A shadow study for a static dyonic black hole with a global monopole surrounded by perfect fluid

Abstract

In this paper, we mainly study the shadow and observable features of a dyonic black hole (DBH) with a global monopole surrounded by perfect fluid under various profiles of accretions. We investigate the influence of model parameters on the observational signatures and space-time structure of black holes (BHs). We observe that the value of $b_{ps}$ increases with the increasing values of $\alpha$ and $\eta$, while it decreases with the increasing values of the electromagnetic parameter. We found that the corresponding regions and the observed specific intensities of the direct, lensing and photon ring emissions dramatically changed according to the variation of BH state parameters. It is noticed that the total observed flux is dominated by the direct emission and the lensing ring makes a small contribution while the photon ring makes a negligible contribution due to its exponential narrowness, even the photon ring intersects the thin plane more than three times to pick up a larger intensity. Assuming the spherically symmetric accretion disk, it is found that due to the Doppler effect of infalling motion, shadows of infalling accretion are found to be darker as compared to static ones. However, the size and position of the DBH shadows do not change in both cases, implying that the BH’s shadow size depends on the geometric space-time and the shadow’s luminosities rely on the accretion flow models. Finally, the discussion is done analytically and numerically, and ray-tracing methods are adopted to obtain the proper visualizations.

1 Introduction

A piece of paper is placed over a coin, and a pencil or crayon is rubbed across the surface of the paper, which is a so-called hobby of coin rubbing. As a result, the rubbing displays a pattern of the coin. As the process is repeated, the rubbing will appear different every time, due to the influence of different factors such as the type and optical appearance of the crayon and the intensity of rubbing. However, with the passage of time, some fundamental guidelines are followed, and the glance of the coin will always remain constant. An analogy can be considered with the physical interpretation of a BH, which itself maintained a constant space-time geometry but was illuminated by external sources of fluorescent matter radiation, which may have different geometrical structures, radiate a range of shining colors map, and behave in a time-dependent way. Physically, the BH cannot be viewed directly, but its footprint on the scattering of light blossoms can be observed, like the coin beneath a piece of paper.

Black holes are one of the fundamental solutions to Einstein’s equations, known as cast-iron exceptional predictions of General Relativity (GR) [1]. There is a historical debate on the existence of BHs and several observations have been made to detect such massive objects. Black holes are unexpected regions of space-time, where the influence of gravity is so strong, even light cannot escape and produce singularities in space-time. In 2016, Laser Interferometer Gravitational-Wave Observatory (LIGO) detected the first gravitational signals, which had emanated from the merger of two BHs, and even LIGO detected the sensitive “ring down”, which is the end stage of the waveform, contains a few rapidly vanishing oscillations [2]. The image received from the event horizon telescope (EHT) observational team shows the shadow of the BH on the center of the milky way galaxy $M87^{*}$, which is surrounded by a bright ring-shaped lump of radiation having a dark interior region of an approximated 6.5 billion solar masses [3,4,5,6,7,8]. It provides strong evidence of the existence of BHs in our universe and put a new spirit among the tabletop scientific community to interpret the dynamics of shadows luminosity around compact objects.

In this perspective, EHT further measures the linear polarization of $M87^{*}$, crucial to the analysis of the launching of highly energetic jets from its core. They also provide the groundbreaking various key aspects of magnetically arrested accretion disks surrounding the $M87^{*}$ [9, 10]. Recently, EHT released the first horizon-scale high-resolution image of the Sagittarius (Sgr $A^{*}$), which is located at the heart of the milky way galaxy and shows that the angular size of the photon ring of the Sgr $A^{*}$ is consistent with the radius of the shadow critical curve, as calculated in GR within the range of 10% nicely [11,12,13,14,15,16]. Since the optical appearance and data of BH released by EHT, its various consequences have been investigated. An astrophysical BH provides a stable space-time geometry, but its physical interpretation shows different types of shapes and radiates a blossom of colors due to some external sources of the luminous accretion material. If the light crosses near BH, which is emitted from accretion material, is bent towards the singularity of the BH’s gravitational region.

Theoretically, a stellar body represents a critical curve and is illuminated by an accretion disk, then a uniform spherical screen around the BH may generate a series of complex patterns of participation to the whole luminosity driven by various colored light ray curves. When traced backward from the observer, the trajectories of light from the critical curve will asymptotically reach a bound thin photon ring. These trajectories revolve around the central object many times on the observer’s screen. The radius of bound orbit for Schwarzschild BH is $r\equiv 3{\mathcal {M}}$, in which ${\mathcal {M}}$ is the mass of the BH, and the radius of the critical curve, so-called impact parameter $b\approx 5.2{\mathcal {M}}$. We know that the possible observational properties of the BHs shadows and their related concepts were discussed for a long time. In 1979, Luminet analyzed the emergence of the BH shadow and its associated thin photon ring, which depends on the accretion flow matter and the outer edge of central brightness depression [17]. He further drew a ray-traced profile of the accretion disk around the BH by hand.

After that, Falcke et al. [18] created a ray-tracing computer program and found that the position of such an edge also depends on the coupling between the geometry of the stellar object and the nature of the accretion flow surrounding a super-massive BH, which is the main source of illumination and hence, it is also critical to describe the optical appearance of BH. Basically, two major characteristics of the accretion disk contribute to this, its optically thin accretion flow, which may be transparent due to its own radiation, and its geometrical appearance, which may be infinitesimally thin or may appear any other possible thickness [19]. The shadow of BH is caused by the deflection of light due to its strong gravitational field and the intensity of the deflected light leading to a main dark area simply extends to the lensed position of the inner edge of the accretion disk. In [20], authors considered the Schwarzschild BH surrounded by a thin and thick accretion flow matter and analyzed the gravitational lensing effect and the position of the equatorial observer who could observe different patches of the sky close to the screen.

By considering the spherical accretion flow model, Narayan et al. analyzed the shadow of Schwarzschild BH and concluded that the optical appearance of the accreting BH does not depend upon the radius of the inner region at which the radiating gas stops [21]. In [22], authors exhibit a backlit BH casting a shadow radius $r\approx 6.17{\mathcal {M}}$, and observe the appearance of radiating gas near the BH, where the radiation and gravitational red-shift plays significant roles in understanding the size of the interior region. They further analyzed the optical behavior of the photon ring that revolves around the BH in the near field region before approaching infinity on the screen, they turn into a ring-shaped curve and concluded that in the case of optically thin emitting matter, the brightness can become arbitrarily approaches to high intensity, which is close to this curve. The arguments in [23] showed that the physical appearance of the shadow can be significantly reduced from the size of the ring-shaped curve down to a minimum interior shadow boundary, which is related to the gravitational lensed and red-shifted geometry of the object.

Although these heuristics configurations provide us with realistic descriptions of the shadow dynamics simulations of the BH, there is still a thrust to further understand the geometrical properties and their associated deeper phenomenological consequences need to be addressed through effective implementations. In the framework of the spherical accretion flow, Zeng et al. [24] explored the possible appearance of the shadow of the four-dimensional Gauss–Bonnet BH and analyzed the specific intensities of all the emission profiles under various accretion flows. Zeng et al. [25] also found some interesting phenomenological features of the charged four-dimensional Gauss–Bonnet BH, when they coupled with strings clouds and non-commutative geometry under the same accretions flow models. In [26], the researchers argued that the accretions flow matter of quantum-corrected Schwarzschild BH may give observational proof for the quantum influence of GR. Li and He [27] analyzed the optical features of the global monopole BH within the framework of f(R) (where R is the Ricci scalar) theory under various accretions flow models and found the significant emission profiles of the BH shadow, which can be used to distinguish the BHs from different modified theories.

Guo et al. [28] investigated the shadow and position of the photon ring of a charged BH within the mechanism of Rastall gravity and perfect fluid radiation field. Saleem and Aslam [29] analyzed the shadow and observable features of non-commutative charged Kiselev BH, under different emission profiles. They found that the specific intensity of the considering BH profile to be darker in the case of infalling gas due to the Doppler effect as compared to static one. Since many other theoretical constrainings of BH shadows and some related geometrical properties are attracted some attention in the community, which are investigated on the basis of theoretically well-grounded models, (for instance see references [30,31,32,33,34,35,36]). Among different types of BHs and thermodynamical properties, DBHs become a subject of special interest in literature. This is because such a BH carries both electric and magnetic charged BH solutions and has its origin in maximal gauged supergravity, which provides wide applications in different regions of the space-time geometry [37].

A DBH has two different source fields, a graviton metric, and a U(1) gauge field, and due to this, it is possible to construct four-dimensional BH solutions, which satisfy the anti-de sitter asymptotic boundary conditions. In the context of dual boundary description, DBHs correspond to a field theory in $(2+1)$ dimensions with a gauge field and a constant electric and magnetic field mechanism [38]. The influence of magnetic charge not only changes the thermodynamic phase diagram of anti-de sitter BH but also plays a significant part in the background magnetic field, which is related to the dual boundary side. Hence, this gives a comprehensive way to probe physics related to the Hall effect [39], ferromagnetism [37], and magnetohydrodynamics [40] and some more related discussions on DBH are found in the literature. Haroon et al. [41] analyzed the shadow of rotating DBH in the presence of a perfect fluid and global monopole. They investigated the influence of perfect fluid and global monopole parameters with three forms of matter on the silhouette of BH and found that the variations of parameters significantly change the dynamics of BHs.

In [42], authors investigated the scalarization of the static and spherically symmetric dyonic RN BHs in Einstein-Maxwell-scalar theory, where the scalar field is coupled to an electromagnetic Chern–Simons term. They found that when both electric and magnetic charges are present, there exists an unstable region of parametric space for the dyonic RN BHs where the scalarization of BHs should occur. Shaymatov et al. [43] investigated the motion of massive charged and spinning test particles around a charged DBH surrounded by a perfect fluid scalar dark matter field. They discussed the trajectories for various values of electric and magnetic charges under the influence of dark matter field $\lambda$. In addition, they investigated the properties of the innermost stable circular orbits (ISCOs) in detail and showed that the particle’s spin, the dark matter field parameter $\lambda$, and the BH charges (both electric and magnetic) have a significant influence on the ISCOs of spinning particles. Dutta et al. [44], discussed the thermodynamic properties of DBH and its dual field theory. They observed that the phase diagram of a DBH in constant electric potential and magnetic charge ensemble is similar to that of a Van der Waals fluid with chemical potential. Finally, they analyzed the magnetic properties of dual conformal field theory and observed a ferromagnetic-like behavior of boundary theory when the external magnetic field vanishes. The authors in [45] considered the dyonic RN BH as the simplest model and argued that the DBH space-times must be studied within the theory of two electromagnetic potentials, where the field of the monopole magnetic charge is correctly described by the t component of the dual electromagnetic potential. As a result, the Dirac string associated with the t component of the usual electromagnetic 4-potential becomes just a mathematical object without any physical content that arises in some calculations when one employs unsymmetrical representations of the electromagnetic field.

Hui and Mu [46] studied the effective potential and echoes from the DBH with quintessence. They found that, for a DBH, quasi-topological electromagnetism provides proper matter energy-momentum tensor to curve the space-time, and quintessence strengthens this force. They further analyze that when the effect of quintessence becomes stronger, the BH potential transforms between single-peak and double-peak, which will influence the existence of BH echoes. Further, due to the interesting features of DBHs, numerous publications have been devoted to exploring the significant features of this BH, for instance, see references [47, 48] and many more. Although different phenomenological properties of DBHs are extensively studied, the optical appearance of DBH shadow with global monopole within the framework of different accretion flow models is essential to be discussed. It is interesting to analyze the observational features of DBH through different emission profiles and to know the influence of each parameter on the shadow of DBH which is the main focus of this study.

The outline of this paper is settled as: In Sect. 2, we briefly define the solution of 4-dimensional DBH under considering framework and analyze the deflection of light by using the ray-tracing method. We examine the direct, lensing and photon ring emissions including the transfer functions in Sect. 3. The optical appearance of the BH shadow images with thin disk accretions is discussed in Sect. 4. We summarize our present discussion in the last section. In addition, we depicted the trajectories of the photon and observed emission profiles for some other values of model parameters in Appendices A and B.

2 Bending of light near a 4-dimensional dyonic black holes

The 4-dimensional DBHs solutions have their origin in maximal gauged supergravity and it can be obtained by the reduction of 5-dimensional Kaluza–Klein theory which has some interesting properties [49, 50]. To understand more deeply and explore the properties of DBHs, one needs to investigate the distinct features of accretion matters around the BH under different accretion flow models. Motivated by this, we consider the metric of 4-dimensional DBH which is given by [41]

$$\begin{aligned} ds^{2}=-h(r)dt^{2}+\frac{dr^{2}}{h(r)}+d\Omega ^{2}, \end{aligned}$$

(1)

where

$$\begin{aligned} h(r)=1-\frac{2{\mathcal {M}}}{r}+\frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{1+3\omega }}-8\pi \alpha ^{2}, \end{aligned}$$

(2)

$d\Omega ^{2}=r^2(d\theta ^2+\sin ^2\theta d\psi ^2)$, Q stands for electric charge, $\beta$ denotes the magnetic charge, $\omega$ is the equation of state parameter characterizing the matter radiation around the BH, $\eta$ is the perfect fluid parameter and $\alpha$ represents the global monopole parameter of the DBH. Since $\omega$ has many possible values, which correspond to different BH topological solutions, for a detailed review one can see [41]. In this paper, we consider $\omega =1/3$, which develops the radiation field around the BH [29]. From the weak energy condition, it follows that the energy density $\rho$ should be positive in the surrounding field, which is defined as [41]

$$\begin{aligned} \rho =-\frac{3\omega \eta }{8\pi r^{3(1+3\omega )}}. \end{aligned}$$

(3)

So, to satisfy the constraint on energy density, we choose the negative values of $\eta$ throughout the paper. Further, global monopoles are the topological defects, which may have been produced during the phase transitions in the early universe and this is just one type of topological defect. Other possible types may be expected to exist, which may include domain walls and cosmic strings [51]. More precisely, a global monopole is a heavy object having a divergent mass, which may have been formed during the phase transition of a system consisting of a self-coupling triplet of scalar fields, which undergoes a spontaneous breaking of global gauge symmetry U(1). So far, there are numerous works in literature that study the solutions of BHs with global monopoles see Refs. [52,53,54]. Solving the equation $h(r)=0$, we obtained two locations of the horizons as given below

$$\begin{aligned} r_{+}&=\frac{2{\mathcal {M}}+\sqrt{4{\mathcal {M}}^{2}-4(1-8\pi \alpha ^{2})(Q^{2}+\beta ^{2}-\eta )}}{2(1-8\pi \alpha ^{2})},\nonumber \\ r_{-}&=\frac{2{\mathcal {M}}-\sqrt{4{\mathcal {M}}^{2}-4(1-8\pi \alpha ^{2})(Q^{2}+\beta ^{2}-\eta )}}{2(1-8\pi \alpha ^{2})}, \end{aligned}$$

(4)

where $r_{+}$ and $r_{-}$ represent the event horizon and the inner horizon, respectively. Now we analyzed the geodesic of photons to investigate the behavior of light rays around the BH. For this purpose, we impose the Euler–Lagrange equation as following

$$\begin{aligned} \frac{d}{d\sigma }\bigg (\frac{\partial {\mathcal {L}}}{\partial \dot{x}^{\kappa }}\bigg )=\frac{\partial {\mathcal {L}}}{\partial x^{\kappa }}, \end{aligned}$$

(5)

where $\sigma$ is an affine parameter, $\dot{x}^{\kappa }$ is the four-velocity of the photon, “.” is the derivative with respect to the affine parameter and ${\mathcal {L}}$ is Lagrangian, which can take the following form

$$\begin{aligned} {\mathcal {L}}= & {} \frac{1}{2}g_{\kappa \tau }\dot{x}^{\kappa }\dot{x}^{\tau }\nonumber \\= & {} \frac{1}{2}\big (-h(r)\dot{t}^{2}+\frac{\dot{r}^{2}}{h(r)}+r^{2}(\dot{\theta }^{2}+\sin ^{2}\theta \dot{\psi }^{2})\big ). \end{aligned}$$

(6)

We focus on the light ray that moves on the equatorial plane as in [24, 25], i.e., we apply the initial conditions $\theta =\pi /2$ and $\dot{\theta }=0$ and the coefficients of DBH is dependent explicitly on both t and $\psi$. Hence, we have two conserved quantities, which are $E=-h(r)dt/d\sigma$ and $L=r^{2}d\psi /d\sigma$ represent the energy and angular momentum of photons, respectively. The four-velocity of the time, the azimuthal angle, and the radial components can be obtained as

$$\begin{aligned} \frac{dt}{d\sigma }= & {} \frac{1}{b\bigg (1-\frac{2{\mathcal {M}}}{r}+\frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{2}}-8\pi \alpha ^{2}\bigg )}, \end{aligned}$$

(7)

$$\begin{aligned} \frac{d\psi }{d\sigma }= & {} \pm \frac{1}{r^{2}}, \end{aligned}$$

(8)

$$\begin{aligned} \frac{dr}{d\sigma }= & {} \sqrt{\frac{1}{b^{2}}-\frac{1}{r^{2}}\bigg (1-\frac{2{\mathcal {M}}}{r}+ \frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{2}}-8\pi \alpha ^{2}\bigg )},\nonumber \\ \end{aligned}$$

(9)

in which the sign “±”, represents the clockwise $(+)$ and anti-clockwise $(-)$ direction of motion of photons, b defines the impact parameter satisfying the $b\equiv \frac{|L|}{|E|}$. The expression of effective potential V(r) can be obtained through Eq. (9) as

$$\begin{aligned} \dot{r}^{2}=\frac{1}{b^{2}}-V(r), \end{aligned}$$

(10)

where

$$\begin{aligned} V(r)=\frac{1}{r^{2}}\bigg (1-\frac{2{\mathcal {M}}}{r}+ \frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{2}}-8\pi \alpha ^{2}\bigg ). \end{aligned}$$

(11)

At the photon sphere, photon trajectories satisfy $\dot{r}=0$ and $\ddot{r}=0$. Now, we are going to obtain the photon sphere and impact parameter of the photon sphere for DBH by employing the ray-tracing method. Therefore, the radius of the photon sphere satisfies the following conditions

$$\begin{aligned} V(r_{ps})=\frac{1}{b_{ps}^{2}}, \quad V'(r_{ps})=0, \end{aligned}$$

(12)

Table 1 The numerical values of $r_{+}$, $b_{ps}$, and $r_{ps}$, for various values of $\alpha$ with $\beta =Q=0.7$, $\eta =-0.1$ and ${\mathcal {M}}=1$

Table 2 The numerical values of $r_{+}$, $b_{ps}$, and $r_{ps}$, for various values of $\eta$ with $\beta =Q=0.6$, $\alpha =0.08$ and ${\mathcal {M}}=1$

Table 3 The numerical values of $r_{+}$, $b_{ps}$, and $r_{ps}$, for various values of $\beta$ and Q with $\eta =-0.1$, $\alpha =0.07$ and ${\mathcal {M}}=1$

Fig. 1

The profiles of the effective potential for various values of $\alpha$, $\eta$, and $\beta =Q$ from left to right panels with ${\mathcal {M}}=1$

where “prime” is the derivative with respect to the radial coordinate r, $r_{ps}$, and $b_{ps}$ denotes the radius and critical impact parameter of the photon sphere, respectively. Further, the quantities $r_{ps}$ and $b_{ps}$ can be encapsulated as

$$\begin{aligned} r^{2}_{ps}=b^{2}_{ps}h(r), \quad 2b^{2}_{ps}h(r)^{2}-r^{3}_{ps}h'(r)=0. \end{aligned}$$

(13)

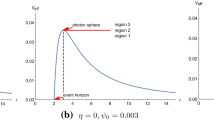
Based on this equation, the numerical values of $r_{+}$, $r_{ps}$, and $b_{ps}$ of the DBH for different values of model parameters are listed in Tables 1, 2 and 3. Because of the change in the correlation parameters, the space-time structure will be changed, which means that the behavior of photons will be different and varies significantly according to the variation of parameters. Table 1 shows that the values of $r_{+}$, $b_{ps}$, and $r_{ps}$ increases with the increasing values of $\alpha$ and it approaches Schwarzschild BH which is $r\approx 3{\mathcal {M}}$ at $\alpha =0.1$. From Table 2, it can be observed that the numerical values of $r_{+}$, $b_{ps}$, and $r_{ps}$ also increase with the increasing values of $\eta$. Further Table 3 depicted that these relevant values decrease smoothly with the increasing values of electric and magnetic charges. In addition, we also depicted the behavior of V(r) for some specific choices of model parameters as shown in Fig. 1. Particularly, when $V(r)=0$ it corresponds to the position of the event horizon and then it increases to a maximum and reaches the peak position of the photon sphere $r_{ps}$ and after that gradually drops down with respect to the radial coordinate r. For instance, one can see from the left panel of Fig. 1, the trajectory of V(r) reaches a peak position when $\alpha =0.08$ and shows a lower position at $\alpha =0.1$. Similarly, the other panels also exhibit different positions of the effective potential corresponding to various values of the involved parameters. Hence, the effective potential is sensitive for all model parameters.

Using the ray-tracing method, the trajectory of the light ray can be depicted based on the equation of motion [24]. Combining Eqs. (8) and (9), we have

$$\begin{aligned} \frac{dr}{d\psi }= & {} \pm r^{2}\nonumber \\{} & {} \times \sqrt{\frac{1}{b^{2}}-\frac{1}{r^{2}}\bigg (1-\frac{2{\mathcal {M}}}{r}+ \frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{2}}-8\pi \alpha ^{2}\bigg )}.\nonumber \\ \end{aligned}$$

(14)

Now, we introduce a parameter $\hat{u}\equiv 1/r$, which led to modify the above equation as

$$\begin{aligned} \Phi (\hat{u})= & {} \frac{d\hat{u}}{d\psi }\nonumber \\= & {} \sqrt{\frac{1}{b^{2}}-\hat{u}^{2}\bigg (1-2M\hat{u}+\hat{u}^{2}(Q^{2}+ \beta ^{2}-\eta )-8\pi \alpha ^{2}\bigg )}.\nonumber \\ \end{aligned}$$

(15)

Fig. 2

The illustrations of light rays for different specific values of model parameters in polar coordinates $(r,\psi )$ with ${\mathcal {M}}=1$. The white lines, white dashed lines, and cyan lines classified the $b<b_{ps}$, $b=b_{ps}$, and $b>b_{ps}$ regions, respectively. The dashed magenta line denotes the photon orbit and BH is shown as a solid black disk

The geometry of the geodesics depends on the roots of the equation $\Phi (\hat{u})=0$. Particularly, for $b>b_{ps}$, the light will be deflected at the radial position $\Phi (\hat{u}_{i})=0$. Hence, to obtain the trajectory of the light ray, it is important to detect the radial position $\hat{u}_{i}$ along with the position of the observer. In general, the observer is located at an infinite boundary for the asymptotically flat space-time. The light trajectories correspond to some specific values of model parameters as mentioned in Tables 1, 2 and 3 are depicted in Fig. 2. All the light rays approach the BH from the right side and there are three different regions of the light rays are observed. For the region of $b<b_{ps}$, the light rays (white lines) fall into the BH singularity because they do not account for any potential limits at this location. For $b>b_{ps}$, here the light rays (cyan lines) are deflected and pass near the BH but never enter the BH whereas in the region $b=b_{ps}$, the light rays (white dashed lines) revolve around the BH. Here, the photon will move in a circular intrinsic form and interpret the unstable behavior [22]. Further, the magenta dashed line depicted the radius of the photon orbit. From Fig. 2, it can be seen that the behavior of the light rays and the size of the BH, including the radius of the photon orbit are different corresponding to each numerical value of the model parameter, and hence these results have justified the Tables 1, 2 and 3 and Fig. 1.

Table 4 The ranges of the impact parameter b under specific values of model parameters for the direct, lensing, and photon ring, respectively with ${\mathcal {M}}=1$

3 Classification of rays and rings

Considering that the BH is illuminated by an accretion disk in the equatorial plane, where the observer is located at the north pole and the disk radiates isotropically in the rest frame of the static world lines. To classify the total number of incoming light rays around the BH, we closely follow Ref. [22] and describe the number of orbits as $n\equiv \psi /2\pi$. Since the deflection angle depends on the impact parameter, n is a function of b as expected. Before carrying out the specific relevant calculations, we would like to describe the configuration of the light rays as

• (1): $n<3/4$: Direct image, intersects the accretion plane once.

• (2): $3/4<n<5/4$: Lensing ring, intersects the accretion plane twice.

• (3): $n>5/4$: Photon ring, intersects the accretion plane at least three times.

Here, we investigate the optical appearance of the BH shadow with different values of the parameters. Currently, we depicted the accretion flow scenario, for three sets of model parameters. The relevant range of b, which is defined as the numerical regions of emissions corresponding to three sets of numerical values, is listed in Table 4. The depicted results in Fig. 3 for the values of the impact parameter $b\in (0,15)$, alongside its comparison, we point out that the observer’s screen is located at the far right side of this plot in all these cases. Taking together Table 4 and Fig. 3, we observe that the influence of each parameter significantly changes the position of the photon orbit and the optical appearance of the BH space-time, which is corresponding to different emission regions. However, the radius of the black disk slightly varies for this set of numerical values. In addition, we also plot the accretion flow scenario for some other specific values of the model parameters. The graphical illustrations and the corresponding emission regions are mentioned in Appendix A.

Fig. 3

Trajectory of photons around the DBH in polar coordinates $(b,\psi )$ with ${\mathcal {M}}=1$. The region inside the event horizon is illustrated by a black circle, while the photon orbit is illustrated by the dashed magenta circumference. The white, magenta, and green lines correspond to direct, lensing, and photon ring trajectories, respectively. We only show a selected portion, where the spacing between impact parameters is 1/5, 1/100, and 1/1000 in the direct, lensed, and photon ring bands, respectively

3.1 Transfer functions

Assuming that the only visible portion is due to the accretion disk, the specific intensity and frequency of the emission will be denoted as $I_{\text {em}}(r)$ and $\nu _{\text {em}}$, respectively. Since $I_{\text {em}}(r)/(\nu _{\text {em}})^{3}$ is conserved along a light ray from Liouville’s theorem [22], the observed specific intensity thus can be written as follows

$$\begin{aligned} I_{\text {obs}}(r)= & {} h(r)^{\frac{3}{2}}I_{\text {em}}(r)\nonumber \\= & {} \bigg (1-\frac{2{\mathcal {M}}}{r}+ \frac{Q^{2}}{r^{2}}+\frac{\beta ^{2}}{r^{2}}-\frac{\eta }{r^{2}} -8\pi \alpha ^{2}\bigg )^{\frac{3}{2}}I_{\text {em}}(r).\nonumber \\ \end{aligned}$$

(16)

Therefore, the total photon intensity can be calculated by integrating over different frequencies:

$$\begin{aligned} I_{\text {o}}=\int I_{\text {obs}}(r)d\nu _{\text {obs}} {=}\int h(r)^{2}I_{\text {em}}(r)d\nu _{\text {em}} {=}h(r)^{2} I_{\text {e}}(r),\nonumber \\ \end{aligned}$$

(17)

in which $I_{\text {e}}(r)=\int I_{\text {em}}(r)d\nu _{\text {em}}$ denotes the total emitted specific intensity near the accretion. Therefore, based on our brightness model having contact with the accretion disk and three different emission regions, the total intensity received by the observer should be given by the sum of all intersections with the disk, defined as

$$\begin{aligned} I_{\text {o}}(b)=\sum \limits _{\begin{array}{c} m \end{array}} h(r)^{2}I_{\text {e}}(r)|_{r= r_{m}(b)}, \end{aligned}$$

(18)

here $r_{m}(b)$ is the radial position of the $m ^{th}$ intersection with the disk plane outside the horizon, which we will call the transfer function. Here, we have ignored the absorption of the light for the thin accretion, which would decrease the observed intensity resulting from the extra passages.

Fig. 4

The $r_{m}(b)$ as a function b for a face-on thin disk in the DBH space-time with ${\mathcal {M}}=1$

The transfer function is directly depicted, where the light ray of impact parameter b will hit on the disk. The slope of the transfer function dr/db, at each b, generates the demagnification factor. For different involved parameters, the first three transfer functions are illustrated in Fig. 4. For the case of $m=1$ (first transfer function), which corresponds to direct emission, indicating a linear function with a slope of 1 and shows that $r_{m}(b)$ is proportional to b. When $m=2$ (second transfer function), it corresponds to lensing ring emission. Here, the function $r_{m}(b)$ behaves as an asymptotic curve, and b has a narrow range around $b\approx 4.84{\mathcal {M}}$ to $7.34{\mathcal {M}}$ and hence, the lensing ring shows up as a thin ring in the shadow profile. Finally, the photon ring emission corresponds to $m=3$ (third transfer function). In this case, $r_{m}(b)$ shows almost a vertical line leads to an infinite slope. Therefore, its contribution can be ignored safely to the total flux of the BH shadow image.

Next, we are going to discuss the distinct features of the free-moving matter around BH through different accretions flows models. To observed the optical appearance of specific intensities, we plot the two-dimensional density maps on the observational plane (x, y) for each model. Since, the photons moving on unstable orbits construct the edges of the shadow. Thus, the apparent shape of the shadow can be found by the stereographic projection of the shadow from the BH’s plane to the observer’s image plane with coordinates (x, y). So we introduce the celestial coordinates, that connected to the actual astronomical measurements that span a two-dimensional plane are defined as [55]

$$\begin{aligned} x= & {} \lim _{r_{o} \rightarrow \infty }\bigg (-r_{o}^{2}\sin \theta _{o}\bigg (\frac{d\psi }{dr}\bigg )_{(r_{o},\theta _{o})}\bigg ), \end{aligned}$$

(19)

$$\begin{aligned} y= & {} \lim _{r_{o} \rightarrow \infty }\bigg (r_{o}^{2}\bigg (\frac{d\theta }{dr}\bigg )_{(r_{o},\theta _{o})}\bigg ), \end{aligned}$$

(20)

where $r_{o}$ is the position coordinate of the observer, lie far away from the BH, and $\theta _{o}$ is the angular position of the observer with respect to the BH’s plane.

4 Geometrically thin disk accretion and shadows

In general, the shadow of BH assumes that photons are all from infinity and deflected due to gravity, when they passed near the BH. As a result, they will not reach the observer’s location and fall into the BH and thus form a shadow having a boundary, which is determined by the critical impact parameter. Hence, there will be a massive amount of accretion flow material surrounding the BHs’ space-times, whose features depend only on space-time or the observer’s geometry. In this scenario, we assume a specific case that there is an optically and geometrically thin disk accretion on the equatorial plane of the BH, from which the photons are emitted, where the influence of absorption and reflection of photons can be disregarded safely [18, 22]. It is well known that an ISCO is one of the relativistic effects, representing the boundary between test particles orbiting the BH and test particles falling into BH. We take the radius of the ISCO as the radiation stop position. To proceed further with the observational features of the DBH, we consider three toy models for the intensity profile of the thin accretion disk, which are listed below [22, 56, 57] as

• First Model: Here, we consider that the emission $I_{\text {emit}}(r)$, suddenly increases and reaches a peaks position, and then decays sharply with second power at the ISCO, while with no emission inside it. The intensity profile of this function is given as

  $$\begin{aligned} I^{a}_{\text {emit}}(r)= {\left\{ \begin{array}{ll} \left( \frac{1}{r-(r_{\text {ISCO}}-1)}\right) ^{2}, &{}\text {if } r>r_{\text {ISCO}} \\ 0,&{}\text {if } r\le r_{\text {ISCO}}, \end{array}\right. } \end{aligned}$$

  (21)

  where ISCO is obtain by [57]

  $$\begin{aligned} r_{\text {ISCO}}=\frac{3h(r_{\text {ISCO}})h'(r_{\text {ISCO}})}{2h'(r_{\text {ISCO}})^{2}-h(r_{\text {ISCO}})h''(r_{\text {ISCO}})}, \end{aligned}$$

  (22)

  in which $h'$, $h''$ denote the first and second partial derivatives of metric potential with respect to r, respectively.

• Second Model: In this case, the emission is assumed that originated from the photon sphere of the radius $r_{ps}$, and the emission intensity profile is defined as

  $$\begin{aligned} I^{b}_{\text {emit}}(r)= {\left\{ \begin{array}{ll} \left( \frac{1}{r-(r_{ps}-1)}\right) ^{3}, &{}\text {if } r>r_{ps} \\ 0,&{}\text {if } r\le r_{ps}. \end{array}\right. } \end{aligned}$$

  (23)

• Third Model: In this model, the emission begins from the event horizon radius $r_{+}$, and we assume that the emission profile in which the decay is more moderate in contrast to the first two models. Its emission intensity can be written as

  $$\begin{aligned} I^{c}_{\text {emit}}(r)= {\left\{ \begin{array}{ll} \frac{\frac{\pi }{2}-\tan ^{-1}(r-r_{\text {ISCO}}+1)}{\frac{\pi }{2}-\tan ^{-1}(r_{ps})}, &{}\text {if } r>r_{+} \\ 0,&{}\text {if } r\le r_{+}. \end{array}\right. } \end{aligned}$$

  (24)

Fig. 5

Observational signatures of thin accretion disk near the DBH, viewed from a face-on orientation. The right panels depicted two-dimensional density maps of the observed emission $I_{\text {obs}}(r)$ for each of the models (in celestial coordinates). The profiles are plotted for $\beta =Q=0.7,~\eta =-0.1,~\alpha =0.08$ with ${\mathcal {M}}=1$

Fig. 6

Observational signatures of thin accretion disk near the DBH, viewed from a face-on orientation. The right panels depicted a two-dimensional density map of the observed emission $I_{\text {obs}}(r)$ for each of the models in celestial coordinates. The profiles are plotted for $\beta =Q=0.6,~\eta =-0.3,~\alpha =0.08$ with ${\mathcal {M}}=1$

The above-mentioned models have their own specific optical features relevant to the BH shadow profiles. These models, despite being rather idealized, however, can provide a comprehensive visual signature of the light waves in the exterior of BHs space-times. Figures 5 and 6 illustrate the optical appearance of the BH shadow for some specific values of the model parameters. To this end, we plot the total emitted intensity with respect to radius r, the total observational intensity $I_{obs}(r)$ as a function of impact parameter b, and two-dimensional density maps in celestial coordinates for each model, in left, middle and right panels, respectively. As an example, from the top row of Fig. 5 (left panel), the disk emission reaches a peak position near the critical curve, and after that, it falls off by the radial distance and approaches zero. We obtain $r_{\text {ISCO}}\simeq 5.58$ by taking the $\beta =Q=0.7,~\eta =-0.1,~\alpha =0.08$ with ${\mathcal {M}}=1$, as shown in the top row of Fig. 5 (left panel). Here, the photon orbits occur inside the region of the disk emission.

From the middle panel of Fig. 5 (top row), the observed intensity has two independent peaks and lies within the domain of the lensing ring and photon ring, and the corresponding direct image decays similarly as $b>7.44{\mathcal {M}}$ due to gravitational lensing. Here, the observed lensing ring emission lie within the range $6.27{\mathcal {M}}<b<7.33{\mathcal {M}}$, and weak contribution in the observed intensity, while the photon ring emission is a highly narrow spike at $b\sim 5.51$ and negligible contribution in total observed intensity. Hence, we can conclude that the intensity of the photon ring is smaller than that of the direct emission and both peaks are of a significantly narrow range, which means that at the observer’s location, the contribution of the lensing and photon rings in the observed intensity is dominated by that of the direct emission. The optical appearance of the corresponding observed intensity is depicted through the two-dimensional density maps, where the photon ring is a thin circle inside the relatively thicker lensing ring and moves continuously toward the interior as shown in Fig. 5 (top row right panel).

The second row of Fig. 5 (left panel) reflects the emitted intensity peaks at $r_{ps}$ and then drops sharply by increasing the radial distance. Here, the observed lensing ring and photon ring emission are now combined on the direct image emission, which decays from $b>3.62{\mathcal {M}}$. The lensing ring has a spike in brightness and a range of $5.34{\mathcal {M}}<b<5.63{\mathcal {M}}$, while the photon ring has an even narrow spike at $b\sim 5.44{\mathcal {M}}$, which can be hardly distinguished from the lensing ring, see middle panel of Fig. 5 (second row). Since, in this case, the lensing ring continues to make very little contribution to the total intensity and the photon ring continues to make an entirely negligible contribution, which is barely visible. The optical appearance corresponding to this emission is provided in the right panel of the second row (Fig. 5).

For the third model, emitted intensity occurs at peak position at $r_{+}$, and then gradually decreases with respect to the radial distance, see left panel of Fig. 5 (bottom row). The very narrow spike at $b\sim 5.45{\mathcal {M}}$ is the photon ring, while the broader bump at $b\sim 5.86{\mathcal {M}}$ represents the lensing ring as shown in the middle panel of Fig. 5 (bottom row). Here, again lensing ring and photon ring are superimposed on the direct image. The right panel of Fig. 5 (bottom row) shows that the optical appearance has a narrow but somewhat brighter extended ring, made up of the contributions of the direct, lensed, and photon ring emission, though as usual the latter can be ignored safely because the photon ring is still entirely negligible. Although, the description of Fig. 5 depicted only a few highly idealized cases of thin accretion material around the DBH, we concluded that the optical appearance is dominated by the direct emission while the lensing ring emission provided only a small contribution to the total intensity and the influence of the photon ring is ignored in all cases. In addition, we also plotted the emission profiles and the observed intensities for some other values of the model parameters as shown in Fig. 6 and Appendix B as an example. The differences are the widths and intensities of the photon and lensing ring and the relevant descriptions as well.

Fig. 7

Observational signatures of the specific observed intensity $I_{s}(b)$ cast by a static spherical accretion, viewed from a face-on orientation. We consider $\alpha =0.08$ (for the left and middle panel) and $\alpha =0.07$ (for the right panel) with ${\mathcal {M}}=1$ as three examples. The bottom panels depicted the optical appearance of the observed specific intensity in two-dimensional density maps in celestial coordinates

4.1 Spherically static accretion and shadows

Now, we will analyze the shadow cast of the DBH with the static spherical accretion. The observed intensity for this model is defined as [58, 59]:

$$\begin{aligned} I_{s}(b)=\int g_{s}^{3}J(\nu _{em})dl_{\text {prop}}, \end{aligned}$$

(25)

in which $g_{s}=\nu _{o}/\nu _{em}$ denotes the red-shift factor, $\nu _{o}$ is the observed frequency of the photon and $\nu _{em}$ is the emission frequency of photon, $J(\nu _{em})$ represents the emission per unit volume, which is obtained in the static frame of emitter and $dl_{\text {prop}}$ is the infinitesimal proper length. The red-shift factor has value $g_{s}=(h(r))^{\frac{1}{2}}$, and assuming that the radiation of specific emission is monochromatic having fixed frequency $\nu _{\text {sf}}$, i.e.,

$$\begin{aligned} J(\nu _{em})\propto \frac{\delta (\nu _{em}-\nu _{\text {sf}})}{r^{2}}. \end{aligned}$$

(26)

Further, we have adopted the $1/r^{2}$ radial coordinate as expressed in [59] and the proper length in the rest frame of the emitter can be calculated as

$$\begin{aligned} dl_{\text {prop}}= & {} \sqrt{(h(r)^{-1}dr^{2}+r^{2}d\psi ^{2})}\nonumber \\= & {} \sqrt{h(r)^{-1}+r^{2}\bigg (\frac{d\psi }{dr} \bigg )^{2}}dr, \end{aligned}$$

(27)

in which $\frac{d\psi }{dr}$ is given by the inverse of Eq. (14). Based on these assumptions, one can obtain the specific observed intensity as

$$\begin{aligned} I_{s}(b)=\int \frac{h(r)^{3/2}}{r^{2}}\sqrt{h(r)^{-1}+r^{2}\bigg (\frac{d\psi }{dr}\bigg )^{2}}dr. \end{aligned}$$

(28)

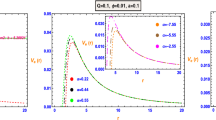
With the help of Eq. (28), we analyzed the optical appearance of the shadow image and the corresponding observed intensity of the DBH, which depends on the trajectory of the light and is determined through the impact parameter b. So, we will investigate how intensity changes with respect to b. In Fig. 7, we have plotted the profiles of the observed intensities and the corresponding two-dimensional density maps (in celestial coordinates) for different values of the model parameters as mentioned in the caption. Here, we observed that the intensity shows increasing behavior initially and reaches a peak position at $b_{ps}$ ($b_{ps}\sim 5.42{\mathcal {M}}$ (left panel), $b_{ps}\sim 5.52{\mathcal {M}}$ (middle panel) and $b_{ps}\sim 5.90{\mathcal {M}}$ (right panel)) and then moving down to lesser values with an increase of b. These results are also consistent with the Figs. 1 and 2.

In this perspective, when $b<b_{ps}$, the intensity comes from the accretion and is mostly absorbed by the BH, and when $b=b_{ps}$, the light rays revolve around the BH many times, so here the intensity obtain the maximum value. After that, for the case of $b>b_{ps}$, only the refracted light contributes to the observed intensity. Further, as the value of b increases, the refracted light starts to obtain smaller values and disappears, when b approaches infinity. In addition, one can also see that from Tables 1, 2 and 3, each value of the model parameter will change the observed intensity significantly. The shadow image cast by the DBH in the circular plane is depicted in the lower panel of Fig. 7. We observe that beyond the BH, there is a bright ring, which is the so-called photon sphere. Note that the radii of the photon sphere are different corresponding to each parameter as calculated in Tables 1, 2 and 3.

Fig. 8

Observational signatures of the specific observed intensity $I_{in}(b)$ cast by an infalling spherical accretion, viewed from a face-on orientation. We consider $\alpha =0.08$ (for the left and middle panel) and $\alpha =0.07$ (for the right panel) with ${\mathcal {M}}=1$ as three examples. The bottom panels depicted the optical appearance of the observed specific intensity in two-dimensional density maps in celestial coordinates

4.2 Spherically infalling accretion and shadows

Here, we assume that the accretion is free-falling onto the BH from infinity. This model is considered to be more realistic as compared to the previous one, as we discuss the static case because most of the accretions are continuously moving in the Universe [58, 59]. We still employ Eq. (28) to investigate the shadow of the DBH, but now the red-shift factor for the infalling accretion should be calculated as

$$\begin{aligned} g=\frac{{\mathcal {D}}_{\kappa }u_{0}^{\kappa }}{{\mathcal {D}}_{\kappa }u_{e}^{\kappa }}, \end{aligned}$$

(29)

where ${\mathcal {D}}^{\kappa }=\dot{x}_{\kappa }$, $u_{0}^{\kappa }=(1,0,0,0)$ and $u_{e}^{\kappa }$ represents the 4-velocity components of the photon, a static observer at infinity and infalling accretion, respectively. The components of $u_{e}^{\kappa }$ for infalling accretion are described as

$$\begin{aligned} u_{e}^{t}=\frac{1}{h(r)}, \quad u_{e}^{r}=-\sqrt{(1-h(r))}, \quad u_{e}^{\theta }\equiv u_{e}^{\psi }\equiv 0, \end{aligned}$$

(30)

and the 4 velocity of the photon can be written as

$$\begin{aligned} {\mathcal {D}}_{t}=\frac{1}{b}, \quad {\mathcal {D}}_{r}=\pm \frac{1}{h(r)b}\sqrt{1-\frac{b^{2}h(r)}{r^{2}}}, \end{aligned}$$

(31)

where the symbol “±” represents the motion of photons traveling towards and moving away from the BH, respectively. Using Eq. (31), the red-shift factor defined in Eq. (29) can be written as

$$\begin{aligned} g=\bigg (u_{e}^{t}+\frac{{\mathcal {D}}_{r}}{{\mathcal {D}}_{t}}u_{e}^{r}\bigg )^{-1}. \end{aligned}$$

(32)

The proper distance can be evaluated as

$$\begin{aligned} dl_{\text {prop}}={\mathcal {D}}_{\kappa }u_{e}^{\kappa }d\sigma = \frac{{\mathcal {D}}_{t}}{g|{\mathcal {D}}_{r}|}dr, \end{aligned}$$

(33)

in which $\sigma$ represents the affine parameter along the path of photon $\kappa$. For simplicity, we assume that the emission of observed intensity is monochromatic, so Eq. (26) is still applicable. Hence, one can obtain the total observed intensity of the DBH under the infalling spherical accretion flow as

$$\begin{aligned} I_{in}(b)\propto \int _{\kappa } \frac{g^{3}}{r^{2}}\frac{{\mathcal {D}}_{t}}{|{\mathcal {D}}_{r}|}dr. \end{aligned}$$

(34)

Figure 8 (upper panel) shows that the total observed intensity function behaves in a similar manner as observed in the static accretion case as shown in Fig. 7 (upper panel), but the difference is that the observed intensity has an extremely sharp rise before to reach the peak position. The two-dimensional density map depicted the corresponding intensity of each panel in celestial coordinates (see Fig. 8 (bottom panel)). Further, we see that the radius of the shadow and the position of the photon ring show a similar description as discussed in the static accretion case. A prominent new feature is observed here, the intensity of the shadow is darker in the central region as compared to the static one since the Doppler effect is caused by the radial infalling accretion flow and this effect is more obvious near the event horizon of the BH. In this scenario, we concluded that the size and the location of the BH shadow do not change in both cases, implying that the BH shadow is a signature of space-time geometry.

5 Conclusions

Once the tabletop is set, the community has launched the search for shadows cast by several compact objects when illuminated by different types of accretion disks. In this sense, they made some feasible assumptions that involved the many ingredients of accretion materials around the BH space-time geometry. Based on the underlying background mechanism, they simplify the assumptions through some numerical simulations and try to investigate the nature of the BH shadows and their related concepts in good approximation. A BH shadow is the projection of its unstable photon region on an observer’s sky. If the BH is surrounded by a massive accretion material, then a step-like dip in brightness will be observed that is coincident with the shadow. Recently, the EHT collaboration published the first image of a BH shadow and reduced its associated uncertainties by using a wide range of self-consistent numerical simulations, which exhibits the realistic nature of plasma radiation around BH. This apparent shape of BH shadow prompts us to better understand and explain what we see, and what we do not see. We have come a long way in understanding the accretions of BHs and their relevant consequences.

Therefore, simple toy models can only be used to guide our intuition and help us to explain what we are seeing. Nonetheless, care must be taken to ensure that these toy models are at least roughly depicted the realistic astrophysical features, which are no longer entirely arbitrary. The purpose of this work is to study the optical appearance and shadow of the DBH surrounded by perfect fluid radiation through some realistic models, which have recently attracted some attention in the community. We have investigated some physical properties of the considering BH, which is relevant to the accreting materials, and then explored the influence of each parameter on the optical appearance and space-time geometry of the BH. We initially show the behavior of effective potential for different values of model parameters, which is based on the technique of null geodesics as shown in Fig. 1. For instance, one can see from the middle panel of Fig. 1, the trajectories of effective potential reach the peak position with the decreasing values of $\eta$ and then decrease smoothly with respect to the radial coordinate r. According to derived effective potential, we found that with the increasing values of $\eta$, the radius of the event horizon, critical impact parameter, and radius of the photon sphere also increases, which confirms that the position of the photon sphere lies far away from the BH.

Similarly, we have analyzed the influence of other BH state parameters and observed that the effective potential is sensitive for all model parameters. The numerical values of the event horizon, critical impact parameter, and radius of the photon spheres are also calculated for various values of model parameters, see Tables 1, 2 and 3. The trajectories of the light rays are plotted on the basis of the equation of motion in Fig. 2, and we observed that the size of the BH and the light curves show different observational appearances corresponding to each value of the BH state parameters. Based on the ray-tracing method, we illustrated the optical appearance of the light trajectories near the BH region and try to understand the total change in the orbital plane from the eye of a distant observer. We define the total number of orbits such as $n\equiv \psi /2\pi$, (in which $\psi$ is the total in azimuthal angle outside the horizon) as a function of b, and plotted the light curves around the BH as shown in Fig. 3. According to the crossing of the equatorial plane, we classify these rays into three major portions such as direct, lensed, and photon ring.

Despite these distinctions, the total observed flux of the DBH is dominated by the direct emission, while the lensing ring makes a minor contribution, and the photon ring makes a negligible contribution. We also discuss the optical appearance of the DBH via three transfer functions as shown in Fig. 4, and the slope of the transfer functions, so-called the demagnification factor. The slope of the first transfer function approaches unity and indicates the direct emission leads to the red-shifted source. The second transfer function corresponding to the lensing ring and its slope greater than unity illustrated that the back side of the accretion disk is demagnified. The photon ring emission corresponds to the third transfer function and its slope approaches infinity, indicating that the front side of the accretion disk is highly demagnified. These results also describe that the contribution of the direct emission is prominent as compared to the lensing ring, while the latter can be ignored safely as a routine. Based on the above discussion, one can notice that the observational features of the DBH surrounded by a thin accretion disk depend both on the BH space-time geometry and the location of the accretion disk with respect to the central dark region.

Fig. 9

The trajectory of photons around the DBH in polar coordinates $(b,\psi )$ with ${\mathcal {M}}=1$. The region inside the event horizon is illustrated by a black circle, while the photon orbit is illustrated by the dashed magenta circumference. The white, magenta, and green lines correspond to direct, lensing, and photon ring trajectories, respectively. We only show a selected portion, where the spacing between impact parameters is 1/5, 1/100, and 1/1000 in the direct, lensed, and photon ring bands, respectively

Table 5 The ranges of the impact parameter b under specific values of model parameters for the direct, lensing, and photon ring, respectively with ${\mathcal {M}}=1$

We further considered a scenario for the observational appearance of thin accretion disks through three toy models. We choose these models on the grounds bases because they simulate different physical properties and generate qualitative different observed emission profiles and their corresponding optical appearance for the considering framework as shown in Figs. 5 and 6. We observed specific intensities of direct, lensing, and photon ring emissions. In all cases, we notice that the main contribution in the total flux obtained from the direct emission, yielding a wide rim, while the lensing ring provided only a small contribution and appeared in the interior of the wide rim, whereas the photon ring provided a negligible contribution, lies in the innermost region, which is hardly to see. Further, the size of the central dark region changes with the emission models. Finally, we considered here two relativistic spherical accretions models such as the static and infalling spherical accretions, and calculated the total observed intensity for different values of BH state parameters as shown in Figs. 7 and 8, respectively. In both cases, we noticed that the images of the BH would have a dark interior and there is a bright photon ring outside the dark region. In addition, we found that there is a darker interior in the infalling accretion case as compared to the static one, which is due to the Doppler effect of the infalling matter.

Based on our analysis, we concluded that the above discussion may provide fruitful results for the theoretical study of the BH shadow profiles and their relevant dynamics. Of course, for minimum uncertainties, some new ideas will require more theoretical investigations, more observations, and highly precise experiments, including space experiments [60, 61]. Given the continuous rubbing of the coin, a more prominent outline of the BH space-time structure will appear, which may lead to reading the mint markings of BHs more obviously in the future.

Appendices

Appendix A

The classification of rays and rings for some other values of the model parameters (Fig. 9; Table 5).

Fig. 10

Observational signatures of thin accretion disk near the DBH, viewed from a face-on orientation. The right panels depicted two-dimensional density maps of the observed emission $I_{\text {obs}}(r)$ for each of the models in celestial coordinates. The profiles are plotted for $\beta =Q=0.4,~\eta =-0.1,~\alpha =0.07$ with ${\mathcal {M}}=1$

Appendix B

Thin disk accretion and shadows for some other values of the model parameters (Fig. 10).