1 Introduction

The study of cosmos and its components inspired many researchers in the last few years due to their mysterious nature. Stars are considered the basic components of astronomy and the essential building blocks of galaxies. Fusion processes have significant effects on the development of stars and planets. The equilibrium position of stars is maintained through the fusion process if there is a balance between the inward force of gravity and the outward pressure. After the consumption of nuclear fuel, the star collapses and as a result new compact objects like white dwarfs, neutron stars and black holes are formed depending on their initial mass. Compact stars have a different nature than ordinary stars as they have large masses and small radii. These cosmic objects have attracted the attention of many researchers due to their significant features. Baade and Zwicky [1] investigated the geometry of compact objects and proposed the concept of pulsars like Her X-1. After discovering pulsars, the theory of neutron stars acquired observational validation [2]. Dev and Gleiser [3, 4] analyzed the physical behavior of pulsars with different considerations. Mak and Harko [5] used the mass-radius relationship to analyze the stability of pulsars. Kalam et al. [6] examined the viability and stability of compact stars using the Karori–Barua technique. The dynamics of compact objects near the boundary with massless and massive scalar field are explored in [7, 8].

The anisotropy modifies some significant characteristics of relativistic objects. According to Ruderman [9], nuclear matter demonstrates anisotropy if the matter density of relativistic particles is equivalent to \(10^{15}~\text {g}/\text {cm}^{3}\). Due to phase transition and viscosity, the distribution of matter exhibits pressure anisotropy [10,11,12]. Bowers and Liang [13] examined the anisotropy of a relativistic sphere and the physical characteristics of anisotropic pressure. The effects of local anisotropy for self-gravitating systems have been examined in [14]. The equilibrium composition and static spherical anisotropic solution have been studied in [15]. Karori–Barua solutions were used to analyze the behavior of anisotropic quark stars in [16]. Dourah and Ray [17] studied the metric solutions for compact stars. Later, Finch and Skea [18, 19] modified the metric solutions in four dimensions for anisotropic star models. The Finch–Skea solutions were used to develop relativistic star models [20]. Bhar [21] determined the physical characteristics of compact stars by using the equation of state (EoS) parameter and Finch–Skea solutions. Anisotropic stellar structures using Finch–Skea potentials have been examined in [22]. These solutions were also used to evaluate the anisotropic compact configurations [23].

In modified theories of gravity, the study of stellar structures is a major topic for discussion. Numerous studies on star structures have been analyzed in the last few decades. Accordingly, the Symmetric teleparallel gravity, which is also known as \(f({\mathcal {Q}})\) is an intriguing theory that has gained attention in recent years [24,25,26]. The study of \(f({\mathcal {Q}})\) gravity is the most debatable phenomenon of the current time. Lazkoz et al. [27] established a credible set of limitations on \(f({\mathcal {Q}})\) gravity, where the polynomial expression of gravity is given as a function of redshift. Moreover, the \(f({\mathcal {Q}})\) gravity showed some fascinating results using observational measurements [28,29,30,31,32,33]. Furthermore, the study of different cosmic objects with different matter configurations in the framework of \(f({\mathcal {Q}})\) gravity has been discussed in [34,35,36,37]. Olmo [38] studied the geometry of compact stellar objects using polytropic EoS in Palatini f(R) gravity. Arapoglu et al. [39] used barotropic EoS to examine the compactness of pulsars in the same theory. Zubair et al. [40] investigated the viable behavior of rotating neutron stars in the background of f(R, T) theory. Mustafa and his collaborators [41,42,43,44,45,46,47] studied compact spherical structures with different considerations. Maurya et al. [48] analyzed the effect of charge on the stability of spherical objects through the Karmarkar condition in f(G, T) gravity. Sharif and Gul studied the Noether symmetry approach [49,50,51,52,53,54,55], stability of the Einstein universe [56,57,58] and dynamics of gravitational collapse [59,60,61,62,63] in modified theory. In the framework of off-diagonal tetrad, the study of anisotropic strange stars in \(f (\tau , T )\) gravity presented in [64]. Das et al. [65] considered Finch–Skea geometry to study the viable behavior of pulsars in the context of Einstein Gauss-Bonnet gravity. Dita et al. [66] studied the characteristics of celestial objects using a modified Van der Waals EoS in the presence of charge in \(f({\mathcal {Q}})\) gravity. Recently, the study of observational constraints in modified f(Q) gravity discussed in [67] and thermal fluctuations of compact objects as charged and uncharged BHs in f(Q) gravity are explored in [68, 69]. Some people have also studied the characteristics of celestial objects in different scenarios of modified gravity and obtained interesting results [70,71,72,73,74].

In this article, we analyzed the viability and stability of compact objects by considering Finch Skea solutions in \(f({\mathcal {Q}})\) theory. The manuscript is arranged as follows. The basics of \(f({\mathcal {Q}})\) gravity with anisotropic matter configuration is presented in Sect. 2. The geometrical explanation of metric and the evaluation of unknown constant is given in Sect. 3. Section 4 analyzes some physical features to determine the viability of compact stars. Further, we check the stability analysis in Sect. 5. Our results are summarized in Sect. 6.

2 \(f({\mathcal {Q}})\) theory: field equations

The corresponding integral action with coupling constant as a unity is expressed as

$$\begin{aligned} S=\frac{1}{2}\int f({\mathcal {Q}})\sqrt{-g}d^4x+\int L_{m}\sqrt{-g}d^4x, \end{aligned}$$
(1)

where \(L_{m}\) represents Lagrangian density of matter and g is determinant of metric tensor. The non-metricity tensor is defined as

$$\begin{aligned} {\mathcal {Q}}_{k \eta \xi }=\nabla _{k} g_{\eta \xi }=g_{\xi k}- \Gamma _{\eta \xi }^{l}g_{lk}-\Gamma _{\eta k}^{l}g_{\xi l}, \end{aligned}$$
(2)

where \(\nabla _{k}\) covariant derivative and \(\Gamma _{\eta \xi }^{l}\) is affine connection, given by

$$\begin{aligned} \Gamma _{\eta \xi }^{l}=K_{\eta \xi }^{l}+ L_{\eta \xi }^{l}, \end{aligned}$$
(3)

where \( L_{\eta \xi }^{l}\) and \(K_{\eta \xi }^{l}\) are deformation and contortion tensors, respectively, defined as

$$\begin{aligned} L_{\eta \xi }^{l}=\frac{1}{2}{\mathcal {Q}}_{\eta \xi }^{l}-{\mathcal {Q}}_{(\eta \xi )}^{l}, \quad K_{\eta \xi }^{l}=\frac{1}{2}T_{\eta \xi }^{l}+ T_{(\eta \xi )}^{l}. \end{aligned}$$
(4)

The antisymmetric component of affine connection reduces to torsion tensor as \( T_{\eta \xi }^{k} = 2\Gamma _{[\eta \xi ]}^{l}\). The super potential can be written as

$$\begin{aligned} P_{\eta \xi }^{k}=\frac{1}{4}[-{\mathcal {Q}}_{\eta \xi }^{k}+2 {\mathcal {Q}}_{(\eta \xi )}^{k}+{\mathcal {Q}}^{k}g_{\eta \xi } -\tilde{{\mathcal {Q}}^{k}}g_{\eta \xi } -\delta _{(\eta {\mathcal {Q}}_{\xi })}^{k}].\nonumber \\ \end{aligned}$$
(5)

The non-metricity scalar is expressed as

$$\begin{aligned} {\mathcal {Q}}=-{\mathcal {Q}}_{\eta \xi k}P^{\eta \xi k}. \end{aligned}$$
(6)

Variation of action (1) corresponding to metric tensor yields field equations of \(f({\mathcal {Q}})\) gravity as

$$\begin{aligned}{} & {} \frac{2}{\sqrt{-g}}\nabla _{k}(\sqrt{-g} f_{{\mathcal {Q}}}P_{\eta \xi }^{k})+ \frac{1}{2}g_{\eta \xi } f \nonumber \\{} & {} \quad + f_{{\mathcal {Q}}}( P_{\eta kl}{\mathcal {Q}}^{kl}_{\xi }-2{\mathcal {Q}}_{kl\xi } P_{\xi }^{kl}) = -T_{\eta \xi }, \end{aligned}$$
(7)

where \(f_{{\mathcal {Q}}}\) depicts the partial derivative with respect to non-metricity.

Now, we use the static spherically symmetric spacetime to examine the stellar structures as

$$\begin{aligned} ds^{2}=-e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}. \end{aligned}$$
(8)

We assume anisotropic matter distribution as

$$\begin{aligned} T_{\eta \xi }=(\rho +P_{t})u_{\eta }u_{\xi }+P_{t}g_{\eta \xi }+(P_{r}-P_{t})\xi _{\eta } \xi _{\xi }, \end{aligned}$$
(9)

where \(\rho \), \(P_{t}\) and \(P_{r}\) depict the energy density, tangential pressure and radial pressure, respectively. By using Eq. (9), the value of non-metricity becomes

$$\begin{aligned} {\mathcal {Q}}=-\frac{2e^{-\lambda (r)}(1+r \nu ^{\prime }(r))}{r^{2}}, \end{aligned}$$
(10)

where prime is the derivative with respect to radial coordinate. The resulting field equations turn out to be

$$\begin{aligned} \rho= & {} \frac{f({\mathcal {Q}})}{2}- f_{{\mathcal {Q}}}\left[ {\mathcal {Q}} + \frac{1}{r^{2}}+ \frac{e^{-\lambda }}{r}(\nu ^{\prime }+\lambda ^{\prime })\right] , \end{aligned}$$
(11)
$$\begin{aligned} P_{r}= & {} -\frac{f({\mathcal {Q}})}{2}+f_{{\mathcal {Q}}}[{\mathcal {Q}} + \frac{1}{r^{2}}], \end{aligned}$$
(12)
$$\begin{aligned} P_{t}= & {} -\frac{f({\mathcal {Q}})}{2}+ f_{{\mathcal {Q}}}\left[ \frac{{\mathcal {Q}}}{2}-e^{-\lambda }\frac{\nu ^{''}}{2} +\left( \frac{\nu ^{\prime }}{4}+\frac{1}{2r}\right) \right. \nonumber \\{} & {} \left. \quad \times (\nu ^{\prime }-\lambda ^{\prime })\right] , \end{aligned}$$
(13)
$$\begin{aligned} 0= & {} \frac{cot\theta }{2}{\mathcal {Q}}^{\prime }f_{{\mathcal {Q}}{\mathcal {Q}}}. \end{aligned}$$
(14)

Solving Eq. (14), we have

$$\begin{aligned} f_{{\mathcal {Q}}{\mathcal {Q}}}=0\Rightarrow f_{{\mathcal {Q}}} = k_{1}\Rightarrow f({\mathcal {Q}})= k_{1}{\mathcal {Q}} + k_{2}, \end{aligned}$$
(15)

where \(k_{1}\) and \(k_{2}\) are integration constants. Now using Eqs. (10)–(15), the corresponding equations of motion become

$$\begin{aligned} \rho= & {} \frac{1}{2r^{2}}[2k_{1}+ 2e^{-\lambda } k_{1}(r \lambda ^{\prime }-1)-r^{2}k_{2}], \end{aligned}$$
(16)
$$\begin{aligned} P_{r}= & {} \frac{1}{r^{2}}[-2k_{1}+2e^{-\lambda } k_{1}(r \nu ^{\prime }+1)+r^{2}k_{2}], \end{aligned}$$
(17)
$$\begin{aligned} P_{t}= & {} \frac{e^{-\lambda }}{4r}[2e^{\lambda }rk_{2} + k_{1}(2+r \nu ')(\nu '-\lambda ')+ 2rk_{1}{\nu ''}].\nonumber \\ \end{aligned}$$
(18)

By using field equations (16)–(18), we obtain

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}(\rho +P_{r})-(P_{r})^{\prime }+\frac{2}{r}(P_{t}-P_{r})=0. \end{aligned}$$
(19)

This is known as Tolman–Oppenheimer–Volkoff (TOV) equation in \(f({\mathcal {Q}})\) gravity.

3 Finch–Skea solutions and matching conditions

Compact stars are fascinating objects that result from the gravitational collapse of massive stars. Understanding their structure, composition and behavior is crucial for advancing our knowledge of fundamental physics and astrophysics. Different solutions, including Finch–Skea solutions are considered to describe the properties of compact stars and their various aspects, such as density profiles, pressure, and temperature distributions. Finch–Skea solutions provide insights into the behavior of matter at extreme conditions in compact stars. These solutions predict distinct gravitational wave signatures that could be compared with observations to validate or refine the models. Finch–Skea solutions provide insights into the interior structure of compact stars, helping astrophysicists to understand phenomena such as the formation of quark–gluon plasma or other exotic states of matter. The Finch–Skea solutions are finite and non-singular, ensuring that the spacetime is smooth and free from singularities.

Table 1 For the considered compact star approximate values of unknown constants
Full size table
Fig. 1
figure 1

Plot of metric elements versus \({{\textrm{r}}}\)

Full size image

The modeling of stellar objects using Finch–Skea solutions has attained a lot of interest in recent years due to their non-singular behavior. These solutions are defined as [18, 19]

$$\begin{aligned} e^{\nu }=\left( A+\frac{1}{2}Br \sqrt{r^{2}C}\right) ^{2}, \quad e^{\lambda } = (1+Cr^{2}), \end{aligned}$$
(20)

where arbitrary constants are denoted by A, B and C, respectively. The set of constants can be evaluated by smoothly matching the inner and outer regions. The Schwarzschild spacetime is used to investigate the outer geometry of the compact stars as

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}\right) dt^{2}+ \left( 1-\frac{2M}{r}\right) ^{-1}dr^{2}\nonumber \\{} & {} -\,r^{2}d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}, \end{aligned}$$
(21)

where M and R depict the total mass and radius of the sphere, respectively. The continuity of metric tensors at the boundary surface gives

$$\begin{aligned} A= & {} \frac{3M-2R}{2\sqrt{R}\sqrt{R-2M}}, \quad B = \frac{\sqrt{\frac{M}{R-2M}}\sqrt{R-2M}}{\sqrt{2}R^{\frac{3}{2}}}\nonumber \\ C= & {} \frac{2M}{R^{2}(R-2M)}. \end{aligned}$$
(22)

Now, using the Finch Skea metric in Eqs. (16)–(18), we obtain

$$\begin{aligned} \rho= & {} \frac{1}{2r^{2}}\bigg [4 - 2C r^{2}-r^{2}\bigg ], \end{aligned}$$
(23)
$$\begin{aligned} P_{r}&{=}&\frac{1}{2r^{2}}\bigg [{-}2{-}2(1{+}Cr^{2}) \Bigg (\frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}1\Bigg ){+}r^{2}\bigg ],\nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned} P_{t}= & {} \frac{-(1+Cr^{2})}{4}\left[ 2(1+Cr^{2})+ \Bigg (\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\Bigg )\right. \nonumber \\{} & {} \times \Bigg (\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}-\frac{2Cr}{1+Cr^{2}}\Bigg )\nonumber \\{} & {} \left. +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}-2BCr^{3}}{\Big (\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\Big )^{2}}\right] . \end{aligned}$$
(25)

We use green, red, blue, orange, purple, brown, yellow, black, pink and gray colors for Her X-1, EXO 1785-248, Vela X-1, PSR J1614-2230, LMC X-4, SMC X-4, PSR J1903+327, 4U 1538-52, 4U 1820-30, Cen X-3 compact stars, respectively for all graphs. Table 1 provides the values of unknown constants. Figure 1 shows that the metric elements are regular and show positively increasing behavior as required.

4 Physical attributes

In this section, we examine the physical characteristics of compact stars through graphs in the background of \(f({\mathcal {Q}})\) gravity. We evaluate the behavior of effective matter variable, anisotropy, energy condition, mass, compactness, redshift and EoS parameters in the interior of proposed compact stars. Further, we use the TOV equation, sound speed and adiabatic index to analyze the equilibrium stability state of considered stars.

4.1 Energy density and pressure components

Figure 2 shows that the behavior of energy density, radial pressure and tangential pressure is positive and decreasing for all considered compact star candidates. It can also be seen that matter variables are maximum at the center of stars. Figure 3 represents that the radial derivative of energy density, radial and tangential pressure components are negative, which ensures the presence of a highly compact picture of the considered compact stars in the framework of \(f({\mathcal {Q}})\) gravity.

Fig. 2
figure 2

Behavior of energy matter variables versus \({\textrm{r}}\)

Full size image
Fig. 3
figure 3

Behavior of energy density and pressure for gradient versus \({\textrm{r}}\)

Full size image

4.2 Anisotropy

The anisotropy of compact objects can be evaluated by using Eqs. (24) and (25) as

$$\begin{aligned} \Delta= & {} P_{t}-P_{r}\\= & {} \frac{-(1+Cr^{2})}{4}\left[ 2(1+Cr^{2})+ \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\right) \right. \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2} Br\sqrt{r^{2}C}}-\frac{2Cr}{1+Cr^{2}}\right) \nonumber \\{} & {} +\left. \frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}-2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2}}\right] \\{} & {} {-} \frac{1}{2r^{2}}\bigg [{-}2{-}2(1{+}Cr^{2}) \bigg (\frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}1\bigg )+r^{2}\bigg ]. \end{aligned}$$

Anisotropy determines the direction of pressure, i.e., when \(\Delta >0\) the pressure is directed outward and when \(\Delta <0\), the direction of the pressure is inward. Figure 4 determines that the pressure is in the outward direction as anisotropy is positive, which is required for compact star configuration.

Fig. 4
figure 4

Plot of anisotropy versus \({\textrm{r}}\)

Full size image
Fig. 5
figure 5

Behavior of energy conditions versus \({\textrm{r}}\)

Full size image

4.3 Energy bounds

Energy conditions are essential for understanding several cosmological findings connected to significant gravitational fields. Due to the vital role of energy bounds, some interesting results have been published in [75,76,77]. For anisotropic fluid, \({\mathcal {NEC}}\) (null energy condition), \({\mathcal {WEC}}\) (weak energy condition), \({\mathcal {SEC}}\) (strong energy condition) and \({\mathcal {DEC}}\)( dominant energy condition) can be classified as

  • \({\mathcal {NEC}}:\rho +P_{r}\ge 0, \quad \rho +P_{t}\ge 0\),

  • \({\mathcal {WEC}}:\rho \ge , \quad \rho +P_{r}\ge 0, \quad \rho +P_{t} \ge 0\),

  • \({\mathcal {DEC}}:\rho -P_{r}\ge 0, \quad \rho -P_{t} \ge 0\),

  • \({\mathcal {SEC}}:\rho +P_{r}\ge 0, \quad \rho +P_{t}\ge 0,\rho +2P_{t}+P_{r}\ge 0\).

Figure 5 shows that all energy conditions are satisfied for all star models.

Fig. 6
figure 6

Behavior of EoS parameters versus \({\textrm{r}}\)

Full size image

4.4 EoS parameters

Here, we investigate the crucial EoS parameters in describing the relationship between pressure and energy density in various physical systems. The radial \((\phi _{r}=\frac{P_r}{\rho })\) and transverse \((\phi _{t}=\frac{P_t}{\rho })\) components must lie in [0, 1] for a physically viable model. The corresponding parameters are expressed as

$$\begin{aligned} \phi _{r}= & {} \left[ \frac{1}{2r^{2}}\left\{ \left( \frac{-4B\sqrt{r^{2}C}- 4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) \right. \right. \\{} & {} \left. \left. \quad -\left( \frac{4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) +2r\right\} \right] \\{} & {} \quad \times \bigg [\frac{1}{2r^{2}}(4 - 2C r^{2}-r^{2})\bigg ]^{-1},\\ \phi _{t}&{=}&\left[ \left\{ \frac{{-}(1{+}Cr^{2})}{4}(2(1{+}Cr^{2}){+} \left( \frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}2\right) \right. \right. \\{} & {} \quad \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} \quad \left. \left. +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\right\} \right] \\{} & {} \quad \times \bigg [\frac{1}{2r^{2}}(4 - 2C r^{2}-r^{2})\bigg ]^{-1}. \end{aligned}$$

The graphical behavior of \(\phi _{r}\) and \(\phi _{t}\) for considered compact star models is given in Fig. 6, which shows that EoS parameters satisfy the required condition \((0<\phi _{r}<1\) and \(0<\phi _{t}<1).\)

4.5 Mass, compactness and redshift

Mass function for the anisotropic compact stars is given by

$$\begin{aligned} m=\frac{Mr^{3}e^{\frac{M(R^{2}-r^{2})}{R^{2}(2M-R)}}}{R^{2} (2M-R)+2Mr^{2}e^{\frac{M(R^{2}-r^{2})}{R^{2}(2M-R)}}}. \end{aligned}$$
(26)

Figure 7 shows that the mass is increasing in a positive direction and regular at the center of stars. The compactness function is essential for examining the viability of compact stars, expressed as

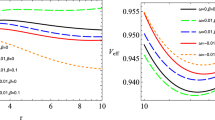
$$\begin{aligned} \mu (r)=\frac{m(r)}{r}=\frac{Mr^{2}e^{\frac{M(R^{2}-r^{2})}{R^{2} (2M-R)}}}{R^{2}(2M-R)+2Mr^{2}e^{\frac{M(R^{2}-r^{2})}{R^{2}(2M-R)}}}. \end{aligned}$$
(27)

According to Buchdahl [78] compact stellar objects are feasible if this factor has the limit \(\mu (r)<\frac{4}{9}\). The gravitational redshift \(( Z = (1-2\mu )^{\frac{-1}{2}}-1)\) is considered to be the key concept to understand the nature of compact objects.

Figure 8 determines that the compactness and redshift lie in the required limits \((\mu <\frac{4}{9}, Z \le 5.2)\).

5 Stability analysis

It is more interesting to examine celestial objects that maintain their stability in the presence of external disturbances. Here, we use the TOV equation to explore the equilibrium state of the star candidates and sound speed/adiabatic index to check the stability.

5.1 Tolman–Oppenheimer–Volkoff equation

The TOV equation in the framework of f(Q) is formulated in Eq. (19). This provides information regarding the cosmic balance as a consequence of the several forces, including the gravitational force \((F_{g})\), anisotropic force \((F_{a})\) and the hydrostatic force \((F_{h})\), expressed as

Fig. 7
figure 7

Plot of mass function versus \({\textrm{r}}\)

Full size image
Fig. 8
figure 8

Behavior of Compactness and redshift functions versus \({\textrm{r}}\)

Full size image
Fig. 9
figure 9

Behavior of TOV equation versus \({\textrm{r}}\)

Full size image
$$\begin{aligned} F_{g}= & {} \bigg [-\frac{\nu ^{\prime }}{2}\left\{ \frac{1}{2r^{2}}(4 - 2C r^{2}-r^{2})\right\} \bigg ]\\{} & {} + \left[ \frac{1}{2r^{2}}\left\{ -2-2(1+Cr^{2}) \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+1\right) \right. \right. \\{} & {} \left. \quad \left. +r^{2}\right\} \right] ,\\ F_{h}&{=}&\left[ \frac{{-}1}{r^{3}}\left\{ {-}2{-}2(1{+}Cr^{2}) \left( \frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}1\right) {+}r^{2}\right\} \right] \\{} & {} +\left[ \frac{1}{2r^{2}}\left\{ \left( \frac{-4B\sqrt{r^{2}C}- 4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) \right. \right. \\{} & {} \left. \left. \quad -\left( \frac{4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) +2r\right\} \right] ,\\ F_{a}= & {} \frac{2}{r}\left[ \left\{ \frac{-(1+Cr^{2})}{4}(2(1+Cr^{2})\right. \right. \\{} & {} \quad +\left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\right) \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} \quad \left. \left. +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\right\} \right] \\{} & {} -\left[ \frac{1}{2r^{2}}\left\{ \Bigg (\frac{-4B\sqrt{r^{2}C} -4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\Bigg ) \right. \right. \\{} & {} \left. \left. \quad -\Bigg (\frac{4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\Bigg )+2r\right\} \right] . \end{aligned}$$

Figure 9 shows that the our system is in the equilibrium state as the sum of all forces is zero \((F_{g}+F_{h}+F_{a}=0)\).

Fig. 10
figure 10

Behavior of components of sound speed versus \({\textrm{r}}\)

Full size image

5.2 Sound speed

The development of cracking technique has been explored spherically for compact objects using various methodologies [79,80,81]. The radial and transverse sound speed components, represented as \(\nu ^{2}_{sr}\) and \(\nu ^{2}_{sr}\) are used to determine the stability of compact star candidates. The expressions for speed of sounds are given as follows

$$\begin{aligned} \nu ^{2}_{sr}= & {} \left[ \frac{-1}{r^{3}}\left\{ -2-2(1+Cr^{2}) \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+1\right) \right. \right. \\{} & {} \left. \left. +r^{2}\right\} \right] \\{} & {} +\left[ \frac{1}{2r^{2}}\left\{ \left( \frac{-4B\sqrt{r^{2}C}- 4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) \right. \right. \\{} & {} \left. \left. -\left( \frac{4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) +2r\right\} \right] \\{} & {} \times \bigg [\frac{1}{2r^{2}}(-4Cr-2r)-\frac{1}{r^{3}}(4-2Cr^{2}-r^{2})\bigg ]^{-1},\\ \nu ^{2}_{st}= & {} \left[ \left\{ \frac{-(1+Cr^{2})}{4}(2(1+Cr^{2})\right. \right. \\{} & {} + \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\right) \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} \left. \left. +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\right\} \right] \\{} & {} \times \bigg [\frac{1}{2r^{2}}(-4Cr-2r)-\frac{1}{r^{3}}(4-2Cr^{2}-r^{2})\bigg ]^{-1}. \end{aligned}$$

The causality condition in the case of anisotropic matter configuration is defined as

$$\begin{aligned} 0\le v^{2}_{r}\le 1, \quad 0\le v_{t}^{2}\le 1. \end{aligned}$$

The range for radial sound speed and transverse sound speed must satisfy the following inequality \(0\le |\nu ^{2}_{sr}-\nu ^{2}_{st}|\le 1\) for stable compact stars. We observed that desired condition are fulfilled as shown in Figs. 10 and 11. This proves the stability of our compact star models in the framework of \(f({\mathcal {Q}})\) gravity.

5.3 Adiabatic index

The another alternative technique to investigate the stability of compact stars is adiabatic index. The radial and transverse components of adiabatic index are defined as

$$\begin{aligned} \Gamma _{r}{} & {} = \frac{P_{r}+ \rho }{P_{r}} \frac{dP_{r}}{d\rho }= \frac{P_{r}+ \rho }{P_{r}}\nu ^{2}_{sr}, \quad \Gamma _{t} = \frac{P_{t}+ \rho }{P_{t}} \frac{dP_{t}}{d\rho }\nonumber \\{} & {} = \frac{P_{t}+ \rho }{P_{t}}\nu ^{2}_{st}. \end{aligned}$$
(28)

Using Eqs. (23)–(25), we have

Fig. 11
figure 11

Behavior of \(| \nu ^{2}_{t}-\nu ^{2}_{r}|\) versus \({\textrm{r}}\)

Full size image
Fig. 12
figure 12

Behavior of adiabatic index versus \({\textrm{r}}\)

Full size image
$$\begin{aligned} \Gamma _{r}= & {} \bigg [\left\{ \frac{1}{2r^{2}}(4 - 2C r^{2}-r^{2})\right\} \bigg ] \\{} & {} + \bigg [ \frac{1}{2r^{2}}\bigg \{-2-2(1+Cr^{2}) \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+1\right) \\{} & {} +r^{2}\bigg \}\bigg ]\times \bigg [ \frac{1}{2r^{2}}\{-2-2(1+Cr^{2}) \\ {}{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+1\right) +r^{2}\bigg \}\bigg ]^{-1}\\{} & {} {\times }\bigg [\frac{{-}1}{r^{3}}\left\{ {-}2{-}2(1{+}Cr^{2}) \left( \frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}1\right) {+}r^{2}\right\} \bigg ]\\{} & {} +\bigg [\frac{1}{2r^{2}}\Bigg \{\left( \frac{-4B\sqrt{r^{2}C}- 4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) \\{} & {} -\left( \frac{4BCr^{2}\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}\right) +2r\Bigg \}\bigg ]\\{} & {} \times \bigg [\frac{1}{2r^{2}}(-4Cr-2r)-\frac{1}{r^{3}}(4-2Cr^{2}-r^{2})\bigg ]^{-1},\\ \Gamma _{t}&{=}&\bigg [\bigg \{\frac{1}{2r^{2}}(4 {-} 2C r^{2}{-}r^{2})\bigg \}\bigg ] {+} \bigg [\bigg \{\frac{{-}(1{+}Cr^{2})}{4}(2(1{+}Cr^{2})\\{} & {} +\left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\right) \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\bigg \}\bigg ]\\{} & {} {\times }\bigg [\bigg \{\frac{{-}(1{+}Cr^{2})}{4}(2(1{+}Cr^{2}){+} \left( \frac{Br\sqrt{r^{2}C}}{A{+}\frac{1}{2}Br\sqrt{r^{2}C}}{+}2\right) \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\bigg \}\bigg ]^{-1}\\{} & {} \times \bigg [\bigg \{\frac{-(1+Cr^{2})}{4}(2(1+Cr^{2})\\{} & {} +\left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}}+2\right) \\{} & {} \times \left( \frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}} -\frac{2Cr}{1+Cr^{2}}\right) \\{} & {} +\frac{Ar+\frac{1}{2}Br^{2}\sqrt{r^{2}C}- 2BCr^{3}}{(\frac{Br\sqrt{r^{2}C}}{A+\frac{1}{2}Br\sqrt{r^{2}C}})^{2})})\bigg \}\bigg ]\\{} & {} \times \bigg [\frac{1}{2r^{2}}(-4Cr-2r)-\frac{1}{r^{3}}(4-2Cr^{2}-r^{2})\bigg ]^{-1}. \end{aligned}$$

According to adiabatic index criteria, the system is stable if \(\Gamma >\frac{4}{3}\) otherwise, it is unstable [82]. Figure 12 shows that our system is stable in the presence of modified terms corresponding to all considered compact stars.

6 Final remarks

In this paper, we have examined the viability and stability of compact stars in the background of \(f({\mathcal {Q}})\) theory. To evaluate the graphical characteristics of compact stars, we formulate the functional form as \(f({\mathcal {Q}})=k_{1}{\mathcal {Q}}+k_{2}\). The main results are given by

  • The graphical behavior of energy density versus radial coordinate depicts that energy density approaches to the maximum value when \(r\rightarrow 0\) as shown in Fig. 2. We have noted the same behavior for \(P_{t}\) and \(P_{r}\) that is positive and decreasing. The radial derivative of the energy density and pressure components are negative for considered compact star candidates as shown in Fig. 3.

  • The anisotropy for the compact star candidates is directed outward as shown in Fig. 4.

  • Energy conditions for compact star candidates are positive, which ensure the presence of normal matter in the proposed compact stars as shown in Fig. 5.

  • It is examined that the EoS parameters satisfy the required bound for radial component \( 0< \phi _{r} <1\) and tangential component \( 0< \phi _{t} <1\) as given in Fig. 6.

  • There is a direct relation between the mass and radius of the compact stars, suggesting that the mass function remains regular at the center of the compact stars (Fig. 7).

  • Compactness and redshift functions satisfied the required limits in the presence of modified terms as presented in Fig. 8.

  • It is found that the proposed compact stars are stable as all the necessary conditions are fulfilled as shown in Figs. 9, 10, 11 and 12.

It is noteworthy to mention here that we have obtained more stable anisotropic stellar structures due to the presence of \(f({\mathcal {Q}})\) terms as compared to GR and other modified theories [83,84,85,86,87,88]. We can conclude that viable and stable compact stars exist in this modified theory.