Abstract
We investigate the quantum dynamics of the quasi-isotropic inflationary solution. This is achieved by deriving the Lagrangian and Hamiltonian for both the FLRW background and the inhomogeneous correction, via an expansion of the Einstein–Hilbert action up to second order in the perturbation amplitudes. Then we implement a semiclassical WKB scenario for which the inhomogeneous component of the Universe is treated as a “small” quantum subsystem, evolving on the classical isotropic background. Starting from the Wheeler–DeWitt equation, we recover a Schrödinger dynamics for the perturbations, in which the time dependence of the wave function emerges thanks to the classicality of the background, and we solve it for an inflationary phase. The main result of this paper is to show that, while the scalar component of the power spectrum has the standard scale invariant profile, the tensor one results to be not constrained by the inflationary expansion, apart from an overall normalization factor which guarantees a small tensor-to-scalar ratio. This means that the spatial distribution of the quasi-isotropic correction to the metric remains preserved, with the consequence that some information about the pre-inflationary Universe survives to the de Sitter expansion.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The isotropic Universe, as described by the Robertson–Walker geometry [1,2,3], models a large part of the present Universe evolution, as confirmed by the nucleosynthesis of the light elements [4] and, overall, the isotropy of the microwave background temperature [5].
However, as outlined mainly by the activity of the Landau School, the Robertson–Walker geometry is far from being the most general dynamical approach to the cosmological singularity [3, 6,7,8,9].
An interesting generalization of the isotropic Universe has been derived in [10] by Lifshitz and Khalatnikov, where, by a Taylor expansion in the synchronous time of the metric component, it was constructed the so-called quasi-isotropic solution. Its physical meaning is given by the fact that it represents the most generic spatially inhomogeneous generalization of the FLRW model in which the spacetime is locally FLRW-like near the cosmological singularity. This solution, existing in the presence of ultrarelativistic matter, contains three physically arbitrary functions of the spatial coordinates and the metric splits into a background isotropic-like component and a small correction, controlled by a different scale factor with respect to the background one. This solution has a certain degree of isotropy, although being an inhomogeneous cosmology. For other generalizations of the quasi-isotropic solution in the presence of a scalar field, of viscous dissipation and during the de Sitter phase, see [11,12,13] respectively. It is worth remarking that, for such different physical contexts, the quasi-isotropic solution is no longer a Taylor expansion of the three-metric in the synchronous time, but it retains the same structure with two (one larger and one smaller) scale factors, having, in principle, generic functional form, as a result of the dynamics – for instance, in the presence of a scalar field these scale factors are suitable power laws. Here, we study the quasi-isotropic solution during a de Sitter phase of the Universe and in the presence of an inhomogeneous quantum scalar field. In other words, we are considering the generation of the primordial inflaton and gravitational field fluctuations during the inflationary expansion [4, 14].
The peculiar point of our analysis consists of treating the correction, due to the small scale factor (actually, the ratio of the smaller to the larger scale factor), as a quantum degree of freedom.
We implement to our model the ideas discussed in [15, 16], see also [17]. That is, we treat the inhomogeneous correction to the metric and the scalar field as a “small” quantum subset, living on the classical isotropic background. Thus, from a WKB expansion in the Planck constant of the Wheeler–DeWitt (WDW) equation and implementing a Born–Oppenheimer-like approximation, we recover a Schrödinger-like dynamics for the two quantum degrees of freedom, where the time dependence of the wave function comes out from the dependence of the background metric on the label time (for a critical analysis and a reformulation of this scheme, when the WKB expansion is extended to higher orders, see [18, 19]).
After a detailed construction of the Lagrangian and Hamiltonian for the model, as splitted into the zero, first and second order of approximation in the perturbation variables, we derive the quantum dynamics of the metric (actually a tensor degree of freedom) and the scalar field. To deal with a gauge invariant formulation, we adopt the Mukhanov–Sasaki variable for the scalar component, and we retain as factorized between a time dependent and a space dependent function the tensor degree of freedom. In other words, preserving also on a quantum level the structure of the quasi-isotropic solution has the non-trivial implication that the spatial dependence of the metric is not coupled to the quantum evolution of the tensor component. The scalar field is, instead, treated as an intrinsically inhomogeneous degree of freedom and it is analyzed via a Fourier decomposition, leading to a mini-superspace dynamics for each independent mode.
The main result of the present study is to outline the real nature of the primordial spectrum, associated to the proposed dynamical scenario. In particular, while the scalar field, i.e. the scalar component of the spectrum, corresponds to the usual scale invariant profile of the predicted spectrum, the tensor component preserves the generic fingerprint contained in the space dependence of the quasi-isotropic correction, and we show that such a contribution is smaller than the scalar one (the tensor-to-scalar ratio remains much less than unity), but it is not suppressed.
The merit of the present analysis is to demonstrate that, under suitable conditions, corresponding to the validity of the quasi-isotropic scheme also in the WKB scenario here discussed, it is possible that a pre-inflationary information survives to the de Sitter expansion of the Universe. In fact, the inhomogeneous component of the tensor perturbation is not fixed by the slow-rolling evolution, but it contains, in the Fourier transform of the original space dependence, an arbitrary shape, in principle corresponding to non-gaussian features of the tensor spectrum, to be identified by future experiments aimed to measure the cosmological background of gravitational waves [20] (for a review of the main mechanisms of gravitational wave production related to inflation see [21]).
The manuscript is structured as follows. In Sect. 2 we present the quasi-isotropic solution, both in the presence of ultrarelativistic matter and during the de Sitter phase. In Sect. 3 we review the quantization scheme à la Vilenkin. In Sect. 4 we construct the gauge invariant action of the quasi-isotropic Universe in presence of a real self-interacting scalar field. We discuss the different nature of the scalar and tensor degrees of freedom and derive the total Hamiltonian of the background and perturbations. Then, in Sect. 5 we quantize the perturbations implementing the semiclassical and Born–Oppenheimer-like approximation. We derive a time dependent Schrödinger equation for the wave function of each independent mode and find the solution. Finally, we derive the Power Spectrum of both the scalar and tensor perturbations. We do this both in the case of a purely de Sitter expansion and in the first slow-roll approximation. In Sect. 6 some concluding remarks and future perspectives follow.
2 Quasi-isotropic solution
The original Lifshitz–Khalatnikov quasi-isotropic solution [10, 22] considers an inhomogeneous Universe filled by ultrarelativistic matter nearby the cosmological singularity. The peculiar feature of this solution consists in the fact that the inhomogeneity is managed through a Taylor expansion of the spatial metric \(\gamma _{ij}(t,{{\textbf {x}}})\) in the synchronous time.Footnote 1 The idea is that, order by order, space contracts (going backward in time) maintaining the same time dependence of linear distance changes.
Because the FLRW solution for a relativistic perfect fluid with equation of state \(p=\rho /3\) is linear in the synchronous time t, the expansion should consist of integer powers of t. Therefore, considering only the first two terms of the expansion, the quasi-isotropic spatial metric results to have the following structure
All the operations of index raising and covariant differentiation are made using the time-independent tensor \(h_{ij}\), so that it takes a metric role. For example \(\theta ^i_j=h^{ik}\theta _{kj}\).
The choice of a synchronous reference frame allows to perform arbitrary transformations of the spatial coordinates, that can be used, for example, to diagonalize \(h_{ij}\). As a consequence, this tensor contains only three independent components. Then, inserting the metric (1) into the Einstein equations and solving them asymptotically for \(t\rightarrow 0\), it is possible to express all the other quantities in terms of these three degrees of freedom. Therefore, in this context the quasi-isotropic solution contains three physically arbitrary functions of the spatial coordinates, specified by the initial conditions.
In particular, \(\theta _{ij}\) is given by a linear combination of the Ricci tensor and the scalar curvature corresponding to \(h_{ij}\).
For what concerns the fluid, the first two terms of the energy density expansion are given by
where \(\theta =\theta ^i_i\) and \(\kappa _g = 8\pi G\) is the Einstein constant. As a consequence, the density contrast, defined as the ratio between the first and zeroth-order energy density terms, is linear in t. Therefore, the singularity is naturally approached with a vanishing density contrast, in agreement with the standard cosmological model.
Moreover, at this level of approximation, no rotations take place in the fluid. This is because the spatial dependence of the velocity field \(u_i\) reduces to the divergence of \(\theta \), i.e.
and therefore the curl of the velocity vanishes.
Finally, let us point out that the pure isotropic and homogeneous model results to be a special case of this solution, for \(h_{ij}\) corresponding to spaces of constant curvature.
2.1 Inflationary scenario
The scheme previously outlined can be applied also in the context of inflation, with two differences: (i) the presence of a scalar field allows to relax the assumption of expandability in integer powers of t adopted in Eq. (1); (ii) the asymptotic solution is searched in the limit \(t \rightarrow \infty \). Therefore, we require a three-dimensional metric tensor having the following structure
where \(\eta = b^2/a^2\) is the square of the ratio between the scale factor b, which governs the inhomogeneous dynamics, and the FLRW-like scale factor a and is assumed to satisfy the condition
As shown in Ref. [13], the coupling between the metric (4), a scalar field \(\phi (t,{{\textbf {x}}})\) governed by an effective cosmological constant \(\Lambda \) and an ultrarelativistic perfect fluid yields an isotropic, flat and exponentially growing background metric
perturbed by an exponentially decreasing inhomogeneous term. i.e.
In Eqs. (6) and (7) \(H_0=\sqrt{\kappa _g\Lambda /3}\) is the (constant) Hubble parameter. The energy density and velocity of the ultrarelativistic field are given by
which implies \(\theta < 0\) for each point of the allowed domain of the spatial coordinates. Furthermore, the spatial distribution of the metric correction reduces to \(\theta _{ij} = \theta \delta _{ij}/3\). Finally, the two leading orders of the scalar field, modulo a multiplicative integration constant, read as
where \(t_r\) is a constant which satisfies the condition \(t_r\gg t\) during all the slow-rolling expansion. This condition guarantees that the dominant term of the scalar field is almost constant such that it actually evolves very slowly on the plateau region.
The peculiar feature of this solution lies in the free character of the function \(\theta ({{\textbf {x}}})\) which, being a three-scalar, is not affected by spatial coordinate transformations. From a cosmological point of view, this implies the existence of a quasi-isotropic inflationary solution together with an arbitrary spatial distribution of ultrarelativistic matter and of the scalar field. Nevertheless, given the extremely fast decaying of the inhomogeneities, they are not able to account for the observed cosmological structures,Footnote 2 therefore supporting the idea that the latter cannot have a classical origin in the presence of an inflationary scenario.
3 Semiclassical approximation
During the slow-roll phase the Universe is essentially classical and the quantum fluctuations of the inflaton and gravitational fields evolve as small quantum fields around a classical FLRW background [23]. This situation is particularly suitable to implement the scheme proposed by Vilenkin in [15], which we are now going to review. The idea is that in cosmology a well-defined evolutionary quantum dynamics can emerge from the timeless WDW equation only when some of the degrees of freedom of the Universe become classical. The reason for that is due to the essential role played by classical measuring devices in quantum mechanics. The existence of a classical background during inflation would thus ensure the presence of an “observer” of the quantum subsystem represented by the fields fluctuations.
Here we restrict the discussion to homogeneous minisuperspace models, but we will see that the formalism can be straightforwardly applied to our model which includes also a certain degree of inhomogeneity. In this case, the geometric and matter variables are independent of \({{\textbf {x}}}\) and the momentum constraint identically vanishes. The quantum dynamics of the Universe follows from the WDW equation [24]
where we used a unified notation for metric and matter variables, all labeled as \(h^\alpha \), and \(\nabla ^2\) denotes the Laplace–Beltrami operator of the superspace metric \(G_{\alpha \beta }\). The physical states are the solutions of the WDW equation (10) and \(\Psi = \Psi (h)\) is called the wave function of the Universe.
However, in a fully quantum regime two main problems arise [25]: it is not clear how to recover an explicit evolution with respect to a time variable (the so called problem of time); in general a satisfactory definition of probability associated to \(\Psi (h)\) has not yet been found and, therefore, it is not clear what is its meaning. Indeed, since Eq. (10) is formally a Klein-Gordon equation with a variable mass, it is common to consider the corresponding Klein-Gordon current
This current gives the probability \(dP=j^\alpha d\Sigma _\alpha \) to find the system in a surface element \(d\Sigma _\alpha \) of the configuration-space. The problem is that, in this context, this quantity is not positive-defined in general.
Both problems can be solved if we assume the system to be composed of \(n-m\) semiclassical variables and m quantum variables, that we label respectively \(\lbrace c^\alpha \rbrace \) and \(\lbrace q^\nu \rbrace \). Furthermore, we suppose that the quantum subsystem can be considered “small” (so that its backreaction on the classical variables is negligible) and “fast” with respect to the classical one. In this way it is possible to implement a Born–Oppenheimer approximation to decouple the quantum and classical dynamics.
More precisely, we assume that the subspaces defined by the semiclassical and quantum variables are approximately orthogonal, such that \(G_{\alpha \nu }\) is negligible with respect to \(G_{\alpha \beta }\). Then, we can write the WDW equation (10) in the following convenient form
where \(H_{c} = -\hbar ^2\nabla _0^2 + U_0\) is obtained neglecting all the contributes of the quantum variables. We can also write the wave function as
where S(c) is assumed to be real valued in order to avoid classically forbidden regions for the semiclassical variables.
As shown in [15], the two leading orders in \(\hbar \) of the WKB expansion of Eq. (12), considering also that the wave function \(\psi _0 = Ae^{iS/\hbar }\) satisfies the equation \(H_c\psi _0=0\), lead to:
-
(1)
The Hamilton–Jacobi equation
$$\begin{aligned} {\mathcal {H}}(c^\alpha ,\nabla _\alpha S) = G^{\alpha \beta } \nabla _\alpha S \, \nabla _\beta S + U_0 = 0. \end{aligned}$$(14)\(S=S(c)\) is the classical action and describes a congruence of classical trajectories. Equation (14) defines the classical Hamiltonian \(H=N{\mathcal {H}}\), where N is the lapse function, and one can use the Hamilton equations to relate the “velocities” \(\dot{c}^\alpha \) to the action S. As we are going to show explicitly in Sect. 5, from this relation it is then possible to define a time variable t which parametrizes the evolution of each trajectory.
-
(2)
The Schrödinger equation for the quantum subsystem
$$\begin{aligned} i\hbar \frac{d\chi }{dt} = NH_q\chi , \end{aligned}$$(15)where now the quantum wave function \(\chi = \chi (t,q)\) depends on time t.
-
(3)
An equation for the amplitude A expressing the conservation of the classical probability current \(j_0^\alpha = |A|^2\nabla _0^\alpha S\) for the variables \(h^\alpha \), obtained from the leading order of Eq. (11). In this way one gets two different parts of the probability current, one related to the components of the classical subspace and the other one to those in the quantum one, ending with a normalizable probability distribution for the quantum variables \(q^\nu \), given by \(\rho _\chi = |\chi |^2\).
Hence, the standard interpretation of the wave function has been recovered for a small subsystem of the Universe.
4 Quasi-isotropic action functional
Now let’s consider a quasi-isotropic scenario in presence of a real and self-interacting scalar field \(\Phi \). The Einstein–Hilbert action for the gravity and matter system under consideration is
We assume that the contribution of the inhomogeneities is small enough to treat them as a first order correction to the FLRW background, so that the metric and the scalar field can be written as
where the metric \(\gamma _{ij}(t,{{\textbf {x}}})\) of the spatial slicing takes the quasi-isotropic form (4). Since we are interested in the inflationary dynamics, we assume from the beginning a background metric with null curvature.
Expanding the action (16) in \(\delta g_{\mu \nu }\) and \(\varphi \), the background dynamics and the perturbations dynamics follow respectively from the zeroth and second order terms of the expansion, since they give the unperturbed and linearized Einstein equations [23, 26]. Therefore, the steps toward the quantization of the perturbations are: expand the action (16) up to second order in perturbations, find the constraints and apply Vilenkin’s procedure discussed in Sect. 3.
4.1 Gauge invariant variables
In order to obtain the canonical action we write (16) in terms of the ADM variables [27]. Comparing the metric in Eq. (17) with the line element
we obtain the lapse function \({\mathcal {N}}\) and shift vector \({\mathcal {N}}^i\) (note that each quantity must be expanded up to second order in the perturbation variables)
where we have defined the variables
From the condition \(\gamma ^{ik}\gamma _{kj}=\delta ^i_j+{\mathcal {O}}(\eta ^3)\) we get the inverse three-metric tensorFootnote 3
Finally, the squared root of the spatial metric’s determinant reads as
Only the scalar and tensor components of the perturbations “survive” the inflationary expansion, so that we can write
where \(\psi ({{\textbf {x}}}),\ \mu ({{\textbf {x}}}),\ B(t,{{\textbf {x}}})\) are scalar functions, \((\ldots )_{,i}=\partial _i(\ldots )\) and \(\vartheta _{ij}({{\textbf {x}}})\) is a symmetric, traceless and divergenceless three-tensor.
It is easy to see that the tensor sector of the perturbations (which represents the gravitational degrees of freedom \(\delta g_{ij}^{(t)} = \eta \vartheta _{ij}\)) is gauge invariant while the scalar component is not. Therefore, we need to express the latter in terms of a scalar gauge invariant variable, which represents the true physical degree of freedom of the perturbations.
This variable can be constructed combining the two Bardeen’s potentials [28] with the scalar field perturbation and reads as
However, in practice it is more useful to work with an auxiliary field defined as
which is called the Mukhanov–Sasaki variable [23].
Let us point out the following property of the scalar sector. The variables \(\xi _S\) and \(v_S\) factorize into a product of a space and a time function only if \(\varphi \) also does. Nevertheless, this does not happen in general as it is easy to see looking at the de Sitter limit \(\dot{\phi }\rightarrow 0\). In this case \(\varphi \) does not couple to the metric (the gauge invariant variables (24) and (25) become independent from it) and there is no reason to impose any factorization. Therefore, the quasi-isotropic factorization disappears in the scalar sector and the dynamics follows from the standard treatment given for example in [23] (see Ref. [29] for a derivation of the quantum theory of cosmological perturbations in the Schrödinger picture).
Differently, the tensor component preserves its quasi-isotropic form under gauge transformations, such that the inhomogeneities evolve with a frozen spatial distribution \(\vartheta _{ij}({{\textbf {x}}})\) and the dynamics is governed by the only degree of freedom \(\eta (t)\).
What we are going to show (Sect. 5) is that the inflationary expansion does not suppress these perturbations, whose spectrum is determined by the free functions \(\vartheta _{ij}({{\textbf {x}}})\).
4.2 Gauge invariant action
The expansion of the action (16) in the perturbations \(\delta g_{\mu \nu }\) and \(\varphi \),
gives the action \(S_0\) of the background variables a and \(\phi \), its first-order variation \(\delta S\) and the action \(\delta ^2S\) of the perturbations. The latter splits into the sum of two terms, one containing only scalar degrees of freedom, \(S_S\), and one only the tensor ones, \(S_T\).
Using the conformal time \(d\tau =dt/a\) and the notation \('=d/d\tau \), \(S_0\) results to be the usual FLRW action in presence of a scalar field
Applying the background equation of motion derived from (27) to the unperturbed variables a and \(\phi \) makes, as expected, the first order term \(\delta S\) identically vanish. Furthermore, it simplifies a lot the second-order term \(\delta ^2S\).
The scalar component \(S_S\) contains the first variation of the background constraints. Following, e.g., Ref. [23], one can write it in terms of the Mukhanov–Sasaki variable. This is done imposing the constraint given by the variation of \(S_S\) with respect to the metric variable B and then expressing the gauge dependent variables in terms of \(v_S\). In this way one ends with the following action for \(v_S\)
Here, \({{\textbf {k}}}\) is the comoving wave-vector, related to the physical wave-vector by \({{\textbf {k}}}_{phys} = {{\textbf {k}}}/a\). The quantities \(\omega _k^2\) are functions of the unperturbed variables only and are defined as
where \({\mathscr {H}}=a'/a\). We will see in the following that they take the role of time dependent frequencies. Note that in Eq. (28) appears only the module of the wave-vector. This is because, as we will see in Sect. 5, the equations of motion and the initial conditions for the modes depend only on \(k=|{{\textbf {k}}}|\). Let us point out that in the synchronous frame, where \(N=1\), Eq. (28) reduces to the expression obtained by Mukhanov in [23].
The tensor perturbation action obtained from the expansion of Eq. (16) results to be in a gauge invariant form. Thanks to the quasi-isotropic factorization the spatial dependence of the Lagrangian density can be integrated in the action. All the information about the spatial distribution of the inhomogeneities results to be encoded into the two constants \({\mathcal {C}}_\vartheta = \int d^3x \vartheta _{ij}\vartheta _{ij}\) and \({\mathcal {C}}_\vartheta ' = \int d^3x \vartheta _{ij,k}\vartheta _{ij,k}\). Therefore, we are left with just one degree of freedom in the action. In analogy to Eqs. (24) and (25), we now define the tensor gauge invariant variables
In this way the tensor perturbation action becomes the following
In this case the time dependent frequency of the tensor degree of freedom is given by
where \(K =\sqrt{{\mathcal {C}}_\vartheta '/{\mathcal {C}}_\vartheta }\). The meaning of the constant K results clearer in Fourier space: it is the square root of the expectation value of \(k^2\) with respect to the probability distributionFootnote 4\(p_\vartheta ({{\textbf {k}}})=|\hat{\vartheta }_{ij}({{\textbf {k}}})|^2/\int d^3k|{\hat{\vartheta }}_{ij}|^2\). Indeed, it results to be equal to
We shall see that this quantity represents the reference scale for the evolution of the tensor degree of freedom (30), playing a role equivalent to the wave vector module k for the scalar mode-k.
Observe that in Eqs. (27) and (28) should appear a fiducial length \(l=\big (\int d^3x\big )^{1/3}\), which has to be included in the action since we are considering both homogeneous and inhomogeneous quantities. However one can avoid to show it explicitly simply considering the following redefinition of the variables
Because the interval ds has dimension of a length, we can initially choose \([a]=L^0\), \([dx]=[d\tau ]=L\) and thus \([l] = L\), and so after the rescaling (34) the scale factor has the dimension of a length while \(\tau \), the spatial variables, k and K become dimensionless.
4.3 Super-Hamiltonian constraint
In order to quantize the system, it is convenient to replace the complex amplitudes \(v_{k}\) with real variables given by their real and imaginary part
Defining from the Lagrangians (27), (28) and (31) the canonical momenta
where the index i labels the real and imaginary components (35) of the scalar modes, we obtain a Hamiltonian \(H=N{\mathcal {H}} = N({\mathcal {H}}_0+{\mathcal {H}}_S+{\mathcal {H}}_T)\) which contains the background constraint \({\mathcal {H}}_0\) and its second variation \(\delta ^2{\mathcal {H}} = {\mathcal {H}}_S+{\mathcal {H}}_T\), given in the following expressions
Let us observe that once the frequencies (29) and (32) are expressed in terms of the momenta (36), the unperturbed component N of the lapse function is removed from the super-Hamiltonian \({\mathcal {H}}\) and appears in the Hamiltonian only as a multiplicative factor. Therefore, we obtain the super-Hamiltonian constraint
Note that here we are considering a total Hamiltonian for both the background and perturbative degrees of freedom. In this way, what we are going to do, is to directly quantize all degrees of freedom with the total constraint (38). This is, in principle, different from solving separately the dynamics of the background and then the dynamics of the perturbations. In this second case there would be two different Hamiltonians, the first containing only unperturbed variables and the other terms quadratic in the perturbations. The background variable N would appear in the Hamiltonian of the perturbations as a given, non-dynamical variable, so that \(H_{pert}=N({\mathcal {H}}_S+{\mathcal {H}}_T)\) would represent a physical (i.e. non-vanishing) Hamiltonian for the perturbative degrees of freedom. Therefore, once quantized, it would lead to an evolutive Schrödinger equation for the perturbations.
We stress that only the method used here is able to give the quantum-gravitational corrections to the background dynamics [31,32,33,34,35]. Nonetheless, as long as we are interested, as in this work, in the linear regime for the perturbations and in the limit of quantum field theories on a fixed background spacetime, the two approaches are equivalent.
5 Quantum dynamics
Let us now face the problem of quantization. The phase space variables are promoted to quantum operators which satisfy the canonical commutation relations
In the following it will be convenient to introduce a unified notation for the scalar and tensor modes, labelling all the perturbations as \(q_\nu \).
The super-Hamiltonian constraint (38) now becomes a quantum operator which annihilates the wave function \(\psi =\psi (a,\phi ,\{q_\nu \})\), yielding the WDW equation \({\mathcal {H}}\psi =0\).
Now we apply the semiclassical scheme à la Vilenkin. We treat the background degrees of freedom a and \(\phi \) as classical and impose the following WKB ansatz
The wave function \(\psi _0 = Ae^{iS/\hbar }\) satisfies the equation \({\mathcal {H}}_0\psi _0=0\) which gives, at the zeroth-order in \(\hbar \), the Hamilton–Jacobi equation
One can demonstrate that this equation is equivalent to the Friedmann equation. Consequently, the variables a and \(\phi \) follow classical trajectories with “velocities” given by
From Eq. (42) it is then possible to define a WKB time in terms of the background variables. This time variable is given by the following relation
and we shall show that it will be identified with the classical conformal time.
Now considering the full wave function (40) we find that the leading order in \(\hbar \) of the WDW equation yields the following equation for the quantum wave function \(\chi \)
where we recognize on the left side the time derivative defined in (43). So, we obtain the following Schrödinger equation for the quantum subsystem
where now \(\chi =\chi (\tau ,\{q_\nu \})\) and \(H_q\) is the Hamiltonian of the perturbations
Let us note that the semiclassical approximation simplifies drastically the expression of the frequencies \(\omega _{k}\) and \(\omega _T\). In a fully quantum gravitational regime, because of the presence of the unperturbed momenta, they would be quantum operators. However, at the order of approximation considered here, the background variables are pure classical functions of time.
It must be observed that, in order to solve Eq. (45), we need to fix the lapse function and solve the dynamics of the background so that the frequencies \(\omega _k\) and \(\omega _T\) can be expressed as functions of time. This means that we must fix the reference frame, which is now possible thanks to the semiclassical regime. We thus choose to work in a synchronous frame and set \(N(t) = 1\).
Thanks to the linear character of the perturbations it is possible to simplify Eq. (45). In this regime different modes do not interact with each other and they can be considered as independent. This assumption allows us to factorize \(\chi \) into a product of wave functions describing the single modes, that is
In this way Eq. (45) reduces to an infinite set of decoupled Schrödinger equations which read as
Such a system can be solved analytically using the exact invariant method developed in [36, 37] and summarized in [38]. The general solution of Eq. (48) is a linear combination \(\chi _\nu = \sum _{n}c_\nu ^{(n)}\chi _\nu ^{(n)}\), were
Here, \(H_n\) are the Hermite polynomials and \(\varphi _{\nu }^{(n)}(\tau )\) are time dependent phases. We point out that, because in the following we are interested just in the calculus of the power spectra, the phases do not play any role and thus it is not necessary to calculate them.
Therefore, the wave function of the perturbations is known once the functions \(\rho _\nu (\tau )\) are given and these are the solutions of the differential equations
The general solution of Eq. (50) can be obtained [39] from the following relation
where \(f(\tau )\) e \(g(\tau )\) are two linearly independent solutions of the linear system associated to Eq. (50), A and B are arbitrary constants, \(\alpha = fg'-gf'\) and \(\gamma _{1,2} = \pm 1\).
As usual in the context of inflationary models we assume that the perturbations are initially in the ground state, which here correspond to \(n=0\) for which the energy is minimal. Hence, we choose the following gaussian wave functions
Now we must note that all the modes of astrophysical interest today had, at the beginning of inflation, a physical wavelength much smaller than the Hubble radius, which means that \(k/aH \rightarrow \infty \). In this regime the perturbations are not affected by the expansion of the background and the modes behave as harmonic oscillators with constant frequencies \(\omega _{{\textbf {k}}}=k\) and \(\omega _T=K\). Hence, we will fix the constants A and B such that for each mode the wave function (52) approaches asymptotically the ground state of a Minkowskian harmonic oscillator.
5.1 Power spectra of the perturbations
Now that the wave function of the perturbations is known, we can derive the power spectra.
Let us consider first the scalar sector. As we have seen the quantum amplitudes \(v_k\) have gaussian probability distributions, in agreement with the most recent measurements of the CMB anisotropies which do not show any hint of primordial non-Gaussianity [40]. This implies that the statistical properties of the scalar modes are entirely given by the two-point correlation function
Here, \({|{\chi }\rangle } \) is the ground state of the scalar sector given in Eq. (47). Making use of the Fourier transform of \(v_S({{\textbf {x}}})\) and the explicit expression of the wave functions (52), the correlation function results to be (see, e.g., Ref. [41] for details) the following
The power spectrum is defined as the Fourier amplitude of the variance \(\Xi _S|_{r=0}=\langle v_S^2\rangle \) per unit logarithmic interval. Therefore we find for it the expression
The connection between the primordial quantum perturbations and the observable fluctuations of temperature and density appears in the comoving curvature perturbation \(\zeta \). As it is well known, its spectrum, calculated at the end of inflation, can directly be propagated to the time when perturbations re-enter the horizon without the need to consider the details of the cosmological evolution [14, 42]. During the matter-dominated era, when the temperature anisotropies of the CMB are created, the relation of \(\zeta \) to the Mukhanov–Sasaki variable is given by [41]
where \(\epsilon = 1 - {\mathscr {H}}'/{\mathscr {H}}^2\) is the slow-roll parameter. From Eqs. (55) and (56) follows the expression of the power spectrum of the comoving curvature perturbation
where the ratio \(\rho _k/a\) has to be calculated in the super-Hubble limit \(\tau \rightarrow 0\).
For what concerns the tensor sector, it is given by the component of the metric \(\delta g_{ij}^{(t)}=\eta \vartheta _{ij}\), where \(\eta \) is a quantum operator and \(\vartheta _{ij}\) are classical functions of the spatial coordinates. Therefore, the two-point correlation function factorizes into a time dependent quantum amplitude and a stochastic average containing the statistical properties of the spatial distribution. The latter is determined by the probability distribution governing the variable \(\vartheta _{ij}\) and can be, in principle, different from the gaussian one, thus leading to non-gaussian features of the spectrum.
It is easy to derive the time dependent component which is proportional to
Assuming that the variable \(\vartheta _{ij}\) is governed by a translationally and rotationally invariant probability distribution function as well as space-inversion invariance, the stochastic term can be written as
where \(\Pi _{ij,kl}({\hat{p}}) = \sum _{\lambda }e_{ij}({\hat{q}},\lambda )e_{kl}^*({\hat{q}},\lambda )\), being \(e_{ij}({\hat{p}},\lambda )\) the polarization tensor and \(\lambda \) the helicity.
As for the comoving curvature perturbation, the spectrum of the tensor perturbations becomes a constant in the limit \(\tau \rightarrow 0\), i.e. when the perturbations are outside the horizon. This means that its value calculated in this limit provides an initial condition for the gravitational waves when they re-enter the horizon. From Eqs. (58) and (59) we finally obtain the power spectrum of the tensor perturbations which reads as
where, again, the ratio \(\rho _T/a\) has to be evaluated in the super-Hubble limit.
We shall now apply what we have found here first to the de Sitter and then to the slow-rolling expansion.
5.2 De Sitter case
In the de Sitter case the potential of the scalar field takes a constant value \(V (\phi ) = \Lambda \) and plays the role of an effective cosmological constant. The unperturbed scalar field takes a constant value as well and, therefore, the gauge invariant scalar potential (24) reduces to the (gauge invariant) scalar field perturbation, \(\xi _S = \varphi \). Note that the slow-roll parameter appearing in the power spectrum of the scalar modes (57) should be zero. Indeed, in this scenario the matter-dominated era never happens, therefore the relation (56) does not hold anymore and it makes no sense to speak about a power spectrum since the modes never re-enter the horizon. For this reason it is necessary to perform the computations imposing \(\epsilon \) to be a non-vanishing constant.
The Hamilton–Jacobi equation (41) reduces here to the following simple equation
From Eq. (42) it results that the explicit expression of the scale factor in terms of the new time coordinate reads as
where \(H_0 = \sqrt{\kappa _g\Lambda /3}\). Therefore \(\tau \) is equal to the conformal time.
It is now possible to express the frequencies as functions of time, which result to be the following
The linear equation for the tensor gaussian width reads as \(\rho _T''+(K^2-2/\tau ^2)\rho _T=0\) and yields the following two linearly independent solutions
The general solution is thus given by inserting the functions (64) into Eq. (51). Our “Minkowskian” initial conditions are satisfied by setting \(A^2=B^2=1/2\) and \(\gamma _1=1\) and give the following gaussian width
For what concerns the scalar modes, we note that the equation for \(\rho _k\) is equal to the one for \(\rho _T\) with the substitution \(k\rightarrow K\). So it is sufficient to replace K with k in Eq. (65) and we find the following scalar gaussian width
We can finally give the expressions of the power spectra for the quasi-isotropic de Sitter evolution. This is done evaluating the ratios \(\rho _k/a\) and \(\rho _T/a\) in the super-Hubble limit and inserting the results into Eqs. (57) and (60). We, thus, obtain the following power spectrum for the scalar modes
where, because of the presence of the slow-roll parameter \(\epsilon \), it has to be evaluated at the instant of time at which a certain mode-k crosses the horizon, i.e. when \(k = H_0a\); and the following power spectrum for the tensor modes
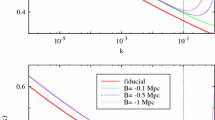
We can see that Eq. (67) is the standard power spectrum of curvature perturbations for the de Sitter inflationary model, while Eq. (68) results to be radically different from the standard scale invariant spectrum, since the scale dependence is contained in the power spectrum \({\mathcal {P}}_\vartheta (k)\) of the functions \(\vartheta _{ij}\), which are fixed by the initial conditions and remain frozen during the subsequent de Sitter evolution. We note also that, in agreement with the current observations, the tensor contribution is much smaller than the scalar one, being the tensor-to-scalar ratio \(r = {\mathcal P_T(k)}/{{\mathcal {P}}_S(k)}\) proportional to \(\epsilon \).
5.3 Slow-rolling case
Here we generalize the results (67) and (68) to the regime in which the inflaton field undergoes a generic slow-roll dynamics. In this case the matter potential \(V(\phi )\) develops a small dependence on \(\phi \) and the background component of the scalar field acquires a finite velocity, i.e. \(\phi '\ne 0\).
The analytical calculation of the power spectra is achieved making use of an expansion in the slow-roll parameters
which must be small in order to guarantee the slow-roll approximation. Here we consider only the first order slow-roll approximation so that in the following we will drop quadratic and higher order terms.
First we need to derive the background quantities. Integrating the relation \(d\tau =adt\), i.e.
we get the explicit expression of the scale factor in terms of the slow-roll parameters and conformal time
where C is an integration constant. Therefore, the Hubble parameter takes the following form
in which the constant C it’s been replaced by
Physically \(H_0\) represents the reference de Sitter spacetime. We set it as the value of the Hubble parameter at the time \(\tau _k\) of horizon crossing of the mode-k, that is \(H_0 = H(\tau _k) = k/a(\tau _k)\), which implies \(\tau _0(\tau _k) = -1/k\). Analogously, for what concerns the tensor degree of freedom we choose to set \(H_0=K/a\) and \(\tau _0=1/K\), since \(v_T\) behaves like an oscillator with comoving wave-vector norm K. In this way both \(H_0\) and \(\tau _0\) become k-dependent.
Note that Eq. (72) fixes the range of validity of the approximation, that is given by the request that the expansion rate is almost constant. Thus we must impose \(\epsilon |\log (\tau /\tau _0)|\ll 1\), that gives
and assuming \(\epsilon \) to be very small, this range is very large.
The Friedmann equation can be written without approximations in terms of the first slow-roll parameter as
It is easy then to derive the explicit expressions of V and \(\phi '\) in terms of \(\tau \) and finally find the frequencies (29) and (32), which result to be the following
where we have defined the parameter \(\gamma = 2\epsilon -\delta \).
The linearly independent solutions \(f(\tau )\) and \(g(\tau )\) of the linear system of differential equations for the gaussian widths can be obtained in terms of the Bessel functions \(J_{\pm (3/2+\gamma )}(-k\tau )\) and \(J_{\pm (3/2+\epsilon )}(-K\tau )\), for the scalar and tensor sector respectively. Again, the gaussian widths are constructed from Eq. (51) and imposing the “Minkowskian” initial conditions. In the super-Hubble limit they read as
Now we can derive the power spectra linearizing Eq. (77) with respect to the slow-roll parameters and evaluating the ratio between the gaussian widths and a in the super-Hubble limit. In this way Eq. (57) gives the following power spectrum of the curvature perturbation
and Eq. (60) gives the power spectrum of the tensor perturbations which reads as
Again, the result (78) is exactly the standard power spectrum of the scalar perturbations while in (79) the contribution of each mode-k is fixed only by the initial conditions on \(\vartheta _{ij}\). Furthermore, the tensor-to-scalar ratio is proportional to \(\epsilon \ll 1\), therefore the tensor contribution is much smaller than the scalar one.
6 Concluding remarks
Our analysis was based on the implementation of the so-called quasi-isotropic solution in the early Universe dynamics, in which the standard FLRW Universe presents a small inhomogeneous correction, evolving according to a second scale factor different from the background one. The smallness of the inhomogeneities is guaranteed by the correspondingly small ratio \(\eta (t)\) between the FLRW scale factor and the perturbation one, which has been taken as the fundamental dynamical variable in our study.
Here, we implemented the idea proposed in [15] of considering the inhomogeneous correction and, in particular, the small variable controlling their values, as associated to a “small quantum” subspace, living on the quasi-classical framework of the isotropic Universe.
In this way, the variable \(\eta (t)\) was, de facto, treated as a small quantum correction to the standard primordial cosmology, whose dynamics is described by a Schrödinger equation, resembling a time dependent harmonic oscillator.
We studied the resulting dynamics of the proposed picture during the de Sitter phase of an inflationary era and we involved in the problem of characterizing both the scalar perturbation of the corresponding inflaton field and the tensor perturbation of the gravitational degrees of freedom.
We constructed the Lagrangian and Hamiltonian formulation of this cosmological scenario, up to the second order of approximation in the perturbation amplitude and adopting the gauge invariant formulation, guaranteed by the use of the Mukhanov–Sasaki variables.
We then calculated the spectrum of the primordial fluctuations emerging from the de Sitter phase, comparing the tensor and scalar spectrum properties. While the latter retains its standard scale invariant form, the former has a peculiar dependence on the wave-vectors, fixed, ab initio, from the nature of the considered inhomogeneous term perturbing the isotropic Universe.
Actually, the resulting feature of our dynamical setting is that the tensor spectrum, emerging from inflation, can have a generic (non-necessarily gaussian) profile. We stress that the tensor-to-scalar ratio, being proportional to the slow-roll parameter \(\epsilon \), is very small, such that our results are in perfect agreement with the available experimental constraints.
The obtained results are a direct consequence of the factorization of the time and space dependence that naturally takes place in the quasi-isotropic solution. Indeed, we have shown that, while the scalar component behaves as an intrinsically inhomogeneous degree of freedom, such a quasi-isotropic character leads to a factorization of the tensor component of the metric. Thus, if this feature can be postulated also for a quantum Universe (no objection exists a priori to this statement), we can infer that, since the isotropic Universe emerges as the main classical component of the dynamics, a factorized perturbation can still evolve on such a background, becoming responsible for a generic spectral feature of the primordial tensor spectrum.
The robustness of the quasi-classical solution in the Planckian representation of the Universe could also be inferred from a quantum dynamical process of isotropization of the generic cosmological solution [6, 43, 44]. According to the ideas discussed in [45], the emergence of a classical Universe from a quantum Mixmaster scenario [46, 47] can approach a classical limit only when the anisotropy degrees of freedom becomes small enough and a quasi-classical isotropic Universe starts to emerge. It is exactly this dynamical picture the most convincing motivation for the present analysis.
Finally, we point out that at a classical level it was demonstrated in [48,49,50] that the backreaction on the metric of the particles produced during the BKL oscillatory regime leads to a quick isotropization of the cosmological expansion, actually yielding a quasi-isotropic evolution of the Universe. Therefore, in the light of our results, it would be interesting to see if an analogous mechanism exists also in the quantum regime, allowing one to study the space distribution of the tensor inhomogeneity \(\vartheta _{ij}({{\textbf {x}}})\). This would relate the tensor power spectrum to the pre-inflationary Universe, giving the unexpected opportunity to gain information about such unknown epoch of the Universe from future observations of the cosmological background of gravitational waves, thus opening a new phenomenological window on, possibly, beyond standard model physics and quantum gravity.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The present manuscript is a theoretical work without any data.]
Notes
In the following Latin indices run through the three spatial values 1, 2, and 3, while Greek indices run through the values 0, 1, 2 and 3.
Given that the minimum number of e-folds necessary to solve the shortcomings present in the standard cosmological model is typically \({\mathcal {E}} \simeq 60\) [4], any perturbation that could exist before inflation would be reduced at the end by a factor \(\sim \eta _f/\eta _i \sim (a_i/a_f)^4 \sim {\mathcal {O}}(10^{-108})\).
From now on we will adopt the convention \(\delta ^{ij}V_iW_j = V_iW_i\), while \(\gamma ^{ij}V_iW_j = V^iW_i\).
It is easy to see that \(p_\vartheta \) satisfies all the requirements to be a probability distribution, in particular the three Kolmogorov axioms [30].
References
H.P. Robertson, Kinematics and world-structure. Astrophys. J. 82, 284 (1935)
A.G. Walker, On Milne’s theory of world-structure. Proc. Lond. Math. Soc. 42, 90–127 (1937)
G. Montani, M.V. Battisti, R. Benini, G. Imponente, Primordial Cosmology (World Scientific, Singapore, 2011)
E.W. Kolb, M.S. Turner, The Early Universe (CRC Press, Boca Raton, 2018)
Y. Akrami, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A.J. Banday, R.B. Barreiro, N. Bartolo, S. Basak, K. Benabed et al., Planck 2018 results-VII. Isotropy and statistics of the CMB. Astron. Astrophys. 641, 7 (2020)
V.A. Belinskii, I.M. Khalatnikov, E.M. Lifshitz, A general solution of the Einstein equations with a time singularity. Adv. Phys. 31(6), 639–667 (1982)
K.S. Thorne, C.W. Misner, J.A. Wheeler, Gravitation (Freeman, San Francisco, 2000)
C.W. Misner, The isotropy of the universe. Astrophys. J. 151, 431 (1968)
G. Montani, M.V. Battisti, R. Benini, G. Imponente, Classical and quantum features of the mixmaster singularity. Int. J. Mod. Phys. A 23(16n17), 2353–2503 (2008)
E.M. Lifshitz, I.M. Khalatnikov, On the singularities of cosmological solutions of the gravitational equations. I. ZhETF 39(149), 149 (1960)
G. Montani, On the quasi-isotropic solution in the presence of ultrarelativistic matter and a scalar field. Class. Quantum Gravity 16(3), 723 (1999)
N. Carlevaro, G. Montani, Study of the quasi-isotropic solution near the cosmological singularity in the presence of bulk viscosity. Int. J. Mod. Phys. D 17(06), 881–896 (2008)
G. Imponente, G. Montani, On the quasi-isotropic inflationary solution. Int. J. Mod. Phys. D 12(10), 1845–1857 (2003)
S. Weinberg, Cosmology (OUP, Oxford, 2008)
A. Vilenkin, Interpretation of the wave function of the universe. Phys. Rev. D 39(4), 1116 (1989)
C. Kiefer, T.P. Singh, Quantum gravitational corrections to the functional Schrödinger equation. Phys. Rev. D 44(4), 1067 (1991)
G. Maniccia, M. De Angelis, G. Montani, WKB approaches to restore time in quantum cosmology: predictions and shortcomings. Universe 8(11), 556 (2022)
F. Di Gioia, G. Maniccia, G. Montani, J. Niedda, Nonunitarity problem in quantum gravity corrections to quantum field theory with Born–Oppenheimer approximation. Phys. Rev. D 103(10), 103511 (2021)
G. Maniccia, G. Montani, Quantum gravity corrections to the matter dynamics in the presence of a reference fluid. Phys. Rev. D 105(8), 086014 (2022)
P. Campeti, E. Komatsu, D. Poletti, C. Baccigalupi, Measuring the spectrum of primordial gravitational waves with CMB, PTA and laser interferometers. J. Cosmol. Astropart. Phys. 2021(01), 012 (2021)
M.C. Guzzetti, N. Bartolo, M. Liguori, S. Matarrese, Gravitational waves from inflation. La Rivista del Nuovo Cimento 39(9), 399–495 (2016)
E.M. Lifshitz, I.M. Khalatnikov, Investigations in relativistic cosmology. Adv. Phys. 12(46), 185–249 (1963)
V.F. Mukhanov, H.A. Feldman, R.H. Brandenberger, Theory of cosmological perturbations. Phys. Rep. 215(5–6), 203–333 (1992)
B.S. DeWitt, Quantum theory of gravity. I. The canonical theory. Phys. Rev. 160(5), 1113 (1967)
C.J. Isham, Canonical quantum gravity and the problem of time, in Integrable Systems, Quantum Groups, and Quantum Field Theories (Springer, Berlin, 1993), pp. 157–287
A.H. Taub, Stability of general relativistic gaseous masses and variational principles. Commun. Math. Phys. 15(3), 235–254 (1969)
F. Cianfrani, O.M. Lecian, M. Lulli, G. Montani, Canonical Quantum Gravity: Fundamentals and Recent Developments (World Scientific, Singapore, 2014)
J.M. Bardeen, Gauge-invariant cosmological perturbations. Phys. Rev. D 22, 1882–1905 (1980)
C. Gundlach, Cosmological quantum fluctuations: gauge-invariance and Gaussian states. Class. Quantum Gravity 10(6), 1103 (1993)
A.N. Kolmogorov, A.T. Bharucha-Reid, Foundations of the Theory of Probability, 2nd English edition (Courier Dover Publications, New York, 2018)
D. Brizuela, C. Kiefer, M. Krämer, Quantum-gravitational effects on gauge-invariant scalar and tensor perturbations during inflation: the de Sitter case. Phys. Rev. D 93, 104035 (2016)
D. Brizuela, C. Kiefer, M. Krämer, Quantum-gravitational effects on gauge-invariant scalar and tensor perturbations during inflation: the slow-roll approximation. Phys. Rev. D 94, 123527 (2016)
A.Y. Kamenshchik, A. Tronconi, G. Venturi, Inflation and quantum gravity in a Born–Oppenheimer context. Phys. Lett. B 726(1–3), 518–522 (2013)
A. Kamenshchik, A. Tronconi, G. Venturi, Signatures of quantum gravity in a Born–Oppenheimer context. Phys. Lett. B 734 (2014)
A.Y. Kamenshchik, A. Tronconi, G. Venturi, Quantum gravity and the large scale anomaly. J. Cosmol. Astropart. Phys. 2015(04), 046 (2015)
H.R. Lewis Jr., Class of exact invariants for classical and quantum time-dependent harmonic oscillators. J. Math. Phys. 9(11), 1976–1986 (1968)
H.R. Lewis Jr., W.B. Riesenfeld, An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J. Math. Phys. 10(8), 1458–1473 (1969)
I.A. Pedrosa, Exact wave functions of a harmonic oscillator with time-dependent mass and frequency. Phys. Rev. A 55(4), 3219 (1997)
H.R. Lewis Jr., Classical and quantum systems with time-dependent harmonic-oscillator-type Hamiltonians. Phys. Rev. Lett. 18(13), 510 (1967)
Y. Akrami, F. Arroja, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A.J. Banday, R.B. Barreiro, N. Bartolo, S. Basak et al., Planck 2018 results-IX. Constraints on primordial non-Gaussianity. Astron. Astrophys. 641, 9 (2020)
J. Martin, V. Vennin, P. Peter, Cosmological inflation and the quantum measurement problem. Phys. Rev. D 86(10), 103524 (2012)
D.H. Lyth, Large-scale energy-density perturbations and inflation. Phys. Rev. D 31, 1792–1798 (1985)
G. Montani, On the general behaviour of the universe near the cosmological singularity. Class. Quantum Gravity 12(10), 2505 (1995)
A.A. Kirillov, The nature of the spatial distribution of metric inhomogeneities in the general solution of the Einstein equations near a cosmological singularity. JETP 76(3), 355–358 (1993)
A.A. Kirillov, G. Montani, Origin of a classical space in quantum inhomogeneous models. J. Exp. Theor. Phys. Lett. 66(7), 475–479 (1997)
R. Benini, G. Montani, Inhomogeneous quantum mixmaster: from classical towards quantum mechanics. Class. Quantum Gravity 24(2), 387 (2006)
G. Montani, M.V. Battisti, R. Benini, G. Imponente, Classical and quantum features of the mixmaster singularity. Int. J. Mod. Phys. A 23(16n17), 2353–2503 (2008)
V.N. Lukash, A.A. Starobinsky, The isotropization of the cosmological expansion owing to particle production. Sov. J. Exp. Theor. Phys. 39, 742 (1974)
A.G. Doroshkevich, V.N. Lukash, I.D. Novikov, The isotropization of homogeneous cosmological models. Sov. Phys. JETP 37, 739–746 (1973)
V.N. Lukash, I.D. Novikov, A.A. Starobinsky, Y.B. Zeldovich, Quantum effects and evolution of cosmological models. Il Nuovo Cimento B (1971–1996) 35(2), 293–307 (1976)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Bortolotti, N., Montani, G. Inflationary quantum spectrum of the quasi-isotropic Universe. Eur. Phys. J. C 84, 23 (2024). https://doi.org/10.1140/epjc/s10052-023-12359-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-12359-0