1 Introduction

Recently, there has been rapid development in the field of gravitational wave astronomy, which has provided us with new insights into compact objects such as the black holes (BHs) and the neutron stars (NSs) [1,2,3]. The advancements in gravitational wave detection technology have also made it possible to search for exotic compact objects (ECOs) similar to the BHs. One prominent class of ECOs is the bosonic stars, which are particle-like configurations of massive scalar fields [4,5,6,7,8,9] or vector fields [10,11,12,13,14] that form under their own gravitational attraction. The repulsive force balancing gravity is provided by the Heisenberg uncertainty principle. The bosonic stars provide a promising framework for studying compact objects, and certain models of the bosonic stars can mimic the BHs [15,16,17,18,19]. Additionally, the bosonic stars are also considered candidates for dark matter [20,21,22,23,24,25].

However, particle-like configurations can also be formed by spin-1/2 fermion fields. For non-gravitational cases, attempts to construct particle-like solutions for the Dirac equation were made as early as the 1930s by Ivanenko [26]. Subsequent studies have also been conducted in this regard [27,28,29,30]. However, it was not until 1970 that the exact numerical solutions for such particle-like configurations were first studied by Soler [31]. When gravitational interactions are considered, numerical calculations become more challenging. In 1999, Finster et al. constructed the exact numerical solutions for the Einstein–Dirac system, which couples spinor fields with Einstein’s gravity, for the first time [32]. These particle-like configurations, formed by spin-1/2 fermions under their own gravitational attraction, are known as the Dirac stars. Subsequently, research on the Dirac stars has been extended to include charged [33] and gauge field [34] additions, and the existence of the Dirac star solutions has been proven [35, 36]. Recently, the rotational Dirac star solutions [37] and their charged counterparts [38] have been provided for the first time by Herdeiro et al. Some comparative studies between the bosonic stars and the Dirac stars have been conducted in [39, 40]. Additionally, various interesting studies on the Einstein–Dirac system have been carried out [41,42,43,44,45,46,47,48,49].

In 2010, Bernal et al. constructed the multi-state boson stars (MSBSs) composed of two complex scalar fields in their ground state and the first excited state and analyzed the stability of the solutions [50]. Subsequently, the MSBSs were extended to include rotation [51] and self-interactions [52]. It is possible that the Dirac field, under its own gravitational attraction, can also form multi-state configurations. In this work, we numerically solve the Einstein–Dirac system and construct spherically symmetric multi-state Dirac stars (MSDSs), where two coexisting states of the Dirac field are present.

The paper is organized as follows. In Sec. 2, we introduce the Einstein–Dirac system, which couples four-dimensional Einstein’s gravity with two sets of Dirac fields. In Sec. 3, we investigate the boundary conditions of the MSDSs. In Sec. 4, we present the numerical results and analyze the solutions of the MSDSs under synchronized and nonsynchronized frequencies. We also discuss the binding energy of the solutions and the problem of the galactic halos. In Sec. 5, we provide a summary and outline the scope of future research.

2 The model setup

We consider a system composed of multiple matter fields that are minimally coupled to Einstein gravity. The matter fields consist of two sets of Dirac spinor fields, each set containing two spinors of opposite spin (thus ensuring the system has spherical symmetry), with one set in the ground state and the other set in the first excited state. For such a system, the action is given by:

$$\begin{aligned} S=\int \sqrt{-g} d^4 x \left( \frac{R}{16\pi G} + {{\mathcal {L}}}_{0} + {{\mathcal {L}}}_{1}\right) , \end{aligned}$$
(1)

where R is the Ricci scalar, G is the gravitational constant,and \({{\mathcal {L}}}_{0}\) and \({{\mathcal {L}}}_{1}\) are the Lagrangians of the spinor fields in the ground state and first excited state, respectively,

$$\begin{aligned} {{\mathcal {L}}}_{0}= & {} -i\sum \limits _{k=1}^2 \left[ \frac{1}{2}\left( {\hat{D}}_\mu {\overline{\Psi }}^{(k)}_0\gamma ^\mu \Psi ^{(k)}_0 -{\overline{\Psi }}^{(k)}_0\gamma ^\mu {\hat{D}}_\mu \Psi ^{(k)}_0\right) \right. \nonumber \\{} & {} \left. + \mu _0{\overline{\Psi }}^{(k)}_0\Psi ^{(k)}_0\right] , \end{aligned}$$
(2)
$$\begin{aligned} {{\mathcal {L}}}_{1}= & {} -i\sum \limits _{k=1}^2 \left[ \frac{1}{2}\left( {\hat{D}}_\mu {\overline{\Psi }}^{(k)}_1\gamma ^\mu \Psi ^{(k)}_1 - {\overline{\Psi }}^{(k)}_1\gamma ^\mu {\hat{D}}_\mu \Psi ^{(k)}_1\right) \right. \nonumber \\{} & {} \left. + \mu _1{\overline{\Psi }}^{(k)}_1\Psi ^{(k)}_1\right] , \end{aligned}$$
(3)

where \(\Psi ^{(k)}_n\) are spinors with mass \(\mu _n\) and n radial nodes, and the index \(k=1,2\), corresponds to spinors with opposite spin. The variations of the action (1) with respect to the metric and the field functions yield the Einstein equations and the Dirac equation:

$$\begin{aligned}{} & {} R_{\alpha \beta } - \frac{1}{2}g_{\alpha \beta }R = 8\pi G\left( T^0_{\alpha \beta } + T^1_{\alpha \beta }\right) , \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \gamma ^\mu {\hat{D}}_\mu \Psi ^{(k)}_n - \mu _n\Psi ^{(k)}_n = 0,\quad n = 0,\,1. \end{aligned}$$
(5)

where \(T^0_{\alpha \beta }\) and \(T^1_{\alpha \beta }\) are the energy-momentum tensors of the two sets of spinor fields,

$$\begin{aligned} T^0_{\alpha \beta }= & {} \sum \limits _{k=1}^2 -\frac{i}{2}\left( {\overline{\Psi }}^{(k)}_0\gamma _\alpha {\hat{D}}_\beta \Psi ^{(k)}_0 + {\overline{\Psi }}^{(k)}_0\gamma _\beta {\hat{D}}_\alpha \Psi ^{(k)}_0\right. \nonumber \\{} & {} \left. - {\hat{D}}_\alpha {\overline{\Psi }}^{(k)}_0\gamma _\beta \Psi ^{(k)}_0 -{\hat{D}}_\beta {\overline{\Psi }}^{(k)}_0\gamma _\alpha \Psi ^{(k)}_0\right) , \end{aligned}$$
(6)
$$\begin{aligned} T^1_{\alpha \beta }= & {} \sum \limits _{k=1}^2 -\frac{i}{2}\left( {\overline{\Psi }}^{(k)}_1\gamma _\alpha {\hat{D}}_\beta \Psi ^{(k)}_1 + {\overline{\Psi }}^{(k)}_1\gamma _\beta {\hat{D}}_\alpha \Psi ^{(k)}_1\right. \nonumber \\{} & {} \left. - {\hat{D}}_\alpha {\overline{\Psi }}^{(k)}_1\gamma _\beta \Psi ^{(k)}_1 -{\hat{D}}_\beta {\overline{\Psi }}^{(k)}_1\gamma _\alpha \Psi ^{(k)}_1\right) . \end{aligned}$$
(7)

Furthermore, it can be seen from Eqs. (2) and (3) that the Lagrangians of the spinor fields are invariant under a global U(1) transformation \(\Psi ^{(k)}_n\rightarrow e^{i\alpha }\Psi ^{(k)}_n\), where \(\alpha \) is an arbitrary constant. As a result, the system possesses a conserved current:

$$\begin{aligned} J_n^{\mu } = {\overline{\Psi }}_n\gamma ^\mu \Psi _n,\quad n = 0,\,1. \end{aligned}$$
(8)

Integrating the timelike component of the conserved current over a spacelike hypersurface \({\mathcal {S}}\) yields the Noether charge:

$$\begin{aligned} Q_n = \int _{{\mathcal {S}}}J_n^t,\quad n = 0,\,1. \end{aligned}$$
(9)

To construct spherically symmetric solutions, we choose the metric to be of the following form:

$$\begin{aligned} ds^2= & {} -N(r)\sigma ^2(r)dt^2 + \frac{dr^2}{N(r)} \nonumber \\{} & {} + r^2\left( d\theta ^2 + \sin ^2\theta d\varphi ^2\right) , \end{aligned}$$
(10)

where \(N(r) = 1 - {2m(r)}/{r}\). The two sets of Dirac fields are given by [39]:

$$\begin{aligned} \Psi ^{(1)}_n= & {} \begin{pmatrix}\cos (\frac{\theta }{2})[(1 + i)f_n(r) - (1 - i)g_n(r)]\\ i\sin (\frac{\theta }{2})[(1 - i)f_n(r) - (1 + i)g_n(r)]\\ -i\cos (\frac{\theta }{2})[(1 - i)f_n(r) - (1 + i)g_n(r)]\\ -\sin (\frac{\theta }{2})[(1 + i)f_n(r) - (1 - i)g_n(r)] \end{pmatrix}e^{i\frac{\varphi }{2} - i\omega _nt},\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} \Psi ^{(2)}_n= & {} \begin{pmatrix}i\sin (\frac{\theta }{2})[(1 + i)f_n(r) - (1 - i)g_n(r)]\\ \cos (\frac{\theta }{2})[(1 - i)f_n(r) - (1 + i)g_n(r)]\\ \sin (\frac{\theta }{2})[(1 - i)f_n(r) - (1 + i)g_n(r)]\\ i\cos (\frac{\theta }{2})[(1 + i)f_n(r) - (1 - i)g_n(r)] \end{pmatrix}e^{-i\frac{\varphi }{2} - i\omega _nt},\nonumber \\ \end{aligned}$$
(12)

where the index n also represents the number of radial nodes, and \(\omega _n\) is the frequency of the Dirac field with n radial nodes. We only consider the cases of \(n=0,1\) in this paper.

Substituting the above ansatz into the field equations (4–5) yields the following system of ordinary differential equations:

$$\begin{aligned}{} & {} f^\prime _n + \left( \frac{N^\prime }{4N} + \frac{\sigma ^\prime }{2\sigma } + \frac{1}{r\sqrt{N}} + \frac{1}{r}\right) f_n\nonumber \\{} & {} \quad + \left( \frac{\mu _n}{\sqrt{N}} - \frac{\omega _n}{N\sigma }\right) g_n = 0 , \end{aligned}$$
(13)
$$\begin{aligned}{} & {} g^\prime _n + \left( \frac{N^\prime }{4N} + \frac{\sigma ^\prime }{2\sigma } - \frac{1}{r\sqrt{N}} + \frac{1}{r}\right) g_n\nonumber \\{} & {} \quad + \left( \frac{\mu _n}{\sqrt{N}} + \frac{\omega _n}{N\sigma }\right) f_n = 0. \end{aligned}$$
(14)
$$\begin{aligned}{} & {} m^\prime = \frac{32\pi G r^2}{\sqrt{N}\sigma } \left[ \omega _0(f^2_0 + g^2_0) + \omega _1(f^2_1 + g^2_1) \right] , \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \frac{\sigma ^\prime }{\sigma } = \frac{32\pi Gr}{\sqrt{N}}\left[ g_0f_0^\prime - f_0g_0^\prime + g_1f_1^\prime - f_1g_1^\prime \right. \nonumber \\{} & {} \quad \left. + \frac{\omega _0(f_0^2 + g_0^2)}{N\sigma } + \frac{\omega _1(f_1^2 + g_1^2)}{N\sigma }\right] . \end{aligned}$$
(16)

And the Noether charges of the system are:

$$\begin{aligned} Q_n = 16\pi \int _0^\infty r^2\frac{f^2_n + g^2_n}{\sqrt{N}}dr,\quad n = 0,\,1. \end{aligned}$$
(17)

3 Boundary conditions

To solve the system of ordinary differential equations obtained in the previous section, appropriate boundary conditions need to be imposed. First, for a regular, asymptotically flat spacetime, the metric function should satisfy the following boundary conditions:

$$\begin{aligned} m(0) = 0,\quad \sigma (0) = \sigma _0,\quad m(\infty ) = M,\quad \sigma (\infty ) = 1, \end{aligned}$$
(18)

where the ADM mass m and \(\sigma _0\) are unknown constants. In addition, the matter field vanishes at infinity:

$$\begin{aligned} f_n(\infty ) = 0,\qquad g_n(\infty ) = 0,\quad n=0,1. \end{aligned}$$
(19)

Expanding Eqs. (13–14) near the origin, we obtain that the field function satisfies the following condition at the origin:

$$\begin{aligned} f_n(0) = 0,\qquad \left. \frac{dg_n(r)}{dr}\right| _{r = 0} = 0. \end{aligned}$$
(20)

4 Numerical results

In order to facilitate numerical calculations, we employ the following dimensionless quantities:

$$\begin{aligned}{} & {} r \rightarrow r/\rho ,\quad f_n \rightarrow \frac{\sqrt{4\pi \rho }}{M_{Pl}}f_n,\quad g_n \rightarrow \frac{\sqrt{4\pi \rho }}{M_{Pl}}g_n,\nonumber \\{} & {} \quad \omega _n \rightarrow \omega _n\rho ,\quad \mu _n \rightarrow \mu _n\rho , \end{aligned}$$
(21)

where \(M_{Pl} = 1/\sqrt{G}\) is the Planck mass. For any physical quantity A, we denote the dimensionless A under the conditions of \(\rho = 1/\mu _0\) and \(\rho = 1/\mu _1\) as \({\tilde{A}}\) and \({\overline{A}}\) respectively. For ease of computation, we define the radial coordinate x as follows:

$$\begin{aligned} x = \frac{{\tilde{r}}}{1+{\tilde{r}}}, \end{aligned}$$
(22)

where the radial coordinate \({\tilde{r}}\in [0,\infty )\), so \(x\in [0,1]\). We employ the finite element method to numerically solve the system of differential equations. The integration region \(0\le x\le 1\) is discretized into 1000 grid points. The Newton-Raphson method serves as our iterative approach. In order to ensure the accuracy of the computational results, we enforce a relative error criterion of less than \(10^{-5}\).

In order to ensure the accuracy of our numerical calculations, it is crucial to verify the numerical precision through physical constraint validation, in addition to employing the aforementioned numerical analysis methods. In this study, we examined the equivalence between the asymptotic mass and the Komar mass of the numerical solution, and the results consistently maintained a discrepancy of less than \(10^{-5}\) between these two quantities.

We denote the Dirac stars in the ground state and the first excited state as \(D_0\) and \(D_1\), respectively, and the multi-state Dirac stars as \(D_0D_1\) (or MSDSs). The representation of the gamma matrices and the choice of the tetrad in the Dirac equation are the same as in [41].

4.1 Synchronized frequency

Through the analysis of the numerical calculations, we found that the solution of the MSDSs under synchronized frequency (\(\omega =\omega _0=\omega _1\)) depends on the ratio of the masses of the excited state and ground state Dirac fields: \(\mu _1/\mu _0\), which is the dimensionless mass of the first excited state Dirac field, denoted as \({\tilde{\mu }}_1\). By varying the value of the mass \({\tilde{\mu }}_1\), various MSDSs solutions can be obtained. According to the number of branches of the obtained MSDSs solutions, we divide the solutions into single-branch and double-branch solutions. When \(0.7694 \le {\tilde{\mu }}_1 < 1\), the solution of the MSDSs is a single-branch solution; when \(0.7573 \le {\tilde{\mu }}_1 < 0.7694\), the solution of the MSDSs is a double-branch solution. Next, we will discuss the characteristics of these two types of solutions.

Fig. 1
figure 1

The matter functions \({\tilde{f}}_0\), \({\tilde{g}}_0\), \({\tilde{f}}_1\) and \({\tilde{g}}_1\) as functions of x and \({\tilde{\omega }}\) for \({\tilde{\mu }}_1 = 0.898\)

Full size image
Fig. 2
figure 2

The ADM mass M of the MSDSs as a function of the synchronized frequency \({\tilde{\omega }}\) (\({\overline{\omega }}\)) for several values of \({\tilde{\mu }}_1\) (\(1/{\overline{\mu }}_0\))

Full size image

4.1.1 Single-branch

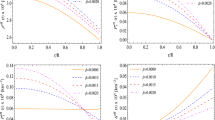
We first discuss the more general single-branch solution in the multi-field system [41, 42, 51,52,53]. The characteristic of the change in the radial profile of the matter field forming the MSDSs as the synchroniezd frequency \({\tilde{\omega }}\) continuously varies is shown in Fig. 1. The field functions depicted in the figure were obtained under the condition of a fixed mass \({\tilde{\mu }}_1 = 0.898\). The two upper plots correspond to the ground state Dirac field functions \({\tilde{f}}_0\) and \({\tilde{g}}_0\), revealing the absence of nodes in these field functions. The two lower plots represent the excited state Dirac field functions \({\tilde{f}}_1\) and \({\tilde{g}}_1\), where each of these field functions exhibits a single node, indicating that the Dirac field is in the first excited state. It is easy to see that as the synchroniezd frequency \({\tilde{\omega }}\) increases, the peak values of the ground state Dirac field functions \({\tilde{f}}_0\) and \({\tilde{g}}_0\) also increase gradually, while the peak values of the excited state Dirac field functions \({\tilde{f}}_1\) and \({\tilde{g}}_1\) decrease gradually. In addition, when the synchroniezd frequency approaches the minimum value at which the single-branch solution can exist, the ground-state Dirac field tends to disappear, while the opposite is true for the excited state Dirac field.

Next, we analyze the characteristics of the ADM mass M of the single-branch solution of the MSDSs as the synchroniezd frequency \({\tilde{\omega }}\) varies. As shown in Fig. 2, the black dashed line represents the ground state Dirac stars (\(D_0\)), the blue dashed line represents the first excited state Dirac stars (\(D_1\)), and the orange line represents the MSDSs (\(D_0D_1\)). The ADM mass of the system monotonically decreases as the synchroniezd frequency increases. It can be seen that the upper end of the orange line intersects with the blue dashed line, where the MSDSs degenerate into the \(D_1\); the lower end of the orange line intersects with the black dashed line, where the MSDSs degenerates into the \(D_0\). This degeneration of the MSDSs is manifested in Fig. 1 as the disappearance of the ground state or excited state field functions. In addition, when the mass \({\tilde{\mu }}_1\) of the excited state Dirac field is small, both endpoints of the orange line are located on the first branch of the black and blue dashed lines; when the mass \({\tilde{\mu }}_1\) decreases to 0.801, the intersection point of the orange line and the blue dashed line is located at the inflection point between the first and second branches of the blue dashed line; as the mass \({\tilde{\mu }}_1\) continues to decrease to 0.771, the intersection point of the orange line and the black dashed line is located at the inflection point between the first and second branches of the black dashed line; when \({\tilde{\mu }}_1\) decreases to the minimum frequency at which the single-branch solution can exist, 0.7694, the orange line and the black dashed line show a "tangent" form. The two plots at the bottom of Fig. 2 intuitively illustrate the variation of the orange line endpoints. It should be noted that the horizontal axis of the lower right plot represents \({\overline{\omega }}\), not \({\tilde{\omega }}\), in order to show the changing trend of the intersection points of the orange line and the blue dashed line.

Fig. 3
figure 3

The matter functions \({\tilde{f}}_0\), \({\tilde{g}}_0\), \({\tilde{f}}_1\) and \({\tilde{g}}_1\) on the first (left column) and second branches (right column) of the MSDSs solution function as functions of x and \({\tilde{\omega }}\) for \({\tilde{\mu }}_1 = 0.7645\)

Full size image
Fig. 4
figure 4

The ADM mass M of the MSDSs as a function of the synchronized frequency \({\overline{\omega }}\) for several values of \(1/{\overline{\mu }}_0\)

Full size image

4.1.2 Double-branch

In addition to the single-branch solution described in the preceding section, the solutions of MSDSs exhibit two branches when the synchronized frequency \({\tilde{\omega }}\) is sufficiently low. In the following, we will first discuss the variation of the matter field functions with respect to the synchronized frequency \({\tilde{\omega }}\) for the double-branch solution. As shown in Fig. 3, We demonstrate the relationship between the radial profile of the matter fields which constitute the MSDSs, and the synchronized frequency \({\tilde{\omega }}\), under the condition of a fixed mass \({\tilde{\mu }}_1 = 0.898\). For the first branch field functions of the MSDSs displayed in the left column of the figure, as the synchronized frequency increases, the peak values of the ground state Dirac field functions, \({\tilde{f}}_0\) and \({\tilde{g}}_0\), also increase, while the peak values of the excited state Dirac field functions, \({\tilde{f}}_1\) and \({\tilde{g}}_1\), gradually decrease. For the second branch field functions displayed in the right column, as the synchronized frequency decreases, the peak values of the ground state field functions, \({\tilde{f}}_0\) and \({\tilde{g}}_0\), gradually decrease, while the peak values of the excited state field functions, \({\tilde{f}}_1\) and \({\tilde{g}}_1\), gradually increase. It is worth noting that the ground state Dirac field disappears at the minimum synchronized frequency of the first and second branches, while the excited state field always exists.

Fig. 5
figure 5

The matter functions \({\tilde{f}}_0\), \({\tilde{g}}_0\), \({\tilde{f}}_1\) and \({\tilde{g}}_1\) as functions of x and \({\tilde{\omega }}_1\) for \({\tilde{\omega }}_0 = 0.819\)

Full size image

Next, we analyze the characteristics of the ADM mass M of the double-branch solutions of the MSDSs as a function of synchronized frequency. Figure 4 shows the relationship between the ADM mass M and the synchronized frequency \({\overline{\omega }}\) for different masses \({\overline{\mu }}_0\) of the MSDSs. The blue dashed line represents the \(D_1\) solutions, while the red and green lines represent the first and second branch solutions of the MSDSs, respectively. As shown in Fig. 4, the two branches of the double-branch solution are very close to each other, but their intersections with the blue dashed line are clearly different. As \(1/{\overline{\mu }}_0\) decreases, the synchronized frequency range of the two branches of the MSDSs gradually decreases. For all double-branch solutions, the intersections of the two branches with the blue dashed line are always in the second branch of the blue dashed line. When \(1/{\overline{\mu }}_0\) decreases to 0.7573, the second branch solution is very close to some of the solutions in the first branch, to the extent that the two branches almost coincide. It is noteworthy that at this time, the first branch of the MSDSs appears to be "tangential" to the blue dashed line, which is a similar feature as the single-branch solution of the MSDSs mentioned earlier.

4.2 Nonsynchronized frequency

In this section, we discuss the nonsynchronized frequency solutions of the MSDSs. To analyze the influence of the parameters on the numerical solutions, we set the masses of the ground state and excited state Dirac fields to be the same (\(\mu _0 = \mu _1 = \mu \)), and investigate how the MSDSs change with the frequency of the excited state Dirac field \({\tilde{\omega }}_1\) under a fixed frequency of the ground state Dirac field \({\tilde{\omega }}_0\). Through a series of numerical calculations, we find that the nonsynchronized frequency solutions of the system can be divided into two types. When the frequency of the ground state Dirac field is in the range of \(0.733 \le {\tilde{\omega }}_0 < 1\), the solution of the MSDSs is a single branch solution; when the frequency of the ground state Dirac field is in the range of \(0.6971 \le {\tilde{\omega }}_0 < 0.733\), the solution of the MSDSs is a double branch solution.

4.2.1 Single-branch

We first discuss the single-branch solution. The radial profile of the ground-state and excited state Dirac field functions as a function of the excited state frequency \({\tilde{\omega }}_1\) is shown in Fig. 5. It can be seen that as the frequency \({\tilde{\omega }}_1\) increases, the maximum values of the ground state Dirac field functions \({\tilde{f}}_0\) and \({\tilde{g}}_0\) also increase gradually, while the maximum and minimum absolute values of the first excited-state Dirac field functions \({\tilde{f}}_1\) and \({\tilde{g}}_1\) decrease. Similar to the single-branch solution at synchronized frequency, for the single-branch solution at nonsynchronized frequency, the ground state fields almost disappears at the minimum value of the frequency \({\tilde{\omega }}_1\), and the excited state fields tends to disappear at the maximum value of the frequency \({\tilde{\omega }}_1\).

Fig. 6
figure 6

The ADM mass M of the MSDSs as a function of the frequency \({\tilde{\omega }}_1\) for several values of \({\tilde{\omega }}_0\)

Full size image
Fig. 7
figure 7

The matter functions \({\tilde{f}}_0\), \({\tilde{g}}_0\), \({\tilde{f}}_1\) and \({\tilde{g}}_1\) on the first (left column) and second branches (right column) of the MSDSs solution function as functions of x and \({\tilde{\omega }}_1\) for \({\tilde{\omega }}_0 = 0.721\)

Full size image

The relationship between the ADM mass M of nonsynchronized frequency single-branch solutions of the MSDSs and the frequency \({\tilde{\omega }}_1\) of the excited Dirac field is shown in Fig. 6. The black and blue dashed lines represent the ground state and the first excited state of the Dirac star solutions (\(D_0\) and \(D_1\)), the orange line represents the MSDSs solution, and the red dashed line represents the ADM mass of the \(D_0\) when the frequency \({\tilde{\omega }}_0\) of the ground state Dirac field takes the values indicated in each plot. When the frequency \({\tilde{\omega }}_0\) of the ground state Dirac field is close to 1, the range of the frequency \({\tilde{\omega }}_1\) corresponding to the obtained single-branch solution is very narrow. Then, as the frequency \({\tilde{\omega }}_0\) gradually decreases, the range of the frequency \({\tilde{\omega }}_1\) increases gradually. In addition, for a fixed frequency \({\tilde{\omega }}_0\), as the frequency \({\tilde{\omega }}_1\) increases, the ADM mass of the system decreases gradually. When the ADM mass reaches its maximum value, the frequency \({\tilde{\omega }}_1\) reaches its minimum value, and the ground state Dirac field disappears, the MSDSs degenerates into the \(D_1\). When the ADM mass reaches its minimum value, this minimum value is the same as the ADM mass of the \(D_0\) when the frequency \({\tilde{\omega }}_0\) takes the values indicated in each plot. This is because when the ADM mass of the MSDSs reaches its minimum value, the frequency \({\tilde{\omega }}_1\) reaches its maximum value, and the excited state Dirac field disappears, and the system degenerates into the \(D_0\). In other words, the minimum ADM mass of MSDSs is dependent on the frequency \({\tilde{\omega }}_0\) of the ground state Dirac field.

Fig. 8
figure 8

The ADM mass M of the MSDSs as a function of the frequency \({\tilde{\omega }}_1\) for several values of \({\tilde{\omega }}_0\)

Full size image

4.2.2 Double-branch

Next, we discuss the double-branch solutions of the MSDSs under nonsynchronized frequency. In the single-branch solution discussed earlier, the minimum value of the frequency \({\tilde{\omega }}_0\) of the ground state Dirac field is 0.733. Since there is no solution with a frequency less than 0.733 for the \(D_0\), the MSDSs cannot degenerate into the \(D_0\) when the frequency \({\tilde{\omega }}_0\) is less than 0.733, and thus the single-branch solution cannot be obtained. Through a series of numerical calculations, we found that when the ground state field frequency satisfies \(0.6971 \le {\tilde{\omega }}_0 < 0.733\), the double-branch solutions of the MSDSs will be obtained. Figure 7 shows the relationship between the radial profile of the matter fields which constitute the MSDSs, and the nonsynchronized frequency \({\tilde{\omega }}_1\). The left column shows the field functions on the first branch. As the frequency \({\tilde{\omega }}_1\) increases, the peak values of the ground state Dirac field functions \({\tilde{f}}_0\) and \({\tilde{g}}_0\) gradually increase, while the changes in the excited state field functions \({\tilde{f}}_1\) and \({\tilde{g}}_1\) are relatively small. The right column shows the field functions on the second branch. As the frequency \({\tilde{\omega }}_1\) decreases, the peak values of the ground state Dirac field functions \({\tilde{f}}_0\) and \({\tilde{g}}_0\) gradually decrease, while the excited state field functions \({\tilde{f}}_1\) and \({\tilde{g}}_1\) gradually increase. It can be seen that when the frequency \({\tilde{\omega }}_1\) of the first and second branch solutions reaches the minimum value, the ground state Dirac field disappears, while the excited state Dirac field does not disappear for any \({\tilde{\omega }}_1\).

Fig. 9
figure 9

The binding energy \(E_B\) of the MSDSs as a function of the synchronized frequency \({\overline{\omega }}\) for several values of \(1/{\overline{\mu }}_0\)

Full size image
Fig. 10
figure 10

The binding energy \(E_B\) of the MSDSs as a function of the nonsynchronized frequency \({\tilde{\omega }}_1\) for several values of \({\tilde{\omega }}_0\)

Full size image

The relationship between the ADM mass M of the nonsynchronized frequency double-branch solution of the MSDSs and the frequency \({\tilde{\omega }}_1\) is shown in Fig. 8. The black and blue dashed lines represent the ground state and first excited state solutions of the Dirac star (\(D_0\) and \(D_1\)), and the orange line represents the double-branch solution of the MSDSs (\(D_0D_1\)). As the frequency \({\tilde{\omega }}_0\) of the ground state Dirac field decreases, the range of existence of the two branches of the double-branch solution gradually decreases with respect to the frequency \({\tilde{\omega }}_1\). For a fixed ground state field frequency \({\tilde{\omega }}_0\), when the frequency \({\tilde{\omega }}_1\) reaches its maximum value, the MSDSs does not degenerate into the \(D_0\), but turns to another new branch. Afterwards, as the frequency \({\tilde{\omega }}_1\) decreases, the ADM mass of the system gradually increases, and eventually the MSDSs transform into the \(D_1\). This characteristic change in the system mass is also reflected in the profile of the field functions presented in Fig. 7, where the disappearance of the ground state Dirac field functions on the two branches when the frequency \({\tilde{\omega }}_1\) reaches its minimum indicates the transformation of the MSDSs into the \(D_1\).

4.3 Binding energy

After obtaining various different solutions for the MSDSs, we will analyze the stability of the system from the perspective of binding energy. Consider a MSDS with ADM mass M, where the Noether charge for the ground state Dirac field is denoted as \(Q_0\), and the Noether charge for the first excited state Dirac field is denoted as \(Q_1\). The binding energy \(E_B\) of the system can be expressed as:

$$\begin{aligned} E_B = M - 2\left( \mu _0 Q_0 + \mu _1 Q_1 \right) , \end{aligned}$$
(23)

where the coefficient 2 outside the parentheses on the right-hand side of the equation arises from the fact that in a spherically symmetric MSDS, both the ground state and the first excited state of the Dirac field have two components.

We first analyze the binding energy of the MSDSs under synchronized frequency. Figure 9 shows the relationship between the binding energy \(E_B\) and the synchronized frequency \({\overline{\omega }}\) of the MSDSs. The left plot represents the single-branch solutions of the MSDSs. When \(1/{\overline{\mu }}_0 > 0.863\), for a fixed value of \({\overline{\mu }}_0\), the binding energy \(E_B\) of the MSDSs monotonically increases with the synchronized frequency \({\overline{\omega }}\), and the binding energy is always less than zero. When \(1/{\overline{\mu }}_0 \le 0.863\), for a given \({\overline{\mu }}_0\), the binding energy initially decreases and then increases as the synchronized frequency increases. When \(1/{\overline{\mu }}_0\) becomes sufficiently small, the solutions become unstable (e.g., the red curve). Therefore, when \(1/{\overline{\mu }}_0\) is sufficiently large, i.e., when the masses \(\mu _0\) and \(\mu _1\) of the ground state and excited state Dirac fields are sufficiently close, the MSDSs are more stable. The right plot represents the double-branch solutions of the MSDSs. As \(1/{\overline{\mu }}_0\) increases, the minimum value of the binding energy gradually decreases, but the binding energies of these double-branch solutions are all greater than zero, indicating that the solutions are unstable.

Fig. 11
figure 11

Upper row: the ADM mass M, field mass \(\mu _1\) and frequency \(\omega \) vs. field mass \(\mu _0\) for synchronized frequency solutions. Bottom row: the ADM mass M, frequency \(\omega _0\) and frequency \(\omega _1\) vs. field mass \(\mu \) for nonsynchronized frequency solutions

Full size image

Next, we consider the binding energy of the MSDSs under nonsynchronized frequency. Figure 10 shows the relationship between the binding energy \(E_B\) and the frequency \({\tilde{\omega }}_1\) for the nonsynchronized frequency solutions of the MSDSs. The left plot represents the single-branch solutions, where for a fixed \({\tilde{\omega }}_0\), the binding energy \(E_B\) increases monotonically with the frequency \({\tilde{\omega }}_1\) and remains negative when the frequency \({\tilde{\omega }}_0\) is sufficiently large. However, for small values of \({\tilde{\omega }}_0\) (e.g. \({\tilde{\omega }}_0=0.733\)), the MSDSs can undergo a transition from a stable solution to an unstable one as the frequency \({\tilde{\omega }}_1\) increases. The right plot represents the double-branch solutions, where the negative binding energy solutions appear when the frequency \({\tilde{\omega }}_0\) is sufficiently large (e.g. \({\tilde{\omega }}_0=0.732\)). As the frequency \({\tilde{\omega }}_0\) decreases, the stable solutions in the double-branch solutions gradually disappear, and all solutions eventually become unstable. Therefore, in the case of nonsynchronized frequency, there exist stable solutions in the double-branch solutions.

4.4 Single particle condition

In the preceding text, we have computed the classical Dirac field coupled with gravity through the Einstein–Dirac equations and have investigated the resultant soliton solutions. However, in a quantum universe, the quantum nature of the Dirac field must also be considered. By taking into account the Pauli exclusion principle and setting Q=1 for each spinor field, we arrive at the results illustrated in Fig. 11.

In Fig. 11, the black curve represents the single-branch solutions, while the red, green, and orange curves denote the double-branch solutions (corresponding to Figs. 4, 8). Insets provide a magnified view of the double-branch regions. The first and second rows correspond to synchronized and nonsynchronized frequency solutions, respectively. Within the same row, identical numbers on blue dots indicate identical solutions. Regardless of the synchronicity of the frequency, the maximum masses of the spinors \(\mu _0\) and \(\mu _1\) are approximately \(0.5M_{pl}\), akin to the scenario of Dirac stars subjected to a single-particle condition as in Ref. [39]. The ADM mass of the MSDSs can reach about \(2M_{pl}\), nearly double that of the Dirac stars mentioned in [39]. We speculate that with the addition of a sufficient number of spinor fields, even under the imposition of the single-particle condition, the mass ratio of the MSDSs to the spinor field mass could still achieve a significant magnitude, rendering them analogous to macroscopic quantum states akin to the bosonic stars.

4.5 Galactic halos as MSDSs

The velocity of stars orbiting the central core of a galaxy remains constant over a large range of distances starting from the galactic center. This phenomenon may be attributed to the presence of a dark matter halo in the outer regions of the galaxy. By using boson stars to simulate the dark matter halo, it is possible to obtain results that are consistent with real observational data [20, 50, 54]. In the following, we will analyze the feasibility of simulating the dark matter halo using MSDSs by computing the velocities of test particles orbiting around them. Considering timelike circular geodesics on the equatorial plane, the rotational velocity of the test particles is given by [50, 54]:

$$\begin{aligned} v^2 = r\sqrt{-g_{tt}}\partial _r \sqrt{-g_{tt}}, \end{aligned}$$
(24)

Substituting Eq. (10) into the expression, we obtain

$$\begin{aligned} v = \sqrt{\frac{r\sigma (\sigma N^\prime + 2N \sigma ^\prime )}{2}}. \end{aligned}$$
(25)
Fig. 12
figure 12

Left panel: the rotational curves of the MSDSs for several values of \({\tilde{\mu }}_1\). Right panel: the rotational curves of the Dirac stars at different energy levels

Full size image

Next, we proceed to analyze the rotational curves of the MSDSs. As shown in Fig. 12, the red, green, and blue curves in the left panel represent the rotation curves of the MSDSs synchronized frequency solutions for different values of the mass \({\tilde{\mu }}_1\). In the right panel, the red, green, and blue curves represent the rotation curves of the ground state, first excited state, and second excited state Dirac stars, respectively. The synchronized frequency of all solutions in the figure is \({\tilde{\omega }} = 0.92\). By observing the left panel, we can find that when the excited state Dirac field mass \({\tilde{\mu }}_1 = 0.964\), the rotation curve of the MSDSs does not decrease significantly after reaching its peak velocity. Instead, it exhibits a relatively flat region with slight oscillations. If we increase the mass \({\tilde{\mu }}_1\), the oscillation amplitude of the curve will increase, resembling the green curve in the right panel (first excited state Dirac star). Conversely, it will resemble the red curve in the right panel (ground state Dirac star) as the mass \({\tilde{\mu }}_1\) decreases.

5 Conclusion

In this paper, we investigate the Einstein–Dirac system and construct spherically symmetric multistate Dirac stars, where two coexisting states of the Dirac field are present. We discuss the field functions, ADM mass, and binding energy of the solutions for the multistate Dirac star under synchronized and nonsynchronized frequency conditions. Additionally, we analyze the feasibility of considering the multistate Dirac star as a candidate for dark matter halos.

In the case of synchronized frequency, we explore different solutions for the MSDSs by varying the ratio of masses between the ground state and excited state Dirac fields (\(\mu _0/\mu _1\)). Based on the number of solution branches, we classify the obtained numerical results into single-branch solutions and double-branch solutions. For single-branch solutions, the peak values of the ground state and excited state Dirac field functions exhibit monotonic behavior as the synchronized frequency changes. The ADM mass monotonically decreases with increasing synchronized frequency, and at the minimum and maximum synchronized frequencies, the MSDSs degenerate into the first excited state Dirac stars and the ground state Dirac stars, respectively. For double-branch solutions, as the synchronized frequency varies, the excited state Dirac field functions persist, while the ground state field functions disappear at the minimum synchronized frequency on both branches, resulting in the degeneration of the MSDSs into the first excited state Dirac stars. As the mass of the ground state field decreases, the range of synchronized frequency values on the two branches of the double-branch solution gradually diminishes.

Then, for the case of nonsynchronized frequency, we set the ratio of masses between the ground state and excited state Dirac fields as \(\mu _0/\mu _1 = 1\) and obtain different solutions by varying the frequency of the ground state Dirac field. Similar to the synchronized frequency case, the nonsynchronized frequency solutions of the MSDSs can also be classified into single-branch solutions and double-branch solutions. For single-branch solutions, the variations of the ground state and excited state field functions with respect to the frequency of the excited state Dirac field exhibit monotonic behavior. The ADM mass decreases as the frequency of the excited state field increases, with its minimum value depending on the frequency of the ground state Dirac field. For double-branch solutions, as the frequency of the ground state field decreases, the minimum ADM mass of the MSDSs gradually increases, the range of nonsynchronized frequency values on the two branches diminishes, and the MSDSs degenerate into the first excited state Dirac stars when the nonsynchronized frequency becomes sufficiently small.

Subsequently, we computed the binding energy of various solutions for the MSDSs. For synchronized frequency solutions, stable solutions only exist in the single-branch solutions, and when \(1/{\overline{\mu }}_0\) is sufficiently small, all stable solutions within the single-branch solutions vanish. For nonsynchronized frequency solutions, stable solutions exist in both single-branch and double-branch solutions. However, the double-branch solutions become unstable when the frequency of the ground state field reaches a sufficiently low value, whereas the single-branch solutions maintain stable solutions for any frequency of the ground state field. In the subsequent analysis, we have deliberated upon the MSDSs under the imposition of the single particle condition. Our findings suggest that the ratio of the mass of MSDSs to the mass of the Dirac spinor field is approximately twice that of the Dirac stars. Introducing additional spinor fields into the system is anticipated to further augment this ratio, potentially qualifying MSDSs as candidates for star-like objects.

Finally, we computed the rotation curves of the MSDSs. It has been observed that the rotation curves of MSDSs containing excited state matter fields exhibit a nearly flat region near the velocity peak, resembling the shape of rotation curves of multi-state boson stars discussed in [50]. In future work, we plan to construct MSDSs with a greater number of matter field nodes. Perhaps the rotational curves of models with a higher number of nodes can provide a closer fit to the observed data [54].