1 Introduction

Investigations of the S-matrix over the past decade have revealed deep connections among amplitudes of various different theories, which are invisible upon inspecting traditional Feynman rules. For instance, tree-level gravitational (GR) and Yang–Mills (YM) amplitudes are related by the so-called Kawai–Lewellen–Tye (KLT) relation [1] and Bern–Carrasco–Johansson (BCJ) color–kinematics duality [2,3,4,5]. In the well-known Cachazo–He–Yuan (CHY) formalism [6,7,8,9,10], tree amplitudes for a large variety of theories can be generated from tree GR amplitudes through compactification, squeezing, and generalized dimensional reduction procedures. Similar unifying relations were proposed by introducing appropriate differential operators, which transmute tree GR amplitudes to others [11,12,13]. At the same time, another type of relation that has attracted attention is the expansion of amplitudes, where tree amplitudes of one theory can be expanded to tree amplitudes of other theories [14,15,16,17,18,19,20]. Indeed, the expansions serve as the dual picture of differential operators, as interpreted in [20]. In the dual web, tree amplitudes for a wide range of theories can be expanded to tree bi-adjoint scalar (BAS) amplitudes.

In this note, we focus on the expansion of the tree single-trace Yang–Mills-scalar (YMS) amplitudes [3, 21,22,23,24,25,26], due to the special role of these amplitudes. Both tree YM and BAS amplitudes can be regarded as special cases of tree single-trace YMS amplitudes. When performing the squeezing procedure iteratively the CHY framework, or acting differential operators, the YM amplitudes are transmuted to single-trace YMS amplitudes, then end with pure BAS ones. These connections can be directly extended to tree GR amplitudes, tree YM amplitudes, and single-trace tree EYM amplitudes [8,9,10, 12, 13]. Furthermore, single-trace tree YMS amplitudes exhibit double-copy structure and color–kinematics duality in an elegant manner [3, 8,9,10, 23, 27]. The single-trace YMS amplitudes which describe the scattering of massless gluons and scalars can be expanded to YMS ones with fewer external gluons and more external scalars [14,15,16,17,18, 28]. Such recursive expansion can be performed iteratively, ending with the expansion to pure BAS amplitudes.

In the recursive expansion given in [14, 15, 18], a fiducial external gluon is required. This special gluon breaks the manifest permutation symmetry among external gluons: if one re-chooses the fiducial gluon, we expect that the new expansion is equivalent to the old one, but such equivalence is hard to prove. Another disadvantage of the expansion in [14, 15, 18] is related to the gauge invariance. Here, the gauge invariance for the polarization vector carried by the fiducial gluon is obscure, that is, if one replaces the polarization with the corresponding momentum, the vanishing of amplitude is not manifest. Suppose one uses this expansion iteratively to expand the YMS amplitude to BAS amplitudes. In the resulting expansion, none of polarizations has the manifest gauge invariance, since each external gluon will play the role of the fiducial gluon once in the iterative process. As is well known, the gauge invariance plays a crucial role in the modern S-matrix program, and always hints at a new understanding and new mathematical structure for scattering amplitudes. For instance, tree amplitudes in general relativity and Yang–Mills theory are found to be completely determined by gauge invariance and singularity structures [29, 30]. Another well-known example is that the Britto–Cachazo–Feng–Witten (BCFW) on-shell recursion relation expresses YM amplitudes in gauge-invariant formulas which include spurious poles [31, 32]. These new formulas motivated elegant new constructions of amplitudes, such as Grassmannian representation and amplituhedron [33,34,35]. These experiences force us to seek the new expansion with the explicit gauge invariance. After expanding to BAS amplitudes, the BAS basis contributes only poles, so the gauge invariance for each polarization is completely determined by coefficients. Thus, it is natural to expect a formula of coefficients which manifests the gauge invariance. The above consideration leads to an important question: how to achieve new expansions which have manifest permutation symmetry among external gluons and gauge invariance for each polarization.

Such new expansion was first found by Clifford Cheung and James Mangan in [27] via the so-called covariant color–kinematics duality method. The approach in [27] is based on the traditional Lagrangian and equations of motion. The very premise of the modern S-matrix program is to bootstrap scattering amplitudes without the aid of an action or equation of motion (for reviews see [36, 37]). Thus, it is natural to ask whether the new expansion in [27] can be obtained through bottom-up construction which uses only on-shell information. This question is the main motivation for the current short note.

Herein, we reconstruct the expansion in [27] from a totally different perspective based on universal soft behaviors of massless particles. We first bootstrap the lowest three-point tree single-trace YMS amplitudes with only one external gluon, by imposing general principles including the appropriate mass dimension and Lorentz invariance. Then, we invert the soft theorem for external scalars to construct the expanded single-trace YMS amplitudes with more external scalars while keeping the number of external gluons unaltered. After such construction, we use the well-known BCJ relation [2,3,4,5] to convert the resulting expansion into the new formula which manifests the gauge invariance. Next, we invert the sub-leading soft theorem for external gluons to construct the expanded single-trace YMS amplitudes with more external gluons. Such procedure inserts external gluons into the lower-point amplitude in a manifestly gauge-invariant pattern; thus the explicit gauge invariance will be kept if the starting point is expressed in a gauge-invariant form. The manifest permutation symmetry among external gluons is also kept at each step.

The remainder of this note is organized as follows. In Sect. 2, we briefly introduce the necessary background including the expansions of tree massless amplitudes to BAS amplitudes, the recursive expansion of single-trace YMS amplitudes, and soft theorems for external scalars and gluons. In Sect. 3, we construct the expansion in [27] by using our recursive method based on inverting soft theorems. Then, we end with a brief summary in Sect. 4.

2 Background

For the reader’s convenience, in this section we provide a brief review of the necessary background. In Sect. 2.1, we introduce the tree-level amplitudes of BAS theory, as well as expansions of tree amplitudes to BAS amplitudes. In Sect. 2.2, we discuss the recursive expansion of YMS amplitudes. In Sect. 2.3, we review the soft theorems for external scalars and gluons.

2.1 Expanding tree-level amplitudes to BAS basis

The BAS theory describes the massless BAS fields \(\phi ^{Aa}\) with cubic interaction. The Lagrangian is given as

$$\begin{aligned} {{\mathcal {L}}}_\textrm{BAS}={1\over 2}\,\partial _\mu \phi ^{Aa}\,\partial ^{\mu }\phi ^{Aa}+{\lambda \over 3!}\,F^{ABC}f^{abc}\, \phi ^{Aa}\phi ^{Bb}\phi ^{Cc}, \end{aligned}$$
(1)

where the structure constant \(F^{ABC}\) and generator \(T^A\) satisfy

$$\begin{aligned}{}[T^A,T^B]=iF^{ABC}T^C, \end{aligned}$$
(2)

and the dual algebra encoded by \(f^{abc}\) and \(T^{a}\) is analogous.

Tree amplitudes of this theory contain only propagators for massless scalars. Decomposing the group factors via the standard procedure gives

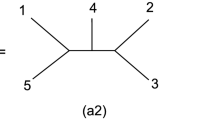
$$\begin{aligned} {{\mathcal {A}}}_n{} & {} =\sum _{\sigma \in {{\mathcal {S}}}_n}\,\sum _{\widetilde{\sigma }_n\in \widetilde{\mathcal{S}}_n}\,\textrm{Tr}[T^{A_{\sigma _1}},\ldots T^{A_{\sigma _n}}]\nonumber \\{} & {} \quad \times \textrm{Tr}[T^{a_{\widetilde{\sigma }_1}}\ldots T^{a_{\widetilde{\sigma }_n}}]\,\mathcal{A}_{S}(\sigma _1,\ldots ,\sigma _n|\widetilde{\sigma }_1,\ldots ,\widetilde{\sigma }_n), \end{aligned}$$
(3)

where \({{\mathcal {A}}}_n\) denotes the kinematic part of n-point amplitude in which the coupling constants are dropped, and \({{\mathcal {S}}}_n\) and \(\widetilde{{\mathcal {S}}}_n\) are non-cyclic permutations of external legs. In this note, partial amplitudes \(\mathcal{A}_{S}(\sigma _1,\ldots ,\sigma _n|\widetilde{\sigma }_1,\ldots ,\widetilde{\sigma }_n)\) play a crucial role when considering expansions of amplitudes. Each partial amplitude is simultaneously planar with respect to two color orderings \((\sigma _1,\ldots ,\sigma _n)\) and \((\widetilde{\sigma }_1,\ldots ,\widetilde{\sigma }_n)\). In other words, it is double-color-ordered. Let us take the five-point amplitude \({{\mathcal {A}}}_\textrm{S}(1,2,3,4,5|1,4,2,3,5)\) as an example. In Fig. 1, the first diagram is allowed by both orderings (1, 2, 3, 4, 5) and (1, 4, 2, 3, 5), while the second one violates the ordering (1, 4, 2, 3, 5). Other diagrams which satisfy the ordering (1, 2, 3, 4, 5) are also forbidden by the ordering (1, 4, 2, 3, 5); thus the first diagram in Fig. 1 is the only candidate for the amplitude \({{\mathcal {A}}}_{\textrm{S}}(1,2,3,4,5|1,4,2,3,5)\). Then the amplitude \({{\mathcal {A}}}_{\textrm{S}}(1,2,3,4,5|1,4,2,3,5)\) can be evaluated as

$$\begin{aligned} {{\mathcal {A}}}_{\textrm{S}}(1,2,3,4,5|1,4,2,3,5)={1\over s_{23}}{1\over s_{51}}, \end{aligned}$$
(4)

up to an overall sign. The Mandelstam variable \(s_{i\ldots j}\) is defined as

$$\begin{aligned} s_{i\ldots j}\equiv k_{i\ldots j}^2,~~~~k_{i\ldots j}\equiv \sum _{a=i}^j\,k_a,~~~~ \end{aligned}$$
(5)

where \(k_a\) is the momentum carried by the external leg a.

Fig. 1
figure 1

Two five-point diagrams

Full size image

Each double-color-ordered partial BAS amplitude carries an overall ± sign, arising from swapping two lines at the common vertex, due to the anti-symmetry of structure constants \(F^{ABC}\) and \(f^{abc}\). In this note, we choose the convention that the overall sign is \(+\) if two orderings carried by the BAS amplitude are the same. For instance, the amplitude \({{\mathcal {A}}}_{\textrm{S}}(1,2,3,4|1,2,3,4)\) carries the overall sign \(+\) under the above convention. Note that this convention is different from that in [8]. The overall signs for other BAS amplitudes with general orderings can be determined by counting the number of flippings [8].

The double-color-ordered partial amplitudes can be systematically evaluated by applying the diagrammatic rules proposed by Cachazo, He and Yuan in [8]. We do not introduce this method in this note, but the reader can see this interesting and useful approach in [8].

Any tree-level amplitudes for massless particles and cubic interactions can be expanded to double-color-ordered partial BAS amplitudes, since each associated topology of Feynman diagrams can be included in at least one partial BAS amplitude. For higher-point vertices, one can transmute them to cubic ones by simultaneously inserting the propagator 1/D and the numerator D, as shown in Fig. 2. This manipulation expands any tree amplitude to tree Feynman diagrams with only cubic vertices. Since each Feynman diagram contributes propagators which can be provided by partial BAS amplitudes, accompanied by a numerator, one can conclude that each tree amplitude for massless particles can be expanded to double-color-ordered partial BAS amplitudes. In such expansions, coefficients are polynomials dependent on Lorentz invariants created by external kinematic variables, without any pole.

Fig. 2
figure 2

Turning the four-point vertex to three-point ones. The bold line corresponds to the inserted propagator 1/D. This manipulation turns the original numerator N to DN

Full size image

The expansion requires appropriate basis. Such basis can be determined by employing the well-known Kleiss–Kuijf (KK) relation [38]

(6)

where \(\vec {\pmb {{\alpha }}}\) and \(\vec {\pmb {{\beta }}}\) are two ordered subsets of external scalars, and \(|\pmb {{\beta }}|\) stands for the number of elements included in \(\vec {\pmb {{\beta }}}\). The ordered set \(\vec {\pmb {{\beta }}}^T\) is the inversion of \(\vec {\pmb {{\beta }}}\). For example, \(\vec {\pmb {{\beta }}}^T=\{3,2,1\}\) if \(\vec {\pmb {{\beta }}}=\{1,2,3\}\). The n-point BAS amplitude \({{\mathcal {A}}}_\textrm{S}(1,\vec {\pmb {{\alpha }}},n,\vec {\pmb {{\beta }}}|\sigma _n)\) at the l.h.s of (6) carries two orderings, which are encoded by \((1,\vec {\pmb {{\alpha }}},n,\vec {\pmb {{\beta }}})\) and \(\sigma _n\), respectively. The symbol means summing over all possible shuffles of two ordered sets \(\vec {\pmb {\gamma }}_1\) and \(\vec {\pmb {\gamma }}_2\), i.e., all permutations in the set \(\vec {\pmb {\gamma }}_1\cup \vec {\pmb {\gamma }}_2\), while preserving the orderings of \(\vec {\pmb {\gamma }}_1\) and \(\vec {\pmb {\gamma }}_2\). For instance, suppose \(\vec {\pmb {\gamma }}_1=\{1,2\}\) and \(\vec {\pmb {\gamma }}_2=\{3,4\}\); then

(7)

The analogous KK relation holds for another ordering \(\sigma _n\). The KK relation among partial BAS amplitudes implies that the basis can be chosen as amplitudes \({{\mathcal {A}}}_\textrm{S}(1,\sigma _1,n|1,\sigma _2,n)\), with legs 1 and n fixed at two ends in each ordering. Such basis is called the KK BAS basis. Consequently, any tree amplitude for massless particles can be expanded to this basis. The basis provides poles, while the coefficients contribute numerators.

The double-color-ordered partial BAS amplitudes also satisfy the well-known BCJ relations [2,3,4,5]. Here we give the explicit formula of the fundamental BCJ relation,

(8)

since it will be used subsequently. The combinatorial momentum \(Y_s\) is defined as the summation of external momenta carried by legs at the l.h.s of s in the ordering , and the ordering \(\sigma _{n+1}\) is defined for \(n+1\) legs in \(\{1,\ldots ,n\}\cup s\). BCJ relations imply the linear dependence of BAS amplitudes in the KK basis; thus, the so-called BCJ basis can be chosen as BAS amplitudes with three legs fixed in color orderings. However, in BCJ relations, coefficients of BAS amplitudes depend on Mandelstam variables, and this characteristic leads to poles in coefficients when expanding amplitudes to the BCJ basis. On the other hand, when expanding to the KK basis, coefficients contain no poles. In this note, we choose the KK basis since we expect that all poles are included in the basis, and coefficients only contribute numerators.

2.2 Recursive expansion of single-trace YMS amplitudes

The YMS theory under consideration is the massless \(\textrm{YM}\oplus \textrm{BAS}\) theory with Lagrangian [23]

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{YM}\oplus \textrm{BAS}}{} & {} =-{1\over 4}\,F^{a}_{\mu \nu }\,F^{a\mu \nu }+{1\over 2}\,D_\mu \phi ^{Aa}\,D^{\mu }\phi ^{Aa}\nonumber \\{} & {} \quad -{g^2\over 4}\,f^{abe}\,f^{ecd}\,\phi ^{Aa}\phi ^{Bb}\phi ^{Ac}\phi ^{Bd}\nonumber \\{} & {} \quad +{\lambda \over 3!}\,F^{ABC}f^{abc}\, \phi ^{Aa}\phi ^{Bb}\phi ^{Cc}.~~ \end{aligned}$$
(9)

The indices a, b, c and d run over the adjoint representation of the gauge group. Scalar fields carry additional flavor indices A, B, C. The field strength and covariant derivative are defined in the usual way

$$\begin{aligned}{} & {} F^{a}_{\mu \nu }=\partial _\mu \,A^a_\nu -\partial _\nu \,A^a_\mu +g\,f^{abc}\,A^b_\mu A^c_\nu ,\nonumber \\{} & {} D_\mu \phi ^{Aa}=\partial _\mu \phi ^{Aa}+g\,f^{abc}\,A^b_\mu \phi ^{Ac}. \end{aligned}$$
(10)

The general tree amplitude of this theory includes both massless external scalars and massless external gluons. Through the standard technique, one can decompose the gauge group factors to obtain

$$\begin{aligned} {{\mathcal {A}}}_{n+m}=\sum _{\sigma \in {{\mathcal {S}}}_{n+m}}\,\textrm{Tr}[T^{a_{\sigma _1}}\ldots T^{a_{\sigma _{n+m}}}]\,\mathcal{A}_{n+m,1}(\sigma _1,\ldots ,\sigma _{n+m}),~~\nonumber \\ \end{aligned}$$
(11)

where \({{\mathcal {S}}}_{n+m}\) denotes non-cyclic permutations among n external scalars and m external gluons, and \(T^{a_{\sigma _i}}\) encodes generators of the gauge group. Here, \({{\mathcal {A}}}_{n+m}\) is the kinematic part of the amplitude without coupling constants. Meanwhile, decomposition of the flavor group factors leads to a structure of tree amplitudes which is similar to that of loop amplitudes, in that, unlike pure gauge theories, it is not restricted to having only single-trace terms [3, 23]:

$$\begin{aligned} {{\mathcal {A}}}_{n+m}{} & {} =\sum _{\sigma \in {{\mathcal {S}}}_n}\,\textrm{Tr}[T^{A_{\sigma _1}}\ldots T^{A_{\sigma _m}}]\,\mathcal{A}_{n+m,1}(\sigma _1,\ldots ,\sigma _n)\nonumber \\{} & {} \quad +\sum _{n_1+n_2=n}\,\sum _{{\alpha }\in {{\mathcal {S}}}_{n_1}}\,\sum _{{\beta }\in \mathcal{S}_{n_2}}\,\textrm{Tr}[T^{A_{{\alpha }_1}}\ldots T^{A_{{\alpha }_{n_1}}}]\nonumber \\{} & {} \quad \times \textrm{Tr}[T^{A_{{\beta }_1}}\ldots T^{A_{{\beta }_{n_2}}}]\,\mathcal{A}_{n+m,2}({\alpha }_1,\ldots ,{\alpha }_{n_1}|{\beta }_1,\ldots ,{\beta }_{n_2})\nonumber \\{} & {} \quad +\cdots ,~~ \end{aligned}$$
(12)

where \({{\mathcal {S}}}_{n_i}\) again stands for the set of non-cyclic permutations. The single-trace and double-trace terms are collected in the first and second lines, respectively, and \(\cdots \) in the third line denotes the remaining multi-trace terms. External scalars for the partial amplitudes \(\mathcal{A}_{n+m,2}({\alpha }_1,\ldots ,{\alpha }_{n_1}|{\beta }_1,\ldots ,{\beta }_{n_2})\) in the second line are grouped into two orderings which are \(({\alpha }_1,\ldots ,{\alpha }_{n_1})\) and \(({\beta }_1,\ldots ,{\beta }_{n_2})\). Analogously, partial amplitudes in multi-trace terms in the third line include more orderings among external scalars.

In this note, we focus on single-trace partial tree amplitudes \({{\mathcal {A}}}_{n+m,1}(\sigma _1,\ldots ,\sigma _n)\) in the first line of (12), for the following reasons. First, there are special connections between tree YM amplitudes, tree BAS amplitudes and single-trace tree YMS amplitudes [8, 10]. These relations can be extended to tree GR amplitudes, tree YM amplitudes, and single-trace tree EYM amplitudes, via the well-known double-copy structure [8,9,10, 12, 13]. Secondly, single-trace tree YMS amplitudes play a crucial role when studying color–kinematics duality [3, 8,9,10, 23, 27]. By definition, the single-trace YMS amplitudes under consideration are partial amplitudes \({{\mathcal {A}}}_\textrm{YS}(\sigma _n;\{p_i\}_m|\sigma _{n+m})\), obtained by decomposing flavor and gauge group factors simultaneously. Here, the color ordering in (11) among all external legs is denoted as \(\sigma _{n+m}\), while the flavor ordering among external scalars for single-trace terms in the first line in (12) is labeled as \(\sigma _n\). The unordered set of m external gluons is denoted by \(\{p_i\}_m\equiv \{p_1,\ldots ,p_m\}\). In other words, gluons belong to only one ordering \(\sigma _{n+m}\). Note that the single-trace sector of YMS theory is equivalent to dropping the \(\phi ^4\) terms in the Lagrangian (9), see in [3, 23, 27].

The discussion for expansions of tree-level amplitudes in the previous Sect. 2.1 indicates that the single-trace tree YMS amplitude \({{\mathcal {A}}}_\textrm{YS}(1,\ldots ,n;\{p_i\}_m|1,\sigma _{n+m-2},n)\) can be expanded to the KK BAS basis as

$$\begin{aligned}{} & {} {{\mathcal {A}}}_\textrm{YS}(1,\ldots ,n;\{p_i\}_m|1,\sigma _{n+m-2},n)\nonumber \\{} & {} \quad =\sum _{\widetilde{\sigma }_{n+m-2}}\,\mathcal{C}(\widetilde{\sigma }_{n+m-2},\epsilon _i,k_j)\,{{\mathcal {A}}}_\textrm{S}(1,\widetilde{\sigma }_{n+m-2},n|1,\sigma _{n+m-2},n),~~~\nonumber \\ \end{aligned}$$
(13)

where \(\sigma _{n+m-2}\) and \(\widetilde{\sigma }_{n+m-2}\) denote orderings among external legs in \(\{2,\ldots ,n-1\}\cup \{p_i\}_m\). The double-copy structure [1,2,3,4,5, 8] indicates that the coefficient \(\mathcal{C}(\widetilde{\sigma }_{n+m-2},\epsilon _i,k_j)\) depends on polarization vectors \(\epsilon _i\) carried by external gluons, momenta \(k_i\) carried by either gluons or scalars, and orderings \(\widetilde{\sigma }_{n+m-2}\), but is independent of the ordering \(\sigma _{n+m-2}\).Footnote 1 The independence of the ordering \(\sigma _{n+m-2}\) leads to the more general ansatz

$$\begin{aligned}{} & {} {{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m})\nonumber \\{} & {} =\sum _{\widetilde{\sigma }_{n+m-2}}\,\mathcal{C}(\widetilde{\sigma }_{n+m-2},\epsilon _i,k_j)\,{{\mathcal {A}}}_\textrm{S}(1,\widetilde{\sigma }_{n+m-2},n|\sigma _{n+m}),~~~ \end{aligned}$$
(14)

where \(\sigma _{n+m}\) stands for the general ordering among all external legs, without fixing any one at any particular position.

The expansion in (14) can be achieved by iteratively applying the following recursive expansion [14, 15, 18],

(15)

where p is the fiducial gluon which can be chosen as any element in \(\{p_i\}_m\), and \(\pmb {{\alpha }}\) are subsets of \(\{p_i\}_m{\setminus } p\) which are allowed to be empty. When \(\pmb {{\alpha }}=\{p_i\}_m{\setminus } p\), the YMS amplitudes in the second line of (15) are reduced to pure BAS amplitudes. The ordered set \(\vec {\pmb {{\alpha }}}\) is generated from \(\pmb {{\alpha }}\) by giving an order among elements in \(\pmb {{\alpha }}\). The tensor \(F^{\mu \nu }_{\vec {\pmb {{\alpha }}}}\) is defined as

$$\begin{aligned} F^{\mu \nu }_{\vec {\pmb {{\alpha }}}}\equiv \big (f_{{\alpha }_k}\cdot f_{{\alpha }_{k-1}}\ldots f_{{\alpha }_2}\cdot f_{{\alpha }_1}\big )^{\mu \nu }, \end{aligned}$$
(16)

for \(\vec {\pmb {{\alpha }}}=\{{\alpha }_1,\ldots {\alpha }_k\}\), where each anti-symmetric strength tensor \(f_i\) is given as \(f^{\mu \nu }_i\equiv k^\mu _i\epsilon ^\nu _i-\epsilon ^\mu _i k^\nu _i\). The combinatorial momentum \(Y_{\vec {\pmb {{\alpha }}}}\) is the summation of momenta carried by external scalars at the l.h.s of \({\alpha }_1\) in the color ordering , where \({\alpha }_1\) is the first element in the ordered set \(\vec {\pmb {{\alpha }}}\). The symbol means summing over permutations of \(\{2,\ldots ,n-1\}\cup \{\vec {\pmb {{\alpha }}},p\}\) which preserve the orderings of two ordered sets \(\{2,\ldots ,n-1\}\) and \(\{\vec {\pmb {{\alpha }}},p\}\), as explained around (7). The summation in (15) is over all inequivalent ordered sets \(\vec {\pmb {{\alpha }}}\). In the recursive expansion (15), the YMS amplitude is expanded to YMS amplitudes with fewer gluons and more scalars. Repeating such expansion, one can finally expand any YMS amplitude to pure BAS amplitudes.

In the recursive expansion (15), the gauge invariance for each gluon in \(\{p_i\}_m{\setminus } p\) is manifest, since the tensor \(f^{\mu \nu }\) vanishes automatically under the replacement \(\epsilon _i\rightarrow k_i\). However, the gauge invariance for the fiducial gluon p has not been manifested. When applying (15) iteratively, a fiducial gluon will be required at each step. Consequently, in the resulting expansion to pure BAS amplitudes, the gauge invariance for each polarization will be spoiled. Furthermore, the manifest permutation invariance among external gluons is also broken. Note that the breaking of manifest permutation invariance among external scalars cannot be avoided, since the KK basis requires fixing two legs at two special positions in orderings. However, a special external gluon is not necessary. To obtain the expansion which manifests the gauge invariance and permutation invariance for external gluons simultaneously, one should employ another recursive expansion

(17)

where \(k_r\) is a reference massless momentum. Here, the notations are parallel to those for (15). The formula (17) is equivalent to that found by Clifford Cheung and James Mangan, in the so-called covariant color–kinematics duality framework [27]. This new expansion does not require any fiducial gluon, the gauge invariance for any polarization and the permutation symmetry among external gluons are manifested. Using (17) iteratively, one finally obtains the new expansion of YMS amplitudes to the KK BAS basis, with explicit gauge and permutation invariance for gluons. Reconstructing the expansion (17) through the bottom-up method is the main purpose of this note.

2.3 Soft theorems for external scalars and gluons

In this subsection, we briefly review the soft theorems for external scalars and gluons, which are basic tools for subsequent constructions in the next section.

For the double-color-ordered BAS amplitude \({{\mathcal {A}}}_\textrm{S}(1,\ldots ,n|\sigma _n)\), we rescale \(k_i\) as \(k_i\rightarrow \tau k_i\), and expand the amplitude by \(\tau \). The leading order contribution arises from propagators \(1/s_{1(i+1)}\) and \(1/ s_{(i-1)i}\), which are at the \(\tau ^{-1}\) order,

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(0)_i}_{\textrm{S}}(1,\ldots ,n|\sigma _n)={1\over \tau }\Bigg ({\delta _{i(i+1)}\over s_{i(i+1)}}+{\delta _{(i-1)i}\over s_{(i-1)i}}\Bigg )\,\nonumber \\{} & {} \qquad \times {{\mathcal {A}}}_{\textrm{S}}(1,\ldots ,i-1,\not {i},i+1,\ldots ,n|\sigma _n{\setminus } i)\nonumber \\{} & {} \quad =S^{(0)_i}_s\,{{\mathcal {A}}}_\textrm{S}(1,\ldots ,i-1,\not {i},i+1,\ldots ,n|\sigma _n{\setminus } i),~~~ \end{aligned}$$
(18)

where \(\not {i}\) means removing the leg i, and \(\sigma _n{\setminus } i\) stands for the color ordering generated from \(\sigma _n\) by eliminating i. The superscript \((0)_i\) is introduced for denoting the leading-order contribution when considering the soft behavior of \(k_i\). The symbol \(\delta _{ab}\) is defined as followsFootnote 2 [28]. In an ordering, if two legs a and b are adjacent, then \(\delta _{ab}=1\) if a precedes b, and \(\delta _{ab}=-1\) if a follows b. If a and b are not adjacent, \(\delta _{ab}=0\). From this definition, it is straightforward to observe that \(\delta _{ab}=-\delta _{ba}\). In (18), \(\delta _{i(i+1)}\) and \(\delta _{(i-1)i}\) are defined for the ordering \(\sigma _n\), and the leading soft operator \(S^{(0)_i}_s\) for the scalar i is given as

$$\begin{aligned} S^{(0)_i}_s={1\over \tau }\,\Bigg ({\delta _{i(i+1)}\over s_{i(i+1)}}+{\delta _{(i-1)i}\over s_{(i-1)i}}\Bigg ).~~~~ \end{aligned}$$
(19)

The term “soft” means taking the limit \(\tau \rightarrow 0\). In such limit, we have \(\sum _{j\ne i}k_j\rightarrow 0\). In other words, external momenta carried by legs in \(\{1,\ldots ,n\}{\setminus } i\) satisfy the momentum conservation condition. Thus, on-shell amplitudes \(\mathcal{A}_{\textrm{S}}(1,\ldots ,i-1,\not {i},i+1,\ldots ,n|\sigma _n{{\setminus }} i)\) in (18) are well defined. By requiring the universality of soft behavior, the above result can be generalized to YMS amplitudes as [28]

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(0)_i}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m}) =S^{(0)_i}_s\,\nonumber \\{} & {} {{\mathcal {A}}}_\textrm{YS}(1,\ldots ,i-1,\not {i},i+1,\ldots ,n;\{p_i\}_m|\sigma _{n+m}{\setminus } i),~~~ \end{aligned}$$
(20)

where the soft factor \(S^{(0)_i}_s\) is the same as in (19). This means that the soft operator \(S^{(0)_i}_s\) does not act on any external gluon.

The soft theorems for external gluons at leading and sub-leading orders can be obtained by various approaches [39, 40].One of these methods is to use the expanded formula of YMS amplitude in (15), as can be seen in [28]. Such soft theorems are

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(0)_{p_j}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m}) \nonumber \\{} & {} \quad =S^{(0)_{p_j}}_g\,{{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m{\setminus } p_j|\sigma _{n+m}{\setminus } p_j),~~~ \end{aligned}$$
(21)

and

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(1)_{p_j}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m}) \nonumber \\{} & {} \quad =S^{(1)_{p_j}}_g\,{{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m{\setminus } p_j|\sigma _{n+m}{\setminus } p_i),~~~ \end{aligned}$$
(22)

where the external momentum \(k_{p_j}\) is rescaled as \(k_{p_j}\rightarrow \tau k_{p_j}\). The soft factors at leading and sub-leading orders are given as

$$\begin{aligned} S^{(0)_{p_j}}_g={1\over \tau }\,\sum _{a\in \{1,\ldots ,n\}\cup \{p_i\}_m{\setminus } p_j}\,{\delta _{ap_j}\,(\epsilon _{p_j}\cdot k_a)\over s_{ap_j}},~~ \end{aligned}$$
(23)

and

$$\begin{aligned} S^{(1)_{p_j}}_g=\sum _{a\in \{1,\ldots ,n\}\cup \{p_i\}_m{\setminus } p_j}\,{\delta _{ap_j}\,\big (\epsilon _{p_j}\cdot J_a\cdot k_{p_j}\big )\over s_{ap_j}},~~ \end{aligned}$$
(24)

respectively. In (23) and (24), one should sum over all external legs a; i.e., these soft operators for external gluons act on both external scalars and gluons.

The sub-leading soft operator (24) for external gluons plays a central role in the next section. Here we list some useful results for the action of this operator. The angular momentum operator \(J_a^{\mu \nu }\) acts on the Lorentz vector \(k^\rho _a\) with the orbital part of the generator, and on \(\epsilon ^\rho _a\) with the spin part of the generator in the vector representation

$$\begin{aligned} J_a^{\mu \nu }\,k_a^\rho =k_a^{[\mu }\,{\partial k_a^\rho \over \partial k_{a,\nu ]}},~~~~ J_a^{\mu \nu }\,\epsilon _a^\rho =\big (\eta ^{\nu \rho }\,\delta ^\mu _\sigma -\eta ^{\mu \rho }\,\delta ^\nu _\sigma \big )\,\epsilon ^\sigma _a. \nonumber \\ \end{aligned}$$
(25)

Then the action of \(S^{(1)_p}_g\) can be re-expressed as

$$\begin{aligned} S^{(1)_p}_g= & {} -\sum _{V_a}\,{\delta _{ap}\over s_{ap}}\,V_a\cdot f_p\cdot {\partial \over \partial V_a},~~ \end{aligned}$$
(26)

due to the observation that the amplitude is linear in each polarization vector. In (26), the summation over \(V_a\) is among all Lorentz vectors including both momenta and polarizations. The operator (26) is a differential operator which satisfies the Leibniz rule. Using (26), we immediately obtain

$$\begin{aligned}{} & {} \big (S^{(1)_p}_g\,k_a\big )\cdot V=-{\delta _{ap}\over s_{ap}}\,(k_a\cdot f_p\cdot V),\nonumber \\{} & {} ~~~~\big (S^{(1)_p}_g\,\epsilon _a\big )\cdot V=-{\delta _{ap}\over s_{ap}}\,(\epsilon _a\cdot f_p\cdot V),~~~~ \end{aligned}$$
(27)

where V is an arbitrary Lorentz vector, and

$$\begin{aligned} V_1\cdot \big (S^{(1)_p}_g\,f_a\big )\cdot V_2={\delta _{ap}\over s_{ap}}\,V_1\cdot (f_p\cdot f_a-f_a\cdot f_p)\cdot V_2,~~~~\nonumber \\ \end{aligned}$$
(28)

for two arbitrary Lorentz vectors \(V_1\) and \(V_2\), where the anti-symmetric tensor \(f_i\) is defined as \(f_i^{\mu \nu }\equiv k_i^\mu \epsilon _i^\nu -\epsilon _i^\mu k_i^\nu \), as introduced previously.

3 Expansion of single-trace YMS amplitude

In this section, we study the expansion of single-trace tree YMS amplitudes. Our purpose is to reconstruct the expansion in (17) through a purely bottom-up approach. For simplicity, we will choose the reference momentum \(k_r\) in (17) as \(k_r=k_n\). We first bootstrap the three-point YMS amplitudes with only one external gluon. Then, we invert the soft theorem for BAS scalars to construct YMS amplitudes with more external scalars, while keeping the number of external gluons fixed. After this construction, we use the BCJ relation to transmute the resulting expansion of such special BAS amplitudes with only one external gluon to a manifestly gauge-invariant form. Next, we invert the sub-leading soft theorem for external gluons to obtain a recursive pattern which leads to the general expansion of single-trace YMS amplitudes with an arbitrary number of external gluons, which is manifestly gauge-invariant for any polarization. Through the whole process, the manifest permutation symmetry among external gluons is retained at each step.

3.1 YMS amplitude with one external gluon

In this subsection, we construct the single-trace YMS amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;p|\sigma _{n+1})\) which contains external scalars \(i\in \{1,\ldots ,n\}\) and only one external gluon p, using the purely bottom-up method. To start, we first bootstrap the three-point one \({{\mathcal {A}}}_{\textrm{YS}}(1,2;p|\sigma _3)\). In d-dimensional spacetime, any n-point amplitude has the mass dimension \(d-{d-2\over 2}n\); thus the three-point one has the mass dimension \(3-{d\over 2}\). On the other hand, the coupling constant g in Lagrangian (9) has mass dimension \(2-{d\over 2}\), and thus the kinematic part \({{\mathcal {A}}}_{\textrm{YS}}(1,2;p|\sigma _3)\) has mass dimension 1. Meanwhile, the amplitude \({{\mathcal {A}}}_\textrm{YS}(1,2;p|\sigma _3)\) with one external gluon p should be linear in \(\epsilon _p\), where \(\epsilon _p\) is the polarization vector carried by p. Finally, the three-point amplitude does not include any pole since it can never be factorized into lower-point amplitudes. The above constraints uniquely fix \({{\mathcal {A}}}_{\textrm{YS}}(1,2;p|\sigma _3)\) to be \(\epsilon _p\cdot k_1\), up to an overall sign.Footnote 3 Note that \(\epsilon _p\cdot k_2\) is equivalent to \(\epsilon _p\cdot k_1\), due to the momentum conservation and the on-shell condition \(\epsilon _p\cdot k_p=0\). Using the observation \({{\mathcal {A}}}_\textrm{S}(1,p,2|1,p,2)=1\), we arrive at the following expansion

$$\begin{aligned} {{\mathcal {A}}}_{\textrm{YS}}(1,2;p|\sigma _3)=(\epsilon _p\cdot k_1)\,\mathcal{A}_{\textrm{S}}(1,p,2|\sigma _3),~~ \end{aligned}$$
(29)

which coincides with the general ansatz in (14). Here the overall sign of \({{\mathcal {A}}}_{\textrm{YS}}(1,2;p|1,p,2)\) is chosen to be 1, which forces the overall sign of \({{\mathcal {A}}}_\textrm{YS}(1,2;p|2,p,1)\) to be \(-1\). Note that \(\sigma _3\) has only two inequivalent choices, which are (1, p, 2) and (2, p, 1), due to the cyclic symmetry of orderings.

Then we invert the leading soft theorem for external scalars in (18) and (19) to insert external scalars into \({{\mathcal {A}}}_{\textrm{YS}}(1,2;p|2,p,1)\). Consider the four-point amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,2,3;p|\sigma _4)\) with external scalars \(i\in \{1,2,3\}\) and external gluon p. The soft theorem in (18) and (19) indicates the following leading soft behavior when taking \(k_2\rightarrow \tau k_2\),

$$\begin{aligned}{} & {} {{\mathcal {A}}}_{\textrm{YS}}^{(0)_2}(1,2,3;p|\sigma _4)=S^{(0)_2}_s\,\mathcal{A}_{\textrm{YS}}^{(0)_2}(1,3;p|\sigma _4{\setminus }2)\nonumber \\{} & {} \quad =\Bigg ({\delta _{12}\over s_{12}}+{\delta _{23}\over s_{23}}\Bigg )\,\Bigg ((\epsilon _p\cdot k_1)\,{{\mathcal {A}}}_\textrm{S}(1,p,3|\sigma _4{\setminus }2)\Bigg )\nonumber \\{} & {} \quad =\Big ({\delta _{12}\over s_{12}}+{\delta _{2p}\over s_{2p}}+{\delta _{p2}\over s_{p2}}+{\delta _{23}\over s_{23}}\Big )\,\Bigg ((\epsilon _p\cdot k_1)\,{{\mathcal {A}}}_\textrm{S}(1,p,3|\sigma _4{\setminus }2)\Bigg )\nonumber \\{} & {} \quad =(\epsilon _p\cdot k_1)\,\Bigg ({{\mathcal {A}}}^{(0)_2}_\textrm{S}(1,2,p,3|\sigma _4)+{{\mathcal {A}}}^{(0)_2}_\textrm{S}(1,p,2,3|\sigma _4)\Bigg ),~~\nonumber \\ \end{aligned}$$
(30)

where the second equality uses the soft factor in (19) and the expansion (29) simultaneously, the third one uses the anti-symmetry of \(\delta _{ab}\), and the last one uses the inversion of the soft theorem in (18) and (19). The soft behavior in (30) implies that \({{\mathcal {A}}}_{\textrm{YS}}(1,2,3;p|\sigma _4)\) can be expanded as

$$\begin{aligned}{} & {} {{\mathcal {A}}}_{\textrm{YS}}(1,2,3;p|\sigma _4)=C(1,2,p,3)\,{{\mathcal {A}}}_\textrm{S}(1,2,p,3|\sigma _4)\nonumber \\{} & {} \quad +C(1,p,2,3)\,{{\mathcal {A}}}_{\textrm{S}}(1,p,2,3|\sigma _4), \end{aligned}$$
(31)

where coefficients C(1, 2, p, 3) and C(1, p, 2, 3) satisfy

$$\begin{aligned} C^{(0)_2}(1,2,p,3)=C^{(0)_2}(1,p,2,3)=\epsilon _p\cdot k_1.~~ \end{aligned}$$
(32)

The constraint (32) requires C(1, 2, p, 3) and C(1, p, 2, 3) to have the form

$$\begin{aligned} C(1,2,p,3){} & {} =\epsilon _p\cdot k_1+{\alpha }_1\,\epsilon _p\cdot k_2,\nonumber \\ C(1,p,2,3){} & {} =\epsilon _p\cdot k_1+{\alpha }_2\,\epsilon _p\cdot k_2. \end{aligned}$$
(33)

To determine \({\alpha }_1\) and \({\alpha }_2\), one can consider the leading soft behavior of \(k_1\rightarrow \tau k_1\) to obtain

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(0)_1}_{\textrm{YS}}(1,2,3;p|\sigma _4)=S^{(0)_1}_s\,\mathcal{A}_{\textrm{YS}}(2,3;p|\sigma _4{\setminus }1)\nonumber \\{} & {} \quad =\Bigg ({\delta _{31}\over s_{31}}+{\delta _{12}\over s_{12}}\Bigg )\,\Bigg ((\epsilon _p\cdot k_2)\,{{\mathcal {A}}}_\textrm{S}(2,p,3|\sigma _4{\setminus }1)\Bigg )\nonumber \\{} & {} \quad =-\Bigg ({\delta _{21}\over s_{21}}+{\delta _{1p}\over s_{1p}}+{\delta _{p1}\over s_{1p}}+{\delta _{13}\over s_{13}}\Bigg )\,\Bigg ((\epsilon _p\cdot k_2)\,{{\mathcal {A}}}_\textrm{S}(2,p,3|\sigma _4{\setminus }1)\Bigg )\nonumber \\{} & {} \quad =-(\epsilon _p\cdot k_2)\,\Bigg ({{\mathcal {A}}}^{(0)_1}_\textrm{S}(2,1,p,3|\sigma _4{\setminus }1)+{{\mathcal {A}}}^{(0)_1}_\textrm{S}(2,p,1,3|\sigma _4{\setminus }1)\Bigg )\nonumber \\{} & {} \quad =(\epsilon _p\cdot k_2)\,{{\mathcal {A}}}^{(0)_1}_\textrm{S}(1,2,p,3|\sigma _4{\setminus }1),~~ \end{aligned}$$
(34)

where the last equality uses the KK relation in (6). The soft behavior in (34) indicates that

$$\begin{aligned} C^{(0)_1}(1,2,p,3)=\epsilon _p\cdot k_2,~~~~C^{(0)_1}(1,p,2,3)=0.~~ \end{aligned}$$
(35)

Comparing (35) with (32), we find \({\alpha }_1=1\), \({\alpha }_2=0\); thus the full expansion of \({{\mathcal {A}}}_\textrm{YS}(1,2,3;p|\sigma _4)\) is given as

(36)

where the symbol is defined around (7), and the combinatorial momentum \(Y_p\) is defined as the summation over momenta carried by scalars at the l.h.s of p in the color ordering .

Repeating the above manipulation, one can determine the general YMS amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;p|\sigma _{n+1})\) with an arbitrary number of external scalars and one external gluon p, in the expanded formula

(37)

where the combinatorial momentum \(Y_p\) was defined analogously. In the above expansion, one can clearly observe the gauge invariance for the polarization \(\epsilon _p\), since the replacement \(\epsilon _p^\mu \rightarrow k_p^\mu \) yields the BCJ relation (8),

(38)

However, if one uses the formula (37) and the soft theorem for external gluons to construct YMS amplitudes with more external gluons, the resulting expansion is in the formula (15) [28], and the gauge invariance for the polarization of the fiducial gluon is obscure. The proof of gauge invariance for such special polarization requires the application of BCJ relations in a complicated way, and the complexity increases rapidly as the number of external gluons increases. To avoid this disadvantage, we want to rewrite (37) so that the manifest gauge invariance is carried by coefficients. To this end, we can use the BCJ relation to modify (37) as

(39)

In the last line at the r.h.s of (39), the coefficients vanish under the replacement \(\epsilon _p^\mu \rightarrow k_p^\mu \), due to the definition \(f^{\mu \nu }_p\equiv k^\mu _p\epsilon ^\nu _p-\epsilon ^\mu _p k^\nu _p\). This is the desired new expansion for the single-trace YMS amplitudes with one external gluon, which trivializes the gauge invariance of polarization \(\epsilon ^\mu _p\), with the cost that a spurious pole \(k_n\cdot k_p\) is introduced. As will be seen, by applying the recursive technique based on the soft theorem for external gluons, this new expansion leads to a general expansion of YMS amplitudes with an arbitrary number of external gluons, which manifests the gauge invariance for each polarization.

3.2 YMS amplitude with two external gluons

Now we turn to the single-trace YMS amplitude \({{\mathcal {A}}}_\textrm{YS}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\) with two external gluons labeled \(p_1\) and \(p_2\). Let us consider the soft behavior of gluon \(p_2\), i.e., we rescale \(k_{p_2}\) as \(k_{p_2}\rightarrow \tau k_{p_2}\), and expand \({{\mathcal {A}}}_\textrm{YS}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\) in \(\tau \). The soft theorem (22) indicates that the contribution at sub-leading order should be

(40)

where

(41)
(42)

and

(43)

The second equality of (40) is obtained by substituting the expansion (39). Three parts \(B_1\), \(B_2\) and \(B_3\) arise from acting \(S^{(1)_{p_2}}_g\) on , \(k_n\cdot f_{p_1}\cdot Y_{p_1}\) and \(k_n\cdot k_{p_1}\), respectively, due to the Leibniz rule. The expression for the first part \(B_1\) in (41) is obtained via the soft theorem

(44)

The second part \(B_2\) can be calculated as follows. Using relations (27) and (28), we have

$$\begin{aligned} S^{(1)_{p_2}}_g\,(k_n\cdot f_{p_1}\cdot Y_{p_1})=H_1+H_2, \end{aligned}$$
(45)

where

$$\begin{aligned} H_1{} & {} =-{\delta _{np_2}\,(k_n\cdot f_{p_2}\cdot f_{p_1}\cdot Y_{p_1})\over s_{np_2}} +{\delta _{p_1p_2}\,(k_n\cdot f_{p_2}\cdot f_{p_1}\cdot X_{p_1})\over s_{p_1p_2}}\nonumber \\ H_2{} & {} =-{\delta _{p_1p_2}\,(k_n\cdot f_{p_1}\cdot f_{p_2}\cdot Y_{p_1})\over s_{p_1p_2}} \nonumber \\{} & {} \quad +\sum _{i=1}^j\,{\delta _{ip_2}\,(k_n\cdot f_{p_1}\cdot f_{p_2}\cdot k_i)\over s_{ip_2}},~~~~ \end{aligned}$$
(46)

with \(Y_{p_1}=\sum _{i=1}^j\,k_i\). We use \(\delta _{ab}=-\delta _{ba}\) to reorganize \(H_1\) as

$$\begin{aligned} H_1{} & {} =\Bigg [\Bigg ({\delta _{p_1p_2}\over s_{p_1p_2}}+{\delta _{p_2(j+1)}\over s_{p_2(j+1)}}\Bigg )\nonumber \\{} & {} \quad +\sum _{k=j+1}^{n-1}\,\Bigg ({\delta _{kp_2}\over s_{kp_2}}+{\delta _{p_2(k+1)}\over s_{p_2(k+1)}}\Bigg )\Bigg ]\,(k_n\cdot f_{p_2}\cdot f_{p_1}\cdot Y_{p_1}).~~~~\nonumber \\ \end{aligned}$$
(47)

The reason for expressing \(H_1\) in the above manner is that we want to interpret as coefficients times leading or sub-leading terms of amplitudes, as can be seen in (42). Combining (47) and the leading soft factor (19) for the scalar, we find

(48)

We emphasize that is the leading-order contribution of , which is at the \(\tau ^{-1}\) order, while \(f_{p_2}\) in the coefficients is accompanied by \(\tau \). Combining them leads to the \(\tau ^0\) order contribution which satisfies the order of \({{\mathcal {A}}}^{(1)_{p_2}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\). For reasons similar to those for rewriting \(H_1\), we reorganize \(H_2\) as

$$\begin{aligned} H_2{} & {} =\sum _{i=1}^j\,\Bigg ({\delta _{ip_2}\over s_{ip_2}}-{\delta _{p_1p_2}\over s_{p_1p_2}}\Bigg )\,(k_n\cdot f_{p_1}\cdot f_{p_2}\cdot k_i)\nonumber \\{} & {} =\sum _{i=1}^j\,\Bigg [\sum _{l=i}^{j-1}\,\Bigg ({\delta _{lp_2}\over s_{lp_2}}+{\delta _{p_2(l+1)}\over s_{p_2(l+1)}}\Bigg )+{\delta _{jp_2}\over s_{jp_2}}+{\delta _{p_2p_1}\over s_{p_2p_1}}\Bigg ]\,\nonumber \\{} & {} \quad \times (k_n\cdot f_{p_1}\cdot f_{p_2}\cdot k_i)\nonumber \\{} & {} =\sum _{l=1}^{j}\,\Bigg ({\delta _{lp_2}\over s_{lp_2}}+{\delta _{p_2(l+1)}\over s_{p_2(l+1)}}\Bigg )\,\Bigg [k_n\cdot f_{p_1}\cdot f_{p_2}\cdot \Bigg (\sum _{i=1}^l\,k_i\Bigg )\Bigg ],\nonumber \\ \end{aligned}$$
(49)

where \(\delta _{q(j+1)}\) and \(s_{q(j+1)}\) in the last line should be understood as \(j+1=p_1\). Thus,

(50)

Combining (48) and (50) yields the expression of \(B_2\) in (42). The third part \(B_3\) in (43) can be calculated using the relation (27)

$$\begin{aligned}{} & {} S^{(1)_{p_2}}_g\,{1\over k_n\cdot k_{p_1}}=-{k_n\cdot f_{p_2}\cdot k_{p_1}\over (k_n\cdot k_{p_1})^2}\,\Bigg ({\delta _{p_1p_2}\over s_{p_1p_2}}-{\delta _{np_2}\over s_{np_2}}\Bigg )\nonumber \\{} & {} \quad =-{k_n\cdot f_{p_2}\cdot k_{p_1}\over (k_n\cdot k_{p_1})^2}\,\Bigg [{\delta _{p_1p_2}\over s_{p_1p_2}}+{\delta _{p_2a}\over s_{p_2a}}+\sum _{k=a}^{n-1}\,\Bigg ({\delta _{kp_2}\over s_{kp_2}}+{\delta _{p_2(k+1)}\over s_{p_2(k+1)}}\Bigg )\Bigg ],\nonumber \\ \end{aligned}$$
(51)

which indicates that

(52)

We will use \(B_1\), \(B_2\) and \(B_3\) to reconstruct the complete expansion of \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\). Mathematically, it is impossible to restore the full amplitude from the sub-leading contribution, so further physical constraints are needed. The most important one is the symmetry under the permutation \(p_1\leftrightarrow p_2\). The physical amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\) should be invariant under such relabeling. In the expansion (15), since a fiducial gluon \(p_1\) is required, such symmetry is not manifest. However, one can use the BCJ relations to prove that the resulting expansions obtained by choosing different fiducial gluons are equivalent to each other. On the other hand, the purpose of the current work is to seek the new expansion which manifests the gauge invariance for all polarizations, which implies democracy among all external gluons; thus it is natural to expect manifest symmetry under \(p_1\leftrightarrow p_2\).

With the additional condition of symmetry \(p_1\leftrightarrow p_2\), let us try to determine the expansion of the amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\). It is straightforward to recognize that \(B_2\) arises as the leading term of

(53)

which is at the \(\tau ^0\) order. The reason for turning \(k_n\cdot k_{p_1}\) in the denominators into \(k_n\cdot k_{p_1p_2}\) is to keep the symmetry \(p_1\leftrightarrow p_2\). There is another way to keep such symmetry, which is adding terms with \(1/k_n\cdot k_{p_2}\). However, \({{\mathcal {A}}}^{(1)_{p_2}}_{\textrm{YS}}(1,\ldots ,n;p_1,p_2|\sigma _{n+2})\) will receive contributions from such terms; for example, the coefficients carry \(1/(\tau k_n\cdot k_{p_2})\) under the rescaling \(k_{p_2}\rightarrow \tau k_{p_2}\), and the amplitudes contribute \(\tau ^1\), which combine to terms at the \(\tau ^0\) order. Since such contributions do not exist in \({{\mathcal {A}}}^{(1)_{p_2}}_{\textrm{YS}}(1,\ldots ,n;p_1,p_2|\sigma _{n+2})\) in (40), the \(1/k_n\cdot k_{p_2}\) terms are excluded. Then the symmetry \(p_1\leftrightarrow p_2\) also excludes the \(1/k_n\cdot k_{p_1}\) terms, and the remaining choice is only \(1/k_n\cdot k_{p_1p_2}\).

One can also observe that \(B_1\) comes from the sub-leading term of

(54)

which is also at the \(\tau ^0\) order. Again, the denominator is set to be \(k_n\cdot k_{p_1p_2}\) due to the symmetry. However, the sub-leading contribution of \(P_2\) receives an additional contribution from expanding the denominator in \(\tau \). Furthermore, the symmetry between two gluons requires the existence of

(55)

which serves as the counterpart of \(P_2\) under the permutation \(p_1\leftrightarrow p_2\). These missing terms will be determined by considering \(B_3\). The expression of \(B_3\) in (43) also breaks the manifest symmetry between \(p_1\) and \(p_2\). Based on such symmetry, the appearance of in (43) implies the existence of . To realize this, we observe that

(56)

where the combinatorial momentum \(X_a\) is defined as the summation of momenta carried by external legs at the l.h.s of a in the color ordering, without distinguishing scalars or gluons (recall that \(Y_a\) only includes momenta carried by external scalars). Then, \(B_3\) can be identified as

$$\begin{aligned} B_3=B_4+B_5, \end{aligned}$$
(57)

where

(58)

and

(59)

Here we have used expansions

(60)

Note that \(Y_{p_2}\) in (60) is equal to \(X_{p_2}\) in (56), since in the second line of (60) the leg \(p_1\) is a scalar. The combinatorial momentum \(Y_{p_1}\) in (60) is equal to \(Y_{p_1}\) in (43) and (60) at the leading order, since \(k_{p_2}\) is accompanied by \(\tau \) thus is dropped into the sub-leading term.

Now one can observe that \(B_4\) is the leading term of \(P_3\), and \(B_5\) arises from the term at \(\tau ^1\) order in the expansion of the denominator of \(P_2\). Thus, we conclude that

(61)

One can verify that taking \(k_{p_1}\rightarrow \tau k_{p_1}\) and expanding (61) in \(\tau \) gives the correct behavior at sub-leading order, namely,

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(1)_{p_1}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_2|\sigma _{n+2})\nonumber \\{} & {} \quad =S^{(1)_{p_1}}_g\,{{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;p_2|\sigma _{n+2}{\setminus } p_1). \end{aligned}$$
(62)

Note that in the formula (61), both the symmetry between two gluons and the gauge invariance for each polarization are manifested.

3.3 YMS amplitude with three external gluons

The next example is the single-trace YMS amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_3|\sigma _{n+3})\), which includes three external gluons \(p_1\), \(p_2\) and \(p_3\). The treatment is parallel to that in the previous subsection for the two-gluon case, and such similarity exhibits a recursive pattern. We consider \(k_{p_3}\rightarrow \tau k_{p_3}\), and expand \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_3|\sigma _{n+3})\) in \(\tau \). The soft theorem requires the sub-leading term to be

(63)

where the expanded formula (61) for YMS amplitude with two external gluons is used. Applying the Leibniz rule, we obtain

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(1)_{p_3}}_{\textrm{YS}}(1,\ldots ,n;p_1,p_2,p_3|\sigma _{n+3})\nonumber \\{} & {} \quad =B_1+B_2+B_3+B_4+B_5+B_6, \end{aligned}$$
(64)

where

(65)
(66)
(67)
(68)
(69)
(70)

The first and second parts \(B_1\) and \(B_2\) in (65) and (66) are analogous to \(B_1\) in (41), and come from the soft theorem. The computation of \(B_3\) and \(B_4\) in (67) and (68 is parallel to that for obtaining \(B_2\) in (42). The calculation of \(B_5\) and \(B_6\) in (69) and (70) is parallel to the process for obtaining \(B_3\) in (43). The combinatorial momentum \(K_{p_3}\) is defined as the summation of momenta in \(\{k_{p_1},k_{p_2}\}\) whose corresponding legs are at the l.h.s of \(p_3\) in the color ordering. The notation in the last line of (69) means expanding to pure BAS basis, and \(K_{p_3}\) are defined for the corresponding color orderings carried by these BAS amplitudes. If one uses other expressions for , (69) does not hold.

Using \(K_{p_3}=Y_{p_3}-X_{p_3}\), where for (69) \(X_{p_3}\) is defined for BAS amplitudes after expanding , one can separate \(B_5\) and \(B_6\) as

$$\begin{aligned} B_5=B_7+B_8,~~~~B_6=B_9+B_{10}, \end{aligned}$$
(71)

where

(72)
(73)
(74)
(75)

The resulting \(B_8\) in (73) can be obtained as follows. Using the expansion of , we have

(76)

since all other terms are at the \(\tau ^1\) order. Then we use the expansion of to obtain

(77)

Note that for pure BAS amplitudes, \(Y_{p_3}\) is equivalent to \(X_{p_3}\). Expanding will not alter \(Y_{p_2}\) in (76) at the leading order, since \(k_{p_3}\) is accompanied by \(\tau \) and thus does not contribute. Substituting (77) into (76), we find

(78)

where the expansion of has been used. The relation (78) yields the expression of \(B_8\) in (73). The expression of \(B_9\) in (75) can be calculated in an analogous way.

Now one can recognize that \(B_1\) in (65) together with \(B_8\) in (73) gives the sub-leading term of

(79)

while \(B_2\) in (66) and \(B_{10}\) in (75) give the sub-leading term of

(80)

Similar to the two-gluon case, \(k_n\cdot k_{p_1p_2}\) in the denominator is turned into \(k_{n}\cdot k_{p_1p_2p_3}\), to maintain the manifest permutation symmetry among external gluons \(p_1\), \(p_2\), \(p_3\). The block \(B_3\) in (67) can be interpreted as the leading term of

(81)

\(B_4\) in (68) can be interpreted as the leading term of

(82)

Finally, combining \(B_7\) in (72) and \(B_9\) in (74) gives the leading contribution of

(83)

Thus, we arrive at

(84)

where \(j\in \{1,2,3\}\) in the final line.

3.4 General case

Comparing the constructions in Sects. 3.2 and 3.3, we see that the processes bear strong similarity. This similarity implies a recursive pattern which yields the general expansion for single-trace YMS amplitudes with an arbitrary number of external gluons. Such general expansion is the goal of this subsection.

In general, the single-trace YMS amplitude \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m})\) with m external gluons can be expanded as in (17). When \(\pmb {{\alpha }}=\{p_i\}_m\), the YMS amplitudes at the second line of (17) are reduced to pure BAS amplitudes. As mentioned previously, in this note we restrict ourselves to the special choice of the reference momentum \(k_r\) in (17), which is \(k_r=k_n\).

Obviously, expansions in (39), (61), (84) satisfy the general formula in (17) with \(k_r=k_n\). To achieve the general formula, let us suppose that (17) is satisfied for a particular m, then it is also satisfied for \(m+1\). Consider \(k_{p_{m+1}}\rightarrow \tau k_{p_{m+1}}\), and expand \({{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_{m+1}|\sigma _{n+m+1})\) in \(\tau \); we obtain

$$\begin{aligned}{} & {} {{\mathcal {A}}}^{(1)_{p_{m+1}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_{m+1}|\sigma _{n+m+1})\nonumber \\{} & {} \quad =S^{(1)_{p_{m+1}}}_g\,{{\mathcal {A}}}_{\textrm{YS}}(1,\ldots ,n;\{p_i\}_m|\sigma _{n+m+1}{\setminus } p_{m+1})\nonumber \\{} & {} \quad =B_1+B_2+B_3,~~ \end{aligned}$$
(85)

where

(86)
(87)

with , and

(88)

The calculations are parallel to those in Sects. 3.2 and 3.3. Again, the notation is understood as expanding to the BAS basis. To obtain \(B_2\) in the second line of (87), we used the property

(89)

where \(\vec {\pmb {a}}\), \(\vec {\pmb {b}}\) and \(\vec {\pmb {c}}\) are three ordered sets. In (88), \(K_{p_{m+1}}\) stands for the summation of momenta carried by external gluons \(p_i\) at the l.h.s of \(p_{m+1}\) in the color ordering. We emphasize that the external leg \(p_{m+1}\) is not included in the set \(\pmb {{\alpha }}\) appearing in \(B_1\), \(B_2\) and \(B_3\).

Using \(K_{p_{m+1}}=Y_{p_{m+1}}-X_{p_{m+1}}\), one can split \(B_3\) as

$$\begin{aligned} B_3=B_4+B_5, \end{aligned}$$
(90)

where

(91)
(92)

The computations of \(B_4\) and \(B_5\) are analogous to those for obtaining \(B_7\), \(B_8\), \(B_9\) and \(B_{10}\) in Sect. 3.3. It is worth providing a brief discussion of how to generalize the manipulation from (76) to (78) to the current general case. We first observe that

(93)

Here, \(\pmb {{\beta }}\) is a subset of \(\{p_i\}_m{\setminus }\pmb {{\alpha }}\) which does not include \(p_{m+1}\), since otherwise \(k_{p_{m+1}}\) will occur in \(F_{\vec {\pmb {{\beta }}}}\) and contribute \(\tau \) under the rescaling \(k_{p_{m+1}}\rightarrow \tau k_{p_{m+1}}\). The combinatorial momentum \(k_{\{p_i\}_m{\setminus }\pmb {{\alpha }}}\) is the summation of momenta for external legs in the set \(\{p_i\}_m{\setminus }\pmb {{\alpha }}\). Applying the above procedure iteratively, one can further expand the leading terms of YMS amplitudes in the second line of (93), until there is only one remaining gluon \(p_{m+1}\). In other words, can be expanded to . Then, we expand them further by employing

(94)

and reorganize the full expansion as

(95)

based on the observation that \(k_{p_{m+1}}\) which is accompanied by \(\tau \) does not contribute to any Y at the leading order. The relation (95) is the generalization of the previous result (78). Using (95), we arrive at the expression of \(B_5\) in (92).

Now we observe that \(B_1\) in (86) together with \(B_5\) in (92) gives the sub-leading term of

(96)

\(B_2\) in (87) can be interpreted as the leading term of

(97)

where \(\pmb {{\alpha }}'\) includes the external leg \(p_{m+1}\) and \(\pmb {{\alpha }}'{\setminus } p_{m+1}\ne \emptyset \), and \(B_4\) in (91) corresponds to the leading terms of

(98)

Combining \(P_1\), \(P_2\) and \(P_3\), we see that the general formula (17) is correct for single-trace YMS amplitude with \((m+1)\) external gluons, and this completes the proof.

4 Summary

In this note, we reconstructed the expansion of single-trace YMS amplitudes proposed by Clifford Cheung and James Mangan in [27], by using the bottom-up method based on soft theorems, without the aid of a Lagrangian or equations of motion. The whole process is on-shell, without using any off-shell ansatz. Our recursive method inserts gluons into the lower-point amplitude in a manifestly gauge-invariant manner, resulting in an expansion which manifests the gauge invariance for all polarizations carried by external gluons, and the permutation symmetry among external gluons, at the cost of sacrificing the manifest locality. One can apply such expansion iteratively to expand the single-trace YMS amplitudes to pure BAS ones without breaking the manifest gauge invariance for any polarization, but a variety of spurious poles will be created.

Through the double-copy structure, our result can be directly extended to the expansion of single-trace Einstein–Yang–Mills amplitudes,

(99)

where \(1,\ldots ,n\) are color-ordered gluons, and elements in \(\{p_i\}_m\) are gravitons without any ordering.

It is straightforward to verify that the expansion (17) is equivalent to that found by Clifford Cheung and James Mangan in [27]. After some modifications of notation, the expansion in [27] is given as

(100)

up to an overall sign. Here, \(k_i\) contributes when i is at the l.h.s of the first element in \(\vec {\pmb {{\alpha }}}\) in the ordering; therefore, the definition of \(Y_{\vec {\pmb {{\alpha }}}}\) is satisfied. On the other hand, the momentum conservation gives \(k_{1\ldots n}=-k_{p_1\ldots p_m}\). Thus, the equivalence between (17) and (100) is proved.

The sub-leading soft theorem for external gluons plays a crucial role in our recursive method. One may ask the reason for choosing the sub-leading soft theorem rather than the leading-order one. The answer is that the leading-order soft theorem cannot detect all terms in the expansion. Suppose we rescale \(k_{p_j}\) as \(k_{p_j}\rightarrow \tau k_{p_j}\), as can be seen in the general expanded formula (17). Various terms including \(f_{p_j}^{\mu \nu }\) in coefficients are therefore accompanied by \(\tau \); these terms have no contribution to the leading order. Another question is whether the sub-leading soft theorem is sufficient to detect all terms in the complete expansion. For example, if the coefficient of one term behaves as \(\tau ^2\), then this coefficient cannot be detected at both leading and sub-leading orders. This question was answered in [28], by employing the universality of soft factor for external scalars, as well as the counting of mass dimensions. The argument in [28] at least shows that the old expansion (15) can be fully detected by the sub-leading soft theorem for external gluons. Since any correct expansion must be equivalent to (15), we claim that the new expansion, which manifests gauge invariance for all polarizations, can also be completely detected.

A related interesting future direction is seeking the expanded formula for pure YM amplitudes which manifests the gauge invariance for each polarization. Such expansion leads to the manifestly gauge-invariant BCJ numerators. We expect that the recursive method in this note can be applied to solve the challenge.