1 Introduction

Cosmological models can be used to describe black holes after imposing the condition that involves dealing with isolated objects. In the case of spherically symmetric objects, this issue may be reduced to the problem of matching the Schwarzschild spacetime with a finite region of specific spacetime [1, 2]. This idea was recently used to obtain the Oppenheimer–Snyder (OS) and Lemaître–Tolman–Bondi (LTB) models of isolated objects within one formalism (see [3] and references therein). The former model concerns a spherical cloud of homogeneous dust (pressureless matter), whereas the latter deals with a spherical but inhomogeneous cloud of dust. However, the merging condition sometimes leads to complicated equations defining variables, which cannot be resolved analytically but only numerically, creating additional difficulties in analyses (e.g., see [3]).

A different strategy for obtaining a description of an isolated astrophysical object was recently proposed for the LTB model [4,5,6,7]. A metric of both interior and exterior regions of an isolated body is expressed in one coordinate system, which obviates the need to impose matching conditions across the interface between the matter and vacuum regions provided that certain functions are continuous across the boundary. We apply this approach in the present paper.

In this article we present the quantum system ascribed to the OS model of a collapsing pressureless dust star. For this purpose we use the so-called integral quantization (IQ) method applied quite recently to the quantization of the Schwarzschild spacetime [8] and a thin matter shell in vacuum [9].

In this article, we disregard the black hole evaporation by Hawking radiation. Thus, the global mass of the considered star is conserved during its evolution.

Following the idea presented in [8], we quantize both the spatial and the temporal coordinates. The rationale for such an approach is the covariance of general relativity with respect to the transformations of these coordinates. Treating temporal and spatial coordinates on the same footing at the quantum level has enabled the construction of a consistent quantum theory.

One of the main issues addressed in the quantization of black holes is the singularity avoidance, which has been widely discussed in the literature. In the case of the OS black hole, various approaches motivated by loop quantum gravity have led to resolution of the singularity of the classical model (see, e.g., [10,11,12,13,14,15,16] and references therein). Many investigations have been conducted in the context of quantum geometrodynamics (see, e.g., [17] and references therein). On the other hand, few results have been obtained within the IQ method based on coherent states [18, 19]. The latter method is applicable even in cases in which the canonical quantization has methodological problems [19]. We extend this discussion in the conclusion section.

The paper is organized as follows: In Sect. 2, we recall the formalism of spherically symmetric spacetime specialized to black holes. The singularities and horizon issues are exhibited. The specific case of the dust black hole is considered. Section 3 is devoted to the quantization of the OS model, which includes recalling an essence of the IQ quantization, and presents the quantum dynamics of the considered black hole. In particular, we discuss the fate of the classical singularities at the quantum level. We reduce the results to the case of the quantum Schwarzschild black hole in Sect. 4. We conclude in Sect. 5. Appendix A recalls a general solution for the dynamics of the LTB spacetime. Appendix B specifies the transformation between the two coordinate systems applied in our paper. The two state spaces used in the affine quantization are discussed in Appendix C.

In the following we choose \(\;G = c =1 = \hbar \;\) except where otherwise noted.

2 Spherically symmetric spacetime

2.1 The perfect fluid case

We begin our considerations by recalling the metric and field equations of the LTB model of black holes presented in [5], and describing a general spherically symmetric perfect fluid.

The metric of the collapsing massive star of a spherically symmetric spacetime in the coordinates \((t,r,\theta ,\phi )\) (see, e.g., [20]) and considered in [5] reads

$$\begin{aligned} \textrm{d}s^2 = - \alpha ^2 \textrm{d}t^2 + \frac{(\alpha \sqrt{2 M/r + E}\, \textrm{d}t + \textrm{d}r)^2}{1+E} + r^2 \textrm{d}\Omega ^2 \,, \end{aligned}$$
(1)

where \((t,r) \in {\mathbb {R}}\times {\mathbb {R}}_+\), with \( {\mathbb {R}}_+:= \{r \in {\mathbb {R}}~|~r > 0\}\), and where \(\alpha (t,r) > 0\) is the lapse function (specific to the \(3+ 1\) decomposition of the spacetime metric), whereas \(\textrm{d}\Omega ^2:= \textrm{d}\theta ^2 +\sin ^2\theta \textrm{d}\phi ^2\). The so-called energy function E(t, r), arbitrary up to the constraint \(E > -1\), is a measure of the energy of a shell at a radius r. The so-called mass function M(t, r), at some radius r, is defined as

$$\begin{aligned} M(t,r) = 4\pi \int _0^r \rho (t,\sigma ) \sigma ^2 \; \mathrm{{d}} \sigma \,. \end{aligned}$$
(2)

The field equations have the form [5]

$$\begin{aligned}{} & {} \frac{\partial M}{\partial t} - \alpha \,\sqrt{\frac{2M}{r}+E} \;\; \Bigg (\frac{\partial M}{\partial r} + 4\pi P r^2 \Bigg ) = 0 \,, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \frac{\partial E}{\partial t} - \alpha \,\sqrt{\frac{2M}{r}+E} \;\; \Bigg (\frac{\partial E}{\partial r} + 2\, \frac{1+E}{\rho +P}\; \frac{\partial P}{\partial r} \Bigg ) = 0 \,, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \frac{1}{\alpha }\;\frac{\partial \alpha }{\partial r} + \frac{1}{\rho + P}\; \frac{\partial P}{\partial r} = 0 \,, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} f(\rho , P) = 0 \,. \end{aligned}$$
(6)

The energy-momentum tensor for a perfect fluid reads

$$\begin{aligned} T^{\mu \nu } = (\rho + P)\,n^\mu n^\nu + P g^{\mu \nu }\,, \end{aligned}$$
(7)

where P is the pressure, \(\rho \ne -P\) is the energy density, \(n^\mu \) is the vector field tangent to the fluid, and (6) is an equation of state.

In the OS collapse model of a black hole, we have two regions: a “star region” defined by non-vanishing \(\rho \), and a vacuum region with vanishing energy density. In this configuration, the system is asymptotically flat, and M presents the global mass/energy of the system. This energy is conserved during the evolution, as a static spherically symmetric black hole does not radiate gravitational waves.

Equations  (3)–(6) require the specification of initial and boundary conditions to be well defined. Additionally, one should impose the boundary conditions at the interface between the matter that fills the interior of the ball of matter and the vacuum exterior. For these important issues, we recommend Sec. III of Ref. [5].

The metric (1) is expressed in terms of a generalization of the Painlevé–Gullstrand (PG) coordinates [21, 22]. In this choice of coordinates, the radial coordinate r is always space-like. We call the above formalism the spherically symmetric spacetime model in the PG coordinates.

2.2 The dust case

In what follows, we consider the dust case. It can be introduced by the conditions

$$\begin{aligned} P=0\;,\;\;\alpha = 1, \end{aligned}$$
(8)

implemented in Eqs. (1)–(5). As a result, the metric and field equations become

$$\begin{aligned} \textrm{d}s^2= & {} - \textrm{d}t^2 + \frac{(\sqrt{2 M/r + E}\, \textrm{d}t + \textrm{d}r)^2}{1+E} + r^2 \textrm{d}\Omega ^2 \,, \end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial M}{\partial t}- & {} \sqrt{\frac{2M}{r}+E} \;\; \frac{\partial M}{\partial r} = 0 \,, \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial E}{\partial t}- & {} \sqrt{\frac{2M}{r}+E} \;\; \frac{\partial E}{\partial r} = 0 \,, \end{aligned}$$
(11)

where M is defined by Eq. (2), and where t is the time measured by an in-falling geodesic observer.

The system (9)–(11) can describe the interior and exterior regions of the LTB dust star in the single PG coordinate patch. Given the initial density profile with the density vanishing at some finite radius, the latter region can be shown to be diffeomorphic to the Schwarzschild spacetime [4]. The so-called marginally bound model [23] considered in this article is the case with \(E = 0\) (see Appendix A). The classical dynamics of this model are defined, due to (10), by the equation

$$\begin{aligned} \frac{\partial M}{\partial t} - \sqrt{\frac{2M}{r}} \;\; \frac{\partial M}{\partial r} = 0 \,. \end{aligned}$$
(12)

This equation has a general implicit solution (as presented in [5]):

$$\begin{aligned} M = \mathcal {F}\left( \frac{2}{3}r^{3/2}+t\sqrt{M}\right) , \end{aligned}$$
(13)

where \(\mathcal {F}\) is a function of integration coming from solving the equation with the method of characteristics. In what follows we present a simpler but explicit separable analytical solution to Eq. (12), which is a particular case satisfying Eq. (13) (see Appendix A for a general solution in (t, R) coordinates).

Making the assumption \(M(t,r)=M_1(t)M_2(r)\) splits (12) into the two equations

$$\begin{aligned}{} & {} \frac{\partial M_1}{\partial t} - \lambda M_1^{\frac{3}{2}} =0 \,, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \frac{\partial M_2}{\partial r} - \lambda \sqrt{\frac{M_2 r}{2}} =0. \end{aligned}$$
(15)

Direct integration of Eq. (14) gives the solution

$$\begin{aligned} \sqrt{M_1}= \frac{-2}{\lambda t + C_1} \, \end{aligned}$$
(16)

where \(\lambda \) is the separation parameter and \(C_1\) an arbitrary constant.

Similarly, integration of Eq. (15) gives the following solution:

$$\begin{aligned} \sqrt{M_2}= \frac{\lambda }{3\sqrt{2}} r^{\frac{3}{2}} +C_2 \, \end{aligned}$$
(17)

where \(C_2\) is an arbitrary constant.

Combining both factors \(M_1\) and \(M_2\), the full solution of the dust equation can be written as

$$\begin{aligned}{} & {} \sqrt{M(t,r)}=\sqrt{M_1(t)}\sqrt{M_2(r)}\nonumber \\{} & {} \quad = \left( \frac{-2}{\lambda t + C_1}\right) \left( \frac{\lambda }{3\sqrt{2}} r^{\frac{3}{2}} +C_2 \right) \,, \end{aligned}$$
(18)

so that

$$\begin{aligned} M(t,r)= & {} \left( \sqrt{M_1(t)}\sqrt{M_2(r)} \right) ^2\nonumber \\= & {} \left\{ \left( \frac{-2}{\lambda t + C_1}\right) \left( \frac{\lambda }{3\sqrt{2}} r^{\frac{3}{2}} +C_2 \right) \right\} ^2 \,. \end{aligned}$$
(19)

Formally, the derivation of the solution (19) requires the restrictions of the domains of the functions \(\sqrt{M_1(t,r)}\) and \(\sqrt{M_2(t,r)}\), which also implies the restriction for the domain of M(t, r). However, since the function (19) fulfills the condition of mass positivity for arbitrary (t, r), we take the mass (19) to be defined on the full domain \((t,r)\in \mathbb {R}\times \mathbb {R}_+\), except for the singularities at \(t_c = -C_1/\lambda \). This result can be well defined mathematically by taking the definition of the complex root in the solutions to Eqs. (14) and (15).

2.3 Singularities

In the synchronous co-moving coordinates \((\tau , R, \theta , \phi )\), the line element and field equations read (see, e.g., [24])

$$\begin{aligned} \textrm{d}s^2= & {} -\textrm{d}\tau ^2 + \frac{\left( \frac{\partial r}{\partial R}\right) ^2}{1+2E}\textrm{d}R^2 + r^2 \textrm{d}\Omega ^2, \end{aligned}$$
(20)
$$\begin{aligned} \left( \frac{\partial r}{\partial \tau }\right) ^2= & {} \frac{2M}{r}+E , \end{aligned}$$
(21)
$$\begin{aligned} 4\pi \rho= & {} \frac{\partial M}{\partial R}\left( r^2\frac{\partial r}{\partial R}\right) ^{-1}. \end{aligned}$$
(22)

Equation (21) describes the dynamics of the shells. Taking a square root of this equation requires choosing a sign, which represents expanding or collapsing shells for a negative or positive sign, respectively. The second equation (22) defines the density, which can become singular under two conditions, leading to two different types of singularities. The \(\partial r /\partial R = 0\) is usually referred to as a shell crossing and may be viewed as a weak singularity, inherent to the lack of pressure in the matter model. The second one, however, i.e. \(r=0\), is a strong singularity and cannot be avoided for the collapsing scenarios. For the relationship between the line elements (9) and (20) expressed in two different coordinate systems, see Appendix B.

2.3.1 Shell-crossing singularity

Let us find an explicit form of the condition \(\partial r /\partial R = 0\) for the separable solution (19). We rewrite it as

$$\begin{aligned} M(t,r) = \left( A r^{\frac{3}{2}}+B\right) ^2 , \end{aligned}$$
(23)

where

$$\begin{aligned} A = \frac{-2\lambda }{\left( \lambda t+C_1\right) 3\sqrt{2}} \;,\;\;B = \frac{-2C_2}{\lambda t+C_1}. \end{aligned}$$
(24)

Let us take some instance of time \(t=0\) so that

$$\begin{aligned} M(t_i, r_i)= & {} \left( \left( \frac{-2}{C_1}\right) \left( \frac{\lambda }{3\sqrt{2}}r_i^{\frac{3}{2}}+C_2\right) \right) ^2\nonumber \\= & {} \left( A_i r_i^{\frac{3}{2}}+B_i\right) ^2 . \end{aligned}$$
(25)

We can use the freedom to choose our radial coordinate and set \(R = r_i\), where \(r_i\) is the areal radius at \(t=0\). We then have

$$\begin{aligned} M(0,R) = \left( A_i R^{\frac{3}{2}}+B_i\right) ^2 . \end{aligned}$$
(26)

We also get from (23)

$$\begin{aligned} r = \left( \frac{\sqrt{M}-B}{A}\right) ^{\frac{2}{3}} . \end{aligned}$$
(27)

Differentiating the above equations leads to

$$\begin{aligned} \frac{\partial r}{\partial R} = \frac{1}{3A}r^{-\frac{1}{2}}M^{-\frac{1}{2}}\frac{\partial M}{\partial R}, \end{aligned}$$
(28)

and

$$\begin{aligned} \frac{\partial M}{\partial R} = 3\sqrt{M}A_iR^{\frac{1}{2}}. \end{aligned}$$
(29)

From the two equations above, it is evident that the shell-crossing cannot occur, as for our setup we have

$$\begin{aligned} \frac{\partial r}{\partial R} = \frac{\lambda t +C_1}{3\sqrt{2}\, C_1} \ne 0~~~~\text{ for }~~~~t \ne t_c = - C_1/\lambda . \end{aligned}$$
(30)

2.3.2 Gravitational singularities

The existence of a gravitational singularity is usually signaled by the blow-up of the curvature scalars. The Kretschmann scalar can be decomposed in the following way:

$$\begin{aligned} K = R_{\mu \nu \lambda \sigma }R^{\mu \nu \lambda \sigma } = C_{\mu \nu \lambda \sigma }C^{\mu \nu \lambda \sigma } + 2R_{\mu \nu }R^{\mu \nu } - \frac{1}{3}{\mathcal {R}}^2 ,\nonumber \\ \end{aligned}$$
(31)

where \(R_{\mu \nu \lambda \sigma }\), \(C_{\mu \nu \lambda \sigma }\), \(R_{\mu \nu }\), and \({\mathcal {R}}\) are the Riemann, Weyl, and Ricci tensors and the scalar curvature. Term by term, we have

$$\begin{aligned}{} & {} C_{\mu \nu \lambda \sigma }C^{\mu \nu \lambda \sigma } = 48\left( \frac{1}{3}\frac{\partial M}{\partial R}\left( \frac{\partial r}{\partial R}\right) ^{-1}r^{-2}-Mr^{-3}\right) ^2 , \qquad \end{aligned}$$
(32)
$$\begin{aligned}{} & {} R_{\mu \nu }R^{\mu \nu }= 64 \pi ^2 \rho ^2 = \left( 2\frac{\partial M}{\partial R}\left( \frac{\partial r}{\partial R}\right) ^{-1}r^{-2}\right) ^2 , \end{aligned}$$
(33)
$$\begin{aligned}{} & {} {\mathcal {R}}= 8\pi \rho = 2\frac{\partial M}{\partial R}\left( \frac{\partial r}{\partial R}\right) ^{-1}r^{-2} . \end{aligned}$$
(34)

For the separable solution (19), with \(C_2 = 0\) corresponding to the OS model (see, Sect. 2.4), we obtain

$$\begin{aligned}{} & {} C_{\mu \nu \lambda \sigma }C^{\mu \nu \lambda \sigma } = 48\left( AM^{\frac{1}{2}}r^{-\frac{3}{2}}-Mr^{-3}\right) ^2 = 0 , \end{aligned}$$
(35)
$$\begin{aligned}{} & {} R_{\mu \nu }R^{\mu \nu }= 36A^2Mr^{-3} = 576\, \lambda ^4\, \epsilon ^{-4} , \end{aligned}$$
(36)
$$\begin{aligned}{} & {} {\mathcal {R}}= 6AM^{\frac{1}{2}}r^{-\frac{3}{2}}= 24\, \lambda ^2\,\epsilon ^{-2} , \end{aligned}$$
(37)
$$\begin{aligned}{} & {} K = 108 A^2Mr^{-3}-96A M^{\frac{3}{2}}r^{-\frac{9}{2}}\nonumber \\ {}{} & {} \qquad \quad +48M^2r^{-6} = \frac{240}{81}\,\lambda ^4\, \epsilon ^{-4} , \end{aligned}$$
(38)

where \(\epsilon := \lambda t + C_1\). The solution (19) implies that for \(\epsilon \rightarrow 0\), we have the gravitational singularity.

2.3.3 Apparent horizon

In the case of dynamical spacetimes, very often it is not possible to establish the event horizon (EH), since it requires knowledge of the whole spacetime, including null and spatial infinities. One way to replace the notion of the event horizon by something in principle determinable locally is to resort to the outermost marginally outer trapped surface, called the apparent horizon (AH). Although its definition is dependent on the foliation of spacetime, it is still one of the most convenient ways to define a black hole, especially in numerical general relativity. In the spherically symmetric configuration, the AH is a sphere residing on the hyper-surface. The condition for this sphere to be an outer trapped surface requires us to calculate the divergence of the outgoing (from the surface) null vectors and demand it to be zero. The radial null vector associated with the LTB metric (for \(E=0\)) in PG coordinates (see, e.g., [4] for derivation) reads

$$\begin{aligned} k^{\mu } = \left( 1, 1-\sqrt{\frac{2M}{R}}, 0, 0\right) . \end{aligned}$$
(39)

The condition for the divergence of (39) to be zero, \(k^{\mu }_{\;\;;\mu } = 0\), on a given surface is equivalent to requiring that we have for this surface

$$\begin{aligned} r(t) = 2M(t,r(t)) . \end{aligned}$$
(40)

It is worth noting that for the surfaces located in the vacuum part of the solution, this condition is equivalent to the condition for the EH.

2.4 Oppenheimer–Snyder black hole

In the following we will focus on the interior region of the solution.

For \(C_2 = 0\), we have from (19) the formula

$$\begin{aligned} M(t,r) = \frac{2}{9}\,\frac{\lambda ^2\,r^3}{(\lambda t + C_1)^2} \,, \end{aligned}$$
(41)

which resolved with respect to r gives

$$\begin{aligned} r = \Big (\frac{9}{2} \Big )^{1/3}M^{1/3} \Big (\frac{\lambda t +C_1}{\lambda } \Big )^{2/3} \,. \end{aligned}$$
(42)

Equation (42) shows that specifying M and t leads to corresponding r. Thus, inserting into (42) \(M = M(0, R) = M_0\) leads to

$$\begin{aligned} r = r_0 (t,R) =: f(R) g(t) \,. \end{aligned}$$
(43)

The covariant condition for a spherically symmetric dust solution of Einstein equations to be equivalent to the Friedmann–Lemaître–Robertson–Walker (FLRW) model is vanishing of the shear, acceleration, and rotation (see, e.g., [24]). The only nontrivial quantity in our case is the shear \(\sigma \), which reads

$$\begin{aligned} \sigma = \frac{1}{3}\left( \frac{1}{r}\frac{\partial r}{\partial t} -\left( \frac{\partial r}{\partial R}\right) ^{-1} \frac{\partial ^2 r}{\partial t \partial R}\right) . \end{aligned}$$
(44)

Taking \(r = f(R) g(t)\) gives \(\sigma = 0\), and hence \(C_2=0\) leads to the FLRW model and, after imposing the Schwarzschild solution in the outer region, to the OS black hole. This can be achieved by prescribing the initial density profile, e.g., with the use of the Heaviside step function. Such setup guarantees the Schwarzschild solution in the exterior region throughout the evolution.

The equation defining the horizon can be written, due to (40), in the form

$$\begin{aligned} r_0 (t_h,R) = 2 M_0 \,, \end{aligned}$$
(45)

where \(t_h\) denotes the time at which the outermost shell reaches the horizon. Resolving (43) with respect to \(t_h\) leads to the formula \( t_h=t_c \mp \frac{4}{3} M_0 \).

Since we consider the collapsing star, the co-moving observer passes the horizon before approaching the gravitational singularity. At the singularity, the classical dynamics break down. Thus, there is no classical evolution for \(t \ge t_c\), so we choose

$$\begin{aligned} t_h=t_c - \frac{4}{3} M_0 \,. \end{aligned}$$
(46)

3 Quantum Oppenheimer–Snyder black hole

In the standard approach to quantization of classical dynamics defined by the Hamiltonian H, which is a generator of the dynamics, one maps H onto an operator \(\hat{H}\) defined in some Hilbert space \(\mathcal {H}\). If \(\hat{H}\) is self-adjoint in \(\mathcal {H}\), it can be used to define quantum dynamics in the form of the Schrödinger equation defined in \(\mathcal {H}\).

In the case considered in this paper, we do not quantize Hamilton’s dynamics, but we use the solution to the classical dynamics to construct three quantum observables generated by their classical counterparts: the time operator \(\hat{t}\), the radius operator \(\hat{r}\), and the total mass operator \(\hat{M}\). For this purpose, we use the classical dynamics similarly as in the cosmological case considered in [25]. The classical dynamics are defined by the equations of motion obtained by inserting the metric (9) into the Einstein equations. In what follows, we consider the marginally bound model so that the dynamics are defined by Eq. (12). The equations of motion, with a suitable set of boundary conditions, carry the same information as the general solution to these equations. In our case, as Eq. (19) presents the solution to Eq. (12), the solution M(t, r) includes the dynamics of this gravitational system.

3.1 Integral quantization method

In what follows, we apply the affine coherent states (ACS) quantization (see [8, 25,26,27,28] and references therein) to the quantization of the classical dynamics (12) corresponding to the marginally bound case. The extension to the general dust case (10)–(11) and perfect fluid case can be done by analogy.

We begin by introducing the extended configuration space T for our system. It is defined as follows [8]:

$$\begin{aligned} T = \{(t,r) \in {\mathbb {R}}\times {\mathbb {R}}_+\},~~~~{\mathbb {R}}_+ = (0, +\infty ) \,, \end{aligned}$$
(47)

where t and r are the time and radial coordinates, respectively, which occur in the line element (9).

Since the configuration space is a half-plane, it can be identified with the affine group \(\text {Aff}(\mathbb {R})=:G\), for which the multiplication rule is given by

$$\begin{aligned} (t^\prime , r^\prime )\cdot (t, r) = (r^\prime t + t^\prime , r^\prime r ), \end{aligned}$$
(48)

with the unity (0, 1) and the inverse

$$\begin{aligned} (t, r)^{-1} = \left( -\frac{t}{r}, \frac{1}{r}\right) . \end{aligned}$$
(49)

The affine group has two nontrivial, nonequivalent irreducible unitary representations. Both are realized in the Hilbert space \(\mathcal {H}=L^2({\mathbb {R}}_+, \mathrm{{d}}\nu (x))\), where \(\mathrm{{d}}\nu (x)=\mathrm{{d}}x/x\) is the invariant measure on the multiplicative group \(({\mathbb {R}}_+,\cdot )\). In what follows we choose the one defined by

$$\begin{aligned} U(t,r)\psi (x)= e^{i t x} \psi (rx)\,. \end{aligned}$$
(50)

The integration over the affine group reads

$$\begin{aligned} \int _G \mathrm{{d}}\mu (t,r):= \frac{1}{2\pi }\int _{-\infty }^\infty \mathrm{{d}}t \int _0^\infty \mathrm{{d}}r /r^2\,, \end{aligned}$$
(51)

where the measure \(\mathrm{{d}}\mu (t,r)\) is left-invariant.

Fixing the normalized vector \(\vert \Phi _0 \rangle \in L^2({\mathbb {R}}_+, \mathrm{{d}}\nu (x))\), called the fiducial vector, one can define a continuous family of affine coherent states \(\vert t,r \rangle \in L^2({\mathbb {R}}_+, \mathrm{{d}}\nu (x))\) as follows:

$$\begin{aligned} \vert t,r \rangle = U(t,r) \vert \Phi _0 \rangle . \end{aligned}$$
(52)

The fiducial vector can be taken to be any vector of \(\mathcal {H}\) that satisfies certain conditions to be specified during the quantization process. It is a sort of free “parameter” of ACS quantization. First of all, it should be normalized so that we should have

$$\begin{aligned} \langle \Phi _0 \vert \Phi _0 \rangle:= & {} \int _0^{\infty } \mathrm{{d}}\nu (x) \langle \Phi _0 \vert x \rangle \langle x \vert \Phi _0 \rangle \nonumber \\= & {} \int _0^{\infty } \mathrm{{d}}\nu (x) |\Phi _0(x)|^2 = 1, \end{aligned}$$
(53)

where we have used the formula [27]

$$\begin{aligned} \int _0^{\infty } \mathrm{{d}}\nu (x) \vert x \rangle \langle x \vert = \hat{1\hspace{-4.75pt}1}, \end{aligned}$$
(54)

which applies to \(\mathcal {H}\).

The space of coherent states is highly entangled in the sense that we have

$$\begin{aligned}{} & {} \langle t,r |t^\prime ,r^\prime \rangle \ne 0~~~ \text{ if }~~~t \ne t^\prime ~~\text{ or }~~ r \ne r^\prime \,, \end{aligned}$$
(55)
$$\begin{aligned}{} & {} \langle t,r | t,r \rangle = 1~~~ \text{ if }~~~\langle \Phi _0|\Phi _0 \rangle = 1 \,. \end{aligned}$$
(56)

The irreducibility of the representation used to define the coherent states (52) allows us to make use of Schur’s lemma, which leads to the resolution of the unity \(\hat{1\hspace{-4.75pt}1}\) in \(L^2({\mathbb {R}}_+, \mathrm{{d}}\nu (x))\):

$$\begin{aligned} \int _{G} \mathrm{{d}}\mu (t,r) \vert t,r \rangle \langle t,r \vert = A_{\Phi _0}\; \hat{1\hspace{-4.75pt}1}\;, \end{aligned}$$
(57)

where

$$\begin{aligned} A_{\Phi _0}:= \int _0^\infty \frac{\mathrm{{d}}p}{p^2} |\Phi _0(p)|^2 < \infty \,. \end{aligned}$$
(58)

Making use of the resolution of the unity (57), we define the quantization of a classical observable \(f: T \rightarrow {\mathbb {R}}\) as follows:

$$\begin{aligned} f \longrightarrow \hat{f}:= \frac{1}{A_{\Phi _0}}\int _{\text {G}} \mathrm{{d}}\mu (t,r) \vert t,r \rangle f(t,r) \langle t,r \vert \,, \end{aligned}$$
(59)

where \(\hat{f}: \mathcal {H} \rightarrow \mathcal {H}\) is the corresponding quantum observable.

The mapping (59) is covariant in the sense that one has

$$\begin{aligned} U(\xi _0) \hat{f} U^\dag (\xi _0)= & {} \frac{1}{A_{\Phi _0}}\int _{\text {G}} \mathrm{{d}}\mu (\xi ) U(\xi _0)\vert \xi \rangle f(\xi ) \langle \xi \vert U^\dag (\xi _0) \nonumber \\= & {} \frac{1}{A_{\Phi _0}}\int _{\text {G}} \mathrm{{d}}\mu (\xi ) \vert \xi \rangle f(\xi _0^{-1}\cdot \xi ) \langle \xi \vert \,, \end{aligned}$$
(60)

where \(\xi _0^{-1}\cdot \xi = (t_0,r_0)^{-1}\cdot (t,r) = (\frac{t-t_0}{r_0},\frac{r}{r_0})\), with \(\xi := (t,r)\). This means that no point in the configuration space T is privileged.

Equation (59) defines a linear mapping, and the observable \(\hat{f}\) is a symmetric operator by the construction. It results from the Schwartz inequality that \(|\langle t,r \vert \Psi \rangle | \le \Vert \Psi \Vert \) for every vector \(\Psi \in \mathcal {H}\) and every (t, r). This implies that the sesquilinear form corresponding to the operator \(\hat{f}\) fulfills the following inequalities:

$$\begin{aligned} |\langle \Psi _2 \vert \hat{f}\vert \Psi _1 \rangle |\le & {} \frac{1}{A_\phi } \int _{\text {G}} \mathrm{{d}}\mu (t,r) |f(t,r)| |\langle t,r \vert \Psi _2 \rangle ^\star ||\langle t,r \vert \Psi _1 \rangle | \nonumber \\\le & {} \left[ \frac{1}{A_\phi } \int _{\text {G}} \mathrm{{d}}\mu (t,r) |f(t,r)| \right] \Vert \Psi _2 \Vert \Vert \Psi _1 \Vert . \end{aligned}$$
(61)

The second inequality proves that for every finite value of the integral in the square bracket, i.e., \(\int _{\text {G}} \mathrm{{d}}\mu (t,r) |f(t,r)| < \infty \), the operator \(\hat{f}\) is bounded so that it is a self-adjoint operator.

3.2 Quantum dynamics

We propose applying the procedure of mapping classical dynamics onto quantum dynamics considered in [25]. In that method, the time variable of the classical level is mapped onto an operator acting at the quantum level so that it is no longer an evolution parameter of the quantum level, but a quantum observable like other quantum observables. In this way, the time is considered on the same footing as the spatial coordinates.

In our classical model we have three observables: the time-like t, the space-like r, and the mass M(t, r). The maximum M(t, r) equal to \(M_0\) represents the total energy of this system, which has to be a conserved quantity. The imposition of the energy conservation constraint onto the mass operator \(\hat{M}\), calculated in the appropriate Hilbert space, leads to quantum dynamics.

Classical observables should be related to the corresponding quantum observables by their expectation values. This is the leading idea we use to find quantum states of our system in a Hilbert space. In our case, these three classical basic observables are mapped onto the corresponding operators \(\hat{t}\), \(\hat{r}\), and \(\hat{M}\) using Eq. (59). Since M is of fundamental importance, as it represents the global energy of the considered gravitational system, we treat the corresponding operator \(\hat{M}\) as the main quantum observable. We use the expectation value of \(\hat{M}\) to determine the family of vector states \(\psi _\eta (t,r)\) in the Hilbert space \(\mathcal K= L^2(G,\mathrm{{d}}\mu (t,r))\), where \(\eta = (\eta _1,\eta _2)\) are the parameters specifying the quantum evolution.

Consistently, we require the states \(\vert \psi _\eta \rangle \) to satisfy the constraint

$$\begin{aligned} \langle \psi _\eta \vert \hat{M} \vert \psi _\eta \rangle = M_0 \,, \end{aligned}$$
(62)

where \(M_0\) is the mass of the considered dust star defined by the density \(\rho \) of the star with radius \(r_0\). For the OS star with density

$$\begin{aligned} \rho (t,r) =\left\{ \begin{array}{lll} \frac{\lambda ^2}{6\pi }\frac{1}{(\lambda t+ C_1)^2}&{}\text{ for }&{} r \le r_0 (t)\\ 0&{}\text{ for }&{}r > r_0 (t) \end{array} \right. \;, \end{aligned}$$
(63)

the corresponding mass defined by Eq. (2) reads

$$\begin{aligned} M (t,r) =\left\{ \begin{array}{lll} \frac{2\lambda ^2}{9}\frac{r^3}{(\lambda t+ C_1)^2}&{}\text{ for }&{} r \le r_0 (t)\\ M_0&{}\text{ for }&{}r > r_0 (t) \end{array} \right. \;, \end{aligned}$$
(64)

so that the relationship between \(M_0\) and \(r_0\) is

$$\begin{aligned} r_0 (t) = \Big (\frac{9 M_0}{2 \lambda ^2} \Big )^{1/3}(\lambda t + C_1)^{2/3} \,. \end{aligned}$$
(65)

According to (64), the expression for the mass operator can be rewritten as

$$\begin{aligned} \hat{M}= & {} \frac{1}{2\pi A_\phi } \int _{-\infty }^{\infty } \mathrm{{d}}t \, \left\{ \int _{0}^{r_0(t)} \frac{\mathrm{{d}}r}{r^2} \vert t,r \rangle \left[ \frac{2\lambda ^2}{9}\frac{r^3}{(\lambda t+ C_1)^2} \right] \langle t,r \vert \right. \nonumber \\{} & {} \left. + M_0 \int _{r_0(t)}^{\infty } \frac{\mathrm{{d}}r}{r^2} \vert t,r \rangle \langle t,r \vert \right\} \,. \end{aligned}$$
(66)

This operator fulfills the condition (61)

$$\begin{aligned} |\langle \Psi _2 \vert \hat{M} \vert \Psi _1 \rangle | \le M_0 \Vert \Psi _2 \Vert \Vert \Psi _1 \Vert \,, \end{aligned}$$
(67)

which implies that \(\hat{M}\) is a bounded operator.

Using the resolution of the unity (57), the mass operator can be rewritten as

$$\begin{aligned}{} & {} \hat{M} = M_0 \hat{1\hspace{-4.75pt}1}+ \frac{1}{2\pi A_\phi } \int _{-\infty }^{\infty } \mathrm{{d}}t \, \int _{0}^{r_0(t)} \frac{\mathrm{{d}}r}{r^2} \vert t,r \rangle \nonumber \\{} & {} \left[ \frac{2\lambda ^2}{9}\frac{r^3}{(\lambda t+ C_1)^2} -M_0 \right] \langle t,r \vert \,. \end{aligned}$$
(68)

This form of the mass operator shows that the calculated mass is independent of the shape of the wave function \(\Psi (t,r):=\langle t,r \vert \Psi \rangle \) outside of the star, i.e., for \(r \ge r_0(t)\). This also implies that all states \(\vert \Psi _{M_0} \rangle \in \mathcal H\) satisfying the condition \(\langle t,r \vert \Psi _{M_0} \rangle =0\) for all \(r \le r_0(t)\) are eigenstates of the mass operator which belongs to the eigenvalue \(M_0\)

$$\begin{aligned} \hat{M} \vert \Psi _{M_0} \rangle = M_0 \vert \Psi _{M_0} \rangle \,, \end{aligned}$$
(69)

i.e., \(M_0\) is the upper bound of the mass spectrum. On the other hand, the mass function is non-negative. The condition \(M(t,r) \ge 0\) determines the lower bound of the mass operator spectrum to be equal to zero.

According to the interpretation of the state spaces of our quantum system described in Appendix (C), the corresponding scalar product \(\langle t,r \vert \Psi _{M_0} \rangle \) should be interpreted as the probability amplitude of finding our OS star at time t in the form of a spherical three-dimensional object with radius r. The constructed mass operator \(\hat{M}\) (see (66)) measures the full mass of the OS star bounded by the classical radius \(r_0(t)\). This feature and the fact that \(M_0\) is the maximum of the mass operator imply that all the amplitudes \(\langle t,r \vert \Psi \rangle \) have to be equal to zero inside the star, for every acceptable physical state \(\vert \Psi \rangle =\vert \Psi _{M_0} \rangle \in \mathcal H\).

The above suggests that the mass operator (66) also has eigenstates corresponding to masses smaller than \(M_0\). It is clear that all the states \(\vert \Psi \rangle \in \mathcal H\) for which the amplitudes \(\langle t,r \vert \Psi \rangle \) are not identically equal to zero inside the star correspond to smaller masses than \(M_0\). In the case of an isolated OS star, such states do not occur because of the conservation of the total energy. However, some perturbations of the eigenstates (69) can lead to a mass smaller than \(M_0\) and possibly new dynamics of the OS star.

Such mass variation may come, for example, from the physical process of Hawking radiation. However, some analyses (see, e.g., [29]) suggest that this dissipative process has minor effects on the deeply quantum regime inside a black hole (but should be implemented into analysis for completeness). Our formalism gives some possibility of a description of such a process. However, a mathematical description requires the preparation of a kind of transition operator which transforms a state of given mass to a state of lower mass. This interesting feature requires further analysis and will be consider elsewhere.

In what follows, we consider the quantum states corresponding to the total mass \(M_0\), defined to be wave packets localized within given time and space intervals, and additionally having a “hole” including the singularity at \(t=t_c\). Qualitatively, each packet represents a wave function with compact support. The wave function without a hole can be obtained in the limit \(\epsilon \rightarrow 0^+\). This type of wave packet can be written as

$$\begin{aligned} \psi _{\eta _1,\eta _2}(t,r)= & {} \frac{1}{\sqrt{N}}\,r\,\chi _{\left( r(t,\eta _1),r(t,\eta _1+\delta _1) \right) }(r)\, \chi _{\left( \eta _2-\frac{\delta _2}{2},\eta _2+\frac{\delta _2}{2}\right) }(t)\,\nonumber \\{} & {} \times \left( 1-\chi _{\left( t_c-\frac{\epsilon }{2},t_c +\frac{\epsilon }{2}\right) }(t)\right) \,, \end{aligned}$$
(70)

where \(\delta _1,\delta _2>0\), \(\eta _1\in \langle 0,\infty )\), and \(\eta _2 \in (-\infty ,\infty )\). In addition, we assume the condition \(0< \epsilon < \delta _2\), which defines the wave functions with width larger than the hole around the singularity. This means that we consider a subset of wave functions which totally cover the hole. They are equal to zero within the hole and are different from zero outside the hole. In this way, they connect both regions separated by the singularity.

In what follows, we use the following auxiliary functions: The characteristic function \(\chi _{(a,b)}(x)\) of the set (a, b) defined as

$$\begin{aligned} \chi _{(a,b)}(x)=\left\{ \begin{array}{lll} 1&{}\text{ for }&{}x\in (a,b)\\ 0&{}\text{ for }&{}x\not \in (a,b) \end{array} \right. \;, \end{aligned}$$
(71)

and the function r(x, y) defined as

$$\begin{aligned} r(x,y)=\root 3 \of {\frac{9}{2}}y^{\frac{1}{3}}(x-t_c)^{\frac{2}{3}}\;, \qquad t_c=-\frac{C_1}{\lambda } \,, \end{aligned}$$
(72)

which represents the radius of the shell with mass y at time x.

Next, we define two new functions in terms of integrals

$$\begin{aligned} \mathcal {G}_\alpha (a,b) =\int _a^b \mathrm{{d}}x\, x^{\alpha -1} =\frac{1}{\alpha }\left( b^\alpha -a^\alpha \right) \,,\quad \alpha \ne 0 \,, \end{aligned}$$
(73)

and

$$\begin{aligned}{} & {} \mathcal {F}_\alpha (\eta _2)= \int _{\eta _2-\frac{\delta _2}{2}}^{\eta _2+\frac{\delta _2}{2}}\mathrm{{d}}x\, (x-t_c)^{\alpha -1} \left( 1-\chi _{\left( t_c-\frac{\epsilon }{2},\;t_c+\frac{\epsilon }{2}\right) }(x) \right) \end{aligned}$$
(74)
$$\begin{aligned}{} & {} = \left\{ \begin{array}{lll} \mathcal {G}_\alpha \left( \eta _2^-,\eta _2^+\right) &{}\text{ for }&{} \eta _2 \le t_c-\frac{\epsilon +\delta _2}{2} \\ \mathcal {G}_\alpha \left( \eta _2^-,-\frac{\epsilon }{2}\right) &{}\text{ for }&{} t_c-\frac{\epsilon +\delta _2}{2}< \eta _2 \le t_c-\frac{\delta _2-\epsilon }{2} \\ \mathcal {G}_\alpha \left( \eta _2^-,-\frac{\epsilon }{2}\right) + \mathcal {G}_\alpha \left( \frac{\epsilon }{2},\eta _2^+\right) &{}\text{ for }&{} t_c-\frac{\delta _2-\epsilon }{2}< \eta _2 \le t_c+\frac{\delta _2-\epsilon }{2} \\ \mathcal {G}_\alpha \left( \frac{\epsilon }{2},\eta _2^+\right) &{}\text{ for }&{} t_c+\frac{\delta _2-\epsilon }{2}< \eta _2 \le t_c+\frac{\delta _2+\epsilon }{2} \\ \mathcal {G}_\alpha \left( \eta _2^-,\eta _2^+\right) &{}\text{ for }&{} \eta _2 > t_c+\frac{\delta _2+\epsilon }{2} \end{array} \right. \nonumber \\ \end{aligned}$$
(75)

where

$$\begin{aligned} \eta _2^-:=\eta _2-\frac{\delta _2}{2}-t_c, \qquad \eta _2^+:=\eta _2+\frac{\delta _2}{2}-t_c~\,. \end{aligned}$$
(76)

It is worth noting that we have

$$\begin{aligned} \mathcal {F}_{\alpha }(\eta _2)\xrightarrow []{\epsilon \rightarrow 0}\left\{ \begin{array}{lll} \mathcal {G}_\alpha (\eta _2^-,\eta _2^+)&{}\text{ for }&{}\alpha >0\\ \infty &{}\text{ for }&{} \alpha < 0 \,. \end{array} \right. \end{aligned}$$
(77)

The normalization constant of the wave packets (70) reads

$$\begin{aligned} N=\frac{1}{2\pi A_\phi }\frac{1}{3}\,\root 3 \of {\frac{9}{2}}\; \mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)\; \mathcal {F}_{\frac{5}{3}}(\eta _2) \,. \end{aligned}$$
(78)

The expectation value of the operator \(\hat{t}\) is

$$\begin{aligned}{} & {} t_Q(\eta _1,\eta _2):= \langle \psi _{\eta _1,\eta _2} \vert \hat{t} \vert \psi _{\eta _1,\eta _2} \rangle \nonumber \\{} & {} =\frac{1}{2\pi A_\phi }\frac{1}{N} \int _{\eta _2-\frac{\delta _2}{2}}^{\eta _2+\frac{\delta _2}{2}}\mathrm{{d}}t\, t \left( 1-\chi _{ \left( t_c-\frac{\epsilon }{2},t_c+\frac{\epsilon }{2}\right) }(t) \right) \int _{r(t,\eta _1)}^{r(t,\eta _1+\delta _1)}\mathrm{{d}}r \nonumber \\{} & {} =\frac{\mathcal {F}_{\frac{8}{3}}(\eta _2)}{\mathcal {F}_{\frac{5}{3}}(\eta _2)} +t_c . \end{aligned}$$
(79)

The expectation value of the operator \(\hat{r}\) is found to be

$$\begin{aligned}{} & {} r_Q(\eta _1,\eta _2):= \langle \psi _{\eta _,\eta _2} \vert \hat{r} \vert \psi _{\eta _1,\eta _2} \rangle \nonumber \\{} & {} =\frac{1}{2\pi A_\phi }\frac{1}{N} \int _{\eta _2-\frac{\delta _2}{2}}^{\eta _2+\frac{\delta _2}{2}}\mathrm{{d}}t \left( 1-\chi _{\left( t_c-\frac{\epsilon }{2},t_c+\frac{\epsilon }{2}\right) }(t) \right) \, \int _{r(t,\eta _1)}^{r(t,\eta _1+\delta _1)}\mathrm{{d}}r\, r \nonumber \\{} & {} =\root 3 \of {\frac{9}{2}}\; \frac{\mathcal {G}_{\frac{2}{3}}(\eta _1,\eta _1+\delta _1)}{ \mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}\; \frac{\mathcal {F}_{\frac{7}{3}}(\eta _2)}{\mathcal {F}_{\frac{5}{3}}(\eta _2)} . \end{aligned}$$
(80)

The expectation value of the mass operator \(\hat{M}\) reads

$$\begin{aligned} \langle \psi _{\eta _1,\eta _2} \vert \hat{M} \vert \psi _{\eta _1,\eta _2} \rangle = M_0 \,, \end{aligned}$$
(81)

where \(\eta _1 \ge M_0\).

For very small values of \(\delta _2\) and \(\epsilon \), the functions \(t_Q(\eta _1,\eta _2)\) and \(r_Q(\eta _1,\eta _2)\) can be approximated as

$$\begin{aligned}{} & {} t_Q(\eta _1,\eta _2) \approx \eta _2 \,, \end{aligned}$$
(82)
$$\begin{aligned}{} & {} _Q(\eta _1,\eta _2) \approx \root 3 \of {\frac{9}{2}} \eta _1^{\frac{1}{3}} (\eta _2-t_c)^{\frac{2}{3}} \,. \end{aligned}$$
(83)

Comparing these formulae with their classical counterparts, we get \(\eta _1 = M_0\), and we see that the parameter \(\eta _2\) corresponds to the classical time (but only to some extent).

With fixed \(\eta _1\), the quantum radius of the OS star \(r_Q(\eta _1,\eta _2)\) is found to achieve its minimum at \(\eta _2=t_c\) and reads

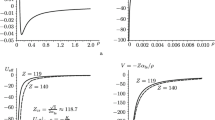
$$\begin{aligned} r_{Q}(\eta _1,t_c)= \root 3 \of {\frac{9}{2}}\; \frac{ \mathcal {G}_{\frac{2}{3}}(\eta _1,\eta _1+\delta _1)}{ \mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}\; \frac{5}{7} \left( \frac{1}{2}\right) ^{\frac{2}{3}} \frac{ \delta _2^{\frac{7}{3}}-\epsilon ^{\frac{7}{3}} }{ \delta _2^{\frac{5}{3}}-\epsilon ^{\frac{5}{3}} }.\nonumber \\ \end{aligned}$$
(84)

The radius \(r_{Q}(\eta _1,t_c)\) represents the bouncing radius of the OS star. The corresponding quantum time \(t_{Q}(\eta _1,t_c)=t_c\), as \(\mathcal {F}_{\frac{8}{3}}(t_c)=0\) in (79), so that it is equal to the time at which the classical singularity is achieved. After the bounce, the quantum star expands (see Fig. 1). This phenomenon does not disappear even for the states without the whole, i.e., for \(\epsilon =0\).

Fig. 1
figure 1

The \(r_{Q}(\eta _1,\eta _2)\) function (see Eq. (80)) for \(\eta _2 \in [-10,10]\), with \(\eta _1=2=M_0\) (blue curve), \(\eta _1=5\) (orange curve), \(\eta _1=20\) (green curve), where \(\delta _1=\delta _2=1\), \(\epsilon =10^{-5}\), and \(t_c=5\)

Full size image

Another interesting aspect of the evolution of the OS star is its horizon, which the collapsing star reaches, corresponding to the classical time \(t_h\) given by the formula (40). To estimate the parameters \(\eta _2\), while \(\eta _1 = M_0\), let us impose the condition

$$\begin{aligned} t_Q(M_0,\eta _2)= t_h = t_c - \frac{4}{3} M_0. \end{aligned}$$
(85)

For small \(\delta _1,\delta _2\), and \(\epsilon \), the approximate solution of Eq. (85) is found to be \(\eta _2 = t_c - \frac{4}{3} M_0\). In this approximation, the horizon radius \(r_Q(M_0,\eta _{2}) \approx 2M_0\), i.e., it reproduces the classical condition for the horizon.

The vector state in the form of the wave packet (70) is well defined for any t, including the neighborhood of the singularity at \(t_c\). Thus, the quantum dynamics in terms of expectation values (79) and (80) are well defined before and after the singularity. See, for instance, the case of a very small \(\delta _2\) and \(\epsilon \) presented by (82) and (83). In particular, the equation

$$\begin{aligned} \langle \psi _{\eta _1,\eta _2} \vert \hat{r} \vert \psi _{\eta _1,\eta _2} \rangle = 2\; \langle \psi _{\eta _1,\eta _2} \vert \hat{M} \vert \psi _{\eta _1,\eta _2} \rangle \,, \end{aligned}$$
(86)

for \(\eta _1 = M_0\), is formally well defined. This equation corresponds to the classical equation (40) that determines the horizon (46), but is defined at the quantum level. Due to (80) and (81), Eq. (86) can be rewritten as

$$\begin{aligned} \root 3 \of {\frac{9}{2}}\; \frac{\mathcal {G}_{\frac{2}{3}}(M_0,M_0+\delta _1)}{ \mathcal {G}_{\frac{1}{3}}(M_0,M_0+\delta _1)}\; \frac{\mathcal {F}_{\frac{7}{3}}(\eta _2)}{\mathcal {F}_{\frac{5}{3}}(\eta _2)} = 2 M_0 \,. \end{aligned}$$
(87)

Let us solve Eq. (87) numerically. We take \(t_c = 1\) and \(M_0=\eta _1=1\); the state parameters \(\delta _1=0.01\), \(\delta _2=0.2\), and \(\epsilon =0.1\). For such values of the state parameters, Eq. (86) has two solutions for \(\eta _2\), which we denote as \(\eta _{2\,h} = 1 \mp 1.32877 \approx t_c \mp \frac{4}{3}M_0\). The second solution, \(\eta _{2\,h} = 1 + 1.32877\), that follows the bounce does not have as clear a physical meaning as the one preceding the bounce. This will be further discussed in Sect. 5.

These numerical results are not changed qualitatively for a different choice of parameters or for the states without a hole, i.e., for \(\epsilon =0\).

3.3 Fate of classical singularities

In what follows, we address the issue of the classical singularities of the Oppenheimer–Snyder black hole at the quantum level.

Let us introduce the following function:

$$\begin{aligned} \mathcal {A}(\alpha ,\beta ,\gamma )=\frac{1}{(t-t_c)^\alpha }M(t,r)^\beta r^{-\gamma } . \end{aligned}$$
(88)

Our curvature invariants (36)–(38) can be expressed in terms of \(\mathcal {A}\) in the following way:

$$\begin{aligned}{} & {} R_{\mu \nu }R^{\mu \nu }=8\,\mathcal {A}(2,1,3) \,, \end{aligned}$$
(89)
$$\begin{aligned}{} & {} \mathcal {R}=(-2\sqrt{2})\,\mathcal {A}\left( 1,\frac{1}{2},\frac{3}{2}\right) \,, \end{aligned}$$
(90)
$$\begin{aligned}{} & {} K=48\,\mathcal {A}(2,1,3)+32\sqrt{2}\,\mathcal {A}\left( 2,\frac{3}{2},\frac{9}{2}\right) +48\,\mathcal {A}(0,2,6).\nonumber \\ \end{aligned}$$
(91)

The expectation value of the operator \(\hat{\mathcal {A}}(\alpha ,\beta ,\gamma )\) is found to be

$$\begin{aligned}{} & {} \langle \psi _{\eta _1,\eta _2} \vert \hat{\mathcal {A}}(\alpha ,\beta ,\gamma ) \vert \psi _{\eta _1,\eta _2} \rangle \nonumber \\{} & {} \quad =\frac{1}{2\pi A_\psi }\, \frac{1}{N} \int _{\eta _2-\frac{\delta _2}{2}}^{\eta _2+\frac{\delta _2}{2}}\mathrm{{d}}t \left( 1-\chi _{\left( t_c-\frac{\epsilon }{2},t_c +\frac{\epsilon }{2}\right) }(t)\right) \,\nonumber \\{} & {} \qquad \times \int _{r(t,\eta _1)}^{r(t,\eta _1+\delta _1)}\mathrm{{d}}r \frac{M(t,r)^\beta }{(t-t_c)^\alpha r^\gamma } \nonumber \\{} & {} \quad =\left( \frac{2}{9}\right) ^{\frac{\gamma }{3}} \frac{\mathcal {F}_{\frac{5}{3}-\frac{2}{3}\gamma -\alpha }(\eta _2)}{ \mathcal {F}_{\frac{5}{3}}(\eta _2)}\cdot \\{} & {} \qquad \cdot \nonumber \left\{ \begin{array}{lll} \frac{\mathcal {G}_{\beta -\frac{\gamma }{3}+\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}{ \mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}&{}\text{ for }&{} \eta _1<M_0-\delta _1 \\ \frac{ \mathcal {G}_{\beta -\frac{\gamma }{3}+\frac{1}{3}}(\eta _1,M_0)+ M_0^\beta \mathcal {G}_{\frac{1}{3}-\frac{\gamma }{3}}(M_0,\eta _1+\delta _1) }{\mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}&{} \text{ for } &{} M_0-\delta _1 \le \eta _1 < M_0 \,. \nonumber \\ M_0^\beta \frac{\mathcal {G}_{\frac{1}{3} -\frac{\gamma }{3}}(\eta _1,\eta _1+\delta _1)}{ \mathcal {G}_{\frac{1}{3}}(\eta _1,\eta _1+\delta _1)}&{} \text{ for } &{} \eta _1 \ge M_0 \end{array} \right. \end{aligned}$$
(92)

Is it possible for the expectation value of the operator \(\hat{\mathcal {A}}\) to be infinite? Let us examine this issue.

Since the numerators in Eq. (92) are defined in terms of the functions \(\mathcal {G}_\alpha (a,b)\), the infinity can be achieved if and only if one has division by zero. In the denominators, we obtain two kinds of functions which can potentially be equal to zero. The first one is \(\mathcal {G}_{\frac{1}{3}}(a,b)=0\) for \(a=b\). This condition cannot be satisfied for \(\delta _1>0\). The second one is the function \(\mathcal {F}_{\frac{5}{3}}(\eta _2)\), which is a combination of the functions \(\mathcal {G}\). Making use of the definition (74) and the fact that \(\mathcal {G}_{\frac{5}{3}}(a,b)=0\) is true only for \(a=b\), the only case of division by zero is when \(\eta _2^- \le -\frac{\epsilon }{2}\) and \(\frac{\epsilon }{2} \le \eta _2^+\). However, in the case \(\delta _2>\epsilon \), the two boundary conditions \(\eta _2^- =-\frac{\epsilon }{2}\) and \(\frac{\epsilon }{2} =\eta _2^+\) cannot be fulfilled simultaneously. Therefore, the function \(\mathcal {F}_{\frac{5}{3}}(\eta _2)\) is not equal to zero for any \(\eta _2\). We conclude that the expectation value of the operator \(\hat{\mathcal {A}}\) for the states \(\psi _{\eta _1\eta _2}\) is not singular. Therefore, the expectation values of the operators corresponding to the invariants (89)–(91) do not diverge anywhere.

On the other hand, according to Eq. (77), it is easy to see that we have

$$\begin{aligned} \langle \psi _{\eta _1,\eta _2} \vert \hat{\mathcal {A}}\vert \psi _{\eta _1,\eta _2} \rangle \xrightarrow [] {\epsilon \rightarrow 0}\infty \,, \end{aligned}$$
(93)

so that the expectation values of the operators corresponding to (89)–(91) diverge.

It is instructive to examine the variance of this operator in the case \(\epsilon \rightarrow 0^+\). The variance of the symmetric operator \(\hat{\mathcal {A}}\) in the quantum state \(|\psi \rangle \in \mathcal {K}\) with compact support, for \(\epsilon > 0\), is as follows [8, 30]:

$$\begin{aligned} \textrm{var}(\hat{\mathcal {A}},\psi ):= & {} \langle \psi |\big (\hat{\mathcal {A}}- \langle \hat{\mathcal {A}}\rangle _\psi \hat{1\hspace{-4.75pt}1}\big )^2 \psi \rangle \nonumber \\{} & {} = \langle \big (\hat{\mathcal {A}}- \langle \hat{\mathcal {A}}\rangle _\psi \hat{1\hspace{-4.75pt}1}\big )\psi |\big (\hat{\mathcal {A}}- \langle \hat{\mathcal {A}}\rangle _\psi \hat{1\hspace{-4.75pt}1}\big )\psi \rangle \nonumber \\= & {} \Vert \big (\hat{\mathcal {A}}- \langle \hat{\mathcal {A}}\rangle _\psi \hat{1\hspace{-4.75pt}1}\big )\psi \Vert ^2 , \end{aligned}$$
(94)

where \(\langle \hat{\mathcal {A}}\rangle _\psi := \langle \psi | \hat{\mathcal {A}}\psi \rangle \). Thus, \(\textrm{var}(\hat{\mathcal {A}},\psi ) >0\) for any nonzero vector of the Hilbert space \(\mathcal {K}\) if and only if \(\hat{\mathcal {A}}|\psi \rangle \ne \langle \hat{\mathcal {A}}\rangle _\psi \hat{1\hspace{-4.75pt}1}\psi \rangle \). The latter means that \(|\psi \rangle \) is not an eigenstate of \(\hat{\mathcal {A}}\), which is the case for the wave packet (70) for any \(\epsilon \), and in particular for \(\epsilon = 0\) due to (93). Thus, the singularity in this case does occur, but it is smeared. Consequently, the expectation values of the operators corresponding to the invariants (89)–(91) are singular, but these singularities occur with nonzero fluctuations.

4 Quantum Schwarzschild black hole

Recently, we quantized the Schwarzschild spacetime with the negative mass parameter, \(M <0\), to address the case with a naked singularity [8, 31]. Here, we consider the case with a covered singularity \(M>0\). The case \(M=0\) corresponds to the Minkowski spacetime.

The Schwarzschild black hole (SBH) is a spherically symmetric, static solution of the Einstein field equations, parameterized by the constant \(M > 0\), having the horizon at \(r=2M\) and the gravitational singularity at \(r = 0\). It is an exact spacetime geometry of a non-rotating “point particle” with the mass parameter M devoid of “internal” dynamics [32].

Let us identify the SBH within our formalism. To this end, let us consider the line element defined by (9) and (10) with \(E=0\). It is clear that the constant M satisfies Eq. (12). To see that it corresponds to the SBH, we argue as follows. Evaluating the Einstein tensor with the metric so obtained leads to zero, which means that it corresponds to the vacuum case. The Birkhoff theorem implies that this spherically symmetric vacuum solution must be diffeomorphic to the Schwarzschild metric (for more detail, see [4]).

It results from (31)–(46) that the only non-vanishing invariant is the Kretschmann scalar \(K = 48 M^2 r^{-6}\). In our recent paper [8], we showed that quantization smears the singularity indicated by the Kretschmann scalar, avoiding its localization in the configuration space. Here, we can obtain quite similar results using the quantum state (70) with \(\epsilon = 0\). Applying the reasoning following Eq. (93) leads to the result

$$\begin{aligned} \textrm{var}(\hat{K}; \psi _{\eta _1,\eta _2}) > 0, \end{aligned}$$
(95)

where \(\hat{K}\) is the quantum operator corresponding to the Kretschmann scalar K. Thus, the singularity in this case does occur, but it is smeared.

However, making use of the quantum state (70) with \(\epsilon > 0\), we obtain the result (92) specialized to the case of the Kretschmann operator. Therefore, we conclude that the expectation value of the Kretschmann operator is finite, which resolves the classical singularity problem.

5 Conclusions

We have shown in this paper that the evolution of the OS dust star model under consideration consists of three phases: classical collapse towards the gravitational singularity, quantum evolution, and classical expansion away from the singularity. The quantum evolution consists of quantum collapse, strongly quantum regime, and quantum expansion. The quantum collapse and expansion are described by the evolution of the expectation value of the position operator. The strong quantum regime may present a regular quantum bounce or smeared singularity.

We have obtained the above scenario by making use of the vector state in the form of the wave packet with compact support parameterized by two real parameters \(\eta _1\) and \( \eta _2\). Thus, these vector states represent a wide class of quantum states in the considered Hilbert space \(\mathcal K'\) (see Appendix C). Therefore, our resolution of the classical gravitational singularity of the OS model is not generic but is possible within the considered quantum system ascribed to that classical one.

As the system is spherically symmetric, it possesses a horizon that is formed during the first classical phase of its evolution if the dust density is high enough (due indirectly to the Birkhoff theorem). The second expression for the horizon, derived from Eq. (86), following the bounce does not have as clear a meaning. We suggest that it may describe the disappearance of the first horizon created before the bounce. In such case, the bouncing time of the considered black hole can be estimated by \(\frac{8}{3}M_0\). The quantum evolution may describe the so-called black-to-white hole transition (see, e.g., [14] and references therein).

We present the quantum Schwarzschild spacetime for the positive mass parameter, \(M>0\), that we promised to carry out in our recent paper [8] concerning the case \(M<0\). That paper concerns the naked singularity. Here, we are concerned with the covered singularity, i.e., the black hole case. The resolution of the classical singularity is done in a way quite similar to that for the OS spacetime, as the former is a special case of the latter.

Our quantum description of the collapsing dust star corresponds to the flat sector of the dust collapse presented in [19] (while described in co-moving coordinates). However, we apply different parameterization of the affine group. It is worth mentioning that different parameterizations may lead to unitarily nonequivalent quantum theories [27]. In our parameterization, the expectation values of elementary observables calculated in coherent states coincide with corresponding classical observables. Therefore, we use the quantum states in the form of wave packets. They enable us to obtain the quantum bounce of the space operator. All the states parameterized by parameters such as deltas and epsilon in Eq. (70) satisfy the required physical condition and improve the flexibility of the model. In principle, such parameters can be determined either by observational data or by a more realistic model of the matter field. Another difference is that we have analyzed the evolution of the curvature invariants. The expectation values obtained for the corresponding quantum operators are either singular but smeared, or regular.

In both approaches, ours and that of [19], the bouncing time of the considered quantum black hole is numerically similar. In both papers, the issue of possible Hawking radiation is relegated to future papers.

In this paper we have used an idea of time as a quantum observable, similar to the space position quantum observable. A proposal for treating time on the same footing as other quantum observables was recently published as the projection evolution approach (PEv) in [33]. In the present paper, we do not apply the full PEv formalism, which allows us, in principle, to obtain detailed dynamics of the system by constructing the so-called evolution operators. Instead, we build a family of some, but not all, possible evolution scenarios of our OS star by constructing a family of states with required physical properties. One of the most important feature of our wave packets is that in a limit of very narrow functions \(\psi _{\eta _1,\eta _2}\), the expectation values of \(\hat{t}\),\(~\hat{r}\) and \(\hat{M}\) operators reproduce the classical motion of the OS star, far from singularity. This constraint allows us to choose some possible evolution paths and calculate them as relations among expectation values of the fundamental observables in this model, i.e., the time, the position, and the global mass.

Our next paper will concern the quantum system ascribed to the LTB model of a collapsing star. Within this model, one can consider the inclusion of realistic features of a matter field, such as pressure and inhomogeneity in density distribution, and a reasonable equation of state. Considering the cases with a covered singularity and a naked singularity separately will make it possible to gain deeper insight into the issue of the quantum bounce.