Gauge waves generation and detection in Aharonov–Bohm electrodynamics

Abstract

The extended Aharonov–Bohm electrodynamics has a simple formal structure and allows to couple the e.m. field also to currents which are not locally conserved, like those resulting from certain non-local effective quantum models of condensed matter. As it often happens in physics and mathematics when one tries to extend the validity of some equations or operations, new perspectives emerge in comparison to Maxwell theory, and some “exotic” phenomena are predicted. For the Aharonov–Bohm theory the main new feature is that the potentials $A^\mu$ become univocally defined and can be measured with probes in which the “extra-current” $I=\partial _\mu j^\mu$ is not zero at some points. As a consequence, it is possible in principle to detect pure gauge-waves with ${\textbf{E}}={\textbf{B}}=0$, which would be regarded as non-physical in the Maxwell gauge-invariant theory with local current conservation. We discuss in detail the theoretical aspects of this phenomenon and propose an experimental realization of the detectors. A full treatment of wave propagation in anomalous media with extra-currents and of energy–momentum balance issues is also given.

1 Introduction

Although classical and quantum electrodynamics are among the most precise and successful theories in physics, there are reasons to look for extensions of Maxwell equations in various directions and physical contexts [1, 2]. In particular, we are interested into the extension first proposed by Ohmura [3] and often called “Aharonov–Bohm electrodynamics” because of their major contribution ([4]; see also [5,6,7,8,9,10,11,12,13]). The logical motivation for this extension, at least from today’s perspective, is the quest for a Lagrangian density which has the most general covariant form, in terms of four-potentials $A_\mu$ and sources $j^\mu$ (not necessarily locally conserved). Apart from the addition of a total four-divergence, this form is

$$\begin{aligned} L_{A.-B.}=\frac{1}{4\mu _0} F_{\mu \nu }F^{\mu \nu }-\frac{\lambda }{2\mu _0} (\partial _\mu A^\mu )^2+A_\mu j^\mu \end{aligned}$$

(1)

where a possible additional photon mass term proportional to $A_\mu A^\mu$ has been excluded based on experimental evidence.

1.1 Formal structure of local Aharonov–Bohm electrodynamics

We shall call (1) the “Aharonov–Bohm Lagrangian”, even though it is in fact a well-known expression contained in textbooks (see e.g. [14, 15]) and its unicity has been proven by Woodside [16] in vector formalism. This Lagrangian is gauge-invariant in the familiar sense only if $\lambda =0$. Therefore by considering extensions with non-zero $\lambda$ we are sacrificing gauge invariance to extended relativistic invariance and especially to the possibility of coupling $A_\mu$ to a current $j^\mu$ which is not locally conserved.

Maxwell theory with full gauge invariance can be of course re-obtained from this extended theory in the special case when $\lambda =0$ and current is locally conserved everywhere. The power of gauge theories in quantum field theory and particle physics of course strongly suggests to make this symmetrical choice whenever possible.

The special choice $\lambda =1$ is known in the literature as “Feynman gauge” (although it is not a gauge condition in the usual sense) and leads to a quantization method which is alternative to the Gupta–Bleuler method or to canonical quantization [15]. As we show in the following, in the extended Aharonov–Bohm theory this choice is natural and almost mandatory in the presence of currents which are not locally conserved.

The field equations derived from the Lagrangian (1) are

$$\begin{aligned} \partial ^2 A^\mu + (\lambda -1) \partial ^\mu \partial _\nu A^\nu =\mu _0 j^\mu \end{aligned}$$

(2)

with $\partial ^2=\partial _\mu \partial ^\mu$. From this one has by contraction

$$\begin{aligned} \partial ^2 (\partial _\nu A^\nu )= \frac{\mu _0}{\lambda }I \end{aligned}$$

(3)

where I is called “extra-current” and defined as

$$\begin{aligned} I=\partial _\mu j^\mu \end{aligned}$$

(4)

This allows to rewrite Eq. (2), for $\lambda \ne 0$, as

$$\begin{aligned} \partial ^2 A^\mu = \mu _0 j^\mu + \mu _0 \frac{1-\lambda }{\lambda } \partial ^\mu [(\partial ^2)^{-1} I] \end{aligned}$$

(5)

Now, on physical grounds it is very tempting to add the condition that in these equations the fields are “locally forced” by the physical sources $j^\mu$, in the sense that second derivatives of the fields at one point in spacetime are determined by the values of the sources at that point. All fundamental theories for massless fields give, at least in their linearized versions, wave equations for the field which have this property.

In this case, this is accomplished by setting $\lambda =1$. As a consequence, the four-potentials of Aharonov–Bohm theory resemble those of Maxwell theory in Lorentz gauge or Feynman gauge, and in fact we shall express them routinely as retarded integrals over the sources. There is a clear difference, however, apparent from Eq. (3): if charge is not locally conserved everywhere, it is not possible in general to impose the gauge condition $\partial _\nu A^\nu =0$. Actually, there is no gauge freedom in the AB theory, except for the possibility of reduced gauge transformations of the form $A^\mu \rightarrow A^\mu +\partial ^\mu \chi$, where the function $\chi$ satisfies $\partial ^2 \chi =0$.

Therefore in most physical situations where the physical sources are localized, the potentials are completely determined. As we shall see in the following, they can even be measured using hypothetical material probes in which $\partial _\mu j^\mu \ne 0$ ! All other “standard” probes can only measure the fields $F^{\mu \nu }$ (i.e., ${\textbf{E}}$ and ${\textbf{B}}$).

From the discussion above it is also clear that in A.-B. electrodynamics there is a sort of additional degree of freedom, namely a scalar field $S=\partial _\mu A^\mu$ satisfying the equation $\partial ^2 S=\mu _0 I$. It is not really an independent degree of freedom because it is expressed in terms of $A_\mu$, but it appears explicitly in the extended field equations. The scalar field becomes automatically decoupled from the sources if $I = 0$.

We do not think that S can have any relevant physical effects in normal laboratory conditions, because we hypothesize that violations of local charge conservation can only occur in microscopic quantum sources whose emission is very weak at the macroscopic scale (the situation may be different at an astrophysical or cosmological scale, see e.g. [17]). Nevertheless, precise measurements could allow to detect the generation of an S field [18, 19]. Also, in order to check the general consistency of the theory, we have computed the propagation of S in material media and found that it is completely reflected by ohmic conductors and pure dielectrics (see [20], preferably in the arXiv version).

Table 1 Formal framework of Aharonov–Bohm extended electrodynamics with the choice $\lambda =1$ which ensures local field equations. The “minimalistic” structure of the theory appears: given the currents $j^\mu$, one directly solves for $A^\mu$ and computes the Lorenz four-force density on a probe with current $j^\mu _p$ and extra-current $I_p$. The four-force density is given here also in vector form in view of the simple application to a $\phi$-probe described later; the relation between four- and three-vectors is $A^\mu =(\phi /c,{\textbf{A}})$, $j^\mu =(c\rho ,{\textbf{j}})$

1.2 Energy conservation. Lorenz force

The conceptual structure of the theory is summarized in Table 1. In order to complete the picture we still need the conservation laws of energy and momentum of the extended e.m. field and the generalization of the formula for the Lorenz force.

The conservation laws have been derived in [12] by coupling the field to a generic gravitational background. The calculation is complex, but the result is relatively simple and the energy density u, for example, can be written in vector formalism as

$$\begin{aligned} u=\frac{1}{\mu _0} \left( \frac{{\textbf{E}}^2}{2c^2} + \frac{{\textbf{B}}^2}{2} + \frac{\phi }{c^2} \frac{\partial S}{\partial t} - {\textbf{A}} \cdot \nabla S - \frac{S^2}{2} \right) \end{aligned}$$

(6)

Some contributions depending on S and explicitly dependent on the potentials can be seen here.

For the Lorenz force density and for the power exerted on a probe p with charge density $\rho _p$, current density ${\textbf{j}}_p$ and extra-current $I_p$ one finds

$$\begin{aligned} {\textbf{f}}= & {} \rho _p{\textbf{E}}+{\textbf{j}}_p\times {\textbf{B}}-I_p{\textbf{A}} \end{aligned}$$

(7)

$$\begin{aligned} w= & {} {\textbf{j}}_p\cdot {\textbf{E}}-I_p\phi \end{aligned}$$

(8)

This means that anomalous extra-sources not only generate a (usually small) scalar field contributing to the energy density, but can also feel the effect of the potentials ${\textbf{A}}$, $\phi$, and act as probes for measuring them. It is thus confirmed that the Aharonov–Bohm potentials should be regarded as physical. In Sect. 3 we will study a possible concrete realization of a $\phi$-detector.

1.3 In which physical systems can the extra-current I be non-zero?

The physical systems where a violation of local conservation might occur, yielding $I\ne 0$ in some regions, are thought to be mainly the following:

• 1. Complex condensed-matter systems described by a quantum field theory, in which the local conservation of the current operator is spoiled by anomalies occurring in the renormalization process [21, 22].

• 2. Molecular devices, like e.g. carbon nanotubes and other molecular “wires”, in which the effect of bound electrons in the inner orbitals upon the conduction electrons is well modelled through a non-local potential, and the anomaly is not due to the use of a reduced eigenstates base, but remains at any order in the computations [23,24,25,26].

• 3. Systems with explicitly non-local wave equations, e.g. fractional quantum mechanics and other phenomenological models [27,28,29,30,31,32,33,34,35].

• 4. Macroscopic quantum systems like Josephson junctions and superconductors in general. For a system with macroscopic wavefunction, the charge density and current density are represented by non-commuting operators. It follows that the extra-current $I=\partial _t \rho + \nabla \cdot {\textbf{j}}$, being essentially a linear combination of these two operators in the frequency-momentum domain, does not admit eigenstates and has a minimum uncertainty fixed by the Heisenberg relation $\Delta N \Delta \phi \simeq 1$ which involves the occupation number and the phase of the wavefunction. In [12] we have given an estimate of the minimum uncertainty in the case of a tunnel Josephson junction made of Nb.

1.4 Definition and properties of gauge waves

We define a gauge wave as a plane wave with potentials

$$\begin{aligned} \phi= & {} \phi _0 e^{i(\omega t - {\textbf{k}}{\textbf{x}})} \end{aligned}$$

(9)

$$\begin{aligned} {\textbf{A}}= & {} {\textbf{A}}_0 e^{i(\omega t - {\textbf{k}}{\textbf{x}})} \end{aligned}$$

(10)

for which the relation

$$\begin{aligned} \omega {\textbf{A}}_0={\textbf{k}}\phi _0 \end{aligned}$$

(11)

holds. It is therefore a longitudinal wave, with Fourier amplitudes $\phi _0$ and ${\textbf{A}}_0$ connected in absolute value by $|\phi _0|=c|{\textbf{A}}_0|$, as follows from (11) and from $\omega /|{\textbf{k}}|=c$. It is a solution of the AB equations in vacuum $\partial ^2 A^\mu =0$.

Taking the scalar product by ${\textbf{k}}$ in Eq. (11) we also find that

$$\begin{aligned} {\textbf{k}} \cdot {\textbf{A}}_0=\frac{\omega }{c^2}\phi _0 \end{aligned}$$

(12)

This means that the potentials defined by (9), (10) satisfy the equation

$$\begin{aligned} \nabla \cdot {\textbf{A}}+\frac{1}{c^2} \frac{\partial \phi }{\partial t}=0 \end{aligned}$$

(13)

which is the vector equivalent of the Lorentz gauge condition $\partial _\mu A^\mu =0$.

Remembering the definition of the scalar field S as $S=\partial _\mu A^\mu$ we thus see that $S=0$ in a gauge wave. It is also straightforward to prove that in this wave ${\textbf{E}}$ and ${\textbf{B}}$ are zero, using the general relations between fields and potentials, namely

$$\begin{aligned} {\textbf{E}}= & {} \nabla \phi -\frac{1}{c} \frac{\partial {\textbf{A}}}{\partial t}=i({\textbf{k}}\phi _0-\omega {\textbf{A}}_0)e^{i(\omega t - {\textbf{k}}{\textbf{x}})}=0 \end{aligned}$$

(14)

$$\begin{aligned} {\textbf{B}}= & {} \nabla \times {\textbf{A}}=i({\textbf{k}}\times {\textbf{A}}_0)e^{i(\omega t - {\textbf{k}}{\textbf{x}})}=0 \end{aligned}$$

(15)

This property justifies the name chosen for the gauge wave.

Since the fields S, ${\textbf{E}}$ and ${\textbf{B}}$ are all zero in a gauge wave, the wave does not carry any energy and momentum, according to the general expressions in [12] (for the energy flux see also Eq. (48)). In a gauge-invariant theory it would be regarded as non-physical, also because it would be equivalent, via a gauge transformation, to a four-potential which is identically zero. We know, however, that in AB electrodynamics the potentials are physical and interact with an anomalous matter probe with extra-current $I_p$ through the terms $I_p\phi$ and $I_p{\textbf{A}}$ in the Lorenz force density.

In [20] we have proven that, consistently with the picture above, a gauge wave propagates without attenuation in normal media where local charge conservation holds. In Sect. 2.4 of this work the propagation of general plane waves in anomalous media is analysed using the “$\gamma$-model” approximation for the anomalous current density.

1.5 Generation of gauge waves

Concerning the generation of gauge waves, in [20] it was shown that when a plane wave of the S field encounters a normal medium, it cannot enter it but is totally reflected, possibly generating a gauge wave at the interface. This process, however, is not the most efficient way of producing gauge waves, since it requires an incident S wave, which can only be generated by an anomalous oscillating source (see computation in Sect. 4).

It is thus far more convenient to take advantage of the gauge wave components which are generated in normal oscillating dipoles and go unnoticed unless they impinge on a material probe containing an extra-current $I_p$.

In fact, the physical AB potentials of an oscillating dipole are (like in Maxwell theory in Lorentz gauge)

$$\begin{aligned} \phi ({\textbf{x}},t)= & {} \frac{\mu _0 c}{4\pi r} \dot{{\textbf{p}}}(t-r/c)\cdot {\textbf{n}} \end{aligned}$$

(16)

$$\begin{aligned} {\textbf{A}}({\textbf{x}},t)= & {} \frac{\mu _0}{4\pi r} \dot{{\textbf{p}}}(t-r/c) \end{aligned}$$

(17)

where $r=|{\textbf{x}}|$ and ${\textbf{n}}={\textbf{x}}/r$ is the local propagation direction, such that the spherical wave can be approximated at each point by a plane wave with vector ${\textbf{k}}=|{\textbf{k}}|{\textbf{n}}$.

The vector ${\textbf{A}}$ can be decomposed into a longitudinal component

$$\begin{aligned} {\textbf{A}}_{\textbf{n}}=({\textbf{A}}\cdot {\textbf{n}}){\textbf{n}}=\frac{\phi }{c} {\textbf{n}} \end{aligned}$$

(18)

satisfying the gauge wave condition $|{\textbf{A}}_{\textbf{n}}|=\phi /c$, and a transverse component ${\textbf{A}}_T$.

Along the oscillation axis of the dipole we have that ${\textbf{A}}_T=0$, so that the wave is longitudinal and a purely gauge wave. At any other point, the four-potential can be considered as the sum of a gauge wave $(\phi ,{\textbf{A}}_{\textbf{n}})$ and a transverse vector potential $(0,{\textbf{A}}_T)$. If the gauge wave encounters a normal conducting medium it is not affected (supposing the process is linear). The transverse component, on the other hand, generally interacts with the medium and in several cases can be strongly dampened, leaving as a result a pure gauge wave which propagates in the medium and then possibly gets out of the medium again into free space.

A hypothetical detection antenna for gauge waves will be described in Sect. 3.

1.6 Outline

After this long Introduction, the rest of the work will be organized as follows. Section 2 is devoted to what we call the “$\gamma$-model”, namely a simplified one-parameter model for the description of material media containing currents non locally conserved. The non-dimensional parameter $\gamma$ quantifies in a well-defined sense the average, macroscopic effect of the conservation violations which occur at the microscopic level. In Sect. 2.1 the model is applied to free charges, in Sect. 2.2 to dielectric media, where $\gamma$ appears in the relations among ${\textbf{j}}$, ${\textbf{P}}$ (local polarization vector) and ${\textbf{M}}$ (local magnetization vector). As a consequence, in Sect. 2.3 we write the extended AB field equations in a medium and in Sect. 2.4 the wave propagation equations in the medium. Section 3 contains a discussion of possible observable effects of AB extended electrodynamics. In Sect. 3.1 we describe a basic DC circuit for detection of gauge-waves. It contains a voltage generator and a resistor made of a material with conservation violation parameter $\gamma$. The scalar potential $\phi$ of a gauge-wave can interact with the fraction $\gamma$ of the resistor current that is not locally conserved. Using one of the fundamental relations of the $\gamma$-model, namely $\langle \phi I \rangle = \gamma \langle {\textbf{j}}\cdot \nabla \phi \rangle +$ surface term, and imposing energy conservation and conditions for the surface term to be negligible, one can prove that an additional voltage $\delta V$ arises in the resistor, of order $\delta V \sim \gamma \Delta \phi$, where $\Delta \phi$ is the variation of the potential $\phi$ across the conductor length. Section 3.2 contains a description of the possible measurable effects of gauge waves. We first describe the basic scheme of a DC circuit for the detection of a generic potential gradient $\Delta \phi$ through an extra-current flowing in a conductor. Then we consider an antenna detector and its response to an harmonic gauge wave propagating along the direction of the antenna. Section 4 contains a general calculation of radiation fields generated by harmonic currents in anomalous conductors with negligible polarization described by the $\gamma$ model. Fields are computed in the dipole approximation. An evaluation of the time-averaged energy flow at large distance from the source closes the section. Finally, Sect. 5 contains our Conclusions.

2 Material media with non-conserved currents: the $\gamma$ model

In order to build up a theory of Aharonov–Bohm (AB) extended electrodynamics in material media with non-conserved currents we need to reconsider the usual models for the macroscopic description of fields and sources in those media.

To begin, we start with the AB equations in vacuum

$$\begin{aligned} \nabla \cdot {\textbf{E}}= & {} \frac{\rho }{\varepsilon _{0}}-\frac{\partial S}{ \partial t}, \end{aligned}$$

(19a)

$$\begin{aligned} \nabla \cdot {\textbf{B}}= & {} 0, \end{aligned}$$

(19b)

$$\begin{aligned} \nabla \times {\textbf{E}}= & {} -\frac{\partial {\textbf{B}}}{\partial t}, \end{aligned}$$

(19c)

$$\begin{aligned} \nabla \times {\textbf{B}}= & {} \mu _{0}\varepsilon _{0}\frac{\partial {\textbf{E}} }{\partial t}+\mu _{0}{\textbf{j}}+\nabla S, \end{aligned}$$

(19d)

$$\begin{aligned} {\textbf{E}}= & {} -\nabla \phi -\frac{\partial {\textbf{A}}}{\partial t}, \end{aligned}$$

(19e)

$$\begin{aligned} {\textbf{B}}= & {} \nabla \times {\textbf{A}}, \end{aligned}$$

(19f)

$$\begin{aligned} S= & {} \mu _{0}\varepsilon _{0}\frac{\partial \phi }{\partial t}+\nabla \cdot {\textbf{A}}, \end{aligned}$$

(19g)

From Eqs. (19) it results that the extra source I, defined as

$$\begin{aligned} I=\frac{\partial \rho }{\partial t}+\nabla \cdot {\textbf{j}}, \end{aligned}$$

is the source of the scalar, which satisfies

$$\begin{aligned} \mu _{0}\varepsilon _{0}\frac{\partial ^{2}S}{\partial t^{2}}-\nabla ^{2}S=\mu _{0}I. \end{aligned}$$

(20)

These equations are valid if all sources $\varrho$ and ${\textbf{j}}$ are known, which is the main difficulty in dealing with material media. The usual approach is then to consider for all magnitudes macroscopic averages (introduced below), that should average out the small scale, rapid fluctuations of the sources and fields. Furthermore, the sources are separated into free and molecular. Molecular sources are those due to microscopic charges and currents that are highly localized in space, in or around the molecules they belong to. Free charges, on the other hand, are those that are not bounded to a particular molecule and can more or less freely move in the medium.

2.1 Free charges

In the model presented in [13], which we refer here as the I-$\gamma$-j model, or simply $\gamma$ model, it is considered that a likely candidate to account for non-local conservation of charge in material media is the tunnel effect of electrons. If a microscopic free electron current of value $i_{n}$ discontinuously crosses from the point ${\textbf{x}}_{n}$ to the point ${\textbf{x}}_{n}+{\textbf{d}}_{n}$, the corresponding extra source is

$$\begin{aligned} I_{n}=i_{n}\left[ \delta \left( {\textbf{x}}-{\textbf{x}}_{n}-{\textbf{d}} _{n}\right) -\delta \left( {\textbf{x}}-{\textbf{x}}_{n}\right) \right] . \end{aligned}$$

(21)

This relation results from the definition of the extra source I and the semiclassical conceptualization of instantaneous tunneling as the disappearance of the current at ${\textbf{x}}_{n}$ with its simultaneous reappearance at ${\textbf{x}}_{n}+{\textbf{d}}_{n}$, which corresponds to a spatial redistribution of charge without an accompanying electric current. It is to be noted that extra sources with similar opposite peaks appear in the solution of the Schrödinger equation with non-local interactions [35].

Furthermore, in the I-$\gamma$-j model the tunneled current $i_{n}$ in the volume element $d^{3}x=dSdL$ represents a fraction of the current ${\textbf{j}} \cdot d{\textbf{S}}$ traversing it, while the tunneled distance is a fraction of the volume length dL, so that $i_{n}{\textbf{d}}_{n}=\gamma {\textbf{j}}d^{3}x$, with $\gamma$ the product of those fractions. In a sense, the I-$\gamma$-j model represents the simplest phenomenological model one can conceive based on a single parameter.

The idea is now to consider a macroscopically small volume $\delta \Omega$ centered at position ${\textbf{x}}={\textbf{X}}$, with dimensions much larger than the characteristic tunneling distance $\left| {\textbf{d}} _{n}\right|$, which is taken as a measure of the microscopic scale. For a generic microscopic field $F\left( {\textbf{x}},t\right)$ one thus defines a macroscopic corresponding field by spatial averaging (at each time) of the form

$$\begin{aligned} \left\langle F\right\rangle _{{\textbf{X}}}=\frac{1}{\delta \Omega } \int _{\delta \Omega }F\left( {\textbf{x}},t\right) d^{3}x, \end{aligned}$$

(22)

where $\delta \Omega$ is the same for all ${\textbf{X}}$.

Immediate properties from the very definition (22) are

$$\begin{aligned} \frac{\partial }{\partial t}\left\langle F\right\rangle _{{\textbf{X}}}= & {} \frac{1}{\delta \Omega }\int _{\delta \Omega }\frac{\partial }{\partial t} F\left( {\textbf{x}},t\right) d^{3}x, \\ \frac{\partial }{\partial X_{i}}\left\langle F\right\rangle _{{\textbf{X}}}= & {} \frac{1}{\delta \Omega }\int _{\delta \Omega }\frac{\partial }{\partial x_{i}} F\left( {\textbf{x}},t\right) d^{3}x. \end{aligned}$$

Using these properties, since Eqs. (19) are linear their average results in identical equations, but now applied to the corresponding macroscopic magnitudes.

Special care must be taken when considering the macroscopic current density, because, according to the $\gamma$ model, part of charge is redistributed in a microscopically discontinuous manner. Indeed, if one considers the electric charge contained in a given elementary volume

$$\begin{aligned} \delta Q=\int _{\delta \Omega }\rho \left( {\textbf{x}},t\right) d^{3}x, \end{aligned}$$

its time variation depends on the net flow of charge across $\Sigma \left( \delta \Omega \right)$, the boundary of $\delta \Omega$,

$$\begin{aligned} \frac{\partial }{\partial t}\delta Q=-\oint _{\Sigma \left( \delta \Omega \right) }{\textbf{j}}\left( {\textbf{x}},t\right) \cdot d{\textbf{S}} +\sum _{n}i_{n}, \end{aligned}$$

where ${\textbf{j}}\left( {\textbf{x}},t\right)$ represents the flow of charge that is transported continuously, and $\sum _{n}i_{n}$ represents the sum of the elementary currents that tunnel across $\Sigma \left( \delta \Omega \right)$ (with their corresponding sign, according to whether they enter or leave the volume).

Using Gauss theorem and the average properties we can write

$$\begin{aligned} \frac{1}{\delta \Omega }\oint _{\Sigma \left( \delta \Omega \right) }\textbf{ j }\left( {\textbf{x}},t\right) \cdot d{\textbf{S}}= & {} \frac{1}{\delta \Omega } \int _{\delta \Omega }\nabla _{{\textbf{x}}}\cdot {\textbf{j}}\left( {\textbf{x}},t\right) d^{3}x \\= & {} \nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle _{\textbf{ X }}, \end{aligned}$$

so that the macroscopic charge density $\left\langle \rho \right\rangle _{ {\textbf{X}}}=\delta Q/\delta \Omega$ satisfies the relation

$$\begin{aligned} \frac{\partial }{\partial t}\left\langle \rho \right\rangle +\nabla _{ {\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle =\frac{1}{\delta \Omega }\sum _{n}i_{n}. \end{aligned}$$

(23)

In order to proceed we expand on the $I-\gamma -j$ model. In this model the tunneled current $i_{n}$ in a given volume element is a fraction of the normal current flowing through it, and the total tunneled distance is also a fraction of the length traversed by the normal current in that volume. Furthermore, we take into consideration that in order that a given $i_{n}$ contributes to the charge transport across $\Sigma \left( \delta \Omega \right)$ the corresponding tunneled length ${\textbf{d}}_{n}$ must cross the surface (with either ${\textbf{x}}_{n}$ or ${\textbf{x}}_{n}+{\textbf{d}}_{n}$ outside $\delta \Omega$). In this way, if normal current crosses a given surface element (${\textbf{j}}\cdot d{\textbf{S}}\ne 0$), the probability that tunneled currents cross the surface element is given by the fraction of tunneled to normal current, times the fraction of tunneled distance to total distance (the latter accounts for the probability that ${\textbf{d}}_{n}$ crosses the surface). Both mentioned fractions make up the coefficient $\gamma$, so that the current that actually tunnels across a given surface element is $\gamma {\textbf{j}}\cdot d{\textbf{S}}$. We thus have

$$\begin{aligned} \frac{1}{\delta \Omega }\sum _{n}i_{n}= & {} -\frac{1}{\delta \Omega } \oint _{\Sigma \left( \delta \Omega \right) }\gamma {\textbf{j}}\left( \textbf{x },t\right) \cdot d{\textbf{S}} \nonumber \\= & {} -\frac{1}{\delta \Omega }\int _{\delta \Omega }\gamma \nabla _{{\textbf{x}} }\cdot {\textbf{j}}\left( {\textbf{x}},t\right) d^{3}x\nonumber \\= & {} -\gamma \nabla _{\textbf{X }}\cdot \left\langle {\textbf{j}}\right\rangle . \end{aligned}$$

(24)

Using (23) and (24), the relation between macroscopic free charge and current densities is finally expressed as

$$\begin{aligned} \frac{\partial }{\partial t}\left\langle \rho \right\rangle +\left( 1+\gamma \right) \nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle =0. \end{aligned}$$

(25)

A related important magnitude is the macroscopic extra source

$$\begin{aligned} \left\langle I\right\rangle _{{\textbf{X}}}=\frac{1}{\delta \Omega } \int _{\delta \Omega }\sum _{n\subseteq \delta \Omega }I_{n}d^{3}x, \end{aligned}$$

which is determined, according to (21), by only those microscopic currents for which the corresponding tunneled length ${\textbf{d}}_{n}$ crosses the surface with either ${\textbf{x}}_{n}$ or ${\textbf{x}}_{n}+\textbf{ d }_{n}$ outside $\delta \Omega$. This gives precisely the same result as (24)

$$\begin{aligned} \left\langle I\right\rangle _{{\textbf{X}}}=-\gamma \nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle . \end{aligned}$$

(26)

An important result of the $I-\gamma -j$ model, from (25) and (26), is that for a stationary case the macroscopic extra source due to free charges is zero: $\left\langle I\right\rangle _{{\textbf{X}}}=0$ if $\partial \left\langle \rho \right\rangle / \partial t=0$

Finally, it will also be necessary to consider averages of the type

$$\begin{aligned} \left\langle FI\right\rangle _{{\textbf{X}}}=\frac{1}{\delta \Omega } \int _{\delta \Omega }F\left( {\textbf{x}}\right) \left( \sum _{n\subseteq \delta \Omega }I_{n}\right) d^{3}x, \end{aligned}$$

for different fields $F\left( {\textbf{x}}\right)$. Using (21) we have

$$\begin{aligned} \left\langle FI\right\rangle _{{\textbf{X}}}= & {} \frac{1}{\delta \Omega } \sum _{n\subseteq \delta \Omega }i_{n}\left[ F\left( {\textbf{x}}_{n}+{\textbf{d}} _{n}\right) -F\left( {\textbf{x}}_{n}\right) \right] \\{} & {} +\frac{1}{\delta \Omega }\sum _{n\subseteq \Sigma \left( \delta \Omega \right) }sg_{n}i_{n}F\left( {\textbf{x}}_{n}\right) . \end{aligned}$$

where the second term in the right-hand side accounts for the contribution of those microscopic currents for which the corresponding tunneled length ${\textbf{d}}_{n}$ crosses the surface with either ${\textbf{x}}_{n}$ or $\textbf{ x}_{n}+{\textbf{d}}_{n}$ outside $\delta \Omega$, and $sg_{n}$ is the corresponding sign, positive when $i_{n}$ enters the volume, and negative when it leaves it. We now write

$$\begin{aligned} F\left( {\textbf{x}}_{n}+{\textbf{d}}_{n}\right) -F\left( {\textbf{x}}_{n}\right) =\nabla F\cdot {\textbf{d}}_{n}, \end{aligned}$$

and use the $I-\gamma -j$ model as before, which allows us to write the contributions of the volume and of the surface terms as

$$\begin{aligned} \left\langle FI\right\rangle _{{\textbf{X}}}=\frac{1}{\delta \Omega } \int _{\delta \Omega }\gamma {\textbf{j}}\cdot \nabla Fd^{3}x-\frac{1}{\delta \Omega }\oint _{\Sigma \left( \delta \Omega \right) }\gamma F{\textbf{j}}\cdot d {\textbf{S}}. \nonumber \\ \end{aligned}$$

(27)

Using Gauss theorem in the surface term we finally obtain

$$\begin{aligned} \left\langle FI\right\rangle _{{\textbf{X}}}=-\frac{1}{\delta \Omega } \int _{\delta \Omega }\gamma F\nabla \cdot {\textbf{j}}d^{3}x=-\gamma \left\langle F\nabla \cdot {\textbf{j}}\right\rangle _{{\textbf{X}}}. \end{aligned}$$

(28)

Care must be taken in the evaluation of averages of this form due to their being non-linear in the microscopic fields. To proceed we follow the formalism in [36] in which the averages of the form (22) are complemented with the definition of the fluctuations, relative to the averages, as

$$\begin{aligned} \delta F\left( {\textbf{x}},{\textbf{X}},t\right) \equiv F\left( {\textbf{x}},t\right) -\left\langle F\right\rangle _{{\textbf{X}}}. \end{aligned}$$

This particular definition of fluctuations satisfies the relation

$$\begin{aligned} \left\langle \delta F\left( {\textbf{x}},{\textbf{X}},t\right) \left\langle G\right\rangle _{{\textbf{X}}}\right\rangle _{{\textbf{X}}}=0, \end{aligned}$$

(29)

for any two fields $F\left( {\textbf{x}},t\right)$ and $G\left( {\textbf{x}},t\right)$. In this way, by writing

$$\begin{aligned} F\left( {\textbf{x}},t\right)= & {} \left\langle F\right\rangle _{{\textbf{X}} }+\delta F\left( {\textbf{x}},{\textbf{X}},t\right) , \\ \nabla \cdot {\textbf{j}}\left( {\textbf{x}},t\right)= & {} \nabla _{{\textbf{X}} }\cdot \left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}}+\delta \nabla \cdot {\textbf{j}}\left( {\textbf{x}},{\textbf{X}},t\right) \end{aligned}$$

we have

$$\begin{aligned} \left\langle F\nabla \cdot {\textbf{j}}\right\rangle _{{\textbf{X}} }=\left\langle F\right\rangle _{{\textbf{X}}}\nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}}+\left\langle \delta F\delta \nabla \cdot {\textbf{j}}\right\rangle _{{\textbf{X}}}. \end{aligned}$$

The average of fluctuations in this expression results from two contributions: that due to fluctuations of scale much smaller than the macroscopic one, $\delta L$, and that due to fluctuations of scale close to $\delta L$. The latter contribution can be determined using the method in [36], while the contributions of fluctuations of very small scale need to be modeled independently. The fluctuations of scale not too small contribute to a generic average of fluctuations $\left\langle \delta F\delta G\right\rangle$ a term [36]

$$\begin{aligned} \left\langle \delta F\delta G\right\rangle \simeq \frac{\left( \delta L\right) ^{2}}{24}\nabla _{{\textbf{X}}}\left\langle F\right\rangle \cdot \nabla _{{\textbf{X}}}\left\langle G\right\rangle , \end{aligned}$$

and since $\left\langle F\right\rangle$ and $\left\langle G\right\rangle$ are macroscopic fields their variation over $\delta L$ is small,

$$\begin{aligned} \left| \frac{\left( \delta L\right) ^{2}}{24}\nabla _{{\textbf{X}} }\left\langle F\right\rangle \cdot \nabla _{{\textbf{X}}}\left\langle G\right\rangle \right| \ll \left| \left\langle F\right\rangle \left\langle G\right\rangle \right| , \end{aligned}$$

so that one can safely neglect this contribution. Concerning the contribution of the scales much smaller than $\delta L$, we will also neglect it considering that the level of those fluctuations is not supposed to be highly excited above their thermal level, in the absence of a mechanisms leading to a non-linear energy cascade. In this way, we finally obtain

$$\begin{aligned} \left\langle FI\right\rangle _{{\textbf{X}}}=-\gamma \left\langle F\right\rangle _{{\textbf{X}}}\nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}} \right\rangle _{{\textbf{X}}}. \end{aligned}$$

(30)

We can now analyze the application of Ohm law. The point is that in [12] the following expression for the force density on matter due to the fields was obtained

$$\begin{aligned} {\textbf{f}}=\rho {\textbf{E}}+{\textbf{j}}\times {\textbf{B}}-I{\textbf{A}}. \end{aligned}$$

Using the previous considerations we obtain

$$\begin{aligned} \left\langle I{\textbf{A}}\right\rangle _{{\textbf{X}}}= & {} -\gamma \left\langle {\textbf{A}}\right\rangle _{{\textbf{X}}}\nabla _{{\textbf{X}}}\cdot \left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}}, \end{aligned}$$

(32)

$$\begin{aligned} \left\langle {\textbf{j}}\times {\textbf{B}}\right\rangle _{{\textbf{X}}}= & {} \left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}} \times \left\langle {\textbf{B}} \right\rangle _{{\textbf{X}}} =\left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}} \times \left( \nabla _{ {\textbf{X}}}\times \left\langle {\textbf{A}}\right\rangle _{{\textbf{X}}} \right) . \end{aligned}$$

(33)

This allows us to estimate the relative order of magnitude of these two terms, considering that the averaged magnitudes have spatial variations of the same relative order. This shows that the additional force coming from the non-conserved currents is a term of small magnitude (for $\gamma$ small) compared to the Lorentz force. In this way, we take as a reasonable approximation the usual relation between local electric field and total current to be $\left\langle {\textbf{j}}\right\rangle _{{\textbf{X}}} =\sigma {\textbf{E}}$, with $\sigma$ the conductivity of the medium, even if it has to be extended to include magnetic forces, like in the Hall effect.

2.2 Dielectric media

We consider now the macroscopic relations for polarizable media, in which the molecular sources play a fundamental role.

To begin, the usual expression of averaged molecular charge density (no explicit distinction between the spatial coordinates of volume centers and space coordinates would be made from now on)

$$\begin{aligned} \left\langle \rho _{m}\right\rangle =-\nabla \cdot {\textbf{P}}, \end{aligned}$$

(34)

expressed in terms of a vector ${\textbf{P}}$, is justified considering that the total molecular charge in a medium without added free charges should be zero, irrespective of the shape of the medium. Besides, the interpretation of ${\textbf{P}}$ as the volume density of electric polarization results from expression (34) and the definition of the dipole moment of the medium as $\int \left\langle \rho _{m}\right\rangle {\textbf{x}}d^{3}x$, with the integral extended to the whole medium.

We thus see that expression (34) can be taken over for the description of media with non-conserved currents. Furthermore, the phenomenological relation ${\textbf{P}}=\varepsilon _{0}\varkappa \left\langle {\textbf{E}}\right\rangle$ for a linear, isotropic medium, with a polarization coefficient $\varkappa$, should also be an acceptable model in our case, since it does not conflict with any assumption in the $\gamma$ model.

We now consider the macroscopic averages ${\textbf{J}}_{m}$ of molecular currents. The condition that molecular currents are highly localized implies that their flux across any macroscopic cross section of the medium should be zero, which translates into the relation ${\textbf{J}}_{m}=$ $\nabla \times {\textbf{M}}$ for a generic vector ${\textbf{M}}$. This is valid under the assumption that the spatial averaging process cancels the rapidly fluctuating in time, instantaneous unbalances of molecular currents crossing the surface element. However, when the macroscopic fields are not stationary, a time variation of a polarization vector ${\textbf{P}}$ with non-zero divergence corresponds to an orderly redistribution of charges, crossing the boundary of the element, but remaining localized in the molecules that cross that boundary. This effect gives rise to a contribution to the macroscopic molecular current of the form $\partial {\textbf{P}} /\partial t$. It is thus customary to include both contributions in the expression

$$\begin{aligned} {\textbf{J}}_{m}=\frac{\partial {\textbf{P}}}{\partial t}+\nabla \times \textbf{ M }. \end{aligned}$$

Moreover, for stationary situations, the interpretation of ${\textbf{M}}$ as the volume density of magnetic moment results from the very definition of total magnetic moment of the medium: $\frac{1}{2}\int {\textbf{x}}\times {\textbf{J}}_{m}d^{3}x$, with the integral extended to the whole medium, and the expression of ${\textbf{J}}_{m}$ valid in this case.

Furthermore, for linear, isotropic media the idea of the orientation of the molecular magnetic dipoles along the magnetic field leads to a model with a linear relation between ${\textbf{M}}$ and ${\textbf{B}}$, usually expressed through the auxiliary vector ${\textbf{H}}=\left( \left\langle {\textbf{B}} \right\rangle -{\textbf{M}}\right) /\mu _{0}$ as ${\textbf{M}}=\chi {\textbf{H}}$, where $\chi$ is the magnetic susceptibility coefficient. This latter phenomenological model can also be taken over to our case, since it is fully compatible with the $\gamma$ model.

Note that the macroscopic molecular sources so far considered satisfy the continuity relation

$$\begin{aligned} \frac{\partial }{\partial t}\left\langle \rho _{m}\right\rangle +\nabla \cdot {\textbf{J}}_{m}=0. \end{aligned}$$

However, we must take into account that in the spirit of the $\gamma$ model some of the molecular charge redistribution can take place discontinuously, even within the molecule in which it is localized. The likely candidate for this is the redistribution of charge leading to variation of the dipole moment in each molecule. For this reason, we assume that only a fraction $\alpha$ of $\partial {\textbf{P}}/\partial t$ is due to a continuous charge motion. We thus consider that an effective fraction $\gamma ^{\prime }$ (in general different from the $\gamma$ for free currents) of the continuous current crosses a given surface element discontinuously, so that

$$\begin{aligned} \left\langle I\right\rangle _{{\textbf{X}}}=-\gamma ^{\prime }\alpha \nabla \cdot \frac{\partial {\textbf{P}}}{\partial t}. \end{aligned}$$

These considerations lead to a redefinition of the continuous component ${\textbf{J}}_{m}$ as

$$\begin{aligned} {\textbf{J}}_{m}=\alpha \frac{\partial {\textbf{P}}}{\partial t}+\nabla \times {\textbf{M}}, \end{aligned}$$

(35)

so that now the continuity relation is

$$\begin{aligned} \frac{\partial }{\partial t}\left\langle \rho _{m}\right\rangle +\nabla \cdot {\textbf{J}}_{m}=-\gamma ^{\prime }\alpha \nabla \cdot \frac{\partial {\textbf{P}}}{\partial t}, \end{aligned}$$

which using also (34) is written as

$$\begin{aligned} -\frac{\partial }{\partial t}\nabla \cdot {\textbf{P}}+\alpha \nabla \cdot \frac{\partial {\textbf{P}}}{\partial t}=-\gamma ^{\prime }\alpha \nabla \cdot \frac{\partial {\textbf{P}}}{\partial t}, \end{aligned}$$

which requires that

$$\begin{aligned} \alpha =\frac{1}{1+\gamma ^{\prime }}. \end{aligned}$$

resulting in the macroscopic extra source contributed by the polarization of the medium to be

$$\begin{aligned} \left\langle I\right\rangle _{{\textbf{X}}}=-\frac{\gamma ^{\prime }}{1+\gamma ^{\prime }}\nabla \cdot \frac{\partial {\textbf{P}}}{\partial t}. \end{aligned}$$

(36)

As for the contribution from free charges to the macroscopic extra source, also that due to molecular sources turns out to be zero in stationary situations.

2.3 Macroscopic AB equations in media with non-conserved currents

We now recall the relations which, according to the considerations in the previous sections, could serve as a valid model for the macroscopic fields and sources in a linear, homogeneous medium with non-locally conserved currents.

We first recall that, due to their being linear, the volume average procedure can be applied directly to Eq. (19) to yield exactly the same equations, but where all fields and sources are to be considered as macroscopic ones. Besides, the sources are to be considered as including both components, free and molecular.

Furthermore, for easy of notation, from now on all macroscopic fields and sources are represented without the average symbol $\left\langle ...\right\rangle$. The spatial coordinate ${\textbf{x}}$ is also not distinguished from the center of the volume elements, previously designated as ${\textbf{X}}$.

With these considerations, the molecular sources are given by

$$\begin{aligned} \rho _{m}= & {} -\nabla \cdot {\textbf{P}}, \\ {\textbf{j}}_{m}= & {} \frac{1}{1+\gamma ^{\prime }}\frac{\partial {\textbf{P}}}{ \partial t}+\nabla \times {\textbf{M}}, \end{aligned}$$

where the polarization and magnetization have the usual expressions

$$\begin{aligned} {\textbf{P}}= & {} \left( \varepsilon -\varepsilon _{0}\right) {\textbf{E}}, \\ {\textbf{M}}= & {} \left( 1/\mu _{0}-1/\mu \right) {\textbf{B}}. \end{aligned}$$

Using the previous relations to express the macroscopic molecular sources we obtain the equations

$$\begin{aligned} \nabla \cdot {\textbf{E}}= & {} \frac{\rho }{\varepsilon }-\frac{\varepsilon _{0} }{\varepsilon }\frac{\partial S}{\partial t}, \end{aligned}$$

(37a)

$$\begin{aligned} \nabla \cdot {\textbf{B}}= & {} 0,\;{\textbf{B}}=\nabla \times {\textbf{A}}, \end{aligned}$$

(37b)

$$\begin{aligned} \nabla \times {\textbf{E}}= & {} -\frac{\partial {\textbf{B}}}{\partial t},\; {\textbf{E}}=-\nabla \phi -\frac{\partial {\textbf{A}}}{\partial t}, \end{aligned}$$

(37c)

$$\begin{aligned} \nabla \times {\textbf{B}}= & {} \mu {\textbf{j}}+\mu \varepsilon \frac{1+\gamma ^{\prime }\frac{\varepsilon _{0}}{\varepsilon }}{1+\gamma ^{\prime }}\frac{ \partial {\textbf{E}}}{\partial t}+\frac{\mu }{\mu _{0}}\nabla S, \end{aligned}$$

(37d)

$$\begin{aligned} S= & {} \mu _{0}\varepsilon _{0}\frac{\partial \phi }{\partial t}+\nabla \cdot {\textbf{A}}. \end{aligned}$$

(37e)

The sources appearing explicitly in these relations are only the free sources, the molecular ones having been included through their expressions in terms of the fields.

The equations for the potentials can be more simply derived from the original system (19), which after further averaging and use of the expressions of the molecular sources in terms of the fields gives

$$\begin{aligned} \mu _{0}\varepsilon _{0}\frac{\varepsilon _{0}}{\varepsilon }\frac{\partial ^{2}\phi }{\partial t^{2}}-\nabla ^{2}\phi= & {} \frac{\rho }{\varepsilon } +\left( 1-\frac{\varepsilon _{0}}{\varepsilon }\right) \frac{\partial }{ \partial t}\left( \nabla \cdot {\textbf{A}}\right) , \end{aligned}$$

(38a)

$$\begin{aligned} \mu \varepsilon \frac{1+\gamma ^{\prime }\frac{\varepsilon _{0}}{\varepsilon }}{1+\gamma ^{\prime }}\frac{\partial ^{2}{\textbf{A}}}{\partial t^{2}}-\nabla ^{2}{\textbf{A}}= & {} \mu {\textbf{j}}+\left( \frac{\mu }{\mu _{0}}-1\right) \nabla \left( \nabla \cdot {\textbf{A}}\right) \nonumber \\{} & {} +\mu \varepsilon \frac{\frac{\varepsilon _{0}}{\varepsilon }-1}{1+\gamma ^{\prime }}\nabla \left( \frac{\partial \phi }{\partial t}\right) . \end{aligned}$$

(38b)

The previous equations must be complemented with the relation for free sources, Eq. (25),

$$\begin{aligned} \frac{\partial \rho }{\partial t}+\left( 1+\gamma \right) \nabla \cdot {\textbf{j}}=0, \end{aligned}$$

where the free current is related to the electric field by the Ohm law

$$\begin{aligned} {\textbf{j}}=\sigma {\textbf{E}}=-\sigma \left( \nabla \phi +\frac{\partial {\textbf{A}}}{\partial t}\right) . \end{aligned}$$

(39)

2.4 Wave propagation

We study in this section the possible plane-wave modes in which all fields and sources are of the generic form $a_{0}\exp \left[ i\left( {\textbf{k}} \cdot {\textbf{x}}-\omega t\right) \right]$, with constant complex amplitude $a_{0}$.

From Eqs. (25) and (39) we have for the mode amplitudes of the free sources

$$\begin{aligned} \varrho _{0}= & {} -i\frac{\sigma \left( 1+\gamma \right) }{\omega }\left( k^{2}\phi _{0}-\omega {\textbf{k}}\cdot {\textbf{A}}_{0}\right) , \\ {\textbf{j}}_{0}= & {} -i\sigma \left( {\textbf{k}}\phi _{0}-\omega {\textbf{A}} _{0}\right) , \end{aligned}$$

which are used in Eqs. (38) to finally obtain the relations for the potentials amplitudes

$$\begin{aligned}{} & {} \left\{ k^{2}\left[ 1+i\frac{\sigma \left( 1+\gamma \right) }{\omega \varepsilon }\right] -\mu _{0}\varepsilon _{0}\frac{\varepsilon _{0}}{ \varepsilon }\omega ^{2}\right\} \phi _{0}\nonumber \\{} & {} \quad =\omega \left[ 1-\frac{ \varepsilon _{0}}{\varepsilon }+i\frac{\sigma \left( 1+\gamma \right) }{ \omega \varepsilon }\right] {\textbf{k}}\cdot {\textbf{A}}_{0}, \end{aligned}$$

(40a)

$$\begin{aligned}{} & {} \left( k^{2}-\mu \varepsilon \frac{1+\gamma ^{\prime }\frac{\varepsilon _{0} }{\varepsilon }}{1+\gamma ^{\prime }}\omega ^{2}-i\mu \sigma \omega \right) {\textbf{A}}_{0} \nonumber \\{} & {} \quad =\left( 1-\frac{\mu }{\mu _{0}}\right) {\textbf{k}}\left( {\textbf{k}}\cdot {\textbf{A}}_{0}\right) \nonumber \\{} & {} \qquad +\left( \mu \varepsilon \frac{\frac{\varepsilon _{0}}{\varepsilon }-1}{ 1+\gamma ^{\prime }}\omega -i\mu \sigma \right) {\textbf{k}}\phi _{0}. \end{aligned}$$

(40b)

The transverse mode (${\textbf{k}}\cdot {\textbf{A}}_{0}=0$) corresponds to a wave with $\phi _{0}=0$ and dispersion relation

$$\begin{aligned} k^{2}=\mu \varepsilon \frac{1+\gamma ^{\prime }\frac{\varepsilon _{0}}{ \varepsilon }}{1+\gamma ^{\prime }}\omega ^{2}+i\mu \sigma \omega . \end{aligned}$$

For a dielectric without losses ($\sigma =0$) this is an electromagnetic wave with phase speed given by

$$\begin{aligned} c=\sqrt{\mu \varepsilon \frac{1+\gamma ^{\prime }\frac{\varepsilon _{0}}{ \varepsilon }}{1+\gamma ^{\prime }}}, \end{aligned}$$

which indicates a slight (for $\gamma ^{\prime }\ll 1$) decrease of the usual speed of light in the medium.

For the case of a conducting medium there is also the usual decay associated to Joule dissipation, which is very strong in good conductors with $\frac{ \sigma }{\omega \varepsilon }\gg 1$.

For the longitudinal modes (${\textbf{k}}\times {\textbf{A}}_{0}=0$) we obtain the dispersion relation

$$\begin{aligned}{} & {} \left( \frac{k^{2}}{\mu _{0}\varepsilon _{0}\omega ^{2}}-1\right) \left\{ \left( \frac{k^{2}}{\mu _{0}\varepsilon _{0}\omega ^{2}}-1\right) \left[ 1+i \frac{\sigma \left( 1+\gamma \right) }{\omega \varepsilon }\right] \right. \\{} & {} \left. \quad +\frac{ \gamma ^{\prime }\left( 1-\frac{\varepsilon _{0}}{\varepsilon }\right) }{ 1+\gamma ^{\prime }}+i\frac{\gamma \sigma }{\omega \varepsilon }\right\} =0. \end{aligned}$$

We thus see that the branch $k^{2}=\mu _{0}\varepsilon _{0}\omega ^{2}$, corresponding to a wave of pure potentials, or gauge wave, which has zero fields (${\textbf{E}}$, ${\textbf{B}}$ and S), is allowed for all values of $\gamma$, $\gamma ^{\prime }$ and $\sigma$.

The other branch has the dispersion relation

$$\begin{aligned} \frac{k^{2}}{\mu _{0}\varepsilon _{0}\omega ^{2}}=1-\frac{\gamma ^{\prime }\left( 1-\frac{\varepsilon _{0}}{\varepsilon }\right) +i\frac{\gamma \sigma }{\omega \varepsilon }\left( 1+\gamma ^{\prime }\right) }{\left( 1+\gamma ^{\prime }\right) \left[ 1+i\frac{\sigma \left( 1+\gamma \right) }{\omega \varepsilon }\right] }. \end{aligned}$$

(41)

When relation (41) is used in expressions (40), the relation between the amplitudes of the potentials is given for this mode by

$$\begin{aligned} {\textbf{k}}\cdot {\textbf{A}}_{0}=\frac{\mu _{0}\varepsilon _{0}\omega }{1- \frac{\varepsilon _{0}}{\varepsilon }+i\frac{\sigma \left( 1+\gamma \right) }{\omega \varepsilon }}\left( \frac{1-\frac{\varepsilon _{0}}{\varepsilon }}{ 1+\gamma ^{\prime }}+i\frac{\sigma }{\omega \varepsilon }\right) \phi _{0}. \end{aligned}$$

Consequently, the amplitude of the scalar wave, $S_{0}=i\left( {\textbf{k}} \cdot {\textbf{A}}_{0}-\mu _{0}\varepsilon _{0}\omega \phi _{0}\right)$, has the expression

$$\begin{aligned} S_{0}=i\frac{\mu _{0}\varepsilon _{0}\omega }{\left( 1+\gamma ^{\prime }\right) }\left[ \frac{\gamma ^{\prime }\left( \frac{\varepsilon _{0}}{ \varepsilon }-1\right) -i\sigma \frac{\gamma }{\varepsilon \omega }\left( 1+\gamma ^{\prime }\right) }{1-\frac{\varepsilon _{0}}{\varepsilon }+i\frac{ \sigma \left( 1+\gamma \right) }{\omega \varepsilon }}\right] \phi _{0}, \end{aligned}$$

(42)

and the corresponding longitudinal electric field amplitude satisfies

$$\begin{aligned} {\textbf{k}}\cdot {\textbf{E}}_{0}=\frac{\omega \frac{\varepsilon _{0}}{ \varepsilon }}{1+i\frac{\sigma \left( 1+\gamma \right) }{\omega \varepsilon } }S_{0}. \end{aligned}$$

(43)

For the case of a very good conductor, $\frac{\sigma }{\omega \varepsilon } \gg 1$, relation (41) simplifies to

$$\begin{aligned} \frac{k^{2}}{\mu _{0}\varepsilon _{0}\omega ^{2}}=\frac{1}{1+\gamma }, \end{aligned}$$

and (42) to

$$\begin{aligned} S_{0}=-i\frac{\gamma }{1+\gamma }\mu _{0}\varepsilon _{0}\omega \phi _{0}. \end{aligned}$$

The corresponding longitudinal electric field amplitude is

$$\begin{aligned} E_{0}=-\frac{\gamma \varepsilon _{0}\omega ^{2}}{\sigma \left( 1+\gamma \right) }\sqrt{\frac{\mu _{0}\varepsilon _{0}}{1+\gamma }}\phi _{0}. \end{aligned}$$

These relations indicate that a small amplitude (for $\gamma \ll 1$) scalar wave is possible in this case, propagating without decay in a good conductor. Note that, consistently, the dissipated power density, $\sigma E_{0}^{2}$, goes to zero for $\sigma \rightarrow \infty$.

For a dielectric without losses, $\sigma =0$, the dispersion relation is

$$\begin{aligned} \frac{k^{2}}{\mu _{0}\varepsilon _{0}\omega ^{2}}=\frac{1+\gamma ^{\prime } \frac{\varepsilon _{0}}{\varepsilon }}{1+\gamma ^{\prime }}, \end{aligned}$$

and the corresponding amplitudes of the scalar and of the longitudinal electric field are

$$\begin{aligned} S_{0}= & {} -i\frac{\gamma ^{\prime }}{1+\gamma ^{\prime }}\mu _{0}\varepsilon _{0}\omega \phi _{0}, \\ E_{0}= & {} -i\gamma ^{\prime }\frac{\varepsilon _{0}}{\varepsilon }\omega \sqrt{\frac{\mu _{0}\varepsilon _{0}}{\left( 1+\gamma ^{\prime }\right) \left( 1+\gamma ^{\prime }\frac{\varepsilon _{0}}{\varepsilon }\right) }} \phi _{0}. \end{aligned}$$

As in the case of a conductor, a small amplitude (for $\gamma ^{\prime }\ll 1$) scalar wave can propagate also in this case.

3 Possible measurable effects

The general energy–momentum laws in AB electrodynamics were derived in [12]. In relation to the interaction of fields and matter the following expression for the power density on matter due to the fields was obtained

$$\begin{aligned} w={\textbf{j}}\cdot {\textbf{E}}-I\phi . \end{aligned}$$

(44)

This is the microscopic expression that, apart from the usual term found in Maxwell electrodynamics, includes a term proportional to the extra source I. As a consequence, in media with non-conserved currents it would in principle be possible to observe the effect of this extra term.

3.1 Detection of gauge-waves

As mentioned above, the possibility of material media with non-conserved currents allows the detection of gauge-waves. This is so because according to (44) the scalar potential of the wave can interact with any extra source I present in the medium. In the following a basic circuit capable in principle of this detection is presented.

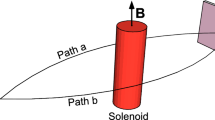
In the conductor represented in Fig. 1 there is a constant current of value $i_{0}=V_{0}/\left( R+R_{0}\right)$. The scalar potential $\phi$ of a gauge wave can then interact with the part of this current that is not locally conserved.

Fig. 1

Possible basic circuit for detection of gauge waves. The conductor of length L and total electrical resistance R sustains a continuous current $i_{0}=V_{0}/\left( R+R_{0}\right)$. The scalar potential of a gauge wave interacts with the not locally conserved part of the current and produces a varying voltage $\delta V$ at the position denoted by the black dot

Since the gauge wave does not transport energy, and energy conservation is already satisfied by the circulating permanent current, the law of conservation of energy is expressed by (44) applied to the whole circuit, expressed as

$$\begin{aligned} \int \left[ \delta \left( {\textbf{j}}\cdot {\textbf{E}}\right) -I\phi \right] d^{3}x=0, \end{aligned}$$

where the integral is extended to the whole volume of the circuit, and $\delta \left( {\textbf{j}}\cdot {\textbf{E}}\right) =\delta {\textbf{j}}\cdot {\textbf{E}}+{\textbf{j}}\cdot \delta {\textbf{E}}$ represents the small change in the corresponding magnitudes due to the interaction with the wave (it is assumed that $I\phi$, induced by the wave, is a small perturbation), while ${\textbf{E}}$ and ${\textbf{j}}$ are the values of the magnitudes when no gauge wave is present. In this way, denoting as $\delta i$ the change of current that arises due to interaction with the gauge wave, we can write

$$\begin{aligned} \int \delta {\textbf{j}}\cdot {\textbf{E}}d^{3}x= & {} \delta i\left( -V_{0}+Ri_{0}+R_{0}i_{0}\right) , \\ \int {\textbf{j}}\cdot \delta {\textbf{E}}d^{3}x= & {} i_{0}\left( R\delta i+R_{0}\delta i\right) , \end{aligned}$$

so that

$$\begin{aligned} \int \delta \left( {\textbf{j}}\cdot {\textbf{E}}\right) d^{3}x=\left[ -V_{0}+2\left( R+R_{0}\right) i_{0}\right] \delta i=V_{0}\delta i. \end{aligned}$$

In order to evaluate $\int I\phi d^{3}x$ we use the general expression (27) with $\phi$ in place of F, and extend the integration to the whole circuit, so that

$$\begin{aligned} \int I\phi d^{3}x=\int \gamma {\textbf{j}}\cdot \nabla \phi d^{3}x-\oint \gamma \phi {\textbf{j}}\cdot d{\textbf{S}}\text {,} \end{aligned}$$

where ${\textbf{j}}$ is the current density in the circuit when there is no gauge wave. Note that the surface integral in this expression applies if the current that crosses the surface of the detecting element has a discontinuous component described by the same $\gamma$ coefficient as that of the bulk of the detecting medium. In that case, after use of Gauss law we would obtain

$$\begin{aligned} \int I\phi d^{3}x=-\gamma \int \phi \nabla \cdot {\textbf{j}}d^{3}x, \end{aligned}$$

which is zero, since $\nabla \cdot \mathbf {j=0}$ for the DC circuit when no gauge wave is present. We must thus consider that the detecting medium is electrically fed by conductors with zero, or a much smaller value of $\gamma$ than that of the detecting element, so as to neglect the surface contribution, and finally obtain

$$\begin{aligned} V_{0}\delta i= & {} \int I\phi d^{3}x=\int \gamma {\textbf{j}}\cdot \nabla \phi d^{3}x \\= & {} \gamma i_{0}\int \nabla \phi \cdot {\textbf{n}}dl=\gamma i_{0}\Delta \phi , \end{aligned}$$

where the integral in the second line is preformed along the length of the conductor, the unit vector ${\textbf{n}}$ indicates the direction of the circulating current, and the resulting $\Delta \phi$ is the difference of potential across the conductor length.

Using again $V_{0}=i_{0}\left( R+R_{0}\right)$ we thus have

$$\begin{aligned} \delta i=\frac{\gamma }{\left( R+R_{0}\right) }\Delta \phi , \end{aligned}$$

or, from $\delta V=R_{0}\delta i$,

$$\begin{aligned} \delta V=\gamma \frac{R_{0}}{\left( R+R_{0}\right) }\Delta \phi . \end{aligned}$$

3.2 Antenna detector

We consider as a relatively simple example a linear dipole of length d and negligible cross dimensions, fed by a source of voltage V of (angular) frequency $\omega$. Taking the coordinate z along the dipole, with the origin at the dipole half point (where the power is fed to the antenna), a good approximation to the current circulating in the dipole is [37]

$$\begin{aligned} i\left( z,t\right) =i_{0}\sin \left( \frac{kd}{2}-k\left| z\right| \right) \cos \left( \omega t\right) . \end{aligned}$$

In terms of the antenna impedance, $Z_{A}=R_{A}+iX_{A}$, and that of the source and circuit, $Z_{S}=R_{S}+iX_{S}$, the corresponding voltage is

$$\begin{aligned} V=i_{0}\left| Z_{A}+Z_{S}\right| \cos \left( \omega t+\varphi \right) , \end{aligned}$$

where

$$\begin{aligned} \tan \left( \varphi \right) =\left( X_{A}+X_{S}\right) /\left( R_{A}+R_{S}\right) . \end{aligned}$$

We consider that the condition for maximum power delivered to the antenna by the circuit is fulfilled: $R_{S}=R_{A}$, $X_{S}=-X_{A}$, so that

$$\begin{aligned} V=2R_{A}i_{0}\cos \left( \omega t\right) . \end{aligned}$$

If a gauge wave propagates along the z direction with potential given by

$$\begin{aligned} \phi \left( z,t\right) =\phi _{0}\cos \left( k^{\prime }z-\omega ^{\prime }t+\theta \right) , \end{aligned}$$

the instantaneous power exchanged with the antenna is given by (the integral is extended to the antenna volume)

$$\begin{aligned}{} & {} -\int I\phi d^{3}x =\gamma \int \phi \nabla \cdot {\textbf{j}}d^{3}x \\{} & {} \quad =-\gamma ki_{0}\phi _{0}\cos \left( \omega t\right) \\{} & {} \qquad \times \int _{-d/2}^{d/2}sign\left( z\right) \cos \left( \frac{kd}{2}-k\left| z\right| \right) \cos \left( k^{\prime }z-\omega ^{\prime }t+\theta \right) dz \\{} & {} \quad =2\gamma i_{0}\phi _{0}kk^{\prime }\frac{\cos \left( \frac{kd}{2}\right) -\cos \left( \frac{k^{\prime }d}{2}\right) }{\left( k-k^{\prime }\right) \left( k+k^{\prime }\right) }\cos \left( \omega t\right) \sin \left( \omega ^{\prime }t-\theta \right) . \end{aligned}$$

Conservation of energy requires that the additional $\delta i$ generated by the interaction with the gauge wave satisfies

$$\begin{aligned} -V\delta i+\delta \left( 2R_{A}i^{2}\right) -\int I\phi d^{3}x=0, \end{aligned}$$

which, since $V=2R_{A}i$, reduces to

$$\begin{aligned} V\delta i-\int I\phi d^{3}x=0, \end{aligned}$$

that determines the additional current in the circuit

$$\begin{aligned} \delta i=\frac{\gamma \phi _{0}}{R_{A}}kk^{\prime }\frac{\cos \left( \frac{kd }{2}\right) -\cos \left( \frac{k^{\prime }d}{2}\right) }{\left( k-k^{\prime }\right) \left( k+k^{\prime }\right) }\sin \left( \omega ^{\prime }t-\theta \right) . \end{aligned}$$

The previous analysis is valid for $\omega ^{\prime }$ close to $\omega$ because the reactive component of the impedances was taken for simplicity as the same for both frequencies. For the case $\omega ^{\prime }=\omega$ the expression of the additional current simplifies to

$$\begin{aligned} \delta i=-\frac{\gamma \phi _{0}}{2R_{A}}\frac{kd}{2}\sin \left( \frac{kd}{2} \right) \sin \left( \omega t-\theta \right) . \end{aligned}$$

It is interesting to note that a half-wavelength dipole, $d=\lambda /2$, would be the best suited for the detection of a gauge wave at resonant conditions.

4 Radiating systems

An important point for possible applications and/or experiments is the prediction of the fields radiated by a system in the context of the I-$\gamma$-j model. We will consider the fields generated by harmonic in time currents in conductors in which polarization effects can be neglected.

We first recall that in AB electrodynamics the equations for the potentials derived from (19) coincide with the corresponding Maxwell equations in the Lorentz gauge

$$\begin{aligned} \frac{1}{c^{2}}\frac{\partial ^{2}\phi }{\partial t^{2}}-\nabla ^{2}\phi= & {} \frac{\varrho }{\varepsilon _{0}}, \\ \frac{1}{c^{2}}\frac{\partial ^{2}{\textbf{A}}}{\partial t^{2}}-\nabla ^{2} {\textbf{A}}= & {} \mu _{0}{\textbf{j}}, \end{aligned}$$

which after averaging result in equations with the same form for the macroscopic potentials, but with the sources replaced by the macroscopic ones, free plus molecular.

The general solutions in free space are given by

$$\begin{aligned} \phi \left( {\textbf{x}},t\right)= & {} \frac{1}{4\pi \varepsilon _{0}}\int \frac{ \varrho \left( {\textbf{x}}^{\prime },t^{\prime }\right) }{\left| \textbf{x }^{\prime }-{\textbf{x}}\right| }d^{3}x^{\prime }, \\ {\textbf{A}}\left( {\textbf{x}},t\right)= & {} \frac{\mu _{0}}{4\pi }\int \frac{ {\textbf{j}}\left( {\textbf{x}}^{\prime },t^{\prime }\right) }{\left| {\textbf{x}}^{\prime }-{\textbf{x}}\right| }d^{3}x^{\prime }, \end{aligned}$$

where $t^{\prime }=t-\left| {\textbf{x}}^{\prime }-{\textbf{x}}\right| /c$. For harmonic in time fields and sources the corresponding Fourier-transformed-in-time amplitudes satisfy

$$\begin{aligned} \phi \left( {\textbf{x}},\omega \right)= & {} \frac{1}{4\pi \varepsilon _{0}} \int \frac{\varrho \left( {\textbf{x}}^{\prime },\omega \right) }{R}\exp \left( ikR\right) d^{3}x^{\prime }, \\ {\textbf{A}}\left( {\textbf{x}},\omega \right)= & {} \frac{\mu _{0}}{4\pi }\int \frac{{\textbf{j}}\left( {\textbf{x}}^{\prime },\omega \right) }{R}\exp \left( ikR\right) d^{3}x^{\prime }, \end{aligned}$$

with $R=\left| {\textbf{x}}^{\prime }-{\textbf{x}}\right|$, and $k=\omega /c$.

In the non-polarizable conductors considered the relation between the sources is given by (25), which results for the Fourier amplitudes in

$$\begin{aligned} \varrho \left( {\textbf{x}},\omega \right) =-i\frac{1+\gamma }{\omega }\nabla \cdot {\textbf{j}}. \end{aligned}$$

We can thus write

$$\begin{aligned} \phi \left( {\textbf{x}},\omega \right)= & {} -i\frac{1+\gamma }{4\pi \varepsilon _{0}\omega }\int \frac{\nabla ^{\prime }\cdot {\textbf{j}}}{R}\exp \left( ikR\right) d^{3}x^{\prime } \\= & {} -i\frac{1+\gamma }{4\pi \varepsilon _{0}\omega }\oint \frac{\exp \left( ikR\right) }{R}{\textbf{j}}\cdot d{\textbf{S}}^{\prime } \\{} & {} +i\frac{1+\gamma }{4\pi \varepsilon _{0}\omega }\int {\textbf{j}}\left( {\textbf{x}}^{\prime },\omega \right) \cdot \nabla ^{\prime }\left[ \frac{\exp \left( ikR\right) }{R}\right] d^{3}x^{\prime }. \end{aligned}$$

Since the volume of integration contains all sources, no current traverses its boundary, so that the surface integral is zero. Also, $\nabla ^{\prime }R=-\nabla R$, allowing to finally obtain

$$\begin{aligned} \phi \left( {\textbf{x}},\omega \right)= & {} -i\frac{1+\gamma }{4\pi \varepsilon _{0}\omega }\nabla \cdot \int \frac{{\textbf{j}}\left( {\textbf{x}} ^{\prime },\omega \right) }{R}\exp \left( ikR\right) d^{3}x^{\prime } \\= & {} -i\frac{\left( 1+\gamma \right) c^{2}}{\omega }\nabla \cdot {\textbf{A}} \left( {\textbf{x}},\omega \right) . \end{aligned}$$

In this way, all fields outside the sources can be determined from the solution for the vector potential alone

$$\begin{aligned} {\textbf{A}}\left( {\textbf{x}},\omega \right) =\frac{\mu _{0}}{4\pi }\int \frac{ {\textbf{j}}\left( {\textbf{x}}^{\prime },\omega \right) }{R}\exp \left( ikR\right) d^{3}x^{\prime }, \end{aligned}$$

(45)

using the fields definitions in terms of the potentials, and the previous expression of $\phi \left( {\textbf{x}},\omega \right)$, to obtain

$$\begin{aligned} {\textbf{B}}\left( {\textbf{x}},\omega \right)= & {} \nabla \times {\textbf{A}} \left( {\textbf{x}},\omega \right) , \\ {\textbf{E}}\left( {\textbf{x}},\omega \right)= & {} -\nabla \phi \left( {\textbf{x}},\omega \right) +i\omega {\textbf{A}}\left( {\textbf{x}},\omega \right) \\= & {} i\frac{\left( 1+\gamma \right) c^{2}}{\omega }\nabla \times {\textbf{B}} \left( {\textbf{x}},\omega \right) -i\gamma \omega {\textbf{A}}\left( {\textbf{x}},\omega \right) , \\ S\left( {\textbf{x}},\omega \right)= & {} -i\frac{\omega }{c^{2}}\phi \left( {\textbf{x}},\omega \right) +\nabla \cdot {\textbf{A}}\left( {\textbf{x}},\omega \right) \\= & {} -\gamma \nabla \cdot {\textbf{A}}\left( {\textbf{x}},\omega \right) . \end{aligned}$$

We can now use the usual approximations for the far field, or radiation region, in the solution of (45), with sources located around the origin of coordinates, and $R\simeq \left| {\textbf{x}}\right| - {\textbf{x}}^{\prime }\cdot {\textbf{n}}$, with ${\textbf{n}}={\textbf{x}} /\left| {\textbf{x}}\right|$. By further denoting $r\equiv \left| {\textbf{x}}\right|$ the far-field term is

$$\begin{aligned} {\textbf{A}}\left( {\textbf{x}},\omega \right)= & {} \frac{\mu _{0}}{4\pi r}\exp \left( ikr\right) \nonumber \\{} & {} \times \int {\textbf{j}}\left( {\textbf{x}}^{\prime },\omega \right) \exp \left( -ik{\textbf{x}}^{\prime }\cdot {\textbf{n}}\right) d^{3}x^{\prime }. \end{aligned}$$

(46)

Since space derivatives of $r^{-1}$ and of ${\textbf{n}}$ generate additional factors $r^{-1}$, the only space derivatives of (46) that contribute in the radiation region are those of $\exp \left( ikr\right)$, so that the general expression of the fields in the radiation region are

$$\begin{aligned} {\textbf{B}}\left( {\textbf{x}},\omega \right)= & {} ik{\textbf{n}}\times {\textbf{A}} \left( {\textbf{x}},\omega \right) , \end{aligned}$$

(47a)

$$\begin{aligned} {\textbf{E}}\left( {\textbf{x}},\omega \right)= & {} -i\omega \left( 1+\gamma \right) {\textbf{n}}\times \left[ {\textbf{n}}\times {\textbf{A}}\left( {\textbf{x}},\omega \right) \right] -i\gamma \omega {\textbf{A}}\left( {\textbf{x}},\omega \right) \nonumber \\= & {} i\omega {\textbf{A}}_{\perp }\left( {\textbf{x}},\omega \right) -i\gamma \omega {\textbf{A}}_{\parallel }\left( {\textbf{x}},\omega \right) , \end{aligned}$$

(47b)

$$\begin{aligned} S\left( {\textbf{x}},\omega \right)= & {} -ik\gamma {\textbf{n}}\cdot {\textbf{A}} \left( {\textbf{x}},\omega \right) , \end{aligned}$$

(47c)

$$\begin{aligned} \phi \left( {\textbf{x}},\omega \right)= & {} \left( 1+\gamma \right) c{\textbf{n}} \cdot {\textbf{A}}\left( {\textbf{x}},\omega \right) \end{aligned}$$

(47d)

with ${\textbf{A}}$ given by (46), and where ${\textbf{A}}_{\parallel }=\left( {\textbf{n}}\cdot {\textbf{A}}\right) {\textbf{n}}$, ${\textbf{A}}_{\perp }={\textbf{A}}-{\textbf{A}}_{\parallel }$. Relation $\omega =kc$ was also used.

We thus see that the transverse components of the electromagnetic radiation field generated by a given current distribution coincide with those predicted by Maxwell electrodynamics. The additional terms are the longitudinal component of the electric field and the scalar field.

The instantaneous energy flow has in AB electrodynamics the expression [12]

$$\begin{aligned} {\textbf{S}}_{u}=\frac{1}{\mu _{0}}\left( {\textbf{E}}\times {\textbf{B}}-\phi \nabla S+{\textbf{A}}\frac{\partial S}{\partial t}\right) . \end{aligned}$$

(48)

In terms of the Fourier amplitudes the time-averaged energy flow is thus expressed as (the asterisk indicates complex conjugation)

$$\begin{aligned} \overline{{\textbf{S}}}_{u}= & {} \frac{1}{4\mu _{0}}\left[ {\textbf{E}}^{*}\times {\textbf{B}}+{\textbf{E}}\times {\textbf{B}}^{*}\right. \\{} & {} \left. +ik\left( \phi S^{*}-\phi ^{*}S\right) +i\omega \left( {\textbf{A}}S^{*}-{\textbf{A}}^{*}S\right) \right] . \end{aligned}$$

Using expressions (47) we readily obtain

$$\begin{aligned} \overline{{\textbf{S}}}_{u}=\frac{\omega ^{2}}{2\mu _{0}c}\left[ {\textbf{A}} _{\perp }\cdot {\textbf{A}}_{\perp }^{*}-\gamma \left( 1+\gamma \right) {\textbf{A}}_{\parallel }\cdot {\textbf{A}}_{\parallel }^{*}\right] \textbf{n }. \end{aligned}$$

The term that contains the perpendicular component ${\textbf{A}}_{\perp }$ coincides with the usual Poynting vector in Maxwell electrodynamics. The interesting point is that the term containing the parallel component ${\textbf{A}}_{\parallel }$ represents an “incoming” energy flow. This indicates that the tunneling currents lead to a “gain” of energy for the radiating system.

As an example we take the finite-length dipole antenna previously considered, for which

$$\begin{aligned} {\textbf{A}}\left( {\textbf{x}},\omega \right)= & {} {\textbf{e}}_{z}\frac{\mu _{0}i_{0} }{4\pi r}\exp \left( ikr\right) \\{} & {} \times \int _{-d/2}^{d/2}\sin \left( \frac{kd}{2} -k\left| z^{\prime }\right| \right) \exp \left( -ikz^{\prime }\cos \theta \right) dz^{\prime }, \end{aligned}$$

where $\theta$ is the angle between ${\textbf{x}}$ and the z axis ($\textbf{ e}_{z}$ is the unit vector along the z axis). An elementary integration gives

$$\begin{aligned} {\textbf{A}}\left( {\textbf{x}},\omega \right) =\frac{\mu _{0}i_{0}}{2\pi kr} \exp \left( ikr\right) \frac{\cos \left( \frac{kd}{2}\cos \theta \right) -\cos \left( \frac{kd}{2}\right) }{\sin ^{2}\theta }{\textbf{e}}_{z}. \end{aligned}$$

The resulting magnetic far field has only azimuthal component

$$\begin{aligned} {\textbf{B}}\left( {\textbf{x}},\omega \right) =i\frac{\mu _{0}i_{0}}{2\pi r} \exp \left( ikr\right) \frac{\cos \left( \frac{kd}{2}\right) -\cos \left( \frac{kd}{2}\cos \theta \right) }{\sin \theta }{\textbf{e}}_{\varphi }, \end{aligned}$$

which is transverse to the propagation direction ${\textbf{n}}$.

The electric far field has the transverse $\theta$-component

$$\begin{aligned} E_{\theta }\left( {\textbf{x}},\omega \right) =i\frac{i_{0}}{2\pi \varepsilon _{0}cr}\exp \left( ikr\right) \frac{\cos \left( \frac{kd}{2}\right) -\cos \left( \frac{kd}{2}\cos \theta \right) }{\sin \theta }, \end{aligned}$$

and the radial, longitudinal component

$$\begin{aligned} E_{r}\left( {\textbf{x}},\omega \right)= & {} i\gamma \frac{i_{0}}{2\pi \varepsilon _{0}cr}\exp \left( ikr\right) \nonumber \\{} & {} \times \frac{\cos \left( \frac{kd}{2}\right) -\cos \left( \frac{kd}{2}\cos \theta \right) }{\sin ^{2}\theta }\cos \theta . \end{aligned}$$

(49)

The scalar far field is

$$\begin{aligned} S\left( {\textbf{x}},\omega \right)= & {} i\gamma \frac{\mu _{0}i_{0}}{2\pi r}\exp \left( ikr\right) \nonumber \\{} & {} \times \frac{\cos \left( \frac{kd}{2}\right) -\cos \left( \frac{kd }{2}\cos \theta \right) }{\sin ^{2}\theta }\cos \theta . \end{aligned}$$

(50)

The time-averaged energy flow is

$$\begin{aligned} \overline{{\textbf{S}}}_{u}= & {} \frac{\mu _{0}i_{0}^{2}c}{8\pi ^{2}r^{2}}\left[ \frac{\cos \left( \frac{kd}{2}\cos \theta \right) -\cos \left( \frac{kd}{2} \right) }{\sin ^{2}\theta }\right] ^{2}\\{} & {} \times \left[ \sin ^{2}\theta -\gamma \left( 1+\gamma \right) \cos ^{2}\theta \right] {\textbf{n}}. \end{aligned}$$

5 Conclusions

Building upon previous work, we have proven that the Aharonov–Bohm extended electrodynamics with the parameter choice $\lambda =1$ (corresponding to the so-called Feynman gauge Lagrangian in Maxwell theory) is the only theory of the electromagnetic field which allows a coupling to non-conserved currents and preserves the locality of field equations. In this theory the potentials $A^\mu$ are fixed, apart from a small class of residual gauge transformations, and can in principle be physically measured using anomalous conducting probes (i.e., probes made of materials in which the continuity $\partial _\mu j^\mu =0$ is violated at some points). As briefly recalled in Sect. 1.3, such anomalies may exist, at the microscopic and quantum level, in various physical systems.

We can thus conclude that, although the exact local conservation of the current and the associated gauge symmetry are important and “desirable” properties, they do not constitute an absolute necessity, because the equations of the electromagnetic field make perfectly sense without them, and even become logically simpler.

On the other hand, we have proven that since it is still possible to introduce auxiliary, non-physical potentials with the familiar gauge-fixing choices, the extended theory is well compatible with Maxwell theory and inherits from it most of the usual computational techniques.

In order to demonstrate the consistency of the extended theory we have elaborated in detail on a phenomenological model of anomalous media, in which the continuity equation is replaced by the relation (derived from some microscopic fundamental hypotheses) $\partial _t \langle \rho \rangle + (1+\gamma ) \nabla \cdot \langle {{\textbf {j}}} \rangle =0$. Here $\gamma$ is in general an adimensional parameter much smaller than 1; however, calculations of radiation emission in Sect. 4 indicate that $\gamma$ can approach 1 from below without giving rise to any singularity. In Sect. 2.4 the propagation of plane waves in anomalous media has been computed.

Possible physical realizations of anomalous conductors are represented by molecular devices [23,24,25,26]. We would like to point out that the parts of Ref. [24] most in line with our ideas are the Supplementary Materials, where the method by Wang et al. for the calculations of the non-local part of the current [38] is applied. The authors find that a part of the current “does not follow the bonds” (i.e., the wavefunctions) also when the basis of states employed for the first-principles calculations is much enlarged. It should be stressed that first-principles calculations give excellent results for observable quantities like energy spectra etc., so they appear to produce a good picture of the physics of the system, probably equivalent to that of an hypothetical renormalized quantum field theory, in which anomalies can play a role.

Another kind of macro-molecule exhibiting high conductivity and a charge transmission mechanism which is still not completely understood is graphene. Due to the chiral nature of quasi-particles in single and bi-layer graphene, quantum tunneling in these materials becomes highly anisotropic and markedly different from the case of normal, non-relativistic electrons. It is in fact a condensed-matter realization of the Klein tunneling, which raises a paradox concerning local charge conservation [39, 40]. The solutions of the paradox that have been proposed go beyond single-particle wavefunctions and involve multi-particle quantum field theory processes (see e.g. [41] and refs.). However, it is well known that chiral symmetry is often broken at the quantum level.

For this reason we believe that in the detection circuits for gauge waves proposed in Sect. 3 it might be convenient to use graphene or graphite as possible anomalous medium with non-zero extra-current I. However, a detailed discussion of those detectors concerning signal/noise sensitivity and possible error sources is beyond the scope of this paper and will be the subject of future work.