Abstract
We write down the teleparallel equivalent to Hassan–Rosen bigravity, which is written using a torsionful but curvature-free connection. The theories only differ by a boundary term. The equivalence was proven, both by using perturbation theory and Hamiltonian analysis. It is further shown how one can construct novel bigravity theories within the teleparallel framework. Some of those are analyzed through perturbation theory, and it is found that all of the considered novel bigravity theories suffer from pathologies. In particular, it is found that a construction with two copies of new general relativity leads to ghostly degrees of freedom which are not present in the single tetrad teleparallel corresponding theory. We demonstrate how the teleparallel framework allows to easily create theories with derivative interaction. However, it is shown through perturbation theory that the simplest model is not viable. Furthermore, we demonstrate some steps in the Hamiltonian analysis of teleparallel bigravity with two copies of new general relativity and some toy models. The results rule out some of the novel teleparallel bigravity theories, but also demonstrate techniques in perturbation theory and Hamiltonian analysis which could be further used for more profound theories in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum field theory has successfully led to a consistent description of all fundamental forces of nature within the standard model of particle physics, except gravity. The standard model in its present form has passed numerous experimental tests, including most prominently the discovery of the Higgs boson almost half a century after its prediction. Modifying such a robust theory, to make it consistent with general relativity seems very difficult. A more natural approach would be to look at modifications of general relativity. The gauge structure encountered in the standard model and unexplained observations in Nature guide us towards the most motivated ways to explore theories beyond general relativity.
General relativity has also been very successful in passing experimental tests. It has successfully predicted the deflection of light from the sun and the precession of Mercury. One may ask why we should consider theories beyond general relativity. Beside a philosophically appealing idea, that there would exist a theory for everything, we need a quantum theory of gravity in order to understand the early universe and black holes. However, general relativity is a notoriously non-renormalizable theory, as is very nicely explained in [1], so that the usual quantization methods used in the standard model cannot be applied.
From observations at scales of galaxies and larger, we conclusively find evidence for the so-called dark sector of the universe. The dark sector consists of dark matter and dark energy, which make up about 95% of our observable universe. Dark energy gives rise to an expanding universe at an accelerating speed. The existence of dark matter can be inferred indirectly by its gravitational effects on the motion of stars within galaxies, gravitational lensing, and structure formation. However, neither of these components has been observed in any laboratory experiment searching for a suitable extension of the standard model. Since gravity is the dominant force at the scales where dark matter and dark energy are observed, it is motivating to look at extensions of general relativity which could give us an understanding of the dark sector of the universe.
The first question to ask before investigating modifications of general relativity is “which formulation of general relativity should be modified?”. In [2] the different formulations of general relativity are explained. Einstein already proposed an alternative formulation of general relativity, which is nowadays called “teleparallel equivalent to general relativity” [3, 4], or “TEGR”. However, the third equivalent formulation called “symmetric teleparallel equivalent to general relativity”, or “STEGR”, was not found until 1998 in [5] and only more recently unified into the general teleparallel theory in [6]. In this article we will work in the framework of “teleparallel gravity”, where our starting point will be the teleparallel equivalent to general relativity. For reviews about teleparallel gravity, see [7,8,9,10,11,12]. For literature about the viability of teleparallel gravity theories, see [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. Teleparallel gravity, in contrast to the conventional curvature-based formulation of gravity in terms of the Einstein–Hilbert Lagrangian, is a gauge theory of gravity with a Yang–Mills-like structure.Footnote 1 [51, 52], similar to that of the standard model. Thus, teleparallel gravity theories are more reminiscent of the standard model of particle physics.
The second question to ask is “how to modify gravity?”. In this article we want to investigate the possibility of adding a massive spin-2 field. Already in 1939 Fierz and Pauli addressed the question of a possible formulation of a massive gravity theory [53]. There were some further historical attempts, such as [48, 54], but not until 2010 a consistent theory of massive gravity was formulated which avoids the previously encountered problems of ghost instabilities [55]. Shortly after Hassan and Rosen wrote down a consistent gravitational theory for a massless and a massive spin-2 field [56]. This theory was named “bimetric gravity” but is sometimes referred as “bigravity” or “bimetric theory”. For a review about bimetric gravity, see [57, 58]. For work on the consistency of bigravity theories, see [59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77]. Bimetric gravity has the potential of describing dark matter [78, 79] and viable cosmological solutions [80,81,82,83,84,85,86,87,88]. The aim of this article is to investigate if we can write down viable teleparallel bigravity theories, that is, to formulate a self-consistent theory of two dynamical tetrads using a flat, metric compatible, but torsionful connection.
A promising feature coming from the structure of teleparallel bigravity is the possibility to construct terms with derivative interactions which are much more symmetric than those constructed in curvature based theories of bigravity (see for example [61, 62, 89]). Derivative interaction has gained interest in bigravity since they are related to theories with conformal symmetries [90, 91]. These theories exhibit a symmetry which manifests with the existence of a partially massless spin-2 field instead of the massive spin-2 field. There is, however, a no-go theoremFootnote 2 forbidding self-interactions for a single partially massless spin-2 field [92]. This no-go theorem is here avoided, by the fact that this is a theory of several interacting fields as in [93].
We provide a new teleparallel equivalent formulation for Hassan–Rosen bigravity (TEHR) where curvature is replaced by torsion analogously to the teleparallel formulation of general relativity. This provides a theory of a massless and a massive spin-2 field, which, in addition, more evidently exhibits a Yang–Mills-like gauge structure. These properties make the theory more reminiscent of the standard model of particle physics compared to the formulation of general relativity the curvature formulation of the theory of general relativity (see though footnote 1 in this paper and the first paragraph in the paper [49]).
We show that the Hamiltonian of TEHR has the same structure as in [60] so we expect the number of degrees of freedom to be consistent. Furthermore, the linear analysis around a Minkowski background describes massless and massive spin-2 fields just as in Hassan–Rosen bimetric gravity. This formulation will work as a conceptually different view of Hassan–Rosen bimetric gravity, as well as a new base for possible extensions of the theory. Furthermore, we present a very general class of novel theories within the TEHR framework and look at the linear level of some interesting cases and use the Dirac-Bergmann algorithm to express the Hamiltonians for some examples.
In Sect. 2, we describe the theories of bigravity and teleparallel gravity to finally introduce our novel theory of teleparallel bigravity. In Sect. 3 we make the linear analysis for a large subclass of teleparallel bigravity, and in Sect. 4 we derive the primary constraints for these theories and the Hamiltonian for two specific examples.
We adopt to the following conventions: metrics follow the \(\eta _{AB}=\textrm{diag}(-1,1,1,1)\) sign convention. Greek indices denote global coordinate indices, capital Latin indices represent Lorentz indices, and small Latin indices denote spatial coordinate indices. We use the notation for symmetrizing indices of a tensor by \(2A_{(\mu \nu )}:=A_{\mu \nu }+A_{\nu \mu }\) and, similarly, for antisymmetrizing indices of a tensor we have \(2A_{[\mu \nu ]}:=A_{\mu \nu }-A_{\nu \mu }\).
2 Teleparallel bigravity
In this section we formulate a novel class of theories of gravity which we choose to call teleparallel bigravity. The basic idea of this theory is quite simple. By taking the Hassan–Rosen bimetric gravity theory as our starting point, which is based on a formulation with a metric compatible and torsion-free connection, one can view this action in the teleparallel framework. In this formulation we are able to construct novel theories of gravity, as well as recovering equivalent theories, such as the teleparallel equivalent to Hassan–Rosen bimetric gravity. In order to reach a construction of teleparallel bigravity we start by reviewing Hassan–Rosen bimetric gravity in Sect. 2.1. Then, in order to clarify the distinction between the idea of teleparallel bigravity and other novel theories with names which suggest very similar ideas, we devote Sect. 2.2 to shortly review these theories. In Sect. 2.3 we give a short review for teleparallel equivalent to general relativity, and its extension to new general relativity is reviewed in Sect. 2.4. Section 2.5 is devoted to the introduction of teleparallel bigravity.
2.1 Hassan–Rosen bimetric gravity
Bimetric gravity (or bigravity, bimetric relativity, or bimetric theory) is an extension to general relativity where one metric is added to the theory and is given dynamics. It is a theory of two interacting spin-2 fields. One of the fields is massless (as in general relativity) and the other is massive. In [56] the unique ghost-free bimetric gravity theory with the kinetic terms being two copies of the Einstein–Hilbert action is presented. We refer to this theory as Hassan–Rosen bimetric gravity, and its corresponding action is

where,  and
and  are two dynamical metrics (with corresponding tetrads \(\mathfrak {e}, \mathfrak {f}\) to be defined later), and \(\beta _{n}\) are arbitrary parameters in front of the elementary symmetric polynomials of the eigenvalues \(\lambda _i\): of the matrix
are two dynamical metrics (with corresponding tetrads \(\mathfrak {e}, \mathfrak {f}\) to be defined later), and \(\beta _{n}\) are arbitrary parameters in front of the elementary symmetric polynomials of the eigenvalues \(\lambda _i\): of the matrix  , given by
, given by





As in general relativity

and  is the Ricci scalar of the Levi-Civita connection, which essentially consists of up to second order derivatives of the metric
is the Ricci scalar of the Levi-Civita connection, which essentially consists of up to second order derivatives of the metric  . The parameters \(m, \ m_{\mathfrak {e}}, \ m_{\mathfrak {f}}\) have a dimension of mass and are needed to make the action dimensionless.
. The parameters \(m, \ m_{\mathfrak {e}}, \ m_{\mathfrak {f}}\) have a dimension of mass and are needed to make the action dimensionless.
Hassan–Rosen bimetric gravity can also be formulated in the vielbein (or tetrad) formalism [60]. In this formalism the action becomes:
where \(R^{CD}(E)\) and \(R^{CD}(F)\) are the curvature 2-forms of the Levi-Civita connection constructed from the cotetrads \(E^A\) and \(F^A\) respectively, which relates to the metrics  and
and  in the following way:
in the following way:


We also define the tetrads  , and
, and  , dual to the cotetrads \(\mathfrak {e}^A{}_\mu \), and \(\mathfrak {f}^A{}_\mu \) respectively. For objects which are not metrics, we may suppress metrics and place indices in the wrong position in order to make expressions look more compact. For instance, if we have a cotetrad \(\mathfrak {e}^A{}_\mu \), we may, instead of
, dual to the cotetrads \(\mathfrak {e}^A{}_\mu \), and \(\mathfrak {f}^A{}_\mu \) respectively. For objects which are not metrics, we may suppress metrics and place indices in the wrong position in order to make expressions look more compact. For instance, if we have a cotetrad \(\mathfrak {e}^A{}_\mu \), we may, instead of  , write \(\mathfrak {e}_A{}^\mu \). This takes the correct index positions as the tetrad, but it should not be confused with the tetrad which we, in this case, denote by
, write \(\mathfrak {e}_A{}^\mu \). This takes the correct index positions as the tetrad, but it should not be confused with the tetrad which we, in this case, denote by  . Note that the action is written slightly differently from [60] and rather as in [61]. This will then only be equivalent to (1) up to a reparametrisation of the coefficients \(\beta _{n}\).
. Note that the action is written slightly differently from [60] and rather as in [61]. This will then only be equivalent to (1) up to a reparametrisation of the coefficients \(\beta _{n}\).
2.2 Other bigravity theories
Our aim is to look at bigravity theories in the teleparallel framework, which assumes vanishing curvature. This includes novel theories of gravity. Recently, other novel bigravity theories have been proposed in articles where either the title is reminiscent to the concept of teleparallel gravity, or the structure of the theory is similar. Before going into the theory of teleparallel gravity, we highlight the main differences between these bigravity theories and teleparallel bigravity, in order to avoid any confusion. In [94,95,96] a novel theory named torsion bigravity has been considered. Here, a theory of both curvature and torsion is formulated, where a massless spin-2 field is mediated by the curvature, whereas the massive spin-2 field is mediated by the torsion, which avoids the notion of two metrics (or tetrads) in the construction of a bigravity theory.
In [97] a bigravity theory is constructed with vierbeins as the fundamental field in order to yield an antisymmetric part of the field equations. It was motivated by the fact that antisymmetric field equations played a big role in the quantization of string theory, which suggests that it would make sense to include antisymmetric parts in a gravity theory. Their construction differs from ours by being curvature-based. However, we cannot exclude cases where the field equations might be equivalent. This theory was extended from the single vierbein massive gravity theory proposed in [98]. In [99] the structure of the action seems to yield a physics similar to that of our theory, and even closer to that of [61]. The crucial difference with respect to our approach is that our construction uses more than one connection. In teleparallel bigravity the action contains two connections (corresponding to the two tetrad fields), but only one spin connection. The construction of a bigravity theory with only one connection was found to yield one graviton, instead of two as in other bigravity theories, making this scheme significantly different from teleparllel bigravity [99].
2.3 Teleparallel equivalent to general relativity
General relativity is formulated with the Ricci scalar which depends on the spin connection, which is taken to be torsion-free. However, an equivalent formulation can be made by setting the spin connection to be curvature-free and replacing curvature with torsion. The resulting action reads:

where \(\mathfrak {e}=\det (\mathfrak {e}^A{}_\mu )\),  ,
,  and
and  are the coefficients of the two-form
are the coefficients of the two-form

and where, for our purposes, we chose to set a priori the so-called spin connection to zero. In particular, it is known that this works for the teleparallel equivalent of general relativity and its most popular modifications [17, 100,101,102].
This action is equivalent to the Einstein–Hilbert action modulo a boundary term [4, 7] (which does not appear in this theory). This can be seen by realizing that the Ricci scalar of the teleparallel connection which vanishes due to the flatness condition can be written as

where  denotes the curvature of the torsion-free Levi-Civita connection and
denotes the curvature of the torsion-free Levi-Civita connection and  . One realize immediately from this relation that
. One realize immediately from this relation that

where B.T. denotes the apparent boundary term. From this equation we identify the curvature of the Levi-Civita connection and realize that in teleparallel gravity it is equivalent to (13) up to a boundary term.
2.4 New general relativity
Considering (13) it is apparent that one easily can formulate more theories quadratic in the torsion than the special case equivalent to general relativity. By relaxing the coefficients in (13) to be arbitrary constants, we get a generalized theory of gravity. It appears that any other term quadratic in the torsion tensor and without any derivatives acting on the torsion would violate parity [47]. Our starting point is then

This class of theories have extensively been studied in [15, 17, 18, 22, 31, 33, 34, 42, 47, 103, 104]. Sometimes this theory is named new general relativity, however, the original name was reserved for only a restricted class by forcing  [47]. It is known that if one does not force this restriction the parameterized post Newtonian parameters will deviate from those of general relativity [47, 104] and ghost instabilities are bound to arise [33, 34, 36, 46]. The ghost instabilities will not get removed in the extension to teleparallel bigravity. Since our goal is to make some prior investigation for what novel teleparallel bigravity theories can be viable, this restriction makes sense. However, to canonically write the action for this restricted case one should add a Lagrange multiplier corresponding to the primary constraints imposed by this restriction to (17).Footnote 3 Despite this naming, it makes sense to not fix the coefficients
[47]. It is known that if one does not force this restriction the parameterized post Newtonian parameters will deviate from those of general relativity [47, 104] and ghost instabilities are bound to arise [33, 34, 36, 46]. The ghost instabilities will not get removed in the extension to teleparallel bigravity. Since our goal is to make some prior investigation for what novel teleparallel bigravity theories can be viable, this restriction makes sense. However, to canonically write the action for this restricted case one should add a Lagrange multiplier corresponding to the primary constraints imposed by this restriction to (17).Footnote 3 Despite this naming, it makes sense to not fix the coefficients  , and
, and  beforehand since we can then realize how the choice of parameters has to be chosen to remove ghost-instabilities.
beforehand since we can then realize how the choice of parameters has to be chosen to remove ghost-instabilities.
2.5 Teleparallel bigravity
Hassan–Rosen bimetric gravity is given by the action of either (1) or (8). It has two Einstein–Hilbert terms, one for each metric, and an interaction potential. Many equations are similar to general relativity, with the addition of an analogous equation depending on the second metric.
In this section we will consider a new framework of gravity theories which we call “teleparallel bigravity”. We write down a general action quadratic in the torsion and that does not violate parity. Then we count degrees of freedom for the special case of “teleparallel equivalent to Hassan–Rosen bigravity”, showing that the theory is a ghost-free theory of massless and massive spin two fields.
2.5.1 Novel terms with derivative interactions
Bigravity theories with derivative interactions have been considered in [61, 62, 90]. The naïve actions provided in [61, 89, 105] generically have ghost instabilities due to a relative sign and the full Hamiltonian analysis of [90] have not been carried out. The teleparallel gravity framework, however, gives much more freedom to create bigravity theories with derivative interactions. In this section we explore if examples that are potentially ghost-free can be created. The most general action which is quadratic in torsion in this framework reads

where V(E, F) is an interaction potential, and \(\overset{\mathfrak {e}}{G}_{AB}{}^{\mu \nu \rho \sigma },\)\( \ \overset{kin}{G}_{AB}{}^{\mu \nu \rho \sigma },\) and \(\overset{\mathfrak {f}}{G}_{AB}{}^{\mu \nu \rho \sigma }\) are some combinations of tetrads and metrics not containing any derivatives. Analogously to new general relativity, we introduced

where we again set the spin connection to zero, which we have shown to not affect the number of degrees of freedom in Appendix A. Below, we display a figure for teleperallel bigravity and its limits.

The figure should be understood in the following way. In the lower part in green color we display two equivalent formulations of general relativity. That is, the standard formulation with a metric compatible and torsion free connection and the teleparallel equivalent to general relativity. With the standard formulation of general relativity, it is known from the literature that one can add a second metric and make it dynamical to create a bimetric gravity theory (following the red arrow in the figure). We note that the concept bigravity can be used for more theories than just the standard Hassan–Rosen bimetric gravity, with some of them briefly discussed in Sect. 2.2. From bimetric gravity, one can first look into the tetrad formulation of the theory, and then take inspiration from the known teleparallel gravity theories to construct a teleparallel bigravity theory by changing to the teleparallel framework (blue arrow).
Another logical path for constructing teleparallel bigravity is to start with the teleparallel equivalent to general relativity. By just looking at this action, one can realize that it can be generalized to new general relativity. With new general relativity we can then add a second tetrad which we make dynamical in a very similar way to what was done in the construction of bimetric gravity. This as well leads to the formulation of teleparallel bigravity. Teleparallel bigravity, hence, have the limits of Hassan–Rosen bimetric gravity, new general relativity, and general relativity. In teleparallel bigravity there are novel theories of gravity which may, or may not be viable.
2.5.2 Teleparallel equivalent to Hassan–Rosen bigravity
We will work in the tetrad formalism since this has been useful in both teleparallel and bimetric gravity. We make an ansatz that we simply replace the Einstein–Hilbert terms in (8) with two copies of (13). We will in Sect. 3 show that it reproduces the linear equations of Hassan–Rosen bimetric gravity, and in Sect. 2.5.3 that the counting gives the expected degrees of freedom. The action then is:

Here \(\mathfrak {f}=\det (\mathfrak {f}^A{}_\mu )\), and, \(E^A\), \(F^B\),  , and
, and  are defined in (9), (10), (11), (12) respectively,
are defined in (9), (10), (11), (12) respectively,  is defined in equation (13) and defines \(\mathcal {L}_{\textrm{TEGR}}\) together with the volume element \(\mathfrak {e}\). This is formulated in a gauge where the spin connection vanishes (which is not the canonical formulation). We show in appendix A that the counting of degrees of freedom at the nonlinear level (using Hamiltonian analysis) is independent of our gauge choice. Since this greatly simplifies the Hamiltonian analysis, we choose to set the spin connection to zero.
is defined in equation (13) and defines \(\mathcal {L}_{\textrm{TEGR}}\) together with the volume element \(\mathfrak {e}\). This is formulated in a gauge where the spin connection vanishes (which is not the canonical formulation). We show in appendix A that the counting of degrees of freedom at the nonlinear level (using Hamiltonian analysis) is independent of our gauge choice. Since this greatly simplifies the Hamiltonian analysis, we choose to set the spin connection to zero.
It is well known that the action given by (13) is equivalent to the Einstein–Hilbert action up to a surface term given by (16). Hence, the kinetic part of (20) is equivalent to the kinetic part of Hassan–Rosen bimetric gravity up to a couple of surface terms.
To get a true equivalence we need to make sure that the theory contains the same number of degrees of freedom as in Hassan–Rosen bimetric gravity. We should also investigate whether the consistency-tests performed in Hassan–Rosen bimetric gravity still holds in this new formulation of the theory.
2.5.3 Counting degrees of freedom
In [15, 39, 41] it is shown that the degrees of freedom count for (13) coincides with that of general relativity. Hence the teleparallel formulation of general relativity is a ghost free theory for a spin-2 field as in general relativity.
We now describe how degrees of freedom are counted in Hassan–Rosen bimetric gravity, since we are looking at an extension to this theory. Hassan–Rosen bimetric gravity is formulated in terms of two dynamical metrics. Note that first class constraints remove 2 degrees of freedom each in phase-space, whereas second class constraints remove only 1. Starting with 20 degrees of freedom for each metric (including conjugate momenta). 8 degrees of freedom can be removed from first class constraints associated with a common diffeomorphism invariance for the two metrics. 4 additional degrees of freedom can be removed from gauge fixing one set of lapse and shift. 4 more are removed by Hamiltonian and momentum constraints, normally realized from the field equations of analogous to (25). One set of lapse and shift appears as Lagrange multipliers which gives us 4 first class primary constraints which removes 8 additional degrees of freedom. Finally, 2 more degrees of freedom are removed by an additional second class constraint with an associated secondary second class constraint. This leaves us with \(40-26=14=(2+5)\times 2\) degrees of freedom corresponding to a massless and massive spin-2 field and its corresponding conjugate momenta. Note that the 2 last second class constraints follow from the specific form of the interaction potential [56, 73] and removes the pathological Boulware-Deser ghost.Footnote 4 We should, hence, carefully check whether this constraint still remains in our new theory.
In order to make the Hamiltonian analysis, we need the conjugate momenta, which comes from the fields which have time-derivatives. Hence, we need to distinguish between space and time and make a so-called 3+1 decomposition.Footnote 5 To avoid cumbersome repetition only the objects associated with one metric ( ) will be displayed, and the analogous parts follows. In the case of TEGR there are 6 additional primary constraints compared the metric GR and they have been shown to be of first class, thus removing the dynamics of all the extra components introduced when treating tetrads as canonical fields instead of the metric. These are only slightly different from the usual tetrad formulation of bigravity [60] due to the presence of torsion terms.
) will be displayed, and the analogous parts follows. In the case of TEGR there are 6 additional primary constraints compared the metric GR and they have been shown to be of first class, thus removing the dynamics of all the extra components introduced when treating tetrads as canonical fields instead of the metric. These are only slightly different from the usual tetrad formulation of bigravity [60] due to the presence of torsion terms.
By making a 3+1 decomposition of spacetime in ADM variables we can express the Hamiltonian for teleparallel equivalent to general relativity [15, 17, 39, 41]. Following the notation of [17], but adding an overset label \(\mathfrak {e}\) which will be important when extending the result to the teleparallel equivalent to Hassan–Rosen bigravity. The ADM-variables used are  (lapse),
(lapse),  (shift), spatial tetrad \(\mathfrak {e}^A{}_i\) and its conjugate momenta
(shift), spatial tetrad \(\mathfrak {e}^A{}_i\) and its conjugate momenta  , induced metric
, induced metric  and its Levi-Civita covariant derivative \(D_i\) and spatial volume element
and its Levi-Civita covariant derivative \(D_i\) and spatial volume element  , a normal vector to constant hypersurfaces
, a normal vector to constant hypersurfaces  , and the resulting Hamiltonian reads
, and the resulting Hamiltonian reads

where \(\equiv \) signifies that a boundary term have been dropped as discussed in [107] and

with the 6 primary first class constraints

and

where \(\mathcal {V}\) stands for “vector part” and \(\mathcal {A}\) for “antisymmetric” part of the irreducible decomposition under the rotation group as in [15, 17]. Note that [60] did not find the important  constraints and resorted instead to the field equations to demonstrate Lorentz invariance. The constraint algebra satisfy the Lorentz algebra [4, 15, 23] which is essential for realizing they are of first class.
constraints and resorted instead to the field equations to demonstrate Lorentz invariance. The constraint algebra satisfy the Lorentz algebra [4, 15, 23] which is essential for realizing they are of first class.
From (20) it is straightforward to write down the Lagrangian as the back-transformation of the primary Hamiltonian, for teleparallel equivalent to Hassan–Rosen bigravity in a form like the one used in [60]:

where  comes, and are defined, from the interaction potential which is linear in lapse and shifts due to the fact that they only appear (and are linear) in \(\mathfrak {e}^A{}_0\) and \(\mathfrak {f}^A{}_0\) terms and the antisymmetric property of the wedge product ensures that they appear exactly one time in each term as discussed in [60]. Now we have reproduced the tetrad formulation of bigravity and we, hence, do not expect any difference in the results of Hassan–Rosen bigravity. In sect 2.5.2 we find that at the linear level we recover the linearized modes of Hassan–Rosen bigravity as expected.
comes, and are defined, from the interaction potential which is linear in lapse and shifts due to the fact that they only appear (and are linear) in \(\mathfrak {e}^A{}_0\) and \(\mathfrak {f}^A{}_0\) terms and the antisymmetric property of the wedge product ensures that they appear exactly one time in each term as discussed in [60]. Now we have reproduced the tetrad formulation of bigravity and we, hence, do not expect any difference in the results of Hassan–Rosen bigravity. In sect 2.5.2 we find that at the linear level we recover the linearized modes of Hassan–Rosen bigravity as expected.
However, one should be cautious since in the special case of choosing the kinetic action to be two copies of TEGR (and similarly by taking two copies of the tetrad formulation of Einstein–Hilbert terms) the antisymmetric components of the tetrads become non-dynamical [76].Footnote 6 Variation with respect to the antisymmetric components generate the following field equations [60, 76] which turns out to be constraints. Thus, the antisymmetric components are subject to the following 12 constraints:


Note that this is special for TEHR (and for the tetrad HR formulation of HR bigravity and multigravity extensions [76]) and in general teleparallel bigravity theories the antisymmetric part of the tetrads become dynamical, and the above constraints will be spoiled in the absence of  , which constrains the antisymmetric kinetic part. Absence of primary constraints for the the antisymmetric sector will reduce the number of constraints, also in the case where at least one of
, which constrains the antisymmetric kinetic part. Absence of primary constraints for the the antisymmetric sector will reduce the number of constraints, also in the case where at least one of  , or their corresponding \(\mathfrak {f}\) constraints, is absent.
, or their corresponding \(\mathfrak {f}\) constraints, is absent.
We will now turn to the linear analysis of general quadratic teleparallel bigravity theories to confirm the results of Hassan–Rosen bigravity and new general relativity, and further explore what novel theories might be viable. In section 4 we will do some preliminary investigation of these novel theories.
2.5.4 Explicit examples worth considering
In this section we argue for what kind of choice of supermetrics provided in teleparallel bigravity (18) are worth taking a deeper look into. We assume that the interaction potential V(E, F) is as in Hassan Rosen bigravity. That is,
This interaction potential has a clear interpretation when expressed in tetrads. Namely, the terms are the volume forms one can create by general combinations of two tetrads in four dimensions. Furthermore, we have a special case  where the first kinetic term is that of new general relativity. We get another copy of new general relativity by assuming
where the first kinetic term is that of new general relativity. We get another copy of new general relativity by assuming  . This is already interesting since these include novel theories for which we already have some insights from the literature of new general relativity and Hassan–Rosen bigravity. For the rest of the article we assume that the interaction potential takes the form as in Hassan–Rosen bigravity, that
. This is already interesting since these include novel theories for which we already have some insights from the literature of new general relativity and Hassan–Rosen bigravity. For the rest of the article we assume that the interaction potential takes the form as in Hassan–Rosen bigravity, that  , and
, and  . By including a non-zero
. By including a non-zero  we will get novel terms which can be motivated from its conformal symmetry. This term alone does, however, suffer from ghost-instabilities. However, if one later would consider a similar theory with complex tetrads similar to the constructions in [90, 91] the theory might turn out to be viable. For the linearized level the explicit expressions of the non-vanishing supermetrics does not play a role in the perturbations we define around a Minkowski background. For the non-linear level we will assume that
we will get novel terms which can be motivated from its conformal symmetry. This term alone does, however, suffer from ghost-instabilities. However, if one later would consider a similar theory with complex tetrads similar to the constructions in [90, 91] the theory might turn out to be viable. For the linearized level the explicit expressions of the non-vanishing supermetrics does not play a role in the perturbations we define around a Minkowski background. For the non-linear level we will assume that  , where we define the cotetrad \(\ae ^A{}_\mu \) to satisfy
, where we define the cotetrad \(\ae ^A{}_\mu \) to satisfy

with its corresponding tetrad denoted by  , and
, and  being some new Lorentzian metric.
being some new Lorentzian metric.
For the Hamiltonian analysis we derive the primary constraints for the theory corresponding to this action. However, we restrict further analysis to the special case  , which should be viewed as a toy-model since it contains ghosts. The cotetrad \(\ae ^A{}_\mu \) for a bigravity theory should depend on the two other cotetrads \(\mathfrak {e}^A{}_\mu \) and \(\mathfrak {f}^A{}_\mu \), since the theory describes only two dynamical tensor fields. However, the Hamiltonian analysis can be made without much complications to the point where velocities have been Legendre transformed to conjugate momenta. For this reason we leave \(\ae ^A{}_{\mu }\) undetermined until this stage of the analysis. We could already make some speculations of what \(\ae ^A{}_\mu \) could be. In order to make the term with derivative interactions completely symmetric in \(\mathfrak {e}\) and \(\mathfrak {f}\) there are in particular two choices. First one is to assume
, which should be viewed as a toy-model since it contains ghosts. The cotetrad \(\ae ^A{}_\mu \) for a bigravity theory should depend on the two other cotetrads \(\mathfrak {e}^A{}_\mu \) and \(\mathfrak {f}^A{}_\mu \), since the theory describes only two dynamical tensor fields. However, the Hamiltonian analysis can be made without much complications to the point where velocities have been Legendre transformed to conjugate momenta. For this reason we leave \(\ae ^A{}_{\mu }\) undetermined until this stage of the analysis. We could already make some speculations of what \(\ae ^A{}_\mu \) could be. In order to make the term with derivative interactions completely symmetric in \(\mathfrak {e}\) and \(\mathfrak {f}\) there are in particular two choices. First one is to assume  . The second choice is to take it to depend on the so-called geometric mean defined via the relation
. The second choice is to take it to depend on the so-called geometric mean defined via the relation

where  is an intermediate metric between
is an intermediate metric between  and
and  [106]. The explicit expressions for the supermetrics are,
[106]. The explicit expressions for the supermetrics are,



where we introduced, a priory, arbitrary coefficients  , for the part which only depends on \(\mathfrak {f}\) and
, for the part which only depends on \(\mathfrak {f}\) and  for the terms with derivative interactions. For the linear analysis, we will use a different supermetric
for the terms with derivative interactions. For the linear analysis, we will use a different supermetric

pointing out that its use in our perturbation theory still gives compatible results since we only look at lower order expansions around a Minkowski background, where the contractions are reduced to contractions with the Minkowski metric.
3 Linear analysis of teleparallel bigravity
In this section we examine teleparallel bigravity at the linear level, where we retain only linear perturbations of the field equations or, equivalently, second order perturbations of the Lagrangian. The results motivate a further examination of these theories at the nonlinear level, which we carry out in Sect. 4.
3.1 The spectrum of teleparallel bigravity
The full action and Lagrangian density of the theory are specified as
where



The expressions used for the perturbations of the tetrad, cotetrad and volume form are



where we used the permutation symbol \(\epsilon _{ABCD}\). Analogous relations hold for the  tetrad. Notice the presence of the background metric
tetrad. Notice the presence of the background metric  and that
and that  .
.
The resulting linearized Lagrangian then is
with the second order expansions given by:













where we defined  and
and  .
.
3.2 Linear analysis of the teleparallel equivalent to Hassan–Rosen bimetric gravity
As a first application of the general theory, we recover the standard bimetric theory in tetrad formulation. To this purpose we eliminate the new terms brought by the kinetic mixing in the Lagrangian setting  . For the sake of visualization, we also rewrite the above Lagrangian in matrix formalism, using a basis where the field vector has the components \(\Phi :=\)(
. For the sake of visualization, we also rewrite the above Lagrangian in matrix formalism, using a basis where the field vector has the components \(\Phi :=\)( ,
,  ,
,  ,
,  )\(^T\) and by integrating by parts if required
)\(^T\) and by integrating by parts if required
The matrices \(\mathbb {K}\) and \(\mathbb {M}^2\) for the general case can be straightforwardly read from the Lagrangian in Eq. (43). Below we give their explicit forms only for the cases under consideration.
Requiring the absence of linear terms for  and
and  in the bimetric Lagrangian yields the following conditions on the coefficients entering the interaction term
in the bimetric Lagrangian yields the following conditions on the coefficients entering the interaction term
and, as a result, we also obtain that
in the same fashion, for instance, as the condition (3.2) and (3.3) of [60]. After the cancellation of these tadpole terms, enforcing \(\overset{int}{\mathcal {L}}_1=\overset{int}{\mathcal {L}}_0=0\), the mass term reduces to
where, in the last step, we used  .
.
As for the kinetic terms, in order to recover standard bimetric theory, we enforce the cancellation of the \(h-b\) mode mixing by setting  , as well as
, as well as  yielding two copies of the one parameter family of new general relativity introduced in [47]. The resulting kinetic term presents then the following structure
yielding two copies of the one parameter family of new general relativity introduced in [47]. The resulting kinetic term presents then the following structure

where the Lichnerowicz operator is defined as
and we have again used the fact that  .
.
With the kinetic term being already in a diagonal form, we need only to diagonalize the remaining mass term. As a first step, we give the fields the canonical mass dimension through the field redefinition

which puts the Lagrangian in the form:

with

and
Before analyzing the two emerging blocks in isolation, we further simplify the Lagrangian by writing, without loss of generality,
As usual in bimetric theories, we have re-absorbed the dependence of the Lagrangian on \(\beta _{i=1,2,3}\) into the definition of the mass scale \(m_{FP}\).
3.2.1 Symmetric sector
Focusing now on the symmetric perturbations, we have

which is diagonalized through the usual field redefinition

ensuring that the norm of \(M_{AB}\) in field space is the unity.
The orthogonal combination  is determined through
is determined through
where the \(\cdot \) operator stands for the scalar product in field space. As a result, we obtain

showing that the field transformation linking the mass eigenstates to the original fields is simply a rotation in field space:

In terms of the mass eigenstates, the Lagrangian of the symmetric sector is then given by

showing that the condition  is necessary for a complete diagonalization of the symmetric sector. In fact, because the performed field redefinition is simply a rotation, the kinetic term matrix of the original field must be proportional to the unit matrix in order to be unaffected by the field redefinition.
is necessary for a complete diagonalization of the symmetric sector. In fact, because the performed field redefinition is simply a rotation, the kinetic term matrix of the original field must be proportional to the unit matrix in order to be unaffected by the field redefinition.
3.2.2 Antisymmetric sector
As for the antisymmetric sector, we have

which is diagonalized through a rotation analogous to that of the symmetric sector. In particular, by defining

we have

In analogy with the case of the symmetric sector, the condition  ensures the decoupling of the modes.
ensures the decoupling of the modes.
3.2.3 Teleparallel equivalent of bimetric gravity
In terms of the mass eigenstates we have identified and through the above conditions, the full Lagrangian then becomes:

Setting now the remaining coefficients to their TEGR values, we notice that  ensures a proper normalizes the Lichnerowicz operator \(\mathcal {E}^{ABDE}\) and casts the Lagrangian of the symmetric sector into the usual bimetric form:
ensures a proper normalizes the Lichnerowicz operator \(\mathcal {E}^{ABDE}\) and casts the Lagrangian of the symmetric sector into the usual bimetric form:
Differently, the choice  prevents the propagation of all antisymmetric modes, reducing the corresponding Lagrangian to
prevents the propagation of all antisymmetric modes, reducing the corresponding Lagrangian to
The resulting equation of motion then forces constraint \(E_{AB} = 0\), which through Eq. (74) recovers

At the first order of the perturbation expansion, this condition coincides with the requirement \(\eta _{AB}{\mathfrak {e}^A}_{[\mu } {\mathfrak {f}^B}_{\nu ]}{\mathop {=}\limits ^{!}}0\), often discussed in the literature of bigravity [60, 65, 66, 106].
We remark that the final form of the Lagrangian was obtained by using a rotation in field space, rather than a generic linear transformation, to diagonalize the mass term. Whether this might seem as an overly restrictive choice, we remind that in the teleparallel equivalent of bimetric gravity, the coefficients \(C_i\) of the two tetrads are set from the very beginning to their TEGR values and, as a consequence, the identified rotation is the only transformation that recasts the symmetric sector in the standard form.
We also notice that prior to setting the coefficients \(C_i\) to their TEGR values, the Lagrangian of the antisymmetric sector mirrors that of the symmetric one, albeit an important distinction. The mass terms of the massive modes, in fact, have opposite signs. Whether a generic theory containing propagating symmetric and antisymmetric modes would probably contain ghosts, at this stage it seems still possible to recover a regime of the theory characterized by the propagation of a massive and a massless antisymmetric mode and no symmetric perturbations.
3.3 Linear analysis of the full Lagrangian
We now face the full Lagrangian, allowing for the kinetic mixing terms that we neglected in the previous section. Note that in the limit \(m_{FP} \rightarrow 0\) of vanishing Fierz-Pauli mass, a kinetic coupling in the symmetric sector, which contains two massless spin-2 fields in this case, inevitably leads to the existence of a scalar ghost mode [108]. For this reason, such kinetic coupling is not considered in the Hassan–Rosen bigravity [56].
The treatment of the linear and 0-th order terms proceeds as in the standard bimetric case: enforcing the absence of tadpole term by setting
we obtain \(\beta _0 + \beta _1 + \beta _2 + \beta _3 + \beta _4 \equiv 0\), and the mass term consequently acquires again the form
in terms of the properly normalized fields given by

As for the kinetic term of the normalized fields, in this first analysis we choose to set

in order to obtain the same block diagonal structure of the mass term. Whereas this condition is in principle unnecessary, it allows us to tackle the symmetric and antisymmetric modes separately, with a considerable simplification of the diagonalization procedure. In order to further simplify the Lagrangian, we also opt to set \(m^2_{\mathfrak {e}\mathfrak {f}}{\mathop {=}\limits ^{!}}m_\mathfrak {e}m_\mathfrak {f}\), obtaining:

with the Lichnerowicz operator \(\mathcal {E}^{ABDE}\) defined as in the standard case. Because the interaction term is the same as in the standard bimetric gravity, the field rotations in Eqs. (71) and (74) certainly diagonalize it. However, if we restrict ourselves to these transformations, the coefficients in the kinetic term will have to be set in a way that the kinetic term becomes proportional to the unit matrix in field space. In particular, this choice will force the absence of kinetic mixing, leading inevitably to scenarios close to the standard bimetric case or that, at most, allow for the propagation of a massless and a negative mass antisymmetric mode. For this reason, in the following we consider instead generic superpositions of symmetric and antisymmetric perturbations rather than rotations in the corresponding field spaces.
3.3.1 Symmetric sector
Upon partial integration of the off-diagonal kinetic terms, the Lagrangian for the symmetric perturbation is written as:

where, without loss of generality, we have set \(\left( 3\beta _1 + 4\beta _2 \right. \)\( \left. +3\beta _3 \right) =24\). In order to diagonalize the Lagrangian, we now consider the generic linear transformation

where \(G_{AB}\) and \(M_{AB}\) are respectively the graviton and massive bigraviton excitation. However generic the transformation be, we still require that an inverse exists by imposing that the determinant of the transformation never vanishes. We will verify that the solutions we identify indeed satisfy this criterion.
Analyzing the mass term in isolation, we see that

and analogous expressions hold for the remaining terms. It is then clear that setting
forbids a mass term for the G perturbation. Similarly, requiring that the kinetic terms for G and M have the canonical form, as well as the presence of no mixing, results in three further conditions that fully determine the parameters in Eq. (86). Explicitly, we have

where \(\supset \) denotes that some terms in the Lagrangian are omitted, and imposing the above condition, as well as

results in four possible solutions for the involved parameters which differ only by the verse associated to the selected linear combinations in field space. In particular, the choice

correctly reduces to the (inverse of the) rotation matrix in Eq. (71). Real and finite coefficients are obtained when

which also ensure that the transformation is invertible:

We notice the following particular values of  :
:
-
 . In this case the kinetic term acquires the form
. In this case the kinetic term acquires the form\(\mathcal {L}\supset A^2 \,M_{AB} \,\tilde{\mathcal {E}}^{ABDE}\,M_{DE} + B^2 \,G_{AB} \,\tilde{\mathcal {E}}^{ABDE}\,G_{DE} + 2AB \,G_{AB} \,\tilde{\mathcal {E}}^{ABDE}\,M_{DE}\), implying that a vanishing mixing term necessarily requires at least either of the kinetic terms to vanish.
-
 . Once Eq. (88) is imposed to prevent a mass term for the \(G_{AB}\) perturbation, this particular value of
. Once Eq. (88) is imposed to prevent a mass term for the \(G_{AB}\) perturbation, this particular value of  nullifies the kinetic term of the same perturbation.
nullifies the kinetic term of the same perturbation.
Excluding the above values of  , the Lagrangian of the symmetric sector simply becomes
, the Lagrangian of the symmetric sector simply becomes
where the involved perturbations are determined from the original  and
and  fields through the inverse of Eq. (86) and where we have defined
fields through the inverse of Eq. (86) and where we have defined

Notice that the Fierz–Pauli mass is positive defined if the conditions in Eq. (92) are satisfied, and becomes vanishing or singular in correspondence of the two values of  that make the transformation singular. This seems to imply that if a fluctuation does not propagate, the other must necessarily be massless.
that make the transformation singular. This seems to imply that if a fluctuation does not propagate, the other must necessarily be massless.
3.3.2 Antisymmetric sector
Analogously, for the antisymmetric perturbations we have

where we used \(\left( 3\beta _1 + 4\beta _2 +3\beta _3 \right) =24\). In order to diagonalize the above Lagrangian we introduce the states \(E_{AB}\) and \(F_{AB}\) such that

and express the mass term as
Imposing the absence of mass mixing then forces, again, the presence of a massless state. In analogy to the symmetric case, we choose here
so that
Notice that \(\mu ^2_{FP}\ge 0\) and consequently the mass term appears in the Lagrangian inevitably with the wrong sign. Leaving this issue aside for the moment, we proceed to express the kinetic term in terms of the newly defined perturbations


Requiring now

results in

and every other result can, likewise, be derived from those of the symmetric sector via the substitution  ,
,  ,
,  .
.
As in the case with vanishing kinetic mixing, the general theory seems to admit the propagation of a ghost-like massive antisymmetric perturbation. Although it is certainly possible to force the kinetic terms of this problematic perturbation to vanish through a proper choice of the coefficients, we argue below that this might not be necessary. As antisymmetric perturbations correspond, in essence, to the propagation of scalar fields, the presence of a negative mass term could simply indicate the emergence of a spontaneously broken symmetry. In fact, for the sake of the viability of the theory, it could be enough that the terms of higher order in the perturbative expansion give rise to self interactions of the scalar field which result in a potential bounded from below. The situation is analogous to that of the Higgs boson in the standard model, where the negative mass term of the field triggers the electroweak symmetry breaking.
4 Nonlinear analysis of teleparallel bigravity
We saw in the previous section that some teleparallel bigravity theories contain ghosts. Still, it is of interest to understand their symmetries and view them as toy models. For instance, the terms with derivative interactions might be constructed in a viable way if we allow for a construction with complex tetrads similar to the theory considered in [90, 91]. We dedicate this section to investigate teleparallel bigravity at the nonlinear level. For this we make a 3+1 decomposition and find primary constraints for the action considered in the linear analysis.
4.1 Primary constraints
We remind ourselves that the linear analysis applies to the action (18) with the supermetrics defined by (31), (32), and (33). Note that the interaction potential is independent of velocities in the fields and, hence, do not contribute to the conjugate momenta. Furthermore, \(\overset{\mathfrak {e}}{\mathcal {L}}\) and \(\overset{\mathfrak {f}}{\mathcal {L}}\) are just new general relativity terms which are already known from the literature [11, 15, 17, 18, 40]. Hence, we can determine the primary constraints by making the 3+1 decomposition of \(\overset{kin}{\mathcal {L}}\) and calculate its primary constraints and add this information. The lapse and shift are denoted by  , respectively and the induced metric is denoted by
, respectively and the induced metric is denoted by  , whereas the normal vector components to the hypersurface of constant time slices is denoted by
, whereas the normal vector components to the hypersurface of constant time slices is denoted by  . The Lagrangian 3+1 decomposition of \(\overset{kin}{\mathcal {L}}\) is
. The Lagrangian 3+1 decomposition of \(\overset{kin}{\mathcal {L}}\) is

where

and

The conjugate momenta hence becomes


We decompose everything into irreducible parts, with respect to \(\ae \), as done in [15, 17].




The inversion for a general theory (18) is quite involved and lies beyond the scope of this article. However, we can, as a toy example, derive the inversion formula between the velocities and conjugate momenta for the subtheory  , for which the results are very similar to [17]. First we define the sources which are independent of velocities:
, for which the results are very similar to [17]. First we define the sources which are independent of velocities:


where  and its inverse can be written in irreducible parts:
and its inverse can be written in irreducible parts:

which yields:

where




Putting  ) we get the following primary constraints \({}^{\mathcal {I}}C \approx 0\) and \({}^{\mathcal {I}}\tilde{C} \approx 0\):
) we get the following primary constraints \({}^{\mathcal {I}}C \approx 0\) and \({}^{\mathcal {I}}\tilde{C} \approx 0\):




We now want to include the contribution from \(\overset{\mathfrak {e}}{\mathcal {L}}\) and \(\overset{\mathfrak {f}}{\mathcal {L}}\). The 3+1 decomposition of this Lagrangian reads

where we introduce




The conjugate momenta for this action are


We can, as in the \(\overset{kin}{\mathcal {L}}\) case, define sources which are independent of velocities so that


with

or equivalently

It is possible to find the Moore–Penrose pseudo inverse of a matrix to the block matrix in Eq. (136) analogous to [17,18,19]. This is done by using the usual inverse formula for block matrices, assuming that the determinants of the submatrices are non-zero. This can then be decomposed into irreducible parts under the rotation group, and if the corresponding primary constraints are imposed, then that part of the irreducible decomposition is simply removed in order to get the correct inverse. The Hamiltonian can then straightforwardly be derived. However, due to the lengthiness of these calculations we leave this for the future. Note that a proper 3+1 decomposition assumes that all tetrads are timelike with respect to each other and, hence, the following is true

and so on. This will also be useful when considering other bigravity theories.
4.2 Specific examples
In this section we go into two examples for which we write down the Hamiltonian (to the step before using Dirac’s algorithm to calculate Poisson brackets and find all constraints). The first example is two copies of new general relativity which is very easy to get from previous results [17, 18]. The second is the \(\overset{kin}{\mathcal {L}}\)-term which share a lot of similarities with new general relativity. This theory, however, contains ghosts and only acts as a toy model. Note that \(\mathcal {H}\left( \overset{\mathfrak {e}}{\mathcal {L}}+\overset{\mathfrak {f}}{\mathcal {L}}+\overset{kin}{\mathcal {L}}+\overset{int}{\mathcal {L}}\right) \ne \overset{\mathfrak {e}}{\mathcal {H}}+\overset{\mathfrak {f}}{\mathcal {H}}+\overset{kin}{\mathcal {H}}+\overset{int}{\mathcal {H}}\). The inversion of velocities to conjugate momenta will in this case be different than simply the sum of them due to the derivative interactions between the tetrads in \(\overset{kin}{\mathcal {L}}\). The interaction potential transforms under Legendre transformation just by changing its sign. We, hence, focus only on kinetic terms for the Hamiltonian analysis (until the step when Poisson brackets are calculated).
4.2.1 Two copies of new general relativity: \(\overset{\mathfrak {e}}{\mathcal {L}}+\overset{\mathfrak {f}}{\mathcal {L}}\)
A straightforward example of a Hamiltonian for novel teleparallel bigravity terms is obtained by restricting to the case with no derivative interaction. Then the conjugate momenta for the tetrads will only be related to the velocity of the tetrad for which this conjugate momenta was defined. In this case, the Legendre transformation of the total Lagrangian equals the addition of the Lagrangians individually Legendre transformed,
Since we already know \(\overset{\mathfrak {e}}{\mathcal {H}}\) from the literature [17,18,19], and \(\overset{\mathfrak {f}}{\mathcal {H}}\) will just be another copy of the same Hamiltonian, but with respect to the f-tetrad we have

Now the interaction potential should be added and it will modify the secondary constraints in lapse and shift. Since in general we do not have the special case where the antisymmetric modes become non-dynamical, we avoid that non-linearities in lapse and shift appear from solving the equations of motion for the antisymmetric tetrad components. However, one should still be cautious since for particular theories there exists constraints making certain tetrad components non-dynamical and we might end up in a similar situation. From this point Poisson brackets need to be calculated for whichever sub-theory one is interested in, from which eventual secondary, tertiary, ...constraints can be found. In particular, this theory has two subcases. One is new general relativity in the single tetrad limit. The other is teleparallel equivalent to Hassan–Rosen bigravity (see Eq. (20)), when  . For any other choice of parameters we get novel theories of gravity. However, according to the linear analysis all those novel theories appear to be pathological.
. For any other choice of parameters we get novel theories of gravity. However, according to the linear analysis all those novel theories appear to be pathological.
4.2.2 Term with derivative interactions: \(\overset{kin}{\mathcal {L}}\)
We have already established the 3+1 decomposition of the Lagrangian in equation (105) and derived its primary constraints. In order to invert velocities into conjugate momenta we have to find the inverse of \(M^{i \ j}_{ \ A \ B}\) which turns out to be

where the irreducible parts are identified using \((\mathcal {I} \ \in \ \{\mathcal {V},\mathcal {A},\mathcal {S},\mathcal {T}\})\)  . We can write the Hamiltonian as
. We can write the Hamiltonian as

We have that

We note that this expression appears in (141) and is always contracted with something antisymmetric in k and l. One can now quite easily show, by the use of the decomposition of the conjugate momenta into irreducible parts (112) and (113), that the Hamiltonian expressed in the possible primary constraints becomes:

Now we perform an integration by parts and get:

Again, the fact that the equations of motion for the antisymmetric parts of the tetrads introduce non-linearities in lapse and shift is avoided. One still needs to be cautious for certain choices of parameters that one can still end up in similar situations. Now it is time to choose the metric  . One prominent choice would be the so-called geometric mean [65, 106] for which the two metrics
. One prominent choice would be the so-called geometric mean [65, 106] for which the two metrics  and
and  appear on equal footing by satisfying (30). However, this could only be viewed as a toy model when demanding the theory to be ghost-free. Another prominent choice would be to consider
appear on equal footing by satisfying (30). However, this could only be viewed as a toy model when demanding the theory to be ghost-free. Another prominent choice would be to consider  constructed from complex tetrads similar to what have been considered in [90, 91]. In this case more primary constraints are expected in the Hamiltonian analysis and the shape of the Hamiltonian may alter. For the case of the linear analysis it would be considerably different involving complex tetrads and this is, thus, beyond the scope of this article.
constructed from complex tetrads similar to what have been considered in [90, 91]. In this case more primary constraints are expected in the Hamiltonian analysis and the shape of the Hamiltonian may alter. For the case of the linear analysis it would be considerably different involving complex tetrads and this is, thus, beyond the scope of this article.
5 Discussion and conclusions
The teleparallel equivalent of Hassan–Rosen bimetric gravity (TEHR) has been formulated and it admits almost the same structure of constraints as the tetrad formulation of Hassan–Rosen bimetric gravity. The primary constraints associated with the antisymmetric part of the conjugate momenta differ, however, by the presence of torsion terms originating from differences in the boundary [11]. Nevertheless, the symmetries the theory admits are the same, and thus, the degrees of freedom coincide with other formulations of Hassan–Rosen bimetric gravity [56, 60]. With TEHR as a starting point we found several possibilities to create novel modified theories of gravity. For instance, one can make two copies of NGR. As an initial assumption, the NGR coefficients in the  sector can be different from the
sector can be different from the  sector. However, analyzing the perturbations around the Minkowski background reveals that the coefficients need to be proportional to each other for the modes to be decoupled. The only difference is absorbed in the mass constant in front of the respective kinetic term used to define the Fierz–Pauli mass. It is already known that NGR suffer from the strong coupling problem in Minkowski backgrounds [22, 33] and ghost instabilities in the generic case [46]. We confirm this result and find that the problem worsens in the case of teleparallel bigravity since we find that ghostly modes propagate in this theory.Footnote 7
sector. However, analyzing the perturbations around the Minkowski background reveals that the coefficients need to be proportional to each other for the modes to be decoupled. The only difference is absorbed in the mass constant in front of the respective kinetic term used to define the Fierz–Pauli mass. It is already known that NGR suffer from the strong coupling problem in Minkowski backgrounds [22, 33] and ghost instabilities in the generic case [46]. We confirm this result and find that the problem worsens in the case of teleparallel bigravity since we find that ghostly modes propagate in this theory.Footnote 7
As another example, we introduce terms with derivative interactions. It appears that the teleparallel framework makes construction of such examples more easy, however, likewise the Riemannian case is known to introduce ghost instabilities in the symmetric sector [108] in the massless case, this may be retained in the massive case. In future works, it would be interesting to investigate constructions with complex tetrads similar to what have been done in the Riemannian case [90, 91]. The motivation for this would be to investigate if viable theories with partially massless symmetry can be constructed in a viable way. Previous results suggest that this is strongly coupled around Minkowski backgrounds, and one would need to extend the linear analysis in this work to perturbations around complex De Sitter tetrads. It is also outlined how the Hamiltonian can be obtained in the model considered in this article, and with more details in a simpler model where the derivation is easier to carry out.
Furthermore, it is shown in app. A that as in other teleparallel theories [17, 19, 100,101,102], the so-called Weitzenböck gauge can safely be assumed. One may easily be mistaken, trying to include two spin connections in the construction of teleparallel bigravity theories since bimetric gravity assumes two Levi-Civita connections. However, that would have little sense and miss the point of the theory covariant under Lorentz transformations [29, 35]. Overall, our work has made the initial investigations for teleparallel bigravity. Providing details about teleparallel and bimetric gravity and explained the difference between these theories and a couple of other theories that would appear to be similar. Some novel theories have been ruled out by our analysis, which also provides useful tools to further investigate perturbation theory and Hamiltonian analysis in the future.
Currently, the perhaps most promising avenue to pursue is paved by the parameterised field theory approach to gauging translations [49, 50]. The conventional approach, adopted also in this paper, is well established to describe gauge interactions of fields and particles in spacetime, in continuum as well as in lattice models. However, if we would rather consider gravity as the gauge theory of spacetime, we should not assume the inhomogeneous extension of the symmetry group to begin with. In the parameterised field theory approach, the fundamental field giving rise to the spacetime metric is not its extension to a tetrad, but its reduction to a scalar. Recently, a viable theory with two interacting frame fields emerging from two scalar fields and giving rise to two independent but non-trivially coupled metrics, has been constructed in this approach, though not for bigravity but for the unification of gravity and the particle physics Yang–Mills theories [109]. Some of the methods and results we presented in this paper could be useful also in the potentially interesting application of the parameterised field theory approach to interacting multiple spin-2 field theories.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data sharing not applicable to this article as no datasets were generated or analysed during the current study.]
Notes
The alleged similarity with Yang–Mills is though compromised by the degeneracy of the gauge group, the inconsistency of the minimal coupling, the need for a non-canonical Lagrangian, the violation of Yang–Mills Bianchi identity etc There is, however, a new approach to gauging translations which may alleviate these issues [49, 50].
This is rather a conjecture, since the argument only holds up to cubic order, whereas the interacting theory might only start at quartic order, as the authors stress in their conclusions.
And as well one should not put the spin connection to vanish beforehand, however, this is shown in Appendix A to not affect the counting of the number of degrees of freedom.
Note that in the absence of the interaction potential, there are no connection between the kinetic terms and there will be two sets of diffeomorphism invariances and this will bring us down to two massless spin-2 fields.
This is manifest in Sect. 3 where the antisymmetric modes disappear for the TEGR coefficients.
The strong coupling problem could in theory be avoided by going to less trivial backgrounds and analyze the viability of the theory in more generic backgrounds. An example of such an attempt can be found in f(T)-gravity [30].
References
A. Zee, Quantum field theory in a nutshell (2003)
J.B. Jiménez, L. Heisenberg, T.S. Koivisto, The geometrical trinity of gravity. Universe 5(7), 173 (2019). https://doi.org/10.3390/universe5070173. arXiv:1903.06830 [hep-th]
A. Einstein, Riemann-Geometrie mit Aufrechterhaltung des Begriffes des Fernparallelismus (Wiley, New York, 2006), pp.316–321. https://doi.org/10.1002/3527608958.ch36
J.W. Maluf, The teleparallel equivalent of general relativity. Ann. Phys. 525, 339–357 (2013). https://doi.org/10.1002/andp.201200272. arXiv:1303.3897 [gr-qc]
J.M. Nester, H.-J. Yo, Symmetric teleparallel general relativity. Chin. J. Phys. 37, 113 (1999). arXiv:gr-qc/9809049
J. Beltrán Jiménez, L. Heisenberg, D. Iosifidis, A. Jiménez-Cano, T.S. Koivisto, General teleparallel quadratic gravity. Phys. Lett. B 805, 135422 (2020). https://doi.org/10.1016/j.physletb.2020.135422. arXiv:1909.09045 [gr-qc]
R. Aldrovandi, J.G. Pereira, Teleparallel Gravity: An Introduction (Springer, Dordrechts, 2012)
S. Bahamonde, Modified teleparallel theories of gravity. Ph.D. thesis, U. Coll. London (2018). http://discovery.ucl.ac.uk/10055604/1/Thesis%20Sebastian%20Bahamonde%20Final%20version%20electronic%20copy.pdf
S. Bahamonde, K.F. Dialektopoulos, M. Hohmann, J.L. Said, Teleparallel Gravity: Foundations and Cosmology (2021)
S. Bahamonde, K.F. Dialektopoulos, C. Escamilla-Rivera, G. Farrugia, V. Gakis, M. Hendry, M. Hohmann, J. Levi Said, J. Mifsud, E. Di Valentino, Teleparallel gravity: from theory to cosmology. Rep. Prog. Phys. 86(2), 026901 (2023). https://doi.org/10.1088/1361-6633/ac9cef. arXiv:2106.13793 [gr-qc]
D. Blixt, M.-J. Guzmán, M. Hohmann, C. Pfeifer, Review of the Hamiltonian analysis in teleparallel gravity. Int. J. Geom. Methods Mod. Phys. 18(supp01), 2130005 (2021). https://doi.org/10.1142/S0219887821300051. arXiv:2012.09180 [gr-qc]
M. Krssak, R.J. Van Den Hoogen, J.G. Pereira, C.G. Boehmer, A.A. Coley, Teleparallel theories of gravity: illuminating a fully invariant approach. arXiv:1810.12932 [gr-qc]
S. Bahamonde, K.F. Dialektopoulos, M. Hohmann, J. Levi Said, C. Pfeifer, E.N. Saridakis, Perturbations in non-flat cosmology for f(T) gravity. Eur. Phys. J. C 83(3), 193 (2023). https://doi.org/10.1140/epjc/s10052-023-11322-3. arXiv:2203.00619 [gr-qc]
J. Beltrán Jiménez, A. Golovnev, T. Koivisto, H. Veermäe, Minkowski space in \(f(T)\) gravity. Phys. Rev. D 103(2), 024054 (2021). https://doi.org/10.1103/PhysRevD.103.024054. arXiv:2004.07536 [gr-qc]
M. Blagojevic, I.A. Nikolic, Hamiltonian structure of the teleparallel formulation of GR. Phys. Rev. D 62, 024021 (2000). https://doi.org/10.1103/PhysRevD.62.024021. arXiv:hep-th/0002022
M. Blagojević, J.M. Nester, Local symmetries and physical degrees of freedom in \(f(T)\) gravity: a Dirac Hamiltonian constraint analysis. Phys. Rev. D 102(6), 064025 (2020). https://doi.org/10.1103/PhysRevD.102.064025. arXiv:2006.15303 [gr-qc]
D. Blixt, M. Hohmann, C. Pfeifer, Hamiltonian and primary constraints of new general relativity. Phys. Rev. D 99(8), 084025 (2019). https://doi.org/10.1103/PhysRevD.99.084025. arXiv:1811.11137 [gr-qc]
D. Blixt, M. Hohmann, M. Krššák, C. Pfeifer, Hamiltonian analysis in new general relativity, in 15th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, vol. 5 (2019). https://doi.org/10.1142/9789811258251_0038. arXiv:1905.11919 [gr-qc]
D. Blixt, M. Hohmann, C. Pfeifer, On the gauge fixing in the Hamiltonian analysis of general teleparallel theories. Universe 5(6), 143 (2019). https://doi.org/10.3390/universe5060143. arXiv:1905.01048 [gr-qc]
S. Capozziello, M. Caruana, J. Levi Said, J. Sultana, Ghost and Laplacian instabilities in teleparallel Horndeski gravity. JCAP 03, 060 (2023). https://doi.org/10.1088/1475-7516/2023/03/060. arXiv:2301.04457 [gr-qc]
P. Chen, K. Izumi, J.M. Nester, Y.C. Ong, Remnant symmetry, propagation and evolution in \(f\)(T) gravity. Phys. Rev. D 91(6), 064003 (2015). https://doi.org/10.1103/PhysRevD.91.064003. arXiv:1412.8383 [gr-qc]
W.-H. Cheng, D.-C. Chern, J.M. Nester, Canonical analysis of the one parameter teleparallel theory. Phys. Rev. D 38, 2656–2658 (1988). https://doi.org/10.1103/PhysRevD.38.2656
R. Ferraro, M.J. Guzmán, Hamiltonian formulation of teleparallel gravity. Phys. Rev. D 94(10), 104045 (2016). https://doi.org/10.1103/PhysRevD.94.104045. arXiv:1609.06766 [gr-qc]
R. Ferraro, M.J. Guzmán, Hamiltonian formalism for f(T) gravity. Phys. Rev. D 97(10), 104028 (2018). https://doi.org/10.1103/PhysRevD.97.104028. arXiv:1802.02130 [gr-qc]
R. Ferraro, M.J. Guzmán, Pseudoinvariance and the extra degree of freedom in f(T) gravity. Phys. Rev. D 101(8), 084017 (2020). https://doi.org/10.1103/PhysRevD.101.084017. arXiv:2001.08137 [gr-qc]
A. Golovnev, T. Koivisto, Cosmological perturbations in modified teleparallel gravity models. JCAP 1811(11), 012 (2018). https://doi.org/10.1088/1475-7516/2018/11/012. arXiv:1808.05565 [gr-qc]
A. Golovnev, M.J. Guzman, Disformal transformations in modified teleparallel gravity. Symmetry 12(1), 152 (2020). https://doi.org/10.3390/sym12010152. arXiv:1912.04604 [gr-qc]
A. Golovnev, Perturbations in \(f(\mathbb{T} )\) cosmology and the spin connection. JCAP 04, 014 (2020). https://doi.org/10.1088/1475-7516/2020/04/014. arXiv:2001.10015 [gr-qc]
A. Golovnev, T. Koivisto, M. Sandstad, On the covariance of teleparallel gravity theories. Class. Quantum Gravity 34(14), 145013 (2017). https://doi.org/10.1088/1361-6382/aa7830. arXiv:1701.06271 [gr-qc]
A. Golovnev, M.-J. Guzman, Nontrivial Minkowski backgrounds in \(f(T)\) gravity. Phys. Rev. D 103(4), 044009 (2021). https://doi.org/10.1103/PhysRevD.103.044009. arXiv:2012.00696 [gr-qc]
M. Hohmann, Hamiltonian of new general relativity using differential forms. Int. J. Mod. Phys. A 35(02n03), 2040014 (2020). https://doi.org/10.1142/S0217751X2040014X. arXiv:1907.08343 [gr-qc]
M. Hohmann, Disformal transformations in scalar-torsion gravity. Universe 5, 167 (2019). https://doi.org/10.3390/universe5070167. arXiv:1905.00451 [gr-qc]
J. Beltrán Jiménez, K.F. Dialektopoulos, Non-linear obstructions for consistent new general relativity. JCAP 01, 018 (2020). https://doi.org/10.1088/1475-7516/2020/01/018. arXiv:1907.10038 [gr-qc]
T. Koivisto, G. Tsimperis, The spectrum of teleparallel gravity. Universe 5(3) (2019). https://doi.org/10.3390/universe5030080. arXiv:1810.11847 [gr-qc]
M. Krššák, E.N. Saridakis, The covariant formulation of f(T) gravity. Class. Quantum Gravity 33(11), 115009 (2016). https://doi.org/10.1088/0264-9381/33/11/115009. arXiv:1510.08432 [gr-qc]
R. Kuhfuss, J. Nitsch, Propagating modes in gauge field theories of gravity. Gen. Relativ. Gravit. 18, 1207 (1986). https://doi.org/10.1007/BF00763447
M. Li, R.-X. Miao, Y.-G. Miao, Degrees of freedom of \(f(T)\) gravity. JHEP 07, 108 (2011). https://doi.org/10.1007/JHEP07(2011)108. arXiv:1105.5934 [hep-th]
J.W. Maluf, J.F. da Rocha-Neto, Hamiltonian formulation of the teleparallel equivalent of general relativity without gauge fixing. arXiv:gr-qc/0002059
J.W. Maluf, Hamiltonian formulation of the teleparallel description of general relativity. J. Math. Phys. 35, 335–343 (1994). https://doi.org/10.1063/1.530774
P. Mitrić, Canonical structure of the teleparallel equivalent of general relativity. arXiv:1910.02810 [gr-qc]
Y.C. Ong, J.M. Nester, Counting components in the lagrange multiplier formulation of teleparallel theories. Eur. Phys. J. C 78(7), 568 (2018). https://doi.org/10.1140/epjc/s10052-018-6050-3. arXiv:1709.00068 [gr-qc]
A. Okolow, J. Swiezewski, Hamiltonian formulation of a simple theory of the teleparallel geometry. Class. Quantum Gravity 29, 045008 (2012). https://doi.org/10.1088/0264-9381/29/4/045008. arXiv:1111.5490 [math-ph]
A. Okolów, ADM-like Hamiltonian formulation of gravity in the teleparallel geometry. Gen. Relativ. Gravit. 45, 2569–2610 (2013). https://doi.org/10.1007/s10714-013-1605-y. arXiv:1111.5498 [gr-qc]
A. Okolów, ADM-like Hamiltonian formulation of gravity in the teleparallel geometry: derivation of constraint algebra. Gen. Relativ. Gravit. 46, 1636 (2014). https://doi.org/10.1007/s10714-013-1636-4. arXiv:1309.4685 [gr-qc]
Y.C. Ong, K. Izumi, J.M. Nester, P. Chen, Problems with propagation and time evolution in f(T) gravity. Phys. Rev. D 88, 024019 (2013). https://doi.org/10.1103/PhysRevD.88.024019. arXiv:1303.0993 [gr-qc]
T. Ortin, Gravity and Strings. Cambridge Monographs on Mathematical Physics, vol. 7, 2nd edn. (Cambridge University Press, Cambridge, 2015). https://doi.org/10.1017/CBO9781139019750
K. Hayashi, T. Shirafuji, New general relativity. Phys. Rev. D 19, 3524–3553 (1979). https://doi.org/10.1103/PhysRevD.19.3524
P. Van Nieuwenhuizen, On ghost-free tensor Lagrangians and linearized gravitation. Nucl. Phys. B 60, 478–492 (1973). https://doi.org/10.1016/0550-3213(73)90194-6
T. Koivisto, M. Hohmann, T. Złośnik, The general linear Cartan Khronon. Universe 5(6), 168 (2019). https://doi.org/10.3390/universe5070168. arXiv:1905.02967 [gr-qc]
T.S. Koivisto, T. Zlosnik, Paths to gravitation via the gauging of parameterized field theories. arXiv:2212.04562 [gr-qc]
M. Blagojević, F.W. Hehl (eds.), Gauge Theories of Gravitation (World Scientific, Singapore, 2013). https://doi.org/10.1142/p781
Y.M. Cho, Einstein Lagrangian as the Translational Yang–Mills Lagrangian. Phys. Rev. D 14, 2521 (1976) (393(1975)). https://doi.org/10.1103/PhysRevD.14.2521
W. Pauli, M. Fierz, On relativistic field equations of particles with arbitrary spin in an electromagnetic field. Helv. Phys. Acta 12, 297–300 (1939)
D.G. Boulware, S. Deser, Can gravitation have a finite range? Phys. Rev. D 6, 3368–3382 (1972). https://doi.org/10.1103/PhysRevD.6.3368
C. de Rham, G. Gabadadze, A.J. Tolley, Resummation of massive gravity. Phys. Rev. Lett. 106, 231101 (2011). https://doi.org/10.1103/PhysRevLett.106.231101. arXiv:1011.1232 [hep-th]
S.F. Hassan, R.A. Rosen, Bimetric gravity from ghost-free massive gravity. JHEP 02, 126 (2012). https://doi.org/10.1007/JHEP02(2012)126. arXiv:1109.3515 [hep-th]
A. Schmidt-May, M. von Strauss, Recent developments in bimetric theory. J. Phys. A 49(18), 183001 (2016). https://doi.org/10.1088/1751-8113/49/18/183001. arXiv:1512.00021 [hep-th]
L. Heisenberg, Massive gravity and bigravity (2021)
S.F. Hassan, A. Schmidt-May, M. von Strauss, Higher derivative gravity and conformal gravity from bimetric and partially massless bimetric theory. Universe 1(2), 92–122 (2015). https://doi.org/10.3390/universe1020092. arXiv:1303.6940 [hep-th]
K. Hinterbichler, R.A. Rosen, Interacting spin-2 fields. JHEP 07, 047 (2012). https://doi.org/10.1007/JHEP07(2012)047. arXiv:1203.5783 [hep-th]
W. Li, Absence of the Boulware–Deser ghost in novel graviton kinetic terms. Phys. Rev. D 94(6), 064079 (2016). https://doi.org/10.1103/PhysRevD.94.064079. arXiv:1512.06386 [hep-th]
G. Tukhashvili, Possible derivative interactions in massive bi-gravity. arXiv:1704.08603 [hep-th]
S.F. Hassan, M. Kocic, A. Schmidt-May, Absence of ghost in a new bimetric-matter coupling. arXiv:1409.1909 [hep-th]
S.F. Hassan, M. Kocic, On the local structure of spacetime in ghost-free bimetric theory and massive gravity. JHEP 05, 099 (2018). https://doi.org/10.1007/JHEP05(2018)099. arXiv:1706.07806 [hep-th]
M. Kocic, Causal propagation of constraints in bimetric relativity in standard 3+1 form. JHEP 10, 219 (2019). https://doi.org/10.1007/JHEP10(2019)219. arXiv:1804.03659 [hep-th]
M. Kocic, Note on bimetric causal diagrams. arXiv:1904.10407 [gr-qc]
M. Kocic, Bimetric interactions based on metric congruences. arXiv:1906.11841 [hep-th]
A. Schmidt-May, Nonlinear interactions for massive spin-2 fields. PoS CORFU2015, 157 (2016). https://doi.org/10.22323/1.263.0157. arXiv:1602.07520 [gr-qc]
S.F. Hassan, A. Schmidt-May, M. von Strauss, Bimetric theory and partial masslessness with Lanczos–Lovelock terms in arbitrary dimensions. Class. Quantum Gravity 30, 184010 (2013). https://doi.org/10.1088/0264-9381/30/18/184010. arXiv:1212.4525 [hep-th]
S.F. Hassan, A. Schmidt-May, M. von Strauss, On partially massless bimetric gravity. Phys. Lett. B 726, 834–838 (2013). https://doi.org/10.1016/j.physletb.2013.09.021. arXiv:1208.1797 [hep-th]
S.F. Hassan, A. Schmidt-May, M. von Strauss, On consistent theories of massive spin-2 fields coupled to gravity. JHEP 05, 086 (2013). https://doi.org/10.1007/JHEP05(2013)086. arXiv:1208.1515 [hep-th]
S.F. Hassan, A. Schmidt-May, M. von Strauss, Proof of consistency of nonlinear massive gravity in the Stúckelberg formulation. Phys. Lett. B 715, 335–339 (2012). https://doi.org/10.1016/j.physletb.2012.07.018. arXiv:1203.5283 [hep-th]
S.F. Hassan, A. Lundkvist, Analysis of constraints and their algebra in bimetric theory. JHEP 08, 182 (2018). https://doi.org/10.1007/JHEP08(2018)182. arXiv:1802.07267 [hep-th]
Z. Molaee, A. Shirzad, Hamiltonian structure of bi-gravity, problem of ghost and bifurcation. Class. Quantum Gravity 36(22), 225005 (2019). https://doi.org/10.1088/1361-6382/ab496b. arXiv:1805.02179 [hep-th]
A. Higuchi, Forbidden mass range for spin-2 field theory in De Sitter space-time. Nucl. Phys. B 282, 397–436 (1987). https://doi.org/10.1016/0550-3213(87)90691-2
S.F. Hassan, A. Schmidt-May, Interactions of multiple spin-2 fields beyond pairwise couplings. Phys. Rev. Lett. 122(25), 251101 (2019). https://doi.org/10.1103/PhysRevLett.122.251101. arXiv:1804.09723 [hep-th]
V.O. Soloviev, Two approaches to Hamiltonian bigravity. Universe 8(2), 119 (2022). https://doi.org/10.3390/universe8020119
E. Babichev, L. Marzola, M. Raidal, A. Schmidt-May, F. Urban, H. Veermäe, M. von Strauss, Heavy spin-2 dark matter. JCAP 1609(09), 016 (2016). https://doi.org/10.1088/1475-7516/2016/09/016. arXiv:1607.03497 [hep-th]
Y. Manita, K. Aoki, T. Fujita, S. Mukohyama, Spin-2 dark matter from anisotropic Universe in bigravity. arXiv:2211.15873 [gr-qc]
Y. Akrami, T.S. Koivisto, M. Sandstad, Accelerated expansion from ghost-free bigravity: a statistical analysis with improved generality. JHEP 03, 099 (2013). https://doi.org/10.1007/JHEP03(2013)099. arXiv:1209.0457 [astro-ph.CO]
Y. Akrami, T.S. Koivisto, M. Sandstad, Cosmological constraints on ghost-free bigravity: background dynamics and late-time acceleration, in 13th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (2015), p. 1252–1254. https://doi.org/10.1142/9789814623995_0138. arXiv:1302.5268 [astro-ph.CO]
A. Bassi, S.A. Adil, M.P. Rajvanshi, A.A. Sen, Cosmological evolution in bimetric gravity: observational constraints and LSS signatures. arXiv:2301.11000 [astro-ph.CO]
M. Högås, F. Torsello, E. Mörtsell, On the stability of bimetric structure formation. JCAP 04, 046 (2020). https://doi.org/10.1088/1475-7516/2020/04/046. arXiv:1910.01651 [gr-qc]
M. Högås, E. Mörtsell, Constraints on bimetric gravity from Big Bang nucleosynthesis. JCAP 11, 001 (2021). https://doi.org/10.1088/1475-7516/2021/11/001. arXiv:2106.09030 [astro-ph.CO]
M. Högås, Was Einstein Wrong? Theoretical and observational constraints on massive gravity. Ph.D. thesis, Stockholm University, Faculty of Science, Department of Physics (2022)
A.R. Solomon, Y. Akrami, T.S. Koivisto, Linear growth of structure in massive bigravity. JCAP 10, 066 (2014). https://doi.org/10.1088/1475-7516/2014/10/066. arXiv:1404.4061 [astro-ph.CO]
M. Lüben, E. Mörtsell, A. Schmidt-May, Bimetric cosmology is compatible with local tests of gravity. Class. Quantum Gravity 37(4), 047001 (2020). https://doi.org/10.1088/1361-6382/ab4f9b. arXiv:1812.08686 [gr-qc]
M. Lüben, A. Schmidt-May, J. Smirnov, Vainshtein screening in bimetric cosmology. Phys. Rev. D 102, 123529 (2020). https://doi.org/10.1103/PhysRevD.102.123529. arXiv:1912.09449 [gr-qc]
W. Li, Novel nonlinear kinetic terms for gravitons. Phys. Rev. D 94(6), 064078 (2016). https://doi.org/10.1103/PhysRevD.94.064078. arXiv:1508.03246 [gr-qc]
L. Apolo, S.F. Hassan, Non-linear partially massless symmetry in an SO(1,5) continuation of conformal gravity. Class. Quantum Gravity 34(10), 105005 (2017). https://doi.org/10.1088/1361-6382/aa69f7. arXiv:1609.09514 [hep-th]
L. Apolo, S.F. Hassan, A. Lundkvist, Gauge and global symmetries of the candidate partially massless bimetric gravity. Phys. Rev. D 94(12), 124055 (2016). https://doi.org/10.1103/PhysRevD.94.124055. arXiv:1609.09515 [hep-th]
S. Garcia-Saenz, K. Hinterbichler, A. Joyce, E. Mitsou, R.A. Rosen, No-go for partially massless spin-2 Yang–Mills. JHEP 02, 043 (2016). https://doi.org/10.1007/JHEP02(2016)043. arXiv:1511.03270 [hep-th]
N. Boulanger, C. Deffayet, S. Garcia-Saenz, L. Traina, Theory for multiple partially massless spin-2 fields. Phys. Rev. D 100(10), 101701 (2019). https://doi.org/10.1103/PhysRevD.100.101701. arXiv:1906.03868 [hep-th]
T. Damour, V. Nikiforova, Spherically symmetric solutions in torsion bigravity. Phys. Rev. D 100(2), 024065 (2019). https://doi.org/10.1103/PhysRevD.100.024065. arXiv:1906.11859 [gr-qc]
V. Nikiforova, Absence of a Vainshtein radius in torsion bigravity. Phys. Rev. D 101(6), 064017 (2020). https://doi.org/10.1103/PhysRevD.101.064017. arXiv:2001.07148 [gr-qc]
V. Nikiforova, Perturbations of a Schwarzschild black hole in torsion bigravity. Phys. Rev. D 105(6), 064060 (2022). https://doi.org/10.1103/PhysRevD.105.064060. arXiv:2201.02259 [gr-qc]
C. Markou, F.J. Rudolph, A. Schmidt-May, Vierbein interactions with antisymmetric components. J. Phys. Commun. 3(7), 075013 (2019). https://doi.org/10.1088/2399-6528/ab33cc. arXiv:1812.07580 [hep-th]
C. Markou, F.J. Rudolph, A. Schmidt-May, Gravity with antisymmetric components. Class. Quantum Gravity 36(9), 095014 (2019). https://doi.org/10.1088/1361-6382/ab0fd6. arXiv:1811.12419 [hep-th]
S. Alexandrov, S. Speziale, Bi-gravity with a single graviton. JHEP 08, 070 (2019). https://doi.org/10.1007/JHEP08(2019)070. arXiv:1904.11906 [hep-th]
D. Blixt, R. Ferraro, A. Golovnev, M.-J. Guzmán, Lorentz gauge-invariant variables in torsion-based theories of gravity. Phys. Rev. D 105(8), 084029 (2022). https://doi.org/10.1103/PhysRevD.105.084029. arXiv:2201.11102 [gr-qc]
A. Golovnev, M.-J. Guzman, Lorentz symmetries and primary constraints in covariant teleparallel gravity. Phys. Rev. D 104(12), 124074 (2021). https://doi.org/10.1103/PhysRevD.104.124074. arXiv:2110.11273 [gr-qc]
A. Golovnev, The geometrical meaning of the Weitzenböck connection. arXiv:2302.13599 [gr-qc]
M. Hohmann, M. Krššák, C. Pfeifer, U. Ualikhanova, Propagation of gravitational waves in teleparallel gravity theories. arXiv:1807.04580 [gr-qc]
U. Ualikhanova, M. Hohmann, Parametrized post-Newtonian limit of general teleparallel gravity theories. Phys. Rev. D 100(10), 104011 (2019). https://doi.org/10.1103/PhysRevD.100.104011. arXiv:1907.08178 [gr-qc]
C. de Rham, A. Matas, A.J. Tolley, New kinetic terms for massive gravity and multi-gravity: a No-Go in Vielbein form. Class. Quantum Gravity 32(21), 215027 (2015). https://doi.org/10.1088/0264-9381/32/21/215027. arXiv:1505.00831 [hep-th]
M. Kocic, Geometric mean of bimetric spacetimes. Class. Quantum Gravity 38(7), 075023 (2021). https://doi.org/10.1088/1361-6382/abdf28. arXiv:1803.09752 [hep-th]
L. Pati, D. Blixt, M.-J. Guzman, Hamilton’s equations in the covariant teleparallel equivalent of general relativity. Phys. Rev. D 107(4), 044071 (2023). https://doi.org/10.1103/PhysRevD.107.044071. arXiv:2210.07971 [gr-qc]
N. Boulanger, T. Damour, L. Gualtieri, M. Henneaux, Inconsistency of interacting, multigraviton theories. Nucl. Phys. B 597, 127–171 (2001). https://doi.org/10.1016/S0550-3213(00)00718-5. arXiv:hep-th/0007220
P. Gallagher, T. Koivisto, L. Marzola, Pregeometric first order Yang–Mills theory. Phys. Rev. D 105(12), 125010 (2022). https://doi.org/10.1103/PhysRevD.105.125010. arXiv:2202.05657 [hep-th]
Acknowledgements
The authors are grateful to Fawad Hassan for very interesting discussions. MH LM and TK gratefully acknowledge the full financial support by the Estonian Research Council through the Personal Research Funding project PRG356 and by the European Regional Development Fund through the Center of Excellence TK133 “The Dark Side of the Universe”.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Gauge fixing
Appendix A: Gauge fixing
We show here that the Hamiltonian analysis can be done in the so-called Weitzenböck gauge in all theories considered in this article. In [17, 19, 100,101,102] it was shown that this is valid in a quite general class of teleparallel theories. However, the results do not cover teleparallel bigravity theories. In this appendix, we will conduct a quite different notation, where we define conjugate momenta without a priori gauge fix, so that the spin connection \(\omega ^A{}_{B\mu }=0\). Furthermore, we denote Lorentz transformations by “ \(\tilde{}\) ”. Consider the teleparallel bigravity theory given by (18). In this expression we know that all derivatives appear in  and
and  . In order to account for the symmetries of the spin connection, we introduce the same auxiliary field as was introduced in [17, 19]
. In order to account for the symmetries of the spin connection, we introduce the same auxiliary field as was introduced in [17, 19]
We introduce conjugate momenta with respect to both tetrads

The conjugate momenta with respect to Lorentz matrices are inherited by the following expression
since the auxiliary field \(a_{AB}\) is linearly related to the time derivatives of the Lorentz matrices. Explicitly, we have



Furthermore, we have

This means that we have the following algebraic relation

for which we get the following primary constraints

Under Lorentz transformation (denoted with “ \(\tilde{}\) ”), the conjugate momenta transforms as



with the inverse transformation



By imposing the primary constraint, given by Eq. (A8), to Eq. (A12) we see that \(\tilde{\hat{\pi }}^{MN}\approx 0\). We can now look at the Lorentz transformed Hamiltonian which schematically will look like

where \(\mathrm {P.C}\) are theory specific primary constraints. It turns out that \(\tilde{\mathcal {L}}\left[ \tilde{\mathfrak {e}},\tilde{\dot{\mathfrak {e}}},\tilde{\mathfrak {f}},\tilde{\dot{\mathfrak {f}}},\tilde{\Lambda }\right] =\tilde{\mathcal {L}}\left[ \tilde{\mathfrak {e}},\tilde{\dot{\mathfrak {e}}},\tilde{\mathfrak {f}},\tilde{\dot{\mathfrak {f}}}\right] \). Furthermore, the Hamiltonian is on-shell independent of both \(\tilde{\Lambda }\) and \(\tilde{\hat{\pi }}\). The evolution of the primary constraints Eq. (A9) is expected to vanish on-shell similar to the case of [101]. Hence, the number of degrees of freedom obtained by the Hamiltonian analysis of (18) in the Weitzenböck gauge will not differ from the canonical Hamiltonian analysis. The results of [100,101,102] can easily be extended to the case of teleparallel bigravity as well. The important point is that the covariantization only involves one spin connection. This is the only sensible way to make the theory Lorentz covariant similar to the more studied cases [29]. The same conclusions about the consistency of working in the Weitzenböck gauge from the start can be argued in a similar way as was done elsewhere in the literature [100, 102].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Blixt, D., Hohmann, M., Koivisto, T. et al. Teleparallel bigravity. Eur. Phys. J. C 83, 1120 (2023). https://doi.org/10.1140/epjc/s10052-023-12247-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-12247-7


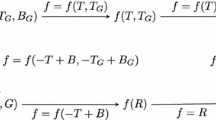

 . In this case the kinetic term acquires the form
. In this case the kinetic term acquires the form . Once Eq. (
. Once Eq. ( nullifies the kinetic term of the same perturbation.
nullifies the kinetic term of the same perturbation.