1 Introduction

Among various fascinating solutions of general relativity (GR), the wormhole (WH) solutions are considered the most interesting and have become the center of attraction for numerous researchers. In accordance with GR, the existence of such exotic objects is made possible by the deformable spacetime evolved by energy/matter. The structure of the WH acts as a bridge, tunnel, or connection between different points at a manifold. Generally, WHs are characterized by asymptotically flat geometry, and the concept of WHs was first introduced by Flamm [1] and then presented by Einstein and Rosen [2]. The geometry proposed in [2] is known as the Einstein–Rosen bridge, and it is considered a vacuum solution of the equations of GR. These WHs are generated through the solution of two Schwarzschild black holes (BHs) combining two different domains of metrics. The appearance of singularity evidences the non-traversable geometry of a WH. Fuller and Wheeler [3] implemented Kruskal coordinates in 1962 to explore the geometry of a Schwarzschild WH exhibiting a non-traversable structure. They showed that the open geometry of a WH would close so rapidly that nothing would pass across it.

Following the theoretical information of Schwarzschild WHs along with Einstein–Rosen bridges, several researchers have been inspired to analyze the appearance of traversable WHs. The primary model of traversable WH geometry is presented by Morris and Thorne [4] as a tunnel that combines two domains of the similar universes or two distinct cosmos with the help of a throat which allows the movement from one domain to another. To pass by this domain, the matter comprising such geometries must defy the usual energy bounds [4,5,6,7]. In light of GR, an exotic component disobeying the standard energy bounds is necessary to obtain a traversable WH geometry. Obviously, it is a huge issue to consider such sort of matter content that has not been inspected directly. In order to deal with this problem, thin-shell WHs were suggested, where the exotic component can be minimized in the throat, creating such WH geometry that disobeys the energy bounds only in this domain [8, 9]. The formation of this WH geometry is accomplished by adopting the well-known cut-and-paste methodology, where cutting and pasting is done with the two manifolds to construct a completely new one having a shell placed in the joining region. During this procedure, the exotic component necessary for the occurrence is engrossed in the WH throat. We can concentrate our research on a thin-shell structure, as the exotic component cannot be fully ignored. At the WH throat, the constituents of the surface stress–energy tensor are computed by implementing the Darmois–Israel conjecture [10, 11], which yields the Lanczos equations [12,13,14]. Employing the solution of the Lanczos equation, one can discuss the dynamics of WH geometry through the equation of state (EoS) describing the exotic component on the thin shell.

However, in alternative theories of gravity, the junction conditions for the thin-shell WHs are extended by inducing some new sorts of geometrical entities, except an extrinsic curvature. It is observed that the contributions from the curvature tensors allow the presence of WHs incorporated by normal matter. In this respect, Richarte and Simeone [15] adopted the generalized Darmois–Israel condition for the Einstein–Gauss–Bonnet (GB) gravity to create a thin-shell WH. They found that for some specific choices of parameters, WHs could be assisted by normal matter not violating the energy constraints. Mazharimousai [16] investigated the stability of thin-shell WH geometry bounded by ordinary matter in five-dimensional Einstein–Maxwell GB gravity and obtained the stable regions for negative choices of GB parameters. In the context of Dvali, Gabadadze, and Porrati (DGP) gravity, Richarte [17] constructed a five-dimensional WH geometry incorporating the normal matter not disobeying the energy constraints. Richarte et al. [18] examined the mechanical stability of traversable thin-shell WHs in Bose–Einstein condensate and emergent gravity. They observed that WHs with a finite radius do not defy the null/strong energy constraint. In light of Rastall gravity, Lobo et al. [19] constructed thin-shell WHs sourced by an anisotropic fluid and checked the energy constraints at the WH’s throat corresponding to the traversability condition. They observed that all energy constraints are satisfied corresponding to the particular choice of Rastall parameter.

It is well known that astronomical entities have huge significance if they exhibit stability against external oscillations. In this regard, several researchers have analyzed the stability of WH geometries and thin-shell WHs under linear perturbations preserving the real symmetries. Poisson and Visser [20] discussed the stable geometry of Schwarzschild thin-shell WHs without considering the EoS for exotic matter. Lobo and Crawford [39] inspected the stability of thin-shell WHs with the inclusion of a cosmological constant (\(\Lambda \)) and demonstrated that the stable solutions of a WH appear only for positive values of \(\Lambda \). Many researchers have discussed thin-shell WH structures and their stability by incorporating various scenarios such as charge, \(\Lambda \), and various other physical factors [21,22,23,24,25,26,27,28,29,30,31,32]. For cylindrical spacetime, the same scenario has been observed by several authors [33,34,35]. Similarly, using various EoSs, the stability of distinct thin-shell WH structures has been inspected in [36,37,38,39,40,41,42].

It is more significant to discuss the different cosmological and astrophysical scenarios in higher dimensions. In this respect, Kaluza and Klein combined gravity and electromagnetism through a five-dimensional theory. By the Kaluza–Klein paradigm, when low-energy physics is taken into account, the additional dimensions compress to a smaller radius of about the Planck length. M-theory/string theory indicates the presence of additional dimensions at small energy levels and gave rise to the idea of Braneworlds. Such conjectures act as crucial participants for a quantum theory and also for the fusion of gravity and quantum effects. In Braneworlds [43,44,45,46], the general particles model is restricted to a 3-brane in which just gravity is permitted to pierce the additional dimensions. In this regard, the four-dimensional cosmos is observed as a hypersurface known as the “brane,” which is endorsed in an additional dimensional spacetime labeled “the bulk.” To further study the behavior of gravity in more dimensions, numerous significant solutions corresponding to Einstein field equations have been discussed in the literature [47,48,49,50,51,52,53].

The investigation of WHs, and particularly thin-shell WHs in higher-dimensional spacetimes, has become a very interesting subject for researchers. In higher dimensions, there exist various captivating scenarios related to Euclidean and Lorentzian WHs. Jianjun and Sicong [54] and Gonzales-Diaz [55] discussed the geometry of Euclidean WHs. Cataldo et al. [56] observed the structure of Lorentzian WHs in N-dimensional Einstein gravity. Cataldo and his collaborators [57] also inspected WHs in \((N+1)\) dimension corresponding to polytropic EoS. On the same ground, various authors presented their results related to WHs in higher dimensions [58,59,60,61,62]. In higher-dimensional gravity, thin-shell WHs along with an electric field and \(\Lambda \) have also been examined in [25, 63]. The non-asymptotically flat geometry of thin-shell WHs in d-dimensional spacetime have been studied in Einstein–Yang–Mills–dilaton (EYMD) gravity and Einstein–Yang–Mills–Gauss–Bonnet gravity [64, 65]. Motivated by these works, Dias and Lemos [66] examined the stability of d-dimensional electrically charged thin-shell WHs with \(\Lambda \). Eiroa and Simeone [67] mathematically created the shell by utilizing the cut-and-paste method and observed some interesting aspects of the spherical shell in d-dimensional spacetime.

The \(\Lambda \) in Einstein’s equations is utilized to specify the present cosmic state. Several astrophysical implications indicate that the present rapid cosmic expansion is caused by some parameter possessing huge negative pressure. To illustrate this pressure, the quintessence is characterized as a crucial alternative of \(\Lambda \) [68, 69]. The first ever solution of the GR equations associated with the quintessence in four dimensions was evaluated by Kiselev [70]. In a higher-dimensional metric, Chen et al. [71] demonstrated the outcomes of Einstein’s equation bounded by quintessence. Banerjee et al. [72] observed the stable geometry of a thin-shell WH in a d dimension comprising a quintessence parameter. On the other hand, a one-dimensional entity called a string can also be considered to characterize the cosmos. Such cosmic strings can extend to any point in the cosmos and are closely related to the rapidly accelerating cosmic expansion [73]. String theory speculates about the presence of quantum gravity by treating particles and the fundamental forces of nature as vibrations of microscopic super-symmetric strings. Motivated by this, a series of studies on the gravitational consequences of matter using string clouds was conducted. Letelier [74] first presented the general solutions of the string clouds for spherical symmetry in order to demonstrate the relationship between the counting string state and the entropy of the BH. Herscovich and Richarte [75] obtained a BH solution with string clouds in five-dimensional Einstein GB gravity. They discussed the thermodynamic properties and observed the existence of stable BHs corresponding to the small values of the string cloud density and GB parameter.

In this manuscript, our key objective is to study the d-dimensional electrically charged thin-shell WH structure for a spherically symmetric line element with quintessence and a cloud of strings. The manuscript is presented as follows: Section II depicts the basics of a d-dimensional spherically symmetric spacetime with quintessence and a cloud of strings. In Section III, the structure of charged thin-shell WHs corresponding to the abovementioned spacetime is presented by adopting the cut-and-paste technique. Further, the geodesic equation related to a test particle is derived directly which firstly is at rest and moves radially. Section IV analyzes the stability of WH geometry by implementing the general linearized expansion approach. We also observe the standard stability criterion for the structure of thin-shell WHs. Section V investigates some interesting specific cases for BH spacetimes with the quintessence and cloud of strings. Moreover, we explore the stability modes that are investigated corresponding to the quintessence and the cloud of strings. Finally, in the last section, we summarize our important results.

2 d-Dimensional spherically symmetric line element with quintessence and a cloud of strings

Consider a static spherically symmetric line element in d dimension with quintessence and cloud of strings as [76]

$$\begin{aligned} ds ^2 = f(r)^{-1}dr^2+ r^2 d\Omega ^{2}_{d-2}-f(r) dt^2, \end{aligned}$$
(1)

in which \(\Omega ^{2}_{d-2}\) indicates the metric corresponding to the \((d-2)\) unit-sphere, and f(r) is characterized as

$$\begin{aligned} f(r)= & {} -\frac{2 a}{(d-2) r ^{d-4}}-\frac{2 \Lambda r ^2}{(d-1) (d-2)} -\frac{2 m}{r ^{d-3}}\nonumber \\{} & {} -\frac{\alpha }{r ^{(d-1) \omega _q+d-3}}+\frac{Q^2}{r ^{2 (d-3)}}+1. \end{aligned}$$
(2)

The d-dimensional line element depends on the quintessence factor \(w_q\le 0\), cloud of string a, the mass m, charge Q, and \(\Lambda \). Different choices of the physical parameters and the metric function lead to different BHs.

  • For a d-dimensional Schwarzschild anti-de Sitter (ADS) BH with quintessence (\(Q=0, a=0\)), it can be presented as

    $$\begin{aligned} f(r)\!=\!-2 m r^{3-d}\!-\!\alpha r^{-(d-1) \omega _q+3-d}\!-\!\frac{2 \Lambda r^2}{(d-2) (d-1)}+1. \end{aligned}$$

  • For a d-dimensional Schwarzschild ADS BH with quintessence and the parameter of cloud strings (\(Q=0, a\ne 0\)), it can be expressed as

    $$\begin{aligned} f(r)= & {} -\frac{2 a r^{4-d}}{d-2}-2 m r^{3-d}-\alpha r^{-(d-1) \omega _q+3-d}\\{} & {} -\frac{2 \Lambda r^2}{(d-1)(d-2)}+1. \end{aligned}$$

  • For a d-dimensional Reissner–Nordström (RN) ADS BH with quintessence and \(a=0\), it can be expressed as as [77]

    $$\begin{aligned} f(r)= & {} -2 m r^{3-d}-\alpha r^{-(d-1) \omega _q+3-d}+Q^2 r^{-2 (d-3)}\\{} & {} -\frac{2 \Lambda r^2}{(d-1)(d-2)}+1. \end{aligned}$$

3 Thin-shell WH structure and the gravitational field

In order to mathematically construct the geometry of a thin-shell WH, we assume two equivalent forms of the considered BH solutions and remove the spacetime region from each copy as \(\Omega ^{{\pm }}\equiv \lbrace r^{{\pm }}\le \xi |\, \xi >r_{h} \rbrace \), in which \(\xi \) indicates the radius constant which is larger than the event horizon \(r_h\) in order to keep the spacetime away from the existence of a horizon as well as singularities of the line element given in Eq. (1). The exclusion of the eras from each line element provides two partially completed manifolds corresponding to the timelike hypersurfaces as boundary surfaces presented by \(\partial \Omega ^{{\pm }}\equiv \lbrace r^{{\pm }}= \xi |\,\xi >r_{h} \rbrace \). By identifying the timelike hypersurface \(\partial \Omega ^{{-}}=\partial \Omega ^{{+}}\), in which two eras are joined through a WH, we obtain a geodesically complete manifold. The identified era \(\partial \Omega \) is known as the WH throat, in which the exotic component is present. The line element on \(\partial \Omega \) yields the expression as

$$\begin{aligned} ds ^2 = \xi ^{2}(\tau )d\Omega ^2_{d-2}-d\tau ^2, \end{aligned}$$
(3)

where \(\tau \) depicts the proper time on \(\partial \Omega \), and \(\xi (\tau )\) indicates the throat radius acts as a function of the proper time. The surface stresses at the boundary region are evaluated by implementing the Darmois–Israel conjecture. The intrinsic surface stress-energy tensor \(S_{ij}\) using the Lanczos equation is given by

$$\begin{aligned} S^{i}_{j} = -\frac{1}{8\pi }\left( \kappa ^i_j-\delta ^i_j\kappa ^m_m\right) , \end{aligned}$$
(4)

where the factor \(\kappa _{ij} = K^{+}_{ij}-K^{-}_{ij}\) displays the discontinuity in the extrinsic curvature \(K_{ij}^{\pm }\). The symbols \(+\) and − specify the exterior and interior line elements, respectively. The second fundamental expression of the extrinsic curvature is described by

$$\begin{aligned} K^{\pm }_{ij} = -\gamma _{\nu }\left( \frac{\partial ^2 x^{\nu }}{\partial \eta ^i \partial \eta ^j}+\Gamma ^{\nu \pm }_{\alpha \beta }\frac{\partial x^{\alpha }}{\partial \eta ^{i}}\frac{\partial x^{\beta }}{\partial \eta ^{j}}\right) , \end{aligned}$$
(5)

in which \(\gamma _{\nu }\) exhibits the unit normal vector at the junction, whereas \(\eta ^i\) symbolizes the intrinsic coordinates. The parametric equation at the hypersurface \(\partial \Omega \) is expressed as \(f\left( x^\mu (\xi ^i)\right) =0\). Employing this expression, the unit normal vector to \(\partial \Omega \) is derived as

$$\begin{aligned} n_{\mu } = \pm \Bigl |g^{\alpha \beta }\frac{\partial f}{\partial x^{\alpha }}\frac{\partial f}{\partial x^{\beta }}\Bigl |^{-\frac{1}{2}}\frac{\partial f}{\partial x^{\mu }}, \end{aligned}$$
(6)

where the unitary condition \(n_{\mu }n^{\mu }= +1\) satisfies, while the discontinuity of the extrinsic curvature \(\kappa _{ij}\) can be expressed as \(\kappa ^i_{j}= \mathrm{{diag}}\left( \kappa ^{\tau }_{\tau },\kappa ^{\theta _1}_{\theta _1}, \ldots ,\kappa ^{\theta _{d-2}}_{\theta _{d-2}}\right) \). Thus, the surface-energy tensor can be presented by \(S^i_j = \mathrm{{diag}}\left( -\sigma , P, ...,P\right) \), where P indicates the surface pressure, and \(\sigma \) depicts the surface-energy density. Implementing the Lanczos equation, it is observed that

$$\begin{aligned} \sigma (\xi )=-\frac{(d-2)}{4\pi \xi }\sqrt{\xi ^{3-2 d} \left( \xi ^d \left( -\frac{2 a \xi }{d-2}-\alpha \xi ^{-(d-1) \omega _q}-2 m\right) +\xi ^3 Q^2\right) -\frac{2 \Lambda \xi ^2}{d^2-3 d+2}+1+{\dot{\xi }}^2}, \end{aligned}$$
(7)

and

$$\begin{aligned} P(\xi )=\frac{(d-3)}{4\pi \xi }\sqrt{\xi ^{3-2 d} \left( \xi ^d \left( -\frac{2 a \xi }{d-2}-\alpha \xi ^{-(d-1) \omega _q}-2 m\right) +\xi ^3 Q^2\right) -\frac{2 \Lambda \xi ^2}{d^2-3 d+2}+1+{\dot{\xi }}^2}+\frac{ f^{\prime }(\xi )+\ddot{\xi }}{8\pi \sqrt{f(\xi )+{\dot{\xi }}^2}}, \end{aligned}$$
(8)
Fig. 1
figure 1

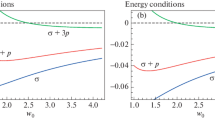
Behavior of energy conditions through \(\sigma (\xi _0), \sigma (\xi _0)+P(\xi _0), and \sigma (\xi _0)+3P(\xi _0)\) with red, blue, and green colors for \(\Lambda =0.02,\alpha =0.2,a=0.4,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) with \(d=4\) (first plot) and \(d=8\) (second plot). It is noted that the null and weak energy conditions are violated

Full size image

where dots and primes demonstrate the differentiation according to \(\tau \) and a, respectively, while the function \(f(\xi )\) is provided in Eq. (2). P and \(\sigma \) satisfy the conservation equation as

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}\tau }\left( \sigma \xi ^{d-2}\right) +P\frac{\mathrm{{d}}}{\mathrm{{d}}\tau }\left( \xi ^{d-2}\right) =0. \end{aligned}$$
(9)

The static state of radius \(\xi =\xi _0\) leads to \(\dot{\xi } = 0 \) and \(\ddot{\xi }= 0 \). From Eqs. (7) and (8), we can obtain

$$\begin{aligned} \sigma (\xi _0)=-\frac{(d-2)}{4\pi \xi _0}\sqrt{-\frac{2 a \xi _0^{4-d}}{d-2}-\frac{2 \Lambda \xi _0^2}{d^2-3 d+2}-2 m \xi _0^{3-d}-\alpha \xi _0^{-(d-1) \omega _q-d+3}+Q^2 \xi _0^{6-2 d}+1}, \end{aligned}$$
(10)

and

$$\begin{aligned} P(\xi _0)=\frac{(d-3)}{4\pi \xi _0}\sqrt{-\frac{2 a \xi _0^{4-d}}{d-2}-\frac{2 \Lambda \xi _0^2}{d^2-3 d+2}-2 m \xi _0^{3-d}-\alpha \xi _0^{-(d-1) \omega _q-d+3}+Q^2 \xi _0^{6-2 d}+1}+\frac{ f^{\prime }(\xi _0)}{8\pi \sqrt{f(\xi _0)}}. \end{aligned}$$
(11)

To inspect the physical objects, energy bounds play a crucial role to investigate their validity. Here, the null (\(\sigma +p\ge 0\)), weak (\(\sigma \ge 0\), \(\sigma +p\ge 0\)), and strong (\(\sigma +2p\ge 0\)) energy bounds are fulfilled for usual matter, whereas the defiance manifests the appearance of exotic substance. For developed thin-shell WHs, the weak and null energy bounds are not satisfied (Fig. 1). This suggests the occurrence of exotic substance at the WH throat.

Now we are going to analyze the repulsive/attractive behavior of the WH on test particles. For this purpose, we evaluate the four-acceleration for the static WH \((\dot{a} =0)\), given by \(a^\mu = u^\mu _{\,\,;\nu } u^\nu \), where the 4-velocity is \( u^\mu =\frac{\mathrm{{d}} x^{\mu }}{\mathrm{{d}}\tau }\)= \((\frac{1}{\sqrt{f(r)}},0,0, \ldots ,0)\). The non-vanishing constituent of the acceleration is presented as

$$\begin{aligned} a^r= & {} \Gamma ^r_{tt} \left( \frac{\mathrm{{d}}t}{\mathrm{{d}}\tau }\right) ^2= \frac{1}{2} \xi \Bigg (\frac{2 a (d-4) \xi ^{2-d}}{d-2}-\frac{4 \Lambda }{d^2-3 d+2}\\{} & {} +2 (d\!-\!3) m \xi ^{1\!-\!d}+\alpha \left( (d\!-\!1) \omega _q\!+\!d\!-\!3\right) \xi ^{-(d\!-\!1) \left( \omega _q\!+\!1\right) }\\{} & {} -2 (d-3) Q^2 \xi ^{4-2 d}\Bigg ). \end{aligned}$$

Taking into account a test particle which is firstly at rest and moves in a radial direction, for this particle, the equation of motion yields

$$\begin{aligned} \frac{\mathrm{{d}}^2r}{\mathrm{{d}}\tau ^2}= -\Gamma ^r_{tt}\left( \frac{\mathrm{{d}}t}{\mathrm{{d}}\tau } \right) ^2 =-a^r, \end{aligned}$$
(12)

which provides the geodesic equation for \(a^{r}=0\). This indicates that the WH is of repulsive nature if \(a^{r}< 0\), while it is of an attractive nature if \(a^{r}> 0\).

4 Linearized Stability Analysis

We can re-express the equations of motion (7) and (9) as

$$\begin{aligned}&{\dot{\xi }}^{2}-\frac{16\pi ^2\xi ^2}{(d-2)^2}\sigma ^2(\xi )=-\frac{2a}{(d-2) \xi ^{d-4}}-\frac{2 \Lambda \xi ^2}{(d-1)(d-2)}\nonumber \\&\quad -\frac{2 m}{\xi ^{d-3}}-\frac{\alpha }{\xi ^{(d-1) \omega _q-3+d}} +\frac{Q^2}{\xi ^{2 (d-3)}}+1\,, \end{aligned}$$
(13)
$$\begin{aligned}&{\dot{\sigma }}=-\frac{{\dot{\xi }}}{\xi }(d-2)\left( \sigma (\xi )+P(\xi )\right) \,. \end{aligned}$$
(14)

We take into account the linear perturbations about a static solution having radius \(\xi _0\) in order to determine the stability constraint for our system [20]. The surface energy density \(\sigma (\xi _0)\) for this solution is explicitly expressed in Eq. (10), whereas the surface pressure \(P(\xi _0)\) for the static solution is presented in Eq. (11). Now, by re-expressing Eq. (13), we get the thin-shell equation of motion given by

$$\begin{aligned} {{\dot{\xi }}}^2+\Omega (\xi )=0, \end{aligned}$$
(15)

in which the potential \(\Omega (\xi )\) is specified as

$$\begin{aligned} \Omega (\xi )= & {} -\frac{2 a}{(d-2) \xi ^{d-4}}-\frac{2 \Lambda \xi ^2}{(d-1) (d-2)}-\frac{2 m}{\xi ^{d-3}}\nonumber \\{} & {} -\frac{\alpha }{\xi ^{(d-1) \omega _q+d-3}}+\frac{Q^2}{\xi ^{2 (d-3)}}+1-\frac{16\pi ^2 \xi ^2}{(d-2)^2} \sigma ^2.\nonumber \\ \end{aligned}$$
(16)

As we are considering the linearization about the static solution \(\xi _0\), we therefore expand \(\Omega (\xi )\) about \(\xi _0\) by employing a Taylor series up to the second order for the powers of \((\xi -\xi _{0})\), which yields

$$\begin{aligned} \Omega (\xi )= & {} \Omega (\xi _0) + \Omega ^\prime (\xi _0) ( \xi - \xi _0) + \frac{1}{2} \Omega ^{\prime \prime }(\xi _0) ( \xi - \xi _0)^2 \nonumber \\{} & {} +{\mathcal {O}}\left[ ( \xi - \xi _0)^3\right] , \end{aligned}$$
(17)

where prime manifests the derivatives associated with \(\xi \). The first-order derivative of \(\Omega (\xi )\) is demonstrated as

$$\begin{aligned}{} & {} \Omega ^{\prime }(\xi )= -\frac{2 a (4-d) \xi ^{3-d}}{d-2}-\frac{4 \Lambda \xi }{(d-2) (d-1)}\nonumber \\{} & {} \quad -2 (3-d) m \xi ^{2-d}-\frac{32 \pi ^2 \xi ^2 \sigma (\xi ) \sigma '(\xi )}{(d-2)^2}-\frac{32 \pi ^2 \xi \sigma (\xi )^2}{(d-2)^2}\nonumber \\{} & {} \quad -\alpha \left( -(d-1) \omega _q+3-d\right) \xi ^{-(d-1) \omega _q-d+2}\nonumber \\{} & {} \quad -2 (d-3) Q^2 \xi ^{-2 (d-3)-1} \end{aligned}$$
(18)

Utilizing the conservation equation (14), the above form becomes

$$\begin{aligned}{} & {} \Omega ^{\prime }(\xi )= -\frac{2 a (4-d) \xi ^{3-d}}{d-2}-\frac{4 \Lambda \xi }{(d-2) (d-1)}\nonumber \\{} & {} \quad -2 (3-d) m \xi ^{2-d}-\frac{32 \pi ^2 \xi \sigma (\xi )^2}{(d-2)^2}\nonumber \\{} & {} \quad +\frac{32 \pi ^2 \xi \sigma (\xi ) (\sigma (\xi )+P(\xi ))}{d-2}-\alpha \left( -(d-1) \omega _q-d+3\right) \nonumber \\{} & {} \quad \times \xi ^{-(d-1) \omega _q-d+2} -2 (d-3) Q^2 \xi ^{-2 (d-3)-1}. \end{aligned}$$
(19)

Now we introduce a factor \(\eta (\sigma )=dp/d\sigma =P^{\prime }/\sigma ^\prime \) that specifies the second differential of the potential. Thus, the second derivative of the potential leads to

$$\begin{aligned}{} & {} \Omega ^{\prime \prime }(\xi )= -\frac{2 a (d-4) (d-3) \xi ^{2-d}}{d-2}-\frac{4 \Lambda }{d^2-3 d+2}\nonumber \\{} & {} \quad -2 (d-3) (d-2) m \xi ^{1-d}-\frac{32 \pi ^2 \sigma (\xi )^2}{(d-2)^2}\nonumber \\{} & {} \quad +\frac{96 \pi ^2 \sigma (\xi ) (\sigma (\xi )+P(\xi ))}{d-2}\nonumber \\{} & {} \quad -\alpha \left( (d-1) \omega _q-3+d\right) \left( (d-1) \omega _q+d-2\right) \nonumber \\{} & {} \xi ^{-(d-1) \left( \omega _q+1\right) }+2 (d-3) (2 d-5) Q^2 \xi ^{4-2 d}\nonumber \\{} & {} \quad -32 \pi ^2 (\eta +1) \sigma (\xi ) (\sigma (\xi )\!+\!P(\xi ))\!-\!32 \pi ^2 (\sigma (\xi )\!+\!P(\xi ))^2.\nonumber \\ \end{aligned}$$
(20)

As we assume the linearization about \(\xi =\xi _0\), we can use Eqs. (16) and (19) to insert \(\xi =\xi _0\) to obtain \(\Omega (\xi _0)=0\) and \( \Omega ^\prime (\xi _0)=0\), respectively. Hence, from Eq. (17), the potential \(\Omega (\xi )\) becomes

$$\begin{aligned} \Omega (\xi )= \frac{1}{2}\Omega ^{\prime \prime }(\xi _0) (\xi -\xi _0)^2+{\mathcal {O}}[(\xi -\xi _0)^3], \end{aligned}$$
(21)

and the equation of motion for the WH throat is provided by

$$\begin{aligned} {\dot{\xi }}^2=-\frac{1}{2}\Omega ^{\prime \prime }(\xi _0) (\xi -\xi _0)^2+{\mathcal {O}}[(\xi -\xi _0)^3]. \end{aligned}$$
(22)

For a more general scenario, we must consider the relationship between the BH mass parameter M and the Arnowitt–Deser–Misner (ADM) mass \({\mathcal {M}}\) for a d-dimensional metric. Further, for a spherical geometry (\(k=1\)), we obtain

$$\begin{aligned} {\mathcal {M}}=\frac{16 \,\pi \, \Gamma (\frac{d-1}{2})}{(d-2) 2 \, \pi ^{\frac{d-1}{2}}} M. \end{aligned}$$
(23)

Hence, the WH structure shows stability just for \(\Omega ^{\prime \prime }(\xi _0)> 0\). Moreover, \(\Omega (\xi _0)\) possesses a local minimum at \(\xi _0\). To perform this inspection, we can discuss the prerequisites for a stable structure of WHs. In our case, we observe that this parameter must satisfy. Further, the stability condition (\(\Omega ^{\prime \prime }(\xi _0)> 0\)) can be reduced in terms of \(\eta _0\) given as follows

$$\begin{aligned} \eta _0>\frac{{\mathcal {A}}_0}{{\mathcal {B}}_0} \quad \text {if} \quad {\mathcal {B}}_0>0, \quad \eta _0<\frac{{\mathcal {A}}_0}{{\mathcal {B}}_0} \quad \text {if} \quad {\mathcal {B}}_0<0, \end{aligned}$$
(24)

where

$$\begin{aligned} {\mathcal {A}}_0= & {} \frac{1}{(d-2)^2}\left( \frac{(d-2)}{d-1} \xi _0 ^{-2 d \omega _q-3 d+\omega _q+1}\right. \\{} & {} \times \left. \left( 2 (d-1) (d-3) \xi _0 ^{(2 d-1) \omega _q+d} \left( \xi _0 ^d\right. \right. \right. \\{} & {} \times \left. \left. \left. \left( a (d-4) \xi _0 +(d-2)^2 m\right) \right. \right. \right. \\{} & {} - \left. \left. \left. (d-2) (2 d-5) \xi _0 ^3 Q^2\right) +\xi _0 ^{d \left( \omega _q+2\right) }\right. \right. \\{} & {} \times \left. \left. \left( \alpha (d-2) (d-1) \left( (d-1) \omega _q+d-3\right) \right. \right. \right. \\{} & {} \times \left. \left. \left. \left( (d-1) \omega _q+d-2\right) +4 \Lambda \xi _0 ^{(d-1) \left( \omega _q+1\right) }\right) \right) \right. \\ {}{} & {} + \left. 32 \pi ^2 \left( (d-3) (2 d-5) \sigma (\xi _0 )^2\right. \right. \\{} & {} \left. \left. +3 (d-3) (d-2) \sigma (\xi _0 ) P(\xi _0 )+(d-2)^2 P(\xi _0 )^2\right) \right) ,\\ {\mathcal {B}}_0= & {} -32 \pi ^2 \sigma (\xi _0 )^2-32 \pi ^2 \sigma (\xi _0 ) P(\xi _0 ). \end{aligned}$$

These inequalities help us to determine the constraints of WH stability under all the parameters of the line element.

5 Stability constraints for some specific cases

In this section, our main focus is to present some specific cases which are of a higher-dimensional BH with quintessence and a cloud of strings. We compute the stability constraints for every choice of four-dimensional BH geometries by considering the constraints (\(\Omega ^{\prime \prime }(\xi _0)> 0\)), which leads to \( \eta _0 >0\) by using \({\mathcal {B}}_0>0\). For calculating the constraints, we only present the conditions of a stable configuration for the case of \({\mathcal {B}}_0>0\), while the case \({\mathcal {B}}_0<0\) is not written in the present manuscript. Moreover, we calculate the stable structure that is based on the quintessence and cloud parameters as mentioned in the following cases:

Fig. 2
figure 2

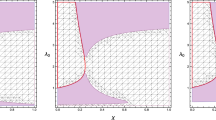
Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH for a d-dimensional RN-ADS BH with quintessence and a cloud of strings. The brown regions represent the stable regions (\(\eta _0 >0\)), and blues regions show an unstable configuration (\(\eta _0<0\)) with \(Q=0.2,\Lambda =0.02,\alpha =0.2,a=0.4,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image
Fig. 3
figure 3

Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH with a d-dimensional RN-ADS BH with quintessence (\(a=0\)). The brown regions represent the stable regions (\(\eta _0 >0\)), and blue regions show an unstable configuration (\(\eta _0<0\)) with \(Q=0.2,\Lambda =0.02,\alpha =0.2,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image
Fig. 4
figure 4

Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH with a d-dimensional RN-ADS BH (\(a=0, \alpha =0\)). The brown regions represent the stable regions (\(\eta _0 >0\)), and blue regions show an unstable configuration (\(\eta _0<0\)) with \(Q=0.2,\Lambda =0.02,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image
Fig. 5
figure 5

Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH with a d-dimensional Schwarzschild-ADS BH with quintessence and a cloud strings (\(Q =0\)). The brown regions represent the stable regions (\(\eta _0 >0\)), and blue regions show an unstable configuration (\(\eta _0<0\)) with \(\Lambda =0.02,\alpha =0.2,a=0.4,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image
Fig. 6
figure 6

Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH with a d-dimensional Schwarzschild-ADS BH with quintessence (\(Q =0=a\)). The brown regions represent the stable regions (\(\eta _0 >0\)), and blue regions show an unstable configuration (\(\eta _0<0\)) with \(\Lambda =0.02,\alpha =0.2,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image
Fig. 7
figure 7

Region plot of \(\eta _0\) versus \(\xi _0\) and d of a thin-shell WH with a d-dimensional Schwarzschild-ADS BH (\(\alpha =0=a,Q=0\)). The brown regions represent the stable regions (\(\eta _0 >0\)), and blue regions show an unstable configuration (\(\eta _0<0\)) with \(\Lambda =0.02,m=0.4,\) for \(\omega _q=-\frac{d-3}{d-1}\) (first plot), \(\omega _q=-1\) (second plot), and \(\omega _q=-\frac{d-2}{d-1}\) (third plot)

Full size image

5.1 Four-dimensional Schwarzschild BH with quintessence and cloud of strings

We assume the four-dimensional spherical symmetric solution with quintessence and cloud of strings in the absence of charge and \(\Lambda \). For this purpose, we substitute \(Q=0, \Lambda =0, and d=4\) with different possibilities of \(\omega _q\) in Eq. (24).

  • For \(\omega _q=-1\), the condition of stability is

    $$\begin{aligned} \eta _0> & {} \frac{(a-1) \xi _0 }{2 \left( \alpha \xi _0 ^3-a \xi _0 -4 m+\xi _0 \right) }\nonumber \\{} & {} +\frac{-a \xi _0 -3 m+\xi _0 }{\xi _0 \left( \alpha \xi _0 ^2+a-1\right) +2 m}+1, \,\,\,\,\,\,\,\,\nonumber \\{} & {} \text {if} \,\,\,\,\, a>\alpha \xi _0 ^2-\frac{4 m}{\xi _0 }+1. \end{aligned}$$
    (25)

  • For \(\omega _q=-\frac{d-2}{d-1}\), we observe the following constraint:

    $$\begin{aligned} \eta _0>-\frac{\xi _0 ^2 \left( \alpha ^2 \xi _0 ^2+\alpha (a-1) \xi _0 +(a-1)^2\right) -2 m \xi _0 (\alpha \xi _0 -2 a+2)+8 m^2}{2 ((a-1) \xi _0 +4 m) (\xi _0 (\alpha \xi _0 +a-1)+2 m)}, \,\,\,\,\,\,\,\,\text {if} \,\,\,\alpha \in {\mathbb {R}}\wedge a+\frac{4 m}{\xi _0 }>1. \end{aligned}$$
    (26)

  • For \(\omega _q=-\frac{d-3}{d-1}\), the stability condition becomes

    $$\begin{aligned} \eta _0> & {} -\frac{\xi _0 ^2 (a+\alpha -1)^2+4 m \xi _0 (a+\alpha -1)+8 m^2}{2 (\xi _0 (a+\alpha -1)+2 m) (\xi _0 (a+\alpha -1)+4 m)}, \,\,\,\,\,\,\,\,\nonumber \\{} & {} \text {if} \,\,\,a+\alpha +\frac{4 m}{\xi _0 }>1. \end{aligned}$$
    (27)

5.2 Four-dimensional Schwarzschild ADS BH with quintessence and cloud of strings

Now we observe the stability constraints for the choice of a four-dimensional Schwarzschild ADS BH with quintessence and a cloud of strings. For this purpose, we consider \(Q=0,\Lambda \ne 0,\) and \(d=4\) with different possibilities of \(\omega _q\) in Eq. (24).

  • For \(\omega _q=-1\), we get

    $$\begin{aligned} \eta _0> & {} -\frac{3 (a-1) \xi _0 }{-2 \xi _0 ^3 (3 \alpha +\Lambda )+6 (a-1) \xi _0 +24 m}\nonumber \\{} & {} +\frac{-3 (a-1) \xi _0 -9 m}{\xi _0 ^3 (3 \alpha +\Lambda )+3 (a-1) \xi _0 +6 m}+1, \end{aligned}$$
    (28)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge a>\frac{1}{3} \xi _0 ^2 (3 \alpha +\Lambda )-\frac{4 m}{\xi _0 }+1. \end{aligned}$$

  • For \(\omega _q=-\frac{d-2}{d-1}\), the stability conditions are

    $$\begin{aligned}{} & {} \eta _0 >\frac{\xi _0 ^2 {\mathcal {J}}_1(\xi _0)+6 m \xi _0 \left( 3 \alpha \xi _0 -6 a+5 \Lambda \xi _0 ^2+6\right) -72 m^2}{2 \left( 3 (a-1) \xi _0 -\Lambda \xi _0 ^3+12 m\right) \left( \xi _0 \left( 3 \alpha \xi _0 +3 a+\Lambda \xi _0 ^2-3\right) +6 m\right) }, \end{aligned}$$
    (29)

    if

    $$\begin{aligned} \alpha \in {\mathbb {R}}\wedge a>\frac{\Lambda \xi _0 ^2}{3}-\frac{4 m}{\xi _0 }+1. \end{aligned}$$

  • For \(\omega _q=-\frac{d-3}{d-1}\), it yields the following condition:

    $$\begin{aligned} \eta _0> & {} -\frac{3 \xi _0 (a+\alpha -1)}{6 \xi _0 (a+\alpha -1)-2 \Lambda \xi _0 ^3+24 m}\nonumber \\{} & {} +\frac{-3 \xi _0 (a+\alpha -1)-9 m}{3 \xi _0 (a+\alpha -1)+\Lambda \xi _0 ^3+6 m}+1, \end{aligned}$$
    (30)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge a+\alpha +\frac{4 m}{\xi _0 }>\frac{\Lambda \xi _0 ^2}{3}+1. \end{aligned}$$

5.3 Four-dimensional RN BH with quintessence and cloud of strings

Now we observe the effect of quintessence and a cloud of strings on the stable constraints of a four-dimensional RN BH; in other words, by setting \(Q\ne 0,\Lambda =0,\) and \(d=4\) with different choices of \(\omega _q\) in Eq. (24).

  • For \(\omega _q=-1\), we get

    $$\begin{aligned} \eta _0 >\frac{\xi _0 ^2 \left( -2 \alpha ^2 \xi _0 ^6+(a-1) \alpha \xi _0 ^4+2 m \xi _0 \left( 5 \alpha \xi _0 ^2-2 a+2\right) -(a-1)^2 \xi _0 ^2-8 m^2\right) +{\mathcal {J}}_2(\xi _0)}{2 \left( \xi _0 \left( \alpha \xi _0 ^3-a \xi _0 -4 m+\xi _0 \right) +3 Q^2\right) \left( Q^2-\xi _0 \left( \xi _0 \left( \alpha \xi _0 ^2+a-1\right) +2 m\right) \right) }, \end{aligned}$$
    (31)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge \alpha \xi _0 ^4+\xi _0 ^2+3 Q^2<\xi _0 (a \xi _0 +4 m). \end{aligned}$$

  • For \(\omega _q=-\frac{d-2}{d-1}\), the stability conditions are

$$\begin{aligned} \eta _0 >\frac{\xi _0 ^2 \left( -\xi _0 ^2 \left( \alpha ^2 \xi _0 ^2+\alpha (a-1) \xi _0 +(a-1)^2\right) +2 m \xi _0 (\alpha \xi _0 -2 a+2)-8 m^2\right) +{\mathcal {J}}_3(\xi _0)}{2 \left( \xi _0 (-a \xi _0 -4 m+\xi _0 )+3 Q^2\right) \left( Q^2-\xi _0 (\xi _0 (\alpha \xi _0 +a-1)+2 m)\right) }, \end{aligned}$$
(32)

if

$$\begin{aligned} \alpha \in {\mathbb {R}}\wedge a>-\frac{4 m}{\xi _0 }+\frac{3 Q^2}{\xi _0 ^2}+1. \end{aligned}$$

  • For \(\omega _q=-\frac{d-3}{d-1}\), it yields the following condition:

    $$\begin{aligned} \eta _0> & {} \frac{4 m \xi _0 -5 Q^2}{2 \xi _0 (\xi _0 (a+\alpha -1)+4 m)-6 Q^2}\nonumber \\{} & {} +\frac{Q^2-m \xi _0 }{\xi _0 (\xi _0 (a+\alpha -1)+2 m)-Q^2}-\frac{1}{2}, \end{aligned}$$
    (33)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge a+\alpha +\frac{4 m}{\xi _0 }>\frac{3 Q^2}{\xi _0 ^2}+1. \end{aligned}$$

5.4 Four-dimensional RN-ADS BH with quintessence and cloud of strings

Finally, we consider a four-dimensional RN-ADS BH with quintessence and a cloud of strings by taking \(Q\ne 0,\Lambda \ne 0, and d=4\) with various choices of \(\omega _q\) in Eq. (24).

  • For \(\omega _q=-1\), the condition of stability becomes

    $$\begin{aligned} \eta _0 >\frac{\xi _0 ^2 \left( 3 (a-1) \xi _0 ^4 (3 \alpha +\Lambda )-2 \xi _0 ^6 (3 \alpha +\Lambda )^2+{\mathcal {J}}_6(\xi _0)\right) -3 \xi _0 Q^2 \left( 10 \xi _0 ^3 (3 \alpha +\Lambda )-3 (a-1) \xi _0 -30 m\right) -36 Q^4}{2 \left( \xi _0 \left( \xi _0 ^3 (3 \alpha +\Lambda )-3 (a-1) \xi _0 -12 m\right) +9 Q^2\right) \left( 3 Q^2-\xi _0 \left( \xi _0 ^3 (3 \alpha +\Lambda )+3 (a-1) \xi _0 +6 m\right) \right) }, \end{aligned}$$
    (34)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge a>\frac{1}{3} \xi _0 ^2 (3 \alpha +\Lambda )-\frac{4 m}{\xi _0 }+\frac{3 Q^2}{\xi _0 ^2}+1. \end{aligned}$$

  • For \(\omega _q=-\frac{d-2}{d-1}\), it leads to the following stability condition:

    $$\begin{aligned} \eta _0 >\frac{\xi _0 ^2 \left( {\mathcal {J}}_7(\xi _0) +6 m \xi _0 \left( 3 \alpha \xi _0 -6 a+5 \Lambda \xi _0 ^2+6\right) -72 m^2\right) -3 \xi _0 Q^2 (\xi _0 (2 \xi _0 (6 \alpha +5 \Lambda \xi _0 )-3 a+3)-30 m)-36 Q^4}{2 \left( \xi _0 \left( \xi _0 \left( -3 a+\Lambda \xi _0 ^2+3\right) -12 m\right) +9 Q^2\right) \left( 3 Q^2-\xi _0 \left( \xi _0 \left( 3 \alpha \xi _0 +3 a+\Lambda \xi _0 ^2-3\right) +6 m\right) \right) }, \end{aligned}$$
    (35)

    if

    $$\begin{aligned} \alpha \in {\mathbb {R}}\wedge \xi _0 \ne 0\wedge a>\frac{\Lambda \xi _0 ^2}{3}-\frac{4 m}{\xi _0 }+\frac{3 Q^2}{\xi _0 ^2}+1. \end{aligned}$$

  • For \(\omega _q=-\frac{d-3}{d-1}\), we get the stability constraint as

    $$\begin{aligned} \eta _0 >\frac{\xi _0 ^2 \left( 3 \Lambda \xi _0 ^4 (a+\alpha -1)-9 \xi _0 ^2 (a+\alpha -1)^2+6 m \xi _0 \left( 5 \Lambda \xi _0 ^2-6 (a+\alpha -1)\right) -2 \Lambda ^2 \xi _0 ^6-72 m^2\right) +{\mathcal {J}}_8(\xi _0)}{2 \left( \xi _0 \left( -3 \xi _0 (a+\alpha -1)-\Lambda \xi _0 ^3-6 m\right) +3 Q^2\right) \left( \xi _0 \left( -3 \xi _0 (a+\alpha -1)+\Lambda \xi _0 ^3-12 m\right) +9 Q^2\right) }, \end{aligned}$$
    (36)

    if

    $$\begin{aligned} \xi _0 \ne 0\wedge a+\alpha +\frac{4 m}{\xi _0 }>\frac{\Lambda \xi _0 ^2}{3}+\frac{3 Q^2}{\xi _0 ^2}+1. \end{aligned}$$

5.5 Graphical analysis via regional plots

Further, we study the stability of the created structure through the region plots of \(\eta _0\) versus \(\xi _0\) and d as shown in Figs. 2, 3, 4, 5, 6, and 7. It is very interesting to note that for a stable configuration, \(\eta _0\) must be greater (less) than zero; otherwise, it represents the unstable configurations for \({\mathcal {B}}_0>0\) (\({\mathcal {B}}_0<0\)). As calculated for different values of d, there is a possibility of stable configurations (\(\eta _0>0\)) with certain conditions on the physical parameters. We are interested in observing these stable regions graphically and also analyzing the impact of dimension, charge, quintessence, and cloud strings on the stability of thin-shell WHs. In Fig. 2, the possibility of a stable geometry of an RN-ADS d-dimensional BH with quintessence and cloud parameters for three different choices of \(\omega _q\), i.e., \(\omega _q=-\frac{d-3}{d-1}, -1,-\frac{d-2}{d-1}\), is presented.The same stable regions are found for every choice of \(\omega _q\), and stable regions shrink for higher-dimensional BHs. For the case of an RN-ADS d-dimensional BH with (\(\alpha \ne 0, a=0\)) and (\(\alpha =0=a\)), stable regions decrease (Figs. 2, 3, and 4). Similarly, we also observe the impact of quintessence and cloud parameters on the stable structure of a thin shell in light of Schwarzschild ADS d-dimensional BHs (Figs. 5, 6, and 7). Finally, it is concluded that the chances of a stable structure are maximum for the choice of an RN-ADS d-dimensional BH with quintessence and cloud strings. In the absence of cloud and quintessence parameters, the stability of charged and uncharged ADS BHs decreases, as shown in Figs. 2, 3, 4, 5, 6, and 7.

6 Conclusions

In this study, we have constructed a d-dimensional thin-shell WH that is bounded by quintessence and a cloud of strings by using the cut-and-paste approach and the Darmois–Israel conjecture. The stress-energy tensor components are determined from the simplified form of the Einstein field equations at the hypersurface, which creates the dynamical equations of these built geometries. A more general model of stability constraints has been inspected under radial oscillations while maintaining the spherically symmetric structure in the framework of Schwarzschild (ADS) and RN (ADS) BHs with the quintessence and cloud of strings. It is noted that the matter constituents violate the energy constraints, which indicates the presence of exotic substance. Such type of matter contents plays a remarkable role in stabilizing the rapidly collapsing and expanding behavior of the WH throat. We have also explored the stability of the developed structure through a regional plot along the equilibrium shell radius and dimension of the BH. For a stable configuration, \(\eta _0\) must be greater or less than zero with respect to the behavior of \({\mathcal {B}}_0\) as \({\mathcal {B}}_0>0\) or \({\mathcal {B}}_0<0\), respectively. As calculated for different values of d, there is a possibility of stable configurations (\(\eta _0>0\)) with certain conditions on the physical parameters. We have observed these stable regions graphically and also analyzed the influences of dimension, charge, quintessence, and cloud strings on the stability of thin-shell WHs, as shown in Figs. 5, 6, and 7. It is concluded that the stability of thin-shell WHs increases in the background of the cloud of strings and quintessence field. Hence, the developed higher-dimensional charged thin-shell WH with quintessence and cloud of strings shows maximum stable configurations. The stability constraints show that for higher dimension, the stable domain decreases. This work can be extended for the dynamics of higher-dimensional thin-shell and gravastar structures with different types of matter contents. It is also beneficial to study the thermodynamic properties of the shell around BH and WH geometries.