1 Introduction

Astrophysical and cosmological observations indicate the existence of cold dark matter as 23% [1] of the Universe’s total energy budget. Promising scenarios include dark matter in the form of extralow mass bosons [2], and one highly motivated candidate is the axion [3,4,5,6,7,8,9,10]. Naturally relaxing the amount of Charge-Parity violation in the Standard Model’s strong interaction [11, 12] (a.k.a. the strong CP problem [13]), the axion emerges from a natural global \(U(1)_{\textrm{PQ}}\) symmetry extension of the Standard Model (SM), which is spontaneously broken at high scale and later explicitly broken at the strong interaction’s confinement scale by the QCD instanton potential [14, 15], making the axion a pseudo-Nambu-Goldstone particle with a small but non-zero mass. Cosmologically, through the ‘misalignment’ mechanism [16,17,18,19,20,21] axions are produced during the QCD phase transition and their collective evolution makes up the dark matter density observed at the current time. Depending on the spontaneous \(U(1)_{\textrm{PQ}}\) breaking scale relative to that of inflation, typically cosmic axions account for the relic density in the classical mass window with \(m_a\sim \mathcal{O}(10^{-5}-10^{-3})\) eV [21] or \(m_a<\mathcal{O}(10^{-7})\) eV [22], and a wider dark matter axion mass range is possible through other production mechanisms.

The axion acquires its characteristic \(\frac{a}{f_a}G\tilde{G}\) coupling through a loop of \(SU(3)_c\)-charged fermions, such as in benchmark invisible axion scenarios such as the KSVZ [7, 8] and the DFSZ [9, 10] models. Generally the axion can also couple to other SM gauge fields, in particular the QED photon, with the interaction Lagrangian term

$$\begin{aligned} \mathcal{L}_{a\gamma \gamma }=g_{a\gamma }a\vec {E}\cdot \vec {B}, \end{aligned}$$
(1)

where \(\vec {E},\vec {B}\) are the electric and magnetic field strengths, the axion-photon coupling is \(g_{a\gamma }=c_{\gamma }\alpha _{\textrm{QED}} / (\pi f_a)\), with \(f_a\) as the \(U(1)_{\textrm{PQ}}\) symmetry’s scale factor, \(\alpha _{\textrm{QED}}=1/137\) is the fine-structure constant and the \(\mathcal{O}(1)\) coefficient \(c_{\gamma }\) is given by the details of the particular UV model. This coupling also characterizes the generalized axion-like particles (ALPs), which can be created from dimension compactification in string theory, or other UV theories with an extra light bosonic mode that may not necessarily couple to the SM gluon field. General ALPs have relaxed \(f_a-m_a\) correlation compared to that of the QCD axion, thus they have a much wider parameter space to serve as a dark matter candidate. In the following we use ‘axion’ to denote both the QCD axion and ALPs if not specified.

The axion-photon coupling \(g_{a \gamma }\) allows the dark matter axion to convert into photons inside a laboratory’s electromagnetic fields, and is being actively searched for by cavity haloscopes including ADMX [23], HAYSTAC [24], CAPP [25], ORGAN [26], CAST-RADES [27], QUAX-\(a\gamma \) [28], TASEH [29], DANCE [30], noncavity experiments such as ABRACADABRA [31], high-frequency dielectric design such as MADMAX [32], BREAD [33], and many others. For recent reviews of axion search methods, see Refs. [34, 35]. To date, resonant cavity haloscopes have achieved the highest sensitivity due to the high-Q front-end enhancement at both classical [36] and quantum levels [37]. However, matching the signal photon’s wavelength in the low axion mass range \(m_a\ll 10^{-6}\) eV, motivated by string theory [38], GUT scale new physics [39,40,41,42,43], etc., faces the practical limitation of cryogenic equipment sizes. For a low axion mass the size of the resonant cavity could be too large, and multiple promising complementary methods are helpful, such as in ABRACADABRA [31], SHAFT [44], ADMX-SLIC [45], BASE [46], and DMRadio [47], each featuring different strengths and limitations.

From the theoretical perspective, the \(m_a\lesssim 10^{-7}\) eV axion does have unique attractions. It has been shown that very light axions have strong implications for inflation [22]. Models with a very light axion typically have a PQ symmetry breaking scale \(f_a\) order of the GUT scale, which results in considerable tensions between the observed isocurvature fluctuations and high-scale inflation. A low energy scale inflation scenario will be necessary if very light dark matter axions are detected. The discovery of very light dark matter axions will also indicate the observed Universe as a highly atypical Hubble volume and possibly the KKLT scenario [22]. Thus, for low-mass axions, an alternative detection method has been proposed in Refs. [48, 49] to utilize the high Q-factor of a resonant LC circuit as a narrow-band pickup. Following this idea, dark matter experiments with LC-enhanced pickup systems have been carried out [31, 47, 49]. However the very strong magnetic fields created by magnets or solenoids inherently possess small fluctuations which would be hard to separate from the tiny axion induced signals.

In this paper, we propose a narrow-band axion dark matter experimental scheme based on an electrified cylindrical capacitor. We investigate the prospective sensitivity to axion-photon coupling \(g_{a\gamma }\) with a resonance circuit as the high Q pickup of induced signals from axion coupling to a strong laboratory electric field. In comparison with using a strong magnetic field as the conversion medium, while the axion-to-photon conversion rate inside an electric field is suppressed by the subunity local dark matter velocity, using the \(\vec {E}\) field [50] can avoids placing a sensitive magnetic probe close to a strong magnetic field. In addition, the signal strength with an electric field is modulated by the relative angle of the \(\vec {E}\) field orientation and the direction of the local dark matter flux, which provides a potential test of the origin of a signal.

In Sect. 2, we describe the experimental schematics with a meter-scale cylindrical capacitor, and calculate the signal strength of the DM axion-induced signal with an LCR resonance pickup. Section 3 discusses the major noises and the prospective sensitivity in an axion mass range \(m_a< 10^{-6}\) eV. We demonstrate that good axion-photon coupling sensitivity can be achieved with a static electric field as the converting medium, and then we conclude in Sect. 4.

2 Cylindrical capacitor setup

For terrestrial laboratories, the dark matter axion can be modeled as a plane wave

$$\begin{aligned} a(x,t)\approx a_0\textrm{cos}\left[ m_a\vec {v}_a\cdot \vec {x}-\left( m_a+{m_a\over 2}v_a^2\right) t \right] ~, \end{aligned}$$
(2)

with a de-Broglie wavelength \(\lambda _a= k_a^{-1}\sim (v_a m_a)^{-1}\). \(v_a\sim 10^{-4}-10^{-3}\) is the Earth’s relative velocity to the local bulk of the galaxy’s dark matter halo, and the local dark matter forms an ‘axion wind’ to the Earth. The local axion field magnitude is \(a_0=\sqrt{2\rho _{\textrm{DM}}}/m_a\) where the local DM halo density is typically \(\rho _{\textrm{DM}}=0.4\) GeV cm\(^{-3}\). For \(\lambda _a\) longer than the dimension of the experimental apparatus, this axion field can be considered a coherent classical background field [51, 52] that oscillates at \(\omega _a = (1+v_a^2/2)m_a\), for which the axion velocity can interchange with the axion field’s spatial gradient up to a small red(blue)-shift due to Earth’s motion. The energy spread due to the halo velocity dispersion is usually small, and it is often denoted by the axion field quality factor as \(\delta \omega _a /\omega _a \equiv Q_a^{-1}\). For conventional dark matter halo models [20], \(Q_a \sim 10^{6}\), any signals from this nearly monochromatic oscillation would be efficiently detected from a narrow-band probe with a matched quality factor.

When the axion is considered as a background field, the axion-modified Maxwell equations [36] observe the addition of an effective 4-current density \(j^\mu =\{\vec {\nabla } a\cdot \vec {B},-g_{a\gamma }\vec { E}\times \vec { \nabla } a+g_{a\gamma }\dot{a}\vec { B} \}\) that simplifies to an effective displacement current density \(\vec {j}_a\) inside a static laboratory electric field. The modified Maxwell equations are

$$\begin{aligned} \begin{aligned} \vec {\nabla }\cdot \vec { E}&= \rho _e,\\ \vec {\nabla }\times \vec { B}-{\partial \vec { E} \over \partial t}&= \vec {j}_e + \vec {j}_a, \\ \vec {\nabla }\cdot \vec { B}&=0,\\ \vec {\nabla }\times \vec {E}&=-{\partial \vec { B}\over \partial t}~, \end{aligned} \end{aligned}$$
(3)

where \(\vec {E}=\vec {E}_0+\vec {E}_a\) is dominated by the static field \(\vec {E}_0\) and \(\vec {j}_e =0\). \(\vec {j}_a=-g_{a\gamma }a \vec {E}_0\times \vec {k}_a\) alternates at the same frequency as the axion field, and it induces a magnetic field signal \(\vec {B}_a\). Since \(\vec {j}_a\) is perpendicular to both \(\vec {E}\) and \(\vec {v}_a\), \(\vec {j}_a\) depends on the angle between the local dark matter density flow density and the applied field \(\vec {E}_0\). This will lead to periodic \(\vec {j}_a\) modulations, for instance, at a 24-hour period due to the Earth’s rotation that orientate the apparatus to the direction of the local dark matter flow. Another shorter-period modulation over \(2\pi (v_a \omega _a)^{-1}\) also arises as the nonrelativistic axion field may have a longer wavelength \(\lambda _a = (\beta m_a)^{-1}\) than the size of the \(\vec {E}_0\)-field region, which causes the strength of \(\vec {\nabla } a\) to fluctuate as the a field propagates. We also note that the amplitude \(j_a= g_{a\gamma }\sqrt{2\rho _\textrm{DM}}\cdot |\vec {v}_a\times \vec {E}_0|\) is insensitive to \(m_a\) for a given dark matter energy density.

With a cylindrical capacitor, as illustrated in Fig. 1, and assuming \(\vec {a}\) is along the cylinder axis, \(\vec {j}_a\) is circularly distributed in the radial \(\vec {E}\)-field region between the capacitor plates, forming an effective current loop and the induced magnetic field amplitude along the cylinder axis [50] is

$$\begin{aligned} B_a= & {} g_{a\gamma }E_0 v_{\textrm{DM}} c_R\sqrt{2\rho _{\textrm{DM}}}R_1 \nonumber \\\sim & {} 2\times 10^{-10} \textrm{T} \cdot \left( \frac{g_{a\gamma }}{\textrm{GeV}}^{-1}\right) \left( \frac{E_0}{10^7 \mathrm{V/m}} \right) \left( \frac{R_1}{ \mathrm{0.1 m}} \right) , \nonumber \\ \end{aligned}$$
(4)

where \(R_1\) is the inner radius of the capacitor and \(E_0\) denotes the strongest electric field strength at the inner radius. \(c_R\) is an \(\mathcal{O}(1)\) parameter determined by the geometry of the capacitor cross-section. \(v_{\textrm{DM}}=10^{-4}\) is the Earth’s local relative velocity to the dark matter halo.

Fig. 1
figure 1

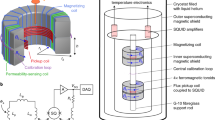
Illustrative experiment setup. Upper: a superconductor coil \(L_1\) is placed in the central region of a cylindrical capacitor, and is connected in a resonant LCR circuit as a narrow-band pickup for the axion-induced signal \(\vec {B}_a\). The inner layer (\(R_1\)) of the capacitor should be non-conducting to let in the induced signal. \(R_s\) denotes the total resistance. Lower: The pickup coil \(L_1\) is loosely winded to reduce its self-inductance and allows the signal to penetrate into the central region. Using superconducting \(L_1\) and \(L_2\) can lower their resistance and reduce thermal noise

Full size image

In a simplified low-frequency and long-solenoid limit, the signal magnetic field can be easily computed by integrating out the total effective current between the capacitor’s inner and outer radii, and the form factor is \(c_R=\textrm{ln}(R_2/R_1)=0.69\) for \(R_2=2R_1\). The realistic evaluation of \(c_R(\omega )\) can be much more involved, which depends on the axion oscillation frequency, radius-length ratio, plate thickness and material, etc. Here we resort to numerical electromagnetic simulation with the Comsol package. For a sample study, we choose the geometry with \(R_2=2R_1\) and a cylinder length equal to twice of \(R_2\). We performed simulations with 5 mm-thick nonconductor material plates and assuming the capacitor was placed inside a shielding box. Simulations show that \(c_R\) at low frequencies is a constant value around 0.3, mostly due to the large opening at the cylinder’s ends, which spoils the long-solenoid symmetry [53] and lets the induced magnetic field be on both the inside and outside of the cylinder; the expected frequency-dependence from decoherence starts to show up near the cut-off frequency, as shown in Table 1. We will assume a similar \(c_R\) behavior with the frequency fraction \(f/f_{\textrm{max}}\) to give sensitivity estimate at our benchmark cases, which scale up with the same ratio of dimensions. In principle \(c_R\) could be improved with a longer cylinder; we will postpone the geometric optimization of \(c_R\) for future work.

Table 1 Simulated \(c_R\) values at different frequencies, \(R_2=2R_1=0.4\) m and \(f_{\textrm{max}}= 0.1875\) GHz. The cylinder length is set to 0.8 m, corresponding to Benchmark A in Sect. 3. The cylinder assumes 5 mm nonconductive material plates and they are enclosed inside an exterior shielding box
Full size table

An \(N_1\)-turn coil of radius \(R_{\textrm{coil}}\sim R_1\) is then placed in the central region of the capacitor to pick up the induced magnetic flux \(\Phi _a=B_a\cdot \pi R_1^2\). This magnetic flux corresponds to the \(B_a\) component parallel to the cylinder axis, and is proportional to the \(v_{a,z}\) component along \(\hat{z}\); the \(\vec {v}_a\) projections in the \(\hat{x}\) and \(\hat{y}\) directions do not contribute to \(\Phi _a\). In our calculations, we assume \(\vec {v}_a //{\hat{z}}\), while in measurement \(\vec {v}_a\cdot {\hat{z}}\) yields a directional dependence in \(\Phi _a\) that in principle can be used as check by adjusting the experiment’s orientation.

The pickup coil is connected as part of an LCR circuit with its resonance point tuned to a target search frequency of the axion field oscillation, e.g. \(LC =\omega ^{-2}\). The total inductance L (without subscript) includes contributions from the pickup coil \(L_1\), the effective inductance \(L_2\) of the inductive coupling to amplifier circuit and any additional inductance from wiring. \(L_2\) includes both the coupled coils’ self-inductance and mutual inductance. We would require \(L_1 \gg L_2\) to ensure \(L\sim L_1\). Note that a single-turn circular loop with wire radius \(d_1\sim \)mm has a self-inductance approximately \(10 \mu \)H per meter. The pickup coil \(L_1\) can be loosely winded to reduce the inductance between its adjacent turns, so that \(L_1\propto N_1\). The LCR resonance requires a capacitance value \(C=(2\pi f)^{-2}/L\sim 0.3\textrm{pF}\cdot (\mu \textrm{H}/L)\left( \mathrm{0.1 ~GHz}/{f}\right) ^2\), which increases toward lower axion mass, and is much larger than typical stray capacitance on meter-scale wiring. Low-temperature tuning of the LCR resonance frequency can be achieved via an adjustable capacitor.

As the signal strength derives from one pickup loop’s enclosed magnetic flux, which are 2D quantities, Eq. (4) seems to have no explicit dependence on the cylinder’s length. However, the cylinder length still affects how many turns \(N_1\) can loosely wind into the pickup, and it is also coherence limited by the signal photon’s half-wavelength [54], and appears in the theoretical upper limit of the axion-photon coherent conversion rate.

The high LCR quality factor at its resonance point allows for an enhanced current in the circuit [49]. The saturated current in the loop is

$$\begin{aligned} I_a =Q_c \cdot (\pi R_1^2 N_1 B_a L^{-1}) \cos \omega t, \end{aligned}$$
(5)

where \(Q_c\) denotes the conventional LCR quality factor \(Q_c=\omega _a L/R_s\). The signal power is stored in the LCR circuit utill the energy dissipation power by the resistance is \(P_\mathrm{dis.}= Q_c\cdot (N_1\Phi _a/L)^2\omega _a L/2\) equals that of the signal feed. For efficient signal pickup, \(Q_c\) should match the order of magnitude of the quality factor in the axion field \(Q_c\sim Q_a\), which also matches the saturated energy dissipation to the dark matter axion-photon energy conversion rate. Here we choose \(Q_c\sim Q_a\) for a proof-of-principle estimate. In practice, \(Q_c\) should be replaced by a ‘loaded’ quality factor after coupling to the amplifier/detector chain, and further optimization is needed [55, 56]. Note that for a high \(Q_c\), saturating the maximal current takes \(Q_c\) oscillation periods, and in the MHz–GHz range it is typically much shorter than the time scale of \(\vec {v}_a\) variation. However, in principle it could require significantly longer time \(Q_c\cdot 2\pi \omega _a^{-1}\) in the case of extremely low axion masses. In the MHz\(\sim \)GHz range, the saturation time is less than a second and we consider that the maximal LCR current is always reached during the observation time.

The inner volume of the cylindrical capacitor, along with the pickup circuit, is placed under cryogenic conditions to suppress thermal noise. Environmental fluctuations can be removed via electromagnetic shielding. Since there is no strong magnetic field in the system, the inductance coils and the capacitor in the LCR loop can be made with superconductor materials, such that the circuit components with the major resistance can be confined to a small spatial region and placed under an extreme cryogenic temperature, \(T_c\sim \) mK. This reduces the cooling requirement on the sizable superconducting pickup \(L_1\), without worsening its noise. For instance, the NbTi superconductor has a transition temperature at 9.7 K and has a good transmission rate for \(10^2\) MHz signals. Denoting \(R_s\) as the total resistance in the LCR circuit, a low effective resistance on the superconducting NbTi pickup coil \(R_{\textrm{coil}}\ll R_s\) would allow a much higher temperature \(T_{\textrm{coil}} = T_c\cdot (R_s/R_\textrm{coil})\) and keep the coil’s thermal noise subdominant. Note for a meter-radius, loosely winded 10 round loop, \(L_1\sim 50-100 \upmu \)F and the LCR resonance requires \(R_s=\omega L/Q_c=~0.04\mathrm{\Omega }\cdot (f/\textrm{GHz})\). The contact resistance can be reduced to \(10^{-3}~\mathrm{\Omega }\). If \(L_1\) is at 1 K with the rest of the LCR at mK, \(L_1\)’s effective resistance needs to be controlled to \(R_{\textrm{coil}}<10^{-5}~\mathrm{\Omega }\).

3 Noise and sensitivity

The induced current \(I_a(t)\) in the LCR circuit is then coupled to the amplifier/detector chain. The leading current noise in the LCR is Johnson-Nyquist noise due to the resistance in the LCR circuit, \(\delta I^2= k_B T_c \Delta f/R_s\). This noise will also be amplified at the subsequent amplifier(s) and can be the major noise in signal measurement. The total noise power is

$$\begin{aligned} P_n = k_B T_c \Delta f + k_B T_D \Delta f, \end{aligned}$$
(6)

where the latter is an equivalent readout noise power that includes the added noises from amplifier and detector chain, etc. For the detection bandwidth we take \(\Delta f = Q_c^{-1} f\) as a reasonable estimate. High sensitivity and low dissipation amplification help maintain the SNR from the LCR loop. For instance, using a SQUID to convert the inductively coupled \(I_a(t)\) into a voltage signal is proposed in Ref. [49], and other amplifications are possible. State-of-the-art cryogenic detectors such as the HEMT have \(T_D\sim K\) noise temperature. Recent developments in interferometry techniques can further reduce the detector noise level to \(T_D \le 0.1\) K [57, 58] and are applicable in axion search [37, 59]. With sufficient amplification it is possible for the amplified JN noise to be larger than the added detector noise. Thus for a proof-of-principle analysis in this paper, we take \(T_c =1\) mK and 10  mK as benchmark scenarios and assume that the pickup circuit’s thermal noise dominates after amplification.

Assuming thermal noise dominates after amplification, the SNR for the signal with \(I_a^2\) and \(\delta I^2\) is

$$\begin{aligned} \textrm{SNR}= & {} \frac{(Q_c N_1 \Phi _a/L)^2R_s}{2 k_B T_{c}}\sqrt{\frac{t}{\Delta f}}~~,\nonumber \\= & {} \frac{Q_c ( N_1\cdot \pi R_1^2B_a)^2}{2 Lk_B T_{c}}\sqrt{Q_c \cdot 2\pi \omega _a\cdot t} \end{aligned}$$
(7)

where t is the integrated total observation time, g is the effective signal power gain from subsequent amplifiers, and we used the relation \(R_s=L\omega _a/Q_c\) at the resonance frequency. This SNR formula is similar to that of a resonant cavity haloscope in the sense of a high Q enhancement from front-end frequency filtering on the near-monochromatic signal. Note that in Eq. (7) the integrated time t is typically longer the than axion field’s coherent time-scale \(t_c=2\pi Q_c/\omega _a\approx (m_a v_a^2)^{-1}\), and the latter is from \(10^{-2}\) s up to a few minutes for \(m_a\) between \(10^{-10}\) eV and \(10^{-6}\) eV. In experiments such as ADMX [60] and ADMX-SLIC [45], data-taking is on a time-scale comparable to \(t_c\) and then repeated. The repeated \(N_{\mathrm{obs.}}=t/t_c\) times of measurement reduce the statistical uncertainty in the noise power by \(1/\sqrt{N_{\mathrm{obs.}}}\). Since the signal power \(\propto g_{a\gamma }^2\), the sensitivity of the axion-photon coupling then scales as \(g_{a\gamma }\propto (t/t_c)^{-1/4}\). Recently, dedicated detector-specific analyses [61, 62] have been performed for continuous measurement over \(t>t_c\), showing a consistent \(g_{a\gamma }\propto (t/t_c)^{-1/4}\) relation for long data-taking times [63]. Without going into detector/amplifier details, in this paper, we will consider the average signal power measurement as a sensitivity estimate.

The shaded benchmark regions in Fig. 2 demonstrate the narrow-band sensitivity in the applicable frequency range of the experimental setup. Incremental narrow-band measurements need to be performed at frequency intervals of \(\Delta f=m_a/Q\) and it typically takes time to scan a significant frequency range. For \(t>t_c\), the sensitivity scales as \(g_{a\gamma }\propto t^{-1/4}\), so that a shorter integration time at each frequency can also yield meaningful results. For instance, reducing t to 1 h will reduce the plotted sensitivities by a factor of 3.6.

Fig. 2
figure 2

Prospective single-frequency sensitivity with benchmark parameter sets listed in Table 2. The projected \(g_{a\gamma }\) sensitivities (dotted lines) assume one week of observation time at each frequency, and the maximal \(m_a\) corresponds to the axion field coherence limit that \(\lambda _\gamma > 8R_1\). The shaded regions (A, B, C) represent the applicable parameter space, rather than the frequency coverage in one single narrow-band measurement. The CAST limit (gray, top) and recent results from cavity haloscopes (vertical, right) and ADMX-SLIC (vertical, middle) are shown for comparison. The red solid line denote the theoretical predicted axion-photon coupling strength in the KSVZ model

Full size image

In Eq. (7), lowering L helps but it is related to the pickup loop’s own geometry. When the \(L_1\) coil is loosely winded, \(L\approx N_1\times R_1\left[ \ln {(8R_1/r_1)}-2\right] \) and the SNR still benefits from increasing the turn number \(N_1\) if \(L_1\) dominates the total L. We take modest numbers \(N_1=5,10\) as it is desirable to have a large \(R_1\) to maximize the pickup area. The benchmark selections of experimental parameters are given in Table 2. Demanding SNR=3 and observation time t on one frequency point, the sensitivity on the axion-photon coupling is

$$\begin{aligned} g_{a\gamma }= & {} \frac{\sqrt{{\textrm{SNR}}\cdot 2N_1L_{1,0}\cdot k_B T_c}}{(\pi R_1^3 N_1 E_0 v_a c_R\sqrt{2\rho _{\textrm{DM}}}) \root 4 \of {Q_c^3~ 2\pi \omega _a t}}, \nonumber \\\approx & {} 1.4\times 10^{-12}{\mathrm{~GeV}}^{-1} \left( \frac{R_1}{1 ~\textrm{m}}\right) ^{-3} \left( \frac{E_0}{\textrm{MV}}m^{-1} \right) \nonumber \\{} & {} \times \left( \frac{m_a}{10^{-6}~\textrm{eV}}\cdot \frac{t}{\textrm{hr}} \right) ^{-1/4}\left( \frac{N_1}{5}\right) ^{-1/2}\left( \frac{T_c}{10~\textrm{mK}}\right) ^{1/2}, \nonumber \\ \end{aligned}$$
(8)

where we take \(v_a=10^{-4}c\), \(N_1=5\), \(c_R\) interpolated from Table 1 and \(L_{1,0}\equiv L_1/N_1\sim \mu \)H which represents the inductance per turn. The sensitivity reach with benchmark parameters is illustrated in Fig. 2, where the sensitivity curves assume one week of integration time at each scanned frequency. As a narrow-band measurement, short-step frequency scanning is necessary, and resonance frequency tuning can be achieved by adjusting the capacitor’s capacitance in the LCR circuit. In practice, the measurement bandwidth at each frequency may need to balance between the dark matter’s intrinsic \(m_a\cdot Q_a^{-1}\) and the practical bandwidth of the readout system. A reasonable strategy would be choosing a frequency below the cut-off frequency, where the projected sensitivity is relatively high, then scan a neighborhood around this frequency.

Benchmark A assumes modest parameter values that can fit into conventional dilution fridges, and for \(t\sim 1\) week observation time, the sensitivity dips below the current solar axion search constraint [64] at the optimal frequency of approximately 0.2 GHz. Note that the sensitivity reach is for a single-frequency measurement, and scanning over a finite neighborhood of \(m_a\) requires spending an total observation time t at each frequency point, with intervals at \(Q_c^{-1} m_a\). Benchmark B assumes more aggressive cryogenic conditions for a multimeter cylinder and the projected sensitivity can reach \(g_{a\gamma }\sim 3\times 10^{-15}\) GeV\(^{-1}\) at \(m_a=0.1~\mu \)eV, or 19 MHz. Here we use an MVm\(^{-1}\) field strength above air’s breakdown limit as a reasonably strong E field. \(E> 30\) Vm\(^{-1}\) is achieved in modern high-voltage cavities [65, 66], and voltage tolerance can be improved with insulator coating on capacitor plates and applying high vacuum [67, 68]. Implementation under cryogenic conditions requires high-voltage R &D at the engineering level. Electric leakage in principle contributes a short noise and its shielding needs further investigation. One also needs to consider the breakdown limit of the electric-field strength in the capacitor. For semiconductors, Ref. [69] found that the breakdown field strength of ultrathin atomic-layers is approximately 30 MV/cm, and the leakage current density between GaAs and Au is low, approximately \(10^{-10}\)A/cm\(^2\), which should not be a concern if we consider a modest vacuum level. For instance, the electrical breakdown of silver/silver-nickel alloy in a 1.4\(^{-4}\) Pa vacuum is approximately 2-4\(\times 10^{9}\) V/m with a negligible leakage current [70]. Other high-voltage designs for low-mass scalar-type dark matter [71] and axion-monopole search [72] have been proposed recently.

Benchmark C shows that an electric field strength in the order of GVm\(^{-1}\) would be required to touch down to the theoretical prediction for the (KSVZ) QCD axion. While a GVm\(^{-1}\) E-field could still be sustained by strong and transparent insulation material (such as diamond), achieving such a colossal voltage over a large distance is a challenge to high-voltage engineering, and here it is only shown for illustrative purposes. As shown in Eq. (8), the sensitivity improves toward larger \(m_a\), but it has its coherence limit: the diameter of the electrified cylinder should not exceed the half-wavelength of the induced electromagnetic wave \(\lambda _\gamma =m_a^{-1}/2\), or \(8R_1> \lambda _a\).

Table 2 Benchmark setups. Common parameters include \(Q_c\sim 10^6\), \(\rho _{\textrm{DM}}=0.4\) GeV cm\(^{-3}\), and pickup wire radius \(r_1=1\) cm. The corresponding \(g_{a\gamma }\) sensitivity is shown in  Fig. 2
Full size table

As shown in Eq. (8), increasing the cylinder size and/or the electric field strength is efficient for improving the \(g_{a\gamma }\) sensitivity. This corresponds to a stronger induced \(\vec {B}_a\) field. Improvements from more pickup coil turns, lowering the noise temperature and a longer observation time are less effective. The \(g_{a\gamma }\) limit scales with the quality factor as \(Q^{-3/4}\), which shows the necessity of exploiting the dark matter’s coherence via proper frequency filtering.

4 Summary and discussion

In this paper we explore the concept of a narrow-band axionic dark matter detection scheme with a strong laboratory static electric field as the \(a\rightarrow \gamma \) converting medium. The geometry of a cylindrical capacitor allows the axion-induced effective current to form a solenoid pattern and yield a concentrated magnetic field signal in the inner region of the capacitor. As axion-photon conversion is suppressed by axion velocity under a static electric field, we adopt a narrow band approach to enhance signal detection. Working at relatively long wavelengths, an LC resonance offers front-end high Q-factor frequency filtering, which can be matched to the dark matter field’s energy dispersion. The high Q-factor allows the signal to build up in the LCR circuit that effectively enhances the signal strength, and can be probed by cryogenic amplifiers and detectors with high sensitivity.

We propose three benchmark scenarios, and demonstrate that a submeter capacitor scheme with mainstream cryogenic technology is sensitive to \(g_{a\gamma }\sim 10^{-12}\) GeV\(^{-1}\). For a multimeter cylindrical capacitor and mK-level noise temperature, the projected sensitivity can be further improved to the \(10^{-15}\) GeV\(^{-1}\) scale with 10 MVm\(^{-1}\) static E field strength. The theoretical QCD axion prediction requires a high field \(E\sim \mathcal{O}(10^9)\) Vm\(^{-1}\) setup that involves further R &D on implementing high dielectric materials.

In addition to avoiding magnetic fluctuations, the absence of a strong magnetic field allows the pickup coils to use superconductor materials as an option to reduce the LCR circuit’s resistance, and in principle low-resistance material needs to be used when \(\omega L/Q\) is small. For thermal noise control, only the circuit parts with resistance need to be restricted to the lowest (\(\sim \)mK) temperature. Given the meter-scale size of the cylinder, this reduces the overall cooling requirement of the system.

Due to the direction dependence in the effective \(\vec {j}_a=-g_{a\gamma }a\vec {E}\times {\vec {k}}_a\), the signal strength with a static electric field is modulated by both the axion field periodicity and apparatus orientation. Adjustment of capacitor direction, as well as daily modulation, can be used as an additional method of differentiation of the axion-induced signal from the system’s own systematics.