Analysis of exponential corrected thermodynamic geometries in $AdS_5\times S^5$ black hole

Abstract

This paper delves the thermodynamics of 5-dimensional Schwarzschild $AdS_5 \times S^5$ black hole by considering the recently proposed effective models of exponential entropies. The conventional understanding of cosmological constant $\Lambda$ as thermodynamic pressure with volume being its counterpart cannot be directly applied in the framework of the AdS/CFT correspondence. In order to resolve this issue, we establish a connection between the cosmological constant $\Lambda$ in the boundary gauge theory and number of colors N while chemical potential is considered as thermodynamic conjugate. In this study, we replace the geometric parameters L and r of the AdS black hole with two thermodynamic parameters $N^2$ and S in the micro-canonical ensemble. Additionally, we explore the various thermodynamic geometry models such as Ruppeiner, Quevedo and Weinhold to derive the associated scalar curvatures for the 5-D Schwarzschild AdS BH. We analyze that these geometries exhibit microscopic attraction/repulsion forces on the particles of black hole.

1 Introduction

The Bekenstein–Hawking entropy, named after physicists Jacob Bekenstein and Stephen Hawking, constitutes a pivotal bridge between classical general relativity and quantum mechanics. Bekenstein’s ground-breaking insight in the early 1970s proposed that black holes (BHs) possess an intrinsic entropy, a measure of microscopic disorder associated with the BH’s horizon area. This revolutionary idea challenged the classical view and hinted at a deeper connection between BHs and the statistical behavior of particles. The subsequent work of Stephen Hawking in the mid-1970s further transformed our understanding of BHs. Hawking demonstrated that due to quantum effects near the event horizon, BHs are not truly black - they emit a faint radiation now known as “Hawking radiation.” This radiation, which carries away energy and reduces the mass of the BH over time, implies that black holes have a temperature and a corresponding entropy linked to their surface area. The expression for the entropy of BH is given by [1,2,3,4,5,6,7,8]

$$\begin{aligned} S_{BH}=\frac{c^3 k_B A_H}{4 G \hbar }, \end{aligned}$$

where c is speed of light, G is Newton’s constant, $k_B$ is Boltzmann constant, $\hbar$ is Planck’s constant and $A_H$ is area of event horizon. Bekenstein–Hawking entropy $S_{BH}$ serves essentially the same purpose in BH physics as it does in conventional thermodynamics. In particular, it enables one to determine how much of a BH’s internal energy may be converted into work. This formula is a purely classical result and does not account for quantum effects. However, when considering the principles of quantum mechanics, such as the quantization of energy levels and the nature of microstates, physicists have speculated that there could be quantum corrections to this formula. Exponential corrections to BH entropy might arise as a result of quantum gravitational effects, which are expected to become important at extremely small length scales near the Planck scale. These corrections could modify the form of the entropy formula to include exponential terms that depend on the area of the event horizon. These corrections are generally anticipated to become relevant in the context of a full theory of quantum gravity, which is currently a topic of active research and remains largely speculative. Chatterjee and Ghosh [9] worked on the exponential corrections to BH entropy. They have shown that the area spectrum of a BH horizon must be discrete and independent of any specific quantum theory of gravity. Recently in the remarkable works of Nojiri et al. [10, 11] they proposed a novel entropy framework that generalizes the Tsallis, R$\acute{\textrm{e}}$nyi, Sharma-Mittal, Barrow, Kaniadakis, and loop quantum gravity (LQG) entropies and in a specific limit, it converges to the Bekenstein–Hawking entropy. That model is given by

$$\begin{aligned} S_{G}(\alpha _\pm ,~ \beta _\pm ,~ \gamma _{\pm })= & {} \frac{1}{\alpha _{+}+\alpha _{-}}\bigg [\bigg (1+\frac{\alpha _{+}}{\beta _{+}}S^{\gamma _{+}}\bigg )^{\beta _{+}}\\{} & {} -\bigg (1+\frac{\alpha _{-}}{\beta _{-}}S^{\gamma _{-}}\bigg )^{-\beta _{-}}\bigg ], \end{aligned}$$

where all $(\alpha _\pm ,~ \beta _\pm ,~ \gamma _{\pm })$ are positive. Setting $\alpha _{+}=\alpha _{-}\rightarrow 0$, $\gamma _{+}= \gamma _{-}=\gamma$ and further for $\gamma =\delta$ or $\gamma =1+\frac{\Delta }{2}$, the generalized entropy turns to Tsallis or Barrow entropy respectively. For $\alpha _{-}=0$, $\alpha _{+}=R$, $\beta _{+}=\frac{R}{\delta }$ and $\gamma _{+}=\delta$, it yields Sharma-Mittal entropy. For $\alpha _{-}=0$, $\alpha _{+}\rightarrow 0$ simultaneously with $\beta _{+}\rightarrow 0$ keeping $\alpha \equiv \frac{\alpha _{+}}{\beta _{+}}$ finite and considering $\gamma _{+}=1$ produces R$\acute{\textrm{e}}$nyi entropy. Moreover, $\beta _\pm ,\rightarrow 0,~\gamma _{\pm }=1$ and $\alpha _\pm =K$ give Kaniadakis entropy. Finally $\alpha _{-}=0$, $\gamma _{+}=1$ and in addition limit $\beta _{+}\rightarrow +\infty$ in conjunction with $\alpha =1-q$ yields

$$\begin{aligned} S_{G}=\frac{1}{1-q}\bigg (e^{(1-q)S}-1\bigg ), \end{aligned}$$

which is LQG entropy and it reduces to the Bekenstein–Hawking entropy for $q\rightarrow 1$. This particular case of the generalized entropy also have exponential term but this entropy is different from the above discussed exponential entropy. The focus of our current research is to investigate the implications of these exponential entropy models on the thermodynamic quantities and thermodynamic geometries of BHs. It is important to highlight that while we are exploring these exponential entropy models in the present study, we anticipate that utilizing the generalized entropy model (proposed by Nojiri et al.) may help us understand the structure of quantum gravity and it will be of significant interest in upcoming research endeavors.

The BH physics can be explained in two complementary ways, one using thermodynamics and the other using only space-time geometry. The two descriptions are connected to one another by the BH thermodynamics “first law” which is $dM = TdS +\phi _H dQ +\Omega _H dJ$, where M is the total mass, S is entropy, T is the Hawking temperature, $\phi _H$ is the Coulomb potential on horizon, $\Omega _H$ is the angular velocity, Q is the electric charge, and J is angular momentum [13]. BHs in de Sitter (dS) or asymptotically flat space differ significantly from BHs in AdS space in terms of their thermodynamic properties. The cosmological constant $\Lambda$ is a realistic option for BHs in the Anti de Sitter (AdS) background [14,15,16,17,18,19,20]. In dual conformal field theory(CFT), the degrees of freedom N is treated as a negative cosmological constant $\Lambda$ in relationship between AdS and CFT. Cosmological constant is considered as the varying number of colors of the dual CFT and its conjugate can be associated to chemical potential $\mu$ with finite temperature $N=4$ of the super conformal Yang Mills theory and large N in case of $AdS_5\times S^5$. In Yang Mills theory, $\mu$ is negative in high temperature phase and it decreases when the temperature increases [21,22,23].

Numerous researchers have developed new methods to investigate phase transitions in classical thermodynamical systems by utilizing geometrical ideas. As BH is assumed to be thermodynamic system therefore it is natural to investigate its thermodynamic geometries. It has been revealed that the thermodynamic geometry of BH has structure that can be used to draw scientific conclusions [24]. Weinhold has proved two Reimannian structures that define the notion of length for fluctuations in thermodynamic processes via equilibrium states [25]. Furthermore, Quevedo has showed that metrics are not invariant under Legendre transformation and this problem can be solved through geometrothermodynamics method. Using this method, we can interpret thermodynamics both at phase space and at equilibrium state. This thermodynamical geometry technique was used to study phase transitions of BHs [26,27,28,29,30].

The paper is organized as follow: In Sect. 2, we provide thermal stability of Schwarzschild $AdS_5\times S^5$ BH through exponential corrected entropy. In Sect. 3, we obtain scalar curvature of the considered BH by using Ruppeiner, Quevedo and Weinhold geometries. In Sect. 3, we summarize our results in conclusion.

2 Thermal stability of Schwarzschild $AdS_5\times S^5$ black hole with exponential entropy

The concept of entropy plays a crucial role in understanding the thermodynamics of BHs. In the context of BHs, entropy is closely linked to the idea that these enigmatic objects exhibit thermodynamic properties analogous to those of ordinary physical systems, such as gases and liquids. This connection was famously established by Bekenstein–Hawking’s ground-breaking work on entropy $S_{BH}= \frac{A}{4G}$ and the subsequent development of BH thermodynamics [7]. As it is well-known that the entropy of large BHs, when compared to the Planck scale, is directly proportional to the area of their event horizon. Additionally, the BH size decreases due to Hawking radiation, necessitating corrections to the entropy of small BHs. Exploring the microscopic origins of entropy constitutes a significant focus within the field of quantum BH physics. There is a general expectation that any quantum theory concerning BHs should provide an explanation for the Bekenstein–Hawking area law governing entropy. Both string theory and LQG engage in microstate counting and not only reproduce the Bekenstein–Hawking area law but also introduce corrections to it, expressed as an expansion involving $\frac{l_{p}^{2}}{A}$. These corrections, which include a logarithmic term, become relevant for horizons with areas significantly larger than $l_{p}^{2}$. If we consider a BH composed of a total of N particles, we can calculate the overall microstates to determine its entropy. According to statistical mechanics, the total number of microstates for a specific system can be expressed as follows

$$\begin{aligned} \Omega =\frac{(\Sigma n_{i})!}{\Pi n_{i}!}. \end{aligned}$$

(1)

Assuming that each number $n_{i}$ is distributed among $s_{i}$ pieces, thus,

$$\begin{aligned} \Omega =\frac{(\Sigma s_{i})!}{\Pi s_{i}!}. \end{aligned}$$

(2)

Additionally, $\varepsilon _{i}$ represents the energy associated with the microstate numbered $n_{i}$. Consequently, $N=\Sigma s_{i}n_{i}$ is total number and $E=\Sigma s_{i}n_{i}\varepsilon _{i}$ is the overall energy. Employing the Stirling formula for the case of a large N limit

$$\begin{aligned} \ln N!=N\ln N-N, \end{aligned}$$

(3)

and varying $\ln \Omega$ subject to the following conditions

$$\begin{aligned} \delta \Sigma s_{i}n_{i}= & {} 0,\end{aligned}$$

(4)

$$\begin{aligned} \Sigma \varepsilon _{i}\delta (s_{i}n_{i})= & {} 0. \end{aligned}$$

(5)

We can acquire the configuration most likely to occur as

$$\begin{aligned} s_{i}=\bigg (\Sigma n_{i}\bigg )e^{-\lambda n_{i}}, \end{aligned}$$

(6)

where $\lambda$ is referred to the variation parameter and serving as Lagrange multipliers adheres to the following condition

$$\begin{aligned} \Sigma e^{-\lambda n_{i}}=1, \end{aligned}$$

(7)

which provides

$$\begin{aligned} \lambda \simeq \ln 2-2^{N}, \end{aligned}$$

(8)

and $O(2^{-2N})$ is being neglected. So, the entropy is given by $S_{e} = \lambda N$, substituting N yields the exponential correction to Bekenstein–Hawking entropy as follows [9, 31]

$$\begin{aligned} S_e=\frac{A\ln 2}{8\pi \gamma l_p^2}+e^{A\ln 2/8\pi \gamma l_p^2}, \end{aligned}$$

(9)

where A is the horizon area, $l_p$ is the Planck length and $\gamma$ is constant. The exponential entropy turns into the leading order Bekenstein–Hawking entropy for $\gamma =\frac{\ln 2}{2\pi }$. The Bekenstein Hawking entropy can be express in terms of exponential corrected entropy as follows

$$\begin{aligned} S_{BH}=\sqrt{2(S_e - 1)}. \end{aligned}$$

(10)

The five-dimensional Schwarzschild BH metric is an extension of the well-known four-dimensional Schwarzschild metric, which describes a non-rotating and uncharged BH. The fundamental illustration of asymptotically AdS BH is the Schwarzschild AdS solution which is defined as

$$\begin{aligned} ds^2=-g(r)dt^2+g(r)^{-1}dr^2+r^2d\Omega _3, \end{aligned}$$

(11)

where g(r) is the metric function which is given by [32]

$$\begin{aligned} g(r)=k-\frac{8G_5M}{3\pi r^2}+\frac{r^2}{L^2}. \end{aligned}$$

(12)

Here $L={(\frac{\sqrt{2} N l_p^4}{\pi ^2})}^{\frac{1}{4}}$ is radius of AdS space time with $\Lambda = \frac{-6}{L^2},~G_5 =\frac{l_p^8}{\pi ^3\,L^5},~k=0,\pm 1$ is the scalar curvature and M represents mass of BH [33]. Another alternative to Bekenstein Hawking entropy of BH is given as [34]

$$\begin{aligned} S_{BH}=\frac{\pi ^2 r^3}{2G_{(5)}} = \frac{\pi ^5 L^5 r^3}{2l_p^8}. \end{aligned}$$

(13)

Using Eqs. (10) and (13), the expression for the exponential entropy takes the form

$$\begin{aligned} S_e=\frac{1}{2}{\left( \frac{\pi ^5 L^5 r^3}{2l_p^8}\right) }^2 +1. \end{aligned}$$

(14)

Setting $g(r)=0$ in Eq. (12), the mass of five-dimensional Schwarzschild AdS BH becomes

$$\begin{aligned} M=\frac{3\pi ^4 r^2 L^3(kL^2+r^2)}{8l_p^8}. \end{aligned}$$

(15)

Solving the horizon radius in terms of exponential entropy and using the above equation, one can rewrite the mass of BH in terms of $S_e$ and N as follows

$$\begin{aligned} M(S_e,N)= \frac{3 \left( 2^{\frac{7}{8}} (S_e-1)^{\frac{2}{3}} l_{p}^{\frac{5}{3}} + 2^{\frac{3}{8}} k \pi ^{\frac{4}{3}} (S_e-1)^{\frac{1}{3}} l_p^{\frac{1}{3}} N \right) }{4 \pi ^{\frac{4}{3}} N^{\frac{1}{4}}}. \end{aligned}$$

(16)

The relation for the Hawking temperature for the considered BH by using $T=\frac{\partial M}{\partial S_e}\bigg |_N$ turns out to be

$$\begin{aligned} T(S_e,N)= \frac{2^{\frac{7}{8}} (S_e-1)^{\frac{1}{3}} l_p^{\frac{5}{3}} + 2^{\frac{3}{8}} k \pi ^{\frac{4}{3}} l_p^{\frac{1}{3}} N}{2 \pi ^{\frac{4}{3}} N^{\frac{1}{4}} (S_e-1)^{\frac{2}{3}}}. \end{aligned}$$

(17)

Fig. 1

Plots of Hawking temperature T versus exponential corrected entropy $S_e$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

In Fig. 1 the relationship between T and exponential entropy ($S_e$) is shown. It can be seen that for $k=0$ and $k=1$, T is monastically decreasing as $S_e$ increases, which leads to stable behavior of BHs. For $k=-1$, T is increasing as $S_e$ increases, which leads to unstable behavior of BH.

The Gibbs free energy is a key state function which plays vital role to determine the global stability of the BH. It can be determined by using $G= M-TS$, the relation for Gibbs free energy for the five-dimensional Schwarzschild AdS BH takes the following form

$$\begin{aligned} G=-\frac{A}{B}, \end{aligned}$$

(18)

where

$$\begin{aligned} A= & {} a_1 N^{\frac{3}{4}}\Bigg ( \frac{2 a_2 N^{-\frac{1}{2}} + \sqrt{4 a_2^{2} N + 12 T a_1 N^{\frac{3}{2}}}}{3 T}-1\Bigg ) \\{} & {} + a_2N^{-\frac{1}{4}}\Bigg (\Bigg (2 a_2 N^{-\frac{1}{2}} \\{} & {} + \sqrt{4 a_2^{2} N + 12 T a_1 N^{\frac{3}{2}}}\Bigg )(6 T)^{-1}\Bigg )^4\\{} & {} - a_2 N^{-\frac{1}{4}}\Bigg (\frac{2 a_2 N^{-\frac{1}{2}} + \sqrt{4 a_2^{2} N + 12 T a_1 N^{\frac{3}{2}}}}{3 T}\Bigg ), \end{aligned}$$

and $B=3 \left( \frac{2 a_2 N^{-\frac{1}{2}} + \sqrt{4 a_2^{2} N + 12 T a_1 N^{\frac{3}{2}}}}{6 T}\right) ^2$ with $a_1=\frac{3 k l_p^{\frac{1}{3}}}{2^{\frac{13}{8}}}$ and $a_2=\frac{3 l_p^{\frac{5}{3}}}{2^{\frac{9}{8}} \pi ^{\frac{4}{3}}}$ are the constant values. Figure 2 manifests the relationship between Gibbs free energy G versus Hawking temperature T of Schwarzschild AdS BH. The positive and negative behavior of G yields global stability and instability respectively and it is given as

• For $k=0$, $\left\{ \begin{array}{ll} G>0~~in ~~ T=[0, 0.2], &{} \hbox {} \\ G<0~~in ~~T>0.24. &{} \hbox {} \end{array} \right.$

• For $k=1$, $\left\{ \begin{array}{ll} G>0~~in ~~T=[0, 3],&{}\\ \qquad G<0~~in ~~T>3, &{} \hbox {when}~~N =2, \\ G>0~~in ~~T=[0, 5.7],&{}\\ \qquad G<0~~in ~~T>5.7, &{} \hbox {when}~~N =3, \\ G>0~~in ~~T=[0, 9],&{}\\ \qquad G<0~~in ~~T>9, &{} \hbox {when}~~N =4. \end{array} \right.$

• For $k=-1$, $\left\{ \begin{array}{ll} G>0~~in ~~T<0.02, &{} \hbox {when}~~N =2, \\ G>0~~in ~~T<0.017, &{} \hbox {when}~~N =3, \\ G>0~~in ~~T<0.015, &{} \hbox {when}~~N =4. \end{array} \right.$

One can analyze that the global stability of the BH increases with high values of N. During chemical reaction or phase transition energy can be absorbed or released which leads to the change in mass of the BH. In BH thermodynamics, the change in energy is known as chemical potential ($\mu$) which can be computed as

$$\begin{aligned} \mu= & {} \frac{\partial M}{\partial N^2} \bigg |_{S_e},\nonumber \\ \mu= & {} \frac{3 (S_e-1)^{\frac{1}{3}} l_p^{\frac{1}{3}}}{16 2^{\frac{5}{8}} N^{\frac{9}{4}}} \Bigg (3 k \sqrt{N} - \frac{\sqrt{2} (S_e-1)^{\frac{1}{3}} l_p^{\frac{4}{3}}}{\pi ^{\frac{4}{3}}}\Bigg ). \end{aligned}$$

(19)

Fig. 2

Plots of Gibbs free energy G versus Hawking temperature T of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Fig. 3

Plots of chemical potential $\mu$ versus exponential corrected entropy $S_{e}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 3 shows the relationship between chemical potential $\mu$ and $S_e$. The results for this analysis are concluded as

• For $k=0$, $\mu <0$ when $S_e>1$.

• For $k=1$, $\mu >0$ when $S_e>1$.

• For $k=-1$, $\mu <0$ when $S_e>1$.

The region where $\mu <0$ represents stable branch of BH while its positive values leads to unstable branch of BH. From above conclusion, it can be observed that BH (corresponding to $k=0,~-1$) remains stable while BH (corresponding to $k=1$) shows unstable behavior. Another important thermodynamic quantity is specific heat which investigates the thermal stability of BH and determines the phase transition point [35]. The BH’s specific heat for fixed $N^2$ can be obtained as

$$\begin{aligned} C_{N^2}= & {} T \left( \frac{\partial S_e}{\partial T} \right) _{N^2} \nonumber \\= & {} -\frac{6\sqrt{2}l_{p}^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}+3k\pi ^{\frac{4}{3}}N}{(S_e-1)^{\frac{1}{3}}\left( 2^{\frac{3}{2}}(S_e-1)^{\frac{1}{3}}l_P^{\frac{4}{3}}+2k\pi ^{\frac{4}{3}}N \right) }. \end{aligned}$$

(20)

Fig. 4

Plots of specific heat $C_{N^2}$ versus exponential corrected entropy $S_{e}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 4 shows the relationship between specific heat $C_{N^2}$ versus exponential corrected entropy $S_e$. The results for the local stability of the BH are summarized as follow

• For $k=0$, $C_{N^2}<0$ when $S_e>1$.

• For $k=1$, $C_{N^2}<0$ when $S_e>1$.

• For $k=-1$, $C_{N^2}<0$ when $S_e>1$.

One can observed that for all the cases ($k=0,~-1,~1$), the specific heat $C_{N^2}$ remains negative which shows the instability of the BH. In order to conform our analysis, we find out the system’s specific heat for fixed $\mu$ which is given by

$$\begin{aligned} C_{\mu }= & {} \left( \frac{\partial \phi }{\partial T} \right) _{\mu }\nonumber \\= & {} -\frac{9N^{\frac{1}{4}}\left( 18\sqrt{2}(S_e-1)^{\frac{1}{3}}l_{p}^{\frac{4}{3}}+5k\pi ^{\frac{4}{3}}N\right) }{32\sqrt{2}(S_e-1)^{\frac{4}{3}}l_{P}^{\frac{4}{3}}N^{\frac{1}{4}}+48kN^{\frac{1}{4}} \pi ^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}N}.\nonumber \\ \end{aligned}$$

(21)

Fig. 5

Plots of specific heat $C_{\mu }$ versus exponential corrected entropy $S_{e}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 5, shows the relationship between $C_{\mu }$ and $S_e$ which is given as

• For $k=0$, $C_{\mu }<0$ when $S_e>1.3$.

• For $k=1$, $C_{\mu }<0$ when $S_e>1.4$ for $N=2$ and $C_{\mu }<0$ when $S_e>1.3$ for $N=3$ and $N=4$.

• For $k=-1$; $C_{\mu }<0$ when $S_e=[1.2,6.6]$, $C_{\mu }=0$ when $S_e=[6.7,7.0]$ and $C_{\mu }>0$ when $S_e>7$ for $N=2$. $C_{\mu }<0$ when $S_e>1.2$ for $N=3$ and $N=4$.

This analysis confirm our findings that Schwarzschild AdS BH is unstable.

2.1 Exponential form of q-entropy

In this subsection, we consider exponential form of q-entropy in non-extensive loop quantum gravity which posses four properties like generalized third law, monotonicity, positivity and Bekenstein–Hawking limit which are mainly required for any alternative entropy proposal. The mathematical expression for this important model of entropy is given by [36]

$$\begin{aligned} S_q=\frac{1}{1-q} [e^{(1-q)\Lambda (\gamma _0) S_{BH}}-1], \end{aligned}$$

(22)

where q is the entropic index, $\Lambda (\gamma _0)=\frac{\ln {(2)}}{\sqrt{2} \pi \gamma _0}$ where $\gamma _0$ is the Barbero–Immirzi parameter. The Bekenstein entropy from the above equation can be obtained as

$$\begin{aligned} S_{BH}= \frac{\sqrt{3} \pi \gamma _0}{(1-q) \ln {(2)}} \ln {|(1-q)S_q +1|}. \end{aligned}$$

(23)

Using Eq. 15, the mass of BH by taking taking $l_p=1$ can be rewritten as

$$\begin{aligned} M(S_q,N)= & {} \frac{3^{\frac{4}{3}} \sqrt{\pi } \gamma ^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{2}{3}}}{4~2^{\frac{1}{8}} (1-q)^{\frac{4}{3}} \ln {(2)}^{\frac{4}{3}} N^{\frac{11}{12}}}\nonumber \\{} & {} \times \left( 3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}\right. \nonumber \\{} & {} \left. + k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}} N^{\frac{4}{3}}\right) . \end{aligned}$$

(24)

The Hawking temperature in terms of q-entropy turns out to be

$$\begin{aligned}{} & {} T(S_q,N)=\frac{3^{\frac{1}{3}} \sqrt{\pi } \gamma ^{\frac{2}{3}}(2 3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}+k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}} N^{\frac{4}{3}})}{2^{\frac{9}{8}} (1-q)^{\frac{1}{3}} ((1-q) S_q+1) \ln {(2)}^{\frac{4}{3}} \ln {|(1-q)S_q+1|}^{\frac{1}{3}} N^{\frac{11}{12}}}. \end{aligned}$$

(25)

Fig. 6

Plots of temperature T versus q-entropy $S_{q}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 6 manifests the graph of Hawking temperature T versus exponential form of q-entropy ($S_q$). The results for the plots are given by

• For $k=0$, T increases as entropy $S_q$ increases.

• For $k=1$, the minimal Hawking temperature is

  $T\approx 6.3$ occurs at $S_q\approx 0.09$ when $N=2$,

  $T\approx 6.4$ at $S_q\approx 0.17$ when $N=3$ and

  $T\approx 6.7$ at $S_q\approx 0.15$ when $N=4$.

• For $k=-1$;

  $T<0$ when $S_q=(0,0.4)$, $T=0$ when $S_q=0.4$ and $T>0$ when $S_q= (0.4,0.8)$ for $N=2$.

  $T<0$ when $S_q=(0,0.7)$, $T=0$ when $S_q=0.7$ and $T>0$ when $S_q= (0.7,0.92)$ for $N=3$.

  $T<0$ when $S_q=(0,0.8)$, $T=0$ when $S_q=0.8$ and $T>0$ when $S_q= (0.8,0.96)$ for $N=4$.

We can analyze that temperature is monotonically increasing for $S_q$ ($k=0, -1$) which shows the unstable behavior of BH while for $k=1$ there exist minimal Hawking temperature and BH does not exist below the minimal temperature. Above this temperature there are two branches unstable and stable branch. Unstable branch exists for small values of $S_q$ and stable branch exist for large values of $S_q$. The relation for Gibbs free energy in terms of q-entropy turns out to be

$$\begin{aligned} G(S_q,N^2)= \frac{A}{B}, \end{aligned}$$

(26)

where

$$\begin{aligned} A= & {} 3^{\frac{1}{3}} \sqrt{\pi } \gamma ^{\frac{2}{3}} (4~3^{\frac{1}{3}}(q-1) S_q \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}\\{} & {} +3^{\frac{4}{3}}((q-1)S_q+1)\gamma ^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{5}{3}}\\{} & {} +2 k (1-q)^{\frac{5}{3}} S_q \ln {2}^{\frac{2}{3}}(N)^{\frac{4}{3}}-3 k(1-q)^{\frac{2}{3}}\\{} & {} ((1-q)S_q+1) \ln {(2)}^{\frac{2}{3}} \ln {|(1-q)S_q+1|} N^{\frac{4}{3}}), \end{aligned}$$

and

$$\begin{aligned} B= & {} 4~2^{\frac{1}{8}}(1-q)^{\frac{4}{3}} ((q-1)S_q-1) \ln {(2)}^{\frac{4}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{1}{3}} N^{\frac{11}{12}}. \end{aligned}$$

Fig. 7

Plots of Gibbs free energy G versus q-entropy $S_{q}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 7 shows the plot of Gibbs free energy versus $S_q$. The Gibbs free energy of Schwarzschild AdS BH remains negative for all cases which exhibits the unstable behavior of BHs. The chemical potential of Schwarzschild AdS BH in the form q-entropy becomes

$$\begin{aligned} \mu= & {} \frac{3^{\frac{1}{3}}\sqrt{\pi } \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}}{32~2^{\frac{1}{8}} (1-q)^{\frac{4}{3}} \ln {(2)}^{\frac{4}{3}} N^{\frac{35}{24}}}\nonumber \\{} & {} \times \left[ 5 k(1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}}N^{\frac{2}{3}}\right. \nonumber \\{} & {} \left. -11~3^{\frac{1}{3}}\gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}\right] . \end{aligned}$$

(27)

Fig. 8

Plots of chemical potential $\mu$ versus q-entropy $S_{q}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Figure 8 shows the plot of $\mu$ versus $S_q$ of Schwarzschild AdS BH. The results are summarized as follow

• For $k=0$,

  $\mu <0$ in $S_q=[0,0.83]$ for $N=2$,

  $\mu <0$ in $S_q=[0,0.99]$ for $N=3$, and

  $\mu <0$ in $S_q=[0,1]$ for $N=4$.

• For $k=1$,

  $\mu >0$ in $S_q=[0,0.39)$, $\mu =0$ in $S_q=0.39$, $\mu <0$ in $S_q=(0.39,0.78]$ for $N=2$,

  $\mu >0$ in $S_q=[0,0.65)$, $\mu =0$ in $S_q=0.65$, $\mu <0$ in $S_q=(0.65,0.97]$ for $N=3$, and

  $\mu >0$ in $S_q=[0,0.84)$, $\mu =0$ in $S_q=0.84$, $\mu <0$ in $S_q=(0.84,1]$ for $N=4$.

• For $k=-1$,

  $\mu <0$ in $S_q=[0,0.86]$ for $N=2$,

  $\mu <0$ in $S_q=[0,0.99]$ for $N=3$, and

  $\mu <0$ in $S_q=[0,1]$ for $N=4$.

The positive behavior of $\mu$ shows that BH is in unstable branch while the negative behavior of chemical potential shows that BH is in stable branch. The specific heat of Schwarzschild AdS BH by considering the q-entropy takes the following form

$$\begin{aligned} C_{N^2}= \frac{A}{B}, \end{aligned}$$

(28)

where

$$\begin{aligned} A= & {} 3 ((1-q) S_q+1) \ln {|(1-q)S_q+1|}~\Bigg [2~3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}\\{} & {} + k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}} N^{\frac{2}{3}}\Bigg ], \\ B= & {} (1-q)(2 \ln {|(1-q)S_q+1|}^{\frac{2}{3}} (-1+3^{\frac{4}{3}} \gamma ^{\frac{2}{3}} \\{} & {} \ln {|(1-q)S_q+1|})\\{} & {} + k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}} (1+3 \ln {|(1-q)S_q+1|}) N^{\frac{2}{3}}). \end{aligned}$$

Fig. 9

Plots of specific heat $C_{N^2}$ versus q-entropy $S_{q}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Fig. 10

Plots of specific heat $C_{\mu }$ versus q-entropy $S_{q}$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

The plots of specific heat versus $S_q$ are shown in Fig. 9, the results are summarized as follow

• For $k=0$, $C_{N^2}<0$.

• For $k=1$,

  $C_{N^2}>0$ in $S_q=[0,0.11]$ and $C_{N^2}<0$ in $S_q=[0.19,1]$ when $N=2$,

  $C_{N^2}>0$ in $S_q=[0,0.13]$ and $C_{N^2}<0$ in $S_q=[0.23,1]$ when $N=3$ and

  $C_{N^2}>0$ in $S_q=[0,0.15]$ and $C_{N^2}<0$ in $S_q=[0.26,1]$ when $N=4$,

• For $k=-1$,

  $C_{N^2}>0$ in $S_q=[0,0.41)$, $C_{N^2}=0$ in $S_q=0.41$ and $C_{N^2}<0$ in $S_q=(0.41,1]$ when $N=2$,

  $C_{N^2}>0$ in $S_q=[0,0.70)$, $C_{N^2}=0$ in $S_q=0.70$ and $C_{N^2}<0$ in $S_q=(0.70,1]$ when $N=3$ and

  $C_{N^2}>0$ in $S_q=[0,0.88)$, $C_{N^2}=0$ in $S_q=0.88$ and $C_{N^2}<0$ in $S_q=(0.88,1]$ when $N=4$.

The positive value of specific heat shows stability and negative value shows instability of BH. Finally, the specific heat for fixed chemical potential turns out to be

$$\begin{aligned} C_{\mu }= \frac{A}{B}, \end{aligned}$$

(29)

where

$$\begin{aligned} A= & {} ((1-q) S_q+1) \ln {|(1-q)S_q+1|}~(70~3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}\\{} & {} + 19 k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}} N^{\frac{2}{3}}), \\ B= & {} 8 (1-q)~(2 \ln {|(1-q)S_q+1|}^{\frac{2}{3}} ~(-1+ 3^{\frac{4}{3}} \gamma ^{\frac{2}{3}} \\{} & {} \ln {|(1-q)S_q+1|})\\{} & {} + k (1-q)^{\frac{2}{3}} \ln 2^{\frac{2}{3}}(1+3\ln {|(1-q)S_q+1|}) N^{\frac{2}{3}}). \end{aligned}$$

The plots of specific heat versus $S_q$ for fixed $\mu$ are shown in Fig. 10, the results are summarized as

• For $k=0$, $C_{\mu }<0$.

• For $k=1$,

  $C_{\mu }>0$ in $S_q=[0,0.11]$ and $C_{\mu }<0$ in $S_q=[0.19,1]$ when $N=2$,

  $C_{\mu }>0$ in $S_q=[0,0.13]$ and $C_{\mu }<0$ in $S_q=[0.23,1]$ when $N=3$ and

  $C_{\mu }>0$ in $S_q=[0,0.15]$ and $C_{\mu }<0$ in $S_q=[0.26,1]$ when $N=4$,

• For $k=-1$,

  $C_{\mu }>0$ in $S_q=[0,0.19)$, $C_{\mu }=0$ in $S_q=0.19$ and $C_{\mu }<0$ in $S_q=(0.19,1]$ when $N=2$,

  $C_{\mu }>0$ in $S_q=[0,0.39)$, $C_{\mu }=0$ in $S_q=0.39$ and $C_{\mu }<0$ in $S_q=(0.39,1]$ when $N=3$ and

  $C_{\mu }>0$ in $S_q=[0,0.59)$, $C_{\mu }=0$ in $S_q=0.59$ and $C_{\mu }<0$ in $S_q=(0.59,1]$ when $N=4$.

It can be concluded from the above analysis that BH show stable behavior for $k=0$.

3 Thermodynamic geometries of Schwarzschild $AdS_5\times S^5$ black hole

The term thermodynamic geometries refers to a theoretical framework that connects the thermodynamic properties of BHs to geometric concepts. In particular, it involves the study of BH thermodynamics using tools from differential geometry and topology. This approach seeks to establish analogies between the laws of thermodynamics and properties of BHs, leading to insights about the fundamental nature of BHs and the universe. The study of thermodynamic geometries has crucial role when examining the behavior and properties of BHs during phase transitions. In this section, we consider well known model like Weinhold, Ruppeiner and Quevedo geometries to explore the thermodynamic properties of BHs.

3.1 Weinhold geometry

Weinhold geometry is a concept developed in the field of thermodynamics of the BHs. In traditional thermodynamics, a thermodynamic potential is a function of extensive variables (like volume, entropy, etc.) that defines the equilibrium state of a system. The Hessian matrix of the internal energy with respect to the extensive variables is called the Weinhold metric. Weinhold spacetime is characterized by second derivative of internal energy with respect to entropy and it is given by [37]

$$\begin{aligned} g_{ij}^W= \partial _i \partial _j M(S,N^2), \end{aligned}$$

(30)

the metric is defined as

$$\begin{aligned} ds^2W = M_{SS} dS^2+2M_{SN^2}dSdN^2+ M_{N^2N^2}d(N^2)^2, \end{aligned}$$

(31)

it can also be written in the form of matrix as follows

$$\begin{aligned} \begin{pmatrix} M_{SS} &{} M_{SN^2}\\ M_{N^2S} &{} M_{N^2 N^2}.\\ \end{pmatrix} \end{aligned}$$

The curvature scalar of Weinhold metric for Schwarzschild AdS BH in the presence of exponential entropy takes the following form

$$\begin{aligned} R=-\frac{16 l_p{2}^{\frac{5}{8}}\pi ^{\frac{8}{3}}k(-14N^{\frac{10}{2}}(S_e-1)^{\frac{1}{3}}l_p^{\frac{4}{3}}+13N^6\sqrt{2}\pi ^{\frac{4}{3}}k)}{(21N\pi ^{\frac{8}{3}}k^2+24\sqrt{N}\sqrt{2}(S_e-1)^{\frac{1}{3}}\pi ^{\frac{4}{3}}l_p^{\frac{4}{3}}k-44(S_e-1)^{\frac{2}{3}}l_p^{\frac{8}{3}})^2N^{\frac{30}{8}}}. \end{aligned}$$

(32)

Fig. 11

Plots of scalar curvature $R_W$ versus $S_e$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Fig. 12

Plots of scalar curvature $R_W$ versus $S_q$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

The scalar curvature of the Weinhold metric provides information about the microscopic attractive or repulsive behavior of the molecules. Figure 11 shows the relationship between $R_W$ and $S_e$ and the results are summarize as follow

• For $k=0$, $R_W=0$.

• For $k=1$, $R_W<0$ when $S_e>0.99$.

• For $k=-1$, $R_W<0$ when $S_e>0.99$.

The negative scalar curvature of weinhold metric shows the attractive behavior of particles. The weinhold’s scalar curvature for $S_q$ is given as

$$\begin{aligned} R=\frac{A}{B}, \end{aligned}$$

(33)

where

$$\begin{aligned} A= & {} 20~2^{\frac{1}{8}} (1-q)^{\frac{4}{3}} \ln {(2)}^{\frac{4}{3}} N^{\frac{11}{12}}\Bigg [701316 \gamma ^{2}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{7}{3}}+44k(1-q)^{\frac{2}{3}}\\{} & {} \gamma ^{\frac{4}{3}}\ln {8}^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{2}{3}}(-453-1325\\{} & {} \ln {|(1-q)S_q+1|}+1308\\{} & {} \ln {|(1-q)S_q+1|}^{2})N^{\frac{4}{3}}+k^2(3-3q)^{\frac{1}{3}} (q-1)\gamma ^{\frac{2}{3}}\\{} & {} \ln {(2)}^{\frac{4}{3}}(-10362-31789\ln {|(1-q)S_q+1|}\\{} & {} +15384\ln {|(1-q)S_q+1|}^2)N^{\frac{8}{3}}+1995\\{} & {} k^{3}(q-1)^{2} \ln {(2)}^{2}\ln {|(1-q)S_q+1|}^{\frac{1}{3}} N^{2}\Bigg ], \end{aligned}$$

and

$$\begin{aligned} B= & {} 9~3^{\frac{1}{3}} \sqrt{\pi }\gamma ^{\frac{2}{3}}\Bigg [22~ 3^{\frac{2}{3}}\gamma ^{\frac{4}{3}}\ln {|(1-q)S_q+1|}^{\frac{4}{3}}\\{} & {} (3+35\ln {|(1-q)S_q+1|})+15~3^{\frac{1}{3}}k (1-q)^{\frac{2}{3}}\gamma ^{\frac{2}{3}} \\{} & {} \ln {(2)}^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}(3+13\ln {|(1-q)S_q+1|})\\{} & {} N^{\frac{4}{3}}-5k^{2}(1-q)^{\frac{4}{3}} \ln {(2)}^{\frac{4}{3}}(3+19\\{} & {} \ln {|(1-q)S_q+1|})N^{\frac{8}{3}}\Bigg ]^2. \end{aligned}$$

From the relationship between $R_W$ and $S_q$ as shown in Fig. 12, we can see that

• For $k=0$, $R_W<0$ in $S_q=[0.12,1]$.

• For $k=1$,

  $R_w>0$ for $S_q=[0,0.02]$ and $S_q=0.13$, $R_{W}=0$ for $S_q=0.13$ and $S_q>0.87$, $R_W<0$ for $S_q=0.13$ and $S_q=[0.25, 0.87]$ when $N=2$.

  $R_w>0$ for $S_q=[0,0.07]$ and $S_q=0.16$, $R_{W}=0$ for $S_q=0.16$ and $S_q>0.87$, $R_W<0$ for $S_q=[0.16, 0.27]$ and $S_q=[0.45, 0.87]$ when $N=3$.

  $R_w>0$ for $S_q=[0,0.10]$ and $S_q=0.14$, $R_{W}=0$ for $S_q=0.14$ and $S_q>0.87$, $R_W<0$ for $S_q=[0.14, 0.49]$ and $S_q=[0.58, 0.87]$ when $N=4$.

• For $k=-1$,

  $R_w>0$ for $S_q=[0,0.13]$ and $S_q=0.23$, $R_W<0$ for $S_q=[0.42,1]$ when $N=2$.

  $R_w>0$ for $S_q=[0,0.11]$ and $S_q=0.24$, $R_W<0$ for $S_q=[0.25,0.62]$ and $S_q=[0.72, 1]$ when $N=3$.

  $R_w>0$ for $S_q=[0,0.12]$ and $S_q=[0.18, 0.25]$, $R_W<0$ for $S_q=[0.31,0.86]$ and $S_q=[0.9, 1]$ when $N=4$.

The positive scalar curvature $R_W$ shows the repulsive behavior of particles and negative curvature shows the attractive behavior of BH particles.

3.2 Ruppeiner geometry

The fluctuation theory of equilibrium thermodynamics serves as the foundation for the Ruppeiner thermodynamic geometry [38]. Ruppeiner suggested that the idea of a metric on the spaces of thermodynamic equilibrium state emerges when the concept of fluctuations is introduced into the axioms of equilibrium thermodynamics. The Ruppeiner metric supports the idea that the probability of a thermodynamic state change depends inversely on how close it is to another state. It turns out that the phase transitions and critical points are encoded in R associated with Ruppeiner geometry [39,40,41,42]. Also, it has been claimed that the divergence of R strongly suggests a relationship to microscopic degrees of freedom. While the absolute value of R can be used to calculate the strength of interactions [43,44,45,46,47,48]. The connection between Ruppeiner metric and Weinhold geometry is established by the temperature conformal factor which is given by [49]

$$\begin{aligned} ds^2R= \frac{1}{T} ds^2W. \end{aligned}$$

(34)

In matrix form, the Ruppeiner metric takes the following form

$$\begin{aligned} g^R= \frac{1}{T} \begin{pmatrix} M_{SS} &{} M_{SN^2}\\ M_{N^2S} &{} M_{N^2 N^2}.\\ \end{pmatrix} \end{aligned}$$

The curvature scalar of Ruppeiner metric by using exponential corrected entropy turns out to be

$$\begin{aligned} R=\frac{A}{B}, \end{aligned}$$

(35)

$$\begin{aligned} A= & {} 2k l_p^{\frac{4}{3}}\pi ^{\frac{4}{3}} \Bigg (1020N^9\pi ^{\frac{4}{3}}(S_e-1)^{\frac{7}{3}}l_p^{\frac{8}{3}}\sqrt{2}k\\{} & {} -864N^9\pi ^{\frac{4}{3}}(S_e-1)^{\frac{4}{3}}\\{} & {} l_p^{\frac{8}{3}}\sqrt{2}S_e k+864N^9\pi ^{\frac{4}{3}}(S_e-1)^{\frac{4}{3}}l_p^{\frac{8}{3}}\sqrt{2}k\\{} & {} -288N^9\pi ^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}\\{} & {} l_p^{\frac{8}{3}}\sqrt{2}S_e^2k+576N^9\pi ^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}l_p^{\frac{8}{3}}\sqrt{2}S_e k\\{} & {} -993N^{11}\pi ^4(S_e-1)^{\frac{5}{3}}\sqrt{2}k^3- 288N^9\pi ^{\frac{4}{3}}\\{} & {} (S_e-1)^{\frac{1}{3}}l_p^{\frac{8}{3}}\sqrt{2}k +1152N^{11}\pi ^4(S_e-1)^{\frac{2}{3}} \\{} & {} \sqrt{2}S_e k^3+606N^{10}\pi ^{\frac{8}{3}}l_p^{\frac{4}{3}}S_e^2k^2- 1152N^{11}\pi ^4\\{} & {} (S_e-1)^{\frac{2}{3}}\sqrt{2}k^3 -1212N^{10}\pi ^{\frac{8}{3}}l_p^{\frac{4}{3}}S_e k^2\\{} & {} +606N^{10}\pi ^{\frac{8}{3}}l_p^{\frac{4}{3}}k^2+1800N^8(S_e-1)^{\frac{8}{3}}l_p^4\\{} & {} -2480N^8(S_e-1)^{\frac{5}{3}}l_p^4S_e+ 2480N^8(S_e-1)^{\frac{5}{3}}l_p^4\Bigg ), \end{aligned}$$

and

$$\begin{aligned} B= & {} \Bigg (3\Bigg (21 \pi ^{\frac{8}{3}}N k^2+24\pi ^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}l_p^{\frac{4}{3}}\sqrt{N}\sqrt{2}k\\{} & {} -44(S_e-1)^{\frac{2}{3}}l_p^{\frac{8}{3}}\Bigg )^{2} N^{7}\\{} & {} \Bigg (k\sqrt{N}\pi ^{\frac{4}{3}}+2(S_e-1)^{\frac{1}{3}}l_p^{\frac{4}{3}}\sqrt{2}\Bigg )(S_e-1)^{\frac{7}{3}}\Bigg ). \end{aligned}$$

Fig. 13

Plots of scalar curvature $R_R$ versus $S_e$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Fig. 14

Plots of scalar curvature $R_R$ versus $S_q$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

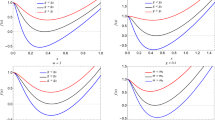
From the relationship between $R_R$ and $S_e$ as shown in Fig. 13, we can see that

• For $k=0$, $R_R=0$.

• For $k=1$, $R_R>0$ for $S_e>1.80$ when $N=2$, $R_R>0$ for $S_e>1.53$ when $N=3$ and $R_R>0$ for $S_e>1.33$ when $N=4$, which shows the attractive behavior of particles.

• For $k=-1$, $R_R<0$ for $S_e>1.56$ when $N=2$, $R_R<0$ for $S_e>1.23$ when $N=3$ and $R_R<0$ for $S_e>1.09$ when $N=4$, which shows the repulsive behavior of particles.

The Ruppeiner scalar curvature of Schwarzschild AdS BH for $S_q$ can be expressed as follow

$$\begin{aligned} R=\frac{A}{B}, \end{aligned}$$

(36)

where

$$\begin{aligned} A= & {} (q-1)N\Bigg (848897280~3^{\frac{1}{3}}\gamma ^{\frac{20}{3}} \ln {|(1-q)S_q+1|}^7\\{} & {} -1024531200~3^{\frac{1}{3}}\gamma ^{\frac{20}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^8- 1596672 k (1-q)^{\frac{2}{3}}\gamma ^6 \ln {(2)}^{\frac{2}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{16}{3}}N^{\frac{4}{3}}\\{} & {} +2967909120 k (1-q)^{\frac{2}{3}}\gamma ^6 \ln {(2)}^{\frac{2}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{19}{3}}N^{\frac{4}{3}}-3660560640\\{} & {} k(1-q)^{\frac{2}{3}}\gamma ^{6}\ln {(2)}^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{22}{3}}N^{\frac{4}{3}}\\{} & {} -3024000~3^{\frac{2}{3}}k^2(1-q)^{\frac{4}{3}}\gamma ^{\frac{16}{3}}\\{} & {} \ln {(2)}^{\frac{4}{3}} \ln {|(1-q)S_q+1|}^{\frac{14}{3}} N^{\frac{8}{3}}\\{} & {} + 1420030080~3^{\frac{2}{3}}k^2 (1-q)^{\frac{4}{3}}\gamma ^{\frac{16}{3}}\ln {(2)}^{\frac{4}{3}}N^{\frac{8}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{17}{3}}- 1814037120~3^{\frac{2}{3}} k^2 (1-q)^{\frac{4}{3}} \gamma ^{\frac{16}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{20}{3}}\ln {(2)}^{\frac{4}{3}}N^{\frac{8}{3}}\\{} & {} - 6350400~3^{\frac{1}{3}} k^3 (1-q)^2 \gamma ^{\frac{14}{3}} \ln {(2)}^2 \\{} & {} \ln {|(1-q)S_q+1|}^{4} N^{4}+\\{} & {} 1037148480~3^{\frac{1}{3}} k^3 (1-q)^2 \gamma ^{\frac{14}{3}} \ln {(2)}^2 \\{} & {} \ln {|(1-q)S_q+1|}^5 N^4-3^{\frac{1}{3}} k^3\\{} & {} 1404077760 (1-q)^2 \gamma ^{\frac{14}{3}} \ln {(2)}^2\ln {|(1-q)S_q+1|}^6 N^4\\{} & {} - 6562080k^4(1-q)^{\frac{8}{3}} \gamma ^4 \\{} & {} \ln {(2)}^{\frac{8}{3}} \ln {|(1-q)S_q+1|}^{\frac{10}{3}}N^{\frac{16}{3}}\\{} & {} + 356610240 k^{4}(1-q)^{\frac{8}{3}}\\{} & {} \gamma ^4 \ln {(2)}^{\frac{8}{3}} \ln {|(1-q)S_q+1|}^{\frac{13}{3}}N^{\frac{16}{3}}\\{} & {} -545650560 k^4 (1-q)^{\frac{8}{3}} \gamma ^4 \ln {(2)}^{\frac{8}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{16}{3}}N^{\frac{16}{3}}-1164240~3^{\frac{2}{3}} k^5 \\{} & {} (1-q)^{\frac{10}{3}} \gamma ^{\frac{10}{3}}\ln {(2)}^{\frac{10}{3}}N^{\frac{20}{3}}\ln {|(1-q)S_q+1|}^{\frac{8}{3}}\\{} & {} + 868560~3^{\frac{2}{3}} k^5 (1-q)^{\frac{10}{3}} \gamma ^{\frac{10}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{11}{3}}\ln {(2)}^{\frac{10}{3}}N^{\frac{20}{3}}\\{} & {} - 14742000~3^{\frac{2}{3}} k^5 (1-q)^{\frac{10}{3}} \gamma ^{\frac{10}{3}}\\{} & {} \ln {(2)}^{\frac{10}{3}} \ln {|(1-q)S_q+1|}^{\frac{14}{3}}\\{} & {} N^{\frac{20}{3}}- 257544~3^{\frac{1}{3}} k^6 (1-q)^4 \gamma ^{\frac{8}{3}} \ln {(2)}^4\\{} & {} \ln {|(1-q)S_q+1|}^2 N^4-3^{\frac{1}{3}} k^6\\{} & {} 12993960 (1-q)^4 \gamma ^{\frac{8}{3}} \ln {(2)}^4 \ln {|(1-q)S_q+1|}^3 N^4\\{} & {} + 15097320~3^{\frac{1}{3}} k^6 (1-q)^4 \gamma ^{\frac{8}{3}} \\{} & {} \ln {(2)}^4 \ln {|(1-q)S_q+1|}^4 N^4\\{} & {} +26460 k^7 (1-q)^{\frac{14}{3}} \gamma ^2 \ln {(2)}^{\frac{14}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{4}{3}}N^{\frac{28}{3}}- 3280620 k^7 (1-q)^{\frac{14}{3}} \gamma ^2\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{7}{3}}\\{} & {} \ln {(2)}^{\frac{14}{3}}N^{\frac{28}{3}}+5068980 k^7 (1-q)^{\frac{14}{3}} \gamma ^2 \\{} & {} \ln {(2)}^{\frac{14}{3}} \ln {|(1-q)S_q+1|}^{\frac{10}{3}}N^{\frac{28}{3}}\\{} & {} +7770~3^{\frac{2}{3}} k^8 (1-q)^{\frac{16}{3}} \gamma ^{\frac{4}{3}} \ln {(2)}^{\frac{16}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}} N^{\frac{32}{3}}+56885~3^{\frac{2}{3}} k^8\\{} & {} (1-q)^{\frac{16}{3}} \gamma ^{\frac{4}{3}} \ln {(2)}^{\frac{16}{3}} \ln {|(1-q)S_q+1|}^{\frac{5}{3}}N^{\frac{32}{3}}\\{} & {} +22905~3^{\frac{2}{3}} k^8 (1-q)^{\frac{16}{3}} \gamma ^{\frac{4}{3}}\\{} & {} \ln {(2)}^{\frac{16}{3}} \ln {|(1-q)S_q+1|}^{\frac{8}{3}}N^{\frac{32}{3}}+1050~3^{\frac{1}{3}} k^9 (1-q)^6 \gamma ^{\frac{2}{3}} \\{} & {} \ln {(2)}^{6} N^{12}+3^{\frac{1}{3}}56980 k^{9} (1-q)^{6} \gamma ^{\frac{2}{3}}\\{} & {} \ln {(2)}^6 \ln {|(1-q)S_q+1|} N^12\\{} & {} -69020~3^{\frac{1}{3}} k^9 (1-q)^6 \\{} & {} \gamma ^{\frac{2}{3}} \ln {(2)}^6 \ln {|(1-q)S_q+1|}^2 N^12+ 6175 k^{10} (1-q)^{\frac{20}{3}} \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{1}{3}}\ln {(2)}^{\frac{20}{3}}N^{\frac{40}{3}}\\{} & {} -9025 k^{10} (1-q)^{\frac{20}{3}} \ln {(2)}^{\frac{20}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{4}{3}} N^{\frac{40}{3}}\Bigg ), \end{aligned}$$

and

$$\begin{aligned} B= & {} -2 ((1-q)S_q+1) \ln {|(1-q)S_q+1|}^{\frac{1}{3}}(2 3^{\frac{1}{3}} \gamma ^{\frac{2}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}+k(1-q)^{\frac{2}{3}}\\{} & {} \ln {(2)}^{\frac{2}{3}}N^{\frac{4}{3}})(2 3^{\frac{1}{3}}\gamma ^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{2}{3}}N^2\\{} & {} + k (1 -q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}}N^{\frac{10}{3}})\\{} & {} (264 3^{\frac{1}{3}}\gamma ^{\frac{8}{3}} \ln {|(1-q)S_q+1|}^{\frac{8}{3}}\\{} & {} (3 + 35 \ln {|(1-q)S_q+1|})+12 k(1 - q)^{\frac{2}{3}} \\{} & {} \gamma ^2 \ln {(2)}^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^2\\{} & {} (111 + 965 \ln {|(1-q)S_q+1|}) N^{\frac{8}{3}}+ 6 3^{\frac{2}{3}} \\{} & {} k^2 (1 - q)^{\frac{4}{3}} \gamma ^{\frac{4}{3}}\ln {(2)}^{\frac{4}{3}} \ln {|(1-q)S_q+1|}^{\frac{4}{3}} \\{} & {} (31 + 195N^{\frac{8}{3}}\ln {|(1-q)S_q+1|}) \\{} & {} - 5 3^{\frac{1}{3}} k^3 (1 - q)^2 \gamma ^{\frac{2}{3}}\ln {(2)}^2\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}(3 +37 \ln {|(1-q)S_q+1|})N^2 \\{} & {} - 5 k^4 (1 - q)^{\frac{8}{3}}\ln {(2)}^{\frac{8}{3}} (3 + 19 \\{} & {} \ln {|(1-q)S_q+1|}) N^{\frac{16}{3}})^2. \end{aligned}$$

From the relationship between $R_R$ and $S_q$ as shown in Fig. 14, we can see that

• For $k=0$, $R_R<0$ for $S_q=[0, 0.03]$ and $S_q=[0.13, 1]$ which leads to repulsive behavior.

• For $k=1$,

  $R_R<0$ for $S_q=[0, 0.13]$ and $S_q=[0.15, 1]$ when $N=2$, which leads to repulsive behavior.

  $R_R>0$ for $S_q=[0, 0.02]$ which leads to attractive bahavior, $R_R<0$ for $S_q=[0, 0.10]$ and $S_q=[0.31, 1]$ when $N=3$, leads to repulsive behavior.

  $R_R>0$ for $S_q=[0, 0.02]$ which leads to attractive bahavior, $R_R<0$ for $S_q=[0, 0.10]$, $S_q=[0.19, 0.44]$ and $S_q=[0.47, 1]$ when $N=4$, leads to repulsive behavior.

• For $k=-1$,

  $R_R<0$ for $S_q=[0.08, 0.13]$, $S_q=[0.15, 0.38]$, $S_q=[0.49, 0.58]$ and $S_q=[0.85, 1]$ when $N=2$, leads to repulsive behavior.

  $R_R<0$ for $S_q=[0, 0.69]$, $S_q=[0.75, 0.88]$ and $S_q=[0.97, 1]$ when $N=3$, leads to repulsive behavior.

  $R_R<0$ for $S_q=[0, 0.87]$, $S_q=[0.92, 0.98]$ and $S_q=1$ when $N=4$, leads to repulsive behavior.

3.3 Quevedo geometry

Quevedo proposed a new method of formalism of geometro-thermodynamics, the metric of his method is Legendre invariant in space of equilibrium and it overcome the invariance of Weinhold and Ruppeiner under the Legendre transformation [50,51,52,53]. Legendre invariance ensures that the geometric properties of metric G when used as a non-degenerate Riemannian metric on space $\mathcal {T}$ have no influence on the choice of thermodynamic potential used in its creation. The non-degenerate Riemannian metric can be written as $G= (d\theta - \delta _{pq}I^p dE^q)^2 + (\delta _{pq}E^p I^q)(\eta _{rs}dE^r dI^s)$, with $\eta _{rs}=diag(-1, 1,...,1)$ [54]. It is also feasible to write the Quevedo metric as

$$\begin{aligned} g=\varphi ^*(G)=\left( E^r \frac{\partial \theta }{\partial E^r} \right) \left( \eta _{pq} \delta ^{qr} \frac{\partial ^2 \theta }{\partial E^r \partial E^s} dE^p dE^s \right) , \end{aligned}$$

(37)

which can also be written as

$$\begin{aligned} g^Q= (ST+N^2 \mu ) \begin{pmatrix} -M_{SS} &{} 0\\ 0 &{} M_{N^2 N^2}\\ \end{pmatrix}. \end{aligned}$$

Fig. 15

Plots of scalar curvature $R_Q$ versus $S_e$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

Fig. 16

Plots of scalar curvature $R_Q$ versus $S_q$ of Schwarzschild AdS BH for $k=0$ (top left panel), $k=1$ (top right panel) and $k=-1$ (bottom panel)

The scalar curvature of Quevedo metric for $S_e$ yields as

$$\begin{aligned} R=\frac{A}{B}, \end{aligned}$$

(38)

$$\begin{aligned} A= & {} 322^{\frac{3}{4}}\pi ^{\frac{8}{3}}(S_e-1)^{\frac{1}{3}}\Bigg (\!-15858N^{13}\pi ^4\sqrt{2}(S_e-1)^{\frac{2}{3}}l_p^{\frac{8}{3}}S_e k^3\\{} & {} -59670 N^{11}\pi ^{\frac{4}{3}}\sqrt{2}(S_e-1)^{\frac{7}{3}}l_p^{\frac{16}{3}}S_e k+39593N^{13}\pi ^4\\ {}{} & {} \sqrt{2}(S_e-1)^{\frac{2}{3}}l_p{}^{\frac{8}{3}}S_e^2k^3+ 18117N^{13}\pi ^4\sqrt{2}(S_e-1)^{\frac{5}{3}}l_p^{\frac{8}{3}}S_e k^3\\{} & {} +12648N^{11}\pi ^{\frac{4}{3}}\sqrt{2}(S_e-1)^{\frac{4}{3}}l_p^{\frac{16}{3}}S_e k+45900N^{15}\pi ^{\frac{20}{3}}\sqrt{2}k^5\\{} & {} - 164268N^{5}(S_e-1)^{\frac{8}{3}}l_p^{\frac{20}{3}}S_e+309420N^{12}\pi ^{\frac{8}{3}}l_p^4k^2-37908N^{10}\\ {}{} & {} (S_e-1)^{\frac{8}{3}}l_p^{\frac{20}{3}}+ 422756N^{12}\pi ^{\frac{8}{3}}l_p^4S_e^2k^2-697908N^{12}\pi ^{\frac{8}{3}}l_p^4S_e k^2\\{} & {} - 164430N^{14}\pi ^{\frac{16}{3}}(S_e-1)^{\frac{4}{3}}l_p^{\frac{4}{3}}k^4+16848 N^{14}\pi ^{\frac{16}{3}}(S_e-1)^{\frac{1}{3}}l_p^{\frac{4}{3}}k^4\\ {}{} & {} - 34268N^{12}\pi ^{\frac{8}{3}}l_p^4 S_e^3k^2-45900 N^{\frac{15}{2}}\pi ^{\frac{20}{3}}\sqrt{2}S_e k^5\\{} & {} + 164268N^{10}(S_e-1)^{\frac{11}{3}}l_p^{\frac{20}{3}}-62140N^{11}\pi ^{\frac{4}{3}}\sqrt{2}\\{} & {} (S_e-1)^{\frac{4}{3}}l_p^{\frac{16}{3}}S_e^2k+ 114750N^{7}\pi ^{\frac{16}{3}}(S_e-1)^{\frac{4}{3}}l_p^{\frac{4}{3}}S_e k^4\\ {}{} & {} +6228N^{11}\pi ^{\frac{4}{3}}\sqrt{2}(S_e\!-\!1)^{\frac{4}{3}}l_p^{\frac{16}{3}}k\!+\! 30996N^{13}\pi ^4\\ {}{} & {} \sqrt{2}(S_e-1)^{\frac{8}{3}}l_p^{\frac{8}{3}}k^3\!+\!23166N^{11}\\{} & {} \pi ^{\frac{4}{3}}\sqrt{2}(S_e\!-\!1)^{\frac{10}{3}}l_p^{\frac{16}{3}}k\!-\! 57528N^{14}\pi ^{\frac{16}{3}}(S_e\!-\!1)^{\frac{1}{3}}l_p^{\frac{4}{3}}S_e^2k^4\!\\{} & {} +\!122310 N^{11}\pi ^{\frac{4}{3}}\sqrt{2}(S_e-1)^{\frac{7}{3}}l_p{}^{\frac{16}{3}}k\!+\! 48552N^{14}\pi ^{\frac{16}{3}}\\ {}{} & {} (S_e\!-\!1)^{\frac{1}{3}}l_p^{\frac{4}{3}}S_e k^4\!+\!N^{13}\\{} & {} 11529\pi ^4\sqrt{2}(S_e-1)^{\frac{2}{3}}l_p^{\frac{8}{3}}k^3+ 37827N^{13}\pi ^4\sqrt{2}(S_e-1)^{\frac{5}{3}}l_p^{\frac{8}{3}}k^3), \\ B= & {} 9l_p^{\frac{2}{3}}(17k \pi ^{\frac{4}{3}}\sqrt{N}S_e-9k \pi ^{\frac{4}{3}}\sqrt{N}+13\sqrt{2}l_p^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}S_e+3\sqrt{2}\\{} & {} l_p^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}})^3N^{\frac{19}{2}}(k \pi ^{\frac{4}{3}}\sqrt{N}+\sqrt{2}l_p^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}})^2(5k\pi ^{\frac{4}{3}}\sqrt{N}\\{} & {} -3\sqrt{2}l_p^{\frac{4}{3}}(S_e-1)^{\frac{1}{3}}\Bigg )^2. \end{aligned}$$

The relationship between $R_Q$ and $S_e$ as shown in Fig. 15 manifests the following results

• For $k=0$, $R_Q>0$ for $S_e>1$, which shows the attractive behavior.

• For $k=1$,

  $R_Q>0$ for $S_e=[0.03, 0.9]$, $R_Q=0$ for $S_e=0.9$, $R_Q>0$ for $S_e=[0, 0.3]$ and $S_e=[0.21, 1]$ when $N=2$.

  $R_Q>0$ for $S_e=[0, 0.13]$, $S_e=[0.20, 0.33]$ and $S_e=[0.37, 1]$ when $N=3$.

  $R_Q>0$ for $S_e=[0, 0.15]$, $S_e=[0.23, 0.53]$ and $S_e=[0.55, 1]$ when $N=4$. It shows attractive behavior for positive values.

• For $k=-1$,

  $R_Q>0$ for $S_e=[1, 6.0]$, $R_Q=0$ for $S_e=6.1$ and $R_Q<0$ for $S_e>6.1$ when $N=2$.

  $R_Q>0$ for $S_e=[1, 7.2]$, $R_Q=0$ for $S_e=(7.2, 8.8]$ and $R_Q<0$ for $S_e>8.8$ when $N=3$.

  $R_Q>0$ for $S_e=[1, 7.3]$, $R_Q=0$ for $S_e=(7.3, 8.8]$ and $R_Q<0$ for $S_e>8.8$ when $N=4$. It shows attractive behavior for positive values and repulsive behavior for negative values.

Finally the scalar curvature of Quevedo metric for $S_q$ turns out to be

$$\begin{aligned} R=\frac{A}{B}, \end{aligned}$$

(39)

where

$$\begin{aligned} A= & {} 128 2^{\frac{1}{4}} (1-q)^{\frac{8}{3}} ((1-q)S_q+1)\\{} & {} \ln {(2)}^{\frac{8}{3}} \ln {|(1-q)S_q+1|}^{\frac{1}{3}} N^{\frac{11}{6}}(-3201660\gamma ^4 \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{13}{3}}(-128 (-1+q)^2 S_q^2\\{} & {} (-55+(34+55 q) S_q+199\\{} & {} (q-1) S_q^2)-8 (q-1)S_q(-1529+(6930 q -7358)\\{} & {} + (-1041+6442 q-5401 q^2)S_q^2+9396 (q-1)^2 S_q^3)\\{} & {} \ln {|(1-q)S_q+1|}+ 4(1298+(14553-14377 q) S_q\\{} & {} + 4(5317-9948 q+4631 q^2)S_q^2\\{} & {} -(q-1)^2 (6683+5445 q) S_q^3+14696(q-1)^3S_q^4)\\{} & {} \ln {|(1-q)S_q+1|}^2-33 (549+(1667-1603 q)\\{} & {} S_q+5(267-502 q+235 q^2) S_q^2-(q-1)^2 \\{} & {} (135+121 q)S_q^3+352(q-1)^3 S_q^4)\ln {|(1-q)S_q+1|}^3\\{} & {} + 8712 ((1-q) S_q+1)^2\ln {|(1-q)S_q+1|}^4)-132 k \\{} & {} (1-q)^{\frac{2}{3}} \gamma ^{\frac{10}{3}} \ln {8}^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{8}{3}}(4096 (q-1)^{3} \\{} & {} S_{q}^{3} (-13475+17080 S_{q}+256 S_q^2)\\{} & {} -128 (q-1)^2 S_q^2(-238700-(298687+149380 q)S_q\\{} & {} +(-3507475+3608147 q) S_q^2+378560 (-1+q) S_q^3)\\{} & {} \ln {|(1-q)S_q+1|}+12 S_q \\{} & {} (3076733-36009686 S_q+739101 S_{q}^{2}+ 46196848 S_{q}^{3}\\{} & {} -9682944 S_q^4+(2627427-41330800 S_q\\ {}{} & {} +9682944 S_q^2)q^3 S_q^2-q^2 S_{q}(20248294+ 4515753 S_q\\{} & {} -S_q^2 128858448 +29048832 S_q^3)+ q(-3076733\\{} & {} +56257980 S_{q}+1149225\\{} & {} S_q^2- 133724496 S_q^3+29048832 S_q^4))\\{} & {} \ln {|(1-q)S_q+1|}^2+3(-16253413+11 (-59581\\{} & {} +1374461 q) S_q+(183177905-141529122 q\\{} & {} -41648783 q^2) S_q^2+49(q-1)^2 (3581211+873125 q) \\{} & {} S_{q}^{3}-192 (q-1)^{2}(61641+41143 q) S_q^4\\{} & {} +19734528 (q-1)^3S_q^5)\ln {|(1-q)S_q+1|}^3+198\\{} & {} (397203-(321403+422277 q) S_q+ S_q^2\\{} & {} (-1411567+1214302 q+197265 q^2)\\{} & {} -(q-1)^2(787553+172191 q) S_q^3\\{} & {} +94592 (q-1)^3 S_q^4)\ln {|(1-q)S_q+1|}^4\\{} & {} +8712(-4408+1153(q-1) S_q) \\{} & {} ((1-q)S_q)^{2} N^{\frac{4}{3}}\ln {|(1-q)S_q+1|}^5)\\{} & {} +3 k^2 (3-3q)^{\frac{1}{3}} \gamma ^{\frac{8}{3}}\ln {(2)}^{\frac{4}{3}} \ln {|(1-q)S_q+1|}^2(-8192\\{} & {} \ln {|(1-q)S_q+1|}^5)(q-1)^4S_q^3(-176561-85716 S_q\\{} & {} +115712 S_q^2)+128 (q-1)^3 S_q^2(15027639 \\ {}{} & {} +(8902778-17814423 q) S_q+(58367619\\{} & {} -54733571 q) S_q^2+11234432 (q-1) S_q^3)\\{} & {} \ln {|(1-q)S_q+1|}- 32 (q-1)\\{} & {} S_q(-28270693+(-52878163+184848026 q)\\{} & {} S_q+11(46967723-\\{} & {} 70142316 q+23174593 q^2) S_q^2\\{} & {} +(-308314553+583141234 q-\\{} & {} 274826681 q^2) S_q^3+14582784 (q-1)^2 S_q^4) \\{} & {} \ln {|(1-q)S_q+1|}^2+ 6\\{} & {} (-257674791-570617399 S_q-3452672681 S_q^2\\{} & {} -3682294345S_q^3-\\{} & {} 130842544 S_q^4+411721728 S_q^5+q^4 S_q^3\\{} & {} (-775192649-542564272 S_q+\\{} & {} 411721728 S_q^2)+(1598853817+6007872292 S_q\\{} & {} +1758535360 S_q^2-\\{} & {} 1646886912S_q^3)q^3 S_q^2+ q^2 S_q (-1081335959\\{} & {} -6650380315 S_q-S_q^2\\{} & {} 13372460982-2020220448 S_q^3+ 2470330368 S_q^4)\\{} & {} + q(257674791+1651953358S_q+8504199179 S_q^2\\{} & {} + 11822075684 S_q^3+935091904 S_q^4-\\{} & {} 1646886912 S_q^5))\ln {|(1-q)S_q+1|}^3\\{} & {} - 99 (q-1) (33815479-145 \\{} & {} (-143825+359057 q)S_q+(-79749699+60636326 q\\{} & {} +19113373q^2) S_q^2-(-1+q)^2 (84435917\\{} & {} +865587 q) S_q^3+17647072 (-1+q)^3 S_q^4)\\{} & {} \ln {|(1-q)S_q+1|}^4+ 8712 (q-1)\\{} & {} (-207371+52106(q-1) S_q) (1+\\{} & {} (1-q)S_q)^2\ln {|(1-q)S_q+1|}^5)N^{\frac{8}{3}}+18 k^3 (q-1)^2 \gamma ^2 \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{4}{3}}\\{} & {} \ln {(2)}^2(-2048(q-1)^3 S_q^3(108955-107978 S_q\\{} & {} +26752 S_q^2)-64 (q-1)^2S_q^2\\{} & {} (-6068068+(1044913-1393292 q)S_q\\{} & {} +(-11485163+11217643 q) S_q^2\\{} & {} +267520 (q-1) S_q^3)\ln {|(1-q)S_q+1|}\\{} & {} +12 S_q (-11781781-32128126 S_q\\ {}{} & {} +35846275 S_q^2+122569324 S_q^3\\{} & {} -41091072 S_q^4+q^3S_q^2(-14177355-\\{} & {} 122569324 S_q+41091072S_q^2)+(-5956426\\{} & {} +64200985 S_q+367707972\\{} & {} S_q^2-123273216S_q^3)q^2 S_q+q(11781781\\{} & {} +38084552S_q-85869905 S_q^2-\\{} & {} 367707972 S_q^3+123273216 S_q^4) \\{} & {} \ln {|(1-q)S_q+1|}^2+3(69630785+5\\{} & {} (-50131581+31911517 q)S_q+(-341575253\\{} & {} +764312506 q-q^2 \\{} & {} 422737253)S_q^2+(q-1)^2 (293447469\\{} & {} +193548883 q) S_q^3- 48 (q-1)^2\\{} & {} (-5486879+6556959 q) S_q^4+51363840 (q-1)^3 S_q^5)\\{} & {} \ln {|(1-q)S_q+1|}^3\\{} & {} -9 (27434785+(151051503-128424143q) S_q\\{} & {} +(173031051-q 314823622+141792571 q^2) S_q^2\\{} & {} -3 (q-1)^2 (-12370351+13601071 q) S_q^3\\{} & {} +12303280 (q-1)^3 S_q^4) \ln {|(1-q)S_q+1|}^4\\{} & {} + 3960 (-46195+19041 (q-1)\\{} & {} S_q)N^4 (1+(1-q) S_q)^2 \ln {|(1-q)S_q+1|}^5)\\{} & {} +2 k^4 (3-3q)^{\frac{2}{3}} (q-1)^2 \gamma ^{\frac{4}{3}}\ln {(2)}^{\frac{8}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}(1024 (q-1)^3 S_q^3(223579\\{} & {} -185398S_q+7296 S_q^2)+64\\{} & {} (q-1)^2S_q^2(2719718+(3972333-5441054 q) S_q\\{} & {} +(4300207-4336687 q)\\{} & {} S_q^2+736896 (q-1) S_q^3) \ln {|(1-q)S_q+1|}\\{} & {} + 4S_q(-20454493+185024930\\{} & {} S_q+566924635 S_q^2-S_q^3191403044 \\{} & {} -20312064 S_q^4+q^3 S_q^2(-391181411+187900964\\{} & {} S_q+20312064 S_q^2)+(40357510\\{} & {} +1349287457S_q-567204972\\{} & {} S_q^2-60936192 S_q^3)q^2S_q+(20454493\\{} & {} -225382440 S_q-1525030681 S_q^2+570707052S_q^3\\{} & {} +60936192 S_q^4)q) \ln {|(1-q)S_q+1|}^2\\{} & {} +3(-108665785+\\{} & {} (124675741-63501821 q) S_q+5(214908625\\{} & {} -330178674 q+115270049\\{} & {} q^2) S_q^2-(q-1)^2 (-820340847+404182639 q) S_q^3\\{} & {} + 48 (q-1)^2 (-580519\\{} & {} +434599 q) S_q^4+7004160 (q-1)^3 S_q^5)\\{} & {} \ln {|(1-q)S_q+1|}^3-18(17095845-\\{} & {} (8518969+12248791 q) S_q-139 (497307\\{} & {} -632254 q+134947 q^2)S_q^2+\\{} & {} (q-1)^2(-46880499+13910579 q) S_q^3\\{} & {} +3369640 (q-1)^3 S_q^4)\\{} & {} \ln {|(1-q)S_q+1|}^4-360 (84908+62731 (q-1) S_q) \\{} & {} (1+(1-q) S_q)^2N^{\frac{16}{3}}\\{} & {} \ln {|(1-q)S_q+1|}^5)-6 k^5 (3-3q)^{\frac{1}{3}} (q-1)^3 \gamma ^{\frac{2}{3}}\\{} & {} \ln {(2)}^{\frac{10}{3}} (1024 (q-1)^3 S_q^3\\{} & {} (-1567+5662 S_q)+64 (q-1)^2 S_q^2(-957864\\{} & {} +(-237679+312824 q) S_q+612807\\{} & {} (q-1) S_q^2) \ln {|(1-q)S_q+1|}\\{} & {} + 4 (q-1)S_q(-8446365-2S_q\\{} & {} (-8055837+5156627 q)+19(1351273\\{} & {} -2100986 q+749713 q^2) S_q^2\\{} & {} +17290228(q-1)^2 S_q^3) \ln {|(1-q)S_q+1|}^2\\{} & {} +(26145635-5(-29206993\\{} & {} +30188913 q) S_q+3 (13823387-57832454q\\{} & {} +44009067 q^2) S_q^2- (q-1)^2\\{} & {} (117606289+7228271 q)S_q^3+39187120 \\{} & {} (q-1)^3 S_q^4) \ln {|(1-q)S_q+1|}^3+15\\{} & {} (4516707-5 (-2174761+2371145 q) S_q\\{} & {} +(5600417-13923154q\\{} & {} +8322737 q^2) S_q^2-(q-1)^2 (1168601\\{} & {} +983719 q)S_q^3+411920 (q-1)^3\\{} & {} S_q^4) \ln {|(1-q)S_q+1|}^4-600(-26207\\{} & {} +3179 (q-1) S_q) (1+(1-q) S_q)^2\\{} & {} \ln {|(1-q)S_q+1|}^5)N^{\frac{20}{3}}+16245 k^6 (q-1)^4 \\{} & {} \ln {(2)}^4\ln {|(1-q)S_q+1|}^{\frac{1}{3}}(384\\{} & {} (q-1)^2 S_q^2(7+(q-1) S_q)-8 (q-1) \\{} & {} S_q(-231-178 (q-1) S_q+25 (q-1)^2\\{} & {} S_q^2) \ln {|(1-q)S_q+1|}+4 (-210\\{} & {} +2671 (q-1) S_q-2536 (q-1)^2S_q^2+75\\{} & {} (q-1)^3 S_q^3)\ln {|(1-q)S_q+1|}^2+5(-629\\{} & {} +1667(q-1) S_q-1063 (q-1)^2\\{} & {} S_q^2+25 (q-1)^3 S_q^3)\ln {|(1-q)S_q+1|}^3\\{} & {} -600N^8 (1+(1-q)S_q)^2\\{} & {} \ln {|(1-q)S_q+1|}^4)), \end{aligned}$$

and

$$\begin{aligned} B= & {} 15 3^{\frac{2}{3}}\pi \gamma ^{\frac{4}{3}}\Bigg (77 3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}\\{} & {} -19 k (1-q)^{\frac{2}{3}} \ln {(2)}^{\frac{2}{3}}N^{\frac{4}{3}})^2\\{} & {} (2 3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}(-1+3 \\{} & {} \ln {|(1-q)S_q+1|})+k (1-q)^{\frac{2}{3}}\\{} & {} \ln {(2)}^{\frac{2}{3}} (1+3 \ln {|(1-q)S_q+1|})N^{\frac{4}{3}})^2(3^{\frac{1}{3}} \gamma ^{\frac{2}{3}} \\{} & {} \ln {|(1-q)S_q+1|}^{\frac{2}{3}}(-32\\{} & {} (q-1) S_q+11 (-1+(-1+q) S_q) \\{} & {} \ln {|(1-q)S_q+1|})+k(1-q)^{\frac{2}{3}} \\{} & {} \ln {(2)}^{\frac{2}{3}} (-16 (q-1)S_q+(5-5 (q-1) S_q)\\{} & {} \ln {|(1-q)S_q+1|})N^{\frac{4}{3}})^2\\{} & {} (3^{\frac{1}{3}} \gamma ^{\frac{2}{3}}\ln {|(1-q)S_q+1|}^{\frac{2}{3}} (-32 (q-1) S_q^2\\{} & {} +11 (-1+(-1+q) S_q)\\{} & {} \ln {|(1-q)S_q+1|})+k (1-q)^{\frac{2}{3}}\ln {(2)}^{\frac{2}{3}} \\{} & {} (-16 (q-1) S_q+(5-5(-1+q)S_q) \\{} & {} \ln {|(1-q)S_q+1|}) N^{\frac{4}{3}}\Bigg )^2. \end{aligned}$$

From the relationship between $R_Q$ and $S_q$ as shown in Fig. 16, we can see that

• For $k=0$,

  $R_Q>0$ for $S_q=[0.01, 0.27]$ and $S_q=[0.30, 1]$ when $N=2$.

  $R_Q>0$ for $S_q=[0.02, 0.25]$ and $S_q=[0.31, 1]$ when $N=3$.

  $R_Q>0$ for $S_q=[0.04, 0.23]$ and $S_q=[0.32, 1]$ when $N=4$. Curvature leads to the attractive behavior of particles.

• For $k=1$,

  $R_Q<0$ for $S_q=[0.03, 0.9]$, $R_Q=0$ for $S_q=0.9$, $R_Q>0$ for $S_q=[0, 0.3]$ and $S_q=[0.21, 1]$ when $N=2$.

  $R_Q>0$ for $S_q=[0, 0.13]$, $S_q=[0.20, 0.33]$ and $S_q=[0.37, 1]$ when $N=3$.

  $R_Q>0$ for $S_q=[0, 0.15]$, $S_q=[0.23, 0.53]$ and $S_q=[0.55, 1]$ when $N=4$. Curvature leads to the attractive behavior of particles for positive values and repulsive behavior for negative values.

• For $k=-1$,

  $R_Q>0$ for $S_q=[0, 0.04]$, $S_q=[0.6, 0.73]$ and $S_q=[0.78, 0.84]$, $R_Q=0$ for $S_q=0.03$ and $S_q>0.84$, $R_Q<0$ for $S_q=[0.03, 0.57]$ and $S_q=[0.66, 0.68]$ when $N=2$.

  $R_Q>0$ for $S_q=[0, 0.32]$, $S_q=[0.85, 0.87]$ and $S_q=[0.89, 0.90]$, $R_Q=0$ for $S_q=0.3$ and $S_q=0.94$, $R_Q<0$ for $S_q=0$ and $S_q=[0.3, 0.81]$ when $N=3$.

  $R_Q>0$ for $S_q=[0, 0.78]$ and $S_q=[0.94, 0.96]$, $R_Q=0$ for $S_q=0.97$, $R_Q<0$ for $S_q=[0.83, 0.92]$ when $N=4$. Curvature shows attractive behavior of particles for positive values and repulsive behavior for negative values.

4 Conclusions

We have discussed the thermodynamical properties of 5-D Schwarzschild-AdS BH in $AdS_5\times S^5$ spacetime in accordance with AdS/CFT. We treated cosmological constant $\wedge$ as number of colors N and used two recently proposed effective models of the exponential corrected entropies. We obtained the well-known thermodynamic quantities in terms of $N^2$, $S_{e}$ and $S_{q}$ to uncover the behavior for three different curvatures correspond to different values of k. First considering $S_{e}$, we analyzed the relationship between the Hawking temperature and exponential entropy. It is observed that T shows stable behavior for $k=0$ and $k=1$ while for the case of $k = -1$, T increases against $S_e$ which shows the instability of BH. We also indicated the negative intervals of Gibbs free energy which manifest the global instability of BH. We studied the relationship between chemical potential and entropy. The $\mu$ remains positive for $k=1$ which shows the unstable branch and it becomes negative for $k=0$ and $k=-1$ which yields the stable branch of BH. The relationship between specific heat and $S_e$ showed the negative behavior which exhibit local instability. We have also analyzed the behavior of scalar curvature for Weinhold, Ruppeiner and Quevedo. It is observed that Weinhold and Quevedo geometries show microscopic attractive behavior while Ruppeiner curvature shows both the attractive and repulsive behaviors.

Utilizing another effective model of the entropy $S_q$, we have found the relationship between the Hawking temperature and $S_q$ and analyzed that there exist a minimal temperature for $k=1$ and no BH exists blow this temperature. Gibbs free energy remains negative in this case as similar to the above case which exhibits the unstable behavior. $\mu$ shows negative trend for $k=0$ and $k=-1$ which show stable behavior while for $k=1$, it becomes positive which show the unstable behavior. Moreover, the specific heat changes its sign from positive to negative for $k=1$ and $k=-1$. Finally, It is observed that Weinhold, Ruppeiner and Quevedo curvatures show attractive and repulsive behavior of the particles of BH.