1 Introduction

Acoustic black holes, also known as sonic black holes, are a fascinating phenomenon that mimics the behavior of real black holes in certain conditions. They are created by the flow of a fluid, such as water or gas, in a specific configuration, and they possess many of the characteristics of real black holes, including an event horizon, a singularity, and an ergoregion. The ergoregion is a region surrounding the black hole where the fluid flow becomes supersonic, and it is this region that we will be focusing on in this study.

Acoustic black holes as an analogy between sound wave crossing a supersonic fluid and light wave crossing an event horizon of a black hole were proposed for the first time by William Unruh in 1981 to explain quantum gravity effects near the black holes [1]. However, its experimental construction had taken quite long time and in 2009 the first acoustic black hole was created in a laboratory that was first generated in a rubidium Bose-Einstein condensate using a technique called density inversion [2]. This technique creates a flow by repelling the condensate with a potential minimum. The surface gravity and temperature of the acoustic black hole were also measured. An acoustic black hole in contrast to an astrophysical black hole (which is an object) is a phenomenon in which sound perturbations called phonons are unable to escape from a region of a fluid that is flowing more quickly than the speed of sound. However, it is a specific representative model of analogy gravity in which the classical or quantum fluid simulates the properties of the black holes in the experiments. This is similar to the behavior of photons which can not escape an area called the event horizon of the astrophysical black hole. There is growing interest to study acoustic black holes because they have many properties similar to astrophysical black holes. The boundary of an acoustic black hole, at which the flow speed changes from being greater than the speed of sound to less than the speed of sound, is called the event horizon in analogy to the astrophysical black hole case. We should mention that it was commonplace to consider that the phonon does not carry the gravitational mass. In [3, 4] it was proven that that statement is correct only in the linear order, but in fact sound wave does carry very small negative mass.

The acoustic black holes are realized in nature because phonons in perfect fluids exhibit the same properties of motion as photons in space-time of black holes. For this reason, a system in which an acoustic black hole can be created is called an acoustic analogue of gravitating black hole. Gravity analogues other than phonons in a fluid, such as slow light and a system of ions, have also been proposed for studying black hole analogues. The fact that so many systems mimic gravity is sometimes used as evidence for the theory of emergent gravity, which could help reconcile relativity, and quantum mechanics. One must note in dealing with the acoustic black holes that they are not solutions of the Einstein equations, despite, they possess all features of that general relativistic black holes have got. Since the analogous gravity provides testing opportunities many phenomena in relativity theories in both experimental and theoretical levels, over the last few decades a vast of work has been done to probe gravitational phenomena such as the Hawking radiation [5,6,7,8] and superradiance [9,10,11] in the analogous black holes. Moreover, there has been published many more papers devoted to the other gravitational phenomena in the acoustic black holes [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

To study the motion of phonons in acoustic black holes, we use a mathematical model that simulates the flow of a fluid in a specific configuration that creates an acoustic black hole. We then use this model to calculate the behavior of phonons in the ergoregion, as well as how their behavior changes as the rotation of the black hole increases.

The paper is organized as follows. Section 2 is devoted to the spacetime properties of the acoustic black hole studied. Equations of motion and dynamics of massless phonons are explored in the next Sect. 3. In Sect. 4 we present results related to the capture of the phonon by the acoustic black hole. The lensing of the phonon in the spacetime of the acoustic black hole in the weak field regime is studied in the Sect. 5. The last Sect. 6 summarizes the main results obtained in the paper.

2 Background

In this section we briefly demonstrate the formalism in which the acoustic black hole metric in the photon-fluid model was obtained by Marino and Ciszak [28, 29]. The propagation of a monochromatic optical beam with wavelength \(\lambda \) at direction z in a two-dimensional nonlinear medium is governed by the nonlinear Schrödinger equation

$$\begin{aligned} \partial _zE=\frac{i}{2k}\nabla ^2E-i\frac{kn_2}{n_0}E|E|^2, \end{aligned}$$
(1)

where E is the slowly varying envelope of the electromagnetic field, \(n_0\) and \(n_2\) are a linear refractive index and medium nonlinear coefficient, respectively, and \(k=2\pi n_0/\lambda \) is the wave number. By applying the Madelung transformation, \(E=\rho ^{1/2}e^{i\phi }\), one can convert Eq. (1) into the hydrodynamic continuity and Euler equations as

$$\begin{aligned}{} & {} \partial _t\rho +\mathbf{\nabla }(\rho \textbf{v})=0, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \partial _t\psi +\frac{1}{2}v^2=-\frac{c^2n_2}{n_0^3}\rho +\frac{c^2}{2k^2n_0^2}\frac{\nabla ^2\rho ^{1/2}}{\rho ^{1/2}}, \end{aligned}$$
(3)

where \(\rho \) is a fluid density, \(\textbf{v}=(c/kn_0){\varvec{\nabla }}\phi \equiv {\varvec{\nabla }}\psi \) is the fluid velocity. The first term on the right hand side of the Euler equation (3) represents the local repulsive bulk pressure, \(P=c^2n_2\rho ^2/2n_0^3\), while the last term represents the analogue quantum pressure. Then, by introducing the linear perturbations to the fixed background (\(\rho _0\), \(\psi _0\)), as

$$\begin{aligned}{} & {} \rho =\rho _0+\epsilon \rho _1+O(\epsilon ^2), \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \psi =\psi _0+\epsilon \psi _1+O(\epsilon ^2), \end{aligned}$$
(5)

and neglecting term corresponding to the quantum pressure, one can write hydrodynamic equations (2) and (3) in the following form of the single second-order differential equation:

$$\begin{aligned}{} & {} -\partial _t\left[ \frac{\rho _0}{c_s^2}(\partial _t\psi _1+\mathbf{v_0}\cdot {\varvec{\nabla }} \psi _1)\right] \nonumber \\{} & {} +{\varvec{\nabla }}\cdot \left[ \rho _0{\varvec{\nabla }}\psi _1-\frac{\rho _0 \mathbf{v_0}}{c_s^2}(\partial _t \psi _1 + \mathbf{v_0}\cdot {\varvec{\nabla }}\psi _1)\right] =0, \end{aligned}$$
(6)

where \(c_s\) is the sound speed defined by \(c_s^2\equiv \partial P/\partial \rho =c^2n_2\rho _0/n_0^3\). The field equation (6) describes the propagation of the massless scalar field \(\psi _1\), in an analog curved spacetime as

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _\mu \left( \sqrt{-g}g^{\mu \nu }\partial _\nu \psi _1\right) =0, \end{aligned}$$
(7)

where the analog curved spacetime is given by

$$\begin{aligned} ds^2= & {} \left( \frac{\rho _0}{c_s}\right) ^2 \left[ -(c_s^2-v_0^2)dt^2-2v_rdrdt\right. \nonumber \\{} & {} \left. -2v_\theta rd\theta dt+dr^2+r^2d\theta ^2\right] , \end{aligned}$$
(8)

with \(v_0^2=v_r^2+v_\theta ^2\), \(v_r=\partial _r\psi _0\), and \(v_\theta =\partial _\theta \psi _0/r\). The spacetime line element (8) is still not similar to the ones of the relativistic compact objects in the Kerr coordinates. Therefore, by applying the following transformations in the region \(\xi ^2/r_0\le r<\infty \):

$$\begin{aligned}{} & {} dt\rightarrow dt+\frac{|v_r|}{(c_{s}^2-v_r^2)}dr, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} d\theta \rightarrow d\theta +\frac{|v_r| v_\theta }{r(c_{s}^2- v_r^2)}dr, \end{aligned}$$
(10)

we write it in the standard Kerr-like geometry as

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{\xi ^2}{r_0r}-\frac{m^2\xi ^2}{\pi ^2 r^2}\right) dt^2\nonumber \\{} & {} +\left( 1-\frac{\xi ^2}{r_0r}\right) ^{-1}dr^2-2\frac{m\xi }{\pi }d\theta dt+r^2d\theta ^2, \end{aligned}$$
(11)

where \(\xi =\lambda /2\sqrt{n_0n_2\rho _0}\). Now by introducing the following notations:

$$\begin{aligned} r_{\textrm{H}}=\frac{\xi ^2}{r_0}, \qquad \Omega _{\textrm{H}}=\frac{mr_0^2}{\pi \xi ^3}, \end{aligned}$$
(12)

we obtain the \((2+1)\)-dimensional acoustic black hole line element [28]

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{h(r)}-2\Omega _{\textrm{H}}r_{\textrm{H}}^2d\theta dt+r^2d\theta ^2, \end{aligned}$$
(13)

with the metric functions

$$\begin{aligned} f(r)=1-\frac{r_{\textrm{H}}}{r}-\frac{\Omega _{\textrm{H}}^2r_{\textrm{H}}^4}{r^2}, \qquad h(r)=1-\frac{r_{\textrm{H}}}{r}, \end{aligned}$$
(14)

where \(r_{\textrm{H}}\) is a radius of the acoustic black hole horizon which is determined as the circular ring at which the inward radial velocity of the fluid flow equals the speed of sound, \(v_r=c_s\), and \(\Omega _{\textrm{H}}\) is the angular velocity of the horizon.

In the context of acoustic black holes, an ergoregion can be created by the flow of a fluid with a sufficiently high speed. This flow can produce an effective “event horizon” similar to the event horizon of a real black hole, beyond which sound waves cannot escape. The ergoregion in this case is the region of the fluid flow inside of this effective horizon. It can be seen from the spacetime metric (13) that the axially symmetric acoustic black hole has not only the event horizon defined by the root of \(h(r)=0\) but also the timelike static limit which is the outer bound of the ergoregion that is defined by solution of equation \(f(r)=0\). Thus, the radius of the outer boundary of the ergoregion is located at

$$\begin{aligned} r_{\textrm{E}}=\frac{r_{\textrm{H}}}{2} \left( 1+\sqrt{1+4 \Omega _{\textrm{H}}^2r_{\textrm{H}}^2}\right) . \end{aligned}$$
(15)

As it can be seen in the expression (15), for the nonrotating black hole, the horizon and static limit coincide, i.e., the ergoregion which is a region between the horizon and static limit vanishes – see Fig. 1.

Fig. 1
figure 1

The ergoregion (blue region) of the acoustic black hole in (\(x=r/r_{\textrm{H}}\sin \theta \), \(y=r/r_{\textrm{H}}\cos \theta \)) plane for different values of the angular velocity which is increased from the left panel to the right one. Where the central black region represents inside the acoustic horizon of the black hole

Full size image

Once the black hole starts to rotate, the ergoregion forms and with increasing its rotation, the size of the ergoregion increases. However, unlike the case of the Kerr-like black holes (or black holes in relativity theories), the radius of the event horizon does not depend on the angular velocity of the black hole and it always remains at \(r=r_{\textrm{H}}\).

3 Equations of motion for phonon

Let us study the massless particle motion along the null geodesics of the acoustic black hole spacetime. Since the central object is the acoustic black hole, we consider this massless particle to be a phononFootnote 1 and in this section we study the phonon motion around acoustic black hole. To do so we should first obtain the equations of motion defining the velocity of the particle along all coordinates. Because of the spacetime symmetries (stationary and axial symmetry) we can solve equations of null geodesics in the integrated form due to existence of conserved components of the 3-momentum and the normalization condition, similarly to the standard black holes in vacuum or in external magnetic fields [31]. We use the conservative quantities that are associated with the spacetime symmetries that are in our case the momentum components corresponding to the time and angular coordinates, namely the energy and angular momentum of the particle, given as

$$\begin{aligned} g_{\mu t}u^\mu =-E,\qquad g_{\mu \theta }u^\mu =L. \end{aligned}$$
(16)

where \(u^\mu \) is the three-velocity of the phonon. By solving the given equations simultaneously, we obtain the following expressions of the velocity along the time and angular coordinates:

$$\begin{aligned}{} & {} u^t=\frac{r}{r-r_{\textrm{H}}}E-\frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r(r-r_{\textrm{H}})}L,\nonumber \\{} & {} u^\theta =\frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r(r-r_{\textrm{H}}) }E+\frac{\left( r^2-r_{\textrm{H}}r-\Omega _{\textrm{H}}^2r_{\textrm{H}}^4\right) }{r^3(r-r_{\textrm{H}})}L. \end{aligned}$$
(17)

Now by using the normalization condition \(u^\mu u_\mu =0\), we obtain expression of the radial velocity of phonon as

$$\begin{aligned} \left( u^r\right) ^2=E^2-2\frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r^2}EL-\frac{\left( r^2-r_{\textrm{H}}r-\Omega _{\textrm{H}}^2r_{\textrm{H}}^4\right) }{r^4}L^2, \end{aligned}$$
(18)

To write expression of the radial velocity (18) in the form of a motion in the central field, we rewrite it using the method of effective potential

$$\begin{aligned} \left( u^r\right) ^2=(E-V_{+})(E-V_{-}), \end{aligned}$$
(19)

where the effective potentials defined as

$$\begin{aligned} V_{\pm }=L\left[ \frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r^2}\pm \frac{\sqrt{r(r-r_{\textrm{H}})}}{r^2}\right] . \end{aligned}$$
(20)

One can notice from (20) that \(V_+\) and \(V_-\) have the following cross symmetry in \(\Omega _{\textrm{H}}\rightarrow -\Omega _{\textrm{H}}\) transformation:

$$\begin{aligned} V_{+}(-\Omega _{\textrm{H}})=-V_{-}(\Omega _{\textrm{H}}), \qquad V_{-}(-\Omega _{\textrm{H}})=-V_{+}(\Omega _{\textrm{H}}). \end{aligned}$$
(21)
Fig. 2
figure 2

Radial profiles of functions \(V_{\pm }\) given by (20) for the different values of the angular velocity of the acoustic horizon (left panel) and angular momentum of the phonon (right panel). Where gray and blue curves represent \(V_{+}\) and \(V_-\) cases, respectively

Full size image

In order to see the behaviours of the functions \(V_{\pm }\), in Fig. 2 we present their radial profiles for different values of the angular momentum of the particle and angular velocity of the black hole. One can see from Fig. 2 that \(V_+\) is mostly positive with potential barrier-like form, while \(V_-\) is negative with hole form. Therefore, we consider \(V_+\) is the effective potential that governs the phonon motion. A barrier form of the effective potential indicates existence of an unstable circular orbit corresponding to the peak of the potential barrier. To find the location (or radius) of the unstable circular null geodesics (or phononring), one must solve the following equation:

$$\begin{aligned} \frac{dV_{+}}{dr}=0, \end{aligned}$$
(22)

that gives a radius of the circular null geodesics to be at

$$\begin{aligned}{} & {} r_{\textrm{ph1}}/r_{\textrm{H}}=1+\frac{(-3)^{2/3}r_{\textrm{H}}\left( 3+16 \Omega _{\textrm{H}} ^2r_{\textrm{H}}^2\right) }{6A}-(-3)^{1/3}A,\nonumber \\{} & {} r_{\textrm{ph2}}/r_{\textrm{H}}=1+\frac{A}{2\times 3^{2/3}r_{\textrm{H}}}+\frac{r_{\textrm{H}}\left( 3+16\Omega _{\textrm{H}}^2r_{\textrm{H}}^2\right) }{2\times 3^{1/3} A}. \end{aligned}$$
(23)

where

$$\begin{aligned} A=\root 3 \of {-9r_{\textrm{H}}^3+i4\sqrt{3}r_{\textrm{H}}^4\Omega _{\textrm{H}}\sqrt{27+144\Omega _{\textrm{H}}^2r_{\textrm{H}}^2+256 \Omega _{\textrm{H}}^4r_{\textrm{H}}^4}}. \end{aligned}$$

As shown by above expressions, and in Fig. 3, around the rotating acoustic black hole two types of circular null geodesics appear: prograde (co-rotating, i.e. \(\Omega _{\textrm{H}}L>0\)) and counter-rotating (\(\Omega _{\textrm{H}}L<0\)). As in the case of the standard Kerr-like black holes [32,33,34], the co-rotating circular null geodesics is located closer to the black hole than the counter-rotating one.

In the asymptotic cases the radius of the circular null geodesics behaves for \(r_{\textrm{H}}\Omega _{\textrm{H}}\ll 1\) as follows [35]:

$$\begin{aligned} r_{\textrm{ph}}=r_{\textrm{H}}\left( \frac{3}{2}\mp \frac{2r_{\textrm{H}}\Omega _{\textrm{H}}}{\sqrt{3}}+\frac{8r_{\textrm{H}}^2\Omega ^2}{9}\right) +O\left[ (r_{\textrm{H}}\Omega _{\textrm{H}})^3\right] , \end{aligned}$$
(24)

where the upper and lower sings correspond to the co- and counter-rotating circular null geodesics, respectively. The radius of the co-rotating circular null geodesics in the regime \(r_{\textrm{H}}\Omega _{\textrm{H}}\gg 1\) behaves as

$$\begin{aligned} r_{\textrm{ph}}=r_{\textrm{H}}\left( 1+\frac{1}{r_{\textrm{H}}^2\Omega _{\textrm{H}}^2}\right) +O\left[ (r_{\textrm{H}}\Omega _{\textrm{H}})^{-3}\right] , \end{aligned}$$
(25)

while the radius of the counter-rotating circular null geodesics in this regime behaves as

$$\begin{aligned} r_{\textrm{ph}}=r_{\textrm{H}}\left( 1+2r_{\textrm{H}}\Omega _{\textrm{H}}\right) +O\left[ (r_{\textrm{H}}\Omega _{\textrm{H}})^{-1}\right] . \end{aligned}$$
(26)
Fig. 3
figure 3

The radii of co-rotating (solid curve) and counter-rotating (dashed curve) circular null geodesics around the acoustic black hole as a function of the angular velocity of the black hole. Where the shaded region represents ergoregion while the dotdashed curve represents the outer boundary of ergoregion

Full size image

One can see from Fig. 3 that the co-rotating phononring is located inside the ergoregion of the acoustic black hole when the angular velocity of the black hole \(\Omega _{\textrm{H}}r_{\textrm{H}}\ge 0.44096\).

4 Capture of phonons

In this section we concentrate on the motion of massless acoustic particle (phonon) around acoustic black hole with more details by using the equations of motion presented in a previous section. In order to analyse the motion, we first rewrite the radial equations of motion (18) so that its right hand side is given in the polynomial form in the radial coordinate as

$$\begin{aligned} r^4\left( u^r\right) ^2=E^2r^4-L(L+2\Omega _{\textrm{H}}r_{\textrm{H}}^2E)r^2+r_{\textrm{H}}L^2r+\Omega _{\textrm{H}}^2r_{\textrm{H}}^4L^2.\nonumber \\ \end{aligned}$$
(27)

It is well-known that the zeros of the function on the right hand side of Eq. (27) correspond to the turning points where the radial velocity vanishes. Despite number of these zeros is four, being dependent on the values of the angular momentum and energy of the phonon, only up to two of them can be physical which are located outside the acoustic horizon (\(r_0>r_{\textrm{H}}\)). This can be confirmed from the single barrier-like shape of the effective potential in Fig. 2.Footnote 2 The variations in the values of the angular momentum and energy delivers more uncertainty in finding critical values for these quantities. Therefore, as we have noticed from the radial equation of motion (27), by dividing both sides of equation by the square of the energy, one can adopt a new parameter, impact parameter, which is defined by the ratio of angular momentum and energy as

$$\begin{aligned} b=\frac{L}{E}. \end{aligned}$$
(28)

Prior to turning to the equations, in order to decrease the number of physical quantities we introduce new parameter, impact parameter b that describes the closest approach distance of the particle to the central object before reaching the observer at spatial infinity.

As we have mentioned above, the number of turning points can be zero, one or at most two. For the phonon approaching the acoustic black hole from from spatial infinity, the following scenarios are possible:

  1. (i)

    No turning point: in this case the phonon coming from infinity has subcritical impact parameter (\(b<b_{\textrm{cr}}\)) and it falls to the black hole. This case corresponds to the shaded region in Fig. 4.

  2. (ii)

    Two turning points (\(r_{\textrm{H}}<r_1<r_2\)): in this case the phonon coming from spatial infinity has greater impact parameter than the critical one (\(b>b_{\textrm{cr}}\)) and it reaches the turning point \(r_2\) and is scattered back to finally escape from the black hole. This case corresponds to the unshaded region in Fig. 4. The turning point at \(r_1\) is relevant for phonons moving in vicinity of the horizon.

  3. (iii)

    One turning point (\(r_{\textrm{H}}<r_1=r_2\)): in this case the phonon has the critical impact parameter (\(b=b_{\textrm{cr}}\)). It reaches the turning point at \(r_1=r_2\) and get captured by the black hole phononcircle. This case corresponds to the solid black curve separating capture and scatter regions in Fig. 4.

Fig. 4
figure 4

The capture and scatter regions of the phonon coming from infinity in the parametric space by the acoustic black hole

Full size image

Note that if one considers the phonon is emitted just outside the horizon and under the phononring (\(r_{\textrm{H}}<r<r_{\textrm{ph}}\)), above listed first and second scenarios would change slightly as in the case there is no turning point, phonon escapes to infinity, while in the two turning points case (\(r_{\textrm{H}}<r_1<r_2\)), the phonon reaches turning point \(r_1\) and falls back to the black hole. Thus, for the phonon emitted just outside the acoustic horizon of the black hole, scatter and capture regions in Fig. 4 would exchange their places.

As we have mentioned in the third scenario above, the critical impact parameter corresponds to the case when both turning points coincide. For this case, one can rewrite the equation of motion (27) in the following form:

$$\begin{aligned} r^4\left( u^r\right) ^2=E^2(r-r_1)^2(r-r_3)(r-r_4), \end{aligned}$$
(29)

where \(r_3\) and \(r_4\) are complex conjugates. To find the critical impact parameter, we should find a condition in which two real zeros coincide, \(r_1=r_2\). This happens only if the discriminant of the polynomial on the right hand side of (27) vanishes. By finding the discriminant of the \(7\times 7\) Sylvester’s matrix, as in [38,39,40] (or alternative method can also be used as in [41,42,43]), we obtain the critical impact parameter as

$$\begin{aligned} b_{\textrm{cr}}=-\frac{2 r_{\textrm{H}}^2 \Omega _{\textrm{H}} \left( 3+16 r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2\right) }{3 \left( 1+4 r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2\right) }+\frac{a}{\root 3 \of {d}}+\frac{\root 3 \of {d}}{c}, \end{aligned}$$
(30)

with

$$\begin{aligned} a= & {} -\frac{\root 3 \of {2} r_{\textrm{H}}^2 \left( 3+16 r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2\right) \left( 27+108 r_{\textrm{H}}^2 \Omega _{\textrm{H}}^2+64 r_{\textrm{H}}^4 \Omega _{\textrm{H}}^4\right) }{3+12r_{\textrm{H}}^2 \Omega _{\textrm{H}}^2},\\ d= & {} 16 (3 \sqrt{3} r_{\textrm{H}}^2 \left( 64 r_{\textrm{H}}^4 \Omega _{\textrm{H}} ^4{+}28 r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2{+}3\right) \left( 9{-}16r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2\right) ^{1/2} \\{} & {} \times ((r_{\textrm{H}}^2 (4 \Omega _{\textrm{H}}(2 \Omega _{\textrm{H}} (512 r_{\textrm{H}}^6 \Omega _{\textrm{H}} ^4 (\Omega +2) \\{} & {} {-}96 r_{\textrm{H}}^4 \Omega ^2 (\Omega _{\textrm{H}} (9 \Omega _{\textrm{H}}{+}22){+}1){+}18 r_{\textrm{H}}^2 (\Omega (3 \Omega _{\textrm{H}}-59)\\{} & {} -12)+189)- 243)-243)+243))^{1/2}\\{} & {} +r_{\textrm{H}}^2 \left( 16r_{\textrm{H}}^2 \Omega _{\textrm{H}} ^2+3\right) (2 r_{\textrm{H}}^2 \Omega _{\textrm{H}} (4 \Omega _{\textrm{H}} (256 r_{\textrm{H}}^6 \Omega _{\textrm{H}}^5\\{} & {} -96 r_{\textrm{H}}^4 \Omega _{\textrm{H}}^3 (9 \Omega _{\textrm{H}} +11)\\{} & {} +9r_{\textrm{H}}^2 \Omega _{\textrm{H}}(6 \Omega _{\textrm{H}}-59)+189)-243)+243)) ,\\ c= & {} 12 \root 3 \of {2} \left( 1+4r_{\textrm{H}}^2 \Omega _{\textrm{H}}^2\right) . \end{aligned}$$

The asymptotic behaviour of the critical impact parameter for \(r_{\textrm{H}}\Omega _{\textrm{H}}\ll 1\) is given as

$$\begin{aligned}{} & {} b_{\textrm{cr}}=r_{\textrm{H}}\left( \frac{3 \sqrt{3} }{2}-3 r_{\textrm{H}} \Omega _{\textrm{H}}+\frac{2r_{\textrm{H}}^2\Omega _{\textrm{H}} ^2}{\sqrt{3}}\right) +O\left[ (r_{\textrm{H}}\Omega _{\textrm{H}})^3\right] ,\nonumber \\ \end{aligned}$$
(31)

while it is given as the following in the regime \(r_{\textrm{H}}\Omega _{\textrm{H}}\gg 1\):

$$\begin{aligned} b_{\textrm{cr}}=\frac{1}{\Omega _{\textrm{H}}}\left( 1-\frac{1}{8\Omega _{\textrm{H}}^2r_{\textrm{H}}^2}\right) +O\left[ (r_{\textrm{H}}\Omega _{\textrm{H}})^{-5}\right] . \end{aligned}$$
(32)

Since the spacetime under consideration is three dimensional, one cannot speak about the area of acoustic shadow (deaf region), instead, \(b_{\textrm{cr}}\) represents the radius of the deaf region.

5 Weak acoustic lensing

In analogy to the gravitational lensing of the photons on a central gravitating object, we study lensing of the phonons on the acoustic black hole in the weak field regime. We consider that the phonon is travelling from source to detector passing by the acoustic black hole. To study this, we use equations of motion (17) and (18) rewritten in terms of the impact parameter as:

$$\begin{aligned}{} & {} u^t=E\frac{r^2-b\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r(r-r_{\textrm{H}})}, \end{aligned}$$
(33)
$$\begin{aligned}{} & {} u^r=E\sqrt{1-\frac{2 b \Omega _{\textrm{H}}r_{\textrm{H}}^2}{r^2}-\frac{b^2\left( r^2-r_{\textrm{H}}r-\Omega _{\textrm{H}} ^2r_{\textrm{H}}^4\right) }{r^4}}, \end{aligned}$$
(34)
$$\begin{aligned}{} & {} u^\theta =E\left[ \frac{b}{r^2}+\frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2}{r(r-r_{\textrm{H}})}-\frac{b\Omega _{\textrm{H}}^2r_{\textrm{H}}^4}{r^3(r-r_{\textrm{H}})}\right] . \end{aligned}$$
(35)

Once the phonon approaches the black hole, its trajectory starts to deviate from the initial straight line and this deviation is measured by the deflection angle of its trajectory from its initial direction. Due to this deflection in the trajectory, its travel time from source to observer (detector) increases. By using these equations of motion we study the deflection angle and time delay of the phonon in the field of the acoustic black hole.

5.1 Deflection angle

Once the phonon approaches the black hole, its trajectory starts to deviate from the initial straight line and this deviation is measured by the deflection angle of its trajectory from its initial direction. The deflection angle, \(\alpha \), can be determined by the following equation:

$$\begin{aligned} \alpha =\int _{-\infty }^{\infty }\left( \frac{d\theta }{dr}\right) dr-\pi . \end{aligned}$$
(36)

Here we consider that the phonon emitted from the source which is located far away the black hole approaches the black hole reaching minimal distance \(r_0\) and travels to the detector (observer) at spatial infinity. Since both the source and the detector are located very far from the black hole and there is negligible deflection far away from the source, we can treat both as located at \(r=\infty \) and (36) can be written as

$$\begin{aligned} \alpha =2\int _{r_0}^{\infty }\left( \frac{d\theta }{dr}\right) dr-\pi , \end{aligned}$$
(37)

where \(d\theta /dr\equiv u^\theta /u^r\) and can be written in terms of the equations of motion (34) and (35) as

$$\begin{aligned} \frac{d\theta }{dr}=\frac{b\left( r^2-r_{\textrm{H}}r-\Omega _{\textrm{H}} ^2r_{\textrm{H}}^4\right) +r^2 \Omega _{\textrm{H}}r_{\textrm{H}}^2 }{(r-r_{\textrm{H}}) r \sqrt{\left( r^2-b\Omega _{\textrm{H}}r_{\textrm{H}}^2\right) ^2 -b^2r\left( r-r_{\textrm{H}}\right) }}, \end{aligned}$$
(38)

One can see that (38) diverges at \(r_0\) and the impact parameter corresponding to this distance equals

$$\begin{aligned} b_\pm =\frac{r_0^2}{\Omega _{\textrm{H}}r_{\textrm{H}}^2\pm \sqrt{r_0(r_0-r_{\textrm{H}})}}. \end{aligned}$$
(39)

One can see from (39) that there are two (plus and minus) families of impact parameter of the null geodesics corresponding to upper and lower signs. However, the value of \(b_-\) is negative or less than the critical value of the impact parameter which ensures the capture of the phonon by the black hole. Therefore, hereafter we write the equations for the both families of phonon, but in calculations we only consider the plus family. From the expression of the impact parameter it is obvious that an increase in the value of the closest approach distance of phonon to the black hole, \(r_0\), the impact parameter of the phonon increases. By replacing impact parameter (39) with (38), the expression (38) takes the new form

$$\begin{aligned} \frac{d\theta }{dr}=\frac{r^2 \sqrt{r_0(r_0-r_{\textrm{H}})}\Omega _{\textrm{H}}r_{\textrm{H}}^2\pm r(r-r_{\textrm{H}})r_0^2\pm \Omega _{\textrm{H}}^2r_{\textrm{H}}^4 (r^2-r_0^2)}{r(r-r_{\textrm{H}}) \sqrt{\left\{ r_0^2\Omega _{\textrm{H}}r_{\textrm{H}}^2+r^2 \left[ \Omega _{\textrm{H}}r_{\textrm{H}}^2 \pm \sqrt{r_0(r_0-r_{\textrm{H}})}\right] \right\} ^2-r_0^4r(r-r_{\textrm{H}})}}. \end{aligned}$$
(40)

Since we are considering the acoustic lensing in the “weak field regime” where \(r_{\textrm{H}}/r_0\ll 1\), in order to simplify integrand (40), we introduce new variable \(u\equiv 1/r\) (where \(dr=-du/u^2\)) and the the deflection angle (37) takes the new form as

$$\begin{aligned} \alpha (r_0)=-2\int _{0}^{1/r_0}du\left[ \frac{\Omega _{\textrm{H}}r_{\textrm{H}}^2\left[ \Omega _{\textrm{H}}r_{\textrm{H}}^2\pm \sqrt{r_0(r_0-r_{\textrm{H}})}\right] +r_0^2(1-r_{\textrm{H}}u-\Omega _{\textrm{H}}^2r_{\textrm{H}}^4u^2)}{(1-r_{\textrm{H}}u)\sqrt{\left\{ \Omega _{\textrm{H}}r_{\textrm{H}}^2\left( r_0^2u^2+1\right) \mp \sqrt{r_0(r_0-r_{\textrm{H}})}\right\} ^2-u^2(1-ur_{\textrm{H}})r_0^4}}\right] -\pi .\nonumber \\ \end{aligned}$$
(41)

Integration of (41) cannot be done analytically. Therefore, as we are considering the weak field lensing, we solve this integral in this limit, considering the spacetime is slowly rotating and obtain the following approximate result:

$$\begin{aligned} \alpha (r_0)= & {} \frac{2r_{\textrm{H}}}{r_0}{-}\left( 1{-}\frac{15\pi }{16}\pm 2\Omega _{\textrm{H}}r_{\textrm{H}}{-}\frac{3\pi }{4}\Omega _{\textrm{H}}^2r_{\textrm{H}}^2\right) \left( \frac{r_{\textrm{H}}}{r_0}\right) ^2\nonumber \\{} & {} +O\left[ \left( \frac{r_{\textrm{H}}}{r_0}\right) ^3, (r_{\textrm{H}}\Omega _{\textrm{H}})^3\right] . \end{aligned}$$
(42)

One can see from the deflection angle (42) that a trajectory of the phonon passing by the corotating acoustic black hole is deflected less than the one passing by the same distance of the counter-rotating side of the black hole.

Fig. 5
figure 5

The deflection angle of the phonon (top panels) passing by the acoustic black hole in the weak field limit (WFL) given by (42) and exact one calculated numerically in (37) and the relative error of the WFL approximation (bottom panels) as a function of the closest approach distance

Full size image

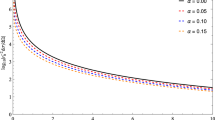
In order to estimate the accuracy of the weak field approximation method, we calculated the relative error as

$$\begin{aligned} \varepsilon =\left| 1-\frac{\mathrm{approx.}}{\textrm{exact}}\right| \times 100\%, \end{aligned}$$
(43)

where approx. refers a result of the weak field limit given by (42). The difference of results of the exact deflection angle and one in the weak field approximation as well as the relative error of the weak field approximation are presented in Fig. 5 for various values of the spacetime angular velocity. We can see in Fig. 5 that as long as the closest-approach point is not very close to the black hole, the weak field approximation provides very accurate results. Moreover, one can notice from these figures that trajectory of the phonon passing by the black hole by co-rotating side is less deflected from its initial direction than for the counter-rotating side. Furthermore, the slow-rotation and weak field regime approximation has very good accuracy.

5.2 Time delay

As we have stated earlier due to the change in the trajectory of the phonon its travel time from the source to the observer increases and it reaches observer with a delay. In this subsection we calculate this delay in time by following similar procedure as in the previous subsection. We first consider the phonon is travelling from the source at \(r_1\), passing close to the acoustic black hole, to observer at \(r_2\) and coming back – see Fig. 6b. Total time of this round trip is calculated by using the following equation:

$$\begin{aligned} t(r_1,r_2)=2\left[ t(r_1,r_0)+t(r_2,r_0)\right] , \end{aligned}$$
(44)

where

$$\begin{aligned} t(r_k,r_0)=\int _{r_0}^{r_k}dr\left( \frac{dt}{dr}\right) , \quad r_k>r_0 \quad \textrm{and} \quad k=1, 2.\nonumber \\ \end{aligned}$$
(45)

The integrand of (45) can be written in terms of equations of motion (33) and (34) in the following form:

$$\begin{aligned} \frac{dt}{dr}=\frac{r \left( r^2-b \Omega _{\textrm{H}} r_{\textrm{H}}^2 \right) }{(r-r_{\textrm{H}}) \sqrt{\left( r^2-b \Omega _{\textrm{H}} r_{\textrm{H}}^2\right) ^2-b^2 r (r-r_{\textrm{H}})}}. \end{aligned}$$
(46)

Again by following the procedure presented in previous subsection, we rewrite integrand (46) in terms of the impact parameter (39) corresponding to the closest approach distance as

$$\begin{aligned} \frac{dt}{dr}=\frac{r \left[ \Omega _{\textrm{H}} r_{\textrm{H}}^2(r^2-r_0^2)\pm r^2\sqrt{r_0(r_0-r_{\textrm{H}})}\right] }{(r-r_{\textrm{H}}) \sqrt{\left\{ r_0^2\Omega _{\textrm{H}}r_{\textrm{H}}^2-r^2 \left[ \Omega _{\textrm{H}}r_{\textrm{H}}^2\pm \sqrt{r_0(r_0-r_{\textrm{H}})} \right] \right\} ^2-r_0^4r(r-r_{\textrm{H}})}}. \end{aligned}$$
(47)
Fig. 6
figure 6

The qualitative picture of round trips of photon from E to O and back in Newtonian (a) and relativistic (b) theories of gravity

Full size image

This integral cannot be solved analytically. Therefore, prior to solving it approximately, we introduce new variable instead of the radial coordinate as \(u\equiv 1/r\) and we write the integral (45) as

$$\begin{aligned} t(r_k,r_0)=\int _{1/r_k}^{1/r_0}du\left[ \frac{\Omega _{\textrm{H}} r_{\textrm{H}}^2(1-r_0^2u^2)\pm \sqrt{r_0(r_0-r_{\textrm{H}})}}{u^2(1-r_{\textrm{H}}u) \sqrt{\left\{ r_0^2\Omega _{\textrm{H}}r_{\textrm{H}}^2u^2- \left[ \Omega _{\textrm{H}}r_{\textrm{H}}^2 \pm \sqrt{r_0(r_0-r_{\textrm{H}})}\right] \right\} ^2-r_0^4u^2(1-r_{\textrm{H}}u)}}\right] . \end{aligned}$$
(48)

In the weak field and slowly rotating black hole regimes, the integrand of above given expression can be expanded and solved analytically. In this case, the integral (48) takes the approximate form

$$\begin{aligned} t(r_k,r_0)= & {} \sqrt{r_k^2{-}r_0^2}{+}\frac{3\Omega _{\textrm{H}}r_{\textrm{H}}^3 }{2r_0}\left[ \frac{\pi \Omega _{\textrm{H}}r_{\textrm{H}}}{2}{-}\frac{(r_0+2 r_k)\sqrt{r_k^2{-}r_0^2}}{r_k(r_0+r_k)}\right] \nonumber \\{} & {} +r_{\textrm{H}} \left[ \frac{\sqrt{r_k^2-r_0^2}}{2 (r_0+r_k)}+\coth ^{-1}\left( \frac{r_k}{ \sqrt{r_k^2-r_0^2}}\right) \right] ,\nonumber \\{} & {} +\frac{r_{\textrm{H}}^2}{8 r_0}\left[ -\frac{(5r_0+4 r_k) \sqrt{r_k^2-r_0^2}}{(r_0+r_k)^2}\right] , \end{aligned}$$
(49)

where we have made use of the inverse hyperbolic function

$$\begin{aligned} \coth ^{-1} x=\frac{1}{2}\ln \left( \frac{x+1}{x-1}\right) . \end{aligned}$$
Fig. 7
figure 7

The Shapiro time delay of the phonon (top panels) passing by the acoustic black hole in the weak field limit (WFL) for the case that the observer and source are located far from the black hole (at \(r_1=r_2=10^3r_0\)) given by (53) and exact one calculated numerically in (48) and the relative error of the WFL approximation (bottom panels) as a function of the closest approach distance

Full size image

If we consider the total time spent for the round trip between \(r_1\) and \(r_2\) in Newtonian gravity (or in the absence of the central gravitational object), in this case the phonon travels along EC and CO adjacents of the two ESC and OSC right triangles, respectively – see Fig. 6a. In this case the total time spent for the round trip equals

$$\begin{aligned} t_{N}(r_1,r_2)=2\left( \sqrt{r_1^2-r_0^2}+\sqrt{r_2^2-r_0^2}\right) . \end{aligned}$$
(50)

By comparing expressions (49) and (50), one can notice that the time spent in the field acoustic black hole (49) is greater than in the Newtonian gravity. This difference, so-called time delay \(\Delta t=t(r_1,r_2)-t_N(r_1,r_2)\), is given by

$$\begin{aligned} \Delta t= & {} \sum _{k=1}^2\left\{ \frac{3\Omega _{\textrm{H}}r_{\textrm{H}}^3 }{2r_0}\left[ \frac{\pi \Omega _{\textrm{H}}r_{\textrm{H}}}{2}-\frac{(r_0+2 r_k)\sqrt{r_k^2-r_0^2}}{r_k(r_0+r_k)}\right] \right. \nonumber \\{} & {} \left. +r_{\textrm{H}} \left[ \frac{\sqrt{r_k^2-r_0^2}}{2 (r_0+r_k)}+\coth ^{-1}\left( \frac{r_k}{ \sqrt{r_k^2-r_0^2}}\right) \right] \right\} . \end{aligned}$$
(51)

In the case of an assumption that the central object is the Schwarzschild black hole (\(\Omega _{\textrm{H}}=0\)), the time delay (51) reduces to the Shapiro time delay given as

$$\begin{aligned} \Delta t= & {} 2r_{\textrm{H}}\left[ \ln \left( \frac{r_1+\sqrt{r_1^2-r_0^2}}{r_0}\right) +\ln \left( \frac{r_2+\sqrt{r_2^2-r_0^2}}{r_0}\right) \right. \nonumber \\{} & {} \left. +\frac{1}{2}\sqrt{\frac{r_1-r_0}{r_1+r_0}}+\frac{1}{2}\sqrt{\frac{r_2-r_0}{r_2+r_0}}\right] . \end{aligned}$$
(52)

If we consider the radii \(r_1\) and \(r_2\) are very far from the black hole, as \(r_0\ll r_1, r_2\), the time delay becomes (51)

$$\begin{aligned} \Delta t= & {} 2r_{\textrm{H}}\left[ 1+2\ln \left( \frac{4r_1r_2}{r_0^2}\right) \right] \nonumber \\{} & {} +\frac{3r_{\textrm{H}}^3\Omega }{r_0}\left( \pi \Omega _{\textrm{H}}r_{\textrm{H}}-4\right) +O(r_1^{-1},r_2^{-1}). \end{aligned}$$
(53)
Table 1 The deflection angle and time delay of the phonon for some values of the acoustic black hole parameters and the locations of emitter and observer. In calculations we set \(r_1=r_2\)
Full size table

In Fig. 7 as in the previous subsection we present the difference in time of the phonon spent for travelling from source to observer and back passing by the acoustic black hole with the closest approach distance \(r_0\) and in the absence of the black hole cases in both numerical (exact) and approximate (weak field limit) cases. Moreover, we estimated the relative error of the approximate method for some values of the spacetime parameters.

In Table 1 we calculate deflection angle of the phonon travelling from \(r_1\) to \(r_2\) passing near by the acoustic black hole and the time delay of the phonon making round trip from \(r_1\) to \(r_2\) and back to \(r_1\) relative to the absence case of the absence of the acoustic black hole for some values of the spacetime parameters. This calculations can be used in laboratory to probe acoustic black hole spacetime.

6 Conclusion

We studied the motion of a phonon that is a particle of the sound wave around (2+1)-dimensional axially symmetric acoustic (sonic) black hole. Since the acoustic black hole for phonon has analogy (several common properties) with the real relativistic black holes for the photon, by studying the motion of phonon (acoustic particle) around acoustic black hole within the relativistic theory framework and generating this process in the laboratory would allow us to verify relativistic effects. Similar to the real black holes in relativity theories, the acoustic black hole possesses the ergoregion whose area only increases with the rotation of the black hole, however, unlike the case of the black holes in relativity theories, its horizon radius does not change with its rotation. Despite the rotation of the black hole does not change size of its horizon, it affects to the radius of the circular null geodesics, as it shrinks (increases) the radius of the co-rotating (counter-rotating) circular null geodesics. Afterwards, one of the effects associated with tests of the relativity theories, weak gravitational lensing that can be easily observed in the laboratories for the acoustic black hole, has been applied to acoustic black hole under study. Since the correctness of the general relativity in the weak fields regime has been verified with high accuracy [44], the kind of calculation we have done in this paper (such as in Table 1) can be used to test the geometry of the acoustic black hole spacetime via the deflection angle of the phonon and its delay in time when it travels from one point to the another one in the field of the acoustic black hole.

Thus, our study has provided new insight into the behavior of phonons in acoustic black holes, specifically in the ergoregion. Our results show that the motion of phonons in this region is affected by the supersonic flow of the fluid and this behavior changes as the rotation of the black hole increases. The study of acoustic black holes opens up new possibilities for further research in the field of black hole physics. It allows scientists to explore the behavior of phonons, which are quanta of sound waves, in a controlled laboratory setting. This can help to gain a deeper understanding of how sound waves behave in the vicinity of black holes, both real and acoustic.

One of the key advantages of studying acoustic black holes in a laboratory setting is that it allows for the testing of various spacetime metrics, which are mathematical models used to describe the properties of black holes. For example, scientists can use laboratory experiments to test the validity of the Schwarzschild and Kerr metrics, which are commonly used metrics to describe the properties of non-rotating and rotating black holes, respectively. Additionally, the study of acoustic black holes can also have important implications for other areas of physics, such as the study of quantum gravity and the behavior of fluids in extreme conditions. Overall, the research on properties of acoustic black holes open new avenue for the researchers to study black holes and their properties in a controlled environment and can lead to a better understanding of black holes.