Abstract
We review recent results for forward jests at the LHC and EIC as obtained within small-x Improved Transverse Momentum Dependent factorization (ITMD). In addition to elementary overview of various approaches to perturbative QCD at high energy, including High Energy Factorization, Color Glass Condensate and ITMD, we describe the Monte Carlo implementation and discuss the existing and unpublished phenomenological results for forward dijets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum Chromodynamics (QCD) is a well established theory that describes interactions of quarks and gluons. However, it still has its challenges. In the high energy domain, one of the long standing problems is finding clear experimental signals of gluon saturation, which is a signature of quasi equilibrium between gluon splitting and gluon fusion in dense nuclear systems. Gluon saturation has been predicted from QCD long time ago [1, 2] and has been extensively studied using various approaches, most recently the Color Glass Condensate (CGC) – i.e. effective theory obtained within QCD (for a reviews see [3,4,5,6,7] and the textbook [8]).
While there is no doubt that gluon distributions must saturate at some point due to the unitarity constraints on the cross section, and there are strong indications of saturation in the data [9,10,11,12,13,14,15,16,17,18,19,20], a complete consensus on reaching it is still to be achieved. This is mainly due to the demanding kinematics, which requires the final states to be measured in the forward region of the detectors. This configuration of jets is triggered by an assymmetry in the partonic state of colliding hadrons – one of the colliding hadron is probed at a very low longitudinal momentum fraction while the other at rather large longitudinal momentum fraction (see also Sect. 2. In this scenario, one expects to reach saturation at values of longitudinal momentum fraction at about \(10^{-5}\). The saturation is also expected to be stronger for nuclei, in the same kinematic domain. Once the saturation is reached the shapes of jet correlation spectra are expected to be broadened as compared to the non-saturated case, although this signal is strongly affected by the Sudakov resummation (see Sect. 6.3). Therefore, it is essential to compare forward jet observables for proton–proton and proton–nucleus collisions.
Another of the challenges in dealing with nuclear targets is the rich collision environment (see e.g. [21]). Moreover, theoretical predictions in high energy QCD are at present not as precise as those requiring ordinary collinear factorization.
Among various final states that can be measured in the context of saturation searches, the system consisting of two identified jets in the forward region (and everything else) plays a special role [22,23,24]. The typical transverse momentum of gluons in a high density medium is of the order of the saturation scale \(Q_s\), which then induces a small imbalance between the jet transverse momenta. The saturation scale is of the order of a few GeV, for sufficiently high collision energy and sufficiently forward. This means, that the jet transverse momenta can be quite large, of the order of twenty GeV or so, and still provide sensitivity to the saturation effects in the back-to-back region. The single inclusive jet production, on the other hand, require jet transverse momenta to be of the order of the saturation scale, thus rather small. Obviously, jets with larger transverse momenta are easier to reconstruct and are “cleaner”. There is also some interest in the forward-central dijets [12, 25,26,27,28], but these do not probe sufficiently low fractions of the longitudinal momenta to be sensitive to saturation. Another appealing feature of harder forward dijets is that their description becomes possible in terms of “generalized” transverse momentum dependent (TMD) factorization, which is easier to implement in Monte Carlo generators than the full CGC.
Dijet yields at relatively forward rapidity have already been measured at the Large Hadron Collider (LHC) by ATLAS collaboration for both proton–proton and proton–lead collisions [29]. Since there was no cross section measurement, the conclusions regarding saturation signals do not give yet a definite answer to whether saturation has been observed or not. Inclusive single forward jet energy spectra for proton–lead collisions measured at CMS CASTOR detector [30] does not provide convincing proof either. Further research and analysis are necessary to gain a better understanding of gluon saturation and its effects on nuclear systems. In particular, more measurements of both proton–proton and proton–lead collisions in the same kinematics are needed. In addition to the ATLAS forward detector, the ALICE collaboration plans to build a more forward detector FoCal [31] that hopefully will shed more light on the saturation phenomenon. The forward jet physics at LHC is complementary to the physics of the Electron Ion Collider (EIC) [32, 33] one of the primary goals of which is to study gluon saturation physics.
In this work, we review the theoretical framework suitable for a description of forward dijet production in hadro and lepto-production in the full azimuthal angle range. The formalism lies in the intersection of the CGC theory and more traditional factorization approach, utilizing TMD gluon distributions. Since the formalism accounts for power corrections it has been dubbed as Improved TMD Factorization (ITMD) [34]. A review of some essential aspects of high energy QCD and the ITMD framework itself is contained in Sect. 4. We shall also review Monte Carlo implementation of the ITMD framework KaTie (Sect. 5), construction of the TMD gluon distributions, as well as recent phenomenological predictions for azimuthal dijet correlations, both for proton–proton and proton–lead collisions, in the kinematics of the forward calorimeters of ATLAS detector and planned FoCal of ALICE (Sect. 6). We also include new unpublished earlier computations of the rapidity distributions for different kinematic cuts.
2 Kinematics
The process in question is the inclusive production of two jets, that is, there are at least two jets with transverse momenta above a certain threshold:
where A is either the proton state p or a nucleus having the four momentum \(P_A\) that is hit by the proton state with four momentum \(P_B\) (see Fig. 1). The produced jets have four momenta \(p_1\) and \(p_2\) and are defined by a proper jet algorithm. X corresponds to other particles produced in the process; there are no kinematic cuts imposed on those additional states. We shall also discuss the complementary DIS process
which will be studied at EIC and will be essential in testing the theoretical formalism and constraining the nonperturbative input.
We are interested in the kinematic regime, where both jets \(J(p_1)\) and \(J(p_2)\) are produced in the “forward” rapidity interval, i.e. both jets have positive (or negative) sufficiently large rapidity. There is no universal definition as to what rapidity is considered sufficiently large. Basing on the current LHC setup, one can consider particles with rapidity \(|y|>2.5\) in the center of mass frame as being produced forward. Taking into account the planned forward calorimeters, the upper limit for the rapidity of reconstructed jets is about \(|y|<5.1\).
In what follows, we define the \(P_A\) and \(P_B\) four momenta as being the two light cone vectors, defining the“plus” and “minus” light cone components:
with the center of mass energy \(s=2P_A\cdot P_B\). Using these, the Sudakov decomposition of any four vector reads:
where
The central assumption in our investigations is that the nucleus (or a proton) is probed at small longitudinal momentum transfers compared to the hadron longitudinal momentum. That is, we define longitudinal momentum fractions
where \(k_1\) is the momentum transferred to the target A, whereas \(k_2\) is the momentum transferred to the proton target. We assume
These fractions can be also expressed in terms of the final state rapidities \(y_i\) and transverse momenta
Therefore, restricting the final states to a window with large rapidities as explicitly defined above and keeping the jet transverse momenta relatively low guarantees the smallness of \(x_A\). For the LHC conditions, in the considered forward kinematic setup the \(x_A\) can be as low as \(10^{-5}\).
In phenomenological applications, we shall follow the realistic setup of the LHC experiments that measured (or plan to measure) forward dijets in proton–proton and proton–nucleus collisions: ATLAS and ALICE with their planned forward calorimeter FoCal. We shall discuss the kinematic cuts more precisely in Sect. 6 devoted to phenomenology.
3 QCD at high energy
One of the biggest achievements in theoretical developments of perturbative QCD are hard factorization theorems (see [35] for a review). These include the collinear factorization and the TMD factorization. They are applicable for processes that admit a large ”hard scale” \(Q^2\), related to the momentum transfer to a hadron, so that the coupling constant \(\alpha _s(Q^2)\) is small enough to permit the perturbation theory. Both types of factorization can be proved to all orders in coupling constant \(\alpha _s\) and the leading power in the hard scale \(Q^2\), for few sufficiently inclusive processes. In practice, not only the truncation of perturbation series in \(\alpha _s\) is necessary (at present at very low orders), but also the limit \(Q^2 \rightarrow \infty \) is rarely adequate. Indeed, when comparing with experimental data, for example for large transverse momenta dijet production in the central rapidity region [36, 37], both a normalization factor (the so-called K-factor) is needed, as well as a resummation (parton shower) with the addition of semi-nonperturbative effects (like multiple partonic interactions).
In computations within the collinear factorization, one encounters powers of logarithms of the CM energy \(\bar{s}\) of colliding partons at every perturbative order, \(\bar{s}=x_A x_B s\), where s is the total available CM energy. Therefore, at very large total CM energies, small transverse momenta, forward particle production, or a mixture of all of these conditions, these logarithms become large, even at the perturbative orders not accounted for in the computation. Thus, the perturbative expansion becomes less reliable. Although within the collinear factorization, it is in principle possible to resum the logarithms of small x (see [38] and references therein), this does not address the two important issues.
First, within the collinear factorization the evolution of the Parton Distribution Functions (PDFs) describing the nonperturbative input is always linear, which is a result of a simple branching of partons. Denote a PDF as \(f_i(x,\mu ^2)\), where i is a parton type, x is the longitudinal momentum fraction carried by the parton, and \(\mu ^2\) is the factorization scale. The evolution of \(f_i(x,\mu ^2)\) happens in the scale \(\mu ^2\) that, intuitively, is inversely proportional to the spatial resolution scale. Decreasing the resolution scale, we find more gluons in a hadron due to the perturbative gluon emissions, and thus the gluon PDF slowly grows with decreasing \(\mu ^2\). The collinear factorization, however, does not directly restrict the behaviour of the PDFs in x, which turns out to be much more dramatic. The global fits (e.g. [39, 40]) predict a very steep increase of gluon PDF \(f_g(x,\mu ^2)\) in 1/x. This is a consequence of the QCD perturbation theory and simple branching of partons. As mentioned in the previous paragraph, the perturbative calculations admit logarithms of 1/x. Resummation of these leading logarithms to all orders predicts growth of the cross section as a power of 1/x. In fact, this behaviour is usually implied in the initial parametrizations of the gluon PDFs. As we will recall in more detail in the following sections, the linear growth of the PDFs with the energy and, in turn, the cross section is in contradiction with the unitarity of the scattering matrix [41], known as the Froissart bound. Taming this behavior requires including gluon recombination, which cannot be implemented in any kind of linear evolution.
Second, the collinear factorization neglects higher twist effects that contribute to the power corrections of the order \(\mathcal {O}(1/Q^2)\). As mentioned, realistically \(Q^2\) is always finite. Moreover, for many processes, the inverse powers of \(Q^2\) can be enhanced by other scales; for example, dijet production processes involve the dijet momentum imbalance which enhances the power corrections away from the correlation peak. For a discussion of higher twists in inclusive DIS and Drell-Yan see e.g. [42,43,44,45,46,47].
Below, we briefly recall the existing approaches that attempt to address the above issues (for an extensive and pedagogical review of high energy QCD see [8]). We focus on the central ideas and main references, skipping the technical details. We start with recalling the issues of energy dependence of hadronic cross section, a discussion that predates the QCD.
3.1 Pomeron and the Reggeon field theory
Historically, Pomeron – the Regge trajectory with the intercept greater than one and vacuum quantum numbers, was introduced in order to explain the growth of the total hadronic cross section with energy observed in the data gathered in the early 1970s by the Intersecting Storage Rings (ISR) at CERN (see e.g. [48]). The Pomeron exchange results in a behavior of the cross section as \(\sim s^{\omega _0}\), where \(\omega _0>1\). However, according to the Froissart theorem [41] based on the unitarity and analytic properties of the S-matrix, the cross section should not grow faster than \(\sim \ln s\). These facts, although pre-dating QCD, provide a major motivation for the study of high energy QCD.
The nature of the Pomeron quasi-particle is essentially non-perturbative. Together with its parity-odd partner, the Odderon, they constitute a possible effective theory of strong interactions with color singlet degrees of freedom. Typically, their interactions are described by the Euclidean field theory called the Regge field theory [49] (see also [50,51,52]). In its most general form, it includes the multiple Pomeron and Odderon interactions, but in the context of unitarity, one typically studies a truncation to the triple Pomeron vertex.
In perturbative QCD the parity even color singlet state exchanged in the t channel can be made out of two gluons. This leads to the perturbative Pomeron of Balitsky, Fadin, Kuraev and Lipatov (BFKL) [53,54,55,56] (for a pedagogical review see eg. [57]). The corresponding energy evolution equation of the Pomeron Green function gives the power like behavior of the cross section with energy. The triple Pomeron vertex needed for nonlinear taming of the growth can also be constructed in QCD [58,59,60]. The difference in the Pomeron intercept derived in perturbative QCD and the one needed to describe for example elastic hadron-hadron scattering leads to a distinction between the hard and the soft Pomeron.
There are numerous applications of the Pomeron calculus to particle production; in particular, there exist several Monte Carlo event generators: PHOJET and DPMJET [61, 62], EPOS [63, 64], SIBYLL [65, 66], QGSJET [67, 68].
3.2 Lipatov effective action
In view of the BFKL approach to Pomeron physics, it turns out, that the computations in QCD at high energy can be done using the effective building blocks: the “reggeized” gluons R and effective interaction vertices \(RR\rightarrow g\). The former are characterized by the eikonal coupling to ordinary QCD vertices (due to the high energy approximation) and the “reggeization” factor \((-s)^{\omega (t)}\) appearing due to radiative corrections, where \(\omega (t)\) is the perturbative Regge trajectory. The RRg effective vertices are separated in rapidity (the so-called quasi-multi-Regge kinematics).
Stripping off the reggeization factors, the building blocks can be formalized into an effective gauge invariant action [69, 70] that contains both the QCD degrees of freedom, and the reggeized gluon fields \(A_+\), \(A_{-}\), that, roughly, by virtue of equations of motions are straight semi-infinite Wilson lines along two light-cone directions \(P_A\) and \(P_B\). The vertices are naturally generalized into \(RRg\dots g\) vertices, as well as multiple reggeon vertices. For a review see [71] (chapter 11 in [72]).
Using Lipatov’s high energy effective action beyond tree level is rather cumbersome due to double counting between gluon field and composite reggeons, but several results have been obtained (see for example [73,74,75,76,77]). The important feature of that action is that it includes all the necessary ingredients to unitarize the cross section. In particular in [78,79,80,81] a relation to the Color Glass Condensate was established and investigated.
3.3 High energy operator product expansion
It turns out that in high energy QCD, the non-perurbative information is rather naturally contained in hadronic matrix elements of straight infinite Wilson lines, instead of the PDFs. It is convenient to recall the evolution equation for their energy dependence via the high energy operator product expansion (OPE) [82]. Similar to Wilsonian OPE, it is straightforwardly applicable only for fully inclusive quantities.
Consider a projectile, a photon for simplicity, scattering off a hadron in a frame where it is moving slowly. The photon fluctuates into a pair of quarks well before it hits the target and – at high energies – interacts with the target eikonally. In the considered high energy kinematics, the target is made of gluons, that are treated as background field, which shrinks to a shock wave. The quark-antiquark dipole interacts with that shockwave becoming a straight infinite Wilson lines of the background field. Since the scattering cross section is related to the hadronic matrix element of the time ordered product of quark current, effectively, the above picture provides a means of decomposing the hadronic tensor into products of Wilson lines and the so-called impact factors. This is the essence of the high energy operator product expansion [82]. More precisely, the time ordered product of electromagnetic currents at high energy can be decomposed as
where
is the straight infinite Wilson line along the plus light cone direction and fixed transverse position, whereas \(\mathcal {I}^{\mu \nu }_2\) is the leading order impact factor. The dots represent the subleading corrections. In the collinear factorization, usually the hadronic matrix element is traded to the partonic one when deriving the evolution equation via operator renormalization procedure. Analogously, here the hadronic matrix elements is traded to the matrix element of the background gluon field
The distinction between the background field and the projectile is related to the rapidity; formally the matrix elements depend on the rapidity cutoff. This dependence is explicitly introduced when regulating the rapidity divergence appearing when considering perturbative correction. However, a perturbative gluon interacting with the shock wave generates an adjoint Wilson line that gives a product of four fundamental Wilson lines. The evolution of this four-point correlator generates in turn further higher point correlators. Therefore the resulting evolution equation is not closed and consists of a tower of products of an increasing number of Wilson lines, known as the Balitsky hierarchy. However, at the large \(N_c\) limit, the hierarchy is terminated and one obtains a single evolution equation for the product of two Wilson lines, the so-called dipole amplitude
where \(\eta \) is the implicit rapidity cutoff. The evolution equation [82] reads
It was also obtained independently in [83] using the Mueller dipole approach [84] and is therefore called the Balitsky–Kovchegov (BK) equation.
Typically one introduces new variables, the dipole size
and the impact parameter
The usual treatment of that equation assumes an infinite target and thus neglects the impact parameter dependence [85,86,87,88,89,90,91,92,93], but solutions with impact parameter are also known, see [94] and the following works, including [95,96,97,98,99,100].
Let us finally mention the huge progress in controlling next-to-eikonal corrections, see [101,102,103,104,105,106,107], as well as the development of the next-to-leading order BK equation [108,109,110,111,112,113].
3.4 Color glass condensate
The High Energy Operator Product expansion does provide the evolution equation but does not allow for the calculation of the non-perturbative correlators itself. On the other hand, the effective theory of high energy QCD – the Color Glass Condensate (CGC) theory is a convenient framework to approach both the evolution and averages of Wilson lines in the background color field. For a full review of the CGC theory see for example [5].
In this part of the overview, we would like to focus on the essential aspects of the CGC theory, in particular how the saturation of a gluon distribution emerges. The procedure of computing dijet cross section within the CGC will be outlined in the next section.
To this end, let us now review a famous model of large nucleus – the McLerran–Venugopalan (MV) model [114, 115]. Assume we view a large nucleus with a large number of nucleons in a frame where it is moving with a very large velocity. In that boosted frame, large x partons are localized in one of the light-cone directions and can be considered as color sources for the classical Yang–Mills fields. These sources are some, apriori unknown, distributions in the transverse plane \(\rho _a(x_T)\) and are considered independent within the large nucleus because there are large numbers of nucleons inside. One can solve the Yang–Mills equation for such configuration to obtain the gluon “wee” fields. In order to compute observables, one needs to average over the color sources. For example, a basic quantity to consider is the particle number density with the generic definition
where \(\tilde{A}^i_b\) are partially Fourier transformed gauge fields, \(\textbf{k}=(k^+,\vec {k}_T)\) is a three-vector conjugate to \(\textbf{y}=(y^-,\vec {y}_T)\). We have assumed here that the large boost is in the light cone “plus” direction. In the MV model, the hadronic matrix element of the gluon field correlator is traded to
where the averaging is over the color sources in the functional sense. \(\mathcal {W}_{x}\) is the functional weight for random color sources, which in the MV model is a Gaussian. Direct computation of the above gluon distribution leads to the so-called Weizsacker-Williams (WW) gluon distribution [116, 117]. Interestingly, despite it being the most basic quantity in the MV model it is not the easiest one to compute nor can it be probed in the simplest scattering processes. Rather, as we discuss later, the quantities that appear for example in inclusive DIS are correlators of Wilson lines. The WW gluon distribution can be approximated as
where \(\mu _A\) is the average color charge per unit transverse area per color. The saturation phenomenon is visible in the above distribution as follows. If the two-point correlator (16) was an ordinary perturbative correlator it would behave like \(\sim 1/k_T^2\); this behavior leads to the power-like growth of the gluon distribution. It turns out that (18) behaves like \(\sim 1/k_T^2\) in the perturbative domain (large \(k_T\)), but at small \(k_T\) it behaves like \(\frac{1}{\alpha _{s}}\log \frac{Q_{s}^{2}}{k_{T}^{2}}\), where \(Q_s\) is the scale at which the suppression happens, called the saturation scale (see Fig. 2). This dynamical scale depends on x (through the evolution) and increases with decreasing x.
The subscript x in the functional weight \(\mathcal {W}_{x}\) denotes a longitudinal cutoff between the sources and the “wee” partons. Decreasing the cutoff produces new color sources and thus the Gaussian distribution gets distorted. The CGC high energy effective theory predicts the evolution equation of \(\mathcal {W}_x\) in x. It is the so-called Jalilian–Marian–Iancu–McLerran–Weigert–Leonidov–Kovner (JIMWLK) equation [118,119,120,121,122,123] and has the following general form
where \(H_{\textrm{JIMWL}}\) is the so-called JIMWLK Hamiltonian (we skip its exact form here). It gives a nonlinear evolution of \(\mathcal {W}_x\) and in turn also a nonlinear evolution of any gauge field-dependent quantity due to the averaging procedure in \(\rho \). These equations are consistent with the Balitsky hierarchy mentioned earlier, therefore it is often called B-JIMWLK equation.
4 Forward dijet production in high energy QCD
In this section, we shall review the formalism that is suitable for phenomenological studies of forward jet production processes at moderate transverse momenta. The formalism lies at the intersection of the two aspects of QCD that in the past were rarely overlapping and, essentially, were exercised by distinct communities. One is the high energy scattering reviewed in the previous Section and the other is the hard factorization theorems, in particular the TMD factorization (see eg. [35] for a review).
4.1 Dijet production in dilute-dense collisions
We start with a CGC description of a scattering of a proton or a photon off a nuclear target to produce two partons. The basic assumption here is that, in the case of the proton projectile, it is dilute, that is the partons extracted from the projectile are moderate x partons. With that assumption, we can treat the scattering of color dipoles, such as \(\gamma \rightarrow q\bar{q}\), \(q\rightarrow qg \), etc., off a color field of a nucleus. This is the essence of the dilute-dense (or hybrid) approach which, as explained in Sect. 2, is kinematically well suited to study forward jets [124].
Scattering of a color dipole \(q\rightarrow qg\) off a nuclear target in CGC. The shaded ellipses symbolize the color field of a nucleus. This particular diagram corresponds to a contribution, where in the amplitude the incoming quark scatters off the color field of the nucleus before the splitting, while in the amplitude conjugate both gluon and a quark scatter after splitting. Particles scattering off the color field of the nucleus gain infinite straight Wilson line along the light cone, in their respective representations
Consider, as an example, the scattering of a \(q\rightarrow qg\) color system off a nuclear target (Fig. 3). In the shock wave approximation, the interaction with the color field of the nucleus can take place either before the quark splits or after. For example, in Fig. 3 the scattering takes place before the splitting in the amplitude and after the splitting in the amplitude conjugate. Each colored particle gains a nonabelian phase when scattering, given by the Wilson line
where the generator \(T_R^a\) is in the fundamental representation (\(R=F\)) for a quark or in the adjoint representation (\(R=A\)) for a gluon. The cross section for the scattering of that system can be written as [22]
where \(\psi _q(z,\vec {x}_T)\) is the wave function of the qg-dipole, with z being a fraction of the incoming quark momentum taken by a gluon. This wave function can be computed in perturbative QCD. The quantities in the curly bracket correspond to the color averages of the Wilson lines:
The above correlators depend on x through the B-JIMWLK equations. In practice, one often uses the Gaussian approximation [125], which states that the color source distribution stays Gaussian throughout the evolution. This allows us to compute the evolution of correlators in closed form.
In order to compute the differential cross section for dijet production in proton–nucleus scattering in the above setup, one needs to find the remaining color dipole contributions [22, 126] and convolute the parton-nucleus cross section with the ordinary collinear PDFs.
The CGC formulation of the dilute-dense scattering provides the high-energy description of the jet production at both small transverse momenta \(p_T\) of jets and moderate (at very large \(p_T\) one should switch the approach from leading energy to leading power in the hard scale). The drawback of the above approach, in addition to being hard to generalize and implement in a Monte Carlo code, is that the perturbative information is contained not only in the color dipole wave function but also in the correlators. As we discuss later, in certain limits this information can be extracted and combined with the dipole wave function to obtain the hard matrix elements, similar to those known from hard factorization.
In the end, let us mention the huge progress in computing higher orders in particle production within the CGC framework. The NLO results for single inclusive jets have been available already for some time [127,128,129], also with resolutions of the “negative cross section” problem [130,131,132,133]. Further, there are NLO computations for inclusive DIS [19, 134], also with heavy quarks [135, 136], dijets in DIS [137,138,139], vector meson production [140, 141], dijet and dihadron hadroproduction [142,143,144] and Drell–Yan process [145]. Higher multiplicity LO computations in CGC include dijet and photon production [146], trijets [147] and trijets in photoproduction [148].
4.2 High energy (or \(k_T\)) factorization
Usually, the high energy factorization (HEF) (or \(k_T\)-factorization) refers to a description of particle production at asymptotically high energies in terms of “unintegrated” PDFs that undergo the BFKL [149,150,151,152] or CCFM [153, 154] evolution. More precisely, within HEF the cross section for a multi-jet production in a collision of two hadrons can be written as
where \(\mathcal {F}_{g/H}\) are unintegrated gluon distributions defined as
where \(\varPhi _H\) is the non-perturbative impact factor of a hadron and \(\mathcal {G}\) is the BFKL Green’s function. At leading order, the partonic cross section in (25) reads
where \(V_{RR\rightarrow P\dots P}\) (the bar denotes the usual spin/color summation and averaging) is the suitably normalized tree-level \(RR\rightarrow P\dots P\) vertex to produce n partons (jets), with R being reggeon states understood as fields from the high energy Lipatov’s action (i.e. without the “reggeization” factors), while P being on-shell quarks or gluons. Above, \(d\varGamma _n\) is ordinary on-shell phase space and F is a jet function that implements the cuts. The momenta of reggeons are
Notice that they are off-shell \(k_{1,2}^2=-|\vec {k}_{T1,2}|^2\) and lack one of the light-cone components, due to the high energy approximations. In the original work on HEF in heavy quark production [150] the partonic cross section (27) was expressed in terms of off-shell amplitude to produce heavy quark pair, with initial gluons having momenta (28) and projected onto \(P_A\) and \(P_B\) (eikonal coupling). In that simple case, it turns out that the amplitude calculated in terms of ordinary diagrams is gauge invariant, despite the initial gluons being off-shell. In practical applications, it proves to be very convenient to stick to that logic also for more complicated processes, instead of using Lipatov’s effective action. Indeed, it is possible to define off-shell gauge invariant amplitude for arbitrary processes. In addition to ordinary Feynman diagrams (with off-shell space-like gluons), one needs “gauge restoring” contributions. Those additional diagrams can be reconstructed for example by the “embedding” method [155], where an off-shell process is embedded in an on-shell process with special kinematics of the auxiliary quarks or gluons. This method was automatized for arbitrary Standard Model tree level process in the KaTie Monte Carlo discussed in Sect. 5.Footnote 1 Also, other methods suitable for automatization were also developed [158,159,160,161]. In Fig. 4 we illustrate one of the methods.
Off-shell gauge invariant amplitude (upper blob – the zigzag lines represent off-shell gauge invariant gluons) can be constructed by promoting a single off-shell gluon coupled eikonally to a straight infinite Wilson line along corresponding hadron momenta \(P_A\) or \(P_B\). Here we show diagrams for the production of two gluons at tree level. The double line represents the momentum space Wilson line along \(P_A\) (for the top line) and \(P_B\) (for the bottom line). Gluons couple to these Wilson lines via \(igt^a p_{A(B)}^\mu \) and the double-line propagators have form \(i/(k\cdot p_{A(B)}+i\epsilon )\). Only planar diagrams are shown. The blob represents all possible connections of gluons via standard vertices
In the context of forward jets, one can apply similar considerations to the hybrid approach explained before. Namely, when, say, \(x_B\) is moderate and not small, one should extract partons from collinear PDF rather than unintegrated PDF undergoing BFKL evolution. This was discussed in [162] and the corresponding HEF formula reads
where we have explicitly denoted the fact that the partonic cross section is constructed from amplitude with one off-shell (gauge invariant) gluon. Above \(f_{a/B}\) is the collinear PDFs for parton a (quark or gluon) in hadron B.
Let us now refocus our attention to the dijet case. It turns out that the \(k_T\)-factorization formula with proper gauge invariant off-shell amplitudes can be retrieved from the CGC expressions discussed before [34, 126]. In the dilute limit, which corresponds to \(|\vec {k}_T|\gg Q_s\), one can neglect the multiple scattering off the target. This means that the triple and quadrupole operators \(S^{(3)}\), \(S^{(4)}\) can be expressed only in terms of the dipole \(S^{(2)}\). In that limit, one obtains for the \(q\rightarrow qg\) dipole scattering
where
and the unintegrated gluon distribution is related to the average of the weak field limit of the CGC dipole operator as follows
The hard factor obtained above turns out to be exactly the off-shell gauge invariant amplitude.
4.3 TMD factorization
Formally, the TMD factorization is the leading power (in the hard scale \(\mu ^2\)) factorization of a cross section into TMD dependent PDFs and hard factors, that to leading power are on-shell (for a review see [35, 163, 164]). This factorization does not resum the large small-x logarithms and therefore becomes unreliable at very high energies. Moreover, it is not expected to hold to all orders in perturbation theory for the processes we are interested in. However, the formalism provides sturdy theoretical definitions of the TMD gluon distributions that, as it turns out, can be matched to the CGC correlators.
In TMD factorization, gluon distribution is given by the Fourier transform of the bilocal matrix element of the gluon field strength tensor
where \(\hat{F}^{j+}=F^{j+}_at^a\) is the gluon field strength tensor; the two operators are displaced in both the light cone and transverse direction (unlike in the collinear PDF, where the displacement is only along the light cone). The bilocal operator would not be gauge invariant, therefore the proper general definition requires gauge links \(\mathcal {U}_{C_1}\) and \(\mathcal {U}_{C_2}\) (here everything is in the fundamental representation) that connect the two space-time points. There is also a possibility of the double-trace over the fundamental representation (see below). We consider here only the unpolarized case, therefore the transverse index j is summed over. The TMD gluon distributions are connected to a partonic process by virtue of factorization. Since we consider gauge theory, there are multiple soft and collinear gluons that can be connected to various places in the diagrams. The definition given above corresponds to the bare operator. In perturbation theory, it contains UV and rapidity divergences that, for some processes, can be removed order-by-order by the operator renormalization and by (part of) the soft factor accumulating soft gluons. This gives the hard scale and rapidity evolution of the TMD PDFs. The collinear gluons (collinear to the target hadron) can be resummed into the Wilson lines \(\mathcal {U}_{C_1}\) and \(\mathcal {U}_{C_2}\). As can be easily understood, the form of these Wilson lines depends on the actual hard process (its color flow). In [165] a general procedure of determining these Wilson lines via resummation of collinear gluons was given. It turns out, that they can become quite complicated for colored partonic processes, see for example [166]. In Table 1 we collect the operators relevant for the dijet production. The notation \(\mathcal {F}_{gg}^{(i)}\) and \(\mathcal {F}_{gg}^{(i)}\) corresponds to TMD PDFs that appear for incoming gluons (the “gg” subscript) or quark-gluon system (the “qg” subscript), and various color flows (the (i) superscript). The Wilson lines \(\mathcal {U}^{[\pm ]}\) are defined as
which is the past-pointing staple-like gauge link and
is the future pointing “staple”, see Fig. 5. The square brackets above [x, y] is a standard notation for segments of straight gauge link between the points x and y. Out of two staples it is possible to make a Wilson loop
The relation of the field theoretical definitions of TMD PDFs and small-x QCD has been a subject of intense work, see for example [167,168,169,170,171,172,173,174,175,176,177,178]. In the context of forward dijet production, we are interested in the small-x limit of the TMD gluon distributions. This is achieved by literally taking the limit \(x_A\rightarrow 0\) in the definitions. On the other hand, one can consider the leading power limit of the CGC expressions (21). This leads to the identification of the TMD gluon distributions and the leading terms in the gradient expansions of the CGC correlators [168]. For example
that is, the \(\mathcal {F}_{qg}^{(1)}\) is identified with the expansion of the dipole operator. For the complete list of similar relations for other TMDs see [168, 179]. Ultimately, in the leading power limit, the CGC formula for the \(qg\rightarrow qg \) contribution can be written as
where s is the hadronic center of mass energy and \(\mathcal {H}_{qg\rightarrow qg}^{(i)}\) are on-shell hard factors corresponding to the two independent color flows. They read
where \(\hat{s}\), \(\hat{t}\), \(\hat{u}\) are the Mandelstam variables.
In collinear LO factorization, both TMD gluon distributions would be replaced by the collinear gluon PDFs and the above hard factors would be added. It is easy to check that the sum corresponds to the known on-shell hard factor for \(qg\rightarrow qg\) process. The list of all hard factors for all subprocesses beyond the large \(N_c\) limit is given in [159].
In the end, let us mention progress in establishing the CGC-leading power TMD factorization correspondence. In [166] the Authors explicitly obtained the structure of all TMD operators corresponding to five and six colored parton processes. In [148] the TMD factorization limit was studied for three jet production in CGC. Finally, in [144] the TMD factorization was studied in the context of dijet production in photoproduction at NLO.
The ITMD factorization (pure gluon channel) of the p+A dijet cross section into TMD PDF (upper blob), the collinear PDF (lower blob) and the off-shell hard part (center blow). Since the exchanged momentum between the upper blob and the center is off-shell, multiple eikonal gluon exchanges are required to maintain the gauge invariance. In ITMD factorization, these gluons do not increase the genuine twist of the TMD operator. The TMD distribution is given by a certain linear combination of the operators listed in Table 1
4.4 Improved TMD factorization and resummation of kinematic twists
It is important to stress, that the TMD factorization in dilute-dense collisions, despite being leading power, does take into account the gluon saturation, although certain contributions that affect the saturation are neglected. The leading power means here the regime \(k_T \ll P_T\), where \(P_T\) is related to the transverse momenta of the jets. The saturation scale is taken into account by the leading twist TMD gluon distribution which is considered in the strict high energy limit and undergoes the nonlinear evolution, even at leading twist (for an interesting discussion of two types of saturation see [180]). To summarize, the dilute-dense TMD factorization is suitable when the transverse momenta of dijets are rather large and when we are interested in the back-to-back dijet region. For very large transverse momenta of the jets, the highest scale is not given by the energy but the hard scale and one should switch the framework to the collinear factorization.
The main limitation of the dilute-dense TMD factorization is that it works only in the back-to-back region. In dijet studies, especially at small x, dijet azimuthal correlations are the most important observables and can be measured over a wide range of the azimuthal angle. Therefore, it is essential to account not only for jet correlations but also decorrelations. A related issue is that of the transverse momentum conservation. In the TMD factorization, the transverse momentum \(k_T\) of the gluon scattered (or extracted) from the target nucleus enters only TMD gluon distributions, and not the hard process. This complicates for example Monte Carlo realization of such an approach.
It turns out, that, in practical terms, it is actually quite easy to improve the dilute-dense TMD factorization. The hard factors have to take into account power corrections due to the transverse momentum of the incoming gluon. This is uniquely realized in the high energy limit by promoting the on-shell hard factors to the gauge invariant off-shell ones, following the rules described in the part devoted to HEF. This procedure was described in detail in [34], where also off-shell gauge invariant hard factors are calculated for all channels and color flows. A proof and proper interpretation within the CGC was later given in [181]. First, a formal distinction between kinematic and genuine twist is made. The genuine twist counting can be simply understood as counting gluon operators in the TMD matrix element (but not the Wilson lines), for example, an operator with two strength field tensors corresponds to twist two and two-body contribution. The kinematic twists are power corrections in \(k_T\) to the n-body process and come from the hard matrix element. In [181] a resummation of the kinematic twists was performed for the two-body contributions, showing that the resulting hard factors indeed correspond to the off-shell gauge invariant hard factors.
Before we review the dilute-dense improved TMD (ITMD) factorization framework, let us first comment, that when determining the TMD gluon distribution functions it is important to work with gauge invariant subset of diagrams and not the individual ones. The systematic way of doing that in small-x physics was suggested in [159], where a decomposition of an amplitude into color-ordered amplitudes was used. The color-ordered amplitudes [182] are gauge invariant, but contain only planar diagrams and correspond to the different ordering of the external partons. Each color-ordered amplitude comes with a color structure, for which the TMD operator can be determined. It is then usually given as some combination of the basic operators build from \(\mathcal {U}^{[\pm ]}\) Wilson lines, but corresponds to the gauge invariant hard factor. The ITMD framework given below was formulated with that feature in mind.
The ITMD factorization formula, accounting for all channels (Fig. 6), reads
where \(K_{ag^*\rightarrow cd}^{(i)}\big (\vec {k}_T\big )\) are off-shell gauge invariant hard factors and \(\varPhi _{ag\rightarrow cd}^{(i)}\big (x_A,|\vec {k}_T|\big )\) are the corresponding TMD gluon distributions. We collect them in Table 2. They are expressed in terms of the ordinary Mandelstam variables, as well as “modified” Mandelstam variables. The former read explicitly
where the incoming momenta are
and
They sum up to \({{\hat{s}}}+ {{\hat{t}}}+ {{\hat{u}}}= -|\vec {k}_T|^2\). The “modified” Mandelstam variables take into account only the longitudinal component of the off-shell initial state \(k_1\) and read
which are related via the equation
The ITMD factorization was also investigated for other processes than dijets in proton–nucleus collisions. In [183] heavy quark pair production was studied and the problem of longitudinal gluons was discussed in depth. In [184] the effect of the genuine twists vs kinematic twists was studied in detail for dijets in DIS. Finally, neglecting the longitudinal gluon contribution, the ITMD framework was formulated and applied to the trijet production [166, 185].
5 ITMD with the Monte Carlo tool KaTie
KaTie [186] is a parton-level Monte Carlo event generator that can deal with space-like initial-state partons for arbitrary tree-level processes within the Standard Model. This means that it can be provided with \(k_T\)-dependent PDFs and that it will automatically calculate the necessary matrix elements with space-like initial-state partons to create parton-level event files. These event files can be chosen to be in the LHEF-format [187]. The \(k_T\)-dependent PDFs can be provided via TMDlib [188], or via independent grid files, which however must be in a specific format. Furthermore, KaTie can perform calculations within ITMD factorization, and automatically calculates the necessary gauge invariant matrix elements corresponding to the color structures associated with the several gluon distributions that appear in this factorization scheme. While KaTie primarily creates event files, it also provides tools to create histograms of differential distributions.
KaTie can be downloaded from https://bitbucket.org/hameren/katie/downloads/define the following Fourier transforms, and a description of use is provided in the manual there. Here, we provide some background on the Monte Carlo method it employs, elucidating the procedures to be followed when using KaTie.
In hybrid factorization like ITMD factorization, the cross section can be written as a 3n-dimensional integral
where n is the number of final-state momenta. There are 4 initial-state variables and \(3n-4\) final-state variables. For hadro-production of dijets at tree-level the number \(n=2\). The function F includes the collinear PDF, the TMDS, the flux factor, and the hard matrix elements. Given a probability density \(G(\omega )\) in the integration space (or phase space) that is non-zero whenever \(F(\omega )\) is non-zero, we can write
The Monte Carlo method is based on the Central Limit Theorem, which dictates that if \(\{\omega _1,\omega _2,\) \(\ldots ,\) \(\omega _{N}\}\) is a sequence of random phase space points, or events, independently drawn from density \(G(\omega )\), then
Clearly, the approximation converges to the correct result faster if the fluctuation over the terms in the sum is smaller, with the optimum when \(G(\omega )=F(\omega )/\sigma \). Successfully applying the Monte Carlo method means that one solves the problem of bringing \(G(\omega )\) to this optimum to a satisfactory degree. Reaching the optimum implies having solved the integration problem and eliminates the need for the Monte Carlo procedure. Satisfaction means that the result can be obtained within an acceptable time, and in practice means finding a compromise between the number of terms needed, and the complexity of the algorithm to produce the sequence of events.
An advantage of the Monte Carlo method is that, given a “satisfactory” sequence generator to calculate the cross section \(\sigma \), it can also be used to estimate differential distributions. Let \(\varphi (\omega )\) be an observable, and \(\textrm{b}_{j}(\varphi )=\theta (\varphi -\varphi _j)\theta (\varphi _{j+1}-\varphi )\) be a bin for this observable between values \([\varphi _j,\varphi _{j+1}]\), then
The idea of an event file is to store events \(\omega _i\) and their weight \(W_i=F(\omega _i)/G(\omega _i)\) to produce arbitrary distributions without having to redo the generation of events.
In the context of the foregoing, KaTie performs roughly speaking two tasks: it calculates the hard matrix elements, automatically and efficiently, as part of the evaluation of \(F(\omega )\), and, provided with PDFs and TMDs, it creates reasonably-sized event files. In order to perform the first task, KaTie employs the Dyson–Schwinger approach to calculate tree-level helicity amplitudes numerically, as first proposed in [189] and also utilized in other tree-level programs, notably Alpgen [190]. The feature of space-like initial-state momenta is dealt with following the auxiliary-parton method outlined in [155]. The second task is achieved through the application of many well-known optimization techniques, a few of which are worth mentioning in order to understand the procedures in KaTie’s operation.
One is adaptive importance sampling, which optimizes adaptable probability densities iteratively, using the information of events generated so far in each iterative step. While being very effective, it can cause bias in those events, and they must not be used for the actual event file. Consequently, there must be a separate optimization stage before the generation of the event file starts. This happens for each partonic subprocess separately. Once this has been performed, the information of the optimized densities is stored, and is from then on used to generate an arbitrary number of event files.
Secondly, KaTie employs rejection. Phase space cuts are required to mimic detector acceptance and to avoid singularities in tree-level matrix elements. These typically are formulated in terms of variables that are non-trivial functions of the variables in \(\omega \) that are actually generated, and cannot be implemented as exact integration bounds. Instead, the integrand \(F(\omega )\) is imagined to vanish outside those phase space cuts, and a bigger enveloping space is generated. This leads to many events with \(W_i=0\), which are however not stored but are included in the eventual normalization of the weights. In order to achieve the unbiased normalization of the event weights in case several event files are generated, so called raw files are stored instead of actual event files, containing non-normalized weights and more statistical information. Event files in the LHF format can be extracted from these.
The third method that needs to be mentioned is unweighting. This is a statistical procedure to reduce the fluctuations of the weights \(W_i\) while keeping the event file sound. In practice this procedure “weeds out” low-weight events and reweighs remaining ones. The cross section estimate is not affected (is also not getting better) but it allows to reduce the required size of the event file. While it causes many events to get the same constant weight, there may occur events with higher weights.
The phase space is only 3n-dimensional, but it is much more convenient to write the events in terms of the \(4(n+2)\) variables being the parton-level initial-state and final-state momenta. We will still denote events with the symbol \(\omega \). While all components of \(F(\omega _i)\), like the matrix element, the PDFs, the strong coupling etc., can be re-evaluated using these, it is more convenient to also store their values besides \(W_i\). This is useful if one wants to employ the reweighting procedure. For example, let an event file be created within hybrid \(k_T\)-factorization with a TMD \(\mathcal {F}(\omega )\) (we simply imply that this function selects the appropriate variables from \(\omega \). Realize that this in practice includes the final-state ones due to the factorization scale dependence). Suppose a user has their own TMD \(\mathcal {F}'\) but only in a numerical form that cannot (yet) be married with KaTie or TMDlib. The value of \(\mathcal {F}_i=\mathcal {F}(\omega _i)\) is stored for each event, and the event file can be transformed to be valid for \(\mathcal {F}'\) by multiplying
for each event. It will increase the fluctuation of the weighs and reduce the quality of the event file, but most likely not in a drastic way.
As mentioned earlier, the use of KaTie is described in the manual, but below we present the complete single input card that allows to create event files for dijets within ITMD.

6 Gluon densities saturation and Sudakov form factor
6.1 BK equation for dipole gluon density
From the BK equation discussed in the earlier sections, one can obtain TMD dipole gluon density. The steps outlined below will closely follow the results obtained in [60, 85, 191].
In this section, we will use \(k^2=|\vec {k}_T|^2\) as an argument of gluon density. This is the standard notation used in the discussion of angular averaged distributions.
Let’s define the following Fourier transforms [191, 192]
The function \({\mathcal F}(x,k^2)\) is the dipole gluon density already introduced in the previous sections. The function \(\varPhi (x,k^2)\) is an auxiliary quantity for which the BK equation has a simple form with local nonlinear term as will be shown below.
The explicit relation between the two functions \({\mathcal F}(x,k^2)\) and \(\varPhi (x,k^2)\). is
It has been shown in [85] that once one considers homogenous infinite nucleus the b integral on the formula 53 can be factorized and enters only via initial condition
and one gets the following BK equation
In the equation above, the impact parameter is not a dynamic quantity. On top of that it does not describe physics at large distances correctly as it does not take into account confinement effects [193]. Taking the above into account in order to obtain the integrated over impact parameter gluon density one needs to assume some impact parameter dependence since one needs to perform the integration over it to calculate gluon density. For cylinder like target, one may use the following ansatz for factorization [191]
with normalization conditions
where S(b) is the profile function \( S(b)=\theta (R-b)/\pi R^2\).
The momentum space equation for the integrated over impact parameter dependence \(\varPhi (x,k^2)\) assumes the form:
where \(\overline{\alpha }=N_c\alpha _s/\pi \).
The the equation for \({\mathcal F}(x,k^2)\) is obtained from Eq. (56) by inserting in the nonlinear part of it relation expressing \(\varPhi (x,k^2)\) in terms of \({\mathcal F}(x,k^2)\) and acting on the whole equation with the operator that transforms \(\varPhi (x,k^2)\) to \({\mathcal F}(x,k^2)\) see [191] for the details of this transformations. In the end one obtains [60, 191, 194]
The linear part of the equation above is the well known BFKL kernel while the nonlinear part is the triple pomeron vertex. The triple pomeron vertex has such property that it is dominated by the anticollinear pole. We see that as one evaluates the gluon at lower and lower values of \(k^2\) the integration in the nonlinear term is over a larger domain giving a larger contribution and suppressing the gluon density. One can also see that in the collinear limit, the nonlinear term completely drops and one is left with a linear equation.
6.2 BK equation within Kwiecinski Martin Staśto model
The (60) is a leading order BK equation for dipole gluon density. So far there is no direct momentum space extension of the equation beyond LO approximation. It is known that higher-order corrections slow down the rapid growth of gluon density and are relevant for phenomenology. Therefore in order to make it applicable to phenomenology it has been extended to account for higher order corrections following Kwiecinski–Martin–Stasto (KMS) model [195] that was originally applied to the BFKL equation. Those include
-
kinematical constraints which enforce that the virtuality of the exchanged gluon is dominated by its transverse component \(k^2=|\vec {k}_T|^2\). This constraint suppresses the anticollinear pole and therefore suppresses the diffusion into the infrared. Furthermore, this contribution can be shown to account for resummation of collinear logs
-
nonsingular at small z pieces of the splitting function in order to be consistent in the collinear limit with the DGLAP system of equations in the collinear limit
-
running coupling constant
-
sea quark singlet contribution to match the DGLAP limit at large z
With these corrections, the equation assumes the form [191]
where \(\varSigma (x,k^2)\) is a sea quark distribution obeying essentially DGLAP equation in unintegrated form (further details can be found in [191]). Please note that in the equation above lower cut in \(k^2=k_0^2\) was introduced. The origin of the cut is related to the method of solving of the equation and in principle can be set to an arbitrarily small value.
In Ref. [12], the following initial condition for Eq. (62) was fitted to the \(F_2\) proton structure data from HERA [196]
with
For \(k^2 \le 1\, \text {GeV}^2\), the gluon distribution was taken as \(\mathcal {F} (x,k^2) = k^2 \mathcal {F}(x,1)\), which is motivated by the shape obtained from the solution of the LO BK equation in the saturation regime [197].
The fitting procedure gave the following numerical values for the parameters: \(N=0.94\), \(\beta =18.6\), \(D=-82.1\) and \(R=2.40 \,\textrm{GeV} ^{-1}\). The overall quality of the fit was good, with \(\chi ^2/\text {ndof} = 1.73\). We shall refer to this gluon distribution as the Kutak-Sapeta or KS gluon.
For completeness, the fit of a linearized version of Eq. (62), i.e. with the last term dropped, was performed as well, and the following parameters were obtained: \(N=0.004\), \(\beta =26.7\), \(D=-51102\) and \(\chi ^2/\text {ndof} = 3.86\). The presence of the parameter R, characterizing the target, allows one to obtain the dipole gluon distribution of nuclei. In order to do that, one uses relation \(R_A=d\, A^{1/3} R \), which in the end gives the enhancement by \(A^{1/3}\) of the nonlinear term for gluon density normalized to the number of nucleons [12]. The parameter d is a phenomenological factor that was varied between \(d=0.5\) and \(d=1.0\). In the following computations, we used the “least saturation” scenario with \(d=0.5\).
6.3 The Sudakov resummation
An important class of perturbative corrections to the scattering process, appearing when the emitted partons are both collinear and soft, is resummed in terms of the Sudakov form factor. It appears due to not exact cancellation of virtual corrections and real corrections, as a consequence of certain exclusivity of the final state. The Sudakov resummation is used to formulate DGLAP evolution equations in unintegrated form [198,199,200] and in Monte Carlo simulations [201]. In the latter application, it leads to finite transverse momentum even in the absence of any other mechanism generating transverse momentum. Finally, it is also independent of any saturation effects.
In the processes considered here the largest effect of the Sudakov is expected to affect the cross section when the jets are in a nearly back-to-back configuration. The large logarithm appears because the transverse momenta of jets can be sizable while the imbalance \(k_T\) of incoming space-like parton is small. The effect of the Sudakov form factor is to suppress the back-to-back configuration and enhance the moderate angle part of the distribution, leading to so-called broadening. Within the small-x formalism, the Sudakov form factor can be factorized at one loop level, in the coordinate space, from the hard process [202,203,204]. The complete cross-section accounting for the Sudakov form factor reads:
where \(\widetilde{\varPhi }_{ag\rightarrow cd}^{\left( i\right) }\) is the Fourier transform of the TMD gluon distributions and \(S^{ag\rightarrow cd}\) are the Sudakov factors written for each channel
where \(S_p^{i}\) and \(S_{np}^{i}\) are the perturbative and non-perturbative contributions. The perturbative Sudakov factors, including double and single logarithms, are given by [202, 205]
where \(\beta _0 = (11-2n_f/N_c)/12\). The \(g g \rightarrow q {\bar{q}}\) channel is negligible in the kinematic domain considered here. In the above the scale \(\mu _b\) is the inverse of the impact parameter:
with
Given this selection, the scale \(\mu _b\) becomes constant at the point of high \(b_T\), where its value is determined to be \(2 e^{-\gamma _E}/b_{\max }\), which is considerably greater than \(\varLambda _\text {QCD}\). Following Ref. [206], we will adopt \(b_{\max } = 0.5, \text {GeV}^{-1}\).
For completeness, we comment briefly on DGLAP based prescriptions for incorporating the Sudakov form factor. The method relies on constructing the Sudakov form factor from the DGLAP splitting function and using it to reshuffle events according to the relation between hard scale and transverse momentum of the gluon. In such constructions, one chooses some inclusive quantity to be unmodified while allowing for modification of unintegrated quantity. Two such methods were presented in [24, 27]. In the former, the total cross section was preserved while in the latter the integrated gluon density was unmodified.
6.4 Kutak–Sapeta (KS) gluon distribution
We shall now discuss the KS gluon, introduced above, in variants with and without the Sudakov resummation. The parameters were fixed by the original fit [12] with no Sudakov factors and the gluon was later used without any modifications. Hence, combining it with the Sudakov does not introduce new parameters. This is true because the perturbative part (67) and (68) is parameter-free while the non-perturbative terms are universal in the kinematic domain of our study [207].
We introduce the Sudakov effects into the KS gluon distribution following the formalism described above. In addition, for reference, we use two methods employed in our earlier studies [24, 27]. Those calculations used the Sudakov form factor, understood as the DGLAP evolution kernel, that has been applied on the top of the gluon TMD, together with constraints such as unitarity. Those methods should therefore be considered as models, in contrast to the proper resummation of Sudakov logarithms described in the preceding section. Nevertheless, the approaches used in Refs. [24, 27] were phenomenologically successful (see also [14]), and it is therefore useful and interesting to compare the predictions of those simplistic models with the proper way of including the Sudakov effects into the small-x gluon.
The reference models are:
-
Model 1: The survival probability model [27], where the Sudakov factor of the form [208]
$$\begin{aligned} T_s(\mu _{F}^2,k_{T}^2)= & {} \exp \left( -\int _{k_{T}^2}^{\mu _F^2}\frac{dk_{T}^{\prime 2}}{k_{T}^{\prime 2}}\nonumber \right. \\{} & {} \times \left. \frac{\alpha _s(k^{\prime 2}_{T})}{2\pi }\sum _{a^\prime }\int _0^{1-\varDelta }dz^{\prime }P_{a^\prime a}(z^\prime )\right) , \end{aligned}$$(71)is imposed at the level of the cross section. This procedure corresponds to performing a DGLAP-type evolution from the scale \(\mu _0\sim k_T\) to \(\mu \), decoupled from the small-x evolution.
-
Model 2: The model with a hard scale introduced in Ref. [24]. The Sudakov form factor of the same form as in Eq. (71) is imposed on top of the KS gluon distribution in such a way that, after integration of the resulting hard scale dependent gluon TMD, one obtains the same result as by integrating the KS gluon distribution.
In Fig. 7, we show the KS gluon distributions, with and without Sudakov form factors, as functions of the transverse momentum \(k_T\) and the hard scale \(\mu \). Three columns correspond to three different x values. The first row shows the original KS gluon distribution, which, as expected, does not depend on the value of \(\mu \). In the second row, we show the KS hardscale gluon distribution of Ref. [24] (the other model [27] does not allow one to plot gluon distribution, as it applies Sudakov effects at the cross section level via a reweighting procedure). Here, the dependence on \(\mu \) is non-trivial and we see that the gluon develops a maximum in that variable. As shown in the figure, this maximum is rather broad. In the third and the fourth row of Fig. 7, we present the KS gluon distribution with the Sudakov form factor from Eqs. (66)–(68). As explained earlier, this gluon exists in two versions, one for the qg and the other for the gg channel. The dependence on \(k_T\) and \(\mu \) is qualitatively similar between these gluons and the naive KS hardscale gluon distribution. In the former case, however, the peak is significantly narrower in \(\mu \) as compared to the naive model of Ref. [24]. It is interesting to note that the qg gluon is broader than the gg gluon. This can be understood by comparing the colour factors in the Sudakov functions (67) and (68). Since the colour factor for the gg channel is larger than for the qg, the Sudakov suppression is stronger along the \(\mu \) direction in the former case.
We have as well computed linear versions of the KS gluon distributions with the Sudakov, using the KS linear gluon distribution of Ref. [12]. The gluons discussed in this section are available publicly as part of the KS package and can be downloaded from http://nz42.ifj.edu.pl/~sapeta/KSgluon-2.0.tar.gz.
6.5 ITMD gluons distributions
In the limit of small x and assuming the mean field approximation, the gluons listed in the table (1) can be expressed in terms of dipole gluon density as [168]
where
and \(F\big (x,|\vec {k}_T|\big )\) is a Fourier transform of the fundamental dipole
The gluons listed above form a set from which one can construct the gluon densities \(\varPhi ^{(i)}\) entering the ITMD factorization formula (42) as obtained in [34]:
6.6 ITMD distributions from KS gluon
All the gluon TMDs (72)–(76) can be calculated from a single \(xG^{(2)}\big (x,|\vec {k}_T|\big )\) distribution in the above Gaussian approximation. However, because the KS gluon provides directly an impact-parameter-integrated distribution, it is not straightforward to identify \(S_\perp \) and obtain \(F\big (x,|\vec {k}_T|\big )\) from Eq. (77). To address this issue, we applied the following procedure [209]. We first computed the dipole cross section \(\sigma _\textrm{dipole}(x,r\!=\!|\mathbf{{r}}|)=2\int d^2b\ N_F(x, \mathbf{{r}})\) from \(xG^{(2)}\big (x,|\vec {k}_T|\big )\) by inverse Fourier transformation of Eq. (78), and then defined \(S_\perp \) as its value at large r, i.e. when it saturates (since in that limit \(N_F\rightarrow 1\)):
We can now obtain \(F\big (x,|\vec {k}_T|\big )\) and calculate all the needed gluon TMDs. Their behavior as a function of \(k_t=|\vec {k}_T|\) is plotted in Fig. 8, both for the proton and the lead nucleus. The small mismatch between their high-\(k_t\) behavior, expected due to the initial condition for the x evolution, can be observed.
Similarly, we computed [210] the ITMD distributions from the KS gluon with the proper QCD Sudakov, shown in Fig. 7.
Within the Gaussian approximation, one can also derive the following formula for the WW gluon density [209]
where \({\mathcal F}_{qg}^{(1)}\) is the dipole gluon density and \(S_\perp \) is the target’s transverse area.
Using the procedure described above, we computed also the WW gluon, which we show in Fig. 9 in proton (left) and lead (right), with and without Sudakov form factors, as functions of the transverse momentum \(|\vec {k}_T|\) and the hard scale \(\mu \), for one particular \(x = 10^{-3}\). (The gluon density is available from the TMDlib [188]).
First of all, let us notice that the WW gluon distribution has no maximum, contrary to the dipole gluon [12, 209]. Secondly, we see that the Sudakov factor suppresses the gluon distribution at low \(|\vec {k}_T|\) and enhances it at higher \(|\vec {k}_T|\). Because the Sudakov form factor is derived in the regime \(\mu \propto |\vec {p}_T| \gg |\vec {k}_T|\), we apply it only to that part of the gluon density where \(\mu >|\vec {k}_T|\). In the remaining domain, we use the gluon without Sudakov, given in Eq. (83). This is visible in Fig. 9 as a kink of the curve corresponding to \(\mu = 17\, \,\textrm{GeV} \). (A similar kink exits also for the \(\mu = 67\, \,\textrm{GeV} \) curve but it is located at larger values of \(\log |\vec {k}_T|^2\)).
All the ITMD gluons discussed above are available publicly and can be downloaded from http://nz42.ifj.edu.pl/~sapeta/itmd-KS.tar.gz.
7 Phenomenology of forward jets
7.1 Forward dijets at the LHC
In the following section we review some existing predictions for forward dijet production in proton–proton and proton–lead collisions at LHC energies, obtained within the ITMD framework. We also include some new computations, not published before.
Before we proceed, it is important to mention, that the first predictions for forward dijets in saturation formalism using the ITMD, that – as discussed in Sect. 4.4 – approximates the CGC for sufficiently large transverse momenta, appeared in [209]. This computation significantly improved the predictions of [23] obtained with \(k_T\)-factorization, which is not entirely accurate at small dijet imbalance. Later, in [211] a full computation within CGC was compared to ITMD, confirming, that at larger transverse momenta ITMD is adequate.
None of the above computations included the Sudakov resummation, however. In [14] a calculation has been performed that included both the full ITMD and the Sudakov resummation “model” [27], based on the reweighting the events with the DGLAP Sudakov form factor. The Authors compared the shape of the obtained azimuthal dijet correlations for proton–proton and proton–lead with those obtained by ATLAS collaboration [29] (no dijet cross section was actually measured, only the conditional yields). Interestingly, when the shapes of the azimuthal correlations for p–p and p–Pb are stacked together so that they match in the first bin, one can clearly see broadening of the p–Pb cross section. It turns out, that similar broadening is obtained within the ITMD, if both the saturation as well as the Sudakov resummation are present. We show this result in Fig. 10.
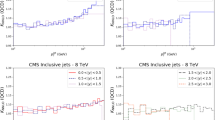
Broadening of azimuthal correlations in p–Pb collisions vs p–p collisions for different sets of cuts imposed on the jets’ transverse momenta. The blue and red bands show the normalized differential cross sections in azimuthal angle \(\varDelta \phi \), respectively for for p–Pb and p–p, shifted so that they match in the first bin. The points show the experimental data [29] for p–p and p–Pb, where the p–Pb data were shifted by a pedestal, so that the values in the bin \(\varDelta \phi \sim \pi \) are the same. Theoretical calculations are represented by the histograms with uncertainty bands coming from varying the scale by factors 1/2 and 2
In the following, we shall report on further advances in dijet computations within ITMD, with the full Sudakov resummation [212]. In particular, we will present the numerical results for the differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at LHC energies. We shall also discuss the nuclear modification ratio \(R_{\mathrm {p-Pb}}\)
where \(\mathcal {O}\) is a differential related to an observable. Finally, we shall investigate differential cross sections in the rapidity of the leading and sub-leading jet.
The cross sections were computed using the KaTie Monte Carlo program [186] within the ITMD factorization, both described in the preceding Sections. We considered the proton–proton and proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\), \(8.16\,\textrm{TeV}\) and \(8.8\, \textrm{TeV}\) per nucleon. For proton–proton collisions, we also computed the proton–proton cross section for \(\sqrt{s}=14\,\textrm{TeV}\). In order to define the leading and the sub-leading jets, mentioned above, we used the anti-\(k_T\) jet clustering algorithm [213] with a radius of \(R = 0.4\). Since our computation is leading order, the jet algorithm is actually equivalent to a simple cut in rapidity-azimuthal plane. Motivated by the current and planned LHC experiments, we applied the following cuts to the transverse momentum of these jets:
The differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the FCal ATLAS kinematics. These were computed using KaTie within the ITMD factorization formula with: the simplified Sudakov resummation Eq. (42) (solid lines), the full b-space resummation Eq. (65) (dotted lines). The plots were taken from [212]
The differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the FCal ATLAS kinematics. The solid lines represent the results from KaTie computed within the ITMD approach, the points represent the results from Pythia with different components, and the dotted lines represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. The plots were taken from [212]
The differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the FCal ATLAS kinematics. The solid lines represent the results from KaTie computed within the ITMD approach, and the dotted lines represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. The bands represent the error due to the variation of the factorization/renormalization scales from a value of \((p_{T1}+p_{T2})/2\) by a factor of 1/2 and 2. The plots were taken from [212]
Nuclear modification ration \(R_{\mathrm {p-Pb}}\) in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the FCal ATLAS kinematics. The solid lines represent the results from KaTie computed within the ITMD approach with: the simplified Sudakov resummation Eq. (42) (red line), the full b-space resummation Eq. (65) (blue line). The band represents the error due to the variation of the factorization/renormalization scales from a value of \((p_{T1}+p_{T2})/2\) by a factor of 1/2 and 2. The points \(\triangledown \) represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. The error bars associated with these points account for both errors due to variation of scale in KaTie and the statistical uncertainties in the correction factor from Pythia. The plots were taken from [212]
The differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the ALICE FoCal kinematics. The first plot represents the cross sections computed using KaTie within the ITMD factorization formula with: the simplified Sudakov resummation Eq. (42) (solid lines), the full b-space resummation Eq. (65) (dotted lines). In the second plot, the solid lines represent the cross sections from KaTie computed within the ITMD approach, the points represent the results from Pythia with different components, and the dotted lines represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. In the third plot, the solid lines represent the cross sections from KaTie computed within the ITMD approach, and the dotted lines represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. The bands represent the error due to the variation of the factorization/renormalization scales in KaTie from a value of \((p_{T1}+p_{T2})/2\) by a factor of 1/2 and 2. The plots were taken from [212]
Nuclear modification ration \(R_{\mathrm {p-Pb}}\) in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\) in the ALICE FoCal kinematics. The solid lines represent the results from KaTie computed within the ITMD approach with: the simplified Sudakov resummation Eq. (42) (red line), the full b-space resummation Eq. (65) (blue line). The band represents the error due to the variation of the factorization/renormalization scales from a value of \((p_{T1}+p_{T2})/2\) by a factor of 1/2 and 2. The points \(\triangledown \) represent the KaTie results corrected with the non-perturbative correction factor extracted from Pythia. The error bars associated with these points account for both errors due to variation of scale in KaTie and the statistical uncertainties in the correction factor from Pythia. The plots were taken from [212]
The differential cross sections in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\) (blue) and \(8.8\,\textrm{TeV}\) (red) in the ALICE FoCal kinematics. For the same kinematics, each plot also represents the differential cross section for the proton–proton collision at \(\sqrt{s}=5.02\,\textrm{TeV}\) (black). Since proton–lead collisions are not feasible at this energy, we didn’t compute those. All of these cross sections were computed using KaTie within the ITMD factorization formula with the simplified Sudakov resummation Eq. (42) The solid lines represent the results for proton–lead collisions and the dotted lines represent the results for the proton–proton collisions
The differential cross sections in terms of the rapidity of the leading jet \(y_1^{\star }\) for the proton–proton and the proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\) (blue) and \(8.8\,\textrm{TeV}\) (red) in the ALICE FoCal kinematics. For the same kinematics, each plot also represents the differential cross section for the proton–proton collision at \(\sqrt{s}=5.02\,\textrm{TeV}\) (black). Since proton–lead collisions are not feasible at this energy, we didn’t compute those. All of these cross sections were computed using KaTie within the ITMD factorization formula with the simplified Sudakov resummation Eq. (42) The solid lines represent the results for proton–lead collisions and the dotted lines represent the results for the proton–proton collisions
The differential cross sections in terms of the rapidity of the sub-leading jet \(y_2^{\star }\) for the proton–proton and the proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\) (blue) and \(8.8\,\textrm{TeV}\) (red) in the ALICE FoCal kinematics. For the same kinematics, each plot also represents the differential cross section for the proton–proton collision at \(\sqrt{s}=5.02\,\textrm{TeV}\) (black). Since proton–lead collisions are not feasible at this energy, we didn’t compute those. All of these cross sections were computed using KaTie within the ITMD factorization formula with the simplified Sudakov resummation Eq. (42) The solid lines represent the results for proton–lead collisions and the dotted lines represent the results for the proton–proton collisions
-
i)
\(28\, \textrm{GeV}< p_{T1},p_{T2} < 35\, \textrm{GeV}\),
-
ii)
\(35\, \textrm{GeV}< p_{T1},p_{T2} < 45\, \textrm{GeV}\),
-
iii)
\(35\, \textrm{GeV}< p_{T1} < 45\, \textrm{GeV}\) and \(28\, \textrm{GeV}< p_{T2} < 35\, \textrm{GeV}\),
-
iv)
\(p_{T1}, p_{T2} > 10\, \textrm{GeV}\),
-
v)
\(p_{T1}, p_{T2} > 20\, \textrm{GeV}\).
Specifically, we used the first three cuts \(i)--iii)\) for the transverse momentum of the jets in the rapidity range \(2.7<y^{\star }_{1},y^{\star }_{2}<4.0\), both for proton–proton and proton–lead collisions at \(\sqrt{s}=8.16\,\textrm{TeV}\). These cuts correspond to the FCal calorimeter of the ATLAS detector and are motivated by the measurement [29]. The last two cuts \(iv)- v)\) were applied in the rapidity range \(3.8<y^{\star }_{1},y^{\star }_{2}<5.1\), both for proton–proton and proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\), and \(8.8\, \textrm{TeV}\) energies per nucleon. These correspond to the planned FoCal extension of the ALICE detector [31]. For the same kinematic domain (rapidity and transverse momentum cuts for the jets), we also considered protons collisions at \(\sqrt{s}=14\,\textrm{TeV}\) (proton–lead collisions are not feasible at this energy). The result for \(5.02\,\textrm{TeV}\) and \(14\,\textrm{TeV}\) were not published in [212] and are thus new.
The factorization and renormalization scales were set using the transverse momentum of the leading and the sub-leading jets \(\mu =(p_{T1}+p_{T2})/2\). For the TMD gluon distributions, we used the ones calculated in [209] based on the Kutak-Sapeta (KS) fit of the dipole gluon density [12], as described in the preceding subsections. For the collinear PDFs we used the CTEQ10NLO PDF set [214] from LHAPDF6 [215]. For the computation of the cross sections, we included the channels \(qg^*\rightarrow qg\), with five quark flavours, and \(gg^* \rightarrow gg\). The channel \( gg^*\rightarrow {\overline{q}} q\) was neglected because its contribution, for the considered kinematic domain, is quite small [12, 209].
Let us now discuss the results. In Fig. 11 we show the results for the azimuthal correlations for p–p and p–Pb collisions in the ATLAS kinematics at \(\sqrt{s}=8.16\,\textrm{TeV}\). We compare the Sudakov resummation obtained via two methods, the full-b space resummation (dotted) and the simplified approach, where the collinear PDF is not affected by the Sudakov form factor. As can be seen, they differ a bit, but as we shall see below, the difference cancels in the nuclear modification ratio, and thus does not affect the saturation signal. Moreover, as we also show below, there are very large scale uncertainties, within which both methods are qualitatively similar. In our computations, we used the ITMD factorization alone, without parton shower or hadronisation corrections. In order to asses this effect, we computed cross section with PYTHIA [216, 217] with all correction turned on, and then just with initial-state parton shower. The latter roughly corresponds to the TMD framework (as discussed eg. in [218]), therefore both calculations allow for the extraction of a “correction factor”. We repeated the same procedure using the nucler PDFs in PYTHIA. In Fig. 12 we applied that correction to KaTie results and compared with PYTHIA computations. Although the correction factor is rather large, as we shall see below it does not affect the saturation signal in the nuclear modification ratio. Next, in Fig. 13 we show the error bands due to both scale variation. Finally, in Fig. 14 we compute the nuclear modification ratio. For all three \(p_T\) cuts, we show the ITMD result with simplified Sudakov resummation, with the full-b space resummation, and the result where the non-perturbative correction factor from PYTHIA was applied. We also compute the error band due to scale variation and due to the correction factor. We see, that the saturation effect due to the nonlinear evolution is visible, but not very significant for the considered kinematics. For the lower \(p_T\) cut, we observe suppression of about 15%, but the uncertainty due to the correction factor is not much less. Interestingly (but understandably) this error decreases for larger \(p_T\) bins.
Next, we move on to the more forward region with FoCal kinematics. Here we focus first on the \(p_T>10\) GeV cut. The results for azimuthal correlations are shown in Fig. 15. In one figure we show ITMD results with Sudakov obtained via both models, as well as PYTHIA corrections and errorbands, as discussed before. In Fig. 16 we compute the nuclear modification ratio for that case. As can be seen from the plot, the suppression due to saturation is very large, about 25–30%, and is not destroyed by the errors, both due to the scale variation and due to the non-perturbative effects. In Fig. 17 we show the latest results, where we compare p–p and p–Pb cross sections at different energies, computed also with larger \(p_T>20\) GeV cut. As expected, the difference between p–p and p–Pb is smaller in that case. Next, in Figs. 18 and 19 we present the latest results for rapidity distributions for the two \(p_T\) cuts, for the leading jet, and the sub-leading jet. As the shape of the rapidity distribution is correlated with the x dependence, and thus with the evolution in the energy, measurement of the rapidity distribution may provide a valuable discriminatory tool for the evolution equations. Finally, in Fig. 20 we show the nuclear modification ratio for the two energies and both \(p_T\) cuts. As can be seen, with forward FoCal kinematics, even with the \(p_T\) cut of 20 GeV the suppression is about 20%.
Nuclear modification ration \(R_{\mathrm {p-Pb}}\) in terms of the azimuthal angle \(\varDelta \phi \) between the leading and the sub-leading jets for the proton–proton and the proton–lead collisions at \(\sqrt{s}=5.02\,\textrm{TeV}\) (blue) and \(8.8\,\textrm{TeV}\) (red) in the ALICE FoCal kinematics. The solid lines represent the results from KaTie computed within the ITMD approach with the simplified Sudakov resummation Eq. (42) for \(p_{T1}, p_{T2} > 10\, \textrm{GeV}\). And the dotted lines represent the results for \(p_{T1}, p_{T2} > 20\, \textrm{GeV}\)
7.2 Forward dijets at electron ion collider
While the focus of this review is on forward jets at LHC, the new accelerator Electron Ion Collider (EIC) is just around the corner [33]. A vital part of its research program is to look for gluon saturation. However, since the involved hard scales are lower than at the LHC, in fact, hadrons constitute better probes of the saturation physics than jets. Nevertheless, there has been a large interest in jets at EIC, see for example [184, 219, 220]. Moreover, at the partonic level, both hadron and jet production need classes of the same diagrams. Therefore, the upcoming EIC experiment triggered tremendous progress in computing NLO corrections for the DIS process within the CGC formalism, see for example [101, 106, 139, 144, 221, 222].
In the context of the ITMD factorization, dijet production at EIC is actually a very interesting and important process. As discussed eg. in [168] the only TMD gluon distribution that is relevant for dijets in DIS, in the back-to-back limit, is the Weizsacker–Williams (WW) gluon distribution \(F_{gg}^{(3)}\) (called also \(xG^{(1)}\)).Footnote 2 For the ITMD factorization, this is only true for sufficiently small photon virtuality \(Q^2\ll p_T\), otherwise longitudinally polarized gluons contribute, and they are not formally accounted for in the ITMD approach. Due to this fact, for processes where such contributions formally enter, the ITMD factorization is called ITMD\(^*\) (see for example [185] for the trijet production case).
The dijet production in the DIS process gives actually more interesting observables than dijets in hadron-hadron scattering. This is because there is also an identified electron in the final state. Thus, in addition to dijet azimuthal correlations, one can also study correlations with the outgoing electron.
Azimuthal correlations between the total transverse momentum of the dijet system and the transverse momentum of the scattered electron at EIC in two frames: the LAB frame (left), and the Breit frame (right). The calculation has been done within the ITMD* framework with the Weizsäcker–Williams gluon distribution obtained from the Kutak–Sapeta fit to HERA data
The ITMD\(^*\) factorization formula for the process
reads
As mentioned above, there is only WW gluon distribution in the above formula.
In [224] we computed several observables using the above framework, not only to quantify possible saturation effects in dijet observable at EIC but also to demonstrate the relevance of interplay of the saturation, the Sudakov effect, and the exact kinematics.
First, we found that in the context of saturation physics, it is best to consider forward dijets. This provides a very good focusing of the \(x_A\) distribution around the sufficiently small values so that the use of the small-x formalism is well justified. For the WW gluon distribution, we used the Kutak–Sapeta fit of the dipole TMD to HERA data, and then the WW TMD distribution was calculated in the mean field approximation (see Sect. 6.5). The calculation was supplemented with the Sudakov form factor, see Fig. 9 and the corresponding discussion in the text. In Fig. 21 we show prediction for the cross section dependence on azimuthal angle between the dijet system and the scattered electron for CM energy per nucleon \(\sqrt{s}=90\) GeV. The calculations are done both in the lab frame and the Breit frame. One clearly sees effects coming from the Sudakov form factor while the saturation is rather mild, despite the cut on the jet transverse momentum (in the Breit frame) is very low. Primarily, it is a consequence of the saturation pattern visible in the WW gluon distribution. Unlike the dipole gluon distribution, it does not have a peak as a function of the transverse momentum, c.f. Figs. 9 and 8. In our computation, we put quite a low cut on the photon virtuality \(Q^2>1\) GeV\(^2\) in order to suppress the longitudinal gluons. For a complete discussion see [224, 225].
8 Summary and outlook
The text discusses the challenges and selected ongoing research related to searches of gluon saturation in QCD using dijet observables. Although there are indications of saturation in the experimental data, achieving a complete consensus on its existence is still a challenge due to demanding kinematics and the complex collision environment. While there are simpler observables than dijets, the latter have the advantage of providing the azimuthal correlations, which in the back-to-back kinematics are sensitive to saturation even for relatively hard jets.
The study of forward dijet production, using the Improved TMD Factorization (ITMD) framework, is a relatively novel proposal in the search for gluon saturation. The framework has been already used in addressing many dijet related observables that were reviewed in this work. The text highlights the need for more measurements and the construction of the FoCal detector by the ALICE collaboration to shed more light on the saturation phenomenon. Furthermore, it discusses complementary dijet measurements in photon nucleus scattering that can be done at the Electron Ion Collider.
While in the review we focused our attention on dijets, there are other forward physics final states that can be used to search for saturation effects [226]. Those include di-hadrons [13, 227, 228], \(J/\psi \) production [229], and trijets [148, 185]. The processes are complementary to dijets, however, in some aspects more challenging. The di-hadrons require knowledge of fragmentation function and are sensitive to longitudinal polarization effects while trijets are just more difficult to measure and interpret.
Future research will be focused on increasing the precision of the calculations. The ITMD framework is well suited to extrapolate methods known in collinear factorization to compute higher order corrections to off-shell gauge invariant matrix elements, and in principle to automatize NLO computations. First steps toward that goal have already been undertaken [230,231,232,233]. Also, it is important to increase the accuracy of the evolution equations, parton densities and there is also a substantial progress in this direction, see for example [112, 178, 234,235,236,237,238,239,240,241,242]. Last but not least, the ITMD framework should account for the longitudinally polarized gluons, which contribute to some processes (see eg. [243]). The corresponding amplitudes should be obtainable automatically, similarly to off-shell gauge invariant amplitudes coupled eikonally that are used currently in the ITMD. Research in that direction is also ongoing.
Data availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical paper and has no data.]
Notes
This distribution is also probed in forward Ultra Peripheral Collisions at LHC. We however do not discuss this process here. The first application of ITMD to UPC processes can be found in [223].
References
L. Gribov, E. Levin, M. Ryskin, Semihard Processes in QCD. Phys. Rep. 100, 1–150 (1983). https://doi.org/10.1016/0370-1573(83)90022-4
A.H. Mueller, J.-W. Qiu, Gluon recombination and shadowing at small values of x. Nucl. Phys. B 268, 427–452 (1986). https://doi.org/10.1016/0550-3213(86)90164-1
E. Iancu, R. Venugopalan, The Color glass condensate and high-energy scattering in QCD. 3, 249–3363 (2003). https://doi.org/10.1142/9789812795533_0005. arXiv:hep-ph/0303204
J. Jalilian-Marian, Y.V. Kovchegov, Saturation physics and deuteron-Gold collisions at RHIC. Prog. Part. Nucl. Phys. 56, 104–231 (2006). https://doi.org/10.1016/j.ppnp.2005.07.002. arXiv:hep-ph/0505052
F. Gelis, E. Iancu, J. Jalilian-Marian, R. Venugopalan, The color glass condensate. Ann. Rev. Nucl. Part. Sci. 60, 463–489 (2010). https://doi.org/10.1146/annurev.nucl.010909.083629. arXiv:1002.0333
J.L. Albacete, C. Marquet, Gluon saturation and initial conditions for relativistic heavy ion collisions. Prog. Part. Nucl. Phys. 76, 1–42 (2014). https://doi.org/10.1016/j.ppnp.2014.01.004. arXiv:1401.4866
J.-P. Blaizot, High gluon densities in heavy ion collisions. Rep. Prog. Phys. 80, 032301 (2017). https://doi.org/10.1088/1361-6633/aa5435. arXiv:1607.04448
Y.V. Kovchegov, E. Levin, Quantum Chromodynamics at High Energy, vol. 33 (Cambridge University Press, Cambridge, 2012). https://doi.org/10.1017/CBO9781139022187
K.J. Golec-Biernat, M. Wusthoff, Saturation effects in deep inelastic scattering at low Q**2 and its implications on diffraction. Phys. Rev. D 59, 014017 (1998). https://doi.org/10.1103/PhysRevD.59.014017. arXiv:hep-ph/9807513
J.L. Albacete, C. Marquet, Azimuthal correlations of forward di-hadrons in d+Au collisions at RHIC in the Color Glass Condensate. Phys. Rev. Lett. 105, 162301 (2010). https://doi.org/10.1103/PhysRevLett.105.162301. arXiv:1005.4065
K. Dusling, R. Venugopalan, Evidence for BFKL and saturation dynamics from dihadron spectra at the LHC. Phys. Rev. D 87, 051502 (2013). https://doi.org/10.1103/PhysRevD.87.051502. arXiv:1210.3890
K. Kutak, S. Sapeta, Gluon saturation in dijet production in p-Pb collisions at Large Hadron Collider. Phys. Rev. D 86, 094043 (2012). https://doi.org/10.1103/PhysRevD.86.094043. arXiv:1205.5035
A. Stasto, S.-Y. Wei, B.-W. Xiao, F. Yuan, On the Dihadron angular correlations in forward \(pA\) collisions. Phys. Lett. B 784, 301–306 (2018). https://doi.org/10.1016/j.physletb.2018.08.011. arXiv:1805.05712
A. van Hameren, P. Kotko, K. Kutak, S. Sapeta, Broadening and saturation effects in dijet azimuthal correlations in p–p and p–Pb collisions at \( \sqrt{s} = \) 5.02 TeV. Phys. Lett. B 795, 511–515 (2019). https://doi.org/10.1016/j.physletb.2019.06.055. arXiv:1903.01361
H. Mäntysaari, H. Paukkunen, Saturation and forward jets in proton–lead collisions at the LHC. Phys. Rev. D 100, 114029 (2019). https://doi.org/10.1103/PhysRevD.100.114029. arXiv:1910.13116
B. Ducloué, E. Iancu, G. Soyez, D.N. Triantafyllopoulos, HERA data and collinearly-improved BK dynamics. Phys. Lett. B 803, 135305 (2020). https://doi.org/10.1016/j.physletb.2020.135305. arXiv:1912.09196
A. Arroyo Garcia, M. Hentschinski, K. Kutak, QCD evolution based evidence for the onset of gluon saturation in exclusive photo-production of vector mesons. Phys. Lett. B 795, 569–575 (2019). https://doi.org/10.1016/j.physletb.2019.06.061. arXiv:1904.04394
STAR collaboration, M.S. Abdallah et al., Evidence for nonlinear gluon effects in QCD and their mass number dependence at STAR. Phys. Rev. Lett. 129, 092501 (2022). https://doi.org/10.1103/PhysRevLett.129.092501. arXiv:2111.10396
G. Beuf, H. Hänninen, T. Lappi, H. Mäntysaari, Color glass condensate at next-to-leading order meets HERA data. Phys. Rev. D 102, 074028 (2020). https://doi.org/10.1103/PhysRevD.102.074028. arXiv:2007.01645
A. Morreale, F. Salazar, Mining for gluon saturation at colliders. Universe 7, 312 (2021). https://doi.org/10.3390/universe7080312. arXiv:2108.08254
M. Cacciari, J. Rojo, G.P. Salam, G. Soyez, Jet reconstruction in heavy ion collisions. Eur. Phys. J. C 71, 1539 (2011). https://doi.org/10.1140/epjc/s10052-011-1539-z. arXiv:1010.1759
C. Marquet, Forward inclusive dijet production and azimuthal correlations in p(A) collisions. Nucl. Phys. A 796, 41–60 (2007). https://doi.org/10.1016/j.nuclphysa.2007.09.001. arXiv:0708.0231
A. van Hameren, P. Kotko, K. Kutak, C. Marquet, S. Sapeta, Saturation effects in forward-forward dijet production in p\(+\)Pb collisions. Phys. Rev. D 89, 094014 (2014). https://doi.org/10.1103/PhysRevD.89.094014. arXiv:1402.5065
K. Kutak, Hard scale dependent gluon density, saturation and forward-forward dijet production at the LHC. Phys. Rev. D 91, 034021 (2015). https://doi.org/10.1103/PhysRevD.91.034021. arXiv:1409.3822
M. Deak, F. Hautmann, H. Jung, K. Kutak, Forward-central jet correlations at the large hadron collider. arXiv:1012.6037
M. Deak, F. Hautmann, H. Jung, K. Kutak, Forward jets and energy flow in hadronic collisions. Eur. Phys. J. C 72, 1982 (2012). https://doi.org/10.1140/epjc/s10052-012-1982-5. arXiv:1112.6354
A. van Hameren, P. Kotko, K. Kutak, S. Sapeta, Small-\(x\) dynamics in forward-central dijet decorrelations at the LHC. Phys. Lett. B 737, 335–340 (2014). https://doi.org/10.1016/j.physletb.2014.09.005. arXiv:1404.6204
A. van Hameren, P. Kotko, K. Kutak, S. Sapeta, Sudakov effects in central-forward dijet production in high energy factorization. Phys. Lett. B 814, 136078 (2021). https://doi.org/10.1016/j.physletb.2021.136078. arXiv:2010.13066
ATLAS collaboration, M. Aaboud et al., Dijet azimuthal correlations and conditional yields in pp and p+Pb collisions at sNN=5.02TeV with the ATLAS detector. Phys. Rev. C 100, 034903 (2019). https://doi.org/10.1103/PhysRevC.100.034903. arXiv:1901.10440
CMS collaboration, A.M. Sirunyan et al., Measurement of inclusive very forward jet cross sections in proton–lead collisions at \( \sqrt{s_{\rm NN}} \) = 5.02 TeV. JHEP 05, 043 (2019). https://doi.org/10.1007/JHEP05(2019)043. arXiv:1812.01691
C. ALICE Collaboration, Letter of Intent: A Forward Calorimeter (FoCal) in the ALICE experiment, tech. rep., CERN, Geneva, Jun (2020)
A. Accardi et al., Electron ion collider: the next QCD frontier: understanding the glue that binds us all. Eur. Phys. J. A 52, 268 (2016). https://doi.org/10.1140/epja/i2016-16268-9. arXiv:1212.1701
R. Abdul Khalek et al., Science requirements and detector concepts for the electron-ion collider: EIC yellow report. Nucl. Phys. A 1026, 122447 (2022). https://doi.org/10.1016/j.nuclphysa.2022.122447. arXiv:2103.05419
P. Kotko, K. Kutak, C. Marquet, E. Petreska, S. Sapeta, A. van Hameren, Improved TMD factorization for forward dijet production in dilute-dense hadronic collisions. JHEP 09, 106 (2015). https://doi.org/10.1007/JHEP09(2015)106. arXiv:1503.03421
J. Collins, Foundations of Perturbative QCD, vol. 32 (Cambridge University Press, Cambridge, 2013)
ATLAS collaboration, G. Aad et al., Measurement of Dijet Azimuthal Decorrelations in \(pp\) Collisions at \(\sqrt{s}=7\) TeV. Phys. Rev. Lett. 106, 172002 (2011). https://doi.org/10.1103/PhysRevLett.106.172002. arXiv:1102.2696
CMS collaboration, V. Khachatryan et al., Dijet Azimuthal Decorrelations in \(pp\) Collisions at \(\sqrt{s} = 7\) TeV. Phys. Rev. Lett. 106, 122003 (2011). https://doi.org/10.1103/PhysRevLett.106.122003. arXiv:1101.5029
M. Bonvini, Small-x resummation in PDF fits and future prospects, in Diffraction and Low-x 2022, 12 (2022). arXiv:2212.14231
T.-J. Hou et al., New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC. arXiv:1912.10053
NNPDF collaboration, R.D. Ball et al., The path to proton structure at 1% accuracy. Eur. Phys. J. C 82, 428 (2022). https://doi.org/10.1140/epjc/s10052-022-10328-7. arXiv:2109.02653
M. Froissart, Asymptotic behavior and subtractions in the Mandelstam representation. Phys. Rev. 123, 1053–1057 (1961). https://doi.org/10.1103/PhysRev.123.1053
J. Bartels, K. Golec-Biernat, L. Motyka, Twist expansion of the nucleon structure functions, F(2) and F(L), in the DGLAP improved saturation model. Phys. Rev. D 81, 054017 (2010). https://doi.org/10.1103/PhysRevD.81.054017. arXiv:0911.1935
L. Motyka, M. Sadzikowski, W. Slominski, Evidence of strong higher twist effects in diffractive DIS at HERA at moderate \(Q^2\). Phys. Rev. D 86, 111501 (2012). https://doi.org/10.1103/PhysRevD.86.111501. arXiv:1203.5461
L. Motyka, M. Sadzikowski, Twist decomposition of proton structure from BFKL and BK amplitudes. Acta Phys. Pol. B 45, 2079 (2014). https://doi.org/10.5506/APhysPolB.45.2079. arXiv:1411.7774
L. Motyka, M. Sadzikowski, T. Stebel, Twist expansion of Drell–Yan structure functions in color dipole approach. JHEP 05, 087 (2015). https://doi.org/10.1007/JHEP05(2015)087. arXiv:1412.4675
D. Brzeminski, L. Motyka, M. Sadzikowski, T. Stebel, Twist decomposition of Drell–Yan structure functions: phenomenological implications. JHEP 01, 005 (2017). https://doi.org/10.1007/JHEP01(2017)005. arXiv:1611.04449
L. Motyka, M. Sadzikowski, W. Słomiński, K. Wichmann, Evidence of quasi-partonic higher-twist effects in deep inelastic scattering at HERA at moderate \(Q^2\). Eur. Phys. J. C 78, 80 (2018). https://doi.org/10.1140/epjc/s10052-018-5548-z. arXiv:1707.05992
U. Amaldi, R. Biancastelli, C. Bosio, G. Matthiae, J.V. Allaby, W. Bartel et al., The Energy dependence of the proton proton total cross-section for center-of-mass energies between 23 and 53 GeV. Phys. Lett. B 44, 112–118 (1973). https://doi.org/10.1016/0370-2693(73)90315-8
H.D.I. Abarbanel, J.B. Bronzan, R.L. Sugar, A.R. White, Reggeon field theory: formulation and use. Phys. Rep. 21, 119–182 (1975). https://doi.org/10.1016/0370-1573(75)90034-4
J. Bartels, C. Contreras, G.P. Vacca, Could reggeon field theory be an effective theory for QCD in the Regge limit? JHEP 03, 201 (2016). https://doi.org/10.1007/JHEP03(2016)201. arXiv:1512.07182
A. Kovner, E. Levin, M. Li, M. Lublinsky, The JIMWLK evolution and the s-channel unitarity. JHEP 09, 199 (2020). https://doi.org/10.1007/JHEP09(2020)199. arXiv:2006.15126
A. Kovner, E. Levin, M. Li, M. Lublinsky, Reggeon field theory and self duality: making ends meet. JHEP 10, 185 (2020). https://doi.org/10.1007/JHEP10(2020)185. arXiv:2007.12132
I. Balitsky, L. Lipatov, The Pomeranchuk singularity in quantum chromodynamics. Sov. J. Nucl. Phys. 28, 822–829 (1978)
E.A. Kuraev, L.N. Lipatov, V.S. Fadin, Multi-Reggeon processes in the Yang–Mills theory. Sov. Phys. JETP 44, 443–450 (1976)
E.A. Kuraev, L.N. Lipatov, V.S. Fadin, The Pomeranchuk singularity in nonabelian gauge theories. Sov. Phys. JETP 45, 199–204 (1977)
V.S. Fadin, E. Kuraev, L. Lipatov, On the Pomeranchuk singularity in asymptotically free theories. Phys. Lett. B 60, 50–52 (1975). https://doi.org/10.1016/0370-2693(75)90524-9
J.R. Forshaw, D.A. Ross, Quantum Chromodynamics and the Pomeron, vol. 9 (Oxford University Press, Oxford, 1998). https://doi.org/10.1017/9781009290111
J. Bartels, M. Wusthoff, The Triple Regge limit of diffractive dissociation in deep inelastic scattering. Z. Phys. C 66, 157–180 (1995). https://doi.org/10.1007/BF01496591
J. Bartels, Unitarity corrections to the Lipatov pomeron and the four gluon operator in deep inelastic scattering in QCD. Z. Phys. C 60, 471–488 (1993). https://doi.org/10.1007/BF01560045
J. Bartels, K. Kutak, A momentum space analysis of the triple Pomeron vertex in pQCD. Eur. Phys. J. C 53, 533–548 (2008). https://doi.org/10.1140/epjc/s10052-007-0501-6. arXiv:0710.3060
R. Engel, Photoproduction within the two component dual parton model. 1. Amplitudes and cross-sections. Z. Phys. C 66, 203–214 (1995). https://doi.org/10.1007/BF01496594
S. Roesler, R. Engel, J. Ranft, The Monte Carlo event generator DPMJET-III, in International Conference on Advanced Monte Carlo for Radiation Physics, Particle Transport Simulation and Applications (MC 2000), 12 (2000), p. 1033–1038. https://doi.org/10.1007/978-3-642-18211-2_166. arXiv:hep-ph/0012252
K. Werner, F.-M. Liu, T. Pierog, Parton ladder splitting and the rapidity dependence of transverse momentum spectra in deuteron-gold collisions at RHIC. Phys. Rev. C 74, 044902 (2006). https://doi.org/10.1103/PhysRevC.74.044902. arXiv:hep-ph/0506232
K. Werner, On a deep connection between factorization and saturation: new insight into modeling high-energy proton–proton and nucleus-nucleus scattering in the EPOS4 framework. arXiv:2301.12517
R.S. Fletcher, T.K. Gaisser, P. Lipari, T. Stanev, SIBYLL: an event generator for simulation of high-energy cosmic ray cascades. Phys. Rev. D 50, 5710–5731 (1994). https://doi.org/10.1103/PhysRevD.50.5710
E.-J. Ahn, R. Engel, T.K. Gaisser, P. Lipari, T. Stanev, Cosmic ray interaction event generator SIBYLL 2.1. Phys. Rev. D 80, 094003 (2009). https://doi.org/10.1103/PhysRevD.80.094003. arXiv:0906.4113
N.N. Kalmykov, S.S. Ostapchenko, A.I. Pavlov, Quark-gluon string model and EAS simulation problems at ultra-high energies. Nucl. Phys. B Proc. Suppl. 52, 17–28 (1997). https://doi.org/10.1016/S0920-5632(96)00846-8
S. Ostapchenko, Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: I. QGSJET-II model. Phys. Rev. D 83, 014018 (2011). https://doi.org/10.1103/PhysRevD.83.014018. arXiv:1010.1869
L. Lipatov, Gauge invariant effective action for high-energy processes in QCD. Nucl. Phys. B 452, 369–400 (1995). https://doi.org/10.1016/0550-3213(95)00390-E. arXiv:hep-ph/9502308
E. Antonov, L. Lipatov, E. Kuraev, I. Cherednikov, Feynman rules for effective Regge action. Nucl. Phys. B 721, 111–135 (2005). https://doi.org/10.1016/j.nuclphysb.2005.013. arXiv:hep-ph/0411185
M. Hentschinski, Chapter 11: Lipatov’s QCD high energy effective action: past and future. 283–310 (2021). https://doi.org/10.1142/9789811231124_0011. arXiv:2010.14748
J. Bartels, V. Fadin, E. Levin, A. Levy, V. Kim, A. Sabio-Vera (eds.), From the Past to the Future (World Scientific, Singapore, 2021). https://doi.org/10.1142/12127
G. Chachamis, M. Hentschinski, J.D. Madrigal Martinez, A. Sabio Vera, Quark contribution to the gluon Regge trajectory at NLO from the high energy effective action. Nucl. Phys. B 861, 133–144 (2012). https://doi.org/10.1016/j.nuclphysb.2012.03.015. arXiv:1202.0649
G. Chachamis, M. Hentschinski, J.D. Madrigal Martínez, A. Sabio Vera, Forward jet production \(\backslash \) & quantum corrections to the gluon Regge trajectory from Lipatov’s high energy effective action. Phys. Part. Nucl. 45, 788–799 (2014). https://doi.org/10.1134/S1063779614040030. arXiv:1211.2050
G. Chachamis, M. Hentschinski, J.D. Madrigal Martínez, A. Sabio Vera, Next-to-leading order corrections to the gluon-induced forward jet vertex from the high energy effective action. Phys. Rev. D 87, 076009 (2013). https://doi.org/10.1103/PhysRevD.87.076009. arXiv:1212.4992
G. Chachamis, M. Hentschinski, J.D. Madrigal Martinez, A. Sabio Vera, Gluon Regge trajectory at two loops from Lipatov’s high energy effective action. Nucl. Phys. B 876, 453–472 (2013). https://doi.org/10.1016/j.nuclphysb.2013.08.013. arXiv:1307.2591
M. Hentschinski, J.D. Madrigal Martínez, B. Murdaca, A. Sabio Vera, The next-to-leading order vertex for a forward jet plus a rapidity gap at high energies. Phys. Lett. B 735, 168–172 (2014). https://doi.org/10.1016/j.physletb.2014.06.022. arXiv:1404.2937
S. Bondarenko, L. Lipatov, A. Prygarin, Effective action for reggeized gluons, classical gluon field of relativistic color charge and color glass condensate approach. Eur. Phys. J. C 77, 527 (2017). https://doi.org/10.1140/epjc/s10052-017-5101-5. arXiv:1706.00278
M. Hentschinski, Color glass condensate formalism, Balitsky-JIMWLK evolution, and Lipatov’s high energy effective action. Phys. Rev. D 97, 114027 (2018). https://doi.org/10.1103/PhysRevD.97.114027. arXiv:1802.06755
S. Bondarenko, L. Lipatov, S. Pozdnyakov, A. Prygarin, One loop light-cone QCD, effective action for reggeized gluons and QCD RFT calculus. Eur. Phys. J. C 77, 630 (2017). https://doi.org/10.1140/epjc/s10052-017-5208-8. arXiv:1708.05183
S. Bondarenko, S. Pozdnyakov, On correlators of Reggeon fields and operators of Wilson lines in high energy QCD. Int. J. Mod. Phys. A 33, 1850204 (2018). https://doi.org/10.1142/S0217751X18502044. arXiv:1806.02563
I. Balitsky, Operator expansion for high-energy scattering. Nucl. Phys. B 463, 99–160 (1996). https://doi.org/10.1016/0550-3213(95)00638-9. arXiv:hep-ph/9509348
Y.V. Kovchegov, Small x F(2) structure function of a nucleus including multiple pomeron exchanges. Phys. Rev. D 60, 034008 (1999). https://doi.org/10.1103/PhysRevD.60.034008. arXiv:hep-ph/9901281
A.H. Mueller, Soft gluons in the infinite momentum wave function and the BFKL pomeron. Nucl. Phys. B 415, 373–385 (1994). https://doi.org/10.1016/0550-3213(94)90116-3
Y.V. Kovchegov, Unitarization of the BFKL pomeron on a nucleus. Phys. Rev. D 61, 074018 (2000). https://doi.org/10.1103/PhysRevD.61.074018. arXiv:hep-ph/9905214
E. Levin, K. Tuchin, Solution to the evolution equation for high parton density QCD. Nucl. Phys. B 573, 833–852 (2000). https://doi.org/10.1016/S0550-3213(99)00825-1. arXiv:hep-ph/9908317
E. Levin, K. Tuchin, New scaling at high-energy DIS. Nucl. Phys. A 691, 779–790 (2001). https://doi.org/10.1016/S0375-9474(01)00590-5. arXiv:hep-ph/0012167
E. Levin, K. Tuchin, Nonlinear evolution and saturation for heavy nuclei in DIS. Nucl. Phys. A 693, 787–798 (2001). https://doi.org/10.1016/S0375-9474(01)00880-6. arXiv:hep-ph/0101275
M. Braun, Structure function of the nucleus in the perturbative QCD with N(c)–\({>}\) infinity (BFKL pomeron fan diagrams). Eur. Phys. J. C 16, 337–347 (2000). https://doi.org/10.1007/s100520050026. arXiv:hep-ph/0001268
N. Armesto, M.A. Braun, Parton densities and dipole cross-sections at small x in large nuclei. Eur. Phys. J. C 20, 517–522 (2001). https://doi.org/10.1007/s100520100685. arXiv:hep-ph/0104038
M. Lublinsky, E. Gotsman, E. Levin, U. Maor, Nonlinear evolution and parton distributions at LHC and THERA energies. Nucl. Phys. A 696, 851–869 (2001). https://doi.org/10.1016/S0375-9474(01)01150-2. arXiv:hep-ph/0102321
M. Lublinsky, Scaling phenomena from nonlinear evolution in high-energy DIS. Eur. Phys. J. C 21, 513–519 (2001). https://doi.org/10.1007/s100520100752. arXiv:hep-ph/0106112
K.J. Golec-Biernat, L. Motyka, A.M. Stasto, Diffusion into infrared and unitarization of the BFKL pomeron. Phys. Rev. D 65, 074037 (2002). https://doi.org/10.1103/PhysRevD.65.074037. arXiv:hep-ph/0110325
K.J. Golec-Biernat, A.M. Stasto, On solutions of the Balitsky–Kovchegov equation with impact parameter. Nucl. Phys. B 668, 345–363 (2003). https://doi.org/10.1016/j.nuclphysb.2003.07.011. arXiv:hep-ph/0306279
E. Gotsman, M. Kozlov, E. Levin, U. Maor, E. Naftali, Towards a new global QCD analysis: solution to the nonlinear equation at arbitrary impact parameter. Nucl. Phys. A 742, 55–79 (2004). https://doi.org/10.1016/j.nuclphysa.2004.05.018. arXiv:hep-ph/0401021
T. Ikeda, L. McLerran, Impact parameter dependence in the Balitsky–Kovchegov equation. Nucl. Phys. A 756, 385–398 (2005). https://doi.org/10.1016/j.nuclphysa.2005.03.119. arXiv:hep-ph/0410345
J. Berger, A. Stasto, Numerical solution of the nonlinear evolution equation at small x with impact parameter and beyond the LL approximation. Phys. Rev. D 83, 034015 (2011). https://doi.org/10.1103/PhysRevD.83.034015. arXiv:1010.0671
A.H. Rezaeian, I. Schmidt, Impact-parameter dependent color glass condensate dipole model and new combined HERA data. Phys. Rev. D 88, 074016 (2013). https://doi.org/10.1103/PhysRevD.88.074016. arXiv:1307.0825
D. Bendova, J. Cepila, J.G. Contreras, M. Matas, Solution to the Balitsky–Kovchegov equation with the collinearly improved kernel including impact-parameter dependence. Phys. Rev. D 100, 054015 (2019). https://doi.org/10.1103/PhysRevD.100.054015. arXiv:1907.12123
J. Cepila, J.G. Contreras, M. Matas, Collinearly improved kernel suppresses Coulomb tails in the impact-parameter dependent Balitsky–Kovchegov evolution. Phys. Rev. D 99, 051502 (2019). https://doi.org/10.1103/PhysRevD.99.051502. arXiv:1812.02548
T. Altinoluk, G. Beuf, A. Czajka, A. Tymowska, Quarks at next-to-eikonal accuracy in the CGC: forward quark-nucleus scattering. Phys. Rev. D 104, 014019 (2021). https://doi.org/10.1103/PhysRevD.104.014019. arXiv:2012.03886
G.A. Chirilli, High-energy operator product expansion at sub-eikonal level. JHEP 06, 096 (2021). https://doi.org/10.1007/JHEP06(2021)096. arXiv:2101.12744
Y.V. Kovchegov, M.G. Santiago, Quark sivers function at small \(x\): spin-dependent odderon and the sub-eikonal evolution. JHEP 11, 200 (2021). https://doi.org/10.1007/JHEP11(2021)200. arXiv:2108.03667
T. Altinoluk, G. Beuf, Quark and scalar propagators at next-to-eikonal accuracy in the CGC through a dynamical background gluon field. Phys. Rev. D 105, 074026 (2022). https://doi.org/10.1103/PhysRevD.105.074026. arXiv:2109.01620
P. Agostini, T. Altinoluk, N. Armesto, F. Dominguez, J.G. Milhano, Multiparticle production in proton–nucleus collisions beyond eikonal accuracy. Eur. Phys. J. C 82, 1001 (2022). https://doi.org/10.1140/epjc/s10052-022-10962-1. arXiv:2207.10472
T. Altinoluk, G. Beuf, A. Czajka, A. Tymowska, DIS dijet production at next-to-eikonal accuracy in the CGC. Phys. Rev. D 107, 074016 (2023). https://doi.org/10.1103/PhysRevD.107.074016. arXiv:2212.10484
T. Altinoluk, N. Armesto, G. Beuf, Probing quark transverse momentum distributions in the Color Glass Condensate: quark-gluon dijets in Deep Inelastic Scattering at next-to-eikonal accuracy. arXiv:2303.12691
I. Balitsky, G.A. Chirilli, Next-to-leading order evolution of color dipoles. Phys. Rev. D 77, 014019 (2008). https://doi.org/10.1103/PhysRevD.77.014019. arXiv:0710.4330
A. Kovner, M. Lublinsky, Y. Mulian, J.-M. Iancu, M. Weigert, L. Kovner, Evolution at next to leading order. Phys. Rev. D 89, 061704 (2014). https://doi.org/10.1103/PhysRevD.89.061704. arXiv:1310.0378
A. Kovner, M. Lublinsky, Y. Mulian, NLO JIMWLK evolution unabridged. JHEP 08, 114 (2014). https://doi.org/10.1007/JHEP08(2014)114. arXiv:1405.0418
T. Lappi, H. Mäntysaari, Direct numerical solution of the coordinate space Balitsky–Kovchegov equation at next to leading order. Phys. Rev. D 91, 074016 (2015). https://doi.org/10.1103/PhysRevD.91.074016. arXiv:1502.02400
T. Lappi, H. Mäntysaari, Next-to-leading order Balitsky–Kovchegov equation with resummation. Phys. Rev. D 93, 094004 (2016). https://doi.org/10.1103/PhysRevD.93.094004. arXiv:1601.06598
B. Ducloué, E. Iancu, A.H. Mueller, G. Soyez, D.N. Triantafyllopoulos, Non-linear evolution in QCD at high-energy beyond leading order. JHEP 04, 081 (2019). https://doi.org/10.1007/JHEP04(2019)081. arXiv:1902.06637
L.D. McLerran, R. Venugopalan, Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 49, 2233–2241 (1994). https://doi.org/10.1103/PhysRevD.49.2233. arXiv:hep-ph/9309289
L.D. McLerran, R. Venugopalan, Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 49, 3352–3355 (1994). https://doi.org/10.1103/PhysRevD.49.3352. arXiv:hep-ph/9311205
Y.V. Kovchegov, NonAbelian Weizsacker–Williams field and a two-dimensional effective color charge density for a very large nucleus. Phys. Rev. D 54, 5463–5469 (1996). https://doi.org/10.1103/PhysRevD.54.5463. arXiv:hep-ph/9605446
J. Jalilian-Marian, A. Kovner, L.D. McLerran, H. Weigert, The Intrinsic glue distribution at very small x. Phys. Rev. D 55, 5414–5428 (1997). https://doi.org/10.1103/PhysRevD.55.5414. arXiv:hep-ph/9606337
J. Jalilian-Marian, A. Kovner, A. Leonidov, H. Weigert, The BFKL equation from the Wilson renormalization group. Nucl. Phys. B 504, 415–431 (1997). https://doi.org/10.1016/S0550-3213(97)00440-9. arXiv:hep-ph/9701284
A. Kovner, J.G. Milhano, H. Weigert, Relating different approaches to nonlinear QCD evolution at finite gluon density. Phys. Rev. D 62, 114005 (2000). https://doi.org/10.1103/PhysRevD.62.114005. arXiv:hep-ph/0004014
A. Kovner, J.G. Milhano, Vector potential versus color charge density in low x evolution. Phys. Rev. D 61, 014012 (2000). https://doi.org/10.1103/PhysRevD.61.014012. arXiv:hep-ph/9904420
H. Weigert, Unitarity at small Bjorken x. Nucl. Phys. A 703, 823–860 (2002). https://doi.org/10.1016/S0375-9474(01)01668-2. arXiv:hep-ph/0004044
E. Iancu, A. Leonidov, L.D. McLerran, Nonlinear gluon evolution in the color glass condensate. 1. Nucl. Phys. A 692, 583–645 (2001). https://doi.org/10.1016/S0375-9474(01)00642-X. arXiv:hep-ph/0011241
E. Ferreiro, E. Iancu, A. Leonidov, L. McLerran, Nonlinear gluon evolution in the color glass condensate. 2. Nucl. Phys. A 703, 489–538 (2002). https://doi.org/10.1016/S0375-9474(01)01329-X. arXiv:hep-ph/0109115
A. Dumitru, A. Hayashigaki, J. Jalilian-Marian, The color glass condensate and hadron production in the forward region. Nucl. Phys. A 765, 464–482 (2006). https://doi.org/10.1016/j.nuclphysa.2005.11.014. arXiv:hep-ph/0506308
H. Fujii, F. Gelis, R. Venugopalan, Quark pair production in high energy pA collisions: General features. Nucl. Phys. A 780, 146–174 (2006). https://doi.org/10.1016/j.nuclphysa.2006.09.012. arXiv:hep-ph/0603099
E. Iancu, J. Laidet, Gluon splitting in a shockwave. Nucl. Phys. A 916, 48–78 (2013). https://doi.org/10.1016/j.nuclphysa.2013.07.012. arXiv:1305.5926
G.A. Chirilli, B.-W. Xiao, F. Yuan, One-loop factorization for inclusive hadron production in \(pA\) collisions in the saturation formalism. Phys. Rev. Lett. 108, 122301 (2012). https://doi.org/10.1103/PhysRevLett.108.122301. arXiv:1112.1061
G.A. Chirilli, B.-W. Xiao, F. Yuan, Inclusive Hadron Productions in pA collisions. Phys. Rev. D 86, 054005 (2012). https://doi.org/10.1103/PhysRevD.86.054005. arXiv:1203.6139
A.M. Stasto, B.-W. Xiao, D. Zaslavsky, Towards the test of saturation physics beyond leading logarithm. Phys. Rev. Lett. 112, 012302 (2014). https://doi.org/10.1103/PhysRevLett.112.012302. arXiv:1307.4057
B. Ducloué, T. Lappi, Y. Zhu, Single inclusive forward hadron production at next-to-leading order. Phys. Rev. D 93, 114016 (2016). https://doi.org/10.1103/PhysRevD.93.114016. arXiv:1604.00225
E. Iancu, A.H. Mueller, D.N. Triantafyllopoulos, CGC factorization for forward particle production in proton-nucleus collisions at next-to-leading order. JHEP 12, 041 (2016). https://doi.org/10.1007/JHEP12(2016)041. arXiv:1608.05293
H.-Y. Liu, Y.-Q. Ma, K.-T. Chao, Improvement for color glass condensate factorization: single hadron production in pA collisions at next-to-leading order. Phys. Rev. D 100, 071503 (2019). https://doi.org/10.1103/PhysRevD.100.071503. arXiv:1909.02370
H.-Y. Liu, K. Xie, Z. Kang, X. Liu, Single inclusive jet production in pA collisions at NLO in the small-x regime. JHEP 07, 041 (2022). https://doi.org/10.1007/JHEP07(2022)041. arXiv:2204.03026
B. Ducloué, H. Hänninen, T. Lappi, Y. Zhu, Deep inelastic scattering in the dipole picture at next-to-leading order. Phys. Rev. D 96, 094017 (2017). https://doi.org/10.1103/PhysRevD.96.094017. arXiv:1708.07328
G. Beuf, T. Lappi, R. Paatelainen, Massive quarks in NLO dipole factorization for DIS: transverse photon. Phys. Rev. D 106, 034013 (2022). https://doi.org/10.1103/PhysRevD.106.034013. arXiv:2204.02486
H. Hänninen, H. Mäntysaari, R. Paatelainen, J. Penttala, Proton structure functions at next-to-leading order in the dipole picture with massive quarks. Phys. Rev. Lett. 130, 192301 (2023). https://doi.org/10.1103/PhysRevLett.130.192301. arXiv:2211.03504
P. Caucal, F. Salazar, R. Venugopalan, Dijet impact factor in DIS at next-to-leading order in the color glass condensate. JHEP 11, 222 (2021). https://doi.org/10.1007/JHEP11(2021)222. arXiv:2108.06347
P. Caucal, F. Salazar, B. Schenke, R. Venugopalan, Back-to-back inclusive dijets in DIS at small \(x\): Sudakov suppression and gluon saturation at NLO. arXiv:2208.13872
P. Caucal, F. Salazar, B. Schenke, T. Stebel, R. Venugopalan, Back-to-back inclusive dijets in DIS at small \(x\): Gluon Weizsäcker–Williams distribution at NLO. arXiv:2304.03304
H. Mäntysaari, J. Penttala, Exclusive production of light vector mesons at next-to-leading order in the dipole picture. Phys. Rev. D 105, 114038 (2022). https://doi.org/10.1103/PhysRevD.105.114038. arXiv:2203.16911
H. Mäntysaari, J. Penttala, Complete calculation of exclusive heavy vector meson production at next-to-leading order in the dipole picture. JHEP 08, 247 (2022). https://doi.org/10.1007/JHEP08(2022)247. arXiv:2204.14031
E. Iancu, Y. Mulian, Forward dijets in proton–nucleus collisions at next-to-leading order: the real corrections. JHEP 03, 005 (2021). https://doi.org/10.1007/JHEP03(2021)005. arXiv:2009.11930
E. Iancu, Y. Mulian, Dihadron production in DIS at NLO: the real corrections. arXiv:2211.04837
P. Taels, T. Altinoluk, G. Beuf, C. Marquet, Dijet photoproduction at low \(x\) at next-to-leading order and its back-to-back limit. arXiv:2204.11650
P. Taels, Forward production of a Drell–Yan pair and a jet at small \(x\) at next-to-leading order. arXiv:2308.02449
T. Altinoluk, R. Boussarie, C. Marquet, P. Taels, TMD factorization for dijets + photon production from the dilute-dense CGC framework. JHEP 07, 079 (2019). https://doi.org/10.1007/JHEP07(2019)079. arXiv:1810.11273
E. Iancu, Y. Mulian, Forward trijet production in proton–nucleus collisions. Nucl. Phys. A 985, 66–127 (2019). https://doi.org/10.1016/j.nuclphysa.2019.02.003. arXiv:1809.05526
T. Altinoluk, R. Boussarie, C. Marquet, P. Taels, Photoproduction of three jets in the CGC: gluon TMDs and dilute limit. JHEP 07, 143 (2020). https://doi.org/10.1007/JHEP07(2020)143. arXiv:2001.00765
J.C. Collins, R. Ellis, Heavy quark production in very high-energy hadron collisions. Nucl. Phys. B 360, 3–30 (1991). https://doi.org/10.1016/0550-3213(91)90288-9
S. Catani, M. Ciafaloni, F. Hautmann, High-energy factorization and small x heavy flavor production. Nucl. Phys. B 366, 135–188 (1991). https://doi.org/10.1016/0550-3213(91)90055-3
S. Catani, F. Hautmann, Quark anomalous dimensions at small x. Phys. Lett. B 315, 157–163 (1993). https://doi.org/10.1016/0370-2693(93)90174-G
S. Catani, F. Hautmann, High-energy factorization and small x deep inelastic scattering beyond leading order. Nucl. Phys. B 427, 475–524 (1994). https://doi.org/10.1016/0550-3213(94)90636-X. arXiv:hep-ph/9405388
M. Ciafaloni, Coherence effects in initial jets at small q**2 / s. Nucl. Phys. B 296, 49–74 (1988). https://doi.org/10.1016/0550-3213(88)90380-X
S. Catani, F. Fiorani, G. Marchesini, Small x behavior of initial state radiation in perturbative QCD. Nucl. Phys. B 336, 18–85 (1990). https://doi.org/10.1016/0550-3213(90)90342-B
A. van Hameren, P. Kotko, K. Kutak, Helicity amplitudes for high-energy scattering. JHEP 01, 078 (2013). https://doi.org/10.1007/JHEP01(2013)078. arXiv:1211.0961
CASCADE collaboration, H. Jung et al., The CCFM Monte Carlo generator CASCADE version 2.2.03. Eur. Phys. J. C 70, 1237–1249 (2010). https://doi.org/10.1140/epjc/s10052-010-1507-z. arXiv:1008.0152
CASCADE collaboration, S. Baranov et al., CASCADE3 A Monte Carlo event generator based on TMDs. Eur. Phys. J. C 81, 425 (2021). https://doi.org/10.1140/epjc/s10052-021-09203-8. arXiv:2101.10221
A. van Hameren, P. Kotko, K. Kutak, Multi-gluon helicity amplitudes with one off-shell leg within high energy factorization. JHEP 12, 029 (2012). https://doi.org/10.1007/JHEP12(2012)029. arXiv:1207.3332
P. Kotko, Wilson lines and gauge invariant off-shell amplitudes. JHEP 07, 128 (2014). https://doi.org/10.1007/JHEP07(2014)128. arXiv:1403.4824
A. van Hameren, BCFW recursion for off-shell gluons. JHEP 07, 138 (2014). https://doi.org/10.1007/JHEP07(2014)138. arXiv:1404.7818
A. van Hameren, M. Serino, BCFW recursion for TMD parton scattering. JHEP 07, 010 (2015). https://doi.org/10.1007/JHEP07(2015)010. arXiv:1504.00315
M. Deak, F. Hautmann, H. Jung, K. Kutak, Forward jet production at the large hadron collider. JHEP 09, 121 (2009). https://doi.org/10.1088/1126-6708/2009/09/121. arXiv:0908.0538
R. Angeles-Martinez et al., Transverse momentum dependent (TMD) parton distribution functions: status and prospects. Acta Phys. Pol. B 46, 2501–2534 (2015). https://doi.org/10.5506/APhysPolB.46.2501. arXiv:1507.05267
R. Boussarie et al., TMD Handbook. arXiv:2304.03302
C.J. Bomhof, P.J. Mulders, F. Pijlman, The construction of gauge-links in arbitrary hard processes. Eur. Phys. J. C 47, 147–162 (2006). https://doi.org/10.1140/epjc/s2006-02554-2. arXiv:hep-ph/0601171
M. Bury, P. Kotko, K. Kutak, TMD gluon distributions for multiparton processes. Eur. Phys. J. C 79, 152 (2019). https://doi.org/10.1140/epjc/s10052-019-6652-4. arXiv:1809.08968
B.-W. Xiao, F. Yuan, Non-universality of transverse momentum dependent parton distributions at small-x. Phys. Rev. Lett. 105, 062001 (2010). https://doi.org/10.1103/PhysRevLett.105.062001. arXiv:1003.0482
F. Dominguez, C. Marquet, B.-W. Xiao, F. Yuan, Universality of unintegrated gluon distributions at small x. Phys. Rev. D 83, 105005 (2011). https://doi.org/10.1103/PhysRevD.83.105005. arXiv:1101.0715
A. Metz, J. Zhou, Distribution of linearly polarized gluons inside a large nucleus. Phys. Rev. D 84, 051503 (2011). https://doi.org/10.1103/PhysRevD.84.051503. arXiv:1105.1991
E. Akcakaya, A. Schäfer, J. Zhou, Azimuthal asymmetries for quark pair production in pA collisions. Phys. Rev. D 87, 054010 (2013). https://doi.org/10.1103/PhysRevD.87.054010. arXiv:1208.4965
I. Balitsky, A. Tarasov, Rapidity evolution of gluon TMD from low to moderate x. JHEP 10, 017 (2015). https://doi.org/10.1007/JHEP10(2015)017. arXiv:1505.02151
I. Balitsky, A. Tarasov, Gluon TMD in particle production from low to moderate x. JHEP 06, 164 (2016). https://doi.org/10.1007/JHEP06(2016)164. arXiv:1603.06548
Y.V. Kovchegov, M.D. Sievert, Calculating TMDs of a large nucleus: quasi-classical approximation and quantum evolution. Nucl. Phys. B 903, 164–203 (2016). https://doi.org/10.1016/j.nuclphysb.2015.12.008. arXiv:1505.01176
Y.V. Kovchegov, D. Pitonyak, M.D. Sievert, Helicity evolution at small-x. JHEP 01, 072 (2016). https://doi.org/10.1007/JHEP01(2016)072. arXiv:1511.06737
Y.V. Kovchegov, D. Pitonyak, M.D. Sievert, Small-\(x\) asymptotics of the gluon helicity distribution. JHEP 10, 198 (2017). https://doi.org/10.1007/JHEP10(2017)198. arXiv:1706.04236
Y.V. Kovchegov, M.D. Sievert, Small-\(x\) helicity evolution: an operator treatment. Phys. Rev. D 99, 054032 (2019). https://doi.org/10.1103/PhysRevD.99.054032. arXiv:1808.09010
R. Boussarie, Y. Mehtar-Tani, A novel formulation of the unintegrated gluon distribution for DIS. Phys. Lett. B 831, 137125 (2022). https://doi.org/10.1016/j.physletb.2022.137125. arXiv:2006.14569
R. Boussarie, Y. Mehtar-Tani, Gluon-mediated inclusive deep inelastic scattering from Regge to Bjorken kinematics. JHEP 07, 080 (2022). https://doi.org/10.1007/JHEP07(2022)080. arXiv:2112.01412
C. Marquet, E. Petreska, C. Roiesnel, Transverse-momentum-dependent gluon distributions from JIMWLK evolution. JHEP 10, 065 (2016). https://doi.org/10.1007/JHEP10(2016)065. arXiv:1608.02577
T. Altinoluk, R. Boussarie, Low \(x\) physics as an infinite twist (G)TMD framework: unravelling the origins of saturation. JHEP 10, 208 (2019). https://doi.org/10.1007/JHEP10(2019)208. arXiv:1902.07930
T. Altinoluk, R. Boussarie, P. Kotko, Interplay of the CGC and TMD frameworks to all orders in kinematic twist. JHEP 05, 156 (2019). https://doi.org/10.1007/JHEP05(2019)156. arXiv:1901.01175
M.L. Mangano, S.J. Parke, Multiparton amplitudes in gauge theories. Phys. Rep. 200, 301–367 (1991). https://doi.org/10.1016/0370-1573(91)90091-Y. arXiv:hep-th/0509223
T. Altinoluk, C. Marquet, P. Taels, Low-x improved TMD approach to the lepto- and hadroproduction of a heavy-quark pair. JHEP 06, 085 (2021). https://doi.org/10.1007/JHEP06(2021)085. arXiv:2103.14495
R. Boussarie, H. Mäntysaari, F. Salazar, B. Schenke, The importance of kinematic twists and genuine saturation effects in dijet production at the electron-ion collider. JHEP 09, 178 (2021). https://doi.org/10.1007/JHEP09(2021)178. arXiv:2106.11301
M. Bury, A. van Hameren, P. Kotko, K. Kutak, Forward trijet production in p–p and p–Pb collisions at LHC. JHEP 09, 175 (2020). https://doi.org/10.1007/JHEP09(2020)175. arXiv:2006.13175
A. van Hameren, KaTie: for parton-level event generation with \(k_T\)-dependent initial states. Comput. Phys. Commun. 224, 371–380 (2018). https://doi.org/10.1016/j.cpc.2017.11.005. arXiv:1611.00680
J. Alwall et al., A Standard format for Les Houches event files. Comput. Phys. Commun. 176, 300–304 (2007). https://doi.org/10.1016/j.cpc.2006.11.010. arXiv:hep-ph/0609017
N.A. Abdulov et al., TMDlib2 and TMDplotter: a platform for 3D hadron structure studies. Eur. Phys. J. C 81, 752 (2021). https://doi.org/10.1140/epjc/s10052-021-09508-8. arXiv:2103.09741
F. Caravaglios, M. Moretti, An algorithm to compute Born scattering amplitudes without Feynman graphs. Phys. Lett. B 358, 332–338 (1995). https://doi.org/10.1016/0370-2693(95)00971-M. arXiv:hep-ph/9507237
M.L. Mangano, M. Moretti, F. Piccinini, R. Pittau, A.D. Polosa, ALPGEN, a generator for hard multiparton processes in hadronic collisions. JHEP 07, 001 (2003). https://doi.org/10.1088/1126-6708/2003/07/001. arXiv:hep-ph/0206293
K. Kutak, J. Kwiecinski, Screening effects in the ultrahigh-energy neutrino interactions. Eur. Phys. J. C 29, 521 (2003). https://doi.org/10.1140/epjc/s2003-01236-y. arXiv:hep-ph/0303209
M.A. Kimber, J. Kwiecinski, A.D. Martin, Gluon shadowing in the low x region probed by the LHC. Phys. Lett. B 508, 58–64 (2001). https://doi.org/10.1016/S0370-2693(01)00235-0. arXiv:hep-ph/0101099
A. Kovner, U.A. Wiedemann, No Froissart bound from gluon saturation. Phys. Lett. B 551, 311–316 (2003). https://doi.org/10.1016/S0370-2693(02)02907-6. arXiv:hep-ph/0207335
N.N. Nikolaev, W. Schafer, Quenching of leading jets and particles: the p perp dependent Landau–Pomeranchuk–Migdal effect from nonlinear k perp factorization. Phys. Rev. D 74, 014023 (2006). https://doi.org/10.1103/PhysRevD.74.014023. arXiv:hep-ph/0604117
J. Kwiecinski, A.D. Martin, A. Stasto, A unified BFKL and GLAP description of F2 data. Phys. Rev. D 56, 3991–4006 (1997). https://doi.org/10.1103/PhysRevD.56.3991. arXiv:hep-ph/9703445
H1, ZEUS collaboration, F. Aaron et al., Combined measurement and QCD analysis of the inclusive e+- p scattering cross sections at HERA. JHEP 01, 109 (2010). https://doi.org/10.1007/JHEP01(2010)109. arXiv:0911.0884
S. Bondarenko, Gluon density and F(2) functions from BK equation with impact parameter dependence. Phys. Lett. B 665, 72–78 (2008). https://doi.org/10.1016/j.physletb.2008.05.053. arXiv:0802.1802
M.A. Kimber, A.D. Martin, M.G. Ryskin, Unintegrated parton distributions and prompt photon hadroproduction. Eur. Phys. J. C 12, 655–661 (2000). https://doi.org/10.1007/s100520000326. arXiv:hep-ph/9911379
F. Hautmann, H. Jung, A. Lelek, V. Radescu, R. Zlebcik, Soft-gluon resolution scale in QCD evolution equations. Phys. Lett. B 772, 446–451 (2017). https://doi.org/10.1016/j.physletb.2017.07.005. arXiv:1704.01757
F. Hautmann, H. Jung, A. Lelek, V. Radescu, R. Zlebcik, Collinear and TMD quark and gluon densities from parton branching solution of QCD evolution equations. JHEP 01, 070 (2018). https://doi.org/10.1007/JHEP01(2018)070. arXiv:1708.03279
R.K. Ellis, W.J. Stirling, B.R. Webber, QCD and collider physics, vol. 8 (Cambridge University Press, 2011). https://doi.org/10.1017/CBO9780511628788
A. Mueller, B.-W. Xiao, F. Yuan, Sudakov double logarithms resummation in hard processes in the small-x saturation formalism. Phys. Rev. D 88, 114010 (2013). https://doi.org/10.1103/PhysRevD.88.114010. arXiv:1308.2993
A.H. Mueller, L. Szymanowski, S. Wallon, B.-W. Xiao, F. Yuan, Sudakov Resummations in Mueller–Navelet Dijet production. JHEP 03, 096 (2016). https://doi.org/10.1007/JHEP03(2016)096. arXiv:1512.07127
A. Mueller, B. Wu, B.-W. Xiao, F. Yuan, Medium induced transverse momentum broadening in hard processes. Phys. Rev. D 95, 034007 (2017). https://doi.org/10.1103/PhysRevD.95.034007. arXiv:1608.07339
A. Mueller, B.-W. Xiao, F. Yuan, Sudakov resummation in small-\(x\) saturation formalism. Phys. Rev. Lett. 110, 082301 (2013). https://doi.org/10.1103/PhysRevLett.110.082301. arXiv:1210.5792
C. Marquet, S.-Y. Wei, B.-W. Xiao, Probing parton saturation with forward \(Z^0\)-boson production at small transverse momentum in p+p and p+A collisions. Phys. Lett. B 802, 135253 (2020). https://doi.org/10.1016/j.physletb.2020.135253. arXiv:1909.08572
P. Sun, J. Isaacson, C.P. Yuan, F. Yuan, Nonperturbative functions for SIDIS and Drell–Yan processes. Int. J. Mod. Phys. A 33, 1841006 (2018). https://doi.org/10.1142/S0217751X18410063. arXiv:1406.3073
G. Watt, A. Martin, M. Ryskin, Unintegrated parton distributions and inclusive jet production at HERA. Eur. Phys. J. C 31, 73–89 (2003). https://doi.org/10.1140/epjc/s2003-01320-4. arXiv:hep-ph/0306169
A. van Hameren, P. Kotko, K. Kutak, C. Marquet, E. Petreska, S. Sapeta, Forward di-jet production in p+Pb collisions in the small-x improved TMD factorization framework. JHEP 12, 034 (2016). https://doi.org/10.1007/JHEP12(2016)034. arXiv:1607.03121
M.A. Al-Mashad, A. van Hameren, H. Kakkad, P. Kotko, K. Kutak, P. van Mechelen et al., Dijet azimuthal correlations in p-p and p-Pb collisions at forward LHC calorimeters. JHEP 12, 131 (2022). https://doi.org/10.1007/JHEP12(2022)131. arXiv:2210.06613
H. Fujii, C. Marquet, K. Watanabe, Comparison of improved TMD and CGC frameworks in forward quark dijet production. JHEP 12, 181 (2020). https://doi.org/10.1007/JHEP12(2020)181. arXiv:2006.16279
M.A. Al-Mashad, A. van Hameren, H. Kakkad, P. Kotko, K. Kutak, P. van Mechelen et al., Dijet azimuthal correlations in p–p and p–pb collisions at forward lhc calorimeters (2022)
M. Cacciari, G.P. Salam, G. Soyez, The anti-\(k_t\) jet clustering algorithm. JHEP (04) (2008). https://doi.org/10.1088/1126-6708/2008/04/063. arXiv:0802.1189
H.-L. Lai, M. Guzzi, J. Huston, Z. Li, P.M. Nadolsky, J. Pumplin et al., New parton distributions for collider physics. Phys. Rev. D 82 (2010). https://doi.org/10.1103/physrevd.82.074024
A. Buckley, J. Ferrando, S. Lloyd, K. Nordström, B. Page, M. Rüfenacht et al., LHAPDF6: parton density access in the LHC precision era. Eur. Phys. J. C 75 (2015). https://doi.org/10.1140/epjc/s10052-015-3318-8
T. Sjöstrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 Physics and Manual. JHEP 05, 026 (2006). https://doi.org/10.1088/1126-6708/2006/05/026. arXiv:hep-ph/0603175
T. Sjöstrand, S. Ask, J.R. Christiansen et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012
M. Bury, A. van Hameren, H. Jung, K. Kutak, S. Sapeta, M. Serino, Calculations with off-shell matrix elements, TMD parton densities and TMD parton showers. Eur. Phys. J. C 78, 137 (2018). https://doi.org/10.1140/epjc/s10052-018-5642-2. arXiv:1712.05932
M. Arratia, Y. Song, F. Ringer, B.V. Jacak, Jets as precision probes in electron-nucleus collisions at the future electron-ion collider. Phys. Rev. C 101, 065204 (2020). https://doi.org/10.1103/PhysRevC.101.065204. arXiv:1912.05931
H.T. Li, I. Vitev, Nuclear matter effects on jet production at electron-ion colliders. arXiv:2010.05912
F. Bergabo, J. Jalilian-Marian, Single inclusive hadron production in DIS at small x: next to leading order corrections. JHEP 01, 095 (2023). https://doi.org/10.1007/JHEP01(2023)095. arXiv:2210.03208
F. Bergabo, J. Jalilian-Marian, Dihadron production in DIS at small x at next-to-leading order: transverse photons. Phys. Rev. D 107, 054036 (2023). https://doi.org/10.1103/PhysRevD.107.054036. arXiv:2301.03117
P. Kotko, K. Kutak, S. Sapeta, A.M. Stasto, M. Strikman, Estimating nonlinear effects in forward dijet production in ultra-peripheral heavy ion collisions at the LHC. Eur. Phys. J. C 77, 353 (2017). https://doi.org/10.1140/epjc/s10052-017-4906-6. arXiv:1702.03063
A. van Hameren, P. Kotko, K. Kutak, S. Sapeta, E. Żarów, Probing gluon number density with electron-dijet correlations at EIC. Eur. Phys. J. C 81, 741 (2021). https://doi.org/10.1140/epjc/s10052-021-09529-3. arXiv:2106.13964
T. Goda, K. Kutak, S. Sapeta, Effects of gluon kinematics and the Sudakov form factor on the dipole amplitude. arXiv:2305.14025
M. Hentschinski et al., White paper on forward physics, BFKL, saturation physics and diffraction. Acta Phys. Pol. B 54, 2 (2023). https://doi.org/10.5506/APhysPolB.54.3-A2. arXiv:2203.08129
J.L. Albacete, G. Giacalone, C. Marquet, M. Matas, Forward dihadron back-to-back correlations in \(pA\) collisions. Phys. Rev. D 99, 014002 (2019). https://doi.org/10.1103/PhysRevD.99.014002. arXiv:1805.05711
J. Jalilian-Marian, A.H. Rezaeian, Hadron production in pA collisions at the LHC from the color glass condensate. Phys. Rev. D 85, 014017 (2012). https://doi.org/10.1103/PhysRevD.85.014017. arXiv:1110.2810
B. Ducloué, T. Lappi, H. Mäntysaari, Forward \(J/\psi \) production in proton-nucleus collisions at high energy. Phys. Rev. D 91, 114005 (2015). https://doi.org/10.1103/PhysRevD.91.114005. arXiv:1503.02789
M. Hentschinski, J.D. Madrigal Martínez, B. Murdaca, A. Sabio Vera, NLO vertex for a forward jet plus a rapidity gap at high energies. AIP Conf. Proc. 1654, 070013 (2015). https://doi.org/10.1063/1.4916003. arXiv:1409.7731
E. Blanco, A. van Hameren, P. Kotko, K. Kutak, All-plus helicity off-shell gauge invariant multigluon amplitudes at one loop. JHEP 12, 158 (2020). https://doi.org/10.1007/JHEP12(2020)158. arXiv:2008.07916
A. van Hameren, L. Motyka, G. Ziarko, Hybrid k\(_{T}\) -factorization and impact factors at NLO. JHEP 11, 103 (2022). https://doi.org/10.1007/JHEP11(2022)103. arXiv:2205.09585
E. Blanco, A. Giachino, A. van Hameren, P. Kotko, One-loop gauge invariant amplitudes with a space-like gluon. arXiv:2212.03572
M. Hentschinski, A. Sabio Vera, C. Salas, Hard to soft pomeron transition in small-x deep inelastic scattering data using optimal renormalization. Phys. Rev. Lett. 110, 041601 (2013). https://doi.org/10.1103/PhysRevLett.110.041601. arXiv:1209.1353
E. Iancu, J.D. Madrigal, A.H. Mueller, G. Soyez, D.N. Triantafyllopoulos, Collinearly-improved BK evolution meets the HERA data. Phys. Lett. B 750, 643–652 (2015). https://doi.org/10.1016/j.physletb.2015.09.071. arXiv:1507.03651
M. Hentschinski, A. Kusina, K. Kutak, Transverse momentum dependent splitting functions at work: quark-to-gluon splitting. Phys. Rev. D 94, 114013 (2016). https://doi.org/10.1103/PhysRevD.94.114013. arXiv:1607.01507
M. Hentschinski, A. Kusina, K. Kutak, M. Serino, TMD splitting functions in \(k_T\) factorization: the real contribution to the gluon-to-gluon splitting. Eur. Phys. J. C 78, 174 (2018). https://doi.org/10.1140/epjc/s10052-018-5634-2. arXiv:1711.04587
Y. Shi, L. Wang, S.-Y. Wei, B.-W. Xiao, Pursuing the precision study for color glass condensate in forward hadron productions. Phys. Rev. Lett. 128, 202302 (2022). https://doi.org/10.1103/PhysRevLett.128.202302. arXiv:2112.06975
W. Li, A.M. Stasto, Structure functions from renormalization group improved small x evolution. Eur. Phys. J. C 82, 562 (2022). https://doi.org/10.1140/epjc/s10052-022-10523-6. arXiv:2201.10579
F. Hautmann, M. Hentschinski, L. Keersmaekers, A. Kusina, K. Kutak, A. Lelek, A parton branching with transverse momentum dependent splitting functions. Phys. Lett. B 833, 137276 (2022). https://doi.org/10.1016/j.physletb.2022.137276. arXiv:2205.15873
M. Hentschinski, Transverse momentum dependent gluon distribution within high energy factorization at next-to-leading order. Phys. Rev. D 104, 054014 (2021). https://doi.org/10.1103/PhysRevD.104.054014. arXiv:2107.06203
M. Hentschinski, K. Kutak, A. van Hameren, Forward Higgs production within high energy factorization in the heavy quark limit at next-to-leading order accuracy. Eur. Phys. J. C 81, 112 (2021). https://doi.org/10.1140/epjc/s10052-021-08902-6. arXiv:2011.03193
C. Marquet, C. Roiesnel, P. Taels, Linearly polarized small-\(x\) gluons in forward heavy-quark pair production. Phys. Rev. D 97, 014004 (2018). https://doi.org/10.1103/PhysRevD.97.014004. arXiv:1710.05698
Acknowledgements
We would like to thank Jacek Otwinowski for interesting and stimulating discussions and Francesco Hautmann for useful comments. HK is supported by the National Science Centre, Poland Grant no. DEC-2021/41/N/ST2/02956. PK is partially supported by the National Science Centre, Poland Grant no. DEC-2020/39/O/ST2/03011. KK acknowledges the Polish National Science Centre Grant no. DEC-2017/27/B/ST2/01985. AvH is supported by the National Science Centre, Poland Grant no. DEC-2019/35/B/ST2/03531.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
van Hameren, A., Kakkad, H., Kotko, P. et al. Searching for saturation in forward dijet production at the LHC. Eur. Phys. J. C 83, 947 (2023). https://doi.org/10.1140/epjc/s10052-023-12120-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-12120-7