Implications of pressure anisotropy and complexity factor on the gravitational cracking phenomenon

Abstract

In this study, we are investigating the stability of some stellar configurations evolving under anisotropic environment, in the background of gravitational cracking. The models we consider pertain to anisotropic versions of Durgapal–Fuloria model, which are established using the gravitational decoupling framework and present diverse scenarios involving complexity factor. Our analysis delves into the impact of anisotropy on the occurrence of cracking, as well as the influence of the complexity factor, which was introduced by Herrera (Phys Rev D 97:044010, 2018). We thoroughly examine how variations in the decoupling parameter and the compactness of the source contribute to the behavior of the radial force. It is found that more compact objects are more prone to gravitational cracking.

1 Introduction

The term “cracking” is used metaphorically to depict the presence of internal forces within the fluid distribution that resemble the behavior of a cracked or fragmented solid. This phenomenon describes the formation of regions or regions with opposing forces, leading to a departure from the overall equilibrium state. In a spherical fluid distribution, the concept of cracking, as described by Herrera and elaborated upon in subsequent works [1,2,3,4], refers to the behavior exhibited by the fluid distribution immediately after it departs from equilibrium. At this stage, the system experiences non-vanishing radial forces of different signs within it. Specifically, cracking occurs when, the radial force is directed inward in the inner part of a sphere and then changes direction beyond a certain radial coordinate. On the other hand, if the radial force changes direction from outward to inward, it is referred to as overturning. In this way, it provides a framework to analyze and model the intricate behavior of fluid distributions, allowing us to explore the consequences and implications of such phenomena in various fields including astrophysics and cosmology [5,6,7,8].

When cracking occurs, it directly affects the structure formation of the compact object at time scales that are less than or equivalent to the hydrodynamic time scale [9,10,11]. This is the case because what we do is examine the system’s trend immediately after it departs from its equilibrium state. Due to the significant impact on the development of the compact stellar objects, the occurrence of cracking increases its importance and interest. It was found in [4] that cracking occurs only if the local anisotropy is disturbed, which indicates that the fluctuation of this quantity plays a key role in the occurrence of cracking. Furthermore, the presence of cracks in initially isotropic configurations highlights that even slight deviations from local isotropy can lead to significant changes in the evolution of the system [12]. Therefore, there is a clear and undeniable relationship between anisotropy and the phenomenon of cracking. In [13], the concept of cracking is utilized as a means to detect instabilities and examine the stability properties of isotropic and anisotropic matter configurations.

The concept of pressure anisotropy was introduced in the pioneering work of Ruderman [14], where it was demonstrated that the high density of nuclear matter, which interacts relativistically, plays a crucial role in the formation of this anisotropy. Here, anisotropy refers to the difference between the radial component of pressure and transversal component of pressure leading to variations in the internal structure and physical properties of these objects, while the equality of pressure arises from assuming the spherical symmetry of the stellar system. Further investigations by Bowers and Liang [15] revealed that anisotropy in spherically symmetric stellar systems can emerge due to the presence of complex strong interactions, such as superconductivity and superfluidity of ultradense matter. Herrera and Santos [16] provided a comprehensive review discussing the potential reasons behind the formation and existence of local anisotropic stress in self-gravitating systems. They also studied the effects of anisotropy on static spherically symmetric stellar systems.

Building on this line of research, several authors [17,18,19,20,21,22,23,24,25,26] have investigated the effects of anisotropy on spherically symmetric compact stellar systems. They have examined how anisotropy influences various physical properties of the stellar system and explored its implications. The above discussion provide a rationale for the renewed interest in the study of fluids that do not satisfy the isotropic condition, specifically in the context of compact stars. However, it is important to notice that anisotropy, whether arising from intrinsic properties of the system or external influences, is a crucial factor in the occurrence of cracking. It introduces the necessary conditions for the emergence of non-vanishing radial forces and contributes to the dynamic behavior and evolution of the system.

In addition to considering anisotropy as a fundamental factor in the occurrence of cracking, exploring it in terms of another physical quantity known as the complexity factor can provide valuable insights. The complexity factor incorporates both anisotropy and gradients in energy density, offering a comprehensive measure of the system’s complexity. This complexity factor based on a scalar quantity $Y_{TF}$ appearing in the orthogonal splitting of the Riemann tensor, has gained attention in the study of self-gravitating systems [27]. It differs significantly from previous definitions found in different researches [28,29,30,31,32,33]. It is characterized by the inclusion of contributions from both energy density inhomogeneity and local pressure anisotropy, combined in a specific manner. Notably, the complexity factor defined by $Y_{TF}$ focuses on the simplicity of an isotropic homogeneous fluid as a baseline, allowing for a natural definition of a system with zero complexity. It is worth emphasizing that the complexity factor defined in this way not only vanishes for the simple configuration mentioned earlier but also has the potential to vanish when the two terms appearing in its definition cancel each other out. The concept of assessing the complexity of a given fluid distribution involves addressing two distinct challenges. Firstly, it entails evaluating the intricacy of the fluid’s structure, which is quantified by a complexity factor. Secondly, when dealing with systems operating outside of equilibrium conditions (it is important to note that cracking occurs when the system departs from equilibrium), one must not only consider the complexity of the fluid itself but also examine the intricacy of its evolutionary pattern. To delve further into the second aspect, it becomes crucial to identify the simplest mode of evolution for such systems. In [34, 35], Herrera and his co-researchers explored two distinct patterns of evolution as potential candidates for being the “simplest”. These were referred to as (i) the homologous regime and (ii) the quasi-homologous regime. While considering the occurrence of cracking, it becomes imperative to account for the specific mode of evolution that the fluid distribution undergoes precisely at the moment it departs from equilibrium.

Moreover, the complexity factor $Y_{TF}$ not only quantifies complexity in the physical systems but also facilitates the classification of systems into equivalence classes based on their complexity level. Thus, it allows us to identify the shared features and phenomenon in each class. Moreover, some recent works can be found in [36,37,38,39,40,41,42,43,44], where complexity factor has been used to close the system of Einstein’s field equations (EFEs), particularly in the domain of gravitational decoupling (GD) by means of Minimal Geometric Deformation (MGD) [45, 46, 48,49,50, 56]. Analyzing the impact of complexity on cracking helps us understand how the degree of intricacy in a system affects its stability and response to perturbations. By considering systems with different complexity levels, researchers can investigate how cracking phenomena vary and whether there are specific complexity thresholds that lead to its occurrence or suppression.

In this work, we investigate different anisotropic versions of the Durgapal-Fuloria model [51, 52], where our primary focus lies in assessing their stability within the framework of cracking phenomenon. To achieve this, we employ a generalized approach introduced in a previous work [53] The article is arranged as follows: Sect. 2 provides a concise overview of the fundamental concepts underlying the definition of the complexity factor. Section 3 is related to the basic equations of MGD framework. Section 4 is specifically focused on the examination of cracking within selected models. Concluding remarks are presented in the last section.

2 Generalization of complexity factor

In this section, we discuss the essential features of the definition of complexity factor $\mathcal {Y_{TF}}$. In recent years, the concept of complexity for static and spherically symmetric self-gravitating systems was introduced by Herrera [28]. This definition of complexity is characterized by the inclusion of contributions from both energy density inhomogeneity and local pressure anisotropy, and vanishes for a homogeneous and locally isotropic fluid distribution, which is regarded as the least complex system.

Let us begin by considering a static, spherically symmetric space-time, whose metric (in Schwarzschild-like coordinates) is given as

$$\begin{aligned} ds^2=e^{\nu (r)}dt^2-e^{\lambda (r)}dr^2-r^2(d\sigma ^2+sin^2\sigma d\phi ^2), \end{aligned}$$

(1)

where $\nu$ and $\lambda$ are the functions of r. Here, EFEs for a static anisotropic fluid with spherical symmetry metric is given below

$$\begin{aligned} R_{ab}-\frac{1}{2}g_{ab}R=\kappa T_{ab}, \end{aligned}$$

(2)

where $R_{ab}$ is the Ricci tensor, $g_{ab}$ is metric tensor, $\kappa$ is the coupling constant. In the case of anisotropic fluid distribution, the matter sector on right hand side is defined by EMT, given below

$$\begin{aligned} T^{a}_{b}= & {} diag(\rho , -p_r, -p_t, -p_t), \end{aligned}$$

(3)

Moreover, the Riemann tensor can be decomposed in the form of following three tensors [54]

$$\begin{aligned} \mathcal {Y}_{ab}= & {} R_{abcd}s^c s^d, \end{aligned}$$

(4)

$$\begin{aligned} N_{ab}= & {} *R_{abcd}s^c s^d, \end{aligned}$$

(5)

$$\begin{aligned} O_{ab}= & {} *R*_{abcd}s^c s^d, \end{aligned}$$

(6)

where $s^a$ is a four velocity vector, which is defined by $s^a=(0, e^{-\frac{\nu }{2}}, 0, 0)$. Moreover, $*$ symbolizes the dual tensor such that $R*_{abcd}=\frac{1}{2}\eta _{efcd} R_{ab}^{ef}$, while $\eta _{efcd}$ is Levi-Civita tensor. The above-mentioned tensor $\mathcal {Y}_{ab},$ $N_{ab}$ and $O_{ab}$ assume the expressions, when expressed in the form of matter variables, as [27]

$$\begin{aligned} \mathcal {Y}_{ab}= & {} \frac{4\pi }{3}(\rho +p_r+2p_t)k_{ab}+4\pi \bar{\Pi }_{ab}+E_{ab}, \end{aligned}$$

(7)

$$\begin{aligned} N_{ab}= & {} 0, \end{aligned}$$

(8)

$$\begin{aligned} O_{ab}= & {} \frac{8\pi }{3}\rho k_{ab}++4\pi \bar{\Pi }_{ab}+E_{ab}, \end{aligned}$$

(9)

where

$$\begin{aligned} \bar{\Pi }_{b}^{a}= & {} \Pi \big (\bar{s}^a \bar{s}_b+\frac{1}{3}k^a_b\big ), \end{aligned}$$

(10)

$$\begin{aligned} \bar{\Pi }= & {} p_t-p_r, \end{aligned}$$

(11)

$$\begin{aligned} k^a_b= & {} \delta ^a_b-s^a s_b. \end{aligned}$$

(12)

Here, $\bar{s}^a$ is defined as $\bar{s}^a=(0, e^{-\frac{\lambda }{2}}, 0, 0)$, and satisfies the relations $\bar{s}^a\bar{s}_a=-1$ and $\bar{s}^a s_a=0$. In the expressions (7) and (9), we find $E_{ab}=C_{acbd}s^c s^d$ which corresponds to the electric part of the Weyl tensor, whereas magnetic one is vanished in the case of spherical symmetry. We can define $E_{ab}$ in the following form as well [55]

$$\begin{aligned} E_{ab}=E\big (\bar{s}_a \bar{s}_b+\frac{1}{3}k_{ab}\big ), \end{aligned}$$

(13)

where E is defined as

$$\begin{aligned} E=-\frac{e^{-\lambda }}{4}\Bigg [\nu ''+\frac{\nu '^2-\nu '\lambda }{2}-\frac{\nu '-\lambda '}{r}+\frac{2(1-e^\lambda )}{r^2}\Bigg ].\nonumber \\ \end{aligned}$$

(14)

Now, we can define four scalar functions consisting on traced and traced-free parts of $O_{ab}$ and $\mathcal {Y}_{ab}$. Here, we have trace-free parts in the following form

$$\begin{aligned} \mathcal {Y_{TF}}=4\pi \bar{\Pi } -E, \end{aligned}$$

(15)

and

$$\begin{aligned} O_{TF}=4\pi \bar{\Pi } +E. \end{aligned}$$

(16)

From (15) and (16), it can be noticed clearly that total anisotropy of the system can be expressed as

$$\begin{aligned} \mathcal {Y_{TF}}+O_{TF}=8\pi \bar{\Pi }. \end{aligned}$$

(17)

In [55], it has been shown that $\mathcal {Y_{TF}}$ can expressed in terms of energy density inhomogeneity and anisotropy of the system, and such an expression of trace-free tensor takes the form as

$$\begin{aligned} \mathcal {Y_{TF}}=8\pi \bar{\Pi }-\frac{4\pi }{r^3}\int _{0}^{r}\hat{r}^3\rho 'd\hat{r}. \end{aligned}$$

(18)

Here, we can see that complexity factor $\mathcal {Y_{TF}}$, as a single scalar function, captures all the modifications introduced by the energy density inhomogeneity and the anisotropy of the pressure. This argument suggests that the complexity factor can be defined based on this scalar function. With the help of this function, Tolman’s mass can be defined as

$$\begin{aligned} m_T=\Bigg (\frac{r}{r_\Sigma }\Bigg )^3 (m_T)_\Sigma +r^3\int _r^{r_\Sigma }\frac{\mathcal {Y_{TF}}}{\hat{r}}e^{\frac{\lambda +\nu }{2}}d\hat{r}. \end{aligned}$$

(19)

This expression supports our previous argument, and also shows that $\mathcal {Y_{TF}}$ quantifies the modifications induced by both quantities, i.e., energy density inhomogeneity and pressure anisotropy, on the active gravitational mass. Moreover, it is assumed that one of the simplest systems has a homogeneous energy density distribution with isotropic pressure. In such a system, the structure scalar $\mathcal {Y_{TF}}$ is zero, indicating a lack of complexity or vanishing complexity. From (18), we find that vanishing of complexity factor provides the following condition

$$\begin{aligned} \bar{\Pi }=\frac{1}{2r^3}\int _{0}^{r}\hat{r}^3\rho 'd\hat{r}. \end{aligned}$$

(20)

The complexity factor $\mathcal {Y_{TF}}$ against specific choices can be used to solve the field equations in general relativity and other modified theories. Equation (20) may be regarded as a non-local equation of state, which is obtained against the vanishing of complexity condition and can be used to impose a condition on the matter variables when solving the EFEs for a static, spherically symmetric anisotropic fluid sphere.

3 Einstein field equations and MGD

Now, we present a brief review of GD by means of MGD. For this, we take EFEs (2) into account. However we choose a total EMT $T_{ab}$ on the right hand side of the EFEs, which is combination of two sources, given by

$$\begin{aligned} T_{ab}=T_{ab}^{o} +\alpha \sigma _{ab}. \end{aligned}$$

(21)

In Eq. (21), $T_{ab}^{o}$ represents the seed sector, which is the matter of a standard solution of EFEs, while $\sigma _{ab}$ represents an extra source. Both of these sources are connected through $\alpha$ which controls the anisotropy of the system and measures the effects of $\sigma _{ab}$. Moreover, extra source $\sigma _{ab}$ can be defined through the following diagonal form, i.e.,

$$\begin{aligned} \sigma _{b}^{a}=diag(\sigma _{0}^{0}, \sigma _{1}^{1}, \sigma _{2}^{2}, \sigma _{3}^{3}). \end{aligned}$$

(22)

Further, EMT $T_{ab}$ satisfies the conservation equation, which is described by the following mathematical expression

$$\begin{aligned} \nabla _a T^{ab}=0. \end{aligned}$$

(23)

Next, the components of the EFEs (2) are expressed explicitly using the EMT (21) and line-element (1). With these assumptions, EFEs are expressed as follows

$$\begin{aligned} \kappa (\rho ^{o}+\alpha \sigma _{0}^{0})= & {} \frac{1}{r^2}+e^{-\lambda }\bigg (\frac{ \lambda '}{r}-\frac{1}{r^2}\bigg ), \end{aligned}$$

(24)

$$\begin{aligned} \kappa (p^{o}_r-\alpha \sigma ^{1}_{1})= & {} -\frac{1}{r^2}+e^{-\lambda }\bigg (\frac{1}{r^2}+\frac{\nu '}{r}\bigg ) , \end{aligned}$$

(25)

$$\begin{aligned} \kappa (p_t^{o}-\alpha \sigma ^{2}_{2})= & {} \frac{1}{4}e^{-\lambda }\bigg (2\nu ''-\nu '\lambda '+\nu '^2+2\frac{\nu '-\lambda '}{r}\bigg ).\nonumber \\ \end{aligned}$$

(26)

The right sides of these equations can be related with the effective quantities in the following manner

$$\begin{aligned} \rho= & {} (\rho ^{o}+\alpha \sigma _{0}^{0}), \end{aligned}$$

(27)

$$\begin{aligned} p_r= & {} (p^{o}_r-\alpha \sigma ^{1}_{1}), \end{aligned}$$

(28)

$$\begin{aligned} p_t= & {} (p_t^{o}-\alpha \sigma ^{2}_{2}). \end{aligned}$$

(29)

For the implementation of MGD, a deformation is introduced in the radial component of metric, given by

$$\begin{aligned} e^{-\lambda }\rightarrow & {} e^{-\eta }+\alpha f, \end{aligned}$$

(30)

where f represents the deformation function in the corresponding metric component. This deformation function has only radial dependence. Now this transformation allows us to split the field Eqs. (23–26) into two sets of equations. One set representing a seed sector obtained against the EMT of usual matter sector, is described as

$$\begin{aligned} \kappa \rho ^{o}= & {} \frac{1}{r^2}+e^{-\eta }\bigg (\frac{ \eta '}{r}-\frac{1}{r^2}\bigg ), \end{aligned}$$

(31)

$$\begin{aligned} \kappa p^{o}_r= & {} -\frac{1}{r^2}+e^{-\eta }\bigg (\frac{1}{r^2}+\frac{\nu '}{r}\bigg ) , \end{aligned}$$

(32)

$$\begin{aligned} \kappa p_t^{o}= & {} \frac{1}{4}e^{-\eta }\bigg (2\nu ''-\nu '\eta '+\nu '^2+2\frac{\nu '-\eta '}{r}\bigg ). \end{aligned}$$

(33)

However, the other set sourced by $\sigma _{ab}$ is given by

$$\begin{aligned} \kappa \sigma _{0}^{0}= & {} -\frac{f}{r^2}-\frac{f'}{r}, \end{aligned}$$

(34)

$$\begin{aligned} \kappa \sigma _{1}^{1}= & {} -f\bigg (\frac{\nu '}{r}+\frac{1}{r^2}\bigg ), \end{aligned}$$

(35)

$$\begin{aligned} \kappa \sigma _{2}^{2}= & {} -\frac{f}{4}\bigg (2\nu ''+\nu '^2+\frac{2\nu '}{r}\bigg )-\frac{f'}{4}\bigg (\nu '+\frac{2}{r}\bigg ). \end{aligned}$$

(36)

with the following conservation equation

$$\begin{aligned} \sigma _{1}^{'1}-\frac{\nu '}{2}(\sigma _{0}^{0}-\sigma _{1}^{1})-\frac{2}{r}(\sigma _{2}^{2}-\sigma _{1}^{1})=0. \end{aligned}$$

(37)

Next we discuss the exterior geometry. In the present situation, the standard Schwarzschild solution is suitable for the description of exterior spacetime [56]. Thus, we have

$$\begin{aligned} ds^2{} & {} =\Bigg (1-\frac{2M}{r}\Bigg )dt^2-\Bigg (\frac{r}{r-2M}\Bigg )dr^2\nonumber \\{} & {} \quad -r^2 d\theta ^2-r^2 sin^{\theta }d\phi ^2. \end{aligned}$$

(38)

For the smooth matching of internal configuration with exterior spacetime, the well-known Israel-Darmois junction condition [57, 58] can be used here, which establish the conditions, known as first and second fundamental form, as follows

$$\begin{aligned} e^\nu (R)\mid _{\Sigma }= & {} \left( 1-\frac{2M}{r}\right) \mid _{\Sigma }, \end{aligned}$$

(39)

$$\begin{aligned} e^{-\lambda }(R)\mid _{\Sigma }= & {} \left( 1-\frac{2M}{r}\right) \mid _{\Sigma }, \end{aligned}$$

(40)

$$\begin{aligned} p_r(R)\mid _{\Sigma }= & {} 0, \end{aligned}$$

(41)

where M is the total mass. In subscript, $\Sigma$ shows that the value is evaluated at the boundary surface, and Eq. (41) expresses that in the final combined solution radial pressure must disappear at the boundary surface. Further, we close this section by presenting conservation equation corresponding to the total fluid (21), given by

$$\begin{aligned} p'_r=-\frac{\nu '}{2}(\rho +p_r)+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(42)

which is nothing more than an anisotropic fluid’s hydrostatic equilibrium (Tolman-Oppenheimer Volkoff) equation. It is important to note that in Eq. (42), the local anisotropic distribution and a gravitational term that includes the metric variable $\nu$ work together to balance the pressure gradient. However, the TOV equation contains dimensions of force per unit volume; as a result we have the following quantity

$$\begin{aligned} \textit{R}\equiv p'_r+\frac{\nu '}{2}(\rho +p_r)-\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(43)

is the total force per unit volume acting on each fluid element. When a fluid system is in equilibrium, the total force per unit volume on each fluid element is indeed zero, i.e., $\textit{R} = 0$, as there are no net external forces acting on the fluid. However, when a fluid system is perturbed or not in equilibrium, the total force per unit volume on each fluid element is is no longer zero.

The mass function m can be defined in the following manner

$$\begin{aligned} e^{-\lambda }=1-\frac{2m}{r}, \end{aligned}$$

(44)

then, (32) can be used to find $\nu '$ in the following form

$$\begin{aligned} \nu '=\frac{2m+4\pi p_r r^3}{r(r-2m)}. \end{aligned}$$

(45)

These constructions makes us to write (43) as

$$\begin{aligned} \mathbb {R}{} & {} =\frac{dp_r}{dr}+\frac{4\pi p_{r}^2r}{(1-2m/r)}+\frac{4\pi rp_r\rho }{(1-2m/r)}\nonumber \\{} & {} \quad +\frac{m\rho }{r^2(1-2m/r)}+\frac{mp_r}{r^2(1-2m/r)}+\frac{2(p_t-p_r)}{r}=0.\nonumber \\ \end{aligned}$$

(46)

In the following section, we will examine the implications of perturbing the system, causing the total force $\textit{R}$ to no longer be zero. Moreover, we will discuss subsequently, this perturbation is expected to result in the system experiencing cracks.

4 Gravitational cracking for self-gravitating fluid spheres

In this study, we assume that the perturbation is applied in a way that the radial pressure profile remains unchanged, while other quantities such as density and anisotropy undergo modifications through the model parameters, resulting in ${\mathbb {R}}=0$. For instance, if $\alpha$ and $\beta$ are the model parameters, the modified TOV equation can be expressed as $\hat{\mathbb {R}}$, with parameters $\{\alpha +\delta \alpha , \beta +\delta \beta \}$. Consequently, considering the first-order perturbation, we can derive the following results

$$\begin{aligned} \hat{\mathbb {R}}=\frac{\partial \hat{\mathbb {R}}}{\partial \alpha }\delta \alpha +\frac{\partial \hat{\mathbb {R}}}{\partial \beta }\delta \beta +\textit{O}(\delta \alpha ^2, \delta \beta ^2). \end{aligned}$$

(47)

Based on the previous discussion, gravitational cracking occurs when $\hat{\mathbb {R}}$ changes its sign at a specific radius r within the body. More precisely, it occurs when $\hat{\mathbb {R}}$ has at least one real root. It is worth noting that if we define $\delta \beta =-\Gamma \delta \alpha$, with $\Gamma$ being a constant, the condition for cracking corresponds to a condition for the existence of a $\Gamma$ such that

$$\begin{aligned} \Gamma =\frac{\partial \hat{\mathbb {R}}/\partial \alpha |_{\beta , \alpha }}{\partial \hat{\mathbb {R}}/\partial \beta |_{\beta , \alpha }}. \end{aligned}$$

(48)

In the following section, we will utilize the concepts introduced in the above sections to examine specific interior solutions that are distinguished based on their gravitational complexity parameter, and study the impacts of different scenarios in compact star’s arena through gravitational cracking. Thus, we use anisotropic solutions previously constructed based on different constraints [52].

4.1 Model-I

The first solution we are going to consider was constructed in [52] by assuming the isotropization of an anisotropic solution through GD, and it can be read as

$$\begin{aligned} e^{\Xi }= & {} B(Ar^2+1)^4, \end{aligned}$$

(49)

$$\begin{aligned} e^{-\lambda }= & {} \frac{Ar^2+1}{9Ar^2+1}+\frac{16Ar^2}{7(Ar^2+1)^2}\aleph , \end{aligned}$$

(50)

$$\begin{aligned} \hat{\rho }= & {} \frac{A\alpha }{7\pi }\biggl (\frac{21(3Ar^2+1)}{(9Ar^2+1)^2}-\frac{2\aleph }{(Ar^2+1)^2}(\zeta -4Ar^2\aleph \nonumber \\{} & {} \quad +2(Ar^2+1)\aleph \biggl )\div \biggl ((Ar^2+1)\aleph \biggl ), \end{aligned}$$

(51)

$$\begin{aligned} \hat{p}_r= & {} \frac{2A\alpha }{7\pi (Ar^2+1)^2}\biggl (9-\frac{8}{Ar^2+1}\biggl ) \aleph , \end{aligned}$$

(52)

$$\begin{aligned} \hat{\Pi }= & {} \frac{6A^2 r^2(3Ar^2+1)(1-\alpha )}{\pi (9Ar^2+1)^2(Ar^2+1)}, \end{aligned}$$

(53)

$$\begin{aligned} \hat{m}= & {} \frac{1}{2} r\bigg (1 - \frac{Ar^2 + 1}{9 Ar^2 + 1} - \frac{\alpha \aleph }{7 (Ar^2 + 1)^2}\bigg ), \end{aligned}$$

(54)

where

$$\begin{aligned} \aleph= & {} \biggl (\frac{2-Ar^2(7+Ar^2)}{1+9Ar^2}\nonumber \\{} & {} \quad +\frac{(1+5AR^2)^{\frac{2}{5}}(-2+AR^2(7+AR^2))}{(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2)}\biggl ), \end{aligned}$$

(55)

$$\begin{aligned} \zeta= & {} \biggl (1+\biggl (2Ar^2(Ar^2+1)\biggl (-\frac{7+2Ar^2}{9Ar^2+1}\nonumber \\{} & {} \quad +\frac{9(-2+Ar^2(Ar^2+7))}{(9Ar^2+1)^2}\nonumber \\ {}{} & {} -\frac{2(5AR^2+1)^{\frac{2}{5}}(-2+AR^2(AR^2+7))}{(5Ar^2+1)^{\frac{7}{5}}(9AR^2+1)}\biggl ). \end{aligned}$$

(56)

In the above equations, r is the radius of the star, and the parameters A and B, which provide a smooth matching of interior geometry with the Schwarzschild exterior, are given by

$$\begin{aligned} A= & {} \frac{u}{R(4R-9M)}, \end{aligned}$$

(57)

$$\begin{aligned} B= & {} (1-2u)\biggl (\frac{4R-9M}{4R-8M}\biggl )^4, \end{aligned}$$

(58)

where $u=M/R$ is the compactness parameter. Moreover, $\alpha \in [0, 1]$ is the decoupling parameter appearing in the mechanism of GD. It, in the present scenario, controls the anisotropy of the system. Note that the system is in an anisotropic state for $\alpha = 0$, and that the anisotropy reduces as the value of $\alpha$ approaches to 1; it reaches its minimum value at $\alpha = 1$.

Let us some define non-dimensional quantities, i.e.,

$$\begin{aligned} x= & {} \frac{r}{R}, \end{aligned}$$

(59)

$$\begin{aligned} A= & {} \frac{\beta }{R^2}. \end{aligned}$$

(60)

These definitions allow us to rewrite the set (49–54) in terms of x and A as

$$\begin{aligned} \rho= & {} \frac{1}{7\pi R^2} \bigg [\frac{\alpha \beta }{\aleph (\beta , x) (\beta x^2 + 1)}\bigg (\frac{21 (3\beta x^2 + 1)}{(9\beta x^2 + 1)^2} \nonumber \\{} & {} - \frac{2}{(\beta x^2 + 1)^2}\aleph (\beta , x)(\zeta (\beta , x) - 4\beta x^2 \aleph (\beta , x) \nonumber \\ {}{} & {} + 2 (\beta x^2 + 1)\aleph (\beta , x))\bigg )\bigg ], \end{aligned}$$

(61)

$$\begin{aligned} \rho= & {} \frac{1}{7\pi R^2} \hat{\rho }(\alpha ,\beta ,x), \end{aligned}$$

(62)

$$\begin{aligned} p_r= & {} \frac{1}{7\pi R^2} \bigg [\frac{2\alpha \beta }{(\beta x^2 + 1)^2}\bigg (\frac{8\beta x^2}{\beta x^2 + 1} + 1\bigg )\aleph (\beta , x)\bigg ], \end{aligned}$$

(63)

$$\begin{aligned} p_r= & {} \frac{1}{7\pi R^2} \hat{p}_r(\alpha ,\beta ,x), \end{aligned}$$

(64)

$$\begin{aligned} \Pi= & {} \frac{1}{7\pi R^2} \bigg [ -\frac{42\beta ^2 x^2 (3\beta x^2 + 1) (\alpha - 1)}{(9\beta x^2 + 1)^2 (\beta x^2 + 1)}\bigg ], \end{aligned}$$

(65)

$$\begin{aligned} \Pi= & {} \frac{1}{7\pi R^2} \hat{\Pi }(\alpha ,\beta ,x), \end{aligned}$$

(66)

$$\begin{aligned} m= & {} R\bigg [\frac{x}{2}\bigg (1 - \frac{\beta x^2 + 1}{9\beta x^2 + 1} - \frac{16\alpha \beta x^2 \aleph (\beta , x)}{7 (\beta x^2 + 1)^2}\bigg )\bigg ], \end{aligned}$$

(67)

$$\begin{aligned} m= & {} R \hat{m}(\alpha ,\beta ,x), \end{aligned}$$

(68)

where

$$\begin{aligned} \aleph (\beta , x)&{=}&\frac{2 - 7\beta x^2 - \beta ^2 x^4}{9\beta x^2 + 1} {+} \frac{(5\beta + 1)^{2/5} (\beta ^2 + 7\beta - 2)}{(5\beta x^2 {+} 1)^{2/5} (9\beta + 1)},\nonumber \\ \end{aligned}$$

(69)

$$\begin{aligned} \zeta (\beta , x)= & {} \bigg (1 + \bigg (2\beta x^2 (\beta x^2 + 1)\bigg (\frac{9 (\beta ^2 x^4 + 7\beta *x^2 - 2)}{(9\beta x^2 + 1)^2}\nonumber \\{} & {} - \frac{2 (5\beta + 1)^{2/5} (\beta ^2 + 7\beta - 2)}{(5\beta x^2 + 1)^{7/5} (9\beta + 1)} \nonumber \\{} & {} - \frac{2\beta x^2 + 7}{9\beta x^2 + 1}\biggl ). \end{aligned}$$

(70)

Here, Eqs. (69) and (70) are directly written from (55) and (56).

As we are interested to investigate the stability of models in the presence of small perturbations on matter sector, thus we start to perturb the system by varying the parameters $\alpha$ and $\beta$ as follows

$$\begin{aligned} \alpha\rightarrow & {} \hat{\alpha }=\alpha +\delta \alpha , \end{aligned}$$

(71)

$$\begin{aligned} \beta\rightarrow & {} \hat{\beta }=\beta +\delta \beta , \end{aligned}$$

(72)

where ‘hat’ shows that the quantity is being perturbed. Obviously, applying the above perturbation leads to a non-zero TOV equation because the system is no longer in hydro-static equilibrium. Here, substitution of (71) and (72) in (46) provides the following expression

$$\begin{aligned}{} & {} \hat{\mathbb {R}}=\frac{d\hat{p}_r}{dx}\nonumber \\{} & {} {+}\frac{(\hat{p}_r(\hat{\alpha }, \hat{\beta }, x){+}\hat{\rho }(\hat{\alpha }, \hat{\beta }, x))(4x^3\hat{p}_r(\hat{\alpha }, \hat{\beta }, x){+}\hat{m}(\hat{\alpha }, \hat{\beta }, x))}{x^2(1{-}2\hat{m}(\hat{\alpha }, \hat{\beta }, x)/x)}\nonumber \\{} & {} \quad +84\frac{\hat{\Pi }(\hat{\alpha }, \hat{\beta }, x)}{x}, \end{aligned}$$

(73)

where

$$\begin{aligned} \hat{\mathbb {R}}=\frac{1}{7\pi R^3} {\mathbb {R}}. \end{aligned}$$

(74)

We can write $\hat{ \mathbb {R}}$ in terms of perturbed quantities as

$$\begin{aligned}{} & {} \hat{\mathbb {R}}(\alpha +\delta \alpha , \beta +\delta \beta , x)=\hat{\mathbb {R}}(\alpha , \beta , x)\nonumber \\{} & {} \quad +\frac{\partial \hat{\mathbb {R}}}{\partial \hat{\beta }}\bigg |_{\alpha , \beta }\delta \beta +\frac{\partial \hat{\mathbb {R}}}{\partial \hat{\alpha }}\bigg |_{\alpha , \beta }\delta \alpha +\textit{O}(\delta \alpha ^2, \delta \beta ^2), \end{aligned}$$

(75)

where $\hat{\mathbb {R}}$ is zero because it is related to the unperturbed values of $\hat{\mathbb {R}}$. Moreover, it is worth noticing if cracking occurs, R must have a zero in the range $x\in (0, 1)$. Thus, at this point of cracking

$$\begin{aligned} \delta \beta =-\Gamma \delta \alpha , \end{aligned}$$

(76)

with

$$\begin{aligned} \Gamma =\frac{\partial \hat{\mathbb {R}}/\partial \alpha |_{\beta , \alpha }}{\partial \hat{\mathbb {R}}/\partial \beta |_{\beta , \alpha }}. \end{aligned}$$

(77)

Here, $\Gamma$ is regarded as a perturbation ratio, as it serves as a measure of how much the variations ${\delta \alpha , \delta \beta }$ deviate between them.

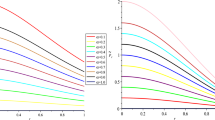
Next, we proceed to plot $\hat{\mathbb {R}}$ as a function of x by taking into different values of parameters $\alpha$, $\beta$ and $\Gamma$, and investigate the potential occurrence of cracking or overturning in the system. First, we fix the values of any two parameters, and check the behavior of system against different values of the third parameter. In Fig. 1, we plot the function $\hat{\mathbb {R}}$ as a function of x, considering $\alpha = 0.1,~\beta = 1$, whereas different values of $\Gamma$ has been considered. It is observed that the system experiences a situation where both cracking (in the internal regions) and overturning (in external regions) occur for all the values of $\Gamma$. However, cracking occurs more abruptly for smaller values of $\Gamma$. We can see that as the value of $\Gamma$ decreases, cracking occurs in the deepest region.

Fig. 1

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =0.1$, $\beta =1$ and $\Gamma =1.2$ (purple curve), $\Gamma =1.4$ (black curve), $\Gamma =1.6$ (red curve) and $\Gamma =1.8$ (green curve)

In Fig. 2, we present $\hat{\mathbb {R}}$ as a function of x for $\Gamma = -1.5$ and $\beta = 0.1$, and varying values of $\alpha$. It is interesting to note that the system changes from a state in which cracking does not occur (purple curve) to one in which it does (green curve). Another interesting fact is that there is no cracking in all anisotropic scenarios and system is stable for all $0\le \alpha <1$, however it begins to lose such a condition when it gets closer to the isotropic state $(\alpha = 1)$. For $\alpha =1$, which corresponds to the isotropic configuration, cracking occurs in the external region. Here, it can be inferred that the absence of anisotropy leads to emergence of instabilities in the systems, which results into cracking.

Fig. 2

$\hat{\mathbb {R}}$ as a function of x, for $\Gamma =-1.5$, $\beta =0.1$ and $\alpha =0$ (purple curve), $\alpha =0.2$ (black curve), $\alpha =0.6$ (red curve) and $\alpha =1$ (green curve)

In Fig. 3, we fix $\alpha$ and $\Gamma$, and varying the values of $\beta$. In this case, In this case, we observe how the compactness affects the appearance of cracking. We see as the compactness increases, the system undergoes a notable transition. It shifts from solely exhibiting overturning to experiencing both cracking and overturning. Additionally, it is evident that more compact objects, characterized by bigger $\beta$, display more internal cracking. Thus, compact objects demonstrate enriched behaviors linked to their cracking characteristics.

Fig. 3

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =1$, $\Gamma =1.5$ and $\beta =1.1$, (u $\approx$ 0.23319—purple curve), $\beta =1.4$, (u $\approx$ 0.20330—black curve), $\beta =1.5$, (u $\approx$ 0.18515—red curve) and $\beta =1.9$ (u $\approx$ 0.15478–green curve)

4.2 Model-II

Here, we consider another anisotropic version of Durgapal-Fuloria model and discuss its stability with the help of gravitational cracking. The model under consideration follows some specific conditions regarding complexity factor. It deals with a situation in which the sum of complexity factor $\tilde{\mathcal {Y}}_{TF}^{m}$ associated with the usual EMT and $8\pi \Pi _{\psi }$ is equal to zero. This situation can be described mathematically as $\mathcal {Y}_{TF}^m+8\pi \Pi _{\psi }=0$, and corresponding solution (for details one can see [52]) can be read as

$$\begin{aligned} e^{\Xi }= & {} B(Ar^2+1)^4, \end{aligned}$$

(78)

$$\begin{aligned} e^{-\lambda }= & {} 1-\frac{8A r^2(Ar^2+3)}{7(Ar^2+1)^2}\nonumber \\{} & {} +\frac{8A\alpha r^2((Ar^2+17)\mathcal {K}-(AR^2+17)\mathcal {J}}{49\mathcal {K}(Ar^2+1)^2}, \end{aligned}$$

(79)

$$\begin{aligned} \tilde{\rho }= & {} \frac{A}{49\pi (Ar^2+1)^3}(7(Ar^2(Ar^2+2)+9)\nonumber \\{} & {} +\frac{1}{(5Ar^2+1)\mathcal {K}}(51(-\mathcal {K}+\mathcal {J}+A(-5A^2\mathcal {K}r^6\nonumber \\{} & {} +3R^2\mathcal {J}+r^2(-243\mathcal {K}+170\mathcal {J}+10AR^2\mathcal {J})\nonumber \\{} & {} +Ar^4(59\mathcal {K}-153\mathcal {J}-9AR^2\mathcal {J})))\alpha ), \end{aligned}$$

(80)

$$\begin{aligned} \tilde{p}_r= & {} \frac{\alpha A}{49\pi (Ar^2+1)^3}\biggl (-14(A^2r^4+7Ar^2-2)\nonumber \\{} & {} +(Ar^2+1)\biggl (1+\frac{8Ar^2}{Ar^2+1}\biggl )\biggl (Ar^2+17\nonumber \\{} & {} -\frac{(AR^2+17)\mathcal {J}}{\mathcal {K}}\biggl )\biggl ), \end{aligned}$$

(81)

$$\begin{aligned} \tilde{\Pi }= & {} \frac{A^2r^2(Ar^2+5)\alpha }{7\pi (Ar^2+1)^3},\end{aligned}$$

(82)

$$\begin{aligned} \tilde{m}= & {} \frac{4 Ar^3}{49 \mathcal {K} (Ar^2 + 1)^2} (7 (Ar^2 + 3) \nonumber \\{} & {} - (A\mathcal {K}r^2 + 17 \mathcal {K} - \mathcal {J} (AR^2 + 17)))\alpha , \end{aligned}$$

(83)

where

$$\begin{aligned} \mathcal {K}= & {} (5Ar^2+1)^{2/5}, \end{aligned}$$

(84)

$$\begin{aligned} \mathcal {J}= & {} (5AR^2+1)^{2/5}, \end{aligned}$$

(85)

Here, A and B are the constants which can easily obtained from the matching conditions, and are given by

$$\begin{aligned} A= & {} \frac{(\sqrt{57} - 7) }{2 R^2}, \end{aligned}$$

(86)

$$\begin{aligned} B= & {} \frac{16 (1 - 2 u)}{(\sqrt{57} - 5)^4 }, \end{aligned}$$

(87)

where, u is compactness parameter, defined by $u=\frac{M}{R}$ with M and R being mass and radius of stellar object, respectively. Here, we use the same definition of the dimensionless quantities $\beta$ and x as it was in the previous section (59, 60), consequently physical quantities take the following form

$$\begin{aligned} \rho= & {} \frac{1}{49\pi R^2}\biggl [\frac{\alpha \beta }{(x^2\beta + 1)^3}\biggl (7 (\beta x^2 (\beta x^2 + 2) + 9) \nonumber \\{} & {} + \frac{1}{(5 x^2\beta + 1)\aleph (\beta , x)} (51 (\mathcal {J} (\beta , x) \nonumber \\{} & {} - \mathcal {K} (\beta , x))+ \beta (-5\beta x^6\mathcal {K} (\beta , x)\nonumber \\{} & {} + 3\mathcal {J} (\beta , x) + x^4\beta (59\mathcal {K} (\beta , x) - 153\mathcal {J} (\beta , x) \nonumber \\{} & {} - 9\beta \mathcal {J} (\beta , x)) + x^2 (-243\mathcal {K} (\beta , x)\nonumber \\{} & {} + 170\mathcal {J} (\beta , x) + 10\beta \mathcal {J} (\beta , x))))\biggl )\biggl ], \end{aligned}$$

(88)

$$\begin{aligned} \rho= & {} \frac{1}{49\pi R^2} \hat{\rho }(\alpha ,\beta ,x), \end{aligned}$$

(89)

$$\begin{aligned} p_r= & {} \frac{1}{49\pi R^2}\biggl [\frac{\alpha \beta }{(x^2\beta + 1)^3}\biggl (-14 (\beta ^2 x^4 + 7\beta x^2 - 2) \nonumber \\{} & {} + (\beta x^2 + 1)\biggl (\frac{8\beta x^2}{\beta x^2 + 1} + 1\biggl ))\Omega (\beta , x)\biggl ], \end{aligned}$$

(90)

$$\begin{aligned} p_r= & {} \frac{1}{49\pi R^2} \hat{p}_r(\alpha ,\beta ,x), \end{aligned}$$

(91)

$$\begin{aligned} \Pi= & {} \frac{1}{7\pi R^2}\biggl [\frac{\beta ^2 x^2 (\beta x^2 + 5)\alpha }{(\beta x^2 + 1)^3}\biggl ], \end{aligned}$$

(92)

$$\begin{aligned} \Pi= & {} \frac{1}{7\pi R^2}\hat{\Pi }(\alpha , \beta , x), \end{aligned}$$

(93)

$$\begin{aligned} m= & {} R\biggl (\frac{4\beta x^3 (7 (\beta x^2 + 3) - \Omega (\beta , x))}{49 (\beta x^2 + 1)^2}\biggl ), \end{aligned}$$

(94)

$$\begin{aligned} m= & {} \frac{4R}{49}\hat{m}(\alpha , \beta , x), \end{aligned}$$

(95)

where

$$\begin{aligned} \Omega (\beta , x)= & {} \beta x^2 +17 - \frac{(\beta + 17)\mathcal {J} (\beta , x)}{\mathcal {K} (\beta , x)}, \end{aligned}$$

(96)

$$\begin{aligned} \mathcal {K}(\beta , x)= & {} (5\beta x^2+1)^{2/5}, \end{aligned}$$

(97)

$$\begin{aligned} \mathcal {J}(\beta , x)= & {} (5\beta +1)^{2/5}. \end{aligned}$$

(98)

Now we expand Eq. (46) to first order, and determine the distribution of radial forces that emerge in the system as a result of the parametric perturbation. Resultantly, we have

$$\begin{aligned}{} & {} \hat{\mathbb {R}} = \frac{d\hat{p} _r}{dx}\nonumber \\{} & {} {+} \frac{(\hat{p} _r (\hat{\alpha }, \hat{\beta }, \!x) {+} \hat{\rho } (\hat{\alpha }, \hat{\beta },\! x)) (4 x^3\hat{p} _r (\hat{\alpha },\! \hat{\beta }, x) {+} 4\hat{m} (\hat{\alpha }, \hat{\beta }, x))}{49 x^2 (1 {-} 2\hat{m} (\hat{\alpha }, \!\hat{\beta }, x)/x)} \nonumber \\{} & {} + 14\frac{\hat{\Pi } (\hat{\alpha }, \hat{\beta }, \!x)}{x}, \end{aligned}$$

(99)

where

$$\begin{aligned} \hat{\mathbb {R}}=\frac{1}{49\pi R^3}\mathbb {R}. \end{aligned}$$

(100)

Now, we again plot $\hat{\mathbb {R}}$ as a function of x for different values of $\alpha$, $\beta$ and $\Gamma$. In Fig. 4, we choose $\alpha =0.1$, $\beta =1$, whereas different values of $\Gamma$ is taken into account. The system is more stable with these choices of parameters. It does not present cracking or overturning anywhere for all the chosen values of $\Gamma$. The system is stable for $\Gamma <0$ and there is no gravitational cracking. For $\Gamma >0$ system does not present overturning.

Fig. 4

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =0.1$, $\beta =1$ and $\Gamma =1$ (purple curve), $\Gamma =1.4$ (black curve), $\Gamma =-1$ (red curve) and $\Gamma =-1.4$ (green curve)

In Fig. 5, we plot $\mathbb {R}$ as a function of x for $\Gamma =-1$, $\beta =1.383$ and various values of $\alpha$. The system again demonstrates stable behavior for these choices of parameters as gravitational cracking does not occur for all the chosen values of $\alpha$.

Fig. 5

$\hat{\mathbb {R}}$ as a function of x, for $\Gamma =-1$, $\beta =1.383$ and $\alpha =0.1$ (purple curve), $\alpha =0.3$ (black curve), $\alpha =0.6$ (red curve) and $\alpha =1$ (green curve)

In Fig. 6, we fix $\alpha =0.8$, $\Gamma =1$ and choose different values of $\beta$. We can easily observe that less compact object, characterized by $\beta$, are more stable (green curve). As the compactness of an object increases, there are more chances for the appearence of cracking (purple curve). Moreover, an increase in compactness moves the cracking radius towards more external regions of the stellar object until no cracking occurs.

4.3 Model-III

In this case, we consider an anisotropic solution which is constructed by generalizing complexity factor $\mathcal {Y_{TF}}$ of Durgapal-Fuloria stellar model. For this, we considered Eq. (78) and found the explicit expression for energy density and anisotropy $\Pi$. After this, we used these expressions in the definition (69), and developed a particular expression for complexity factor $\mathcal {Y_{TF}}$, which takes the form as

$$\begin{aligned} \mathcal {Y_{TF}}=\frac{8A^2r^2(Ar^2+5)}{7(Ar^2+1)^3}. \end{aligned}$$

(101)

This expressions for complexity factor is basically established for the seed source. Then, we generalized the expression (82), which is given as

$$\begin{aligned} \mathcal {Y}_{TF}=\frac{c_1r^4+5c_2r^2}{(Ar^2+1)^3}. \end{aligned}$$

(102)

The above generalized value of $\mathcal {Y}_{TF}$ makes us to constrauct the following differential equation

$$\begin{aligned}{} & {} \frac{\Xi '}{2}f'+\frac{f}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi '^2}{2}\biggl )+\frac{e^{-\eta }}{2}\biggl (\Xi '' -\frac{\Xi '}{r}+\frac{\Xi ^{'2}}{2}\nonumber \\{} & {} \quad -\frac{\Xi '\eta '}{2}\biggl )+\frac{c_1r^4+5c_2r^2}{(Ar^2+1)^3}=0. \end{aligned}$$

(103)

This equation is further solved to evaluate deformation function f(r), which is required to solve additional sector (34–36), while the seed source (31–33) is assumed as Durgapal-Fuloria model (see [52] for details). However, the final results are as follows

Fig. 6

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =0.8$, $\Gamma =1$ and $\beta =1.1$, (u $\approx$ 0.23319–purple curve), $\beta =1.4$, (u $\approx$ 0.20330–black curve), $\beta =1.5$, (u $\approx$ 0.18515–red curve) and $\beta =1.9$ (u $\approx$ 0.15478–green curve)

$$\begin{aligned}{} & {} e^{\Xi }=B(Ar^2+1)^4, \end{aligned}$$

(104)

$$\begin{aligned}{} & {} e^{-\lambda }=1-\frac{8Ar^2(Ar^2+3)}{7(Ar^2+1)^2}+\frac{\alpha [(80 A^2 - 70 c_ 2) r^2 + (8 A^3 - 7 c_ 1) r^4]}{56 A (Ar^2 + 1)^2} \end{aligned}$$

(105)

$$\begin{aligned}{} & {} \tilde{\rho }=\frac{A (A^2 r^4 + 2 Ar^2 + 9)}{7\pi (Ar^2 + 1)^3}+ \frac{(30(-8 A^2 + 7 c_ 2) +5 (8 A^3 - 14 Ac_ 2+ 7 c_ 1 ) r^2 + A (-8 A^3 + 7 c_ 1) r^4)\alpha }{448 A\pi (Ar^2 + 1)^3}, \end{aligned}$$

(106)

$$\begin{aligned}{} & {} \tilde{p}_r=\frac{-7 (10 c_ 2 + c_ 1 r^2)\alpha - 63 Ar^2 (10 c_ 2 + c_ 1 r^2)\alpha + 16 A^2 (5\alpha + 16) + 8 A^4 r^4 (9\alpha - 16) + 56 A^3 r^2 (13\alpha - 16)}{448 A\pi (Ar^2 + 1)^3}, \end{aligned}$$

(107)

$$\begin{aligned}{} & {} \tilde{\Pi }=\frac{r^2 (8 A^4 r^2 - 7 Ac_ 1 r^2 + 24 A^3 - 20 Ac_ 2 - c_ 1)\alpha }{64 A\pi (Ar^2 + 1)^3}, \end{aligned}$$

(108)

$$\begin{aligned}{} & {} \tilde{m}=\frac{r^3 (7 (10 c_ 2 + c_ 1 r^2)\alpha - 8 A^3 r^2 (\alpha - 8) - 16 A^2 (5\alpha - 12))}{112 A (Ar^2 + 1)^2}. \end{aligned}$$

(109)

Here we consider the constant $c_1=0$ and introduce new definition of $c_2$ in terms of dimensionless parameters as follows

$$\begin{aligned} c_2=\frac{\alpha }{R^4}. \end{aligned}$$

(110)

Now using (59), (60) and (110), we can rewrite (106-109) as

$$\begin{aligned}{} & {} \rho =\frac{1}{7\pi R^2}\biggl [\frac{\beta ^2 x^4 + 2\beta x^2 + 9}{\beta x^2 + 1)^3} + \frac{\alpha (30 (7\alpha - 8\beta ^2) + 5 (8\beta ^3 x^2 - 14\alpha \beta x^2) - 8\beta ^4 x^4)}{74\beta (\beta x^2 + 1)^3}\biggl ], \end{aligned}$$

(111)

$$\begin{aligned}{} & {} \rho =\frac{1}{7\pi R^2}\hat{\rho }(\alpha ,\beta ,x), \end{aligned}$$

(112)

$$\begin{aligned}{} & {} p_r=\frac{1}{7\pi R^2}\biggl [\frac{8\beta ^4 x^4 (9\alpha - 16) + 56\beta ^3 x^2 (13\alpha - 16) - 630\alpha \beta x^2 + 16\beta ^2 (5\alpha + 16) - 70\alpha ^2}{74\beta \pi (\beta x^2 + 1)^3}\biggl ], \end{aligned}$$

(113)

$$\begin{aligned}{} & {} p_r=\frac{1}{7\pi R^2}\hat{p}_r(\alpha ,\beta ,x), \end{aligned}$$

(114)

$$\begin{aligned}{} & {} \Pi =\frac{1}{7\pi R^2}\biggl [\frac{7 x^2 (8\beta ^4 + 24\beta ^3 - 20\alpha \beta )}{64\beta \pi (\beta x^2 + 1)^3}\biggl ], \end{aligned}$$

(115)

$$\begin{aligned}{} & {} \Pi =\frac{1}{7\pi R^2}\hat{\Pi }(\alpha ,\beta ,x), \end{aligned}$$

(116)

$$\begin{aligned}{} & {} m=R\biggl [-\frac{x^3 (8\beta ^3 x^2 (\alpha - 8) + 16\beta ^2 (5 \alpha - 12) - 70\alpha )}{112\beta (\beta x^2 + 1)^2}\biggr ], \end{aligned}$$

(117)

$$\begin{aligned}{} & {} m=R\hat{m}(\alpha ,\beta ,x). \end{aligned}$$

(118)

Now, we can perturb the parameters $\alpha$ and $\beta$ for this case. Consequently, the total force after perturbation reads as

$$\begin{aligned}{} & {} \hat{\mathbb {R}} = \frac{d\hat{p} _r}{dx}\nonumber \\{} & {} {+} \frac{(\hat{p} _r (\hat{\alpha }, \hat{\beta }, \!x) {+} \hat{\rho } (\hat{\alpha }, \!\hat{\beta },\! x)) (4 x^3\hat{p} _r (\hat{\alpha }, \hat{\beta }, x) {+} 7\hat{m} (\hat{\alpha },\! \hat{\beta }, x))}{7 x^2 (1 {-} 2\hat{m} (\hat{\alpha }, \hat{\beta }, \!x)/ x)}\nonumber \\{} & {} + \frac{\hat{2\Pi } (\hat{\alpha }, \hat{\beta }, x)}{7 x}, \end{aligned}$$

(119)

where

$$\begin{aligned} \hat{\mathbb {R}}=\frac{1}{7\pi R^3}\mathbb {R}. \end{aligned}$$

(120)

We now plot perturbed total force $\hat{\mathbb {R}}$ as a function of x for various values of $\alpha$, $\beta$, and $\Gamma$ in the same manner as in previous cases. Figure 7 presents the scenario where $\alpha$ and $\beta$ are fixed, but $\Gamma$ assumes different values. It shows the relation between the occurrence of cracking and the parameter $\Gamma$ in the context of third case. One can easily notice that for the values of $\Gamma >3.5$, the cracking occurs in external region of the compact star, while for smaller values of $\Gamma$ it moves towards the center of the star which is evident from black ($\Gamma =3.5$) and purple curves ($\Gamma =2.3$).

Fig. 7

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =0.0188$, $\beta =0.1$ and $\Gamma =2.3$ (purple curve), $\Gamma =3.5$ (black curve), $\Gamma =4.5$ (red curve) and $\Gamma =5.5$ (green curve)

In Fig. 8, we fix $\beta =0.113$ and $\Gamma =-1.5$, varying different values of $\alpha$. The system shows the stable behavior for these choices $\beta$ and $\Gamma$ with $0<\alpha <0.1$. However, if one increases the value of $\alpha$ more the system shows different behavior. For $\alpha >0.1$, it becomes unstable. It is also noted that the change in radial force is not as rapid as when cracking and overturning occur.

Further, Fig. 9 analyzes the relationship between the occurrence of cracking and compactness (characterized by the parameter $\beta$) of the stellar object. For more compact structures, the system is prone to the occurrence of overturning (purple curve) as it is expected. However, for the larger values of $\beta$ the system is more stable (green, red and black curves).

5 Conclusion

The study of cracking in fluid distributions aims to understand the complex dynamics and behavior of the system as it evolves away from equilibrium. By investigating the non-vanishing radial forces, researchers can gain deep insights into the underlying physical processes and the factors influencing the system’s behavior. In this study, we observed how the presence of anisotropy and complexity of the system affect the occurrence of gravitational cracking, when the system is submitted to the perturbations that effectively makes the system to leave the hydrostatic equilibrium. For this, we consider three different stellar models that presents different scenarios regrading the complexity of the system and pressure anisotropy, and analyzed the significance of aforementioned quantities in the occurrence of cracking, varying the parameters like decoupling parameter, compactness of the source and perturbation ratio that measure the difference between the variation of the parameters. Here, we summarize the outcomes obtained for each model.

Fig. 8

$\hat{\mathbb {R}}$ as a function of x, for $\Gamma =-1.5$, $\beta =0.113$ and $\alpha =0.02$ (purple curve), $\alpha =0.04$ (black curve), $\alpha =0.06$ (red curve) and $\alpha =0.08$ (green curve)

Fig. 9

$\hat{\mathbb {R}}$ as a function of x, for $\alpha =1$, $\Gamma =1.5$ and $\beta =1.1$, (u $\approx$ 0.23319—purple curve), $\beta =1.4$, (u $\approx$ 0.20330—black curve), $\beta =1.5$, (u $\approx$ 0.18515—red curve) and $\beta =1.9$ (u $\approx$ 0.15478—green curve)

• The relationship between the occurrence of gravitational cracking and the values of perturbation ratio (77) is different for all the models. For the first model, the system experiences a situation where both cracking and overturning occur for all the chosen values. However, the system shows tendency that it can avoid the appearance of cracking and overturning for larger values of perturbation ratio $\Gamma$. For the second model, cracking or overturning does not occur, as the total perturbed force $\hat{\mathbb {R}}$ does not change the sign in the whole interior region. The third model also shows stable behavior for a wide range of perturbation ratio. it is observed that there is no cracking or overturning for all $\Gamma >3.5$. It can happen, but in the exterior region. However, for $\Gamma <3.5$ with fixed values of $\alpha =.0188$ and $\beta =0.1$, cracking occurs and moves towards the deeper regions as we decrease the values of $\Gamma$. This feature shares all the models that they can avoid overturning or cracking for larger values of $\Gamma$.

• The different values of decoupling parameter $\alpha$ are considered between $0\le \alpha \le 1$, and is observed that decoupling parameter produces a sort of screening effect on the anisotropy of the source, which has an impact on cracking. For the model-I, the system shows stable behavior for all $0\le \alpha <1$, which corresponds to anisotropic stellar environment, however when $\alpha$ grows and the system reaches to the isotropic state, gravitational cracking appears in the system. In the case of model-II, the system is stable for all the chosen values of $\alpha$, as cracking does not appear in the whole interior region. For the model-III, there is no cracking or overturning for all $0<\alpha <0.1$, however system becomes vulnerable for the occurrence of cracking when $\alpha$ assumes the values greater than 0.1.

• Addressing the case of compactness parameter which is characterized by $\beta$, our analysis indicates that more compact stellar configurations are more vulnerable for the occurrence of gravitational cracking. In the case of model-I, a shift occurs in the system’s behavior with the increases in compactness parameter. It transits from solely displaying cracking to encountering a combination of cracking and overturning. For model-II, cracking appears only for the more compact structures. Moreover, the size of of the surface, where cracking appears, increases as the compactness assumes larger values. In the case of model-III, $\hat{\mathbb {R}}$ does not change the sign in the interior region of less dense stars, and hence the system does not experience cracking or overturning. However, overturning appears in the deeper region for highly compact systems. Moreover, the critical radius can move towards the stellar surface as the compactness of the system increases more.