Abstract
In the framework of metric-affine gravity, we consider the role of the boundary term in Symmetric Teleparallel Gravity assuming f(Q, B) models where f is a smooth function of the non-metricity scalar Q and the related boundary term B. Starting from a variational approach, we derive the field equations and compare them with respect to those of f(Q) gravity in the limit of \(B\rightarrow 0\). It is possible to show that \(f(Q,B)=f(Q-B)\) models are dynamically equivalent to f(R) gravity as in the case of teleparallel \(f(\tilde{B}-T)\) gravity (where \(B\ne \tilde{B}\)). Furthermore, conservation laws are derived. In this perspective, considering boundary terms in f(Q) gravity represents the last ingredient towards the Extended Geometric Trinity of Gravity, where f(R), \(f(T,\tilde{B})\), and f(Q, B) can be dealt under the same standard. In this perspective, we discuss also the Gibbons–Hawking–York boundary term of General Relativity comparing it with B in f(Q, B) gravity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
General Relativity (GR) is the best and well-tested theory of gravity so far available. However, it cannot be the final model of gravitational interaction, because of some fundamental reasons related to its infrared (IR) and ultraviolet (UV) behaviors. At astrophysical and cosmological scales, we need mechanisms capable of explaining the clustering of structures and the accelerated expansionFootnote 1 [1,2,3]. Furthermore, at microscopic scales, GR results to be not renormalizable [4, 5]. The fact that a coherent quantum gravity theory does not yet exist [6, 7] means that some extensions or modifications of GR are needed. To address the aforementioned issues, the current most-followed strategy consists of formulating gravitational theories admitting GR in some limits and including, in general, further degrees of freedom [8,9,10,11,12,13,14,15]. All these theories come from motivations related to the fundamental structure and principles of gravitational field (see Refs. [16,17,18], for comprehensive reviews).
In this debate, the validity of the Equivalence Principle at quantum scales, as well as related features like causal and geodesic structure play a main role. In particular, in view of dealing with gravity as a gauge theory, the metricity requirement is of paramount importance. Indeed, relaxing the hypothesis that metricity principle holds in any case can offer a possibility to achieve a fundamental theory overcoming the GR shortcomings. Among metric-affine theories, Symmetric Teleparallel Gravity and its extensions are assuming a prominent role in the discussion to build up a final theory of gravity. In this approach, the dynamics is described by the non-metricity scalar Q, derived from the non-metricity tensor \(Q_{\alpha \mu \nu }=\nabla _\alpha g_{\mu \nu }\) (see e.g. [19, 20]). Recently, the extension f(Q), where f is a smooth function of Q, has been exploited to describe bouncing cosmology [21], late time accelerated expansion [22, 23], and early time inflationary behavior [24], as well as to constrain gravitational wave observations and to test GR [25, 26]. There are also applications in high-energy astrophysics for black hole [20, 27] and wormhole [28, 29] solutions. Other fundamental developments are related to Noether symmetries [30] and minisuperspace quantum cosmology [31] in f(Q) gravity.
In particular, for \(f(Q)=a\ Q+b\), with a, b real constants, it is possible to retrieve the Symmetric Teleparallel Equivalent of GR (STEGR), where the Lagrangian of GR and STEGR differ only for a boundary term B [32]. In other words, the two mathematical frameworks produce exactly the same field equations, albeit they seem to be a-priori completely unrelated theories. Beside them, there is also the Teleparallel Equivalent of GR (TEGR), based on the torsion scalar T and the related boundary term \(\tilde{B}\) (with \(B\ne \tilde{B}\)), which is another equivalent formulation of GR [32,33,34]. The aforementioned three theories, whose dynamics are encoded in the Ricci curvature scalar R for GR, the torsion scalar T for TEGR, and the non-metricity scalar Q for STEGR, constitute the so-called Geometric Trinity of Gravity [32, 35].
The goal of this article aims at presenting the f(Q, B) gravity, configuring as an extension of f(Q) gravity and, more in general, of STEGR. We analyse some features of this model and we discover that \(f(Q,B)=f(Q-B)\) represents a dynamically equivalent formulation of f(R) gravity (being an extension of GR), where f is a smooth function of Q, B in the former case and of R in the latter occurence. The paper is organized as follows: in Sect. 2 we briefly recall the f(Q) gravity and set out our notations. Section 3 is devoted to modified f(Q, B) gravity model verifying the consistency of the obtained equations and introducing the concept of Extended Geometric Trinity of Gravity. A comparison between boundary terms appearing in GR and those in f(Q) gravity is developed. In Sect. 4, we draw the conclusions.
Notations. The spacetime metric is \(g_{\mu \nu }=\eta _{AB} e^A_{\mu }e^B_{\nu }\) where \(e^A_{\mu }\) are the tetrad fields on the tangent space with Minkowskian metric \(\eta _{AB}\). The determinant of the metric \(g_{\mu \nu }\) is denoted by g and \(e=\sqrt{-g}\). Round (square) brackets around a pair of indices stands for the symmetrization (antisymmetrization) procedure, i.e., \(A_{(ij)}=A_{ij}+A_{ji}\) (respectively, \(A_{[ij]}=A_{ij}-A_{ji}\)). All quantities with an over-circle denote objects framed in GR, like  ; whereas quantities without any marked symbols are framed in the Symmetric Teleparallel Gravity, like \(\Gamma ^\lambda {}_{\mu \nu },\nabla _\alpha \). The coupling constant in the metric field equations is \(\chi =\frac{8\pi G}{c^4}\). We indicate the partial derivatives of f with \(f_X(X,Y)=\frac{\partial f}{\partial X}\), and \(f_{XX}(X,Y)=\frac{\partial {}^2f}{\partial X^2}\). The same conventions hold also with respect to Y or mixed derivatives with respect to X and Y.
; whereas quantities without any marked symbols are framed in the Symmetric Teleparallel Gravity, like \(\Gamma ^\lambda {}_{\mu \nu },\nabla _\alpha \). The coupling constant in the metric field equations is \(\chi =\frac{8\pi G}{c^4}\). We indicate the partial derivatives of f with \(f_X(X,Y)=\frac{\partial f}{\partial X}\), and \(f_{XX}(X,Y)=\frac{\partial {}^2f}{\partial X^2}\). The same conventions hold also with respect to Y or mixed derivatives with respect to X and Y.
2 f(Q) symmetric teleparallel gravity
A subclass of metric-affine geometries is represented by the Symmetric Teleparallel Gravity theories, characterized by vanishing curvature and torsion [32]. The only surviving quantity is the non-metricity tensor
expressing the failure of the metric compatibility when different from zero. In this framework, metric and affine connection are two independent geometrical objects. The former is deputed to define the casual structure, whereas the latter describes the geodesic structure.
Specifically, it is possible to take into account the f(Q) gravity, expressed in terms of the following action
where Q is the non-metricity scalar defined as
where \(Q_\alpha =Q_{\alpha \mu }{}^\mu \) and \(\bar{Q}_\alpha =Q^\mu _{\ \mu \alpha }\). The non-metricity scalar can be also written as follows

where
\(\tilde{Q}^\lambda =Q^\lambda -\bar{Q}^\lambda \),
 is the GR Ricci scalar curvature,
is the GR Ricci scalar curvature,  the GR covariant derivative, and B the boundary term.
the GR covariant derivative, and B the boundary term.
If the action \(S_Q\) is derived with respect to the metric (i.e., \(\delta _g S_Q=0\)), we obtain the metric field equations of second-order in \(g_{\mu \nu }\), namely \(\mathcal {M}_{\mu \nu }=\chi \Theta _{\mu \nu }\) (see Appendix A, for derivation and details), with [20]
where
\(\mathcal {M}_{\mu \nu }\) can be recast in the GR-like form as follows [20]

where  is the GR Einstein tensor, and the last term can be written as \(2P^\alpha _{\ \mu \nu }\partial _\alpha f_{Q}=2P^\alpha _{\ \mu \nu }f_{QQ}\partial _\alpha Q\). Here, we use the GR-like form (see Eq. (145) in Ref. [32])
is the GR Einstein tensor, and the last term can be written as \(2P^\alpha _{\ \mu \nu }\partial _\alpha f_{Q}=2P^\alpha _{\ \mu \nu }f_{QQ}\partial _\alpha Q\). Here, we use the GR-like form (see Eq. (145) in Ref. [32])

If we derive the action with respect to the affine connection (i.e., \(\delta _\Gamma S_Q=0\)), we obtain the connection field equations \(\mathcal {C_\alpha }=0\), where [20]
The above equation can be found by introducing the Lagrange multipliers subjected to the constraints of vanishing torsion and curvature. Then, the hypermomentum can be defined as follows [19]
Requiring the hypermomentum conservation (i.e., \(\nabla _\mu \nabla _\nu \mathfrak {H}_\alpha {}^{\mu \nu }=0\)) and using the symmetry properties of the aforementioned Lagrange multipliers, we come to Eq. (9) (see Sec. IV–A in Ref. [19], for more details).
It is worth noticing that the conservation laws of the energy–momentum tensor with respect to the GR covariant divergence (i.e.,  ) implies
) implies

which is not identically satisfied, but it represents an additional constraint to be considered. Of course, Eq. (11) holds in STEGR, as soon as \(f_Q=1\).
3 Improving the theory with a boundary term
We propose an extension of f(Q) gravity, by considering a generic smooth function of the non-metricity scalar and of the boundary term B, namely the f(Q, B) gravity. Let us start from the following action
Varying \(S_{QB}\) with respect to the metric (i.e., \(\delta _g S_{QB}=0\)), we obtain the following metric field equations (see Appendix B, for their derivations and details)
where (cf. Eq. B.14)

Using Eq. (8), the field equations (13) become

The above equation can be also written as

It is possible to prove that (see Appendix B)

Therefore, Eq. (15) becomes


It is important to note that the addition of a boundary term B fulfills an important role, because it allows the f(Q) gravity to ascend from second to fourth order field equations (cf. Eq. (17)). The reader can find a discussion on f(T, B) gravity in Refs. [36,37,38].
Adopting the same strategy employed in Sect. 2 to derive Eq. (9), we finally obtain the connection field equation in f(Q, B) gravity, namely
3.1 Consistency check
This section is dedicated to check the consistency of the ensued results, represented by Eqs. (18) and (19).
-
1.
For \(B=0\), we have \(f_B=0\) and the field equations (18) reduce to f(Q) gravity (7), as well as the connection equations (19) reduce to Eq. (9).
-
2.
For \(R=Q-B\), we have
 and
and  . From this preliminary analysis, we immediately note that Eq. (18) is equivalent to the f(R) gravity, namely [9]
. From this preliminary analysis, we immediately note that Eq. (18) is equivalent to the f(R) gravity, namely [9]  (20)
(20)Clearly, Eq. (19) is trivial in this framework.
-
3.
Finally, we require that the stress-energy tensor is conserved under the action of the GR covariant divergence, namely
 , which implies
, which implies  (21)
(21)being not identically satisfied. This imposes thus a further constraint, as it already occurs in the f(Q) gravity (see Eq. (11) and discussion below). However, it is important to note that Eq. (21) holds in the \(f(Q-B)\) gravity, because \(f_Q=-f_B\).
3.2 The extension of geometric trinity of gravity
As already illustrated above, Geometric Trinity of Gravity gives three dynamically equivalent formulations of GR. They are based on Lagrangians containing R, T, Q, representing the Ricci curvature, the torsion, and the non-metricity scalars, respectively. It is possible to demonstrate that these Lagrangians are equivalent up to a boundary term, which is different in GR, TEGR, and STEGR. This equivalence practically means that TEGR and STEGR have the same field equations of GR.
However, the main issue arises, when we pass to the related extended theories, represented by f(R), f(T), f(Q) gravities, which are not dynamically equivalent, because f(R) gravity, in metric formalism, is a fourth-order theory, whereas f(T) and f(Q) are second-order theories. Nevertheless, it is possible to restore the equivalence among extended theories via the addition of an appropriate boundary term. Indeed, in the general frameworks \(f(T,\tilde{B})\) and f(Q, B) (where usually \(\tilde{B}\ne B\)), we have that \(f(\tilde{B}-T),f(Q-B)\) are dynamically equivalent to f(R) gravity. These three theories constitute what we may dub Extended Geometric Trinity of Gravity (see Fig. 1). While \(R,\tilde{B}-T,Q-B\) is a geometric trinity of gravity of second-order, \(f(R), f(\tilde{B}-T),f(Q-B)\) configures to be as a geometric trinity of gravity of fourth-order. In summary, adding boundary terms means to improve the number of degrees of freedom, because they act as effective scalar fields. Clearly, this procedure can be extended to higher-order metric-affine theories formulated in metric, teleparallel, and symmetric teleparallel formalisms.
3.3 The role of boundary terms in general relativity and f(Q, B) gravity
It is worth noticing that the Gibbons–Hawking–York (GHY) boundary term \(S_\textrm{GHY}\) [39], is fundamental in GR when the underlying spacetime manifold \(\mathcal {M}\) is endowed with a boundary \(\partial \mathcal {M}\). In this case, to recover the Einstein field equations, we must add such a term to the Einstein–Hilbert action. The hypersurface \(\partial \mathcal {M}\) can be described by the parametric equations \(x^\alpha =x^\alpha (y^i)\) with \(i=1,2,3\). Here \(y^i\) are the intrinsic coordinates on \(\partial \mathcal {M}\). Then, we define the unit normal vector \(n^\alpha \) to the hypersurface \(\partial \mathcal {M}\) as followsFootnote 2
It is useful also to introduce the tangent vectors \(t^\alpha _a\) to \(\partial \mathcal {M}\) (being orthogonal to \(n^\alpha \), i.e., \(n_\alpha t^\alpha _a=0\)) as followsFootnote 3
The previous concepts permit to define the induced metric \(h_{ab}\) and the trace of the extrinsic (or Gaussian) curvature K on the hypersurface \(\partial \mathcal {M}\), which read explicitly as [40]


We have now all the ingredients to define the GHY term as
The aim of the above quantity is to cancel out the following GR divergence term [40]
where \(\delta W^\mu =g^{\alpha \beta }\delta \Gamma ^\mu _{\alpha \beta }-g^{\alpha \mu }\delta \Gamma ^\beta _{\alpha \beta }\) vanishes only in the case of a manifold without boundary. The GHY boundary term is also largely employed for path integral in quantum gravity and for calculating the black hole entropy via the Euclidean semi-classical approach [41]. To summarize, we can take into account the GHY boundary term to obtain a conservative action. It assures the validity of GR field equations on a manifold with a boundary.
On the other hand, the boundary term B in f(Q, B) (as well as \(\tilde{B}\) in \(f(T,\tilde{B})\)) allows us to upgrade the theory from a second-order to fourth-order in the field equations. In particular choosing \(f(Q,B)=f(Q-B)\) (or \(f(T,\tilde{B})=f(\tilde{B}-T)\)), we obtain a theory which is equivalent to f(R). In particular, in the case of \(f(Q-B)\), some interesting properties hold as explained in Sect. 3.1. In addition, the boundary term B (cf. Eq. (4)), as well as \(\tilde{B}\), is a second-order invariant. In this case the boundary term fulfills an upgrade action on the underlying theory of gravity.
Although \(S_\textrm{GHY}\) and B are taken into account for different goals, the contact point between the two terms emerges as soon as we consider f(Q, B) and (\(f(T,\tilde{B})\)) models defined on a manifold \(\mathcal {M}\) endowed with a boundary \(\partial \mathcal {M}\). In this case, a GHY-like boundary term, depending on B (\(\tilde{B}\)), should be added in view to recover the appropriate field equations.
4 Discussion and conclusions
In this paper, we have discussed f(Q, B) gravity, which is an extension of Symmetric Teleparallel Gravity endowed with some interesting properties. Thanks to the introduction of an appropriate boundary term B, it is possible to lift up the f(Q) gravity from second-order to fourth-order in the field equations. In particular, the model \(f(Q,B)=f(Q-B)\) is dynamically equivalent to f(R) gravity. Furthermore, the theory is consistent with f(Q) gravity in the limit of \(B\rightarrow 0\). Furthermore, this theory identically satisfy the conservation laws with respect to the GR divergence. We can say that \(f(R),f(\tilde{B}-T),f(Q-B)\) (with \(\tilde{B}\ne B\)) give rise to an extension of trinity gravity, which we have dubbed the Extended Geometric Trinity of Gravity, being three equivalent theories based on fourth-order field equations.
We have also discussed the differences existing between the GHY boundary term of GR and the boundary term B in f(Q, B). The former has a conservative action, because it must reproduce the Einstein field equations on a manifold endowed with a boundary, whereas the latter plays the role to improve the field equations from second-order to fourth-order. In this case, f(Q, B) gravity can be related to f(R) gravity as derived in metric framework.
It is worth noticing that these results provide a sort of route to extend equivalent representations of gravity to any higher-order dynamics (see also Ref. [42], for details), which can be extremely interesting in cosmological and astrophysical applications. As mentioned above, being f(R) gravity of fourth-order in metric formalism, it seems that it cannot be directly compared with f(T) and f(Q), which are of second-order. If one considers cosmology, for example, it seems that dynamics coming from Starobinsky gravity [43], i.e. \(f(R)=R+\alpha R^2\), cannot be theoretically compared with \(f(T)=T+\alpha _1 T^2\) or \(f(Q)=Q+\alpha _2 Q^2\) [24] due to the different order of related field equations. The introduction of boundary terms restores the same differential order into the equations and then information coming from different representations of gravity appears on the same ground. Similar considerations can be developed also for black hole solutions or, in more general, for any self-gravitating compact object.
In a forthcoming paper, we will study how boundary terms impact phenomenology. In particular, it is relatively straightforward to show that the matching of cosmological models against the observations may result improved thanks to the presence of boundary terms.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data.]
Notes
Difficulties in detecting new fundamental particles to explain the dark sector point out that alternative approaches could be pursued in order to match the observed phenomenology.
We are considering the metric signature \((-,+,+,+)\).
The index \(\alpha \) labels the components, whereas a counts the independent tangent vectors, namely \(t^\alpha _1,t^\alpha _2,t^\alpha _3\).
The variation \(=-\frac{1}{2}g_{\mu \nu }e\) can be obtained via the Jacobi formula expressing the derivative of the determinant of a matrix A in terms of the adjugate of A and the derivative of A [44].
In Eq. (A.3), we have used the following relation
$$\begin{aligned} Q_\alpha ^{\ \mu \nu }&=g^{\mu \beta }g^{\nu \gamma }Q_{\alpha \beta \gamma }=g^{\mu \beta }g^{\nu \gamma }(\partial _\alpha g_{\beta \gamma }-\Gamma ^\lambda _{\ \alpha \beta }g_{\lambda \gamma }-\Gamma ^\lambda _{\ \alpha \gamma }g_{\lambda \beta })\nonumber \\&=\partial _\alpha (g^{\mu \beta }g^{\nu \gamma } g_{\beta \gamma })- g^{\nu \gamma } g_{\beta \gamma }\partial _\alpha g^{\mu \beta }- g^{\mu \beta } g_{\beta \gamma }\partial _\alpha g^{\nu \gamma }\nonumber \\&\quad -g^{\mu \beta }g^{\nu \gamma }g_{\lambda \gamma }\Gamma ^\lambda _{\ \alpha \beta }-g^{\mu \beta }g^{\nu \gamma }g_{\lambda \beta }\Gamma ^\lambda _{\ \alpha \gamma }\nonumber \\&=-(\partial _\alpha g^{\mu \nu }+\Gamma ^\nu _{\alpha \beta }g^{\mu \beta }+\Gamma ^\mu _{\alpha \beta }g^{\nu \beta })=-\nabla _\alpha g^{\mu \nu }. \end{aligned}$$(A.4)We remind that the Levi-Civita affine connection
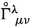 is
is (B.9)
(B.9)
References
S.M. Carroll, Living Rev. Relativ. 4, 1 (2001). https://doi.org/10.12942/lrr-2001-1. arXiv:astro-ph/0004075
S. Capozziello, R. D’Agostino, O. Luongo, Int. J. Mod. Phys. D 28, 1930016 (2019). https://doi.org/10.1142/S0218271819300167. arXiv:1904.01427 [gr-qc]
Planck Collaboration, N. Aghanim, et al., A &A 641, A6 (2020). https://doi.org/10.1051/0004-6361/201833910. arXiv:1807.06209 [astro-ph.CO]
G. ’t Hooft, M.J.G. Veltman, Ann. Inst. H. Poincare Phys. Theor. A 20, 69 (1974)
M.H. Goroff, A. Sagnotti, Phys. Lett. B 160, 81 (1985). https://doi.org/10.1016/0370-2693(85)91470-4
G. ’t Hooft, M. Veltman, Ann. Inst. H. Poincare Sect. (A) Phys. Theor. 20, 69 (1974)
M. Gleiser, Phys. Today 58, 57 (2005)
T. Clifton, Alternative Theories of Gravity, Ph.D. thesis, school (2006)
S. Capozziello, V. Faraoni, Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics (Springer, Dordrecht, 2011). https://doi.org/10.1007/978-94-007-0165-6
S. Nojiri, S.D. Odintsov, Phys. Rep. 505, 59 (2011). https://doi.org/10.1016/j.physrep.2011.04.001. arXiv:1011.0544 [gr-qc]
S. Capozziello, M. de Laurentis, Phys. Rep. 509, 167 (2011). https://doi.org/10.1016/j.physrep.2011.09.003. arXiv:1108.6266 [gr-qc]
S. Nojiri, S.D. Odintsov, V.K. Oikonomou, Phys. Rep. 692, 1 (2017). https://doi.org/10.1016/j.physrep.2017.06.001. arXiv:1705.11098 [gr-qc]
S. Bahamonde, K.F. Dialektopoulos, C. Escamilla-Rivera, G. Farrugia, V. Gakis, M. Hendry, M. Hohmann, J. Levi Said, J. Mifsud, E. Di Valentino, Rep. Prog. Phys. 86, 026901 (2023). https://doi.org/10.1088/1361-6633/ac9cef. arXiv:2106.13793 [gr-qc]
G.A.R. Franco, C. Escamilla-Rivera, J. Levi Said, Eur. Phys. J. C 80, 677 (2020). https://doi.org/10.1140/epjc/s10052-020-8253-7. arXiv:2005.14191 [gr-qc]
L. Heisenberg, M. Hohmann, S. Kuhn, Eur. Phys. J. C 83, 315 (2023). https://doi.org/10.1140/epjc/s10052-023-11462-6. arXiv:2212.14324 [gr-qc]
Y. Akrami, et al., (Collaboration CANTATA), Modified Gravity and Cosmology: An Update by the CANTATA Network ed. by E.N. Saridakis, R. Lazkoz, V. Salzano, P. Vargas Moniz, S. Capozziello, J. Beltrán Jiménez, M. De Laurentis, G.J. Olmo (Springer, 2021). https://doi.org/10.1007/978-3-030-83715-0. arXiv:2105.12582 [gr-qc]
C.G. Böhmer, E. Jensko, Phys. Rev. D 104, 024010 (2021). https://doi.org/10.1103/PhysRevD.104.024010. arXiv:2103.15906 [gr-qc]
C.G. Böhmer, E. Jensko, J. Math. Phys. 64, 082505 (2023). https://doi.org/10.1063/5.0150038. arXiv:2301.11051 [gr-qc]
J. Beltrán Jiménez, L. Heisenberg, T.S. Koivisto, JCAP 2018, 039 (2018). https://doi.org/10.1088/1475-7516/2018/08/039. arXiv:1803.10185 [gr-qc]
F. D’Ambrosio, S.D.B. Fell, L. Heisenberg, S. Kuhn, Phys. Rev. D 105, 024042 (2022). https://doi.org/10.1103/PhysRevD.105.024042. arXiv:2109.03174 [gr-qc]
F. Bajardi, D. Vernieri, S. Capozziello, Eur. Phys. J. Plus 135, 912 (2020). https://doi.org/10.1140/epjp/s13360-020-00918-3. arXiv:2011.01248 [gr-qc]
S. Capozziello, R. D’Agostino, Phys. Lett. B 832, 137229 (2022). https://doi.org/10.1016/j.physletb.2022.137229. arXiv:2204.01015 [gr-qc]
R. Solanki, A. De, S. Mandal, P.K. Sahoo, Phys. Dark Universe 36, 101053 (2022). https://doi.org/10.1016/j.dark.2022.101053. arXiv:2201.06521 [gr-qc]
S. Capozziello, M. Shokri, Phys. Dark Universe 37, 101113 (2022). https://doi.org/10.1016/j.dark.2022.101113. arXiv:2209.06670 [gr-qc]
I. Soudi, G. Farrugia, J.L. Said, V. Gakis, E.N. Saridakis, Phys. Rev. D 100, 044008 (2019). https://doi.org/10.1103/PhysRevD.100.044008. arXiv:1810.08220 [gr-qc]
R. D’Agostino, R.C. Nunes, Phys. Rev. D 106, 124053 (2022). https://doi.org/10.1103/PhysRevD.106.124053
F. Javed, G. Mustafa, S. Mumtaz, F. Atamurotov, Nucl. Phys. B 990, 116180 (2023). https://doi.org/10.1016/j.nuclphysb.2023.116180
F. Parsaei, S. Rastgoo, P.K. Sahoo, Eur. Phys. J. Plus 137, 1083 (2022). https://doi.org/10.1140/epjp/s13360-022-03298-y
U.K.S. Shweta, A.K. Mishra, Int. J. Geom. Methods Mod. Phys. 19, 2250019 (2022).https://doi.org/10.1142/S0219887822500190. arXiv:2108.07174 [physics.gen-ph]
K.F. Dialektopoulos, T.S. Koivisto, S. Capozziello, Eur. Phys. J. C 79, 606 (2019). https://doi.org/10.1140/epjc/s10052-019-7106-8. arXiv:1905.09019 [gr-qc]
F. Bajardi, S. Capozziello, Eur. Phys. J. C 83, 531 (2023). https://doi.org/10.1140/epjc/s10052-023-11703-8. arXiv:2305.00318 [gr-qc]
S. Capozziello, V. De Falco, C. Ferrara, Eur. Phys. J. C 82, 865 (2022). https://doi.org/10.1140/epjc/s10052-022-10823-x. arXiv:2208.03011 [gr-qc]
R. Aldrovandi, J.G. Pereira, Teleparallel Gravity: An Introduction (Springer, Berlin, 2013). https://doi.org/10.1007/978-94-007-5143-9
Y.-F. Cai, S. Capozziello, M. De Laurentis, E.N. Saridakis, Rep. Prog. Phys. 79, 106901 (2016). https://doi.org/10.1088/0034-4885/79/10/106901. arXiv:1511.07586 [gr-qc]
J. Beltrán Jiménez, L. Heisenberg, T.S. Koivisto, Universe 5, 173 (2019). https://doi.org/10.3390/universe5070173. arXiv:1903.06830 [hep-th]
S. Bahamonde, C.G. Böhmer, M. Wright, Phys. Rev. D 92, 104042 (2015). https://doi.org/10.1103/PhysRevD.92.104042. arXiv:1508.05120 [gr-qc]
S. Bahamonde, S. Capozziello, Eur. Phys. J. C 77, 107 (2017). https://doi.org/10.1140/epjc/s10052-017-4677-0. arXiv:1612.01299 [gr-qc]
S. Capozziello, M. Capriolo, L. Caso, Eur. Phys. J. C 80, 156 (2020). https://doi.org/10.1140/epjc/s10052-020-7737-9. arXiv:1912.12469 [gr-qc]
G.W. Gibbons, S.W. Hawking, Phys. Rev. D 15, 2752 (1977). https://doi.org/10.1103/PhysRevD.15.2752
A. Romano, M. Mango Furnari, The Physical and Mathematical Foundations of the Theory of Relativity: A Critical Analysis (Springer International Publishing, Cham, 2019)
E. Dyer, K. Hinterbichler, Phys. Rev. D 79, 024028 (2009). https://doi.org/10.1103/PhysRevD.79.024028
S. Capozziello, M. Capriolo, L. Caso, Class. Quantum Gravity 37, 235013 (2020). https://doi.org/10.1088/1361-6382/abbe71. arXiv:2010.00451 [gr-qc]
A.A. Starobinsky, Phys. Lett. B 91, 99 (1980). https://doi.org/10.1016/0370-2693(80)90670-X
J.R. Magnus, H. Neudecker, Matrix Differential Calculus with Applications in Statistics and Econometrics, 2nd edn. (Wiley, New York, 1999)
Y. Xu, G. Li, T. Harko, S.-D. Liang, Eur. Phys. J. C 79, 708 (2019). https://doi.org/10.1140/epjc/s10052-019-7207-4. arXiv:1908.04760 [gr-qc]
Acknowledgements
This paper is based upon work from COST Action CA21136 Addressing observational tensions in cosmology with systematics and fundamental physics (CosmoVerse) supported by COST (European Cooperation in Science and Technology). Authors acknowledge the Istituto Nazionale di Fisica Nucleare (iniziative specifiche QGSKY, TEONGRAV and MOONLIGHT2). S.C. and V.D.F. thank the Gruppo Nazionale di Fisica Matematica of Istituto Nazionale di Alta Matematica for the support. We are grateful to Francesco Bajardi, Rocco D’Agostino and the anonymous Referee for the useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Variational principle for f(Q) gravity and field equations
Starting from Eq. (2) and considering the variation of the action with respect to the metric, we have
where,Footnote 4
In the above implications we have used the definition of \(P^\alpha _{\ \mu \nu }\) (cf. Eq. (6a)),Footnote 5 and \(q_{\mu \nu }\) (see Eq. (6b)). For an alternative calculation of \(\delta _g Q\), we suggest the reader to see Appendices A and B in Ref. [45].
Inserting the above findings in Eq. (A.1), we obtain
Appendix B: Variational principle for f(Q, B) gravity and field equations
Starting from the modified action (12) and varying it with respect to the metric, we obtain s
where
with \(e(\partial _\lambda f_B)\delta _g \tilde{Q}^\lambda =eU^\lambda _{\ \mu \nu } \delta _g g^{\mu \nu }\). Let us explicitly calculate this last term, where we obtain
Calculating all the above terms, we eventually haveFootnote 6



where in \(A_1\) and \(A_3\) we have employed
instead in \(A_2\) we have exchanged \(\partial _\alpha \) and \(\delta _g\) and used


Therefore, from Eq. (B.7) we have (without \(e\delta _g g^{\mu \nu }\))

where we have used the following identities



Starting from Eq. (B.5) and considering Eqs. (B.6) and (B.14), we obtain the following metric field equations (13). Now, we calculate the following terms

After simple algebra, we obtain Eq. (16). Gathering Eqs. (B.14) and (B.16), we prove Eq. (17). Defined \(\Psi _{\mu \nu }=(\partial _\lambda f_B)(2P^\lambda _{\ \mu \nu }-\frac{1}{2}g_{\mu \nu }\tilde{Q}^\lambda +U^\lambda _{\ \mu \nu })\), we have

The field equations of f(Q, B) gravity are (cf. Eq. (18))

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Capozziello, S., De Falco, V. & Ferrara, C. The role of the boundary term in f(Q, B) symmetric teleparallel gravity. Eur. Phys. J. C 83, 915 (2023). https://doi.org/10.1140/epjc/s10052-023-12072-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-12072-y




 and
and  . From this preliminary analysis, we immediately note that Eq. (
. From this preliminary analysis, we immediately note that Eq. (
 , which implies
, which implies 

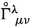 is
is