1 Introduction

In high-energy nuclear physics, the internal structure and dynamics of the proton are still not fully understood. Although decades have passed since the discovery that the proton internal structure consisted of quarks [1,2,3,4] and gluons (partons) [5,6,7,8], we still have limited knowledge about how these partons contribute to the global properties of the proton, such as its mass and spin. The measurement of the fraction of the proton’s spin carried by quarks by the European Muon Collaboration (EMC) in 1987 indicated that only small percentages of the proton’s spin comes from quarks [9]. The data of nucleon’s polarized structure function \(g_{1}\left( x_{B}\right) \) in EMC has deviated significantly from the Ellis–Jaffe sum rule [10]. These results gave rise to the so-called “spin crisis” or, more appropriately, the “spin puzzle”. The discrepancy has since inspired many intensive experimental and theoretical studies of spin dependent nucleon structure [11,12,13,14,15,16,17]. It was proposed that the missing fraction of the proton’s spin comes from the polarized gluon contribution. Recent measurements of the polarized gluon density have shown that gluons indeed contribute, but they cannot fully account for the gap in the spin puzzle [16]. The orbital angular momenta of the quarks and gluons play an important role in the proton’s spin. According to the generator of Lorentz transformation, we can define the angular momentum operator in Quantum Chromodynamics (QCD) [18],

$$\begin{aligned} J^{i}=\frac{1}{2} \epsilon ^{i j k} \int d^{3} x M^{0 j k}, \end{aligned}$$
(1)

where \(M^{0 j k}\) is the angular momentum density, which can be expressed by the energy-momentum tensor \(T^{\mu \nu }\) through

$$\begin{aligned} M^{\alpha \mu \nu }=T^{\alpha \nu } x^{\mu }-T^{\alpha \mu } x^{\nu }. \end{aligned}$$
(2)

\(T^{\mu \nu }\) has the Belinfante-Improved form and is symmetric, gauge-invariant, and conserved. It can be divided into gauge-invariant quark and gluon contributions,

$$\begin{aligned} T^{\mu \nu }=T_{q}^{\mu \nu }+T_{g}^{\mu \nu }, \end{aligned}$$
(3)

and \({\vec {J}}\) has a gauge-invariant form, \({\vec {J}}_{\textrm{QCD}}={\vec {J}}_{q}+{\vec {J}}_{g}\), where

$$\begin{aligned} J_{q, g}^{i}=\frac{1}{2} \epsilon ^{i j k} \int d^{3} x\left( T_{q, g}^{0 k} x^{j}-T_{q, g}^{0 j} x^{k}\right) . \end{aligned}$$
(4)

In pure gauge theory, \({\vec {J}}_{g}\) is a conserved angular momentum charge by itself, generating spin quantum numbers for glueballs. We can observe that \({\vec {J}}_{q}\) and \({\vec {J}}_{g}\) are interaction-dependent. To study the orbital angular momentum of the partons, one needs to study beyond one-dimensional parton distributions.

One-dimensional parton distribution functions (PDFs) provide significant informations about the structure of the proton. Although PDFs have provided us with much knowledge about the proton, one-dimensional distributions cannot give us a complete picture. Therefore, theorists developed a new density function about 30 years ago, which are called GPDs. GPDs provide information that including both transverse spacial and longitudinal momentum distributions. In addition to the momentum fraction, GPDs depend on another independent variable, the negative value of momentum transfer square \(t=-\left( p-p^{\prime }\right) ^{2}\) between the initial and final states of a proton. Thus, GPDs provide extensive information about the three-dimensional dynamics of the nucleon, including the composition of spin and pressure distribution [19,20,21,22,23,24]. Similar to the one dimensional PDFs, GPDs include non-polarized and polarized functions.

GPDs, also known as the off-forward PDFs, have attracted a lot of attention since the spin decomposition rule was first proposed [18]. It was proposed to factorize the hard exclusive processes. The corresponding factorization structure functions that describe the structure of the nucleon are the GPDs \(H^{q}\left( x, \xi , t\right) \), \(E^{q}\left( x, \xi , t\right) \), \(\widetilde{H}^{q}\left( x, \xi , t\right) \) and \(\tilde{E}^{q}\left( x, \xi , t\right) \). These functions correspond to the Fourier transform of the non-diagonal operators [18, 20, 22, 25]:

$$\begin{aligned}{} & {} \left. \frac{P^{+}}{2 \pi } \int d y^{-} e^{j x P^{+} y^{-}}\left\langle p^{\prime }\left| \bar{\Psi }_{q}(0) \gamma ^{+} \Psi _{q}(y)\right| p\right\rangle \right| _{y^{+}=\vec {y}_{\perp }=0}\nonumber \\{} & {} \quad =H^{q}\left( x, \xi , t\right) \bar{N}\left( p^{\prime }\right) \gamma ^{+} N(p)\nonumber \\{} & {} \qquad + E^{q}\left( x, \xi , t\right) \bar{N}\left( p^{\prime }\right) i \sigma ^{+v} \frac{\Delta _{v}}{2 M_{N}} N(p),\nonumber \\{} & {} \left. \frac{P^{+}}{2 \pi } \int d y^{-} e^{x P^{+} y^{-}} \left\langle p^{\prime }\left| \bar{\Psi }_{q}(0) \gamma ^{+} \gamma ^{5} \Psi _{q}(y)\right| p\right\rangle \right| _{y^{+}=\vec {y}_{\perp }=0}\nonumber \\{} & {} \quad =\widetilde{H}^{q}\left( x, \xi , t\right) \bar{N} \left( p^{\prime }\right) \gamma ^{+} \gamma _{5} N(p)\nonumber \\{} & {} \qquad + \widetilde{E}^{q}\left( x, \xi , t\right) \bar{N} \left( p^{\prime }\right) \gamma _{5} \frac{\Delta ^{+}}{2 M_{N}} N(p), \end{aligned}$$
(5)

where y is the coordinate of the two correlated quarks, P is the average nucleon four-momentum in the light-front frame: \(P=\left( p+p^{\prime }\right) / 2\) and \(\Delta =p^{\prime }-p\). The “+” superscript denotes the plus component of four-momentum in the light-front frame. Each GPD function defined above is specific to a particular flavor of quark: \(H^{q}, E^{q}, \widetilde{H}^{q}, \widetilde{E}^{q}(q=u, d, s, \ldots )\). \(H^q\) and \(\widetilde{H}^{q}\) represent spin non-flipped GPD functions, while \(E^{q}\) and \(\widetilde{E}^{q}\) represent spin-flipped ones. The off-forward parton distributions encompass both the ordinary parton distributions and nucleon form factors. In \(t \rightarrow 0\) and \(\xi \rightarrow 0\) limit, we get

$$\begin{aligned}{} & {} H(x, 0, 0)=f_{1}(x),\nonumber \\{} & {} \widetilde{H}\left( x, 0, 0\right) =g_{1}(x), \end{aligned}$$
(6)

where \(f_{1}(x)\) is quark distribution and \(g_{1}(x)\) is quark helicity distribution. According to the Dirac and Pauli form factors \(F_1\), \(F_2\), as well as the axial-vector and pseudo-scalar form factors \(G_A\), \(G_P\), the sum rules can be obtained,

$$\begin{aligned}{} & {} \int d x H\left( x, \xi , t\right) =F_{1}\left( t\right) ,\nonumber \\{} & {} \int d x E\left( x, \xi , t\right) =F_{2}\left( t\right) , \nonumber \\{} & {} \int d x \tilde{H}\left( x, \xi , t\right) =G_{A}\left( t\right) , \nonumber \\{} & {} \int d x \tilde{E}\left( x, \xi , t\right) =G_{P}\left( t\right) . \end{aligned}$$
(7)

The most interesting Ji’s sum rules related to the nucleon spins are described through GPDs [22],

$$\begin{aligned} \int _{-1}^{1} d x x\left[ H\left( x, \xi , t\right) +E\left( x, \xi , t\right) \right] =A(t)+B(t). \end{aligned}$$
(8)

Then the total spin of the proton can be expressed as:

$$\begin{aligned}{} & {} J_{q, g}=\frac{1}{2}\left[ A_{q, g}(0)+B_{q, g}(0)\right] ,\nonumber \\{} & {} J_{q}+J_{g}=\frac{1}{2}, \end{aligned}$$
(9)

where \(A_{q, g}(0)\) gives the momentum fractions carried by quarks and gluons in the nucleon \((A_{q}(0) + A_{g}(0) = 1),\) and B-form factor is analogous to the Pauli form factor for the vector current. By extrapolating the sum rule to \(t = 0\), one gets \(J_{q,g}\). The GPDs can be measured in deep-exclusive processes such as DVCS and Deeply Virtual Meson Production (DVMP) [18, 22, 26,27,28,29,30]. Both of these processes are exclusive hard scattering processes in lepton-nucleon collisions. Theoretical research on these topics has been conducted for many years, and researchers have developed various theoretical models and predictions [18, 21, 22, 31,32,33,34,35,36,37,38,39]. During the past 20 years, the collaborations at HERA, Jefferson Lab (JLab), and CERN have made significant efforts to obtain information about GPDs from the electro-production of real photons (DVCS processes) [31, 40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61], such as DESY with H1 [40, 43], ZEUS [41], HERMES [45, 46], JLab Halls A [31, 50, 52,53,54,55] and Halls B [48, 51, 56,57,58,59], and COMPASS [60, 61]. These experiments have made important contributions to our understanding of the internal structure of the proton. However, the available data from these experiments lack high precision and coverage of a wide kinematic range. Accurately measuring the DVCS process is a significant challenge as it requires high luminosity to compensate for very small cross section and well-designed detector design to ensure the exclusive measurement of the final states. Both EicC and EIC are important future experiments that will provide high luminosity and excellent particle detection capabilities. In this work, we discuss the relation of GPDs and DVCS observables [22], and perform a Monte-Carlo simulation of DVCS + Bethe-Heitler (BH) events to estimate the statistical errors of asymmetry observables in future DVCS experiments at EicC and EIC.

The extraction of Generalized Parton Distributions (GPDs) from exclusive reactions is indirect, and it requires the use of appropriate GPD models. After years of development, numerous theoretical models of GPDs have been developed. Two of these models are based on double distributions (DDs) [20, 62, 63]. One model, known as the VGG model, was proposed by Vanderhaeghen, Guichon, and Guidal [26, 27, 64, 65]. Another model, called the GK model, was presented by Goloskokov and Kroll [28, 66, 67]. Researchers have examined different GPD models using available experimental data and have shown that the data from various experiments agree well with the calculations based on the VGG model [25, 48, 54, 57, 58]. Therefore, in this work, we perform theoretical calculations using the VGG model. In the VGG model, the observable Transverse Target-Spin Asymmetry (TTSA) \(A_{U T}^{\sin (\phi -\phi _s) \cos \phi }\) is particularly sensitive to the quark total angular momentum in the nucleon compared to other observables [31, 68, 69]. Thus we make a constraint on \(J_u\) and \(J_d\) by the pseudo data of \(A_{U T}^{\sin (\phi -\phi _s) \cos \phi }\).

The organization of the paper is as follows. The relationship between GPDs and DVCS is illustrated in Sect. 2. The phenomenological parametrization of GPDs is described in Sect. 3. The invariant kinematic and final state kinematic distributions of the simulation are shown in Sect. 4. The projections of DVCS experiment are shown in Sect. 5. Finally, some discussions and a concise summary are given in Sect. 6.

2 Generalized partons distribution and deeply virtual compton scattering

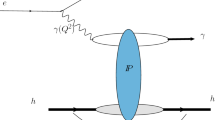
Deeply virtual Compton scattering on a nucleon shown in Fig. 1 left panel is the simplest process to access GPDs. It plays an important role in exploring the internal structure of the nucleon. BH process, illustrated in the middle and right panels of Fig. 1, shares the same initial and final states as the DVCS process.

Fig. 1
figure 1

The Feynman diagram of DVCS (left) and BH (right) processes. e, e\(^{\prime }\) and p, p\(^{\prime }\) are the initial and final states electron and proton respectively. t is the squared four-momentum transfer between the initial and final state proton

Full size image
Fig. 2
figure 2

The reference frame of scattering plane and kinematic variables of \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) reaction in the laboratory [25, 32, 70]

Full size image

The five-fold differential cross section for electro-production of real photon \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) is defined as [32]:

$$\begin{aligned} \frac{d \sigma }{d x_{\textrm{B}} d y d\left| \Delta ^{2}\right| d \phi d \varphi }=\frac{\alpha ^{3} x_{\textrm{B}} y}{16 \pi ^{2} {\mathcal {Q}}^{2} \sqrt{1+\epsilon ^{2}}}\left| \frac{{\mathcal {T}}}{e^{3}}\right| ^{2}. \end{aligned}$$
(10)

The cross section of this process depends on the Bjorken scaling variable \(x_B\), the squared momentum transfer \( \Delta = \left( P_{2}-P_{1}\right) ^{2}\), and the lepton energy fraction \(y=P_{1} \cdot q_{1} / P_{1} \cdot k\), where \(q_{1}=k-k^{\prime }\). Here, \(P_{1}\) and \(P_{2}\) represent the four-momentum of the initial and final state proton, respectively. The azimuthal angle between the lepton plane and the recoiled proton momentum is denoted as \(\phi \). Additionally, \(\varphi \) is the angle between the polarization vector \(S_{\perp }\) and the scattered hadron, as shown in Fig. 2. The parameter \(\epsilon =2 x_{\textrm{B}} M / {\mathcal {Q}}\) incorporates nonvanishing target mass effects [32, 70]. The reaction amplitude \({\mathcal {T}}\) is the linear superposition of the BH and DVCS amplitudes,

$$\begin{aligned} {\mathcal {T}}^{2}=\left| {\mathcal {T}}_{BH}\right| ^{2}+\left| {\mathcal {T}}_{D V C S}\right| ^{2}+{\mathcal {T}}_{I}, \end{aligned}$$
(11)

where \({\mathcal {T}}_{I}={\mathcal {T}}_{D V C S} T_{B H}^{*}+{\mathcal {T}}_{D V C S}^{*} {\mathcal {T}}_{B H}\). The squared BH term \(\left| {\mathcal {T}}_{BH}\right| ^{2}\), squared DVCS amplitude \(\left| {\mathcal {T}}_{D V C S}\right| ^{2}\), and interference term \({\mathcal {T}}_{I}\) are given by:

$$\begin{aligned}{} & {} \left| {\mathcal {T}}_{\textrm{BH}}\right| ^{2}=\frac{e^{6}}{x_{\textrm{B}}^{2} y^{2} \left( 1+\epsilon ^{2}\right) ^{2} \Delta ^{2} {\mathcal {P}}_{1}(\phi ) {\mathcal {P}}_{2}(\phi )}\nonumber \\{} & {} \qquad \qquad \quad \times \left\{ c_{0}^{\textrm{BH}} + \sum _{n=1}^{2} c_{n}^{\textrm{BH}} \cos (n \phi )+s_{1}^{\textrm{BH}} \sin (\phi )\right\} ,\nonumber \\\end{aligned}$$
(12)
$$\begin{aligned}{} & {} \left| {\mathcal {T}}_{\textrm{DVCS}}\right| ^{2}= \frac{e^{6}}{y^{2} {\mathcal {Q}}^{2}}\nonumber \\{} & {} \quad \times \left\{ c_{0}^{\textrm{DVCS}}+\sum _{n=1}^{2}\left[ c_{n}^{\textrm{DVCS}} \cos (n \phi )+s_{n}^{\textrm{DVCS}} \sin (n \phi )\right] \right\} ,\nonumber \\\end{aligned}$$
(13)
$$\begin{aligned}{} & {} {\mathcal {T}}_{I}=\frac{ \pm e^{6}}{x_{\textrm{B}} y^{3} \Delta ^{2} {\mathcal {P}}_{1}(\phi ) {\mathcal {P}}_{2}(\phi )}\nonumber \\{} & {} \quad \times \left\{ c_{0}^{\mathcal {I}}+\sum _{n=1}^{3}\left[ c_{n}^{\mathcal {I}} \cos (n \phi )+s_{n}^{\mathcal {I}} \sin (n \phi )\right] \right\} . \end{aligned}$$
(14)

For \({\mathcal {P}}_{1}\) and \({\mathcal {P}}_{2}\), we use the following parametrization [32, 70]:

$$\begin{aligned} {\mathcal {P}}_{1}= & {} -\frac{1}{y\left( 1+\epsilon ^{2}\right) } \{J+2 K \cos (\phi )\},\nonumber \\ {\mathcal {P}}_{2}= & {} 1+\frac{\Delta ^{2}}{{\mathcal {Q}}^{2}}+ \frac{1}{y\left( 1+\epsilon ^{2}\right) }\{J+2 K \cos (\phi )\}, \end{aligned}$$
(15)

where

$$\begin{aligned} J= & {} \left( 1-y-\frac{y \epsilon ^{2}}{2}\right) \left( 1+\frac{\Delta ^{2}}{{\mathcal {Q}}^{2}}\right) -(1-x)(2-y) \frac{\Delta ^{2}}{{\mathcal {Q}}^{2}},\nonumber \\\end{aligned}$$
(16)
$$\begin{aligned} K^{2}= & {} -\frac{\Delta ^{2}}{{\mathcal {Q}}^{2}}\left( 1-x_{\textrm{B}}\right) \left( 1-y-\frac{y^{2} \epsilon ^{2}}{4}\right) \left( 1-\frac{\Delta _{\min }^{2}}{\Delta ^{2}}\right) \nonumber \\{} & {} \times \left\{ \sqrt{1+\epsilon ^{2}}+\frac{4 x_{\textrm{B}}\left( 1-x_{\textrm{B}}\right) +\epsilon ^{2}}{4\left( 1-x_{\textrm{B}}\right) } \frac{\Delta ^{2}-\Delta _{\min }^{2}}{{\mathcal {Q}}^{2}}\right\} .\nonumber \\ \end{aligned}$$
(17)

It vanishes at the kinematical boundary \(\Delta ^{2} = \Delta _{\min }^{2}\) or \(\Delta ^{2} = \Delta _{\max }^{2}\),

$$\begin{aligned} \Delta _{\min }^2= & {} -{\mathcal {Q}}^2 \frac{2\left( 1-x_{\textrm{B}}\right) \left( 1-\sqrt{1+\epsilon ^2}\right) +\epsilon ^2}{4 x_{\textrm{B}}\left( 1-x_{\textrm{B}}\right) +\epsilon ^2}, \end{aligned}$$
(18)
$$\begin{aligned} t_{\max }= & {} -{\mathcal {Q}}^2 \frac{2\left( 1-x_{\textrm{B}}\right) \left( 1+\sqrt{1+\epsilon ^2}\right) +\epsilon ^2}{4 x_{\textrm{B}}\left( 1-x_{\textrm{B}}\right) +\epsilon ^2}. \end{aligned}$$
(19)

The results for the Fourier coefficients can be found in [32, 70]. The variables \(\xi \) and t (or \(\Delta ^{2}\)) can be computed from the kinematic variables. Since we cannot directly obtain \(x_{B}\) from experiment, the Compton form factors (CFFs) are obtained by integrating the GPDs,

$$\begin{aligned}{} & {} \int _{-1}^{1} \frac{F_{q}(x, \xi , t)}{x-\xi +i \epsilon } d x \nonumber \\{} & {} \quad ={\mathcal {P}} \int _{-1}^{1} \frac{F_{q}(x, \xi , t)}{x-\xi } d x -i \pi F_{q}(\xi , \xi , t), \end{aligned}$$
(20)

where \(F_{q}\) are \(H^q\), \(\widetilde{H}^{q}\), \(E^{q}\), or \(\widetilde{E}^{q}\). These real and imaginary part of Eq. 20, which can be expressed in eight GPD-related quantities that can be extracted from DVCS observables [25]:

$$\begin{aligned} H_{R e}(\xi , t)\equiv & {} {\mathcal {P}} \int _{0}^{1} d x \left[ H\left( x, \xi , t\right) -H\left( -x, \xi , t\right) \right] C^{+}, \nonumber \\ H_{I m}(\xi , t)\equiv & {} H(\xi , \xi , t)-H(-\xi , \xi , t), \nonumber \\ E_{R e}(\xi , t)\equiv & {} {\mathcal {P}} \int _{0}^{1} d x \left[ E\left( x, \xi , t\right) -E\left( -x, \xi , t\right) \right] C^{+},\nonumber \\ E_{I m}(\xi , t)\equiv & {} E(\xi , \xi , t)-E(-\xi , \xi , t), \nonumber \\ \widetilde{H}_{R e}(\xi , t)\equiv & {} {\mathcal {P}} \int _{0}^{1} d x \left[ \widetilde{H}\left( x, \xi , t\right) -\widetilde{H}\left( -x, \xi , t\right) \right] C^{-},\nonumber \\ \widetilde{H}_{I m}(\xi , t)\equiv & {} \widetilde{H}(\xi , \xi , t)- \widetilde{H}(-\xi , \xi , t),\nonumber \\ \widetilde{E}_{R e}(\xi , t)\equiv & {} {\mathcal {P}} \int _{0}^{1} d x \left[ \widetilde{E}\left( x, \xi , t\right) -\widetilde{E}\left( -x, \xi , t\right) \right] C^{-},\nonumber \\ \widetilde{E}_{I m}(\xi , t)\equiv & {} \widetilde{E}(\xi , \xi , t)-\widetilde{E}(-\xi , \xi , t). \end{aligned}$$
(21)

The case with the subscript “Re” is accessed by observables sensitive to the real part of the DVCS amplitude, while the case with the subscript “Im” is accessed by observables sensitive to its imaginary part. The coefficients \(C^{\pm }\) are defined as:

$$\begin{aligned} C^{\pm }=\frac{1}{x-\xi } \pm \frac{1}{x+\xi }. \end{aligned}$$
(22)

As a result, the Compton form factors with four complex functions are written as:

$$\begin{aligned} {\mathcal {H}}(\xi , t)\equiv & {} H_{R e}(\xi , t)-i \pi H_{I m}(\xi , t), \nonumber \\ \tilde{{\mathcal {H}}}(\xi , t)\equiv & {} \widetilde{H}_{R e}(\xi , t)-i \pi \widetilde{H}_{I m}(\xi , t), \nonumber \\ {\mathcal {E}}(\xi , t)\equiv & {} E_{R e}(\xi , t)-i \pi E_{I m}(\xi , t), \nonumber \\ \tilde{{\mathcal {E}}}(\xi , t)\equiv & {} \widetilde{E}_{R e}(\xi , t)-i \pi \widetilde{E}_{I m}(\xi , t). \end{aligned}$$
(23)

For the measurement of CFFs, it is mandatory to consider the interference term from BH events. The production of BH events is a pure QED process, which can be measured precisely from the form factor \(F_1\) and \(F_2\). In addition to the absolute cross section, another way to obtain the CFFs is by measuring the asymmetries. The beam charge asymmetries are defined as:

$$\begin{aligned} A_{C}=\frac{\sigma ^{+}(\phi )-\sigma ^{-}(\phi )}{\sigma ^{+}(\phi )+\sigma ^{-}(\phi )}, \end{aligned}$$
(24)

where \(\sigma ^{+}\) and \(\sigma ^{-}\) refer to the cross sections with lepton beams of opposite charge. It can be observed that the asymmetries only depend on \(\phi \). The observables of interest in this paper are the correlated charge and transversely polarized target-spin asymmetries, which are defined as:

$$\begin{aligned}{} & {} A_{U T, D V C S}=\frac{\left( \sigma _{+}^{+}(\phi )-\sigma _{-}^{+}(\phi )\right) + \left( \sigma _{+}^{-}(\phi )-\sigma _{-}^{-}(\phi )\right) }{\sigma _{+}^{+}(\phi )+ \sigma _{-}^{+}(\phi )+\sigma _{+}^{-}(\phi )+\sigma _{-}^{-}(\phi )},\nonumber \\{} & {} A_{U T, I}=\frac{\left( \sigma _{+}^{+}(\phi )-\sigma _{-}^{+}(\phi )\right) - \left( \sigma _{+}^{-}(\phi )-\sigma _{-}^{-}(\phi )\right) }{\sigma _{+}^{+}(\phi )+ \sigma _{-}^{+}(\phi )+\sigma _{+}^{-}(\phi )+\sigma _{-}^{-}(\phi )}, \end{aligned}$$
(25)

where A with subscripts denote the cross section asymmetries of \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) at certain beam (first subscript) and target (second subscript) polarization sign (“U” stands for unpolarized and “T” for transverse polarized). Note that there are two independent transverse polarization direction of proton: \(UT_x\) is in the hadronic plane and \(UT_y\) is perpendicular to it. There, the superscript and subscript of \(\sigma \) refer to the charge of the lepton beam and the beam (or target) spin projection. One can measure the exclusive \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) cross section with different beam and target polarization since the spin asymmetries provide access to different CFFs through the interference term \(\mathcal {I}\) in the BH and DVCS processes. At leading order and leading twist, the relations linking observables and CFFs for the \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) process have been derived as [32, 71, 72]:

$$\begin{aligned}{} & {} A_{{\textrm{UT}}, \text { DVCS }}^{\sin \left( \phi -\phi _{s}\right) } \propto \left[ {\text {Im}}\left( {\mathcal {H}} {\mathcal {E}}^{*}\right) -\xi {\text {Im}}\left( \widetilde{{\mathcal {H}}} \widetilde{{\mathcal {E}}}^{*}\right) \right] , \end{aligned}$$
(26)
$$\begin{aligned}{} & {} A_{{\textrm{UT}}, {\textrm{I}}}^{\sin \left( \phi -\phi _{s}\right) \cos \phi } \propto {\text {Im}}\left[ -\frac{t}{4 M^{2}}\left( F_{2} {\mathcal {H}}-F_{1} {\mathcal {E}}\right) \right. \nonumber \\{} & {} \quad +\xi ^{2}\left( F_{1}+\frac{t}{4 M^{2}} F_{2}\right) ({\mathcal {H}}+{\mathcal {E}})\nonumber \\{} & {} \quad \left. -\xi ^{2}\left( F_{1}+F_{2}\right) \left( \tilde{{\mathcal {H}}}+ \frac{t}{4 M^{2}} \widetilde{{\mathcal {E}}}\right) \right] . \end{aligned}$$
(27)

These approximations illustrate that different experimental observables are sensitive to different CFFs. We can see that the above asymmetries depend on the CFF \({\mathcal {E}}\), which has important implications for our subsequent study of the total angular momentum of different quarks within the proton.

3 Phenomenological parametrization of GPDs

Assuming a factorized t-dependence, the quark GPD \(H^q\) is given by [26]:

$$\begin{aligned} H^{q}(x, \xi , t)=H^{q}(x, \xi ) \cdot F_{1}^{q}(t). \end{aligned}$$
(28)

The nucleon form factors in dipole form is given by:

$$\begin{aligned} F_{1}^{\text {dipole }}(t)=\frac{1-\left( 1+\kappa ^{P}\right) t / 4 m_{N}^{2}}{1-t / 4 m_{N}^{2}} \frac{1}{(1-t / 0.71)^{2}}. \end{aligned}$$
(29)

For the function \(H^q\) (for each flavor q), the t-independent part \(H^{q}(x, \xi ) \equiv H^{q}(x, \xi , t=0)\) is parametrized by a two-component form,

$$\begin{aligned} H^{q}(x, \xi ) \equiv H^{q}_{DD}(x, \xi , t=0) + \theta (\xi -|x|) D^{q}\left( \frac{x}{\xi }\right) , \end{aligned}$$
(30)

where \(D^{q}\left( \frac{x}{\xi }\right) \) is the D-term, set to 0 in our following calculation. And \(H^q_{DD}\) is the part of the GPD which is obtained as a one-dimensional section of a two-variable double distribution (DD) \(F^q\), imposing a particular dependence on the skewness \(\xi \),

$$\begin{aligned} H_{D D}^{q}(x, \xi )=\int _{-1}^{1} d \beta \int _{-1+|\beta |}^{1-|\beta |} d \alpha \delta (x-\beta -\alpha \xi ) F^{q}(\beta , \alpha ). \nonumber \\ \end{aligned}$$
(31)

For the double distributions, entering Eq. 31, we use the following model,

$$\begin{aligned} F^{q}(\beta , \alpha )=h(\beta , \alpha ) q(\beta ), \end{aligned}$$
(32)

where \(q(\beta )\) is the forward quark distribution (for the flavor q) and where \(h(\beta , \alpha )\) denotes a profile function. In the following estimates, we parametrize the profile function through a one-parameter ansatz, following [26, 62, 63]:

$$\begin{aligned} h(\beta , \alpha )=\frac{\Gamma (2 b+2)}{2^{2 b+1} \Gamma ^{2}(b+1)} \frac{\left[ (1-|\beta |)^{2}-\alpha ^{2}\right] ^{b}}{(1-|\beta |)^{2 b+1}}. \end{aligned}$$
(33)

For \(\beta > 0\), \(q(\beta )=q_{\textrm{val}}(\beta )+\bar{q}(\beta )\) is the ordinary PDF for the quark flavor q. In this work, we use IMParton as input [73]. The negative \(\beta \) range corresponds to the antiquark density: \(q(-\beta )=-\bar{q}(\beta )\). The parameter b characterizes to what extent the GPD depends on the skewness \(\xi \), and fixed to 1 in this work.

The spin-flip quark GPDs \(E_q\) in the factorized ansatz are given by:

$$\begin{aligned} E_{q}(x, \xi , t)=E_{q}(x, \xi ) \cdot F_{2}^{q}(t) / \kappa ^{q}. \end{aligned}$$
(34)

Here \(F_2^q(t)\) denotes the Pauli FF for quark flavor q, and is parameterized by:

$$\begin{aligned} F_{2}^{q}=\frac{\kappa ^{q}}{\left( 1-t / 4 m_{p}^{2}\right) \cdot \left( 1-t / m_{D}^{2}\right) ^{2}}, \end{aligned}$$
(35)

where \(\kappa _{q}\) is the anomalous magnetic moment of quarks of flavor q, \(\kappa ^{u}=2\kappa ^{p}+\kappa ^{n}=1.67\), \(\kappa ^{d}=\kappa ^{p}+2\kappa ^{n}=-2.03\). Same as Eq. 30, the t-independent part of the quark GPDs, \(E_q(x, \xi )\) is defined as:

$$\begin{aligned} E_{q}(x, \xi )=E_{q}^{D D}(x, \xi )-\theta (\xi -|x|) D_{q}\left( \frac{x}{\xi }\right) . \end{aligned}$$
(36)

The part of the GPD E that can be obtained from the double distribution has a form analogous to the spin-nonflip case:

$$\begin{aligned} E_{q}^{D D}(x, \xi )=\int _{-1}^{1} d \beta \int _{-1+|\beta |}^{1-|\beta |} d \alpha \delta (x-\beta -\alpha \xi ) K_{q}(\beta , \alpha ),\nonumber \\ \end{aligned}$$
(37)

there, \(K_{q}(\beta , \alpha )\) is given by:

$$\begin{aligned} K_{q}(\beta , \alpha )=h(\beta , \alpha ) e_{q}(\beta ), \end{aligned}$$
(38)

and \(e_q(\beta )\) denotes the spin-flip can be written as:

$$\begin{aligned} e_{q}(x)=A_{q} \cdot q_{\textrm{val}}(x)+B_{q} \cdot \delta (x), \end{aligned}$$
(39)

with:

$$\begin{aligned} A_{q}= & {} \frac{2 J_{q}-M_{q}^{(2)}}{M_{q_{\text {val }}}^{(2)}}, \nonumber \\ B_{u}= & {} 2\left[ \frac{1}{2} \kappa _{u}-\frac{2 J_{u}-M_{u}^{(2)}}{M_{u_{\text {val }}}^{(2)}}\right] , \nonumber \\ B_{d}= & {} \kappa _{d}-\frac{2 J_{d}-M_{d}^{(2)}}{M_{d_{\text {val }}}^{(2)}}. \end{aligned}$$
(40)

By defining the total fraction of the proton momentum carried by the quarks and antiquarks of flavor q as:

$$\begin{aligned} M_{2}^{q}= & {} \int _{0}^{1} d x x[q(x)+\bar{q}(x)]\nonumber \\ {}= & {} \int _{0}^{1} d x x\left[ q_{\text {val }}(x)+2 \bar{q}(x)\right] , \end{aligned}$$
(41)

and the momentum fraction carried by the valence quarks as:

$$\begin{aligned} M_{2}^{q_{v a l}}=\int _{0}^{1} d x x q_{\text {val }}(x). \end{aligned}$$
(42)

The parameterizations of \(\widetilde{H}\) and \(\widetilde{E}\) are introduced in [26, 27, 64, 65]. For the parameterization of \(\widetilde{H}\), we use polIMParton as input [74]. In this model, the total angular momentum carried by u-quarks and d-quarks, \(J_u\) and \(J_d\), are free parameters in the parameterization of the spin-flip GPD \(E_q(x,\xi ,t)\). Therefore, this parameterization can be used to study the sensitivity of hard electroproduction observables to variations in \(J_u\) and \(J_d\). The main objective of this article is to predict the errors in future EIC and EicC experiments. The D-term and the parameters introduced by the VGG model, have a minimal impact on the errors. Therefore, we have adopted a concise computational form.

4 Distributions of invariant and final-state kinematics

There is a Monte-Carlo (MC) simulation package for DVCS and BH processes called MILOU [75]. We used this software to generate 5 million events for EicC and EIC. We utilized the PARTONS (PARtonic Tomography Of Nucleon Software) package as input for observables [76]. Thus, we obtained pseudo data for subsequent theoretical calculations. We focus on two future experiments (EIC and EicC). For EicC, we assume an incoming electron beam energy of \(E_{e}=3.5\) GeV and an incoming proton beam energy of \(E_{p}=20\) GeV [77]. For EIC, the assumed beam energies are \(E_{e}=5\) GeV for the incoming electron and \(E_{p}=100\) GeV for the incoming proton [78]. We propose to perform measurements of spin azimuthal asymmetries in deeply virtual Compton scattering on transverse polarized protons. In addition to the scattered electron, the real photon and the scattered proton will be measured after the incoming unpolarized electron. The observable \(A_{U T}^{\sin (\phi -\phi _s) \cos \phi }\) will be extracted from the data. The EicC facility can provide a beam integrated luminosity up to 50 fb\(^{-1}\), corresponding to the effective running time of one year [77]. EicC also has a large kinematic acceptance capacity, which can complement the current vacant data. Compared to EicC, EIC offers a beam integrated luminosity up to 60 fb\(^{-1}\) in less running time [78, 79]. By combining data from the EIC and EicC experiments, high precision data covering most kinematic regions will be available.

In order to efficiently generate events in the kinematic region of interest, we apply the following kinematic ranges for MC sampling: \(10^{-4}<x_{B}<1\), 1 GeV\(^2<Q^2< 100\) GeV\(^2\), and \(10^{-3}\) GeV\(^2\) \(<-t<\) 3 GeV\(^2\). Figures 3 and 4 show the momentum vs. polar angle coverage for the final state electrons, real photons, and scattered protons from the DVCS and BH processes at EicC and EIC. We observe that the final proton typically carries a large fraction of the momentum of the incoming proton and has a small scattering angle. Most protons are located at very small polar angles, and their momentum difference with the beam is so small that we require a high-resolution momentum measurement for the forward detector. On the other hand, the final electron has a larger scattering angle compared to the final proton. Based on the distribution of the final state particles, we can appropriately position the detectors to collect more events. Figures 5 and 6 illustrate the cross-section weighted invariant kinematics distributions of the \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) reaction at EicC and EIC. These color z-axis distributions are weighted by the cross-section computed in VGG model implemented in the MILOU software, and they are shown on a logarithmic z-scale. We observe that the \(Q^2\) range covers from 1.0 GeV\(^2\) to 10.0 GeV\(^2\), \(x_B\) ranges from 0.003 to 0.05, and t goes from 0 down to \(-0.2\) GeV\(^2\). Approximately 92\(\%\) of the total events fall within this region. When comparing the results of EicC and EIC, we observe that EIC has more data in the smaller \(x_B\) and smaller \(-t\) regions compared to EicC.

Fig. 3
figure 3

The cross-section weighted momentum and polar angles distributions of the final-state particles (scattered protons, scattered electrons and real photons) in the MC simulation at EicC

Full size image
Fig. 4
figure 4

The cross-section weighted momentum and polar angles distributions of the final-state particles (scattered protons, scattered electrons and real photons) in the MC simulation at EIC

Full size image
Fig. 5
figure 5

The cross-section weighted distributions of the invariant kinematics in the MC simulation at EicC

Full size image
Fig. 6
figure 6

The cross-section weighted distributions of the invariant kinematics in the MC simulation at EIC

Full size image

5 Projection of DVCS experiment

The statistical uncertainty of the measured experimental observable is directly related to the number of events collected during an experiment. To estimate the number of events for an experiment, we need to know the cross section of the reaction, the integrated luminosity of the experiment, and the event selection criteria for the reaction. EIC provides an integrated luminosity of 1.5 fb\(^{-1}\) per month [78]. We assume an integrated luminosity of 50 fb\(^{-1}\) for the EicC experiment, which corresponds to three to four years of data collection. The integrated luminosity for EIC is assumed to be 60 fb\(^{-1}\) over a period of approximately 3 years. To ensure that the collected events are valid for our study, we have applied the following event selection conditions: \(0.01<{\textrm{y}}<0.85\), \(t>-0.5\) GeV\(^2\), \({\textrm{W}}>2.0\) GeV, \({\textrm{P}}_{{\textrm{e}}^{\prime }}>0.5\) GeV. Figure 7 shows the kinematic regions of EIC and EicC, which represent the simulated region in this work. EIC and EicC will provide data in small x region, with the red area indicating EIC and the green area indicating EicC. In the small \(Q^2\) region, EicC can provide data where x is close to \(x\sim 0.005\). Since EIC has a higher center-of-mass energy, it can provide data for an even smaller x region in the range of \(x\sim 0.0007\). The DVCS experiment poses significant challenges for detecting the recoiled proton with small t. In order to ensure that the recoiled proton can be detected by forward detector, we have imposed certain constraints on the detection of the final state protons. This low-t acceptance eliminates many forward events, as exemplified by EicC in Fig. 8.

Fig. 7
figure 7

Kinematic range in the x, \(Q^2\) plane at EicC (\(\sqrt{s}=16.7\) GeV) and EIC (\(\sqrt{s}=45\) GeV) [80,81,82]. The hatched areas indicate the areas simulated in this work, which correspond to \(0.01 \le y \le 0.85\). The red dashed line and green dashed line indicate \(y = 0.6\)

Full size image
Fig. 8
figure 8

The cross-section weighted momentum and polar angles distributions of the scattered protons with the geometric cut. The square breach at the right side shows the eliminated data with proton momentum larger than 99\(\%\) of beam momentum and scattering angle smaller than 2 mrad

Full size image

Based on the event selection criteria discussed above, the number of events in each bin is calculated using the following formula,

$$\begin{aligned} N=\sigma ^{a v g} \cdot \text { Lumi } \cdot \text { Time } \cdot \epsilon _{\textrm{eff}} \cdot \Delta x_{B} \cdot \Delta t \cdot \Delta Q^{2}, \end{aligned}$$
(43)

where N is the total number of events in each kinematical bin, \(\sigma ^{a v g}\) is the average of the four cross section with different electron and proton beam polarization directions, “Lumi” is the beam luminosity, “Time” is the beam duration, \(\epsilon _{\textrm{eff}}\) is the overall detector efficiency, and the remaining terms represent the sizes of the kinematical bins. In this work, we conservatively assumed a particle acceptance of 25\(\%\) at EIC and 20\(\%\) at EicC [77, 78].

The counts of events in each bin are denoted as \(N^{++}\), \(N^{+-}\), \(N^{-+}\), and \(N^{--}\), corresponding to different electron and nucleon polarization directions. One can obtain the asymmetries quantities of the target spin asymmetry \((A_{TS})\) using the formula:

$$\begin{aligned} A_{TS}=\frac{N^{++}+N^{-+}-N^{+-}-N^{--}}{N^{++}+N^{+-}+N^{-+}+N^{--}} \frac{1}{P_{T}}, \end{aligned}$$
(44)

where \(P_{T}\) stands for the polarization degree of nucleon (assumed to be 70\(\%\)) [77, 78]. Considering that the asymmetries quantities are at the several percent level, we use the unpolarized events generated by MILOU for the projection, and the total number of events for all polarization conditions is denoted as N. Thus, the absolute statistical uncertainty of the asymmetries quantities can be approximately expressed as:

$$\begin{aligned} \delta A_{TS}\approx \frac{1}{P_{T}} \frac{1}{\sqrt{N}}. \end{aligned}$$
(45)

Figures 9 and 10 show the projection of statistical errors in a low \(Q^2\) bin ranging from 1 to 3 GeV\(^2\) for EicC and EIC experiments. We focus on the small \(x_B\) and \(-t\) region and divide the \(x_B\) vs. \(-t\) plane into very small bins. In these plots, we observe that the statistical uncertainty increases as \(x_B\) increases. For most of the data at EicC and EIC, the projected statistical uncertainty is smaller than 3\(\%\). When \(x_B\) reaches around 0.12, the statistical uncertainty is around 5\(\%\). These precise data will be of great help for future theoretical research. Now we can provide the pseudo-data for the asymmetry of the cross-section in the region of interest at EicC and EIC. We divide \(x_B\), t, and \(Q^2\) in different bins, as shown in Table 1. This table corresponds to Figs. 11 and 12. For cases where only \(x_B\), t or \(Q^2\) changes, we applied a similar division approach. Here \(x_B\) ranges from 0.01 to 0.17 in steps of 0.02 (\(t:-0.11\sim -0.09\) GeV\(^2\), \(Q^2:1.13\sim 1.38\) GeV\(^2\)), t ranges from \(-0.19\) GeV\(^2\) to \(-0.03\) GeV\(^2\) in steps of 0.02 (\(x_B:0.01\sim 0.03\), \(Q^2:1.13\sim 1.38\) GeV\(^2\)) and \(Q^2\) ranges from 1.13 to 3.13 GeV\(^2\) in steps of 0.25 (\(x_B:0.01\sim 0.03\), \(t:-0.11\sim -0.09\) GeV\(^2\)). As shown in Fig. 11, EicC provides a large phase space coverage and good statistics, especially for the small \(x_B\),\(-t\) and \(Q^2\) regions. Similar results at EIC [83] are shown in Fig. 12. Since we also divide the \(Q^2\) into small bins, the statistical errors of the pseudo-data in Figs. 11 and 12 are much larger than those shown in Figs. 9 and 10.

Fig. 9
figure 9

The statistical errors projection of the Transverse Target-Spin Asymmetry at low \(Q^2\) at EicC. We calculate the statistical errors at each bin center. The right axis shows how large the statistical errors are

Full size image
Fig. 10
figure 10

The statistical errors projection of the Transverse Target-Spin Asymmetry at low \(Q^2\) at EIC. We calculate the statistical errors at each bin center. The right axis shows how large the statistical errors are

Full size image
Table 1 Binning scheme for \(x_B\), t, and \(Q^2\)
Full size table
Fig. 11
figure 11

Asymmetries with polarized electron beam and proton beam in some typical bins at EicC

Full size image

We have developed a code to calculate observables in the exclusive reaction \(e p \rightarrow e^{\prime } p^{\prime } \gamma \) to LO precision in perturbative theory. This calculation follows the VGG model described in Sect. 3. In order to compare the results from theoretical calculations with the pseudo data for the TTSA amplitudes shown in Fig. 13, the \(\chi ^{2}\) is defined as:

$$\begin{aligned}{} & {} \chi ^{2}\left( J_{u}, J_{d}\right) \nonumber \\{} & {} \quad =\frac{\left[ \left. A_{U T}^{\sin \left( \phi -\phi _{s}\right) \cos \phi } \right| _{(\text { Pseudo data })}-\left. A_{U T}^{\sin \left( \phi -\phi _{s}\right) \cos \phi }\right| _{\text {theory }}\right] ^{2}}{\delta A_{\text {stat }}^{2} + \delta A_{\text {syst}}^{2}}.\nonumber \\ \end{aligned}$$
(46)

To account for systematic errors, we need to consider the previous experiments [31, 40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. Based on these previous experiments, we make a conservative estimate for EicC and EIC. Therefore, for EicC and EIC, we assume the experimental systematic errors to be 10\(\%\). The constraints on \(J_u\) and \(J_d\) obtained for the extracted TTSA amplitudes from the pseudo data are shown in Fig. 13. We calculate the TTSA amplitudes for \(J_u\) \((J_d)\) ranging from 0 to 1 (\(-1\) to 1) in steps of 0.2 and set the D-term = 0 \((D^{q}\left( \frac{x}{\xi }\right) \) in Eq. 30). We make the assumption that the D-term is equal to zero, as the value of D-term has little significance on the final distribution of angular momentum [84]. Figure 14 shows the model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) in the same kinematic region as HERMES [68, 69]. Here we only consider the influences from statistical errors. The result of EicC, which is shown in Fig. 14, can be expressed as

$$\begin{aligned} J_u + J_d/2.9 = 0.41 \pm 0.06, \end{aligned}$$
(47)
Fig. 12
figure 12

Asymmetries with polarized electron beam and proton beam in some typical bins at EIC

Full size image
Fig. 13
figure 13

Asymmetries with polarized electron beam and proton beam in small x region at EicC (Table 2) and EIC (Table 3)

Full size image

and the result of EIC is

$$\begin{aligned} J_u + J_d/3.0 = 0.39 \pm 0.04. \end{aligned}$$
(48)

If we consider both statistical and systematic errors (\(A_{U T}^{\sin (\phi -\phi _s) \cos \phi } = -0.142 \pm 0.020 \pm 0.014\) at EicC, \(A_{U T}^{\sin (\phi -\phi _s) \cos \phi } = -0.020 \pm 0.002 \pm 0.002\) at EIC), the result (shown in Fig. 15) is

$$\begin{aligned} J_u + J_d/2.9 = 0.41 \pm 0.08, \end{aligned}$$
(49)

for EicC, and

$$\begin{aligned} J_u + J_d/3.0 = 0.39 \pm 0.06. \end{aligned}$$
(50)

for EIC. The uncertainty is propagated from the TTSA amplitudes uncertainty of the pseudo data, and experimental systematic errors dominate. According to the results of HERMES [68, 69, 85],

$$\begin{aligned} J_u + J_d/2.9 = 0.42 \pm 0.21, \end{aligned}$$
(51)

we ignore the effects of parameter b and D-term. As the Fig. 15 shows, EicC and EIC have higher accuracy to obtain smaller uncertainty for constraint on u-quark and d-quark total angular momentum.

Table 2 Asymmetries with polarized electron beam and proton beam at EicC
Full size table
Table 3 Asymmetries with polarized electron beam and proton beam at EIC
Full size table
Fig. 14
figure 14

The result of model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) at EIC and EicC compared with HERMES [68, 69]. Only statistical errors are considered

Full size image
Fig. 15
figure 15

The result of model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) at EIC and EicC compared with HERMES [68, 69]. Both statistical and systematic errors are considered

Full size image

Since EIC and EicC can provide a large amount of accurate data in the small x region, we performed some calculations in this region. Both statistical and systematic errors are considered in these results. At \(x = 0.01\), the results of EicC and EIC are shown in Fig. 16, where EicC is

$$\begin{aligned} J_u + J_d/2.6 = 0.39 \pm 0.05, \end{aligned}$$
(52)

and EIC is

$$\begin{aligned} J_u + J_d/2.7 = 0.38 \pm 0.05. \end{aligned}$$
(53)
Fig. 16
figure 16

The result of model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) in the region of \(x\sim 0.01\) at EIC and EicC. Both statistical and systematic errors are considered

Full size image

In the region of \(x\sim 0.006\), we obtained the following results, where

$$\begin{aligned} J_u + J_d/2.5 = 0.38 \pm 0.05, \end{aligned}$$
(54)

is the result of EicC shown in Fig. 17. The result of EIC in this kinematic region is

$$\begin{aligned} J_u + J_d/2.5 = 0.39 \pm 0.05. \end{aligned}$$
(55)
Fig. 17
figure 17

The result of model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) in the region of \(x\sim 0.006\) at EIC and EicC. Both statistical and systematic errors are considered

Full size image

As Fig. 7 shows, EIC also provides accurate data in the area of \(x\sim 0.002\). In this very small x region, we present the result of EIC,

$$\begin{aligned} J_u + J_d/2.4 = 0.35 \pm 0.04, \end{aligned}$$
(56)

which is shown in Fig. 18.

Fig. 18
figure 18

The result of model-dependent constraint on u-quark total angular momentum \(J_u\) vs d-quark total angular momentum \(J_d\) in the region of \(x\sim 0.002\) at EIC. Both statistical and systematic errors are considered

Full size image

The results of EicC and EIC are both within the error range of HERMES and exhibit small uncertainties. Without precise experiments, it is challenging for theoretical advancements to occur. These accurate experimental data will greatly contribute to our future understanding of nucleon structure.

6 Discussions and summary

The internal structure of the nucleon remains mysterious, and researchers explore it through various methods. Following the EMC experiment, numerous detailed studies on nucleon spins were conducted. The proposed theory of GPDs has opened new avenues for investigating the three-dimensional structure and spin of the nucleon. Ji’s sum rule establishes a direct relationship between GPDs and the total angular momentum carried by the partons. DVCS experiments serve as a valuable choice for obtaining GPDs, albeit not through direct extraction. Despite significant progress in the theoretical exploration of GPDs, relatively little advancement has been made on the experimental front. This is primarily due to the demanding requirements of high statistical accuracy, necessitating exceptional detectors and high luminosity.

In this study, we performed simulations of the DVCS process at EicC and EIC to investigate the internal structure of the proton. We predicted the statistical errors for these two future experiments. Based on the very small statistical errors, we conclude that the measurement accuracy of future DVCS experiments will be predominantly limited by systematic errors. A notable improvement in data accuracy is expected for EIC and EicC compared to existing data obtained from different experimental groups. This development holds significant implications for future experimental studies on the internal structure of the nucleon. Advanced experimental equipment can help reduce systematic errors, while better detection of final-state particles can minimize statistical errors. With excellent detectors and high accelerator luminosity, DVCS experiments at EicC and EIC hold promising prospects.

Using high-precision pseudo-data for TTSA from EIC and EicC measurements, we can effectively study the nucleon’s helicity-flip GPD E. Through the VGG model, GPD E is parameterized by the total angular momentum of the up and down quarks within the nucleon. By combining DVCS experiments with nucleon spin studies, we can constrain the total angular momentum carried by up and down quarks inside the proton during future EIC and EicC experiments, taking into account the constraints provided by HERMES and JLab experiments on the total angular momentum of quarks in the proton and neutron. Comparison of the differences between the different models is necessary.The viability of the VGG model in the valence quark energy region is unquestionable, but there is a restriction on its use in the gluon as well as in the sea quark energy region at small x. Measurements and analyses of nucleon angular momentum in recent years have used the VGG model as a benchmark, e.g., HERMES, JLab experiments. As a first step, we use the same VGG model and parameters for the simulations in this paper, with the aim of comparing the results with those of other collaborations. In future work we will focus on the discretization of the VGG model with respect to the GK model, the later one increases the rationality of the parameterization of GPDs in the small x gluon and sea quark energy regions.