The spatial string tension from the field correlator method

Abstract

The behaviour of spatial string tension $\sigma _s(T)$ as a function of the temperature T is found in the framework of the Field Correlator Method (FCM). Here the string tension is calculated using the gluelump Green’s function, where gluons in the gluelump are interacting via the same spatial string tension. The resulting T-dependence was obtained without extra parameters in the region $T_c< T < 5 T_c$ using the formalism of elliptic functions $\theta _3$, demonstrating good agreement with available lattice data.

1 Introduction

The confinement in QCD is a basic phenomenon which ensures more than 90% of the visible mass in the Universe and makes the world such as we see it. At zero temperature the theory of confinement in QCD was formulated in the framework of the Field Correlator Method (FCM) [1,2,3,4,5,6,7], via the vacuum field correlators of the colorelectric (CE) and the colormagnetic (CM) fields $E_i^a,H_i^a$, and at the temperature $T=0$ the behaviour of all physical quantities is expressed via the basic nonperturbative parameter – the string tension, which can have different values in the light-like $\sigma _E$ and space-like $\sigma _H$ areas, but at zero temperature T, $\sigma _E(T=0)=\sigma _H(T=0)= \sigma$. Very important role in FCM plays bilocal correlator (BC) of gluonic fields strength:

$$\begin{aligned} \frac{g^{2}}{N_{c}} \bigg \langle tr_{f}\Phi (y,x)F_{\mu \nu }(x)\Phi (x,y)F_{\lambda \rho }(y) \bigg \rangle \equiv D_{\mu \nu ,\lambda \rho }(x,y). \nonumber \\ \end{aligned}$$

(1)

From this moment we use $F_{\mu \nu }\equiv F^{a}_{\mu \nu }T^{a}$, $a=1..N_{f},T^{a}$ – are generators of fundamental representation of $SU(N_{c})$. In Eq. (1) symbol $\langle \rangle$ means averaging over Yang-Mills action $S=\frac{1}{4\,g^{2}}\int {d^{4}x}(F^{a}_{\mu \nu }), F^{a}_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }+gf^{abc}A^{b}_{\mu }A^{c}_{\nu }, a=1..N^{2}_{c}-1$, $\Phi (x,y)=Pexp(i\int ^{x}_{y}A_{\mu }dz^{\mu }), \mu =1..4$¹ is the Wilson line in fundamental representation. We can write BC as follows:

$$\begin{aligned} D_{\mu \nu ,\lambda \rho }(x,y)= & {} (\delta _{\mu \lambda }\delta _{\nu \rho }-\delta _{\mu \rho }\delta _{\nu \lambda })D(x-y)\nonumber \\{} & {} +\frac{1}{2}\bigg (\frac{\partial }{\partial x_{\mu }}(x-y)_{\lambda }\delta _{\nu \rho }+perm.)\bigg )D_{1}(x-y),\nonumber \\ \end{aligned}$$

(2)

$D(x-y),D_{1}(x-y)$ – are scalar functions. We also can add index E or H² to $D,D_{1}$, because $E_{i}=F_{0i},H_{i}=\epsilon _{ijk}F^{jk}/2, i=1,2,3$ and $\langle EH \rangle =0$. Functions $D^{E,H}(x),D^{E,H}_{1}(x)$ define all confining QCD dynamics and in particular the string tensions:

$$\begin{aligned} \sigma _E= 1/2 \int (d^2z)_{i4} D^{E}(z), \sigma _H= 1/2 \int (d^2z)_{ik} D^{H}(z) . \end{aligned}$$

(3)

These functions were calculated in good agreement between the FCM [8] and the lattice data [4, 6], while $D^E(x),D^H(x)$ were also studied in details at $T>0$ on the lattice [6]. The most interesting fact is that at $T>0$ $\sigma _E(T)$ and $\sigma _H(T)= \sigma _s(T)$ behave differently. Namely: $\sigma _E(T)$ displays a spectacular drop before $T=T_c$ and disappears above $T=T_c$, while in contrast to that $\sigma _s(T)$ grows almost quadratically at large T, as was found on the lattice [5, 9,10,11,12] and supported by the studies in the framework of the FCM [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Indeed, as it was found in Refs. [11, 12] that the dominant part of the spatial string tension $\sigma _s(T)$ grows quadratically at large T

$$\begin{aligned} \sigma _s(T)= (c_{\sigma })^2 g^4(T) T^2 , \end{aligned}$$

(4)

where $c_{\sigma }$ was defined numerically in the lattice calculations [11, 12] in case $N_c=3, N_f=0$ as

$$\begin{aligned} c_{\sigma }= 0.566\pm 0.013. \end{aligned}$$

(5)

On the theoretical side the quadratic growth of the $\sigma _s(T)$ was derived in the framework of FCM [8, 13, 18, 21], and the value of $c_{\sigma }$ was found in Ref. [22] in good agreement with the lattice data of [11, 12].

However, in the full FCM expression for the spatial string tension the term in the Eq. (4) is only a fast-growing part of the whole expression, which was hitherto not known.

The purpose of this paper is to derive the total expression of the spatial string tension including the linear in T part, to calculate the numerical value of $\sigma _s(T)$ in the region of $[T_{c}..5T_{c}]$³ and compare it with the lattice data. As will be seen, the results, obtained within the FCM, will provide the values of $\sigma _s (T)$ in good agreement with the lattice data. In the next section we discuss connection between BC and gluelump Green’s function. In Sect. 3 we discuss the general expression for $\sigma _s(T)$ in terms of the field correlators (and gluelump Green’s functions respectively), we formulate its final form and obtain the expression of the string tension, which is discussed and compared with the lattice data in Sect. 4. The renormalized coupling constant $g^2(T)$ is given in Appendix A1, the detailed discussion of two-gluelump Green’s function is given in Appendix A2. We discuss diagonalization of the two-glulump Hamiltonian in Appendix A3. Calculations of the two-gluelump Hamiltonian eigenvalues and eigenfunctions is given in Appendix A4.

2 Gluelump and bilocal correlator of gluonic field strength

We need to find a connection between D(x) and so called gluelump Green’s function [29, 30]. For this purpose we rewrite the expression in Eq. (2) in the form:

$$\begin{aligned}{} & {} \frac{g^{2}}{N_{c}} \bigg \langle tr_{f}\Phi (y,x)F_{\mu \nu }(x)\Phi (x,y)F_{\lambda \rho }(y) \bigg \rangle \nonumber \\{} & {} \quad = \frac{g^{2}}{N_{c}}tr_{f} \bigg \langle F^{a}_{\mu \nu }(x)[T^{a}\Phi (x,y)T^{b}\Phi (y,x]F_{\lambda \rho }(y) \bigg \rangle . \end{aligned}$$

(6)

The integration in the last expression is performed along the straight line connecting the points x and y, so we can rewrite the expression in square brackets in the form [17]:

$$\begin{aligned} 2tr(T^{a}\Phi (x,y)T^{b}\Phi (y,x))=\Phi ^{ab}_{adj}(x,y), \end{aligned}$$

(7)

and finally we have:

$$\begin{aligned} D_{\mu \nu ,\lambda \rho }(x,y)=\frac{g^{2}}{2N^{2}_{c}}tr_{adj} \bigg \langle F^{a}_{\mu \nu }(x)\Phi ^{ab}_{adj}(x,y)F^{b}_{\lambda \rho }(y) \bigg \rangle . \end{aligned}$$

(8)

Last equation coincides with the expression from the paper [31]. For our purposes we rewrite it as:

$$\begin{aligned} D_{\mu \nu ,\lambda \rho }(x,y)=\frac{g^{2}}{2N^{2}_{c}} \bigg \langle tr_{adj}{\hat{F}}_{\mu \nu }(x) {\hat{\Phi }}(x,y){\hat{F}}_{\lambda \rho }(y)\bigg \rangle , \end{aligned}$$

(9)

here all dashed letters stand for operators in the adjoint representation. At the next step we need to find connection between BC and so called gluelump Green’s functions. Expanding $F_{\mu \nu }$ into abelian (parentheses ) and nonabelian parts:

$$\begin{aligned} F_{\mu \nu }=(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })-ig[A_{\mu },A_{\nu }], \end{aligned}$$

(10)

we can write BC as:

$$\begin{aligned} D_{\mu \nu ,\lambda \rho }(x,y)= & {} D^{0}_{\mu \nu ,\lambda \rho }(x,y)+D^{1}_{\mu \nu ,\lambda \rho }(x,y)\nonumber \\{} & {} \quad +D^{2}_{\mu \nu ,\lambda \rho }(x,y), \end{aligned}$$

(11)

where the number at the top of the letter D means power minus two of coupling constant g. For $D^{0}(x,y)$ we obtain:

$$\begin{aligned} D^{0}_{\mu \nu ,\lambda \rho }(x,y)= & {} \frac{g^{2}}{2N_{c}^{2}}\bigg ( \frac{\partial }{\partial x_{\mu }} \frac{\partial }{\partial y_{\nu }} G^{1g}(x,y) +perm. \bigg )\nonumber \\{} & {} +\Delta ^{0}_{\mu \nu ,\lambda \rho }, \end{aligned}$$

(12)

where $\Delta ^{0}_{\mu \nu ,\lambda \rho }(x,y)$ contains contribution of higher field cumulants, which we systematically discard. Here $G^{1g}$ is one-gluelump Green’s function:

$$\begin{aligned} G^{1g}_{\mu \nu }(x,y)= \bigg \langle tr_{adj}{\hat{A}}_{\mu }(x){\hat{\Phi }}_{adj}(x,y){\hat{A}}_{\nu }(y)\bigg \rangle , \end{aligned}$$

(13)

$tr_{adj}$ is a trace over adjoint indices. As shown in Ref. [32], this term is connected with the functions $D^{E,H}_{1}$.From the physical point of view the Eq. (13) describes the gluon that is moving in the field of adjoint source (see Fig. 4 in Appendix A.5). Interaction between two objects in the adjoint representation is leading to formation of the string that according to Casimir scaling law found in the framework of FCM in [33] and supported by lattice data in [34, 35] have a tension $\sigma _{adj}=\frac{C_{2}(adj)}{C_{2}(f)}\sigma _{f}=9/4 \sigma _{f}$, $C_{2}(adj),C_{2}(f)$ are Casimir operators for adjoint and fundamental representations. This hypothesis give us a chance to calculate one-gluelump mass $M_{0}$. This mass governs the nonconfinig part of the colour Coulomb’s potential (we can calculate it from the correlator of Polyakov lines), and from our reasoning it is obvious that we can make the assumption that $M_{0} \sim \sqrt{\sigma _{adj}}$. From direct calculations we have [27]:

$$\begin{aligned} V_{1}(r,T)= & {} -\frac{C_{2}(f)\alpha _{s}}{r}exp(-M_{0} r), M_{0} \nonumber \\\simeq & {} 2.06 \sqrt{\sigma _{s}}, rT\ll 1 \end{aligned}$$

(14)

r-is a distance, T is a temperature, $\alpha _{s}$ is a strong coupling constant. From comparison of the last equation with a simple Debye potential [36] we can say that $M_{0}$ is playing the role of Debye mass.

As for $D^{2}_{\mu \nu ,\lambda \rho }(x,y)$, it is of basic importance, since ensures confinement via D(x-y) and is expressed via two-gluon gluelump Green’s function $G^{2g}(x,y)$. The expression for $D^{2}_{\mu \nu ,\lambda \rho }(x,y)$ reads as:

$$\begin{aligned} D^{2}_{\mu \nu ,\lambda \rho }(x,y)= & {} -\frac{g^{4}}{2N^{2}_{c}} \bigg \langle tr_{adj}\bigg ([A_{\mu }(x),A_{\nu }(x)]{\hat{\Phi }}(x,y)\nonumber \\{} & {} \times [A_{\lambda }(x),A_{\rho }(x)]\bigg )\bigg \rangle . \end{aligned}$$

(15)

We remind that:

$$\begin{aligned}{}[A_{i},A_{k}]=iA^{a}_{i}A^{b}_{k}f^{abc}T^{c}. \end{aligned}$$

(16)

Let’s consider:

$$\begin{aligned}{} & {} G_{\mu \nu ,\lambda \rho }(x,y)=tr_{adj}\nonumber \\{} & {} \quad \times \bigg \langle f^{abc}f^{def}A^{a}_{\mu }(x)A^{b}_{\nu }(x)T^{c}{\hat{\Phi }}(x,y)A^{d}_{\lambda }(y)A^{e}_{\rho }(y)T^{f}\bigg \rangle .\nonumber \\ \end{aligned}$$

(17)

We can fix in Eq. (17) color indices a, b; d, e and average Green’s function over all fields $A^{h}_{\mu }$ with $h \ne a, b; d, e$. This averaging will produce the white string (of triangle shape at any given moment), and hence it will ensure terms ($\delta _{ad} \delta _{be}$+ permutations). As a result we can represent $G_{\mu \nu ,\lambda \rho }(x,y)$ in the form:

$$\begin{aligned} G_{\mu \nu ,\lambda \rho }(x,y)= & {} N^{2}_{c}(N^{2}_{c}-1)\nonumber \\{} & {} (\delta _{\mu \lambda }\delta _{\nu \rho }-\delta _{\mu \rho }\delta _{\nu \lambda })G^{2gl}(x,y), \end{aligned}$$

(18)

where $G^{2gl}(x,y)$ is the Green’s function of the two-gluon gluelump.

Comparison of Eqs. (2), (15) and (18) immediately yields the following expression for D(x-y):

$$\begin{aligned} D(x-y)=\frac{g^{4}(N^{2}_{c}-1)}{2}G^{2gl}(x,y) . \end{aligned}$$

(19)

Both one- and two-gluon gluelump functions can be written in terms of path integrals [37] and finally expressed via eigenvalues and eigenfunctions of relativistic string Hamiltonian [38,39,40].

3 The spatial string tension in the FCM

We need to clarify some important moments: at temperatures above deconfinement, $T > T_{c}$, large spatial Wilson loops still comply with the area law. For pure gauge SU(3) Yang–Mills theory $T_{c}=270$ MeV. This behaviour of spatial Wilson loops [41] is the main well established nonperturbative phenomenon at $T > T_{c}$, which is usually called “magnetic ” or “spatial” confinement. Of course, it does not contradict true deconfinement of a static quark–antiquark pair [42,43,44,45,46], because spatial-time Wilson loops indeed lose the exponential damping with the area for $T > T_{c}$. To illustrate this phenomenon one can calculate polarization operator $\Pi (x,y)$ in Yang–Mills theory [47]. As a standard step we need to decompose gluon field in non-perturbative $B^{a}_{\mu }$ and perturbative $a^{b}_{\mu }$ parts:

$$\begin{aligned} A^{a}_{\mu }=B^{a}_{\mu }+a^{a}_{\mu }, \end{aligned}$$

(20)

usually field B is treated as external. The expression for scalar part of polarization operator reads as:

$$\begin{aligned} \langle \Pi (x,y) \rangle _{B}= \bigg \langle tr (D^{2}[B]_{xy})^{-1}(D^{2}[B]_{yx})^{-1}\bigg \rangle _{B} , \end{aligned}$$

(21)

where

$$\begin{aligned} (D_{\mu }[B]a_{\nu })^{c}=\partial _{\mu }a_{\nu }^{c}+gf^{cde}B^{d}_{\mu }a^{e}_{\nu }. \end{aligned}$$

(22)

In Eq. (21) averaging is over $B^{a}_{\mu }$. At $T>T_{c}, T \ll \sigma _{s} R, (\sigma _{s}=\sigma _{H})$ one observes dramatic difference for spatial and time-like domains. For the first one ($x_{0}-y_{0}=0,{x}-{y}={R}$) one obtains at large distance:

$$\begin{aligned} \Pi (0,R) \approx \frac{\sigma _{s}}{R^{2}}exp(-C\sqrt{\sigma _{s}}R), \sigma _{s}R^{2}\gg 1, C\approx 2\sqrt{2}, \end{aligned}$$

(23)

and at small distance polarization operator tends to non-interacting case:

$$\begin{aligned} \Pi (0,R) \rightarrow \bigg (\frac{1}{4\pi ^{2} R^{2}}\bigg )^{2},\sigma _{s}R^{2}\ll 1. \end{aligned}$$

(24)

For a time-like domain at zero temperature we have $\sigma _{E}=\sigma _{H}$, but at $T>T_{c}$ $\sigma _{E}=0$ as a manifestation of the confinement–deconfinement phase transition.

With these examples in mind we can focus on calculations of two-gluelump Green’s function at non-zero temperature. The Eq. (17) describes two gluons moving in the field of adjoint source and interacting nonperturbatively (via $\sigma _{E,s}$) with it and between themselves.

The spatial string tension is proportional to the integral of two-gluon gluelump Green’s function in the 3d space, where one of three space coordinates can be treated as an evolution parameter (“‘the Euclidean time”). Using the technic, developed in Refs. [13, 18,19,20,21] we can write $G^{(2\,g)}_{4d} (z) = G_{4d}^{(g)}\otimes G_{4d}^{(g)}$. We neglect the spin interactions in the first approximation. Concerning $G_{4d}^{(g)}$ we have [21, 22]:

$$\begin{aligned} (-D^2)^{-1}_{xy}= & {} \left\langle x\left| \int ^{\infty }_0 dt e^{tD^2(B)}\right| y\right\rangle \nonumber \\= & {} \int ^{\infty }_0dt(Dz)^{w}_{xy}e^{-K}\Phi (x,y), \end{aligned}$$

(25)

where

$$\begin{aligned} K= & {} \frac{1}{4}\int ^s_0d\tau \left( \frac{dz_\mu }{d\tau } \right) ^2, ~~\Phi (x,y)\nonumber \\= & {} P \exp ig\int ^x_yB_{\mu }dz_{\mu }, \end{aligned}$$

(26)

and a winding path measure is

$$\begin{aligned} (Dz)^w_{xy}= & {} \lim _{N\rightarrow \infty }\prod ^{N}_{m=1}\frac{d^4\zeta (m)}{(4\pi \varepsilon )^2} \sum ^{+\infty }_{n=-\infty }\nonumber \\{} & {} \times \int \frac{d^4p}{(2\pi )^4}e^{ip(\sum \zeta (m)-(x-y)-n\beta \delta _{\mu 4})}. \end{aligned}$$

(27)

The important point for the resulting T dependence of the string tension is the integration in the gluon propagator $G^{(g)}_{4d}$ over the 4-th direction in Eq. (25) with the exponent $K_4 = \frac{1}{4} \int ^s_0 d\tau \left( \frac{d z_4}{d\tau }\right) ^2,$ which gives for the spatial string tension with $x_4=y_4$, and for the temporal string tension with the nonzero $x_4-y_4$ completely different behaviour, namely for the $\sigma _s$ case:

$$\begin{aligned} J_4 \equiv \int (Dz_4)_{x_4x_4} e^{-K_4} = \sum ^{+\infty }_{n=-\infty } \frac{1}{2 \sqrt{\pi s}} e^{-\frac{(n\beta )^2}{4s}} . \end{aligned}$$

(28)

One can notice that the sum in the Eq. (28) is a known function:

$$\begin{aligned} \sum ^{+\infty }_{n=-\infty }e^{-\frac{n^2}{4sT^2}}\equiv \vartheta _3(q),~~~q=e^{-\frac{1}{4sT^2}}, \end{aligned}$$

(29)

where the function $\vartheta _3(q)$ is defined as:

$$\begin{aligned} \vartheta _3(q)=\sum ^{+\infty }_{n=-\infty }q^{n^2}=1+2q+2q^4+O(q^9) , \end{aligned}$$

(30)

and thus, the first term in this expression is connected with the vacuum contribution. Then starting from low temperature there is an expansion:

$$\begin{aligned} J_4= & {} \frac{1}{2\sqrt{\pi s}}\sum ^{+\infty }_{n=-\infty }e^{-\frac{n^2}{4sT^2}} \equiv \frac{1}{2\sqrt{\pi s}}\vartheta _3(e^{-\frac{1}{4sT^2}})\nonumber \\= & {} \frac{1}{2\sqrt{\pi s}}(1+2e^{-\frac{1}{4sT^2}}+O(e^{-\frac{1}{sT^2}})) . \end{aligned}$$

(31)

To find the asymptotics at high T one can use the relation:

$$\begin{aligned} \sum ^{+\infty }_{n=-\infty }e^{-\frac{\beta ^2n^2}{4s}}= \frac{2\sqrt{\pi s}}{\beta } \sum ^{+\infty }_{n=-\infty } e^{-\frac{4\pi ^2n^2}{\beta ^2}s}. \end{aligned}$$

(32)

As a result at large T one obtains an equality:

$$\begin{aligned} J_4= & {} T\sum ^{+\infty }_{n=-\infty }e^{-4\pi ^2sT^2n^2}\equiv T\vartheta _3(e^{-4\pi ^2sT^2})\nonumber \\= & {} T(1+2e^{-4\pi ^2sT^2}+O(e^{-16\pi ^2sT^2})) . \end{aligned}$$

(33)

Here we use the elliptic functions $\vartheta _{3}(q)$ defined in Eq. (30).

Their behaviour as function of q is given in Fig. 1.

Fig. 1

$\vartheta _{3}(q)$ as a function of q

As a result we can use $J_{4}$ at an arbitrary T in the form:

$$\begin{aligned} J_4(s,T)\equiv \frac{1}{2\sqrt{\pi s}}\vartheta _3(e^{-\frac{1}{4sT^2}}) . \end{aligned}$$

(34)

In this way starting from low T one obtains an exact expression for $J_4(T)$ valid in the whole range of T. One could approximate this behaviour as a sum of linear and constant terms implying a soft transition from $T=0$ case to the linear in T behaviour however this approximation fails numerically and actually one observes a sharp transition at some intermediate point $T^*$ from the regime $T=0$ to the large T behaviour as given by the Eq. (34). For simplification we define:

$$\begin{aligned} \vartheta _3(e^{-\frac{1}{sT^2}})= f(\sqrt{s}T). \end{aligned}$$

(35)

At this point we turn to the general form of the field correlator $D^H(z)$ with the aim to express the string tension via the factors f(x). Rewriting the Eq. (19) with index “H” we have:

$$\begin{aligned} D^H(z) = \frac{g^{4}(T)(N^2_c-1) }{2} \langle G^{(2g)} (z,T) \rangle , \end{aligned}$$

(36)

where $G^{(2g)}(z,T)$ is the two-gluelump Green’s function. In the path integral representation we can write it (see Appendix A2 for details) as:

$$\begin{aligned} G^{(2g)}(z,T)= & {} \frac{z}{8\pi } \int \frac{d\omega _1}{\omega _1^{3/2}} \frac{d\omega _2}{\omega _2^{3/2}}\int {} D^{2}r_1 D^{2}r_2\nonumber \\{} & {} \times \exp {(-K_1-K_2-V({\varvec{\textrm{r}}}_1,{\varvec{\textrm{r}}}_2)z)}I(z,T,\omega _{1},\omega _{2}), \end{aligned}$$

$$\begin{aligned} I(z,T,\omega _{1},\omega _{2})=f(\sqrt{z/2\omega _1}T)f(\sqrt{z/2\omega _2}T) . \end{aligned}$$

(37)

As a result we obtain $\sigma _s(T)$ in the following form:

$$\begin{aligned} \sigma _s(T)= & {} \frac{g^{4}(T)(N_c^2-1)}{4}\int d^2z z/(8\pi ) \nonumber \\{} & {} \times \int d\omega _1 d\omega _2 (\omega _1\omega _2)^{-3/2}\sum _{n=0,1,} |\psi _n(0,0)|^2 \end{aligned}$$

(38)

$$\begin{aligned}{} & {} \times \exp (-M_n(\omega _1,\omega _2)z) f(\sqrt{z/2\omega _1}T)f(\sqrt{z/2\omega _2}T).\nonumber \\ \end{aligned}$$

(39)

One can see in Eq. (39) the only T-dependent factors $g^4(T)$ and $f(\sqrt{z/2\omega _1}T)$ which define the dependence of $\sigma _s(T)$. Therefore one can write $\sigma _{s}(T)$ (denoting the z- and $\omega$-integration in Eq. (39) with the average sign $\langle ... \rangle$) in the following form:

$$\begin{aligned} \sigma _s(T)= & {} \textrm{const} g^4(T) \bigg \langle f^2(\sqrt{z/(2\omega )T}) \bigg \rangle \nonumber \\= & {} \textrm{const} g^4(T) f^2(\sqrt{\overline{ \mathrm z/2\omega }} T), \end{aligned}$$

(40)

$$\begin{aligned} \sigma _{s}(T)= & {} \textrm{const} g^4(T) f^2(\overline{\textrm{w}}T), \end{aligned}$$

(41)

where we have denoted the average values of $\sqrt{\overline{\mathrm{z/2\omega }}}$ (obtained as a result of integration over the T-independent region of parameters with the T-independent kernel. We have also taken into account the symmetries of the Hamiltonian $H(\omega _{1},\omega _{2})$ with respect to permutation of $\omega _{1}$ and $\omega _{2}$) as $\overline{\textrm{w}}= \rho /T_c$ and both $\rho ,T_c$ are fixed parameters. The appearance of $g^4(T)$ which is decreasing with T as $(\ln T)^{-2}$ defines the T dependence of $\sigma _s(T)$ to be lower than $T^2$, thus confirming the behaviour of $\sigma _s(T)$ in the lattice data of [11], where the data were fitted as $\sigma _s(T)= \textrm{const} g^4(T) T^2$. However this fit fails for $T<2T_c$ claiming the necessity of another factor in Eq. (41). Correspondingly we are writing the resulting equation for the $\sigma _s(T)$ denoting the average value of $\sqrt{z/(2\omega )}T$ as $\rho T/T_c$.

In the next sections we try to test our arguments and to demonstrate that this new form with the well-defined factor $f(\overline{\textrm{w}}T)$ describes the whole region of $T>T_c$ with good accuracy.

4 General expression for the spatial string tension vs lattice data

For approve our predictions we need to find the parameter $\rho$ that describes the all data from the lattice simulations. For $f(\rho T/Tc)$ we have:

$$\begin{aligned} F(T/Tc)=f(\rho T/T_c)= \vartheta _3 \bigg (e^{-\frac{T_c^2}{\rho ^{2} T^2}}\bigg ) . \end{aligned}$$

(42)

The numerical analysis of the data [11] allows to reproduce well the data with the Eq. (41), derived in the previous section

$$\begin{aligned} \sigma _s(T)=\sigma _s(T_c) \frac{g^4(T) F^2(T/T_c)}{g^4(T_c)F^2(1)} . \end{aligned}$$

(43)

The comparison with the lattice data of [11] for Eq. (43) is shown in Fig. 2, and the expression for $g^4(T)$ is given in the Appendix 1 and the value of the $\rho$-parameter $\rho =1/\sqrt{3.2}$. The Fig. 2 demonstrates a good agreement between the lattice data and Eq. (43), including the region $T< 2.5 T_c$ where the lattice fit $T^2 g^4(T)$ in [11] starts to disagree with numerical data.

Fig. 2

Spatial string tension $\sigma _s (T)/\sigma$ for SU(3) gauge theory as function of $T/T_c$. The lattice data with errors are from Ref. [11]. $T_{c}$=270 MeV

The points on Fig. 2 as functions of $T/T_{c}$ completely coincide with the points from Fig. 3 in Ref. [17]. This fact means that at sufficiently high temperatures we numerically reproduce the Eq. (4). We also show the dependence of running coupling as function of temperature (see Fig. 3 in the Appendix A1). As for the dependence of $\frac{\vartheta _3(e^{-\frac{T_c^2}{\rho ^{2} T^2}})}{T^{2}},\rho =1/\sqrt{3.2}$ it is equal to one with accuracy of 2% for temperatures higher than 1.3$T_{c}$. From these data we also can understand that in the absence of running coupling the string tension at high T is proportional to $T^{2}$. Thus one can conclude that running coupling has a small effect in comparison with $\vartheta ^{2}_{3}$. From all this facts we can say that temperature of dimensional reduction should be $T_{d}\ge 1.3 Tc$. That doesn’t contradict neither the lattice data no earlier FCM predictions [17].

5 Discussion of results and conclusions

The main purpose of our work is the construction of the detailed mechanism of the spatial confinement in the whole region of the temperature from $T=T_c$ to asymptotically large temperatures. The previous analysis in Ref. [28] has shown that the qualitative behaviour near $T=T_c$ can be continuously connected with the asymptotic behaviour of the $\sigma _s(T)$. Due to complications of analytic calculations we tried to find the form of dependence of spatial string tension from the main QCD parameters. And for this dependence we found the behaviour that well describes the lattice data. As can be seen in Fig. 2 our resulting curve for the spatial string tension is in a good agreement with the accurate lattice data in the whole measured region $T_c< T < 5 T_c$. We have exploited the coupling constant depending on the temperature T given in the Appendix A1, which has also allowed the authors of [11] to get agreement with their data in the asymptotic region. Also to describe the region of smaller T we have used the formalism of the elliptic functions $\vartheta _3(z)$ which describe well the sharp transition of the gluon propagator in the two-gluelump Green’s function from the constant to the linear behaviour.It should be emphasized that the formalism presented in the paper is standard for the temperature dependence of any Green’s functions developing in the spacial or time-like continuum with inclusion of interaction via the field correlators [13, 18,19,20]. In particular the same spatial string tension appears in the expression for the screening mass (we have called it “Debye mass” $m_D(T)= 2.06 \sqrt{\sigma _s(T)}$ in [27, 28]) characterizing the spatially oriented parts of the area of the Wilson loops. The inclusion of the temperature via the Matsubara-type formalism with the T-dependent factors $I(x_4-y_4,T)= exp(-ip_4(x_4-y_4 -n/T))$ in the gluon Green’s functions is shown in the Eq. (27). For the space-like correlators with $x_4=y_4$ the use of the Poisson summation formula $1/(2\pi ) \sum _n \exp (ip_4 n\beta )= \sum _k \delta (p-4 \beta -2\pi k), \beta =1/T$, brings about an additional factor of T. This finally leads to the $T^2$ dependence of the leading term in the $\sigma _s(T)$ as in the Eq. (4). On the contrary for the time-like Green’s functions with the nonzero $x_4-y_4$ the T dependence is dictated by the corresponding mass parameters and for $\sigma _E(T)$ the situation is even more dramatic since it drops to zero (deconfinement) at $T=T_c$ approximately as $(1-(T/T_c)^4)^{1/2}$ [48]. One can wonder why these two phenomena – spatial (colormagnetic) confinement and colorelectric confinement are so different and hence disconnected and as follows from the lattice data (see Figs. 9, 10 in Ref. [6]) the CE gluon condensate $<G_2^E (T)>$ and the CM condensate $<G_2^M (T)>$ being equal at $T=0$ behave also in a similarly different manner with growing T? The answer lies in the different active regions of these phenomena – the space-like continuum for CM and the time-like continuum for CE confinement which have a little dynamical intersection as space-like and time-like surfaces, which is evident in the FCM and is an additional argument in favor of its selfconsistency. As it is, we have found good agreement of our FCM approach for CM string tension with lattice data [11] in this paper as well as good agreement of all our CE calculations with the corresponding lattice and experimental data [2, 4,5,6, 8, 13, 18,19,20,21,22] including the latest CE calculations of the deconfining process [48]. Turning back to the CM physics it was found within our approach that an even more important role of the spatial string tension may be in the high T thermodynamics where in the framework of FCM it provides the basic nonperturbative contribution to the pressure and other observables, see e.g. Ref. [25], in good agreement with the lattice data and solving as in Ref. [21] the old “Linde problem” which precludes pure perturbative thermodynamic calculations of interacting systems at large temperature. Another interesting development of this method is the dynamical theory of QCD systems in the external magnetic field where the FCM yields all results in good agreement with lattice data without any parameters, see e.g. [49, 50]. In this way the FCM plays an important role in the development of the present QCD theory.

Appendices

Appendix A1: Two-loop expression for $g^{-2} (t)$

From the point of view of FCM the running coupling enters naturally in the formalism qualitatively in the same way as in the standard theory [51]. One can decompose the non-Abelian gauge field into the low- and the high-energy parts: $A_{\mu }=B_{\mu }+a_{\mu }$. At this step one can treat $B_{\mu }$ as an external gauge field and at after that integrate out perturbative fields in the path integral. This procedure in the UV domain produces the running coupling constant and it can be used for calculation of beta-function for example in three loops order [52]. As a result one can use the two-loop beta-function calculations on the lattice in SU(3) gluodynamics [11] where the expression has the standard form as a function of $t= \frac{T}{T_c}$:

$$\begin{aligned} g^{-2}(t)= c_0 \ln \frac{t}{L_{\sigma }} + c_1 \ln \left( 2 \ln \frac{t}{L_{\sigma }}\right) , \end{aligned}$$

(A1.1)

where

$$\begin{aligned} c_0= \frac{11}{8\pi ^2}, c_1= \frac{51}{88\pi ^2}. \end{aligned}$$

(A1.2)

Here $L_\sigma = \frac{\Lambda _\sigma }{T_c}= 0.104 \pm 0.009$ as in Refs. [11, 12]. All other parameters that we used for the calculations involving g(t) are the same as in Ref. [11]. We also show behaviour of $\frac{g(T)^{4}}{g(T_{c})^4}$ as a function of $\frac{T}{T_{c}}$ on Fig. 3.

Fig. 3

Behaviour of $\frac{g(T)^{4}}{g(T_{c})^4}$ as a function of $\frac{T}{T_{c}}$

Appendix A2: Gluelump Green’s function

There are two different ways to calculate two-gluelump Green’s function and thus to obtain the spatial string tension from Eqs. (19), (3). Two- gluelump Green’s function at non-zero temperature reads as:

$$\begin{aligned}{} & {} G^{2g}(x-y,T) =\int ^{\infty }_{0}{ds}\int ^{\infty }_{0}{d{\bar{s}}}\int {D^{w}z_{4}D^{w}{\bar{z}}_{4}}\nonumber \\{} & {} \times \int {D^{3}zD^{3}{\bar{z}}}exp(-S) \langle W(C_{z{\bar{z}}}) \rangle , \end{aligned}$$

(A2.1)

$$\begin{aligned} S= & {} \frac{1}{4}\int ^{s}_{0}{d\tau }\bigg (\frac{d z_{\mu }}{d\tau }\bigg )^{2}+\frac{1}{4}\int ^{{\bar{s}}}_{0}{d{\bar{\tau }}}\bigg (\frac{d {\bar{z}}_{\mu }}{d {\bar{\tau }}}\bigg )^{2}, \end{aligned}$$

(A2.2)

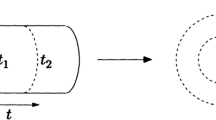
x–y is a distance in four-space between beginning and ending points. The Wilson loop $W(C_{z{\bar{z}}})$ is averaged over gluon fields along the paths z, ${\bar{z}}$ in the field of a static adjoint source with spatial coordinate ${r}=(0,0,0)$ that moves along z-axis entirely. This procedure leads to formation of strings between gluons themselves and glouns and the source. The distance of movement along z-axes is t. This interval must be large enough to avoid contribution of gluon fields fluctuations. With the help of Eq. (28) one can integrate out fourth component of Eq. (A2.1) and obtain:

$$\begin{aligned} G^{2g}(x-y,T)= & {} \int ^{\infty }_{0}{ds}\int ^{\infty }_{0}{d{\bar{s}}}\nonumber \\{} & {} \times \int {D^{3}zD^{3}{\bar{z}}}exp(-S_{spatial})J_{s,{\bar{s}}}(s,{\bar{s}},T),\nonumber \\ \end{aligned}$$

(A2.3)

$$\begin{aligned} J_{s,{\bar{s}}}(s,{\bar{s}},T)= & {} \frac{1}{4\pi \sqrt{s{\bar{s}}}}\vartheta _3 \big (e^{-\frac{1}{4sT^2}}\big )\vartheta _3\big (e^{-\frac{1}{4{\bar{s}}T^2}}\big ), \end{aligned}$$

(A2.4)

$S_{spatial}$ – is a rest part of the action without fourth component containing “spatial” Wilson factor. Changing $s=\frac{t}{2\omega _{1}},{\bar{s}}=\frac{t}{2\omega _{2}}$ and Eq. (34) with third coordinate as “Euclidean time”⁴ we can rewrite the last equation in the following form:

$$\begin{aligned} G^{2g}(t,T)= & {} t^{2}\int ^{\infty }_{0}{\frac{d\omega _{1}}{2\omega _{1}^{2}}}\int ^{\infty }_{0}{\frac{d\omega _{2}}{2\omega _{2}^{2}}}\nonumber \\{} & {} \times \int {D^{3}zD^{3}{\bar{z}}}exp(-S_{spatial})J(t,\omega _1,\omega _{2}),\nonumber \\ \end{aligned}$$

(A2.5)

$$\begin{aligned} J(t,\omega _1,\omega _{2})= & {} \frac{2\sqrt{\omega _{1}\omega _{2}}}{4\pi t }\vartheta _3(e^{-\frac{\omega _{1}}{2tT^2}})\vartheta _3(e^{-\frac{\omega _{2}}{2tT^2}}), \end{aligned}$$

(A2.6)

and according to [53] we can average Wilson line over the “euclidean time direction”. Thus we obtain:

$$\begin{aligned} G^{2g}(t,T)= & {} \frac{t}{8\pi } \int ^\infty _0 \frac{d\omega _1}{\omega _1^{3/2}} \int ^\infty _0 \frac{d\omega _2}{\omega _2^{3/2}}\int { (D^2z_1)_{xy}(D^2{\bar{z}}_2)_{xy}}\nonumber \\{} & {} \times e^{-\sum _{i=1,2}K_{i}(\omega _{i})-Vt}\vartheta _3\big (e^{-\frac{\omega _{1}}{2tT^2}}\big )\vartheta _3\big (e^{-\frac{\omega _{2}}{2tT^2}}\big ),\nonumber \\ \end{aligned}$$

(A2.7)

here label xy means xy-plane. For $K_i(\omega _i),i,j=1,2$:

$$\begin{aligned} K_i(\omega _i)= \int ^{t}_{0}d\tau _{E}\bigg (\frac{\omega _{i}}{2}+\frac{\omega _{i}}{2}\bigg (\frac{dx_{j}}{d\tau _{E}}\bigg )^{2}\bigg ). \end{aligned}$$

(A2.8)

The potential of interaction between gluons themselves and gluons with adjoint source reads as:

$$\begin{aligned} V(z,{\bar{z}})=\sigma _{f}(|{z}|+|{{\bar{z}}}|+|{z}-{{\bar{z}}}|), \end{aligned}$$

(A2.9)

$\sigma _{f}$ – is string tension in the fundamental representation. We can construct the three-body Hamiltonian in the exponent of the Eq. (A2.7) in the 2d spatial coordinates:

$$\begin{aligned} H(\omega _1, \omega _2) = \frac{ \omega _1^2+ {p}^2_1}{2\omega _1}+ \frac{ \omega _2^2+ {p}^2_2}{2\omega _2}+ V({z}, {{\bar{z}}}). \end{aligned}$$

(A2.10)

If we obtain the spectrum of Eq. (A2.10) we can rewrite the Eq. (A2.7) as follows (see [21]):

$$\begin{aligned} G^{(2g)}(t)= & {} \frac{t}{8\pi } \int ^\infty _0 \frac{d\omega _1}{\omega _1^{3/2}} \int ^\infty _0 \frac{d\omega _2}{\omega _2^{3/2}} \nonumber \\{} & {} \times \sum ^\infty _{n=0} |\psi _n (0,0)|^2 e^{-M_n (\omega _1,\omega _2) t}. \end{aligned}$$

(A2.11)

Here $\Psi _n(0,0)\equiv \Psi _n ({\varvec{\textrm{z}}}_1,{\varvec{\textrm{z}}}_2)|_{{\varvec{\textrm{z}}}_1={\varvec{\textrm{z}}}_2=0}$, and $M_n$ is the eigenvalue of $H(\omega _1, \omega _2)$. The latter was studied in Ref. [8] in three spatial coordinates. For our purpose here we only mention that the integral in Eq. (39) is dimensionless. One can note that procedure described above implies possibility of representation of 4d gluon propagator at sufficiently large temperatures in the form:

$$\begin{aligned} G_{4d}^{(g)}(z,T) = T G_{3d}^{(g)}(z)+K_{3d}(z). \end{aligned}$$

(A2.12)

Appendix A3: Diagonalization of gluelump Hamiltonian

We can argue that the Hamiltonian in Eq. (A2.10) describes two non-interacting oscillators. Using standard technique we can rewrite it in the form:

$$\begin{aligned} H= & {} \frac{\omega ^2_1 + {\varvec{\textrm{p}}}^2_1}{2\omega _1} + \frac{\omega ^2_2 + {\varvec{\textrm{p}}}^2_2}{2\omega _2} + \frac{\sigma _{f}^2{\varvec{\textrm{z}}}^{2}}{2 \nu _{1}} + \frac{\sigma _{f}^2 {\bar{{\varvec{\textrm{z}}}}}^2}{2 \nu _{2}} \nonumber \\{} & {} + \frac{\sigma _{f}^2 ({\varvec{\textrm{z}}}-{\bar{{\varvec{\textrm{z}}}}})^2}{2 \nu _{3}} + \frac{\nu _{1}+\nu _{2}+\nu _{3}}{2}. \end{aligned}$$

(A3.1)

Canonical transformation of coordinates reads as:

$$\begin{aligned} {z}={x}+a {y}, \bar{{z}}=b{x}+ {y} , \end{aligned}$$

(A3.2)

and for momentums:

$$\begin{aligned} {p_{1}}=c \varvec{\pi }_{x}+ d \varvec{\pi }_{y},{p_{2}}=e \varvec{\pi }_{x}+ f \varvec{\pi }_{y} , \end{aligned}$$

(A3.3)

where a, b, c, d – are some parameters that we need to calculate. Momentum and coordinates obey the relations:

$$\begin{aligned}{}[p_{1,i},z_{j}]= & {} -i\delta _{ij},[p_{2,i},{\bar{z}}_{j}]=-i\delta _{ij},[p_{2,i},z_{j}]\nonumber \\= & {} 0,[p_{1,i},{\bar{z}}_{j}]=0, \end{aligned}$$

(A3.4)

$$\begin{aligned}= & {} -i\delta _{\alpha x}\delta _{ij},[\pi _{\alpha ,i},y_{j}]=-i\delta _{\alpha y}\delta _{ij}. \end{aligned}$$

(A3.5)

To define coefficients in Eqs. (A3.2), (A3.3) we can substitute them into commutation relations and in the Hamiltonian Eq. (A3.1). Requiring of vanishing of the cross terms (${\pi _{x}}{\pi _{y}}, {x}{y}$) we obtain:

$$\begin{aligned} \omega _{1}a+\omega _{2}b=0, \nu _{1}^{-1}a+\nu _{2}^{-1}b=(a-1)(b-1)\nu _{3}^{-1}.\nonumber \\ \end{aligned}$$

(A3.6)

For coefficients in Eqs. (A3.2), (A3.3) we have:

$$\begin{aligned} c+ad= & {} 1,bc+d=0 , \end{aligned}$$

(A3.7)

$$\begin{aligned} e+af= & {} 0,be+f=1 , \end{aligned}$$

(A3.8)

thus:

$$\begin{aligned} c=\frac{1}{1-ab},d=\frac{b}{ab-1}, f=\frac{1}{1-ab},e=-\frac{a}{1-ab}.\nonumber \\ \end{aligned}$$

(A3.9)

And for the Hamiltonian we have:

$$\begin{aligned} H= & {} \bigg (\frac{c^{2}}{2\omega _{1}}+\frac{e^{2}}{2\omega _{2}}\bigg )\varvec{\pi _{x}^{2}}+\bigg (\frac{d^{2}}{2\omega _{1}}+\frac{f^{2}}{2\omega _{2}}\bigg )\varvec{\pi ^{2}_{y}}+V({x},{y}),\nonumber \\ \end{aligned}$$

(A3.10)

$$\begin{aligned} V({x},{y})= & {} \frac{\sigma _{f}}{2}\bigg ({x}^{2}\bigg (\frac{1}{\nu _{1}}+\frac{b^2}{\nu _{2}}+\frac{(1-b)^{2}}{\nu _{3}}\bigg )\nonumber \\{} & {} +{y}^{2}\bigg (\frac{a^{2}}{\nu _{1}}+\frac{1}{\nu _{2}}+\frac{(1-a)^{2}}{\nu _{3}}\bigg )\bigg ). \end{aligned}$$

(A3.11)

This is the Hamiltonian that describes two non-interacting two-dimensional oscillators and thus we can easily obtain its spectrum. Minimizing Eq. (A3.10) with respect to $\omega _{1},\omega _{2},\nu _{1},\nu _{2},\nu _{3}$ we will obtain gluelump spectrum in the next section.

Appendix A4: Numerical calculation of gluelump eigenvalues and eigenfunctions in the lowest approximation

We calculate here eigenvalues and eigenfunctions of the Hamiltonian in the Eq. (A2.10). We start from the expression:

$$\begin{aligned} H= & {} \frac{\omega ^2_1 + {p}^2_1}{2\omega _1} + \frac{\omega ^2_2 + {\varvec{\textrm{p}}}^2_2}{2\omega _2} + \frac{\sigma _{f}^2{\varvec{\textrm{z}}}^{2}}{2 \nu _{1}} \nonumber \\{} & {} + \frac{\sigma _{f}^2 {\bar{{\varvec{\textrm{z}}}}}^2}{2 \nu _{2}} + \frac{\sigma _{f}^2 ({\varvec{\textrm{z}}}-{\bar{{\varvec{\textrm{z}}}}})^2}{2 \nu _{3}} + \frac{\nu _{1}+\nu _{2}+\nu _{3}}{2}. \end{aligned}$$

(A4.1)

For simplicity we assume that $\omega _1 =\omega _2=\omega$, $\nu _1 = \nu _2 =\nu _3 =\nu$.⁵ We calculate all quantities in Eqs. (A3.2), (A3.3) and obtain mass of the lowest two-gluelump:

$$\begin{aligned} E=(\sqrt{3}+1)\frac{\sigma _{f}}{\sqrt{\omega \nu }}+\frac{3\nu }{2}+{\omega }. \end{aligned}$$

(A4.2)

The conditions of minima yields the final result with notation $\omega ,\nu$ for the extremal values. At final step we obtain⁶:

$$\begin{aligned} M\approx 5.53 \sqrt{\sigma _{f}}. \end{aligned}$$

(A4.3)

As for the eigenfunctions, they are given by the product of the eigenfunctions of two non-interacting two-dimensional oscillators. That means that we can obtain all eigenvalues and eigenfunctions that we need in Eq. (39).

Appendix A5: Gluelumpls Green functions

See Figs. 4 and 5.

Fig. 4

Two-gluelump Green function. Continuous and dashed lines are gluons trajectories. Bold straight line is trajectory of adjoint source. Shaded domain is x–y plane that is perpendicular to z axes. Sides of shaded triangle are fundamental strings

Fig. 5

One-gluelump Green function. Bold straight line is trajectory of adjoint source that interacts with gluon (dashed line) through adjoint string)