1 Introduction

In 1918, Hermann Weyl [1,2,3,4,5] attempted to unify the theory of general relativity (GR) with electromagnetism. In this theory of gravity, the metric transforms under a conformal transformation \(g_{\mu \nu }\rightarrow \Omega ^{2}(x)g_{\mu \nu }\) whenever the electromagnetic field undergoes a gauge transformation \(A_{\mu }\rightarrow A_{\mu }-\partial _{\mu }\log (\Omega (x))\), where \(\Omega (x)\) is the local spacetime stretching. Consequently, the covariant derivative in Weyl’s theory no longer preserves the metric, and as a result, Weyl’s theory of gravity never became a serious competitor for GR. However, Bach [6] derived a different theory of conformal gravity in 1921, whose action is constructed from contractions and squares of the Weyl tensor \({{\mathcal {C}}}_{\mu \nu \rho \sigma }\) in four dimensions which is conformally invariant, and it is usually called Weyl or Weyl-squared gravity. It is important to point out that in four dimensions, the Weyl-squared action is a unique conformally invariant action constructed solely from the Weyl tensor. On the other hand, the action of the theory gives rise to fourth-order equations of motion for the gravitational field which make it difficult to reconcile it with Newtonian gravity. One of the immediate consequences of postulating a gravitational theory with conformal invariance is that the artificially implanted cosmological constant, \(\Lambda \), present in the Einstein–Hilbert action must be withdrawn, since to not do so would introduce a length scale that breaks the conformal symmetry of the theory. However, the same term will naturally emerge out of the metric, which provides further circumstantial evidence for the effectiveness of the principle under consideration.

Despite the absolute success of the GR theory, it fails to describe observations on scales much higher than the solar system without the presence of a large amount of dark matter; however, the absence of any direct experimental evidence for dark matter [7] has led to the consideration of various modified theories of gravity, among which is conformal Weyl gravity, which may not require a dark matter component to explain the astrophysical data. The static and spherically symmetric vacuum solution describing a black hole was obtained by Mannheim and Kazanas [8], where a particular parameter of the solution can explain the flat rotation of galaxies without introducing dark matter. Also, the theory is intended to cover dark energy-related phenomena [9, 10]. Moreover, three new exact solutions of this four-order theory were found: the Reissner–Nordström, Kerr, and Kerr–Newmann solutions [11]. Other solutions of conformal Weyl gravity can be found in [12,13,14,15,16,17].

In the context of the detection of gravitational waves [18], the detected signal is also consistent with GR [19]. However, there are possibilities for alternative theories of gravity due to the large uncertainties in mass and angular momenta of the ringing black hole [20]. Therefore, the study of quasinormal modes (QNMs) and quasinormal frequencies (QNFs) [21,22,23,24,25,26] nowadays plays an important role. QNMs and QNFs give information about the stability of matter fields that evolve perturbatively in the exterior region of a black hole without back-reacting on the metric. Also, the QNMs are characterized by a spectrum that is independent of the initial conditions of the perturbation and depends on the black hole parameters, the probe field parameters, and the fundamental constants of the system. QNFs are an infinite discrete spectrum of complex frequencies in which the real part determines the oscillation timescale of the modes, while the complex part determines their exponential decay timescale; for a review on QNMs see [23, 26].

The tensor QNM spectrum for the Schwarzschild and Kerr black hole backgrounds shows that the longest-lived modes are always the ones with lower angular numbers. This can be understood from the fact that the more energetic modes with high angular numbers would have faster decay rates. However, for the propagation of a massive scalar field, a different behaviour was found [27,28,29,30], at least for the fundamental mode. If the mass of the scalar field is light, then the longest-lived QNMs are those with a high angular number, whereas if the mass of the scalar field is large, the longest-lived modes are those with a low angular number. This behaviour, known as an anomalous decay rate, is expected, since if the probe scalar field is massive, its fluctuations can maintain the QNMs to live longer even if the angular number is large. This behaviour of the QNMs introduces an anomaly of the decay modes which depends on whether the mass of the scalar field exceeds a critical value. Thus, by introducing another scale in the theory through the presence of a cosmological constant, anomalous behaviour of QNMs was found in [31] as a result of the interplay of the mass of the scalar field and the value of the cosmological constant. Anomalous decay rates of QNMs were also found if the background metric was the Reissner–Nordström and the probe scalar field was massive [32] or massive and charged [33], depending on the critical values of the charge of the black hole,the charge of the scalar field, and its mass. The presence of anomalous behaviour for a generalized Bronnikov–Ellis wormhole and a Morris–Thorne wormhole was studied in Ref. [34]. The anomalous decay rate of QNMs has been studied in various setups; see [35,36,37,38,39,40].

The aim of this work is to study the propagation of massive scalar fields in Weyl black hole backgrounds in order to study the effect of the scalar field mass in such propagation. Issues that we will address include the anomalous decay rate of QNMs, as well as whether there is a critical scalar field mass. We will also study the dominance between the family of modes in order to determine whether the dominant family suffers such anomalous behaviour. It is worth mentioning that massless scalar field perturbations, dynamical evolution, and Hawking radiation were recently studied for this spacetime, and it was shown that the propagation of massless scalar fields is stable. Also, it was established that the dominance between the two families of modes was dependent on the parameter \(\lambda \), with the photon sphere (PS) modes being dominant for small \(\lambda \). However, as \(\lambda \) increases, the imaginary part of the PS mode decreases, whereas the de Sitter (dS) mode increases [41]. The parameter \(\lambda \) has been considered in dark energy scenarios and plays a role as the inverse proportion of the cosmological constant. In addition, the behaviour of the QNMs was used to study the thermal stability of black holes in conformal Weyl gravity, comparing these results with Schwarzschild black holes [42]. In the particular case of a near-extremal black hole in Weyl gravity, the correspondence between the parameters of the circular null geodesic and the QNFs in the eikonal limit was demonstrated in [43], and the QNMs of the gravitational and electromagnetic perturbations on a black hole in (exact) Weyl gravity were calculated and studied in [44]. Important theorems on photon spheres were proved in the comprehensive article by [45], and the implications of the photon sphere for gravitational lensing can be found in [46]. The spacetime considered was recently investigated regarding the motion of massless, neutral massive, and electrically charged particles [47,48,49,50].

The remainder of the manuscript is organized as follows: In Sect. 2, we provide a brief review of Weyl black holes. Then, in Sect. 3, we study massive scalar perturbations in the background of Weyl black holes. In Sect. 4, we consider the PS modes and find the critical scalar field mass, and we also show the anomalous behaviour of the decay rate using the WKB method. Then, we analyse the dS modes via the pseudo-spectral Chebyshev method, and we study the dominant family modes. Finally, we conclude in Sect. 5.

2 Four-dimensional Weyl black holes

The action of four-dimensional Weyl gravity is given by [8]

$$\begin{aligned} S=-\alpha \int \textrm{d}^{4}x\sqrt{-g}C_{\mu \nu \rho \sigma }C^{\mu \nu \rho \sigma }+ I_{M}~, \end{aligned}$$
(1)

where \(\alpha \) is a dimensionless gravitational coupling constant which is usually chosen to be positive in order to satisfy the Newtonian lower limit, \(I_{M}\) is the matter part of the action, and \(C_{\mu \nu \rho \sigma }\) is the Weyl tensor given by

$$\begin{aligned} C_{\mu \nu \rho \sigma }= & {} R_{\mu \nu \rho \sigma }+\frac{R}{6}\left( g_{\mu \rho }g_{\nu \sigma }-g_{\mu \sigma }g_{\nu \rho }\right) \nonumber \\{} & {} -\frac{1}{2}\left( g_{\mu \rho }R_{\nu \sigma }-g_{\mu \sigma }R_{\nu \rho }-g_{\nu \rho }R_{\mu \sigma }+g_{\nu \sigma }R_{\mu \rho }\right) ,\nonumber \\ \end{aligned}$$
(2)

which satisfies the conformal invariance condition

$$\begin{aligned} C_{\mu \nu \rho \sigma }\rightarrow {\tilde{C}}_{\mu \nu \rho \sigma }=\Omega ^{2}(x)C_{\mu \nu \rho \sigma }. \end{aligned}$$
(3)

By using the definition of the Weyl tensor and making use of the Gauss–Bonnet theorem, it is possible to express the action (1) in the following form:

$$\begin{aligned} S=-\alpha \int \textrm{d}^{4}x\sqrt{-g}\left( R^{\mu \nu }R_{\mu \nu }-\frac{1}{3}R^{2}\right) + I_{M}. \end{aligned}$$
(4)

This theory of gravity is governed by field equations that can be derived by the functional variation of the action with respect to the metric \(g_{\mu \nu }\) and take the following form:

$$\begin{aligned} W_{\mu \nu }= & {} 2C^\rho \,_{\mu \nu }\,{}^\sigma {}_{;\alpha \sigma }+C^\rho \,_{\mu \nu }{}^{\sigma }R_{\rho \sigma }\nonumber \\= & {} \nabla ^{\rho }\nabla _{\mu }R_{\nu \rho }+\nabla ^{\rho }\nabla _{\nu }R_{\mu \rho }-\square R_{\mu \nu }-g_{\mu \nu }\nabla _{\rho }\nabla _{\sigma }R^{\rho \sigma }\nonumber \\{} & {} -2R_{\rho \nu }R^{\rho }_{\mu }+\frac{1}{2}g_{\mu \nu }R_{\rho \sigma }R^{\rho \sigma }\nonumber \\{} & {} -\frac{1}{3}\left( 2\nabla _{\mu }\nabla _{\nu }R-2g_{\mu \nu }\square R-2R R_{\mu \nu }+\frac{1}{2}g_{\mu \nu }R^{2}\right) \nonumber \\= & {} \frac{1}{4\pi }T_{\mu \nu }, \end{aligned}$$
(5)

where \(W_{\rho \sigma }\) is the Bach tensor. It is important to note from (5) that in vacuum \(T_{\mu \nu }=0\) \((W_{\mu \nu }=0)\), every solution \(R_{\mu \nu }=0\) in Einstein–Hilbert action also leads to a solution in Weyl gravity; however, not every vacuum solution from Weyl gravity implies a solution for GR. The first static and spherically symmetric vacuum solution describing a black hole in this theory was obtained by Mannheim and Kazanas [8]. The lapse function, used in the line element, is given by

$$\begin{aligned} f(r)=1-3\beta \gamma -\frac{2\beta -3\gamma \beta ^{2}}{r}+\gamma r-k r^{2}, \end{aligned}$$
(6)

where the parameters \(\beta \), \(\gamma \), and k are integration constants. In this solution, the parameter \(\gamma \) measures the departure of Weyl theory from GR, and so for a sufficiently small measure, the two theories have similar predictions. On the other hand, it was argued that Weyl gravity can explain the flat rotation of galaxies without introducing dark matter, for which \(\gamma \) must be of the order of the inverse of the Hubble radius (\(\gamma \approx \frac{1}{R_{H}}\)) [8]. It is important to point out that this solution reduces to Schwarzschild black holes when \(k=\gamma =0\) and to Schwarzschild–de Sitter black holes if \(\gamma =0\).

In [11], the authors extended their first work [8] and presented the exact solution to the Reissner–Nordström problem associated with a static, spherically symmetric point electric and/or magnetic charge coupled to Weyl gravity. The charged black hole solution is given by

$$\begin{aligned} f(r)= 1-3\beta \gamma -\frac{2\beta -3\gamma \beta ^{2}}{r}+\gamma r-k r^{2}-\frac{Q^{2}}{8 r\alpha \gamma }, \end{aligned}$$
(7)

where Q is the electric charge, and the electrostatic vector potential considered is \(A_\mu = (Q/r,0,0,0)\). As noted by the authors, the first principal difference from the Reissner Nordström solution in standard Einstein theory is that the effect of the electromagnetic energy of a point electric charge is to produce a 1/r term in the exterior geometry of the black holes rather than the \(1/r^2\) term present in GR. The second difference is that the geometry is not asymptotically conformally flat.

In this work, we consider an alternative charged Weyl black hole solution [51] constructed using the background field method and linear approximation [52]. The RN-like solution of Weyl gravity in the presence of a charged source is given by [51]

$$\begin{aligned} \textrm{d}s^{2}=-f(r)\textrm{d}t^{2}+f^{-1}(r)\textrm{d}r^{2}+r^2 \textrm{d} \Omega ^2, \end{aligned}$$
(8)

where \(d\Omega ^{2}\) is the line elements of the 2-sphere, and the lapse function is

$$\begin{aligned} f(r)=1-\frac{r^2}{\lambda ^{2}}-\frac{Q^2}{4r^2}, \end{aligned}$$
(9)

where \(\lambda \) and Q are the black hole parameters, and the term \(r^2/\lambda ^2\) is related to the dark energy scenario. Also, the electrostatic vector potential considered is \(A_\mu = (Q/r,0,0,0)\). It should be noted that its attractive inverse square potential is due to the charged body, instead of the repulsion in the Reissner–Nordström–de Sitter black hole. For \(\lambda >Q\), the roots of the lapse function are

$$\begin{aligned}{} & {} r_{h}=\lambda \sin {\left( \frac{1}{2}\arcsin {\left( \frac{Q}{\lambda }\right) }\right) }~,\,\, \text {and} \nonumber \\{} & {} r_{c}=\lambda \cos {\left( \frac{1}{2}\arcsin {\left( \frac{Q}{\lambda }\right) }\right) }~.\,\, \end{aligned}$$
(10)

The extremal black hole is obtained when \(\lambda =Q\), and both horizons coalesce to \(r_{ext}=\frac{\lambda }{\sqrt{2}}\). On the other hand, for \(\lambda <Q\), a naked singularity is encountered. In Fig. 1 we plot the lapse function, where for a fixed value of the black hole charge \(Q=1\), it is possible to observe the transition among a naked singularity \(\lambda =0.5\), the extremal black hole \(\lambda =1\), and a black hole with two horizons \(\lambda > 1\).

Fig. 1
figure 1

The behaviour of f(r) with \(Q=1\), and different values of \(\lambda \)

Full size image

3 Massive scalar field perturbations

In order to obtain the QNMs of scalar field perturbations in the background of the metric (9), we consider the Klein–Gordon equation

$$\begin{aligned} \Box \psi = \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g} g^{\mu \nu }\partial _{\nu }\right) \psi =m^2\psi ~, \end{aligned}$$
(11)

with suitable boundary conditions, that is, only ingoing waves on the horizon and on the cosmological horizon. In the expression above, m is the mass of the scalar field \(\psi \). It is worth mentioning that the Weyl tensor is traceless, which implies that the stress–energy tensor of the matter fields must be traceless too. However, for a probe field, it is not actually necessary to respect the same symmetries of the Weyl tensor.

Now, by means of the ansatz \(\psi =e^{-i\omega t} Y_{l,m}(\theta ,\phi ) R(r)\), the Klein–Gordon equation (11) can be written as

$$\begin{aligned} \frac{1}{r^{2}}\frac{\textrm{d}}{\textrm{d}r}\left( r^{2} f(r)\frac{\textrm{d}R}{\textrm{d}r}\right) +\left( \frac{\omega ^2}{f(r)}+\frac{\kappa ^2}{r}-m^{2} \right) R(r)=0, \nonumber \\ \end{aligned}$$
(12)

where \(\kappa ^2 = -l(l+1)\), with \(l = 0, 1, 2,\ldots \) representing the eigenvalues of the Laplacian on the 2-sphere, and l the multipole number or the angular momentum of the field. Now, defining \(R(r) =\frac{F (r)}{r}\) and the tortoise coordinate \(\textrm{d}r^{*} =\frac{\textrm{d}r}{f(r)}\), the wave equation can be written as a one-dimensional Schrödinger-like equation given by

$$\begin{aligned} -\frac{\textrm{d}^{2}F(r^*)}{\textrm{d}r^{*2}}+V_{eff}(r)F(r^*)=\omega ^{2}F(r^*), \end{aligned}$$
(13)

with an effective potential \(V_{eff}(r)\), which is parametrically considered as \(V_{eff}(r^*)\), and it is given by

$$\begin{aligned} V_{eff}(r) =\frac{\left( -\frac{{\tilde{Q}}^2}{4 {\tilde{r}}^2}-{\tilde{r}}^2+1\right) \left( l^2+l+{\tilde{r}}^2 \left( {\tilde{m}}^{2}-2\right) +\frac{{\tilde{Q}}^2}{2 {\tilde{r}}^2}\right) }{\lambda ^2 {\tilde{r}}^2},\nonumber \\ \end{aligned}$$
(14)

where we have defined the dimensionless quantities \({\tilde{r}} \equiv r/\lambda \), \({\tilde{Q}} \equiv Q /\lambda \), and \({\tilde{m}} \equiv \lambda m\). In Fig. 2, we show the effective potential for fixed values of the parameter \({\tilde{Q}}\), different values of the angular number l, and a mass \(m=0.1\) of the scalar field. It can be seen that for \(l=0\), part of the effective potential is negative, and when l increases, the height of the potential barrier increases. However, when the parameter \({\tilde{Q}}\) increases, the height of the potential barrier decreases. It is worth noting that by means of the identification \(\lambda =\sqrt{\frac{3}{\Lambda _{eff}}}\), the effective spacetime potential is asymptotically de Sitter and tends to \(-\frac{r^{2}}{\lambda ^{4}}(m^2\lambda ^{2}-2)\) for \(l=0\), reproducing the result obtained in [31].

Fig. 2
figure 2

The behaviour of \(V_{eff}({\tilde{r}})\lambda ^2\) for a massive scalar field with \(m=0.1\). The left panel is for \({\tilde{Q}}=0.50\), \({\tilde{r}}_h\approx 0.259\), and \({\tilde{r}}_c\approx 0.966\), and the right panel is for \({\tilde{Q}}=0.75\), \({\tilde{r}}_h\approx 0.411\), and \({\tilde{r}}_c\approx 0.911\)

Full size image

4 Quasinormal modes

4.1 Photon sphere modes

Anomalous decay rate and an approach to the critical scalar field mass. In order to gain analytical insight into the behaviour of the QNFs, and to determine the critical scalar field mass, we use the WKB method at third order [53,54,55,56,57,58]. The WKB method can be used for effective potentials which have the form of a barrier potential, approaching a constant value at the event horizon and at the cosmological horizon or spatial infinity [25]. Here, we consider the eikonal limit \(l \rightarrow \infty \) to estimate the critical scalar field mass by considering \(\omega _I^l=\omega _I^{l+1}\) as a proxy for where the transition or critical behaviour occurs [59]. The QNMs are determined by the behaviour of the effective potential near its maximum value \(r^*_{\textrm{max}}\). The Taylor series expansion of the potential around its maximum is given by

$$\begin{aligned} V(r^*)= V(r^*_{\textrm{max}})+ \sum _{i=2}^{\infty } \frac{V^{(i)}}{i!} (r^*-r^*_{\textrm{max}})^{i}, \end{aligned}$$
(15)

where

$$\begin{aligned} V^{(i)}= \frac{\textrm{d}^{i}}{\textrm{d} r^{*i}}V(r^*)|_{r^*=r^*_{\textrm{max}}} \end{aligned}$$
(16)

corresponds to the ith derivative of the potential with respect to \(r^*\) evaluated at the location of the maximum of the potential. Using the WKB approximation up to third order, the QNFs are given by the following expression [60]:

$$\begin{aligned} \omega ^2= & {} V(r^*_{\textrm{max}}) -2 i U, \end{aligned}$$
(17)

where

$$\begin{aligned} U= & {} N\sqrt{-V^{(2)}/2}\\{} & {} +\frac{i}{64} \left( -\frac{1}{9}\frac{V^{(3)2}}{V^{(2)2}} (7+60N^2)+\frac{V^{(4)}}{V^{(2)}}(1+4 N^2) \right) \\{} & {} +\frac{N}{2^{3/2} 288} \Bigg ( \frac{5}{24} \frac{V^{(3)4}}{(-V^{(2)})^{9/2}} (77+188N^2) \\{} & {} +\frac{3}{4} \frac{V^{(3)2} V^{(4)}}{(-V^{(2)})^{7/2}}(51+100N^2) \\{} & {} +\frac{1}{8} \frac{V^{(4)2}}{(-V^{(2)})^{5/2}}(67+68 N^2)\\{} & {} +\frac{V^{(3)}V^{(5)}}{(-V^{(2)})^{5/2}}(19+28N^2)+\frac{V^{(6)}}{(-V^{(2)})^{3/2}} (5+4N^2) \Bigg ), \end{aligned}$$

and \(N=n_{\textrm{PS}}+1/2\), where \(n_{\textrm{PS}}=0,1,2,\dots \) is the overtone number. Now, defining \(L^2= l (l+1)\), we find that for large values of L, the maximum of the potential is at approximately

$$\begin{aligned} \frac{r_{\textrm{max}}}{\lambda }\approx \frac{-\sqrt{2} {\tilde{m}}^2 {\tilde{Q}}^5+\sqrt{2} {\tilde{m}}^2 {\tilde{Q}}^3+2 \sqrt{2} {\tilde{Q}}^5-2 \sqrt{2} {\tilde{Q}}}{16 L^2}+\frac{{\tilde{Q}}}{\sqrt{2}},\nonumber \\ \end{aligned}$$
(18)

and

$$\begin{aligned} \lambda ^2 V(r^*_{\textrm{max}})\approx & {} \left( \frac{1}{{\tilde{Q}}^2}-1 \right) L^{2}\nonumber \\ {}{} & {} +\left( -2-\frac{ {\tilde{m}}^2 {\tilde{Q}}^2}{2}+\frac{{\tilde{m}}^2}{2}+{\tilde{Q}}^2+\frac{1}{{\tilde{Q}}^2}\right) , \end{aligned}$$
(19)

while the second derivative of the potential evaluated at \(r^*_{\textrm{max}}\) yields

$$\begin{aligned}{} & {} \lambda ^4 V^{(2)}(r^*_{\textrm{max}})\nonumber \\{} & {} \quad \approx \frac{\left( 1-{\tilde{Q}}^2\right) ^2 \left( -6-3 {\tilde{m}}^2 {\tilde{Q}}^4+{\tilde{m}}^2 {\tilde{Q}}^2+6 {\tilde{Q}}^4\right) }{{\tilde{Q}}^4}\nonumber \\{} & {} \qquad -\frac{L^2 \left( 4 \left( {\tilde{Q}}^2-1\right) ^2\right) }{{\tilde{Q}}^4}. \end{aligned}$$
(20)

For the higher derivatives of the potential, we consider only the leading terms that are important in the limit considered. Therefore,

$$\begin{aligned} \lambda ^5 V^{(3)}(r^*_{\textrm{max}}){} & {} \approx -\frac{L^2 \left( 6 \sqrt{2} \left( -1+{\tilde{Q}}^6-3{\tilde{Q}}^4+3 {\tilde{Q}}^2\right) \right) }{{\tilde{Q}}^5}, \end{aligned}$$
(21)
$$\begin{aligned} \lambda ^6V^{(4)}(r^*_{\textrm{max}}){} & {} \approx L^2 \left( -40+\frac{58}{{\tilde{Q}}^6}-\frac{168}{{\tilde{Q}}^4}-6 {\tilde{Q}}^2+\frac{156}{{\tilde{Q}}^2}\right) ,\end{aligned}$$
(22)
$$\begin{aligned} \lambda ^7 V^{(5)}(r^*_{\textrm{max}}){} & {} \approx -\frac{L^2 \left( 360 \sqrt{2} \left( 1+{\tilde{Q}}^8-4 {\tilde{Q}}^6+6 {\tilde{Q}}^4-4 {\tilde{Q}}^2\right) \right) }{{\tilde{Q}}^7},\nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} \lambda ^8 V^{(6)}(r^*_{\textrm{max}}){} & {} \approx L^2 \left( 6344-\frac{472}{{\tilde{Q}}^8}+\frac{184}{{\tilde{Q}}^6}+\frac{3984}{{\tilde{Q}}^4}\right. \nonumber \\{} & {} \quad \left. -1704 {\tilde{Q}}^2-\frac{8336}{{\tilde{Q}}^2}\right) . \end{aligned}$$
(24)

Now, using these results, we find that U evaluated at \(r^*_{\textrm{max}}\) is approximately given by

$$\begin{aligned} \lambda ^2 U\approx & {} \frac{B\left( n_{\textrm{PS}}+\frac{1}{2}\right) }{\sqrt{2}}+\frac{1}{576\sqrt{2}}\left( n_{\textrm{PS}}+\frac{1}{2}\right) \nonumber \\{} & {} \times \Bigg (\frac{1080L^{8}\left( 77+188\left( n_{\textrm{PS}}+\frac{1}{2}\right) ^{2}\right) ({\tilde{Q}}^{2}-1)^{12}}{{\tilde{Q}}^{20}B^{9}}\nonumber \\{} & {} -\frac{108 L^6 \left( 100 \left( n_{\textrm{PS}}+\frac{1}{2}\right) ^2+51\right) \left( {\tilde{Q}}^2-1\right) ^9 \left( 29+3 {\tilde{Q}}^2\right) }{B^7 {\tilde{Q}}^{16}}\nonumber \\{} & {} +\frac{4 L^4 \left( 68 \left( n_{\textrm{PS}}+\frac{1}{2}\right) ^2+67\right) \left( {\tilde{Q}}^2-1\right) ^6 \left( 29 +3 {\tilde{Q}}^2\right) ^2}{8B^{5} {\tilde{Q}}^{12}}\nonumber \\{} & {} +\frac{4320 L^{4} \left( 28\left( n_{\textrm{PS}}+\frac{1}{2}\right) ^2+19\right) \left( {\tilde{Q}}^{2}-1\right) ^7}{B^{5} {\tilde{Q}}^{12}}\nonumber \\{} & {} -\frac{L^2 \left( 4 \left( n_{\textrm{PS}}+\frac{1}{2}\right) ^{2}+5\right) \left( {\tilde{Q}}^{2}-1\right) ^{4} \left( 59 +213 {\tilde{Q}}^{2}\right) }{B^{3} {\tilde{Q}}^{8}}\Bigg )\nonumber \\{} & {} +\frac{i}{64}\left( -\frac{8 L^{4}\left( 60\left( n_{\textrm{PS}}+\frac{1}{2}\right) ^{2}+7\right) \left( {\tilde{Q}}^{2}-1\right) ^{6}}{B^4 {\tilde{Q}}^{10}}\right. \nonumber \\{} & {} \left. +\frac{2 L^{2} \left( 4\left( n_{\textrm{PS}}+\frac{1}{2}\right) ^{2}+1\right) \left( {\tilde{Q}}^{2}-1\right) ^{3} \left( 29 +3 {\tilde{Q}}^{2}\right) }{B^2 {\tilde{Q}}^{6}}\right) ,\nonumber \\ \end{aligned}$$
(25)

where \(B \equiv \frac{\left( {\tilde{Q}}^2-1\right) \sqrt{\left( 2 \left( 2\,L^2+3\right) +3 {\tilde{Q}}^4 \left( {\tilde{m}}^2-2\right) -{\tilde{m}}^2 {\tilde{Q}}^2\right) }}{{\tilde{Q}}^2}\). So, using these results together with Eq. (17), we obtain the following analytical QNF that is valid for large values of L:

$$\begin{aligned} {\tilde{\omega }} \equiv \lambda \omega \approx {\tilde{\omega }}_{1m}L+{\tilde{\omega }}_{0}+{\tilde{\omega }}_{1}L^{-1}+{\tilde{\omega }}_{2}L^{-2}, \end{aligned}$$
(26)

where

$$\begin{aligned}{} & {} {\tilde{\omega }}_{1m}=\frac{\sqrt{1-{\tilde{Q}}^{2}}}{{\tilde{Q}}},\,\, {\tilde{\omega }}_{0}=\frac{i\left( -1-2n_{\textrm{PS}}+2n_{\textrm{PS}} {\tilde{Q}}^{2}+ {\tilde{Q}}^{2}\right) }{{\tilde{Q}}\sqrt{2}\sqrt{1-{\tilde{Q}}^2}}, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} {\tilde{\omega }}_{1}=\frac{\sqrt{1-{\tilde{Q}}^2} \left( \left( 2 {\tilde{m}}^2 {\tilde{Q}}^2-3 n_{\textrm{PS}} (n_{\textrm{PS}}+1)+1\right) +3 \left( n_{\textrm{PS}}(n_{\textrm{PS}}+1) -1\right) {\tilde{Q}}^2\right) }{8 {\tilde{Q}}}, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} {\tilde{\omega }}_{2}=\frac{i (2 n_{\textrm{PS}}+1) \left( 1-{\tilde{Q}}^2\right) ^{3/2} \left( {\tilde{Q}}^2 \left( 48 {\tilde{m}}^2+17 n_{\textrm{PS}} (n_{\textrm{PS}}+1)-87\right) - (17 n_{\textrm{PS}} (n_{\textrm{PS}}+1)+9)\right) }{128 \sqrt{2} {\tilde{Q}}}. \end{aligned}$$
(29)

Now, the term proportional to \(1/L^{2}\) is zero at the value of the critical mass \({\tilde{m}}_{c}\), which is given by

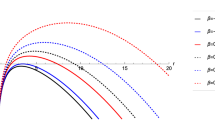
$$\begin{aligned} {\tilde{m}}_c \equiv \lambda m_c = \frac{\sqrt{17 n_{\textrm{PS}} (n_{\textrm{PS}}+1)+9+(87-17 n_{\textrm{PS}} (n_{\textrm{PS}}+1)) {\tilde{Q}}^2}}{4 \sqrt{3} {\tilde{Q}}}.\nonumber \\ \end{aligned}$$
(30)

In Fig. 3, we show the behaviour of \({\tilde{m}}_c\) as a function of \({\tilde{Q}}\). We observe that \({\tilde{m}}_c\) decreases when \({\tilde{Q}}\) increases, and for a fixed value of \({\tilde{Q}}<1\), \({\tilde{m}}_c\) increases when the overtone number \(n_{\textrm{PS}}\) increases. However, when \({\tilde{Q}} \rightarrow 1\) (or \(r_c\) \(\rightarrow \) \(r_h\)), then \({\tilde{m}}_c \rightarrow \sqrt{2}\), and it does not depend on the overtone number \(n_{\textrm{PS}}\). Also, when \({\tilde{Q}} \rightarrow 0\), \({\tilde{m}}_c \rightarrow \infty \).

Fig. 3
figure 3

The behaviour of \({\tilde{m}}_c\) as a function of \({\tilde{Q}}\) for different values of the overtone number \(n_{\textrm{PS}}=0,1,2\) and 5

Full size image

Anomalous decay rate. Here, for simplicity, we use the sixth-order WKB method to show the anomalous decay rate; however, at the end, we compare the QNFs via the sixth-order WKB method and the the pseudo-spectral Chebyshev method to show the accuracy of the sixth-order WKB method. So, in Figs. 4 and 5, we show the behaviour of \(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{m}}\). We can observe an anomalous decay rate; that is, for \({\tilde{m}}<{\tilde{m}}_c\), the longest-lived modes are those with the highest angular number l, whereas for \({\tilde{m}}>{\tilde{m}}_c\), the longest-lived modes are those with the smallest angular number. Also, when the parameter \({\tilde{Q}}\) increases, the parameter \({\tilde{m}}_c\) decreases, and when the overtone number \(n_{\textrm{PS}}\) increases, the parameter \({\tilde{m}}_c\) increases.

Fig. 4
figure 4

The behaviour of \(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{m}}\), with \({\tilde{Q}}=0.5\). Left panel for \(n_{\textrm{PS}}=0\), central panel for \(n_{\textrm{PS}}=1\), and right panel for \(n_{\textrm{PS}}=2\). Here, the WKB method gives via Eq. (30) \({\tilde{m}}_{c} \approx 1.601\) for \(n_{\textrm{PS}}=0\), \({\tilde{m}}_{c} \approx 2.165\) for \(n_{\textrm{PS}}=1\), and \({\tilde{m}}_{c} \approx 2.990\) for \(n_{\textrm{PS}}=2\). Black lines for \(l=20\), blue lines for \(l=40\), and red lines for \(l=60\)

Full size image
Fig. 5
figure 5

The behaviour of \(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{m}}\), with \({\tilde{Q}}=0.75\). Left panel for \(n_{\textrm{PS}}=0\), central panel for \(n_{\textrm{PS}}=1\), and right panel for \(n_{\textrm{PS}}=2\). Here, the WKB method gives via Eq. (30) \({\tilde{m}}_{c} \approx 1.465\) for \(n_{\textrm{PS}}=0\), \({\tilde{m}}_{c} \approx 1.642\) for \(n_{\textrm{PS}}=1\), and \({\tilde{m}}_{c} \approx 1.949\) for \(n_{\textrm{PS}}=2\). Black lines for \(l=20\), blue lines for \(l=40\), and red lines for \(l=60\)

Full size image

Now, in Figs. 6 and 7, we show the behaviour of \(Re({\tilde{\omega }})\) as a function of \({\tilde{m}}\). We can observe that the frequency of oscillation increases when the scalar field mass increases, and the frequency of oscillation decreases when the overtone number increases. Also, when the parameter \({\tilde{Q}}\) increases, the frequency of oscillation decreases.

Fig. 6
figure 6

The behaviour of \(Re({\tilde{\omega }})\) as a function of \({\tilde{m}}\), with \({\tilde{Q}}=0.5\). Left panel for \(l=20\), central panel for \(l=40\), and right panel for \(l=60\). Solid lines for \(n_{\textrm{PS}}=0\), dashed lines for \(n_{\textrm{PS}}=1\), and dotted lines for \(n_{\textrm{PS}}=2\)

Full size image
Fig. 7
figure 7

The behaviour of \(Re({\tilde{\omega }})\) as a function of \({\tilde{m}}\), with \({\tilde{Q}}=0.75\). Left panel for \(l=20\), central panel for \(l=40\), and right panel for \(l=60\). Solid lines for \(n_{\textrm{PS}}=0\), dashed lines for \(n_{\textrm{PS}}=1\), and dotted lines for \(n_{\textrm{PS}}=2\)

Full size image
Table 1 Quasinormal frequencies \(\omega \) for massless scalar fields in the background of Weyl black holes, with \(Q=1\), \(l=1\), and \(\lambda = 10, 40, 100\), and 200. Here, the QNFs are obtained via the pseudo-spectral Chebyshev method using a number of Chebyshev polynomials in the range 95–100. The values inside the quotation marks “...” mean that the QNF converges for a number of polynomials in the range 165–170, and...means that there is no convergence until 170 polynomials with nine decimal places of accuracy for the QNF. The values between parentheses are obtained via Eq. (32)
Full size table
Fig. 8
figure 8

de Sitter modes \({\tilde{\omega }}_{\textrm{dS}}\) for massless scalar fields in the background of Weyl black holes for several values of \({\tilde{Q}}\) in the range 0.25–0.95. Black points for \(l=0\), blue points for \(l=1\), and red points for \(l=2\). Left panel for \(n_{\textrm{dS}}=0\), central panel for \(n_{\textrm{dS}}=1\), and right panel for \(n_{\textrm{dS}}=2\). Some numerical values are shown in Appendix B Table 4

Full size image

Accuracy of the numerical techniques. Now, in order to check the correctness and accuracy of the sixth-order WKB method, we will compare some QNFs with the pseudo-spectral Chebyshev method. Thus, we show in Table 3 (see Appendix B) the QNFs using the pseudo-spectral Chebyshev method and the WKB method. Also, we show the relative error, which is defined by

$$\begin{aligned} \epsilon _{{\text {Re}}({\tilde{\omega }})}= & {} \frac{\mid {\text {Re}}({\tilde{\omega }}_1)\mid - \mid {\text {Re}}({\tilde{\omega }}_0)\mid }{\mid {\text {Re}}({\tilde{\omega }}_0)\mid }\cdot 100\%,\,\, \text {and}\nonumber \\ \epsilon _{{\text {Im}}({\tilde{\omega }})}= & {} \frac{\mid {\text {Im}}({\tilde{\omega }}_1)\mid - \mid {\text {Im}}({\tilde{\omega }}_0)\mid }{\mid {\text {Im}}({\tilde{\omega }}_0)\mid } \cdot 100\%, \end{aligned}$$
(31)

where \({\tilde{\omega }}_1\) corresponds to the QNFs via the sixth-order WKB method, and \({\tilde{\omega }}_0\) denotes the QNFs via the pseudo-spectral Chebyshev method. We can observe that the error does not exceed 117.964 \((\%)\) in the imaginary part and 40.308 \((\%)\) in the real part. These maximum values occur for small values of l, where the sixth-order WKB method does not provide high accuracy. It is known that the WKB method provides better accuracy for larger l (and \(l>n\)). Note that the error increases for higher values of the scalar field mass and for higher values of the overtone number. Note also that the WKB method has good accuracy for \(l\ge 20\), where the error does not exceed \(8.813\times 10^{-6}\) \((\%)\) in the imaginary part and \(1.639\times 10^{-7}\) \((\%)\) in the real part. Therefore, this method with \(l\ge 20\) is appropriate for showing the anomalous behaviour of the decay rate.

4.2 de Sitter modes

These modes are associated with the presence of the cosmological horizon—in this spacetime, the effective cosmological constant \(\Lambda _{eff} = 3/ \lambda ^2\) provides the asymptotically de Sitter solution—and resemble those of a pure de Sitter spacetime [61], which are given by

$$\begin{aligned} \omega _{{\text {pure-dS}}} = - i \sqrt{\frac{\Lambda }{3}} \left( 2n_{\textrm{dS}} + l + 3/2 \pm \sqrt{\frac{9}{4}-3 \frac{m^2}{\Lambda }} \right) , \end{aligned}$$
(32)

where \(\Lambda \) is the (positive) cosmological constant of pure de Sitter spacetime. The purely imaginary QNMs of asymptotically de Sitter black holes cannot be found by the standard WKB method [62, 63]. It it worth noting that for \(m^2 \le 3 \Lambda /4\), the QNFs of pure de Sitter spacetime are purely imaginary, whereas for \(m^2 > 3 \Lambda /4\), the QNFs acquire a real part. We can observe in Table 1 that for \(Q=1\) and for large values of the parameter \(\lambda \) (or small values of \({\tilde{Q}}= Q/ \lambda \)), the modes resemble those of the pure de Sitter spacetime (32). Also, note that for the massless scalar field with \(n_{\textrm{dS}}=0\), \(l=0\), there is a branch where \(\omega _{\textrm{dS}}=0\), the zero mode. By considering this fact, one could say that the zero mode is associated with the dS family. Thus, in the following, we will consider the zero mode as a dS mode.

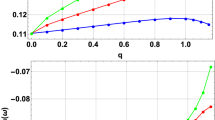
In Fig. 8, we plot the behaviour of the decay rate as a function of the parameter \({\tilde{Q}}\). For massless scalar fields, we can observe that for \(n_{\textrm{dS}}=0\) (left panel), the decay rate is not sensitive to the increase in \({\tilde{Q}}\), giving an approximately null slope. However, it is possible to observe a positive slope for \(n_{\textrm{dS}}>0\) and \(l>0\); see central and right panels.

Now, in order to analyse the effect of the scalar field mass on the decay rate, we consider \({\tilde{Q}}=0.50\) in Table 2 and \({\tilde{m}}=0, 1, 1.5, 1.6, 1.7, 1.8\). We can observe that for \(l=0,1,2\), \(n_{\textrm{dS}}=0\), and for purely imaginary QNFs, the decay rate increases when the scalar field mass increases. However, in general, this is not true for higher overtone numbers. Also, note that the dS modes also can acquire a real part if the mass of the scalar field increases enough, which is similar to what happens to the modes of pure de Sitter spacetime.

Table 2 de Sitter modes \({\tilde{\omega }}_{\textrm{dS}}\) for massive scalar fields in the background of Weyl black holes, with \({\tilde{Q}}= 0.5\). Here, the QNFs are obtained via the pseudo-spectral Chebyshev method using a number of Chebyshev polynomials in the range 50–60, with eight decimal places of accuracy for the QNFs
Full size table

4.3 Dominant family modes

As we mentioned, the purely imaginary modes belong to the family of dS modes, and they continuously approach those of pure de Sitter space in the limit that \({\tilde{Q}}\) vanishes. However, the dS modes can also acquire a real part if the mass of the scalar field increases sufficiently, which is similar to what happens to the modes of pure de Sitter spacetime. The other family corresponds to complex modes for massless and massive scalar fields with a non-null real part, namely PS modes. Thus, in order to analyse the dominance between the family modes, in Fig. 9 we plot both families, where black points correspond to dS modes and red points to PS modes. So, for massless scalar fields, we can observe that the dS family is dominant for \(l=0\). Also, the dS modes are dominant for \(l=1,2\) and small values of the parameter \({\tilde{Q}}\), but for higher values of \({\tilde{Q}}\), the PS modes are dominant for a massless scalar field. Therefore, there is a critical value of \({\tilde{Q}}_c\), where for \({\tilde{Q}}<{\tilde{Q}}_c\), the dominant family is the dS; otherwise, the dominant family is the PS mode for \(l>0\) and a massless scalar field.

Fig. 9
figure 9

\(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{Q}}\) for massless scalar fields in the background of Weyl black holes. Here, the QNFs are obtained via the pseudo-spectral Chebyshev method. Black points correspond to dS modes, while red points correspond to PS modes. Left panel for \(l=0\), central panel for \(l=1\), and right panel for \(l=2\). Some numerical values are shown in Appendix B Table 5

Full size image

Then, in order to analyse the effect of the scalar field mass on the dominance, we plot in Figs. 10 and 11 both families for \({\tilde{Q}}=0.5\) and 0.75, respectively. Black points correspond to dS modes with a purely imaginary QNF, blue points correspond to dS modes with a complex QNF, and red points to PS modes. Interestingly, for \(l=0\), the dominance of the dS modes depends on the scalar field’s mass. For small values of \({\tilde{m}}\), the dS family with purely imaginary QNF is dominant. Otherwise, the PS family is dominant; see left panels. Therefore, there is a critical value of \({\tilde{m}}=\mu _c\) such that, for \({\tilde{m}}<\mu _c\), the dS modes with a purely imaginary QNF are dominant; otherwise, the PS modes are dominant. Note that the dS family with complex QNF is not dominant. Also, the same behaviour is observed for \(l=1\) and small values of \({\tilde{Q}}\); see central panel of Fig. 10. Remarkably, for higher values of \({\tilde{Q}}\) and \(l>0\), the dominance of the PS family does not depend on the scalar field mass (see central and right panels of Fig. 11), and the PS is the dominant family.

Fig. 10
figure 10

\(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{m}}\) for scalar fields in the background of a Weyl black hole with \({\tilde{Q}}=0.5\). Here, the QNFs are obtained via the pseudo-spectral Chebyshev method. Black points correspond to dS modes with a purely imaginary QNF, blue points correspond to dS modes with a complex QNF, and red points to PS modes. Left panel for \(l=0\), central panel for \(l=1\), and right panel for \(l=2\). Some numerical values are shown in Appendix B Table 6

Full size image
Fig. 11
figure 11

\(-\text {Im}({\tilde{\omega }})\) as a function of \({\tilde{m}}\) for scalar fields in the background of a Weyl black hole with \({\tilde{Q}}=0.75\). Here, the QNFs are obtained via the pseudo-spectral Chebyshev method. Black points correspond to dS modes with a purely imaginary QNF, blue points correspond to dS modes with a complex QNF, and red points to PS modes. Left panel for \(l=0\), central panel for \(l=1\), and right panel for \(l=2\). Some numerical values are shown in Appendix B Table 7

Full size image
Fig. 12
figure 12

The solid line corresponds to \(\mu _c\) as a function of \({\tilde{Q}}\) for \(l=1\) (left panel) and \(l=8\) (right panel), and separates regions in the parameter space where a family of QNFs dominates according to the analytical approximation. In the region to the left of the line, the de Sitter modes always dominate, while in the region to the right, the PS modes dominate. The numerical results using the pseudo-spectral Chebyshev method are represented by points. The points are close to the frontier where the change in dominance occurs. The black points are in the side where the de Sitter modes dominate, while the red points are in the side where the PS modes dominate. The coincidence of the line with the points for \(l=1\) is more accurate for low values of \(\mu _c\), while for larger values of \(\mu _c\), the difference between the analytical and the numerical results increases. However, for \(l=8\), the analytical approximation is accurate even for high values of \(\mu _c\)

Full size image

Now, in order to give an approximate value of \({\tilde{m}}=\mu _c\) where there is an interchange in the family dominance, we consider \(Im(\omega _{\textrm{dS}})=Im(\omega _{\textrm{PS}})\) as a proxy for where the interchange in the family dominance occurs, where for \(\omega _{\textrm{PS}}\) we consider the analytical expression given by Eq. (26), which yields the QNFs at third order beyond the eikonal limit, and for \(\omega _{\textrm{dS}}\) we consider the analytical expression given by Eq. (32) for the pure de Sitter spacetime \(\omega _{{\text {pure-dS}}}\) with \(\Lambda _{eff} = 3/ \lambda ^2\), which yields well-approximated QNFs for the dS family for high values of l. It is important because it allows us to discern whether the dominant family is able to suffer the anomalous behaviour of the decay rate. Thus, the equality of \(Im(\omega _{{\text {pure-dS}}})\) with \(Im(\omega _{\textrm{PS}})\) for \(n_{\textrm{PS}}=0\) and \(n_{\textrm{dS}}=0\) yields

$$\begin{aligned} \mu _c^2= & {} -\Bigg [ -27 + 1024 l^4 + 9 {\tilde{Q}}^4 \left( 78-84{\tilde{Q}}^2+29 {\tilde{Q}}^4 \right) \nonumber \\{} & {} +192 l (1-{\tilde{Q}}^2) \left( -2(1-{\tilde{Q}}^2)+ 3 \sqrt{2}{\tilde{Q}}\sqrt{1-{\tilde{Q}}^2} \right) \nonumber \\{} & {} +128 l^3 \left( 16+3 \sqrt{2} {\tilde{Q}} (1-{\tilde{Q}}^2)^{3/2} \right) \nonumber \\{} & {} - 64 l^2 \left( -10+ 3 {\tilde{Q}} \left( -5 \sqrt{2} \sqrt{1-{\tilde{Q}}^2} \right. \right. \nonumber \\{} & {} \left. \left. + {\tilde{Q}} \left( -4+ 2 {\tilde{Q}}^2 + 5\sqrt{2} {\tilde{Q}} \sqrt{1-{\tilde{Q}}^2} \right) \right) \right) \nonumber \\{} & {} - 4 {\tilde{Q}}^2 \Bigg ( 45+ \frac{8 \sqrt{2} l(l+1)}{{\tilde{Q}}^2} \Bigg [ 512 l^4 +9 (1-{\tilde{Q}}^2)^3 (-3+7 {\tilde{Q}}^2) \nonumber \\{} & {} -192 l (1-{\tilde{Q}}^2) \left( 2 (1-{\tilde{Q}}^2)- 3 \sqrt{2} {\tilde{Q}} \sqrt{1-{\tilde{Q}}^2} \right) \nonumber \\{} & {} -128 l^3 \left( -8 - 3\sqrt{2}{\tilde{Q}} (1-{\tilde{Q}}^2)^{3/2} \right) \nonumber \\{} & {} -64 l^2 \left( -2+3 {\tilde{Q}} \left( -5 \sqrt{2} \sqrt{1-{\tilde{Q}}^2}\right. \right. \nonumber \\{} & {} \left. \left. +{\tilde{Q}} \left( -4+2{\tilde{Q}}^2 + 5\sqrt{2} {\tilde{Q}} \sqrt{1-{\tilde{Q}}^2} \right) \right) \right) \Bigg ]^{1/2} \Bigg )\Bigg ] \Bigg /\nonumber \\ {}{} & {} \times \left( 144 {\tilde{Q}}^2 (1-{\tilde{Q}}^2)^3 \right) \end{aligned}$$
(33)

for \(\mu _c \le 3/2\), and

$$\begin{aligned} \mu _c^2 = -\frac{256 l^3 {\tilde{Q}}-3 \sqrt{2} (1-{\tilde{Q}}^2)^{3/2} (3+29{\tilde{Q}}^2)-128 l^2 \left( -5 {\tilde{Q}} + \sqrt{2} \sqrt{1-{\tilde{Q}}^2} \right) -128 l \left( -3 {\tilde{Q}}+ \sqrt{2} \sqrt{1-{\tilde{Q}}^2} \right) }{48 \sqrt{2} {\tilde{Q}}^2 (1-{\tilde{Q}}^2)^{3/2}} \end{aligned}$$
(34)

for \(\mu _c > 3/2\). The mass where the transition of dominance occurs, \(\mu _c\), depends on the parameters \({\tilde{Q}}\) and l.

Note that the imaginary part of the QNFs of the pure de Sitter depends on m for \(m^2 \le 3 \Lambda _{eff}/4\) (\({\tilde{m}} < 3/2 \)), while that in the opposite case does not depend on m, and the QNFs acquire a real part. This is reflected in the behaviour of \(\mu _c\), which is different for \(\mu _c \le 3/2\) and \(\mu _c > 3/2\), as shown in Fig. 12. Also, in that figure, we show numerical results using the pseudo-spectral Chebyshev method (red and blue points), where there is a change in dominance of the families. We observe that the analytical values of \(\mu _c\), represented by the solid line, is more accurate for high values of l.

5 Conclusions

In this work, we studied the propagation of massive scalar fields in the Weyl black hole as a background, and we analysed their QNFs. Essentially, we showed that two families of modes are present—one is a family of complex QNFs, and the other is a family of purely imaginary modes for massless scalar fields (for massive scalar fields, the dS modes also can be complex). We showed that the purely imaginary modes belong to the family of de Sitter modes, and they continuously approach those of pure de Sitter space in the limit that the black hole parameter Q vanishes, and the complex ones correspond to the photon sphere modes. Both families of modes show that the propagation of massless and massive scalar fields is stable in Weyl black hole backgrounds for the cases considered.

For the PS modes, and using the WKB method at third order beyond the eikonal limit, we were able to estimate the value of the critical scalar field mass, and we found its dependence on \({\tilde{Q}}\) and on the overtone number \(n_{\textrm{PS}}\) in the eikonal limit. We found that the critical scalar field mass decreases when \({\tilde{Q}}\) increases, and it increases when the overtone number \(n_{\textrm{PS}}\) increases. Interestingly, at the extremal limit \({\tilde{Q}} \rightarrow 1\) or \((r_{c}\rightarrow r_{h})\), \({\tilde{m}}_c \rightarrow \sqrt{2}\), and it does not depend on the overtone number \(n_{\textrm{PS}}\). Also, when \({\tilde{Q}} \rightarrow 0\), \({\tilde{m}}_c \rightarrow \infty \). Then we showed the anomalous decay rate of the QNMs via the WKB method at sixth order beyond the eikonal limit, where both methods, the WKB method and the pseudo-spectral Chebyshev, show high accuracy. We also showed that the frequency of oscillation increases when the scalar field mass increases, and such frequency decreases when the overtone number \(n_{\textrm{PS}}\) or the parameter \({\tilde{Q}}\) increases.

For the dS modes, we found that for massless scalar fields and l null, the decay rate is not sensitive to the increase in \({\tilde{Q}}\). However, the decay rate increases when \({\tilde{Q}}\) increases \(n_{\textrm{dS}}>1\), and \(l>0\). Also, we showed that when the scalar field acquires mass, the decay rate increases when the scalar field mass increases for \(l=0,1,2\), \(n_{\textrm{dS}}=0\), and purely imaginary QNFs; however, in general, this is not true for higher overtone numbers.

Finally, using the pseudo-spectral Chebyshev method, we studied the dominance between the families of modes. We showed that for a massless scalar field, the dS modes are dominant for \(l=0\). However, for \(l=1,2\), there is a critical value of \({\tilde{Q}}_c\) such that if \({\tilde{Q}}<{\tilde{Q}}_c\), the dominant family is the dS; otherwise, the dominant family is the PS. Interestingly, when the scalar field acquires mass, and for \(l=0\), the dominance of the dS modes depends on the scalar fields mass, and there is a critical value of \({\tilde{m}}=\mu _c\) such that for \({\tilde{m}}<\mu _c\), the dS modes with purely imaginary QNFs are dominant; otherwise, the PS modes are dominant. The same behaviour was observed for \(l=1\) and small values of \({\tilde{Q}}\). Remarkably, for higher values of \({\tilde{Q}}\), and \(l>0\), the dominance of the PS family does not depend on the scalar field mass. Then, by considering as a proxy \(Im(\omega _{\textrm{dS}})=Im(\omega _{\textrm{PS}})\), we were able to estimate the value of \(\mu _c\) where there is an interchange in the family dominance for a null overtone number, the value of which depends on the parameters \({\tilde{Q}}\) and l.

It is worth mentioning that even though the effective potential is negative for a range of values of r for \(l=0\), the propagation of a massive scalar field is stable. However, it would be interesting to extend this work to the case of a charged massive scalar field in order to study the superradiance and the existence of bound states which could trigger an instability for \(l=0\).