1 Introduction

In recent years, LHC experiments provided rich experimental data of hadron production in pp collisions at LHC energies, from which many new features of hadron production are found. For example, in production of light-flavor hadrons, experiments found the enhancement of baryon to meson ratio (such as \(p/\pi \), \(\varLambda /K_{s}^{0}\), \(\varOmega /\phi \)) at intermediate \(p_{T}\) [1, 2] and the enhancement of multi-strange hadrons in high multiplicity events [3]. We also found a quark number scaling property for \(p_{T}\) spectra of hadrons at mid-rapidity by further analyzing experimental data of ALICE collaboration [4,5,6]. In production of open heavy-flavor hadrons, LHC experiments found the enhancement of \(\varLambda _{c}^{+}/D^{0}\) in the low \(p_{T}\) range (\(p_{T}\lesssim 10\) GeV/c) in pp collisions at LHC energies in comparison with measurements in \(e^{+}e^{-}\) and ep collisions at early years [7,8,9,10].

The production enhancement of light-flavor baryons and, in particular, heavy-flavor baryons such as \(\varLambda _{c}^{+}\) attracts lots of theoretical studies. Many new phenomenological mechanisms and/or details in the framework of parton fragmentation [11,12,13,14,15,16,17], quark (re-)combination [18, 19] and statistical hadronization [20,21,22] are proposed to describe the hadronization of final parton system created in pp collisions at LHC energies and explain new experimental data at LHC, which greatly enriches people’s understandings for the property of hadron production in high energy collisions. Recently, ALICE collaboration reported their precise measurement for the multiplicity dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio in the low \(p_{T}\) range [23] and the preliminary data of \(\varLambda _{c}^{+}/D^{0}\) ratio at small \(p_{T}\) (\(p_{T}<1\) GeV/c) [24, 25]. These newest data will further test the existing hadronization models [18,19,20, 26].

In this paper, we apply a quark combination model [4, 18, 27] to study the \(p_{T}\) and multiplicity dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio in pp collisions at \(\sqrt{s}=13\) TeV. The model has a good performance in systematically explaining the production of light-flavor hadrons and single-charm hadrons in pp collisions at LHC and RHIC [5, 6, 18, 28, 29]. The model applies an equal-velocity combination (EVC) mechanism to approximately describe the combination of constituent (anti-)quarks at hadronization and therefore has a good analytic property in describing the momentum distribution and integrated yield of identified hadrons. Taking advantage of this analytic property, we derive the analytic formula of the \(\varLambda _{c}^{+}/D^{0}\) ratio and study several physical ingredients that influence the multiplicity and \(p_{T}\) dependence of the ratio \(\varLambda _{c}^{+}/D^{0}\). We demonstrate how the property of light-flavor quark \(p_{T}\) spectra and charm quark \(p_{T}\) spectra leads to, in an intuitive way, the non-monotonic \(p_{T}\) dependence the ratio \(\varLambda _{c}^{+}/D^{0}\). Finally, we compare our theoretical calculations with the latest experimental data of ALICE collaboration [23].

The paper is organized as follows. Section 2 gives a brief introduction of our quark combination model with EVC mechanism. In Sect. 3, we derive the ratio \(\varLambda _{c}^{+}/D^{0}\) and decompose it into four parts. In Sects. 4–7, we discuss the influence of these four parts, i.e., quark numbers, light-flavor quark \(p_{T}\) spectra, charm quark \(p_{T}\) spectrum, and \(p_{T}\) correlation between charm and light-flavor (anti-)quarks, on the ratio \(\varLambda _{c}^{+}/D^{0}\). In Sect. 8, we compare our theoretical results of ratio \(\varLambda _{c}^{+}/D^{0}\) with experimental data. In Sect. 9, we give the summary and discussions.

2 A brief introduction of EVC model

In this paper, we apply a quark combination model proposed in previous works [4, 18, 27] to study ratio \(\varLambda _{c}^{+}/D^{0}\). This model is inspired by the quark number scaling property found from experimental data for \(p_{T}\) spectra of light-flavor hadrons at mid-rapidity in pp and p-Pb collisions at LHC energies [4, 28]. We have applied the model to describe the yields and \(p_{T}\) spectra of light-flavor hadrons and those of single-charm hadrons in pp, p-Pb and AA collisions at RHIC and LHC energies, and found generally good agreement with experimental data [6, 29,30,31,32]. In this section, we briefly introduce the model and, in particular, the relevant physical approximations and parameters in the model which may influence the ratio \(\varLambda _{c}^{+}/D^{0}\).

2.1 General framework

We start from the inclusive momentum distribution of single-charm hadron in general framework of quark combination mechanism

$$\begin{aligned} f_{M_{c\bar{l}}}(p)&=\int dp_{1}dp_{2}f_{c\bar{l}}(p_{1},p_{2})\,{\mathscr {R}}_{M_{c\bar{l}}}(p_{1},p_{2};p), \end{aligned}$$
(1)
$$\begin{aligned} f_{B_{cll'}}(p)&=\int dp_{1}dp_{2}dp_{3}f_{cll'}(p_{1},p_{2},p_{3})\,{\mathscr {R}}_{B_{cll'}} \nonumber \\&\quad \times (p_{1},p_{2},p_{3};p). \end{aligned}$$
(2)

Here, \(f_{c\bar{l}}(p_{1},p_{2})\) is the joint momentum distribution of charm (c) quark and light antiquark \((\bar{l}).\) \({\mathscr {R}}_{M_{c\bar{l}}}(p_{1},p_{2};p)\) is the combination function denoting the probability density for the given \(c\bar{l}\) with momenta \(p_{1}\), \(p_{2}\) combining into a meson \(M_{c\bar{l}}\) with momentum p. It is similar for the baryon formula.

Different implementations of combination functions have been used in literature. In the well-known parton recombination and parton coalescence models [33,34,35,36,37,38,39], instantaneous hadronization is assumed and the combination function depends on the overlap of wave function of quarks with that of the formed hadron and is finally determined by the Wigner function of the formed hadron. In the recombination model [40,41,42] combination function is determined from the valon model description of hadron structure [41, 43]. In addition, combination function can also be manifested by phenomenological combination conditions in a multi-phase transport (AMPT) model [44, 45] and a quark combination model [46, 47], etc.

In this paper, we adopt a simplified form of combination functions in order to derive the analytic expression of \(\varLambda _{c}^{+}/D^0\) ratio. It is based on the equal velocity combination approximation of charm quarks and light-flavor (anti)quarks at hadronization, which was firstly studied in elliptic flow of charm hadrons [48] and is used in our recent works to explain the observed constituent quark number scaling property for \(p_T\) spectra and elliptic flow of identified hadrons [4, 6, 28, 30, 49]. In this approximation, the combination function is simply the product of Dirac delta functions

$$\begin{aligned}&{\mathscr {R}}_{M_{c\bar{l}}}(p_{1},p_{2};p) =\kappa _{M_{c\bar{l}}}\prod _{i=1}^{2}\delta (p_{i}-x_{i}p), \end{aligned}$$
(3)
$$\begin{aligned}&{\mathscr {R}}_{B_{cll'}}(p_{1},p_{2},p_{3};p) =\kappa _{B_{cll'}}\prod _{i=1}^{3}\delta (p_{i}-x_{i}p). \end{aligned}$$
(4)

Here \(\kappa _{M_{c\bar{l}}}\) and \(\kappa _{B_{cll'}}\) are independent of momentum but are dependent on quarks numbers due to the unitarity constraint of hadronization. Momentum fraction reads as \(x_{i}=m_{i}/(m_{1}+m_{2})\) in meson formula with momentum conservation constraint \(x_{1}+x_{2}=1\) and \(x_{i}=m_{i}/(m_{1}+m_{2}+m_{3})\) in baryon formula with momentum conservation constraint \(x_{1}+x_{2}+x_{3}=1\). The masses of constituent quarks are taken as \(m_u=m_d=0.3\) GeV, \(m_s=0.5\) GeV and \(m_c=1.5\) GeV, respectively.

Substituting Eqs. (3) and (4) into (1) and (2), we obtain

$$\begin{aligned} f_{M_{c\bar{l}}}(p)&=\kappa _{M_{c\bar{l}}}f_{c\bar{l}}(x_{1}p,x_{2}p), \end{aligned}$$
(5)
$$\begin{aligned} f_{B_{cll'}}(p)&=\kappa _{B_{cll'}}f_{cll'}(x_{1}p,x_{2}p,x_{3}p). \end{aligned}$$
(6)

For the integral of joint distribution of quarks, we have

$$\begin{aligned}&\int dp_{1}dp_{2}f_{c\bar{l}}(p_{1},p_{2}) =N_{c}N_{\bar{l}}\equiv N_{c\bar{l}}, \end{aligned}$$
(7)
$$\begin{aligned}&\int dp_{1}dp_{2}dp_{3}f_{cll'}(p_{1},p_{2},p_{3}) =N_{c}N_{ll'}\equiv N_{cll'} \end{aligned}$$
(8)

where \(N_{ll'}\) equals to \(N_{l}N_{l'}\) as \(l\ne l'\) and \(N_{l}(N_{l}-1)\) as \(l=l'\). Obviously, \(N_{c\bar{l}}\) is the number of all \(c\bar{l}\) pair and \(N_{cll'}\) is the number of all possible \(cll'\) combinations. Under EVC constraint, the integrals become

$$\begin{aligned}&\int dpf_{c\bar{l}}(x_{1}p,x_{2}p) \equiv \frac{N_{c\bar{l}}}{A_{c\bar{l}}}, \end{aligned}$$
(9)
$$\begin{aligned}&\int dpf_{cll'}(x_{1}p,x_{2}p,x_{3}p) \equiv \frac{N_{cll'}}{A_{cll'}}, \end{aligned}$$
(10)

where we use coefficient \(A_{c\bar{l}}\) to denote the effect of equal-velocity constraint on the effective number of \(c\bar{l}\) pairs and \(A_{cll'}\) to denote that on the effective number of \(cll'\) combinations.

Integrating Eqs. (5) and (6) over p, we obtain the number of charm hadrons

$$\begin{aligned} N_{M_{c\bar{l}}}&=\kappa _{M_{c\bar{l}}}\frac{N_{c\bar{l}}}{A_{c\bar{l}}}=N_{c\bar{l}}\frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}}, \end{aligned}$$
(11)
$$\begin{aligned} N_{B_{cll'}}&=\kappa _{B_{cll'}}\frac{N_{cll'}}{A_{cll'}}=N_{cll'}\frac{\kappa _{B_{cll'}}}{A_{cll'}}. \end{aligned}$$
(12)

We see that \(\frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}}\) has the meaning of the average probability of a \(c\bar{l}\) pair forming a meson, and it is similar for baryon term.

If we neglect the contribution of multi-charm hadrons, the unitarity of charm quark hadronization gives

$$\begin{aligned} \sum _{M_{c\bar{l}}}N_{M_{c\bar{l}}}+\sum _{B_{cll'}}N_{B_{cll'}}=N_{c}, \end{aligned}$$
(13)

which means

$$\begin{aligned} \sum _{M_{c\bar{l}}}N_{\bar{l}}\frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}}+\sum _{B_{cll'}}N_{ll'}\frac{\kappa _{B_{cll'}}}{A_{cll'}}=1. \end{aligned}$$
(14)

At charm quark hadronization, light-flavor quarks serve as the background and their property, i.e., numbers \(N_{l}\) and momentum distributions \(f_{l}(p)\) relating to A, can be freely changed. With this consideration, we expect \(\frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}}\sim \frac{1}{N_{\bar{q}}}\) and \(\frac{\kappa _{B_{cll'}}}{A_{cll'}}\sim \frac{1}{N_{q}^{2}}\) with \(N_{\bar{q}}=\sum _{\bar{l}}N_{\bar{l}}\) and \(N_{q}=\sum _{l}N_{l}\) so that the unitarity constraint can be satisfied in an easy manner. In this philosophy, we introduce a dynamic parameter \(R_{B/M}^{(c)}\) to denote the competition between the formation of charm baryon and the formation of charm meson as a charm quark hadronizes. Then we can write

$$\begin{aligned}&\sum _{M_{c\bar{l}}}N_{\bar{l}}\frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}} =\frac{1}{1+R_{B/M}^{(c)}}, \end{aligned}$$
(15)
$$\begin{aligned}&\sum _{B_{cll'}}N_{ll'}\frac{\kappa _{B_{cll'}}}{A_{cll'}} =\frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}}. \end{aligned}$$
(16)

Following the spirit in our previous works [18, 27], we can take the following parameterizations

$$\begin{aligned} \frac{\kappa _{M_{c\bar{l}}}}{A_{c\bar{l}}}&=C_{M_{c\bar{l}}}\frac{1}{N_{\bar{q}}}\frac{1}{1+R_{B/M}^{(c)}}=C_{M_{c\bar{l}}}\frac{1}{N_{c\bar{q}}}\frac{1}{1+R_{B/M}^{(c)}}N_{c}, \end{aligned}$$
(17)
$$\begin{aligned} \frac{\kappa _{B_{cll'}}}{A_{cll'}}&=C_{B_{cll'}}N_{iter,ll'}\frac{1}{N_{qq}}\frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}} \nonumber \\&=C_{B_{cll'}}N_{iter,ll'}\frac{1}{N_{cqq}}\frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}}N_{c}, \end{aligned}$$
(18)

which can be understood as follows. In the second equality, \(N_{c}/(1+R_{B/M}^{(c)})\) denotes the number of charm quarks that will form charm mesons. \(N_{c\bar{q}}\) equals to \(N_{c}N_{\bar{q}}\) and denotes the number of all possible \(c\bar{q}\) pair. Then \(N_{c}/(1+R_{B/M}^{(c)})/N_{c\bar{q}}\) denotes the average probability of a \(c\bar{q}\) pair forming a charm meson. Because a \(c\bar{q}\) pair can form the charm meson with different total angular moments, here we introduce a parameter \(C_{M_{c\bar{l}}}\) to denote the probability of a \(c\bar{l}\) pair forming a given state \(M_{c\bar{l}}\). Obviously, unitarity requires \(\sum _{M_{c\bar{l}}}C_{M_{c\bar{l}}}=1\) where summation runs over all meson states with the same \(c\bar{l}\) composition. It is similar for Eq. (18) of the baryon, i.e., \(\sum _{B_{cll'}}C_{B_{cll'}}=1\). Here, \(N_{iter,ll'}\) is the permutation factor of \(ll'\) and is 2 for \(l\ne l'\) and 1 for \(l=l'\), respectively. We expect \(C_{M_{c\bar{l}}}\) and \(C_{B_{cll'}}\) are stable. Because \(\sum _{M_{c\bar{l}}}N_{\bar{l}}C_{M_{c\bar{l}}}=\sum _{\bar{l}}N_{\bar{l}}=N_{\bar{q}}\) and \(\sum _{B_{cll'}}C_{B_{cll'}}N_{iter,ll'}N_{ll'}=\sum _{ll'}N_{iter,ll'}N_{ll'}=N_{qq}\), the unitarity of charm quark hadronization is naturally satisfied via \(\sum _{M_{c\bar{l}}}N_{M_{c\bar{l}}}=\sum _{M_{c\bar{l}}}N_{c\bar{l}}\kappa _{M_{c\bar{l}}}/A_{c\bar{l}}=N_{c}/(1+R_{B/M}^{(c)})\) and \(\sum _{B_{cll'}}N_{B_{cll'}}=\sum _{B_{cll'}}N_{cll'}\kappa _{B_{cll'}}/A_{cll'}=N_{c}R_{B/M}^{(c)}/(1+R_{B/M}^{(c)})\).

Finally, numbers of charm hadrons are

$$\begin{aligned} N_{M_{c\bar{l}}}&=C_{M_{c\bar{l}}}\frac{1}{1+R_{B/M}^{(c)}}\frac{N_{c\bar{l}}}{N_{\bar{q}}}, \end{aligned}$$
(19)
$$\begin{aligned} N_{B_{cll'}}&=C_{B_{cll'}}\frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}}N_{iter,ll'}\frac{N_{cll'}}{N_{qq}}, \end{aligned}$$
(20)

and momentum distributions of charm hadrons are

$$\begin{aligned} f_{M_{c\bar{l}}}(p)&=N_{M_{c\bar{l}}}f_{c\bar{l}}^{(n)}(x_{1}p,x_{2}p), \end{aligned}$$
(21)
$$\begin{aligned} f_{B_{cll'}}(p)&=N_{B_{cll'}}f_{cll'}^{(n)}(x_{1}p,x_{2}p,x_{3}p), \end{aligned}$$
(22)

where \(f_{c\bar{l}}^{(n)}(x_{1}p,x_{2}p)\) and \(f_{cll'}^{(n)}(x_{1}p,x_{2}p,x_{3}p)\) are the normalized distributions under integral over p.

2.2 Application to high-energy collisions

In this paper, we study the production of charm hadrons at mid-rapidity in pp collisions at \(\sqrt{s}=13\) TeV and compare our theoretical results with experimental data at mid-rapidity. The quark momentum distribution dN/dp at rapidity \(y=0\) in our model is reduced to \(f(p_{T})\equiv dN/dp_{T}\). The joint quark momentum distributions are also reduced to \(f_{c\bar{l}}(p_{T,c},p_{T,\bar{l}})\) and \(f_{cll'}(p_{T,c},p_{T,l},p_{T,l'})\). The rapidity densities of charm and light-flavor quarks are denoted as \(N_{l}\) and \(N_{c}\) for convenience.

In experimental measurement, momentum spectra and yield densities of hadrons are mainly reported via their averaged values in the selected event class. We can extend the above formulas to follow the experimental statistics by re-defining quark momentum distributions \(f_{c\bar{l}}(p_{T,c},p_{T,\bar{l}})\) and \(f_{cll'}(p_{T,c},p_{T,l},p_{T,l'})\) and quark numbers \(N_{l}\), \(N_{c}\) as these in the select event class.

Finally, \(p_{T}\) spectra of hadrons in our model are

$$\begin{aligned} f_{M_{c\bar{l}}}(p_{T})&=\left\langle N_{M_{c\bar{l}}}\right\rangle f_{c\bar{l}}^{(n)}(x_{1}p_{T},x_{2}p_{T}), \end{aligned}$$
(23)
$$\begin{aligned} f_{B_{cll'}}(p_{T})&=\left\langle N_{B_{cll'}}\right\rangle f_{cll'}^{(n)}(x_{1}p_{T},x_{2}p_{T},x_{3}p_{T}), \end{aligned}$$
(24)

with

$$\begin{aligned} \left\langle N_{M_{c\bar{l}}}\right\rangle&=C_{M_{c\bar{l}}}\frac{1}{1+R_{B/M}^{(c)}}\left\langle \frac{N_{c\bar{l}}}{N_{\bar{q}}}\right\rangle , \end{aligned}$$
(25)
$$\begin{aligned} \left\langle N_{B_{cll'}}\right\rangle&=C_{B_{cll'}}\frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}}N_{iter,ll'}\left\langle \frac{N_{cll'}}{N_{qq}}\right\rangle . \end{aligned}$$
(26)

In the following studies, we also assume several symmetry property for numbers and momentum distributions of quarks produced at mid-rapidity in pp collisions at LHC energy. We consider the iso-spin symmetry between up and down quarks, i.e., \(\left\langle N_{u}\right\rangle =\left\langle N_{d}\right\rangle \) and \(f_{u}(p_{T})=f_{d}(p_{T})\), and also the charge conjugation symmetry, i.e., \(\left\langle N_{l}\right\rangle =\left\langle N_{\bar{l}}\right\rangle \) and \(f_{l}(p_{T})=f_{\bar{l}}(p_{T})\). These symmetry assumptions will greatly simplify our theoretical expressions.

3 \(p_{T}\) dependence of ratio \(\varLambda _{c}^{+}/D^{0}\)

According to Eqs. (5) and (6), \(p_{T}\) spectra of \(\varLambda _{c}^{+}\) and \(D^{0}\) are

$$\begin{aligned} f_{\varLambda _{c}}(p_{T})&=\kappa _{\varLambda _{c}}f_{cud}\left( x_{c}p_{T},x_{u}p_{T},x_{d}p_{T}\right) , \end{aligned}$$
(27)
$$\begin{aligned} f_{D^{0}}(p_{T})&=\kappa _{D^{0}}f_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{\bar{u}}^{\prime }p_{T}\right) , \end{aligned}$$
(28)

where \(x_{u}=x_{d}=m_{u}/(2m_{u}+m_{c})\), \(x_{c}=m_{c}/(2m_{u}+m_{c})\) for the baryon and \(x_{\bar{u}}^{\prime }=m_{u}/(m_{u}+m_{c})\), \(x_{c}^{\prime }=m_{c}/(m_{c}+m_{u})\) for the meson.

We express the joint distribution functions of (anti-)quarks as

$$\begin{aligned}&f_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right) \end{aligned}$$
(29)
$$\begin{aligned}&\quad =f_{c}(p_{T,c})f_{u}(p_{T,u})f_{d}(p_{T,d})\left[ 1+{\mathscr {C}}_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right) \right] , \nonumber \\&f_{c\bar{u}}\left( p_{T,c},p_{T,\bar{u}}\right) =f_{c}(p_{T,c})f_{\bar{u}}(p_{T,\bar{u}}) \left[ 1+{\mathscr {C}}_{c\bar{u}}\left( p_{T,c},p_{T,\bar{u}}\right) \right] , \end{aligned}$$
(30)

where \(f_{q_{i}}(p_{T})\) is inclusive distribution of \(q_{i}\)-flavor quarks and \({\mathscr {C}}_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right) \) is the correlation term. By rewriting \(f_{q_{i}}(p_{T})=N_{q_{i}}f_{q_{i}}^{(n)}(p_{T})\) with \(f_{q_{i}}^{(n)}(p_{T})\) being the normalized distribution, we can further write the joint distributions as

$$\begin{aligned} f_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right)&=N_{cud}f_{c}^{(n)}(p_{T,c})f_{u}^{(n)}(p_{T,u})f_{d}^{(n)}(p_{T,d})\nonumber \\&\quad \times \left[ 1+{\mathscr {C}}_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right) \right] , \end{aligned}$$
(31)
$$\begin{aligned} f_{c\bar{u}}\left( p_{T,c},p_{T,\bar{u}}\right)&=N_{c\bar{u}}f_{c}^{(n)}(p_{T,c})f_{\bar{u}}^{(n)}(p_{T,\bar{u}})\nonumber \\&\quad \times \left[ 1+{\mathscr {C}}_{c\bar{u}}\left( p_{T,c},p_{T,\bar{u}}\right) \right] . \end{aligned}$$
(32)

With the above form of \(f_{cud}\left( p_{T,c},p_{T,u},p_{T,d}\right) \) and \(f_{c\bar{u}}\left( p_{T,c},p_{T,\bar{u}}\right) \), we can calculate \(p_{T}\) spectra of \(\varLambda _{c}^{+}\) and \(D^{0}\) by formulas in Sect. 2.1 and then consider the event average convention in Sect. 2.2, and finally we get the ratio

$$\begin{aligned} \frac{f_{\varLambda _{c}}(p_{T})}{f_{D^{0}}(p_{T})}&=R_{B/M}^{(c)}\frac{C_{\varLambda _{c}}}{C_{D^{0}}}N_{iter,ud}\frac{\left\langle \frac{N_{cud}}{N_{qq}}\right\rangle }{\left\langle \frac{N_{c\bar{u}}}{N_{\bar{q}}}\right\rangle }\frac{A_{\varLambda _{c}}}{A_{D^{0}}}\frac{f_{c}^{(n)}(x_{c}p_{T})}{f_{c}^{(n)}(x_{c}^{\prime }p_{T})}\nonumber \\&\quad \times \frac{\left[ f_{u}^{(n)}(x_{u}p_{T})\right] ^{2}}{f_{u}^{(n)}(x_{u}^{\prime }p_{T})}\frac{1+{\mathscr {C}}_{cud}\left( x_{c}p_{T},x_{u}p_{T},x_{d}p_{T}\right) }{1+{\mathscr {C}}_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) }\nonumber \\&=R^{(N_{q_{i}})}\left[ \frac{A_{\varLambda _{c}}}{A_{D^{0}}}R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) R_{corr}^{(cl)}\left( p_{T}\right) \right] . \end{aligned}$$
(33)

Here, we have used the symmetry property \(f_{u}^{(n)}(p_{T}) = f_{d}^{(n)}(p_{T})\) \(= f_{\bar{u}}^{(n)}(p_{T})=f_{\bar{d}}^{(n)}(p_{T})\) in the mid-rapidity range at LHC energies. In the second line, we split the ratio into several parts

$$\begin{aligned}&R^{(N_{q_{i}})} \equiv 2R_{B/M}^{(c)}\frac{C_{\varLambda _{c}}\left\langle N_{cud}/N_{qq}\right\rangle }{C_{D^{0}}\left\langle N_{c\bar{u}}/N_{\bar{q}}\right\rangle }, \end{aligned}$$
(34)
$$\begin{aligned}&R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \equiv \frac{f_{c}^{(n)}(x_{c}p_{T})}{f_{c}^{(n)}(x_{c}^{\prime }p_{T})}, \end{aligned}$$
(35)
$$\begin{aligned}&R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \equiv \frac{\left[ f_{u}^{(n)}(x_{u}p_{T})\right] ^{2}}{f_{u}^{(n)}(x_{u}^{\prime }p_{T})}, \end{aligned}$$
(36)
$$\begin{aligned}&R_{corr}^{(cl)}\left( p_{T}\right) =\frac{1+{\mathscr {C}}_{cud}\left( x_{c}p_{T},x_{u}p_{T},x_{d}p_{T},\right) }{1+{\mathscr {C}}_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) } \end{aligned}$$
(37)

which reflect the influence of different physical ingredients on the ratio \(\varLambda _{c}^{+}/D^{0}\).

4 The property of \(R^{(N_{q_{i}})}\)

With Eqs. (9), (10) and (31), we can see that

$$\begin{aligned}&A_{\varLambda _{c}}\int dp_{T}\left[ f_{u}^{(n)}(x_{u}p_{T})\right] ^{2}f_{c}^{(n)}(x_{c}p_{T})\nonumber \\&\quad \times \left[ 1+{\mathscr {C}}_{cud}\left( x_{c}p_{T},x_{u}p_{T},x_{d}{p_{T}}\right) \right] =1,\end{aligned}$$
(38)
$$\begin{aligned}&A_{D^{0}}\int dp_{T} f_{c}^{(n)}(x_{c}^{\prime }p_{T})f_{\bar{u}}^{(n)}(x_{u}^{\prime }p_{T})\nonumber \\&\quad \times \left[ 1+{\mathscr {C}}_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) \right] =1, \end{aligned}$$
(39)

which means that terms in square bracket in Eq. (33), as a global quantity, mainly influences the shape of the \(\varLambda _{c}^{+}/D^{0}\) ratio but not its global magnitude. Therefore, \(R^{(N_{q_{i}})}\) in Eq. (33) plays the role of controlling the global magnitude of \(\varLambda _{c}^{+}/D^{0}\) ratio. In this section, we discuss the property of \(R^{(N_{q_{i}})}\) defined in Eq. (34).

We take

$$\begin{aligned} \left\langle \frac{N_{udc}}{N_{qq}}\right\rangle&\approx \frac{\left\langle N_{u}\right\rangle ^{2}\left\langle N_{c}\right\rangle }{\left\langle N_{q}\right\rangle ^{2}},\end{aligned}$$
(40)
$$\begin{aligned} \left\langle \frac{N_{c\bar{u}}}{N_{\bar{q}}}\right\rangle&\approx \frac{\left\langle N_{\bar{u}}\right\rangle \left\langle N_{c}\right\rangle }{\left\langle N_{\bar{q}}\right\rangle }. \end{aligned}$$
(41)

Here, we use the approximations \(\left\langle N_{\bar{u}}\right\rangle =\left\langle N_{\bar{d}}\right\rangle =\left\langle N_{u}\right\rangle =\left\langle N_{d}\right\rangle \) and \(\left\langle N_{\bar{q}}\right\rangle =\left\langle N_{q}\right\rangle \) in the mid-rapidity range at LHC energies. We neglect quark number correlations among different flavors by considering the small off-diagonal susceptibilities of quark flavors in Lattice-QCD calculations [50].

In order to obtain intuitive expression, we define a strangeness suppression factor

$$\begin{aligned} \lambda _{s}=\frac{\left\langle N_{\bar{s}}\right\rangle }{\left\langle N_{\bar{u}}\right\rangle }. \end{aligned}$$
(42)

By noticing that \(\left\langle N_{q}\right\rangle =\left\langle N_{u}\right\rangle +\left\langle N_{d}\right\rangle +\left\langle N_{s}\right\rangle =(2+\lambda _{s})\left\langle N_{u}\right\rangle \), we obtain

$$\begin{aligned} R^{\left( N_{q_{i}}\right) }=2R_{B/M}^{(c)}\frac{C_{\varLambda _{c}}}{C_{D^{0}}}\frac{1}{2+\lambda _{s}}. \end{aligned}$$
(43)

The branch fraction parameters \(C_{\varLambda _{c}}\) and \(C_{D^{0}}\) directly influence \(R^{\left( N_{q_{i}}\right) }\). However, experimental data of \(\varLambda _{c}^{+}\) and \(D^{0}\) usually contain the contribution of strong and electromagnetic decays of other single-charm hadrons. Considering these decay contributions, the numerator in Eq. (34) for final-state \(\varLambda _{c}^{+}\) is

$$\begin{aligned} {\varLambda _{c}^{+}}^{(final)}&= \left( C_{\varLambda _{c}^{+}}+C_{\varSigma _{c}^{+}} + C_{\varLambda _{c}^{(*+)}} + C_{\varSigma _{c}^{(*+)}}\right) N_{iter,ud}\left\langle \frac{N_{udc}}{N_{qq}}\right\rangle \nonumber \\&\quad +\left( C_{\varSigma _{c}^{++}}+C_{\varSigma _{c}^{*++}} +C_{\varSigma _{c}^{(*++)}} \right) N_{iter,uu}\left\langle \frac{N_{uuc}}{N_{qq}}\right\rangle \nonumber \\&\quad +\left( C_{\varSigma _{c}^{0}}+C_{\varSigma _{c}^{*0}} + C_{\varSigma _{c}^{(*0)}} \right) N_{iter,dd}\left\langle \frac{N_{ddc}}{N_{qq}}\right\rangle \nonumber \\&=\left\langle \frac{N_{uuc}+2N_{udc}+N_{ddc}}{N_{qq}}\right\rangle \nonumber \\&\approx \frac{4}{\left( 2+\lambda _{s}\right) ^{2}}\left\langle N_{c}\right\rangle . \end{aligned}$$
(44)

Here, \(\varLambda _{c}^{+}\), \(\varSigma _{c}^{0,+,++}\) and \(\varSigma _{c}^{*0,*+,*++}\) denote ground states, which are major contribution to final-state \(\varLambda _{c}^{+}\). \(\varLambda _{c}^{(*+)}\) and \(\varSigma _{c}^{(*0,*+,*++)}\) denote excitation states, which have weak contribution due to the smaller production abundance. We have considered that the dominant decay channels of these hadrons are \(\varLambda _c^{+}+\pi 's\). We have used the summation rule \(\sum _{B_{cll'}}C_{B_{cll'}}=1\) with same quark \(cll'\) composition, see discussions below Eq. (18). For final-sate \(D^{0}\), the dominant decay contribution comes from \(D^{*0}\) and \(D^{*+}\) in ground state. Decay contributions from excitation states such as \(D_{0}^{*}(2300)\), \(D_1(2430)\) and \(D_{2}^{*}(2460)\) are small due to heavier masses. Because the decay branch ratios of these hadrons are poorly measured at present, we neglect them in final-state \(D^0\) calculation and obtain

$$\begin{aligned}&{D^{0}}^{(final)} \nonumber \\&\quad = C_{D^{0}}\left\langle \frac{N_{c\bar{u}}}{N_{\bar{q}}}\right\rangle +C_{D^{*0}}\left\langle \frac{N_{c\bar{u}}}{N_{\bar{q}}}\right\rangle +{\mathscr {B}}_{D^{*+}\rightarrow D^{0}}C_{D^{*+}}\left\langle \frac{N_{c\bar{d}}}{N_{\bar{q}}}\right\rangle \nonumber \\&\quad =\left( 1+{\mathscr {B}}_{D^{*+}\rightarrow D^{0}}C_{D^{*+}}\right) \left\langle \frac{N_{c\bar{u}}}{N_{\bar{q}}}\right\rangle \nonumber \\&\quad \approx \left( 1+{\mathscr {B}}_{D^{*+}\rightarrow D^{0}}C_{D^{*+}}\right) \frac{1}{2+\lambda _{s}}\left\langle N_{c}\right\rangle . \end{aligned}$$
(45)

Here, we have simplified the summation rule \(\sum _{M_{c\bar{u}}}C_{M_{c\bar{u}}}=1\) by \(C_{D^0}+C_{D^{*0}}=1\) to exhaust all destination of \(c\bar{u}\) combinations, which can compensate effects of excitation states to a certain extent. The decay branch ratio \({\mathscr {B}}_{D^{*+}\rightarrow D^{0}}=0.677\) is taken from particle data group [51]. The branch fraction parameter \(C_{D^{*+}}\) is about 0.6 since the ratio \(D^{*0}/D^{0}\) is about 0.43 [52].

With Eqs. (44) and (45) we obtain \(R^{\left( N_{q_{i}}\right) }\) for final-state \(\varLambda _{c}^{+}/D^{0}\) ratio

$$\begin{aligned} R^{\left( N_{q_{i}},final\right) }&=R_{B/M}^{(c)}\frac{1}{1+0.677C_{D^{*+}}}\frac{4}{2+\lambda _{s}}\nonumber \\&=R_{B/M}^{(c)}\frac{2.85}{2+\lambda _{s}}. \end{aligned}$$
(46)

According to our estimations in previous work [5, 28], strangeness suppression factor \(\lambda _{s}\) in low multiplicity events is about 0.3 and that in high multiplicity events is about 0.36 in pp collisions at LHC energies. This change of \(\lambda _{s}\) causes little influence on \(R^{\left( N_{q_{i}}\right) }\) through the term \(2+\lambda _{s}\) and therefore contribute little to multiplicity dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio.

\(R_{B/M}^{(c)}\) is a dynamic parameter in our model that denotes the production competition between baryon formation via combination with two light-flavor quarks and meson formation via combination with an antiquark at a charm quark hadronization. In the environment of abundant light-flavor quarks and antiquarks, the charm quark has sufficient chance to interact with surrounding light-flavor quarks and antiquarks, and the baryon-to-meson production competition is sufficient and therefore we expect \(R_{B/M}^{(c)}\) should be saturated. Assuming color of quarks and antiquarks is stochastically distributed, the probability of a charm quark with the given color encountering an antiquark with right anti-color to form a colorless state is 1/3 while that of a charm quark with the given color encountering two light-flavor quarks with right colors to form a colorless state is 1/9. This color counting gives the relative probability 1/3 of baryon formation against meson formation at charm quark hadronziation. There may exist some correlation in colors of two light-flavor quarks. In one gluon exchange picture, two quarks in color anti-triplet state have attractive interactions and these in color sextet have repulsive interactions. The probability of two light-flavor quarks in color anti-triplet state will be greater than that in color sextet state. This will increase the relative probability of baryon formation at charm quark hadronization. In Refs. [53, 54] the correlated two light-flavor quarks in color and flavor anti-triplet are regarded as a kind of quasi-particle (i.e., diquark) at hadronization and their recombination with charm quark contributes a new source of charm baryon production which can significantly increase the production of \(\varLambda _c^+\). From these considerations we generally expect \(R_{B/M}^{(c)}\gtrsim 1/3\) for the charm quark hadronization in the environment of rich light-flavor quarks and antiquarks.

In the low multiplicity events this baryon-to-meson production competition is not sufficient due to the restricted numbers of light-flavor quarks and/or antiquarks. For example, in event multiplicity class X with mid-rapidity \(\left\langle dN_{ch}/d\eta \right\rangle =2.52\) in pp collisions at \(\sqrt{s}=\) 13 TeV [55], the up quark number density is \(\left\langle dN_{u}/dy\right\rangle =1.48\) at mid-rapidity according to our previous study on multiplicity dependence of light-flavor hadron production [5]. Events with a charm quark and up/down quark with numbers \((N_{u},N_{d})=(2,0),(0,2)\) can not form \(\varLambda _{c}^{+}\). Events with \((N_{u},N_{d})=(2,1)\) only provide one effective ud pair for \(\varLambda _{c}^{+}\) formation but can provide three light-flavor antiquarks for charm meson formation. Therefore, the formation of \(\varLambda _{c}^{+}\) in these events is suppressed relative to D mesons. The fraction of these events should not be too small due to the small values of \(\left\langle dN_{u,d}/dy\right\rangle \) in low multiplicity events. Therefore, we can expect the suppression of \(R_{B/M}^{(c)}\) and corresponding \(\varLambda _{c}^{+}/D^{0}\) ratio to a certain extent in low multiplicity events in pp collisions at \(\sqrt{s}= 13\) TeV.

The exact magnitude of such suppression is dependent on the property of quark number distribution event-by-event, which is little known at present. Here, we take the Poisson distribution as an example to roughly estimate the magnitude of this suppression. We assume the joint distribution of quark numbers as

$$\begin{aligned} P(N_{u},N_{d})={{\text {Poi}}}(N_{u}){\text {Poi}}(N_{d}) \end{aligned}$$
(47)

with mean number \(\left\langle N_{u}\right\rangle =\left\langle N_{d}\right\rangle \). The number of \(\bar{u}\) and that of \(\bar{d}\) are taken to be \(N_{\bar{u}}=N_{u}\) and \(N_{\bar{d}}=N_{d}\), respectively. That is, we consider the pair production in each event, for simplicity. For events with V0M multiplicity classes IX and X with \(\left\langle dN_{ch}/d\eta \right\rangle =4.64, 2.52\) [55], the u quark number is about \(\left\langle N_{u}\right\rangle =1.5{-}2.5\) according to our previous study of light-flavor hadrons in pp collisions at \(\sqrt{s}=13\) TeV [5]. The fraction of events that can form \(D^{0}\) but not \(\varLambda _{c}^{+}\) is

$$\begin{aligned} P^{\prime }=\frac{1}{P_{nor}}\sum _{N_{u}=1}^{\infty }P(N_{u},0)=0.08{-}0.18 \end{aligned}$$
(48)

with \(P_{nor}=\sum _{N_{u},N_{d}}P(N_{u},N_{d})-P(0,0)\). In addition, the fraction of events that can form \(D^{0}\) but not \(\varSigma _{c}^{0}\) or \(\varSigma _{c}^{*0}\) which finally decays into \(\varLambda _{c}^{+}\) is

$$\begin{aligned} P^{''}=\frac{1}{P_{nor}}\sum _{N_{u}=1}^{\infty }P(N_{u},1)=0.19{-}0.27. \end{aligned}$$
(49)

The fraction of events that can not form \(\varSigma _{c}^{++}\) or \(\varSigma _{c}^{*++}\) is also \(P^{''}\). These estimations therefore indicate a magnitude of about 20% suppression for \(R_{B/M}^{(c)}\) in low multiplicity events in comparison with that in high multiplicity events where the above suppression is absent.

In our previous works in study of single-charm hadrons in pp and pPb collisions at LHC energies [18, 27], we use \(R_{B/M}^{(c)}=0.425\pm 0.025\). If we take this value as the possibly saturated value in high multiplicity event, we estimate that \(R_{B/M}^{(c)}\) in low multiplicity events is about 0.34. Therefore, we expect

$$\begin{aligned} R^{\left( N_{q_{i}},final\right) }&=R_{B/M}^{(c)}\frac{2.85}{2+\lambda _{s}}\nonumber \\&\approx {\left\{ \begin{array}{ll} 0.51 &{} \text {in high }\left\langle dN_{ch}/d\eta \right\rangle \ \text {events}\\ 0.42 &{} \text {in low }\left\langle dN_{ch}/d\eta \right\rangle \ \text {events} \end{array}\right. }. \end{aligned}$$
(50)
Fig. 1
figure 1

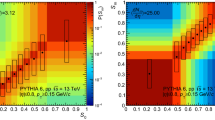
The normalized \(p_{T}\) spectra of up quarks in three multiplicity classes in pp collisions at \(\sqrt{s}=13\) TeV (a), the calculated \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) in multiplicity class I with \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) at mid-rapidity (b) and that in multiplicity class IX with \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\) (c). The solid lines in b and c are directly calculated from the definition by Eq. (36) and the dashed lines are the approximations by Eq. (53)

Full size image

5 The property of \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \)

Because \(m_{c}\approx 5m_{u}\), the momentum fraction of up/down quark \(x_{u}^{\prime }=m_{u}/(m_{c}+m_{u})=0.167\) in \(D^{0}\) is close to \(x_{u}=m_{u}/(m_{c}+2m_{u})\approx 0.143\) in \(\varLambda _{c}^{+}\). The difference between them is quite small

$$\begin{aligned} \varDelta x_{u} =x_{u}^{\prime }-x_{u}=\frac{m_{u}^{2}}{(m_{c}+m_{u})(m_{c}+2m_{u})}\approx 0.024. \end{aligned}$$
(51)

In the studied range \(p_{T}\lesssim 8\) GeV/c, the momentum difference \(\varDelta x_{u}p_{T}\lesssim 0.2\) GeV/c is also small. In order to simplify \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \), we can take Taylor expansion for \(f_{u}(x_{u}p_{T})\)

$$\begin{aligned} f_{u}^{(n)}\left( x_{u}p_{T}\right)&=f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) \Bigg [1-\frac{f_{u}^{(n)'}\left( x_{u}^{\prime }p_{T}\right) }{f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) }\varDelta x_{u}p_{T} \nonumber \\&\quad +\frac{1}{2}\frac{f_{u}^{(n)''}\left( x_{u}^{\prime }p_{T}\right) }{f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) }\left( \varDelta x_{u}p_{T}\right) ^{2}+\cdots \Bigg ], \end{aligned}$$
(52)

where the contribution of perturbative terms is quite small, i.e., about \(0.01\sim 0.07\) as \(p_{T}<8\) GeV/c. Therefore, the light-flavor part \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) becomes

$$\begin{aligned}&R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) =\frac{\left[ f_{u}^{(n)}(x_{u}p_{T})\right] ^{2}}{f_{u}^{(n)}(x_{u}^{\prime }p_{T})} \nonumber \\&\quad =f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) \Bigg [1-\frac{f_{u}^{(n)'}\left( x_{u}^{\prime }p_{T}\right) }{f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) }\varDelta x_{u}p_{T} \nonumber \\&\qquad +\frac{f_{u}^{(n)''}\left( x_{u}^{\prime }p_{T}\right) }{f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) }\left( \varDelta x_{u}p_{T}\right) ^{2}+\cdots \Bigg ]^{2}\nonumber \\&\quad =f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) \left[ 1-2\frac{f_{u}^{(n)'}\left( x_{u}^{\prime }p_{T}\right) }{f_{u}^{(n)}\left( x_{u}^{\prime }p_{T}\right) }\varDelta x_{u}p_{T}+\cdots \right] \nonumber \\&\quad \approx f_{u}^{(n)}\left( (x_{u}^{\prime }-2\varDelta x_{u})p_{T}\right) . \end{aligned}$$
(53)

We see that \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) directly depends on the property of \(p_{T}\) spectrum of up/down quarks.

In Fig. 1a, we show the normalized \(p_{T}\) spectra of up quarks \(f_{u}^{(n)}(p_{T})\) in the low \(p_{T}\) range (i.e., \(p_{T,u}\lesssim 2\) GeV/c) in three multiplicity classes in pp collisions at \(\sqrt{s}=13\) TeV, which are obtained in previous work [5] by fitting experimental data for \(p_{T}\) spectra of proton at mid-rapidity using our EVC model. We see that \(f_{u}^{(n)}(p_{T})\) is different in three multiplicity classes. In Fig. 1b, we show the property of \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) in high multiplicity class I with \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) at mid-rapidity. Here, the V0M multiplicity classes are defined in Ref. [55]. The solid line denotes the result of direct calculation of \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) by the definition Eq. (36) and the dashed line is the approximation by Eq. (53). We see that the approximation is very good. We further see that \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) increases with \(p_{T}\) in the range \(0<p_{T}\lesssim 3\) GeV/c and decreases with \(p_{T}\) at larger \(p_{T}\). This property will cause the non-monotonic \(p_{T}\) dependence of ratio \(\varLambda _{c}^{+}/D^{0}\) which is exhibited in experimental data in high multiplicity class. We emphasize that the property of \(f_{u}^{(n)}(p_{T})\) actually determines the \(p_{T}\) dependence of the ratio \(\varLambda _{c}^{+}/D^{0}\) to a large extent. In Fig. 1c, we show the property of \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) in low multiplicity class IX with \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\) at mid-rapidity. We see that \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) only has a small shoulder structure in the range \(p_{T}\lesssim 1\) GeV/c and then decreases with \(p_{T}\). This is the direct consequence of \(f_{u}^{(n)}(p_{T})\) in the low multiplicity class which exhibits less convex behavior in the low \(p_{T}\) range, see the dot-dashed line in Fig. 1a. Comparing Fig. 1b and c, we emphasize that the multiplicity dependence of light-flavor quark spectrum \(f_{u}^{(n)}(p_{T})\) will lead to the significant multiplicity dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio as a function of \(p_{T}\).

Fig. 2
figure 2

Panel a: The differential cross-section of charm quarks at mid-rapidity in pp collisions at \(\sqrt{s}=13\) TeV calculated by FONLL method. The shadow area denotes scale uncertainties. The solid line shows the fit of central points of theoretical calculations with Eq. (55). Panel b: \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \) for the result of FONLL and these of PYTHIA8 in three multiplicity classes

Full size image

6 The property of \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \)

Because the difference between momentum fraction of charm quarks in \(D^{0}\) and that in \(\varLambda _{c}^{+}\)

$$\begin{aligned} \varDelta x_{c} =x_{c}^{\prime }-x_{c}=\frac{m_{c}m_{u}}{(m_{c}+m_{u})(m_{c}+2m_{u})}\approx 0.12 \end{aligned}$$
(54)

is not quite small, the momentum difference is \(\varDelta x_{c}p_{T}\lesssim 1.2\) GeV/c in the studied range \(p_{T}\lesssim 10\) GeV/c. Taylor expansion is not generally effective to simplify \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) =f_{c}^{(n)}(x_{c}p_{T})/f_{c}^{(n)}(x'_{c}p_{T})\). Therefore, we take the specific form of \(f_{c}^{(n)}(p_{T})\) and directly evaluate \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \).

In practice, we take the following parameterization for \(p_{T}\) spectrum of charm quarks

$$\begin{aligned} f_{c}^{(n)}\left( p_{T}\right) =\mathscr {N}p_{T}^{b}\left( 1+\frac{\sqrt{p_{T}^{2}+M^{2}}-M}{nc}\right) ^{-n}, \end{aligned}$$
(55)

where b, n, M, c are parameters with positive values and \(\mathscr {N}\) is the normalization coefficient. This function can usually well fit the \(p_{T}\) spectrum of charm quarks obtained from theoretical method as well as these of single-charm hadrons measured by experiments. Substituting Eq. (55) into (35), we obtain

$$\begin{aligned} R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right)&=\frac{f_{c}^{(n)}(x_{c}p_{T})}{f_{c}^{(n)}(x_{c}^{\prime }p_{T})}\nonumber \\&=\left( \frac{x_{c}}{x_{c}^{\prime }}\right) ^{b}\left( \frac{nc-M+\sqrt{\left( x_{c}^{\prime }p_{T}\right) ^{2}+M^{2}}}{nc-M+\sqrt{\left( x_{c}p_{T}\right) ^{2}+M^{2}}}\right) ^{n}, \end{aligned}$$
(56)

which is increasing slowly with \(p_{T}\) due to the positive exponent n and \(x_{c}^{\prime }>x_{c}\).

We apply the online calculator of FONLL theoretical method [56, 57] to calculate \(p_{T}\) spectrum of charm quarks in pp collisions at \(\sqrt{s}= 13\) TeV. The result is shown in Fig. 2a, where the shadow area denotes the scale uncertainties in calculations. The solid line is the fit to center values of FONLL calculations by Eq. (55) with parameter values \(b=1.3\), \(M=6.4\) GeV/c, \(n=4.16\), and \(c=0.34\) GeV/c. Figure 2b shows the calculated \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \). We see that it monotonically increases with \(p_{T}\) and changes about one time in the range \(p_{T}<10\) GeV/c. We also run PYTHIA 8 (version 8.243) [58] to obtain the \(p_{T}\) spectra of charm quarks in three multiplicity classes and calculate their \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \). Here, the low, intermediate and high multiplicity classes are defined as events within multiplicity intervals [1,10], [11,19] and [20,60] with the multiplicity \(\left\langle dN_{ch}/d\eta \right\rangle = 4.4, 14.3\) and 25.0 within the pseudo-rapidity interval \(\left| \eta \right| <0.5\), respectively. Results of \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \) are shown in Fig. 2b. We see that \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \) calculated by PYTHIA8 has a certain multiplicity dependence and its \(p_{T}\) dependence is similar to that of FONLL calculations.

7 The possible property of \(R_{corr}^{(cl)}\left( p_{T}\right) \)

The term \(R_{corr}^{(cl)}\left( p_{T}\right) \) defined in Eq. (37) denotes effects of momentum correlations among different quark flavors on the \(p_{T}\) dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio. It contains two correlation functions \(C_{cud}(x_{c}p_{T},x_{u}p_{T},x_{d}p_{T})\) and \(C_{c\bar{u}}(x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T})\). In the case of vanishing momentum correlations \(C_{cud}=0\) and \(C_{c\bar{l}}=0\), \(R_{corr}^{(cl)}\left( p_{T}\right) =1\) and contributes trivially to \(\varLambda _{c}^{+}/D^{0}\) ratio.

In high energy pp collisions, charm quarks are dominantly produced by initial hard parton-parton scattering process and possibly interact with neighboring light-flavor (anti-)quarks before they hadronize. Part of these interactions is non-perturbative and is difficult to calculated from the first principles. On the other hand, quark momentum correlations are also difficult to be reversely obtained from experimental data which are mainly of inclusive distributions of particles at present.

In order to roughly understand the possible property of \(R_{corr}^{(cl)}\left( p_{T}\right) \) and its influence on \(\varLambda _{c}^{+}/D^{0}\) ratio in pp collisions, we apply the event generator PYTHIA 8 (version 8.243) with default tunes, as an example, to study the possible property of \(R_{corr}^{(cl)}\left( p_{T}\right) \). We use PYTHIA8 to firstly calculate \(f_{c\bar{u}}(\) \(p_{T,c}, p_{T,\bar{u}},\varDelta \phi _{c\bar{u}})\) at \(\left| y\right| <0.5\) where \(\varDelta \phi _{c\bar{u}}\) is the azimuthal angle difference between \(\bar{u}\) and c. Then we take the limit \(p_{T,\bar{u}}\rightarrow p_{T,c}m_{u}/m_{c}\) and \(\varDelta \phi _{c\bar{u}}\rightarrow 0\) for \(f_{c\bar{u}}(p_{T,c},p_{T,\bar{u}},\varDelta \phi _{c\bar{u}})\) to obtain the \(f_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) \) and corresponding \({\mathscr {C}}_{c\bar{u}}\big (x_{c}^{\prime }p_{T},\) \(x_{u}^{\prime }p_{T}\big )\) by Eq. (30).

Because the fraction of the event simultaneously consisting of u, d, and c in the mid-rapidity range \(\left| y\right| <0.5\) is very small, it is very hard to directly calculate \(f_{cud}\big (x_{c}p_{T},x_{u}p_{T},\) \(x_{d}p_{T}\big )\), in particular, in low multiplicity events. In the general multi-variable statistics \(\left\langle abc\right\rangle =\left\langle a\right\rangle \left\langle b\right\rangle \left\langle c\right\rangle +\left\langle a\right\rangle C_{bc}+\left\langle b\right\rangle C_{ac}+\left\langle c\right\rangle C_{ab}+C_{abc}\), \(C_{ab}\) is standard two-body correlation and \(C_{abc}\) is three-body correlation which is a higher order term compared with two-body correlations. Here, we neglect the contribution of high-order correlation \(C_{cud}\) and obtain

$$\begin{aligned}&{\mathscr {C}}_{udc}\left( x_{u}p_{T},x_{d}p_{T},x_{c}p_{T}\right) \nonumber \\&\quad \approx {\mathscr {C}}_{ud}\left( x_{u}p_{T},x_{d}p_{T}\right) + {\mathscr {C}}_{cu}\left( x_{c}p_{T},x_{u}p_{T}\right) \nonumber \\&\qquad + {\mathscr {C}}_{cd}\left( x_{c}p_{T},x_{d}p_{T}\right) , \end{aligned}$$
(57)

and then we obtain

$$\begin{aligned}&R_{corr}^{(cl)}\left( p_{T}\right) \nonumber \\&\quad =\frac{1}{1+{\mathscr {C}}_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) } \Big ( 1+{\mathscr {C}}_{ud}\left( x_{u}p_{T},x_{d}p_{T}\right) \nonumber \\&\qquad +{\mathscr {C}}_{cu}\left( x_{c}p_{T},x_{u}p_{T}\right) +{\mathscr {C}}_{cd}\left( x_{c}p_{T},x_{d}p_{T}\right) \Big ) \nonumber \\&\quad \approx 1+{\mathscr {C}}_{ud}\left( x_{u}p_{T},x_{d}p_{T}\right) +2{\mathscr {C}}_{cu}\left( x_{c}p_{T},x_{u}p_{T}\right) \nonumber \\&\qquad -{\mathscr {C}}_{c\bar{u}}\left( x_{c}^{\prime }p_{T},x_{u}^{\prime }p_{T}\right) . \end{aligned}$$
(58)

In the second line, we have assumed that \({\mathscr {C}}_{c\bar{u}}\) is small and \({\mathscr {C}}_{cu}\approx {\mathscr {C}}_{cd}\).

In Fig. 3, we show results of two-quark correlation \({\mathscr {C}}_{q_{1}q_{2}}\) as the function of \(p_{T}\) in low multiplicity events with \(\left\langle dN_{ch}/d\eta \right\rangle \) \(=4.4\) and those in high multiplicity events with \(\left\langle dN_{ch}/d\eta \right\rangle =25.0\). We see that \({\mathscr {C}}_{ud}\), \({\mathscr {C}}_{cu}\) and \({\mathscr {C}}_{c\bar{u}}\) are very small in both low and high multiplicity events. We emphasize that these statistics only serve as a qualitatively estimation because of the following reasons. Quarks and antiquarks are only small fractions of final-state parton system in PYTHIA simulations. Gluons that take large fraction of the parton system are not involved in current statistics. Non-perturbative interactions of these quarks and gluons near hadronization are not fully simulated in PYTHIA8, which may generate some momentum correlations among quarks and antiquarks of different flavors. In addition, collectivity or collective flow of partons may be formed in high multiplicity events [59,60,61,62,63], which may also generate some momentum correlations among quarks and antiquarks. These possible influences on \(R_{corr}^{(cl)}\left( p_{T}\right) \) are left for future study. In this paper, we take \(R_{corr}^{(cl)}\left( p_{T}\right) \approx 1\) for the moment in the following studies.

Fig. 3
figure 3

Two quark correlations \({\mathscr {C}}_{q_{1}q_{2}}\) as the function of \(p_{T}\) in low and high multiplicity events calculated by PYTHIA8

Full size image
Fig. 4
figure 4

\(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) in low and high multiplicity events in pp collisions at \(\sqrt{s}=13\) TeV (a) and the comparison with experimental data [23] (b). See text for the detailed discussions

Full size image

8 Result of \(\varLambda _{c}^{+}/D^{0}\) ratio

In this section, we combine effects of above four terms to calculate the \(\varLambda _{c}^{+}/D^{0}\) ratio and compare with the latest data of ALICE collaboration [23]. Here, we neglect the effect of the momentum correlation \(R_{corr}^{(cl)}\left( p_{T}\right) \) between charm quarks and light-flavor (anti-)quarks by taking \(R_{corr}^{(cl)}\left( p_{T}\right) \approx 1\). This is equivalent to the independence approximation for the joint momentum distribution \(f_{c\bar{l}}\left( p_{T,c},p_{T,\bar{l}}\right) =f_{c}\left( p_{T,c}\right) f_{\bar{l}}\left( p_{T,\bar{l}}\right) \) and \(f_{cll'}\left( p_{T,c},p_{T,l},p_{T,l'}\right) =f_{c}\left( p_{T,c}\right) \) \(f_{l}\left( p_{T,l}\right) f_{l'}\left( p_{T,l'}\right) \). In this case,

$$\begin{aligned} \frac{f_{\varLambda _{c}}(p_{T})}{f_{D^{0}}(p_{T})}\approx R^{(N_{q_{i}})}\left[ \frac{A_{\varLambda _{c}}}{A_{D^{0}}}R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \right] \end{aligned}$$
(59)

where the properties of \(R^{(N_{q_{i}})}\), \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) and \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \) are already shown in Eqs. (46), (53) and (56). Coefficients \(A_{D^{0}}\) and \(A_{\varLambda _{c}}\) can be calculated by Eqs. (9) and (10) with the inclusive distributions of charm and light-flavor quarks shown in Figs. 1 and 2.

In order to study the multiplicity dependence of the \(\varLambda _{c}^{+}/D^{0}\) ratio, we take the light-flavor quark spectrum \(f_{l}(p_{T})\) in event class \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) (class I) and \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\) (class IX) as examples of high multiplicity events and low multiplicity events, respectively. For charm quark \(p_{T}\) spectrum \(f_{c}(p_{T})\), we have two choices. One is that of FONLL calculation and we use it in both high multiplicity events and low multiplicity events. Another is that of PYTHIA8 calculation in Sect. 6 where we have obtained \(f_{c}(p_{T})\) in high multiplicity events \(\left\langle dN_{ch}/d\eta \right\rangle =25.0\) and that in low multiplicity events \(\left\langle dN_{ch}/d\eta \right\rangle =4.4\). The term \(R^{(N_{q_{i}})}\) contains two multiplicity-dependent factors \(\lambda _{s}\) and \(R_{B/M}^{(c)}\). As shown by Eq. (46), strangeness suppression factor \(\lambda _{s}\) causes little change on \(\varLambda _{c}^{+}/D^{0}\) ratio and we can safely neglect its multiplicity dependence. Baryon-to-meson production competition factor \(R_{B/M}^{(c)}\) is a relatively-free parameter which cannot be fixed in our model at present. In Sect. 4, we have discussed its possible multiplicity dependence.

In Fig. 4a, we show results of \(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) in high multiplicity events and low multiplicity events at given \(R_{B/M}^{(c)}=0.425\). The purpose of taking the same \(R_{B/M}^{(c)}\) is to let us focus on the influence of \(p_{T}\) spectra of light-flavor quarks and charm quarks on the \(p_{T}\) dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio. Here, high multiplicity corresponds to \(\left\langle dN_{ch}/d\eta \right\rangle \approx 25\) since we combine effect of \(f_{l}(p_{T})\) in event class \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) (class I) and that of \(f_{c}(p_{T})\) in events with \(\left\langle dN_{ch}/d\eta \right\rangle =25.0\) in PYTHIA8 calculations. Low multiplicity corresponds to \(\left\langle dN_{ch}/d\eta \right\rangle \approx 4.5\) since we combine effect of \(f_{l}(p_{T})\) in event class \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\) (class IX) and that of \(f_{c}(p_{T})\) in events with \(\left\langle dN_{ch}/d\eta \right\rangle =4.4\) in PYTHIA8 calculations. The dot-dashed line with shadow band is the result when \(f_{c}(p_{T})\) calculated by FONLL and \(f_{l}(p_{T})\) in high multiplicity events are used. The dotted line with shadow band is the result when \(f_{c}(p_{T})\) calculated by FONLL and \(f_{l}(p_{T})\) in low multiplicity events are used. Comparing two results, we see an obvious multiplicity dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio caused by that of light-flavor quark spectrum. As \(p_{T}\gtrsim 3\) GeV/c, the \(\varLambda _{c}^{+}/D^{0}\) ratio in high multiplicity events is obviously higher than that in low multiplicity events. This is because \(f_{l}(p_{T})\) in high multiplicity events is obviously flatter than that in low multiplicity events, see Fig. 1a. As \(p_{T}\lesssim 3\) GeV/c, the situation is reversed. This is because at the same \(R_{B/M}^{(c)}\) the ratio of \(p_{T}\)-integrated yield of \(\varLambda _{c}^{+}\) to \(D^{0}\) is almost the same, the suppression of \(\varLambda _{c}^{+}\) at \(p_{T}\gtrsim 3\) GeV/c in low multiplicity events is offset by the enhancement of \(\varLambda _{c}^{+}\) at low \(p_{T}\). We also show the result of \(\varLambda _{c}^{+}/D^{0}\) ratio when the \(f_{c}(p_{T})\) calculated by PYTHIA8 in high multiplicity events is applied. The result, the solid line, is higher than that with FONLL calculated \(f_{c}(p_{T})\) in low \(p_{T}\) range and is slightly smaller than the latter as \(p_{T}\gtrsim 3\) GeV/c. In the range \(3\lesssim p_{T}\lesssim 8\) GeV/c, the result of \(\varLambda _{c}^{+}/D^{0}\) ratio with \(f_{c}(p_{T})\) calculated by PYTHIA8 in low multiplicity events, the dashed line, is also slightly smaller than that with FONLL calculated \(f_{c}(p_{T})\). Comparing results using FONLL calculated \(f_{c}(p_{T})\) with those using PYTHIA8 calculated \(f_{c}(p_{T})\), we see a weak influence of \(f_{c}(p_{T})\) uncertainty on \(\varLambda _{c}^{+}/D^{0}\) ratio.

In addition, we see that \(\varLambda _{c}^{+}/D^{0}\) ratios in our model in both high and low multiplicity events always exhibit a non-monotonic \(p_{T}\) dependence. This is mainly because of the property of \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) in Eq. (53), which is determined by the property of \(p_{T}\) spectrum of light-flavor quark as shown in Fig. 1b and c. The term \(R_{\varDelta x_{c}}^{(c)}\left( p_{T}\right) \), as shown in Fig. 2b, strengthens the increase of the \(\varLambda _{c}^{+}/D^{0}\) ratio in the low \(p_{T}\) range \((p_{T}\lesssim 2-{3}\) GeV/c) but offsets the decrease of the \(R_{\varDelta x_{l}}^{(l)}\left( p_{T}\right) \) as \(p_{T}\gtrsim 3\) GeV/c to a certain extent and leads to the relatively weak decrease of the \(\varLambda _{c}^{+}/D^{0}\) ratio as \(p_{T}\gtrsim 3\) GeV/c.

Fig. 5
figure 5

\(p_{T}\) spectra of \(D^{0}\), \(D_{s}^{+}\) (a) and \(\varLambda _{c}^{+}\) (b) in inelastic pp collisions at \(\sqrt{s}=13\) TeV. Lines are model results and symbols are experimental data [23]

Full size image

In Fig. 4b, we test above theoretical results by experimental data of \(\varLambda _{c}^{+}/D^{0}\) ratio in pp collisions at \(\sqrt{s}=13\) TeV [23]. Here, we show data of \(\varLambda _{c}^{+}/D^{0}\) ratio in V0M multiplicity class with \(\left\langle dN_{ch}/d\eta =31.5\right\rangle \) as an example of high multiplicity events and data in V0M multiplicity class with \(\left\langle dN_{ch}/d\eta =4.4\right\rangle \) as an example of low multiplicity events. Because the light-flavor quark \(p_{T}\) spectrum used in our calculation is extracted from experimental data of light-flavor hadrons in V0M event class I with \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) and class IX with \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\), the underlying events of our theoretical calculations are not exactly the same as those for data of \(\varLambda _{c}^{+}/D^{0}\) ratio but the difference should be small due to the similar multiplicity. In high multiplicity events, we see that theoretical result with FONLL calculated \(f_{c}(p_{T})\), the dot-dashed line, is consistent with the first two datum points with \(p_{T}<3\) GeV/c and is higher than data at larger \(p_{T}\) to a certain extent. Theoretical result with PYTHIA8 calculated \(f_{c}(p_{T})\) in high multiplicity events, the solid line, is closer to experimental data in comparison with that with FONLL calculated \(f_{c}(p_{T})\). Here, the baryon-to-meson competition factor \(R_{B/M}^{(c)}\) is taken to be 0.425, the possible saturation value in high multiplicity events.

According to discussions in Sect. 4, we expect a suppression of \(R_{B/M}^{(c)}\) in low multiplicity events and a rough estimation based on Poisson distribution of quark numbers gives about 20% suppression. Therefore, here we use \(R_{B/M}^{(c)}=0.34\) to calculate the \(\varLambda _{c}^{+}/D^{0}\) ratio in low multiplicity events. We see a good agreement with experimental data in the available \(p_{T}\) range. This indicates that the essential baryon/meson competition dynamics after peeling off the effect of finite quark numbers in low multiplicity events can be similar to that in high multiplicity events. In above comparison with experimental data, we have considered the decay contributions of other single-charm hadrons to \(\varLambda _{c}^{+}/D^{0}\) ratio by the yield term \(R^{(N_{q_{i}})}\) Eq. (46). The decay influence on the shape of \(\varLambda _{c}^{+}/D^{0}\) ratio (as the function of \(p_{T}\)) is numerically studied and is found to be quite small and therefore the comparison with experimental data in Fig. 4b is little changed.

Some comments on the comparison of our model results with available predictions of other theoretical models are necessary. Two theoretical predictions were compared with the experimental data of \(\varLambda _{c}^{+}/D^{0}\) ratio in publication of ALICE collaboration [23]. One is the calculation of the event generator PYTHIA 8 that includes color reconnection mechanisms beyond the leading-color approximation (CR-BLC) [15] and another is that of canonical-ensemble statistical hadronization (CE-SH) model [26]. It was shown that the PYTHIA 8 with CR-BLC tunes and CE-SH model can predict a dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio with multiplicity but fail to describe the non-monotonic \(p_T\) dependence of the \(\varLambda _{c}^{+}/D^{0}\) ratio in the low and intermediate \(p_T\) range in high multiplicity events. Here, we emphasize that such a \(p_T\) dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio shown in Fig. 4b can be naturally explained by our model after considering the property of \(p_T\) distribution of light-flavor quarks and that of charm quarks discussed in Sects. 5 and 6, respectively. Therefore, we argue that the non-monotonic \(p_T\) dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio shown in Fig. 4b is a possible signal of quark combination at hadronization in high multiplicity events in pp collisions at \(\sqrt{s}=13\) TeV.

In Fig. 5, we show \(p_{T}\) spectra of \(D^{0}\), \(D_{s}^{+}\) and \(\varLambda _{c}^{+}\) in inelastic pp collisions at \(\sqrt{s}=13\) TeV and compare them with experimental data [23]. Here, \(p_{T}\) spectra of light-flavor quarks in inelastic events have been obtained in Ref. [5] and \(p_{T}\) spectrum of charm quarks is taken from FONLL calculations shown in Fig. 2a with a \(p_{T}\)-integrated yield density \(dN_{c}/dy=0.025\). The model parameter \(R_{B/M}^{(c)}\) is set to be 0.38, which falls in between the value in high multiplicity events and that in low multiplicity events. The decay contributions from other single-charm hadrons in ground state are systematically considered. We see that experimental data of \(D^{0}\), \(D_{s}^{+}\) and \(\varLambda _{c}^{+}\) are self-consistently explained in our model.

9 Summary and discussion

We have applied an equal-velocity quark combination model to study the \(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) in pp collisions at \(\sqrt{s}=13\) TeV. Taking advantage of the analytic feature of the model, we decomposed the \(\varLambda _{c}^{+}/D^{0}\) ratio into four parts and studied their individual influence on the ratio. Finally, we combined effects of these parts to calculate \(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) and compared theoretical results with experimental data of \(\varLambda _{c}^{+}/D^{0}\) ratio in high and low multiplicity events in pp collisions at \(\sqrt{s}=13\) TeV.

The first part of \(\varLambda _{c}^{+}/D^{0}\) decomposition is the term of light-flavor quark numbers. We summarized this part into a compact form containing a strangeness factor and a baryon-to-meson competition factor defined in our model. The multiplicity dependence of strangeness has very weak influence on the \(\varLambda _{c}^{+}/D^{0}\) ratio. The global effect of light-flavor quark numbers is manifested by the baryon-to-meson competition factor. In low multiplicity events where quark numbers are relatively small, charm quark has relatively small chance to interact with two light-flavor quarks and thus the production of charm baryon should be suppressed to a certain extent. We adopted a Poisson distribution as an example to roughly estimate this suppression and found about 20% suppression of the \(\varLambda _{c}^{+}/D^{0}\) ratio in low multiplicity events with mid-rapidity \(\left\langle dN_{ch}/d\eta \right\rangle \approx 4.5\) in comparison with that in high multiplicity events with \(\left\langle dN_{ch}/d\eta \right\rangle \approx 25\).

The second part of \(\varLambda _{c}^{+}/D^{0}\) decomposition is the term containing the normalized \(p_{T}\) spectrum of up/down quarks. Considering the small difference between momentum fraction \((x_{u})\) of up/down quark in \(\varLambda _{c}^{+}\) and that \((x_{u}^{\prime })\) in \(D^{0}\), we adopted the Taylor expansion method and reduced this part to the inclusive distribution of up/down quarks \(f_{u}^{(n)}\big ((2x_{u}-x_{u}^{\prime })p_{T}\big )\) with a good numerical accuracy. This suggests that the shape of up quark \(p_{T}\) spectrum directly transmits to the \(p_{T}\) dependence of the \(\varLambda _{c}^{+}/D^{0}\) ratio. In particular, \(p_{T}\) spectrum of up/down quarks in high multiplicity events behaves as a thermal like distribution in the low \(p_{T}\) range, which will lead to an obviously non-monotonic \(p_{T}\) dependence of \(\varLambda _{c}^{+}/D^{0}\) ratio in the low and intermediate \(p_{T}\) range.

The third part of \(\varLambda _{c}^{+}/D^{0}\) decomposition is the term containing the normalized \(p_{T}\) spectrum of charm quarks. We adopted FONLL method and PYTHIA8 to calculate charm quark \(p_{T}\) spectrum, respectively. This part increases with \(p_{T}\) and therefore weakens the effect of the second part. We found that results of PYTHIA8 are roughly close to those of FONLL calculations but have a weak multiplicity dependence. The fourth part of \(\varLambda _{c}^{+}/D^{0}\) decomposition is the term containing momentum correlation between up/down quarks and charm quarks. PYTHIA8 simulation on two-quark correlations shows a negligible momentum correlation between up/down quarks and charm quarks. Therefore, we neglect the effect of this part in calculation of \(\varLambda _{c}^{+}/D^{0}\) ratio in this paper.

Finally, we combined these parts and calculated \(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) in pp collisions at \(\sqrt{s}=13\) TeV. In calculations, we chose the \(p_{T}\) spectrum of up/down quarks in multiplicity class IX with \(\left\langle dN_{ch}/d\eta \right\rangle =4.64\) as an example of low multiplicity events and that in multiplicity class I with \(\left\langle dN_{ch}/d\eta \right\rangle =25.75\) as an example of high multiplicity events. \(p_{T}\) spectrum of charm quarks from PYTHIA8 calculation with \(\left\langle dN_{ch}/d\eta \right\rangle =4.4\) and that with \(\left\langle dN_{ch}/d\eta \right\rangle =25\) are taken in order to be consistent with the selected \(p_{T}\) spectrum of light-flavor quarks at similar \(\left\langle dN_{ch}/d\eta \right\rangle \). Finally, we obtained \(\varLambda _{c}^{+}/D^{0}\) ratio as the function of \(p_{T}\) in high multiplicity events with \(\left\langle dN_{ch}/d\eta \right\rangle \approx 25\) and that in low multiplicity events with \(\left\langle dN_{ch}/d\eta \right\rangle \approx 4.5\). We compared our theoretical results with experimental data of \(\varLambda _{c}^{+}/D^{0}\) ratio in multiplicity class with \(\left\langle dN_{ch}/d\eta \right\rangle =31.5\) and those with \(\left\langle dN_{ch}/d\eta \right\rangle =4.4\). In high multiplicity events with a baryon-to-meson competition factor \(R_{B/M}^{(c)}=0.425\), we found that theoretical result with PYTHIA8 calculated charm \(p_{T}\) spectrum is in better agreement with experiment data than that with FONLL calculated charm \(p_{T}\) spectrum. In low multiplicity events with a suppressed \(R_{B/M}^{(c)}=0.34\), theoretical result with FONLL calculated charm \(p_{T}\) spectrum and that with PYTHIA8 calculated charm \(p_{T}\) spectrum are both in good agreement with experimental data.

\(R_{B/M}^{(c)}\) is a dynamical parameter of our model which denotes the competition between the formation of charm baryon and that of charm meson at a charm quark hadronization and can not be predicted by the model of present version. Based on the present work and our previous studies [6, 18, 27, 29], we found that \(R_{B/M}^{(c)}\) is about \(0.385-0.425\) in inelastic and relatively-high multiplicity events pp and pPb collisions and is suppressed in small multiplicity events but it may also increase to a certain extent in AA collisions [32]. This possibly multiplicity-dependent property of \(R_{B/M}^{(c)}\) is an interesting property of charm quark hadronization, which is not seen in the hadronization of light-flavor quarks where we found an relatively stable baryon-to-meson production competition [64]. Its explanation is beyond the model of current version and should introduce further dynamic considerations. For example, by considering the possible production of some \(cll'\) resonances which is predicted by quark model but is not observed yet in experiments [26, 65], the hadronization channel of charm quark to charm baryons can increase which may prompt the possible increase of \(R_{B/M}^{(c)}\) in high multiplicity events where those resonances will have more practical chance to produce. Also, by considering the competition of quark combination mechanism and quark fragmentation mechanism and, in particular, the multiplicity dependence of such competition [19, 66], the effective \(R_{B/M}^{(c)}\) can also be changed in our model. These possible dynamics at charm quark hadronization are deserved to study in the future to improve our model.

The decomposing method used in this work can be applied to the study of other charm baryon/meson ratios such as \(\varXi _c/D\) and \(\varOmega _c/D\). Because \(\varXi _c\) and \(\varOmega _c\) contain strange quarks, their productions in our model are influenced by the properties of strange quarks at hadronization. In particular, ratios \(\varXi _c/D^0\) and \(\varOmega _c/D_{s}\) are influenced by the relative ratio of strange quarks to up/down quarks at hadronization. Ratio \(\varOmega _c/D^0\) depends on the square of the relative ratio but ratio \(\varXi _c/D_s\) weakly depends on that. Therefore, these ratios are good probes of charm quark hadronization with the participancy of strange quarks. We will study them in the future works and compare model results with the latest experimental data of LHC experiments.