Shadow and deflection angle of asymptotic, magnetically-charged, non-singular black hole

Abstract

In this paper, we investigate a solution for an asymptotic, magnetically-charged, non-singular (AMCNS) black hole. By utilizing the Gauss–Bonnet theorems, we aim to unravel the intricate astrophysics associated with this unique black hole. The study explored various aspects including the black hole’s gravitational field, intrinsic properties, light bending, the shadow and greybody bounding of the black hole. Through rigorous calculations and simulations, we derive the weak deflection angle of the optical metric of AMCNS black hole. Additionally, we investigate the impact of the dark matter medium on the deflection angle, examined the distinctive features of the black hole’s shadow, and bound its greybody factors. Our findings not only deepen our understanding of gravitational lensing but also pave the way for future improvements in black hole theories by minimizing restrictive assumptions and incorporating a more realistic representation of these cosmic phenomena.

1 Introduction

The evolution of black hole physics can be traced all the way back to the year 1784 when the English philosopher John Michell [1]. He theorized that all light emitted by an invisible central body having a radius more than five hundred times that of the sun but with a density equal to that of the sun would return to itself due to its own gravity. Essentially, when an object falls from infinity into the central body, it acquires a velocity greater than that of light at the surface of the central body owing to the latter’s force of attraction.

Laplace followed this by proposing an invisible star that could potentially be the largest and highly gravitating luminous object in the universe in the year 1796 [2]. His speculations were connected to the observations on an astronomical body with a density equal to that of the Earth but with a diameter more than 250 times that of the sun, not allowing its light to reach us, thanks to its strong attraction.

Einstein’s ground-breaking theory formulated in 1915 suggests that the apparent gravitational force originates from the curvature of the fabric of spacetime [3]. Schwarzschild gave the first solution for the simplest black holes in the year 1916 depicting the gravitational field from a spherical mass with no angular momentum, charge, or universal cosmological constant [4]. Between then and the year 1918, the combined works of four European physicists discovered the Reissner–Nordström metric solved using the Einstein-Maxwell equations representing an electrically charged black holes [5].

Centuries of research have enabled humanity to understand the concept of a star collapsing due to its own intense gravity into a black hole to an extent that nothing can escape its gravitational pull beyond its horizon. Being a consequence of General Relativity, black holes are enigmatic objects of the universe that started off as a bunch of mathematical equations which were written down only to take form in the sky hundred years later, only to be confirmed with recent observations by Event Horizon Telescopes (EHT) [6,7,8,9].

Now that their existence is proven, the notion of singularity inside a black hole becomes the next question of interest [10]. Quantum Field Theory is sought for answers in this regard with the novelty idea of Hawking radiation for a stationary black hole suggesting that the black holes shrink until the point of singularity is reached at its center. This stems from a semi-classical approximation that radiation has a negative flux of energy contradicting the singularity assumptions [11].

When there is no existing singularity, a “regular” black hole is a good prospect to proceed with, as pioneered by Bardeen. These non-singular black holes are deemed to possess regular centers with a core of collapsed charged matter instead of singularity [12, 13]. The ensuing Einstein tensor is not only reasonable for a physical domain but also satisfies the necessary conditions that eventually give rise to a static, spherically symmetric, and asymptotically flat metric. A non-singular spacetime is defined locally for a black hole forming initially from a vacuum region and evaporating subsequently to a vacuum region, with its quiescence described as a static region [14].

The invisibility of a black hole has not stopped its distant observers from seeing it, thanks to the existence of a shadow [15]. The accretion disk that is formed due to the immense gravity of a black hole attracting everything in its path such as dust, photons, radiation, etc., constitutes the shadow shape and size, hence, indirectly making it visible and observable [16, 17]. The shadow is imagined to be a circular ring of light around its host; however, in reality, this is not the case. It is a region that is geometrically thick and optically thin, especially for regular black holes, that is not so circular. In relativistic models, the size and shape of a shadow is found to be dependant on the geometry of the spacetime, rather than the characteristics of the accretion [18].

The extreme gravitational pull of the black hole compels the light rays to be deflected towards the singularity, causing those that skim the photon sphere to start looping around it. When a photon ends up precisely on the photon sphere, it will continue to encircle the black hole forever. This phenomenon occurring for the light rays passing in the neighborhood of the unstable photon region abets the intensity of the original source through the extended path length of the light rays, thus, increasing its brightness around the shadow’s edge; consecutively, the cloud’s brightness just outside the shadow appears to be enhanced as well. The captured light rays spiraling into a black hole and the scattered light rays veering away from it are separated by a shadow, giving it the facade of a bright surrounding illuminating a dark disk. Therefore, it is also known as the critical curve that manifests as an isotropic and homogenous emission ring. For a given black hole, its intrinsic parameters play a major role in determining the size of the shadow, whereas, the light rays and the instabilities of their orbits in the photosphere affect its contour. Numerous researchers have explored the distinct imprints that alternative gravitational theories leave behind by studying the phenomenon of shadows [8, 9, 19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90].

Apart from accretion, the other factor that enables the visibility of the shadow is a phenomenon that occurs due to the deflection of light rays by the gravity fields of a massive object in their path to a distant observer. Called gravitational lensing, the light rays from the source in the background are distorted owing to the massive object acting as a lens [91,92,93,94,95,96,97]. When the lensing is weak, the magnifications are too minute to be detected, yet, enable the observer to study the structural aspects in its periphery. The effects of lensing were seen to influence the shadow dramatically through the radiation from the accretion [16, 17]. In the realm of astrophysics, the determination of object distances plays a pivotal role in unraveling their inherent qualities and quantities. Remarkably, Virbhadra demonstrated that solely by observing relativistic images, devoid of any knowledge regarding masses and distances, it is feasible to accurately establish an upper limit on the compactness of massive dark entities [98]. Furthermore, Virbhadra unveiled a distortion parameter, leading to the cancellation of the algebraic sum of all singular gravitational lensing images. This groundbreaking discovery has undergone rigorous testing using Schwarzschild lensing within both weak and strong gravity fields [99]. Weak gravitational lensing exhibits the property of differential deflection and can be utilized to distinguish between mass distributions. The extent of the light deflection and lensing is denoted by the deflection angle or the bending angle. In order to evaluate the weak deflection angle, the Gauss–Bonnet theorem is used to derive the optical geometry of the corresponding spacetime by Gibbons and Werner in 2008 [100]. Subsequently, this methodology has been extensively employed to investigate a wide array of phenomena [101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119]. The specialty of this formula is the relationship it establishes between the surface curvature and the underlying topology for a given differential geometry as [100]:

$$\begin{aligned} \iint _{D_{R}}{\mathcal {K}} \text { d}S+\oint _{\partial D_{R}}{\hat{k}} \text { d}\sigma + \sum _{j}{\tilde{\theta }}_{j}=2\pi ~{\mathcal {X}}(D_{R}), \end{aligned}$$

(1)

where ${\mathcal {K}}$ is the Gaussian optical curvature, ${\hat{k}}$ is the geodesic curvature, ${\tilde{\theta }}_j$ is an exterior angle at the vertex j, and $D_R$ is the boundary along which the line element$\sigma$ pertains. For a two-dimensional manifold, a regular domain $D_{R}$ aligned by the two-dimensional surface S with the Riemannian metric ${\hat{g}}_{ij}$ is considered, along with its piece-wise smooth boundary $\partial D_{R}=\gamma _{g}\cup C_{R}$. Also, for a regular domain, it is known that the Euler characteristic is unity, ${\mathcal {X}}_{D_{R}}=1$.

The Gibbons and Werner method: If $\gamma$ is taken to be a smooth curve in the said domain, then ${\dot{\gamma }}$ becomes the unit-speed vector. The geodesic curvature $\kappa$ is given by [100, 102]:

$$\begin{aligned} \kappa =g^{opt}(\nabla _{{\dot{\gamma }}}{\dot{\gamma }}, \ddot{\gamma }), \end{aligned}$$

(2)

having the unit-speed condition $g^{opt}({\dot{\gamma }}, {\dot{\gamma }})=1$. Here, $\ddot{\gamma }$ is the unit-acceleration vector that is perpendicular to ${\dot{\gamma }}$. When $R\rightarrow \infty$, the relevant jump angles are considered to be $\pi /2$; that is to say, the angles respective to the source and the observer sum up as ${\tilde{\theta }}_{S}+{\tilde{\theta }}_{O}\rightarrow \pi$. Putting all this together, Eq. (1) now becomes:

$$\begin{aligned} \iint \limits _{{\mathcal {D}}_{R}}{\mathcal {K}}\,\text { d}S+\oint \limits _{C_{R}}\kappa \, \text { d}t\overset{{R\rightarrow \infty }}{=}\iint \limits _{{\mathcal {D}} _{\infty }}{\mathcal {K}}\,\text { d}S+\int \limits _{0}^{\pi +{\hat{\alpha }}}\text { d}\phi =\pi , \end{aligned}$$

(3)

where, $\phi$ is the angular coordinate centered at the lens and ${\hat{\alpha }}$ is the small, positive, non-trivial, asymptotic angle of deflection. Knowing that $\gamma _{{\tilde{g}}}$ is a geodesic and the geodesic curvature offers zero contribution i.e., $\kappa (\gamma _{{\tilde{g}}})=0$, the curve $C_{R}$ is pursued which contributes in such a manner that:

$$\begin{aligned} \kappa (C_{R})=\mid \nabla _{{\dot{C}}_{R}}{\dot{C}}_{R}\mid . \end{aligned}$$

(4)

Considering $C_{R}:=r(\phi )=R= \text {constant}$, R is the distance from the origin of the selected coordinate system. The radial component of $\kappa$ becomes:

$$\begin{aligned} (\nabla _{{\dot{C}}_{R}}{\dot{C}}_{R})^{r}={\dot{C}}_{R}^{\phi }(\partial _{\phi } {\dot{C}}_{R}^{\phi })+\Gamma ^{\, r}_{\phi \phi }({\dot{C}}_{R}^{\phi })^{2}. \end{aligned}$$

(5)

Evidently, the first term disappears from the presumptions and the second term can be obtained using the unit-speed condition. Then:

$$\begin{aligned}{} & {} \lim _{R \rightarrow \infty } \kappa (C_{R}) =\lim _{R\rightarrow \infty }\left| \nabla _{{\dot{C}}_{R}}{\dot{C}}_{R}\right| \rightarrow \frac{1}{R} \quad \text {and at higher limits} \\{} & {} \qquad \text {of radial distance,} \,\, \lim _{R \rightarrow \infty } \text { d}t\rightarrow R \text { d}\phi . \end{aligned}$$

When gravitational lensing is approached geometrically, this proves effective in finding the deflection caused by any curved surface. In the weak lensing regime, it becomes possible to relate the geometry and the topology with the Gauss–Bonnet theorem to determine the bending angle through the optical metric because:

• the metric evolves from the surface curvature relating it to its geometry

• the geodesics of the metric are spatial light rays regarding the focused light rays as a topological effect.

Gibbons and Werner obtained the bending angle as a consequence of weak lensing using the Gauss–Bonnet theorem with the Gaussian curvature of the optical metric directed outwards from the light ray [100]. For a simply connected and an asymptotically flat domain $D_R$ in which the lens is not an element of the regime but the source and the observer are, with the differential domain consisting of a bounding geodesic at the source, the weak deflection angle is evaluated as [100, 102]:

$$\begin{aligned} {\hat{\alpha }} = -\iint _{D_R} {\mathcal {K}} \text { d}S. \end{aligned}$$

(6)

These are the foundations of this paper with the target of finding the weak deflection angle for an asymptotic magnetically charged non-singular (AMCNS) black hole. The paper is organized as follows: Sect.  2, the solution of the AMCNS black hole is analyzed, followed by its application in Sect. 3 using the Gauss–Bonnet theorem and the Gibbons and Werner method. Section 3.1 deals with the influence of dark matter on the bending angle. We then carry on to explore the shadow of the AMCNS black hole in Sect.  4. Finally, the greybody factor is investigated in Sect. 5 before concluding in Sect. 6.

2 Asymptotic, magnetically-charged, non-singular (AMCNS) black hole

Extensive research has been conducted on the solutions that depict black holes within the framework of non-linear electrodynamics in the context of general relativity [120,121,122,123,124,125,126]. Initially, we outline the action of General Relativity (GR) combined with Nonlinear electrodynamics (NED)

$$\begin{aligned} S = \frac{1}{16\pi } \int d^4 x\sqrt{-g}\ [R - \pounds (F)], \ \ F {\mathop {=}\limits ^\textrm{def}}F_{\mu \nu }F^{\mu \nu }. \end{aligned}$$

(7)

Here, R denotes the scalar curvature, $F_{\mu \nu }= \partial _\mu A_\nu - \partial _\nu A_\mu$ represents the electromagnetic field, and $\pounds$ stands for an arbitrary function that result in the emergence of Maxwell’s theory when F is small: $\pounds (F)\approx F$ as F tends to 0. The tensor $F_{\mu \nu }$ adheres to the dynamic equations and satisfies the Bianchi identities $\nabla _\mu (\pounds _F F^{\mu \nu })=0, \nabla _\mu {}^*F^{\mu \nu }=0.$ Here, the Hodge dual is indicated by an asterisk, and $\pounds _F$ corresponds to the derivative of $\pounds$ with respect to F.

A spherically symmetric metric can be expressed using a structure:

$$\begin{aligned} ds^2 = {\,{\textrm{e}}}^{2\gamma (r)}dt^2 - {\,{\textrm{e}}}^{2\alpha (r)}dr^2 - r^2\,d\Omega ^2 \end{aligned}$$

(8)

where $d\Omega ^2 = d\theta ^2 + \sin ^2\theta \, d\phi ^2$ and r is a radial coordinate. A regular center, by definition, takes place where $r=0$, if all algebraic curvature invariants are finite there.

The tensor $F_{\mu \nu }$ that aligns with spherical symmetry can exclusively encompass a radial electric field $F_{01} = -F_{10}$ and a radial magnetic field $F_{23} = -F_{32}$. Maxwell equations provide the following information:

$$\begin{aligned} r^2 {\,{\textrm{e}}}^{\alpha +\gamma }\pounds _F F^{01} = q_{\textrm{e}}, F_{23} = q_{\textrm{m}}\sin \theta \end{aligned}$$

(9)

Here, $q_{\textrm{e}}$ and $q_{\textrm{m}}$ represent the electric and magnetic charges, respectively. It can be deduced from Eq. (9) that:

$$\begin{aligned} f_{\textrm{e}}&{\mathop {=}\limits ^\textrm{def}}2F_{01}F^{10}= 2q_{\textrm{e}}^2\,\pounds _F^{-2} r^{-4} \ge 0, \end{aligned}$$

(10)

$$\begin{aligned} f_{\textrm{m}}&{\mathop {=}\limits ^\textrm{def}}2F_{23}F^{23}= 2q_{\textrm{m}}^2\,r^{-4} \ge 0. \end{aligned}$$

(11)

Furthermore, the Einstein equations can be formulated in

$$\begin{aligned} -G_{\mu }^{\nu }&= T_{\mu }^{\nu }= -2 \pounds _F F_{\mu \alpha }F^{\nu \alpha } +{\textstyle \frac{1}{2}}\delta _{\mu }^{\nu }\pounds \nonumber \\&= {\textstyle \frac{1}{2}}\textrm{diag}( \pounds {+} 2f_{\textrm{e}}\pounds _F,\, \pounds {+} 2f_{\textrm{e}}\pounds _f,\, \pounds {-}2f_{\textrm{m}}\pounds _F,\, \pounds {-}2f_{\textrm{m}}\pounds _F). \end{aligned}$$

(12)

Because of the equivalence between $T^0_0$ and $T^1_1$, the task at hand involves expressing the familiar connection involving $\alpha (r)$ using the energy density $T_0^0$. This connection can be derived from the Einstein equation pertaining to the ${0\atopwithdelims ()0}$ component

$$\begin{aligned} {\,{\textrm{e}}}^{2\gamma }= & {} {\,{\textrm{e}}}^{-2\alpha } = A(r) = 1 - \frac{2M(r)}{r} \end{aligned}$$

(13)

$$\begin{aligned} M(r)= & {} \frac{1}{2} \int T^0_0(r) \, r^2 \, dr. \end{aligned}$$

(14)

The metric takes on the configuration described in Eq. (8), accompanied by the representation provided in Eq. (13), wherein

$$\begin{aligned} M(r)=\frac{1}{4}\int \pounds (F) r^2 dr \end{aligned}$$

(15)

and $F = 2q_{\textrm{m}}^2/r^4$. It is observed that a spacetime featuring a regular center which is indeed achieved for any function $\pounds (F)$ that satisfies the condition $\pounds \rightarrow \pounds _\infty < \infty$ as $F\rightarrow \infty$, when performing integration in equation (15) from 0 to r (yielding a singular mass value $m = M(\infty )$, establishing a regular center for a given $q_{\textrm{m}}$). Consequently, the entire mass stems from electromagnetic sources.

Hence, one can propose the metric incorporating the variable mass M(r) and explore this metric within the framework of modified General Relativity (GR) through quantum corrections, introducing the fundamental length l. A similar approach has been adopted in previous works [127,128,129,130] for other NEDs.

Assume that the BH is magnetically charged and the mass function of the BH varies with r [131],

$$\begin{aligned} M(r)&=m_0+\int _0^r\rho (r) r^2dr=m_0+\int _0^\infty \rho (r) r^2dr \nonumber \\&\quad -\int _r^\infty \rho (r) r^2dr, \end{aligned}$$

(16)

Here, $m_0$ stands for the integration constant, representing the Schwarzschild mass, while $m_M = \int _0^\infty \rho (r) r^2 \, dr$ denotes the magnetic mass of the black hole, with $\rho (r)$ being the magnetic energy density.

Let’s examine the particular form of non-linear electrodynamics by elucidating the solution for a magnetically charged black hole. In this context, we explore the non-linear electrodynamics introduced in the work by Kruglov [125], wherein the Lagrangian density takes on an exponential structure:

$$\begin{aligned} \pounds =-P\exp (-\beta P), \end{aligned}$$

(17)

where, $P \equiv \nicefrac {1}{4} \left( F_{\mu \nu }\, F^{\mu \nu }\right) =\nicefrac {1}{2}\left( {\textbf{B}}^{2}-{\textbf{E}}^{2}\right) ,~\text {and}~F^{\mu \nu }=\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }.$ $F^{\mu \nu }$ is the electromagnetic field tensor, ${\textbf{B}}$ is the magnetic field, ${\textbf{E}}$ is the electric field, $A^{\mu }$ is the four-potential, and $\beta$ is a parameter with the dimensions of [Length]$^{4}$ having an upper bound of $\left( \beta \le 1\times 10^{-23}\text {T}^{-2}\right)$. The Euler–Lagrange equation is formulated as:

$$\begin{aligned} \partial _{\mu }\left( \frac{\partial \pounds }{\partial \left( \partial _{\mu }A_{\nu }\right) }\right) -\frac{\partial \pounds }{\partial A_{\nu }}=0, \end{aligned}$$

(18)

where $\mu ,~\nu \in [0,3]$. Thus, the field equations come to be:

$$\begin{aligned} \partial _{\mu }\left[ \left( \beta P-1\right) \exp \left( -\beta P\right) F^{\mu \nu }\right] =0, \end{aligned}$$

(19)

The energy–momentum tensor takes the form of:

$$\begin{aligned} T ^{\mu \upsilon }=H^{\mu \lambda }F_{\lambda }^{\upsilon }-g^{\mu \upsilon }\pounds , \end{aligned}$$

(20)

where, $g^{\mu \upsilon }={1}/{g_{\mu \upsilon }}$ and:

$$\begin{aligned} H^{\mu \lambda }\equiv \frac{\partial \pounds }{\partial F_{\mu \lambda }}=-\left( 1-\beta P\right) \exp \left( -\beta P\right) F^{\mu \lambda }. \end{aligned}$$

(21)

Thus, the energy–momentum tensor derived from the Lagrangian density is:

$$\begin{aligned} T ^{\mu \upsilon }=\exp \left( -\beta P\right) \left[ \left( \beta P-1\right) F^{\mu \lambda }F_{\lambda }^{\upsilon }+g^{\mu \upsilon }P\right] , \end{aligned}$$

(22)

whose trace is:

$$\begin{aligned} T =4\beta P^{2}\exp \left( -\beta P\right) . \end{aligned}$$

(23)

The instance of $\beta \rightarrow 0$ not only signifies weak limits, but also reverts to classical electrodynamics as $\pounds \rightarrow -P$ and $T=0$ in Eq. (23).

Typically, when $\beta$ is not zero and the energy–momentum tensor has a non-zero trace, it entails that the scale invariance is violated. That’s why, if any forms of nonlinear electrodynamics incorporate a dimensional parameter, they would also break the scale invariance, prompting the dilation current to be non-trivial: $\partial _{\upsilon }\, x^{\mu }\,T _{\mu }^{\upsilon } = T$

This can be overruled by the general principles of causality together with unitarity according to which the group velocity of the background perturbations are less than c. The sustaining of the causality principle necessitates that $\pounds _{P}=\partial \pounds /\partial P \le 0 \Rightarrow \beta P\le 1$. For a purely magnetic field, $B\le \sqrt{\nicefrac {2}{\beta }}$ ought to be fulfilled. Besides, the constraint $\pounds _{P}+2P\pounds _{PP}\le 0$ allows the unitarity principle to hold provided $\pounds _{PP}\ge 0$. While Eq. (17) construes $\beta P\le 0.219$ agreeing with, it is clear that the limitations for both the causality and unitarity principles incur for $\beta P\le 0.219$ giving:

$$\begin{aligned} {\textbf{B}}\le \sqrt{\frac{5-\sqrt{17}}{2\beta }}\simeq \frac{0.66}{\sqrt{\beta }}. \end{aligned}$$

(24)

Deriving the metric of a static AMCNS black hole in a spherically symmetric spacetime is our next goal. For a pure magnetic field, the governing equations are as follows: The invariant P is deliberated in terms of an electric charge q to be:

$$\begin{aligned} P=\frac{q^{2}}{2r^{4}}. \end{aligned}$$

(25)

The generic line element of a spherically symmetric black hole with a time coordinate t, radial coordinate r, co-latitude $\theta$ and longitude $\phi$ both outlined for a point on the two-sphere, and mass M is given by:

$$\begin{aligned} \text { d}s^2 = - f(r) \text { d}t^2 + f(r)^{-1} \text { d}r^2 + r^2 (\text { d}\theta ^2 + \sin ^2 \theta \text { d}\phi ^2). \end{aligned}$$

(26)

Computing the function f(r) specific to the AMCNS black hole is necessary to go on. To pursue this, putting:

$$\begin{aligned} f=1-\frac{2mr^{2}}{r^{3}+2ml^{2}}, \end{aligned}$$

(27)

engenders the Hayward metric [14] of a non-singular black hole that is static, has no charge, and emerges as the solution of a certain modified gravity theory. The quantity l is an approximate parameter in the length-scale under which the corollaries of the cosmological constant prevail. If M is assumed to vary with r, then:

$$\begin{aligned} M(r)=\int _{0}^{r}\rho (r)r^{2} \text { d}r=m-\int _{r}^{\infty }\rho (r)r^{2}\text { d}r, \end{aligned}$$

(28)

where, $m=\int _{0}^{\infty }\rho (r)r^{2}\text { d}r$ describes the magnetic mass of the black hole that is responsible for screening the magnetic interactions so that the perturbative divergences of magnetostatics can be eliminated. The energy density, in the absence of an electric field, ensues from Eq. (22) to be:

$$\begin{aligned} \rho =\frac{q^{2}}{2r^{4}}\exp \left( \frac{-\beta q^{2}}{2r^{4}}\right) . \end{aligned}$$

(29)

This transforms the mass function to:

$$\begin{aligned} M(r)=\frac{q^{2}}{2}\int _{0}^{r}\exp \left( \frac{-\beta q^{2}}{ 2r^{4}}\right) \frac{\textrm{d}r}{r^{2}}=\frac{{q^{3/2}}\, \Gamma \left( \frac{1}{4},\frac{\beta q^{2}}{2r^{4}}\right) }{2^{11/4}\, \beta ^{1/4}}, \end{aligned}$$

(30)

where, the incomplete gamma function is characterized by:

$$\begin{aligned} \Gamma (s,x)=\int _{x}^{\infty }t^{s-1}e^{-t}\text { d}t. \end{aligned}$$

(31)

Therefore, rewriting the magnetic mass as:

$$\begin{aligned} m=M(\infty )=\frac{q^{\frac{3}{2}}\Gamma \left( \frac{1}{4}\right) }{2^{\frac{11}{4}}\beta ^{\frac{1}{4}}}\simeq \frac{0.54q^{\frac{3}{2}}}{\beta ^{\frac{1}{4}}}. \end{aligned}$$

(32)

Consolidating all of the above, the metric function is discovered to be [127]:

$$\begin{aligned} f\left( r\right) =1-\frac{r^{2}q^{\frac{3}{2}}\Gamma \left( \frac{1}{4},\frac{\beta q^{2}}{2r^{4}}\right) 2^{\frac{-7}{4}}\beta ^{\frac{-1}{4}}}{r^{3}+l^{2}q^{\frac{3}{2}}2^{\frac{-7}{4}}\beta ^{\frac{-1}{4}}\Gamma \left( \frac{1}{4},\frac{\beta q^{2}}{2r^{4}}\right) }. \end{aligned}$$

(33)

The metric function in the circumstance of $l=0$ reduces to Reissner–Nordström solution [125]. In the vicinity of radial infinity, its asymptotic value is attained using the expansion of the series:

$$\begin{aligned} \Gamma (s,z)= & {} \Gamma (s)-z^{s}\left[ \frac{1}{s}-\frac{z}{s+1}+\frac{z^{2}}{2\left( s+2\right) }+O\left( z^{3}\right) \right] ,{ \ }\nonumber \\{} & {} z\rightarrow 0. \end{aligned}$$

(34)

Ultimately, the metric function f(r) at $r\rightarrow \infty$ is structured as [127]:

$$\begin{aligned} f\left( r\right) =1-\frac{r^{2}\left[ 2m-\frac{q^{2}}{r}+\frac{\beta q^{4}}{ 20r^{5}}+O(r^{-9})\right] }{r^{3}+l^{2}\left[ 2m-\frac{q^{2}}{r}+\frac{\beta q^{4}}{20r^{5}}+O(r^{-9})\right] }. \end{aligned}$$

(35)

This will be used for the subsequent computations of the AMCNS black hole. The black hole horizon radius $r_H$, the distance measured from the center of the black hole to its event horizon, can be evaluated by finding the larger root of $f(r)=0$ from this equation which locates the outer horizon. As shown in Fig. 1, the number of horizons are dependent on the parameters of l.

2.1 Calculation of Hawking radiation in Jacobi metric formalism

To calculate a black hole’s Hawking temperature, we use the Jacobi metric corresponding to the four-dimensional covariant metrics to calculate Hawking temperature by obtaining the tunneling probability of the particle through the horizon [132]. In this semi-classical method, we use the wave function of the particle as $\psi =e^{(i/\hbar )S}$. The corresponding Jacobi metric will be [133,134,135],

$$\begin{aligned} \textrm{d}s^2&= j_{ij} \text { d}x^{i}\text { d}x^{j} \nonumber \\&= \Big (E^2-m^2f(r)\Big ) \left( \frac{\textrm{d}r^2}{f^2(r)} + \frac{r^2}{f(r)}(\textrm{d}\theta ^2 + \sin ^2\theta \text { d}\phi ^2)\right) ~. \end{aligned}$$

(36)

Now, the action for a moving particle in this scenario where Hawking radiation occurs at the near-horizon via radial tunneling is found to be:

$$\begin{aligned} S = -\int \sqrt{j_{ij}\frac{\textrm{d}x^i}{\textrm{d}s}\frac{\textrm{d}x^j}{\textrm{d}s}} \textrm{d}s~, \end{aligned}$$

(37)

where the integrand is

$$\begin{aligned} \sqrt{j_{ij}\frac{\textrm{d}x^i}{\textrm{d}s}\frac{\textrm{d}x^j}{\textrm{d}s}} = {\pm } \left( E^2-m^2f(r)\right) ^{\frac{1}{2}} \left( f^{-1}(r)\right) \left( \frac{\textrm{d}r}{\textrm{d}s}\right) ~, \end{aligned}$$

(38)

Fig. 1

Figure shows the lapse function f(r) as a function of r for $q=0.5$, $\beta =0.00001$ and for the different values of l

The radial momentum of the particle using the (38) in (37) is calculated as [132]

$$\begin{aligned} p_r=\partial _r S= {\mp }(E^2-m^2f(r))^{\frac{1}{2}} (f^{-1}(r))~. \end{aligned}$$

(39)

As in our tunneling model, the particle is located near the horizon and so the condition $f(r)<0$ must be satisfied. Therefore, since $p_r>0$ is negative in our equation, it corresponds to the particle going outwards (identical to the conventional tunneling approaches in [136]). Since tunneling occurs near the horizon, the metric is effectively simplified to $(1+1)$-dimensions near the horizon, where only the radial movement is significant [137,138,139] so one can use the Taylor series expansion and apply it to f(r) for $r=r_H$ to expand it around the horizon as: $f(r) = f(r_H) + f'(r_H)(r-r_H) + {\mathcal {O}}(r-r_H)^2 = 2{{\tilde{\kappa }}}(r-r_H) + {\mathcal {O}}(r-r_H)^2~,$ where ${{\tilde{\kappa }}} = h^\prime (r_H)/2$ is the surface gravity of the black hole. Afterward, we substitute this in (38), and obtain near horizon action for radial motion is [132]

$$\begin{aligned} S= & {} {\mp } \frac{E}{2{{\tilde{\kappa }}}} \int _{r_H-\epsilon }^{r_H+\epsilon } \frac{1}{(r-r_H)} \textrm{d}r {\pm } \frac{m^2}{2E}\int _{r_H-\epsilon }^{r_H+\epsilon } \textrm{d}r \nonumber \\{} & {} \quad {\mp } \int _{r_H-\epsilon }^{r_H+\epsilon } {\mathcal {O}}(r-r_H) \textrm{d}r~, \end{aligned}$$

(40)

with note that $r_H-\epsilon$ is close to horizon and $r_H+\epsilon$ is across the horizon, with $\epsilon (>0)$. Using the change of variable $r-r_H = \epsilon e^{i\theta }$ in Eq. (40) and $\int _{r_H-\epsilon }^{r_H+\epsilon } \frac{1}{(r-r_H)} \textrm{d}r = - i\pi ~,$ for first integral, $\sim \epsilon \approx 0$ for second integral, we obtain the action as

$$\begin{aligned} S = {\pm } \frac{i\pi E}{2{{\tilde{\kappa }}}} + \text {real part}, \end{aligned}$$

(41)

where the positive $+$ is for the outgoing trajectory and negative − is for the incoming trajectory of tunneling particles. We then write the WKB wave function for outgoing and incoming particles $\psi _{out} =A e^{\frac{i}{\hbar }S_{out}}, ~~~ \psi _{in} = Ae^{\frac{i}{\hbar }S_{in}}~,$ with A being a normalization constant and corresponding probabilities of the outgoing and incoming particles, become

$$\begin{aligned} P_{out} = |\psi _{out}|^2 = \mid A\mid ^2|e^{\frac{i}{\hbar }S_{out}}|^2 =\mid A\mid ^2 e^{-\frac{\pi E}{\hbar {{\tilde{\kappa }}}}}~, \end{aligned}$$

(42)

and

$$\begin{aligned} P_{in} = |\psi _{in}|^2 = \mid A\mid ^2|e^{\frac{i}{\hbar }S_{in}}|^2 = \mid A\mid ^2 e^{\frac{\pi E}{\hbar {{\tilde{\kappa }}}}}. \end{aligned}$$

(43)

Note that real part has no contribution to probability. Using the outgoing and ingoing particles probabilities, one can calculate the tunneling rate as

$$\begin{aligned} \Gamma = \frac{P_{out}}{P_{in}} = e^{-\frac{2\pi E}{\hbar {{\tilde{\kappa }}}}} \equiv e^{-\frac{E}{T_{H}}}, \end{aligned}$$

(44)

which is similar to the Boltzmann factor with $T_H$ recognized as the Hawking temperature,

$$\begin{aligned} T = \frac{{{\tilde{\kappa }}}}{2\pi }. \end{aligned}$$

(45)

Fig. 2

Left: Hawking temperature T versus r for $q=0.5$, $\beta =0.00001$ and for the various values of l. Right: Hawking temperature T versus q for $q=0.5$, and $\beta =0.00001$

Fig. 3

Left: Hawking temperature T versus l for $q=0.5$, and $\beta =0.0001$. Right: Hawking temperature T versus $\beta$ for $q=0.5$, and $l=0.5$

With the surface gravity expressed as:

$$\begin{aligned} {{\tilde{\kappa }}}=\left. \sqrt{-\frac{1}{2} \nabla _{\mu } \chi _{\nu } \nabla ^{\mu } \chi ^{\nu }} \equiv \frac{1}{2} \frac{\partial f(r)}{\partial r}\right| _{r=r_{H}}, \end{aligned}$$

(46)

the Hawking temperature related to $r_{H}$ is determined to be:

$$\begin{aligned} T=\frac{-\frac{r_H^2 \left( \frac{q^2}{r_H^2}-\frac{\beta q^4}{4 r_H^6}\right) }{l^2 \left( \frac{\beta q^4}{20 r_H^5}-\frac{q^2}{r_H}+\frac{1.08 q^{3/2}}{\root 4 \of {\beta }}\right) +r_HH^3}+\frac{r_H^2 \left( \frac{\beta q^4}{20 r_H^5}-\frac{q^2}{r_H}+\frac{1.08 q^{3/2}}{\root 4 \of {\beta }}\right) \left( l^2 \left( \frac{q^2}{r_H^2}-\frac{\beta q^4}{4 r_H^6}\right) +3 r_H^2\right) }{\left( l^2 \left( \frac{\beta q^4}{20 r_H^5}-\frac{q^2}{r_H}+\frac{1.08 q^{3/2}}{\root 4 \of {\beta }}\right) +r_H^3\right) {}^2}-\frac{2 r_H \left( \frac{\beta q^4}{20 r_H^5}-\frac{q^2}{r_H}+\frac{1.08 q^{3/2}}{\root 4 \of {\beta }}\right) }{l^2 \left( \frac{\beta q^4}{20 r_H^5}-\frac{q^2}{r_H}+\frac{1.08 q^{3/2}}{\root 4 \of {\beta }}\right) +r_H^3}}{4 \pi }, \end{aligned}$$

(47)

and is plotted in Figs. 2 and 3 for different values of l, q and $\beta$. Moreover, the horizon area is plainly calculated as $A=\int _{0}^{2 \pi } \textrm{d} \phi \int _{0}^{\pi } \sqrt{-g} \text { d} \theta =4 \pi r_{H}^2,$ which gives the black hole entropy to be $S_{B H}=\frac{A}{4}=\pi r_{H}^2$.

3 Weak deflection angle of AMCNS black hole using the Gauss–Bonnet theorem

The deflection angle of a photon approaching the said black hole with the distance of closest approach $r_0$ corresponds to [140,141,142]:

$$\begin{aligned} {\hat{\alpha }}(r_0) = -\pi + 2 \int _{r_0}^\infty \text { d}r \frac{\sqrt{f(r)^{-1}}}{r \sqrt{\frac{r^2}{r_0^2}\frac{f(r_0)}{f(r)}-1}}. \end{aligned}$$

(48)

Fig. 4

Geodesics of AMCNS black hole for $q=0.5$, $\beta =0.001$, and varying l; $l=0.5$ (left), and $l=0.7$ (right)

The condition $M/r_0 \ll 1$ is satisfied for weak lensing since the deflection angle will be too small [143]. As $r_0$ verges on the photon sphere, ${\hat{\alpha }}$ increases until it diverges, hence, giving rise to strong lensing. Considering the equatorial plane in which $\theta =\pi /2$ equation Eq. (26) reduces to the optical metric for null geodesics:

$$\begin{aligned} \text { d}t^2 = \frac{\text { d}r^2}{f(r)^2} + \frac{r^2}{f(r)} \text { d}\phi ^2. \end{aligned}$$

(49)

As mentioned above, the optical metric takes advantage of its geodesics for the topological effect that relates it to the Gauss–Bonnet theorem. The photon behaviors within the AMCHS black hole for a range of l values are illustrated in Fig. 4. Subsequently, Fig. 5 presents the paths followed by light rays as they orbit around the AMCHS black hole using the method defined in [41].

In that context, we delve deeper into the geodesics of the optical metric that governs the AMCNS black hole in Fig. 4. Notice the slightest difference in the light ray trajectory approaching from infinity towards the black hole that determines the fate of the light ray, an expected repercussion of the electric charge to starkly either pull the ray in or divert it around. Besides, an increase in l is observed to retract the light rays more swiftly towards the black hole center. Extrapolating this further, Fig. 5 encapsulates the raytracing of the AMCNS metric. The abrupt coiling is more obvious in the myriad of light rays in this figure.

Fig. 5

Raytracing of AMCNS black hole for $q=0.5$, $\beta =0.001$, and varying l; $l=0.5$ (left), and $l=0.7$ (right). The lines colored in black, gold, and red represent the direct, lensed, and photon rings correspondingly. On the panel located to the right, a chosen assortment of related trajectories in Euclidean polar coordinates, denoted as (r, $\phi$), is depicted. The black hole is symbolized by a black disk, and the circular orbit of light is a dashed yellow circular

The Gaussian curvature is computed from the non-zero Christoffel symbols due to its proportionality${\mathcal {K}} = {R}/{2}$ where R is the Ricci scalar and is found to be:

$$\begin{aligned} {\mathcal {K}}= & {} \frac{q^4 \left( -21 \beta +40 r^2+1050\right) }{20 r^8}+\frac{3 q^2}{r^4} \nonumber \\{} & {} \quad +m \left( \frac{q^4 \left( 225 \beta +19 \beta r^2-1830 r^2-22950\right) }{10 r^{11}}\right. \nonumber \\{} & {} \left. \quad -\frac{6 q^2 \left( r^2+25\right) }{r^7}-\frac{2}{r^3}\right) \nonumber \\{} & {} \quad {+} m^2 \left( {-}\frac{3 q^4 \left( 1326 \beta {-}130 r^4{+}124 \beta r^2{-}18410 r^2{-}202800\right) }{10 r^{14}}\right. \nonumber \\{} & {} \left. \quad +\frac{6 q^2 \left( 50 r^2+612\right) }{r^{10}}+\frac{3 r^2+100}{r^6}\right) \nonumber \\{} & {} \quad +l^2 \left( m^2 \left( \frac{30 q^2}{r^8}-\frac{3 q^4 \left( 23 \beta +65 r^2-3640\right) }{10 r^{12}}\right) -\frac{21 m q^4}{r^9}\right) .\nonumber \\ \end{aligned}$$

(50)

Employing the straight-line approximation $r = b/ \sin \phi$ for the impact parameter b, the Gauss–Bonnet theorem suggests that [100, 102]:

$$\begin{aligned} {\hat{\alpha }} = - \int _0^\pi \int _{{b}/{\sin \phi }}^\infty {\mathcal {K}} \text { d}S, \end{aligned}$$

(51)

where $\text { d}S\approx (r+3m) \text { d}r \text { d}\phi$. Owing to the complexity of this calculation, the Gaussian curvature was reduced to ${\mathcal {O}}\left( m^2\right)$ and the integral was simplified by ignoring the higher-order terms ${\mathcal {O}}\left( q^5\right)$. Thus, the deflection angle due to weak lensing for an asymptotic, magnetically charged, non-singular black hole is estimated to be:

$$\begin{aligned} \begin{aligned} {\hat{\alpha }}&= -\frac{1.43139 l^2 q^5}{b^6 \sqrt{\beta }}+\frac{7.15694 q^5}{b^6 \sqrt{\beta }}+\frac{7 \pi \beta q^4}{128 b^6}\\&\quad -\frac{175 \pi q^4}{64 b^6}-\frac{10.0777 q^{9/2}}{b^5 \beta ^{3/4}}+\frac{17.28 q^{7/2}}{b^5 \root 4 \of {\beta }}\\&\quad -\frac{0.6912 q^{11/2}}{b^5 \root 4 \of {\beta }}+\frac{1.5459 q^5}{b^4 \sqrt{\beta }}\\&\quad -\frac{3 \pi q^4}{16 b^4}-\frac{8.58833 q^3}{b^4 \sqrt{\beta }}-\frac{0.629856 q^{9/2}}{b^3 \beta ^{3/4}}\\&\quad -\frac{0.72 q^{7/2}}{b^3 \root 4 \of {\beta }}+\frac{0.687066 q^3}{b^2 \sqrt{\beta }}-\frac{3 \pi q^2}{4 b^2}+\frac{2.16 q^{3/2}}{b \root 4 \of {\beta }}, \end{aligned} \end{aligned}$$

(52)

in the weak-field limit. Note that the mass function defined by Eq. (32) is employed here in the place of m. From this result, the deflection angle is expected to change significantly because of the parameters that govern the black hole, reducing it to the case of a Schwarzschild black hole when $\beta =0$, $q=0$, and $l=0$. This relation is depicted in Fig. 6.

Taking a look at this equation graphically, the deflection angle is seen to be vividly affected by l and more intensely for q. The ranges of values for l and q are chosen according to the acquirable potentialities of a charged particle in the black hole locale. The deviating curve shows that the deflection angle is more than the Schwarzschild case when there is an electric charge, and it keeps increasing as q increases. The deceiving large contribution from l is seemingly increasing the deflection angle.

Fig. 6

Weak deflection angle plotted against the impact parameter. The solid black line denotes the Schwarzschild case and the gradient of grey shows the case of the asymptotic, magnetically-charged, non-singular black hole, Left: with $\beta =0.00001$, $q=0.5$, and $0< l< 1$. Right: Figure is plotted for $\beta =0.00001$, $l=0.5$, and $0< q< 1$

Therefore, the presence of the charge q appears to be enhancing the deflection angle. This suggests that the distortions will be stronger, more evident, and could contain more information about the characteristics of the black hole’s structure and of the light source.

3.1 Weak deflection angle in dark matter medium

The presence of a medium significantly affects the dispersive properties of light rays compared to those in a vacuum. One such medium that is known to exist almost always is the one surrounded by dark matter. The observations from the Event Horizon Telescope of enormous dark matter halos around the black holes in the galactic centers. Its ability to engulf galaxies and to invade the interstellar and intergalactic media makes it a matter of inquisitivity. When surrounding a black hole, the extreme gravity experienced by the dark matter added to its already enduring gravitational impacts constitutes an important component of astrophysics that would greatly aid the gravitational lensing analyses.

To evaluate the consequences of dark matter on the deflection angle, the refractive index computed from the scatterers is defined as outlined in references [107, 144, 145]:

$$\begin{aligned} n = 1 + B u + v w^2. \end{aligned}$$

(53)

In the given equation, w represents the frequency of light. The term $B \equiv { \rho _0 }/{ 4 m ^ { 2 }w ^ { 2 } }$ introduces a quantity denoted as B, where $\rho _0$ denotes the mass density of the scattered particles of dark matter. The parameter $u= - 2 \varepsilon ^ { 2 } e ^ { 2 }$ is defined, where $\varepsilon$ represents the charge of the scatterer in units of e, and v is a non-negative value. The terms of order ${\mathcal {O}} \left( w^2\right)$ and higher account for the polarizability of the dark matter particle. This expression presents the refractive index expected for an optically inactive medium. The term of order $w^{-2}$ corresponds to a charged dark matter candidate, while $w^{2}$ corresponds to a neutral dark matter candidate. Additionally, a linear term in w may be present if there exist parity and charge-parity asymmetries.

The line element in Eq. (26) can be reformulated using the optical metric as follows [106, 108, 146]:

$$\begin{aligned} \text { d} \sigma ^2 = g _ { i j }^{ \textrm{ opt } } \text { d} x^i \text { d} x^j = \frac{n^2}{f (r)} \left[ \frac{\text { d} r^2}{f(r)} + r^2 \text { d} \phi ^ { 2 }\right] . \end{aligned}$$

(54)

As in the previous section, the weak deflection angle of an asymptotic, magnetically charged, non-singular black hole enveloped by dark matter can be expressed as:

$$\begin{aligned} {\hat{\alpha }}= & {} -\frac{1.43139 l^2 q^5}{b^6 \sqrt{\beta } \left( B u+v w^2+1\right) ^2}-\frac{14.3139 q^5}{b^6 \sqrt{\beta } \left( B u+v w^2+1\right) ^2}\nonumber \\{} & {} \quad +\frac{7 \pi \beta q^4}{128 b^6 \left( B u+v w^2+1\right) ^2}-\frac{175 \pi q^4}{64 b^6 \left( B u+v w^2+1\right) ^2}\nonumber \\{} & {} \quad +\frac{17.28 q^{7/2}}{b^5 \root 4 \of {\beta } \left( B u+v w^2+1\right) ^2}-\frac{3 \pi q^4}{16 b^4 \left( B u+v w^2+1\right) ^2}\nonumber \\{} & {} \quad -\frac{8.58833 q^3}{b^4 \sqrt{\beta } \left( B u+v w^2+1\right) ^2}\nonumber \\{} & {} \quad +\frac{1.44 q^{7/2}}{b^3 \root 4 \of {\beta } \left( B u+v w^2+1\right) ^2}-\frac{0.687066 q^3}{b^2 \sqrt{\beta } \left( B u+v w^2+1\right) ^2}\nonumber \\{} & {} \quad -\frac{3 \pi q^2}{4 b^2 \left( B u+v w^2+1\right) ^2}+\frac{2.16 q^{3/2}}{b \root 4 \of {\beta } \left( B u+v w^2+1\right) ^2}.\nonumber \\ \end{aligned}$$

(55)

Fig. 7

Weak deflection angle plotted against the impact parameter in the presence of dark matter medium. The rainbow gradient represents the AMCNS black hole when the light frequency $w=1$ at the red end to the black hole in vaccum at the blue end, with $\beta =0.00001$, $l=0.5$, and $q=0.5$

In Fig. 7, it is demonstrated that the deflection angle exhibits an upward trend as the parameter w increases within the weak field limits, implying more dark matter activity engenders more distortions in the lensing profile. While it is not possible to predict how dark matter behaves around a black hole as opposed to the well-understood outer-galactic distribution, its fundamentality of augmenting the distortions, and by extension, the deflection angle, is unchanging.

4 Accretion disk and shadow cast of AMCNS black hole

In this section, the shadow that is formed by a black hole that has a thin-accretion disk is examined. An accretion disk refers to the structure that arises from the gravitational pull of a central gravitating object on the adjacent matter like gas or dust [41, 147,148,149]. As this matter moves toward the central object, it gains kinetic energy and generates a rapidly rotating disk around it. The temperature and density of the disk can cause it to emit radiation in different forms, such as X-rays, visible light, or radio waves. Accretion disks serve as an essential component in the development and progression of gravitating objects since they facilitate the transfer of mass and angular momentum.

When the accretion disk concurs with the lensing effect, produces the appearance of a shadow of a black hole. In essence, the phenomenon of gravitational lensing is the key factor that distinguishes the black hole shadow in the Newtonian case in contrast to that of the general-relativistic case, thus, exaggerating the shadow with the bending of light. The critical curve segregating the capture orbits and the scattering orbits forms the shadow with a geometrically thick, optically thin region filled with emitters (that either spiral into the black hole or swerve away from it) and is associated with a distant, homogeneous, isotropic emission ring. The former property is important while talking about an emission region since the intensity takes a dip that is coincident with the shadow, making it observable through this strong visual signature. The size of the shadow is mainly determined by the inherent parameters of the black hole, and its contour is shape-shifting owing to the instability in the orbits of the light rays from the photon sphere. For a distant observer, the shadow appears as a dark, two-dimensional disk, which is illuminated by its bright and uniform surroundings.

For the line element given by Eq. (26), introducing the function h(r) such that:

$$\begin{aligned} h^2(r) = \frac{r^2}{A(r)}, \end{aligned}$$

(56)

which is equivalent to the effective potential for photon motion [150]. Not that according to line element in 26, $A(r)=\frac{1}{B(r)}=f(r)$. Equation (57) can be rearranged and rewritten as:

$$\begin{aligned} \left( \frac{\textrm{d} r}{\textrm{d} \phi }\right) ^2=\frac{r^4}{B(r)}\left( \frac{1}{b^{2} A(r)}-\frac{1}{r^{2}}\right) = \frac{r^2}{B(r)}\left( \frac{r^2}{b^{2} A(r)}-1\right) , \end{aligned}$$

(57)

where, the impact parameter $b \equiv L / E$ yet again. This equation is analogous to the traditional energy-conservation law described for one-dimensional motion in classical mechanics:

$$\begin{aligned} \left( \frac{\textrm{d}r}{\textrm{d}\phi }\right) ^2 + V(r) =0, \end{aligned}$$

(58)

with $\phi$ taking the place of the temporal variable and the effective potential V(r) displaying its dependence on r, and by extension, b. This is also known as the orbit equation.

To determine the circular trajectories, the equations $V = 0$ and $\nicefrac {\textrm{d}V}{\textrm{d}r} = 0$ can be solved. For a light ray approaching the center, if there exists a point at which it turns back around to exit the orbit after the ray reaches the minimum radius R, then the condition $\nicefrac {\textrm{d}r}{\textrm{d}\phi }|_R = 0$ needs to be complied with, yielding the orbit equation to be:

$$\begin{aligned} \frac{1}{b^2} = \frac{A(R)}{R^2}. \end{aligned}$$

(59)

This relation between the constant of motion and R instigates the following relationship:

$$\begin{aligned} b = h(R), \end{aligned}$$

(60)

which in turn yields:

$$\begin{aligned} \left( \frac{\textrm{d} r}{\textrm{d} \phi }\right) ^2=\frac{r^2}{B(r)}\left( \frac{h^2(r)}{h^2(R)}-1\right) , \end{aligned}$$

(61)

Say, a static observer located at a radial coordinate $r_o$ shoots one light ray to the past. The dimensionless quantity $\psi$ is identified in terms of the cotangent to be:

$$\begin{aligned} \cot \psi =\left. \sqrt{\frac{g_{r r}}{g_{\phi \phi }}}\, \frac{\textrm{d} r}{\textrm{d} \phi }\right| _{r=r_O}=\left. \frac{\sqrt{B(r)}}{r} \,\frac{\textrm{d} r}{\textrm{d} \phi }\right| _{r=r_O}, \end{aligned}$$

(62)

as represented by Fig. 8 to be the measurable angle between the light ray and the radial coordinate which is directed towards the point of closest approach. It is termed as the angular radius of the shadow.

Fig. 8

Description of the turning point with the minimum radius R and the shadow’s angular radius $\psi$ in the Schwarzschild spacetime when a light ray is sent to the past by an observer located at $r_o$ in the present

Squaring this equation and substituting Eqs. (60) and (61) in it gives:

$$\begin{aligned} \cot ^2 \psi =\frac{h^2 r_o)}{h^2(R)}-1 \quad \quad \text {i.e.,}\quad \quad \sin ^2 \psi =\frac{h^2(R)}{h^2\left( r_o\right) }. \end{aligned}$$

(63)

Here, the light ray approaching the circular (with radius $r_{ph}$), unstable photon orbits asymptotically is oriented to the past, and so is the shadow’s boundary curve. In the limit where where $R \rightarrow r_{ph}$, the above expression can be rewritten as:

$$\begin{aligned} \sin ^2 \psi _{sh}=\frac{h^2\left( r_{ph}\right) }{h^2\left( r_o\right) }\quad \quad \text {and} \quad \quad b_{cr}=h\left( r_{ph}\right) . \end{aligned}$$

(64)

This implies:

$$\begin{aligned} \sin ^2 \psi _{sh}=\frac{b_{cr}^2}{h^2(r_o)} =\frac{b_{\textrm{cr}}^2}{r_o^2/ A(r_o)}. \end{aligned}$$

(65)

In the pursuit of calculating $r_{ph}$ for the metric in Eq. (26) next, it is essential to realize that both $\textrm{d}r/\textrm{d}\phi$ and $\textrm{d}^2 r/ \textrm{d}\phi ^2$ should simultaneously be zero. Differentiating Eq. (57), all terms vanish following the conditions except the third term acquired from the parentheses which are equated to zero resulting in:

$$\begin{aligned} 0=\frac{\textrm{d}}{\textrm{d} r} h^2(r). \end{aligned}$$

(66)

The range of values that r can take is extensive inferring that there could be multiple photon orbits – stable and unstable, existing together, with the light rays oscillating and spiraling respectively – impinging on the construction of the black hole shadow. For $r=r_{ph}$, the shadow can be determined for any distance, small or large, in a static, spherically-symmetric, asymptotically-flat spacetime with h(r) from Eq. (64) by:

$$\begin{aligned} b_{cr}=\frac{r_{ph}}{\sqrt{A\left( r_{ph}\right) }} \quad \quad \text {and} \quad \quad R_{sh}=\psi _{sh} \approx \frac{b_{cr}}{r_o}\sqrt{A(r_o)}. \end{aligned}$$

(67)

In the numerical plot depicted in Fig. 9, the radius of the black hole’s shadow ($R_{sh}$) is calculated for different values of $l$ for asymptotically flat case $A(r_o=1)$, and $(r_0=1$). It is intriguing to observe the exponential and inverse relationship exhibited by $l$, irrespective of the range within which the parameters vary. In Fig. 9, the upper limits of $l$ are presented based on EHT observational results on the Sgr. A* tabulated in Table 1. According to the $68\%$ confidence level (C.L.) [9], the upper limit for $l$ is $0.6$.

Table 1 Observational constraints from the supermassive black hole Sgr. A*

Fig. 9

Constraints from the Event Horizon Telescope horizon-scale image of Sagıttarius A* at $1\sigma$ [9], after averaging the Keck and VLTI mass-to-distance ratio priors for the same with $q=0.5$, $\beta =0.001$, and varying l

4.1 Spherically infalling accretion

In this section, we explore the model of spherically free-falling accretion around AMCNS black hole from an infinite distance. The approach described in references [147, 149] is employed for this investigation. By utilizing this method, we can generate a realistic representation of the shadow produced by the accretion disk. However, in reality, the actual image of the black hole cannot be observed as a discernible boundary in the universe. Additionally, employing a static accretion-disk model is not feasible due to the presence of a dynamic accretion disk surrounding the black hole. This dynamic disk also generates synchrotron emission as part of the accretion process. To accomplish this, our initial focus is on studying the specific intensity observed at the frequency of the photon $\nu _{\textrm{obs}}$ by solving the following integral along the path of light:

$$\begin{aligned} I(\nu _{\textrm{obs}},b_\gamma ) = \int _\gamma g^3 j(\nu _e) \textrm{d} l_{\textrm{prop}}. \end{aligned}$$

(68)

We should mention that $b_{\gamma }$ represents the impact parameter, $j(\nu _e)$ corresponds to the emissivity per unit volume, $\textrm{d} l_{\textrm{prop}}$ represents the infinitesimal proper length, and $\nu _e$ denotes the frequency of the emitted photon. In this context, we introduce the redshift factor for the accretion in free-fall using the following definition:

$$\begin{aligned} g = \frac{k_\mu u^\mu _o}{k_\mu u^\mu _e}, \end{aligned}$$

(69)

The equation provided states that the 4-velocity of the photon is represented by $k^\mu ={\dot{x}}_\mu$, while the 4-velocity of the distant observer is denoted as $u^\mu _o=(1,0,0,0)$. Furthermore, $u^\mu _e$ represents the 4-velocity of the infalling accretion:

$$\begin{aligned} u_{\textrm{e}}^{t}=\frac{1}{A(r)}, \quad u_{\textrm{e}}^{r}=-\sqrt{\frac{1-A(r)}{A(r) B(r)}}, \quad u_{\textrm{e}}^{\theta }=u_{\textrm{e}}^{\phi }=0. \end{aligned}$$

(70)

By utilizing $k_{\alpha } k^{\alpha }=0$, one can derive the constants of motion $k_{r}$ and $k_{t}$ for the photons.

$$\begin{aligned} k_{r}={\pm } k_{t} \sqrt{B(r)\left( \frac{1}{A(r)}-\frac{b^{2}}{r^{2}}\right) }. \end{aligned}$$

(71)

It is worth noting that the sign of ${\pm }$ indicates whether the photon approaches or deviates away from the black hole. Based on this, the redshift factor g and proper distance $\textrm{d} l_\gamma$ can be expressed as follows:

$$\begin{aligned} g = \Big ( u_e^t + \frac{k_r}{k_t}u_e^r \Big )^{-1}, \end{aligned}$$

(72)

and

$$\begin{aligned} \textrm{d} l_\gamma = k_\mu u^\mu _e \textrm{d} \lambda = \frac{k^t}{g |k_r|}\textrm{d} r. \end{aligned}$$

(73)

Next, we restrict our analysis to monochromatic emission, where the specific emissivity is considered with a rest-frame frequency $\nu _*$.

$$\begin{aligned} j(\nu _e) \propto \frac{\delta (\nu _e - \nu _*)}{r^2}. \end{aligned}$$

(74)

Subsequently, the intensity equation, given in equation (68), can be expressed as follows:

$$\begin{aligned} F(b_\gamma ) \propto \int _\gamma \frac{g^3}{r^2} \frac{k_e^t}{k_e^r} \textrm{d} r. \end{aligned}$$

(75)

To analyze the shadow created by the thin accretion disk around the black hole, we begin by numerically solving the aforementioned equation. This numerical calculation is performed using the Einsteinpy library [151] and the Mathematica notebook package [32], which have also been utilized in previous studies [29, 54, 56, 59]. The integration of the flux reveals the impact of the parameter l on the specific intensity observed by a distant observer for an in-falling accretion. The corresponding results are presented in Figs. 10, 11, and 12.

Fig. 10

$q=0.5$, $\beta =0.001$, and varying l; $l=0.3$ (blue), $l=0.5$ (green), and $l=0.7$ (red)

Fig. 11

$q=0.5$, $\beta =0.001$, and $l=0.3$ (left), $l=0.5$ (middle), and $l=0.7$ (right)

Fig. 12

$q=0.5$, $\beta =0.001$, and $l=0.3$ (left), $l=0.5$ (middle), and $l=0.7$ (right)

The figures in Figs. 11, and 12 show the intensity plots and stereographic projections of the AMCNS black hole described following the method of [41, 148, 149]. The intensity plot shows the smooth transition between the layers in the journey directed away from the event horizon. The sharpness in every photon band in Fig. 12 indicates the effect of the parameters q, l, and $\beta$ appearing to be brighter.

The difference in the appearance of the shadow sizes between the three images in Fig. 11 is hard to miss. The emissivity from the innermost photon orbit is seen to get brighter as l increases. Consequently, the size of dark shadow region appears to be decreasing. Numerically speaking, Fig. 10 depicts how small yet non-trivial this difference is. The shadow outline seen in the images of Fig. 12 clearly exemplifies that the manifestation of additional inner-orbits of photons proportionally increasing with l instigates the peak intensity to grow.

When compared with the shadow of a Schwarzschild black hole, the crucial factor that brings about a striking distinction between them is singularity. The Schwarzschild black hole is singular at its center meaning that it is a point of infinite density and zero volume. Among all the properties of a black hole that are disturbed by this (such as curvature, geometry, density profile, etc.), the one that is sizably impacted is the event horizon which is a mathematical construct that assumes the black hole is a point singularity. For a non-singular black hole, this assumption does not hold; in that case, the event horizon becomes an apparent boundary beyond which light cannot escape to infinity, but can still escape to some finite distance. This leads the non-singular black hole to have a smaller event horizon than the Schwarzschild black hole, which in turn explains the former’s smaller shadow size.

In summary, any entity that skirts around a black hole rendering a time-dependent appearance of the shadow will inexorably give rise to distortions, big or small, contingent on its characteristics. Also, the singularity at the center of a black hole can cause its space-time geometry to curve more bringing about a wider event horizon and a bigger shadow size. On the other hand, a non-singular black hole would have a smoother geometry and a smaller horizon that results in a smaller shadow size. Furthermore, dark matter intensifies the extent of distortions because of dispersion.

5 Bounding the greybody factors of AMCNS black hole

The equivalence of black holes to black bodies inspires curiosity about their relationship. This section is devoted to inspecting that correlation. A black body is an idealized object that absorbs all radiation that strikes it and emits radiation without incurring any loss at all wavelengths and at the maximum frequency; for a given spectrum, although the wavelength is dependent on temperature, its efficiency is 100%. Whereas, black holes absorb all radiation and matter inside the event horizon and emit Hawking radiation that is dependent on the mass of the black hole preserving the quantum information of the engulfed particles [11, 152]. While the gravity field and the matter encompassing a black hole deteriorates its energy eventually impairing the Hawking radiation emitted by the black hole from being fully efficient, its resemblance to a pure black body at its horizon, when isolated (resulting from quantum effects), is impeccable.

The deteriorating aspects of a radiating black hole are given by the greybody factor: the nomenclature underlines the departure from the black body behavior. It is a function of frequency and angular momentum that typifies the degree of deviation in the emission spectrum of a black hole from a perfect black body spectrum. The main culprit for this digression is the scattering of the radiation by the geometry of the black hole itself relating to the captured/radiated particles that fall back into the extreme force. This causes the spectrum emitted by the black hole to deviate and can be observed as the greybody factor [153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171].

By the scattering of a wave packet off a black hole, the greybody factor can be determined with the help of the classical Klein-Gordon equation – the Schrödinger-like equation that governs the modes for a wave function $\varphi (r)$ relating the position of an electron to its wave amplitude is written as:

$$\begin{aligned} \left( \frac{\textrm{d}^2}{\textrm{d} r_{*}^2}+\omega ^2-{V}(r)\right) \varphi (r)=0, \end{aligned}$$

(76)

where, $r_*$ is commonly known as the tortoise coordinate. Its purpose is to evolve to infinity in a manner that counters the singularity of the metric under scrutiny. The time of an object looming towards the event horizon in the constructed system of coordinates grows to infinity... so does $r_*$ but at a rate that is appropriate. Mathematically:

$$\begin{aligned} \textrm{d} r_*=\frac{1}{f(r)} \text { d} r, \end{aligned}$$

(77)

and the potential V(r) for the azimuthal quantum number $\ell$ specifying the mode can accordingly be formulated as:

$$\begin{aligned} {V}(r)=\frac{f(r) f^{\prime }(r)}{r}+\ell (\ell +1) \frac{f(r)}{r^2}. \end{aligned}$$

(78)

This embodies the potential energy of the particle when there is an external force/field. The information about the wavefunction, the bound and scattering states, etc. can be begotten from this quantity.

Assuming that the energy of the particles emitted by the black hole falls in the range $\hbar \omega$ to $\hbar (\omega + \textrm{d}\omega )$ for a given wave frequency $\omega$, let $\Upsilon$ be a positive function that obeys $\Upsilon (-\infty ) = \sqrt{\omega ^2 -V_{-\infty }}$ and $\Upsilon (\infty ) = \sqrt{\omega ^2 -V_\infty }$ when $V_{{\pm }\infty } = V{\pm } \infty$. To find the lower bound, the condition $V_{{\pm }\infty } =0$ must be satisfied, implying that $\Upsilon =\omega$ and the transmission probability is deduced as follows [172,173,174]:

$$\begin{aligned} T_b&\ge \textrm{sech}^2\left( \int _{-\infty }^{\infty } {V}(r) \text { d} r_*\right) \nonumber \\&=\textrm{sech}^2\left[ \frac{1}{2 \omega } \int _{r_H}^{\infty }\left( \frac{f^{\prime }(r)}{r}+\frac{\ell (\ell +1)}{r^2}\right) \text { d} r\right] \end{aligned}$$

(79)

This expression for T offers insight into the probability of a particle with a specific energy and angular momentum escaping the black hole and being detected at infinity. Yet again, $r_H$ is the radius of the event horizon of the black hole: it directly affects the details of the emitted radiation spectrum. Because of the intricacy of solving for the polynomial, we procure $r_H$ numerically.

The term $\ell (\ell +1)$ describes the discrete robustness of quantum mechanics in general relativity by providing a measure of the angular momentum carried by the particles that the black hole emits. Also called the angular momentum quantum number, the value that $\ell$ takes says quite a lot about the emitted particles and spectrum:

• $~\ell =0$ insinuates that the emitted particles have zero angular momentum and are moving in a direction away from the black hole. The probability of a particle escaping the black hole in this case is maximum at low energies and it decreases as the energy of the particle increases. The spectrum of emitted radiation for the particles in this state is typically dominated by low-energy photons.

• $~\ell =1$ insinuates that the emitted particles have some angular momentum and are moving in a circular orbit around the black hole. The probability of a particle escaping the black hole in this case is maximum at intermediate energies and it decreases at both low and high energies. The spectrum of emitted radiation for the particles in this state typically peaks at intermediate energy.

Therefore, the value of $\ell$ particularizes the detailed shape of the spectrum of the radiation that a black hole emits, granting information about the features of the black hole itself. The graphical representation of the results acquired for V(r) and T is presented in Fig. 13a and b respectively for an AMCNS black hole.

Plotted to show the variation of the potential V(r) in terms of the radial coordinate r for varying l, Fig. 13a is perceived to show a negative intercept that rises to positive until a certain value before falling again when $\ell =0$. However, for $\ell =1$, Fig. 13b has a negative trough that briskly rises with l to positive.

Fig. 13

Potential plotted against radial distance

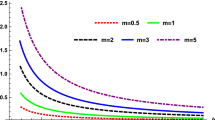
Figure 14 illustrates the variation of the Transmission probability T in terms of the frequency $\omega$ for different values of l for an AMCNS black hole when $\ell =0$. While the graph traits of all cases in Fig. 14a are analogous to each other with the same probability, a closer look at the ascension in the frequency range of $0.05 \le \omega \le 0.2$ infers that any and every variation (even the ones of the smallest magnitude) in the parameters of a black hole gives rise to an innate frequency.

Fig. 14

Transmission probability plotted against frequency for $q=0.5$, and $\beta =0.001$ for $\ell =0$

Figure 15 illustrates the variation of the Transmission probability T in terms of the frequency $\omega$ for different values of l for an AMCNS black hole when $\ell =1$. In Fig. 15a, the probability of transmission of each case is discrete from the others and is noticed to be higher for lower values of l, converging to unity as $\omega$ increases. The offsetting of every different l in Fig. 15b is highly conspicuous attributable to the factor of angular momentum that prevails. Recalling that l is a length-scale parameter, the decrease in $T_b$ with increasing l can be explained by the inverse proportionality exhibited by frequency with respect to wavelength.

Fig. 15

Transmission probability plotted against frequency for $q=0.5$, and $\beta =0.001$ for $\ell =1$

Nevertheless, the overall nature of the AMCNS black hole plots is adequately comparable to that of the Schwarzschild case and to Figs. 2 and 5 in in which the author handles a regular Hayward black hole.

6 Conclusion

In this article, we have attempted to analyze the astrophysics of an asymptotic, magnetically-charged, non-singular black hole. o find its solution, we commenced with the Euler–Lagrange equation for nonlinear electrodynamics and applied it to the Hayward metric through the trace of the energy–momentum tensor. Establishing its connection to the energy density eased us in uncovering the mass function and, with additional computations, the metric function of the AMCNS black hole.

This illation was then employed in the Gauss–Bonnet theorem and modified with the Gibbons and Werner method to obtain the weak deflection angle of the AMCNS black hole. This is done with the aim of examining the black hole’s gravitational field, its intrinsic attributes such as mass, spin, etc., the nature of the light bending, and, ultimately, the validity of Einstein’s theory deeper. These help us comprehend the dynamics of black holes better and prepares Observational Astrophysicists on what to or not to expect. The deflection angle that was obtained was observed to be vastly variant for the AMCNS black hole with an increase that is triggered by its governing parameters.

We then proceeded to calculate the effects of the dark matter medium on the deflection angle. Numerous theoretical and experimental endeavors are adopted to bridge the gap between physics and astrophysics; incorporating the consequences of dark matter majorly subsidizes that. Dark matter plays a key role in the intensified regime of black holes accreting and jets launching. The dark matter medium was perceived to increase the deflection more, and for the AMCNS balc hole, the slightest drop in the refractive index generated an immense upshot.

The greybody factor was then investigated using the Schrödinger-like equation. The potential and the transmission probability were derived for the AMCNS black hole and were plotted against a Schwarzschild black hole. One can discern the sizable differences in each of the curves for every case of the azimuthal quantum number.

Finally, the black hole shadow was probed for the AMCNS case. Although many parameters affect the shadow size, the factors assumed here for this particular black hole display highly distinguished traits, making the black hole fairly distinctive from a Schwarzschild black hole. With the assistance of the Euler–Lagrange equation once again, the critical curve and the shadow’s angular radius were determined. They were scrutinized thoroughly with stereographic projections; the singularity at the center of the Schwarzschild black hole curves and distorts its spacetime geometry more than that of a non-singular black hole, therefore, having a larger horizon and shadow size. The smoother spacetime geometry of the AMCNS black hole gives it a relatively smaller horizon and shadow size.

The allowed values of the shadow radius within the context of the Event Horizon Telescope (EHT) observations of the supermassive black holes, specifically Sgr. A*, serve as constraints on the emergent parameter denoted as l. These observational findings are systematically organized in Table 1. In conjunction with this dataset, we derive the 1$\sigma$ confidence intervals for the Schwarzschild deviation, as outlined in references [6,7,8,9]. These intervals are presented as $4.55M \le R_{\textrm{sh}} \le 5.22M$ for Sgr. A*, where $R_{\textrm{sh}}$ denotes the shadow radius and M symbolizes the black hole’s mass. In Fig. 9, we present the upper limits of the parameter $l$ based on the Sgr. A* observational outcomes tabulated in Table 1 as a result of the EHT observations. According to the $68\%$ confidence level (C.L.) analysis [9], $l$ is bounded by an upper limit of $0.6$. This implies that the potential impacts of nonsingular black holes could be tightly constrained through forthcoming high-precision observations involving supermassive and other black holes.

Upcoming advancements in astronomical instrumentation hold the potential to thoroughly explore the parameter space of nonsingular black holes. Notable among these instruments is the EHT, which aims to achieve angular resolutions of 10–15 $\upmu$as at $345$ GHz. Additionally, the ESA GAIA instrument is anticipated to possess the capacity to resolve angular details at levels between 7 and 20 $\upmu$as [175]. Another influential tool in this pursuit is the potent VLBI RadioAstron, capable of attaining remarkably fine angular resolutions as diminutive as 1–10 $\upmu$as [176]. These advancements have the potential to revolutionize our understanding of nonsingular black holes by significantly enhancing our ability to observe and analyze their characteristics.

Meticulous methodologies of maximal parametric inclusiveness facilitate us in refining our comprehension of gravitational lensing. The distortions that every black hole produces offer so much information about the source of the light rays along with the black hole, which in turn motivates us to come up with new hypotheses that could polish and perfect our perception: our future work is directed toward the same. we intend to gather as many contributing factors that affect our grasp of black hole theories as possible and enhance them, no matter how complex it is, so that both theoretical and observational astrophysics can use them as a resource for improvement. We hope to attain ways that could minimize our assumptions like zero spin, staticity, spherical symmetry, and so many other constraints, and deal with the black hole realistically instead to the greatest degree feasible.