1 Introduction

The study of wormhole (WH) solutions is recognized as the most fascinating speculation in general relativity (GR), which has gained much attention from several authors. According to GR, such exotic geometries are possible because of the deformability of spacetime caused by matter/energy. In fact, the WHs are bridges between distinct points at a manifold. In general, the WHs are asymptotically flat and the notion associated with their structures was first proposed by Flamm [1] and later suggested by Einstein and Rosen [2]. The structure introduced by the latter is characterized as the “Einstein–Rosen bridge” and is known as a vacuum solution of Einstein’s field equations. Such types of WHs are constructed with the Schwarzschild solution by taking into account two black holes (BHs) connecting two distinct regions of spacetime. Due to the presence of singularity, it was shown that such WH geometry is not traversable. Fuller and Wheeler [3] adopted Kruskal components to narrate the structure of Schwarzschild WH depicting its non-traversable nature. They demonstrated that if the WH were to open, it would close so swiftly that not even a single photon could get over it.

Great cosmologists as well as astrophysicists have started to inspect the possibility of the occurrence of traversable WHs by considering the theoretical predictions of Schwarzschild WHs and Einstein–Rosen bridges. The first structure of traversable WH is displayed by Morris and Thorne [4] as a connection that joins two eras of the same cosmos or two different universes via a throat that permits the way from one spacetime era to another. The same researchers explained that to get through this era, the matter incorporating those structures must violate the general energy constraints [4,5,6,7]. Thus, in the background of GR, the “exotic matter” violating the usual energy constraints is required to obtain a traversable WH. No doubt, it is a serious theoretical problem to deal with such type of matter that has not been straightly examined. To overcome this issue, thin-shell WHs were introduced in which the quantity of exotic matter inside the throat or thin-shell can be restricted as small as required constructing such type of WH geometries that violate the energy constraints only in this era [8, 9]. The construction of such WH geometry is done by considering the famous cut-and-paste method in which cutting and pasting the two manifolds create an entirely new one with a shell inserted in the connection surface. In this process, the exotic matter needed for their presence is concentrated in the shell or WH throat. Since it cannot be entirely ignored, therefore, we can focus our research on a thin-shell model. The constituents of the surface stress-energy tensor at the WH throat are evaluated by employing the Darmois–Israel condition [10, 11], that provides the Lanczos equations [12,13,14]. One can determine the dynamic change in the WH structure by solving the Lanczos equation with the help of the equation of state (EoS) for the exotic matter on the thin-shell.

As those astrophysical objects are of significant importance if they show stability against perturbations. For this purpose, many authors explored the stable geometries of WH as well as thin-shell WHs with linear perturbations to maintain the original symmetries. Poisson and Visser [15] presented the stability of Schwarzschild thin-shell WH. Lobo and Crawford [16] discussed the stable structure of spherically symmetric thin-shell WHs with cosmological constant and exhibited that the stable WH solutions occur just for the positive range of cosmological constant. Eiroa and Romero [17] investigated the WH geometry and its stability using linearized perturbations with the existence of an electric field and found the stable structure of WHs for suitable values of charge parameter. Bronnikov et al. [18] analyzed the stability of WH as well as regular BH with a phantom scalar field. Sharif and Azam [19] demonstrated the thin-shell WH with charged regular BH in a non-linear electrodynamics field and found a stable structure corresponding to some particular choice of parameters. On the same ground, several researchers studied the thin-shell WH geometries and their stability adopting different conjectures like charge, various EoS, and other distinct physical parameters [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].

In Einstein’s field equations, the cosmological constant is usually employed to characterize the current state of the cosmos. The various astronomical observations manifest that the current rapid expansion of the cosmos is due to some factor having large negative pressure. To describe this negative pressure, the quintessence is considered a significant alternative candidate of cosmological constant [37, 38]. The solution of the Einstein equation corresponding to quintessence was first determined by Kiselev in 4-dimensions [39]. Chen et al. [40] presented the solution of Einstein’s equation associated with quintessence in higher dimensional spacetime. Banerjee et al. [41] inspected the stability of a thin-shell wormhole in d-dimension with quintessence.

A novel semi-classical strategy for quantum gravity has recently been proposed in [42], where it is demonstrated that the Raychaudhuri equation is corrected by substituting quantal trajectories for classical geodesics. Thus, by the Hawking-Penrose theorem [43], these new quantum corrections will have an impact on all plausible spacetimes that are incomplete or singular in some particular sense. It has been discovered that the quantum Raychaudhuri equation inhibits the creation of singularities by preventing the focussing of geodesics [42]. In cosmology using the Friedmann–Robertson–Walker universe model, it is observed that the big bang singularity can be avoided by employing quantal geodesics [44]. Moreover, it was discovered that the Friedmann equation acquires a quantum correction factor that is equivalent to a cosmological constant and provides a feasible approximation of its observed value [44, 45]. Motivated by this Ali and Khalil [46] first inspected the BH physics with quantum correction. Shahjalal [47] discussed the thermodynamic properties of quantum-corrected Schwarzschild BH with quintessence. Jusufi [48] examined the stable structure of quantum-corrected thin-shell WH and found that quantum correction greatly affects the stability of WH.

It is well-known that the stability of thin-shell WHs is widely affected by the choice of BH as well as EoSs. Due to this reason, various researchers adopted different EoSs to discuss the different physical aspects of WHs and Chaplygin gas (CG) EoS have attained great attention in this respect. Eiroa and Simeone [49] constructed the spherically symmetric thin-shell WHs using CG and analyzed the stability of their solutions. They also found the parametric values for which stable solutions exist. Eiroa [50] explored the structure of spherical thin-shell WHs with generalized CG and studied their stability with the electric field as well as the cosmological constant. Sharif and Azam [51, 52] considered charged BH for the creation of a thin-shell WH with CG and generalized CG. They observed the stability of static solutions and found stable/unstable structures for cylindrical thin-shell WHs. Varela [53] determined the stable thin-shell WH models with Schwarzschild BH using variable EoS and presented the perturbative analysis of WH equation of motion for variable Chaplygin EoS. Eid [54] presented the dynamical analysis of charged thin-shell WHs by employing the variable EoS. Sharif and Javed inspected the stability of thin-shell WHs constructed by Bardeen BH [55] as well as Bardeen AdS BH [56] by using different choices of variable EoS. The same authors [57] compared the stable structures of thin-shell (internal Minkowski metric and the external Reissner–Nordström BH) and charged thin-shell (inner and outer Reissner–Nordström BH) WHs using generalized barotropic, generalized phantom-like, and CG EoSs. Recently, Li et al. [58] obtained a (3+1)-dimensional static spherically-symmetric BH solution to the Einstein field equations in the background of dark fluid and Chaplygin-like EoS. They also investigated the physical characteristics of BH solutions, i.e., thermodynamics, shadow, and critical values of temperature and pressure.

Motivated by all the above-mentioned works, in the present article, we examine the stability of thin-shell WH with quantum-corrected charged BH surrounded by quintessence. The manuscript is arranged as follows: next section provides the general interpretation of quantum corrected charged BH and the thin-shell WH are constructed with the help of two similar forms of adopted BHs via cut and paste technique. Section 3 is dedicated to observing the stable structure of constructed geometries via radial perturbation corresponding to the barotropic, generalized phantom-like, and Chaplygin-like EoS. The last section summarizes our important results.

2 Equation of motion of thin-shell wormholes

This section deduces the equation of motion of the thin-shell wormholes mathematically constructed from two equivalent copies of quantum corrected charged BHs surrounded by quintessence. The considered BH metric can be displayed as

$$\begin{aligned} ds^2=-{\mathcal {F}}(r)dt^2+\frac{1}{{\mathcal {F}}(r)} dr^2+r^2 d\Omega ^2, \end{aligned}$$
(1)

in which \({\mathcal {F}}(r)\) is a lapse function based upon the radial component r and \(d\theta ^2+\textrm{sin}^2\theta d\phi ^2=d\Omega ^2\). The lapse function can be defined as [47, 59]

$$\begin{aligned} {\mathcal {F}}(r)=\frac{\sqrt{r^2-a^2}}{r}-\frac{2 M}{r}-\frac{\chi }{r^{3 \omega _q+1}}+\frac{Q^2}{r^2}, \end{aligned}$$
(2)

here a denotes the quantum correction factor, M represents the mass of BH, \(\chi \) symbolizes the quintessence field and \( \omega _q\) denotes the quintessence state parameter and Q shows the the electric charge of the BH. Also, a corresponds to the behavior of spherical symmetric quantum fluctuations via \(a\equiv 4l_p\) where \(l_p\) is the Planck length [47, 59]. In the absence of \(\chi \) and Q, we get the quantum corrected Schwarzschild BH solution [47].

In order to create thin-shell WHs, we take two similar copies of the proposed BH solution. The cut and paste technique is used to define thin-shell WHs. It is well known that the geometry of WHs joins two distant and distinct regions of the spacetimes with the help of a tunnel recognized as the WH throat. In cosmology as well as astrophysics, the description of the observers moving from one region to another via WH throat is a fascinating scenario. No observer is able to move freely through the WH throat because of its rapidly collapsing and expanding phenomenon. To prevent the WH throat from collapsing, a certain kind of matter distribution must be needed for traversable WH. As we know that there must occur some matter configuration with exotic characteristics because the ordinary matter is not feasible for the traversable WH. The matter with exotic features does not fulfill the weak and null energy bounds and is termed exotic matter. To reduce the amount of such matter components, Visser defined the cut and paste strategy to create thin-shell WHs by combining two similar forms of BH metrics at the hypersurface. We employ this strategy in this manuscript to create thin-shell WHs in the framework of two similar forms of BH along with the nonlinear impact of electrodynamics. In this respect, we cut this metric as follows

$$\begin{aligned} {\mathcal {M}}^{\pm }=\left\{ r^{\pm }\le \lambda ,\lambda >r_{h}\right\} , \end{aligned}$$
(3)

with \(\lambda \) acts as a radius of WH throat and \(r_h\) exhibits the event horizon radius. Such manifolds are joined at (2+1)-dimensional manifold known as hypersurface provided by

$$\begin{aligned} \Sigma =\left\{ r^{\pm }=\lambda ,\lambda >r_{h}\right\} . \end{aligned}$$
(4)

This technique provides a unique regular manifold and mathematically, it is displayed as \({\mathcal {M}}={\mathcal {M}}^{+}\cup {\mathcal {M}}^{-}\). Notice that by considering \(\lambda >r_h\), the singularity and event horizon formation in the constructed geometry can be prevented. In accordance with the Darmois and Israel junction conditions, the components of hypersurface and manifolds yield the forms \(\xi ^{i}=(\tau ,\theta ,\phi )\) and \(x^{\gamma }=(t,r,\theta ,\phi )\), respectively with \(\tau \) as the proper time on the hypersurface. These systems are linked together with the coordinate transformation given by

$$\begin{aligned} g_{ij}=\frac{\partial x^{\gamma }}{\partial \xi ^{i}}\frac{\partial x^{\beta }}{\partial \xi ^{j}}g_{\gamma \beta }. \end{aligned}$$
(5)

For the hypersurface, the associated parametric equation is written by \(\Sigma :R(r,\tau )=r-\lambda (\tau )=0.\) The geometry of a thin shell is investigated by taking into account the dependency of shell radius (\(\lambda \)) on the proper time. Hence, the shell radius is depicted as a function of proper time given by \(\lambda =\lambda (\tau )\). The respective induced metric becomes

$$\begin{aligned} ds_{\Sigma }^{2}=\lambda ^2(\tau )\sin ^2\theta d\phi ^2+\lambda ^2(\tau )d\theta ^2-d\tau ^2. \end{aligned}$$
(6)

The matter components of the thin shell possess a significant role in the dynamics as well as the stability of the WH throat. The Lanczos equations are derived to describe the field equations at the boundary surface, such as the surface of a massive object or a BH event horizon. In this regime, the gravitational field is expected to behave classically, as the quantum effects become significant only at very small scales, such as the Planck scale. Therefore, macroscopic objects described by the Lanczos equations do not experience significant quantum-generated corrections. For very small scales, quantum gravity effects become important, and one expects deviations from the classical equations of GR. These effects are negligible for macroscopic objects or on scales that are relevant to the applications of the Lanczos equations. It is only in extreme conditions, such as near the singularity of a BH or during the very early stages of the universe, that quantum gravitational effects become dominant. At the hypersurface, the physical factors of matter are derived via reduced expressions of GR equations. Such equations are recognized as Lanczos equations presented by

$$\begin{aligned} {S^{i}}_{j}=-\frac{1}{8\pi }\left( \left[ {K^{i}}_{j}\right] -{\delta ^{i}}_{j}\,K\right) . \end{aligned}$$
(7)

where \({K^{i}}_{j}\) indicates the constituents of extrinsic curvature, while K acts as the trace part of extrinsic curvature (\([{K^{i}}_{i}]=K\)) and \(diag(\sigma ,{\mathcal {V}},{\mathcal {V}})={S^{i}}_{j}\) manifests the stress-energy tensor. The surface pressure and material energy density situated at \(\Sigma \) is specified by \({\mathcal {V}}\) and \(\sigma \), respectively. This matter configuration generates discontinuity in the external as well as internal constituents of extrinsic curvature mathematically expressed by \([{K^{i}}_{j}]={K^{+i}}_{j}-{K^{-i}}_{j}\ne 0\). The extrinsic curvature of internal and external regions is provided by

$$\begin{aligned} K_{ij}^{(\pm )}=-n_{\mu }^{(\pm )}\left( \frac{\partial ^{2}x^{\mu }}{\partial \xi ^{i}\partial \xi ^{j}}+\Gamma _{\gamma \beta }^{\mu }\frac{\partial x^{\gamma }}{\partial \xi ^{i}}\frac{\partial x^{\beta }}{\partial \xi ^{j}}\right) _{\Sigma }. \end{aligned}$$
(8)

The radial as well as the temporal constituents of the unit normals on \({\mathcal {M}}^{\pm }\) lead to

$$\begin{aligned}\nonumber n^{\pm }_{t}=-{\dot{\lambda }},\quad n^{\pm }_{r}=\frac{\lambda ^2 \sqrt{\frac{\lambda \left( \sqrt{\lambda ^2-a^2}-2 M-\chi \lambda ^{-3 \omega _q}\right) +Q^2}{\lambda ^2}+{\dot{\lambda }}^2}}{\lambda \left( \sqrt{\lambda ^2-a^2}-2 M-\chi \lambda ^{-3 \omega _q}\right) +Q^2}, \end{aligned}$$

respectively. Here, overdot describes the derivative corresponding to proper time. The constituents of respective extrinsic curvature are

$$\begin{aligned}{} & {} K_{\tau \tau }^{\pm }=\pm \frac{-\frac{3 a^2 \lambda ^3}{\left( \lambda ^2-a^2\right) ^{3/2}}+\frac{2 a^4 \lambda }{\left( \lambda ^2-a^2\right) ^{3/2}}-4 \lambda M-\chi \left( 9 \omega _q \left( \omega _q+1\right) +2\right) \lambda ^{1-3 \omega _q}+6 Q^2}{2 \lambda ^4 \sqrt{\frac{\lambda \left( \sqrt{\lambda ^2-a^2}-2 M-\chi \lambda ^{-3 \omega _q}\right) +Q^2}{\lambda ^2}+{\dot{\lambda }}^2}}, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} K_{\theta \theta }^\pm =\pm \lambda \sqrt{\frac{\lambda \left( \sqrt{\lambda ^2-a^2}-2 M-\chi \lambda ^{-3 \omega _q}\right) +Q^2}{\lambda ^2}+{\dot{\lambda }}^2}, \end{aligned}$$
(10)

and \(K^{\pm }_{\phi \phi }=\sin ^2\theta K_{\theta \theta }^\pm \). Insertion of Eqs. (9) and (10) into Lanczos equations (7) yields

$$\begin{aligned}{} & {} 2 \pi \lambda \sigma =-\sqrt{\frac{\sqrt{\lambda ^2-a^2}}{\lambda }+{\dot{\lambda }}^2-\frac{2 M}{\lambda }-\frac{\chi }{\lambda ^{3 \omega _q+1}}+\frac{Q^2}{\lambda ^2}}, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} 8\pi \lambda {\mathcal {V}}{=}\frac{\frac{1}{\lambda }\left( \frac{2 \lambda ^2{-}a^2}{\sqrt{\lambda ^2{-}a^2}}{+}2 \ddot{\lambda } \lambda ^2{-}2 M{-}\chi \lambda ^{-3 \omega _q}\right) {+}2 {\dot{\lambda }}^2{+}3 \chi \omega _q \lambda ^{-3 \omega _q{-}1}}{\sqrt{\frac{\lambda \left( \sqrt{\lambda ^2{-}a^2}{-}2 M{-}\chi \lambda ^{-3 \omega _q}\right) {+}Q^2}{\lambda ^2}{+}{\dot{\lambda }}^2}}.\nonumber \\ \end{aligned}$$
(12)

Here, we suppose that the shell of the constructed model does not pass through the radial direction at the equilibrium radius of the shell \(\lambda _0\). So, it is worthwhile to write here that the proper time derivative of the radius of the shell disappears, i.e., \(\dot{\lambda _0}=0=\ddot{\lambda _0}\). Thus, one can obtain

$$\begin{aligned}{} & {} 2\pi \lambda _0\sigma _{0}=-\sqrt{\frac{\sqrt{\lambda ^2-a^2}}{\lambda }-\frac{2 M}{\lambda }-\frac{\chi }{\lambda ^{3 \omega _q+1}}+\frac{Q^2}{\lambda ^2}}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} 8 \pi \lambda _0^2 {\mathcal {V}}_{0}=\frac{\lambda ^{-3 \omega _q-1} \left( -\chi \sqrt{\lambda ^2-a^2}-2 M \sqrt{\lambda ^2-a^2} \lambda ^{3 \omega _q}+3 \chi \sqrt{\lambda ^2-a^2} \omega _q+\left( 2 \lambda ^2-a^2\right) \lambda ^{3 \omega _q}\right) }{\sqrt{\lambda ^2-a^2} \sqrt{\frac{\lambda \left( \sqrt{\lambda ^2-a^2}-2 M-\chi \lambda ^{-3 \omega _q}\right) +Q^2}{\lambda ^2}}}, \end{aligned}$$
(14)

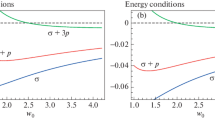
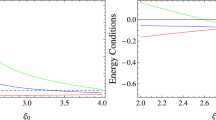
in which \(\sigma _0\) and \({\mathcal {V}}_0\) interpret the matter energy density and pressure at equilibrium points, respectively. There exist three famous energy constraints, i.e., null (\({\mathcal {V}}+\sigma \ge 0\)), weak (\({\mathcal {V}}+\sigma \ge 0\), \(\sigma \ge 0\)) and strong (\(3{\mathcal {V}}+\sigma \ge 0\)) energy constraints. Observed that \(\sigma _{0}<0\) provides the defiance of dominant and weak energy bounds. This nullification displays that the constructed geometry is occupied by exotic matter. Such matter contents at the throat create abhorrence for collapse and provide help to hold it open. Thus, our constructed geometry is physically viable for the WH structure.

The equation of motion by adopting the shell energy density (11) leads to

$$\begin{aligned} {\dot{\lambda }}^{2}=-\Upsilon (\lambda ), \end{aligned}$$
(15)

and the shell effective potential is characterized by

$$\begin{aligned} \Upsilon (\lambda ){=}\frac{\sqrt{\lambda ^2-a^2}}{\lambda }{-}4 \pi ^2 \lambda ^2 \sigma ^2{-}\frac{2 M}{\lambda }-\chi \lambda ^{-3 \omega _q-1}{+}\frac{Q^2}{\lambda ^2}.\nonumber \\ \end{aligned}$$
(16)

With the help of 4-acceleration of the observer, the attractive and repulsive features of WH throat are evaluated as

$$\begin{aligned}\nonumber a^\beta =v^\beta _{;\lambda }v^\lambda , \end{aligned}$$

where the 4-velocity of the observer is exhibited by \(v^\lambda =\left( \frac{1}{\sqrt{{\mathcal {Y}}(r)}}, 0,0,0\right) \). Then, we get

$$\begin{aligned}\nonumber \frac{d^2r}{d\tau ^2}=-\Gamma ^{r}_{tt}\left( \frac{dt}{d\tau }\right) ^2=-a^r, \end{aligned}$$

providing

$$\begin{aligned}\nonumber a^r{=}\frac{1}{2 \lambda ^3}\left( \frac{a^2 \lambda }{\sqrt{\lambda ^2-a^2}}{+}2 \lambda M{+}\chi \left( 3 \omega _q{+}1\right) \lambda ^{1{-}3 \omega _q}{-}2 Q^2\right) . \end{aligned}$$

The gravitational field surrounding by WHs can exhibit two types of behavior: attractive or repulsive. For an attractive WH, it means that the gravitational field near the WH pulls objects towards it. In this case, if an observer wants to avoid being pulled into the WH, they must exert an outward directed force. This means they need to move away from the WH with a force that counteracts the attractive gravitational pull. If they do not exert this outward force, they will be gradually drawn towards the WH. On the other hand, a repulsive WH has a gravitational field that pushes objects away from it. In this case, in order to avoid being pushed by the WH, an observer must have an inward directed force. By exerting this force towards the WH, they can counteract the repulsive gravitational force and maintain a distance from the WH. If they do not exert this inward force, they will be pushed further away from the WH. In summary, the attractive or repulsive nature of a WH’s gravitational field determines the type of force that an observer needs to exert to avoid being influenced by the WH. Consequently, an attractive WH requires an outward force, while a repulsive WH requires an inward force. The radial part of the 4-acceleration describes the attractive (\(a^r>0\)) and repulsive (\(a^r<0\)) behavior of the throat.

3 Stability analysis

In order to analyze the stable structure, we take the equilibrium shell radius \(\lambda _0\) and expanding the effective potential \(\Upsilon (\lambda )\) around \(\lambda _0\) with the help of Taylor series up to second-order factors given by

$$\begin{aligned} \Upsilon (\lambda )= & {} \Upsilon (\lambda _{0})+\Upsilon '(\lambda _{0})(\lambda -\lambda _{0})+\frac{1}{2} \Upsilon ''(\lambda _{0})(\lambda -\lambda _{0})^2\nonumber \\{} & {} +O[(\lambda -\lambda _{0})^3]. \end{aligned}$$
(17)

It is noteworthy that the throat demands that the potential component and its 1st differential form must disappear at the equilibrium point for both the stable and unstable structure of the WH, i.e., \(\Upsilon (\lambda _0)=0=\Upsilon '(\lambda _0)\). Thus, it can be derived as:

  • The stable configuration is obtained if the 2nd differential form of the potential at \(\lambda =\lambda _0\) is positive and if \(\Upsilon ''(\lambda _0)<0\), then it shows unstable structure.

  • If \(\Upsilon ''(\lambda _0)=0\), then it is neither stable nor unstable.

Equation (17) at equilibrium point leads to

$$\begin{aligned} \Upsilon (\lambda )=\frac{1}{2}\Upsilon ''(\lambda _{0})(\lambda -\lambda _{0})^2. \end{aligned}$$
(18)

Notice that \({\mathcal {V}}\) and \(\sigma \) obey the conservation law expressed by

$$\begin{aligned} {\mathcal {V}} \frac{d}{d\tau }(4\pi \lambda ^2)+\frac{d}{d\tau }(4\pi \lambda ^2\sigma )=0. \end{aligned}$$
(19)

The selection of matter configuration that can be characterized by EoS determines the exact solution associated with the conservation equation. Now, we adopt two kinds of EoS \({\mathcal {V}}={\mathcal {V}}(\sigma )\) and \({\mathcal {V}}={\mathcal {V}}(\sigma ,\lambda )\) [53]. The second case depicts the generalized form where shell surface pressure is based on both throat radius and surface energy density. For both choices, one can get \({\mathcal {V}}'=\frac{d{\mathcal {V}}(\sigma )}{d\sigma }\sigma '\) and \({\mathcal {V}}'=\frac{d{\mathcal {V}}}{d\sigma }\sigma '+\frac{d{\mathcal {V}}}{d\lambda }\), respectively. Thus, the conservation equation leads to

$$\begin{aligned} \sigma '=-\frac{2}{\lambda }\{\sigma +{\mathcal {V}}(\sigma ,\lambda )\}. \end{aligned}$$
(20)

Corresponding to different selections of variable EoS, every result of Eq. (20) yields a particular expression of \(\Upsilon (\lambda )\). At \(\lambda =\lambda _{0}\), the \(2^{nd}\) differential form of effective potential becomes

$$\begin{aligned}\nonumber{} & {} \Upsilon ''(\lambda _0)=-\frac{1}{\lambda ^4}\Bigg (\frac{3 a^2 \lambda ^3}{\left( \lambda ^2-a^2\right) ^{3/2}}-\frac{2 a^4 \lambda }{\left( \lambda ^2-a^2\right) ^{3/2}}\\{} & {} \quad +2 \left( 4 \pi ^2 \lambda ^4 \left( \lambda ^2 \sigma '(\lambda )^2+\lambda \sigma (\lambda ) \left( \lambda \sigma ''(\lambda )+4 \sigma '(\lambda )\right) +\sigma (\lambda )^2\right) \right. \\ {}{} & {} \quad \left. +2 \lambda M-3 Q^2\right) +\chi \left( 9 \omega _q \left( \omega _q+1\right) +2\right) \lambda ^{1-3 \omega _q}\Bigg ). \end{aligned}$$

Above equation and Eq. (20) express that the type of matter constituents situated at thin-shell contribute a remarkable role to examine the stable state of the obtained structure. It is obtained that \(\Upsilon ''(\lambda _{0})\) is greatly based upon the EoS parameters \(\gamma _{0}\) and \(\beta _{0}^2\). In the next sections, we examine the influences of barotropic as well as variable EoS on the stable state of the constructed structure.

Fig. 1
figure 1

Region plots of uncharged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for barotropic EoS with different values of a as 0 (first plot), 0.2 (second plot), 0.3 (third plot) using \(M=0.5,Q=0,\omega _q=-2/3\). Here, the colored region represents the stable region (\(\Upsilon ''(\lambda _{0})>0\)) and remaining region shows unstable configuration (\(\Upsilon ''(\lambda _{0})\le 0\)). The region bounded by the red lines shows the behavior of the metric function \({\mathcal {F}}(r)>0\) and other white as well as filled region shows \({\mathcal {F}}(r)<0\). It is noted that the inner red line shows the position of the event horizon. Hence, the stable configuration found after the position of the event horizon

Full size image

3.1 Barotropic EoS

This is the first case in which we adopt barotropic EoS to inspect the stable structure of thin-shell WHs. It is related to the energy density and surface pressure associated with the matter components by

$$\begin{aligned} {\mathcal {V}}=\gamma \sigma , \end{aligned}$$
(21)

here \(\gamma \) symbolizes the parameter for barotropic EoS. Utilizing the Eqs. (21) in (20), we get

$$\begin{aligned} \sigma '(\lambda )=-\frac{2}{\lambda }(1+\gamma )\rho (\lambda ), \end{aligned}$$
(22)

which yields

$$\begin{aligned} \sigma (\lambda )=\sigma (\lambda _{0}) \left( \frac{\lambda _{0}}{\lambda }\right) ^{2(1+\gamma )}. \end{aligned}$$
(23)

The form of effective potential yields

$$\begin{aligned} \Upsilon (\lambda )= & {} \frac{\sqrt{\lambda ^2-a^2}}{\lambda }-4 \pi ^2 \lambda ^2 \sigma _0^2 \left( \frac{\lambda _0 }{\lambda }\right) ^{4 (\gamma +1)}-\frac{2 M}{\lambda }\nonumber \\{} & {} -\chi \lambda ^{-3 \omega _q-1}+\frac{Q^2}{\lambda ^2}, \end{aligned}$$
(24)

The first derivative associated with throat radius \(``\lambda ''\) at \(\lambda _{0}\) takes the form

$$\begin{aligned}\nonumber{} & {} \Upsilon '(\lambda _{0})=\frac{\frac{a^2 \lambda _0 }{\sqrt{\lambda _0 ^2-a^2}}+2 (2 \gamma +1) \left( \lambda _0 \left( \sqrt{\lambda _0 ^2-a^2}-2 M-\chi \lambda _0 ^{-3 \omega _q}\right) +Q^2\right) +2 \lambda _0 M+\chi \left( 3 \omega _q+1\right) \lambda _0 ^{1-3 \omega _q}-2 Q^2}{\lambda _0 ^3}. \end{aligned}$$

It is noted that \(\Upsilon '(\lambda _{0})\) vanishes if and only if

$$\begin{aligned} \gamma =\frac{\lambda _0 \left( \frac{\left( 2 M \sqrt{\lambda _0 ^2-a^2}+a^2-2 \lambda _0 ^2\right) \lambda _0 ^{3 \omega _q}}{\sqrt{\lambda _0 ^2-a^2}}-3 \chi \omega _q+\chi \right) }{4 \left( \lambda _0 \left( \left( \sqrt{\lambda _0 ^2-a^2}-2 M\right) \lambda _0 ^{3 \omega _q}-\chi \right) +Q^2 \lambda _0 ^{3 \omega _q}\right) }.\nonumber \\ \end{aligned}$$
(25)

Also, it is found that

$$\begin{aligned}\nonumber \Upsilon ''(\lambda _{0})= & {} -\frac{3 a^2}{\lambda _0 \left( \lambda _0 ^2-a^2\right) ^{3/2}}+\frac{2 a^4}{\lambda _0 ^3 \left( \lambda _0 ^2-a^2\right) ^{3/2}}\\{} & {} -64 \pi ^2 \gamma ^2 \sigma _0^2-80 \pi ^2 \gamma \sigma _0^2-\frac{4 M}{\lambda _0 ^3}\\{} & {} -9 \chi \omega _q^2 \lambda _0 ^{-3 \omega _q-3}-2 \chi \lambda _0 ^{-3 \omega _q-3}\\ \nonumber{} & {} -9 \chi \omega _q \lambda _0 ^{-3 \omega _q-3}+\frac{6 Q^2}{\lambda _0 ^4}-24 \pi ^2 \sigma _0^2. \end{aligned}$$

This equation is very useful to discuss the dynamical configuration of thin-shell WH in the background of barotropic EoS. In this regard, we consider the region plot as shown in Figs. 1 and 2 along \(\lambda _0\) and \(\chi \) with suitable values of physical parameters. To discuss the stability of the developed structure with charged quantum corrected BHs surrounded by a quintessence field, we consider regions. It is worth writing that the region bounded by red cures represents the positive behavior of the lapse function while in the remaining region, the lapse function shows negative behavior. The red line between the bounded region and the filled as well as the white region shows the position of the event horizon for different values of physical parameters. It is found that stable and unstable configurations of the shell must be evaluated after the position of the event horizon. The stable regions for different values of physical parameters via the effective potential are displaced through the filled region (\(\Upsilon ''(\lambda _{0})>0\)) while white region (\(\Upsilon ''(\lambda _{0})<0\)) shows unstable configuration as shown in Figs. 1 and 2. It is found that the Schwarzschild BH surrounded by the quintessence parameter shows more stability in the absence of a quantum correction parameter. Also, the charge of the BH geometry enhances the stable regions of the developed thin-shell WHs as shown in Fig. 2. By using a particular range that is obtained in the quantum Schwarzschild BH and quantum charged BH, we get \(\Upsilon ''(\lambda _{0})>0\) as shown in Fig. 3. Hence, the presence of charge over the geometry of BHs enhances the stable form of thin-shell WHs.

Fig. 2
figure 2

Region plots of quantum corrected charged thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for barotropic EoS with different values of a as 0 (first plot), 0.4 (second plot), 0.6 (third plot) using \(M=0.5,Q=0.5,\omega _q=-2/3\)

Full size image
Fig. 3
figure 3

Plots of uncharged and charged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) by considering the range of stable regions as given for the parameters \(M=0.5,Q=0,\omega _q=-2/3,a=0.3\) (left plot) and \(M=0.5,Q=0.5,\omega _q=-2/3,a=0.6\) (right plot)

Full size image

3.2 Phantomlike variable EoS

Fig. 4
figure 4

Region plots of uncharged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for phantomlike variable EoS with different values of n as 0 (first plot), 0.35 (second plot), 0.65 (third plot) using \(M=0.5,\, Q=0,\omega _q=-2/3\)

Full size image
Fig. 5
figure 5

Region plots of charged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for phantomlike variable EoS with different values of n as 0 (first plot), 0.35 (second plot), 0.65 (third plot) using \(M=0.5,Q=0.5,\omega _q=-2/3\)

Full size image
Fig. 6
figure 6

Plots of \(\Upsilon ''(\lambda _{0})\) for phantomlike variable EoS by considering the range of stable region as given for the parameters \(q=1,\Lambda =-1,{\mathcal {M}}=0.5\) (left plot) and \(q=0.5,\Lambda =-1,{\mathcal {M}}=0.5\) (right plot)

Full size image

Here, we take phantom-like variable EoS to inspect the stable geometry of thin-shell WHs [53]. It’s mathematical expression is given by

$$\begin{aligned} {\mathcal {V}}=\frac{{\mathcal {N}}}{\lambda ^n}\sigma , \end{aligned}$$
(26)

where \({\mathcal {N}}\) depicts the EoS parameter while n acts as a real constant. This equation manifests the modified expression of phantom-like EoS. It is converted into phantom-like on putting \(n \rightarrow 0\). The conservation equation by implementing this EoS leads to

$$\begin{aligned} \sigma (\lambda )=\sigma _{0}e^{\frac{ {\mathcal {N}}}{n} \left( \frac{1}{\lambda ^n}-\frac{1}{\lambda _0^n}\right) }\left( \frac{\lambda _{0}}{\lambda }\right) ^2. \end{aligned}$$
(27)

The associated effective potential function becomes

$$\begin{aligned} \Upsilon (\lambda )= & {} \frac{\sqrt{\lambda ^2-a^2}}{\lambda }-4 \pi ^2 \lambda ^2 \sigma _0^2 \left( \frac{\lambda _0 }{\lambda }\right) ^4 e^{\frac{(2 {\mathcal {N}}) \left( \frac{1}{\lambda ^n}-\frac{1}{\lambda _0 ^n}\right) }{n}}\nonumber \\{} & {} -\frac{2 M}{\lambda }-\chi \lambda ^{-3 \omega _q-1}+\frac{Q^2}{\lambda ^2}. \end{aligned}$$
(28)

Notice that the effective potential disappears at \(\lambda =\lambda _0\) and the first derivative of this is calculated as

$$\begin{aligned} \Upsilon '(\lambda _0)= & {} \frac{1}{\lambda _0 ^3}\Bigg (\frac{a^2 \lambda _0 }{\sqrt{\lambda _0 ^2-a^2}}+8 \pi ^2 \sigma _0^2 \lambda _0 ^{4-n} \left( {\mathcal {N}}+\lambda _0 ^n\right) \nonumber \\{} & {} +2 \lambda _0 M+\chi \left( 3 \omega _q+1\right) \lambda _0 ^{1-3 \omega _q}-2 Q^2\Bigg ), \end{aligned}$$
(29)

By taking \(\Upsilon '(\lambda _{0})=0\), we obtain

$$\begin{aligned} {\mathcal {N}}= & {} -\frac{\lambda _0 ^{n-4}}{8 \pi ^2 \sigma _0^2} \Bigg (\frac{a^2 \lambda _0 }{\sqrt{\lambda _0 ^2-a^2}}+8 \pi ^2 \lambda _0 ^4 \sigma _0^2+2 \lambda _0 M\nonumber \\{} & {} +\chi \left( 3 \omega _q+1\right) \lambda _0 ^{1-3 \omega _q}-2 Q^2\Bigg ). \end{aligned}$$
(30)

Hence, we have

$$\begin{aligned}\nonumber{} & {} \Upsilon ''(\lambda _0)=-\frac{1}{\lambda _0 ^4}\Bigg (\frac{3 a^2 \lambda _0 ^3}{\left( \lambda _0 ^2-a^2\right) ^{3/2}}-\frac{2 a^4 \lambda _0 }{\left( \lambda _0 ^2-a^2\right) ^{3/2}}\nonumber \\{} & {} \quad +8 \pi ^2 \sigma _0^2 \lambda _0 ^{4-2 n} \left( 2 {\mathcal {N}}^2+{\mathcal {N}} (n+5) \lambda _0 ^n+3 \lambda _0 ^{2 n}\right) +4 \lambda _0 M\nonumber \\ {}{} & {} \quad +\chi \left( 9 \omega _q \left( \omega _q+1\right) +2\right) \lambda _0 ^{1-3 \omega _q}-6 Q^2\Bigg ). \end{aligned}$$
Fig. 7
figure 7

Region plots of uncharged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for Chaplygin variable EoS with different values of n as 0 (first plot), 0.35 (second plot), 0.65 (third plot) using \(M=0.5,Q=0,\omega _q=-2/3\)

Full size image
Fig. 8
figure 8

Region plots of charged quantum corrected thin-shell WHs effective potential \(\Upsilon ''(\lambda _{0})\) verses \(\lambda _0\) and \(\chi \) for Chaplygin variable EoS with different values of n as 0 (first plot), 0.35 (second plot), 0.65 (third plot) using \(M=0.5,Q=0.5,\omega _q=-2/3\)

Full size image

Figures 4 and 5 are considered to explore the stable ranges of the shell composed with phantomlike variable EoS and observe the effects of quantum correction parameters on the stable ranges of the physical parameters. It is found that the phantomlike EoS \(n{=}0\) shows more stable behavior as compared to variable phantomlike EoS (\(n{\ne }0\)). It is found that for higher values of n the stable ranges of the physical parameters of shell decreases. By considering the specific ranges as obtained for charged and uncharged geometry, we obtain the stable configuration of the shell \(\Upsilon ''(\lambda _{0})\). Hence, the stable structure is greatly based upon the physical parameters as well as the matter thin layer located at the WH throat (Fig. 6).

3.3 Chaplygin variable EoS

Fig. 9
figure 9

Plots of \(\Upsilon ''(\lambda _{0})\) for Chaplygin variable EoS by considering the range of stable regions as given for the parameters \(q=1,\Lambda =-1,{\mathcal {M}}=0.5\) (left plot) and \(q=0.5,\Lambda =-1,{\mathcal {M}}=0.5\) (right plot)

Full size image

Now, Chaplygin variable EoS is taken into account which is expressed by [53]

$$\begin{aligned} {\mathcal {V}}=\frac{1}{\lambda ^n}\frac{{\mathcal {K}}}{\sigma }, \end{aligned}$$
(31)

where \({\mathcal {K}}\) indicates the parameter of EoS. This transforms into Chaplygin EoS on substituting \(n\rightarrow 0\). In terms of surface energy density, the solution of the conservation equation is

$$\begin{aligned} \sigma ^2(\lambda )=\frac{4{\mathcal {K}}\left( \lambda ^4\lambda _0^n-\lambda ^n\lambda _0^4\right) + \sigma _{0}^2\lambda _0^{n+4}\lambda ^n(n-4)}{(n-4)\lambda ^{n+4}\lambda _0^{n}}. \end{aligned}$$
(32)

The associated potential function with respect to this matter configuration is obtained and found that \(\Upsilon (\lambda _0)=0\). Further, \(\Upsilon '(\lambda )\) is calculated and adopting \(\Upsilon '(\lambda _0)=0\), we get

$$\begin{aligned} {\mathcal {K}}= & {} -\frac{\lambda _0 ^{n-4}}{16 \pi ^2} \Bigg (\frac{a^2 \lambda _0 }{\sqrt{\lambda _0 ^2-a^2}}+8 \pi ^2 \lambda _0 ^4 \sigma _0^2+2 \lambda _0 M\nonumber \\{} & {} +\chi \left( 3 \omega _q+1\right) \lambda _0 ^{1-3 \omega _q}-2 Q^2\Bigg ). \end{aligned}$$
(33)

The second differential form of potential function associated with the radius of the shell at \(\lambda =\lambda _0\) is expressed as

(34)

To observe the effect of Chaplygin variable EoS on the stable structure of thin-shell WH, we use region plots for different values of n as shown in Figs. 7 and 8. It is noted that the system becomes more stable as \(n\Rightarrow 0\) and stability regions decrease rapidly for higher values of n. The quantum correction parameter decreases the uncharged and charged stable ranges of the physical parameters. Hence, the Chaplygin variable EoS plays a remarkable role to maintain the stability of the shell. We obtain the maximum stable ranges for such type of matter contents of the shell. As the variable \(n\Rightarrow 0\), the stable ranges of the physical parameters of the shell enhance (Fig. 9).

4 Concluding remarks

This article is dedicated to discussing the influences of quantum correction, quintessence, and charge on the dynamical configuration of thin-shell WHs developed from two similar forms of charged quantum corrected BHs with quintessence field. We have considered the cut and paste strategy to overcome the formation of event horizon and singularity in the geometry of thin-shell WH. Then, we used the Einstein field equations for the hypersurface to calculate the energy density and surface pressure of matter thin layer situated at the shell. These matter constituents are very interesting and possess a very important role to preserve the stability of the WH throat. In order to discuss the effects of matter contents on the stability of WH structure, we have considered three distinct EoS, i.e., barotropic, phantom-like, and Chaplygin variable EoS. For the choice of variable EoS, the shell stability can be determined more effectively as compared to other choices of EoS.

First, we have considered the barotropic EoS to inspect the stability of the shell via region plots for a charge as well as uncharged quantum corrected BHs with quintessence. It is found that the Schwarzschild BH surrounded by the quintessence parameter shows more stability in the absence of a quantum correction parameter. Also, the charge of the BH geometry enhances the stable regions of the developed thin-shell WHs as shown in Fig. 2. Moreover, corresponding to the specific range that is attained in the quantum Schwarzschild BH and quantum charged BH, we have obtained \(\Upsilon ''(\lambda _{0})>0\) (Fig. 3).

Secondly, we have considered the phantom-like variable EoS to examine the stable regions of thin-shell WH with and without charge as shown in Figs. 4 and 5. It is worth stating that phantom-like EoS enhances the stability of WH structure while variable EoS decreases the stable ranges (Fig. 4). Hence, the stable geometry is widely based upon the physical parameters as well as the matter thin layer present at the WH throat. Finally, Chaplygin variable EoS is considered to explore the stable structure of thin-shell WH. We have used region plots for several choices of n as displayed in Figs. 7 and 8. It is noted that the system becomes more stable as \(n \rightarrow 0\) and stability regions decrease rapidly for higher values of n.

It is concluded that thin-shell WH becomes more stable for the choice of Chaplygin EoS with minimum values of quantum correction parameter.