1 Introduction

Neutrino is a massless and weakly interacting fermion in the standard model description [1]. In the three-generation neutrino framework, neutrinos have previously been detected in three types, called flavors, known as electron e, muon \(\mu \) and tau \(\tau \) neutrinos [2]. The flavor states of neutrinos are a linear combination of the mass eigenstates [3, 4]. Neutrino oscillation (NO) suggests that neutrino can take the periodical variation with a given flavor transforms into anther flavor as it propagates a large distance, on account of the neutrino masses and neutrino mixing. The probability of detecting a particular flavor can be measured anytime during neutrino propagation that can be used to study the classical and quantum properties among neutrino systems. The last few years have seen that many theoretical and experimental study of the oscillation parameters [5,6,7,8]. The quantumness of neutrino oscillations (NOs) has been tested using the Leggett–Garg inequality (LGI) regarded as the temporal analogue of Bell’s inequality [9,10,11,12,13,14], which implies that the experimentally observed NOs possess a violation of classical bounds imposed by the LGI [15]. Recently, Blasone et al. studied the existence of the quantum nonclassical features in NOs by means of testing the necessary and sufficient conditions for macrorealism [16].

Investing quantumness in NO is a very interesting issue, as in this situation, NOs are inherently associated with quantum correlations, such as quantum coherence and entanglement. Since such linkage established between particle physics and quantum information is of importance to study primary properties of these fundamental particles and explore the possibility of utilizing neutrinos as a resource in quantum information processing. Therefore, using the tools of quantum resource theory (QRT) to determine the quantumness in NOs has been attached much attention of the researchers [17,18,19,20,21,22,23,24,25,26,27]. As the essential tools in QRT, quantum correlations, such as entanglement and quantum discord (QD), are of great research significance and play a crucial role in quantum information processing, including quantum teleportation [28, 29], quantum computation [30, 31], quantum key distribution [32, 33], and so on.

One of the most important properties occurring in studying multipartite quantum correlation is monogamy relation which characterizes the constraints for sharing correlation resources among different constituents in a multipartite system. For example, in a tripartite system, the more correlation between two parties A and B, the less lay in two parties A and C, which exhibit a complementary behavior. The monogamy property provides significant information about the structure of quantum correlations. Monogamy property has many applications in quantum physics [34, 35]. Particularly, monogamy relation is also a crucial character guaranteeing security in quantum key distribution [36]. One of the important issue in this field is to determine whether a given correlation measure is monogamous. A bipartite quantum correlation measure Q applied to a quantum state \(\rho _{ABC}\) has typically considered as monogamous if it satisfies the following relation

$$\begin{aligned} Q_{A \mid BC }\ge Q_{AB}+Q_{AC}, \end{aligned}$$
(1)

where \(Q_{AB}\), \(Q_{AC}\) denote the correlations of the corresponding reduced bipartite systems \(\rho _{AB}\) and \(\rho _{AC}\), respectively, and \(Q_{A \mid BC }\) stands for the correlation of the state \(\rho _{ABC}\) considered in the A : BC bipartite split. This relation was first proposed by Coffman et al. [37] using the squared concurrence \(C^2\) as the correlation measure for three-qubit states, generally referred to as the CKW inequality. Since than, the research on the original CKW inequality was extend to other quantum correlation measures. Prabhu et al. proved that the QD violate the monogamy relation even for the three-qubit W state [38], while the square of quantum discord (SQD) and the geometric measure of quantum discord (GQD) is monogamous in this case [39, 40]. Reference [41] shown that the squared entanglement of formation (SEF), which quantifies the bipartite entanglement, fulfill the monogamy relation in multipartite mixed states. Some similar monogamy relations were also investigated for negativity [42, 43], Tsallis q-entropy entanglement [44], steering [45, 46], and arbitrary quantum entanglement measures [47, 48].

In this paper, we employ the monogamy relation related to the SEF, the SQD and the GQD to investigate the distribution of these quantum correlations in the three-flavor NO systems. Based on these monogamy relations, we construct the residual correlations, which can detect the genuine correlation of three-qubit quantum systems. Through the positive or negative of the residual correlations to judge whether these correlations satisfy the monogamy relation. The results show that all these correlation measures distribute in a monogamous way in three-flavor neutrino NO systems, meaning that the correlation transformations are limited by the related monogamy relations in NOs.

The article is organized as follows. In Sect. 2, we give a brief introduction of three-flavor NOs model. In Sect. 3, we introduce the monogamy relations in terms of SEF, SQD and GQD. In Sect. 4, we investigate those monogamy relations in the three-flavor electron and muon antineutrino oscillations, respectively. Finally, we end with a summary in Sect. 5.

2 Three-flavor NOs

The three flavors of neutrinos, \(\left| {{\nu _e}} \right\rangle \), \(\left| {{\nu _\mu }} \right\rangle \), and \(\left| {{\nu _\tau }} \right\rangle \), as a liner superposition of mass eigenstates, \(\left| {{\nu _1}} \right\rangle \), \(\left| {{\nu _2}} \right\rangle \), and \(\left| {{\nu _3 }} \right\rangle \), can be expressed as

$$\begin{aligned} {\left| {{v_\alpha }} \right\rangle = \sum \limits _i {U_{\alpha k}^ * } \left| {{v_k}} \right\rangle ,} \end{aligned}$$
(2)

where \(\alpha = e, \mu , \tau , \) \(k = 1, 2, 3\), and \(U_{\alpha k}^ *\) is the complex conjugate of the \(\alpha k-th\) elements of a leptonic mixing matrix, namely, the Pontecorvo–Maki–Nakagara–Sakata (PMNS) matrix, which is characterized by three mixing angles (\(\theta _{12}\), \(\theta _{23}\), \(\theta _{13}\)) and a charge conjugation and parity (CP) violating phrase \(\delta _{cp}\). The corresponding matrix can be written as

$$\begin{aligned}&{U}= \nonumber \\&{\left( {\begin{array}{*{11}{c}} {{c_{12}}{c_{13}}}&{}{{s_{12}}{c_{13}}}&{}{{s_{13}}{e^{ - i{\delta _{cp}}}}}\\ {- {s_{12}}{c_{23}}-{c_{12}}{s_{13}}{s_{23}}{e^{ - i{\delta _{cp}}}}}&{}{{c_{12}}{c_{23}}-{s_{12}}{s_{13}}{s_{23}}{e^{ i{\delta _{cp}}}}}&{}{{c_{13}}{s_{23}}}\\ {{s_{12}}{s_{23}}-{c_{12}}{s_{13}}{c_{23}}{e^{ i{\delta _{cp}}}}}&{}{- {c_{12}}{c_{23}}-{s_{12}}{s_{13}}{s_{23}}{e^{ i{\delta _{cp}}}}}&{}{{c_{13}}{c_{23}}} \end{array}} \right) }, \end{aligned}$$
(3)

where \({c_{ij}}=\cos {\theta _{ij}}\) and \({s_{ij}} = \sin {\theta _{ij}}\) (\(i, j=1, 2, 3\)). As the CP violating fails to be observed experimentally, so we ignore it in the following discussion. The massive neutrino states \(\left| {{v_k}} \right\rangle \) are eigenstates of the Hamiltonian with energy eigenvalues \(E_k\). In the plane wave picture, the time evolution of the mass eigenstates \(\left| {{v_k}} \right\rangle \) during propagation is given by

$$\begin{aligned} {\left| {{v_k }(t)} \right\rangle =e^{-\frac{i}{\hbar } E_k t}\left| {{v_k} (0)} \right\rangle ,} \end{aligned}$$
(4)

where \(\left| {{v_k} (0)} \right\rangle \) indicates the mass eigenstates at \(t=0\). Using the Eqs. (2), (3) and (4), one obtains the evolved neutrino flavor states as

$$\begin{aligned} \left| {{v_\alpha }(t)} \right\rangle ={a_{\alpha e}}(t)\left| {v_e} \right\rangle + {a_{\alpha \mu }}(t)\left| {v_\mu } \right\rangle + {a_{\alpha \tau }}(t)\left| {v_\tau }\right\rangle , \end{aligned}$$
(5)

where \(a_{\alpha \beta }(t)=\sum _{k}U^*_{\alpha k}e^{-iE_kt/\hbar }U_{\beta k}\).

The probability of detecting another flavor neutrino \(\beta \) with energy E, evolved from the initial \(\alpha \) flavor neutrino, is

$$\begin{aligned} P_{\alpha \rightarrow \beta }&= \delta _{\alpha \beta }-4 \sum _{i>j} {\text {Re}}\left( {\hat{U}}_{\alpha i}^{*} {\hat{U}}_{\beta i} {\hat{U}}_{\alpha j} {\hat{U}}_{\beta j}^{*}\right) \sin ^{2}\left( \varDelta m_{i j}^{2} \frac{L c^{3}}{4 \hbar E}\right) \nonumber \\&\quad +2 \sum _{i>j} {\text {Im}}\left( {\hat{U}}_{\alpha i}^{*} {\hat{U}}_{\beta i} {\hat{U}}_{\alpha j} {\hat{U}}_{\beta j}^{*}\right) \sin \left( \varDelta m_{i j}^{2} \frac{L c^{3}}{2 \hbar E}\right) , \end{aligned}$$
(6)

where \( \varDelta m_{i j}^{2}=m_{i}^{2}-m_{j}^{2}\), E is the energy of the neutrino which take different values in different neutrino experiments, and \(L=ct\) (c is the speed of light ) is the distance propagated by the neutrino between the source and the detector. It was nothing that the survival probability \(P_{v_{\alpha } \rightarrow v_{\alpha }}=\left| a_{\alpha \alpha }(t)\right| ^{2}\) and the oscillation probability \(P_{v_{\alpha } \rightarrow v_{\beta }}=\left| a_{\alpha \beta }(t)\right| ^{2}\) satisfy the normalization constraint: \(P_{v_{\alpha } \rightarrow v_{\alpha }}+P_{v_{\alpha } \rightarrow v_{\beta }}=\left| a_{\alpha \alpha }(t)\right| ^{2}+\left| a_{\alpha \beta }(t)\right| ^{2}=1\).

To simplify further the calculation, the oscillatory quantity of Eq. (7),\(\sin ^{2}\left( \varDelta m_{i j}^{2} \frac{L c^{3}}{4 \hbar E}\right) \) can be written as

$$\begin{aligned} \sin ^2\left( \varDelta m^2_{ij}\frac{Lc^3}{4E\hbar }\right) =\sin ^2\left( 1.27\varDelta m^2_{ij}[eV^2]\frac{L[km]}{E[GeV]}\right) . \nonumber \\ \end{aligned}$$
(7)

The allowed ranges of the oscillation parameters are determined by experimental data within the framework of three- flavor neutrino oscillations. The best values of the three-flavor oscillation parameters with the normal ordering of neutrino mass spectrum (\(m_{1}<m_{2}<m_{3}\)) are given by

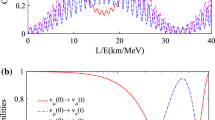
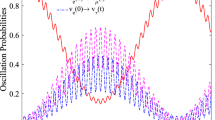
$$\begin{aligned} \varDelta m_{21}^2= & {} 7.50 \times {10^{ - 5}}e{V^2},\nonumber \\ \varDelta m_{31}^2= & {} 2.457 \times {10^{ - 3}}e{V^2},\nonumber \\ \varDelta m_{32}^2= & {} 2.382 \times {10^{ - 3}}e{V^2},\nonumber \\ {\theta _{12}}= & {} {33.48^ \circ }, {\theta _{23}} = {42.3^ \circ }, {\theta _{13}} = {8.50^ \circ }. \end{aligned}$$
(8)

Adopting the above values of parameters, the transition probabilities \(P_{v_{e} \rightarrow v_{\beta }}=\left| a_{e \beta }(t)\right| ^{2}\) and \(P_{v_{\mu } \rightarrow v_{\beta }}=\left| a_{\mu \beta }(t)\right| ^{2}\) corresponds to initial electron and muon neutrino are plotted in Fig. 1 as a function of the ratio L/E. Figure 1a shows that the survival probability of electron flavor state is always higher than 0.1, and the transition probabilities of other two flavors are smaller than 0.7 in a range [0, 40] of L/E with dimension \(\mathrm km/MeV\). From Fig. 1b, the survival probability of muon flavor decreases first then grows with the variation from 0 to 1, while the probability of detecting the electron flavor is always smaller than 0.04 in a range [10, 1000] of L/E with dimension \(\mathrm km/GeV\). According to Ref. [17], we can present the neutrino modes in occupation number basis in the following correspondence

$$\begin{aligned}&\left| {{\nu _e }} \right\rangle \equiv {\left| 1 \right\rangle _e} \otimes {\left| 0 \right\rangle _\mu } \otimes {\left| 0 \right\rangle _\tau } \equiv \left| {100} \right\rangle ,\nonumber \\&\left| \!{{\nu _\mu }} \right\rangle \!\equiv {\left| 0 \right\rangle _e} \otimes {\left| 1 \right\rangle _\mu } \otimes {\left| 0 \right\rangle _\tau } \equiv \left| {010} \right\rangle ,\nonumber \\&\left| {\nu {}_\tau } \right\rangle \!\equiv {\left| 0 \right\rangle _e} \otimes {\left| 0 \right\rangle _\mu } \otimes {\left| 1 \right\rangle _\tau } \equiv \left| {001} \right\rangle . \end{aligned}$$
(9)
Fig. 1
figure 1

Figure a gives the oscillation probability \(P_{{v_e}(0) \rightarrow {v_e}(t)}\) (red, solid line), \(P_{{v_e}(0) \rightarrow {v_\mu }(t)}\) (purple, dashed line), \(P_{{v_e}(0) \rightarrow {v_\tau }(t)}\) (blue, dashed-dotted line) when the initial neutrino flavor is electron flavor. The figure b gives the oscillation probability \(P_{{v_\mu }(0) \rightarrow {v_\mu }(t)}\) (red, solid line), \(P_{{v_\mu }(0) \rightarrow {v_e}(t)}\) (purple, dashed line), \(P_{{v_\mu }(0) \rightarrow {v_\tau }(t)}\) (blue, dashed-dotted line) when the initial neutrino flavor is muon flavor

Full size image

Consequently, the time evolution a flavor state \(\left| {v_\alpha } \right\rangle \) (\(\alpha \)=e, \(\mu \), \(\tau \)) can be written as

$$\begin{aligned} {\left| {\psi (t)} \right\rangle _\alpha } = {a_{\alpha e}}(t)\left| {100} \right\rangle + {a_{\alpha \mu }}(t)\left| {010} \right\rangle + {a_{\alpha \tau }}(t)\left| {001} \right\rangle . \end{aligned}$$
(10)

Therefore, we can discuss the monogamy properties in terms of the SEF, SQD, GQD in this three-flavor neutrino system which is treated as a three-qubit system.

3 Monogamy relation for quantum correlation measures

For any pure state \(|\psi \rangle _{A B}\), The entanglement of formation is defined as

$$\begin{aligned} E_f(|\psi \rangle _{A B})=S(\rho _A)=-\sum \mu _{j} \log _{2} \mu _{j}, \end{aligned}$$
(11)

where \(\rho _{\textrm{A}}={\text {Tr}}_{\textrm{B}}\left( |\psi \rangle _{\textrm{AB}}\langle \psi |\right) \) and \(\mu _j\) are the eigenvalues of \(\rho _A\). When \(\rho _{AB}\) is a bipartite mixed state, using the convex roof extension method, the EOF is defined as

$$\begin{aligned} E_f\left( \rho _{A B}\right)= & {} \min _{\left\{ p_{i},\left| \phi _{i}\right\rangle _{A B}\right\} } \sum _{i} p_{i} E_f\left( \left| \phi _{i}\right\rangle _{A B}\right) , \end{aligned}$$
(12)

where the maximization is taken over all possible pure state decompositions of \(\rho _{A B}=\sum _{i} p_{i}\left| \phi _{i}\right\rangle _{A B}\left\langle \phi _{i}\right| \) with \(p_i \ge 0\), \(\sum _{i} p_i=1\). For a two-qubit mixed state \(\rho _{AB}\), an analytical formula for calculation of EOF was derived by Wootters [49],

$$\begin{aligned} E_{f}\left( \rho _{A B}\right) =H\left( \frac{1+\sqrt{1-\left| C(\rho _{A B})\right| ^{2}}}{2}\right) , \end{aligned}$$
(13)

where \( H(x)= -x \log _{2} x-(1-x) \log _{2}(1-x)\) is the binary entropy and \(C(\rho _{A B})=\max \left\{ \sqrt{\lambda _{1}}-\sqrt{\lambda _{2}}-\sqrt{\lambda _{3}}-\sqrt{\lambda _{4}}, 0\right\} \) is the concurrence of the density \(\rho _{A B}\), where \(\lambda _{i}\)s the eigenvalues of the matrix \(\rho _{AB}\widetilde{\rho _{AB}}\) with decreasing order, in which \(\widetilde{\rho _{AB}}=\left( \sigma _{y} \otimes \sigma _{y}\right) \rho _{A B}^{*}\left( \sigma _{y} \otimes \sigma _{y}\right) \).

For any three-qubit state \(\rho _{ABC}\), the bipartite entanglement quantified by SEF obeys the following monogamy inequality [41]

$$\begin{aligned} E_{f}^{2}(\rho _{A\mid BC}) \ge E_{f}^{2}(\rho _{A B})+E_{f}^{2}(\rho _{A C}), \end{aligned}$$
(14)

where \(E_{f}^{2}(\rho _{A\mid BC})\) quantifies the entanglement between A and the single object BC, and \(E_{f}^{2}(\rho _{A B})\) (\(E_{f}^{2}(\rho _{A C})\)) quantifies the entanglement between A and B(C).

Besides entanglement, QD is also a prominent bipartite quantum correlation measure, which is defined as [50, 51]

$$\begin{aligned} D(\rho _{AB})={\widetilde{S}}(\rho _A \mid \rho _B)-S( \rho _A\mid \rho _B), \end{aligned}$$
(15)

where \({\widetilde{S}}(\rho _A \mid \rho _B)=\min _{\left\{ M_{j}^{B}\right\} } \mathop {\sum \limits _{j}} p_{j} S\left( \rho _{A\mid j}\right) \) is the measurement-induced quantum conditional entropy, in which \(\left\{ M_{j}^{B}\right\} \) is POVM measurement performed on subsystem B, and \(S(\rho A | \rho B) = S (\rho A) -S (\rho B)\) is the entropy of A condition on B. Particularly, for a tripartite pure state \(\left| \psi _{A B C}\right\rangle \), combining Eq. (15) with the Koashi–Winter formula [52], one obtains the pairwise QD as

$$\begin{aligned} {D}(\rho _{ik})=E_{f}(\rho _{ij})-S(\rho _i\mid \rho _k), \end{aligned}$$
(16)

where the measurement is carried out on subsystem k, and \(i \ne j \ne k \in \{A, B, C\}\). Moreover, there exists a relation between the QD and the entanglement of formation [53, 54]

$$\begin{aligned} D\left( \rho _{i \mid j k}\right) =E\left( \rho _{i \mid j k}\right) =S\left( \rho _{i}\right) . \end{aligned}$$
(17)

For any three-qubit pure state \(\rho _{ABC}\), the bipartite correlation quantified by SQD fulfill the monogamy relation [39]

$$\begin{aligned} D^{2}(\rho _{A\mid BC}) \ge D^{2}(\rho _{A B})+D^{2}(\rho _{A C}). \end{aligned}$$
(18)

On the other hand, the geometric measure of quantum discord is defined as the the minimal square Hilbert-Schmidt distance between a given quantum state of a bipartite system AB and the closest classical state [55]

$$\begin{aligned} D_{G}\left( \rho _{A B}\right) =\min _{\sigma _{A B} \in \varOmega }\left\| \rho _{A B}-\sigma _{A B}\right\| _{2}^{2}, \end{aligned}$$
(19)

where the minimum is over the set of classical-quantum states \(\varOmega \) presenting zero discord, and the distance is the square of the 2-norm, also referred to as Hilbert-Schmidt norm. It is given by

$$\begin{aligned} \Vert \rho -\sigma \Vert ^{2}={\text {Tr}}(\rho -\sigma )^{2} \end{aligned}$$

For any two-qubit quantum state in terms of Bloch representation

$$\begin{aligned} {\rho =\frac{1}{4}\left[ I \otimes I+\sum _{i}^{3}\left( x_{i} \sigma _{i} \otimes I+y_{i} I \otimes \sigma _{i}\right) +\sum _{i, j=1}^{3} t_{i j} \sigma _{i} \otimes \sigma _{j}\right] ,} \end{aligned}$$
(20)

where I is the \(2\times 2\) identity matrix and the operators \(\sigma _{i}\) \((i=1, 2, 3)\) represent the three Pauli matrices, \(x_{i}={\text {Tr}} \rho \left( \sigma _{i} \otimes I\right) \), \(y_{i}={\text {Tr}} \rho \left( I \otimes \sigma _{i}\right) \) are the components of local Bloch vectors, \(t_{ij}={\text {Tr}} \rho \left( \sigma _{i} \otimes \sigma _{j}\right) \) is the elements of the correlation matrix T. The explicit expression of the GQD is given by [55]

$$\begin{aligned} D_G(\rho )=\frac{1}{4}\left( \Vert x\Vert ^{2}+\Vert T\Vert ^{2}-\lambda _{\max }\right) , \end{aligned}$$
(21)

where \(x=\left( x_{1}, x_{2}, x_{3}\right) ^{T}\), and \(\lambda _{max}\) is the largest eigenvalue of the \(3\times 3\) matrix defined by

$$\begin{aligned} M=x x^{T}+T T^{T}. \end{aligned}$$
(22)

By simple computation, one can also obtain the alternative compact form of GQD [56]

$$\begin{aligned} D_G(\rho )=\frac{1}{4} \min \left\{ \lambda _{1}+\lambda _{2}, \lambda _{1}+\lambda _{3}, \lambda _{2}+\lambda _{3}\right\} , \end{aligned}$$
(23)

where \(\lambda _i\) (\(i=1,2,3\)) are the eigenvalues of the matrix M. For an arbitrary three-qubit pure state, the monogamy relation for GQD is described as [40]

$$\begin{aligned} D_G(\rho _{A\mid BC})\ge D_G(\rho _{AB})+D_G(\rho _{AC}). \end{aligned}$$
(24)

4 Monogamy relations in NOs

Here, we will test the monogamy relation related to the SEF, the SQD and the GQD in electron and muon NOs, respectively.

4.1 Monogamy relation in the electron antineutrino oscillations

If the electron-neutrino produced in the initial time \(t=0\), from Eq. (10), the time evolution of the initial electron neutrino can be written as

$$\begin{aligned} {\left| {\psi _e (t)} \right\rangle } = {a_{e e}}(t)\left| {100} \right\rangle + {a_{e \mu }}(t)\left| {010} \right\rangle + {a_{e \tau }}(t)\left| {001} \right\rangle , \end{aligned}$$
(25)

Now, we take the trace of density matrix \(\rho _{ABC}^e(t)={\left| {\psi (t)} \right\rangle _e}\left\langle \psi (t)\right| \) over qubit C resulting in the reduced density matrix of the two qubit system

$$\begin{aligned} \underline{}\rho _{AB}^e = \textrm{Tr}_c(\left| \psi \right\rangle \left\langle \psi \right| )\mathrm{{ = }}\left( {\begin{array}{*{20}{c}} {{{\left| {{a_{e\tau }}} \right| }^2}}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad {{{\left| {{a_{e\mu }}} \right| }^2}}&{}\quad {{a_{e\mu }}{a_{ee}}^*}&{}\quad 0\\ 0&{}\quad {{a_{ee}}{a_{e\mu }}^*}&{}\quad {{{\left| {{a_{ee}}} \right| }^2}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}} \right) . \end{aligned}$$
(26)

Similarly, when traced over the qubit B, we can get the reduced density matrix \(\rho _{AC}^e \). Using Eqs. (11) and (13), the pairwise SEF of in the three-flavor electron neutrino system can be calculated as

$$\begin{aligned} E_{f}^{2}(\rho ^e_{A\mid BC})&=[(P_{e\tau }+P_{e\mu })\log _{2}({P_{e\tau }+P_{e\mu }})+P_{ee}\log _{2}{P_{ee}}]^2, \nonumber \\ E_{f}^{2}\left( \rho _{A B}^{e}\right)&= \left( \frac{1+\sqrt{1-4 P_{e \mu } P_{e e}}}{2} \log _{2} \frac{1+\sqrt{1-4 P_{e \mu } P_{e e}}}{2}\right. \nonumber \\&\quad \left. +\frac{1-\sqrt{1-4 P_{e \mu } P_{e e}}}{2} \log _{2} \frac{1-\sqrt{1-4 P_{e \mu } P_{e e}}}{2}\right) ^{2}, \nonumber \\ E_{f}^{2}\left( \rho _{A C}^{e}\right)&= \left( \frac{1+\sqrt{1-4 P_{e \tau } P_{e e}}}{2} \log _{2} \frac{1+\sqrt{1-4 P_{e \tau } P_{e e}}}{2}\right. \nonumber \\&\quad \left. +\frac{1-\sqrt{1-4 P_{e \tau } P_{e e}}}{2} \log _{2} \frac{1-\sqrt{1-4 P_{e \tau } P_{e e}}}{2}\right) ^{2}. \end{aligned}$$
(27)

To determine the monogamy of entanglement measured by SEF in the three-flavor electron antineutrino oscillations, we can define the residual SEF as

$$\begin{aligned} E_R^{2}\left( \rho _{A B C}^{e}\right) =E_{f}^{2}(\rho ^e_{A\mid BC})-E_{f}^{2}\left( \rho _{A B}^{e}\right) -E_{f}^{2}\left( \rho _{A C}^{e}\right) , \end{aligned}$$
(28)

which can detect the three-qubit entanglement in pure state.

Fig. 2
figure 2

The monogamy of SEF tests for electron. Figure a gives \(E^{2}(\rho ^e_{A\mid BC})\) (red, solid line), \(E^2(\rho ^e_{AB})\) (blue, dashed line), \(E^2(\rho ^e_{AC})\) (purple, dashed-dotted line) vs. L/E. Figure b gives the residual SEF (red, solid line) in the electron antineutrino oscillations

Full size image

In Fig. 2, we plot the time evolutions of bipartite entanglement \(E_{f}^{2}(\rho ^e_{A\mid BC})\), \(E_{f}^{2}\left( \rho _{A B}^{e}\right) \) and \(E_{f}^{2}\left( \rho _{A C}^{e}\right) \) as a function of the ratio L/E as well as the related residual SEF \(E^2_R(\rho ^e_{A\mid BC})\). The bipartite entanglement \(E_{f}^{2}(\rho ^e_{A\mid BC})\), \(E_{f}^{2}\left( \rho _{A B}^{e}\right) \) and \(E_{f}^{2}\left( \rho _{A C}^{e}\right) \) all exhibit a obvious oscillatory behavior with the variation that increases firstly and then decreases. At around \(L/E = 10.8~\mathrm km/MeV\), \(E_{f}^{2}(\rho ^e_{A\mid BC})\) reaches the maximum value 1. From Fig. 2b, at \(L/E=0\), the residual SEF \(E^2_R(\rho ^e_{A\mid BC})=0\), which implies the initial electron flavor state is a biseparable state. Furthermore, the residual SEF is always greater than or equal to zero, meaning the monogamy relation \(E_{f}^{2}(\rho ^e_{A\mid BC})\ge E_{f}^{2}(\rho ^e_{A B})+ E_{f}^{2}(\rho ^e_{A C})\) is valid in electron antineutrino oscillation. Note also from the plot that the monogamy relation is considerably tight in the case that, for whole range of L/E, the value of \(E_{f}^{2}(\rho ^e_{A\mid BC})\) is sufficiently limited to ensure that the subsystems between A, B, and A, C are not freely share entanglement in the oscillation process.

Fig. 3
figure 3

The monogamy of SQD tests for electron. Figure a gives \(D^{2}(\rho ^e_{A\mid BC})\) (red, solid line), \(D^2(\rho ^e_{AB})\) (blue, dashed line), \(D^2(\rho ^e_{AC})\) (purple, dashed-dotted line) vs. L/E. Figure b gives the residual SQD \(D_R^{2}(\rho _{A B C}^{e})\) (red, solid line) in comparison to the residual QD \(D_R(\rho _{A B C}^{e})\) (blue, dashed line) in electron antineutrino oscillations

Full size image

Now, we study the monogamy relation of SQD in the electron antineutrino oscillation system. Consider a von Neumann measurement on the subsystem B for three-flavor electron neutrino state, then according to Eq. (16), we can obtain the SQD of subsystem \(\rho ^e_{AB}\) and \(\rho ^e_{AC}\) as

$$\begin{aligned} D^2(\rho ^e_{AB})&=\left[ -\frac{1+\sqrt{1-4P_{e\tau }P_{ee}} }{2}\log _{2}{\frac{1+\sqrt{1-4P_{e\tau }P_{ee}} }{2}}\right. \nonumber \\&\quad \left. -\frac{1-\sqrt{1-4P_{e\tau }P_{ee}} }{2}\log _{2}{\frac{1-\sqrt{1-4P_{e\tau }P_{ee}} }{2}} \right. \nonumber \\&\quad \left. +P_{e\tau }\log _{2}{P_{e\tau }}+(P_{e\mu }+P_{ee})\log _{2}({P_{e\mu }+P_{ee}})\right. \nonumber \\&\quad \left. -P_{e\mu }\log _{2}{P_{e\mu }}-(P_{e\tau }+P_{ee})\log _{2}({P_{e\tau }+P_{ee}})\right] ^2, \end{aligned}$$
(29)
$$\begin{aligned} D^2(\rho ^e_{AC})&=\left[ -\frac{1+\sqrt{1-4P_{e\mu }P_{ee}} }{2}\log _{2}{\frac{1+\sqrt{1-4P_{e\mu }P_{ee}} }{2}}\right. \nonumber \\&\quad \left. -\frac{1-\sqrt{1-4P_{e\mu }P_{ee}} }{2}\log _{2}{\frac{1-\sqrt{1-4P_{e\mu }P_{ee}} }{2}} \right. \nonumber \\&\quad \left. +P_{e\mu }\log _{2}{P_{e\mu }}+(P_{e\tau }+P_{ee})\log _{2}({P_{e\tau }+P_{ee}})\right. \nonumber \\&\quad \left. -P_{e\tau }\log _{2}{P_{e\tau }}-(P_{e\mu }+P_{ee})\log _{2}({P_{e\mu }+P_{ee}})\right] ^2. \end{aligned}$$
(30)

Using Eq. (17), the SQD of the system \(\rho ^e_{ABC}\) between A and BC can be obtained as

$$\begin{aligned} D^{2}(\rho ^e_{A\mid BC})=[(P_{e\tau }+P_{e\mu })\log _{2}({P_{e\tau }+P_{e\mu }})+P_{ee}\log _{2}{P_{ee}}]^2. \end{aligned}$$
(31)

Then, similar to the definition of residual SEF, we can define the residual SQD corresponding to the monogamy relation in Eq. (18),

$$\begin{aligned} D_R^{2}\left( \rho _{A B C}^{e}\right) =D^{2}(\rho ^e_{A\mid BC})-D^{2}\left( \rho _{A B}^{e}\right) -D^{2}\left( \rho _{A C}^{e}\right) , \end{aligned}$$
(32)

which are plotted in Fig. 3b in comparison with the residual QD \(D_R\left( \rho _{A B C}^{e}\right) \) as will as the bipartite correlations \(D_R^{2}\left( \rho _{A B C}^{e}\right) \), \(D_{f}^{2}\left( \rho _{A B}^{e}\right) \) and \(D_{f}^{2}\left( \rho _{A C}^{e}\right) \) are plotted as a function of ratio L/E in Fig. 3a. We can observe that the residual QD is always negative. That is to say, the QD is not monogamous for the electron antineutrino oscillations. The residual SQD \(D_R^{2}\left( \rho _{A B C}^{e}\right) \) is always greater than or equal to zero, suggesting that the monogamy relation \(D^{2}(\rho ^e_{A\mid BC}) \ge D^2(\rho ^e_{AB})+D^2(\rho ^e_{AC})\) works for electron antineutrino oscillation system. Thus, the single-site correlation \(D^{2}(\rho ^e_{A\mid BC})\) can set a limit for the pairwise correlations \(D^2(\rho ^e_{AB})\) and \(D^2(\rho ^e_{AC})\), which can reflect in in Fig. 3a that the evolutions of \(D^2(\rho ^e_{AB})\) and \(D^2(\rho ^e_{AC})\) coincide with the \(D^{2}(\rho ^e_{A\mid BC})\).

To study the monogamy relation of GQD in three-qubit neutrino system, we firstly evaluate the pairwise GQD in pure bipartite state of three-flavor electron neutrino system. For this, we write the three-flavour electron neutrino state in Schmidt decomposition form

$$\begin{aligned} |\psi (t)\rangle _{e}&= \sqrt{P_{e \tau }+P_{e \mu }}|0\rangle ^{A}\left[ \sqrt{ \frac{ P _ { e \mu } }{ P _ { e \tau } + P _ { e \mu } } } \right. \nonumber \\&\quad \left. \times \left( \sqrt{\frac{P_{e \tau }}{P_{e \mu }}}|01\rangle +|10\rangle \right) \right] ^{B C}+\sqrt{P_{e e}}|1\rangle ^{A}|00\rangle ^{B C}, \end{aligned}$$
(33)

where \(\left| {0} \right\rangle ^A\) (\(\left| {1} \right\rangle ^A\)) are the eigenvectors of the reduced density matrix \(\rho ^e_A\). Similarly, \(\sqrt{\frac{P_{e\mu }}{P_{e\tau }+P_{e\mu }}}(\sqrt{\frac{P_{e\tau }}{P_{e\mu }} }\left| {01} \right\rangle +\left| {10} \right\rangle )\) (\(\left| {00} \right\rangle \)) are the eigenvectors of the reduced density matrix \(\rho ^e_{BC}\), and \(P_{ee}\), \(P_{e\tau }+P_{e\mu }\) are nonzero eigenvalues for \(\rho ^e_A\) and \(\rho ^e_{BC}\), respectively. In this case, the matrix M, defined by Eq. (22), can be expressed as the diagonal form

$$\begin{aligned}&{M_{AB}^e} \nonumber \\&\quad =\left( {\begin{array}{*{20}{c}} {4P_{ee}(P_{e\tau }+P_{e\mu }) }&{}\quad 0&{}\quad 0\\ 0&{}\quad {4P_{ee}(P_{e\tau }+P_{e\mu }) }&{}\quad 0\\ 0&{}\quad 0&{}\quad {2[P_{ee}^2+(P_{e\tau }+P_{e\mu })^2]} \end{array}} \right) . \end{aligned}$$
(34)

and using Eq. (23), we can obtain the GQD for subsystem A and BC as

$$\begin{aligned} D_G(\rho ^e_{A\mid BC})=2P_{ee}(P_{e\tau }+P_{e\mu }). \end{aligned}$$
(35)
Fig. 4
figure 4

The twice of GQD \(2D_G(\rho ^e_{A\mid BC})\) (red, solid line), \(2D_G(\rho ^e_{AB})\) (blue, dashed line), and \(2D_G(\rho ^e_{AC})\) (purple, dashed-dotted line) vs. L/E. One can see that the monogamy relation \(D_G(\rho ^e_{AB})+D_G(\rho ^e_{AC})=D_G(\rho ^e_{A\mid BC})\) holds in electron antineutrino oscillations

Full size image

Similarly, we can get the matrices \(M^e_{AB}\) and \(M^e_{AC}\). Then the GQD of reduced matrix density \(\rho ^e_{AB}\) and \(\rho ^e_{AC}\) can be calculated as

$$\begin{aligned} D_G(\rho ^e_{AB})&=2P_{ee}P_{e\mu }, \end{aligned}$$
(36)
$$\begin{aligned} D_G(\rho ^e_{AC})&=2P_{ee}P_{e\tau }. \end{aligned}$$
(37)

Using the Eqs. (35), (36) and (37), we obtain the following relation

$$\begin{aligned} D_G(\rho ^e_{AB})+D_G(\rho ^e_{AC})=D_G(\rho ^e_{A\mid BC}). \end{aligned}$$
(38)

which shows that the monogamy relation of GQD is saturated for the electron antineutrino oscillation system. Here, we use \(2D_G\) as a suitable correlation measure, as GQD is not normalized to one. In Fig. 4, we plot the time evolution of \(2D_G(\rho ^e_{AB})\), \(2D_G(\rho ^e_{AC})\) and \(2D_G(\rho ^e_{A\mid BC})\). At the point \(L/E=0\), \(2D_G(\rho ^e_{A\mid BC})=0\), which means the initial flavor electron state is a biseparable state under the bipartition \(A\mid BC\). Moreover, we can find that \(D_G(\rho ^e_{AB})\) and \(D_G(\rho ^e_{AC})\) always exhibit inverse change trends that \(D_G(\rho ^e_{AB})\) increase along with \(D_G(\rho ^e_{AC})\) decrease, and the sum of \(D_G(\rho ^e_{AB})\) and \(D_G(\rho ^e_{AC})\) is always equal to \(D_G(\rho ^e_{A\mid BC})\) with respect to L/E.

4.2 Monogamy relations in the muon antineutrino oscillations

When a muon flavor state generated at the source in initial time \(t=0\), using Eq. (11), the evolution of states for the three-flavor NOs can be expressed as

$$\begin{aligned} {\left| {\psi _\mu (t)} \right\rangle } = {a_{\mu e}}(t)\left| {100} \right\rangle + {a_{\mu \mu }}(t)\left| {010} \right\rangle + {a_{\mu \tau }}(t)\left| {001} \right\rangle , \end{aligned}$$
(39)

The reduced density matrix \(\rho _{AB}^\mu \) is given by tracing of density matrix \(\rho _{ABC}^\mu (t)={\left| {\psi (t)} \right\rangle _\mu }\left\langle \psi (t)\right| \) over qubit C

$$\begin{aligned} {\rho _{AB}^\mu }\! =\!\textrm{Tr}_c(\left| \psi \right\rangle \langle \psi |)\mathrm{{ = }}\left( {\begin{array}{*{20}{c}} {{{\left| {{a_{\mu \tau }}} \right| }^2}}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad {{{\left| {{a_{\mu \mu }}} \right| }^2}}&{}\quad {{a_{\mu \mu }}{a_{\mu e}}^*}&{}\quad 0\\ 0&{}\quad {{a_{\mu e}}{a_{\mu \mu }}^*}&{}\quad {{{\left| {{a_{\mu e}}} \right| }^2}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}} \right) . \end{aligned}$$
(40)
Fig. 5
figure 5

The monogamy of SEF tests for muon. Figure a gives \(E^{2}(\rho ^\mu _{A\mid BC})\) (red, solid line), \(D^2(\rho ^\mu _{AB})\) (blue, dashed line), \(D^2(\rho ^\mu _{AC})\) (purple, dashed-dotted line) vs. L/E. Figure b gives the residual SEF (red, solid line) in the muon antineutrino oscillations

Full size image

For the reduced density matrix state of the subsystem \(\rho ^\mu _{AB}\) and \(\rho ^\mu _{AC}\), The corresponding matrix \(\rho _{AB}^\mu \widetilde{\rho _{AB}^\mu }\) and \(\rho _{AC}^\mu \widetilde{\rho _{AC}^\mu }\) can be simply obtained. Then the SEF of pairwise qubits are given by

$$\begin{aligned} E_{f}^{2}\left( \rho _{A B}^{\mu }\right)&= \left( \frac{1+\sqrt{1-4 P_{\mu \mu } P_{\mu e}}}{2} \log _{2} \frac{1+\sqrt{1-4 P_{\mu \mu } P_{\mu e}}}{2}\right. \nonumber \\&\quad \left. +\frac{1-\sqrt{1-4 P_{\mu \mu } P_{\mu e}}}{2} \log _{2} \frac{1-\sqrt{1-4 P_{\mu \mu } P_{\mu e}}}{2}\right) ^{2}, \nonumber \\ E_{f}^{2}\left( \rho _{A C}^{\mu }\right)&= \left( \frac{1+\sqrt{1-4 P_{\mu \tau } P_{\mu e}}}{2} \log _{2} \frac{1+\sqrt{1-4 P_{\mu \tau } P_{\mu e}}}{2}\right. \nonumber \\&\quad \left. +\frac{1-\sqrt{1-4 P_{\mu \tau } P_{\mu e}}}{2} \log _{2} \frac{1-\sqrt{1-4 P_{\mu \tau } P_{\mu e}}}{2}\right) ^{2}. \end{aligned}$$
(41)

and the SEF of bipartite system \(\rho ^\mu _{A\mid BC }\) is calculated as

$$\begin{aligned}&E_{f}^{2}(\rho ^\mu _{A\mid BC})=[(P_{\mu \tau }+P_{\mu \mu })\log _{2}({P_{\mu \tau }+P_{\mu \mu }})\nonumber \\ {}&+P_{\mu e}\log _{2}{P_{\mu e}}]^2. \end{aligned}$$
(42)

The residual SEF corresponding to the monogamy relation in Eq. (14) in muon antineutrino oscillations system is

$$\begin{aligned} E_R^{2}\left( \rho _{A B C}^{\mu }\right) =E_{f}^{2}(\rho ^\mu _{A\mid BC})-E_{f}^{2}\left( \rho _{A B}^{\mu }\right) -E_{f}^{2}\left( \rho _{A C}^{\mu }\right) . \end{aligned}$$
(43)

Figure 5 has drawn the dynamics of the \(E_{f}^{2}(\rho ^\mu _{A\mid BC})\), \(E_{f}^{2}(\rho ^\mu _{A B})\) and \(E_{f}^{2}(\rho ^\mu _{A C})\) as a function of ratio L/E, and to examine the monogamy relation of SEF in muon neutrino oscillations, we plotted the residual SEF in Fig. 5b. This figure shows that as the ratio L/E increase, \(E^{2}(\rho ^\mu _{A\mid BC})\) increases from zero to the maximum 0.06 at around \(L/E = 495 ~ \mathrm km/GeV\), and then decreases. The bipartite entanglement \(E_{f}^{2}(\rho ^\mu _{A B})\) and \(E_{f}^{2}(\rho ^\mu _{A C})\) show complementary behavior in a range [261, 762] of L/E– an increase of \(E_{f}^{2}(\rho ^\mu _{A B})\) lead to a corresponding decrease of the \(E_{f}^{2}(\rho ^\mu _{A C})\). It can be seen from Fig. 5b that the residual SEF is positive or equal to zero in the range [10, 1000] of L/E with dimension \(\mathrm km/GeV\). It turns out that the monogamy relation \(E_{f}^{2}(\rho ^\mu _{A\mid BC})\ge E_{f}^{2}(\rho ^\mu _{A B})+ E_{f}^{2}(\rho ^\mu _{A C})\) holds for the muon antineutrino oscillations.

Fig. 6
figure 6

The monogamy of SQD tests for muon. Figure a gives \(D^{2}(\rho ^\mu _{A\mid BC})\) (red, solid line), \(D^2(\rho ^\mu _{AB})\) (blue, dashed line), \(D^2(\rho ^\mu _{AC})\) (purple, dashed-dotted line) vs. L/E. Figure b gives the \(D_R^{2}(\rho ^\mu _{ABC})\) (red, solid line) in comparison with the \(D_R(\rho ^\mu _{ABC})\) (blue, dashed line) in the muon antineutrino oscillations

Full size image

To examine the monogamy relation of SQD in the three-flavor muon NOs, we primarily calculate the SQD for the subsystems \(\rho ^\mu _{AB}\), \(\rho ^\mu _{AC}\) and \(\rho ^\mu _{A\mid BC}\) as

$$\begin{aligned}&D^2(\rho ^\mu _{AB})=\left[ -\frac{1+\sqrt{1-4P_{\mu \tau }P_{\mu e}} }{2}\log _{2}{\frac{1+\sqrt{1-4P_{\mu \tau }P_{\mu e}} }{2}}\right. \nonumber \\&\quad \left. -\frac{1-\sqrt{1-4P_{\mu \tau }P_{\mu e}} }{2}\log _{2}{\frac{1-\sqrt{1-4P_{\mu \tau }P_{\mu e}} }{2}}\right. \nonumber \\&\quad \left. +P_{\mu \tau }\log _{2}{P_{\mu \tau }}+(P_{\mu \mu }+P_{\mu e})\log _{2}({P_{\mu \mu }+P_{\mu e}})\right. \nonumber \\&\quad \left. -P_{\mu \mu }\log _{2}{P_{\mu \mu }}-(P_{\mu \tau }+P_{\mu e})\log _{2}({P_{\mu \tau }+P_{\mu e}}) \right] ^2, \end{aligned}$$
(44)
$$\begin{aligned}&D^2(\rho ^\mu _{AC})=\left[ -\frac{1+\sqrt{1-4P_{\mu \mu }P_{\mu e}} }{2}\log _{2}{\frac{1+\sqrt{1-4P_{\mu \mu }P_{\mu e}} }{2}}\right. \nonumber \\&\quad \left. -\frac{1-\sqrt{1-4P_{\mu \mu }P_{\mu e}} }{2}\log _{2}{\frac{1-\sqrt{1-4P_{\mu \mu }P_{\mu e}} }{2}}\right. \nonumber \\&\quad \left. +P_{\mu \mu }\log _{2}{P_{\mu \mu }}+(P_{\mu \tau }+P_{\mu e})\log _{2}({P_{\mu \tau }+P_{\mu e}})\right. \nonumber \\&\quad \left. -P_{\mu \tau }\log _{2}{P_{\mu \tau }}-(P_{\mu \mu }+P_{\mu e})\log _{2}({P_{\mu \mu }+P_{\mu e}}) \right] ^2. \end{aligned}$$
(45)
$$\begin{aligned}&D^{2}(\rho ^\mu _{A\mid BC})=[(P_{\mu \tau }+P_{\mu \mu })\log _{2}({P_{\mu \tau }+P_{\mu \mu }})+P_{\mu e}\log _{2}{P_{\mu e}}]^2. \end{aligned}$$
(46)

According to monogamy relation in Eq. (24), we can construct the residual SQD in the three-flavor muon antineutrino oscillations as

$$\begin{aligned} D_R^{2}\left( \rho _{A B C}^{\mu }\right) =D^{2}(\rho ^\mu _{A\mid BC})-D^{2}\left( \rho _{A B}^{\mu }\right) -D^{2}\left( \rho _{A C}^{\mu }\right) . \end{aligned}$$
(47)

Figure 6a has drawn the \(D^{2}(\rho ^\mu _{A\mid BC})\), \(D^2(\rho ^\mu _{AB})\), \(D^2(\rho ^\mu _{AC})\) as a function of L/E. From Fig. 6a, one can see that the bipartite correlations \(D^{2}(\rho ^\mu _{A B})\) and \(D^{2}(\rho ^\mu _{A C})\) show complementary behavior in a range [335, 665] of L/E, where at around \(L/E=510 ~ \mathrm km/GeV\), \(D^{2}(\rho ^\mu _{A B})\) increases the maximal value with 0.04, while \(D^{2}(\rho ^\mu _{A C})\) reaches its minimal value with 0.0014. In order to examine the monogamy of SQD in the muon antineutrino oscillation system, we plotted the residual SQD \(D_R^{2}\left( \rho _{A B C}^{\mu }\right) \) in comparison to that of QD \(D_R\left( \rho _{A B C}^{\mu }\right) \)in Fig. 6b. From Fig. 6b, although the QD is not monogamous in three-flavored muon NOs, we can see that the residual SQD is positive or equal to zero as the L/E increases, showing that SQD is monogamous i.e, \(D^{2}(\rho ^\mu _{A\mid BC}) \ge D^2(\rho ^\mu _{AB})+D^2(\rho ^\mu _{AC})\).

Now, we want to detect how the correlations measured by GQD distributed in the muon antineutrino oscillation system. Similar to the case of electron antineutrino oscillation system, we can calculate the \(D_G(\rho ^e_{A\mid BC})\) as

$$\begin{aligned} D_G(\rho ^\mu _{A\mid BC})=2P_{\mu e}(P_{\mu \tau }+P_{\mu \mu }), \end{aligned}$$
(48)

where \(D_G(\rho ^\mu _{A\mid BC})\) is the GQD of \(\rho ^\mu _{A\mid BC}\) with respect to bipartition between A and BC. Resorting to Eq. (23), the GQD for subsystems \(\rho ^\mu _{AB}\) and \(\rho ^\mu _{AC}\) are given by

Fig. 7
figure 7

The twice of GQD \(2D_G(\rho ^\mu _{A\mid BC})\) (red, solid line), \(2D_G(\rho ^\mu _{AB})\) (blue, dashed line), and \(2D_G(\rho ^\mu _{AC})\) (purple, dashed-dotted line) vs. L/E. One can see that the monogamy relation \(D_G(\rho ^\mu _{AB})+D_G(\rho ^\mu _{AC})=D_G(\rho ^\mu _{A\mid BC})\) holds in muon antineutrino oscillations

Full size image
$$\begin{aligned} D_G(\rho ^\mu _{AB})&=2P_{\mu e}P_{\mu \mu }, \end{aligned}$$
(49)
$$\begin{aligned} D_G(\rho ^\mu _{AC})&=2P_{\mu e}P_{\mu \tau }, \end{aligned}$$
(50)

respectively. Thus using Eqs. (48), (49) and (50), we obtain the relation that

$$\begin{aligned} D_G(\rho ^\mu _{AB})+D_G(\rho ^\mu _{AC})=D_G(\rho ^\mu _{A\mid BC}). \end{aligned}$$
(51)

Therefore, the monogamous behavior of GQD is saturated for the muon antineutrino oscillation system. In Fig. 7, we plot the dynamics of \(2D_G(\rho ^\mu _{AB})\), \(2D_G(\rho ^\mu _{AC})\) and \(2D_G(\rho ^\mu _{A\mid BC})\) as a function of ratio L/E. From Fig. 7, we can find that the sum of pairwise \(D_G(\rho ^\mu _{AB})\) and \(D_G(\rho ^\mu _{AC})\) is always equal to \(D_G(\rho ^e_{A\mid BC})\) with respect to L/E. This suggests that the correlation measured by GQD between the subsystem A and BC contains correlation of the subsystem between A, B and A, C in the muon antineutrino oscillation system.

5 Conclusions

In this paper, we have explored the distributions of quantum correlations in three-flavor neutrino systems, by investigating several monogamy relations related to the SEF, SQD, and GQD, for initial electron-neutrino and muon-neutrino oscillations. We have shown that the SEF, SQD, and GQD display monogamy behaviors in three-flavor NOs systems by examining the fulfillment of monogamy relations of these quantum correlations. These relations will restrict the correlations evolutions in NOs, i.e., the correlations between part A and BC of NOs systems, which provide a tight bound to limit the correlations between the subsystem A, B and A, C in the neutrino propagation. This limitation makes a complementary behavior between two pairwise neutrino flavor systems arise in Nos. Among these monogamy relations, we find that SQD is monogamous in NOs, while QD is not monogamous in this case, indicating that investing the monogamy property in NOs is essentially rely on the choice of suitable correlation measures. For GQD, it is demonstrated that the monogamy relation is saturated for three-flavor neutrino systems, i.e., the correlation measured by GQD between a single subsystem and remaining subsystems of the three-flavor NOs contains correlations of the reduced pairwise neutrino subsystems. The results also show the residual correlation is a reasonable measure which can not only explicitly characterizes the structure of quantum correlations in NOs, but also quantify the constraints imposed by monogamy relations in NOs. These monogamy relations give us a better understanding of the distribution of correlations in the three-flavor neutrino systems and provide a promise way towards studying the information flows and transformations in neutrino communications.

As an extension of our work, we plan to consider a more complete monogamy relation which exhibits the correlations between ABC, AB, AC, and BC of a tripartite system in three-flavor NOs. In this case, we can not only explore the multipartite correlation in a effective way, but also can investigate the distribution of quantum correlations in NOs in more details.