1 Introduction

In 1977 Blandford and Znajek (BZ) proposed a mechanism that efficiently extracts the rotational energy of black holes by magnetic field [1]. The BZ process is realizable in an astrophysical environment, since the magnetic fields can be supported by accretion disks around stellar-mass and supermassive black holes (BH). Thus the BZ process is thought to be the most promising candidate for the power source of ultra high energy cosmic rays, such as gamma-ray bursts and relativistic jets from active galactic nuclei. In the BZ process, the ergosphere of a rotating BH is immersed in a poloidal magnetic field. Due to frame-dragging, the magnetic field lines twist in the toroidal direction, resulting in the emergence of a poloidal electric field. In this way the rotational energy of a BH is transferred into the energy of the currents outside the BH.

This process has been extensively studied by analytical method [1,2,3,4,5,6,7,8,9,10] and numerical simulations [5, 12,13,14,15] during the past four decades in general relativity (GR). The simplest analytical study of the BZ mechanism is based on the “split monopole” configuration [1]. These studies allow for the computation of the fields perturbatively up to a particular order of the BH’s spin, making them valid only for slowly rotating BH. For the investigation of BZ process in rapidly rotating BH, numerical simulations are usually necessary. Recently Armas et al. have extended the perturbative scheme to arbitrary orders of spin and any magnetic field configuration [10], and the perturbative expansions were improved in [11].

Since the BZ process depends on the ergosphere of BH, studying the process and its observational signatures can provide insights into gravity in the strong-field regime. Specifically, investigating the BZ process in deformed Kerr geometry, resulting from modifications of GR or certain astrophysical environments, can help constrain the metric deformation parameters using BZ power. Some attempts were made in this direction, such as studying BZ process for parametrically deformed Kerr BHs [16,17,18], for Kerr-Sen BH in heterotic string theory [19] and for slowly rotating BH in scalar Gauss–Bonnet gravity and dynamical Chern–Simons gravity [20].

The analysis in [20] shows a degeneracy between BH spin and the coupling constants of modified terms at leading order in slow rotation approximation which is broken at higher orders. As a result, if we want to distinguish GR from other theories of gravity using BZ power, we must study the BZ process to high orders of spin. Roughly speaking, amplitude of rotation amplifies the differences between GR and modified gravities. Another evidence for this cognition can be found in recent paper [21]. In this paper, we study the BZ process to the second relative order in spin for Einsteinian cubic gravity (ECG) which is a well-motivated high derivative gravity [22]. This can be a further example that enhances the comprehension of how to learn about new physics from BH observations related to BZ mechanism.

This paper is organized as follows. In Sect. 2 we give a brief introduction to BZ mechanism. In Sect. 3 we construct slowly rotating BH in ECG. Then we obtain magnetosphere solution around the BH in Sect. 4. In Sect. 5 we analysis the BZ power in ECG. We conclude in Sect. 6.

2 Blandford–Znajek process

In this section, we show the main ingredients of Blandford–Znajek process. In the split monopole configuration, the accretion disk is considered as a thin current sheet in the equatorial plane of the BH, and the magnetosphere around the BH is determined by force-free electrodynamics which implies [23]

$$\begin{aligned} F_{\mu \nu }J^\nu =0 \,, \end{aligned}$$
(2.1)

where \(F_{\mu \nu }\) is the field strength tensor, and \(J^\nu =\nabla _\mu F^{\mu \nu }\) is the four-current.

In Boyer–Lindquist coordinates (\(t,r,\theta ,\phi \)), a stationary and axisymmetric metric can be decomposed in the following form

$$\begin{aligned} ds^2=g_{\mu \nu }dx^\mu dx^\nu =g^T_{AB}dx^Adx^B+g^P_{ab}dx^adx^b\,. \end{aligned}$$
(2.2)

\(g^T_{AB}\) is referred to as the toroidal metric \((t, \phi )\), and \(g^P_{ab}\) is referred to as the poloidal metric \((r, \theta )\). A stationary and axisymmetric electromagnetic field can always be represented by [23]

$$\begin{aligned} F_{tr}= & {} -F_{rt}=\Omega \partial _r\psi ,\nonumber \\ F_{t\theta }= & {} -F_{\theta t}=\Omega \partial _\theta \psi ,\nonumber \\ F_{r\phi }= & {} -F_{\phi r}=\partial _r\psi ,\nonumber \\ F_{\theta \phi }= & {} -F_{\phi \theta }=\partial _\theta \psi ,\nonumber \\ F_{r\theta }= & {} -F_{\theta r}=\frac{I}{2\pi }\sqrt{\frac{g^P}{-g^T}}, \end{aligned}$$
(2.3)

with all other components zero. Here \(\psi , I, \Omega \) are functions of \(r, \theta \). The t and \(\phi \) components of the force-free condition (2.1) imply that \(I, \Omega \) are functions of \(\psi \). To summarize, the force-free electromagnetic field is characterized by three quantities: the magnetic flux \(\psi (r,\theta )\) and the electric current \(I(\psi )\) through a surface bounded by the loop of revolution at (\(r,\theta \)), and the angular velocity of magnetic field lines \(\Omega (\psi )\) being dragged by the rotation of the BH. The r and \(\theta \) components of the force-free conditions (2.1) give the so-called stream equation

$$\begin{aligned} \nabla _\mu (|\eta |^2\nabla ^\mu \psi )+\Omega '(\eta \cdot dt)|\nabla \psi |^2-\frac{II'}{4\pi ^2g^T}=0\,, \end{aligned}$$
(2.4)

where the prime denotes a derivative with respect to \(\psi \), and \(\eta \equiv d\phi -\Omega dt\).

To solve the above stream equation, we must impose reasonable boundary conditions for \(\psi \). Here we follow a recent work by Armas et al. [10], imposing the boundary conditions for \(\psi \) as

$$\begin{aligned} \psi =0,{} & {} \theta =0,\nonumber \\ \psi =\psi _0,{} & {} \theta =\pi /2,\nonumber \\ \psi ~\text {finite},{} & {} r=r_H,\nonumber \\ \psi ~\text {finite},{} & {} r\rightarrow \infty , \end{aligned}$$
(2.5)

where \(\psi _0\) is the monopole charge, and \(r_H\) is the horizon radius. These are natural boundary conditions for split monopole configuration. The solutions of \(I, \Omega \) can be obtained by the so-called Znajek conditions [23, 24]

$$\begin{aligned} I= & {} 2\pi (\Omega -\Omega _H)\partial _\theta \psi \sqrt{\frac{g_{\phi \phi }}{g_{\theta \theta }}}, \quad r=r_H,\nonumber \\ I= & {} -2\pi \Omega \partial _\theta \psi \sin \theta ,\quad r\rightarrow \infty , \end{aligned}$$
(2.6)

where \(\Omega _H\) is the horizon angular velocity. The Znajek conditions are derived from the requirement that fields are finite in regular coordinates. Then we can resolve the stream equation (2.4) perturbatively order by order in the BH’s spin. It should be pointed out that in order to construct consistent and physical solutions at arbitrary relative order in spin, we must demand regularity at the light surfaces, on which a co-rotating observer would need to travel at the speed of light [10, 11, 15]. Having obtained the solutions of field variables \(\psi , I, \Omega \), the total electromagnetic energy flux extracted from the BH, also known as the BZ power, is given by [23]

$$\begin{aligned} P= & {} -\int I\Omega d\psi \nonumber \\= & {} 4\pi \int _0^{\pi /2}\left. \left[ \Omega (\Omega _H-\Omega )(\partial _\theta \psi )^2\sqrt{\frac{g_{\phi \phi }}{g_{\theta \theta }}}\right] \right| _{r=r_H}d\theta \,.\nonumber \\ \end{aligned}$$
(2.7)

3 Slowly rotating black hole in Einsteinian cubic gravity

The action of Einsteinian cubic gravity includes a particular combination of cubic curvature terms [22]. The ECG has two remarkable properties. First the vacuum static spherically symmetric solution is characterized by only one function in four dimension, which is determined by a two derivatives differential equation. Second, the linearized equations of motion on maximally symmetric backgrounds coincide with the linearized Einstein equations up to an overall factor. Thus it is free of massive spin-2 ghost for general higher curvature gravity. The action of ECG is

$$\begin{aligned} \mathcal {S}=\frac{1}{16\pi G}\int dx^4 \sqrt{-g} (R+\lambda \mathcal {P})\,, \end{aligned}$$
(3.8)

where the cubic curvature term is

$$\begin{aligned} \mathcal {P}= & {} 12R_\mu {}^\rho {}_\nu {}^\sigma R_\rho {}^\gamma {}_\sigma {}^\delta R_\gamma {}^\mu {}_\delta {}^\nu +R_{\mu \nu }^{\rho \sigma }R_{\rho \sigma }^{\gamma \delta } R_{\gamma \delta }^{\mu \nu }\nonumber \\{} & {} -12R_{\mu \nu \rho \sigma }R^{\mu \rho }R^{\nu \sigma } +8R_\mu ^\nu R_\nu ^\rho R_\rho ^\mu . \end{aligned}$$
(3.9)

The covariant equation of motion is

$$\begin{aligned} \mathcal {E}_{ab} \equiv P_{acde}R_b{}^{cde}-{\textstyle {\frac{\scriptstyle 1}{\scriptstyle 2} } }g_{ab}{L}-2\nabla ^c\nabla ^dP_{acdb} = 0\,, \end{aligned}$$
(3.10)

where

$$\begin{aligned}{} & {} P_{abcd} \equiv \frac{\partial {L}}{\partial R^{abcd}}\nonumber \\{} & {} ={\textstyle {\frac{\scriptstyle 1}{\scriptstyle 2} } }(g_{ac}g_{bd}-g_{ad}g_{bc})\nonumber \\{} & {} \qquad +6\lambda \Big (R_{ad}R_{bc}-R_{ac}R_{bd}+g_{bd}R_a{}^eR_{ce}-g_{ad}R_b{}^eR_{ce}\nonumber \\{} & {} \qquad -g_{bc}R_a{}^eR_{de}+g_{ac}R_b{}^eR_{de}-g_{bd}R^{ef}R_{aecf}\nonumber \\{} & {} \qquad +g_{bc}R^{ef}R_{aedf}+g_{ad}R^{ef}R_{becf}\nonumber \\{} & {} \qquad -3R_a{}^e{}_d{}^fR_{becf}-g_{ac}R^{ef}R_{bedf}\nonumber \\{} & {} \qquad +3R_a{}^e{}_c{}^fR_{bedf}+{\textstyle {\frac{\scriptstyle 1}{\scriptstyle 2} } }R_{ab}{}^{ef}R_{cdef}\Big ). \end{aligned}$$
(3.11)

The static spherically symmetric BH in ECG is obtained in [25, 26]. The bouncing universe in critical ECG is obtained in [27]. The slowly rotating BH to leading order in spin for ECG with arbitrary coupling constant of cubic term is obtained in [28]. To study the BZ process in ECG to the second relative order in spin, we need construct the slowly rotating BH in Boyer–Lindquist coordinates, to cubic order in spin and to leading order in coupling constant of cubic terms. Following the scheme in [29], we can expand the metric as

$$\begin{aligned} g_{\mu \nu }= & {} g^{(0,0)}_{\mu \nu }+\chi g^{(1,0)}_{\mu \nu }+\chi ^2g^{(2,0)}_{\mu \nu }+\chi ^3g^{(3,0)}_{\mu \nu }+\zeta g^{(0,1)}_{\mu \nu }\nonumber \\{} & {} +\zeta \chi g^{(1,1)}_{\mu \nu }+\zeta \chi ^2g^{(2,1)}_{\mu \nu }+\zeta \chi ^3g^{(3,1)}_{\mu \nu }, \end{aligned}$$
(3.12)

where \(g^{(0,0)}_{\mu \nu }\) is the Schwarzschild solution, and \(g^{(m,n)}_{\mu \nu }\) is a metric perturbation away from the Schwarzschild solution in order \(\mathcal {O}(\zeta ^n\chi ^m)\). Note that, we have introduced the dimensionless coupling constant \(\zeta \) and dimensionless spin \(\chi \) by setting

$$\begin{aligned} \lambda =M^4\zeta \,,\quad a=M\chi \,, \end{aligned}$$
(3.13)

where M is the mass of BH, and a is the spin of BH. After gauge fixing, the metric ansatz for slowly rotating BH take the form

$$\begin{aligned} ds^2= & {} -(f+\zeta f^{(0,1)}+\chi ^2f^{(2,0)}+\zeta \chi ^2f^{(2,1)})dt^2\nonumber \\{} & {} +\frac{dr^2}{f+\zeta g^{(0,1)}+\chi ^2g^{(2,0)}+\zeta \chi ^2g^{(2,1)}}\nonumber \\{} & {} +r^2\big [(1+\chi ^2\Theta ^{(2,0)}+\zeta \chi ^2\Theta ^{(2,1)})d\theta ^2\nonumber \\{} & {} +(1+\chi ^2\Phi ^{(2,0)}+\zeta \chi ^2\Phi ^{(2,1)})\sin ^2\theta d\phi ^2\big ]\nonumber \\{} & {} -2(\chi \omega ^{(1,0)}+\zeta \chi \omega ^{(1,1)}+\chi ^3\omega ^{(3,0)}\nonumber \\{} & {} +\zeta \chi ^3\omega ^{(3,1)})\sin ^2\theta dtd\phi , \end{aligned}$$
(3.14)

where \(\omega ^{(1,0)}, f^{(2,0)}, g^{(2,0)}, \Theta ^{(2,0)}, \Phi ^{(2,0)}\) can be read off by taking the slowly rotating limit of Kerr BH up to the cubic order of spin

$$\begin{aligned} f^{(2,0)}= & {} \frac{2M^3}{r^3}\cos ^2\theta ,\quad g^{(2,0)}=\frac{M^2}{r^2}-\frac{M^2}{r^2}f\cos ^2\theta ,\quad \nonumber \\ \Theta ^{(2,0)}= & {} \frac{M^2}{r^2}\cos ^2\theta ,\nonumber \\ \Phi ^{(2,0)}= & {} \frac{M^2}{r^2}+\frac{2M^3}{r^3}\sin ^2\theta ,\quad \nonumber \\ \omega ^{(1,0)}= & {} \frac{2M^2}{r},\quad \omega ^{(3,0)}=-\frac{2M^4}{r^3}\cos ^2\theta . \end{aligned}$$
(3.15)

The \(f^{(0,1)}, g^{(0,1)}, \omega ^{(1,1)}\) can be obtained by taking small coupling approximation

$$\begin{aligned} f^{(0,1)}=g^{(0,1)}=\frac{216 M^6}{r^6}-\frac{368 M^7}{r^7}\,,\quad \omega ^{(1,1)}=\frac{368 M^8}{r^7}\,. \end{aligned}$$
(3.16)

We can decompose the \(\mathcal {O}(\zeta \chi ^2)\) and \(\mathcal {O}(\zeta \chi ^3)\) perturbations as [30]

$$\begin{aligned} f^{(2,1)}(r,\theta )= & {} H_0^0(r)+H_0^2(r)P_2(\cos \theta ),\nonumber \\ g^{(2,1)}(r,\theta )= & {} H_1^0(r)+H_1^2(r)P_2(\cos \theta ),\nonumber \\ \Theta ^{(2,1)}(r,\theta )= & {} \Phi ^{(2,1)}(r,\theta )=H_2^2(r)P_2(\cos \theta ),\nonumber \\ \omega ^{(3,1)}(r,\theta )= & {} H_3^0(r)+H_3^2P_2(\cos \theta ). \end{aligned}$$
(3.17)

The solution of \(H_0^0, H_0^2, H_1^0, H_1^2, H_2^2\) are given in the appendix A. The horizon is determined by \(g_{tt}g_{\phi \phi }-g_{t\phi }^2=0\), and the solution is

$$\begin{aligned} r_H=2M-\chi ^2\frac{M}{2}-\zeta M-\zeta \chi ^2\frac{11M}{48}+\mathcal {O}(\zeta ^2,\chi ^4)\,. \end{aligned}$$
(3.18)

The angular velocity of the horizon is

$$\begin{aligned} \Omega _H\equiv & {} -\frac{g_{tt}}{g_{t\phi }}\Big |_{r=r_H}\nonumber \\= & {} \frac{\chi }{4M}+\frac{\chi ^3}{16M}+\zeta \chi \frac{35}{32M}+\zeta \chi ^3\frac{7}{64M}+\mathcal {O}(\zeta ^2,\chi ^5)\,.\nonumber \\ \end{aligned}$$
(3.19)

The ergosphere is determined by \(g_{tt}=0\)

$$\begin{aligned} r_\textrm{ergo}= & {} 2M-\chi ^2\frac{M}{2}\cos ^2\theta -\zeta M \nonumber \\{} & {} -\zeta \chi ^2\frac{11M}{48}(1-15\sin ^2\theta )+\mathcal {O}(\zeta ^2,\chi ^4)\,. \end{aligned}$$
(3.20)

4 Magnetosphere solution in Einsteinian cubic gravity

We now derive the magnetosphere solution around the slowly rotating BH in ECG by solving the stream equation (2.4) under the boundary conditions (2.5) and Znajek conditions (2.6). First we expand the field variables \(\psi , I, \Omega \) as follows [20]

$$\begin{aligned} \psi= & {} \psi ^{(0,0)}+\chi ^2\psi ^{(2,0)}+\zeta \psi ^{(0,1)}+\zeta \chi ^2\psi ^{(2,1)},\nonumber \\ I= & {} \chi i_{(1,0)}(\psi )+\chi ^3i_{(3,0)}(\psi )+\zeta \chi i_{(1,1)}(\psi )+\zeta \chi ^3i_{(3,1)}(\psi )\nonumber \\= & {} \chi I^{(1,0)}+\chi ^3I^{(3,0)}+\zeta \chi I^{(1,1)}+\zeta \chi ^3I^{(3,1)},\nonumber \\ \Omega= & {} \chi \omega _{(1,0)}(\psi )+\chi ^3\omega _{(3,0)}(\psi )\nonumber \\{} & {} +\zeta \chi \omega _{(1,1)}(\psi )+\zeta \chi ^3\omega _{(3,1)}(\psi )\nonumber \\= & {} \chi \Omega ^{(1,0)}+\chi ^3\Omega ^{(3,0)}+\zeta \chi \Omega ^{(1,1)}+\zeta \chi ^3\Omega ^{(3,1)}. \end{aligned}$$
(4.21)

It is easy to obtain the expansion coefficients

$$\begin{aligned} I^{(1,0)}= & {} i_{(1,0)}(\psi ^{(0,0)}),\nonumber \\ I^{(3,0)}= & {} i_{(3,0)}(\psi ^{(0,0)})+i'_{(1,0)}(\psi ^{(0,0)})\psi ^{(2,0)},\nonumber \\ I^{(1,1)}= & {} i_{(1,1)}(\psi ^{(0,0)})+i'_{(1,0)}(\psi ^{(0,0)})\psi ^{(0,1)},\nonumber \\ I^{(3,1)}= & {} i_{(3,1)}(\psi ^{(0,0)})+i'_{(1,0)}(\psi ^{(0,0)})\psi ^{(2,1)}\nonumber \\{} & {} +i'_{(1,1)}(\psi ^{(0,0)})\psi ^{(2,0)},\nonumber \\{} & {} +i'_{(3,0)}(\psi ^{(0,0)})\psi ^{(0,1)}+i''_{(1,0)}(\psi ^{(0,0)})\psi ^{(0,1)}\psi ^{(2,0)},\nonumber \\ \end{aligned}$$
(4.22)

and similar relations between \(\Omega ^{(n,m)}\) and \(\omega _{(n,m)}\). Then we can compute the field variables \(\psi , I, \Omega \) order by order of \(\mathcal {O}(\zeta ^n\chi ^m)\).

4.1 Leading order in spin

$$\begin{aligned} {\underline{Contribution~from~GR:}}\, \underline{\mathcal {O}(\zeta ^0\chi ^0)} \end{aligned}$$

At order \(\mathcal {O}(\zeta ^0\chi ^0)\), the stream equation is

$$\begin{aligned} L\psi ^{(0,0)}=0\,, \end{aligned}$$
(4.23)

where L is a separable differential operator defined by

$$\begin{aligned} L=\frac{\partial }{\partial x}\left[ \left( 1-\frac{2}{x}\frac{\partial }{\partial x}\right) \right] +\frac{\sin \theta }{x^2}\frac{\partial }{\partial \theta }\left( \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\right) \,, \end{aligned}$$
(4.24)

where we have introduced \(x \equiv r/M\) as a dimensionless radial coordinate. Imposing the boundary conditions (2.5), one obtains

$$\begin{aligned} \psi ^{(0,0)}=\psi _0(1-\cos \theta )\,, \end{aligned}$$
(4.25)

which is the exact monopole solution. Note that \(x_H=2+\mathcal {O}(\chi ^2)\), so we impose the horizon boundary conditions at \(x=2\) instead of \(x_H\). The Znajek conditions give

$$\begin{aligned} \quad I^{(1,0)}=-2\pi \psi _0\Omega ^{(1,0)}\sin ^2\theta ,\quad \Omega ^{(1,0)}=\frac{1}{8M}\,. \end{aligned}$$
(4.26)

These are just the leading order results in GR [1, 4].

$$\begin{aligned} \underline{Contribution~from~cubic~term:} \,\underline{\mathcal {O}(\zeta ^1\chi ^0)} \end{aligned}$$

At order \(\mathcal {O}(\zeta ^1\chi ^0)\), the stream equation is the same as the leading equation of GR

$$\begin{aligned} L\psi ^{(0,1)}=0\,. \end{aligned}$$
(4.27)

Since the GR solution \(\psi ^{(0,0)}\) account for all the monopole charge \(\psi _0\), we take

$$\begin{aligned} \psi ^{(0,1)}=0\,. \end{aligned}$$
(4.28)

The Znajek conditions give

$$\begin{aligned} \quad I^{(1,1)}=-2\pi \psi _0\Omega ^{(1,1)}\sin ^2\theta ,\quad \Omega ^{(1,1)}=\frac{35}{64M}. \end{aligned}$$
(4.29)

4.2 Second relative order in spin

$$\begin{aligned} \underline{Contribution~from~GR:}\, \underline{\mathcal {O}(\zeta ^0\chi ^2)} \end{aligned}$$

At order \(\mathcal {O}(\zeta ^0\chi ^2)\), the stream equation is

$$\begin{aligned} L\psi ^{(2,0)}=-\psi _0\frac{x+2}{x^4}\cos \theta \sin ^2\theta \,. \end{aligned}$$
(4.30)

This equation can be solved by separating variables. Imposing the boundary conditions (2.5), the general solution is

$$\begin{aligned} \psi ^{(2,0)}=\psi _0\varphi (x)\cos \theta \sin ^2\theta \,. \end{aligned}$$
(4.31)

Substituting it into the stream equation (2.4), we obtain the equation for \(\varphi (x)\)

$$\begin{aligned} \frac{d}{dx}\left( \Big (1-\frac{2}{x}\Big )\varphi '(x)\right) -\frac{6\varphi (x)}{x^2}+\frac{x+2}{x^4}=0\,. \end{aligned}$$
(4.32)

The solution of \(\varphi (x)\) satisfying the boundary conditions (2.5) is

$$\begin{aligned} \varphi (x)= & {} \frac{1}{8}x^2(2x-3)\left[ \text {Li}_2\Big (\frac{2}{x}\Big )+\ln \Big (\frac{2}{x}\Big )\ln \Big (1-\frac{2}{x}\Big )\right] \nonumber \\{} & {} +\frac{1}{12}(6x^2-3x-1)\ln \Big (\frac{2}{x}\Big )\nonumber \\{} & {} -\frac{1}{6}x^2(x-1)+\frac{11}{72}+\frac{1}{3x}. \end{aligned}$$
(4.33)

The Znajek conditions give

$$\begin{aligned} I^{(3,0)}= & {} -2\pi \psi _0\sin ^2\theta \left[ \Omega ^{(3,0)}+2\Omega ^{(1,0)}\varphi (x)\right] \nonumber \\ \Omega ^{(3,0)}= & {} \frac{1}{32M}+\frac{67-6\pi ^2}{1152M}\sin ^2\theta . \end{aligned}$$
(4.34)

These are just the second relative order results in GR [4, 10].

$$\begin{aligned} \underline{Contribution~from~cubic~term:}\, \underline{\mathcal {O}(\zeta ^1\chi ^2)} \end{aligned}$$

At order \(\mathcal {O}(\zeta ^1\chi ^2)\), the stream equation is

$$\begin{aligned} L\psi ^{(2,1)}=-\psi _0s(x)\cos \theta \sin ^2\theta \,, \end{aligned}$$
(4.35)

where s(x) is given by (B.48) in appendix B. Similarly the general solution of \(\psi ^{(2,1)}\) takes the form

$$\begin{aligned} \psi ^{(2,1)}=\psi _0\varphi _\zeta (x)\cos \theta \sin ^2\theta \,, \end{aligned}$$
(4.36)

and \(\varphi _\zeta (x)\) is determined by the equation

$$\begin{aligned} \frac{d}{dx}\left( \Big (1-\frac{2}{x}\Big )\varphi _\zeta '(x)\right) -\frac{6\varphi _\zeta (x)}{x^2}+s(x)=0\,, \end{aligned}$$
(4.37)

whose solution satisfying the boundary conditions (2.5) is given by (B.49) in appendix B. The Znajek conditions give

$$\begin{aligned} I^{(3,1)}= & {} -2\pi \psi _0\sin ^2\theta \Big [\Omega ^{(3,1)}+2\Omega ^{(1,0)}\varphi _\zeta \cos ^2\theta \nonumber \\{} & {} +2\Omega ^{(1,1)}\varphi \cos ^2\theta \Big ],\nonumber \\ \Omega ^{(3,1)}= & {} \frac{7}{128M}+\frac{120543743-9101400 \pi ^2 }{129024000 M}\sin ^2\theta .\nonumber \\ \end{aligned}$$
(4.38)

5 The power of energy extraction

Up to second relative order in spin, the power of energy extraction can be obtained by (2.7)

$$\begin{aligned} P= & {} \left[ \frac{\pi }{24}+\frac{35\pi }{96}\zeta \right] \frac{\psi _0^2\chi ^2}{M^2}\nonumber \\{} & {} +\left[ \frac{\pi \left( 56-3\pi ^2\right) }{1080} +\frac{\pi \left( 61414581-4013800\pi ^2\right) }{80640000}\zeta \right] \nonumber \\{} & {} \frac{\psi _0^2\chi ^4}{M^2}. \end{aligned}$$
(5.39)

In order to discuss our result, we arrange the horizon angular velocity in the same relative order

$$\begin{aligned} \Omega _H=\left[ \frac{1}{4}+\frac{35}{32}\zeta \right] \frac{\chi }{M}+\left[ \frac{1}{16}+\frac{7}{64}\zeta \right] \frac{\chi ^3}{M}+\mathcal {O}(\zeta ^2,\chi ^5),\nonumber \\ \end{aligned}$$
(5.40)

and the angular velocity of the magnetic field lines

$$\begin{aligned} \Omega= & {} \left[ \frac{1}{8}+\frac{35}{64}\zeta \right] \frac{\chi }{M}+\left[ \frac{1}{32}+\frac{7}{128}\zeta +\left( \frac{67-6\pi ^2}{1152}\right. \right. \nonumber \\{} & {} \left. \left. +\frac{120543743-9101400 \pi ^2 }{129024000}\zeta \right) \sin ^2\theta \right] \frac{\chi ^3}{M}. \end{aligned}$$
(5.41)

The leading BZ power correction with respect to GR is

$$\begin{aligned} \frac{P_\textrm{ECG}-P_\textrm{GR}}{P_\textrm{GR}}\approx 27.5\zeta \,. \end{aligned}$$
(5.42)

For given mass of BH M and magnetic flux \(\psi _0\), our result shows that the BZ power is dependent on two parameters: the coupling constant \(\zeta \) and the spin of BH \(\chi \). So if we have independent and high quality measurements of the jet power and the spin of BH, we can distinguish GR from other theories of gravity by fitting data in principle. However even within GR, a clear observational signature of the BZ mechanism is still missing. Analytical calculation and numerical simulations show that for general rotating BH the maximum rate of energy extraction is achieved when \(\Omega ={\textstyle {\frac{\scriptstyle 1}{\scriptstyle 2} } }\Omega _H\), and takes the form

$$\begin{aligned} P=k\Omega _H^2\Phi _\textrm{BH}^2\,, \end{aligned}$$
(5.43)

where \(k=1/6\pi \) for a split monopole field profile and \(k = 0.044\) for a paraboloidal profile, and \(\Phi _\textrm{BH}\) is the total magnetic flux through the BH horizon. Numerical simulations show that this result is accurate even for large spins up to \(\chi \lesssim 0.95\) for Kerr black hole [5, 14]. It is easy to check that this general character of BZ process still holds at leading order in spin for ECG, i.e.

$$\begin{aligned} \Omega= & {} {\frac{1}{2}}\Omega _H+\mathcal {O}(\zeta ^2,\chi ^3),\nonumber \\ P= & {} \frac{1}{6\pi }\Omega _H^2\Phi _\textrm{BH}^2+\mathcal {O}(\zeta ^2,\chi ^4), \end{aligned}$$
(5.44)

where \(\Phi _\textrm{BH}=2\pi \psi _0\). Since P is a function which only depends on \(\Omega _H\) at leading order in spin, the two parameters \(\zeta \) and \(\chi \) are degenerate to this order. This implies that we will not be able to determine both the coupling constant \(\zeta \) and the spin of BH \(\chi \) even if both the BZ power P and the horizon angular velocity \(\Omega _H\) are measured. However this degeneracy breaks when higher orders in spin are considered. We can see this by rewriting the BZ power as

$$\begin{aligned} P=\frac{1}{6\pi }\frac{\Phi ^2}{M^2}[(M\Omega _H)^2+(\alpha +\beta \zeta )(M\Omega _H)^4]+\mathcal {O}(\zeta ^2,\chi ^6)\,, \end{aligned}$$
(5.45)

where

$$\begin{aligned} \alpha= & {} \frac{8(67-6\pi ^2)}{45}\approx 1.38,\nonumber \\ \beta= & {} \frac{22053743}{630000}-\frac{67 \pi ^2}{150}\approx 30.60. \end{aligned}$$
(5.46)

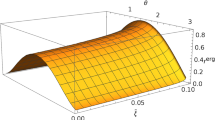
When \(\zeta =0\), we recover the GR result which is accurate for large spins up to \(\chi \lesssim 0.99\) for Kerr black hole [5, 14]. However, at even high spins, \(\chi \gtrsim 0.99\), the authors of Ref. [5] have shown that the expression for the power should be corrected with a further \(\Omega _H^6\) term, which they determined numerically. Recently analytical studies show that the horizon angular velocity dependence in the BZ power is far richer and can also contain odd powers and logarithms [10, 11]. These can help extend our work to near-extreme regime which should exist obvious difference compared to GR. We can see from Fig. 1 that though the spacetime geometry is modified by the cubic interactions, the BZ power has uniform feature with respect to the horizon angular velocity when the BH spin is small. With the increase of BH spin, the relation between the BZ power and horizon angular velocity deviates from the one in GR gradually.

Fig. 1
figure 1

The plot of BZ power as a function of the horizon angular velocity for a split monopole field profile

Full size image

6 Conclusion

The BZ process can be viewed as a magnetic version of Penrose process, whose primary mechanism is frame dragging due to the rotation of BH [31, 32] (see detail discussions on the motion of charged particle around a magnetized Kerr BH in [33, 34]). In general, a magnetic version of Penrose process depend both on the spacetime geometry and the magnetic field configuration. Since the rest-mass density of plasma is many orders of magnitude lower than the electromagnetic field energy density, we can neglect the energy and momentum transfer between magnetic field and accretion disk (see also Refs. [35, 36] in which the interaction between magnetic field and accretion disk was taken into account). Thus in the BZ process, we can determine the magnetosphere around the BH based on solving the force-free electrodynamics under reasonable boundary conditions. Theoretical analysis and numerical simulations of this model in Kerr BH indicate that the power of outflowing jet depends on both the angular velocity of BH horizon \(\Omega _\textrm{H}\) and the amount of magnetic flux threading the BH horizon \(\Phi _\textrm{BH}\), with jet power \(\propto \Omega _\textrm{H}^2\Phi _\textrm{BH}^2\).The Event Horizon Telescope (EHT) observation of M87\(^*\), especially the polarization data favors this model strongly [37, 38].

In this paper, we study the BZ process in the framework of ECG. As expected, the BZ power is modified by the coupling constant of higher curvature terms \(\zeta \). However testing this result with jet power is extremely challenging, even though the BZ mechanism is well understood, since we need so many data to be measured independently, especially the BH spin \(\chi \). In fact our result show that the BH spin \(\chi \) and coupling constant \(\zeta \) are degenerate in the BZ power at leading order in spin. The degeneracies between the astrophysical or theory-dependent parameter and BH spin are common for slow rotating BH. However, in ECG and quadratic gravities, this degeneracy breaks down at higher orders in spin. To summarize, the feature of BZ power in higher derivative gravities deviate from the one in GR for BH with large spin. Consequently, we expect that it is possible to distinguish GR from higher derivative gravities using jet power with rapidly rotating BH.