The b quark fragmentation fractions at LHCb and meson decays with heavy quark spectators

Abstract

We study the current estimates of $B_c\rightarrow B_s \pi$ to extract the fragmentation fraction $f_c/f_s$ at the LHCb. A rather robust estimate of $Br(B_c\rightarrow B_s \pi )$ based on factorization and lattice results for the form factor gives $f_c/f_s \sim 0.056$ with a 16% error. We also revisit the extraction of $f_s/f_d$ using $B\rightarrow D\pi$ instead of the theoretical cleaner but more suppressed channel $B\rightarrow DK$. We also find a tension on the predictions of $Br(B_c\rightarrow J/\psi \pi )$ and $Br(B_c\rightarrow B_s\pi )$ considering the measurements of these modes at LHCb, and find that, within a 23% uncertainty, only the lower end of the current prediction range $Br(B_c\rightarrow J/\psi )\sim 0.4\% - 1.7\%$ would be consistent with the LHCb measurements.

1 Introduction

The heavy meson decay $B_c\rightarrow B_s \pi$ is a remarkable case of a decay of a heavy meson where the heavy quark is a spectator of the weak interaction process, in contrast to the much studied transitions such as $B\rightarrow D$, where it is the heavy quark that decays and the light degrees of freedom act as spectators. The latter case has been extensively studied, giving birth to the systematic treatment called heavy quark effective theory (HQET), which is a expansion in operators with coefficients in powers of $\Lambda _{QCD}/m_b$ and $\Lambda _{QCD}/m_c$ [1,2,3]. As such, in the infinite mass limit, the results are relatively simple [4,5,6]. For example, for a transition $B\rightarrow D \ell \nu$ at the kinematic point where B and D are at relative rest (the so-called zero recoil point), the wave functions of the two heavy mesons should be the same and the overlap of the form factors should be equivalent to their normalization (in the appropriate normalization, this means the form factor should be unity). In contrast, here we are interested in transitions such as $B_c\rightarrow B_s$, where the heavy (or better said the heaviest) quark is the spectator and the weak transition occurs in the lighter degrees of freedom. Now the wavefunctions will not coincide, not even at zero recoil, so there is no a priori known value for the form factor at any kinematic point. These decays, where the heavy quark is a spectator, therefore offer new information for hadron structure and bound states under the strong interactions. To have an intuitive picture let us consider the heavy meson as a bound state of two constituent quarks. The Bohr radius of the wavefunction goes as the inverse of the reduced mass. In decays such as $B\rightarrow D \ell \nu$, in the limit $m_b, m_c\rightarrow \infty$ the reduced mass is the same in both mesons, so one expects that the form factor at zero recoil, which is the overlap of the B and D wavefunctions, should be the same as their normalization (i.e. the form factor goes to a known value, usually taken as unity). However in $B_c\rightarrow B_s$ transitions the $B_c$ and $B_s$ reduced masses and Bohr radii are different, so the form factor at zero recoil is not a fixed norm but depends on the bound state dynamics. The first measurement (and so far the only one) of a $B_c \rightarrow B_s$ transition was done by LHCb [7] in the two-body decay $B_c^+\rightarrow B_s \pi ^+$, however the result on this branching ratio comes combined with the ratio of the fragmentation fractions of the b quarks produced in the pp collisions into the different B mesons, in this case $\sigma (B_c)/\sigma (B_s) \equiv f_c/f_s$. It is therefore necessary to have an independent estimate of either the branching ratio or of $f_c/f_s$, in order to extract a value for the other. In Ref. [7] the authors exemplify the use of independent $f_c/f_s$ estimates to determine the $B_c\rightarrow B_s\pi$ branching ratio. Here we will take the opposite avenue, namely to use the best theoretical estimate we find for the branching ratio, which is based on current lattice results for the form factors [8], in order to extract the value of $f_c/f_s$ from the LHCb measurement. Using this estimate for $f_c/f_s$ we then obtain estimates for other $B_c$ branching ratios such as $B( B_c^+ \rightarrow J/\psi \pi ^+)$, which in Ref. [7] was used as an input.

Concerning the b fragmentation fractions at LHCb, another important ratio is $f_s/f_d$. This ratio was estimated earlier at LHCb, using the decays $B_s\rightarrow D_s^- \pi ^+$ and $B^0\rightarrow D^-K^+$ [9], and more recently doing a global fit using several other decays [10], thus reducing the uncertainty. In the former study, the reason for using $B\rightarrow D K$ instead of the more numerous $B\rightarrow D\pi$ was that its theoretical calculation contains an additional amplitude that is more difficult to estimate. Here we revisit these estimates using updated B meson branching ratios as well as more recent lattice results for the relevant form factors. In Sect. 2 we address the analysis of $f_c/f_s$ and $B_c\rightarrow B_s$ transitions. In Sect. 3 we revisit the estimates and uncertainties of $f_s/f_d$ and the non-factorizable amplitude of $B\rightarrow D\pi$. In Sect. 4 we revisit $Br(B_c\rightarrow J/\psi \, \pi ^+)$ and the extraction of $f_c/f_d$. Our conclusions are in Sect. 5.

2 $B_c\rightarrow B_s$ transitions and $f_c/f_s$

The decay $B_c\rightarrow B_s\pi$ was observed at LHCb [7] and its branching ratio was determined up to the factor $f_c/f_s$:

$$\begin{aligned}{} & {} \frac{f_c}{f_s} \times Br(B_c^+\rightarrow B_s \pi ^+) \nonumber \\{} & {} \quad = (2.37 \pm 0.31 \pm 0.11 {}^{+0.17}_{-0.13})\times 10^{-3}. \end{aligned}$$

(1)

Here $f_c$ and $f_s$ are the fragmentation fractions, i.e.  the probabilities that a b quark produced in the pp collisions hadronizes into a $B_c$ or a $B_s$ meson, respectively, and Br stands for branching ratio. The ratio $f_c/f_s$ appears because one does not know a priori the number of $B_c$ produced in the collisions, and so the count of $B_c \rightarrow B_s\pi$ events is given relative to the number of $B_s$ produced. Since in that analysis the $B_s$ were identified only by their decays $B_s\rightarrow D_s\pi$ and $B_s\rightarrow J/\psi \,\phi$, then $B_c\rightarrow B_s\pi$ are identified by the events $(D_s\pi )\pi$ and $(J/\psi \ \phi )\pi$, where the pair reconstructs the ${B_s}$ mass and the pair plus the bachelor pion reconstructs the $B_c$ mass. One can understand Eq. (1) by first denoting $B_s\rightarrow D_s \pi$ and $B_s\rightarrow J/\psi \phi$ generically as $B_s\rightarrow X$; then the number of observed events $B_c\rightarrow X \pi$, where X reconstructs the $B_s$ mass, can be expressed as:

$$\begin{aligned} n(B_c\rightarrow X\pi ) = N_b\cdot f_c \cdot Br(B_c\rightarrow B_s \pi ) \cdot Br(B_s\rightarrow X) \end{aligned}$$

where $N_b$ is the number of b quarks produced in the pp collisions and $N_b\cdot f_c$ – an unknown – is the total number of $B_c$ produced. In the same way, the total number of observed $B_s\rightarrow X$ events (regardless whether $B_s$ comes from a $B_c$ decay or not) is:

$$\begin{aligned} n(B_s\rightarrow X) = N_b\cdot f_s \cdot Br(B_s\rightarrow X). \end{aligned}$$

Dividing these two expressions one obtains Eq. (1), where the ratio of counts $n(B_c\rightarrow X \pi )/n(B_s \rightarrow X)$ is the result on the right hand side, measured by LHCb [7].

In order to separate $Br(B_c\rightarrow B_s\pi )$ from $f_c/f_s$ in Eq. (1), one needs an independent input. In Ref. [7] this was done by separately estimating $f_c/f_s$, expressing it as:

$$\begin{aligned} \frac{f_c}{f_s} = \frac{f_c/f_d}{f_s/f_d}, \end{aligned}$$

where the denominator was previously given in Ref. [9] as $f_s/f_d = 0.256 \pm 0.020$, and the numerator $f_c/f_d$ was extracted from a previous LHCb result [11]:

$$\begin{aligned}{} & {} \frac{f_c}{f_d} \times \frac{Br(B_c\rightarrow J/\psi \,\pi )}{Br(B\rightarrow J/\psi \, K)} \nonumber \\{} & {} \qquad = \left( 0.68 \pm 0.10\pm 0.03 \pm 0.05 \right) \%. \end{aligned}$$

(2)

While $Br(B\rightarrow J/\psi \,K) = \left( 1.016 \pm 0.033\right) \times 10^{-3}$ has been measured [12], for $Br(B_c\rightarrow J/\psi \,\pi ) \sim 0.06\% \rightarrow 0.18\%$ these are only theoretical estimates [13]. The latter clearly brought the largest uncertainty, while the next largest uncertainties are $\pm 17\%$ in Eq. (2), $\pm 15\%$ in Eq. (1) and $\pm 7.8\%$ in $f_s/f_d$ according to Ref. [9]. Consequently the extracted $Br(B_c \rightarrow B_s \pi )$ from this method reproduces the large uncertainty present in $Br(B_c\rightarrow J/\psi \, \pi )$:

$$\begin{aligned} Br(B_c\rightarrow B_s\pi ) \sim 5\% \rightarrow 15\%, \end{aligned}$$

(3)

and similar uncertainties were then obtained for $f_c/f_s \sim 1.6\% \rightarrow 4.6\%$ and $f_c/f_d \sim 0.4\% \rightarrow 1.2\%$.

Here we take the opposite avenue, namely to start from current lattice estimates for the relevant form factor of $Br(B_c\rightarrow B_s\pi )$ [8] to derive the value of $f_c/f_s$ from Eq. (1).

The expression for the amplitude of $B^+_c \rightarrow B^0_s\pi ^+$, assuming factorization, is [14],

$$\begin{aligned}{} & {} {\mathcal {M}} (B_c^+\rightarrow B_s \pi ^+) \nonumber \\{} & {} \qquad = \frac{G_F}{\sqrt{2}} V_{cs}V^*_{ud}\ a_1 \, \left<\pi ^+|({\bar{u}} d)|0\right> \left<B_s|({\bar{s}} c)|B_c\right>, \end{aligned}$$

(4)

where $({\bar{u}} d)$ and (${\bar{s}} c)$ denote $V-A$ color singlet currents. Within this assumption the matrix element of the 4-quark operator is separated into a product of current matrix elements. Non-factorizable contributions, where gluons are exchanged between these currents, are neglected (for more details see Sect. 3).

Moreover, $a_1$ is the corresponding combination of Wilson coefficients at the renormalization scale of B mesons, $\mu \sim m_b$ [15]. In Ref. [15], a value $a_1 \simeq 1.02 \pm 0.01$ is estimated, but one can find other estimates as well, which depend also on the flavor transition. Larger values at the B scale have also been used, e.g. $a_1 = 1.14$ [13, 16, 17], or even $a_1 = 1.26$ [18]. Several authors have used a value $a_1 \simeq 1.2$ for transitions $c\rightarrow s$ in beauty meson decays such as $B_c \rightarrow B_s \pi$, and a value $a_1 \simeq 1.14$ for transitions $b\rightarrow c$ such as $B_c \rightarrow J/\psi \pi$ [13, 14, 16,17,18,19,20,21,22]. Since $a_1$ is a combination of Wilson coefficients that integrate QCD corrections from the electroweak scale $M_W$ down to $\mu \sim m_b$, its estimates can be done systematically. In a detailed work that includes next-to-leading-order (NLO) calculations the authors of Ref. [23] find $a_1 \simeq 1.05$ with a $2\%$ uncertainty by varying the scale $\mu \sim m_b/2 \rightarrow 2 m_b$. A more recent result at NNLO can be found in Ref. [24] where $a_1=1.070_{-0.013}^{+0.010}$ is obtained for ${\overline{B}}_d\rightarrow D^+K^-$ and very similar results for other final state mesons; here the quoted errors include the uncertainties from the variation of the scale $\mu$ of the Wilson coefficients, quark masses, Gegenbauer moments of the light meson wave functions, and the strong coupling $\alpha _s(m_Z)$ [24]. In order to separate the uncertainties in B meson decays coming from $a_1$, wherever possible we will cite the results on theoretical branching ratios with $a_1$ exhibited as an explicit factor (see Tables I and II).

In Eq. (4) the first matrix element involves the pion decay constant $f_\pi$ and the pion momentum $q_\mu$:

$$\begin{aligned} \left<\pi ^+|({\bar{u}} d)|0\right> = if_\pi q_\mu . \end{aligned}$$

(5)

The second matrix element involves two form factors [8]:

$$\begin{aligned}{} & {} \left<B_s(p_2)|({\bar{s}} c)|B_c(p_1)\right>\nonumber \\{} & {} \quad = f_0(q^2) \left( \frac{m_{B_c}^2 - m_{B_s}^2}{q^2} q^\mu \right) \nonumber \\{} & {} \qquad + f_+(q^2) \left( p_1^\mu + p_2^\mu - \frac{m_{B_c}^2 - m_{B_s}^2}{q^2} q^\mu \right) . \end{aligned}$$

(6)

The term with $f_+(q^2)$ vanishes when contracted with $q^\mu$, so we only need the longitudinal form factor $f_0(q^2)$ at $q^2 = m_\pi ^2$:

$$\begin{aligned} {\mathcal {M}} (B_c^+\rightarrow B_s \pi ^+)= & {} i \frac{G_F}{\sqrt{2}} V_{cs}V^*_{ud}\ a_1\ f_\pi \ f_0(m_\pi ^2 ) \nonumber \\{} & {} \times \left( m_{B_c}^2 - m_{B_s}^2 \right) . \end{aligned}$$

(7)

The value of the form factor according to lattice fits in the physical-continuum limit is [8]:

$$\begin{aligned} f_0(m_\pi ^2) = 0.624 \pm 0.011. \end{aligned}$$

(8)

It is now straightforward to obtain the decay rate:

$$\begin{aligned} \Gamma ( B_c^+ \rightarrow B_s \pi ^+) = \frac{p_{CM}}{8\pi m_{B_c}^2} |{{\mathcal {M}}}|^2, \end{aligned}$$

(9)

where $p_{CM} =\sqrt{(m_{B_c}^2 - m_{B_s}^2 + m_\pi ^2)^2 - 4 m_{B_c}^2 m_\pi ^2}/(2 m_{B_c}) \simeq 831.84 \,\text{ MeV }$ is the 3-momentum of the final state mesons in the CM frame. Here we use $m_{B_c} = 6,274.47\pm 0.32$ MeV, $m_{B_s} = 5,366.92\pm 0.10$ MeV, $m_\pi = 139.57039$ MeV, $V_{ud} = 0.97373 \pm 0.00031$, $V_{cs}= 0.975 \pm 0.006$, $f_\pi = 130.2 \pm 1.2$ MeV. To obtain the branching ratio we use the experimental value of the width $\Gamma (B_c) \simeq (1.291 \pm 0.023) \times 10^{-3}\,\text{ eV }$.

The prediction for the branching ratio using the data above is then:

$$\begin{aligned} Br(B_c^+\rightarrow B_s \pi ^+) = (2.942 \pm 0.104)\times 10^{-2}\ a_1^2. \end{aligned}$$

(10)

The uncertainty in this branching ratio is dominated by $f_0^2(m_\pi ^2)$ [see Eq. (8)] which is near $3.5\%$. We have left out the factor $a_1^2$ as explained above, as it is usually done in the literature. Besides $a_1$, there is the uncertainty of neglecting non-factorizable contributions, but these are not expected to be large for a decay such as $B_c\rightarrow B_s\pi ^+$, a Class 1 decay [14, 15], where only a charged meson with large momentum –in this case $\pi ^+$– is generated directly from the color-singlet current.

Table 1 Predictions for the branching ratio $Br(B_c\rightarrow B_s\pi )$ from different authors. The values listed are the partial widths extracted from their respective cited article divided by the full width also cited therein. The last line is our calculation based on the lattice result for the form factor as explained in the text

Our result in Eq. (10) for $Br(B_c^+\rightarrow B_s \pi ^+)$ is quite similar to several of the other theoretical predictions shown in Table 1, and almost all of them are lower than the LHCb estimate of Eq. (3) based on the theoretical predictions for $Br(B_c^+\rightarrow J/\psi \, \pi ^+)$. Therefore the LHCb results shown in Eqs. (1) and (2) reveal a tension in the theoretical predictions of $Br(B_c^+\rightarrow J/\psi \, \pi ^+)$ and $Br(B_c^+\rightarrow B_s \pi ^+)$. If we trust the result of Eq. (10) and most predictions in Table 1 for $Br(B_c^+\rightarrow B_s \pi ^+)$, we conclude that the actual value of $Br(B_c^+\rightarrow J/\psi \, \pi ^+)$ should be smaller than the lowest estimate $\sim 0.06\%$ considered in Ref. [7].

We will review the branching ratio $Br(B_c^+\rightarrow J/\psi \, \pi ^+)$ in Sect. 4. In the present section we focus on obtaining $f_c/f_s$ based on the theoretical estimate for $Br(B_c^+\rightarrow B_s \pi ^+)$ in Eq. (10), and the LHCb measurement [7] shown in Eq. (1). A straightforward calculation gives the result:

$$\begin{aligned} \frac{f_c}{f_s} = \left( 8.06 \pm 1.22\pm 0.28\right) \times 10^{-2}\,a_1^{-2}, \end{aligned}$$

(11)

where $a_1 \simeq 1.2$ is the accepted value for $c\rightarrow s$ transitions [13, 14, 16,17,18,19,20,21,22]. The first uncertainty is from the LHCb measurement [7] shown in Eq.  (1), which is about $\sim 15\%$, and the second uncertainty is from the lattice estimate of the form factor [8], which is near $3.5\%$. Clearly the first uncertainty dominates. In the next section we examine $f_s/f_d$.

3 On $f_s/f_d$ and $B_s \rightarrow D_s$ transitions

Concerning the determination of the ratio of fragmentation fractions $f_s/f_d$, LHCb has first used $B_s\rightarrow D_s\pi$ vs. $B\rightarrow D K$ in pp collisions at 7 TeV [9], and lately [10] used several non-leptonic and semileptonic decays of $B_s$ and B at 7, 8 and 13 TeV [9, 26,27,28,29]. In their first study, a ratio of events analogous to Eq. (2) was obtained:

$$\begin{aligned} \frac{f_s}{f_d} \times \frac{Br(B_s \rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^-K^+)} \ =\ \frac{n_{cor}(B_s\rightarrow D_s\pi )}{n_{cor}(B^0\rightarrow DK)}, \end{aligned}$$

(12)

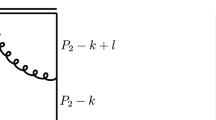
where we have denoted $n_{cor}(B_s \rightarrow D_s\pi )$ the efficiency-corrected number of $B_s\rightarrow D_s\pi$ events and a similar definition for $n_{cor}(B^0\rightarrow DK)$. To extract $f_s/f_d$ from Eq. (12) one needs independent estimates of the branching ratios. For that purpose, Ref. [9] uses the theoretical expressions based on factorization, where the main theoretical uncertainties are (i) the ratio of the form factors in $\langle D_s|J^\mu |B_s\rangle$ and $\langle D^-|J^\mu |B^0\rangle$, and (ii) the neglect of nonfactorizable contributions. Moreover, they use $B^0\rightarrow D^-K^+$ instead of the more abundant mode $B^0 \rightarrow D^-\pi ^+$ precisely because the latter mode has an additional diagram with an internal W exchange, as shown in Fig. 1, for which factorization may not be a good approximation [30].

Fig. 1

Tree level diagrams for $B^0\rightarrow D^-\pi ^+$: a color-allowed, dominant diagram; b color-suppressed, internal W-exchange diagram

Here we consider two other options in this analysis: on the one hand, today we have good experimental data for $B^0\rightarrow D^-\pi ^+$ and $B^0\rightarrow D^- K^+$ so we may try to use the $B^0 \rightarrow D^-\pi ^+$ data instead of the theoretical estimates to extract $f_s/f_d$ from the result in Eq. (12), provided we have good theoretical estimates for $Br(B_s\rightarrow D_s^-\pi ^+)$ on the numerator. On the other hand, there are theoretical estimates for the subdominant diagram of $B^0\rightarrow D^-\pi ^+$ (see Fig. 1), so we can verify the uncertainty they bring to the determination of $f_s/f_d$.

The tree level amplitude for $B_s\rightarrow D^-_s\pi ^+$ has a similar diagram as $B_c\rightarrow B_s\pi ^+$ (see Fig. 2) and therefore a similar expression as Eq. (7):

$$\begin{aligned}{} & {} {\mathcal {M}} (B_s\rightarrow D_s^- \pi ^+) = i \frac{G_F}{\sqrt{2}} V_{cb}^*V_{ud}\ a_1\ \nonumber \\{} & {} \quad f_\pi \ f_0^{(s)}(m_\pi ^2 ) \left( m_{B_s}^2 - m_{D_s}^2 \right) , \end{aligned}$$

(13)

but the form factor $f_0^{(s)}(q^2)$ corresponds to the current matrix element $\langle D_s |({\bar{b}} c)|B_s\rangle$. Similarly the tree level amplitude for $B^0\rightarrow D^-K^+$ is:

$$\begin{aligned}{} & {} {\mathcal {M}} (B^0\rightarrow D^- K^+) = i \frac{G_F}{\sqrt{2}} V_{cb}^*V_{us}\ a_1\ \nonumber \\{} & {} \quad f_K\ f_0^{(d)}(m_K^2 ) \left( m_{B}^2 - m_{D}^2 \right) , \end{aligned}$$

(14)

with the form factor $f^{(d)}_0(q^2)$ corresponding to $\langle D |({\bar{b}} c)|B\rangle$.

Fig. 2

Tree level diagrams for a $B_c^+\rightarrow B_s\pi ^+$, b $B_s\rightarrow D_s^- \pi ^+$ and c $B^0\rightarrow D^-K^+$. All of them are color allowed diagrams in the factorization hypothesis

Let us make a brief parenthesis here to review the significance of non factorizable contributions. All of these two-body nonleptonic weak decays can be treated by means of a low-energy effective weak interaction hamiltonian [15], which at leading order contains two 4-quark operators, $O_1$ and $O_2$, both products of two $V-A$ color singlet currents, the former a product of charged currents and the latter of neutral currents. As an example, the effective interaction hamiltonian for the decay $B_s\rightarrow D_s^-\pi ^+$ is:

$$\begin{aligned} {{\mathcal {H}}}_{eff} = \frac{G_F}{\sqrt{2}}V_{ud} V^*_{cb} \Big \{ C_1(\mu )\ O_1 + C_2(\mu )\ O_2 \Big \}, \end{aligned}$$

where $O_1 \equiv ( {\bar{u}} d) ({\bar{b}} c)$ and $O_2 \equiv ({\bar{u}} c) ({\bar{b}} d)$ (factors in parenthesis represent color-singlet $V-A$ currents). $C_i(\mu )$ are Wilson coefficients at the renormalization scale $\mu \sim m_b$. The matrix elements of these 4-quark operators, $\langle D_s^-\pi ^+|O_1|B_s\rangle$ and $\langle D_s^-\pi ^+|O_2|B_s\rangle$, are difficult to calculate because of the strong interactions. Factorization is the assumption that these matrix elements can be separated as the product of current matrix elements. Looking at the flavor content of the mesons, the first matrix element could be approximated as:

$$\begin{aligned} \langle D_s^-\pi ^+|O_1|B_s\rangle \rightarrow \langle \pi ^+|( {\bar{u}} d)|0\rangle \ \langle D_s^-|({\bar{b}} c) |B_s\rangle \ \equiv \langle O_1\rangle _F. \nonumber \\ \end{aligned}$$

(15)

Since the currents are color singlets, this is expected to be a good approximation. Instead, the matrix element of $O_2$ requires a Fierz rearrangement, causing a color-suppressed factorized term and a non factorizable one:

$$\begin{aligned} \langle D_s^-\pi ^+|O_2|B_s\rangle \&\rightarrow \frac{1}{N_c} \langle \pi ^+|( {\bar{u}} d)|0\rangle \ \langle D_s^-|({\bar{b}} c) |B_s\rangle \nonumber \\&\qquad + 2 \ \langle D_s^- \pi ^+|( {\bar{u}}\, t^a \, d)({\bar{b}} \, t^a\, c) |B_s\rangle \nonumber \\&= \frac{1}{N_c} \langle O_1\rangle _F \quad + \quad nonfact. \end{aligned}$$

(16)

Notice that, in this case, the factorized matrix element is still $\langle O_1\rangle _F$. This is the case for all three processes shown in Fig. 2, where only one diagram enters. As a result, the whole amplitude within factorization contains only $\langle O_1\rangle _F$:

$$\begin{aligned}{} & {} \langle D_s^- \pi ^+ |{{\mathcal {H}}}_{eff} | B_s\rangle = \frac{G_F}{\sqrt{2}} V_{ud} V_{cb}^* \nonumber \\{} & {} \quad \times \Big ( \ a_1 \ \langle O_1\rangle _F + C_2(m_b) \times nonfact \ \Big ) \quad \equiv \ T, \end{aligned}$$

(17)

where $a_1 = C_1(\mu ) + \frac{C_2(\mu )}{N_c}.$ Since $C_1 =1$ and $C_2=0$ at the fundamental (electroweak) scale, $C_2(m_b)$ is small and therefore the non-factorizable term is expected to be relatively small. On the right hand side, we follow the notation of Ref. [31] and refer to this colored-allowed amplitude as T. In contrast, $B^0\rightarrow D^-\pi ^+$ (Fig. 1) has two diagrams: one of type T, dominant and similar to the case above, and the other, called E, the internal W exchange, which is subdominant but contains relatively larger non-factorizable contributions. The presence of two diagrams corresponds to the two different contractions of the operators $O_1$ and $O_2$ for this process. Using a definition for the factorized matrix element $\langle D^-\pi ^+|( {\bar{u}} c)|0\rangle \langle 0|({\bar{b}} d) |B\rangle \equiv \langle O_2\rangle _F$, analogous to that of $\langle O_1\rangle _F$ in Eq. (15), one can see that, for this process:

$$\begin{aligned} \langle D^-\pi ^+|O_1|B^0\rangle \ = \langle O_1\rangle _F + \frac{1}{N_c} \langle O_2 \rangle _F + nonfact. \end{aligned}$$

and

$$\begin{aligned} \langle D^-\pi ^+|O_2|B^0\rangle \ = \langle O_2\rangle _F + \frac{1}{N_c} \langle O_1\rangle _F + nonfact. \end{aligned}$$

Thus the $\langle O_2\rangle _F$ terms add up to a second amplitude, called E [31]:

$$\begin{aligned}{} & {} E \ \equiv \langle D^- \pi ^+ |{{\mathcal {H}}}_{eff} | B^0\rangle _E\nonumber \\{} & {} \quad \rightarrow \ \frac{G_F}{\sqrt{2}} V_{ud} V_{cb}^* \Big (\ a_2 \ \langle O_2\rangle _F + C_1(m_b)\times nonfact \ \Big ) \nonumber \\{} & {} \quad \equiv E_{fact} + E_{nonfact}. \end{aligned}$$

(18)

where $a_2 = C_2(\mu ) + \frac{C_1(\mu )}{N_c}.$ Here the non factorizable part is not suppressed relative to the term containing $\langle O_2\rangle _F$. Because of this uncertainty, the mode $B\rightarrow DK$ was preferred instead of $B\rightarrow D\pi$.

Now, the determination of $f_s/f_d$ using the method of Eq. (12) requires a theoretical expression for $B_s\rightarrow D_s\pi$, since there is no other independent measurement of this rate. Using $B\rightarrow DK$ instead of $B\rightarrow D\pi$ in the denominator has the advantage that the theoretical expression for it is similar and several factors tend to cancel, except for the form factors and uncertainties due to the non-factorizable contributions. The non-factorizable contributions are expected to be smaller in $B\rightarrow DK$ than in $B\rightarrow D\pi$, so $B\rightarrow DK$ was preferred even when the number of events of that mode is smaller. Using Eqs. (9), (13) and (14), one obtains:

$$\begin{aligned}{} & {} \frac{Br(B_s\rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^- K^+)} \nonumber \\{} & {} \quad =\Phi _{sK} \frac{\tau _{B_s}}{\tau _{B^0}} \left| \frac{V_{ud}}{V_{us}} \right| ^2\left( \frac{f_\pi }{f_K}\right) ^2 \times {{\mathcal {N}}}_F^{(K)} \times {{\mathcal {N}}}_a. \end{aligned}$$

(19)

Here $\Phi _{sK}$ is a kinematic factor:

$$\begin{aligned} \Phi _{sK} = \left( \frac{m_{Bs}^2 - m_{D_s}^2}{m_{B^0}^2 - m_{D^-}^2}\right) ^2 \left( \frac{m_{B^0}}{m_{B_s}}\right) ^2 \frac{p_{CM}^{(s)}}{p_{CM}^{(K)}} \quad \simeq 1.0302, \end{aligned}$$

where $p_{CM}^{(s)} \simeq 2.3201$ GeV and $p_{CM}^{(K)} \simeq 2.27901$ GeV are the CM 3-momenta of the final particles in the corresponding decays. The factor ${{\mathcal {N}}}_F^{(K)}$ is the ratio of form factors at the corresponding kinematic points:

$$\begin{aligned} {{\mathcal {N}}}_F^{(K)} = \left( \frac{f_0^{(s)}(m_\pi ^2)}{f_0^{(d)}(m_K^2)}\right) ^2, \end{aligned}$$

while ${{\mathcal {N}}}_a$ is the ratio of non-factorizable corrections. ${{\mathcal {N}}}_F^{(K)}$ and ${{\mathcal {N}}}_a$ are the main sources of theoretical uncertainty in Eq. (19).

Now, using $Br(B^0\rightarrow D^-\pi ^+)$ instead of $Br(B^0\rightarrow D^-K^+)$ in the denominator would presumably introduce larger uncertainties from non-factorizable contributions. We could avoid them if we use the experimental result of $B^0\rightarrow D^-\pi ^+$ instead, which will be sensitive to the experimental error only, but then we will need the full theoretical estimate of the numerator, which includes the absolute value of the form factor, not just a ratio of form factors:

$$\begin{aligned}{} & {} \frac{Br(B_s\rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^- \pi ^+)} \nonumber \\{} & {} \quad =\frac{ G_F^2 |V_{cb}V_{ud}|^2 a_1^2 f_\pi ^2 \left[ f_0^{(s)}(m_\pi ^2)\right] ^2 (m_{B_s}^2-m_{D_s}^2)^2 p_{CM}^{(s)}/(16\pi m_{B_s}^2 \Gamma _{B_s})}{Br(B^0 \rightarrow D^-\pi ^+)_{exp}}. \end{aligned}$$

(20)

Currently $Br(B^0 \rightarrow D^-\pi ^+)_{exp} = (2.51 \pm 0.08)\times 10^{-3}$ [32], i.e. it is known with a $3.2\%$ uncertainty. Possibly Belle II may provide a measurement with even better precision in the near future. However the theoretical uncertainty in the numerator of Eq. (20) is presumably larger.

Instead, let us then reevaluate the theoretical uncertainties using $Br(B^0\rightarrow D^-\pi ^+)$. We will again have a cancellation of form factors (possibly better than in Eq. (19) by being both evaluated at the same $q^2$), but we need to assess the E amplitude. Compared to Eq. (19), in this case we have:

$$\begin{aligned} \frac{Br(B_s\rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^- \pi ^+)} = \Phi _{s\pi } \frac{\tau _{B_s}}{\tau _{B^0}} \times {{\mathcal {N}}}_F^{(\pi )}\times {{\mathcal {N}}}_E, \end{aligned}$$

(21)

with the kinematic factor $\Phi _{s\pi } \simeq 1.0179$ (using now $p_{CM}^{(\pi )} \simeq 2306.41$ MeV for $B\rightarrow D\pi$), while the ratio of lifetimes [32] $\tau _{B_s}/\tau _{B^0} = 1.0007 \pm 0.0042$ is known to a precision better than $0.5\%$. The ratio of form factors is now:

$$\begin{aligned} {{\mathcal {N}}}_F^{(\pi )} = \left( \frac{f_0^{(s)}(m_\pi ^2)}{f_0^{(d)}(m_\pi ^2)}\right) ^2, \end{aligned}$$

and ${{\mathcal {N}}}_E$ is the correction to include the internal W-exchange diagram in $B^0\rightarrow D^-\pi ^+$ (see Fig. 1), namely

$$\begin{aligned} {{\mathcal {N}}}_E = \left| \frac{T}{T + E}\right| ^2, \end{aligned}$$

where T and E are the color-allowed and W-exchange amplitudes respectively [Eqs. (17) and (18)] for the decay $B^0\rightarrow D^-\pi ^+$.

For the estimate of ${{\mathcal {N}}}_E$ we will use two theoretical results, which actually differ and therefore give us a caveat about the correct estimate of this factor. Let us first consider Ref. [33], which uses perturbative QCD including Sudakov factors to estimate the amplitudes of two-body non-leptonic $B\rightarrow D^{(*)}\pi (\rho )$ decays. According to these authors, E has comparable factorized and non-factorizable contributions, but both are much smaller than T and mainly imaginary with respect to T: in a normalization relative to $T\equiv 1$, they find $E_{fact}= - 0.018 + 0.057\, i$, $E_{nonfact} = - 0.0011+0.020\, i$, which they add up to $E= -0.019 + 0.077\, i$. Therefore, the estimate of ${{\mathcal {N}}}_E$ that includes only factorizable terms would be ${{\mathcal {N}}}_E^{(fact)} = 1/((1 - 0.018)^2 + (0.057)^2) \simeq 1.034$, while if the non-factorizable estimates are included the result extracted from Ref. [33] is

$$\begin{aligned} {{\mathcal {N}}}_E = \frac{1}{(1-0.019)^2 + (0.077)^2} \simeq 1.033. \end{aligned}$$

We could then use ${{\mathcal {N}}}_E \simeq 1.033$, where the uncertainty due to neglecting the non-factorizable contributions would be well below $1\%$ if those contributions were anything close to the estimated $E_{nonfact}$ [33], and thus negligible compared to other uncertainties in Eq. (21).

Alternatively, let us consider Ref. [23] for the estimation of ${{\mathcal {N}}}_E$. Here the authors study in systematic detail the different corrections for the factorization hypothesis, including those from the internal W-exchange amplitude E (which they call “annihilation amplitude” A), as well as non-factorizable contributions to the dominant amplitude T. For the first correction they obtain $E/T_{lead} \simeq 0.04$ and the latter correction $T_{non.fact}/T_{lead} \simeq -0.03$. Considering all these estimates from Ref. [23], we obtain

$$\begin{aligned} {{\mathcal {N}}}_E =\frac{1-0.03}{1-0.03+0.04} \simeq 0.97, \end{aligned}$$

while disregarding $T_{non.fact}$ the value changes in only $1\%$. However, the discrepancy in this factor extracted from Refs. [23] and [33] is larger. Taking both results as a range with a central value and an uncertainty, we get:

$$\begin{aligned} {{\mathcal {N}}}_E \simeq 1.00 \pm 0.03 \end{aligned}$$

i.e. a $3\%$ uncertainty. Therefore, considering this estimate on ${{\mathcal {N}}}_E$, still the main source of uncertainty for the ratio of Eq. (21) would come from the ratio of form factors, ${{\mathcal {N}}}_F^{(\pi )}$ which, according to Ref. [10] (see also [34, 35]) it is ${{\mathcal {N}}}_F^{(\pi )} = 1.000\pm 0.042$ (a $4\%$ uncertainty). Consequently we would obtain the ratio

$$\begin{aligned} \frac{Br(B_s\rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^- \pi ^+)} = 1.02 \pm 0.05. \end{aligned}$$

(22)

It is interesting to notice that this result, which is a theoretical estimate of the ratio of branching ratios, slightly differs from the fit from data obtained by LHCb in Ref. [10], which is $1.18 \pm 0.04$, i.e. a discrepancy in the central values by $2.5\, \sigma$, if we consider $\sigma$ as the quadrature combination of the errors in both results. In order to find out the origin of the discrepancy, we cannot analyze the fit by LHCb, but we can examine the sources of uncertainty of our estimate shown in Eq. (22).

As seen in Eq. (21), there are only two possible sources of uncertainty at the level of a few percent or more: the form factor ratio ${{\mathcal {N}}}_F^{(\pi )}$, which is estimated to be known to $4\%$ as cited above, and the internal W exchange correction ${{\mathcal {N}}}_E$ which, according to Refs. [23] and [33], should contain an uncertainty around $3\%$. However, we should be cautious here: there are other estimates that differ from this result. For example, ${{\mathcal {N}}}_E \simeq 0.966 \pm 0.05$ according to Ref. [31]. Notice that this value is also below unity, which means that the real part of E should be positive instead of negative as in Ref.  [33]. But then again, the same Ref. [31] quotes a previous CDF result [36] that leads to a value ${{\mathcal {N}}}_E \sim 1.07 \pm 0.03$ (stat), i.e larger than unity. In summary, there is still an uncertainty in ${{\mathcal {N}}}_E$ that needs to be resolved. Just considering the range of values ${{\mathcal {N}}}_E \sim 0.966$ [31] and 1.033 [33], these differ in near 7$\%$.

Now, if we take this more conservative uncertainty of 7%, the theoretical ratio of Eq. (22) would be known to that level of uncertainty. Then, measurements of $B_s\rightarrow D_s\pi ^+$ and $B^0\rightarrow D^- \pi ^+$ events at LHCb analogous to that of Eq. (12) could be used to extract the ratio of fragmentation fractions $f_s/f_d$, namely:

$$\begin{aligned} \frac{f_s}{f_d} \times \frac{Br(B_s \rightarrow D_s^-\pi ^+)}{Br(B^0\rightarrow D^-\pi ^+)} \ =\ \frac{n_{cor}(B_s\rightarrow D_s^-\pi ^+)}{n_{cor}(B^0\rightarrow D^-\pi ^+) }, \end{aligned}$$

(23)

where $n_{cor}$ are the efficiency-corrected experimental number of events just as in Eq. (12). One could then extract the value for $f_s/f_d$ with a precision up to $7\%$. The actual values of $n_{cor}$ should be determined by experiment, which is of course beyond the scope of our work.

4 On $f_c/f_d$ and $B_c^+\rightarrow J/\psi \, \pi ^+$

As we saw at the end of Sect. 2, there is a tension between the theoretical predictions of $Br(B_c\rightarrow B_s\pi )$ and $Br(B_c\rightarrow J/\psi \, \pi )$ if one tries to relate these processes with $f_c/f_s$, $f_c/f_d$ and the experimental data.

LHCb [7] determined $Br(B_c\rightarrow B_s\pi )$ by measuring the quantity we reproduce here in Eq. (1), and by using $f_c/f_s$ as additional input. This input was in turn estimated using a previous result of $f_s/f_d$ and a value of $f_c/f_d$ obtained from their measurement shown in Eq. (2) together with a broad range of theoretical estimates for $Br(B_c\rightarrow J/\psi \,\pi ) \sim 0.06\% \rightarrow 0.18\%$ [13]. The resulting branching ratio $Br(B_c\rightarrow B_s\pi )\sim 5\% \rightarrow 15\%$, in spite of this broad range, is in slight tension with the direct theoretical estimates of $Br(B_c\rightarrow B_s\pi )$ shown in Table I and Eq. (10): in order to have consistency, one should expect $Br(B_c\rightarrow J/\psi \, \pi )$ to be lower than the aforementioned range.

Let us then derive the values of $Br(B_c\rightarrow J/\psi \, \pi )$ that would be consistent with the theoretical estimates for $Br(B_c\rightarrow B_s \pi )$ given in Sect. 2. To do that, first we take $f_c/f_s$ in Eq. (11), which was derived using the theoretical estimates for $Br(B_c\rightarrow B_s \pi )$, and take $f_s/f_d = 0.2390\pm 0.0076$ obtained by LHCb at 7 TeV [10]. One then finds the values for $f_c/f_d$:

$$\begin{aligned} \frac{f_c}{f_d}= & {} \frac{f_c}{f_s}\times \frac{f_s}{f_d} \nonumber \\= & {} (1.925 \pm 0.291 \pm 0.068 \pm 0.061)\times 10^{-2} a_1^{-2}, \end{aligned}$$

(24)

where the first uncertainty comes from the LHCb measurement of Eq. (1), which is near $15\%$ and by far the largest, the second is near $3.5\%$ and comes from the lattice estimate of the $B_c\rightarrow B_s$ form factor shown in Eq. (8), and the third is near $3.2\%$ and comes from the uncertainty in $f_s/f_d$ according to Ref. [10].

Now, using the LHCb measurement [11] shown in Eq. (2) and the current value of $Br(B^+\rightarrow J/\psi \, K^+) = (1.020\pm 0.019)\times 10^{-3}$ [32], we get:

$$\begin{aligned}{} & {} Br(B_c^+\rightarrow J/\psi \pi ^+) \nonumber \\{} & {} \quad \times = (3.60\pm 0.61 \pm 0.54 \pm 0.18) 10^{-4}\, a_1^2, \end{aligned}$$

(25)

where the first uncertainty (near $17\%$) comes from the LHCb measurement shown in Eq. (2), the second uncertainty (near $15\%$) is from the LHCb measurement shown in Eq. (1), and the last uncertainty (near $5\%$) is the combination of the uncertainties from the branching ratio of $B^+\rightarrow J/\psi K^+$, the form factor of Eq. (8), and $f_s/f_d$ shown above. The combined uncertainty is near 23%. Our result for $Br(B_c^+\rightarrow J/\psi \pi ^+)$ in Eq. (25) contrasts with the theoretical estimates [13] used by LHCb [7] to extract $Br(B_c^+\rightarrow B_s\pi ^+)$, namely:

$$\begin{aligned} Br(B_c\rightarrow J/\psi \pi ) = (6\rightarrow 18)\times 10^{-4}. \end{aligned}$$

(26)

Using $a_1 =1.14$ (the accepted coefficient $a_1$ for $b\rightarrow c$ transitions), our result in Eq. (25) with its 23% uncertainty is still $3\, \sigma$ below the lowest value in Eq. (26). Moreover, other theoretical models (see Table 2) predict values for $Br(B_c^+\rightarrow J/\psi \, \pi ^+)$ in the range $(3.8 \rightarrow 13)\times 10^{-4} a_1^{2}$, and in particular the lowest two values in Table 2 differ in less than $2\sigma$ from the value we calculated in Eq. (25). While there are still large uncertainties in the estimation of the $B_c$ branching ratios and on the ratio of fragmentation functions, these latter comparisons tend to indicate that our results are approaching a consistent set of values.

Table 2 Prediction for the branching ratio $Br(B_c^+\rightarrow J/\psi \pi ^+$) from different models, and our estimate of Eq.  25. The coefficient $a_1 = 1.14$ has been extracted for comparison between the different results

5 Conclusions

We have studied the consistency of current determinations and estimates of the fragmentation fractions $f_c$, $f_s$ and $f_d$, which are the probabilities that a b quark produced at the LHCb hadronizes into a $B_c$, $B_s$ and $B_d$ meson, respectively, together with the predictions of the branching ratios of these mesons into the specific two-body non-leptonic modes that are measured nowadays by LHCb. We compare the theoretical estimates of the branching ratios obtained by different authors using different methods, and in our own estimates we use Lattice results for the corresponding form factors which enter in the theoretical expressions of these decays within the factorization approximation. In the analysis we include the uncertainties due to non-factorizable contributions as well.

In particular, $f_c$ is estimated from the theoretical prediction of $B_c^+ \rightarrow B_s \pi ^+$ based on lattice results, and measurements by LHCb. This decay is a remarkable case, where the heavy quark is a spectator of the weak interaction process, unlike the much studied decays of heavy hadrons where it is the heavy quark that goes through the weak transition. Current theoretical estimates of $Br(B_c^+\rightarrow B_s\pi ^+)$ range from 0.01 to 0.05. Our estimate is $Br(B_c^+\rightarrow B_s\pi ^+)\sim 0.03$, based on Lattice results, with an uncertainty of about 4%, in which case $f_c/f_s\sim 0.08$ could be determined from the LHCb measurement with 15% uncertainty.

Concerning the fraction $f_s/f_d$, we study the possibility obtaining better results by measuring the ratio $Br(B_s \rightarrow D_s \pi )/Br(D^0 \rightarrow D \pi )$ instead of the proposed ratio $Br(B_s \rightarrow D_s \pi )/Br(D^0 \rightarrow D K)$. The latter was proposed because $B\rightarrow D\pi$ contains non factorizable contributions, thus inducing possibly large uncertainties. However, $B\rightarrow D K$ has the disadvantage of being a more suppressed mode, so data is more limited. We therefore investigated the effect of non factorizable contributions in $B\rightarrow D\pi$ to see whether it could compensate the uncertainties by being a more abundant mode. In order to estimate $Br(B^0 \rightarrow D \pi )$ we have discussed various methods, such as using the experimental value from PDG [32], PQCD factorization predictions [23, 33] and the various fittings [31, 36]. We find that the measurements of $B_s \rightarrow D_s\pi$ and $B^0\rightarrow D\pi$ at LHCb can then provide $f_s/f_d$ up to 7% uncertainty, due to the corresponding non-factorizable contributions.

In summary, we predict $Br(B_c\rightarrow B_s\pi ) \simeq 0.04$ (using $a_1 =1.2$ for this $c\rightarrow s$ transition), within 3.5% uncertainty from the Lattice results for the form factor, which then gives $f_c/f_s \simeq 0.056$ with 16% uncertainty using the LHCb measurements of this decay. Concerning $f_s/f_d$, we propose to use again the data on $B_s\rightarrow D_s\pi$ and $B\rightarrow D\pi$ considering our estimate of $Br(B_s\rightarrow D_s\pi )/Br(B^0\rightarrow D^-\pi ^+) \simeq 1.02 \pm 0.05$, where the uncertainties include those from neglecting non factorizable contributions. Finally, we obtain the ratio $f_c/f_d\simeq 0.014$ with a 16% error based on $f_c/f_s$ and current $f_s/f_d$ results, and the estimate $Br(B_c\rightarrow J/\psi \pi )\sim 4 \times 10^{-4}$ which is consistent with $Br(B_c\rightarrow B_s\pi )$ and the current data on the fragmentation fractions, with an uncertainty of 23%. This consistent value is at the lower end of the current theoretical estimates, which still span a rather broad range, from $0.04\%$ to $0.17\%$.