1 Introduction

Drans–Dicke theory, as a special case of scalar–tensor theory, is an alternative gravity theory in which gravity is non-minimally coupled to a scalar field. This theory, which can be regarded as the simplest extension of Einstein’s gravity theory, was initially proposed by Drans and Dicke in 1961 [1]. This extended theory is claimed to be fully Machian and, incorporates Dirac’s large number hypothesis via treating Newton’s constant as a dynamical scalar field [2, 3]. The action of BD theory includes a dimensionless coupling parameter \(\omega \), known as the BD-parameter, such that for its large values Einstein’s theory is recovered. After the discovery of accelerated cosmic expansion in 1998 [4,5,6], an enormous amount of activities, mostly based on the cosmological scalar fields instead of postulating a mysterious form of dark energy, was focused on the context of scalar–tensor gravity [7,8,9,10,11,12,13,14]. Moreover, many authors attempted to address this phenomena without dark energy component. Thus, based on the possibility that this acceleration may be caused by modification of gravity at large scales, generalized the original Einstein-Hilbert action to that of well-known \(f({\mathcal {R}})\) gravity theory [15,16,17,18,19,20,21,22]. Later on, it was shown that metric \(f({\mathcal {R}})\) gravity is similar to BD theory with \(\omega =0\) and Palatini \(f({\mathcal {R}})\) gravity is just \(\omega =-\frac{3}{2}\) BD theory [23]. In addition, it is well-known that string theory and supergravity include BD-like scalars, and low energy limit of string theory is just \(\omega =-1\) BD theory [24,25,26]. Also, it has been shown that scalar–tensor theories can pass the solar system tests and, in the post Newtonian limit, they are consistent with general relativity [27, 28]. The energy conditions and consistency of BD theory with the accelerated expansion of Universe have been confirmed noting the fact that BD and \(f({\mathcal {R}})\)-gravity theories are equivalent [29]. Nowadays, the aforementioned properties of BD theory have renewed the interest in BD and scalar–tensor theories of gravity, mostly on cosmology side and attempts for explaining the present cosmic acceleration. Starting from the (phantom) scalar–tenor action and transforming to its conformal related Einstein frame, the late-time cosmology and acceleration phase have been studied in spatially flat FRW Universe by assuming an exponential function for scalar potential in Ref. [30]. It has been shown that this theory admits acceleration phase of the Universe. Nojiri and Odintsov, after discussing the equivalence of scalar–tensor and \(f({\mathcal {R}})\) gravity theories, proposed a model of \(f({\mathcal {R}})\) theory which in addition to the Einstein’s term includes positive and negative powers of \({\mathcal {R}}\). They show that the terms with negative power serve as effective dark energy and produce cosmic acceleration, while the terms with positive powers support the inflationary epoch. Moreover this theory can pass the solar system tests for scalar–tensor gravity [31]. A detailed discussion on various models of modified gravity, specially \(f({\mathcal {R}})\), f(G), \(f({\mathcal {R}},\;G)\) and scalar–tensor models etc, can be found in Refs. [32, 33]. Different forms of \(f({\mathcal {R}})\) gravity, including logarithmic dependency on R, have been studied. It has been found that, in the case of \(\ln {\mathcal {R}}\) gravity, there are two solutions one corresponds to inflation in the early Universe and the other describes the present cosmic acceleration. Certainly, we have to search for an alternative gravity theory which in one side works as good as general relativity in solar system, and in other side gives a consistent explanation for its shortcomings such as inflation, large scale structure, dark matter, dark energy and cosmic acceleration with acceptable accuracy. For an interesting study on open problems, alternative theories of gravity and the related applications, the readers are referred to [34].

On the gravity side, there many works in which gravitational collapse and various aspects of BD BHs have been studied [35,36,37]. Through analyzing detection of scalar–tensor gravitational waves, based on the existing observational data, it has been found that the scalar field represents a considerable amount of gravitational waves radiated from astronomical sources [38]. Thermodynamics and stability properties of higher-dimensional charged BH solutions, in the presence of both linear and nonlinear models of electrodynamics, have been studied in the BD theory which are not valid for our 4D universe [39,40,41,42,43]. Exact BD BH solutions and related thermodynamics have not been studied in the 4D spacetimes, up to now [44]. The only study dates back to 1997, when Cai and Myung showed that the 4D exact solutions of BDM theory in the absence of scalar potential is non other than RN BHs with a trivial constant scalar field [45]. This result gives rise from the fact that, due to the absence of scalar potential and due to conformal symmetry of Maxwell’s electrodynamics, the source of scalar field equation is zero. While, in the spacetimes with dimensions non-equal to four, the Maxwell’s electrodynamics is no longer conformal-invariant and even in the absence of scalar potential, the scalar field equation appears with a nonzero source and related BH solutions are coupled to nontrivial scalar fields [43, 46].

Although, there are a variety of linear and non-linear models of electrodynamics, the Maxwell’s theory of classical electrodynamics is the only one which remains invariant under 4D CTs [47,48,49,50,51,52,53]. This property plays an important role in constructing AdS/CFT correspondence, based on which there is a relation between a d-dimensional AdS gravity theory in one side and a \(d+1\)-dimensional conformal-invariant field theory on the other side. In addition, it is believed that for solving the problems of gravitational and cosmological physics a conformal-invariant quantum gravity is needed [54, 55]. It means that conformal invariance is an important symmetry which is needed for establishing conformally quantum gravity, and also, for studying quantum aspects of BHs. Since BHs are systems with high energy regime, inclusion of quantum gravity effects is expected to give rise more realistic advantages even in the classical perspectives [56, 57]. Therefore, motivated by the importance of conformal invariance in conformal field theory and quantum gravity, we explore impacts of this property on the behavior of 4D BHs through consideration of Maxwell’s/ or conformal-invariant electrodynamics.

This article is organized as follows: in Sect. 2, by use of the variational principle, equations of motion have been obtained from the action of 4D BDM theory. Since they are too difficult for direct solving, we have translated them from the Jordan to the Einstein frame by applying the conformal transformations (CTs). In Sect. 3, the equations have been solved in the Einstein frame to obtain the exact Einstein-dilaton BH solutions. It has been shown that the 4D BDM theory, in the absence of self-interacting scalar potential, recovers the Einstein–Maxwell-\(\Lambda \) theory coupled to a trivial constant scalar field. Then, It has been shown that the exact solutions, in the presence of a scalar potential, give rise to two novel classes of Einstein-dilaton BHs. In Sect. 4, the 4D BDM exact solutions have been obtained noting their Einstein frame analogous by use of inverse CT, which are coupled to a nontrivial scalar field. Through direct calculations, we have shown that the BHs’ charge and temperature are identical in both of the Einstein and Jordan frames. Also, despite the fact that entropy of BD BHs violates the entropy-area law, Euclidean action method shows that BHs’ mass, entropy and electric potential remain invariant under CTs. Validity of the first law of BH thermodynamics has been proved for both of the BD and dilaton BHs. Finally, stability of the BDM BHs will be studied, using the canonical ensemble method (CEM) and geometrical method (GM), comparatively. Section 5 has been devoted to summarizing and discussing the results.

2 The fundamental equations

The action of 4D BD theory can be presented in the Einstein frame or its conformally related frame known as the Jordan frame. In the Jordan frame, the gravity is nonminimally coupled to the scalar field and, the related equations are strongly nonlinear. Therefore, they are very hard to be solved directly. In order to obtain the exact solutions, one can translate the action from Jordan to Einstein frame use of the CTs. Now, we start with the action of 4D BDM theory, which is written in the Jordan frame, as [58,59,60]

$$\begin{aligned} I^{(BD)}= & {} -\frac{1}{16\pi }\int \sqrt{-\tilde{g}}\;d^{3+1}x \left[ \psi \tilde{{\mathcal {{R}}}}-U(\psi )\right. \nonumber \\{} & {} \left. -\frac{\omega }{\psi }\;\tilde{g}^{\mu \nu }\tilde{\nabla }_\mu \psi \tilde{\nabla }_\nu \psi +L(\tilde{{\mathcal {F}}})\right] . \end{aligned}$$
(1)

Note that, \(\psi \) is a scalar field, \(\tilde{g}_{\mu \nu }\) is the BD metric tensor and \(\tilde{{\mathcal {{R}}}}=\tilde{g}^{\mu \nu }\tilde{{\mathcal {{R}}}}_{\mu \nu }\) denotes related Ricci scalar. \(\omega \) is known as the BD parameter and, the covariant derivative is shown by \(\tilde{\nabla }\). \(L(\tilde{{\mathcal {F}}})= -\tilde{{\mathcal {F}}}\) is the lagrangian of Maxwell’s electromagnetic theory with \(\tilde{{\mathcal {F}}}=\tilde{F}^{\alpha \beta }\tilde{F}_{\alpha \beta }\), \(\tilde{F}_{\alpha \beta }=\partial _\alpha \tilde{A}_\beta -\partial _\beta \tilde{A}_\alpha \), and \(\tilde{F}^{\rho \lambda }=\tilde{g}^{\rho \alpha } \tilde{g}^{\lambda \beta }\tilde{F}_{\alpha \beta }\).

Through application of variational principle, the action (1) leads to the scalar,electromagnetic and gravitation field equations in the following forms [60, 61]

$$\begin{aligned}{} & {} (2\omega +3)\tilde{\square }\psi =\psi \partial _\psi U(\psi )-2U(\psi ), \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \tilde{\nabla }_\mu \tilde{F}^{\mu \nu } =0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \psi \tilde{G}_{\mu \nu }=\psi \left( \tilde{{\mathcal {{R}}}}_{\mu \nu }- \frac{1}{2}\tilde{{\mathcal {{R}}}}\tilde{g}_{\mu \nu }\right) \nonumber \\{} & {} \qquad \qquad \!= \left( \tilde{\nabla }_\mu \tilde{\nabla }_\nu -\tilde{g}_{\mu \nu } \tilde{\square }\right) \psi +T^{(\psi )}_{\mu \nu }+T^{(A)}_{\mu \nu }, \end{aligned}$$
(4)

in which, \( \tilde{\square }=\tilde{\nabla }_\alpha \tilde{\nabla }^\alpha \) is the d’Alembert operator, and

$$\begin{aligned}{} & {} T^{(\psi )}_{\alpha \beta }=\frac{\omega }{\psi }\;\tilde{\nabla }_\alpha \psi \tilde{\nabla }_\beta \psi -\frac{1}{2}\left[ U(\psi ) +\frac{\omega }{\psi }\;(\tilde{\nabla }\psi )^2\right] \tilde{g}_{\alpha \beta }, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} T^{(A)}_{\alpha \beta }=-\frac{1}{2}\tilde{{\mathcal {F}}} \tilde{g}_{\alpha \beta } +2\tilde{F}_{\alpha \nu }\tilde{F}_\beta ^{\;\;\nu }, \end{aligned}$$
(6)

denote the scalar and electromagnetic energy-momentum tensors, respectively [62, 63].

The strong coupling of scalar and gravitational field equations make them difficult for direct solving. The CT is a useful mathematical tool by use of which one can translate the Jordan frame action (1) to its analogous in the Einstein frame. In the new frame, where theory is known as the Einstein–Maxwell-dilaton, the field equations become decoupled and the exact solutions may be obtained easier [64, 65]. In terms of a conformal factor \(\Omega \), which in general is a well-behavior function of spacetime coordinates, the CT defines a connection between \(\tilde{g}_{\mu \nu }\) and Einstein frame metric \(g_{\mu \nu }\) through the following relation [66,67,68]

$$\begin{aligned} \tilde{g}_{\mu \nu }\rightarrow \tilde{g}_{\mu \nu }=\Omega ^2g_{\mu \nu }, \end{aligned}$$
(7)

by use of which the following relation between Ricci scalars (RS)s can be confirmed [69]

$$\begin{aligned} \bar{\mathcal {R}}\longrightarrow \bar{\mathcal {R}}=\Omega ^{-2}{\mathcal {R}}-6\Omega ^{-3}\square \Omega . \end{aligned}$$
(8)

An immediate consequence of substituting (7) and (8) in the BD action (1) is that

$$\begin{aligned} V(\phi )=U(\psi )\Omega ^{4}(\psi ), \quad \hbox {and}\quad \Omega (\psi )=\frac{1}{\sqrt{\psi }}, \end{aligned}$$
(9)

which are useful for decoupling the field equations. Now, we introduce a scalar field \(\phi \) in the frame identified by \(g_{\mu \nu }\) and assume that \(\psi =\psi (\phi )\). Also, the term containing \(\square \Omega \) can be integrated by-part which leaves us with the following differential equation [70]

$$\begin{aligned} \left[ 6\psi \left( \frac{d \Omega (\psi )}{d \psi }\right) ^2+\frac{\omega }{\psi ^2}\right] \left( \frac{d \psi }{d \phi } \right) ^2=2. \end{aligned}$$
(10)

Noting Eqs. (9), (10) can be solved for \(\psi \) as a function of \(\phi \). That is

$$\begin{aligned} \psi =e^{2\beta \phi }, \quad \hbox {and}\quad \beta =\frac{\pm 1}{\sqrt{3+2\omega }}. \end{aligned}$$
(11)

Note that \(\omega \) is restricted to \(\omega >-3/2\). In the limiting case \(\omega \rightarrow \infty \), \(\beta \) vanishes and \(\psi =1\). Thus by considering \(V(\psi =1)=constant=2\Lambda \) the action (1) recovers the Einstein-\(\Lambda \) gravity. It means that, if \(\omega \) is chosen very large, the BD theory recovers the Einstein-\(\Lambda \) theory.

We now return to the electromagnetic Lagrangian by the assumption \(\tilde{A}_\alpha \rightarrow A_\alpha \). Generally it transforms to a new function of \(\phi \) and \({\mathcal {F}}\) and we can write it as

$$\begin{aligned} L(\phi , {\mathcal {F}})=\psi ^{-2}L\left( \psi ^{2}{\mathcal {F}}\right) . \end{aligned}$$
(12)

Here, we have considered Maxwell’s electromagnetic theory. Thus, we have \(L(\phi , {\mathcal {F}})=\psi ^{-2}(-\psi ^2{\mathcal {F}})=L({\mathcal {F}})\). As the result, we obtain \(L(\tilde{{\mathcal {F}}})=L({\mathcal {F}})\), which reminds conformal-invariant property of the 4D Maxwell’s theory. It is worth mentioning that, starting fro Eq. (6), one can show that \(\tilde{g}^{\alpha \beta }T^{(A)}_{\alpha \beta }=0\). Therefore, the trace of Maxwell’s energy-momentum tensor vanishes in 4D spacetimes. It must be emphasized that, among diverse models of electrodynamics, only Maxwell’s electromagnetic theory preserves conformal symmetry in the 4D spacetimes [71]. The final result is that, under CTs the action (1) transforms to that of 4D Einstein-dilaton theory which is coupled to the conformal-invariant Maxwell’s electrodynamics, which can be written as [72, 73]

$$\begin{aligned} I^{(Ed)}= & {} -\frac{1}{16\pi }\int \sqrt{-g}\;d^{3+1}x \nonumber \\ {}{} & {} \times \left[ {\mathcal {R}}-2(\nabla \phi )^2-V(\phi )+L({\mathcal {F}})\right] . \end{aligned}$$
(13)

Here, we have used the definitions: \({\mathcal {R}}=g^{\mu \nu }{\mathcal {R}}_{\mu \nu }\), \((\nabla \phi )^2=g^{\mu \nu }\nabla _\mu \phi \nabla _\nu \phi \) and \(L({\mathcal {F}})=-{\mathcal {F}}\). Note that \({\mathcal {F}}=F^{\mu \nu }F_{\mu \nu }\) with \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \), \(\phi \) and \(V(\phi )\) are the scalar field and potentials in the Einstein frame. Now, we are in the situation to solve the field equations corresponding to the Einstein-dilaton action (13) in the Einstein frame.

3 The Einstein–Maxwell-dilaton BHs

By varying the Einstein–Maxwell-dilaton action (13), with respect to various fields, the related field equations are obtained in the following forms [74]

$$\begin{aligned} 4\square \phi (r)= & {} \frac{d V(\phi )}{d\phi }, \end{aligned}$$
(14)
$$\begin{aligned} \nabla _\mu F^{\mu \nu }= & {} 0, \end{aligned}$$
(15)
$$\begin{aligned} {\mathcal {R}}_{\mu \nu }= & {} 2\partial _\mu \phi (r)\partial _\nu \phi (r)+2F_{\mu \sigma }F_{\nu }^{\;\sigma }\nonumber \\{} & {} + \frac{1}{2}g_{\mu \nu }\left[ V(\phi )- {\mathcal {F}}\right] , \end{aligned}$$
(16)

which are known as the scalar, electromagnetic and gravitational field equations, respectively.

Now, we explore the exact solutions in a static and spherically symmetric spacetime defined by the following line element [75]

$$\begin{aligned} ds^2= & {} g_{\mu \nu }dx^{\mu }dx^{\nu }=-f(r)dt^2 +\frac{1}{f(r)}dr^2\nonumber \\{} & {} +r^2R^2(r)\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) . \end{aligned}$$
(17)

The only nonzero component of \(F_{\mu \nu }\) is \(F_{tr}=E(r)=-A_t'(r)\), and for the Maxwell invariant \({\mathcal {F}}\), one obtains \({\mathcal {F}}=-2F_{tr}^2\). Moreover, the tt, rr and \(\theta \theta \;(\varphi \varphi )\) components of gravitational field equation (16) satisfy the following relations

$$\begin{aligned} C_{tt}\equiv & {} \frac{f''(r)}{2}+\left[ \frac{1}{r}+\frac{R'(r)}{R(r)}\right] f'(r)+\frac{1}{2}\left[ V(\phi )+{\mathcal {F}}\right] =0, \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} C_{rr}\equiv & {} C_{tt}+2f(r)\left[ \frac{R''(r)}{R(r)}+\frac{2R'(r)}{rR(r)}+\phi '^2(r)\right] =0, \end{aligned}$$
(19)
$$\begin{aligned} C_{\theta \theta }= & {} C_{\varphi \varphi }\equiv \left[ \frac{1}{r}+\frac{R'(r)}{R(r)}\right] f'(r)\nonumber \\{} & {} +\left[ \frac{1}{r^2}+\frac{R''(r)}{R(r)} +\frac{4R'(r)}{rR(r)}+\frac{R'^2(r)}{R^2(r)}\right] f(r)\nonumber \\{} & {} -\dfrac{1}{r^2R^2(r)}+\frac{1}{2}\left[ V(\phi )-{\mathcal {F}}\right] =0. \end{aligned}$$
(20)

As matter of calculations, it can be shown that \(C_{tt}=0\) and \(C_{\theta \theta }=0\) are not independent, and the solution of (20) automatically satisfies (18). Therefore, there are five unknowns R(r), \(F_{tr}\), \(\phi (r)\), \(V(\phi )\) and f(r), while the number of unique equations is for. It means that we are confronted with indeterminacy problem [76]. To overcome this problem, we use an exponential ansatz function in the form of \(R(r)=e^{\alpha \phi }\). Thus Eq. (19) can be solved, in terms of a positive constant b, as

$$\begin{aligned} \phi = \gamma \ln \left( \frac{b}{r}\right) , \end{aligned}$$
(21)

with \(\gamma =\alpha (1+\alpha ^2)^{-1}\). Noting Eqs. (11) and (21) the physical scalar field \(\psi \), takes the following form

$$\begin{aligned} \psi =\left( \frac{b}{r} \right) ^{2\beta \gamma }. \end{aligned}$$
(22)

In order to the physical scalar field \(\psi \) vanish at infinite distance from the source, both of \(\beta \) and \(\alpha \) parameters have to be chosen positive.

By solving (15), for the nonzero component of \(F_{\alpha \beta }\), we obtain

$$\begin{aligned} F_{tr}=\frac{q}{b^{2\alpha \gamma }}\;r^{2\alpha \gamma -2}, \end{aligned}$$
(23)

and, for the temporal component of \(A_\mu \), one obtains

$$\begin{aligned} A_{t}=\left\{ \begin{array}{ll} -\frac{q}{b}\ln \left( \frac{r}{\ell }\right) ,&{}\quad \alpha ^2=1,\\ \\ \frac{ qr^{-1}}{1-2\alpha \gamma }\left( \frac{r}{b}\right) ^{2\alpha \gamma },&{}\quad \alpha ^2 <1.\end{array} \right. \end{aligned}$$
(24)

The restriction \(\alpha ^2 <1\) makes \(A_t(r)\) to vanish at the reference point located at infinity.

By use of Eqs. (14) and (20), it is easily shown that the unknown functions \(V(\phi )\) and f(r) are governed by the the following differential equations

$$\begin{aligned}{} & {} \frac{4\gamma }{r}\left( \frac{2\alpha \gamma -1}{r} f(r)-f'(r)\right) =\frac{dV(\phi )}{d\phi }, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \frac{\alpha \gamma -1}{r}\left( \frac{2\alpha \gamma -1}{r}f(r)-f'(r)\right) \nonumber \\{} & {} \quad =\frac{1}{r^2R^2(r)}- \frac{1}{2}\left[ V(\phi )-{\mathcal {F}}\right] . \end{aligned}$$
(26)

Here, we are interested in the special case defining by \(V(\phi )=0\) or \(V(\phi )=2\Lambda =constant\). In that case the action (1) reduces to the original 4D BDM theory studied in Ref. [45]. Now the right-hand side of (14) is zero and, Eqs. (25) and (26) become

$$\begin{aligned}{} & {} \frac{4\gamma }{r}\left( \frac{2\alpha \gamma -1}{r}f(r)-f'(r)\right) =0, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \frac{\alpha \gamma -1}{r}\left( \frac{2\alpha \gamma -1}{r}f(r) -f'(r)\right) \nonumber \\{} & {} \quad =\frac{1}{r^2}e^{-2\alpha \phi }-\frac{1}{2}\left( 2\Lambda -{\mathcal {F}}\right) , \end{aligned}$$
(28)

which are not compatible unless \(\gamma =0\) and, noting (22) results in \(\psi =1\). Consequently, the action (1) reduces to that of Einstein–Maxwell-\(\Lambda \) theory which leads to the well-known RN metric function. That is

$$\begin{aligned} f(r)=1-\frac{m}{r}-\frac{1}{3}\Lambda r^2+\frac{q^2}{r^2}. \end{aligned}$$
(29)

Therefore, when the scalar potential \(U(\psi )\) is absent, the 4D BDM theory is identical to the Einstein–Maxwell-\(\Lambda \) one which is coupled to a trivial constant scalar field. This result is just the same as reported by Cai and Myung in Ref. [45].

Now, we come back to obtain the general solution of differential equations (25) and (26) in the Einstein frame. Through solving the coupled differential equations (27) and (28), for the scalar potential \(V(\phi )\), we obtain

$$\begin{aligned} V(\phi )=\left\{ \begin{array}{ll} 2\Lambda _{_{eff}}e^{2 \phi }+\frac{2q^2}{b^4}e^{4\phi }- \frac{4\phi }{b^2}e^{2\phi },&{}\quad \alpha ^2=1,\\ 2\Lambda e^{2\alpha \phi }+2\Lambda _1e^{2a \phi }+2\Lambda _2e^{a\phi },&{}\quad \alpha ^2<1, \end{array} \right. \end{aligned}$$
(30)

where

$$\begin{aligned} a= & {} 2\alpha ^{-1},\quad \quad \quad \Lambda _1=\frac{\alpha ^2 q^2}{(2-\alpha ^2)\;b^{4}},\quad \quad \quad \nonumber \\ \Lambda _2= & {} -\frac{\alpha ^2}{(1-\alpha ^2)\;b^{2}}, \end{aligned}$$
(31)

and \(\Lambda \) is the cosmological constant while \(\Lambda _{_{eff}}\) denotes the \(\Lambda \) with a constant absorbed in it. Also, after combining (26) and (30) and solving for f(r), we have

$$\begin{aligned} f(r)=\left\{ \begin{array}{ll} -m-2\Lambda _{_{eff}} br -\frac{4q^2}{b^2}\ln \left( \frac{r}{\ell }\right) &{}\\ \quad +\frac{2r}{b}\left[ 2+ \ln \left( \frac{b}{r}\right) \right] , &{}\quad \alpha ^2=1,\\ -m\;r^{2\alpha \gamma -1}-\frac{\Lambda b^2}{\Gamma }\left( \frac{r}{b} \right) ^{2-2 \alpha \gamma }&{}\\ \quad +\frac{2q^2}{b^2\Gamma _1 }\left( \frac{b}{r}\right) ^{2-4 \alpha \gamma } +\Gamma _2\left( \frac{r}{b}\right) ^{2 \alpha \gamma },&{}\quad \alpha ^2 <1, \end{array} \right. \end{aligned}$$
(32)

with

$$\begin{aligned} \Gamma= & {} \frac{3-\alpha ^2}{(1+\alpha ^2)^2},\quad \quad \nonumber \\ \Gamma _1= & {} \frac{(2-\alpha ^2)(1-\alpha ^2)}{(1+\alpha ^2)^2}, \quad \quad \Gamma _2=\frac{1+\alpha ^2}{1-\alpha ^2}. \end{aligned}$$
(33)

Note that when the scalar hair is turned of, by setting \(\alpha =0=\gamma \) in (32), the RN BHs with the metric function (29) are recovered.

The plots of f(r) versus r, for \(\alpha ^2 <1\) and \(\alpha ^2=1\) cases have been depicted in Fig. 1. They show that horizon-less, extreme, one-horizon, two-horizon and multi-horizon BHs can appear for suitable choice of the parameters. Appearance of the multi-horizon BHs, which implies the anti-evaporation quantum effect [77], reveals capability of the model under consideration due to utilizing Maxwell’s conformal-invariant electrodynamics.

Fig. 1
figure 1

f(r) vs r: Left: \(\Lambda =-3,\;m=4,\;q=1,\;b=1.4,\;\alpha =0.5,\;0.5112,\;0.52\) from top to down, Right: \(\alpha ^2=1,\;\Lambda _{_{eff}}=-1,\;m=2.5,\;b=1.4, \;\ell =1.2,\;q=2.35,\;2.392,\;2.44,\;2.475,\;2.5\) from top to down

Full size image

It is worth mentioning that the solutions presented in Eq. (32) can be considered as BHs, if both of the following requirements are fulfilled. (a) The metric functions are necessary to have at least one horizon radius. Existence of the horizon radii is confirmed by diagrams of Fig. 1. (b) At least one physical singularity is required to exist. It can be explored by calculating the Ricci (\({\mathcal {R}}=g^{\mu \nu }{\mathcal {R}}_{\mu \nu }\)) and Kretschmann (\({{\mathcal K}}={\mathcal {R}}^{\alpha \beta \rho \lambda }{\mathcal {R}}_{\alpha \beta \rho \lambda }\)) scalars. As a matter of calculation, one can show that

$$\begin{aligned} {\mathcal {R}}= & {} -f''(r)-4(1-\alpha \gamma )\left( \frac{f'(r)}{r}\right) \nonumber \\{} & {} -2(1-\alpha \gamma )(1-3\alpha \gamma )\left( \frac{f(r)}{r^2}\right) +\frac{2}{r^2}\left( \frac{b}{r}\right) ^{-2\alpha \gamma }, \end{aligned}$$
(34)
$$\begin{aligned} {{\mathcal K}}= & {} \left( f''(r)\right) ^2+4\left( 1-\alpha \gamma \right) ^2\left( \frac{f'(r)}{r}\right) ^2\nonumber \\{} & {} -8\alpha \gamma \left( 1-\alpha \gamma \right) ^2\frac{f(r)f'(r)}{r^3}+\frac{4}{r^4}\left( \frac{b}{r}\right) ^{-4\alpha \gamma }\nonumber \\{} & {} +4\left( 1-\alpha \gamma \right) ^2\left( 3\alpha ^2\gamma ^2-2\alpha \gamma +1\right) \left( \frac{f(r)}{r^2}\right) ^2\nonumber \\{} & {} -8\left( 1-\alpha \gamma \right) ^2\left( \frac{b}{r} \right) ^{-2\alpha \gamma }\left( \frac{f(r)}{r^4}\right) . \end{aligned}$$
(35)

By replacing f(r) from (32) and its first and second derivatives into Eqs. (34) and (35), we found that the Ricci and Kretschmann scalars diverge in the limit \(r\rightarrow 0^+\). As the result, the spacetime under consideration posses a physical singularity at the origin. These facts confirm that the exact solutions presented here, can be interpreted as BHs. Thermodynamic properties of our novel BDM BHs will be investigated in the next section.

4 Thermodynamics of BD BHs

Having the Einstein-dilaton BH solutions, we can introduce the BDM BHs by using inverse CTs. Later, we investigate thermodynamic properties and, analyze thermal stability by use of the CEM. We are interested in the following ansatz for solving the field equations of BDM gravity theory [78]

$$\begin{aligned} d\tilde{s}^2= & {} \tilde{g}_{\mu \nu }dx^\mu dx^\nu =-X(r)dt^2+\frac{1}{Y(r)}dr^2+r^2Z^2(r)\nonumber \\ {}{} & {} \times \left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) . \end{aligned}$$
(36)

The metric coefficients X(r), Y(r), and Z(r) are determined by applying inverse CT and noting the Einstein frame corresponding quantities. By use of Eqs. (7) and (9), we have \(\tilde{g}_{\mu \nu }=\frac{1}{\psi }g_{\mu \nu }\). Then, noting (22), one can write

$$\begin{aligned} X(r)= & {} \left( \frac{b}{r}\right) ^{-2\beta \gamma }f(r), \end{aligned}$$
(37)
$$\begin{aligned} Y(r)= & {} \left( \frac{b}{r}\right) ^{2\beta \gamma }f(r), \end{aligned}$$
(38)
$$\begin{aligned} Z(r)= & {} \left( \frac{b}{r}\right) ^{-\beta \gamma }R(r). \end{aligned}$$
(39)

Note that \(R(r)=e^{\alpha \phi }\) and, the metric function f(r) has been given in Eq. (32). Now, we explore the radius of even horizons through depicting Y(r) versus r. The plots of Fig. 2 show that our exact solutions are capable to produce multi-horizon BDM BHs for the case of well-fixed parameters. Existence of the multi-horizon BHs reveals a quantum effect known as the anti-evaporation [77].

Fig. 2
figure 2

Y(r) vs r: Left: \(0.18 Y(r),\; \beta =2,\;\Lambda =-3,\;m=4,\;q=1,\;b=1.4,\;\alpha =0.5,\;0.5112,\;0.52\) from top to down, Right: \(4 Y(r),\;\alpha ^2=1,\; \beta =1,\;\Lambda _{_{eff}}=-1,\;m=2.5,\;b=1.4,\;\ell =1.2,\;q=2.35,\;2.392,\;2.44,\;2.475,\;2.5\) from top to down

Full size image

At this stage one can calculate the Jordan frame scalar potential \(U(\psi )\) as the physical scalar potential. This is possible noting the Einstein frame scalar potential \(V(\phi )\) presented in Eq. (30) and its relation to \(U(\psi )\) given in Eqs. (9) and (11). After some algebraic calculations we have

$$\begin{aligned} U(\psi )=\left\{ \begin{array}{l} 2\psi ^2\left( \Lambda _{_{eff}}\psi ^{\frac{1}{\beta }}+\frac{q^2}{b^4} \psi ^{\frac{2}{\beta }}-\frac{1}{\beta b^2}\psi ^{\frac{1}{\beta }}\ln \psi \right) ,\\ \qquad \qquad \quad \alpha ^2=1,\\ 2\psi ^2\left( \Lambda \psi ^{\frac{\alpha }{\beta }}+\Lambda _1\psi ^{\frac{2}{\alpha \beta }}+ \Lambda _2\psi ^{\frac{1}{\alpha \beta }}\right) ,\\ \qquad \qquad \quad \alpha ^2<1. \end{array} \right. \end{aligned}$$
(40)

Thus our calculations present the scalar potential in the form of a power law (exponential) function in the Jordan (Einstein) frame. Application of similar functions has produced acceptable results in the context of scalar–tensor cosmology [30, 31].

Here, by calculating mass, charge, temperature, entropy and electric potential, we explore thermodynamic properties of our novel BDM BHs.

By use of the concept of surface gravity \(\kappa \), one can show that for the horizon temperature T can be written as \(\tilde{T}= \frac{1}{4\pi }\left( \sqrt{\frac{Y(r)}{X(r)}}\frac{d X(r)}{dr}\right) _{_{r=r_+}}\). Then, by use of Eqs. (37) and (38), we have [79, 80]

$$\begin{aligned} \tilde{T}=\frac{1}{4\pi }\left( \frac{b}{r_+}\right) ^{2\beta \gamma }\frac{d }{dr}\left[ \left( \frac{b}{r}\right) ^{-2\beta \gamma }f(r)\right] _{_{r=r_+}}=T. \end{aligned}$$
(41)

Note that the condition \(f(r_+)=0\) has been used, here. As the result, based on Eq. (40), the horizon temperature is the same in both of Einstein and Jordan frames. It can be explicitly written as

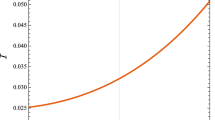
$$\begin{aligned} \tilde{T}(r_{_+})=\left\{ \begin{array}{ll} \frac{1}{2\pi b}\left[ 1-\Lambda _{_{eff}}b^2-\frac{2q^2}{br_{_{+}}}+ \ln \left( \frac{b}{r_{_{+}}}\right) \right] ,&{}\hbox {for}\quad \alpha ^2=1.\\ \frac{1+ \alpha ^2}{4\pi r_{_{+}}}\left[ \frac{1}{1-\alpha ^2}\left( \frac{r_{_{+}}}{b}\right) ^{2 \alpha \gamma }-\Lambda r_{_{+}}^2\left( \frac{b}{r_{_{+}}}\right) ^{2 \alpha \gamma }\right. &{}\\ \left. -\frac{2q^2}{r_{_{+}}^2(2-\alpha ^2)}\left( \frac{r_{_{+}}}{b}\right) ^{4 \alpha \gamma } \right] , &{}\hbox {for}\quad \alpha ^2 <1. \end{array} \right. \end{aligned}$$
(42)

The plots of \(\tilde{T}(r_{_+})\) versus \(r_{_+}\) have been shown in Fig. 3 by blue curves. The left and middle panels show that, for the BHs with \(\alpha ^2 <1\), extreme BHs with horizon radius \(r_{_+}=r_{ext}\) can occur. The BHs with horizon radii greater than \(r_{ext}\) have positive temperature and, are physically reasonable. While the BHs with horizon radius smaller than \(r_{ext}\) have negative temperature, which may be named as the unphysical BHs. The BHs with \(\alpha ^2=1\) show the extreme ones with two horizon radii labeled by \(r_{1ext}\) and \(r_{2ext}\) with \(r_{1ext}<r_{2ext}\). The non-extreme BHs with horizon radii in the range \(r_{1ext}<r_{_+}<r_{2ext}\) have positive temperature and, the unphysical BHs occur with horizon radii less than \(r_{1ext}\) and greater than \(r_{2ext}\) (Right Panel). It must be noted that appearance of extreme BHs with two horizon radii is due to consideration of Maxwell’s electrodynamics which preserves conformal invariance in the 4D spacetimes.

Through the modified Gauss’s law one is able to determine the BH’s electric charge Q in terms of the integration constant q. That is [81, 82]

$$\begin{aligned} \tilde{Q}=\frac{1}{4\pi }\int r^2 Z^2(r)\sqrt{\frac{Y(r)}{X(r)}}F_{tr} d\Omega _2, \end{aligned}$$
(43)

and noting Eqs. (37)–(39) we have

$$\begin{aligned} \tilde{Q}=\frac{1}{4\pi }\int r^2R^2(r)F_{tr} d\Omega _2, \end{aligned}$$
(44)

which is nothing but the BH’s electric charge Q in the Einstein frame. Now, by substituting \(F_{tr}\) from Eq. (23), we have

$$\begin{aligned} \tilde{Q}=q. \end{aligned}$$
(45)

Thus, the BH charge, just like the horizon temperature, is a conformal-invariant quantity. Entropy, mass and electric potential are the other quantities of the BDM BHs which we have to calculate. It must be pointed out that, in the BD theory, the BH entropy cannot be obtained from the entropy-area law [45, 83]. As it has been shown in Refs. [42, 43], the Euclidean action approach is an interesting method by use of which one can calculate the BH mass, entropy and electric charge. The calculations show that these quantities are conformal-invariant too [42, 43]. Therefore, the BH entropy can be written explicitly as

$$\begin{aligned} \tilde{S}=S=\pi r_{_{+}}^2R^2(r_{_+}) =\pi b^{2\alpha \gamma } r_{_{+}}^{2-2\alpha \gamma },\quad \hbox {for}\quad \alpha ^2\le 1, \end{aligned}$$
(46)

and the horizon electric potential, relative to a reference point located at large distance [84, 85], is obtained as

$$\begin{aligned} \tilde{\Phi }(r_{_+})=\Phi (r_{_+})=\left\{ \begin{array}{ll} -\frac{cq}{b}\ln \left( \frac{r_{_+}}{\ell }\right) ,&{}\quad \hbox {for}\quad \alpha ^2=1,\\ \\ \frac{cq}{(1-2\alpha \gamma )r_{_+}} \left( \frac{r_{_+}}{b} \right) ^{2\alpha \gamma },&{}\quad \hbox {for}\quad \alpha ^2 <1, \end{array} \right. \end{aligned}$$
(47)

here, c is an constant coefficient which we fix it later. Also, based on the method of Ref. [59], the BH mass must be written as

$$\begin{aligned} \tilde{M}=M=\frac{m b^{2\alpha \gamma }}{2\left( 1+\alpha ^2\right) },\quad \quad \quad \hbox {for}\quad \alpha ^2\le 1. \end{aligned}$$
(48)

At this stage, using the relation \(Y(r_+)=0\) and combining the obtained equation with that of (48), one can write the BH mass in the following form

$$\begin{aligned} \tilde{M}(r_+, q)=\left\{ \begin{array}{ll} \frac{r_{_{+}}}{2}\left[ 2 +\ln \left( \frac{b}{r_{_{+}}}\right) \right] - \frac{1}{2}\Lambda _{_{eff}} b^2 r_{_+} \\ -\frac{q^2}{b}\ln \left( \frac{r_{_{+}}}{\ell }\right) , &{}\quad \hbox {for}\quad \alpha ^2=1,\\ \frac{r_{_{+}}}{2(1+\alpha ^2)}\left( \frac{b}{r_{_{+}}}\right) ^{2\alpha \gamma } \left[ -\frac{\Lambda b^2}{\Gamma }\left( \frac{r_{_{+}}}{b}\right) ^{2-2\alpha \gamma }\right. \\ \left. +\frac{2q^2}{b^2\Gamma _1}\left( \frac{b}{r_{_{+}}}\right) ^{2-4\alpha \gamma }+ \Gamma _2\left( \frac{r_{_{+}}}{b}\right) ^{2\alpha \gamma }\right] ,&{} \quad \hbox {for}\quad \alpha ^2 <1. \end{array} \right. \nonumber \\ \end{aligned}$$
(49)

From (49), which based on Eqs. (45) and (46) is a function of \(\tilde{Q}\) and \(\tilde{S}\), one can show that

$$\begin{aligned} \tilde{T}= & {} \frac{\partial \tilde{M}(\tilde{S},\tilde{Q})}{\partial \tilde{S}}, \quad \quad \hbox {and}\nonumber \\ \tilde{\Phi }= & {} \frac{\partial \tilde{M}(\tilde{S},\tilde{Q})}{\partial \tilde{Q}},\quad \quad \hbox {for}\quad \alpha ^2\le 1, \end{aligned}$$
(50)

provided that c is fixed to \(c=\frac{2}{2-\alpha ^2}\). Therefore, we can write

$$\begin{aligned} d\tilde{M}(\tilde{S},\tilde{Q})=\tilde{T}d\tilde{S}+\tilde{\Phi }d\tilde{Q}. \end{aligned}$$
(51)

It means that the thermodynamical first law is valid for the novel BDM BHs introduced, here.

Thermal stability of the BHs is an important issue which cannot be forgotten when BH thermodynamics is investigated. A detailed analysis can be performed by using the either of canonical or geometrical approaches. Here, we prefer a comparative study noting the signature of specific heats in the CEM and, divergence points of thermodynamic RSs in the geometrical thermodynamics.

$$\begin{aligned} \bullet \; {{\textbf {The specific heat}}} \end{aligned}$$

In the CEM, thermal stability or phase transition of the BHs can be analyzed regarding the signature of specific heat (SH). The physically reasonable BHs, those with positive temperature, are stable if their SH is positive too. They experience first-order phase transition at the vanishing points of SH. The BH SH diverges at the points of second-order phase transition [86, 87]. Therefore, we need to calculate the BH SH through the following relation [88]

$$\begin{aligned} \tilde{C}_{\tilde{Q}}=\tilde{T}\left( \frac{\partial \tilde{S}}{\partial \tilde{T}}\right) _{\tilde{Q}}=\frac{\tilde{T}}{\tilde{M}_{\tilde{S}\tilde{S}}}, \quad \hbox {with}\quad \tilde{M}_{\tilde{S}\tilde{S}}= \left( \frac{\partial ^2 \tilde{M}}{\partial \tilde{S}^2}\right) _{\tilde{Q}}. \nonumber \\ \end{aligned}$$
(52)

Here, the subscript \({\tilde{Q}}\) means that, when the SH is calculate, the BH charge is treated like a constant. As a matter of calculation, one can show that in our case

$$\begin{aligned} \tilde{M}_{\tilde{S}\tilde{S}}=\left\{ \begin{array}{ll} \frac{1}{2\pi ^2b^2r_{_{+}}}\left( \frac{2q^2}{br_{_{+}}} -1\right) ,&{}\quad \hbox {for}\quad \alpha ^2=1.\\ \\ -\frac{1+ \alpha ^2}{8\pi ^2 r^3_{_{+}}}\left[ \left( \frac{b}{r_{_{+}}}\right) ^{4 \alpha \gamma }-(\alpha ^2-1)\Lambda r_{_{+}}^2\right. \\ -\left. \frac{2q^2(\alpha ^2-3)}{r_{_{+}}^2(\alpha ^2-2)} \left( \frac{r_{_{+}}}{b}\right) ^{6 \alpha \gamma } \right] , &{}\quad \hbox {for}\quad \alpha ^2 <1. \end{array} \right. \nonumber \\ \end{aligned}$$
(53)

Diagrams of \(\tilde{C}_{\tilde{Q}}\) and \(\tilde{T}\) are shown in Fig. 3 for different possible cases. For the case \(\alpha ^2 <1\), they show that there is a first-order phase transition point located at \(r_+=r_{ext}\), the BHs with \(r_+>r_{ext}\) are stable (Left Panel). Moreover, the BHs with \(\alpha ^2 <1\) may show a different behavior: One first-order phase transition point, located at \(r_+=r_{ext}\) and, two second-order ones, labeled by \(r_1\) and \(r_2\) such that \(r_1<r_2\). The BHs with horizon radii in the intervals \(r_{ext}<r_+<r_1\) and \(r_+>r_2\) are stable. While those with the horizon radii in the range \(r_1<r_+<r_2\), with negative specific heat, are unstable ones (Middle Panel). The BHs with \(\alpha ^2 =1\) have two points of first-order phase transition located at the extreme horizons \(r_+=r_{1ext}\) and \(r_+=r_{2ext}\) where \(r_{1ext}<r_{2ext}\). Also, there is a second-order phase transition point which we label by r with \(r_{1ext}<r<r_{2ext}\). The BHs with horizon radii in the range \(r_{1ext}<r_+<r\) are locally stable (Right Panel).

Fig. 3
figure 3

\(\tilde{C}_{\tilde{Q}}\)(black) and \(\tilde{T}\)(blue) vs \(r_+\). Left: \(q=1,\;b=1,\;\Lambda =-3,\;\alpha =0.8,\;3\tilde{C}_{\tilde{Q}},\;\tilde{T},\) Middle: \(q=0.5,\;b=0.5,\;\Lambda =-3,\;\alpha =0.8,\;0.00002\tilde{C}_{\tilde{Q}},\;\tilde{T}.\) Right: \(b=1,\;q=1,\;\Lambda _{_{eff}}=-1,\;\alpha =1,\;0.02\tilde{C}_{\tilde{Q}},\;5\tilde{T}\)

Full size image
$$\begin{aligned} \bullet \;{{\textbf { The thermodynamic RS}}} \end{aligned}$$

Geometrical thermodynamics is an alternative method, by use of which one can determine the points of first-order and second-order phase transition. It is well-known that the divergence points of thermodynamic RS are just the location of phase transition points. The RSs are calculated by use of the thermodynamic metrics and, the most famous thermodynamic metrics are those of the Weinhold (W), Ruppeiner (R), Quevedo-I (QI), Quevedo-II (QII) and HPEM (proposed by Hendi, Panahiyan, Eslam Panah and Momennia) with the following explicit forms [89, 90]

$$\begin{aligned} \begin{array}{ll} {[}ds^{(QI)}]^2=\left( S{M}_S+Q{M}_Q\right) \left( -{M}_{SS}dS^2+{M}_{QQ}dQ^2\right) ,\\ \\ {[}ds^{(QII)}]^2=S{M}_S\left( -M_{SS}dS^2+{M}_{QQ}dQ^2\right) ,\\ \\ {[}ds^{(W)}]^2={M}\;g_{\mu \nu }^W dX^\mu dX^\nu \quad \hbox {with} \;\;\;\;\;g_{\mu \nu }^W=\frac{\partial ^2{M}}{\partial X^\mu \partial X^\nu },\\ \\ {[}ds^{(R)}]^2=-{M}T^{-1}\;g_{\mu \nu }^W dX^\mu dX^\nu ,\\ \\ {[}ds^{(HPEM)}]^2=\frac{SM_S}{M^3_{QQ}}\left( -M_{SS}dS^2+M_{QQ}dQ^2\right) . \end{array} \end{aligned}$$
(54)

Here \( X^\mu \) and \(X^\nu \) are thermodynamic variables of the system. In our case they are BH’s charge and entropy.

It is well-known that the divergence points of RSs are just the zeros of denominators. As a matter of calculation one can show that the denominator of RSs, which we label by \(D[{\mathcal {R}}]\), are given via the following relations [91, 92]

$$\begin{aligned} \begin{array}{ll} D[{\mathcal {R}}^{(QI)}]=2M^2_{SS}M^2_{QQ}(SM_S+QM_Q),\\ D[{\mathcal {R}}^{(QII)}]=2S^3 M^2_{SS}M^2_{QQ} M^3_S,\\ D[{\mathcal {R}}^{(W)}]=M^2\left( M_{SS}M_{QQ}-M^2_{SQ}\right) ^2,\\ D[{\mathcal {R}}^{(R)}]=TM^2\left( M_{SS}M_{QQ}-M^2_{SQ}\right) ^2,\\ D[{\mathcal {R}}^{(HPEM)}]=2S^3 M^3_S M^2_{SS}. \end{array} \end{aligned}$$
(55)

As mentioned above, in the CEM, the points of first and second-order phase transitions are just the real roots of \(T=0\) ( or equivalently \(M_S=0\)) and \(M_{SS}=0\), respectively. In the GM, since the vanishing points of denominator of thermodynamic Recci scalars determine the location of phase transition points, the QI, W and R metrics produce extra divergent points and, their results don’t coincide with those of CEM. The result of QII metric can be consistent with CEM provided that \(M_{QQ}\) does not vanish [see Eq. (49)]. The metric of HPEM is completely successful because it, just like the CEM, diverges at the roots of \(M_S=0\) and \(M_{SS}=0\).

5 Conclusion

We studied thermodynamics of the 4D BD BHs in the presence of Maxwell’s electrodynamics. It is an important subject because Maxwell’s theory is conformal-invariant in the 4D spacetimes and, this property is the basis of AdS/CFT correspondence and necessary for the constructing of conformal quantum gravity. We obtained the Jordan frame equations of BDM theory which are highly nonlinear and very difficult for direct solving. This problem has been removed by use of the CTs which transform the field equations to the Einstein frame, in which they are decoupled and can be solved easily.

In the special case, when the scalar potential is absent or is equal to a constant in the BD action, we showed that the exact solutions are just those of RN-A(dS) coupled to a trivial scalar field \(\psi =1\). This issue is compatible with the advantages of Ref. [45]. Then we obtained the BDM BH solutions under the influence of a varying self-interacting scalar potential which are coupled to a nontrivial scalar field. The Einstein frame solutions, with the suitable choice of the parameters, admits multi-horizon BHs. Existence of the BHs with multi-horizons, which is due to conformal symmetry of Maxwell’s electrodynamics, implies the anti-evaporation quantum effect. Inclusion of the scalar filed makes the asymptotic behavior of the BHs non-flat and non-AdS.

We extracted the exact general solutions of Jordan frame equations from their Einstein frame analogues and, noting the conformal relation between the frames. It has been shown that the BDM BHs, introduced here, can reveal horizon-less, one-horizon, two-horizon and multi-horizons ones too. By direct calculations, and making use of the appropriate methods, we showed that the BH charge and temperature are conformally invariant quantities. The plots of T versus \(r_+\) show that BDM extreme BHs with two horizon radii can occur for the suitably choice of the parameter. Appearance of this property is related to the conformal symmetry of the electromagnetic theory under consideration. Although the BH entropy violates entropy-areal law, the Euclidean action method shoes that the entropy, mass and electric potential of the BDM BHs are just the same of the Einstein frame ones. It reveals that the BHs’ conserved and thermodynamic quantities are invariant under CTs. By writing the BH mass as a function of charge and entropy, we confirmed validity of the first law of BH thermodynamics for both classes of the BDM BHs. We studied stability properties of the BDM BHs in the CEM and GMs, comparatively. Noting the simultaneous plots of \(\tilde{C}_{\tilde{Q}}\) and \(\tilde{T}\) versus \(r_+\) we argued that, for the BDM BHs with \(\alpha ^2 <1\), following cases are distinguishable: 1) there is only one point of first-order phase transition point which appears at \(r_+=r_{ext}\). The BHs with horizon radii greater than \(r_{ext}\) are locally stable. While those with \(r_+\) less than \(r_{ext}\) have negative temperature and physically are not reasonable. 2) A first-order phase transition occurs at \(r_+=r_{ext}\) and, two second-order phase transition take place at \(r_+=r_{1}\) and \(r_+=r_{2}\) with \(r_{ext}<r_{1}<r_2\). The BHs with horizon radii in the ranges \(r_{ext}<r_+<r_1\) and \(r_+>r_{2}\) are locally stable. Moreover, for the BHs with \(\alpha ^2=1\) there are two points of first-order phase transition located at \(r_+=r_{1ext}\) and \(r_+=r_{2ext}\). The BHs with horizon radius equal to \(r_+=r\), where the SH diverges, experience second-order phase transition and those with horizon radii in the interval \(r_{1ext}<r_+<r\) are locally stable. Comparison of the alternative approaches show that among different thermodynamic metrics those of QII and HPEM are the successful ones. A crucial point is that stability properties or phase transitions of the BHs are identical in both of the Einstein and Jordan frames. It means that this issue remains invariant under CTs.