1 Introduction

The general theory of relativity (GTR), developed by Albert Einstein, is a significant gravitational instrument for understanding the fabric of space-time as well as the dynamics of cosmic bodies and other phenomena. Due to the challenges for obtaining the exact analytic solutions of Einstein field equations describing compact configurations such as strange stars, the theoretical studies modeling have significantly improved, in particular designing fluid sphere models with anisotropic matter distributions i.e. unequal radial and tangential pressure: \(p_r \ne p_t.\) Anisotropies play a significant role in the stability and equilibrium of the stellar structure [1]. There is a wealth of research on the impact of local anisotropy on the global characteristics of relativistic compact objects [2,3,4,5,6,7,8,9].

Now it is quite an interesting fact that according to cosmology, the universe’s apparent matter accounts for only \(5\%\) of gravity, with the rest \(26\%\) and \(69\%\) being explained by dark matter and dark energy, respectively. Dark energy is considered a spatially homogeneous cosmic fluid, although it can be developed to non-homogeneous spherically symmetric spacetimes by assuming that the pressure in the dark energy equation of state is negative radial pressure and that the transverse pressure can be obtained using the field equations [10]. The significance of dark energy is not diminished as the universe expands because it is evenly distributed throughout the universe, both in space and in time. The Supernova Cosmology Project at the Lawrence Berkeley National Laboratory and the High-z Supernova Search Team made observations of type-Ia supernovae (“one-A”) in 1998 [11], which led them to hypothesize that the universe is expanding in accelerating manner. These type-Ia supernovae provide the most concrete evidence for dark energy. Numerous studies have been conducted on compact astrophysical objects whose interior pressure p and energy density \(\rho \) obey an equation of state typical of dark energy, such as \(p = -\rho \). In the literature, these objects have been given a variety of names. For ease of use, we call them “dark energy stars” [12, 13]. Perhaps dark energy’s origins remain a mystery but by observing how quickly the universe is expanding and how quickly large-scale structures like galaxies and clusters of galaxies develop as a result of gravitational instabilities, one can determine the presence of dark energy. Even though dark energy stars have a chance to exhibit spacetime singularities, non-singular dark energy stars are more commonly of interest. Astrophysical measurements made recently have shown that the universe is expanding faster than before. Observationally by using the Hubble Space Telescope, Riess and co-researchers discovered that the universe is expanding \(9 \%\) faster than predicted [14]. Although it works against gravity, dark energy speeds up the universe’s expansion and slows down the development of large-scale structures which leads to the violation of the strong energy condition. We naturally seek local astrophysical appearances of dark energy because of the fundamental significance of the phenomenon in cosmology. The equation of state of dark energy may be explained by \(p = \omega \rho \), with \(\omega < -\frac{1}{3}\) [15, 16]. In this connection, Feng et al. examined different phenomenological interaction models for dark energy and dark matter by performing statistical joint analysis with three different observational data [17]

Recently, novel findings of neutron stars and strange stars that meet the exact solutions of the 4-D Einstein field equations have been made possible by astronomical studies of compact objects. Many researchers have created a large number of precise models using the Einstein–Maxwell field equations [18,19,20,21,22,23]. The most significant and logical explanations for the occurrence of tangential pressures inside a star are the existence of a solid core, the presence of type 3A superfluid, magnetic field, phase transitions, a pion condensation, and electric field [24]. Anisotropic pressures are present in several astronomical objects, including the X-ray pulsar, Her X-1, 4U 1820-30, and SAX J1804.4-3658. In order to have a minimal impact on the structure of the star, it is true that all macroscopic entities are charged or that they may have a minor amount of charge, as proposed by Glendening [25]. So, as it is possible to claim that stable charged astrophysical compact objects exist in nature, we have chosen to study the charged case. The electrostatic repulsion of the Coulomb force and the outward pressure gradient will balance the gravitational contraction in the presence of charge. In this scenario, a point singularity caused by the gravitational collapse of a spherically symmetric matter distribution with charge may be removed [26]. Ray et al. studied the effect of electric charge in compact stars assuming that the charge distribution is proportional to the mass density and the relativistic hydrostatic equilibrium equation, i.e., the Tolman–Oppenheimer–Volkoff equation, gets modified due to the inclusion of electric charge [27]. The dynamics of cold star models, compact stars, strange stars, and other stellar configurations with the hybrid coupling of strange matter have been the subject of continuous research during the last decade [28,29,30,31,32,33,34,35,36,37,38,39,40,41].

On the other hand recently many models of particular dark energy stars have been put out in literature [42,43,44,45,46,47]. Bhar and her co-workers have already suggested a model that might be helpful in examining the possible clustering of dark energy and also very recently proposed a model for a dark energy star made up of dark and ordinary matter in which the density of dark energy is proportional to the density of isotropic perfect fluid matter. In-depth research was done on the stability of stellar configuration as well as the model’s physical characteristics such as pressure, density, mass function, and surface redshift [48, 49].

In this paper, we provide a model for a charged strange star coupled to inhomogeneous anisotropic dark energy in Tolman–Kuchowicz spacetime. Here, we made the assumption that the isotropic perfect fluid matter density is proportional to the radial pressure that dark energy exerts on the system. Here, in this case of Einstein–Maxwell field equation one has eight unknown functions i.e. {\(\rho \), \(\rho ^{de}\), p, \(p^{de}_r\), \(p^{de}_t\), \(\nu \), \(\lambda \), E} and four equations. Therefore, in order to solve this system it is necessary to give additional information or conditions that have been discussed in our work. We have described the fundamental field equations for a charged strange star model when inhomogeneous anisotropic dark energy is present in the system. There is a detailed picture of our used metric coefficients. The solutions to the field equations and a smooth correspondence between internal and external spacetime are discussed. A rigorous discussion has been made regarding the physical study of our current model. Also, we summarise some key findings on the formation of a dense, stable stellar structure by the dark energy’s repulsive scalar field.

Our present article is designed as follows. It has five core sections. We have described the technique to solve Einstein–Maxwell field equations for charged static and spherically symmetric matter distribution coupled with dark energy by employing the well-known Tolman–Kuchowicz Metric in Sect. 2 and we fix the constants of our model using junction conditions for a particular compact star candidate Her X - 1. We have analyzed the physical attributes of our model in the next Sect. 3. We perform the stability analysis through different aspects and check the equilibrium of forces for our present model in Sect. 4. In the final Sect. 5, the key findings of our current investigation have been discussed with some concluding remarks.

2 Solutions of Einstein–Maxwell field equations

In order to describe the interior space-time of a static spherically symmetric compact object, here we consider the interior line element in a static spherically symmetric 4D space-time in the Schwarzchild coordinate system \((x^i=t,\,r,\,\theta ,\,\phi )\) as follows,

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(1)

Let us assume that the energy–momentum tensor for an anisotropic charged with two fluids is composed of matter with matter-energy density \(\rho \), pressure p of the corresponding baryonic matter, electric field intensity E, and ‘dark’ energy density \(\rho ^{de}\), corresponding radial pressure \(p_r^{de}\), and tangential pressure \(p_t^{de}\) respectively. The sub-index “de” stands for dark energy throughout the paper. This dark energy density can be expressed in terms of the (variable) cosmological constant (\(\Lambda \)) as \(\rho ^{\textrm{de}}=\frac{\Lambda }{8\pi }\) [50].

We can write the corresponding energy–momentum tensor for an anisotropic charged with two fluids [50] as,

$$\begin{aligned} \begin{array}{l} \left. \begin{aligned} T_0^0 &{}=\rho ^{\textrm{eff}}+E^2= (\rho +\rho ^{de}) +E^2, \\ T_1^1 &{}=-p_r^{\textrm{eff}}+E^2=-(p+p_r^{de}) +E^2, \\ T_2^2 &{}=T_3^3=-p_t^{\textrm{eff}}-E^2=-(p+p_t^{de}) -E^2 ,\\ T_0^1 &{}=T_1^0=0. \end{aligned}\right\} \end{array} \text {Energy-Momentum Tensor} \end{aligned}$$
(2)

where, \(\rho ^{\textrm{eff}}=(\rho +\rho ^{de}\)), \(p_r^{\textrm{eff}}=(p+p_r^{de}\)), and \(p_t^{\textrm{eff}}=(p+p_t^{de}\)) are the effective energy density and pressure components respectively.

Now assuming geometricized unit system (\(G = c = 1\)), the Einstein–Maxwell field equations are given as follows,

$$\begin{aligned}{} & {} T_0^0:~\kappa (\rho +\rho ^{de}) +E^2 =e^{-\lambda }\left( \frac{\lambda '}{r}-\frac{1}{r^{2}} \right) +\frac{1}{r^{2}}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} T_1^1:~\kappa (p+p_r^{de}) -E^2 =e^{-\lambda }\left( \frac{1}{r^{2}}+\frac{\nu '}{r} \right) -\frac{1}{r^{2}}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} T_2^2=T_3^3:~\kappa (p+p_t^{de}) +E^2 \nonumber \\{} & {} \qquad \!= \frac{1}{2}e^{-\lambda } \left( \frac{\nu '^{2}}{2}+\nu ''-\frac{\lambda '\nu '}{2}+\frac{\nu '-\lambda '}{r}\right) \end{aligned}$$
(5)

where prime \((^{\prime })\) denotes the derivative with respect to the radial coordinate ‘r’ and \(\kappa =8\pi \).

Here E is the electric field intensity, \(\sigma =\sigma (r)\) is the proper charge density connected by the relation,

$$\begin{aligned} \kappa \sigma= & {} \frac{2}{r^2} e^{-\lambda /2} (r^2 E)', \end{aligned}$$
(6)

Equation (6) can also be equivalently expressed as,

$$\begin{aligned} E(r)= & {} \frac{\kappa }{2r^2} \int _0^r \sigma r^2 e^{\lambda /2} dr = \frac{q(r)}{r^2}, \end{aligned}$$
(7)

where q(r) represents the total charge contained within the sphere of radius r under consideration.

For our present paper we have taken the well-known metric potentials proposed by Tolman–Kuchowicz [51, 52] (henceforth TK ansatz) as,

$$\begin{aligned} \begin{array}{l} \left. \begin{aligned} \nu (r)= Br^2+2\ln D,\\ \lambda (r)= \ln (1 + ar^2 + br^4) \end{aligned}\right\} \end{array} \text {Tolman-Kuchowicz Metric} \end{aligned}$$
(8)

where a, B and b are constants with units \(\hbox {km}^{-2}\), \(\hbox {km}^{-2}\) and \(\hbox {km}^{-4}\), respectively. D is a dimensionless constant. We shall calculate the numerical values of these constants from a smooth matching of interior and exterior spacetimes. The metric potentials provide a non-singular stellar model which will be described in the coming sections.

With the help of the expressions given in (8), the field equations (3)–(5) take the following form:

$$\begin{aligned}{} & {} \kappa (\rho +\rho ^{de}) +E^2 = \frac{3 a + (a^2 + 5 b) r^2 + 2 a b r^4 + b^2 r^6}{(1 + a r^2 + b r^4)^2}, \nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \kappa (p+p_r^{de}) - E^2 = \frac{2B-a -b r^2}{1 + a r^2 + b r^4}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \kappa (p+p_t^{de}) +E^2 \nonumber \\{} & {} \quad = \frac{2B - a + \big ( B (a + B)-2 b\big ) r^2 + a B^2 r^4 + b B^2 r^6}{(1 + a r^2 + b r^4)^2}.\nonumber \\ \end{aligned}$$
(11)

2.1 Assumption of equation of state due to the dark energy

Obtaining the explicit solutions of the above field equations (9)–(11) is too much complicated due to its non-linearity nature, although the system of equations is mathematically well defined. So to remove this complicacy, we have adopted three assumptions as proposed earlier by the authors mentioned in the Refs. [50, 53, 54] given as follows:

  1. (i)

    The radial dark pressure (\(p_r^{de}\)) is proportional to the density corresponding to dark energy, i.e.,

    $$\begin{aligned} p_r^{de}=-\rho ^{de}, \end{aligned}$$
    (12)
  2. (ii)

    The density corresponding to dark energy (\(\rho ^{de}\)) is proportional to the normal baryonic matter density, i.e.,

    $$\begin{aligned} \rho ^{de}=\alpha \rho , \end{aligned}$$
    (13)

    where \(\alpha (>0)\) is a proportionality constant. Here we called it “coupling parameter”. Clearly, we see that this type of equation of state corresponds to dark energy and is similar to the MIT Bag model for hadrons [25]. The above dark energy EoS relates to the MIT Bag model’s Bag constant contribution. Here we assume the Bag constant to be density-dependent. In astrophysical models of hybrid stars with a deconfined phase of quarks at the core, the MIT Bag model is employed.

  3. (iii)

    lastly, upon following these earlier works in Refs. [26, 54] we preferably assume the difference between radial and tangential pressure corresponding to dark energy is proportional to the square of the electric field intensity E, i.e.

    $$\begin{aligned} p_t^{de} - p_r^{de} = \frac{E^2}{4\pi } \end{aligned}$$
    (14)

2.2 Proposed model of dark energy star

Now solving the Eqs. (9)–(11) by the help of these above assumptions (12)–(14), we obtain the explicit expressions for \(\rho \), p and \(E^2\) as,

$$\begin{aligned} \rho= & {} \frac{12a + (3 a^2 + 21 b + a B - B^2)r^2 + (6 a b + 2 b B - a B^2)r^4 + b (3 b - B^2)r^6}{4\kappa (1 + \alpha ){(1 + ar^2 + br^4)}^2}, \end{aligned}$$
(15)
$$\begin{aligned} p= & {} \frac{1}{4\kappa (1 + \alpha ){(1 + ar^2 + br^4)}^2}\Bigg [a (-4 + 8 \alpha ) + 8 (1 + \alpha ) B + \big (-3 a^2 + (-5 + 16 \alpha ) b + a (7 + 8 \alpha ) B + B^2 \big ) r^2 \nonumber \\{} & {} + \big (2 (3 + 4 \alpha ) b B + a (-6 b + B^2)\big ) r^4 + b (-3 b + B^2) r^6 \Bigg ], \end{aligned}$$
(16)
$$\begin{aligned} E^2= & {} \frac{r^2 \Big [a^2 - a B + B^2 + a (2 b + B^2) r^2 + b \Big (-1 - 2 B r^2 + (b + B^2) r^4\Big )\Big ]}{4 (1 + a r^2 + b r^4)^2}. \end{aligned}$$
(17)

The charge density (\(\sigma \)) is obtained from Eq. (6)as,

$$\begin{aligned} \sigma= & {} \frac{(r^2 E)^{'}}{4\pi r^2\sqrt{e^\lambda }} \nonumber \\= & {} \frac{1}{\kappa (1 + ar^2 + br^4)^{\frac{7}{2}} \sqrt{\frac{r^2[a^2 - aB + B^2 + a(2b + B^2)r^2 + b\{-1 - 2Br^2 + (b + B^2)r^4\}]}{(1 + ar^2 + br^4)^2}}}\nonumber \\{} & {} \times \Bigg [3(a^2 - b - aB + B^2)r + (a^3 + 7ab - {a^2}B - 8bB + 5aB^2)r^3 \nonumber \\{} & {} + \{3b(a^2 + 2b) - 3abB + 2(a^2 + 2b)B^2\}r^5 + 3ab(b + B^2)r^7 + b^2(b + B^2)r^9\Bigg ] \end{aligned}$$
(18)

The expressions for matter-energy density, radial and transverse pressure due to the dark energy are obtained as,

$$\begin{aligned} \rho ^{de}= & {} \frac{\alpha [12a + (3 a^2 + 21 b + a B - B^2)r^2 + (6 a b + 2 b B - a B^2)r^4 + b (3 b - B^2)r^6]}{4\kappa (1 + \alpha ){(1 + ar^2 + br^4)}^2}, \end{aligned}$$
(19)
$$\begin{aligned} p_r^{de}= & {} - \frac{\alpha [12a + (3 a^2 + 21 b + a B - B^2)r^2 + (6 a b + 2 b B - a B^2)r^4 + b (3 b - B^2)r^6]}{4\kappa (1 + \alpha ){(1 + ar^2 + br^4)}^2}, \end{aligned}$$
(20)
$$\begin{aligned} p_t^{de}= & {} \frac{1}{4\kappa (1 + \alpha ){(1 + ar^2 + br^4)}^2}\Bigg [-12a\alpha - \{a^2(-2 + \alpha )\nonumber \\{} & {} + (2 + 23\alpha )b + a(2 + 3\alpha )B - (2 + 3\alpha )B^2\}r^2 \nonumber \\{} & {} +\{-2a(-2 + \alpha )b - 2(2 + 3\alpha )bB + a(2 + 3\alpha )B^2\}r^4 \nonumber \\{} & {} + b\{-(-2 + \alpha )b + (2 + 3\alpha )B^2\}r^6\Bigg ]. \end{aligned}$$
(21)

The expressions for effective matter-energy density, effective radial and transverse pressure for our present model are obtained as,

$$\begin{aligned} \rho ^{\textrm{eff}}= & {} \rho + \rho ^{de} \nonumber \\= & {} \frac{12a + (3a^2 + 21b + aB - B^2)r^2 + (6ab + 2bB - aB^2)r^4 + b(3b - B^2)r^6}{4\kappa {(1 + ar^2 + br^4)}^2}, \end{aligned}$$
(22)
$$\begin{aligned} p_r^{\textrm{eff}}= & {} p + p_r^{de} \nonumber \\= & {} \frac{-4a + 8B + (-3a^2 -5b + 7aB + B^2)r^2 + \{6bB + a(-6b +B^2)\}r^4 + b(-3b + B^2)r^6}{4\kappa {(1 + ar^2 + br^4)}^2}, \end{aligned}$$
(23)
$$\begin{aligned} p_t^{\textrm{eff}}= & {} p + p_t^{de} \nonumber \\= & {} \frac{-4 a + 8 B - (a^2 + 7 b - 5 a B - 3 B^2) r^2 - (2 a b - 2 b B - 3 a B^2) r^4 - b (b - 3 B^2) r^6}{4\kappa {(1 + ar^2 + br^4)}^2}. \end{aligned}$$
(24)

2.3 Determination of constants using junction or matching conditions

In order to develop the profiles of the model parameters, the values of a, b, B, and D must be fixed. So as to investigate the significant values of unknown constants, we match our interior space-time smoothly to the exterior space-time described by the Reissner–Nordström metric [55, 56] given by

$$\begin{aligned} ds_{\Sigma }^{2}= & {} -\left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) dt^2 + \left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) ^{-1}dr^2 \nonumber \\{} & {} + r^2(d\theta ^2+\sin ^2\theta d\phi ^2), \end{aligned}$$
(25)

where Q is the total charge enclosed within the surface \(r = R\). Now the continuity of the metric coefficients \(g_{tt}\), \(g_{rr}\) and \(\frac{\partial g_{tt}}{\partial r}\) across the boundary surface \(r= R\) between the interior and the exterior regions give the following set of relations:

$$\begin{aligned} 1 - 2\tilde{{\mathcal {X}}}+ \tilde{\mathcal {Y}} = e^{\nu (R)}= & {} D^2 e^{BR^2}, \end{aligned}$$
(26)
$$\begin{aligned} 1 - 2\tilde{\mathcal {X}} + \tilde{\mathcal {Y}} = e^{-\lambda (R)}= & {} (1 + a R^2 + b R^4)^{-1}, \end{aligned}$$
(27)
$$\begin{aligned} \tilde{\mathcal {X}} - \tilde{\mathcal {Y}} = R\Big [ \frac{\partial }{\partial r} e^{\nu (r)} \Big ]_{r=R}= & {} B R^2 D^2 e^{BR^2}. \end{aligned}$$
(28)

where, \(\tilde{\mathcal {X}}=\frac{M}{R}\) and \(\tilde{\mathcal {Y}}=\frac{Q^2}{R^2} \) and both \(\tilde{\mathcal {X}},\,\tilde{\mathcal {Y}}\) are dimensionless quantity.

Solving the Eqs. (26)–(28) along with the condition \(p(r=R)=0\), we determine the values of the constants B, D, a and b as,

$$\begin{aligned} B= & {} \frac{M R -Q^2 }{R^2 \Big [Q^2 + R (R-2 M )\Big ]}, \end{aligned}$$
(29)
$$\begin{aligned} D= & {} e^{-BR^2 /2}\sqrt{1 - 2\tilde{\mathcal {X}}+ \tilde{\mathcal {Y}}}, \end{aligned}$$
(30)
$$\begin{aligned} a= & {} -\frac{1}{R^2} - b R^2 + \frac{1}{Q^2 - 2 M R + R^2}, \end{aligned}$$
(31)
$$\begin{aligned} b= & {} \frac{1}{R^4 (1 - 8 \alpha + B R^2) \Big [Q^2 + R (R-2 M )\Big ]^2}\nonumber \\{} & {} \times \Bigg [Q^4 (1 - 8 \alpha + B R^2) \nonumber \\{} & {} + Q^2 R \Big \{4 R - 8 \alpha R + (9 + 8 \alpha ) B R^3 + B^2 R^5 \nonumber \\{} & {} + 4 M (-1 + 8 \alpha - B R^2)\Big \} + R^2 \Big \{4 M^2 (1 - 8 \alpha + B R^2) \nonumber \\{} & {} + B R^4 (8 + 8 \alpha + B R^2) - 2 M R \Big (4 + 8 \alpha (-1 + B R^2)\nonumber \\{} & {} + B R^2 (9 + B R^2)\Big )\Big \}\Bigg ] \end{aligned}$$
(32)

Thus, we have successfully obtained the values of all constants present in our model in terms of M, R, and Q. From (31) and (32) we see that a and b are functions of dark energy coupling parameter \(\alpha \). Now to analyze the physical attributes of our present model we have considered here particularly the compact star Her X - 1 with observed mass and radius \(M = 0.85 \pm 0.15~M_{\odot },\, R = 8.1_{-0.41}^{+0.41}\) km [57]. Along with this, we have also assumed \(Q = 1.31\). The reason behind this particular choice is that according to earlier work by Varela et al. [58], the square of the charge-radius ratio \(\big (\frac{Q^2}{R^2}\big )\) for a charged anisotropic fluid sphere should lie within the interval [0, 0.543). For our chosen compact object HER X-1, the value is \(\frac{Q^2}{R^2} = 0.0237522\) (Approx.), i.e. within the proposed range, and thus we strengthen our numerical calculations as well as graphical analysis.

3 Analysis of stellar physical attributes

3.1 Regularity of metric potentials

Here we have analyzed the behavior of the metric potential temporal components \(e^{\nu (r)}\) and spatial components \(e^{\lambda (r)}\). We can easily check that, \([{e^{\nu (r)}}]_{r = 0}= D^2\), a non-zero constant, and \([{e^{-\lambda (r)}}]_{r=0} = 1\) and which lead to the fact that both metric potential components are finite at the centre and having regularity at all points, \(r < R\) [59, 60]. Moreover, \(\Big [\frac{d(e^{\nu (r)})}{dr}\Big ]_{r=0} = (2B{D^2}r{e^{Br^2}})\Big |_{r=0} =0\) and

\(\Big [\frac{d(e^{\lambda (r)})}{dr}\Big ]_{r=0} = (2ar + 4br^3)\Big |_{r=0} =0\),

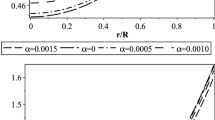
i.e. the derivatives of the metric potential components vanish at the center of the star. They are also positive and consistent within the interior of the star which can be easily verified from the radial profiles of the metric coefficient components shown in Fig. 1. Here we have shown the regularity of the metric potentials with varying coupling parameters \(\alpha \). The internal space-time smoothly matches with the asymptotically flat exterior space-time at the surface (\(r = R\)), fulfilling the Darmois–Israel condition [61,62,63]. By matching these, we obtain the values of the constant parameters that characterize our model. Thus we verify that the metric potential components are well-behaved within the range (0, R).

Fig. 1
figure 1

Variation of metric functions \(e^{-\lambda (r)}\) and \(e^{\nu (r)}\) with respect to ‘r’ with required magnified inset

Full size image

3.2 Stellar profiles of baryonic matter-energy density, pressure, and electric field

The density of the confined matter plays a key role in determining how stable a star structure is against gravitational collapse and similarly pressure plays a significant role in defining the stellar boundary and overall stability [64]. From Eqs. (15) and (16), we get the central values of \(\rho ~ \text {and}~ p\) as, \(\rho _c= [\rho ]_{r=0} = \frac{3a}{\kappa (1 + \alpha )} > 0\), \(p_c= [p]_{r=0} = \frac{a(-1 + 2 \alpha ) + 2 (1 + \alpha ) B }{\kappa (1 + \alpha )} >0\). Figure 2 indicates that matter-energy density and pressure are monotonic decreasing functions of radius r, having the maximum value at the center of the star. \([E^2]_{r=0} = 0.\) i.e. electric field intensity vanishes at the center and gradually increases when r increases as shown in Fig. 2. Finally, it is also observed that \(\rho \), p, and \(E^2\) inside the star are non-negative. We have represented the numerical values of central density (\(\rho _c\)), surface density (\(\rho _s\)), central pressure (\(p_c\)) and the central pressure-density ratio \(p_c/\rho _c\) in Table 1 for different values of the dark energy coupling parameter \(\alpha \).

Furthermore, the density and pressure gradients of the normal baryonic matter for our present model are obtained as,

$$\begin{aligned} \frac{d\rho }{dr}= & {} \frac{r}{2\kappa (1 + \alpha )(1 + ar^2 + br^4)^3}\big [-21a^2 + 21b + aB \nonumber \\{} & {} - B^2 - \{3a^3 + a^2B -4bB + a(57b + B^2)\}r^2 \nonumber \\{} & {} - 3b\{18b + a(3a + B)\}r^4 \nonumber \\{} & {} + b\{-4bB + a(-9b + B^2)\}r^6 \nonumber \\{} & {} + b^2(-3b + B^2)r^8\big ], \end{aligned}$$
(33)
$$\begin{aligned} \frac{dp}{dr}= & {} \frac{r}{2\kappa (1 + \alpha )(1 + ar^2 + br^4)^3}\big [B^2 + 3a^3 r^2 \nonumber \\{} & {} + a^2\{5 - 16\alpha -(7 + 8\alpha )Br^2 + 9br^4\} \nonumber \\{} & {} +a\{-(9 + 8\alpha )B +((9 - 48\alpha )b + B^2))r^2 \nonumber \\{} & {} - 3(7 + 8\alpha )bBr^4 + b(9b - B^2)r^6\} \nonumber \\{} & {} + b\{-5 + 16\alpha - 4(5 + 4\alpha )Br^2 \nonumber \\{} & {} + 6(1- 8\alpha )br^4 - 4(3 + 4\alpha )bBr^6 \nonumber \\{} & {} + b(3b - B^2)r^8\} \big ] \end{aligned}$$
(34)

From Fig. 3, we see that the density and pressure gradients stay negative throughout the fluid sphere and vanish at the core. Also, taking second derivative of \(\rho , p\) we get,

$$\begin{aligned} \Big [\frac{d^2\rho }{dr^2}\Big ]_{r=0}= & {} -\frac{21a^2 -21b -aB + B^2}{2\kappa (1 + \alpha )},\\ \Big [\frac{d^2 p}{dr^2}\Big ]_{r=0}= & {} -\frac{a^2(\alpha - 5) + (16 \alpha -5)b + a(9 + 8\alpha )B - B^2}{2\kappa (1 + \alpha )} \end{aligned}$$

Clearly, the second derivatives take negative values at the center for the dark energy coupling parameter range, \(\alpha \in [0.40, 0.80]\) that we have considered in this investigation and hence we can conclude that both the density and pressure take the maximum value at the core of the stellar configuration.

Fig. 2
figure 2

Profiles of baryonic matter-energy density, pressure, and electric field intensity (\(E^2\)) with respect to ‘r’ with required magnified inset

Full size image
Table 1 The numerical values of \(\alpha \), central density \((\rho _c)\), surface density \((\rho _s)\), central pressure \((p_c)\), compactness ratio (u), surface redshift \((z_s)\), \(p_c/\rho _c\), mass (\(M_{\odot }\)) have been shown for compact star, Her X-1
Full size table
Fig. 3
figure 3

Gradients of matter density and pressure are plotted ‘r’

Full size image
Fig. 4
figure 4

The variation of dark energy density and dark pressure with respect to ‘r’

Full size image

3.3 Dark energy density and dark pressure

In physical cosmology, dark energy is a fictitious type of energy that fills all of space and has the tendency to accelerate the universe’s expansion [65]. It is termed as “dark” because it does not have an electric charge and does not interact with electromagnetic radiation such as light. Dark energy has the reverse effect of positive energy in that it accelerates the expansion of the universe. Dark energy currently occupies over three-quarters of the total mass energy of the universe, according to the conventional cosmological model. Dark energy has recently been employed as an important factor in an attempt [66] to develop a cyclic model of the universe. Unusually, dark energy causes the universe’s expansion because it has very strong negative pressure. This negative pressure induces gravitational repulsion.

In this work, the repulsive nature of dark energy is simulated so that energy density remains positive (\(\rho ^{de}>0\)) and radial dark pressure are negative (\(p_r^{de}<0\)). We have graphically displayed the profiles of dark energy density, radial dark pressure, and transverse dark pressure in Fig. 4. As derived from seed assumption  (14), we can check from Fig. 4 that transverse dark pressure \(p_t^{de}\) remains negative in most of the regions and positive near stellar surface. It is seen that dark energy density gradually decreases within the stellar configuration and its maximum value is at the center. Also from Eq. (19), we get the maximum value, \(\rho ^{de}_{max} = [\rho ^{de}]_{r=0} = \frac{3a\alpha }{\kappa (1+\alpha )}\). Whereas, dark pressures are gradually increasing with \('r'\) whatever the value of \(\alpha \) is. For our model, it is also interesting that at the center \((r = 0)\), \(p^{de}_r = p^{de}_t = - \rho ^{de}_{max}\).

3.4 Mass–radius relationship and compactness factor

We know that the active mass depends on the density profile and it increases with the confining radius [25, 67] as it being gravitationally confined to a finite spatial extent \((r = R)\). We can easily measure the mass function m(r) for an electrically charged fluid sphere by computing the integral connected directly to the energy density (15) using the following expression [68, 69],

$$\begin{aligned} m(r)=4\pi \int ^r_0{\Big (\rho r^2+ r \sigma q e^{\lambda /2}\Big )\,dr},~~~ \end{aligned}$$
(35)

Now employing the metric potentials on (35) we obtain,

$$\begin{aligned} m(r)=\frac{r}{2}\Big (1-e^{-\lambda (r)}+\frac{q^2}{r^2}\Big ). \end{aligned}$$
(36)

This is to be noted that mass function m(r) is a function of r satisfying \(m(r = 0) = 0\) whereas \(m(r = R) = M\). The variation of mass function (35) has been plotted against r with varying \(\alpha \) in Fig. 5.

Clearly mass is regular at the center as it is directly proportional to the radial distance r and maximum mass is attained at the surface \(r=R\) as displayed in Fig. 5.

Fig. 5
figure 5

The mass function and compactness factor are plotted against ‘r’ with required magnified inset

Full size image

Furthermore, the compactness factor is determined by a dimensionless parameter \(u(r) = \frac{m(r)}{r}\). The behavior of compactness factor u(r) is shown in Fig. 5 and see that u(r) increases with r for different values of \(\alpha \).

3.5 Surface redshift and gravitational redshift

The surface redshift \(z_s(r)\) for our model is obtained by using the expression of compactness factor u(r) as, \(z_s(r)=\frac{1}{\sqrt{1-2u(r)}}-1\). We have shown the variation of \(z_s(r)\) in Fig. 6 from center to surface. The surface redshift depends on the stellar mass and star radius, in other words on the surface gravity. In Table 1, we present the numerical results of compactness factor (u(R)), surface redshift (\(z_s(R)\)) and mass (in \(M_{\odot })\)) for different values of the dark energy coupling parameter \(\alpha \). From Table 1, we notice that compactness factor (u(R)), surface redshift (\(z_s(R)\)) and mass (in \(M_{\odot })\)) decrease with increasing \(\alpha \) in our chosen range [0.40,  0.80].

Fig. 6
figure 6

Surface redshift and gravitational redshift are plotted against ‘r’ with required magnified inset

Full size image

On the other hand, the gravitational redshift (or interior redshift) \(z_g(r)\) within a static line element can be expressed as, \(z_g(r)=e^{-\frac{\nu (r)}{2}}-1\). We see that \(z_g(r)\) is maximum at the center and gradually decreases with the increasing radius to attain its minimum at the surface. We have plotted the variation of \(z_g(r)\) in Fig. 6. From these figures, we can easily check that the surface redshift and gravitational redshift have totally opposite trends throughout our model.

The actual reason behind this above trend is that if a photon travels from the center to the stellar surface, it must traverse a much denser region and a longer path, resulting in greater dispersion and a significant loss of energy. This energy must be lost by changing frequency rather than changing speed. When the energy of a photon decreases, so does its frequency. This results in a transition to the red end of the electromagnetic spectrum or an increase in the photon’s wavelength. On another side, when a photon discharges from near the surface, it must travel through a less dense zone and along a shorter trajectory, resulting in lesser dispersion and less loss of energy. As a result, the gravitational (or internal) redshift is minimum at the surface and maximum at the center. On the other side, the surface redshift is maximum near the surface and diminishes towards the core as the radius increases slightly with an increase in mass producing a larger surface gravity. Also from both figures, we can easily check that both types of redshifts have no singularity throughout their configuration.

4 Stability analysis of our model and equilibrium of forces

4.1 Critical stability bound on mass–radius ratio

The mass–radius (M–R) ratio of a compact star cannot be arbitrarily large for physically realistic models. According to Buchdahl [67], for a perfect fluid sphere model without charge, the M–R ratio must satisfy the inequality \(\frac{2M}{R}<\frac{8}{9}\). This upper limit of the M–R ratio was computed using a perfect fluid with decreasing energy density near the boundary. But the presence of electric charge modifies this Buchdahl limit. BÖhmer and Harko [70] suggested the generalized expression of the lower limit for a charged compact object as given following:

$$\begin{aligned} \frac{Q^{2}\left( 18\,R^{2}+Q^{2}\right) }{R^{2}\left( 12\,R^{2}+Q^{2}\right) } \le \frac{2M}{R}. \end{aligned}$$
(37)

Andréasson [71] then showed that, for a relativistic charged sphere, to attain critical stability the model must satisfy the following inequality:

$$\begin{aligned} \sqrt{M} \le \frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9}+\frac{Q^2}{3R}}. \end{aligned}$$
(38)

Now combining these two inequalities (37) and (38), we get both lower and upper bound of \(\frac{M}{R}\) as given following:

$$\begin{aligned} \frac{Q^{2}\left( 18\,R^{2}+Q^{2}\right) }{2\,R^{2}\left( 12\,R^{2}+Q^{2}\right) } \le \frac{{M}}{R}\le \frac{1}{R}\Bigg [\frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9}+\frac{Q^2}{3R}}\Bigg ]^2.\nonumber \\ \end{aligned}$$
(39)

The above inequality (39) is sharp and this sharpness is attained by arbitrarily thin shell solutions [71].

4.2 Causality condition via Herrera’s cracking approach

Now in this subsection, we will discuss another important “physical acceptability condition” for realistic models known as the causality condition using sound velocity along with Herrera’s cracking approach. We start by talking about our model’s causality condition, which states that the square of sound velocity \(V^2\)=\(\frac{dp}{d\rho }\) should be less than unity for a physically realistic model [72, 73]. This means that the speed of sound is not faster than the speed of light. Thus employing expressions (22)–(24), we calculate the effective radial and tangential velocity components for our anisotropic model as,

$$\begin{aligned} V_r^2= & {} \frac{dp_r^{\textrm{eff}}}{d\rho ^{\textrm{eff}}} ~~\textrm{and} \end{aligned}$$
(40)
$$\begin{aligned} V_t^2= & {} \frac{dp_t^{\textrm{eff}}}{d\rho ^{\textrm{eff}}}. \end{aligned}$$
(41)

Because of the complicacy of their analytic expressions, we have analyzed them graphically in Fig. 7 and observe that both lie between the desired range (0, 1) within the stellar object. We clearly notice that the sound velocity components are always positive irrespective of matter density. Hence the causality condition is satisfied for our proposed charged dark energy star model. The unnatural behavior at the initial of the plots of sound velocity components is due to the consideration of well-known dark energy EoS (13) which is similar to the MIT Bag model for hadrons, which may define the quark matter inside the stellar system. Thus these kinds of behavior occur in these plots due to the presence of quark matter inside the stellar system.

Moreover, Herrera has put out the “cracking” (or overturning) technique [72] for relativistic stellar objects under minor radial perturbations. Abreu et al. used the idea of cracking in their research [73] and propose the idea of stability factor, mathematically defined as \(|V_t^2-V_r^2|<1\). The profile of this stability factor is also plotted in Fig. 7 and we see that this condition is also satisfied throughout our model. Henceforth, our model is physically stable and well-behaved.

Fig. 7
figure 7

Square of sound velocity components and the stability factor \(|V_t^2-V_r^2|\) are plotted against ‘r’ with required magnified inset

Full size image

4.3 Energy conditions

Here we shall investigate the energy conditions (ECs) of a charged fluid sphere model coupled to anisotropic dark energy according to the relativistic classical field theories of gravitation. In the context of GR, the ECs are local inequalities that define a relation between matter-energy density and pressure that obeys certain bounds. An anisotropic-charged fluid sphere should satisfy the four standard, model-independent, pointwise ECs termed as (i) null energy condition (NEC), (ii) weak energy condition (WEC), (iii) strong energy condition (SEC), and (iv) dominant energy condition (DEC) [71, 74,75,76,77]. For our present model, the corresponding effective energy conditions must hold simultaneously throughout the stellar model and these are given by these following inequalities:

  • NEC: \(\rho ^{\textrm{eff}}+ p_r^{\textrm{eff}} + \frac{E^2}{4\pi } \ge 0,~\rho ^{\textrm{eff}}+ p_t^{\textrm{eff}} + \frac{E^2}{4\pi } \ge 0\),

  • WEC: \(\rho ^{\textrm{eff}}+ p_r^{\textrm{eff}} + \frac{E^2}{4\pi } \ge 0,~\rho ^{\textrm{eff}}+ p_t^{\textrm{eff}} + \frac{E^2}{4\pi } \ge 0,~ \rho ^{\textrm{eff}} + \frac{E^2}{8\pi } \ge 0\),

  • SEC: \(\rho ^{\textrm{eff}}+ p_t^{\textrm{eff}} + \frac{E^2}{4\pi } \ge 0,~\rho ^{\textrm{eff}} + p_r^{\textrm{eff}} + 2p_t^{\textrm{eff}}+ \frac{E^2}{4\pi } \ge 0\),

  • DEC: \(\rho ^{\textrm{eff}}\!-\!|p_r^{\textrm{eff}}| \!+\! \frac{E^2}{4\pi } \!\ge \! 0,~ \rho ^{\textrm{eff}}-|p_t^{\textrm{eff}}| + \frac{E^2}{4\pi } \ge 0,\rho ^{\textrm{eff}} + \frac{E^2}{8\pi } \ge 0\).

From Fig. 8, we clearly see that our proposed dark energy star model satisfies the above bounds of all energy conditions straightforwardly for all r. Hence, our model is physically realistic.

Fig. 8
figure 8

Behaviour of energy conditions vs. radius ‘r’ with required magnified inset

Full size image

4.4 Hydrostatic equilibrium via modified TOV equation

Now we shall investigate the hydrostatic equilibrium for our present model in the presence of dark energy. To check the equilibrium of our model under various forces acting on it, we shall employ the Tolman–Oppenheimer–Volkoff equation, which is described by [50, 78]:

$$\begin{aligned}{} & {} -\frac{M_G(r)(\rho +p)}{r^2}e^{(\lambda -\nu )/2}-\frac{dp}{dr}-\frac{dp_r^{de}}{dr}\nonumber \\{} & {} \qquad +\frac{2}{r}(p_t^{de}-p_r^{de})+\sigma Ee^{\lambda /2}=0, \end{aligned}$$
(42)

proposed by Tolman, Oppenheimer, and Volkoff and thus named as TOV equation.

Where \(M_G(r)\) is effective gravitational mass inside a sphere of radius r as obtained from the Tolman-Whittaker formula [79] and Einstein’s field equations and is expressed as,

$$\begin{aligned} M_G(r)=\frac{1}{2}r^2 \nu ' e^{(\nu - \lambda )/2}. \end{aligned}$$
(43)

Substituting the expression of \(M_G(r)\) in Eq. (42), we obtain,

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p)-\frac{dp}{dr}-\frac{dp_r^{de}}{dr}+\frac{2}{r}(p_t^{de}-p_r^{de})+\sigma Ee^{\lambda /2}=0. \end{aligned}$$
(44)

The above equation (43) can also be written as,

$$\begin{aligned} F_g + F_h + F_d + F_e=0, \end{aligned}$$
(45)

where \(F_g, F_h\), \(F_e\) represent the gravitational, hydrostatic-gradient, and electric force respectively whereas another force term \(F_d\) arises due to dark energy given as follows:

$$\begin{aligned} \text {Gravitational force:}~ F_g= & {} -\frac{\nu '}{2}(\rho +p) \end{aligned}$$
(46)
$$\begin{aligned} \text {Hydrostatic-gradient force:}~ F_h= & {} -\frac{dp}{dr} \end{aligned}$$
(47)
$$\begin{aligned} \text {Dark energy force:}~ F_d= & {} -\frac{dp_r^{de}}{dr}+\frac{2}{r}(p_t^{de}-p_r^{de})\nonumber \\ \end{aligned}$$
(48)
$$\begin{aligned} \text {Electric force:}~ F_e= & {} \sigma Ee^{\lambda /2}. \end{aligned}$$
(49)
Fig. 9
figure 9

Behavior of different forces, such as the gravitational force \(F_g\), hydrostatic gradient force \(F_h\), dark energy force \(F_d\) and electric force \(F_e\) respectively versus radial coordinate r for different values of \(\alpha \). Here \(F_{\textrm{Sum}}=F_g + F_h +F_d + F_e\)

Full size image

We can check the behavior of the generalized TOV equations from Fig. 9 and the system is counterbalanced by all these four forces present in our system. This concludes that our model attains a static equilibrium. In this context, it is also noted that the hydrostatic gradient (\(F_h\)) and electric forces (\(F_e\)) are positive, whereas the gravitational (\(F_g\)) and dark energy forces (\(F_d\)) are negative. Also to properly justify the counterbalance effect of all these four forces, we have also plotted the overall effect of all four forces \(F_{\textrm{Sum}}=F_g + F_h +F_d + F_e\) and see that it vanishes (magenta line of Fig. 9). This concludes that our present model attains a static equilibrium.

4.5 Equation of state via Zel’dovich condition

The Zel’dovich requirement [80,81,82,83] for the stability of a stellar structure is that the ratio of pressure to density must be less than unity everywhere within the stellar interior. If we define the ratios as: \(\Omega (r) = \frac{p(r)}{\rho (r)}\), then \(\Omega (r)<1\).

From Fig. 10, it is clear that our model satisfies the Zel’dovich ratio \(\Omega (r)<1\) for all \(r < R\) and for all dark energy coupling parameters, \(\alpha \in [ 0.40, 0.80 ]\). This \(\Omega \) explains the idea of the equation of state parameters and it is a key factor to determine the stellar formations.

Now, if we apply the Zel’dovich condition for the central values of stellar parameters \(\rho \)  and  p, we get \(\frac{p_c}{\rho _c} < 1\), from which we obtain the relationship,

$$\begin{aligned} \frac{a (-1 + 2 \alpha ) + 2 (1 + \alpha ) B}{3 a} < 1 \end{aligned}$$
(50)

which implies that,

$$\begin{aligned} \frac{B}{a} < \frac{2-\alpha }{1+\alpha } \end{aligned}$$
(51)

Also from the relation \(p_c > 0\) we get,

$$\begin{aligned} \frac{B}{a} > \frac{1- 2\alpha }{2(1+\alpha )} \end{aligned}$$
(52)

Now combining relations (51) and (52), we finally obtain a boundary representing constraint on \(\frac{B}{a}\) in the following form:

$$\begin{aligned} \frac{1- 2\alpha }{2(1+\alpha )}< \frac{B}{a} < \frac{2-\alpha }{1+\alpha } \end{aligned}$$
(53)

In Fig. 10, we have portrayed the constraint region for B/a given in the expression (53) with respect to \(\alpha \).

Fig. 10
figure 10

(i) Variation of pressure p with respect to density \(\rho \), (ii) the ratio \(\Omega \) are shown inside the stellar interior, and (iii) constraint region plot of B/a with respect to \(\alpha \)

Full size image

4.6 Harrison–Zel’dovich–Novikov’s static stability criterion

Harrison–Zel’dovich–Novikov [81, 84] proposed the criterion for stability of any compact object. According to their criterion, any fluid configuration is stable if its total mass is increasing with increasing central density, i.e. \(\frac{\partial M (\rho _c)}{\partial \rho _c} > 0\), whereas is unstable if the total mass of the star is decreasing with respect to the central density i.e. \(\frac{\partial M (\rho _c)}{\partial \rho _c} < 0\). For this purpose, we have to calculate the mass (M) and its gradient in terms of central density as,

$$\begin{aligned} \rho _c= & {} \frac{3 a}{\kappa (1 + \alpha )} \end{aligned}$$
(54)

For our present model,

$$\begin{aligned} M (\rho _c)= & {} \frac{1}{8 \Big (3 + 3 b R^4 + (1 + \alpha ) \kappa \rho _c R^2 \Big )^2}\nonumber \\{} & {} \times \Bigg [9 R^5 (B^2 + b \Big (3 - 2 B R^2 + (5 b + B^2) R^4)\Big ) \nonumber \\{} & {} + 3 (1 + \alpha ) \kappa R^3 \Big (4 - B R^2 \nonumber \\{} & {} +(10 b + B^2) R^4\Big ) \rho _c + 5 (1 + \alpha )^2 \kappa ^2 R^5 \rho _c^2\Bigg ] \end{aligned}$$
(55)

Now taking partial derivative with respect to \(\rho _c\) we get,

$$\begin{aligned} \frac{\partial M (\rho _c)}{\partial \rho _c}= & {} \frac{1}{8 \Big (3 + 3 b R^4 + (1 + \alpha ) \kappa \rho _c R^2 \Big )^3}\nonumber \\{} & {} \times \Bigg [3\kappa R^3 (1 + \alpha ) \Bigg \{12 + R^2 \Bigg (-3 \Big (B - 8 b R^2 \nonumber \\{} & {} - 3 b B R^4 + B^2 (R^2 + b R^6)\Big ) \nonumber \\{} & {} - \kappa \rho _c(1 +\alpha ) (-3 + B R^2) (2 + B R^2) \Bigg )\Bigg \}\Bigg ] \end{aligned}$$
(56)
Fig. 11
figure 11

Behavior of mass (\(M (\rho _c)\)) and its gradient \(\frac{\partial M (\rho _c)}{\partial \rho _c}\) with respect to central density \(\rho _c\) for the compact star Her X-1

Full size image

From Fig. 11, we can easily verify that the mass (\(M (\rho _c)\)) increases with central density \(\rho _c\). On the other hand, we notice that the gradient \(\frac{\partial M (\rho _c)}{\partial \rho _c}\) becomes monotonically decreasing with increasing central density \(\rho _c\) although it remains positive with respect to central density \(\rho _c\) throughout the stellar interior. This implies that our current stellar model is stable under Harrison–Zel’dovich–Novikov stability criterion.

5 Discussion and concluding remarks

In this present article, we have made an attempt to model a unique charged strange star model coupled with inhomogeneous anisotropic dark energy. We have taken into account the well-known Tolman–Kuchowicz ansatz to solve the Einstein–Maxwell field equations for a static symmetric perfect fluid distribution. We also choose a particular form of EoS. The dark energy follows the distribution of matter at high energy density, with a strength that depends on the parameter \(\alpha \). The fundamental distinction of this type of investigation is that in the original dark energy stellar model, the core is de-Sitter and the shell is close to or replaces the event horizon. Furthermore, there exists a critical parameter \(\alpha _c\), that distinguishes dark energy stars from conventional black hole solutions.

Several research works have been done earlier on dark energy stars composed of ordinary fluid and dark energy. According to Shvartsman [85], stars can carry electric charges. So here we present a model of singularity free charged dark energy star. For many reasons, including its significance as a possible substitute for a black hole, the charged dark energy star model has gained a bigger astrophysical relevance. Also, it has been found that dark energy along with anisotropic stress can help to produce stability for the stars against gravitational collapse as it exerts a repulsive force looking similar to electric charge, on dark energy surrounding.

Here we develop a straightforward numerical technique to integrate the stellar structure equations from the core of the star to its boundary. The compactness of the stars, their structural parameters, and M–R relations have been calculated to compare with the well-known theoretical TOV model.

For this theoretical investigation, we have chosen a particular compact dark energy star HER X-1 to analyze our results numerically as well as graphically throughout this paper. We plot all physical properties for dark energy coupling parameter values \(\alpha = 0.40, 0.50, 0.60, 0.70, 0.80\). Here, to determine the constants present in the TK metric coefficients, we smoothly match the interior metric with the exterior Reissner–Nordström metric by assuming continuity of the metric functions \(g_{tt}\), \(g_{rr}\) and \(\frac{\partial g_{tt}}{\partial r}\) across the boundary surface \(r= R\) along with \(p(r=R)=0\). We require to match our results with available observational data. Because the model meets all of the necessary physical conditions and is horizon free, so this type of star may be realistic in our nature.

The following are the salient key features of our proposed dark energy stellar model:

  1. 1.

    The graphical representations of \(e^{\nu (r)}\) and \(e^{-\lambda (r)}\) in Fig. 1 clearly indicate that they are finite and nonsingular over the radius of stars for varying \(\alpha \), which is necessary to generate physically viable models of compact stellar objects.

  2. 2.

    It is clear from Fig. 2 that the energy density \(\rho (r)\) and pressure p(r) remain continuous, positively finite inside the star, and demonstrate a smooth declining nature towards the surface for various values of \(\alpha \). Pressure and density vanish at the boundary \(r = R\). We see that \(\rho \) and p are maximum at the core (\(r = 0\)). Both density and pressure are at their highest levels at the core, which indicates the presence of highly compact cores. Whereas electric field intensity \(E^2\) increases with r. It remains positive and monotonic increasing throughout the fluid sphere.

  3. 3.

    The gradient components of matter-energy density and pressure show a negative trend in Fig. 3 i.e. from zero to negative region whenever r goes from center to boundary. This scenario remains the same for different considerations of \(\alpha \). The pressure and density gradients vanish at the center (\(r=0\)) and remain negative inside the stellar configuration. Also, double derivatives take negative values at the center which implies that both density and pressure take maximum value at the center of the stellar object.

  4. 4.

    This model represents the repulsive character of dark energy, which leads to the fact that radial dark pressure \((p^{de}_r)\) is negative while energy density \((\rho ^{de})\) is positive (from Fig. 4) whereas in most of the stellar regions, transverse dark pressure \((p^{de}_t)\) is still negative and positive near the stellar surface.

  5. 5.

    In Table 1, the numerical values of central density \((\rho _c)\), surface density \((\rho _s)\), central pressure \((p_c)\), compactness ratio (u(R)), surface redshift \((z_s(R))\), \(p_c/\rho _c\), and mass (\(M_{\odot }\)) have been presented for different values of \(\alpha \). From Fig. 5, it is obvious that the mass function and compactness factor are regular throughout the stellar region and gradually increase with ’r’. Also from Fig. 6, we notice the interesting fact that the gravitational (or internal) redshift \((z_g)\) is minimum at the surface and maximum at the center, in contrast, the surface redshift \((z_s)\) behaves just opposite to \(z_g\).

  6. 6.

    Our proposed charged dark energy stellar model also satisfies the Causality condition i.e. square of the sound velocity \(V^2\) lies within (0, 1) (from Fig. 7) within the stellar body which leads the model to be physically stable and well-behaved.

  7. 7.

    Our obtained model satisfies all four energy conditions viz., NEC, WEC, SEC, and DEC for various values of \(\alpha \), and that is illustrated graphically in Fig. 8. Moreover, these always remain positive in the entire region of the star and it confirms the viability of our proposed solution.

  8. 8.

    Full illustration for the profiles of \(F_g\), \(F_h\), \(F_d\), and \(F_e\) for our proposed stellar structure have been made in Fig. 9. By combining the effects of all these forces, it is obviously conceivable to create a static equilibrium configuration. Here, hydrostatic-gradient and electric forces are repulsive whereas gravitational force and dark energy force are attractive in nature.

  9. 9.

    In Fig. 10, we analyze the equation of state (EoS) parameters via Zel’dovich condition for stability i.e \(\Omega (r)=\frac{p(r)}{\rho (r)}\) should be less than unity, is also verified even though the star comprises electric charge, ordinary matter, and dark energy. So it is obvious that the matter content is non-exotic in nature and the solution of our proposed model is physically well-behaved. Also, we plot p with respect to \(\rho \) and the constraint region for B/a with respect to \(\alpha \) in Fig. 10.

  10. 10.

    From the inequality (39), we can reach the conclusion that the respective M–R ratio values for the presence of anisotropies and electric charge in the matter distribution are higher than the corresponding ones for the isotropic uncharged matter configurations.

  11. 11.

    Finally we analyze the stability situation through Harrison–Zel’dovich–Novikov’s stability condition. We plot mass (\(M (\rho _c)\)) as a function of central density (\(\rho _c\)) and its gradient \(\frac{\partial M (\rho _c)}{\partial \rho _c}\) in Fig. 11. Thus we arrive at a decision that our current stellar model is stable because it meets this Harrison–Zel’dovich–Novikov stability criterion.

Therefore, with respect to all the significant results, we can finally conclude that we are able to structure a physically acceptable, stable, and singularity-free generalized model for charged strange stars employing the dark energy equation of state, which is suitable for studying dark energy stars within the Einstein gravity framework. We expect that our model may hypothetically contribute to the astrophysical scenario on a larger scale.