1 Introduction

The anti-de Sitter/conformal field theories (AdS/CFT) correspondence [1,2,3,4] is a very convenient and efficient tool to model strongly correlated systems in terms of a gravity dual. Since its discovery, this duality has made great development and been extensively used in various areas in physics. The quantum information has important application in the study of quantum gravity and quantum field theory. Two quantities of the boundary field theory, which play important roles in quantum information, are entanglement entropy and complexity. Both of them have gravitational descriptions by certain geometric quantities in the bulk spacetime in holographic framework.

The entanglement entropy is a most studied idea in the last decades. It is directly related to the degrees of freedom in the quantum entangled state [5,6,7,8]. In the light of the AdS/CFT correspondence, the holographic entanglement entropy describes the entanglement properties of the boundary field theory and might be eventually used to understand the quantum structure of spacetime. Ryu and Takayanagi [9, 10] had provided an effective way to calculate the holographic entanglement entropy. The Ryu–Takayanagi proposal states that the entanglement entropy of the CFT in a closed region \(\mathcal {A}\) with its complement is proportional to the area of a minimal surface \(\gamma _{\mathcal {A}}\) extended into the bulk from the boundary of the region \(\mathcal {A}\), and a simple and elegant formula is given as

$$\begin{aligned} S_{\mathcal {A}}=\frac{Area(\gamma _{\mathcal {A}})}{4G_{N}}, \end{aligned}$$
(1)

where \(G_N\) is the Newton constant of the general gravity.

The complexity is recently introduced as a new measure of information of spacetime that can be useful to understand the black hole interior where the entanglement entropy can not cover [11]. In quantum field theory, the complexity is defined as the minimal number of elementary operations (gates) that are required to obtain a desired target state from a reference state. There are two quintessential holographic proposals of the complexity. The first one is called “complexity\(=\)volume” (CV) conjecture [12, 13] which relates the complexity of the boundary state to the volume of a codimension-one maximal hypersurface anchored to the given boundary time. The second one is the “complexity\(=\)action” (CA) conjecture [14, 15] which relates the complexity of the boundary state to the on-shell bulk gravitational action within the Wheeler–DeWitt (WDW) patch. Inspired by the Ryu–Takayanagi proposal of the entanglement entropy, Alishahiha constructed the holographic dual to the complexity for a subsystem on the boundary within the framework of the CV proposal, which is referred to as the holographic subregion complexity [16]. Specifically, the complexity for a subregion \(\mathcal {A}\) equals the volume enclosed by the Ryu–Takayanagi surface \(\gamma _{\mathcal {A}}\)

$$\begin{aligned} C_{\mathcal {A}}=\frac{Volume(\gamma _{\mathcal {A}})}{8\pi LG_{N}}, \end{aligned}$$
(2)

where L is the AdS radius. In this work we will focus on the time-independent holographic subregion complexity, i.e., the minimal surface \(\gamma _{\mathcal {A}}\) totally outside of the black hole horizon.

Among many sectors where the AdS/CFT correspondence has been applied successfully, the holographic realization of high-temperature superconductors has gained plenty of interest for their potential applications to the condensed matter physics. The simplest initial holographic superconductor model is constructed by applying a scalar field and a Maxwell field coupled in an AdS black hole background [17, 18]. The main idea is the spontaneous U(1) symmetry breaking induced by the condensation of the scalar hair close to the horizon of the black hole in low temperature. Since then, kinds of more complete holographic superconductor models have been explored, and many of their interesting features which resemble that of the real superconductors have been revealed, for reviews, see Refs. [19, 20] and references therein. The entanglement entropy was firstly introduced as a tool to describe the phase transitions in the s-wave holographic superconductor in Ref. [21]. By now a lot of works have been carried out for investigating the properties of phase transitions from the entanglement entropy side in various holographic superconductor models and in different backgrounds [22,23,24,25,26,27,28,29,30,31,32,33,34,35]. And the entanglement entropy turns out to be a good probe to the critical point and the order of the phase transition in the holographic superconductor systems. In recent years, as there is a deep connection between the holographic entanglement entropy and holographic complexity, the complexity has also been discussed by using Alishahiha’s subregion CV conjecture in different types of holographic superconductors, such as s-wave model [36, 37], p-wave model [38], d-wave model [39] and so on [40,41,42,43]. These studies show that the holographic complexity may be used as another independent probe to the physics of the phase transition as the holographic entanglement entropy does, though it was found that the complexity behaves in different ways from the entanglement entropy. Specially for the holographic Stückelberg superconductor [41] which allows both first and second order phase transitions to occur, the complexity behaves differently crossing the second order and first order superconducting phase transition point, which indicates that the complexity may also be used to determine the type of transition.

In this paper, we will generalize the investigation on the entanglement entropy and subregion complexity to the holographic model of superfluid with full backreaction, which has not been discussed as far as we know. Supercurrent in superconducting materials is a well studied phenomenon in condensed matter systems. The supercurrent solution can be holographically constructed by performing a deformation of the superconducting black hole, i.e., turning on the spatial component of the U(1) gauge field in the bulk theory [44, 45]. And it was found that the superfluid phase transition can switch from second order to first order when the velocity of the superfluid component increases relative to the normal component. In Ref. [46], considering various scalar field mass in AdS\(_5\), it was observed that the Cave of Winds phase structure exists for some special mass in the superfluid model. Along this line, further efforts in the s-wave holographic superfluid have been made in the related research and discussion [47,48,49,50], and more general and complex models have also been explored, such as p-wave superfluid [51,52,53,54,55] and \(s+p\)-wave superfluid [56]. Besides, considering the holographic superfluid models away from the probe limit, the gravity backreaction also brings some interesting features to the system. In the p-wave superfluid system, it was argued that the order of the phase transition depends on the backreaction [57]. The authors of Ref. [58] further studied the phase diagram modified by the backreaction in the supercurrent solution in the AdS black hole background. Their results showed that the backreaction has different impacts on the condensation behaviors for different operators, i.e., with the increase of the strength of the backreaction, the critical values of the superfluid velocity to accommodate the first order phase transition decreases for the operator \(\mathcal {O}_{+}\) but increases for the operator \(\mathcal {O}_{-}\). Recently, the study has been enlarged to the backreacted superfluid model with the competition between the p-wave solution and the \(p+ip\) solution [59]. Starting with the simple s-wave backreated holographic superfluid model, we would like to carry out a further analysis of this model from the aspects of the entanglement entropy and the complexity. It is meaningful to examine how the two quantities respond to the different types of phase transitions and characterize the phase structure under the influence of the backreaction, which may help us to enhance and supplement the description of the superfluid phase transition. We expect that the entanglement entropy and the complexity can suggest more deeply physical insights so as to better understand the underlying mechanism in the superfluid dual system.

The framework of this paper is as follows. In Sect. 2, we briefly review the construction of a fully backreacted holographic superfluid in the four-dimensional AdS black hole spacetime and show the condensations and phase transitions. In Sect. 3, behaviors of the holographic entanglement entropy and the holographic subregion complexity are investigated in detail to analyze the phase transitions in the superfluid model. The summary and discussions are included in Sect. 4.

2 Holographic model of superfluid with backreactions

We work with the simplest background geometry of a black hole and a U(1) gauge field coupling with a charged scalar field. The lagrangian density reads

$$\begin{aligned} \mathcal {L}= & {} R+\frac{6}{L^2}-\gamma \Bigg (\frac{1}{4}F^{\mu \nu }F_{\mu \nu }+|\nabla _\mu \psi \nonumber \\{} & {} -iqA_\mu \psi |^2+m^2|\psi |^2\Bigg ), \end{aligned}$$
(3)

where R is the Ricci scalar, \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the strength of the electromagnetic field. \(\psi \) denotes a scalar field with charge q and mass m, A represents the gauge field. The AdS radius L and the charge q are set to unity hereafter. And \(\gamma \) here is a parameter measuring the strength of the backreaction.

We are interested in studying the fully backreacted holographic superfluid model, thus we consider the ansatz for the line element of the four-dimensional AdS black hole with the form

$$\begin{aligned} ds^2= & {} -r^2B(r)e^{D(r)}dt^2+\frac{dr^2}{r^2B(r)}\nonumber \\{} & {} \quad +r^2\left[ e^{C(r)}dx^2+dy^2\right] , \end{aligned}$$
(4)

and the gauge field and the charged scalar field to be, respectively,

$$\begin{aligned} A=\phi (r)dt+h(r)dx,\hspace{0.5cm} \psi =\psi (r). \end{aligned}$$
(5)

The function C(r) in the metric ansatz is introduced by considering a nonzero x component of the Maxwell field in order to take the possibility of DC supercurrent into account. The function B(r) gives the position of the event horizon of the black hole, i.e. \(B(r_{h})=0\). The Hawking temperature of the background is expressed as

$$\begin{aligned} T_{H}=\frac{r^{2}_{h}B'(r_{h})e^{D(r_{h})/2}}{4\pi }. \end{aligned}$$
(6)

Then, the equations of motion derived from the action yield

$$\begin{aligned}{} & {} \psi ''+\left( \frac{4}{r}+\frac{D'}{2}+\frac{C'}{2}+\frac{B'}{B}\right) \psi '+\left( \frac{\phi ^2}{r^4B^2e^D}\right. \nonumber \\{} & {} \quad \quad \left. -\frac{h^{2}}{r^4Be^C}-\frac{m^2}{r^2B}\right) \psi =0,\nonumber \\{} & {} \phi ''+\left( \frac{2}{r}+\frac{C'}{2}-\frac{D'}{2}\right) \phi '-\frac{2\psi ^2}{r^2B}\phi =0,\nonumber \\{} & {} h''+\left( \frac{2}{r}+\frac{D'}{2}+\frac{B'}{B}-\frac{C'}{2}\right) h'-\frac{2\psi ^2}{r^2B}h=0,\nonumber \\{} & {} C''\!+\!\frac{C'^2}{2}\!+\!\left( \frac{4}{r}\!+\!\frac{D'}{2}\!+\!\frac{B'}{B}\right) C'\!+\!\gamma \frac{h'^2}{r^2e^C}\!+\!\gamma \frac{2h^2\psi ^2}{r^4Be^C}=0,\nonumber \\{} & {} B'\left( \frac{2}{r}-\frac{C'}{2}\right) -\frac{1}{2}BD'C'+\frac{6}{r^2}B-\frac{6}{r^2}\nonumber \\{} & {} \quad +\gamma \Bigg (\frac{\phi '^2}{2r^2e^D}+\frac{m^2\psi ^2}{r^2}+ B\psi '^2+\frac{\psi ^2\phi ^2}{r^4Be^D}\nonumber \\{} & {} \quad -\frac{Bh'^2}{2r^2e^C}-\frac{h^2\psi ^2}{r^4e^C}\Bigg )=0,\nonumber \\{} & {} D'=\frac{4rC'\!+\!r^2C'^2\!+\!2r^2C''\!+\!\gamma (\frac{2h'^2}{e^C}\!+\!4r^2\psi '^2\!+\!\frac{4\psi ^2\phi ^2}{r^2B^2e^D})}{r(4\!+\!rC')}.\nonumber \\ \end{aligned}$$
(7)

There is a useful scaling symmetry of the above equations

$$\begin{aligned}{} & {} r\rightarrow \lambda r,\hspace{0.5cm}(t,x,y)\rightarrow \frac{1}{\lambda }(t,x,y),\hspace{0.5cm}\phi \rightarrow \lambda \phi ,\hspace{0.5cm}\nonumber \\{} & {} h\rightarrow \lambda h,\hspace{0.5cm}\psi \rightarrow \psi , \end{aligned}$$
(8)

where \(\lambda \) is a real positive number.

For this superfluid phase transition system, there are two classes of the solutions for Eq. (7), i.e., \(\psi =0\) for the normal phase and \(\psi \ne 0\) for the superfluid phase. In order to employ the shooting method to solve the field equations numerically, the adequate boundary conditions on the black hole horizon \(r=r_{h}\) and the asymptotic AdS boundary \(r\rightarrow \infty \) are imposed. Around the horizon we can make the Taylor’s expansion

$$\begin{aligned}{} & {} \psi (r)=\psi _0+\psi _1(r-r_h)+\psi _2(r-r_h)^2+\cdots ,\nonumber \\{} & {} \phi (r)=\phi _1(r-r_h)+\phi _2(r-r_h)^2+\cdots , \nonumber \\{} & {} h(r)=h_0+h_1(r-r_h)+h_2(r-r_h)^2+\cdots , \nonumber \\{} & {} B(r)=B_1(r-r_h)+\cdots ,\nonumber \\{} & {} D(r)=D_0+D_1(r-r_h)+\cdots ,\nonumber \\{} & {} C(r)=C_0+C_1(r-r_h)+\cdots . \end{aligned}$$
(9)

Note that a regular event horizon at \(r=r_{h}\) needs \(B(r_h)=0\). And the requirement of regularity of the matter fields on the horizon leads to \(\phi (r_h)=0\). Near the asymptotic AdS boundary \((r\rightarrow \infty )\), the various fields asymptotically behave like

$$\begin{aligned} \psi \rightarrow \frac{\psi _-}{r^{\Delta _-}}+\frac{\psi _+}{r^{\Delta _+}},\hspace{0.5cm}\phi\rightarrow & {} \mu -\frac{\rho }{r},\hspace{0.5cm}h\rightarrow \sigma -\frac{\xi }{r},\nonumber \\ B\rightarrow 1+\frac{B_3}{r^3},\hspace{0.5cm}D\rightarrow & {} 0,\hspace{0.5cm}C\rightarrow 0, \end{aligned}$$
(10)

where \(\Delta _{\pm }=(3\pm \sqrt{9+4m^{2}})/2\) is the conformal dimension of the operator \(\mathcal {O}_{\pm }\). According to AdS/CFT correspondence, \(\mu \) and \(\rho \) represent the chemical potential and charge density in the dual field theory respectively. \(\xi \) and \(\sigma \) respectively describe the current density and the dual current source. The coefficients \(\psi _-\) and \(\psi _+\) can be regarded as the vacuum expectation value of the operator \(\mathcal {O}\) in the dual field theory while the other is the source. In our analysis, we set the mass-squared of the scalar field \(m^2=-2\), then both \(\psi _-\) and \(\psi _+\) are normalizable. Thus we have two choices of boundary conditions, i.e., \(\psi _-=0\), \(\psi _{+}=\langle \mathcal {O}_{+}\rangle \) and \(\psi _+=0\), \(\psi _{-}=\langle \mathcal {O}_{-}\rangle \), in which \(\psi _+=0\) \((\psi _-=0)\) corresponds to a vanishing source so as to describe a spontaneous symmetry breaking. For the rest of our discussion we would like to consider the both cases in order to explore the properties of the holographic entanglement entropy and complexity for the two different condensation operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\).

Using the scaling symmetry (8), we can rescale the relevant quantities as

$$\begin{aligned} \mu \rightarrow \lambda \mu ,\hspace{0.5cm}\rho\rightarrow & {} \lambda ^{2}\rho ,\hspace{0.5cm}\sigma \rightarrow \lambda \sigma ,\nonumber \\ \xi \rightarrow \lambda ^{2}\xi ,\hspace{0.5cm}\psi _{-}\rightarrow & {} \lambda \psi _{-},\hspace{0.5cm}\psi _{+}\rightarrow \lambda ^{2}\psi _{+}, \end{aligned}$$
(11)

which allow us to employ the dimensionless quantities \(\frac{\sqrt{\langle \mathcal {O}_{+}\rangle }}{\sqrt{\mu ^{2}-\sigma ^{2}}}\), \(\frac{\langle \mathcal {O}_{-}\rangle }{\sqrt{\mu ^{2}-\sigma ^{2}}}\) and \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}\) in the computation of the condensates. Moreover, for the mathematical simplicity, we make a coordinate transformation from r-coordinate to z-coordinate by defining \(z=r_h/r\). The region \(r_h<r<\infty \) now corresponds to \(1>z>0\).

The numerical results of the condensates of the operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\) with the changes of the temperature and the superfluid velocity given by the ratio \(\sigma /\mu \) are plotted in Fig. 1. The scalar field begins to condensate as the temperature reduces to a critical value \(T_c\), and this implies the system undergoes phase transition to a superfluid phase. In particular, from the pictures, it can be seen that there is a threshold value (presented in orange) of the superfluid velocity \(\sigma /\mu \), below which the condensate \(\langle \mathcal {O}_{\pm }\rangle \) grows continuously and monotonically from zero near the critical point, signaling a typically second order phase transition. While we enhance \(\sigma /\mu \) across the threshold, the condensate becomes multi-valued, signaling a first order transition. That is to say, the type of superfluid phase transition is affected by the superfluid velocity, and when the superfluid velocity \(\sigma /\mu \) increases beyond a translating value, the second order phase transition will switch to the first order one.

Fig. 1
figure 1

The condensates \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \) in terms of temperature in the backreacted holographic superfluid model. The left two panels are for the backreaction \(\gamma =0.1\), the middle ones are for \(\gamma =0.2\), and the right ones are for \(\gamma =0.3\)

Full size image

For the second order phase transition, the critical temperature \(T_c\) can be directly read off from Fig. 1, at which the condensation appears. However, for the first order phase transition, the condensate is multi-valued near the transition point. In order to determine the critical temperature, we calculate the free energy of the system which is related to the product of the on-shell Euclidean bulk action and the temperature T as \(\Omega =-TS_E\) [60, 61]. And in our model,

$$\begin{aligned} -S_E= & {} \int dx^4\sqrt{-g}\left( R+\frac{6}{L^2}+\mathcal {L}_m\right) \nonumber \\{} & {} +\int _{z\rightarrow 0}dx^3\sqrt{-h}\left( 2\mathcal {K}-\frac{4}{L^2}\right) , \end{aligned}$$
(12)
$$\begin{aligned} \mathcal {L}_m= & {} -\gamma \left( \frac{1}{4}F^{\mu \nu }F_{\mu \nu }+|\nabla _\mu \psi -iqA_\mu \psi |^2+m^2|\psi |^2\right) , \nonumber \\ \end{aligned}$$
(13)

where h is the determinant of the induced metric on the AdS boundary, and \(\mathcal {K}\) is the trace of the extrinsic curvature \(\mathcal {K}_{\mu \nu }\). Using the equations of motion (7) and the boundary behaviors (10), we obtain the expression for the free energy of the boundary theory as

$$\begin{aligned} \frac{\Omega }{V_2}=B_3, \end{aligned}$$
(14)

with \(V_2=\int dxdy\) which will be set to be unit and \(B_3\) is a coefficient in (10).

As an example, fixing the backreaction parameter \(\gamma =0.2\), we plot the results of the free energy \(\Omega \) for operator \(\mathcal {O}_+\) with \(\sigma /\mu =0.15, 0.25\) and for operator \(\mathcal {O}_-\) with \(\sigma /\mu =0.35, 0.45\) in Fig. 2. Here \(\Omega \) is scaled by the chemical potential \(\mu \) to be dimensionless. The red lines are for the superfluid phases while the blue lines represent the normal phases. The left two panels demonstrate the free energy for the two branches when the system undergoes the second order phase transition. We observe that below the critical temperature \(T_c\) which is marked by the dashed vertical lines, the superfluid phase has lower free energy than the normal phase and becomes physically favorable. For the right two panels, the free energy develops a swallow tail, which is a typical characteristic for first order phase transitions. It is obvious that the temperature \(T=0.0382021\) and \(T=0.165526\) respectively representing the appearance of the condensates \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \), are not the physical critical point. The first order transitions happen at the interaction points \(T_c=0.0385111\) for \(\mathcal {O}_{+}\) and \(T_c=0.166974\) for \(\mathcal {O}_{-}\), and below which the superfluid phase is thermodynamically favorable. Thus, from the free energy, we can obtain \(T_c\) for the first order phase transitions. The results of \(T_c\) for the various superfluid velocity we chosen in Fig. 1 in the case of \(\gamma =0.2\) are listed in Table 1. Obviously, the critical temperature \(T_c\) decreases as the superfluid velocity \(\sigma /\mu \) increases, which indicates that larger superfluid velocity makes the scalar hair more difficult to be developed, and is correct for other values of the backreaction parameter.

Fig. 2
figure 2

the free energy \(\Omega \) as a function of the temperature T for operators \(\mathcal {O}_+\) (top two panels) and \(\mathcal {O}_-\) (bottom two panels) with the strength of the backreaction \(\gamma =0.2\). In each panel, the red lines and blue lines denote the superfluid phases and normal phases, respectively. The dashed vertical lines represent the critical temperature \(T_c\)

Full size image
Table 1 The critical temperature \(T_c\) for operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\) with a number of superfluid velocity \(\sigma /\mu \) and the fixed backreaction parameter \(\gamma =0.2\)
Full size table

Furthermore, we also concern about the dependence of the condensates on the backreaction of the matter fields measured by the parameter \(\gamma \). In Fig. 1, three values of the backreaction parameter have been considered, i.e., \(\gamma =0.1\) (left two panels), \(\gamma =0.2\) (middle two panels), and \(\gamma =0.3\) (right two panels). It is interesting to find that, for the condensates \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \), the backreaction has distinct effects on the translating value of \(\sigma /\mu \) to accommodate the first order phase transition. Concretely, when the strength of backreaction increases, the translating superfluid velocity \(\sigma /\mu \) decreases for \(\langle \mathcal {O}_{+}\rangle \), which shows that the sufficiently strong backreaction can trigger the first order transition of the system even for a small superfluid velocity. However, for \(\langle \mathcal {O}_{-}\rangle \), the translating superfluid velocity \(\sigma /\mu \) increases with the increasing strength of backreaction, which is just opposite to the case of \(\langle \mathcal {O}_{+}\rangle \). Our findings is consistent with the results reported in Ref. [58]. It is of interest to study the holographic entanglement entropy and holographic complexity in this backreacted model of superfluid phase transition. We expect the two quantities would reflect different properties in the two types of phase transition, and provide more detailed physics about the two condensation operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\).

3 Holographic entanglement entropy and subregion complexity

In this section, we will investigate the holographic entanglement entropy and holographic complexity in a strip geometry of the superfluid dual model. We consider a strip subregion \(\mathcal {A}\) which is defined by \(-\frac{l}{2}\le x\le \frac{l}{2}\) and \(-\frac{R}{2}<y<\frac{R}{2}\), where l is the size of region \(\mathcal {A}\) and R is a regulator which can be set to be infinity. The induced metric of the hypersurface \(\gamma _{\mathcal {A}}\) whose boundary is the same as the strip reads

$$\begin{aligned} ds^{2}_{induced}=\frac{1}{z^{2}B}dz^2+\frac{e^C}{z^2}dx^2+\frac{1}{z^2}dy^2. \end{aligned}$$
(15)

Then, using the proposal given by Eq. (1), we have the holographic entanglement entropy connecting with the area of \(\gamma _{\mathcal {A}}\) as

$$\begin{aligned} 4G_{4}S_{\mathcal {A}}=Area(\gamma _{\mathcal {A}})=\int dy\int ^{l/2}_{-l/2}\frac{dx}{z^{2}}\sqrt{\frac{1}{B}\left( \frac{dz}{dx}\right) ^{2}+e^C}.\nonumber \\ \end{aligned}$$
(16)

We now apply the Hamiltonian approach to impose the following minimality condition on the surface area

$$\begin{aligned} \frac{dz}{dx}=\pm \sqrt{e^CB\left( \frac{e^C}{e^{C_*}}\frac{z_{*}^{4}}{z^{4}}-1\right) }, \end{aligned}$$
(17)

where \(z_{*}\) is defined as the turning point of the smooth extremal surface such that \(\frac{dz}{dx}|_{z_{*}}=0\), then \(C_*\) denotes \(C(z_*)\). Integrating the condition (17), we obtain

$$\begin{aligned} x(z)=\int ^{z_{*}}_{z}\frac{z^2dz}{\sqrt{e^CB\left( \frac{e^C}{e^{C_*}}z_{*}^{4}-z^{4}\right) }}, \end{aligned}$$
(18)

which satisfies \(x(z_{*})=0\) and \(x(\epsilon \rightarrow 0)=l/2\) with a UV cutoff \(\epsilon \). Subsequently, we can deduce the resulting holographic entanglement entropy as

$$\begin{aligned} S_{\mathcal {A}}{} & {} =\frac{R}{2G_{4}}\int ^{z_{*}}_{\epsilon }dz\frac{1}{z^{2}}\frac{1}{\sqrt{Be^{C_*}\left( \frac{1}{e^{C_*}}-\frac{1}{e^C}\frac{z^4}{z_{*}^{4}}\right) }}\nonumber \\{} & {} =\frac{R}{2G_4}\left( \frac{1}{\epsilon }+s\right) , \end{aligned}$$
(19)

with \(R=\int dy\). The \(\frac{1}{\epsilon }\) term is the UV divergent term and known as the area law, which will not change since the new solution after the operator condensation still asymptotically approaches to AdS space near the AdS boundary. Subtracting this divergence from \(S_{\mathcal {A}}\), we have the finite term s which is physically important. On the other hand, according to Ref. [16], the complexity for the subregion \(\mathcal {A}\) is holographically related to the volume surrounded by the aforementioned minimal surface (Ryu–Takayanagi surface) \(\gamma _{\mathcal {A}}\). So it can be evaluated as

$$\begin{aligned} C_{\mathcal {A}}=\frac{R}{4\pi G_{4}}\int ^{z_{*}}_{\epsilon }dz\frac{e^{\frac{C}{2}}x(z)}{z^{3}\sqrt{B}}. \end{aligned}$$
(20)

Note that the complexity \(C_{\mathcal {A}}\) also includes a universal term c and a divergent term which is associated with a function of \(z_{*}\) as \(F(z_{*})/\epsilon ^{2}\). Though it is hard to find a general form of the divergence analytically, the value of \(F(z_{*})\) in various situations can be found numerically [37] so that we can confirm the singular part in \(C_{\mathcal {A}}\) and pick up the finite term c.

Due to the presence of the scaling symmetry (8), the strip width l, the entanglement entropy s, and the subregion complexity c can be transformed into

$$\begin{aligned} l\rightarrow \frac{1}{\lambda }l,\hspace{0.5cm}s\rightarrow \lambda s,\hspace{0.5cm}c\rightarrow \lambda c. \end{aligned}$$
(21)

Therefore, it is useful to work with the following dimensionless quantities to study the physics

$$\begin{aligned} l\sqrt{\mu ^2-\sigma ^2},\hspace{0.5cm}\frac{s}{\sqrt{\mu ^2-\sigma ^2}},\hspace{0.5cm}\frac{c}{\sqrt{\mu ^2-\sigma ^2}}. \end{aligned}$$
(22)

Fixing the width \(l\sqrt{\mu ^2-\sigma ^2}=2\) since the other choices will not qualitatively modify our results, we present the holographic entanglement entropy s and subregion complexity c as a function of temperature T for different superfluid velocity \(\sigma /\mu \) with the backreaction \(\gamma =0.1\), 0.2 and 0.3 in Fig. 3 (for operator \(\mathcal {O}_{+}\)) and Fig. 4 (for operator \(\mathcal {O}_{-}\)), where the dashed curves represent the normal state and the solid curves represent the superfluid state. We can clearly observe that the entanglement entropy and complexity exhibit behaviors characterizing two types of phase transition. For the second order phase transition with \(\sigma /\mu \) below the translating value to accommodate the first order phase transition, both the entropy s and complexity c are continuous but have a discontinuous first derivative at the critical point where the superfluid phase (solid curves) intersect with the the normal phase (dashed curves). And under the same conditions, the discontinued slopes of the both quantities occurs at the same critical temperature, at which the condensation appears as shown in Fig. 1. The entropy s monotonously decreases as the temperature decreases, and its value in the superfluid phase is always smaller than in the normal phase. This is comprehensible because the formation of the Cooper pairs in the superfluid phase suppresses the number of the effective degrees of freedom, and the entanglement entropy is just a measure of the degrees of freedom in the field theory. Contrary to s, the complexity c monotonously increases with reducing T, so the superfluid phase has a larger c than the normal phase, which can be interpreted as the quantum state of the system becoming more complicated in the superfluid phase since the complexity describes the difficulty of turning a certain reference state into a target state.

For the first order phase transition with \(\sigma /\mu \) above the translating point, it is interesting to note that both two quantities have a multi-valued region around the critical temperature \(T_c\), and the similar multi-valued behaviors appear in the same temperature region in the free energy diagrams and the condensation diagrams. According to the free energy of the system, below the critical temperature, the lower entanglement entropy and larger complexity are physically important in the multi-valued region. Thus, the real process of entropy s has a discontinuous drop from the dashed curve to the lowest part of the solid curve at the critical point and where the complexity c has a discontinuous jump from the dashed curve to the highest part of the solid curve. Similar phenomena was also found in the first order transition for the holographic Stückelberg superconductor [41]. This is an important distinguishing feature of the first order transition from the second order one in our model. Except the suddenly drop or jump, the entropy s is a monotonic decreasing function but the complexity c is a monotonic increasing function with respect to T, which agree with the case of the second order transition.

In addition, we find that the critical temperature \(T_c\) decreases with the increasing value of the superfluid velocity \(\sigma /\mu \), that is to say, the larger superfluid velocity makes the scalar hair harder to be developed. This observation is consistent with the previous findings in the condensates in Fig. 1 as well.

Fig. 3
figure 3

The holographic entanglement entropy and subregion complexity of the operator \(\mathcal {O}_{+}\) versus temperature for different values of the superfluid velocity \(\frac{\sigma }{\mu }\) with the strength of the backreactions \(\gamma =0.1\) (left two panels), 0.2 (middle two panels) and 0.3 (right two panels)

Full size image
Fig. 4
figure 4

The holographic entanglement entropy and subregion complexity of the operator \(\mathcal {O}_{-}\) versus temperature for different values of the superfluid velocity \(\frac{\sigma }{\mu }\) with the strength of the backreactions \(\gamma =0.1\) (left two panels), 0.2 (middle two panels) and 0.3 (right two panels)

Full size image

Therefore, both of the holographic entanglement entropy and complexity can capture the superfluid phase transition in the backreated dual model and also be a good probe to the type of the phase transition. We argue that the performances of the entropy and complexity crossing the two types of phase transition can be perceived as qualitative characteristic in general holographic model.

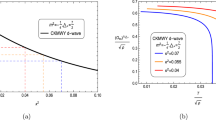
To see clearer of the effect of the superfluid velocity \(\sigma /\mu \) on the entanglement entropy and complexity, the two quantities as a function of \(\sigma /\mu \) in the superfluid phase with chosen values of the backreaction parameter \(\gamma \) are respectively displayed in Fig. 5 for the operator \(\mathcal {O}_{+}\) at \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.028\) and in Fig. 6 for \(\mathcal {O}_{-}\) at \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.145\). We observe that, for a fixed backreaction \(\gamma \), the larger superfluid velocity results in a larger entanglement entropy s, but makes for a smaller complexity c.

All the above features are shared by the case of operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\). Considering the disagreement between the two condensation operators about the effect of the backreaction on the translating superfluid velocity \(\sigma /\mu \) shown in Fig. 1, we expect that the holographic entanglement entropy and complexity for different operators would perform different properties. Comparing the results in Figs. 3 and 4, we are surprised to find that in the normal phase, the larger superfluid velocity results in a smaller complexity c in low temperature region before the condensate \(\langle \mathcal {O}_{+}\rangle \) but a larger c in relatively high temperature region before the condensate \(\langle \mathcal {O}_{-}\rangle \), which can not be seen in the entropy s since it monotonously increases as \(\sigma /\mu \) increase for both the cases. However, from Figs. 5 and 6, we obtain that with the fixed temperature and superfluid velocity, the increasing value of the backreaction parameter \(\gamma \) increases the entropy s for operator \(\mathcal {O}_{+}\) but decreases s for \(\mathcal {O}_{-}\), while the complexity c for both the operators always rises with the strengthening backreaction. These observations indicate that the holographic entanglement entropy and complexity contain different information about the superfluid system, meanwhile both the two quantities may capture the variance between the condensation operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\) and have the potential to help us better understand the physical mechanism behind the two condensates in the dual model.

Fig. 5
figure 5

The holographic entanglement entropy and subregion complexity of the operator \(\mathcal {O}_{+}\) as a function of the superfluid velocity \(\frac{\sigma }{\mu }\) with the strength of the backreactions \(\gamma =0.1\) (left two panels), 0.2 (middle two panels) and 0.3 (right two panels), as \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.028\) in the superfluid phase

Full size image
Fig. 6
figure 6

The holographic entanglement entropy and subregion complexity of the operator \(\mathcal {O}_{-}\) as a function of the superfluid velocity \(\frac{\sigma }{\mu }\) with the strength of the backreactions \(\gamma =0.1\) (left two panels), 0.2 (middle two panels) and 0.3 (right two panels), as \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.145\) in the superfluid phase

Full size image

4 Conclusions

In this paper, we have numerically investigated the holographic entanglement entropy and complexity associated to a strip-shaped subregion for the superfluid phase transition in the four-dimensional AdS black hole with full backreaction. This holographic superfluid model can realize first and second order phase transitions which depends on the superfluid velocity. Moreover, for the different condensates \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \), the strength of the backreaction has different effects on the translating value of superfluid velocity to accommodate the first order transition of the system.

Our results show that regardless of either the operators \(\mathcal {O}_{+}\) or \(\mathcal {O}_{-}\), both the holographic entanglement entropy and complexity present particular features distinguishing the two types of phase transitions, though the two quantities behave differently. For the second order phase transition with \(\sigma /\mu \) below the translating value, both the entropy s and complexity c are continuous but not differentiable at the critical temperature \(T_c\). With the decreasing temperature, the entropy s monotonously decreases while the complexity c increases so that the superfluid phase always has a smaller s but larger c than the normal phase. Some physical interpretations can be given to the behaviors of the both quantities. As temperature goes down, the Cooper pairs forming in the condensed phase makes the reduction of the number of degrees of freedom which causes the drop of the entanglement entropy. And a larger complexity at lower temperatures is related to the quantum state of the system becoming more complicated across the phase transition. For the first order phase transition with \(\sigma /\mu \) above the translating value, both s and c have a multi-valued area around the phase transition point, and the real processes of them are discontinuous at the critical temperature \(T_c\), i.e., from the normal state to the superfluid state, the entropy s experiences a suddenly drop and the complexity experiences a suddenly jump. The discontinuous change of the entropy may be related to some kind of non-trivial reorganization of the degrees of freedom of the system, which probably includes extra degrees of freedom coming from other entanglement apart from the entangled pairs. And the introduction of this extra degrees of freedom may be due to some quantum effect which also possibly causes the discontinuity in the behavior of the complexity.

In addition, we find that under the same conditions, the holographic entanglement entropy and complexity give the same critical temperature of the second order phase transition, at which the condensation appears as shown in Fig. 1. For the first order phase transitions, near the critical temperature the superfluid phase of both the holographic entanglement entropy and complexity have a multi-valued region, and the similar multi-valued behaviors appear in the same temperature region in the free energy diagrams and the condensation diagrams. And we can see that the larger superfluid velocity makes the critical temperature lower, which agrees well with the observation in the condensations. It indicates that the spatial component of the gauge field will hinder the phase transition. Therefore, the transition temperature of the system is quantitatively in agreement with the insights from holographic entanglement entropy and holographic complexity.

We also present the entanglement entropy and complexity in the superfluid phase as a function of the superfluid velocity \(\sigma /\mu \) with different values of the backreaction parameter, i.e., \(\gamma =0.1\), 0.2 and 0.3 at \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.028\) for operator \(\mathcal {O}_{+}\) and at \(\frac{T}{\sqrt{\mu ^{2}-\sigma ^{2}}}=0.145\) for \(\mathcal {O}_{-}\). It is shown that when the value of the superfluid velocity \(\sigma /\mu \) increases, the entanglement entropy always rises and the complexity drops, which is independent of the backreaction.

On the other hand, by comparing our results of the holographic entanglement entropy and complexity for the operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\), it is interesting to find that there exist some inconsistent performances of both the quantities for the two operators. One is that in the normal phase, the increasing superfluid velocity decreases the complexity in low temperature region before the condensate of operator \(\mathcal {O}_{+}\), but increases c in relatively high temperature region before the condensate of operator \(\mathcal {O}_{-}\). The other is that the increasing value of the backreaction parameter increases the entropy s for the operator \(\mathcal {O}_{+}\) but decreases s for \(\mathcal {O}_{-}\). It implies that both the holographic entanglement entropy and complexity have the potential to offer richer physics about the difference between the operators \(\mathcal {O}_{+}\) and \(\mathcal {O}_{-}\) in the dual system, and the information reflected by the complexity is different from the information captured by the entanglement entropy. The physical origins behind them and non-trivial insights from the field theory side deserve further study.

The Cave of Winds is an interesting phenomenon appearing in some holographic superfluid system, such as the five-dimensional gravity dual model and the model in Lifshitz spacetime. Thus, we hope to examine how the holographic entanglement entropy and complexity describe the Cave of Winds phase structure in the near future. And, it would also be interesting to extend our numerical analysis to the holographic superfluid model with the competition and coexistence of different orders, so as to further understand the deep physics involved in the rich phase diagram in holographic superfluid.

It is noticed that here we computed the holographic complexity via Alishahiha’s subregion CV conjecture. As is known that there are also other interesting holographic proposals of the complexity, which have been discussed in various holographic models. In Ref. [62], the authors investigated the complexity of formation, which defined in Ref. [63] within the framework of the CV proposal, in the first holographic superconductor model proposed by Hartnoll et al. [17, 18], and analyzed the full time evolution of the complexity from the normal phase to superconducting phase. It was found that the complexity of formation can also be a good probe to the superconducting phase transition. In Ref. [64], by considering the CA proposal, the holographic complexity was studied in a holographic QCD model proposed by Gubser et al. [65], which can realize three types of phase transition, crossover or first and second order. Their results indicated that the growth rate of the holographic complexity exhibits the behavior characterizing the type of phase transition. Investigating the complexity by other holographic proposals in the holographic superfluid will be another interesting direction. We leave this issue as future works.