1 Introduction

Einstein’s General Relativity (GR), has been working as the basic platform to understand the mechanism of cosmological as well as astrophysical phenomena. However, recently it is under a few crucial issues, like the observational evidences of late-time accelerated phase of the Universe as evident from CMBR [1, 2], high redshift supernovae [3], baryon acoustic oscillations [4], Planck data [5] and supernovae of type Ia [6, 7]. To explain this observed dynamics of cosmology, the simplest prescription was to modify the field equations of GR by introducing the cosmological constant (\(\varLambda \)) which was originally suggested by Einstein himself to construct a static model of the universe [8, 9].

A \(\varLambda \)-cosmological model of GR provides the best fit to the observed data, however, needs further assumption of Dark Matter [10, 11] as well as Dark Energy. The latter one has a huge discrepancy in its value with the theoretical value of \(\varLambda \) [12, 13]. Thus, there was an emergency need to modify GR via different extension schemes of the Einstein-Hilbert action which eventually gave birth to several alternative theories of gravity which are evidently quite different from the traditional dark energy depiction. Till date there are dozens of gravity theories available with numerous modification of GR which present a realistic perspective of the quantum mechanics and gravitational field at the high energy physical arena [14, 15]. Therefore, in the initial phase modifying the Lagrangian density by a simplistic function f(R) in the Einstein-Hilbert action, an extended GR has been provided in f(R) gravity [16,17,18,19]. Later on, several other alternative gravity theories have been proposed by other scientists, such as the f(G) gravity [20, 21], f(R, G) gravity [22], f(T) gravity [23,24,25,26], Brans-Dicke gravity [27,28,29,30,31,32] and so on, where the symbols R, G and T are, respectively, the Ricci scalar, Gauss-Bonnet scalar and the torsion scalar.

Among the above-mentioned alternative gravity theories, it has been observed by the scientists that the f(R) gravity theory suffers from a few problems, e.g. (i) the Solar system tests [33, 34], (ii) the CMBR tests, the strong lensing regime and the galactic scale [35,36,37,38,39,40] and (iii) explanation of the existence of a stable stellar configuration [41,42,43]. As a consequence, the f(R) gravity theory had gone through further generalizations which took place via the inclusion of the coupling between the scalar curvature and matter [19, 44,45,46]. This process of generalization has been continued further by Harko and collaborators [47,48,49] with coupling between the matter and geometry. In this \(f(R,{\mathbb {T}})\) theory the Lagrangian is nothing but an arbitrary function of the Ricci scalar (R) as well as the trace of the energy-momentum tensor (\({\mathbb {T}}\)). Several variants of this gravity theory exist in the literature with successful applications in different areas [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68].

On the other hand, another modified theory of gravity that has a deep-rooted historical background needs here to mention and discuss now. In the year 1928 Einstein [69] proposed a new theory in relation to his fundamental or classical GR. This is originally known as Teleparallelism which nowadays comes in the picture as teleparallel gravity, where an attempt was done by Einstein in connection to unification between the forces like gravity and electromagnetism. Basically, in the mathematical structure a spacetime was characterized by a curvature-free linear connection in conjunction with a metric tensor field and has received much attention in recent research on astrophysics as well as cosmology [70, 71].

In the last few years, there has been greater emphasis on teleparallel theories as one of the alternate gravity theories. Although these theories most often work in a torsion-based environment, however the enthusiasm has shifted to symmetric teleparallelism, where gravity is effectively defined by nonmetricity rather than curvature or torsion. It is worth noting that it is the affine connection, rather than the physical manifold, which takes major role as the mechanism for mediating gravity. This is realized by the fact that, in GR, the curvature is a property of the connection and not of the manifold itself, and hence it can also be characterized by other connection properties like non-metricity. Symmetric teleparallel gravity is formulated in terms of a spacetime metric and Levi-Civita connection or its teleparallel formulation and offers an interesting geometric interpretation of gravitation. It exploits a connection that is torsion-free and curvature-free, but not metric-compatible to describe gravity. By using the so-called ‘coincident gauge’, [72, 73] this connection can be minimized to a partial derivative. From a geometrical point of view, this means that the vectors on a manifold stay parallel over large distances [74]. The rest of the gravitational information is contained in the non-metricity contributions [72, 75,76,77] by requiring the connection to be torsion-free and the curvature to disappear.

The original GR being associated with spacetime curvature, a plausible explanation of the accelerated dynamics of the Universe was to entreat an exotic agent, known as dark energy (DE) [8, 9] and for that, it is necessary to give relaxation to the torsion and nonmetricity. Therefore, as twin baby from the mother GR, one may get two equivalent prescriptions for an alternative gravity: (i) teleparallel equivalent of GR (TEGR) where torsion T has definite role [78,79,80] whereas (ii) symmetric teleparallel general relativity (STGR) where nonmetricity Q has a vital role [72, 81,82,83].

However, in the present work, we are employing STGR theory where the nonmetricity describes the gravity instead of the joint effect of the curvature and the torsion. Recently, f(Q) have gone through several successful applications in cosmology [84,85,86,87,88,89,90,91,92,93] as well as in astrophysics [94,95,96,97,98,99,100,101]. We would like to mention here an important work on f(Q) theory of gravity [102] where the authors considered several cosmological relevance by using the evolution equations and constraining specific functional forms in the Lagrangian \({\mathscr {L}}\). Another work that can claim special mention is that Wang et al. [103] particularly have shown that there does not exist an exact Schwarzschild solution for the nontrivial f(Q) function. Therefore, out of the above-mentioned total scenario we are treating compact stars (specifically neutron and/or strange stars) under the teleparallel f(Q)-gravity as an alternative theory.

A new mathematical technique known as gravitational decoupling has drawn much attention to the scientists to treat compact stellar objects and several astrophysical phenomena under the platform of the standard GR as well as modified gravity theories [104,105,106,107,108,109,110,111,112,113,114,115,116,117] (a detailed discussions with various recent applications are available in the following Refs. [118,119,120,121]). Due to the fruitfulness of the gravitational decoupling approach, it has been applied along with the complexity factor to investigate the compact star models. The concept of complexity in the context of the spherically symmetric metric was originally proposed by Herrera [122] and its generalization as well [123]. Some seminal works on complexity can be seen in the following Refs. [26, 101, 126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141].

In the context of the compact stars, it is now evident that these are endpoints of normal stars due to tremendous gravitational inward pulling under the general relativistic effect of Einstein. They are usually clubbed as a white dwarf, neutron star and black hole where the following internal constitution of the matter content either of the formations into endpoint can take place. From the basic astrophysical point of view, to form a white dwarf the Chandrasekhar limit [142] should be maintained. However, all the ions of a normal star can be inverted into neutral particles to form a neutron star or beyond that the ultra-dense compact objects made up out of u, d and s type quark particles to form strange stars [143, 144]. Eventually one may get a black hole from which nothing can be escaped due to its tremendous potential and hence the escape velocity becomes unattainable for a photon. This obviously makes the compact star invisible, i.e. black to an observer though the Hawking radiation [145] may work from the event horizon because of the relativistic quantum effects.

The outline of the present study is as follows. In Sect. 2 we have provided field equations (i.e. in 2.1 set of field equations in pure f(Q)-gravity whereas in 2.2 set of equations for new source \(\theta _{\epsilon \nu }\)). In Sect. 3 qualitative physical analysis has been performed, e.g. physical behavior of density and pressures (Sect. 3.1), energy conditions (Sect. 3.2), causality and sound velocity (Sect. 3.3), adiabatic stability criterion (Sect. 3.4). The impact of constant \(\beta _1\) on constraining the mass via equi-mass diagram is discussed in Sect. 3.5 while the impact of deformation through constant \(\alpha \) as well as \(\beta _1\) on mass-radii relations via \(M-R\) curves are presented in Sect. 3.6. However, the impact of \(\beta _1\) on physical parameters such as density and pressures is present in Sect. 3.7. We have devoted Sect. 4 for the overall summary and a few final concluding remarks on the investigation.

2 The action under gravitational decoupling for f(Q)-gravity-theory

The action under gravitational decoupling for modified f(Q) gravity introducing new sector \(\theta _{\epsilon \nu }\) is presented as

$$\begin{aligned} {\mathscr {S}}=\int \frac{1}{2}\,f(Q)\sqrt{-g}\,d^4x+\int {\mathscr {L}}_m\,\sqrt{-g}\,d^4x+ \int {\mathscr {L}}^{*}_\theta \,\sqrt{-g}\,d^4x,~~~ \end{aligned}$$
(1)

where \({\mathscr {L}}_m\) is the Lagrangian density for matter distributions as appears in the f(Q) gravity theory, \({\mathscr {L}}^*_{\theta }(= \alpha {\mathscr {L}}_\theta \)) describes the Lagrangian density for new matter source (not given by f(Q) gravity), and \(\alpha \) is a decoupling constant.

In the above, Q denotes a nonmetricity scalar which plays the role of the gravitational interaction. Moreover, this new contribution will introduce some corrections to matter fields in f(Q) which may help us to know the physical properties of the stellar system beyond the f(Q) gravity theory. Also, we consider the energy-momentum tensors (i.e. \(T_{\epsilon \nu }\) and \(\theta _{\epsilon \nu }\)) corresponding to Lagrangian densities (i.e. \({\mathscr {L}}_m\) and \({\mathscr {L}}^{*}_{\theta }\)), respectively as

$$\begin{aligned}{} & {} T_{\nu \epsilon }=g_{\nu \epsilon } {\mathscr {L}}_m-\frac{2\,\partial ({\mathscr {L}}_m)}{\partial g^{\nu \epsilon }},\end{aligned}$$
(2)
$$\begin{aligned}{} & {} \theta ^{*}_{\nu \epsilon }=g_{\nu \epsilon } {\mathscr {L}}^{*}_\theta -\frac{2\,\partial ({\mathscr {L}}^{*}_\theta )}{\partial g^{\nu \epsilon }}, \end{aligned}$$
(3)

whose joint action of both the energy-momentum tensors is denoted by \(T^{\text {eff}}_{\epsilon \nu }~\big (=T_{\epsilon \nu }+\theta ^{*}_{\epsilon \nu }\big )\), where \(\theta ^{*}_{\nu \epsilon }=\alpha \theta _{\nu \epsilon }\).

In terms of the affine connection, the nonmetricity tensor \(Q_{\lambda \epsilon \nu }\) is given by

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\bigtriangledown _{\lambda } g_{\epsilon \nu }=\partial _\lambda g_{\epsilon \nu }-\varGamma ^\delta _{\,\,\,\lambda \epsilon }g_{\delta \nu }-\varGamma ^\delta _{\,\,\,\lambda \nu }g_{\epsilon \delta }, \end{aligned}$$
(4)

where \(\varGamma ^\delta _{\,\,\,\epsilon \nu }\) is defined as the affine connection which takes the form

$$\begin{aligned} \varGamma ^\delta _{\,\,\,\epsilon \nu }=\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace +K^\delta _{\,\,\,\epsilon \nu }+ L^\delta _{\,\,\,\epsilon \nu }, \end{aligned}$$
(5)

where \(\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace \), \(L^\delta _{\,\,\,\epsilon \nu }\), and \(K^\delta _{\,\,\,\epsilon \nu }\), respectively, represent the Levi-Civita connection, disformation, and contortion tensors and are given as:

$$\begin{aligned} \lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace{} & {} =\frac{1}{2}g^{\delta \sigma }\left( \partial _\epsilon g_{\sigma \nu }+\partial _\nu g_{\sigma \epsilon }-\partial _\sigma g_{\epsilon \nu }\right) ,\nonumber \\ L^\delta _{\,\,\,\epsilon \nu }{} & {} =\frac{1}{2}Q^\delta _{\,\,\,\,\epsilon \nu }-Q_{(\epsilon \,\,\,\,\nu )}^{\,\delta },\nonumber \\ K^\delta _{\,\,\,\epsilon \nu }{} & {} =\frac{1}{2} {\mathscr {T}}^\delta _{\,\,\,\,\epsilon \nu }+{\mathscr {T}}_{(\epsilon \,\,\,\,\,\,\nu )}^{\,\,\,\delta }, \end{aligned}$$
(6)

where the torsion tensor \({\mathscr {T}}^\delta _{\,\,\,\epsilon \nu }\) describes the anti-symmetric part realted to affine connection, \({\mathscr {T}}^\delta _{\,\,\,\epsilon \nu }=2\varGamma ^\lambda _{\,\,\,[\epsilon \nu ]}\).

On the other hand, the superpotential connected to the nonmetricity tensor is given as:

$$\begin{aligned} P^\alpha _{\,\,\,\,\epsilon \nu }= & {} \frac{1}{4}\left[ -Q^\alpha _{\,\,\,\,\epsilon \nu }+2 Q_{(\epsilon \,\nu )}^\alpha +Q^\alpha g_{\epsilon \nu }\right. \nonumber \\{} & {} \left. -{\tilde{Q}}^\alpha g_{\epsilon \nu }-\delta ^\alpha _{(\epsilon }Q_{\nu )}\right] , \end{aligned}$$
(7)

where

$$\begin{aligned} Q_{\alpha }\equiv Q_{\alpha \,\,\,\epsilon }^{\,\,\epsilon },\; {\tilde{Q}}_\alpha =Q^\epsilon _{\,\,\,\,\alpha \epsilon }, \end{aligned}$$
(8)

are two traces which being independent can help to describe the nonmetricity scalar term as

$$\begin{aligned} Q=-Q_{\alpha \epsilon \nu }\,P^{\alpha \epsilon \nu }. \end{aligned}$$
(9)

For deriving the field equations in f(Q) gravity, we vary the action (1) with respect to the metric tensor \(g^{\epsilon \nu }\), that provides

$$\begin{aligned}{} & {} \frac{2}{\sqrt{-g}}\bigtriangledown _\gamma \left( \sqrt{-g}\,f_Q\,P^\gamma _{\,\,\,\,\epsilon \nu }\right) +\frac{1}{2}g_{\epsilon \nu }f +f_Q\big (P_{\epsilon \gamma i}\,Q_\nu ^{\,\,\,\gamma i}\nonumber \\ {}{} & {} \quad -2\,Q_{\gamma i \epsilon }\,P^{\gamma i}_{\,\,\,\nu }\big ) =- T^{\text {eff}}_{\epsilon \nu },~~ \end{aligned}$$
(10)

where \(f_Q=\frac{d f}{d Q}\).

With the help of Eq. (1), it is possible to obtain extra constraint over the connection which can be given by

$$\begin{aligned} \bigtriangledown _\nu \bigtriangledown _\epsilon \left( f_Q\,P^\gamma _{\,\,\,\,\nu \epsilon } \sqrt{-g}\right) =0. \end{aligned}$$
(11)

Therefore, the constraints on torsionless and curvatureless provide the affine-connection as

$$\begin{aligned} \varGamma ^\vartheta _{\,\,\,\nu \epsilon }=\left( \frac{\partial x^\vartheta }{\partial \zeta ^\gamma }\right) \partial _\nu \partial _\epsilon \zeta ^\gamma . \end{aligned}$$
(12)

Furthermore, one can opt for a special coordinate system, e.g. coincident gauge, under which \(\varGamma ^\lambda _{\,\,\,\epsilon \nu }=0\). The nonmetricity Eq. (4) then gets the following form

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\partial _\lambda g_{\epsilon \nu }. \end{aligned}$$
(13)

The above form does help immensely to perform the calculation as the fundamental variable being here only the metric function. However, it is to note that the action in this case no longer remains a diffeomorphism invariant unlike the standard GR [93]. Therefore, as an easy path one may undergo the covariant formulation of f(Q) gravity. The affine connection as expressed in Eq. (12) being purely inertial, we can perform the covariant formulation by determining the affine connection when gravity is absent [146].

In the ongoing study, our interest is to find the gravitationally decoupled solutions under the theory of f(Q) gravity for self-bound compact stellar objects. For this we have considered a Schwarzschild-type static spherically symmetric metric as

$$\begin{aligned} ds^2=-e^{\varPhi (r)}dt^2+e^{\mu (r)}dr^2+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2, \end{aligned}$$
(14)

where \(\varPhi (r)\) and \(\mu (r)\), respectively, describe the metric potentials which are mainly functions of r only.

Furthermore, the formula for Q in connection to the spacetime (14), is determined as

$$\begin{aligned} Q=-\frac{2 e^{-\mu (r)} \left( 1+r \varPhi ^\prime (r)\right) }{r^2}. \end{aligned}$$
(15)

On the other hand, we also consider that the interior of the compact star under f(Q) gravity is composed of anisotropic matter distributions. In this situation, one can provide the original source \(T_{\nu \epsilon }\) in the context of f(Q) theory as

$$\begin{aligned} T_{\nu \epsilon }=\rho \eta _{\nu }\,\eta _{\epsilon }+ p_r \eta _{\nu }\,\eta _{\epsilon }-\left( p_t-p_r\right) \chi _{\nu } \chi _{\epsilon }+p_t\,g_{\nu \,\epsilon }, \end{aligned}$$
(16)

where energy density (\(\rho \)), radial pressure (\(p_{r}\)) and tangential pressure (\(p_{t}\)) are the main matter variables in the pure f(Q)-gravity wheres \(\eta ^{\nu }\) and \(\chi ^{\nu }\) satisfies further definition as: \(u^{0} u_{_0}=-1\) and \(\chi ^{1} \chi _{_1}=1\).

The components for effective energy-momentum tensor are defined as

$$\begin{aligned}{} & {} [T^0_0]^{\text {eff}}= -\rho ^{\text {eff}}, \nonumber \\{} & {} [T^1_1]^{\text {eff}}= P^{\text {eff}}_r,~~~[T^2_2]^{\text {eff}}=[T^3_3]^{\text {eff}} = P^{\text {eff}}_t.~~ \end{aligned}$$
(17)

As a result, the \(\theta \)-sector components can be provided as

$$\begin{aligned}{} & {} \theta ^0_0=-\rho ^{\theta },~~~ \theta ^1_1=p^{\theta }_r, ~~~\theta ^2_2=p^{\theta }_t,~~ \text {and}~~ \theta ^3_3=p^{\theta }_t. \end{aligned}$$
(18)

Using above we get

$$\begin{aligned} \rho ^{\text {eff}}= \rho +\alpha \,\rho ^{\theta },~~P^{\text {eff}}_r=p_r+\alpha \,p^{\theta }_r,~~P^{\text {eff}}_t=p_t+\alpha \,p^{\theta }_t,\nonumber \\ \end{aligned}$$
(19)

and effective anisotropy is defined as

$$\begin{aligned} \varDelta ^{\text {eff}}= & {} P^{\text {eff}}_t-P^{\text {eff}}_r= \varDelta _Q+\varDelta _{\theta } \nonumber \\= & {} (p_t-p_r) + \alpha (p^{\theta }_t-p^{\theta }_r). ~~~~~ ~ \end{aligned}$$
(20)

In the above expression it is clear that the effective anisotropy is the combination of two anisotropies corresponding to \(T_{\epsilon \,\nu }\) and \(\theta _{\epsilon \,\nu }\). Here the anisotropy \(\varDelta _{\theta }\) has been invoked due to gravitational decoupling which may enhance the effective anisotropy.

Due to the anisotropic fluid (17), the independent components of the equations of motion (8) under f(Q) gravity can be given as

$$\begin{aligned} \rho ^{\text {eff}}{} & {} =-\frac{f(Q)}{2}+f_{Q}\Big [Q+\frac{1}{r^2}+\frac{e^{-\mu }}{r}(\varPhi ^\prime +\mu ^\prime )\Big ],\end{aligned}$$
(21)
$$\begin{aligned} P^{\text {eff}}_r{} & {} =\frac{f(Q)}{2}-f_{Q}\Big [Q+\frac{1}{r^2}\Big ],\end{aligned}$$
(22)
$$\begin{aligned} P^{\text {eff}}_t{} & {} =\frac{f(Q)}{2}-f_{Q}\Big [\frac{Q}{2}-e^{-\mu } \Big \{\frac{\varPhi ^{\prime \prime }}{2}+\Big (\frac{\varPhi ^\prime }{4}+\frac{1}{2r}\Big ) \nonumber \\{} & {} \quad \times (\varPhi ^\prime -\mu ^\prime )\Big \}\Big ],~~~\end{aligned}$$
(23)
$$\begin{aligned} 0{} & {} =\frac{\text {cot}\theta }{2}\,Q^\prime \,f_{QQ}, \end{aligned}$$
(24)

where \(f_{Q}(Q)=\frac{\partial f(Q)}{\partial Q}\).

Furthermore, according to Wang et al. [149] the exact Schwarzschild anti-de Sitter solution exists for the constraint \(f_{QQ}=0\). On the other hand, functional form derived from \(f_{QQ}=0\) is also compatible with the line element (14) and the coincident gauge [146]. Therefore, we must derive the functional form of f(Q) by considering only \(f_{QQ}\) to be zero in order to obtain the solution for self-gravitating compact star models. Hence

$$\begin{aligned}{} & {} f_{QQ}=0~~~~~\Longrightarrow ~~~~ f(Q)=\beta _1\,Q+\beta _2, \end{aligned}$$
(25)

where \(\beta _1\) and \(\beta _2\) are constants.

By inserting of Eqs. (14) and (25), the Eqs. (21)–(23) give the following set of equations of motion

$$\begin{aligned}{} & {} \quad \rho ^{\text {eff}} = \frac{1}{2\,r^2} \Bigg [2\, \beta _1+2\, e^{-\mu }\, \beta _1 \left( r\, \mu ^\prime -1\right) -r^2 \,\beta _2 \Bigg ],\end{aligned}$$
(26)
$$\begin{aligned}{} & {} \quad P^{\text {eff}}_r=\frac{1}{2\,r^2} \Bigg [-2\, \beta _1+2\, e^{-\mu } \,\beta _1 \left( r\, \varPhi ^\prime +1\right) +r^2\, \beta _2\Bigg ],\nonumber \\\end{aligned}$$
(27)
$$\begin{aligned}{} & {} \quad P^{\text {eff}}_{t}=\frac{e^{-\mu }}{4\,r} \Bigg [2\, e^{\mu }\, r\, \beta _2 +\beta _1\, \left( 2+r \varPhi ^\prime \,\right) \nonumber \\{} & {} \qquad \qquad \left( \varPhi ^\prime -\mu ^\prime \right) +2\, r\, \beta _1 \, \varPhi ^{\prime \prime }\Bigg ],~~~~~~ \end{aligned}$$
(28)

The linear combination of equations (26)-(28) gives,

$$\begin{aligned}{} & {} -\frac{\varPhi ^\prime }{2}(\rho ^{\text {eff}}+P^{\text {eff}}_r)-(P^{\text {eff}}_r)^{\prime }+\frac{2}{r}( P^{\text {eff}}_{t}-P^{\text {eff}}_r)=0.~~~ \end{aligned}$$
(29)

Interestingly, the above-mentioned Eq. (29) is called as the modified TOV equation [147, 148] under f(Q)-gravity theory [149, 150] satisfying the relation (25) which is equivalent to the conservation equation in classical general relativity. Now, our motivation in the present work is to obtain an exact solution of equations of motion (26)–(28) under the vanishing complexity formalism in f(Q)-gravity context. For this purpose, we obtain the condition of vanishing complexity in f(Q)-gravity using the definition of complexity proposed by Herrera [122,123,124,125]. Based on his definition, the complexity factor (\(Y^Q_{TF}\)) is defined for the system (26)–(28) as

$$\begin{aligned}{} & {} \quad Y^Q_{TF} = 8\pi (P^{\text {eff}}_r-P^{\text {eff}}_t)-\frac{4\pi }{2r^3} \int ^r_0 x^3 (\rho ^{\text {eff}})^{\prime } (x) dx. \end{aligned}$$
(30)

On inserting of \(P^{\text {eff}}_r\), \(P^{\text {eff}}_t\) and \(\rho ^{\text {eff}}\) in above equation, we \(Y_{TF}\) as

$$\begin{aligned}{} & {} \quad Y^Q_{TF}=\frac{\beta _1\, \big [\varPhi ^\prime \big \{r (\mu ^\prime -\varPhi ^\prime )+2 \big \}-2 r \varPhi ^{\prime \prime } \big ]}{4\, r\,e^{\mu } }. \end{aligned}$$
(31)

Then \(Y^Q_{TF}=0\) gives

$$\begin{aligned}{} & {} \quad \beta _1\, \big [\varPhi ^\prime \big \{r (\mu ^\prime -\varPhi ^\prime )+2 \big \}-2 r \varPhi ^{\prime \prime } \big ]=0. \end{aligned}$$
(32)

Since \(\beta _1\) can not be zero therefore the second factor must be zero, which gives

$$\begin{aligned}{} & {} \quad \bigg [\varPhi ^\prime \big \{r (\mu ^\prime -\varPhi ^\prime )+2 \big \}-2 r \varPhi ^{\prime \prime } \bigg ] = 0. \end{aligned}$$
(33)

The simplified form of the above differential equation can be written after performing the integration as

$$\begin{aligned}{} & {} \quad \varPhi ^\prime \,e^{\varPhi /2}=A\,r\, e^{\mu /2}. \end{aligned}$$
(34)

Lastly, we derive the bridge equation between \(\varPhi \) and \(\mu \) as

$$\begin{aligned}{} & {} \quad e^{\varPhi }= \left( B+ A\int r\, e^{\mu /2} dr\right) ^2, \end{aligned}$$
(35)

where A and B are two constants of integration. It is very interesting to note that the above relation (35) in f(Q) -gravity theory is similar to the relation derived by Contreras and Stuchlik [151] in the context of Einstein’s GR.

As mentioned above, our primary objective was to get an exact solution to the field equations (26)–(28) describing a compact star beyond the f(Q)-gravity theory. Therefore, we use the well-known technique of gravitational decoupling through the minimal geometric deformation (MGD) approach via a specific transformation

$$\begin{aligned}{} & {} \varPhi (r) \longrightarrow H(r)+\alpha \, \eta (r),~ \end{aligned}$$
(36)
$$\begin{aligned}{} & {} e^{-\mu (r)} \longrightarrow W(r)+\alpha \, \varPsi (r),~~ \end{aligned}$$
(37)

where \(\eta (r)\) denotes the deformation function along the temporal component of spacetime while the deformation function \(\varPsi (r)\) is along the radial metric component.

In the MGD case \(\varPsi (r)\ne 0\) while defromation function \(\eta (r) = 0\) and which we have shown in Fig. 2. Moreover, the MGD technique basically divides the decoupled system (22)–(24) into two subsystems under f(Q)-gravity, where equations of motion for \(T_{\epsilon \,\nu }\) is denoted as first set while the second set is for the new matter source \(\theta _{\epsilon \,\nu }\) as, will be given in the next two subsections.

2.1 Systemic field equations in f(Q)-gravity

We have the following set of equations

$$\begin{aligned} \rho{} & {} = \frac{\beta _1}{r^2} [(1-W) -r W^{\prime } ]-\frac{\beta _2 }{2},\end{aligned}$$
(38)
$$\begin{aligned} p_r{} & {} = \frac{\beta _1}{r^2}[(W-1) +r H^{\prime } ]+\frac{\beta _2 }{2}, \end{aligned}$$
(39)
$$\begin{aligned} p_t{} & {} =\frac{\beta _1( H^{\prime } W^{\prime } + 2 W H^{\prime \prime } +H^{\prime 2} W) }{4} +\frac{\beta _1\,(W^{\prime } + W H^{\prime }) }{2 r}\nonumber \\ {}{} & {} \quad +\frac{\beta _2}{2}, \end{aligned}$$
(40)

and according to Eq. (28) one can get

$$\begin{aligned}{} & {} (p_r)^{\prime }=-\frac{H^\prime \, (p_r+\rho )}{2}-\frac{2}{r}( p_{r}-p_t),~~ \end{aligned}$$
(41)

which is nothing but a TOV equation for the system (31)–(34) and its solution can be provided by the spacetime

$$\begin{aligned} ds^2=-e^{H(r)}dt^2+\frac{dr^2}{W(r)}+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2. \end{aligned}$$
(42)

2.2 Systemic field equations with source \(\theta _{\epsilon \nu }\)

$$\begin{aligned} \rho ^{\theta }{} & {} =-\beta _1 \Big (\frac{\varPsi }{r^2}+\frac{\varPsi ^\prime }{r}\Big ), \end{aligned}$$
(43)
$$\begin{aligned} p^{\theta }_r{} & {} =\beta _1\Big [\frac{\varPsi }{r^2}+\frac{\varPhi ^{\prime } \varPsi }{r}\Big ], \end{aligned}$$
(44)
$$\begin{aligned} p^{\theta }_t{} & {} = \frac{\beta _1}{4r} \Bigg [r (\varPsi ^\prime \varPhi ^{\prime } + 2 \varPhi ^{\prime \prime } \varPsi +\varPhi ^{\prime 2} \varPsi ) +2(\varPsi ^\prime +\varPhi ^{\prime } \varPsi ) \Big ].\nonumber \\ \end{aligned}$$
(45)

The linear combination of equations of motion (43)–(45) yields

$$\begin{aligned}{} & {} -\frac{H^\prime }{2}(\rho ^{\theta }+p^{\theta }_r)-(p^{\theta }_r)^{\prime }+\frac{2}{r}( p^{\theta }_{t}-p^{\theta }_r)=0.~~ \end{aligned}$$
(46)

From the above equation, one important point may be noted that it is not required any energy exchange among the sources for decoupling.

Using Eq. (37), the condition (35) reduce to

$$\begin{aligned}{} & {} e^{{H(r)}}=\left( B+A \int \frac{r}{\alpha \,\varPsi (r)+W(r)}\,dr\right) ^2 \end{aligned}$$
(47)

Now we move on to the solution of field equations for both systems. We have nine unknowns and six independent equations along with vanishing complexity condition (36). Therefore, we need two auxiliary conditions to solve the system completely. For this purpose, we consider well-behaved ansatz for the radial metric function W(r) in pure f(Q)-gravity [152] connected to the spacetime (42) and mimicking of density constraint approach (\(\rho =\rho ^{\theta }\)) as

$$\begin{aligned}{} & {} W(r) =\frac{1+Lr^2}{1+Nr^2}, \end{aligned}$$
(48)
$$\begin{aligned}{} & {} \frac{\beta _1 (1-W) }{r^2}-\frac{W^{\prime } \beta _1 }{r}-\frac{\beta _2 }{2} = -\beta _1 \Bigg (\frac{\varPsi }{r^2}+\frac{\varPsi ^\prime }{r}\Bigg ), \end{aligned}$$
(49)

where L and N are constants with dimension \(length^{-2}\) and \(length^{-4}\), respectively (Fig. 1).

Now the differential Eq. (49) along with Eq. (48) leads the solution for deformation function \(\varPsi (r)\) as

$$\begin{aligned} \varPsi (r)=\frac{r^2 \left( \beta _2+6 \beta _1 L-6 \beta _1 N+\beta _2 N r^2\right) }{6 \beta _1 \left( 1+ N r^2\right) }. \end{aligned}$$
(50)

Now the new form of the gravitational potential \(e^{\mu (r)}\) is given by

$$\begin{aligned} e^{\mu (r)}= \frac{6 \beta _1 \left( N r^2+1\right) }{6 \beta _1 \left[ 1+(\alpha +1) L r^2-\alpha \,N\,r^2\right] +\alpha \beta _2 r^2 \left( N r^2+1\right) }. \nonumber \\ \end{aligned}$$
(51)
Fig. 1
figure 1

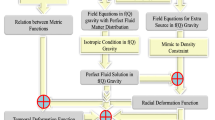
The flow chart for the f(Q)-gravity with the vanishing complexity factor in connection to the Buchdahl metric (vide Eq. (48))

Full size image

Before proceeding further, it is highlighted that the most suitable exterior spacetime under the functional form Eq. (25) in the f(Q)-gravity theory can be given by exact Schwar-zschild (Anti-) de Sitter spacetime. Therefore, the solution’s constant must be calculated by joining of the deformed interior spacetime with the Schwarzschild (Anti-) de Sitter exterior spacetime at the boundary surface \(r=R\). The Schwarzschild (Anti-) de Sitter spacetime and the suitable boundary conditions are:

$$\begin{aligned} ds^2_+{} & {} =-\bigg (1-\frac{2M}{r}-{\varLambda \over 3}~r^2\bigg )\,dt^2+\frac{dr^2}{\bigg (1-\frac{2M}{r}-{\varLambda \over 3}~r^2\bigg )} \nonumber \\ {}{} & {} \quad +r^2 \big (d\theta ^2 +\sin ^2\theta \,d\phi ^2 \big ). \end{aligned}$$
(52)

Now use the Darmois-Israel boundary conditions [153, 154] in order to express the first and second fundamentals mathematically as

$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\varLambda \over 3}~r^2\bigg )= & {} e^{\varPhi (R)},~~~\end{aligned}$$
(53)
$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\varLambda \over 3}~r^2\bigg )= & {} e^{-\mu (R)},~~~\end{aligned}$$
(54)
$$\begin{aligned} P_r^\mathrm{{eff}}(R)= & {} 0, \end{aligned}$$
(55)

where M is the total mass and \(\varLambda \) the cosmological constant. It is noted that cosmological constant \(\varLambda \) can be written in the form of constant \(\beta _1\) and \(\beta _2\) as \(\varLambda =\beta _2/2\beta _1\). As we know that the value of the cosmological constant \(\varLambda \) in the present universe according to the current observational evidence is approx \( 10^{-46}/{\text {km}}^2\). Therefore, there is no effect of \(\varLambda \) on the current stellar models and then it can be considered zero. Due to this assumption, we get \(\beta _2=0\).

By substituting of Eq. (51) into the condition (36) and integrate, we get

$$\begin{aligned} e^{\frac{H(r)}{2}}= & {} \frac{A}{2 \sqrt{N} \sqrt{f(r)} \chi ^{3/2}_1}\nonumber \\{} & {} \times \Bigg [-\sqrt{N} \sqrt{N r^2+1} \sqrt{\chi _1} f(r)+(\alpha +1) \nonumber \\{} & {} \quad \times (L\!-\!N) \sqrt{f(r)} \, \tan ^{-1}\left( \frac{\sqrt{N} \sqrt{f(r)}}{\sqrt{N r^2+1} \sqrt{\chi _1}}\right) \Bigg ]\!+\!B, \nonumber \\ \end{aligned}$$
(56)

where

$$\begin{aligned}{} & {} \chi _1=\big [\alpha N-(\alpha +1)\big ] L,\\{} & {} f(r)=\big [(\alpha +1) L r^2-\alpha N r^2+1\big ]. \end{aligned}$$

Now we have determined the expression for \(\varPhi (r)=H(r)\) and \(\varPsi (r)\). In this way, the matter variables density (\(\rho \)), pressures (\(p_r\) & \(p_t\)), and components of new source \(\rho ^{\theta }\), \(p^{\theta }_r\), and \(p^{\theta }_t\) can be easily found by inserting \(\varPsi (r)\), \(\varPhi (r)=H(r)\), and W(r) into Eqs. (39)–(40) and (43)–(45) and consequently the expression for effective quantities are

$$\begin{aligned} \rho ^{\text {eff}}= & {} \frac{(\alpha +1) \beta _1 (N-L) \left( N r^2+3\right) }{\left( 1+N r^2\right) ^2},\end{aligned}$$
(57)
$$\begin{aligned} P^{\text {eff}}_r= & {} \frac{1}{(1+N r^2)}\Big [\beta _1 \Big ((\alpha +1) \varPsi _{11}(r) L r^2 \nonumber \\{} & {} -\alpha \varPsi _{11}(r) N r^2+\varPsi _{11}(r)+(\alpha +1) (L-N)\Big )\Big ], \nonumber \\ \end{aligned}$$
(58)
$$\begin{aligned} P^{\text {eff}}_t= & {} \frac{1}{4 \left( N r^2+1\right) ^2} \Big [\beta _1 \Big (2 \big \{\psi _{12}(r) \left( N r^2+1\right) \nonumber \\{} & {} \times [(\alpha +1) L r^2-\alpha N r^2 +1]+2 (\alpha +1) (L-N)\big \}\nonumber \\{} & {} +\varPsi _{11}^2(r) r^2 \left( N r^2+1\right) [(\alpha +1) L r^2 \nonumber \\{} & {} -\alpha N r^2+1]+2 \varPsi _{11}(r)\nonumber \\{} & {} \times \big \{(\alpha +1) L r^2 \left( N r^2+2\right) -\alpha N^2 r^4\nonumber \\{} & {} -2 \alpha N r^2+1\big \}\Big )\Big ]. \end{aligned}$$
(59)

3 Qualitative physical analysis

In this Section, we present the analysis of the gravitationally decoupled anisotropic solution to test the regularity conditions of the obtained models in f(Q)-gravity theory. Note that we have checked the model behavior for \(\alpha =0.16\), 0.18, 0.20, and 0.22. It is obvious that when \(\alpha =0\), then the pure f(Q)-gravity model is recovered. It is to be mentioned that the solution is not physically valid when \(\alpha < 0.16\) (due to increasing tangential pressure within the objects) as well as \(\alpha > 0.22\) (due to not preserving the causality condition, especially radial velocity will be more than the speed of light). Therefore, the following range of the decoupling constant \(0.16 \le \alpha \le 0.22 \) yields a physically viable model in f(Q)-gravity theory.

Fig. 2
figure 2

The trend of effective energy density (\(\rho ^{\text {eff}}\times 10^{4}\)) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 3
figure 3

The trend of effective radial pressure (\(P^{\text {eff}}_r\times 10^{4}\)) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 4
figure 4

The trend effective tangential pressure (\(P^{\text {eff}}_t \times 10^{4}\)) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 5
figure 5

The trend effective anisotropy (\(\varDelta ^{\text {eff}} \times 10^{4}\)) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 6
figure 6

Variation of dominant energy conditions versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image

3.1 Physical behavior of density and pressures

In Figs. 2, 3 and 4, the variations of effective energy density, effective radial and tangential pressures with respect to radial distance r for different \(\alpha \) are shown. It is clear that energy density and pressures are monotonically decreasing for increasing r for each \(\alpha \) as expected for a physically viable solution. On the other hand, the central values of density and pressures are increasing when \(\alpha \) increases which implies that a more dense compact object can be obtained in the context of gravitational decoupling. This can be also observed from the increasing value of mass-radius ratios with increasing \(\alpha \) given in Table 1.

Table 1 The values of the physical parameters for different \(\alpha \)
Full size table

3.2 Energy conditions

For investigating the structural properties of our solution, we emphasize the energy conditions (EC) which are really predictable that all of the standard models must satisfy the energy conditions in all kinds of gravity. The necessary energy conditions are groups of inequalities subjected to the energy-momentum tensor of matter. The most viable conditions are Weak energy condition (WEC) (\(\rho ^{\text {eff}}+P^{\text {eff}}_r \ge 0\) and \(\rho ^{\text {eff}}+P^{\text {eff}}_t \ge 0\)), Strong energy condition (SEC) (\(\rho ^{\text {eff}}+P^{\text {eff}}_r+ P^{\text {eff}}_t\ge 0\)), and Dominant energy condition (DEC) (\(\rho ^{\text {eff}}-P^{\text {eff}}_r\ge 0\) and \(\rho ^{\text {eff}}-P^{\text {eff}}_t\ge 0\)). To verify all the above conditions, we first look at Figs. 2, 3, 4, the pressure and density are positive throughout the stellar object. Then WEC and SEC are already satisfying. Now we need to check only DEC. For this purpose, we plotted Fig. 6 to show the variation of quantities \(\rho ^{\text {eff}}-P^{\text {eff}}_r\) and \(\rho ^{\text {eff}}-P^{\text {eff}}_t\) within the stellar object which clearly show that both quantities are positive at each point of the object. This implies that our solution also satisfies the dominant energy condition (Fig. 5).

Fig. 7
figure 7

Variation of the radial velocity of sound \(v^2_r\) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 8
figure 8

Variation of the tangential velocity of sound \(v^2_t\) versus radial coordinate r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image
Fig. 9
figure 9

The behavior adiabatic index (\(\varGamma _r\)) with respect to r for different \(\alpha \) with \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\beta _1=1.2\)

Full size image

3.3 Causality and sound velocity

For preserving the causality condition, it is necessary that the sound velocity does not exceed the velocity of light, i.e. \(0 \le v^2_s = dP^{\text {eff}}_i/ d\rho ^{\text {eff}} <1\) (in geometrical units). We plotted Figs. 7 and 8 to investigate the velocity of sound propagation within the model. It is observed from Figs. 7 and 8 that the velocity of sound is always subluminal (i.e. \(0< \frac{dP^{\text {eff}}_i}{d\rho ^{\text {eff}}} < 1\)) for all decoupling constant \(\alpha \). This implies that the causality conditions preserves throughout the model.

3.4 Adiabatic stability criterion

The adiabatic index (\(\gamma \)) plays an important role in investigating the dynamical stability of a compact object. This adiabatic index \(\varGamma \) for anisotropic matter distribution for the decoupled system is given by

$$\begin{aligned} \varGamma _r \equiv \left( 1+\frac{\rho ^{\text {eff}}}{P ^{\text {eff}}_r}\right) \left( \frac{dP ^{\text {eff}}_r}{d\rho ^{\text {eff}}}\right) _S, \end{aligned}$$
(60)

where the derivation is accomplished at constant entropy S while \(\left( \frac{dP ^{\text {eff}}_r}{d\rho ^{\text {eff}}}\right) _S\) denote the velocity of sound. This shows that the sound velocity is an important measure connected to the adiabatic index, e.g. the adiabatic index for the Schwarzschild solution with constant density is infinite (incompressible fluid). On the other hand, Glass and Harpaz [155] show that the central value of the adiabatic index should be more than 4/3 for a stable polytropic star which will obviously depend on the amount of central velocity as well. Furthermore, based on current investigations, it is argued that the range of \(\varGamma _r\) should be 2 to 4 in massive neutron stars [156]. In Fig. 9 we plot adiabatic index \(\varGamma _r\) as a function of radial distance r for different \(\alpha \). The figure shows that the adiabatic index \(\varGamma _r> 4/3\) when \(\alpha \ge 0.19\). In this connection, Moustakidis [157] proposed a stronger condition on the stability of a self-gravitating system which is \(\varGamma >\varGamma _{crit}\), where \(\varGamma _{crit}\) denotes a critical value of the adiabatic index and it is defined as

$$\begin{aligned} \varGamma _{crit} = \frac{4}{3} + \frac{19 M}{21 R}. \end{aligned}$$
(61)

Table 1 contains the values of \(\varGamma _r\) for different values of \(\alpha \), which shows that \(\varGamma >\varGamma _{crit}\) satisfies when \(\alpha \approx 0.22\). Finally, we conclude that the gravitational decoupling technique may help in stabilizing the stellar configuration.

Fig. 10
figure 10

The equi-mass contour plot on the \(R-\beta _1\) plane for \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\) and \(\alpha =0.2\)

Full size image

3.5 Impact of coupling parameter \(\beta _1\) in constraining the mass via equi-mass diagrams

We discuss here on the impact of coupling parameters \(\beta _1\) on constraining the mass of the object via equi-mass diagram. In Fig. 10 we have shown the equi-mass diagram on \(R-\beta _1\) plane. One can notice from this figure that the pattern mass distribution on \(R-\beta _1\) plane shows that the mass is increasing in this situation when \(\beta _1\) increases with fixed R or R increases with fixed \(\beta _1\). But the effect of \(\beta _1\) can be noticed clearly near the boundary.

Fig. 11
figure 11

The \(M-R\) curve shows the mass-radius relation for different \(\beta _1\) with fixed \(\alpha =0.14\)

Full size image
Fig. 12
figure 12

The \(M-R\) curve shows the mass-radius relation for different \(\alpha \) with fixed \(\beta _1=1.2\,\text {km}^2\)

Full size image
Table 2 The predicted radii of compact stars LMC X-4, PSR J 1614+2230, PSR J 0740+6620, and GW190814 for the different \(\beta _1\) with fixed \(\alpha =0.14\) and different \(\alpha \) with fixed \(\beta _1=1.2\)
Full size table

3.6 Impact of coupling parameters in constraining the radii for different objects via \(M-R\) curves

In this Section, we focus on determining the masses of four neutron star candidates with masses ranging from \(1.29 ^{+ 0.05}_{-0.05}\) to \(2.14 ^{+ 0.2}_{-0.17}\). Furthermore, we also discuss the estimation of massive neutron stars with masses in the range of 2.5–2.67 \({M_\odot }\) came from the GW190814 event. Observations of the masses and their radii for these four neutron stars can be determined from Figs. 11 and 12 for the values of different \(\beta _1\) with fixed \(\alpha \) and different \(\alpha \) with fixed \(\beta _1\), respectively.

It is observed from Fig. 11 that our complexity-free solution expects the presence of low and high-mass neutron stars observed by authors [158,159,160,161]. As \(\beta _1\) increases with fixed \(\alpha \), our solution possesses the higher mass neutron star with larger radii. For \(\beta _1 = 1.4\), our model expects the massive neutron star with masses in the range of 2.5–2.67 with a radius of 14.23\(^{+0.21}_{-0.02}\) km, which is a secondary component of the GW190814 event. However, the masses and radii for other neutron stars for \(\beta _1=1.4\) are as follows: (i) \(M=1.29\pm 0.05~M_\odot \) with \(R=13.01^{+0.05}_{-0.14}\) km for LMC X-1, (ii) \(M=1.97\pm 0.04~M_\odot \) with \(R=14.05^{+0.03}_{-0.03}\) km for PSR J 1614-2230, (iii) \(M=2.14^{+0.2}_{-0.17}~M_\odot \) with \(R=14.18^{+0.07}_{-0.13}\) km for PSR J 0740+6620. It is highlighted that secondary component of the GW190814 is ruled out for low values of \(\beta _1=0.8\). The analysis shows that the constant \(\beta _1\) plays an important role in describing the higher mass neutron star candidates.

As we observed from Fig. 12 that the mass and radii both are increasing when \(\alpha \) increases. Moreover, the secondary component of the GW190814 event with masses \(2.5-2.67\) is ruled out in the absence of deformation. Nevertheless, we predict the presence of a secondary component of the GW190814 event with mass 2.5 in presence of deformation when \(\alpha \ge 0.14\). The predicted radii of different star candidates for \(\alpha =0.21\) are: (i) \(M=1.29\pm 0.05~M_\odot \) with \(R=12.38^{+0.06}_{-0.03}\) km for LMC X-1, (ii) \(M=1.97\pm 0.04~M_\odot \) with \(R=13.39^{+0.01}_{-0.04}\) km for PSR J 1614+2230, (iii) \(M=2.14^{+0.2}_{-0.17}~M_\odot \) with \(R=13.53^{+0.08}_{-0.44}\) km for PSR J 0740+6620, and (iv) \(M=2.5-2.67~M_\odot \) with \(R=13.61^{+0.02}_{-0.04}\) km for secondary component of the GW190814 event. Furthermore, Table 2 includes the predicted radii of different compact objects for different \(\beta _1\) and \(\alpha \). Finally, we can say that higher mass objects can be expected in f(Q)-gravity theory.

It has been noted recently by Rincón et al. [162, 163] that the \(M-R\) profile can be obtained in the context of the vanishing complexity factor and it was also confirmed by the group that the solutions thus obtained exhibit more compact objects than GR. In this regard, we have extended our study to testify self-gravitating compact objects via \(M-R\) profile in f(Q)-gravity theory under complexity formalism. Based on these arguments and the above analysis, we conclude that we get more compact objects when \(\beta _1\) is decreasing while higher \(\beta _1\) gives more massive objects.

Fig. 13
figure 13

The equi-density contour plot on the \(r-\beta _1\) plane for \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\), and \(R=10~\text {km}\)

Full size image
Fig. 14
figure 14

The equi-radial pressure contour plot on the \(r-\beta _1\) plane for \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\), and \(R=10~\text {km}\)

Full size image
Fig. 15
figure 15

The equi-tangential pressure contour plot on the \(r-\beta _1\) plane for \(N = 0.02~\text {km}^{-2}\), \(L = 0.00001~\text {km}^{-2}\), and \(R=10~\text {km}\)

Full size image

3.7 Impact of constant \(\beta _1\) on density and pressures

It is obvious that if \(\beta _1=1\), then f(Q)-gravity theory will be equivalent to GR. The effective energy density distribution on the \(r-\beta _1\) plane via the contour diagram is given in Fig. 13. It clearly shows that the density is decreasing monotonically when we move toward the boundary for any fixed value of \(\beta _1 \in [0.8,1.4]\) and attains its minimum value at the boundary. On the other hand, when we increase \(\beta _1\), then the magnitude of density increase as well, and its maximum value is obtained at the core of the star.

Figures 14 and 15 show the effective radial and tangential pressures (\(p^{\text {eff}}_r\) and \(p^{\text {eff}}_t\)) variations on the \(r-\beta _1\) plane. For fixing \(\beta _1\in [0.8,1.4]\), both pressures are decreasing monotonically with increasing radial distance r while magnitude of \(p^{\text {eff}}_r\) and \(p^{\text {eff}}_t\) increases when \(\beta _1\) increases. The maximum pressure is observed at the center for \(\beta _1 \in [0.8,1.2]\) as expected in our analysis.

Therefore, we may assert that the constant \(\beta _1\) play important roles in constraining the energy density and pressure in f(Q)-gravity theory.

4 Concluding remarks

In this article, we have successfully explored the role of the vanishing complexity factor in generating self-gravitating compact objects in f(Q)-gravity theory. Here, we have mainly adopted the gravitationally decoupled action for modified f(Q) gravity in the form \({\mathscr {S}}={{\mathscr {S}}_{Q}}+\alpha {{\mathscr {S}}_{\theta }}\), which is equivalent to \({\mathscr {S}}={{\mathscr {S}}_{Q}}+ {{\mathscr {S}}^{*}_{\theta }}\), where \({\mathscr {S}}_Q\) designates the Lagrangian density of the fields occurring in the f(Q) gravity theory while \({\mathscr {S}}^{*}_{\theta } (=\alpha {\mathscr {S}}_{\theta })\) represents the Lagrangian density of a new gravitational sector, not described by f(Q) gravity. Since the new sector \(\alpha \theta _{\epsilon \nu }\) is equivalent to \(\theta ^*_{\epsilon \nu }\) because \(\alpha \) is just a control parameter. What’s more, using a systematic approach suggested by Contreras and Stuchlik [151] and the vanishing complexity factor condition stated by Herrera [122], we found a significant relationship between gravitational potentials. The complexity-free anisotropic solution is then generated by combining the Buchdahl model with the mimic-to-density constraints approach.

The eventual model was carefully examined to assess the acceptance of the gravitationally decoupled anisotropic solution via satisfying stringent regularity and stability constraints in f(Q)-gravity in the presence of deformation function via decoupling parameter \(\alpha \). It is interesting to note that the pure f(Q)-gravity theory can be achieved in the absence of deformation, whereas we get a physically viable solution beyond the f(Q)-gravity theory in the presence of deformation function. In the presence of deformation function, the physical behavior of the effective state variables (\(\rho ^{\text {eff}}\), \(P^{\text {eff}}_r\), \(P^{\text {eff}}_t\)), effective anisotropy (\(\varDelta ^{\text {eff}}\)) and the effective energy conditions namely, WEC, SEC, and DEC are analyzed within the stellar object. It is revealed that the limit necessary for the physical viability of the models beyond the f(Q)-gravity theory is satisfied by our anisotropic solution. We have also tested the stability of the resulting solution using the cracking technique and the adiabatic index, and we have discovered that the solution upholds the model-wide stability criterion.

We have then analyzed and made a few notable observations about the impact of coupling parameter \(\beta _1\) in constraining the mass via equi-mass diagrams. We have also shown the effect of the presence of new sector and constant \(\beta _1\) in constraining the Radii for different objects via \(M-R\) curves along with the impact of constant \(\beta _1\) on density and pressures. We specifically observed the impact of \(\beta _1\) on constraining the mass of the object via equi-mass diagrams shown in Fig. 10. We noticed from the mass distribution on \(R-\beta _1\) plane that if \(\beta _1\) increases with fixed R or R increases with fixed \(\beta _1\), the mass magnitude increases. Furthermore, it is evident from the pattern of the mass distribution on \(R-\beta _1\) plane that the increment in mass can be observed when \(R\ge 6\) and high mass can only be achieved for high values of \(\beta _1\) at \(R=10~ \text {km}\).

With an emphasis on the masses of four neutron star candidates with masses ranging from \(1.29 ^{+ 0.05}_{-0.05}\) to \(2.14 ^{+ 0.2}_{-0.17}\) and the estimation of massive neutron stars with masses in the range of 2.5 to 2.67 \({M_\odot }\), came from the GW190814 event, we have discussed the impact of coupling parameters in constraining the Radii via \(M-R\) curves for different values of \(\alpha \) with a fixed \(\beta _1\) and vise-versa. On the one hand, we notice that our solution has the higher mass neutron star with larger radii when \(\beta _1\) increases. For \(\beta _1 = 1.4\), our model predicts the massive neutron star with masses in the range of 2.5 to 2.67 with a radius of 14.23\(^{+0.21}_{-0.02}\) km, which is a secondary component of the GW190814 event. However, the masses and radii for other neutron stars are highlighted that secondary component of the GW190814 is excluded for low values of \(\beta _1=0.8\). On the other hand, we observe that the mass and radii both are increasing when \(\alpha \) increases with fixed \(\beta _1\). It should be highlighted that in the absence of deformation, the secondary component of the GW190814 event with masses \(2.5-2.67\) is ruled out. However, in presence of deformation with \(\alpha \ge 0.14\), we forecast the existence of a secondary component of the GW190814 event with mass 2.5. Moreover, the constant \(\beta _1\) has more impact on the radii than the constant \(\alpha \) (See the predicted radii in Table 2 for more details). Interestingly, we have clearly shown the impact of the constant \(\beta _1\) on the effective energy density distribution and the effective radial and tangential pressure variations on the \(r-\beta _1\) plane via the contour diagram. We notice that all the physical variables are decreasing monotonically with increasing radial distance r while their magnitude increases when \(\beta _1\) increases and their maximum values are obtained at the core of the star. Therefore, we can also state that the constant \(\beta _1\) play important roles in constraining the energy density and pressure in f(Q)-gravity theory.

Finally, it can be claimed that the role of the vanishing complexity factor in generating self-gravitating compact objects under f(Q)-gravity theory is viable for constructing astrophysical models that are congruent with experimental events.