Imprints of Casimir wormhole in Einstein Gauss–Bonnet gravity with non-vanishing complexity factor

Abstract

This article investigates Casimir wormhole solutions in Einstein Gauss–Bonnet (EGB) gravity. We are familiar that Null energy conditions (NEC) need not be satisfied for a stable wormhole due to the existence of exotic matter. As the Casimir effect acts as a negative energy source, it can be treated as a classical applicant for the exotic matter to discuss the stable dynamics of the wormhole. This work explores the Casimir effects with the Generalized Uncertainty Principle (GUP) on wormhole geometry in EGB gravity by confining our results for $D=5$. We have examined two GUP procedures, e.g., Kempf, Mangano, Mann (KMM) and Dentournay, Gabriel, and Spindel (DGS). We have developed shape functions for Casimir wormholes, and GUP corrected Casimir wormholes and studied their existence. In addition, we investigate the behavior of the Gauss–Bonnet (GB) Coupled parameter and minimal uncertainty (MU) parameter on the Equation of state (EOS) parameter. The active gravitational mass and embedding diagrams for all developed shape functions are analysed. Moreover, the violation of the NEC by an exotic matter, the equilibrium forces, and the complexity factor of Casimir wormholes and GUP-corrected Casimir wormholes have also been explored.

1 Introduction

In 1935, Einstein and Rosen discussed the concept of the hypothetical link called the wormholes or Einstein–Rosen bridge via space-time by considering the framework of General Relativity (GR) [1]. These bridges or tunnels connect two different paths of the same cosmos or create a shortcut. Still, the existence of wormholes should be explored experimentally. In 1988 Morris and Thorne established the idea of traversable wormholes [2]. They presented a new class of solutions of Einstein field equations that narrate wormholes and predict the existence of wormhole throat, which does not have a horizon problem. The stability in traversable wormholes depends on the presence of exotic matter. It is known that exotic matter in wormholes violates the NEC. The dynamics of wormholes have been studied with different modified theories in literature intensively [3,4,5,6,7,8,9,10]. The cosmic evolution of wormhole geometries in f(R) modified gravity has been discussed [11, 12]. The exact solution of the wormhole in the presence of phantom energy has been evaluated, and it found out phantom energy is limited in the vicinity of the wormhole throat [13]. The wormhole geometeries are discussed in other modified gravities e.g. f(R) [11, 14], f(T) [15, 16], BD theory [17,18,19,20], f(R, T) [21], scalar–tensor teleparallel gravity [22]. Recently, Kimet Jusufi and his fellow researchers [23] studied the existence of wormholes in 4D EGB gravity. In this article, they have developed shape functions with various techniques and analyzed wormhole conditions. Many efforts have been made in the literature to cut down the exotic matter content. Visser proposed one such model in which he suggested a traversable path should not be fallen in an area of exotic matter [24]. Interestingly, no such traversable wormhole has been found because it is nearly impossible to have enough negative energy density. Scientists have proved that negative energy can be created in laboratories known as Casimir energy [25].

Dutch physicist Hendrik Casimir suggested the phenomenon of the Casimir effect in 1948. A force may exist between the uncharged, parallel, conducting plates [25]. Garattini [26] considered Casimir energy a potential source to study the existence of traversable wormholes. The Casimir effect strongly depends on geometry’s shape and is an artificial source of energy. This form of energy is a suitable source for traversable wormhole as the quantum field of the vacuum between two parallel uncharged plates give rise to negative energy density. The most recent work in quantum mechanics deals with the idea of the minimal length of the order of Planck length. The purpose of using a minimal length scale is to restrict the resolution of small space-time distances. Therefore, it comes up with MU in the position. We can redefine the Casimir energy density with the generalized uncertainty principle (GUP). Therefore, scientists find it quite exciting to work with GUP-corrected wormholes with traversable wormholes. Jusufi et al. [28] studied three types GUP models with the source term Casimir energy density. The GUP-corrected Casimir wormholes are discussed in f(R, T) modified theory by Tripathy [29]. The effects of the MU parameter and theory-coupled parameters on wormhole conditions, EOS, and energy conditions have been studied. In weak limit approximation, Javed et al. [30] investigated the weak deflection angle of the photon by Casimir wormhole. They use Gauss–Bonnet theorem on Gaussian optical space-time to find Gaussian optical curvature. In another article, the authors explore the relationship between an absurdly benign traversable wormhole and Casimir energy [31]. They generalized the idea of Absurdly Benign Traversable Wormhole and explored that wormhole throat is Planckian, but huge. Muniz et al. studied the Casimir effect between the parallel plates in the space-time of a rotating wormhole [32].

The EGB Gravity is a particularly basic example of the larger class of gravitational theories known as Lovelock Gravities, which were proposed by Lovelock [33]. Higher power curvature terms are present in the actions of these gravities, but second-order derivatives in the metric are maintained in the subsequent equations of motion. As a result, Lovelock gravities act as GR most natural extension to higher-dimensional spacetimes. This theory, the most extensive of higher curvature gravities, demonstrates second-order equations of motion and has a number of attractive characteristics in common with Einstein gravity that are missing from other higher curvature gravities theories. Since, we know that the polynomial type of the Lagrangian in Lovelock theories, the first terms is the Einstein–Hilbert action, while the second order term correspond the GB invariant, which is defined as

$$\begin{aligned} {\mathcal {G}}=R^{2}-4R_{\alpha \beta }R^{\alpha \beta }+R_{\alpha \beta \delta \eta }R^{\alpha \beta \delta \eta }. \end{aligned}$$

The Ricci scalar, Ricci tensor, and Riemann curvatures are represented by a particular combination known as the Gauss–Bonnet invariant, abbreviated as ${\mathcal {G}}$. The f(R) formalism has previously been used to study Casimir wormholes in the setting of modified gravity, taking into account two distinct models: $f(R)=R+\alpha R^{2}$ and $f(R)=f_{0}R^{n}$ [34]. We have concentrated on EGB gravity in our research. A noteworthy property of EGB gravity, the potential presence of two separate maximally symmetric solutions, even with distinct curvature scale signs, is what drives the study of wormhole solutions. The flaring-out condition is a crucial need for traversable wormholes. In the background of GR, this condition entails the violation of the NEC. Extensive study has been done to lessen the dependency on exotic matter in light of the energy condition violations [35, 36]. It has been interestingly found that higher-dimensional cosmological wormholes [37] and wormholes in modified gravity theories with higher-order curvature invariants can satisfy the energy requirements at the throat [38,39,40]. Since the higher-order curvature terms, which can be thought of as a gravitational fluid, support these non-conventional wormhole geometries, it has been shown that it is possible to impose matter threading the wormhole throat to stick to all of the energy conditions in modified gravity. In order to alleviate the energy condition violations, particularly at the throat area, wormhole geometries in higher-dimensional theories are therefore strongly encouraged. The GB term is defined in this theory along with the Lanczos tensor, which results in the Weyl tensor. The curvature of spacetime is quantified by the Weyl tensor. The Riemann curvature tensor is used to assess curvature in all other theories using the GB term, such as f(G), f(G, T), f(G, R), etc. The Riemann curvature tensor can offer information on changes in a body’s volume, whereas the Weyl tensor only indicates how tidal forces cause a body’s shape to change. This is where the differences between the two tensors reside. Information on changes in volumes caused by tidal forces is precisely captured by the Ricci curvature, also known as the trace component of the Riemann tensor. As a result, the Weyl tensor can be thought of as the Riemann tensor’s traceless component. The Riemann tensor’s symmetries are shared by this structure, but it also has to be trace-free. The EGB theory thus appears as a plausible and suitable option to study the importance of the GB invariant in respect to the Lanczos tensor.

This article investigates the wormhole space-time geometry in EGB gravity powered by Casimir wormhole. The Lorentzian wormhole solutions were studied in the N-dimensional EGB gravity [41]. The solution of these wormholes greatly depends on the space-time dimension and the GB parameter. These two parameters play an essential role as wormhole throat radius is also constrained by them. Moreover, they studied the dynamics of these parameters for weak energy conditions (WEC) in the neighbourhood of wormhole throats only [41]. Also, authors explored the Lorentzian wormhole solutions of third-order Lovelock gravity [42]. They explored that wormhole throat has a lower bound depending upon the lovelock coefficient, space-time dimension, and function shape. The reference [43] discussed the dynamical wormholes in lovelock gravity. They constructed the shape function by constraining the Ricci scalar and three scale factors. Maeda at el. [44] evaluated static and symmetric wormholes in EGB gravity for $D\ge 5$. In a Similar work, authors discussed the WEC of traversable wormholes in 5D EGB gravity [45]. They have constructed shape functions by considering specific EOS and traceless energy moment tensors (EMT). In the background of N-dimensional EGB gravity, authors studied the Gaussian and Lorentzian distributed noncommutative geometry of wormhole [46]. They studied the dynamics of GB coupled parameters for the fifth and sixth dimensions.

Recently, Herrera [47] introduced the self-gravitating system in an anisotropic system to calculate the vanishing complexity factor. He has explored general mass function and used the orthogonal splitting of the tensor(curvature) for Tolman mass and structure scalars. In 2009, Herrera et al. [48] studied the primary outcomes of gravitational collapse concerning the Israel-Stewart notion for viscid dissipative analysis with bulk shear viscosity. Herrera et al. [49] discussed the solutions for the self-relativistic gravitating collapse in dissipative situations in the background of Post-quasi static estimation. Moreover, by extending the work to the dissipative case in the form of free radiation streaming and heat flow, the scientist Herrera and Santos [50] studied the gravitational collapse in the framework of the Misner and Sharp approach. In addition to this, Herrera et al. [51] concluded their findings in self-gravitating collapsing source with anisotropic matter distribution on the system of the equation, which brings about the actual state for vanishing spatial gradients of energy density. In 2019, the complexity factor for the self-gravitating system in modified GB gravity has also been calculated [52]. Complexity factor for a class of compact stars in f(R, T) modified gravity has been explored by [53]. Moreover, Abbas and Nazar [54] studied the complexity factor in f(R) modified gravity for anisotropic system in non-minimal coupling metric.

The order of the present paper is as follows: in Sect. 2, we presented the basic formalism of higher dimensional EGB gravity and developed the field equations using static wormholes. In the same section, we have discussed the wormhole solution by NEC. The Casimir effect and solution of Casimir wormholes have been discussed in Sect. 3. In the next Sect. 4 we have discussed GUP corrected Casimir wormholes in EGB gravity. The active gravitational mass and wormhole geometry is discussed in Sects. 5 and 6 respectively. In Sects. 7 and 8, we have calculated the equilibrium forces and complexity factor of Casimir wormhole and GUP-corrected Casimir wormholes, respectively. We have summarized our results in the last Sect. 9.

2 Basic formalism of field equations of EGB gravity

The action in the background of EGB is expressed as follows [45],

$$\begin{aligned} \mathcal {I_{G}}=\int d^{D}x\sqrt{-g}\bigg (R+\mu _{2}{\mathcal {G}}\bigg ), \end{aligned}$$

(1)

where R is Ricci scalar, D defines the dimension of spacetime and $\mu _{2}$ is GB coefficient. The GB invariant is expressed by ${\mathcal {G}}$. The expression for GB invariant is

$$\begin{aligned} {\mathcal {G}}=R^{2}-4R_{\alpha \beta }R^{\alpha \beta }+R_{\alpha \beta \delta \eta }R^{\alpha \beta \delta \eta }. \end{aligned}$$

(2)

By varying the action w.r.t metric tensor, the field equations can be written as

$$\begin{aligned} G_{\alpha \beta }+\mu _{2}{\mathcal {H}}_{\alpha \beta }={\mathcal {T}}_{\alpha \beta }, \end{aligned}$$

(3)

Here $G_{\alpha \beta }$ represents Einstein tensor, ${\mathcal {H}}_{\alpha \beta }$ GB tensor and ${\mathcal {T}}_{\alpha \beta }$ is EMT. The expression for ${\mathcal {H}}_{\alpha \beta }$ is as follows

$$\begin{aligned} {\mathcal {H}}_{\alpha \beta }= & {} -\dfrac{1}{2}{\mathcal {G}}g_{\alpha \beta }+2\bigg [RR_{\alpha \beta }-2R_{\alpha \sigma }R^{\sigma }_{\beta }\nonumber \\{} & {} -2R_{\alpha \rho \beta \nu }R^{\rho \nu }-2R_{\alpha a b c }R^{a b c}_{\beta }\bigg ]. \end{aligned}$$

(4)

We have considered that $8\pi G_{D}=1$, where $G_{D}$ is D dimensional gravitational constant. The wormhole geometry for $D-2$ sphere is expressed as [45],

$$\begin{aligned} ds^{2}=-e^{2\Phi (r)}dt^{2}+\bigg (1-\dfrac{b(r)}{r}\bigg )^{-1}dr^{2}+r^{2}d\Omega ^{2}_{D-2}, \end{aligned}$$

(5)

where $\Omega ^{2}_{D-2}$ shows metric on the surface of the $D-2$ sphere. The gravitational redshift function is denoted by $\Phi (r)$ and known as simply redshift function. The gravitational redshift is defined as the required frequency a photon will have when dragged out of gravitational potential. Dragging photons out of gravitational potential requires energy, which is proportional to its frequency. The increase in energy increases frequency called the redshift function. It must be noted that a photon cannot have enough energy to escape if a wormhole has an event horizon. To avoid the horizon, the redshift function should be finite everywhere in the domain. The shape function is denoted by b(r), and it predicts the shape of the wormhole. The shape of the wormhole can be seen through the embedding diagram [2]. The radial coordinate r is nonmonotonic, which ranges from $r_{0}<+\infty$ where $r_{0}$ is the throat of the wormhole. It is defined as a throat that connects two faces since the wormhole has two faces. The b(r) at wormhole throat satisfies $b(r_{0})=r_{0}$. The flaring out condition says that $b'(r_{0})<1$ or it can be understand in this way $\dfrac{b(r)-rb'(r)}{b(r)^{2}}>0$ where $'$ shows derivative with respect to r. The asymptotically flatness condition is defined as $\dfrac{b(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$.

The acquired EMT is expressed as

$$\begin{aligned} T_{\alpha }^{\beta }=diag\bigg (-\rho (r),p_{r}(r),p_{t}(r),p_{t}(r),.....\bigg ), \end{aligned}$$

(6)

here $\rho (r)$ is the energy density. $p_{r}(r)$ signifies radial pressure and $p_{t}(r)$ symbolizes transverse pressures. By using Eq. (3) the field equation in EGB gravity are expressed as follows

$$\begin{aligned} \rho (r)= & {} \dfrac{(D-2)}{2r^{2}}\bigg [\bigg (b'-\dfrac{b}{r}\bigg )\bigg (1+\dfrac{2\mu b}{r^{3}}\bigg )\nonumber \\{} & {} +\dfrac{b}{r}\bigg ((D-3)+(D-5)\dfrac{\mu b}{r^{3}}\bigg )\bigg ], \end{aligned}$$

(7)

$$\begin{aligned} p_{r}(r)= & {} \dfrac{(D-2)}{2r}\bigg [2\Phi '\bigg (1-\dfrac{b}{r}\bigg )\bigg (1+\dfrac{2\mu b}{r^{3}}\bigg )\nonumber \\{} & {} -\dfrac{b}{r^{2}}\bigg ((D-3)+(D-5)\dfrac{\mu b}{r^{3}}\bigg )\bigg ], \end{aligned}$$

(8)

$$\begin{aligned} p_{t}(r)= & {} \bigg (1+\dfrac{2\mu b}{r^{3}}\bigg )\bigg (1-\dfrac{b}{r}\bigg )\bigg [\Phi ''+\Phi '^{2}+\dfrac{(b-rb')\Phi '}{2r(r-b)}\bigg ]\nonumber \\{} & {} +\bigg (\dfrac{b-b'r}{2r^{2}(r-b)}+\dfrac{\Phi '}{r}\bigg )\bigg (1-\dfrac{b}{r}\bigg )\nonumber \\{} & {} \times \bigg [(D-3)+(D-5)\dfrac{2\mu b}{r^{3}}\bigg ]\nonumber \\{} & {} -\dfrac{b}{2r^{3}}\bigg [(D-3)(D-4)+(D-5)(D-6)\dfrac{\mu b}{r^{3}}\bigg ]\nonumber \\{} & {} - \dfrac{2\Phi '\mu }{r^{4}}(D-5)(b-b'r)\bigg (1-\dfrac{b}{r}\bigg ), \end{aligned}$$

(9)

here, the prime signifies a derivative w.r.t r. Also, we define $\mu =(D-3)(D-4)\mu _{2}$ for convenience. We have three field equations that are Eqs. (7)–(9) and five unknown $\rho (r)$, p(r), p(t), $\Phi (r)$ and b(r). Therefore, the number of unknowns exceeds the number of equations. To discuss the wormhole solutions, one may adopt various techniques. We provide below various plan of action for finding the solution of field equations.

2.1 Wormhole solutions

In GR, it is well-known that energy conditions have been violated in static spherically symmetric in four dimensional space-time [55]. The violation of these conditions depends upon the flaring out condition. Moreover, there is a possibility that violation of energy conditions can be avoided or satisfy only in the neighbourhood of wormhole throats, in higher dimensional theories [42]. The NEC can be defined as

$$\begin{aligned} T_{\lambda \delta }{\mathcal {K}}^{\lambda }{\mathcal {K}}^{\delta }\ge 0, \end{aligned}$$

(10)

here, ${\mathcal {K}}$ is null vector. For anisotropic fluid content, we can express NEC as follows

$$\begin{aligned} \rho +p_{r}\ge 0, \quad \rho +p_{t}\ge 0, \end{aligned}$$

(11)

From Eqs. (7)–(9), we have the following relationships of NEC.

$$\begin{aligned} \rho +p_{r}= & {} \dfrac{D-2}{2 r^6}\bigg [\mu b(r)^2 \left( D-4 r \Phi '(r)-7\right) \nonumber \\{} & {} +r^4 \left( b'(r)+2 r \Phi '(r)\right) -b(r)\bigg ((D-5)\mu b(r) \nonumber \\{} & {} + \left( r \left( 2 \left( r^2-2 \mu \right) \Phi '(r)+r\right) -2 \mu b'(r)\right) \bigg )\bigg ],\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} \rho +p_{t}= & {} \dfrac{1}{2r^{6}}\bigg [r^3 \left( b'(r) \left( r-\left( r^2-4 (D-5) \mu \right) \Phi '(r)\right) \right. \nonumber \\{} & {} \left. +2 r^2 \left( (D-3) \Phi '(r)+r \Phi ''(r)+r \Phi '(r)^2\right) \right) \nonumber \\{} & {} + 2 \mu b(r)^2 \left( 2 D-2 r^2 \Phi ''(r)-2 r^2 \Phi '(r)^2\right. \nonumber \\{} & {} \left. +r \Phi '(r)-13\right) +rb(r)\bigg (2\mu b'(r)\nonumber \\{} & {} \times ((9-2 D) r \Phi '(r)+3) \nonumber \\{} & {} {+}r^2 \left( (7{-}2 D) r \Phi '(r){+}2 D{-}2 \left( r^2{-}2 \mu \right) \Phi ''(r)\right. \nonumber \\{} & {} \left. -2 \left( r^2-2 \mu \right) \Phi '(r)^2-7\right) \bigg ) \bigg ]. \end{aligned}$$

(13)

It can be verified from the above equations for $\mu =0$ and $\Phi '(r)=0$, the resulting equations do not satisfy NEC, due to flaring out condition. At wormhole throat $r=r_{0}$ and $D=5$ Eq. (13) can be written as

$$\begin{aligned} \rho (r_{0})+p_{r}(r_{0})=\frac{3 \left( 2 \mu b(r_{0})+3r_{0}\right) \left( r_{0} b'(r_{0})-b(r_{0})\right) }{2 r_{0}^6}\nonumber \\ \end{aligned}$$

(14)

From the flaring out condition, we know that $b'(r_{0})<1$, therefore in the violation of NEC $\mu$ plays a vital role. A particular kind of exotic matter that satisfies the flaring-out criterion and defies the weak energy condition is necessary to maintain the integrity of the wormhole structure [2]. The weak energy conditions are broken by this type of stuff, also known as exotic matter [24], at least close to the wormhole throat. While violations of these requirements may appear unnatural in terms of classical relativity, quantum field theory argues that they occur naturally as a result of the dynamic fluctuations in the topology of spacetime over time. The quantum field between them is perturbed by the existence of uncharged parallel plates, leading to a negative energy density. It is possible to consider this negative energy density as a source of workable traversable wormholes. The introduction of the idea of a minimal length scale, which is on the order of the Planck length, is another important advancement in present-day quantum mechanics. The precision with which short distances in spacetime may be determined is constrained by this minimal length scale. In models of quantum gravity, where the degree of positional uncertainty is constrained, the presence of a minimal length naturally arises. Because of this idea of a minimal length, the position-momentum uncertainty relation must be changed. The negative Casimir energy density is redefined by using the GUP. It is significant to note that the precise design of maximally localised quantum states is a precondition for this redefined Casimir energy density. Therefore, while modelling traversable wormholes, it becomes interesting to take the consequences of GUP into account. As a result, traversable wormholes can be stabilised via the Casimir effect, which produces a negative energy density. Therefore, we can study the possibility of utilising the Casimir effect to accomplish such goals by taking into account quantum phenomena inside a classical framework.

In subsequent sections, we will study the dynamics of GB-coupled parameters, on wormhole conditions and energy conditions by considering cases of Casimir and GUP-corrected Casimir energy densities.

3 Casimir wormholes in EGB gravity

The effects of quantum mechanics within the context of GR have been extensively studied. A universally acknowledged theory of quantum gravity, however, is still elusive despite these attempts. As a result, we are now focusing on investigating how the EGB theory affects this situation. The results of the EGB theory are being investigated in order to learn more about how gravity behaves in quantum mechanical contexts.

Dutch physicist Hendrik Casimir suggested the phenomenon of the Casimir effect in 1948. A force may exist between the uncharged, parallel, conducting plates [25]. This is because the vacuum of the electromagnetic field causes disturbance. It is linked with zero point energy of a quantum electrodynamics vacuum contorted by the plates suggested by Niel Bohar. Later on, it was confirmed from experimental research [56]. The theory of Casimir energy is based on the quantum effect, which says that the initial state of quantum electrodynamics is the main fact that causes the parallel, without charged plates to attract. Moreover, the Casimir energy shows the only unnatural source of exotic matter generated in laboratories. The dependence of Casimir’s energy is on the shape of boundaries [26]. Generally, it has been noticed that exotic matter does not satisfy the energy condition, especially NEC. In particular, it seems logical to assume the Casimir effect in traversable wormholes does not satisfy NEC as it contains exotic matter. Garattini has suggested the idea of traversable wormholes by using an equation of state coming out of Casimir energy. These wormholes are called Casimir Wormholes [26]. The attractive force between two plates arise due to the renormalization of a negative source of energy, according to Casimir effect.

$$\begin{aligned} \mathcal {E}(\textrm{a})=-\dfrac{\pi ^{2}\textrm{A}}{720\mathrm {a^{3}}}, \end{aligned}$$

(15)

where $\textrm{A}$ shows surface area of the the plates and $\textrm{a}$ represents the distance of separation between the plates. It has been noticed that if we move two plates closer together, then Casimir’s energy is lowered. The energy density is expressed as

$$\begin{aligned} \rho (\textrm{a})=-\dfrac{\pi ^{2}}{720\textrm{a}^{4}}. \end{aligned}$$

(16)

We can obtain pressure from the renormalization of the negative energy source expressed in Eq. (15).

$$\begin{aligned} p(\textrm{a})=-\dfrac{d{\mathcal {E}}}{d\textrm{a}}\times \bigg (\dfrac{1}{\textrm{A}}\bigg )=-\dfrac{\pi ^{2}}{240}\times \bigg (\dfrac{1}{\mathrm {a^{4}}}\bigg ). \end{aligned}$$

(17)

The expressions of $\rho (a)$ and p(a) defined in Eqs. (16) and (17) leads to EOS $p=w\rho$ with $w=3$. The Casimir force ${\mathcal {F}}$ is expressed as the surface area multiplies the pressure.

$$\begin{aligned} {\mathcal {F}}=-\textrm{A}\times \bigg (\dfrac{\pi ^{2}}{240\textrm{a}^{4}}\bigg ). \end{aligned}$$

(18)

The above equation shows that the force is attractive as it contains a negative sign.

It is reported that, for existance of traversable wormholes,the NEC is violated as it containts exotic matter. It has been observed by [27] that we can have stable wormhole by allowing wormhole to collapse slowly, moreover, it is also feasible to analyze the stability of a traversable wormhole, if it consists of large throat as contrary to Planck scale. In order to find out the b(r) using Casimir energy density in EGB gravity. We will compare Eqs. (7) and (16), plus the distance between plates which is represented by a is replaced by r. We will get the following form of ODE.

$$\begin{aligned}{} & {} \!\!\!\frac{(D{-}2) \left( b(r) \left( 2 \mu r b'(r){+}(D{-}4) r^3\right) {+}r^4 b'(r){+}(D{-}7) \mu b(r)^2\right) }{2 r^6}\nonumber \\{} & {} \quad +\frac{\pi ^2}{720 r^4}=0. \end{aligned}$$

(19)

Now, confining our analysis to the case of 5D EGB, we find the following b(r).

$$\begin{aligned} b(r)=-\frac{r^3}{2 \mu }\pm \frac{\sqrt{2160 g_{1} \mu r+\frac{540 r^5}{\mu }-2 \pi ^2 r \log (r)}}{12 \sqrt{15}\sqrt{\dfrac{\mu }{r}} }, \end{aligned}$$

(20)

where $g_{1}$ is constant of integration and calculated by $b(r_{0})=r_{0}$.

$$\begin{aligned} g_{1}= \frac{1080 \mu +1080 r_{0}^2+\pi ^2 \log (r_{0})}{1080 \mu }. \end{aligned}$$

(21)

The final form of the shape function is given below

$$\begin{aligned} b(r)= -\frac{r^3}{2 \mu }\pm \dfrac{\sqrt{\frac{540 r^5}{\mu }{+}2160r(r_{0}^{2}{+}\mu ){-}2\pi ^{2}r\log \bigg ({\dfrac{r}{r_{0}}\bigg )}}}{12 \sqrt{15}\sqrt{\dfrac{\mu }{r}}},\nonumber \\ \end{aligned}$$

(22)

Fig. 1

The trajectory a shows dynamics of b(r) versus r whereas $b'(r)<1$ condition is depicted in trajectory (b). Herein, we set $r_{0}=2$

Fig. 2

Trajectory a shows dynamics of $1-\dfrac{b(r)}{r}$ and trajectory b displays dynamics of $b(r)-r$

Fig. 3

Left trajectory shows dynamics of shape function versus radial coordinate in a certain domain of $\mu$ whereas the evolution of $b'(r)$ versus radial coordinate is shown in the right trajectory

here, the above equation contains two shape functions corresponding to the sign of ± i.e. $b(r)_{+}$ and $b(r)_{-}$. We have checked the asymptotically flatness condition for both shape functions, and shape function $b(r)_{+}$ satisfies the criteria, which is $\dfrac{b(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$. Therefore we have used the shape function with the positive sign for further analysis.

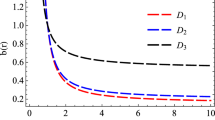
The dynamics of the shape function is plotted in Figs. 1 and 2. It can be observed that from Fig. 1a, when $r_{0}=2$ than $b(2)= 2$. From Fig. 1b flaring out condition is satisfied. The asymptotically flatness condition is also satisfied and graphically plotted in Fig. 2a. Figure 2b says that wormhole throat is located at $r_{0}=2$ where $b(r)-r$ cuts the r-axis.

To understand the dynamics of GB coupled parameter $\mu$, we have plotted the wormhole conditions in terms of contour plots in Fig. 3. It can be seen from Fig. 3a that with the increase in $\mu$, the dynamics of b(r) increases near the wormhole throat. This implies $\mu$ has a direct relationship with the shape function near the wormhole throat. Moreover, Fig. 3b shows that $b'(r)<1$ while $\mu$ increases. Henceforth, we restrict to the $b(r)_{+}$, in this case the 5D EGB wormhole metric reads as

$$\begin{aligned} ds^{2}\!&{=}&\!{-}dt^{2}+\Bigg (1-\dfrac{1}{r}\Bigg [-\frac{r^3}{2 \mu }\nonumber \\{} & {} {+}\dfrac{\sqrt{\frac{540 r^5}{\mu }{+}2160r \mu {+}2160r r_{0}^2{-}2\pi ^{2}r\log \bigg ({\dfrac{r}{r_{0}}\bigg )}}}{12 \sqrt{15}\sqrt{\dfrac{\mu }{r}}}\Bigg ]\Bigg )^{-1}\!\!dr^{2}\nonumber \\{} & {} +r^{2}d\Omega ^{2}_{D-2}. \end{aligned}$$

(23)

By keeping the redshift function constant, the expressions of $p_{r}$ and $p_{t}$ are as follows

$$\begin{aligned} p_{r}(r)= & {} \dfrac{1}{60r\mu }\Bigg [90 r-\sqrt{30} \mu \sqrt{\frac{1}{\mu r^3}} \sqrt{\frac{b_{*}-r\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}\Bigg ], \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} p_{t}(r)= & {} \dfrac{1}{360 \sqrt{\frac{b_{*}-r\pi ^2 \mu \log \Bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}}\bigg [ \sqrt{\frac{30}{\mu r^3}} \left( \mu \left( \pi ^2\right. \right. \nonumber \\{} & {} \left. \left. -2160 \left( \mu +r_{0}^2\right) \right) -1620 r^4\right) +2 \pi ^2 \mu \sqrt{\frac{30}{\mu r^3}} \log \bigg (\dfrac{r}{r_{0}}\Bigg )\nonumber \\{} & {} +540\sqrt{\frac{b_{*}-r\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}\Bigg ], \end{aligned}$$

(25)

where $b_{*}=270r(r^{4}+4\mu (\mu +r_{0}^{2}))$. By using the asymptotically flat shape function, the radial and tangential EOS are defined as $w_{r}(r)=\dfrac{p_{r}}{\rho }$ and $w_{t}(r)=\dfrac{p_{t}}{\rho }$ respectively. The radial and tangential EOS expressions in EGB gravity for $D=5$ are expressed as follows.

$$\begin{aligned} w_{r}= & {} -\dfrac{12 r^3}{\pi ^2 \mu }\Bigg [90 r-\sqrt{30} \mu \sqrt{\frac{1}{\mu r^3}} \sqrt{\frac{b_{*}-r\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}\Bigg ],\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned} w_{t}= & {} -\dfrac{2 r^4}{\pi ^2 \mu \sqrt{\frac{b_{*}-r\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}}\Bigg [ \sqrt{\frac{30}{\mu r^3}} \left( \mu \left( \pi ^2\right. \right. \nonumber \\{} & {} \left. \left. -2160 \left( \mu +r_{0}^2\right) \right) -1620 r^4\right) +2 \pi ^2 \mu \sqrt{\frac{30}{\mu r^3}} \log \bigg (\dfrac{r}{r_{0}}\bigg )\nonumber \\{} & {} +540\sqrt{\frac{b_{*}-r\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )}{\mu }}\Bigg ]. \end{aligned}$$

(27)

The plot of $w_{r}$ and $w_{t}$ against r are displayed in Fig. 4. It can be seen from Fig. 4a that $\mu$ is in direct relationship with $w_{r}$ at wormhole throat $r_{0}=2$. The dynamics of $w_{t}$ is shown in Fig. 4b. Before the wormhole throat, the $w_{t}$ increases while away from the wormhole throat, it decreases in a certain domain of $\mu$. We found the valid regions for NEC to be satisfied. It is found that $\rho +p_{r}\ge 0$ for {$\mu <-3$ }. For $\rho +p_{t}\ge 0$ we have $\{\mu <-90 \}$ and $\{0<\mu <2\}$.

Fig. 4

The trajectory a shows dynamics of $w_{r}$ when $\mu$ is varying while the trajectory b displays dynamics of $w_{t}$ for certain domain of $\mu$

Fig. 5

The dynamics of NEC are displayed for certain domain of $\mu$

In Fig. 5, contour plots of NEC are presented, following the above validity ranges. Evolution of $\rho +p_{r}$ and $\rho +p_{t}$ is depicted for both positive and negative values of $\mu$.

4 GUP-corrected Casimir wormholes in EGB gravity

The concept of existance of minimum length scale leads the way to modify the uncertainty principle. The problems of GUP relating to momentum and position are explored by [57, 58]. We are intended to find the Casimir effect due to GUP. In classical sence, momentum and position are not conjugate variables. Therefore we can consider actual physical position as position eigenspace since we change position momentum relation. There is another method to discuss the position as conditions projected onto the maximally localized state, also called as Quasi position representation [57]. Although there are two ways to have maximally localized states, one is known as KMM [57] and other one is DGS [58]. In this article, we have used both methods to determine the impact on the Casimir wormhole. In N-dimensional minimal length corrected commutation relation is defined as in below equation [59]

$$\begin{aligned}{}[x_{i},p_{j}]=i[f(p^{2})\delta _{ij}+g(p^{2})p_{i}p_{j}], \quad i,j=1,2,3\ldots N \nonumber \\ \end{aligned}$$

(28)

where f(p) and g(p) show generic functions, one can find out by using rotational and translational invariance of the commutation relation. We can introduce various generic functions which express different models and confirms maximally localized states

Now we will discuss two different methods of GUP introduced by Kempf, Mangano, and Mann (KMM) [57] and Detournay, Gabriel and Spindel (DGS) [58]. The two interesting ways are KMM which employs squeezed state, and DGS, which works on variational principle. These models depend upon the number of specific models and dimensions. The model KMM depends on the choice of generic function $f(p^{2})$ and $g(p^{2})$ [60].

$$\begin{aligned} f(p^{2})=\dfrac{\alpha p^{2}}{\sqrt{1+2\alpha p^{2}}-1} \quad g(p^{2})=\alpha , \end{aligned}$$

(29)

The maximally localized states for KMM construction requires

$$\begin{aligned} k_{i}= & {} \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ]p_{i}, \end{aligned}$$

(30)

$$\begin{aligned} w(p)= & {} \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ], \end{aligned}$$

(31)

$$\begin{aligned} \omega (p)= & {} \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ]^{\gamma /2}, \end{aligned}$$

(32)

where $\alpha$ is MU parameter and $\gamma$ is defined as $\gamma =1+\sqrt{1+N/2}$ and N is known as number of spatial dimensions. The maximally localized states for DGS construction requires

$$\begin{aligned} k_{i}= & {} \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ]p_{i}, \end{aligned}$$

(33)

$$\begin{aligned} w(p)= & {} \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ],\end{aligned}$$

(34)

$$\begin{aligned} \omega (p)= & {} \dfrac{\sqrt{2}}{\pi } \bigg [\dfrac{\sqrt{1+2\alpha p^{2}}-1}{\alpha p^{2}}\bigg ]^{\beta /2}\nonumber \\{} & {} \sin \bigg [\dfrac{\sqrt{2}\pi \sqrt{1+2\alpha p^{2}}-1}{2\sqrt{\alpha p^{2}}}\bigg ]. \end{aligned}$$

(35)

Fig. 6

The trajectories a, b show dynamics of b(r) against r for $\zeta _{1}$ and $\zeta _{2}$ respectively. Herein we set $r_{0}=2$

Fig. 7

The trajectories a, b show dynamics of $b'(r)$ against r for $\zeta _{1}$ and $\zeta _{2}$ respectively

The idea of GUP and minimal length to get the finite energy between the uncharged plates was introduced by Frassino and Panella. Both find out the corrections to Hamiltonian and the Casimir energy because of minimal length. The Casimir energy of two different models of fabrication of maximally localized states are expressed as follows [59].

$$\begin{aligned} {\mathcal {E}}(\textrm{a})=-\dfrac{\pi ^{2}\textrm{A}}{720\textrm{a}^{3}}\bigg (1+\zeta _{i}\dfrac{\alpha }{\textrm{a}^{2}}\bigg ), \end{aligned}$$

(36)

where

$$\begin{aligned} \zeta _{1}= & {} \pi ^{2}\bigg [\dfrac{28+3\sqrt{10}}{14}\bigg ],\end{aligned}$$

(37)

$$\begin{aligned} \zeta _{2}= & {} 4\pi ^{2}\bigg [\dfrac{3+\pi ^{2}}{21}\bigg ], \end{aligned}$$

(38)

where $i=1,2$ which depicts two models (a) KMM and (b) DGS. According to the model introduced, the energy densities and pressure becomes as follows,

$$\begin{aligned} \rho ({\textrm{a})}= & {} -\dfrac{\pi ^{2}}{720\textrm{a}^{4}}\bigg (1+\zeta _{i}\dfrac{\alpha }{\textrm{a}^{2}}\bigg ), \end{aligned}$$

(39)

$$\begin{aligned} p({\textrm{a})}= & {} -\dfrac{\pi ^{2}}{720\textrm{a}^{4}}\bigg (1+\dfrac{5\zeta _{i}}{3}\dfrac{\alpha }{\textrm{a}^{2}}\bigg ), \end{aligned}$$

(40)

In order to get GUP corrected Casimir wormholes in EGB gravity, we can replace plate separation distance a by radial coordinate r. By using Eqs. (7) and (39), we will get following equation.

$$\begin{aligned}{} & {} 360 (D-2) \left( b(r) \left( 2 \mu r b'(r)+(D-4) r^3\right) +r^4 b'(r)\right. \nonumber \\{} & {} \quad \left. +(D-7) \mu b(r)^2\right) +\pi ^2 \left( \alpha \zeta _{i}+r^2\right) =0 \end{aligned}$$

(41)

The GUP corrected shape function is expressed as follows.

$$\begin{aligned} b(r) =-\frac{r^3}{2 \mu } \pm \frac{\sqrt{2160 g_{2} \mu r{-}2 \pi ^2 r \left( \log (r){-}\frac{\alpha \zeta _{i}}{2 r^2}\right) {+}\frac{540 r^5}{\mu }}}{12 \sqrt{15} \sqrt{\dfrac{\mu }{r}}},\nonumber \\ \end{aligned}$$

(42)

here we present our results only for $D=5$, and $g_{2}$ is the constant of integration. The constant of integration is evaluated by $b(r_{0})=r_{0}$.

$$\begin{aligned} g_{2}=\frac{-\pi ^2 \alpha \zeta _{i}+2160 r_{0}^4+2160 \mu r_{0}^2+2 \pi ^2 r_{0}^2 \log (r_{0})}{2160 \mu r_{0}^2}.\nonumber \\ \end{aligned}$$

(43)

Therefore, the final form of shape function is expressed as follows.

$$\begin{aligned} b(r)= & {} -\frac{r^3}{2 \mu }\nonumber \\&\pm&\dfrac{\sqrt{\dfrac{540r^{5}}{\mu }{+}2160r(r_{0}^{2}{+}\mu ){-}2r\pi ^{2}\log \bigg (\dfrac{r}{r_{0}}\bigg ){+}\pi ^{2}r\zeta _{i}\alpha \bigg (\dfrac{1}{r^{2}}{-}\dfrac{1}{r_{0}^{2}}\bigg )}}{2 \sqrt{15} \sqrt{\dfrac{\mu }{r}}}.\nonumber \\ \end{aligned}$$

(44)

Fig. 8

The trajectories a, b show dynamics of $1-\dfrac{b(r)}{r}$ against r for $\zeta _{1}$ and $\zeta _{2}$ respectively

Fig. 9

The trajectories a, b show dynamics of $b(r)-r$ against r for $\zeta _{1}$ and $\zeta _{2}$ respectively

The GUP corrected shape function has two branches according to the sign of ±. The shape function $b(r)_{+}$ is asymptotically falt while $b(r)_{-}$ does not satisfy the asymptotically flatness condition. We have considered shape function $b(r)_{+}$ for further analysis. We have studied wormhole conditions from Figs. 6, 7, 8 and 9. The solid lines in Fig. 6 show dynamics of b(r) when $\alpha =2$ while dotted lines show the evolution of b(r) when $\mu =2$. It has been observed from Fig. 6a, b that dynamics of b(r) grow positively as $\mu$ increases. However, the value of b(r) decreases with an increase in the value of $\alpha$ parameter. Figure 7a, b follow the flaring-out condition, which says $b'(r)<1$ for $r>r_{0}$. The Fig. 8a, b confirm the asymptotic flatness condition is satisfied for both models i.e. $\dfrac{b(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$ this implies $1-\dfrac{b(r)}{r}\rightarrow 1$ as $r\rightarrow \infty$. In Fig. 9a, b, we have studied the wormhole throat radii for different values of $\mu$ and $\alpha$. These plots show all conditions of the shape function allow us to study the GUP-corrected wormhole in EGB gravity.

By using an asymptotically flat shape function, expressions of $w_{r}$ and $w_{t}$ are as follows.

$$\begin{aligned} w_{r}= & {} -\dfrac{12 r^5}{\pi ^2 \mu \left( \alpha \zeta _{i}+r^2\right) }\bigg [90 r-\dfrac{\sqrt{15}}{r}\sqrt{\dfrac{\mu }{r}}\times b_{1}^{*}\bigg ], \end{aligned}$$

(45)

$$\begin{aligned} w_{t}= & {} -\dfrac{4 r^9 \left( \frac{1}{\mu r^3}\right) ^{3/2}}{\pi ^2 r_{0}^2 \left( \alpha \zeta _{i}+r^2\right) \times b_{1}^{*}}\nonumber \\{} & {} \times \bigg [-1620 \sqrt{15} r^4 r_{0}^2+\sqrt{15} \pi ^2 \mu r_{0}^2\nonumber \\{} & {} -2160 \sqrt{15} \mu r_{0}^4+\sqrt{15} \pi ^2 \alpha \mu \zeta _{i}-2160 \sqrt{15} \mu ^2 r_{0}^2\nonumber \\{} & {} +2 \sqrt{15} \pi ^2 \mu r_{0}^2 \log (r)-2 \sqrt{15} \pi ^2 \mu r_{0}^2 \log (r_{0})\nonumber \\{} & {} +\dfrac{270 r_{0}^2 }{\times }b_{1}^{*}{\sqrt{\frac{1}{\mu r^3}}}\bigg ]. \end{aligned}$$

(46)

where

$$\begin{aligned} b_{1}^{*}=\sqrt{\dfrac{540r^{5}}{\mu }+2160r(r_{0}^{2}+\mu )-2r\pi ^{2}\log \bigg (\dfrac{r}{r_{0}}\bigg )+\pi ^{2}r\zeta _{i}\alpha \bigg (\dfrac{1}{r^{2}}-\dfrac{1}{r_{0}^{2}}\bigg )} \end{aligned}$$

Fig. 10

The trajectory a shows dynamics of $w_{r}$ when $\alpha =2$ while the trajectory b shows dynamics of $w_{r}$ when $\mu =1$

Fig. 11

The trajectory a shows dynamics of $w_{t}$ when $\alpha =2$ while the trajectory b shows dynamics of $w_{t}$ when $\mu =1$

We have studied the dynamics of radial and tangential EOS parameters from Figs. 10 and 11. The Fig. 10a is plotted in certain domain of $\mu$ when $\alpha$ is held constant while Fig. 10b is plotted in certain domain of $\alpha$ when $\mu$ is held constant for $\zeta _{1}$. It can be seen from Fig. 10a that $\mu$ is directly proportional to $w_{r}$ keeping $\alpha$ constant. And $\alpha$ is inversely proportional to $w_{r}$ keeping $\mu$ constant. Moreover, we have observed that $\mu$ and $w_{r}$ are in an inverse relationship at wormhole throat. At $r=r_{0}$ $\implies$ $\mu = -\frac{2160 r_{0}^6}{\pi ^2 \alpha \zeta _{1} w_r+\pi ^2 r_{0}^2 w_r+2160 r_{0}^4}$. Therefore at wormhole throat, with the increase in the parameter $\mu$, $w_{r}$ decreases. The dynamics of the tangential EOS parameter is plotted in Fig. 11. It can be seen from Fig. 11a that with increase in $\mu$ tangential EOS parameter decreases for $\zeta _{1}$. Figure 11b shows that with the increase in $\alpha$ tangential EOS parameter increases in terms of negative values, while when $\alpha$ decreases $w_{t}$ also decreases. Similar, behaviour of plots have been observed for $\zeta _{2}$ DGS model therefore we haved displayed plots only for KMM model.

Fig. 12

The trajectories a, b show dynamics of NEC against r for $\zeta _{1}$ when $\alpha$ is fixed

Fig. 13

The trajectories a, b show dynamics of NEC against r for $\zeta _{1}$ when $\mu$ is fixed

Some energy conditions are not satisfied due to the presence of exotic matter in the wormholes. We have checked NEC in GUP corrected wormholes in Figs. 12 and 13 for $\zeta _{1}$. Firstly, we calculated valid regions through regional plots and then studied the dynamics of NEC in contour plots. The valid region for $\rho +p_{r}\ge 0$ is $\{ \mu \le -16 \quad \textrm{and} \quad -100<\alpha <100 \}$ for $\zeta _{1}$. For $\rho +p_{t}\ge 0$ we could not found any region in the domain of $2\le r \le 10$ for $\zeta _{1}$. We could not find any region closer to the wormhole throat, which is valid for NEC to be satisfied. We have plotted Fig. 12 by keeping $\alpha =2$ in a certain domain $-10\le \mu \le 10$. For the fixed value of $\mu =1$, we have plotted Fig. 13 in a certain domain of $\alpha$ which is $-10\le \alpha \le 10$. Now, the valid region for $\rho +p_{r}\ge 0$ is $\{ \mu \le -12 \quad \textrm{and} \quad -100 \le \alpha \le 100 \}$ for $\zeta _{2}$. For $\rho +p_{t}\ge 0$ we found $\{\mu \le -13 \quad \textrm{and} \quad -100 \le \alpha \le 100 \}$ for $\zeta _{2}$. Similar, behaviour of plots have been observed for $\zeta _{2}$ DGS model therefore we haved displayed plots only for KMM model.

5 Active gravitational mass

In this section, we will explore the active gravitational mass of Casimir and GUP-corrected Casimir wormholes. This mass exists inside the wormhole’s region from the wormhole’s throat $r_{0}$ to the boundary of the radius r. The active gravitational mass is denoted by $M_{{\mathcal {A}}}$ and calculated by the expression below

$$\begin{aligned} M_{{\mathcal {A}}}=4\pi \int _{r_0}^{r}\rho (r)r^{2}dr. \end{aligned}$$

(47)

The expression for $M_{{\mathcal {A}}}$ of Casimir wormhole is expressed below.

$$\begin{aligned} M_{{\mathcal {A}}}=\dfrac{\pi ^{3}}{180}\bigg (\dfrac{1}{r}-\dfrac{1}{r_{0}}\bigg ). \end{aligned}$$

(48)

The expression for $M_{{\mathcal {A}}}$ of GUP-corrected Casimir wormhole for $\zeta _{1}$ is written below.

$$\begin{aligned} M_{{\mathcal {A}}}=\dfrac{\pi ^{3}}{180}\bigg (\dfrac{1}{r}-\dfrac{1}{r_{0}}\bigg )+\dfrac{(28+3\sqrt{10})\pi ^{2}}{7560}\alpha \bigg (\dfrac{1}{r^{3}}-\dfrac{1}{r_{0}^{3}}\bigg ). \end{aligned}$$

(49)

The expression for $M_{{\mathcal {A}}}$ of GUP-corrected Casimir wormhole for $\zeta _{2}$ is calculated as

$$\begin{aligned} M_{{\mathcal {A}}}=\dfrac{\pi ^{3}}{180}\bigg (\dfrac{1}{r}-\dfrac{1}{r_{0}}\bigg )+\dfrac{16\pi ^{3}(3+\pi ^{2})}{2835}\alpha \bigg (\dfrac{1}{r^{3}}-\dfrac{1}{r_{0}^{3}}\bigg ). \end{aligned}$$

(50)

The $M_{{\mathcal {A}}}$ for Casimir wormhole and GUP-corrected Casimir wormhole is plotted in Figs. 14 and 15 respectively.

Fig. 14

The active gravitational mass of Casimir wormhole. Herein we set $r_{0}=2$

Fig. 15

The active gravitational mass of Casimir wormhole for $\alpha =1$

Fig. 16

The left trajectory shows the dynamics of the embedding diagram, and the right trajectory displays full visualization of the surface generated by the rotation of the embedded curve about the vertical z axis for the Casimir wormhole. Herein, we set $r_{0}=2.0000000001$ and $\mu =1$

It can be observed from Figs. 14 and 15 that $M_{{\mathcal {A}}}$ decays with increase in r. The negative active gravitational mass is a sign of the existence of exotic matter. It is well known that such matter violates energy conditions, and it can be experienced by Sects. 3 and 6. Presently, the Casimir effect is the real representative of such exotic matter. Due to the presence of the Casimir effect, the active gravitational mass in the area of space is measured to be negative.

6 Wormhole geometry

This section focuses on understanding wormhole dynamics geometrically. By taking into account the wormhole space-time represented by Eq. (5), we can envisage or see them. By fixing $t=constant$ and $\theta =\pi /2$, we can obtain an equatorial slice for such wormhole space-time. Consequently, metric becomes

$$\begin{aligned} ds^{2}=r^{2}d\phi ^{2}+\bigg (1-\dfrac{b(r)}{r}\bigg )^{-1}dr^{2}. \end{aligned}$$

(51)

We will now create a 3D space and an embedded Euclidean 2D surface using this wormhole space-time. So, we’ll present $(z, r, \phi )$ cylindrical coordinates. Following is an expression for the embedding space-time.

$$\begin{aligned} ds^{2}=dr^{2}+r^{2}d\phi ^{2}+dz^{2}. \end{aligned}$$

(52)

In order to define $z=z(r)$, we can take advantage of the embedded surface’s axial symmetry. The surface’s line element is expressed as

$$\begin{aligned} da^{2}=\bigg (1+\bigg (\dfrac{dz}{dr}\bigg )^{2}\bigg )dr^{2}+r^{2}d\phi ^{2}. \end{aligned}$$

(53)

By comparing Eqs. (51) and (53), we get

$$\begin{aligned} \dfrac{dz}{dr}=\pm \bigg (\dfrac{r}{b(r)}-1\bigg )^{-1/2}, \end{aligned}$$

(54)

Here, we will use the shape function developed from the Casimir wormhole and GUP-corrected Casimir wormhole expressed in Eqs. (22) and (44) for $\zeta _{1}$ and $\zeta _{2}$.

The embedding diagram for upper $(z>0)$ and lower $(z<0)$ universe for the Casimir wormhole is displayed in Fig. 16. At the same time, the embedding diagram for both models of GUP-corrected wormholes have been evaluated and we have obtained similar results as presented in Fig. 16. Therefore, we have displayed only one figure. Figure 16 shows each wormhole has a radius of $r=r_{0}$, implying an embedded surface is vertical. It can be observed that far away from the throat space showed asymptotically flatness behavior, i.e. $\dfrac{dz}{dr}\rightarrow 0$ as $r\rightarrow \infty$.

7 Equilibrium condition

In this section, we will find the equilibrium configuration of wormhole solutions based on the shape function developed from the Casimir wormhole and GUP-corrected Casimir wormhole in EGB gravity. For this purpose, we will use the generalized Tolman Oppenheimer Volkoff equation and expressed as [46]

$$\begin{aligned} -\dfrac{dp_{r}}{dr}-\dfrac{\Phi '(r)}{2}(\rho +p_{r})-\dfrac{2}{r}(p_{r}-p_{t})=0 \end{aligned}$$

(55)

The above equation tells us about the equilibrium condition for the wormhole geometries based on the following forces.

$$\begin{aligned} {\mathcal {F}}_{g}= & {} -\dfrac{\Phi '(r)}{2}(\rho +p_{r}), \end{aligned}$$

(56)

$$\begin{aligned} {\mathcal {F}}_{h}= & {} -\dfrac{dp_{r}}{dr}, \end{aligned}$$

(57)

$$\begin{aligned} {\mathcal {F}}_{a}= & {} -\dfrac{2}{r}(p_{r}-p_{t}), \end{aligned}$$

(58)

where ${\mathcal {F}}_{g}$, ${\mathcal {F}}_{h}$, ${\mathcal {F}}_{h}$ are known as a gravitational, hydrostatic, and anisotropic force, respectively. For equilibrium condition, ${\mathcal {F}}_{g}+{\mathcal {F}}_{h}+{\mathcal {F}}_{a}=0$ must hold. In our case the equilibrium condition reduces to ${\mathcal {F}}_{h}+{\mathcal {F}}_{a}=0$. Using the shape function developed from the Casimir energy density, expressed in Eq. (22), the forces ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ are calculated and written as follows.

$$\begin{aligned} {\mathcal {F}}_{h}&{=}&{-}\frac{\sqrt{\frac{1}{\mu r^3}} \left( 4320 \mu -4 \pi ^2 \log (r){+}4320 r_{0}^2{+}4 \pi ^2 \log (r_{0}){+}\pi ^2\right) }{4 \sqrt{30} r \sqrt{\frac{r \left( 270 \left( r^4+4 \mu \left( \mu {+}r_{0}^2\right) \right) {-}\pi ^2 \mu \log (r){+}\pi ^2 \mu \log (r_{0})\right) }{\mu }}},\nonumber \\ \end{aligned}$$

(59)

$$\begin{aligned} {\mathcal {F}}_{a}&{=}&\frac{\sqrt{\frac{1}{\mu r^3}} \left( 4320 \mu {-}4 \pi ^2 \log (r){+}4320 r_{0}^2{+}4 \pi ^2 \log (r_{0}){+}\pi ^2\right) }{6 \sqrt{30} r \sqrt{\frac{r \left( 270 \left( r^4+4 \mu \left( \mu {+}r_{0}^2\right) \right) {-}\pi ^2 \mu \log (r){+}\pi ^2 \mu \log (r_{0})\right) }{\mu }}}.\nonumber \\ \end{aligned}$$

(60)

Figure 17 shows the dynamics of hydrostatic and anisotropic forces for different values of $\mu$. We can also observe from the expressions of hydrostatic and anisotropic forces they do not completely quit each other. Therefore, no equilibrium configuration has been examined near wormhole throat but forces are in equilibrium for $r>6$.

Using the shape function developed from the GUP corrected Casimir energy wormholes, expressed in Eq. (44), the forces ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ are calculated and expressed as follows.

$$\begin{aligned} {\mathcal {F}}_{h}= & {} -\dfrac{\mu \left( \frac{1}{\mu r^3}\right) ^{3/2}}{30 \sqrt{21} r_{0}^2\times b3}\bigg [-30 \pi ^4 \alpha r^2\nonumber \\{} & {} +30240 \sqrt{10} r^2 r_{0}^4+7 \pi ^2 \sqrt{10} r^2 r_{0}^245 \pi ^4 \alpha r_{0}^2\nonumber \\{} & {} -28 \sqrt{10} \pi ^4 \alpha r^2+42 \sqrt{10} \pi ^4 \alpha r_{0}^2\nonumber \\{} & {} +30240 \sqrt{10} \mu r^2 r_{0}^2-28 \sqrt{10} \pi ^2 r^2 r_{0}^2 \log (r)\nonumber \\{} & {} +28 \pi ^2 \sqrt{10} r^2 r_{0}^2 \log (r_{0})\bigg ], \end{aligned}$$

(61)

$$\begin{aligned} {\mathcal {F}}_{g}= & {} \dfrac{\mu \left( \frac{1}{\mu r^3}\right) ^{3/2}}{20 \sqrt{21} r_{0}^2\times b3}\bigg [-30 \pi ^4 \alpha r^2+30240 \sqrt{10} r^2 r_{0}^4\nonumber \\{} & {} +7 \pi ^2 \sqrt{10} r^2 r_{0}^245 \pi ^4 \alpha r_{0}^2\nonumber \\{} & {} -28 \sqrt{10} \pi ^4 \alpha r^2+42 \sqrt{10} \pi ^4 \alpha r_{0}^2\nonumber \\{} & {} +30240 \sqrt{10} \mu r^2 r_{0}^2-28 \sqrt{10} \pi ^2 r^2 r_{0}^2 \log (r)\nonumber \\{} & {} +28 \pi ^2 \sqrt{10} r^2 r_{0}^2 \log (r_{0})\bigg ]. \end{aligned}$$

(62)

where

$$\begin{aligned} b3=\sqrt{\frac{7560 r^5}{\mu }+\frac{28 \pi ^4 \alpha }{r}+\frac{3 \pi ^4 \sqrt{10} \alpha }{r}+30240 \mu r-\frac{3 \sqrt{10} \pi ^4 \alpha r}{r_{0}^2}-\frac{28 \pi ^4 \alpha r}{r_{0}^2}+30240 r r_{0}^2+28 \pi ^2 r \log (\dfrac{r_{0}}{r})}. \end{aligned}$$

Figures 18 and 19 displays the dynamics of hydrostatic and anisotropic forces for different values of $\mu$ and $\alpha$. The plot (a) in Fig. 18 shows dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ when $\alpha =2$ is fixed and $\mu$ is varying for KMM. The plot (b) in Fig. 18 shows dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ when $\mu =1$ is fixed and $\alpha$ is varying for KMM. The plot (a) in Fig. 19 shows dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ when $\alpha =2$ is fixed and $\mu$ is varying for DGS. The plot (b) in Fig. 19 shows dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ when $\mu =1$ is fixed and $\alpha$ is varying for DGS. It can be seen from these figures that equilibrium configuration has been experienced for $D=5$ as they do not cancel out each other completely.

Fig. 17

The dynamics of hydrostatic and anisotropic forces for different values of $\mu$ for Casimir wormhole

Fig. 18

The trajectories a, b show dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ for $\zeta _{1}$

Fig. 19

The trajectories a, b show dynamics of ${\mathcal {F}}_{h}$ and ${\mathcal {F}}_{a}$ for $\zeta _{2}$

8 Complexity factor in Casimir sormholes andd GUP corrected Casimir wormholes

In 2018, Herrera introduced the concept of complexity factor in the background of GR, for spherically symmetric and static self-gravitating systems [47]. Mainly, the idea of the complexity factor is based on simple or minimal complicated systems presenting homogeneous energy density and isotopic pressure. This type of fluid distribution shows zero complexity factor. Moreover, with anisotropic pressure and inhomogeneous energy density, zero complexity factor has been calculated in self-gravitating systems, as long as the effects of these two factors on the complexity factor cancel each other. The traced free scalar complexity factor $\mathcal {Y_{TF}}$ is expressed as follows.

$$\begin{aligned} \mathcal {Y_{TF}}=\Pi -\dfrac{1}{2r^{3}}\int _{r_{0}}^{r}r^{3}\dfrac{d\rho (r)}{dr}dr, \end{aligned}$$

(63)

where $\Pi =p_{r}-p_{t}$, which leads us to the following complexity factor for $D=5$ and constant redshift function,

$$\begin{aligned} \mathcal {Y_{TF}}= & {} \frac{r b'(r)-3 b(r)}{r^3}\nonumber \\{} & {} -\dfrac{1}{2r^{3}}\int _{r_{0}}^{r}\bigg (\dfrac{1}{2 r^4}(3 r^5 b''(r)-3 r^4 b'(r)+6 \mu r^2 b'(r)^2\nonumber \\{} & {} -3 r b(r) \left( r \left( 3 r-2 \mu b''(r)\right) +14 \mu b'(r)\right) \nonumber \\{} & {} +36 \mu b(r)^2)\bigg )dr. \end{aligned}$$

(64)

Now, using the shape function developed from Casimir wormhole in the above expression, we have the following results

$$\begin{aligned}{} & {} \!\!\!\mathcal {Y_{TF}}=-\frac{\pi ^2 \left( \frac{1}{r_{0}}-\frac{1}{r}\right) }{360 r^3}\nonumber \\{} & {} \quad {-}\dfrac{\sqrt{\frac{1}{\mu r^3}}\bigg (4320 \mu {+}4320 r_{0}^2{+}\pi ^2{-}4\pi ^{2}\log \bigg (\dfrac{r}{r_{0}}\bigg )\bigg )}{2 \sqrt{30}\sqrt{\dfrac{r \left( 270 \left( r^4+4 \mu \left( \mu {+}r_{0}^2\right) \right) {-}\pi ^2 \mu \log \bigg (\dfrac{r}{r_{0}}\bigg )\right) }{\mu }}}.\nonumber \\ \end{aligned}$$

(65)

It can be seen from Eq. (65), at the wormhole throat, the contribution of the first term, which comes from the integration of the derivative of energy density, becomes zero. The dynamics of complexity factor of casimir wormhole versus radial coordinate are shown in Fig. 20. We have observed that $r\rightarrow \infty$, or away from wormhole throat $\mathcal {Y_{TF}}\rightarrow 0$. According to [47], the minimal complexity factor shows homogenous energy density and isotropic pressure. Moreover, the zero complexity factor predicts inhomogeneous energy density and anisotropic pressure as long as these two effects cancel each other on the complexity factor. Therefore, near the wormhole throat, the complexity factor is monotonically increasing, and for higher values of radial coordinate, ${\mathcal {Y}}_{TF}$ approaches zero. It has also been observed that for $\mu =10$, the energy density is homogenous at very high values of r, and pressure shows isotropic behaviour after $r=10$. Therefore, in the case of a wormhole, we experience complexity factor approaches to zero for higher values of the radial coordinate. Moreover, in the dynamics of complexity factor, pressure isotropy plays a more vital role compared to the homogeneity of energy density.

Fig. 20

The dynamics of $\mathcal {Y_{TF}}$ for different values of $\mu$

Fig. 21

The trajectory a shows dynamics of $\mathcal {Y_{TF}}$ for different values of $\mu$ when $\alpha$ is fixed, and the trajectory b shows dynamics of $\mathcal {Y_{TF}}$ for different values of $\alpha$ when $\mu$ is fixed whereas $\zeta _{i}=\zeta _{1}$

Using GUP corrected Casimir shape function in the definition of complexity factor, we have the following equation

$$\begin{aligned} \mathcal {Y_{TF}}= & {} \dfrac{\mu r \left( \frac{1}{\mu r^3}\right) ^{3/2} \left( -2 \pi ^2 \alpha M r^2+3 \pi ^2 \alpha M r_{0}^2+4320 r^2 r_{0}^4+4320 \mu r^2 r_{0}^2+\pi ^2 r^2 r_{0}^2-4 \pi ^2 r^2 r_{0}^2 \log \bigg (\dfrac{r}{r_{0}}\bigg )\right) }{12 \sqrt{15} r_{0}^2 \sqrt{\frac{\pi ^2 \alpha \zeta _{i}}{r}-\frac{\pi ^2 \alpha \zeta _{i} r}{r_{0}^2}+\frac{540 r^5}{\mu }+2160 \mu r+2160 r r_{0}^2-2 \pi ^2 r \log \bigg (\dfrac{r}{r_{0}}\bigg )}}\nonumber \\{} & {} -\frac{\pi ^2 \left( -\frac{\alpha M}{r^3}+\frac{\alpha M}{r_{0}^3}-\frac{2}{r}+\frac{2}{r_0}\right) }{720 r^3}. \end{aligned}$$

(66)

It can be seen from Eq. (66), the last term disappears at $r=r_{0}$, which is due to the contribution of integration from Eq. (64). We have plotted Fig. 21a for different values of $\mu$ when $\alpha$ is fixed while Fig. 21b shows dynamics of $\mathcal {Y_{TF}}$ for different values of $\alpha$ when $\mu$ is fixed. It can be seen that with increase in $\mu$ and $\alpha$, $\mathcal {Y_{TF}}$ decreases. We have observed that for $r\rightarrow \infty$, implies $\mathcal {Y_{TF}}\rightarrow 0$. Therefore, for GUP-corrected Casimir wormholes, the complexity factor for both models approaches to zero. The plots of the complexity factor have similar behavior for both models, so we have plotted for KMM model only.

9 Deviation of EGB gravity from general relativity

The expressions of shape function for Casimir wormhole and GUP-corrected Casimir wormhole in EGB gravity are expressed in Eqs. (22) and (44). The expression of shape function for Casimir effect in GR [26] is written as

$$\begin{aligned} b(r)=r_{0}+\dfrac{r_{1}^{2}}{r}-\dfrac{r_{1}^{2}}{r_{0}} \end{aligned}$$

(67)

where $r_{1}=\dfrac{\pi ^{3}l_{p}^{2}}{90}$. The Eq.’s (22) and (44) possess two independent maximally symmetric solutions. Both solutions can have different asymptotic behaviour, but this is not the case in GR. Mathematically, the shape function from GR is only a function of r. While in the case of EGB gravity, we have another parameter $\mu$, or we can say that we have an extra degree of freedom to understand the dynamics of shape function in EGB gravity. Similar to this, in the case of a Casimir wormhole with GUP correction, the EGB gravity has degrees of freedom twice of GR i.e., $\mu$ and $\alpha$, whereas GR has only one which is $\alpha$. Here, we present comparison of our results with that of GR.

To measure the contribution of EGB gravity theory in comparison with the theory of GR, we have plotted Figs. 22 and 23, by picking the asymptotically flat shape function. These plots compare shape functions from GR background [26] and EGB gravity framework (Results of a present manuscript). Shape function in EGB background allows us to understand the dynamics of wormhole geometry in a wider range compared to GR. To understand the dynamics of GB coupled parameters on wormhole geometry, we have also studied wormhole conditions in terms of contour plots. We have treated GB coupled parameter as an independent variable in these plots in manuscript.

Fig. 22

Dynamics of b(r) for different values of $\mu$ for Casimir wormhole. Herein, we set $r_{0}=2$

Fig. 23

These trajectories show dynamics of b(r) for different values of $\mu$ for GUP-corrected Casimir wormhole

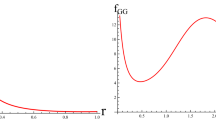
The equation of the state of dark energy can characterize cosmic inflation and the accelerated expansion of the universe. The Fig. 24 shows the dynamics of radial and transverse EOS parameters. We can observe that $w_{r}$ is an increasing function of r while $w_{t}$ is decreasing function of r for the Casimir wormhole for certain values of $\mu$ in EGB gravity and GR. The dynamics of $w_{r}$ is in the phantom phase while $w_{t}$ lies in the non-phantom phase. We have also studied EOS in terms of contour plots to explore the dynamics of GB-coupled parameter.

We have plotted the embedding diagram of Casimir wormhole in the case of shape function in GR and in EBG gravity as shown in Fig. 25. We can see that the shape function expands more in the case of EGB gravity for higher values of theory coupled parameter (Fig. 26).

The dynamics of complexity factors are studied compared to the wormhole solution from GR [26]. It can be seen that the dynamics of both complexity factors are monotonically increasing. The range of modulus value of $\mathcal {Y_{TF}}$ is larger in the case of EGB gravity than for GR.

10 Summary

In this manuscript, we have studied asymptotically flat, static, traversable wormhole geometries in the background of EGB gravity. We have worked with EGB gravity as it has been extensively studied in the scientific literature regarding cosmological phenomena like wormholes, black holes, and stellar structures.

Fig. 24

The trajectory a dynamics of $w_{r}$ and the plot b shows dynamics of $w_{t}$ for Casimir wormhole for different values of $\mu$

Fig. 25

Embedding diagram of Casimir wormhole

Fig. 26

Dynamics of complexity factor of Casimir wormhole

The Casimir effect exists due to distortion between two parallel, without charged, closely spaced plates placed in a vacuum. When two plates move closer to each other, the waves of shorter wavelengths start to fit between the plates, and the total energy between the plates will be less than elsewhere in the vacuum. Due to this, energy plates will attract each other. The concept of the Casimir effect was first predicted theoretically and later confirmed in the Philips laboratories through experimental work. The wormhole connects two points of the same cosmos, and its solution is based on Einstein’s field equations. Since the wormhole contains exotic matter and it violates the NEC. Therefore, the quantum nature of the Casimir effect seems a suitable candidate for the modeling of wormholes in EGB gravity. In this paper, we have studied the traversable wormhole solutions in the framework of EGB gravity by exploring the dynamics of the quantum nature of the Casimir effect. By comparing Casimir energy density with the field equation of EGB gravity, integrating the resulting equation yields a shape function. The obtained shape function has two branches with positive and negative signs. We have selected a positive branch for further analysis, as it satisfies the asymptotically flatness condition. The flaring out and throat conditions are also satisfied and displayed graphically. To understand the dynamics of GB coupled parameter on shape function, we have plotted contour plots in a specific domain of GB parameter. It has been seen that with an increase in the GB parameter, the obtained b(r) of the wormhole increases. The slope of the b(r) is less than one for $\mu <0$ and $\mu >0$. We have also studied the evolution of radial and tangential EOS parameters in specific domains of $\mu$. With the increase in the GB parameter, the value of $w_{r}$ grows positively away from the wormhole throat, while near $r_{0}$, we find decreasing behavior. In the case of $w_{t}$, we have experienced the opposite behavior. We have studied the behavior of NEC for positive and negative values of $\mu$. It can be observed from valid regions and plots of NEC that near the wormhole throat $(r_{0}=2)$, the NEC are not satisfied.

The generalized principle of uncertainty has been studied due to the idea of minimal length in background of quantum gravity theories. In the remaining part of this paper, we have analyzed the dynamics of the GB coupled parameter and MU parameter on the dynamics of the wormhole. There are adequate ways to generate possible generic functions to develop the maximally localized quasi-quantum states. Here, we have considered two models of KMM and DGS to develop quasi-quantum states. In addition, we have modeled Casimir wormhole geometries in the framework of EGB gravity. The behavior of both models in the dynamics of the GB coupled parameter and MU parameter on wormhole geometries is relatively the same. The b(r) of wormhole increases with the increase in GB coupled parameter, while for the MU parameter, we have experienced the opposite results. All wormhole conditions are satisfied for the increasing value of the GB parameter and the decreasing value of the MU parameter. The dynamics of $w_{r}$ and $w_{t}$ have also been studied for both models by keeping one parameter fixed and varying another parameter. The plots of NEC for GUP-corrected wormholes are also displayed, and NEC is violated near the wormhole throat. It has been evidenced that prominent dynamics of GB couple parameter can be seen, despite of the fact which has been discussed in Ref. [29]. We have explored the active gravitational mass of Casimir and GUP-corrected Casimir wormholes. This mass exists inside the wormhole’s region from the wormhole’s throat $r_{0}$ to the boundary of the radius r. In the next section, we aim to discuss wormhole geometry by providing mathematical modeling of obtained wormholes in 3D and 2D space-time. The source is Casimir energy density. We have seen that the developed shape function satisfies all wormhole conditions. We have plotted embedded diagrams to display wormhole shape for $t=constant$ and $\theta =\dfrac{\pi }{2}$ for Casimir wormholes and GUP-corrected Casimir wormholes. Plus, two univereses in 3D and 2D space-time is presented, illustrating asymptotically flat wormhole.

We have also probed the equilibrium forces for the Casimir wormhole and GUP corrected Casimir wormhole. The hydrostatic and anisotropic forces are calculated in each case. The plots show that they do not cancel out each other completely. The complexity factor of Casimir wormholes and GUP-corrected Casimir wormholes have also been calculated and monotonically increasing behaviour of complexity factor have also been experienced. In the present study, we have explored wormhole geometries to study the physical behavior of dynamics of theory-coupled parameters and MU parameter in EGB gravity.

A number of theories of gravity have been tested using useful wormhole solutions, which have been thoroughly researched in a variety of settings [61, 62]. Researchers have also looked into whether modified theories of gravity, such as f(R) gravity [11, 14], ($f(\tau )$ gravity (where $\tau$ denotes torsion) [15, 16, 63,64,65], (f(R, T) gravity (where R represents the Ricci scalar and T is the trace of the energy–momentum tensor) [21], Brans–Dicke (BD) theory [18, 22, 66, 67], scalar–tensor teleparallel gravity [22], and Einstein–Gauss–Bonnet gravity [45]. These investigations aim to explore the dynamics of wormhole properties in alternative theories of gravity. Agnese and Camera [66] investigated static spherically symmetric wormholes in the context of Brans–Dicke (BD) theory, which depend on the post-Newtonian parameter $gamma>1$. In the context of the BD theory, traversable wormhole solutions can be found for both positive ($omega>0$) and negative (omega0) values of the parameter. The scalar field acts as exotic matter in scalar tensor theories [18, 67]. Ebrahim and Riazi [20] introduced two Lorentzian wormhole solutions in BD theory by using a traceless energy–momentum tensor. These solutions were developed taking into account both closed and open universe theories. According to the literature now available, the topic of Casimir wormhole dynamics has been thoroughly investigated both within the framework of GR and in numerous modified theories of gravity. Garattini [26] has put up a model for a static traversable wormhole, looking at the Casimir effect’s negative energy density and analysing the outcomes within the context of GR. Building on a similar strategy, it has been discussed how the GUP affects the geometry of Casimir wormholes [28]. Garattini, [31], conducted additional research into Yukawa Casimir wormholes while assuming no tidal force. Additionally, Sokoliuk [34] has studied the possibility of Casimir wormholes in f(R) modified gravity when there is no tidal force. Three different Casimir wormhole systems have been studied within the framework of f(Q) modified theory, according to Zinnat Hassan [68]. In this work, we analyse Casimir wormhole solutions, concentrating on a five-dimensional ($D=5$) case, utilising the higher-dimensional gravity theory Einstein Gauss–Bonnet (EGB) gravity.

It serves a specific purpose to study the wormhole solution in EGB gravity, highlighting its extraordinary property of having up to two different maximally symmetric solutions, even with various signs of the curvature scale. These solutions display several asymptotic behaviours, which are discussed in the manuscript’s equations (22) and (44). The curvature scale of the maximally symmetric solutions in EGB gravity is still unknown, in contrast to general relativity (GR). Additionally, when investigating EGB black hole solutions, one comes across two unique branches with various asymptotic behaviours [69]. It is important to remember that, according to Zwiebach [70], EGB gravity can be considered the low energy limit of some string theories. Notably, in higher-dimensional gravity theory, Casimir wormholes and GUP-corrected Casimir wormholes have not been discussed before. Existing literature has not yet examined how the “Casimir wormhole”’s active gravitational mass and complexity factor are measured.