1 Introduction

Black hole is excepted by general relativity inside whose event horizon nothing can escape. At first, the black hole is considered to only have mass, angular momentum and charge (if exists) and no temperature or entropy [1,2,3], but the quantum field theory in curved space changes this view. Then the black hole thermodynamics was founded by Bekenstein and Hawking et al. [4,5,6,7,8], suggested that a black hole can have entropy and nonzero temperature. According to the laws of black hole thermodynamics, the entropy of the black hole is proportional to its area and the surface gravity of black hole plays the role of its temperature. The black hole thermodynamics pushes us to consider the black hole as a thermal system [6, 9].

A zero-charged black hole in asymptotically flat space can only have negative heat capacity with standard Gibbs-Boltzmann (GB) statistics, which means the black hole cannot be in thermal equilibrium [10]. But Hawking and Page proved that there are two branches of uncharged black hole in asymptotically anti-de Sitter space, i.e. the small black hole branch is unstable with negative heat capacity and the large black hole branch can be stable with positive heat capacity. Moreover, there is a minimum temperature \(T_{min}\) below which the two branches of black hole cannot occur, and there is another certain temperature \(T_{HP}\) which is the point of Hawking–Page phase transition [9, 10]. With the development of AdS/CFT correspondence, other researches on the black hole thermodynamics were done for the charged AdS black holes [11,12,13].

Some researches [14, 15] suggested that the standard GB statistics will be violated for the long-range interactions (black hole system and etc.). Recently, some authors [9, 16,17,18] also pointed out that the standard stability analysis may not be applicable for the black hole system because it depends strongly on the additivity of entropy function, which fails to hold on the Bekenstein–Hawking entropy. The mentioned problems all suggested that applying GB statistics to a self-gravitation system may bring an uncomplete result. It is well known that the black hole entropy is proportional to its area rather than its volume, which indicates that the black hole entropy is nonextensive. The difficulties force us to consider the black hole thermodynamics with nonextensive statistics and nonextensive entropy. Fortunately, A weaker composition rule [19] which is the famous Abe’s composition rule can be taken to apply for the nonextensive approach,

$$\begin{aligned} H_{\lambda }(S(A,B))= & {} H_{\lambda }(S(A))+H_{\lambda }(S(B))\nonumber \\ {}{} & {} +\lambda H_{\lambda }(S(A))H_{\lambda }(S(B)), \end{aligned}$$
(1)

where H is a differentiable function of entropy S, A, B are two independent systems, and \(\lambda \in {\mathbb {R}}\) is a constant parameter.

One of nonextensive entropy, Tsallis entropy [20,21,22,23] takes the form

$$\begin{aligned} S_{q}=\frac{1-\sum _{i=1}^{W}p^{q}_{i}}{q-1},\,q\in {\mathbb {R}}, \end{aligned}$$
(2)

where \(W\in {\mathbb {N}}\) is the total number of possible (microscopic) configurations and \({p_{i}}\) is the associated possibilities. When \(q\rightarrow 1\), the standard GB entropy \(S_{BG}=-\Sigma _{i=1}^{W}p_{i}lnp_{i}\) will be recovered. The composition rule of nonextensive Tsallis entropy can be written as

$$\begin{aligned} S_{q}(A,B)=S_{q}(A)+S_{q}(B)+(1-q)S_{q}(A)S_{q}(B), \end{aligned}$$
(3)

which satisfies the Abe’s pseudoadditive rule by setting \(H_{\lambda }(S)=S_{q}\) and \(\lambda =1-q\).

The empirical temperature cannot be well defined from the pseudoadditivity of Tsallis entropy, so Biró and Ván [15] considered the logarithmic formal of Tsallis entropy

$$\begin{aligned} L(S_{q})=\frac{1}{1-q}[ln(1+(1-q)S_{q})]=S_{R}. \end{aligned}$$
(4)

Interestingly, it is just the well-known Rényi entropy [24, 25], which is additive under Abe’s composition rule. By defining a nonextensive parameter \(\lambda =1-q\), we have

$$\begin{aligned} S_{R}=\frac{1}{\lambda }ln(1+\lambda S_{q}). \end{aligned}$$
(5)

The Rényi entropy is compatible with the zeroth law of thermodynamics and the empirical temperature can be defined as

$$\begin{aligned} \frac{1}{T_{R}}=\frac{\partial S_{R}(E)}{\partial E}, \end{aligned}$$
(6)

where E is the energy of system.

In Ref. [9] the nonextensive parameter \(\lambda \) plays the role of pressure just like the cosmological constant \(\Lambda \) in anti-de Sitter background. The Rényi statistics has also been applied into several different black holes in different background [14, 16,17,18, 26, 27], but still not been used to consider the regular black holes.

Regular black hole is a set of black hole solutions which origin from preventing the singularity difficulty. Since the first regular black hole solution was found by Bardeen [28], some deeper researches about the regular black hole were done [29,30,31,32,33,34,35,36,37,38,39,40]. Particularly, Eloy Ayó-beato and Alberto García [41,42,43,44] proved that the regular black holes are actually a set of solutions of Einstein equation by considering the nonlinear electromagnetical sources (more references seen [45,46,47,48,49,50]).

When we consider the thermodynamics of regular black holes, the different temperatures will be obtained by the surface gravity approach and the thermodynamic approach, which may lead to giving up one of the first law of thermodynamics or Bekenstein area law. To avoid the different temperatures obtaining by different approaches, Ma and Zhao [51] corrected the first law of black hole thermodynamics.

The thermodynamics of regular black holes has been investigated with several different approaches, but it still has some difficulties which are nonadditivity of entropy function with GB statistics and different temperatures obtaining with different approaches. To solve these problems, we apply the corrected first law of thermodynamics of black hole and Rényi statistics to the thermodynamics of Bardeen black hole.

This paper is organized as follows. In Sect. 2, we briefly review the Bardeen black hole spacetime and its corrected thermal properties. In Sect. 3, we introduce the general Smarr formula of Bardeen black hole via Rényi statistics and derive the corrected first law of regular black hole of Rényi statistics. In Sect. 4, we investigate the thermodynamics quantities of Bardeen black hole with GB statistics and corrected first law of thermodynamics in the grand canonical ensemble and the canonical ensemble. In Sect. 5, the thermodynamic quantities in the Rényi model will be studied. The brief conclusions and discussions are given in the last section. In this paper, the geometric units \(G=\hbar =c=k_{B}=1\) will be chosen.

2 The first law of thermodynamics for regular black holes

In this section, we briefly review the first law of thermodynamics of regular black holes. The line element of spherically symmetric Bardeen black hole is

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2(d\theta ^2+sin^2\theta d\varphi ^2), \end{aligned}$$
(7)

where the function f(r) is

$$\begin{aligned} f(r)=1-\frac{2m(r)}{r}, \end{aligned}$$
(8)

the effective mass m(r) in function f(r) is

$$\begin{aligned} m(r)=\frac{Mr^3}{(r^2+q^2)^\frac{3}{2}}, \end{aligned}$$
(9)

where the parameters M and q are the black hole mass and the magnetic charge, respectively. When \(q>\frac{4\sqrt{3}M}{9}\), there are inner horizon (Killing horizon) and outer horizon (event horizon). Two horizons meet when \(q=\frac{4\sqrt{3}M}{9}\) and there is no horizon when \(q>\frac{4\sqrt{3}M}{9}\). Setting \(r_{h}\) as the radius of event horizon and solving \(f(r_{h})=0\) for M, we can get

$$\begin{aligned} M=\frac{\left( q^2+r_h^2\right) {}^{3/2}}{2 r_h^2}. \end{aligned}$$
(10)

The temperature is defined by surface gravity: \(T_{h}=f'(r_{h})/(4\pi )\), so

$$\begin{aligned} T_{h}=\frac{r_{h}^2-2 q^2}{4 \pi r_{h} \left( q^2+r_{h}^2\right) }. \end{aligned}$$
(11)

On the other hand, the temperature can be calculated from the first law of thermodynamics. For Bardeen black hole the first law of black hole thermodynamics takes the form

$$\begin{aligned} dM=T_{H}dS+\Phi _{h}dq, \end{aligned}$$
(12)

where S is the entropy of black hole which equals to quarter of the area of black hole event horizon and \(\Phi _{h}\) is the magnetic potential of black hole. The temperature calculated with the first law is

$$\begin{aligned} T_{H}=\left( \frac{\partial M}{\partial S}\right) _{q}=\frac{\left( r_h^2-2 q^2\right) \sqrt{q^2+r_h^2}}{4 \pi r_h^4}, \end{aligned}$$
(13)

which is not equal to the temperature taken from the surface gravity way, i.e. \(T_{H}\ne T_{h}\). Considering the correspondence \(\{S,dE,T_{H}\}\leftrightarrow \{A/4,C(M,q,r_{h})dM,T_{h}\}\), the first law of thermodynamics is corrected as [51]

$$\begin{aligned} dE=C(M,q,r_{h})dM=T_{h}dS+\Phi _{H}dq, \end{aligned}$$
(14)

where the parameter \(C(M,q,r_{h})=m(r_{h})/M=r_{h}^3/(r_{h}^2+q^2)^\frac{3}{2}\), A is the area of black hole horizon, \(\Phi _{H}\) is the corrected magnetic potential and E is the internal energy. Thus we have

$$\begin{aligned} T_{h}=C(M,q,r_{h})\left( \frac{\partial M}{\partial S}\right) _{q}=C(M,q,r_{h})T_{H}. \end{aligned}$$
(15)

The magnetic potential of Bardeen black hole can be obtained by the corrected first law

$$\begin{aligned} \Phi _{H}=C(M,q,r_{h})\left( \frac{\partial M}{\partial q}\right) _{S}=\frac{3 q r_h}{2 \left( q^2+r_h^2\right) }. \end{aligned}$$
(16)

3 Thermodynamics and general Smarr formula from Rényi statistics

The thermodynamics and general Smarr formula in the Rényi model will be reviewed in this section. As a self-gravitation system, the black hole thermodynamics can be considered under the nonadditive Tsallis statistics which has the general composition rule. Though the Tsallis statistics can be applied for the non-extensity nature of black hole, the empirical temperature through the zeroth law of thermodynamics cannot be well defined. To avoid this difficulty, the formal logarithm of the Tsallis entropy, which is the well known Rényi entropy, will be taken. The Bekenstein–Hawking entropy of black hole can be considered as the Tsallis entropy from which the Rényi entropy function of black hole takes the form

$$\begin{aligned} S_{R}=\frac{ln(1+\lambda S_{BH})}{\lambda }, \end{aligned}$$
(17)

which is additive with the Abe’s composition rule. The Rényi temperature can be written as

$$\begin{aligned} T_{R}= & {} \frac{1}{\partial S_{R}/\partial E}=\frac{1}{\partial S_{R}/(C(M,q,r_{h})\partial M)}\nonumber \\ {}= & {} T_{h}(1+\lambda S_{BH}). \end{aligned}$$
(18)

The Smarr formula i.e. the mass formula of Bardeen black hole in asymptotically flat space can be written as

$$\begin{aligned} M=\int _{S}(2T_{\nu }^\mu -T\delta _{\nu }^\mu )\xi ^\nu _{(t)}d\Sigma _{\mu }+2\Omega J+\frac{\kappa }{4\pi }A, \end{aligned}$$
(19)

in which the surface gravity term is actually the temperature term 2TS. From the discussion above, the relation of temperature and entropy between the Gibbs–Boltzmann statistics and the Rényi statistics is

$$\begin{aligned} T_{h}=\frac{T_{R}}{e^{\lambda S_{R}}}, \, S_{BH}=\frac{e^{\lambda S_{R}}}{\lambda }. \end{aligned}$$
(20)

From the Ref. [9], the temperature term can be expanded as

$$\begin{aligned} \begin{aligned} M&=2T_{h}S_{BH}+\cdots \\&=2T_{R}S_{R}-\lambda T_{R}S^2_{R}+\cdots +O(\lambda ^2), \end{aligned} \end{aligned}$$
(21)

where the \(S_{R}\) can be expanded as

$$\begin{aligned} S_{R}=\pi r_{h}^2-\frac{\lambda \pi ^2 r^4_{h}}{2}+O(\lambda ^2). \end{aligned}$$
(22)

The pressure P and the volume V will be defined by expanding the temperature term of M, which will be shown latter, and the \(P-v\) criticality and the van der Waals like phase transition of the canonical ensemble will occur naturally.

Fig. 1
figure 1

Left: Rényi temperature of the Bardeen black hole \(T_{R}\) versus event horizon \(r_{h}\) at fixed magnetic potential \(\Phi _{H}=0.3\) for \(\lambda =0.3\) (blue), \(\lambda =0.6\) (green), and \(\lambda =1\) (red) comparing with the GB case i.e. \(\lambda =0\) (black dashed). Right: the heat capacity \(C_{R}\) of the Bardeen black hole versus \(r_{h}\) at fixed potential \(\Phi =0.3\) and \(\lambda =0.3\). The heat capacity is negative when \(r_{h}<r_{c}\) and is positive when \(r_{h}>r_{c}\) while it cannot be positive in the GB case i.e. \(\lambda =0\) (black dashed)

Full size image

Moreover, we can derive the corrected first law of regular black hole of Rényi statistics. Following Ref. [9], substituting Eq. (20) into the corrected first law of regular black hole Eq. (14), we obtain

$$\begin{aligned} dE&=C(M,q,r_{h})dM=\frac{T_{R}}{e^{\lambda S_{R}}}d\left( \frac{e^{\lambda S_{R}}-1}{\lambda }\right) +\Phi _{H}dq \nonumber \\&=T_{R}dS_{R}+\frac{\lambda \pi r_{h}^3(r_{h}^2-2q^2)}{8(r_{h}^2+q^2)}d\lambda +\Phi _{H}dq+O(\lambda ^2)\nonumber \\&\approx T_{R}dS_{R}+VdP+\Phi _{H}dq, \end{aligned}$$
(23)

where \(P=\frac{3 \lambda \left( r_h^2-2 q^2\right) }{32 \left( r_h^2+q^2\right) },\,V=\frac{4 \pi r_h^3}{3}\). From the discussion above and comparing with Eq. (14), the E cannot be interpreted as the internal energy, but reinterpreted as the enthalpy H in the Rényi extended phase space. From the Legendre transformation \(E_{in}=H-PV\), the corrected first law of regular black hole in Rényi statistics is

$$\begin{aligned} dE_{in}=T_{R}dS_{R}-PdV+\Phi _{H}dq, \end{aligned}$$
(24)

where the \(E_{in}\) is the internal energy in Rényi statistics. The internal energy now be defined as \(E_{in}=E-PV\).

4 Thermodynamics of Bardeen black hole from standard Gibbs–Boltzmann statistics with corrected first law of thermodynamics

The physical quantities of a black hole can be treated as thermodynamic quantities because of the analogy between black hole mechanics and the laws of thermodynamics. The thermodynamics of Bardeen black hole can be considered in the grand canonical ensemble and the canonical ensemble.

4.1 Grand canonical ensemble

In the grand canonical ensemble, the magnetic charge q of black hole changes with the surrounding heat bath, and the magnetic potential \(\Phi _{H}\) can be set to be fixed. As mentioned in Sect. 2, the magnetic potential of Bardeen black hole can be written as

$$\begin{aligned} \Phi _{H}=\frac{3 q r_h}{2 \left( q^2+r_h^2\right) }. \end{aligned}$$
(25)

Consequently, the internal energy of black hole can be considered as

$$\begin{aligned} E=C(M,q,r_{h})M=\frac{r_{h}}{2}, \end{aligned}$$
(26)

and the Bekenstein–Hawking entropy is

$$\begin{aligned} S_{BH}=\frac{A}{4}=\pi r_{h}^2. \end{aligned}$$
(27)

Other quantities can be calculated as

$$\begin{aligned} T_{h}= & {} \frac{\sqrt{9-16 \Phi _H^2}-1}{8 \pi r_h}, \end{aligned}$$
(28)
$$\begin{aligned} C_{\Phi _{H}}= & {} T_{h}\left( \frac{\partial S_{H}}{\partial T_{h}}\right) _{\Phi _{H}}=\left( \frac{\partial E}{\partial T_{h}}\right) _{\Phi _{H}}\nonumber \\ {}= & {} -\frac{4 \pi r_h^2}{\sqrt{9-16 \Phi _H^2}-1}, \end{aligned}$$
(29)
$$\begin{aligned} G_{H}= & {} E-T_{h}S_{BH}-q\Phi _{H}=\frac{1}{8} r_h \left( \sqrt{9-16 \Phi _H^2}-1\right) ,\nonumber \\ \end{aligned}$$
(30)

where \(T_{h}\) is the Hawking temperature, \(C_{\Phi _{H}}\) is the heat capacity at fixed magnetic potential \(\Phi _{H}\), and \(G_{H}\) is the Gibbs free energy. The black hole cannot be in stable because the heat capacity \(C_{\Phi _{H}}\) is negative at arbitrary \(r_{h}\). This can be seen from the dashed black line in Fig. 1.

4.2 Canonical ensemble

In the canonical ensemble we fixed the magnetic charge q of black hole. Considering two horizons meet, the mass and the magnetic charge of extremal black hole can be written as \(M_{e}=3 \sqrt{3} q/4\), and the radius of the extremal black hole is \(r_{e}=\sqrt{2}q\). Consequently, the internal energy of black hole is

$$\begin{aligned} E=C(M,q,r_{h})(M-M_{e})=\frac{1}{4} r \left( 2-\frac{3 \sqrt{3} q r^2}{\left( q^2+r^2\right) ^{3/2}}\right) ,\nonumber \\ \end{aligned}$$
(31)

the Bekenstein–Hawking entropy is still \(S_{BH}=\pi r_{h}^2\) and other quantities can be calculated as

$$\begin{aligned} T_{h}= & {} \frac{r_h^2-2 q^2}{4 \pi r_h \left( q^2+r_h^2\right) }, \end{aligned}$$
(32)
$$\begin{aligned} C_{q}= & {} T_{h}\left( \frac{\partial S_{H}}{\partial T_{h}}\right) _{q}=\left( \frac{\partial E}{\partial T_{h}}\right) _{q}\nonumber \\ {}= & {} -\frac{2 \pi r_h^2 \left( r_h^2+q^2\right) {}^2}{-7 q^2 r_h^2+r_h^4-2 q^4}, \end{aligned}$$
(33)
$$\begin{aligned} F_{H}= & {} E-T_{h}S_{BH}=\frac{q^2 r}{q^2+r^2}+\frac{r^3}{4 \left( q^2+r^2\right) }\nonumber \\ {}{} & {} -\frac{3 \sqrt{3} q r^3}{4 \left( q^2+r^2\right) ^{3/2}}, \end{aligned}$$
(34)

where the \(C_{q}\) is the heat capacity of black hole with fixed the magnetic charge q and \(F_{H}\) is the Helmoholtz free energy. From the heat capacity \(C_{q}\), two branches of black hole can be founded, i.e., the one with positive heat capacity and the other with negative heat capacity. From \(C_{q}>0\), \(r_{h}\) can be solved as

$$\begin{aligned} \sqrt{2}q<r_{h}<\frac{\sqrt{\sqrt{57} +7 }q}{\sqrt{2}}. \end{aligned}$$
(35)

The heat capacity will be negative when \(r_{h}>\frac{\sqrt{\sqrt{57} +7 }q}{\sqrt{2}}\), which means that at \(r_{h}=\frac{\sqrt{\sqrt{57} +7 }q}{\sqrt{2}}\) the capacity diverges and temperature gets maximum

$$\begin{aligned} T_{max}=\frac{1}{\sqrt{19 \sqrt{57}+143} \pi q}. \end{aligned}$$
(36)

It is found that the phase transition of Bardeen black hole depends on the choice of ensemble, which may be resulted from the long-range gravitation and electromagnetic interactions of the system.

5 Thermodynamics of Bardeen black hole from Rényi statistics with corrected first law of thermodynamics

In this section, the thermodynamics of Bardeen black hole will be studied with the Rényi approach in the grand canonical ensemble (fixed potential) and the canonical ensemble (fixed charge).

Fig. 2
figure 2

Left: Gibbs free energy versus temperature for fixed \(\Phi _{H}\) in the Rényi model. Right: Gibbs free energy vs. temperature with different nonextensive parameter \(\lambda =0.3\) (blue),0.6 (red),1 (green). The GB case is plotted with dashed black line

Full size image

5.1 Grand canonical ensemble

The thermodynamic quantities of the grand canonical ensemble will be calculated in the Rényi model firstly, then the state equation \(P-v\) will be discussed.

As mentioned in Sect. 3, the Rényi temperature in the grand canonical ensemble can be obtained

$$\begin{aligned} T_{R}=\frac{\left( \sqrt{9-16 \Phi _H^2}-1\right) \left( 1+\lambda \pi r_h^2\right) }{8 \pi r_h}, \end{aligned}$$
(37)

with the above temperature, the heat capacity can be calculated

$$\begin{aligned} C_{R}= & {} T_{R}\left( \frac{\partial S_{R}}{\partial T_{R}}\right) _{\Phi _{H}}=\left( \frac{\partial E}{\partial T_{R}}\right) _{\Phi _{H}}\nonumber \\= & {} \frac{4 \pi r_h^2}{\left( \sqrt{9-16 \Phi _H^2}-1\right) \left( \pi \lambda r_h^2-1\right) }. \end{aligned}$$
(38)

The heat capacity is negative when \(r_{h}<r_{c}\) and is positive when \(r_{h}>r_{c}\). For the critical point \(r_{c}=\sqrt{1/\lambda \pi }\), \(C_{R}\) is divergent. So there are two possible black hole branches, which are the small black hole branch with negative heat capacity and the large black hole branch with positive heat capacity. Substituting \(r_{c}\) into Eq. (10), the critical mass can be obtained

$$\begin{aligned} M_{c}=\frac{3}{32} \sqrt{\frac{3}{2 \pi }} \lambda \left( \frac{3-\sqrt{9-16 \Phi _H^2}}{\lambda \Phi _H^2}\right) ^{3/2}, \end{aligned}$$
(39)

which means that the Bardeen black hole in Rényi statistics is in the small black hole branch when \(M<M_{c}\) and in the large black hole branch when \(M>M_{c}\).

The heat capacity \(C_{R}\) is proportional to the inverse of the slope of the temperature \(T_{R}\), we have

$$\begin{aligned} C_{R}=\frac{1}{2} \left( \frac{1}{\partial T_{R}/\partial r_{h}}\right) . \end{aligned}$$
(40)

The critical radius \(r_{c}\) is the extremum point of \(T_{R}\) i.e. \(T'_{R}(r_{c})=0\). With this relation, the Bardeen black hole can be stable, which has positive heat capacity when \(r_{h}>r_{c}\) and negative heat capacity when \(r_{h}<r_{c}\). While there is no extremum point in the case of GB statistics.

We can also solve Eq. (37) for \(r_{h}(T_{R})\) function of temperature \(T_{R}\) and the minimum temperature can be obtained by solving \(r_{h}(T_{R})=r_{c}=1/\sqrt{\lambda \pi }\)

$$\begin{aligned} T_{R,min}=\frac{1}{4} \left( \frac{\sqrt{9 \lambda -16 \lambda \Phi _H^2}}{\sqrt{\pi }}-\frac{\sqrt{\lambda }}{\sqrt{\pi }}\right) , \end{aligned}$$
(41)

and the minimum temperature \(T_{R,min}=\frac{1}{2}\sqrt{\frac{\lambda }{\pi }}\) corresponds to the Schwarzschild case when \(\Phi _{H}=0\). It is also interesting that the minimum temperature becomes larger with higher level of nonextensivity i.e. higher value of \(\lambda \).

The Rényi statistics, in which black hole can be locally stable in asymptotically flat space with certain level of nonextensivity, gives different conclusions from GB statistics. There is no black hole phase when \(T_{R}<T_{R,min}\), because the event horizon cannot exist due to the imaginary value \(r_{h}(T_{R})\). The hot thermal radiation in asymptotically flat space will collapse to a black hole with higher temperature than a minimum temperature i.e. \(T_{R}>T_{R,min}\), which also occurs in the case of black hole in the AdS background from GB statistics.

In the grand canonical ensemble, the Gibbs free energy will be considered in discussing the global stability of the black hole. So in the Rényi model, the corresponding Gibbs free energy function should be written with Rényi entropy and temperature as

$$\begin{aligned} G_{R}= & {} E-T_{R}S_{R}-q\Phi _{H}=\frac{\left( \sqrt{r_h^2 \left( 9-16 \Phi _H^2\right) }+r_h \left( 4 \Phi _H^2-3\right) \right) \left( \left( \pi \lambda r_h^2+1\right) \ln \left( \pi \lambda r_h^2+1\right) -2 \pi \lambda r_h^2\right) }{2 \pi \lambda r_h \left( \sqrt{r_h^2 \left( 9-16 \Phi _H^2\right) }-3 r_h\right) }, \end{aligned}$$
(42)

The Fig. 2 shows that the Bardeen black hole is globally unstable in the GB case as its free energy is always positive. From Fig. 2, we can see the free energy of black hole will be negative when the temperature is high enough, so the black hole is global stable with the Rényi parameter \(\lambda \). The Hawking–Page temperature \(T_{HP}\) can be obtained from \(G_{R}=0\)

$$\begin{aligned} T_{HP}\approx \sqrt{\lambda } \left( 0.17527 \sqrt{9-16 \Phi _H^2}-0.17527\right) , \end{aligned}$$
(43)

which is about 1.24 times \(T_{R,min}\).

Fig. 3
figure 3

The Hawking–Page temperature \(T_{HP}\) versus the magnetic potential \(\Phi _{H}\). The line corresponds to the Hawking–Page phase transition line which divides the phase space into two regions, the thermal radiation phase and the large black hole phase

Full size image
Fig. 4
figure 4

\(P-v\) diagram of the Bardeen black hole for fixed magnetic potential \(\Phi _{H}=0.3\) (left) and \(\Phi _{H}=0.5\) (right). There are two branches of the black hole for a giving temperature, one of which is small black hole phase (P increases with v) and another is the large black hole phase (P decreases with v)

Full size image

The Hawking–Page temperature \(T_{HP}\) versus magnetic potential \(\Phi _{H}\) is plotted in Fig. 3. The range of magnetic potential can be obtained from the horizon structure of Bardeen black hole mentioned in Sect. 2 and the extreme value of magnetic potential obtained when \(q=4\sqrt{3}M/9\). From Fig. 3, the Hawking-Page transition line is similar to the \(T-\mu \) phase diagram of confining/deconfining phase transition at finite chemical potential. This shows that the properties of asymptotically flat black hole using Rényi statistics is similar to the asymptotically AdS black hole using GB statistics [9, 11,12,13].

Now we turn to the cusp of \(G_{R}\) versus \(T_{R}\), which occurs at \(T_{R,min}\). The cusp corresponds to the small/large black hole phase transition. This cusp corresponds to a second-order phase transition because the heat capacity, which is the second order derivative of Gibbs free energy respect to temperature \(C_{R}=-T_{R}(\frac{\partial ^2 G_{R}}{\partial T_{R}^2})_{\Phi _{H}}\), is divergent. At the cusp, the critical Rényi entropy \(S_{Rc}\) and the critical Gibbs free energy \(G_{Rc}\) is

$$\begin{aligned} S_{Rc}=\frac{ln2}{\lambda },\,G_{Rc}=-\frac{(ln2-1) \left( \sqrt{9-16 \Phi _H^2}-1\right) }{4 \sqrt{\pi } \sqrt{\lambda }}. \end{aligned}$$
(44)

Gibbs free energy has the maximum value \(G_{Rc}\) and the Rényi entropy is a constant with a fixed \(\lambda \) at the cusp point.

Fig. 5
figure 5

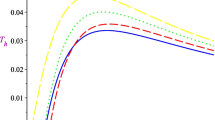
Left: the Rényi temperature of the Bardeen black hole \(T_{R}\) versus event horizon \(r_{h}\) at fixed magnetic charge \(q=0.3\) with different values of the nonextensitive parameter \(\lambda \). There are two turning points for \(\lambda <\lambda _{c}\). Right: the heat capacity \(C_{R}\) of Bardeen black hole versus \(r_{h}\) at fixed \(q=0.3\) with different values of \(\lambda \)

Full size image

Then we focus on the \(P-v\) phase. As mentioned in Sect. 3, the general Smarr formula with Rényi statistics can be written as

$$\begin{aligned} M=2T_{R}S_{R}-\lambda T_{R}S^2_{R}+\dots +O(\lambda ^2). \end{aligned}$$
(45)

For the grand canonical ensemble, substituting the \(T_{R}\) and \(S_{R}\) into Eq. (45), we obtain

$$\begin{aligned} M= & {} 2T_{R}S_{R}-\left( -\frac{\pi \lambda r_h^3 \left( -4 \Phi _H^2-\sqrt{9-16 \Phi _H^2}+3\right) }{6-2 \sqrt{9-16 \Phi _H^2}}\right) \nonumber \\ {}{} & {} +\cdots +O(\lambda ^2), \end{aligned}$$
(46)

with which the pressure P and the volume V can be defined as

$$\begin{aligned} P=-\frac{3 \lambda \left( -4 \Phi _H^2-\sqrt{9-16 \Phi _H^2}+3\right) }{8 \left( 6-2 \sqrt{9-16 \Phi _H^2}\right) },\quad V=\frac{4\pi r_{h}^3}{3},\nonumber \\ \end{aligned}$$
(47)

and the general Smarr formula can be written as

$$\begin{aligned} M=2T_{R}S_{R}-2PV+\cdots . \end{aligned}$$
(48)

It needs to be emphasized that the \(V=4\pi r_{h}^3/3\) is not the geometric spherical volume with the horizon radius \(r_{h}\), but the thermodynamic volume which is the conjugate quantity of the pressure. The specific volume is \(v=8r_{h}/3\), not \(v=2r_{h}\) in AdS case, which allows us to get a better ratio Pv/T in Rényi statistics approaching to the standard van der Waals system [9]. With the specific volume, the equation of state can be written as

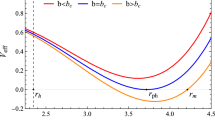
$$\begin{aligned} P= & {} \frac{6 \sqrt{6} \left( 4 \Phi _H^2+\sqrt{9-16 \Phi _H^2}-3\right) T_R}{v \left( \sqrt{9-16 \Phi _H^2}-3\right) \left( \sqrt{16 \Phi _H^2+9}-6\right) \sqrt{\sqrt{16 \Phi _H^2+9}+3}}\nonumber \\ {}{} & {} +\frac{4 \left( 4 \Phi _H^2+\sqrt{9-16 \Phi _H^2}-3\right) }{3 \pi v^2 \left( \sqrt{9-16 \Phi _H^2}-3\right) }. \end{aligned}$$
(49)

The pressure P versus the specific volume v is plotted in Fig. 4 which shows that there is a maximum value of P. The maximum value \(P_{max}\) can be obtained by solving the condition \((\frac{\partial P}{\partial v})_{T_{R},\Phi _{H}}=0\). The corresponding critical volume for \(P_{max}\) is \(v_{c}\). For a given temperature, there are two branches of black hole when \(P<P_{max}\) which are small black hole branch with \(v<v_{c}\) and the large black hole branch with \(v>v_{c}\). For the large black hole branch, the pressure P decreases with the specific volume v, which means the thermodynamic stability for the large black hole branch. In contrary to the large black hole branch, the small black hole branch is unstable. The second derivative \((\frac{\partial ^2 P}{\partial v^2})_{T_{R},\Phi _{H}}\) at \(v_{c}\) is nonzero, which means that there is no critical behavior for Bardeen black hole in the grand canonical ensemble.

5.2 Canonical ensemble

The thermal properties of Bardeen black hole in the canonical ensemble will be investigated in this section. From Eqs. (18) and (32), the Hawking temperature via Rényi model is

$$\begin{aligned} T_{R}=\frac{\left( r_h^2-2 q^2\right) \left( \pi \lambda r_h^2+1\right) }{4 \pi r_h \left( r_h^2+q^2\right) }, \end{aligned}$$
(50)

as the function of event horizon \(r_{h}\) is plotted with fixed \(q=0.3\) and different values of \(\lambda \) in Fig. 5.

These temperature curves of Bardeen black hole in the Rényi model are similar to the uncharged black holes in AdS background. Interestingly, the critical phase transition will occur at different values of \(\lambda \), which can be obtained with the condition

$$\begin{aligned} \left( \frac{\partial T_{R}}{\partial r_{+}}\right) _{q}=\left( \frac{\partial ^2 T_{R}}{\partial r_{+}^2}\right) _{q}=0. \end{aligned}$$
(51)

For this condition, the critical horizon \(r_{c}\), critical nonextensitive parameter \(\lambda _{c}\) and the critical Rényi temperature \(T_{c}\) can be numerically calculated

$$\begin{aligned} \begin{aligned}&r_{c}\approx 4.0552 q, \\&\lambda _{c}\approx \frac{0.00846318}{q^2}, \\&T_{c}\approx \frac{0.0233533}{q}. \end{aligned} \end{aligned}$$
(52)

When \(\lambda <\lambda _{c}\), there are local maximum and local minimum in the temperature curve. When \(\lambda =\lambda _{c}\), these two extremum points meet at the critical event horizon \(r_{c}\).

The Rényi heat capacity is

$$\begin{aligned} C_{R}= & {} T_{R}\left( \frac{\partial S_{R}}{\partial T_{R}}\right) _{q}\nonumber \\= & {} \left( \frac{\partial E}{\partial T_{R}}\right) _{q}\nonumber \\= & {} \frac{2 \pi r_h^2 \left( r_h^2+q^2\right) {}^2}{q^4 \left( 2-2 \pi \lambda r_h^2\right) +q^2 r_h^2 \left( 5 \pi \lambda r_h^2+7\right) +r_h^4 \left( \pi \lambda r_h^2-1\right) }.\nonumber \\ \end{aligned}$$
(53)

Unlike the GB case, three branches of black hole are allowed in the canonical ensemble via Rényi statistics, two positive branches and one negative branch as shown in Fig. 5. It shows that when horizon \(r_{h}\) equals to the extremum points mentioned above, the heat capacity is divergent, which means there is a phase transition. The temperature at these two extremum points are \(T_{1}=0.0695703\) and \(T_{2}=0.0730847\) for the blue curve in Fig. 5.

In the canonical ensemble, it is better to consider the global stability of Bardeen black hole with Helmholtz free energy. The Helmholtz free energy in the Rényi statistics is

$$\begin{aligned} F_{R}= & {} E-T_{R}S_{R}\nonumber \\= & {} \frac{1}{4} r_h \left( 2-\frac{3 \sqrt{3} q r_h^2}{\left( r_h^2+q^2\right) {}^{3/2}}\right) \nonumber \\{} & {} -\frac{\left( r_h^2-2 q^2\right) \left( \pi \lambda r_h^2+1\right) \ln \left( \pi \lambda r_h^2+1\right) }{4 \pi \lambda r_h \left( r_h^2+q^2\right) }, \end{aligned}$$
(54)

where \(E=C(M,q,r_{h})(M-M_{e})\).

Fig. 6
figure 6

The Rényi Helmholtz free energy \(F_{R}\) versus the Rényi temperature \(T_{R}\) with different magnetic charge q and different \(\lambda \). The swallow-tail-shape occurs only at \(\lambda <\lambda _{c}\). As the charge q increases, the swallow-tail-shape deviates from the standard shape, which may be resulted from the nonlinear magnetic charge of Bardeen black hole

Full size image
Fig. 7
figure 7

The pressure P versus v is plotted with different temperatures. The dashed line represents the critical curve \(T_{R}=T_{c}\). The solid curves below to the critical curve are the case of \(T_{R}<T_{c}\), in which there are three branches of black hole, one unstable (P increases with v) and two stable (P decreases with v) branches. The solid curves above the dashed line are the case of \(T_{R}>T_{c}\), which are analogous to the idea gas phase of van der Waals system

Full size image

Figure 6 shows the Helmholtz free energy versus the Rényi temperature of Bardeen black hole. The swallowtail behavior occurs only at \(\lambda <\lambda _{c}\), which is similar to the van der Waals liquid/gas system.

The general Smarr formula in the Rényi model is

$$\begin{aligned} M=2T_{R}S_{R}-\lambda T_{R}S^2_{R}+\cdots +O(\lambda ^2). \end{aligned}$$
(55)

Substituting Eqs. (17) and (50) into Eq. (55) and holding the first order of \(\lambda \), we have

$$\begin{aligned} M=2T_{R}S_{R}-\frac{\pi \lambda r_h^3 \left( r_h^2-2 q^2\right) }{4 \left( r_h^2+q^2\right) }+\cdots \end{aligned}$$
(56)

Defining the pressure P and the volume V as

$$\begin{aligned} P=\frac{3 \lambda \left( r_h^2-2 q^2\right) }{32 \left( r_h^2+q^2\right) },\quad V=\frac{4 \pi r_h^3}{3}, \end{aligned}$$
(57)

the general Smarr formula can be written as

$$\begin{aligned} M=2T_{R}S_{R}-2PV+\cdots \end{aligned}$$
(58)

Using the relation \(v=8r_{h}/3\), the equation of state can be obtained

$$\begin{aligned} P=\frac{T_R}{v}-\frac{18}{64 \pi q^2+9 \pi v^2}+\frac{4}{3 \pi v^2}, \end{aligned}$$
(59)

which the \(P-v\) diagram will behavior like the van der Waals system as shown in Fig. 7. The critical point can be obtained with the conditions

$$\begin{aligned} \left( \frac{\partial P}{\partial v}\right) _{T_{R},q}=0,\,\left( \frac{\partial ^2 P}{\partial v^2}\right) _{T_{R},q}=0. \end{aligned}$$
(60)

The critical pressure \(P_{c}\), specific volume \(v_{c}\) and temperature \(T_{c}\) can be numerically calculated

$$\begin{aligned} \begin{aligned}&P_{c}\approx \frac{0.000917584}{q^2}, \\&v_{c}\approx 10.4641 q, \\&T_{c}\approx \frac{0.0261711}{q}. \end{aligned} \end{aligned}$$
(61)

So, the critical compressibility factor is

$$\begin{aligned} \frac{P_{c}v_{c}}{T_{c}}\approx 0.366882, \end{aligned}$$
(62)

which is independent on the black hole’s mass and magnetic charge. Interestingly, this result is similar to the ratio of standard van der Waals fluid \(\frac{3}{8}\).

The relation P versus v in Fig. 7 is same as van der Waals system. The critical isothermal curve at \(T_{R}=T_{c}\) is plotted with purple dashed line. When \(T_{R}<T_{c}\), there is a small black hole phase corresponding to the liquid phase and a large black hole phase corresponding to the gas phase. The small black hole and the large black hole phase are stable with positive compression coefficient (P decreases with v). There is a unstable part between the small black hole and large black hole phase, which has the negative compression coefficient (P increases with v) and stands for the mixture of liquid and gas phase. Solving the following conditions

$$\begin{aligned} P=0,\,\left( \frac{\partial P}{\partial v}\right) _{T_{R},q}=0, \end{aligned}$$
(63)

the minimum temperature \(T_{0}\) can be obtained at \(v_{0}=\frac{4}{3} \sqrt{2 \left( \sqrt{57}+7\right) } q\),

$$\begin{aligned} T_{0}=\frac{1}{\sqrt{19 \sqrt{57}+143} \pi q}. \end{aligned}$$
(64)

When \(T_{0}<T<T_{c}\), there exists the phase transition similar to van der Waals system. The black hole will be like the ideal gas and there is no phase transition when the temperature is high enough \(T>T_{c}\).

6 Conclusion and discussion

In this paper, to avoid the incompatible temperature of regular black hole obtained with different approaches, we introduced the corrected first law of thermodynamics and studied the thermodynamics of the Bardeen black hole in both the grand canonical ensemble and the canonical ensemble via Rényi statistics. In the grand canonical ensemble (fixed charge potential), the Bardeen black hole can be locally stable and there are small black hole and large black hole branches with the nonextensive parameter \(0<\lambda <1\), while these two branches will not occur in GB statistics. Moreover, there is a Hawking–Page phase transition between the thermal radiation phase and the large black hole phase depending on the nonextensive parameter \(\lambda \). In the canonical ensemble (fixed charge q): (1) when \(\lambda <\lambda _{c}\) (critical nonextensive parameter), there is a small/large black hole phase transition (first order); (2) when \(\lambda >\lambda _{c}\), the phase transition above will disappear and the large black hole phase will just be a possibility. These behaviors are similar to the cases of Bardeen black hole and corrected Bardeen black hole in AdS background via GB statistics (see [48,49,50]). Furthermore, by introducing the general Smarr formula via Rényi statistics, which the parameter \(\lambda \) plays the thermodynamic pressure P, we found that the thermal phase structure in the canonical ensemble just behaves as the van der Waals system. The same phase transition also occurs in the case of Bardeen-AdS black hole via GB statistics.

Both the nonextensive parameter \(\lambda \) in Rényi statistics and the cosmological constant \(\Lambda \) in AdS spacetime play as the thermodynamic pressure P. The analogy between the case of asymptotically flat Bardeen black hole via Rényi statistics and Bardeen-AdS black hole via GB statistics suggests that the nonextensive parameter \(\lambda \) should have some connections with the cosmological constant \(\Lambda \). This connection may lead us to understand the nonextensive parameter \(\lambda \) more deeply.