Abstract
We investigate the space–time picture of string evolution and hadron production in a fully string-based model for high energy collisions involving heavy-ions. We find that although the density of strings is quite large at the time of hadronization in a central heavy-ion collision, the initial overlap between them right after the collisions is not necessarily large. We also find that when including string-string interactions using the so-called shoving model, the density of strings is decreased which should dampen the rapid increase in string tension in the rope hadronization with multiplicity that we found in a previous paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Angantyr [1] model for modelling heavy ion (HI) collisions in  implements a fairly simple procedure for stacking nucleon–nucleon (\(NN\)) sub-collisions on top of each other, to build up full HI events. Each sub-collision is generated using the full power of the
implements a fairly simple procedure for stacking nucleon–nucleon (\(NN\)) sub-collisions on top of each other, to build up full HI events. Each sub-collision is generated using the full power of the  multi-parton interaction (MPI) framework together with initial- and final-state parton showers. The combined parton-level sub-events are then hadronized together with the Lund string fragmentation model [2]. Even though there are no collective effects in this model it is able to adequately describe multiplicities in both \(\text {pPb}\) and \(\text {PbPb}\) events at the LHC, and even predict multiplicities in \(\text {XeXe}\)[3]. This begs the question, if it is possible that the colour degrees of freedom generated in the initial stages on the perturbative level in terms of colour connections (dipoles) between produced partons, can survive the hot and dense environment of a HI collision in the form of strings that then fragment into hadrons.
multi-parton interaction (MPI) framework together with initial- and final-state parton showers. The combined parton-level sub-events are then hadronized together with the Lund string fragmentation model [2]. Even though there are no collective effects in this model it is able to adequately describe multiplicities in both \(\text {pPb}\) and \(\text {PbPb}\) events at the LHC, and even predict multiplicities in \(\text {XeXe}\)[3]. This begs the question, if it is possible that the colour degrees of freedom generated in the initial stages on the perturbative level in terms of colour connections (dipoles) between produced partons, can survive the hot and dense environment of a HI collision in the form of strings that then fragment into hadrons.
In a series of articles [4,5,6,7,8] we have been investigating possible effects of interactions between strings in a dense environment, and have shown that such models may indeed give rise to collective effects such as anisotropic flow and strangeness enhancement, without the need of introducing a thermalised quark–gluon plasma (QGP). In this article we take a step back and investigate in more detail the space–time picture that arises from these models.
Among the string interactions, string shoving [6] and rope hadronization [7, 8] would impact the final-state hadron yields the most in heavy-ion collisions. The novelty of these mechanisms is based on the equilibrium transverse extent of the colour-electric field (E) of each string. Once each string is formed, the colour-electric field spread transversely to reach an equilibrium width R, as established in Ref. [6]. The electric field then is approximate by a Gaussian transverse shape,
where \(\rho \) is the transverse distance from a center of a string of radius R, in cylindrical coordinates. The effect of two strings’ electric fields repelling each other, would give rise to a net ‘shoving’ effect, which would push either string pieces away. In our implementation, this effect is modelled by looking at the strings after the final radius has been reached, and then transferring the push to primary hadrons by shifting their \(p_\perp \) after hadronization.
Also the hadronization process is affected by the interaction between colour-electric fields of the strings. We have suggested that the stings would form wider ‘colour-ropes’ with larger effective string tension \(\kappa _{\text {eff}}\), than just the sum of the tension of the individual strings. When such ropes hadronize, the higher \(\kappa _{\text {eff}}\) is released, which is available for tunnelling mechanism [2], and therefore producing more strange quarks. Thus, rope hadronization influences the strangeness yields in collision systems.
In a recent work [8], where we apply our rope hadronization to \(AA\) collisions, we find that rope hadronization by itself enhances strangeness yields too much in central \(\text {PbPb}\) events as compared to data. We believe that this occurs due to an overestimation of the string density at the time of hadronization in case of heavy-ion collisions. As we noted in that publication, inclusion of string shoving mechanism would produce a more accurate impact-parameter distribution of strings at the time of hadronization. The \(p_\perp \) pushes generated due to shoving would dilute the system due to the dense initial state generating larger shoving force.
In the current implementation, rope hadronization and string shoving mechanisms are not completely compatible. In the perfect case, rope formation would require the precise locations of the string pieces in impact parameter. That would require pushing the string pieces with the \(p_\perp \) generated due to string shoving at each time step during string evolution, but as mentioned above, in our implementation in Ref. [6], the \(p_\perp \) is only transferred to the primary hadrons, formed from hadronization. Therefore, the rope effects are somewhat approximate in all systems, and this mostly affects the yields in \(AA\) collisions, giving an overestimation of the string density.
Further work on reproducing signals such as final-state collective effects in \(AA\) in  would require hadronic rescattering [9, 10] and string interactions to work together. The effectiveness of the implementation will depend on how accurately the string interactions are able to produce the primary hadronic vertices as initial conditions to the hadronic rescattering. In this publication, we investigate the impact of string shoving and rope hadronization on primary hadron vertices.
would require hadronic rescattering [9, 10] and string interactions to work together. The effectiveness of the implementation will depend on how accurately the string interactions are able to produce the primary hadronic vertices as initial conditions to the hadronic rescattering. In this publication, we investigate the impact of string shoving and rope hadronization on primary hadron vertices.
The manuscript is organised as follows. In Sect. 2, we describe the space–time evolution of strings and their transverse overlaps in \(\text {pp}\) and \(AA\) collisions. In Sect. 3, we present how the primary hadron vertices are determined in  , and discuss how these are affected by the shoving and rope models. Lastly, we present our conclusions and further comments in Sect. 4.
, and discuss how these are affected by the shoving and rope models. Lastly, we present our conclusions and further comments in Sect. 4.
2 Space–time evolution of strings
The evolution of the colour fields between partons in a sample PbPb event (top) and a sample pp event (bottom), both generated at \(\sqrt{s_{{\tiny NN}}}=2.76\) TeV. Each circle represents the position in impact parameter space of a colour dipole field that stretches across \(z_{\text {lab}}=0\) at different times after the collision, \(t_{\text {lab}}=0.1\) fm/c (left), 0.3 fm/c (middle), and 0.5 fm/c (right). The radius of each circles corresponds to the transverse extent of the colour field of the dipole as given by the proper time of the string field at that point
The Angantyr model [1] can be said to be a straight forward extension of the multi-parton interaction model for \(\text {pp}\) in  to HI collisions. The model is based on an advanced Glauber [11, 12] calculation, which includes so-called Glauber–Gribov [13] corrections. The obtained nucleon–nucleon (\(NN\)) sub-collisions, are produced with the full
to HI collisions. The model is based on an advanced Glauber [11, 12] calculation, which includes so-called Glauber–Gribov [13] corrections. The obtained nucleon–nucleon (\(NN\)) sub-collisions, are produced with the full  MPI machinery, and are basically stacked together and hadronized. Some modifications are needed when one nucleon in one nuclei interacts with several nucleons in the other. In this case only one such sub-collision is treated as primary and is modelled as a full \(\text {pp}\) collision in
MPI machinery, and are basically stacked together and hadronized. Some modifications are needed when one nucleon in one nuclei interacts with several nucleons in the other. In this case only one such sub-collision is treated as primary and is modelled as a full \(\text {pp}\) collision in  , while the others are treated as diffractive excitations similar to the wounded nuclei model [14] as described in detail in [1].
, while the others are treated as diffractive excitations similar to the wounded nuclei model [14] as described in detail in [1].
As in  , the final-state hadron multiplicity in Angantyr is driven by multiple (semi-hard) scatterings among the partons of the colliding nucleons. These are treated perturbatively, even if they can be rather soft, which means that the scatterings are well localised. In this picture, the partons are then connected by colour lines, or dipoles, and the colour field between the partons in such a dipole is initially also well localised, but will spread out with the speed of light (c) both longitudinally and transversely as the partons fly apart. While the longitudinal extension will continue to grow, the transverse extension will stop due to confinement, and we get a string-like field with a constant string tension, \(\kappa \approx 1\) GeV/fm, that will eventually break and form hadrons.
, the final-state hadron multiplicity in Angantyr is driven by multiple (semi-hard) scatterings among the partons of the colliding nucleons. These are treated perturbatively, even if they can be rather soft, which means that the scatterings are well localised. In this picture, the partons are then connected by colour lines, or dipoles, and the colour field between the partons in such a dipole is initially also well localised, but will spread out with the speed of light (c) both longitudinally and transversely as the partons fly apart. While the longitudinal extension will continue to grow, the transverse extension will stop due to confinement, and we get a string-like field with a constant string tension, \(\kappa \approx 1\) GeV/fm, that will eventually break and form hadrons.
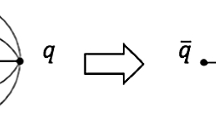
A simplified picture of the time-evolution of a single string piece between a coloured and an anti-coloured parton flying apart with the speed of light is given in Fig. 1. Parameterising a point along the string by the proper time, \(\tau \), and hyperbolic angle, we get in each time step, that the points where the radius reaches the confinement value R, will have \(\tau c=R\).
To illustrate the density of strings in a HI collision we have generated a sample central \(\text {PbPb}\) event at \(\sqrt{s_{{\tiny NN}}}=2.76\) TeV, shown in Fig. 2. The impact parameter is \(\approx 0.2\) fm, resulting in a charged multiplicity in the central pseudorapidity bin of \(dN_{\text {ch}}/d\eta |_{\eta =0}\approx 1750\). We then look at the strings that span \(z=0\) in the laboratory frame. To be precise we look at colour dipoles between a coloured and an anti-coloured parton currently positioned on opposite sides of \(z=0\). For each such dipole we look at its transverse size in different time steps (also in the laboratory frame). For each of these we position in Fig. 2 a correspondingly sized circle in the impact parameter plane. To be more precise, the radius of each circle is given by the proper time (multiplied by c) at the position along the string piece given by \(z=0\) and time in the laboratory frame, limited from above by the final string radius, \(R=0.5\) fm. In addition, since we are interested in the spread of the colour field, we have chosen to also take into account of how well localised the fields were at the time of the scattering. For this reason we limit the diameter of each circle from below by \(\hbar c/p_{\perp \max }\), where \(p_{\perp \max }\) is the largest transverse momentum of the two partons spanning the dipole. This is why there are some large circles already at \(t=0.1\) fm/c.
In the top left plot in Fig. 2, we see that initially, the collision region is only sparsely populated by the colour fields. Comparing to the lower left panel, where we show a high multiplicity (\(dN_{\text {ch}}/d\eta |_{\eta =0}\approx 50\)) \(\text {pp}\) event at the same collision energy (\(\sqrt{s}=2.76\) TeV), there are very few regions in the \(\text {PbPb}\) event where the colour fields are more densely packed. At later times (\(t=0.3\) fm/c in the middle panels), more of the collision area is filled up by colour fields, and at \(t=0.5\) fm/c (right panels), almost the whole area is filled, and this is also when the colour fields start to be confined to their maximum radius (0.5 fm in this simulation). Most dipoles, however, have a transverse momentum, and due to the time-dilation, only some of them has reach their final radius at \(t=0.5\) fm/c.
Clearly the overlap between the colour fields in the \(\text {PbPb}\) event becomes quite large, which raises the question if the string picture is really appropriate for heavy ion collisions. On the other hand, the overlap is also quite high in the \(\text {pp}\) collision, and we know that  is able to describe a vast range of hadronic final-state observables in \(\text {pp}\). We want to see how far we can go with the string picture and, rather than resorting to a hydro-dynamical approach with a quark–gluon plasma, we assume that the string degrees of freedom are still relevant for hadronization.
is able to describe a vast range of hadronic final-state observables in \(\text {pp}\). We want to see how far we can go with the string picture and, rather than resorting to a hydro-dynamical approach with a quark–gluon plasma, we assume that the string degrees of freedom are still relevant for hadronization.
Due to the large overlap among the strings, we need to worry about possible string–string interactions, and in the following sections we will discuss the space–time picture in our models for string shoving and rope hadronization.
There is also a third effect that we will not discuss here, namely colour reconnections. The assignment of colour connections between partons in  is essential, not only for the string fragmentation but also for the parton shower, which is based on the dipole picture. The assignment of colours are, however, made on the perturbative level in the \(N_C\rightarrow \infty \) limit, and in a dense system, there must be corrections to this. Indeed, already in the first multi-parton interaction implementation in
is essential, not only for the string fragmentation but also for the parton shower, which is based on the dipole picture. The assignment of colours are, however, made on the perturbative level in the \(N_C\rightarrow \infty \) limit, and in a dense system, there must be corrections to this. Indeed, already in the first multi-parton interaction implementation in  [15] the concept of colour reconnections was introduced where the colour connections between partons were allowed to change before hadronization, in a way that favoured shorter strings.
[15] the concept of colour reconnections was introduced where the colour connections between partons were allowed to change before hadronization, in a way that favoured shorter strings.
However, the colour reconnection models in  are based on a pure momentum picture and does not take into account the space–time separation between partons, so they are not suitable for heavy ion collisions. And in the Angantyr model, there are therefore only reconnections within each \(NN\) collision, while reconnections between them are not possible. We are currently working on a new reconnection model that takes space–time constraints into account, but it is not yet fully implemented.
are based on a pure momentum picture and does not take into account the space–time separation between partons, so they are not suitable for heavy ion collisions. And in the Angantyr model, there are therefore only reconnections within each \(NN\) collision, while reconnections between them are not possible. We are currently working on a new reconnection model that takes space–time constraints into account, but it is not yet fully implemented.
3 Corrections to hadronic vertices from string interactions
In this section, we present the shoving and rope models and how they affect the primary hadronic vertices. In both of these models, the cumulated effect of interactions between many stings are calculated by summing up pair-wise interactions between string pieces. To calculate the interaction between two string pieces, we use a special Lorentz frame, which we call the parallel frame. Here, any two string pieces spanned between two pairs of (massless) partons in any string system, will at any given time be straight lines lying in parallel planes, moving towards, or away from each other with constant opposite velocity.Footnote 1 This greatly facilitates the calculation of the transverse shoving force, as well as the increased string tension in the rope hadronization.
3.1 String shoving
The distribution of vertices for primary hadrons in the shoving model for \(\text {pp}\) collisions with central charged multiplicity, \(50<dN_{\text {ch}}/d\eta |_{\eta =0}<100\) (top row), and for \(\text {PbPb}\) collisions with \(dN_{\text {ch}}/d\eta |_{\eta =0}>500\) (bottom row). The \(\text {pp}\) events were generated at \(\sqrt{s}=7\) TeV, and the \(\text {PbPb}\) events at \(\sqrt{s_{\text {NN}}}=2.76\) TeV. The left panels show a heat map, giving the number of primary hadrons with \(|\eta |<0.5\) per fm\(^2\) in impact parameter space for  /Angantyr without shoving and the middle panels shows the same with shoving. The right panels compares the distributions with and without shoving in a slice with \(|b_y|<0.5\) fm
/Angantyr without shoving and the middle panels shows the same with shoving. The right panels compares the distributions with and without shoving in a slice with \(|b_y|<0.5\) fm
In our previous implementation of the shoving model [6] we did not treat soft gluons properly. Gluons act like transverse excitations or kinks on a string. Since each gluon is connected to two string pieces, it will lose energy to the strings twice as fast as a quark. In any given reference frame, a gluon with energy e will therefore have lost all its energy after a time \(t=e/2\kappa \). What happens then is that a new string region is formed and will give a straight string piece starting from the point where the gluon stops, expanding as if dragged out by the momenta of the partons to which the stopped gluon is colour connected. In general, a string spanned between a quark to an anti-quark via series of gluons \((q_0, g_1, g_2, \ldots , g_{n-1}, {\bar{q}}_n)\) can be treated as a series of string regions, or plaquettes. In these regions, we have the primary plaquettes spanned between the momenta \((p_i,p_{i+1})\) (where the momenta of the gluons is divided by two), corresponding to the original dipoles, but also secondary ones spanned between \((p_i,p_{i+2})\) with space–time vertices shifted by \(p_{i+1}/\kappa \). Similarly we get higher order plaquettes, spanned by \((p_i,p_{i+n})\) with vertices offset by \(\sum _{j=i+1}^{i+n-1}p_j/\kappa \). This is explained in detail in Refs. [16] and [17].
In our updated shoving implementation, we now allow for all such plaquettes. Just as for the primary dipoles, we can for each plaquette look at any other plaquette in another string, go to the corresponding parallel frame, and calculate the transverse force between them there.
The shoving is implemented as discretised pushes with a small (\(\sim 20\) MeV) transverse momentum, \(\delta p_\perp \). In principle, this would correspond to adding a small gluon to a string, but as its energy would be very small it would stop almost immediately (after a time, \(\delta t=\delta p_\perp /2\kappa \)). This would form a new plaquette which will start to spread out with the speed of light in both directions of the string, resulting in a shift of the string in the z directionFootnote 2 with \(\delta _z=c\delta t\). This is illustrated in Fig. 3 for one of the string pieces (the other string will get a push in the opposite z direction in a similar way).
Implementing each new push with a new plaquette would give forbiddingly complicated string configurations,Footnote 3 and instead the transverse momentum of each push, which is localised in the edges of the expanding region (with \(\delta p_\perp /2\) on each side), is transferred directly to the closest primary hadrons after the hadronization.
Note that, when introducing secondary plaquettes, a push propagating along the straight string piece may encounter a corner between two plaquettes and continue propagating in another plaquette. Currently, such situations are only treated approximately, assuming that the push will continue with in the same directions as in the parallel frame where it is produced and the transverse momentum to the primary hadron closest to that direction.
Previously, our implementation only considered the change in momentum resulting from the shoving, but here we also want to study the space–time picture. We note that the two hadrons receiving a transverse-momentum push would be also pushed in space along the z direction in the parallel frame. This is implemented by simply shifting the production vertices assigned by the  string fragmentation (see description in Sect. 3.2 below) by \(\delta z\). In addition, any hadron produced between these two hadrons along the string will be affected by the push and are also shifted by \(\delta z\). As illustrated in the right panel of Fig. 3, the push spreads out as kinks in opposite directions along the string, and the whole string between the kinks is shifted, however, only the kinks themselves carry the transverse momentum of the push. This means that the two hadrons that include the kinks receive a momentum push, while any other hadron formed between the kinks only gets a shift in transverse position.
string fragmentation (see description in Sect. 3.2 below) by \(\delta z\). In addition, any hadron produced between these two hadrons along the string will be affected by the push and are also shifted by \(\delta z\). As illustrated in the right panel of Fig. 3, the push spreads out as kinks in opposite directions along the string, and the whole string between the kinks is shifted, however, only the kinks themselves carry the transverse momentum of the push. This means that the two hadrons that include the kinks receive a momentum push, while any other hadron formed between the kinks only gets a shift in transverse position.
String shoving therefore, affects the primary hadronic vertices directly via their z component in each parallel frame. This is what we account for in this implementation and its effect is shown in Fig. 4. Shoving would have the most effect in the most dense regions in a collision. The correction due to shoving force would “dilute” the distribution of primary hadrons transverse to the beam axis in the lab frame.
To show the effect of the shoving on the position of the primary hadron vertices, we have generated a large sample of \(\text {pp}\) and \(\text {PbPb}\) events at 7 TeV and 2.76 TeV respectively, and looked at the positions of the centrally produced (\(|\eta |<0.5\)) primary hadrons in impact parameter space. In Fig. 4, we show in the top row the resulting distributions with and without shovingFootnote 4 for high-multiplicity \(\text {pp}\) events (with charged multiplicity, \(N_{\text {ch}}\) between 50 and 100 in the central rapidity bin), and in the bottom row the same for high-multiplicity (\(N_{\text {ch}}>500\)) \(\text {PbPb}\) events.
The first thing to note is that without shoving the high multiplicity \(\text {pp}\) events reaches almost as high densities of primary hadrons as the very central \(\text {PbPb}\) ones, which confirms what we already saw in Fig. 2.Footnote 5 With shoving (middle column), we see that the vertices of primary hadrons are more spread out compared to their distribution without shoving (first column). The impact is most apparent for \(\text {pp}\) collisions in the first row, where the peak at (0, 0) is heavily dampened. This is clearly seen in the right-most column, where for the \(|b_y|<0.5\) fm bins, the number density of primary hadrons are shown as a function of \(b_x\) for both with and without shoving. Also for \(\text {PbPb}\) events the hadronic vertices are more spread out with shoving included, but the effect is not as dramatic. This is because the strings in the centre are shoved from all sides, and therefore do not move as much.
3.2 Rope hadronization
In Refs. [7, 8] we presented a new rope hadronization model for HI collisions in Angantyr, based on the parallel frame technique described above. Depending on the transverse separation between two string pieces at the time of hadronization, the partons at the end of the strings combine to form higher colour-multiplets. This would result in a higher effective string tension, following lattice results and as established in our previous works [7, 8, 18]. When the higher colour-multiplet transitions to lower colour-multiplets in a string breaking, the energy from the higher string tension is released. This results in an effective string tension, \(\kappa _{\text {eff}}\), which is higher than in a single string, increasing the possibility to produce strange quarks in the tunnelling mechanism responsible for the breaking. This would give rise to higher number of strange particles as well as baryons in the final state. This \(\kappa _{\text {eff}}\) would, however, also influence the production vertices of primary hadrons in various stages, which we will describe below.
To calculate vertices of primary hadrons in  , the relation between the energy–momentum picture and space–time picture is used. In the Lund model, the equation of motion of a string between a pair of massless quark q and antiquark \({\bar{q}}\), results in a linear relation between space–time and energy–momentum:
, the relation between the energy–momentum picture and space–time picture is used. In the Lund model, the equation of motion of a string between a pair of massless quark q and antiquark \({\bar{q}}\), results in a linear relation between space–time and energy–momentum:
where \(\kappa \) is the string tension. The location of a break-up point on the string can be given by \(v_i=\frac{x_i^+ p^+ + x_i^- p^-}{\kappa }\), where \(x_i^\pm \) are the light-cone fractions and \(p^+\) (\(p^-\)) is the four-momentum of the q (\({\bar{q}}\)). It is to be noted that these equations are not a function of the width of the string from which the hadron is formed. In case of a string with a radius R the uncertainity of a hadronic vertex point will arise in the transverse plane. This effect is accounted for in the vertex calculation using a Gaussian smearing.Footnote 6 We will return to this effect while discussing the effect on \(\kappa _{\text {eff}}\) on production vertices later.
Since a hadron is formed from two adjacent break-ups, the vertex should be a function of each break-up point, say \(v_i\) and \(v_{i+1}\). Since locating a hadronic vertex is not precise due to a hadron’s transverse extent, they are somewhat approximated. These space–time locations of a hadronic vertex in  can therefore be chosen in three different ways. The default definition is the “middle point” in sampling the hadron vertex. This is given by:
can therefore be chosen in three different ways. The default definition is the “middle point” in sampling the hadron vertex. This is given by:
The “early” position is defined as the space–time point where the backward light cones of the partons forming the hadrons cross. The “late” position is where the forward light cones cross:
For the detailed implementation, we refer the reader to Ref. [17].
For the purpose of this paper we have modified the vertex finding in  , to take into account the increased string tension, \(\kappa _{\text {eff}}\), in the rope model. Since \(\kappa _{\text {eff}}\) varies along the string this is done locally for each vertex.Footnote 7 It should be noted that \(\kappa _{\text {eff}}\) also affects the transverse momentum of the of the \(q{\bar{q}}\) pair in the tunnelling mechanism, giving \(\sqrt{\langle k_\perp ^2\rangle } \propto \sqrt{\kappa _{\text {eff}}}\), and this also results in a corresponding scaling of the transverse momenta of the hadrons. This means that the difference between early and late for the transverse coordinates in (4) would effectively be smaller than for the longitudinal ones. In the following we will only use the default middle option in (3).
, to take into account the increased string tension, \(\kappa _{\text {eff}}\), in the rope model. Since \(\kappa _{\text {eff}}\) varies along the string this is done locally for each vertex.Footnote 7 It should be noted that \(\kappa _{\text {eff}}\) also affects the transverse momentum of the of the \(q{\bar{q}}\) pair in the tunnelling mechanism, giving \(\sqrt{\langle k_\perp ^2\rangle } \propto \sqrt{\kappa _{\text {eff}}}\), and this also results in a corresponding scaling of the transverse momenta of the hadrons. This means that the difference between early and late for the transverse coordinates in (4) would effectively be smaller than for the longitudinal ones. In the following we will only use the default middle option in (3).
When we include the modified \(\kappa _{\text {eff}}\) in calculation of the primary hadron production vertices, the impact on the vertices proved to be rather small. In Fig. 5, we show the effects in \(\text {pp}\) collisions at \(\sqrt{s}=7\) TeV, for a slice around \(|b_y|<0.5\) fm in impact parameter space, as a function of \(b_x\). We show two multiplicity bins \(10< \frac{dN_{\text {ch}}}{d\eta } < 20\) (left) and \(50< \frac{dN_{\text {ch}}}{d\eta } < 100\) (right). As seen in the figure, the effect is barely visible for the lower multiplicities due to lower density of strings, but also for the higher multiplicities the effect is small compared to the effects of shoving in Fig. 4.
We have also studied the effect in HI collisions, and there it is even smaller, since the vertex distribution in impact parameter is less peaked than in the \(\text {pp}\) case. Even for the highest multiplicities in \(\text {PbPb}\) collisions at 2.76 TeV, the effect (not shown here) is barely visible, even though the densities of strings is larger than in \(\text {pp}\).
The distribution of vertices for primary hadrons in the rope hadronization model for \(\text {pp}\) collisions with central charged multiplicity, \(10<dN_{\text {ch}}/d\eta |_{\eta =0}<20\) (top), and \(50<dN_{\text {ch}}/d\eta |_{\eta =0}<100\) (bottom). The events were generated at \(\sqrt{s}=7\) TeV, and the distribution of vertex position along the impact parameter vector (\(b_x\)) is shown for a slice with \(|b_y|<0.5\) fm. The blue line includes the effect of \(\kappa _{\text {eff}}\) on the vertex calculation in  , while the red line does not
, while the red line does not
4 Conclusion and outlook
A correct description of primary hadron vertices in the Lund string picture is essential to arrive at more consistent predictions from string interactions in  /Angantyr. This would help us determine the contribution of such non-perturbative QCD effects on the final-state observables both in small and large systems. As already observed in Refs. [6, 8], both shoving and rope hadronization have non-trivial effects on the final-state in dense systems. The effect is dependent on system size and if accounted for correctly can reproduce QGP-like effects. This would present different underlying mechanisms as origins of QGP-like observations in both small and large systems.
/Angantyr. This would help us determine the contribution of such non-perturbative QCD effects on the final-state observables both in small and large systems. As already observed in Refs. [6, 8], both shoving and rope hadronization have non-trivial effects on the final-state in dense systems. The effect is dependent on system size and if accounted for correctly can reproduce QGP-like effects. This would present different underlying mechanisms as origins of QGP-like observations in both small and large systems.
We have shown here that in the Angantyr model, the initial occupancy of colour fields from the MPIs is not large. As the fields grow transversely they start shoving, giving rise to flow, and when they finally hadronize the increased \(\kappa _{\text {eff}}\) gives rise to strangeness and baryon enhancement. One should note that the rope hadronization and string shoving models used in this publication is rather distinct to CGC-Glasma picture (see e.g. Refs. [19,20,21]). While the Glasma initially contains string-like features, it is assumed to be unstable and will rapidly turn into a QGP. In our picture we instead assume that the strings survive the dense environment and form ropes which then fragments.
In this paper, we have shown that string shoving reduces the string density, resulting in a smaller overlap between the stings forming ropes. This reduces the effective string tension, which is used during rope hadronization. That will in turn cause lower yield of strangeness in dense environments. This would dampen the linear rise in the strangeness yields for \(AA\) using only rope effects as observed before [8]. Whether it will produce the saturation behaviour as observed in data remains to be seen.
We have also observed that the increase of \(\kappa _{\text {eff}}\) in rope hadronization, mainly affects the flavour of the hadrons and its influence on the primary hadron vertices are small, especially when compared to the effects of string shoving. While there are still some caveats as discussed in the Sect. 1, such as the strings not being pushed in space–time before hadronization, we are working towards a proper combination of both string shoving and ropes. This would enable the string shoving to properly affect the space–time overlaps between string, so that the dilution of strings from the shoving can directly affect the \(\kappa _{\text {eff}}\) calculation in the rope hadronization.
The primary hadron vertices are the main input to the hadronic rescattering model in  , hence, one could expect significant effects from the spreading of the vertices due to shoving. Also, the rescattering has effects on the flavour composition of the final state, and it is reasonable to assume that there would be some interplay with rope model.
, hence, one could expect significant effects from the spreading of the vertices due to shoving. Also, the rescattering has effects on the flavour composition of the final state, and it is reasonable to assume that there would be some interplay with rope model.
String shoving and hadronic rescattering together could provide an enhanced final-state collectivity in both small and large systems. Impact from hadronic rescattering in Angantyr ideally would be additive to that from string shoving, and they would build on each other. This non-trivial effect needs proper correction to the vertices of the primary hadrons, which is the work done in this paper. By consistently combining shoving, ropes and rescattering, we hope to achieve a consistent and complete picture for final-state collectivity in all collision systems.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study, with no produced experimental data.]
Notes
In the parallel frame, the two stings pieces lie in planes parallel to the \(x-y\) plane, moving in opposite directions along the z axis (see Ref. [6]).
The complexity of our algorithm is already very high, requiring the construction of several millions parallel frames in a single central \(AA\) event.
All basic
 /Angantyr parameters have their default values, and the shoving model used a string radius of \(R=0.5\) fm and a shoving strength of \(g=0.25\).
/Angantyr parameters have their default values, and the shoving model used a string radius of \(R=0.5\) fm and a shoving strength of \(g=0.25\).Note that the number of primary hadrons from a string is roughly one per unit rapidity.
In
 HadronVertex:xySmear controls the gaussian smearing and has a default value of 0.5 fm, which is the same value for R.
HadronVertex:xySmear controls the gaussian smearing and has a default value of 0.5 fm, which is the same value for R.It should be noted that \(\kappa _{\text {eff}}\) is only approximately localised along the string in our current implementation, and also the effects on the vertices are somewhat approximate.
References
C. Bierlich, G. Gustafson, L. Lönnblad, H. Shah, The Angantyr model for heavy-ion collisions in PYTHIA8. JHEP 10, 134 (2018). arXiv:1806.10820
B. Andersson, G. Gustafson, G. Ingelman, T. Sjöstrand, Parton fragmentation and string dynamics. Phys. Rep. 97, 31–145 (1983)
ALICE Collaboration, S. Acharya et. al., Centrality and pseudorapidity dependence of the charged-particle multiplicity density in Xe–Xe collisions at \(\sqrt{s_{{\rm NN}}}\) =5.44 TeV. Phys. Lett. B 790, 35–48 (2019). arXiv:1805.04432
C. Bierlich, G. Gustafson, L. Lönnblad, A. Tarasov, Effects of overlapping strings in pp collisions. JHEP 03, 148 (2015). arXiv:1412.6259
C. Bierlich, G. Gustafson, L. Lönnblad, Collectivity without plasma in hadronic collisions. Phys. Lett. B 779, 58–63 (2018). arXiv:1710.09725
C. Bierlich, S. Chakraborty, G. Gustafson, L. Lönnblad, Setting the string shoving picture in a new frame. JHEP 03, 270 (2021). arXiv:2010.07595
C. Bierlich, S. Chakraborty, G. Gustafson, L. Lönnblad, Jet modifications from colour rope formation in dense systems of non-parallel strings. arXiv:2202.12783
C. Bierlich, S. Chakraborty, G. Gustafson, L. Lönnblad, Strangeness enhancement across collision systems without a plasma. arXiv:2205.11170
T. Sjöstrand, M. Utheim, A framework for hadronic rescattering in pp collisions. Eur. Phys. J. C 80(10), 907 (2020). arXiv:2005.05658
C. Bierlich, T. Sjöstrand, M. Utheim, Hadronic rescattering in pA and AA collisions. Eur. Phys. J. A 57(7), 227 (2021). arXiv:2103.09665
R.J. Glauber, Cross-sections in deuterium at high-energies. Phys. Rev. 100, 242–248 (1955)
M.L. Miller, K. Reygers, S.J. Sanders, P. Steinberg, Glauber modeling in high energy nuclear collisions. Annu. Rev. Nucl. Part. Sci. 57, 205–243 (2007). arXiv:nucl-ex/0701025
V.N. Gribov, Glauber corrections and the interaction between high-energy hadrons and nuclei. Sov. Phys. JETP 29, 483–487 (1969)
A. Bialas, M. Bleszynski, W. Czyz, Multiplicity distributions in nucleus–nucleus collisions at high-energies. Nucl. Phys. B 111, 461–476 (1976)
T. Sjöstrand, M. van Zijl, A multiple interaction model for the event structure in hadron collisions. Phys. Rev. D 36, 2019 (1987)
T. Sjöstrand, Jet fragmentation of nearby partons. Nucl. Phys. B 248, 469–502 (1984)
S. Ferreres-Solé, T. Sjöstrand, The space–time structure of hadronization in the Lund model. Eur. Phys. J. C 78(11), 983 (2018). arXiv:1808.04619
G.S. Bali, Casimir scaling of SU(3) static potentials. Phys. Rev. D 62, 114503 (2000). arXiv:hep-lat/0006022
T. Lappi, L. McLerran, Some features of the glasma. Nucl. Phys. A 772, 200–212 (2006). arXiv:hep-ph/0602189
R. Venugopalan, From glasma to quark gluon plasma in heavy ion collisions. J. Phys. G 35, 104003 (2008). arXiv:0806.1356
F. Gelis, Color glass condensate and glasma. Int. J. Mod. Phys. A 28, 1330001 (2013). arXiv:1211.3327
Acknowledgements
We thank Gösta Gustafson and Christian Bierlich for interesting discussions and important input to this work. This work was funded in part by the Knut and Alice Wallenberg foundation, contract number 2017.0036, Swedish Research Council, contracts number 2016-03291, 2016-05996 and 2017-0034, in part by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement No 668679, and in part by the MCnetITN3 H2020 Marie Curie Initial Training Network, contract 722104.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Chakraborty, S., Lönnblad, L. Impact of string interactions on the space–time evolution of hadronic vertices. Eur. Phys. J. C 83, 464 (2023). https://doi.org/10.1140/epjc/s10052-023-11652-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-11652-2








 /Angantyr parameters have their default values, and the shoving model used a string radius of
/Angantyr parameters have their default values, and the shoving model used a string radius of 