1 Introduction

The strangeonium \((s{\bar{s}})\) states are the focus of research because they are the bridge between light and heavy quarks [1], and can provide relevant non-perturbative QCD information [2] in the low-energy region where the effective theory of heavy quarks is not suitable. Under the framework of the relativistic quark model [3], the \(s{\bar{s}}\) states are expected to have a spectroscopy similar to that of heavy quarkonia. And their decay is investigated in detail by the theoretical model \(^3P_0\) of the decay of light mesons [4]. However, the current \(s{\bar{s}}\) spectrum is somewhat deficient [2, 5], and only a few experimentally measured vector mesons are broadly accepted as \(s{\bar{s}}\) states: \(\phi (1020)\), \(\phi (1680)\), \(h_{1}(1415)\), \(f^{'}_{2}(1525)\) and \(\phi _{3}(1850)\). This is because the proportion of \(s{\bar{s}}\) states produced among hadrons is small, and decay width exists, which leads to the poor results in strangeonium experiments.

In the particle data group (PDG), \(\phi (1680)\), like \(\phi (1020)\), is listed as a vector state with quantum number \(I^{G}(J^{PC})=0^{-}(1^{--})\). The mass is suggested to be \(1680\pm 20\) MeV and the width is \(150\pm 50\) MeV. The evidence of \(\phi (1680)\) was initially understood in \(p{\bar{p}}\) annihilation experiment [6] and Kp experiment [7]. Then in 1971, the \(m(\pi ^{+}\pi ^{-}\pi ^{0})\) spectrum analysis of \(\pi ^{+}d\rightarrow p p\pi ^{+}\pi ^{-}\pi ^{0}\) revealed the existence of a meson \(\phi (1680)\) at 1.68 GeV mass region [8]. Further research was performed in 1981, the \(\phi (1680)\) was first measured in the \(e^{+} e^{-} \rightarrow K_S K^{\pm } \pi ^{\mp }\) reaction [9] at the energy range 1.4–2.18 GeV, and the fitted mass (\(1.667\pm 0.012\) GeV) and width (\(102\pm 36\) GeV) can be well explained in the quark model. In subsequent analysis, the ratio of \(\phi (1680)\) coupling to \(K^{+}K^{-}\) was found to be very small [10,11,12]. In addition, the various decay properties were predicted in Ref. [1], the decay of \(\phi (1680)\) was found to be dominated by the \(KK^{*}(892)\) mode in their calculations and predicted the partial width ratio,

$$\begin{aligned} \frac{\Gamma (KK)}{\Gamma (KK^{*})}\approx 0.06, \end{aligned}$$
(1)

which was close to \(0.07\pm 0.01\) measured by DMI [9]. At the same time, the ratio of \(\Gamma (\eta \phi )\) and \(\Gamma (KK^{*})\) was predicted as,

$$\begin{aligned} R_{\eta \phi /K K^{*}}=\frac{\Gamma (\eta \phi )}{\Gamma (KK^{*})} \approx 0.20, \end{aligned}$$
(2)

agreeing with the result predicted in Refs. [4, 13, 14]. However, these results is about twice smaller than the 0.37 measured from the BaBar Collaboration [15]. Therefore, the ratio needs to be more accurately measured in future experiments. To clarify the relevant properties of \(\phi (1680)\), we expect to observe the state from photoproduction experiments. The reaction of \(\gamma p\rightarrow K^{+}K^{-}\) shows a clear mass structure with a mass of \(M=1753\pm 3\) MeV/c\(^{2}\) and a width of \(\Gamma =122\pm 63\) MeV. And found that the difference in the mass may be due to interference from other mesons, but it does not rule out the possibility that the 1.75 GeV/c\(^{2}\) is a new state [16]. However, although there has been much research on \(\phi (1680)\) states, the study of \(\gamma p\rightarrow \phi (1680) p\) channel is still relatively inadequate. Therefore, the photoproduction data must be systematically measured through experimental to study the physical properties of the \(\phi (1680)\), especially in the \(\gamma p\rightarrow \phi (1680)p\) channel.

The total cross section and differential cross section of \(\gamma p\rightarrow \phi p\) at the near-threshold were predicted with the two gluon exchange model and the pomeron model [17], which were in good agreement with the experimental data. \(\phi (1680)\) has the same structure as \(\phi (1020)\), so it is reasonable to predict the cross section of \(\gamma p\rightarrow \phi (1680)p\) with the identical models and parameters in this work. In addition, under the definition of the vector meson dominance assumption (VMD), the scattering length of \(\phi (1680)\)-p interaction at the-near threshold is studied as R changes. Here R is proportional to W, which is the ratio of the meson momentum \(\textbf{p}_3\) to the photon momentum \(\textbf{p}_1\).

Collisions between hadrons–hadrons are usually represented as ultraperipheral collisions (UPCs) [18,19,20,21]. When the impact parameter between the two nuclei is larger than the sum of the radii of the two nuclei, the strong interaction between the two nuclei is suppressed. But this effect cannot be ignored because the electromagnetic interaction is a long-range force. In addition, the electron–proton collisions in the Electron-ions collider (EIC) [22,23,24,25] will be an essential reaction in studying the nucleon structure. The major difference between an EICs and a UPCs is that the photons emitted by the electron beam of an EIC are very virtual. Therefore, EICs can be used to study the photoproduction in the large \(Q^2\) range. The STARlight [26] and eSTARlight [27, 28] are two existing and critical Monte Carlo algorithm programs. They can be used to study vector meson and exotic states production at EICs and UPCs [26, 27]. At present, using these two programs can effectively study the XYZ state [29], the bottomonium-like \(Z_b\) [30], the charged final states \(a_2^+(1320)\), and the hidden pentaquark state [31]. Therefore, in this work, the two programs are used to simulate the production of vector meson \(\phi (1680)\). In order to exhibit more distinctly the variation in the relevant kinematics, we set up about 500,000 events and simulated the different consequences in the two \(Q^2\) intervals. This will require higher luminosity EICs and UPCs to satisfy the requirements of future experiments.

A brief outline of the paper is organized as follows. The expression of the scattering length, the two gluon exchange and pomeron models are described in Sect. 2, along with a detailed discussion of vector meson production at EICs and UPCs. The cross section of \(\phi (1680)\), scattering length of \(\phi (1680)\)-p and relevant results are presented in Sect. 3. A simple summary and discussion is given in Sect. 4.

2 Formalism

2.1 Scattering length

The absolute value of the scattering length reflects the coupling strength between the vector meson-proton (V–p) interaction. Under the definition of the vector meson dominance assumption (VMD), the relation between scattering length \(|\alpha _{Vp}|\) and the differential cross section \(d \sigma /d t\) of vector meson photoproduction is [32, 33],

$$\begin{aligned} \left| \alpha _{V p}\right| =\frac{\left| {\textbf{p}}_3\right| g_V}{R\pi } \sqrt{\frac{1}{\alpha _{e m}} \frac{d \sigma ^{\gamma p \rightarrow V p}}{d t}(W_{thr},t_{thr})}, \end{aligned}$$
(3)

with

$$\begin{aligned}{} & {} \left| {\textbf{p}}_1\right| =\frac{1}{2 W} \sqrt{W^4-2\left( m_1^2+m_2^2\right) W^2+\left( m_1^2-m_2^2\right) ^2}\nonumber \\{} & {} \left| {\textbf{p}}_3\right| =\frac{1}{2 W} \sqrt{W^4-2\left( m_3^2+m_4^2\right) W^2+\left( m_3^2-m_4^2\right) ^2} \end{aligned}$$
(4)

where \(R=|\textbf{p}_3|/|\textbf{p}_1|\) represents the ratio of meson momentum \(|\textbf{p}_3|\) to photon momentum \(|\textbf{p}_1|\) and \(g_{v}\) is the VMD coupling constant [34, 35],

$$\begin{aligned} g_{V}=\sqrt{\frac{\pi \alpha _{em}^{2}m_{V}}{3\Gamma _{e^{+}e^{-}}}}, \end{aligned}$$
(5)

where \(m_{V}\) is the mass of \(\phi (1680)\) meson and the lepton decay width \(\Gamma _{e^{+}e^{-}}\) is estimated to be 0.42 keV [36]. In the model definition, the total cross section of vector meson photoproduction is obtained by integrating the differential cross section from \(t_{min}\) to \(t_{max}\),

$$\begin{aligned} \sigma ^{\gamma p\rightarrow V p}=\int ^{t_{max}}_{t_{min}}\frac{d \sigma ^{\gamma p\rightarrow V p}}{d t}dt, \end{aligned}$$
(6)

where \(t_{min}(t_{max})\) is [37, 38],

$$\begin{aligned} t_{min}(t_{max})=\left( \frac{m_{1}^2-m_{3}^2-m_{2}^2+m_{4}^2}{2W}\right) ^{2}-(p_{1cm}\mp p_{3cm})^{2}\nonumber \\ \end{aligned}$$
(7)

with \(p_{icm}=\sqrt{E_{icm}^{2}-m_{i}^{2}}\) \((i=1,3),\) \(E_{1cm}=(W^{2}+m_{1}^{2}-m_{2}^{2})/(2W)\) and \(E_{3cm}=(W^{2}+m_{3}^{2}-m_{4}^{2})/(2W)\).

When the centre of mass energy W approaches the threshold, \(t_{min}\rightarrow t_{max}\), then the Eq. (6) becomes [33],

$$\begin{aligned} \sigma ^{\gamma p\rightarrow V p}(W_{thr})=4|\textbf{p}_1||\textbf{p}_3|\frac{d \sigma ^{\gamma p\rightarrow V p}}{d t}(W_{thr},t_{thr}), \end{aligned}$$
(8)

where the \(4|\textbf{p}_1||\textbf{p}_3|=\Delta t=|t_{max}-t_{min}|\) and \(t_{thr}=-m_{V}^{2}m_{p}/(m_{V}+m_{p})\). Then, by combining Eqs. (3) and (8), the \(|\alpha _{Vp}|\) is calculated by the total cross section of vector meson photoproduction,

$$\begin{aligned} |\alpha _{V p}|=\frac{g_{V}}{2\pi }\sqrt{\frac{\sigma ^{\gamma p\rightarrow V p}}{R\alpha _{em}}}, \end{aligned}$$
(9)

where the \(\alpha _{em}\) is the fine coupling constant

2.2 Pomeron model

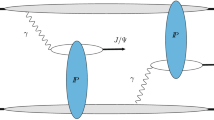
The pomeron-quark interaction is flavour independence in the pomeron model [39], which provides a unique way to describe vector meson photoproduction. The fundamental interactions are described in Fig. 1. In the model, the differential cross section of vector meson is expressed as [39, 40],

$$\begin{aligned} \frac{{\textrm{d}} \sigma }{{\textrm{d}} t}= & {} \frac{81 m_{V}^{3} \beta ^{4} \mu _{0}^{4} \Gamma _{{\textrm{e}}^{+} {\textrm{e}}^{-}}}{\pi \alpha _{em} }\left( \frac{s}{s_{0}}\right) ^{2\alpha (t)-2}\nonumber \\{} & {} \times \left( \frac{F(t)}{\left( Q^{2}+m_{V}^{2}-t\right) \left( Q^{2}+2 \mu _{0}^{2}+m_{V}^{2}-t\right) }\right) ^{2}.\nonumber \\ \end{aligned}$$
(10)

When \(Q^{2}=0\), the formula represents the vector meson photoproduction, otherwise denotes vector meson electroproduction. The relevant coupling constant \(\beta =2\) GeV\(^{-1}\) and \(\mu _{0}=1.1\) Gev\(^{2}\). In Eq. (10), \(\alpha (t)=1.08+0.25t\) is the pomeron Regge trajectory [41], and \(s_{0}=4\) GeV\(^{2}\). F(t) is the isoscalar form factor of the proton,

$$\begin{aligned} F(t)=\frac{4m_{p}^{2}-2.8t}{(4m_{p}^{2}-t)(1-t/0.7)^{2}} \end{aligned}$$
(11)

where \(m_{p}=0.938\) GeV is the mass of proton.

Fig. 1
figure 1

The Feynman diagrams of the pomeron model for the vector mesons photoproduction

Full size image

2.3 Two gluon exchange model

The process of the two gluon exchange model is shown in Fig. 2. The photon is split into \(q{\bar{q}}\), which scatters the initial proton through the exchange of two gluons and finally forms the vector meson. At the lowest order perturbation QCD, the differential cross section of vector meson photoproduction based on the two gluon exchange model is [40],

$$\begin{aligned} \frac{d \sigma }{d t}=\frac{\pi ^{3} \Gamma _{e^{+} e^{-}} \alpha _{s}}{6 \alpha m_{q}^{5}}\left[ x g\left( x, m_{V}^{2}\right) \right] ^{2} \exp \left( b_{0} t\right) . \end{aligned}$$
(12)

Since the vector meson \(\phi (1680)\) has the identical \(s{\bar{s}}\) structure as \(\phi (1020)\), the quark mass of the component is selected as \(m_{q}=0.486\) GeV, and the strong coupling constant \(\alpha _{s}\) is set as 0.701. \(xg(x,m_{V}^{2})\) is the gluon distribution function, because the conventional gluon distribution functions such as the CTEQ6M [42], GRV98 [43], NNPDF [44] and CJ15 [45, 46] cannot effectively interpret the photoproduction data of vector mesons at the near-threshold. Therefore, a parameterized gluon distribution function is introduced as \(xg(x,m_{V}^{2})=A_{0}x^{A_{1}}(1-x)^{A_{2}}\) [37, 47]. The \(A_{0}\), \(A_{1}\), \(A_{2}\), and the slope \(b_{0}\) and are free parameters obtained by fitting experimental data. The total cross section is expressed by integrating Eq. (12) from \(t_{min}\) to \(t_{max}\),

$$\begin{aligned} \sigma (W)=\int _{t_{min}}^{t_{max}}\frac{d \sigma }{d t}d t. \end{aligned}$$
(13)
Fig. 2
figure 2

The Feynman diagrams of the two gluon exchange model for vector mesons photoproduction

Full size image

2.4 The production of vector mesons at EICs and UPCs

For e–p scattering at EICs, the process of vector mesons production by exchanging virtual photons between hadrons and electrons is the vector meson electroproduction, which is closely connected to vector mesons photoproduction. The electroproduction cross section of mesons on a target proton is derived from Refs. [27, 48],

$$\begin{aligned} \sigma (e p \rightarrow e p V){} & {} =\int \frac{d W}{W} \int d k \int d Q^2 \frac{d^2 N_\gamma }{d k d Q^2} \sigma ^{\gamma ^* p \rightarrow V p}\nonumber \\{} & {} \quad \times \left( W, Q^2\right) . \end{aligned}$$
(14)

In the rest target frame, the momentum of the virtual photon emitted from the electron beam is denoted by k. W is the center of mass energy and \(\sigma _{\gamma ^{*}p\rightarrow V p}(W,Q^{2})\) is the cross section of \(\gamma ^{*}p\rightarrow V p\),

$$\begin{aligned} \sigma ^{\gamma ^* p \rightarrow V p}\left( W, Q^2\right){} & {} =\sigma _{\gamma p \rightarrow V p}\left( W, Q^2=0\right) \nonumber \\{} & {} \quad \times \left( \frac{M_V^2}{M_V^2+Q^2}\right) ^\eta , \end{aligned}$$
(15)

where \(\sigma ^{\gamma p \rightarrow V p}\) is the cross section of meson photoproduction. The \(\eta =c_{1}+c_{2}(Q^{2}+m_{V}^{2})\) is the variable which controls the flux, where \(c_{1}=2.15\pm 0.17\) and \(c_{2}=0.0074\pm 0.0046\) GeV\(^{2}\) are two constants determined by HERA data [27]. The photo flux \(d^{2}N_{\gamma }/dkdQ^{2}\) is given as [27, 49],

$$\begin{aligned} \frac{d^2 N_\gamma }{d k d Q^2}=\frac{\alpha }{\pi k Q^2}\left[ 1-\frac{k}{E e}+\frac{k^2}{2 E_e^2}-\left( 1-\frac{k}{E e}\right) \left| \frac{Q_{\min }^2}{Q^2}\right| \right] ,\nonumber \\ \end{aligned}$$
(16)

where \(Q_{min}^{2}=m_{e}^{2}k^{2}/(E_{e}^{2}-E_{e}k)\) with \(E_{e}\) represents the electron energy. The electron energy loss determines the maximum \(Q^{2}\),

$$\begin{aligned} Q_{max}^{2}=4E_{e}(E_{e}-k). \end{aligned}$$
(17)

In the simulation of accelerator experiments, we can set the known electron beam energy \(E_{e}\) and photon virtuality \(Q^{2}\) to calculate the total cross section of electron–proton (e–p) scattering at the near-threshold. In the laboratory frame, the ratio of photon energy K and \(|t_{min}|\) is the rapidity of the final state [50],

$$\begin{aligned} y=\frac{1}{2}\ln {\frac{k}{\sqrt{|t_{min}|}}}=\ln {\frac{2 k}{m_{V}}}. \end{aligned}$$
(18)

In the target frame, the relationship between photon energy and rapidity is \(k=2\gamma _{1}m_{V}/(2\exp {(y)})\), where the \(\gamma _{1}\) represents the Lorentz boost of the ion. Here, the eSTARlight program is used to simulate the total cross-section electroproduction by e–p collision.

For UPCs, Eq. (14) can be rewritten as [26],

$$\begin{aligned} \sigma (p A \rightarrow p A V)=\int dk \frac{d N_{\gamma }(k)}{d k} \sigma ^{\gamma p \rightarrow V p}\left( W, Q^2\right) , \end{aligned}$$
(19)

where \(dN_{\gamma }/dk\) is similar to \(d^2N_{\gamma }/ dk dQ^2\) in the Eq. (14), representing the photon flux of ions [18] and A is heavy ion Au or Pb. Here, we exclusively consider the contribution of \(\gamma p\) in the photon flux emitted by heavy ions. This is because the photon flux is directly proportional to the ion charge, and the photon flux of heavy ions is superior to that of protons [18, 21]. We can simulate the production of vector mesons in proton and heavy ion reactions at the UPCs with STARlight [26].

3 Results

3.1 The reaction of \(\gamma p\rightarrow \phi (1680)p\)

In our previous work [17], the cross section of \(\phi (1020)\) photoproduction was reproduced with the two gluon exchange model and the pomeron model, which was in good agreement with the experimental data. Relevant parameters for the two models are listed in Table 1. Through this set of parameters, the total cross section of \(\phi (1680)\) photoproduction predicted by the two models are shown in Figs. 3 and 4 shows the differential cross section at the center of mass energy \(W\in [2.62,3.02]\) GeV, where \(\Delta W=0.08\) GeV. It can be observed that the cross sections of \(\phi (1680)\) predicted by the two models are adjacent, and the cross section by the pomeron model is smaller than that based on the two gluon exchange model. As can be seen from Fig. 4, the two models exhibit different slopes. The differential cross section obtained by the pomeron model decreases faster with t than the two gluon exchange model, which is similar to the cross section of \(\phi (1020)\) [17]. In addition, it can be found that the total cross section predicted by the theoretical model exceeds 80 nb at \(W=4\) GeV, which indicates that the JLab [51] and CLAS12 [52] laboratories can be carried out for relevant photoproduction experiments.

Table 1 The relevant parameters for the two gluon exchange model and pomeron model
Full size table
Fig. 3
figure 3

The total cross sections of \(\phi (1680)\) photoproduction predicted by the two gluon exchange model (the blue line) and the pomeron model (the magenta dashed-line)

Full size image
Fig. 4
figure 4

The differential cross sections of \(\phi (1680)\) photoproduction as a function of \(-t\) at \(W\in [2.62,3.02]\) GeV, \(\Delta W=0.08\) GeV. Here, the notations are the same as in Fig. 3

Full size image

The variation of scattering length \(|\alpha _{\phi (1680) p}|\) can be effectively observed from the differential cross section. With Eq. (3), the \(|\alpha _{\phi (1680) p}|\) as a function of R based on the differential cross sections predicted by the two models is shown in Fig. 5. Here, the R interval is chosen to be [0, 0.63]. The average scattering length is calculated as \(0.075\pm 0.010\) fm from the two gluon exchange model and 0.047 fm by the pomeron model. There exist some distinctions in consequences between the two models. The \(|\alpha _{\phi (1680) p}|\) obtained based on the pomeron model is smaller than that based on the two gluon exchange model, which can be unambiguously understood from the behaviour of the differential cross section in Fig. 4. In addition, the slope of the differential cross section based on the pomeron is relatively large, resulting in \(d \sigma / d t |_{t=t_{thr}}\) for the pomeron model being less than that for the two gluon exchange model.

Fig. 5
figure 5

The \(|\alpha _{\phi (1680)p}|\) as function of R based on the differential cross sections. Here, the notations are the same as in Fig. 3

Full size image

Since the total cross section of \(\phi (1680)\) predicted by the two models is adjacent at the near-threshold, the \(|\alpha _{\phi (1680) p}|\) obtained does not differ significantly. As shown in Fig. 6, the \(|\alpha _{\phi (1680)p}|\) based on the two models shows an upward trend with R, but the \(|\alpha _{\phi (1680)p}|\) obtained from the two gluon exchange model is more prominent, the average scattering length is \(0.084\pm 0.010\) fm and 0.071 fm, corresponding to the two gluon exchange model and the pomeron model, respectively. Now, revisiting the \(|\alpha _{\phi (1680)p}|\) obtained above, summarized in Table 2. The scattering length \(|\alpha _{\phi (1680)p}|\) calculated based on the total cross section is larger than that derived by the differential cross section. In addition, the \(|\alpha _{\phi (1680)p}|\) calculated by the total and differential cross section of the two gluon model almost coincide with each other when considering the error. In contrast, the consequence derived by the pomeron model are quite different. Moreover, the result obtained by the two gluon exchange model are generally higher than those received by the pomeron model. However, we still require to consider all the results of the two models. This is because the free parameters of the pomeron model are small, which will cause small uncertainty factors. Therefore, considering all the results, the root mean square (RMS) is calculated as \(0.07\pm 0.01\) fm.

Fig. 6
figure 6

The \(|\alpha _{\phi (1680)p}|\) as function of R based on the total cross sections. Here, the notations are the same as in Fig. 3

Full size image
Table 2 Scattering length of \(\phi (1680)\)-p estimated from the differential cross section \(d \sigma /d t\) and total cross section \(\sigma \) based on the two gluon exchange model and pomeron data. The RMS is calculated as \(0.07\pm 0.01\) fm
Full size table
Fig. 7
figure 7

The \(|\alpha _{Vp}|\) as function of \(\exp {(1/m_{V})}\). The \(|\alpha _{\phi (1680)p}|=0.07\pm 0.01\) fm of this work is represented by the magenta triangle. The black diamonds and purple square are from our previous work [53,54,55], the burgundy circle is from the work of Igor I. Strakovsky [35, 56, 57] and the cyan pentagram is from LEPS laboratory [58]

Full size image

In our further discussion, one finds that the lepton decay width \(\Gamma _{e^{+}e^{-}}\) does not affect the value of scattering length of \(\phi (1680)\)-p based on the two gluon exchange model and the pomeron model. This is because both models contain \(\Gamma _{e^{+}e^{-}}\) and are located on the molecule. According to the relationship between the scattering length and the cross section established by the VMD model, \(\Gamma _{e^{+}e^{-}}\) is just in the denominator, so the \(\Gamma _{e^{+}e^{-}}\) cancel each other out in the calculation process. However, because lepton decay width is a critical factor in determining the specific size of the cross section of \(\phi (1680)\) photoproduction based on the two models, it is necessary to measure \(\Gamma _{e^{+}e^{-}}\) more accurately in future experiments.

Figure 7 shows the scattering lengths of different vector mesons \(|\alpha _{V p}|\) calculated with the VMD model. The \(|\alpha _{\phi (1020)p}|=0.10\pm 0.01\) fm (the purple square) is taken from our previous work [53], which is very adjacent to the \(|\alpha _{\phi (1680)p}|\) with a difference of only 0.03 fm. However, \(|\alpha _{\phi (1680)p}|\) deviates from the main line, which is inconsistent with the scattering length of other vector mesons-proton interactions.

3.2 The prediction for \(\phi (1680)\) production at EICs and UPCs

The rate of electroproduction is known to be a few percent of that of photoproduction, the first consideration is to use the eSTARlight code [27, 28] to simulate e-p collisions at EICs. Table 3 displays the total cross section at four EICs at the 0.10 GeV\(^2<Q^2<1.00\) GeV\(^2\), and Table 4 lists the results at 1.00 GeV\(^2<Q^2<5.00\) GeV\(^2\). Obviously, the total cross section produced by high-energy EICs is larger than that produced by low-energy EICs, which means that the production of \(\phi (1680)\) is more likely to be measured from high-energy facilities. In addition, in low-energy devices such as EicC [23], there are at least 300 million events, so the production of \(\phi (1680)\) also has opportunity to be observed at low energy.

Table 3 The total cross sections of \(ep\rightarrow e p \phi (1680)\) and event rates in e–p scattering at \(0.10~\text {GeV}^2<Q^2<1.0~\text {GeV}^2\) at eRHIC [22], EicC [23], JLEIC [24], LHeC [25]
Full size table
Table 4 The total cross sections of \(ep\rightarrow e p \phi (1680)\) and event rates in e–p scattering at \(1.0~\text {GeV}^2<Q^2<5.0~\text {GeV}^2\) at eRHIC [22], EicC [23], JLEIC [24], LHeC [25]
Full size table
Fig. 8
figure 8

The rapidity distribution of \(\phi (1680)\) in EicC (a), eRHIC (b), JLEIC (c) and LHeC (d) at 0.10 GeV\(^2\) \(<Q^2<1.00\) GeV\(^2\)

Full size image
Fig. 9
figure 9

The rapidity distribution of \(\phi (1680)\) at EICs at \(1.00~\text {GeV}^2<Q^2<5.00~\text {GeV}^2\)

Full size image

Figure 8 shows the rapidity distribution of \(e p\rightarrow e p \phi (1680)\) in EICs obtained at \(0.10~\text {GeV}^2<Q^2<1.00~\text {GeV}^2\). And Fig. 9 illustrates the result at \(1.00~\text {GeV}^2<Q^2<5.00~\text {GeV}^2\). As expected, the higher the energy of the electron and proton beam emitted by the collider, the wider the rapidity distribution. This phenomenon is similar to the predicted change in the size trend of the total cross-section of \(\phi (1680)\) electroproduction. Further, the eSTARlight code [27, 28] is used to predict the mass distribution of \(\phi (1680)\), as shown in the Fig. 10. And the variation interval and mass width can be witnessed. Here, only the result predicted at the EicC [23] is exhibited because the trends in the mass distribution produced by the different collider predictions almost overlap.

Fig. 10
figure 10

The mass distribution of \(\phi (1680)\) is simulated at EicC [23] by using eSTARlight code [27, 28]

Full size image

For a more detailed exploration of observations, we require a detector with appropriate capabilities in the experimental aspect of the forward region. For example, the pseudo-rapidity of the final meson is more widely distributed than its own photoproduction rapidity. And reggeon exchange is easier to explore EICs with moderate energy. So a high-energy collider like the LHeC would be difficult to achieve these goals. Therefore, this should be taken very carefully for \(\phi (1680)\) and other vector mesons investigations.

Table 5 Beam energy, production total cross section \(\sigma \) and event for RHIC [20] and LHC [21]
Full size table

For UPCs, the beam energies emitted and the calculation results are listed in Table 5 and Fig. 11 shows the rapidity distribution of \(\phi (1680)\) predicted by the STARlight [26] program. For LHC [21] with high energy, the rapidity distribution is relatively wide. For RHIC [20], the rapidity distribution is mostly concentrated in the middle part, and the events generated are sufficient. Moreover, the cross sections of production are enormous, and the rates are over 2 billion. These phenomena indicate that the \(\phi (1680)\) may be detected by the LHC and RHIC. Investigating p–A scattering in UPCs can quickly measure accurate data of the cross sections of \(\phi (1680)\) production. This may deliver a crucial procedure for further studying the physical properties of \(\phi (1680)\).

Fig. 11
figure 11

The rapidity distribution of \(\phi (1680)\) at eRHIC (top) and LHC (bottom)

Full size image

4 Conclusion

In this work, based on the photoproduction of \(\phi (1020)\) [17], we predict the total and differential cross sections of \(\phi (1680)\) photoproduction at the near-threshold by the two gluon exchange model and the pomeron model. The predicted cross section size is about 1/5 of \(\phi (1020)\). Further, under the guidance of VMD model, the RMS of scattering length of \(\phi (1680)\)-p interaction is calculated as \(|\alpha _{\phi (1680)p}|=0.07\pm 0.01\) fm. This result deviates from the \(\alpha _{V p} \propto \exp {(1/m_{V})}\), which is a little bit different than what we concluded before [53]. Considering that \(\phi (1680)\) is the first excited state of \(\phi (1020)\) and both are \(s{\bar{s}}\) state structure, it is reasonable that the scattering length is close.

Furthermore, we use two existing programs to calculate the total production cross section, event rates and rapidity distribution of \(\phi (1680)\) at four EICs and two UPCs. For the e–p scattering at EICs, the production rates are predicted to exceed 100 million events per year at different \(Q^2\) intervals. At such a production rate, it is possible to observe a wide range of \(W^2\) and \(Q^2\) electroproduction in an acceptable detector. Meanwhile, the p–A scattering at UPCs also have opportunities to detect the production of \(\phi (1680)\). This is an excellent chance for future research on the properties of this state.

In order to comprehensively study the physical characteristics of \(\phi (1680)\), a considerable number of the cross sectional data of \(\gamma p\rightarrow \phi (1680)p\) are required, and the most meaningful data is the result near the threshold. Future United States EIC [22] and the EicC [23] will provide a significant opportunity to probe these cross sections. In addition, the GlueX laboratory [51] at Jefferson Lab intends to conduct photoproduction experiments on a \(LH_2\) target for strangeness states. At the same time, the CLAS12 detector [52] will also provide a world-leading facility to explore strangeness states through e–p scattering experiments. These experiments will produce abundant data for in-depth study in the future.