X(3860) production in association with $J/\psi$ via $e^{+}e^{-}$ annihilation at Belle

Abstract

In this paper, we study the X(3860) production associated with $J/\psi$ via $e^{+}e^{-}$ annihilation at the next-to-leading-order (NLO) accuracy in $\alpha _s$, within the nonrelativistic QCD (NRQCD) framework. With the hypothesis of $J^{PC}_{X(3860)}=0^{++}$, the predictions of $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3860)}$ agree well with the Belle measurements, whereas the results following the $2^{++}$ assignment significantly undershoot the data. This is consistent with the Belle’s conclusion that the $0^{++}$ hypothesis is favored over the $2^{++}$ hypothesis for X(3860). Despite fitting the data of the total cross section, the NRQCD predictions seem to be incompatible with the measured $J/\psi$ angular distributions. We simultaneously calculate the cross section of $e^{+}e^{-} \rightarrow J/\psi +X(3940)$ under the assumption of $J^{PC}_{X(3940)}=0^{-+}$, discovering the consistency of the NRQCD predictions with the light-cone results as well as the experiment.

1 Introduction

In 2005, the Belle Collaboration firstly observed the charmoniumlike state X(3915) through $B \rightarrow J/\psi \omega K$ [1], which was subsequently confirmed by the BABAR Collaboration in the same decay mode [2, 3]. In 2012, BABAR measured $J^{PC}_{X(3915)}=0^{++}$ in the process of $\gamma \gamma \rightarrow X(3915) \rightarrow J/\psi \omega$ [4], following which the X(3915) was identified as the $\chi _{c0}(2P)$ in the 2014 Particle Date Group (PDG) [5].

However, this identification has some problems. As the candidate of $\chi _{c0}(2P)$, the X(3915) is expected to decay dominantly into $D\bar{D}$ ($D=$ $D^{0}$ or $D^{+}$), which, however, has not been observed. On the contrary, the decay mode $X(3915) \rightarrow J/\psi \omega$ that should largely be suppressed by Okubo-Zweig-Liuka [6,7,8,9,10] is detected. In addition, the measured X(3915) width of $20 \pm 5$ Mev is much smaller than the theoretical expectations [11]. In 2015, by reanalyzing the BABAR data [4], Zhou et al. indicated that with the abandonment of $\lambda =2$, the assignment of $J^{PC}_{X(3915)}=2^{++}$ is also permitted [12]. In view of these points, the X(3915) state is no longer identified as the $\chi _{c0}(2P)$ in the 2016 PDG [13].

In 2017, by analyzing the process of $e^{+}e^{-} \rightarrow J/\psi D\bar{D}$ based on a 980 $\text {fb}^{-1}$ data sample, the Belle Collaboration observed a new charmoniumlike state X(3860) with a significance of $6.5\sigma$ [14], claiming that the $J^{PC}=0^{++}$ hypothesis is favored over the $2^{++}$ hypothesis for X(3860). Comparing to the X(3915) state, the X(3860) seems to be a better candidate of the $\chi _{c0}(2P)$ [14,15,16]. For instance, the mass of X(3860) is measured to be $(3862^{+26+40}_{-32-13})~\text {MeV}/c^2$, close to the potential-model expectations; the observed decay mode $X(3860) \rightarrow D\bar{D}$ coincides with the theoretical expectations that the charmonium state above the $D\bar{D}$ threshold should decay primarily to $D\bar{D}$. Moreover, the measured X(3860) width is $(201^{+154+88}_{-67-82})~\text {MeV}$, approaching the theoretical prediction of $\Gamma =(221 \pm 19)$ MeV [11]. In light of these considerations, the X(3860) state has been assigned to the $\chi _{c0}(2P)$ in the recent PDG table.¹

The production of $J/\psi$ in association with positive C-parity charmonium via $e^{+}e^{-}$ annihilation is a beneficial process to search for the $C+$ charmonium. The Belle and BABAR Collaborations have measured the cross sections of $e^{+}e^{-} \rightarrow J/\psi +\eta _c(1\,S,2\,S),\chi _{c0}(1P)$ [19,20,21], which can reasonably be described by the next-to-leading-order (NLO) predictions [22,23,24,25,26,27] built on the nonrelativistic QCD (NRQCD) framework [28]. In 2005, the Belle Collaboration firstly detected the charmoniumlike state X(3940) and measured $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3940)}$ [29], which is in line with the results following the light-cone formalism [30].² Two years later, the Belle Collaboration reported the first observation of the charmoniumlike state X(4160) in the process of $e^{+}e^{-} \rightarrow J/\psi +X(4160)$ [38]. Chao claimed [39], under the assumption of $X(4160)=\eta _c(4S)~(\text {or}~\chi _{c0}(3P))$, that $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(4160)}$ is not small in NRQCD and may be in conformity with experiment.

Inspired by the success of NRQCD in describing the double-charmonium production through $e^{+}e^{-}$ annihilation, in this paper we will adopt the NRQCD factorization to study the process of $e^{+}e^{-} \rightarrow J/\psi +X(3860)$ at the NLO accuracy in $\alpha _s$. Along the same lines, we will also evaluate the cross section of $e^{+}e^{-} \rightarrow J/\psi +X(3940)$ so as to compare with the existing results given by the light-cone formalism.

The rest of the paper is organized as follows: in Sect. 2, we give a description of the calculation formalism. In Sect. 3, the phenomenological results and discussions are presented. Section 4 is reserved as a summary.

2 Calculation formalism

In our calculations, we choose the hypotheses of $J^{PC}_{X(3860)}=0(2)^{++}$ [14,15,16] and $J^{PC}_{X(3940)}=0^{-+}$ [30,31,32,33,34,35], which is to say treating X(3860) and X(3940) as $\chi _{c0(2)}(2P)$ and $\eta _c(3S)$, respectively.

In the context of the NRQCD formalism, the differential cross section of $e^{+}+e^{-} \rightarrow J/\psi +\eta _c(3S),\chi _{c0(2)}(2P)$ can be factorized as

$$\begin{aligned}{} & {} \!\!\!d\sigma \nonumber \\{} & {} =d\hat{\sigma }_{e^{+}e^{-} \rightarrow c\bar{c}[n_1]+c\bar{c}[n_2]}\langle \mathcal {O}^{J/\psi }(n_1)\rangle \langle \mathcal {O}^{\eta _c(3S),\chi _{c0(2)}(2P)}(n_2)\rangle ,\nonumber \\ \end{aligned}$$

(1)

where $d\hat{\sigma }_{e^{+}e^{-} \rightarrow c\bar{c}[n_1]+c\bar{c}[n_2]}$ is the perturbative calculable short distance coefficients, denoting the production of the intermediate state of $c\bar{c}[n_1]$ plus $c\bar{c}[n_2]$. According to the above hypotheses, $n_1=^3S_1$ and $n_2=^1S_0,^3P_{0(2)}$. The universal nonperturbative long distance matrix elements (LDMEs) $\langle \mathcal {O}^{J/\psi }(n_{1})\rangle$ and $\langle \mathcal {O}^{\eta _c(3\,S),\chi _{c0(2)}(2P)}(n_{2})\rangle$ stand for the probabilities of $c\bar{c}[n_{1}]$ and $c\bar{c}[n_{2}]$ into $J/\psi$ and $\eta _c(3S)(~\text {or}~\chi _{c0(2)}(2P))$, respectively.

The $d\hat{\sigma }_{e^{+}e^{-} \rightarrow c\bar{c}[n_1]+c\bar{c}[n_2]}$ can further be expressed as

$$\begin{aligned} d\hat{\sigma }_{e^{+}e^{-} \rightarrow c\bar{c}[n_1]+c\bar{c}[n_2]}=|\mathcal {M}|^2 d\Pi _{2}, \end{aligned}$$

(2)

where $|\mathcal {M}|^2$ is the squared matrix elements and $d\Pi _{2}$ is the standard two-body phase space. As pointed out in Refs. [40, 41], for the $e^{+}e^{-}$ annihilation into double charmonia, at the leading-order (LO) level in $\alpha _s$, besides the primary contributions of the tree-level QCD diagrams, the QED diagrams can also provide nonnegligible contributions by introducing the interference terms ($\alpha ^3$ order) between the QCD and QED diagrams.³ For this reason, to obtain a sound estimation, our calculations will include both the QCD and QED diagrams.

Fig. 1

Representative QCD Feynman diagrams for $e^{+}e^{-} \rightarrow J/\psi +X(3860,3940)$. a ($\mathcal {M}_{\alpha \alpha _s}$) is the QCD tree-level diagram; b–f ($\mathcal {M}_{\alpha \alpha _s^2}$) are the NLO QCD corrections to a. The diagram b with heavy dot denotes the counter-term diagram

Fig. 2

Representative QED Feynman diagrams for $e^{+}e^{-} \rightarrow J/\psi +X(3860,3940)$. a, b ($\mathcal {M}_{\alpha ^2}$) is the QED tree-level diagrams; c–k ($\mathcal {M}_{\alpha ^2\alpha _s}$) are the NLO QCD corrections to a, b. The diagram c with heavy dot denotes the counter-term diagram

Up to the $\alpha ^3$ order and NLO accuracy in $\alpha _s$, the squared matrix elements of $e^{+}+e^{-} \rightarrow J/\psi +\eta _c(3\,S),\chi _{c0(2)}(2P)$ can be written as

$$\begin{aligned}{} & {} \!\!\!\big | \left( \mathcal {M}_{\alpha \alpha _s}+\mathcal {M}_{\alpha \alpha _s^2}\right) + \left( \mathcal {M}_{\alpha ^2}+\mathcal {M}_{\alpha ^2\alpha _s}\right) \big |^2 \nonumber \\{} & {} \quad =\big |\mathcal {M}_{\alpha \alpha _s}\big |^2+2\text {Re}\left( \mathcal {M}^{*}_{\alpha \alpha _s}\mathcal {M}_{\alpha \alpha _s^2}\right) +2\text {Re}\left( \mathcal {M}^{*}_{\alpha \alpha _s}\mathcal {M}_{\alpha ^2}\right) \nonumber \\{} & {} \qquad +2\text {Re}\bigg [\left( \mathcal {M}^{*}_{\alpha \alpha _s}\mathcal {M}_{\alpha ^2\alpha _s}\right) +\left( \mathcal {M}_{\alpha \alpha _s^2}\mathcal {M}^{*}_{\alpha ^2}\right) \bigg ]{+}\cdots . \end{aligned}$$

(3)

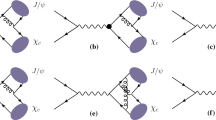
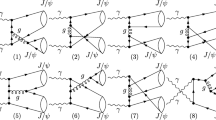
The Feynman diagrams corresponding to $\mathcal {M}_{\alpha \alpha _s}$, $\mathcal {M}_{\alpha \alpha _s^2}$, $\mathcal {M}_{\alpha ^2}$, and $\mathcal {M}_{\alpha ^2\alpha _s}$ are representatively illustrated in Figs. 1 and 2. Figure 1a ($\alpha \alpha _s$ order) denotes the QCD tree-level diagrams, and Fig. 1b–f ($\alpha \alpha _s^2$ order) are the NLO QCD corrections to Figs. 1a and  2a, b ($\alpha ^2$ order) denote the QED tree-level diagrams with Fig. 2c–k ($\alpha ^2\alpha _s$ order⁴) referring to the corrections of high order in $\alpha _s$.

According to Eq. (3), we decompose the differential cross section into four parts,

$$\begin{aligned} d\sigma =d\sigma _2^{(0)}+d\sigma _2^{(1)}+d\sigma _3^{(0)}+d\sigma _3^{(1)}, \end{aligned}$$

(4)

where

$$\begin{aligned} d\sigma _2^{(0)}= & {} \big |\mathcal {M}_{\alpha \alpha _s} \big |^2d\Pi _{2}, \nonumber \\ d\sigma _2^{(1)}= & {} 2\text {Re}\big (\mathcal {M}^{*}_{\alpha \alpha _s} \mathcal {M}_{\alpha \alpha _s^2}\big )d\Pi _{2}, \nonumber \\ d\sigma _3^{(0)}= & {} 2\text {Re}\big (\mathcal {M}^{*}_{\alpha \alpha _s} \mathcal {M}_{\alpha ^2}\big )d\Pi _{2}, \nonumber \\ d\sigma _3^{(1)}= & {} 2\text {Re}\bigg [\left( \mathcal {M}^{*}_{\alpha \alpha _s}\mathcal {M}_{\alpha ^2\alpha _s}\right) +\left( \mathcal {M}_{\alpha \alpha _s^2}\mathcal {M}^{*}_{\alpha ^2}\right) \bigg ]d\Pi _{2}. \end{aligned}$$

(5)

For $e^{+}e^{-}$ annihilation into double charmonia through a virtual photon, $\big |\mathcal {M}\big |^2$ in Eq. (2) is equivalent to $L_{\mu \nu }H^{\mu \nu }$, where $L_{\mu \nu }$ and $H^{\mu \nu }$ are the leptonic and hadronic tensors, respectively. To derive $d\sigma$, with the implementation of the $L_{\mu \nu }$ in Ref. [27] (Eq. (2.7)), we firstly write $d\sigma _{e^{+}e^{-} \rightarrow J/\psi +\eta _c(3\,S),\chi _{c0(2)}(2P)}$ as

$$\begin{aligned} \frac{d\sigma }{d\cos \theta }=A+B\cos ^2\theta =\kappa \left( \mathcal {C}_1 \mathcal {A}_1+\mathcal {C}_2 \mathcal {A}_2\right) , \end{aligned}$$

(6)

where

$$\begin{aligned} \mathcal {A}_1= & {} 1+\cos ^{2}\theta , \nonumber \\ \mathcal {A}_2= & {} 1-3\cos ^{2}\theta . \end{aligned}$$

(7)

For A, B, and $\sigma$, the following relations hold

$$\begin{aligned} A= & {} \kappa (\mathcal {C}_1+\mathcal {C}_2), \nonumber \\ B= & {} \kappa (\mathcal {C}_1-3\mathcal {C}_2), \nonumber \\ \sigma= & {} \frac{8}{3}\kappa \mathcal {C}_1. \end{aligned}$$

(8)

The universal factor $\kappa$ attached to $d\sigma _2^{(0,1)}$ follows as

$$\begin{aligned}{} & {} \!\!\!\kappa _{J/\psi +\eta _c(3S)} = 2 \pi \xi \alpha ^2 \alpha _s^2 |R_{1S}(0)|^2 |R_{3S}(0)|^2, \nonumber \\{} & {} \!\!\!\kappa _{J/\psi +\chi _{cJ}(2P)} = 6 \pi \xi \alpha ^2 \alpha _s^2 |R_{1S}(0)|^2 |R^{'}_{2P}(0)|^2; \end{aligned}$$

(9)

for $d\sigma _3^{(0,1)}$, $\kappa$ reads

$$\begin{aligned}{} & {} \!\!\!\kappa _{J/\psi +\eta _c(3S)} = 4 \pi \xi \alpha ^3 \alpha _s |R_{1S}(0)|^2 |R_{3S}(0)|^2, \nonumber \\{} & {} \!\!\!\kappa _{J/\psi +\chi _{cJ}(2P)} = 12 \pi \xi \alpha ^3 \alpha _s |R_{1S}(0)|^2 |R^{'}_{2P}(0)|^2, \end{aligned}$$

(10)

where

$$\begin{aligned} \xi =\frac{\sqrt{s^2-16 m_c^2 s}}{81 m_c^2 s^{2}}. \end{aligned}$$

(11)

$|R_{1,3S}(0)|$ and $|R^{'}_{2P}(0)|$ are the wave functions at the origin, which can be related to the NRQCD LDMEs by the formulae below:

$$\begin{aligned}{} & {} \!\!\!\langle \mathcal O^{J/\psi }(^3S_1) \rangle = \frac{9}{2\pi }|R_{1S}(0)|^2, \nonumber \\{} & {} \!\!\!\langle \mathcal O^{\eta _c(3S)}(^1S_0) \rangle = \frac{3}{2\pi }|R_{3S}(0)|^2, \nonumber \\{} & {} \!\!\!\langle \mathcal O^{\chi _{cJ}(2P)}(^3P_J) \rangle = (2J+1)\frac{3}{4\pi }|R^{'}_{2P}(0)|^2. \end{aligned}$$

(12)

As to the coefficients $\mathcal {C}^{\text {LO}}_{1,2}$ in $d\sigma ^{(0)}_2$, according to Fig. 1a we have ($r=4m_c^2/s$)

• (i) for $J/\psi +\eta _c(3S)$,

  $$\begin{aligned} \mathcal {C}^{\text {LO}}_1= & {} -\frac{128 r^3(4r-1)}{m_c^4}, \nonumber \\ \mathcal {C}^{\text {LO}}_2= & {} 0, \end{aligned}$$

  (13)

• (ii) for $J/\psi +\chi _{cJ}(2P)$,

  $$\begin{aligned} \mathcal {C}^{\text {LO}}_{1}\big |_{J=0}= & {} \frac{16 r^2 (144 r^4{+}152 r^3{-}428 r^2{+}182 r+1)}{3 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{2}\big |_{J=0}= & {} \frac{16 r^2 (-12 r^2{+}10 r{+}1)^2}{3 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{1}\big |_{J=2}= & {} \frac{32 r^2 (360 r^4{+}308 r^3{-}188 r^2{+}20 r+1)}{3 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{2}\big |_{J=2}= & {} \frac{32 r^2 (360 r^4-96 r^3+4 r^2-4 r+1)}{3 m_c^6}. \nonumber \\ \end{aligned}$$

  (14)

With the aid of Figs. 1a and 2a, b, we obtain the $\mathcal {C}^{\text {LO}}_{1,2}$ in $d\sigma ^{(0)}_3$ in the form

• (i) for $J/\psi +\eta _c(3S)$,

  $$\begin{aligned} \mathcal {C}^{\text {LO}}_1= & {} -\frac{32 r^2(4r-1)(4r+3)}{3m_c^4}, \nonumber \\ \mathcal {C}^{\text {LO}}_2= & {} 0, \end{aligned}$$

  (15)

• (ii) for $J/\psi +\chi _{cJ}(2P)$,

  $$\begin{aligned} \mathcal {C}^{\text {LO}}_{1}\big |_{J=0}= & {} \frac{64 r^2 (36 r^4+56 r^3-59 r^2-7 r+7)}{9 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{2}\big |_{J=0}= & {} \frac{16 r^2 (144 r^4-168r^3+16 r^2+14r+1)}{9 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{1}\big |_{J=2}= & {} \frac{32 r^2 (360 r^4{+}488 r^3{-}104 r^2{-}37 r{+}10)}{9 m_c^6}, \nonumber \\ \mathcal {C}^{\text {LO}}_{2}\big |_{J=2}= & {} \frac{32 r^2 (360 r^4+84 r^3-74 r^2+8 r+1)}{9 m_c^6}. \nonumber \\ \end{aligned}$$

  (16)

For cross-checking purpose, applications of the $\mathcal {C}^{\text {LO}}_{1,2}$ in Eqs. (13)–(16) as well as the relations in Eq. (8) would lead to the LO analytical expressions in Ref. [41].

We utilize the dimensional regularization with $D=4-2\epsilon$ to isolate the ultraviolet (UV) and infrared (IR) divergences. The on-mass-shell (OS) scheme is employed to set the renormalization constants for the c-quark mass ($Z_m$) and heavy-quark filed ($Z_2$); the minimal-subtraction ($\overline{MS}$) scheme is adopted for the QCD-gauge coupling ($Z_g$) and the gluon filed $Z_3$. The renormalization constants are taken as [22]

$$\begin{aligned} \delta Z_{m}^{OS}= & {} -3 C_{F} \frac{\alpha _s}{4\pi }N_{\epsilon }\left[ \frac{1}{\epsilon _{\text {UV}}}+\frac{4}{3}+2\text {ln}{2}\right] , \nonumber \\ \delta Z_{2}^{OS}= & {} - C_{F} \frac{\alpha _s}{4\pi }N_{\epsilon }\left[ \frac{1}{\epsilon _{\text {UV}}}+\frac{2}{\epsilon _{\text {IR}}}+4+6 \text {ln}{2}\right] , \nonumber \\ \delta Z_{3}^{\overline{MS}}= & {} \frac{\alpha _s }{4\pi }(\beta _{0}-2 C_{A})N_{\epsilon }\left[ \frac{1}{\epsilon _{\text {UV}}}+\text {ln}\frac{4m_c^2}{\mu _r^2}\right] , \nonumber \\ \delta Z_{g}^{\overline{MS}}= & {} -\frac{\beta _{0}}{2}\frac{\alpha _s }{4\pi }N_{\epsilon }\left[ \frac{1}{\epsilon _{\text {UV}}}+\text {ln}\frac{4m_c^2}{\mu _r^2}\right] , \end{aligned}$$

(17)

where $N_{\epsilon }= \frac{1}{\Gamma [1-\epsilon ]}\left( \frac{4\pi \mu _r^2}{4m_c^2}\right) ^{\epsilon }$ is an overall factor with $\mu _r$ denoting the renormalization scale, and $\beta _{0}=\frac{11}{3}C_A-\frac{4}{3}T_Fn_f$ is the one-loop coefficient of the $\beta$ function. $n_f(=n_{L}+n_{H})$ represents the number of the active-quark flavors; $n_{L}(=3)$ and $n_{H}(=1)$ denote the number of the light- and heavy-quark flavors, respectively. In $\textrm{SU}(3)$, the color factors are given by $T_F=\frac{1}{2}$, $C_F=\frac{4}{3}$, and $C_A=3$.

After including the QCD corrections, we acquire the $\mathcal {C}^{\text {NLO}}_{1,2}$ involved in $d\sigma _2^{(1)}$ and $d\sigma _3^{(1)}$, which takes the general form

$$\begin{aligned} \mathcal {C}_{1(2)}^{\text {NLO}}= & {} \mathcal {C}_{1(2)}^{\text {LO}} \left[ 1+\frac{\alpha _s}{\pi } \left( \zeta \beta _{0}\text {ln}\frac{\mu _r^2}{4m_c^2}\right. \right. \nonumber \\{} & {} \quad \left. \left. +a_{1(2)}n_{L}+b_{1(2)}n_{H}+c_{1(2)} \right) \right] , \end{aligned}$$

(18)

where $\zeta =\frac{1}{2}$ for $d\sigma _{2}^{(1)}$, and $\frac{1}{4}$ for $d\sigma _{3}^{(1)}$. The coefficients $a_{1(2)}$, $b_{1(2)}$, and $c_{1(2)}$ are functions of r and $m_c$, which can be found in the Appendix (A1–A20).

In our calculations, we use FeynArts [42] to generate all the involved Feynman diagrams and the corresponding analytical amplitudes. The package FeynCalc [43] is then applied to tackle the traces of the $\gamma$ and color matrices, such that the hard-scattering amplitudes can be expressed in terms of the loop integrals. In the next step, with the implementations of Apart [44] and FIRE [45], we reduce the loop integrals to a set of irreducible Master Integrals, which could numerically be evaluated by the package LoopTools [46].

As a cross check, one could use Eqs. (8) and (A1)–(A3) to reproduce the $K(=\sigma ^{\text {NLO}}/\sigma ^{\text {LO}}$, i.e. $(\sigma _{2}^{(0)}+\sigma _{2}^{(1)})/\sigma _{2}^{(0)})$ factor in Refs. [22,23,24,25,26]. We have simultaneously employed the FDC [47] package to calculate $\sigma _{2}^{(0,1)}$, acquiring the same results.

Table 1 Total and differential cross sections of $e^{+}e^{-} \rightarrow J/\psi +X(3860)$ at $\sqrt{s}=\Upsilon (4\,S)$ with $\mu _r=\sqrt{s}/2$. A and $\alpha _{\theta }$ are the coefficients in $\frac{d\sigma }{d\cos \theta }=A(1+\alpha _{\theta }\cos ^{2}\theta )$. The units of A and $\sigma$ are fb. “$0(2)^{++}$” symbolizes the hypothesis of $J^{PC}_{X(3860)}=0(2)^{++}$

Table 2 Total and differential cross sections of $e^{+}e^{-} \rightarrow J/\psi +X(3860)$ at $\sqrt{s}=\Upsilon (5\,S)$ with $\mu _r=\sqrt{s}/2$. A and $\alpha _{\theta }$ are the coefficients in $\frac{d\sigma }{d\cos \theta }=A(1+\alpha _{\theta }\cos ^{2}\theta )$. The units of A and $\sigma$ are fb. “$0(2)^{++}$” symbolizes the hypothesis of $J^{PC}_{X(3860)}=0(2)^{++}$

3 Phenomenological results

In the calculations, $M_{J/\psi } \simeq M_{X(3860)}(\text {or}~M_{J/\psi } \simeq$$M_{X(3940)}) =2m_c$ is implicitly adopted to ensure the gauge invariance of the hard-scattering amplitude. We choose two typical values for charm-quark mass: (1) $m_c=1.4$ GeV, which corresponds to the one-loop charm quark pole mass [48]; (2) $m_c$ is identical to $\frac{m_{J/\psi }+m_{X(3860,3940)}}{4}$, i.e. $m_c \simeq 1.75$ GeV. The wave functions at the origin are taken as: for $m_c=1.4$ GeV, $|R_{1S}(0)|^2=0.81~\text {GeV}^3$, $|R_{3S}(0)|^2=0.455~\text {GeV}^3$, and $|R^{'}_{2P}(0)|^2=0.102~\text {GeV}^5$, corresponding to the BT potential model [49, 50]; regarding the large value of $m_c=1.75$ GeV, the wave functions are given by the Cornell Potential [50], i.e. $|R_{1S}(0)|^2=1.454~\text {GeV}^3$, $|R_{3S}(0)|^2=0.791~\text {GeV}^3$, and $|R^{'}_{2P}(0)|^2=0.186~\text {GeV}^5$. $\alpha$ is identical to 1/130.9 [48]; $\alpha _s$ is determined by the two-loop running coupling.

Table 3 Comparisons with the Belle-measured $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3860)}$. $``\sigma _{\text {theo}}''$ (in units of fb) refers to the theoretical results, comprised of $\sigma ^{(0)}_{2}$, $\sigma ^{(1)}_{2}$, $\sigma ^{(0)}_{3}$, and $\sigma ^{(1)}_{3}$. “$0(2)^{++}$” symbolizes the hypothesis of $J^{PC}_{X(3860)}=0(2)^{++}$

Fig. 3

Normalized $J/\psi$ differential cross section as a function of $\cos \theta$ at $\sqrt{s}=10.58$ GeV with $m_c=1.4$ GeV. The solid line denotes the sum of $d\sigma ^{(0)}_{2}$, $d\sigma ^{(1)}_{2}$, $d\sigma ^{(0)}_{3}$, and $d\sigma ^{(1)}_{3}$. “$0(2)^{++}$” symbolizes the hypothesis of $J^{PC}_{X(3860)}=0(2)^{++}$

We summarize the NRQCD predictions of $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3860)}$ in Tables 1 and 2.⁵ Inspecting the data, one can perceive:

• 1. For the $0^{++}$ hypothesis, the conventional QCD diagrams provide the major contributions (i.e. $\sigma _2^{(0,1)}$), in which the QCD corrections are significant, as can be seen by the ratio of $\sigma _2^{(0)+(1)}/\sigma _2^{(0)}$. The interference terms between the QCD and QED diagrams, i.e. $\sigma _{3}^{(0,1)}$, contribute mildly to the total cross section. As for the angular distribution, the $d\sigma _2^{(1)}$ increases the parameter $\alpha _{\theta }$ predicted by $d\sigma _2^{(0)}$ by about $10\%$; the inclusions of $d\sigma _{3}^{(0)}$ and $d\sigma _{3}^{(1)}$ would enlarge $\alpha _{\theta }$ by about five percent.

• 2. For the $2^{++}$ hypothesis, $\sigma _2^{(1)}$ enhances $\sigma _2^{(0)}$ moderately; including $\sigma _{3}^{(0)+(1)}$ yields a further enhancement that is comparable with $\sigma _2^{(1)}$. As regards the differential cross section, $d\sigma _{2}^{(1)}$ and $d\sigma _{3}^{(0)+(1)}$ simultaneously have crucial influences on $\alpha _{\theta }$.

The impacts of $\sigma _{3}^{(0,1)}$ on the total and differential cross sections manifest the relevance of the interference terms in the study of $e^{+}e^{-} \rightarrow J/\psi +X(3860)$.

We confront our predictions with experiment in Table 3. With the inspection of the data, it can be seen that the predictions built on the $0^{++}$ hypothesis agree well with the Belle measurements within uncertainties; however, the theoretical results provided by the $2^{++}$ hypothesis markedly fall short of the data. These results conform with the Belle’s conclusion that the $0^{++}$ hypothesis is favored over the $2^{++}$ hypothesis for X(3860).

In Figs. 3 and 4, we compare the theoretical results with the measurements of the $J/\psi$ angular distributions. It appears that the NRQCD predictions could not give reasonable explanations for the experiment. Considering the insensitivity of $\left( \frac{d\sigma }{d\cos \theta }\frac{1}{\sigma }\right)$ to $\mu _r$, along with its independence on the LDMEs, the discrepancies between the NRQCD results and the $J/\psi$ angular distributions seem hardly to be cured, at least at the NLO accuracy.

At last, by identifying X(3940) as $\eta _c(3S)$ [30,31,32,33,34,35], we make a comparison between the predicted $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3940)}$ and the Belle data in Table 4. One can see that $\sigma _{3}^{(0)+(1)}$ could enhance the conventional QCD results, i.e. $\sigma _{2}^{(0)+(1)}$, by about 10–15%, indicating the indispensability of considering the interference terms between the QCD and QED diagrams. The NRQCD results are found to be consistent with the light-cone results (i.e. $(11 \pm 3)$ fb [30]) as well as the experimental measurements.

Fig. 4

Normalized $J/\psi$ differential cross section as a function of $\cos \theta$ at $\sqrt{s}=10.58$ GeV with $m_c=1.75$ GeV. The solid line denotes the sum of $d\sigma ^{(0)}_{2}$, $d\sigma ^{(1)}_{2}$, $d\sigma ^{(0)}_{3}$, and $d\sigma ^{(1)}_{3}$. “$0(2)^{++}$” symbolizes the hypothesis of $J^{PC}_{X(3860)}=0(2)^{++}$

Table 4 Comparisons with the Belle-measured $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3940)}$

4 Summary

In this manuscript, we applied the NRQCD factorization to study the production of X(3860) plus $J/\psi$ via $e^{+}e^{-}$ annihilation at the NLO accuracy in $\alpha _s$. We found, in addition to the QCD diagrams, that the QED diagrams can also provide indispensable contributions by introducing the interference terms between the QCD and QED diagrams. The NRQCD predictions obtained by assuming $J^{PC}_{X(3860)}=0^{++}$ match the Belle measurements adequately; however, the results based on the $2^{++}$ hypothesis are far inferior to the data. This coincides with the Belle’s conclusion that the $0^{++}$ hypothesis is favored over the $2^{++}$ hypothesis for X(3860). In spite of the compatibility with the measured total cross section, the NRQCD results seem unlikely to explain the $J/\psi$ angular distributions. With the interpretation of X(3940) as $\eta _c(3S)$, we simultaneously carried out the NLO calculations of $\sigma _{e^{+}e^{-} \rightarrow J/\psi +X(3940)}$, discovering that the NRQCD predictions are in coincidence with the light-cone results and are in good agreement with experiment.

Appendix A

In this section, we list the numerical values of the coefficients $a_{1(2)}$, $b_{1(2)}$, and $c_{1(2)}$ in Eq. (18).

For $d\sigma _{2}^{(1)}$ at $\sqrt{s}=10.58$ GeV:

• I. $m_c=1.4$ GeV,

  • (1) $J/\psi +\eta _c(3S)$,

    $$\begin{aligned}{} & {} a_1=-0.1314,~b_1=-0.3046,~c_1=13.057, \nonumber \\{} & {} a_2=b_2=c_2=0, \end{aligned}$$

    (A1)

  • (2) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.2159,~b_1=-0.4392,~c_1=8.1957, \nonumber \\{} & {} a_2=-0.2981,~b_2=-0.5702,~c_2=7.5214,\nonumber \\ \end{aligned}$$

    (A2)

  • (3) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.4112,~b_1=-0.7505,~c_1=-0.8632, \nonumber \\{} & {} a_2=-0.4534,~b_2=-0.8179,~c_2=-2.4466.\nonumber \\ \end{aligned}$$

    (A3)

• II. $m_c=1.75$ GeV,

  • (1) $J/\psi +\eta _c(3S)$,

    $$\begin{aligned}{} & {} a_1=-0.2802,~b_1=-0.5710,~c_1=12.060, \nonumber \\{} & {} a_2=b_2=c_2=0,\nonumber \\ \end{aligned}$$

    (A4)

  • (2) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.3463,~b_1=-0.7051,~c_1=8.3116, \nonumber \\{} & {} a_2=-0.3973,~b_2=-0.8086,~c_2=7.9286,\nonumber \\ \end{aligned}$$

    (A5)

  • (3) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.5436,~b_1=-1.1055,~c_1=0.5897, \nonumber \\{} & {} a_2=-0.5856,~b_2=-1.1908,~c_2=-0.4977.\nonumber \\ \end{aligned}$$

    (A6)

For $d\sigma _{2}^{(1)}$ at $\sqrt{s}=10.87$ GeV:

• I. $m_c=1.4$ GeV,

  • (1) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.1998,~b_1=-0.4107,~c_1=8.1818, \nonumber \\{} & {} a_2=-0.2856,~b_2=-0.5442,~c_2=7.4574,\nonumber \\ \end{aligned}$$

    (A7)

  • (2) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.3946,~b_1=-0.7139,~c_1=-1.0438, \nonumber \\{} & {} a_2=-0.4365,~b_2=-0.7791,~c_2=-2.6764.\nonumber \\ \end{aligned}$$

    (A8)

• II. $m_c=1.75$ GeV,

  • (1) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.3308,~b_1=-0.6696,~c_1=8.2981, \nonumber \\{} & {} a_2=-0.3856,~b_2=-0.7773,~c_2=7.8893,\nonumber \\ \end{aligned}$$

    (A9)

  • (2) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.5283,~b_1=-1.0571,~c_1=0.4154, \nonumber \\{} & {} a_2=-0.5707,~b_2=-1.1403,~c_2=-0.7404.\nonumber \\ \end{aligned}$$

    (A10)

For $d\sigma _{3}^{(1)}$ at $\sqrt{s}=10.58$ GeV:

• I. $m_c=1.4$ GeV,

  • (1) $J/\psi +\eta _c(3S)$,

    $$\begin{aligned}{} & {} a_1=-0.0657,~b_1=-0.1523,~c_1=2.2357, \nonumber \\{} & {} a_2=b_2=c_2=0, \end{aligned}$$

    (A11)

  • (2) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.0999,~b_1=-0.2068,~c_1=0.3980, \nonumber \\{} & {} a_2=-0.1490,~b_2=-0.2851,~c_2=-2.1628,\nonumber \\ \end{aligned}$$

    (A12)

  • (3) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.1680,~b_1=-0.3153,~c_1=-8.4469, \nonumber \\{} & {} a_2=-0.1651,~b_2=-0.3107,~c_2=-10.176.\nonumber \\ \end{aligned}$$

    (A13)

• II. $m_c=1.75$ GeV,

  • (1) $J/\psi +\eta _c(3S)$,

    $$\begin{aligned}{} & {} a_1=-0.1401,~b_1=-0.2855,~c_1=1.224, \nonumber \\{} & {} a_2=b_2=c_2=0, \end{aligned}$$

    (A14)

  • (2) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.1690,~b_1=-0.3441,~c_1=-0.1032, \nonumber \\{} & {} a_2=-0.1986,~b_2=-0.4043,~c_2=-1.5981,\nonumber \\ \end{aligned}$$

    (A15)

  • (3) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.2264,~b_1=-0.4607,~c_1=-8.0387, \nonumber \\{} & {} a_2=-0.2087,~b_2=-0.4247,~c_2=-8.7074.\nonumber \\ \end{aligned}$$

    (A16)

For $d\sigma _{3}^{(1)}$ at $\sqrt{s}=10.87$ GeV:

• I. $m_c=1.4$ GeV,

  • (1) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.0914,~b_1=-0.1921,~c_1=0.4551, \nonumber \\{} & {} a_2=-0.1428,~b_2=-0.2721,~c_2=-2.2438,\nonumber \\ \end{aligned}$$

    (A17)

  • (2) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.1601,~b_1=-0.2990,~c_1=-8.4891, \nonumber \\{} & {} a_2=-0.1589,~b_2=-0.2971,~c_2=-10.363.\nonumber \\ \end{aligned}$$

    (A18)

• II. $m_c=1.75$ GeV,

  • (1) $J/\psi +\chi _{c0}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.1608,~b_1=-0.3258,~c_1=-0.0405, \nonumber \\{} & {} a_2=-0.1928,~b_2=-0.3886,~c_2=-1.6583,\nonumber \\ \end{aligned}$$

    (A19)

  • (2) $J/\psi +\chi _{c2}(2P)$,

    $$\begin{aligned}{} & {} a_1=-0.2203,~b_1=-0.4425,~c_1=-8.0962, \nonumber \\{} & {} a_2=-0.2044,~b_2=-0.4113,~c_2=-8.8795.\nonumber \\ \end{aligned}$$

    (A20)