1 Introduction

In recent years, a significant amount of astrophysical observational data, such as INTEGRAL [1], Swift [2], IXPE [3], XMM-Newton [4, 5], ATHENA [6], EHT [7, 8], LIGO [9] and Virgo [10], have been employed to describe the evolution of the cosmos. The scientific community is motivated by these observations to investigate, develop more insights, and devise cutting-edge methods for testing gravity in powerful gravitational fields. Meanwhile, the most successful description of gravity, however, is general relativity (GR), whose predictions for gravitational effects on the solar system and cosmological scales closely match the observations. However, over the past few years, a few slight tensions, including the \(H_0\) tension, have emerged. Additionally, the beauty of GR is spoiled by theoretical challenges like singularities, quantum gravity, and a lack of clarification for the genesis of dark energy [11] and dark matter [12]. Further, GR diverges with the present higher-loop contributions and is a non-renormalizable theory. It is therefore useful to consider alternative theories of gravitation that might solve the theoretical and observational problems.

Apart from non-Lagrangian theories (MOND), alternative theories of gravity are typically described by the altered Lagrangian density, which is further altered by the inclusion of the extra geometrodynamical factors in the Einstein–Hilbert action integral. Many such modified theories are currently being explored in the literature, including theories with new scalar and vector dynamical degrees of freedom [13], while some others rely on massive gravitons [14], string-inspired concepts such as brane-worlds [15], and geometric scenarios that deviate from the tradition set by Riemannian geometry. In the latter scenario, we can find theories rely on Einstein–Cartan geometry [16], Palatini (or metric-affine) theories of different sorts [17], incorporating f(R) models [18], and theories with dynamics based completely on torsion and/or non-metricity [19, 20]. In this context, selecting either the torsion (T) or the nonmetricity (Q) as the geometric basis generates two distinct but equivalent representations of gravity so-called GR’s teleparallel equivalent (TEGR) [21, 22] and symmetric teleparallel GR (STGR) [20, 23,24,25]. Even some basic principles are completely different, but these representations are dynamically equivalent to GR. For instance, TEGR considers torsion to be the field that describes gravity. In this case, both curvature and non-metricity are zero, and the Weitzenböck connection serves as the affine connection [26, 27]. Here, tetrads are the fundamental objects from which the affine connection, torsion invariants, and eventually the field equations can be derived. On the other hand, STEGR is based on non-metricity. In this case, the gravitational field is associated with non-metricity and a flat spacetime can be taken into consideration. There is a metric tensor in STEGR, and geometry has a non-metric connection, but torsion and total curvature are vanishing.

Similarly to how curvature may be related to the rotation of vectors when they are transported in parallel on closed curves, non-metricity can be related to the change in length of vectors when they are transported in parallel, allowing gravity to be handled in accordance with the standard of gauge theories. The three equivalent approaches based on the three different connections are often known as: The Geometrical Trinity of Gravity [28, 29]. Although these three theories are completely equivalent from a dynamical perspective, the fundamental principles upon which they are formulated seem to be very different. Further, due to the different geometries involved in formulating the theories, their modifications may not be equivalent at the fundamental level.

Recently, Jiménez et al. [20] constructed an intriguing modified theory of gravity by extending STEGR, known as f(Q)-gravity or symmetric teleparallel gravity. In this f(Q)-gravity, we take into account a flat and vanishing torsion connection, where gravity is characterized by a non-metricity scalar Q, thereby representing one of the geometrical equivalent versions of GR. Intriguingly, partial derivatives may be employed to simplify the associated connection, and they vanish for a particular coordinate choice known as the coincident gauge. Contrary to GR, we can also distinguish gravity from the inertial effects, which is one of the f(Q) theory’s fundamental attributes. It should also be noted that unlike f(R) gravity, where the field equations are of fourth-order [30], f(Q)-gravity has field equations of second-order, which is free from pathologies. Hence, the building of this f(Q) theory provides a novel starting point for several modified gravity theories. Several applications of f(Q) theory have recently been explored, including cosmology [31,32,33,34], the bouncing model [35], wormhole solutions [36,37,38,39,40], energy conditions [41], the Newtonian limit [42], spherically symmetric and stationary black hole spacetimes [43] and star-like objects without singularity present [44], among others.

For decades, the complexity of any system can be analyzed using a variety of factors. The underlying concept relates to measuring the entropy and information of the structure contained within a system. Moreover, the concept of the self-gravitating system’s complexity is extensively analyzed in the study of massive objects. When considering a perfect crystal in physics–which displays a periodic attitude and is symmetrically ordered–the isolated gas–which exhibits disordering and the greatest quantity of information–is considered to be a complicated system with zero complexity. The notion of disequilibrium was introduced by Lopéz-Ruiz et al. [46] to analyze the system’s degree of complexity. In effect, it is a measuring of “distance” from the system’s attainable type’s equally likely dispersion. They came to the conclusion that the notion of complexity dissipated in the situation of an ideal gas and a perfect crystal by defining complexity as the combination of these two components, i.e., information and disequilibrium. In this context, Herrera [47] developed a new notion of complexity incorporating fluid elements such as pressure, energy density, and others after identifying deficiencies in all previous concepts of complexity employed to investigate the self-gravitating system. In a nutshell, it is related to all characteristics of the fluid’s composition. In this situation, the complexity is generated by means of the complexity factor, which is one of the structure scalars acquired from the orthogonal division of the intrinsic curvature. This mechanism for dissipative fluid content was further extended by Herrera et al. [48]. The prerequisites for the progression design with the least amount of complexity were also defined, going beyond simply analyzing the system’s complexity. They found that there are various solutions and that the fluid dissipates shearingly and geodesically.

The axially symmetric geometry was employed by Herrera et al. [49] to further assess the effect of complexity on various geometries, and they discovered three main sources accountable for complexity. They demonstrated how complexity and symmetry are related. In this particular circumstance, they also got some analytical answers. Herrera et al. [50] also study the emergence of spherically symmetric non-static geometry utilizing the notion of complexity, either in terms of dissipation or non-dissipation. Along with developing specific models and calculating their appropriate implications for understanding the emergence, they employed the quasi-homology criterion to relate the areal radius and the areal radius velocity. Using this method, Contreras and Fuenmayor [51] investigated the stability of self-gravitating celestial objects in terms of gravitational cracking. In addition to analyzing the role of extra structure scalars which are obtained by the orthogonal division of the intrinsic curvature, Herrera et al. [52] expanded the concept of the complexity factor on the hyperbolically symmetric geometry. Recently, Contreras et al. [53,54,55,56] and Maurya et al. [57,58,59] succeeded in analyzing the complexity of static and spherically symmetric self-gravitating systems in the context of gravitational decoupling [60] (see [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83] for a list of additional applications of the gravitational decoupling mechanism).

In this study, we are principally interested in investigating the complexity-free spacetime for anisotropic stellar configurations induced by gravitational decoupling in f(Q)-gravity theory. We seek new solutions in a direct way, employing the now-famous gravitational decoupling formalism via the complete geometric deformation (CGD) approach, which has proven to be an efficient tool for exploring the energy exchange between relativistic fluids promoting self-gravitating stellar systems, whatever their nature. The article is organized as follows: In Sect. 2, we thoroughly reviewed the field equations in f(Q)-gravity theory with vanishing complexity factor. By introducing an extra source in f(Q)-gravity, we provide a complexity-free anisotropic solution with gravitational decoupling methodology via CGD approach in Sect. 3. The external spacetime and matching conditions are discussed in Sect. 4, in which we match the decoupled interior solution generated by the anisotropic matter distribution in f(Q)-gravity to the exterior Schwarzschild (Anti-) de Sitter at a suitable boundary. While in Sect. 6, it was addressed how energy is exchanged between the sources \(T_{\epsilon \nu }\) and \(\theta _{\epsilon \nu }\). The full physical analysis of complexity-free anisotropic in f(Q)-gravity is presented in Sect. 5. The concluding remarks are given in Sect. 7, which will be chained by the appendix which comprises some lengthy and pertinent formulations of physical quantities.

2 The field equations

The modified action for f(Q)-gravity by including of an extra Lagrangian \(L_\theta \) connected to the new source \(\theta _{\epsilon \nu }\) through a decoupling constant \(\alpha \) source is defined as:

$$\begin{aligned} \mathcal {S}= & {} \underbrace{\int \frac{1}{2}\,f(Q)\sqrt{-g}\,d^4x+\int \mathcal {L}_m\,\sqrt{-g}\,d^4x}_{\mathcal {S}_{Q}}\nonumber \\{} & {} +\alpha \underbrace{ \int \mathcal {L}_\theta \,\sqrt{-g}\,d^4x}_{\mathcal {S}_{\theta }}, \end{aligned}$$
(1)

As usual, \(\mathcal {L}_m\) denotes the Lagrangian density of matter fields described by energy-momentum tensor \({T}_{\epsilon \nu }\) in the f(Q)-gravity theory with the nonmetricity scalar Q which drives the gravitational interaction. Here, we set \(8 \pi G=1\). The correction in the f(Q)-gravity matter field due to the new contribution may help in understanding the physical properties of the system beyond the f(Q)-gravity theory. We define the sources \(T_{\epsilon \nu }\) and \(T^\theta _{\epsilon \nu }\) as,

$$\begin{aligned}{} & {} {T}_{\epsilon \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\,\mathcal {L}_m\right) }{\delta g^{\epsilon \nu }},\end{aligned}$$
(2)
$$\begin{aligned}{} & {} T^\theta _{\epsilon \,\nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\,\mathcal {L}_\theta \right) }{\delta g^{\epsilon \nu }}, \end{aligned}$$
(3)

along with this, we also denoted the joint action of both sources via decoupling constant \(\alpha \) by \(\bar{T}_{\epsilon \nu }=\big (T_{\epsilon \nu }+\alpha \,T^\theta _{\epsilon \nu }\big )\). As a result of Bianchi’s identity, the total energy-momentum tensor \(\bar{T}_{\epsilon \nu }\) must be covariantly conserved. i.e.

$$\begin{aligned} \bigtriangledown _\epsilon \bar{T}^{\mu \nu }=0, \end{aligned}$$
(4)

The nonmetricity tensor \(Q_{\lambda \epsilon \nu }\) in terms of affine connection is given by

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\bigtriangledown _{\lambda } g_{\epsilon \nu }=\partial _\lambda g_{\epsilon \nu }-\Gamma ^\delta _{\,\,\,\lambda \epsilon }g_{\delta \nu }-\Gamma ^\delta _{\,\,\,\lambda \nu }g_{\epsilon \delta }, \end{aligned}$$
(5)

where \(\Gamma ^\delta _{\,\,\,\epsilon \nu }\) is known as the affine connection which assumes the form

$$\begin{aligned} \Gamma ^\delta _{\,\,\,\epsilon \nu }=\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace +K^\delta _{\,\,\,\epsilon \nu }+ L^\delta _{\,\,\,\epsilon \nu }, \end{aligned}$$
(6)

where \(\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace \), \(L^\delta _{\,\,\,\epsilon \nu }\), and \(K^\delta _{\,\,\,\epsilon \nu }\) are the Levi-Civita connection, disformation, and contortion tensors respectively that are given as:

$$\begin{aligned}{} & {} \lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace =\frac{1}{2}g^{\delta \sigma }\left( \partial _\epsilon g_{\sigma \nu }+\partial _\nu g_{\sigma \epsilon }-\partial _\sigma g_{\epsilon \nu }\right) ,\nonumber \\{} & {} L^\delta _{\,\,\,\epsilon \nu }=\frac{1}{2}Q^\delta _{\,\,\,\epsilon \nu }-Q_{(\epsilon \,\,\,\,\,\,\nu )}^{\,\,\,\,\,\,\delta },\nonumber \\{} & {} K^\delta _{\,\,\,\epsilon \nu }=\frac{1}{2} T^\delta _{\,\,\,\epsilon \nu }+T_{(\epsilon \,\,\,\,\,\,\nu )}^{\,\,\,\,\,\,\delta }, \end{aligned}$$
(7)

here, \(T^\delta _{\,\,\,\epsilon \nu }\) denotes the torsion tensor. This \(T^\delta _{\,\,\,\epsilon \nu }\) describes the anti-symmetric part of the affine connection as \(T^\delta _{\,\,\,\epsilon \nu }=2\Gamma ^\lambda _{\,\,\,[\epsilon \nu ]}\). Moreover, the nonmetricity tensor in connection to superpotential is given as:

$$\begin{aligned} P^\alpha _{\,\,\,\,\epsilon \nu }=\frac{1}{4}\left[ -Q^\alpha _{\,\,\,\,\epsilon \nu }+2 Q_{(\epsilon \,\nu )}^\alpha +Q^\alpha g_{\epsilon \nu }-\tilde{Q}^\alpha g_{\epsilon \nu }-\delta ^\alpha _{(\epsilon }Q_{\nu )}\right] , \end{aligned}$$
(8)

where

$$\begin{aligned} Q_{\alpha }\equiv Q_{\alpha \,\,\,\epsilon }^{\,\,\epsilon },\; \tilde{Q}_\alpha =Q^\epsilon _{\,\,\,\,\alpha \epsilon }. \end{aligned}$$
(9)

are two independence traces that help us to define the nonmetricity scalar term as

$$\begin{aligned} Q=-Q_{\alpha \epsilon \nu }\,P^{\alpha \epsilon \nu }. \end{aligned}$$
(10)

By varying the action (1) with respect to the metric tensor \(g^{\epsilon \nu }\), we obtain the system of governing field equations in f(Q)-gravity as,

$$\begin{aligned}{} & {} \frac{2}{\sqrt{-g}}\bigtriangledown _\gamma \left( \sqrt{-g}\,f_Q\,P^\gamma _{\,\,\,\,\epsilon \nu }\right) +\frac{1}{2}g_{\epsilon \nu }f +f_Q\big (P_{\epsilon \gamma i}\,Q_\nu ^{\,\,\,\gamma i}\nonumber \\ {}{} & {} \quad -2\,Q_{\gamma i \epsilon }\,P^{\gamma i}_{\,\,\,\nu }\big ) =- \bar{T}_{\epsilon \nu },~~ \end{aligned}$$
(11)

where \(f_Q=\frac{d f}{d Q}\). With the help of Eq. (1), it is possible to derive the extra constraint over the connection as

$$\begin{aligned} \bigtriangledown _\epsilon \bigtriangledown _\nu \left( \sqrt{-g}\,f_Q\,P^\gamma _{\,\,\,\,\epsilon \nu }\right) =0. \end{aligned}$$
(12)

The torsionless and curvatureless constraints render the affine connection as

$$\begin{aligned} \Gamma ^\lambda _{\,\,\,\epsilon \nu }=\left( \frac{\partial x^\lambda }{\partial \xi ^\beta }\right) \partial _\epsilon \partial _\nu \xi ^\beta . \end{aligned}$$
(13)

Furthermore, we can choose a special coordinate choice, the so-called coincident gauge, so that \(\Gamma ^\lambda _{\,\,\,\epsilon \nu }=0\). Then, the nonmetricity Eq. (5) reduces to

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\partial _\lambda g_{\epsilon \nu }. \end{aligned}$$
(14)

It makes the calculation more simpler because the only important variable is the metric function. However, excluding the case of conventional GR [85], the action is no longer invariant with regard to the diffeomorphism. To overcome this problem, one may employ the covariant formulation of f(Q)-gravity. One might utilize the covariant formulation by first figuring out the affine connection in the absence of gravity [84], since the affine connection expressed in Eq. (13) is entirely inertial.

The present work mainly focuses on the study of the self-gravitating compact star in f(Q)-gravity theory in the context of gravitational decoupling. For this purpose, we assume a static spherically symmetric line element in the Schwarzschild coordinate as,

$$\begin{aligned} ds^2=-e^{\Phi (r)}dt^2+e^{\mu (r)}dr^2+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2. \end{aligned}$$
(15)

The unknown functions \(\Phi (r)\) and \(\mu (r)\) are called the metric potentials depending on the radial coordinate r. Then the expression of the nonmetricity scalar Q for spherically symmetric line element (15) is determined as:

$$\begin{aligned} Q=-\frac{2 e^{-\mu (r)} \left( 1+r \Phi ^\prime (r)\right) }{r^2}. \end{aligned}$$
(16)

Furthermore, we consider that the internal structure of the self-gravitating system in f(Q)-gravity is made by perfect matter distributions. Then, \(T_{\epsilon \nu }\) can be written as,

$$\begin{aligned} T_{\epsilon \,\nu }=\left( \rho +p\right) u_{\epsilon }\,u_{\nu }+p\,g_{\epsilon \,\nu }, \end{aligned}$$
(17)

where, \(\rho \) and p denote the energy density and fluid pressure, respectively in pure f(Q)-gravity theory. The fluid four-velocity vector is denoted \(u^{\nu }\) such that \(u^{0} u_{0}=-1\). In this connection, we denote the components for \(T^\theta _{\epsilon \nu }\) as

$$\begin{aligned}{}[T^\theta ]^0_0=-\rho ^{\theta },~~~ [T^\theta ]^1_1=p^{\theta }_r, ~~~[T^\theta ]^2_2=[T^\theta ]^3_3=p^{\theta }_t. ~~~~ \end{aligned}$$
(18)

It is noted that we have assumed that \(\theta ^1_1\ne \theta ^2_2\). Then, the new source will generate the anisotropy in the f(Q)-gravity system. In order to write the field equations related to Eq. (11), we define the components of total energy-momentum tensor (\(\bar{T}_{\epsilon \nu }\)) as

$$\begin{aligned} \rho ^{\text {tot}}= \rho +\alpha \,\rho ^{\theta },~~P^{\text {tot}}_r=p+\alpha \,p^{\theta },~~P^{\text {tot}}_t=p+\alpha \,p^{\theta }_t.\nonumber \\ \end{aligned}$$
(19)

Then the independent components of the equation of motion (11) in f(Q)-gravity are,

$$\begin{aligned} \rho ^{\text {tot}}= & {} -\frac{f(Q)}{2}+f_{Q}\Bigg [Q+\frac{1}{r^2}+\frac{e^{-\mu }}{r}(\Phi ^\prime +\mu ^\prime )\Bigg ], \end{aligned}$$
(20)
$$\begin{aligned} P^{\text {tot}}_r= & {} \frac{f(Q)}{2}-f_{Q}\Bigg [Q+\frac{1}{r^2}\Bigg ], \end{aligned}$$
(21)
$$\begin{aligned} P^{\text {tot}}_t= & {} \frac{f(Q)}{2}-f_{Q}\Bigg [\frac{Q}{2}-e^{-\mu } \Bigg \{\frac{\Phi ^{\prime \prime }}{2}+\Bigg (\frac{\Phi ^\prime }{4}+\frac{1}{2r}\Bigg ) \nonumber \\{} & {} \times (\Phi ^\prime -\mu ^\prime )\Bigg \}\Bigg ],~~~ \end{aligned}$$
(22)
$$\begin{aligned} 0= & {} \frac{\text {cot}\theta }{2}\,Q^\prime \,f_{QQ}. \end{aligned}$$
(23)

where \(f_{Q}(Q)=\frac{\partial f(Q)}{\partial Q}\), and consequently the total anisotropy is given as,

$$\begin{aligned}{} & {} \Delta ^{\text {tot}}=p^{\text {tot}}_t-p^{\text {tot}}_r= \Delta _{\theta },~~ \text {where},~\Delta _\theta = \alpha \,(p^{\theta }_t-p^{\theta }_r).\nonumber \\ \end{aligned}$$
(24)

It is observed that the behavior anisotropy in the system will also depend on the signature of decoupling constant \(\alpha \). In order to describe the explicit form of equations of motion (20)–(22), we must define the functional form of f(Q). In this regard, Wang et al. [88] proved that the exterior solution of field equations gives the exact Schwarzschild (anti-) de Sitter solution if and only if \(f_{QQ}=0\). Therefore, the functional form of f(Q) must be derived by assuming \(f_{QQ} =0\) for obtaining the solution of self-gravitating compact star models. Hence,

$$\begin{aligned}{} & {} f_{QQ}=0~~~~~\Longrightarrow ~~~~ f(Q)=\beta _1\,Q+\beta _2, \end{aligned}$$
(25)

where \(\beta _1\) and \(\beta _2\) are constants. In this regard, a well-explanation of the compatibility of the above linear functional form of f(Q) for a static spherically symmetric spacetime with the coincident gauge can be seen in the work of [84].

By inserting of Eqs. (15) and (26), the Eqs. (22)–(24) give the following set of differential equation of motion,

$$\begin{aligned}{} & {} \rho ^{\text {tot}} = \frac{1}{2\,r^2} \Bigg [2\, \beta _1+2\, e^{-\mu }\, \beta _1 \left( r\, \mu ^\prime -1\right) -r^2 \,\beta _2 \Bigg ],\end{aligned}$$
(26)
$$\begin{aligned}{} & {} P^{\text {tot}}_r=\frac{1}{2\,r^2} \Bigg [-2\, \beta _1+2\, e^{-\mu } \,\beta _1 \left( r\, \Phi ^\prime +1\right) +r^2\, \beta _2\Bigg ],\end{aligned}$$
(27)
$$\begin{aligned}{} & {} P^{\text {tot}}_{t}=\frac{e^{-\mu }}{4\,r} \Bigg [2\, e^{\mu }\, r\, \beta _2 +\beta _1\, \left( 2+r \Phi ^\prime \,\right) \left( \Phi ^\prime -\mu ^\prime \right) +2\, r\, \beta _1 \, \Phi ^{\prime \prime }\Bigg ],\nonumber \\ \end{aligned}$$
(28)

and corresponding a conservation equation or a Tolman–Oppenheimer–Volkoff (TOV) equation [86, 87] in f(Q)-gravity [88, 89] under the functional form of f(Q) given by Eq. (25) can be written as,

$$\begin{aligned} -\frac{\Phi ^\prime }{2}(\rho ^{\text {tot}}+P^{\text {tot}}_r)-(P^{\text {tot}}_r)^{\prime }+\frac{2}{r}( P^{\text {tot}}_{t}-P^{\text {tot}}_r)=0.~~~ \end{aligned}$$
(29)

It is noted that Eq. (29) is similar to the TOV equation in classical general relativity. Now we focus on the procedure for finding the solution of field equations (26)–(28) beyond the f(Q)-gravity theory. In this regard, we would like to mention some brief reviews of widely adopted methodologies to solve the field equations in GR and modified gravity theory. There were three main straightforward methodologies where the metric potentials connected through the relations which are well-described by Newton et al. [90]. The first relation proposed by Ivanov [91] in connection to conformally flat geometry [92, 93] is given by,

$$\begin{aligned} e^{\Phi (r)}=A_1^2r^2\, \cosh ^2 \left( \int \sqrt{\frac{e^{\mu (r)}}{r^2}}\,dr +B_1\right) , \end{aligned}$$
(30)

where \(A_1\) and \(B_1\) are constants, which has some drawbacks in determining the redshift at the center of star \(r=0\). In the same spirit, the second method was derived in the context of a conformal killing vector whose relation can be given by the following equation [94,95,96,97],

$$\begin{aligned} e^{\Phi (r)}=A_2^2r^2\, \exp \Bigg (-\frac{2k}{B_2}\sqrt{\frac{e^{\mu (r)}}{r^2}}\, dr\Bigg )^2, \end{aligned}$$
(31)

where \(A_2\) and \(B_2\) denote integration constants. The third relation is known as a Karmarkar condition which has been widely in most of the gravity theories to investigate the solutions of compact star models, wormholes, and black holes. This can be described by following the bridge equation,

$$\begin{aligned} e^{\Phi (r)}=\Bigg (A_3+B_3 \int \sqrt{e^{\mu (r)}-1}\,dr\bigg )^2, \end{aligned}$$
(32)

with \(A_3\) and \(B_3\) being constants of integration. In view of the above relations, now we develop another new bridge equation that relates metric functions through the vanishing complexity factor condition to solve the present system of equations in f(Q)-gravity regime. To do this, we first apply Herrera’s  [98, 99] definition of complexity factor for a self-gravitating system to derive the complexity factor in f(Q)-gravity factor and consequently condition on vanishing complexity factor. Using Herrera’s definition, we define complexity factor (\(Y^Q_{TF}\)) in f(Q)-gravity theory for the system (26)–(28) as,

$$\begin{aligned}{} & {} Y^Q_{TF} = (P^{\text {tot}}_r-P^{\text {tot}}_t)-\frac{1}{2r^3} \int ^r_0 x^3 (\rho ^{\text {tot}})^{\prime } (x) dx.~~~~ \end{aligned}$$
(33)

On inserting of \(P^{\text {tot}}_r\), \(P^{\text {tot}}_t\) and \(\rho ^{\text {tot}}\) in above equation, we \(Y_{TF}\) as

$$\begin{aligned}{} & {} Y^Q_{TF}=\frac{\beta _1\, \big [\Phi ^\prime \big \{r (\mu ^\prime -\Phi ^\prime )+2 \big \}-2 r \Phi ^{\prime \prime } \big ]}{4\, r\,e^{\mu } }. \end{aligned}$$
(34)

Then \(Y^Q_{TF}=0\) gives,

$$\begin{aligned}{} & {} \beta _1\, \big [\Phi ^\prime \big \{r (\mu ^\prime -\Phi ^\prime )+2 \big \}-2 r \Phi ^{\prime \prime } \big ]=0. \end{aligned}$$
(35)

Since \(\beta _1\) can not be zero therefore the second factor must be zero, which gives,

$$\begin{aligned}{} & {} \big [\Phi ^\prime \big \{r (\mu ^\prime -\Phi ^\prime )+2 \big \}-2 r \Phi ^{\prime \prime } \big ] = 0, \end{aligned}$$
(36)

The simplified form of the above differential equation can be written after performing the integration as [100]:

$$\begin{aligned}{} & {} \Phi ^\prime \,e^{\Phi /2}= A r\, e^{\mu /2}. \end{aligned}$$
(37)

where A is a constant on integration. Lastly, we derive the following relation between \(\Phi \) and \(\mu \) as,

$$\begin{aligned} e^{\Phi (r)}=\Bigg (A_1\,\int r\, e^{\mu (r)/2} dr +B_1 \Bigg )^2, \end{aligned}$$
(38)

where \(A_1\) and \(B_1\) are the constants of integration. It is very interesting to note that the vanishing of complexity factor condition under the f(Q)-gravity theory is the same as the condition derived in Einstein GR [100]. As mentioned above, our primary objective was to find an exact solution of the field equations (26)–(28) describing a compact star beyond the f(Q)-gravity theory. Therefore, we use a well-known technique of gravitational decoupling via the complete geometric deformation (CGD) approach in the next section.

3 Complexity free anisotropic solution via gravitational decoupling in f(Q)-gravity

In this section, we start with a complete geometric deformation (CGD) approach through a specific transformation along the gravitational potentials as,

$$\begin{aligned}{} & {} \Phi (r) \longrightarrow H(r)+\alpha \, \eta (r)~ \end{aligned}$$
(39)
$$\begin{aligned}{} & {} e^{-\mu (r)} \longrightarrow W(r)+\alpha \, \Psi (r).~~ ~~ \end{aligned}$$
(40)

here \(\eta (r)\) and \(\Psi (r)\) are known as a geometric deformation function corresponding to the temporal and radial metric components, respectively. The CGD approach gives us to set \( \eta (r) \ne 0\) and \(\Psi (r)\ne 0\). Moreover, this CGD technique divides the decoupled system (26)–(28) in f(Q)-gravity into two subsystems. In this regard, the first system is known as a seed system in pure f(Q)-gravity theory respective to the source \(T_{\epsilon \,\nu }\), while second system is for the new source \(\theta _{\epsilon \,\nu }\), which are given as,

I. System of field equations in pure f(Q)-gravity:

$$\begin{aligned} \rho= & {} \frac{\beta _1 (1-W) }{r^2}-\frac{W^{\prime } \beta _1 }{r}-\frac{\beta _2 }{2}, \end{aligned}$$
(41)
$$\begin{aligned} p= & {} \frac{\beta _1 (W-1) }{r^2}+\frac{H^{\prime } W \beta _1 }{r}+\frac{\beta _2 }{2}, \end{aligned}$$
(42)
$$\begin{aligned} p= & {} \frac{\beta _1(W^{\prime } H^{\prime } + 2 H^{\prime \prime } W +H^{\prime 2} W) }{4} +\frac{\beta _1\,(W^{\prime } +H^{\prime } W) }{2 r}\nonumber \\{} & {} +\frac{\beta _2}{2}, \end{aligned}$$
(43)

and according to the TOV Eq. (29),

$$\begin{aligned} -\frac{H^\prime }{2}(\rho +p)-\frac{dp}{dr}=0,~~ \end{aligned}$$
(44)

which is a TOV equation for the system (41)–(43) whose solution can be given by the following spacetime,

$$\begin{aligned} ds^2=-e^{H(r)}dt^2+\frac{dr^2}{W(r)}+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2, \end{aligned}$$
(45)

II. System of field equations for new source \(\theta _{\epsilon \nu }\):

$$\begin{aligned} \rho ^{\theta }= & {} -\beta _1 \Big (\frac{\Psi }{r^2}+\frac{\Psi ^\prime }{r}\Big ), \end{aligned}$$
(46)
$$\begin{aligned} p^{\theta }_r= & {} \beta _1\Big [\frac{\Psi }{r^2}+\frac{\Phi ^{\prime } \Psi }{r}+\frac{W\,\eta ^{\prime }}{r}\Big ], \end{aligned}$$
(47)
$$\begin{aligned} p^{\theta }_t= & {} \beta _1 \Big (\frac{1}{4} \Psi ^\prime \Phi ^{\prime } +\frac{1}{2} \Phi ^{\prime \prime } \Psi +\frac{1}{4} \Phi ^{\prime 2} \Psi +\frac{\Psi ^\prime }{2 r}+\frac{\Phi ^{\prime } \Psi }{2 r}\Big )\nonumber \\{} & {} +\beta _1\Big [\frac{W}{4}\,\big (2\,\eta ^{\prime \prime }+\beta _1\,\eta ^{{\prime }\,2}+\frac{2\,\eta ^{\prime }}{r}+2\,H^{\prime }\,\eta ^{\prime }\big )+\frac{W^{\prime }\,\eta ^{\prime }}{4}\Big ].~~~~~ \end{aligned}$$
(48)

The system of Eqs. (37)–(39) provide the following conservation equation,

$$\begin{aligned} -\frac{\Phi '}{2}(\rho ^{\theta }+p^{\theta })-(p^{\theta }_r)^{\prime }+\frac{2}{r}( p^{\theta }_{t}-p^{\theta }_r)= \frac{\eta ^\prime }{2}(\rho +p),\nonumber \\ \end{aligned}$$
(49)

which is a linear combination of Eqs. (46)–(48). Now, we have to solve both systems of equations under the condition (38). It is noted that the equation (38) may be solved if the metric potential \(\mu \) is known. For finding the potential \(\mu \), we must have W(r) and \(\Psi (r)\) in our hands. Moreover, the solution second system is also dependent on the first isotropic system. Therefore, we must solve the first system initially. For this purpose, we subtract Eqs. (42) and (43) to get the isotropy condition in f(Q)-gravity as,

$$\begin{aligned} 2 H'' r^2+H^{\prime 2} r^2-2 H' r-4+ \frac{W' r (H' r+2)+4}{ W} =0.\nonumber \\ \end{aligned}$$
(50)

If we look at the above Eq. (50), we find a very interesting result that the isotropic condition in f(Q)-gravity is similar to the isotropic condition in standard GR, which implies that any known isotropic solution in GR will be also an isotropic solution in f(Q)-gravity. Therefore, a well-behaved perfect fluid solution should be considered for which the Eq. (38) must be integrable. For this purpose, we consider a well-known perfect fluid solution corresponding to Buchdahl’s space-time geometry [101],

$$\begin{aligned} W(r)= & {} \frac{2-Cr^2}{2(1+Cr^2)}, \end{aligned}$$
(51)
$$\begin{aligned} H(r)= & {} 2\ln \big [A(1+Cr^2)^{3/2}+B(5+2Cr^2)\sqrt{2-Cr^2}\big ],\nonumber \\ \end{aligned}$$
(52)

Using the above spacetime geometry, the expressions for seed energy density and pressure in f(Q)-gravity are,

$$\begin{aligned} \rho (r)= & {} \frac{3\beta _1 C \left( C r^2+3\right) }{2\left( C r^2+1\right) ^2}-\frac{\beta _2}{2}, \end{aligned}$$
(53)
$$\begin{aligned} p(r)= & {} \frac{9\beta _1 C}{2 f_1(r)}\left[ A \left( 1-C r^2\right) \sqrt{2+C r^2-C^2 r^4}\right. \nonumber \\{} & {} \left. +B \left( 2 C^2 r^4-3 C r^2-2\right) \right] \frac{1}{ \left( C r^2+1\right) }+\frac{\beta _2}{2}, \end{aligned}$$
(54)

where,

$$\begin{aligned} f_1(r)= & {} B \left( 10-C r^2-2 C^2 r^4\right) +A \left( C r^2+1\right) \\ {}{} & {} \times \sqrt{-C^2 r^4+C r^2+2}. \end{aligned}$$

Now we still need to find the deformation function \(\Psi (r)\) to integrate the condition (38). For this purpose, we consider the mimicking of density constraint approach \(\rho =\rho ^\theta \) for determining the deformation function \(\Psi (r)\), which provides the following differential equation in \(\Psi (r)\) as,

$$\begin{aligned} \frac{d\Psi }{dr} + \frac{\Psi }{r} +\frac{3 r C \left( C r^2+3\right) }{2 \left( C r^2+1\right) ^2}- \frac{r \beta _2}{2 \beta _1}=0, \end{aligned}$$
(55)

After integrating the above differential equation, we find the solution of \(\Psi (r)\),

$$\begin{aligned} \Psi (r)=\frac{r^2 \left[ \beta _2 \left( C r^2+1\right) -9 \beta _1 C\right] }{6 \left[ \beta _1 \left( C r^2+1\right) \right] }+\frac{F}{r}. \end{aligned}$$
(56)

Here F denotes the arbitrary constant of integration which is taken F to be zero throughout the study in order to avoid singularity at the center. In this regard, the new form of the metric function \(e^{\mu }\) is,

$$\begin{aligned} e^{-\mu (r)}=\frac{6 \beta _1-3 (3 \alpha +1) \beta _1 C r^2+\alpha \beta _2 r^2 \left( C r^2+1\right) }{6 \beta _1 \left( 1+ C r^2\right) }.\nonumber \\ \end{aligned}$$
(57)

By plugging of deformed metric function \(\mu (r)\) from Eq. (57) into vanishing complexity factor condition (38) we find generalized form of metric function \(\Phi \) as,

$$\begin{aligned} e^{\frac{\Phi (r)}{2}}= & {} \frac{A_1}{\sqrt{2} (3 \alpha +1)^{3/2} C \sqrt{1+C r^2}} \left[ \sqrt{\frac{1+C r^2}{2-(3 \alpha +1) C r^2}}\right. \nonumber \\{} & {} \times \left( \sqrt{3 \alpha +1} \sqrt{C r^2+1} \left\{ (3 \alpha +1) C r^2-2\right\} -3 (\alpha +1)\right. \nonumber \\{} & {} \times \sqrt{2-(3 \alpha +1) C r^2} \tan ^{-1}\nonumber \\{} & {} \left. \left. \times \left( \frac{\sqrt{2-(3 \alpha +1) C r^2}}{\sqrt{3 \alpha +1} \sqrt{C r^2+1}}\right) \right) \right] +B_1, \end{aligned}$$
(58)

and consequently, other deformation function \(\eta (r)\) can be written from Eq. (39) as: \(\eta (r)=\frac{1}{\alpha } \big [\Phi (r)-H(r) \big ]\), which gives the expression of \(\eta (r)\),

$$\begin{aligned} \eta (r)= & {} \frac{1}{\alpha }\left[ 2 \log \Bigg (\frac{A_1\,(3 \alpha +1)^{-3/2}}{\sqrt{2} C \sqrt{1+C r^2}}\right. \nonumber \\{} & {} \times \left\{ \sqrt{\frac{1+C r^2}{2-(3 \alpha +1) C r^2}} \left( \sqrt{3 \alpha +1} \sqrt{C r^2+1}\right. \right. \nonumber \\{} & {} \times \left\{ (3 \alpha +1) C r^2-2\right\} -3 (\alpha +1) \nonumber \\{} & {} \times \sqrt{2-(3 \alpha +1) C r^2} \tan ^{-1}\nonumber \\{} & {} \left. \left. \times \left( \frac{\sqrt{2-(3 \alpha +1) C r^2}}{\sqrt{3 \alpha +1} \sqrt{C r^2+1}}\right) \right) \right\} +B_1\Bigg )\nonumber \\{} & {} \left. -2 \log \left\{ A \left( C r^2+1\right) ^{3/2} +B \frac{\left( 2 C r^2+5\right) }{(2-C r^2)^{-1/2}}\right\} \right] ,\nonumber \\ \end{aligned}$$
(59)
Fig. 1
figure 1

The flow chart for anisotropic generalization of Buchdahl’s perfect fluid model to the anisotropic domain in f(Q)-gravity using gravitational decoupling with the vanishing complexity factor condition

Full size image

On inserting of both deformation functions \(\Psi (r)\) and \(\eta (r)\) in the Eqs. (46)–(48), we find the components for \(\theta \)-sector as,

$$\begin{aligned} \rho ^{\theta }(r)= & {} \frac{3\,C \beta _1 \left( C r^2+3\right) }{2\left( C r^2+1\right) ^2}, \end{aligned}$$
(60)
$$\begin{aligned} p^{\theta }_r(r)= & {} -\frac{\beta _1 }{2 \left( C r^2+1\right) } \left[ 3 C \left( \frac{4 (3 \alpha +1)^{3/2} A_1 C r^2 \sqrt{2 C r^2+2} \sqrt{\frac{C r^2+1}{2-(3 \alpha +1) C r^2}}}{H_{11}(r)}+1\right) +H_1(r) \left( C r^2-2\right) \right] , \end{aligned}$$
(61)
$$\begin{aligned} p^{\theta }_t(r)= & {} -\frac{3\beta _1 C r^2}{4 \left( C r^2+1\right) } \left[ -\frac{8 (3 \alpha +1)^3 A_1^2C^2 r^2 \left( C r^2+1\right) \left( 2C r^2+2\right) }{H^2_{11}(r) \left( (3 \alpha +1)C r^2-2\right) } +\frac{4 (3 \alpha +1)^{3/2} A_1C \sqrt{2C r^2+2} \sqrt{\frac{C r^2+1}{2-(3 \alpha +1)C r^2}}}{H_{11}(r)} +N_1(r) \right] \nonumber \\{} & {} \quad -\frac{3\beta _1C}{2 \left( C r^2+1\right) ^2} \left( \frac{2 (3 \alpha +1)^{3/2} A_1C r^2 \sqrt{2C r^2+2} \sqrt{-\frac{C r^2+1}{2-(3 \alpha +1)C r^2}}}{H_{11}(r)}+1\right) +\beta _1 f_2(r), \end{aligned}$$
(62)

where,

$$\begin{aligned}{} & {} f_2(r)=\frac{1}{8 \left( C r^2+1\right) ^2}\Bigg [\left( 2-C r^2\right) \left( C r^2+1\right) \\{} & {} \quad \times \Bigg (\frac{12 Cr^2 H_1(r) \left( A \sqrt{-C^2 r^4+C r^2+2}-2 B C r^2+B\right) }{A \left( C r^2+1\right) \sqrt{-C^2 r^4+C r^2+2}-B \left( 2 C^2 r^4+C r^2-10\right) }\\{} & {} \quad +2 H_2(r)+\alpha r^2 H^2_1(r)+2 H_1(r)\Bigg )-6 C r^2 H_1(r) \Bigg ]. \end{aligned}$$

The expressions for other symbols used in the above Eqs. (61) and (62) used are given in the appendix. Furthermore, a complete mechanism for generating the anisotropic solution from the perfect fluid solution in f(Q)-gravity theory using extended gravitational decoupling along with the complexity-free condition is shown in Fig. 1. In this regard, it is necessary to mention that the idea of generating the anisotropic solution from perfect fluid distribution using gravitational decoupling was introduced by Ovalle [102]. Some other seminal works can be found in the following Refs. [103,104,105,106,107].

4 Matching condition in f(Q)-gravity

As stated previously that the Schwarzschild (Anti-) de Sitter solution is the most suitable exterior solution in the f(Q)-gravity theory in the context of the linear functional form of f(Q) given in Eq. (25). Therefore, all the solution’s constant must be obtained by joining the interior spacetime with exterior Schwarzschild (Anti-) de Sitter spacetime at the pressure-free boundary \(r=R\). The exterior Schwarzschild (Anti-) de Sitter spacetime is given by

$$\begin{aligned} ds^2_+= & {} -\bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )\,dt^2+\frac{dr^2}{\bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )} \nonumber \\ {}{} & {} +r^2 \Big (d\theta ^2 +\sin ^2\theta \,d\phi ^2 \Big ).~~~~~ \end{aligned}$$
(63)

The suitable boundary conditions are known as the first and second fundamental forms which can be derived by matching the interior spacetime with exterior spacetime at \(r=R\) via Darmois–Israel boundary conditions [108, 109]. These conditions can be expressed mathematically as,

$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{\nu (R)},~~~ \end{aligned}$$
(64)
$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{-\lambda (R)},~~~ \end{aligned}$$
(65)
$$\begin{aligned} P_r(R)= & {} 0. \end{aligned}$$
(66)

Here, M and \(\Lambda \) denote the total mass and the cosmological constant, respectively. Thus, in principle, in the regime restricted by the constants \(\beta _1\) and \(\beta _2\), the cosmological constant \(\Lambda \) can be expressed in the form \(\Lambda =\beta _2/2\beta _1\). Based on the most recent observational evidence, the value of the cosmological constant \(\Lambda \) in the present cosmos is approximately \(10^{-46}/km^2\). Nevertheless, the current stellar configurations will only be slightly affected by this value of the cosmological constant \(\Lambda \), therefore it can be taken to be zero, which indicates that \(\beta _2=0\). For the rest of the study, we will assume that \(\beta _2=0\). We derive formulas for arbitrary constants using the boundary conditions (64)–(66),

$$\begin{aligned} \frac{A_1}{B1}= & {} -\Bigg [3 \sqrt{6 \alpha +2} \left( 3 \alpha ^2+4 \alpha +1\right) C \left( C R^2+1\right) \Bigg ]\Big /\nonumber \\ {}{} & {} \left[ \sqrt{\frac{C R^2+1}{2-(3 \alpha +1) C R^2}} \Bigg (\sqrt{3 \alpha +1} (15 \alpha +7) \left( C R^2+1\right) \right. \nonumber \\ {}{} & {} \times \Big [(3 \alpha +1) C R^2-2\Big ]-9 (\alpha +1)^2 \sqrt{2-(3 \alpha +1) C R^2} \nonumber \\ {}{} & {} \left. \times \sqrt{C R^2+1} ~~\tan ^{-1}\left( \frac{\sqrt{2-(3 \alpha +1) C R^2}}{\sqrt{3 \alpha +1} \sqrt{C R^2+1}}\right) \Bigg )\right] ,~~~~ \end{aligned}$$
(67)
$$\begin{aligned} B_1= & {} \Bigg [(3 \alpha +1)^{3/2} C \sqrt{2 C R^2+2} \sqrt{\frac{2-(3 \alpha +1) C R^2}{2 C R^2+2}}\Bigg ]\Big /\nonumber \\ {}{} & {} \times \Bigg [\frac{A_1}{B_1} \sqrt{-\frac{C R^2+1}{(3 \alpha +1) C R^2-2}} \left( \sqrt{3 \alpha +1} \sqrt{C R^2+1} \right. \nonumber \\ {}{} & {} \times \Big [(3 \alpha +1) C R^2-2\Big ]-3 (\alpha +1) \sqrt{2-(3 \alpha +1) C R^2}\nonumber \\ {}{} & {} \left. \times \tan ^{-1}\left( \frac{\sqrt{2-(3 \alpha +1) C R^2}}{\sqrt{3 \alpha +1} \sqrt{C R^2+1}}\right) \right) +(3 \alpha +1)^{3/2} C\nonumber \\ {}{} & {} \times \sqrt{2 C R^2+2}\Bigg ].~~~ \end{aligned}$$
(68)
Fig. 2
figure 2

The figures show the variation of effective density (\(\rho ^{\text {tot}}\))-top left, radial pressure (\(P^{\text {tot}}_r\))-top right panel, tangential pressure (\(P^{\text {tot}}_t\))-bottom left panel and anisotropy (\(\Delta ^{\text {tot}}\))-bottom right panel versus radial coordinate r within the stellar object for different \(\alpha \) with constant values \(C=0.0043~\text {km}^{-2}\), and \(\beta _1=0.66~\text {km}^{2}\)

Full size image

5 Physical analysis of complexity free anisotropic solution in f(Q)-gravity

In this section, we give a thorough physical analysis of our solutions presented here for anisotropic stellar configurations induced by gravitational decoupling with vanishing complexity factor in f(Q)-gravity theory. To see how they hold up physically, we will examine the graph’s tendencies for different values of decoupling constant \(\alpha =0.0,~0.05,~0.10,~\text {and}~0.15\). The case \(\alpha =0.0\) yields a situation in a pure f(Q)-gravity theory. It is also mentioned that the solution is not well-behaved when \(\alpha > 0.18\) due to a violation of the causality condition.

Fig. 3
figure 3

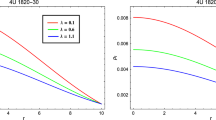
The figures show the variation of the radial velocity of sound (\(\text {v}^2_r\))-left panel and tangential velocity of sound (\(\text {v}^2_t\))-right panel versus radial coordinate r within the stellar object for different \(\alpha \) with constant values \(C=0.0043~\text {km}^{-2}\), and \(\beta _1=0.66~\text {km}^{2}\)

Full size image

5.1 Physical behavior of density, pressures, and anisotropy inside the compact objects

Let us start by analyzing the physical behavior of the matter variables, namely, effective density (\(\rho ^{\text {tot}}\)), radial pressure (\(P^{\text {tot}}_r\)), tangential pressure (\(P^{\text {tot}}_t\)) and anisotropy (\(\Delta ^{\text {tot}}\)) versus radial coordinate r within the stellar configurations. These matter variables are displayed in Fig. 2, at each interior point of the compact objects. The three effective quantities: \(\rho ^{\text {tot}}\), \(P^{\text {tot}}_r\), and \(P^{\text {tot}}_t,\) fall off smoothly as they move from the core toward the stellar surface. We have fixed the contributions from the nonmetricity scalar, Q, denoted by \(\beta _1=0.66~\text {km}^2\), while varying the decoupling constant, \(\alpha \). It is obvious that the magnitude of density for the compact object grows as \(\alpha \) grows. However, since there is no energy transfer to the surrounding space-time, then effective radial pressure disappears at the stellar surface, as we anticipated. We also note that the magnitude of effective pressure components rises when the decoupling constant, denoted by \(\alpha \), increases, as well as the effective tangential pressure dominates its radial counterpart. On the other hand, the effective anisotropy factor \(\Delta ^{\text {tot}}\) is positive in all stellar configurations, which leads to the production of a repulsive force. This repulsive force aids in balancing the inwardly directed gravitational force. It is intriguing to note that the effective anisotropy factor \(\Delta ^{\text {tot}}\) rises as the decoupling constant \(\alpha \) rises, emphasizing that the decoupling constant \(\alpha \) has a significant effect on the strengthening the force owing to anisotropy.

5.2 Causality conditions and stability

In astrophysics, when analyzing any physically viable system, the stability of the stellar configurations plays a crucial role. By using superluminal speeds based on Herrera’s cracking concept [110], we discuss the stability for anisotropic stellar configurations generated by gravitational decoupling with vanishing complexity factor in f(Q)-gravity theory. According to the causality condition, physically stable structures in the interior geometry of stellar objects require that the squared speed of sound, denoted by the formula \(\text {v}_s^2 = dp/d\rho \), must be within the range [0, 1], i.e., \(0\le \text {v}_s^2 = dp/d\rho \le 1\). In this regard, Herrera [110] has developed the idea of cracking, by taking into account a distinct method for obtaining potentially stable or unstable regions of compact stellar structures. These regions are assessed using the formula \(-1\le |\text {v}_{t}^2-\text {v}_{r}^2| \le 0\) (stable regions) and \( 0\le |\text {v}_{t}^2-\text {v}_{r}^2| \le 1\) (unstable regions), where \(\text {v}_{r}^2\) and \(\text {v}_{t}^2\) stand for squared sound speed in the radial and tangential directions, respectively. To ensure the stability analysis, we present the sound speeds in Fig. 3. It is seen that the sound speeds are less than the speed of light (taking into account that the speed of light is unity in relativistic units) and the radial speed of sound is always greater than within the object for each \(\alpha \) which interprets that our resulting complexity free anisotropic stellar solutions in f(Q)-gravity theory generated by gravitational decoupling satisfies the causality and stability condition for all adopted values of the decoupling constant \(\alpha \) and the contributions from the non-metricity scalar, Q, denoted by \(\beta _1\).

Fig. 4
figure 4

The behavior of adiabatic index (\(\Gamma \)) versus radial coordinate r with same constant values as used in Fig. 3

Full size image
Table 1 Numerical values of the physical parameters by taking different values of decoupling constant \(\alpha \) for fixed \(\beta _1=0.66~(\text {km})^2\) and \(R=13.44~\text {km}\)
Full size table

5.3 Adiabatic index and stability

We keep focusing on the stability of our stellar models generated by gravitational decoupling with vanishing complexity factor in f(Q)-gravity theory, but this time, we do so using the adiabatic stability criterion, which was originally inferred by Chandrasekhar [111, 112] for isotropic pressure gradients. This adiabatic stability criterion was described by the following formula:

$$\begin{aligned} \Gamma = \left( 1+\frac{\rho }{p}\right) \left( \frac{dp}{d\rho }\right) _S, \end{aligned}$$
(69)

with \(\Gamma >4/3\) as the limiting case for constrained structures with isotropic pressure, p. Here, the velocity of sound is denoted by \(\frac{dp}{d\rho }\) and the subscript S signifies a constant specific entropy. This condition (69) gets modified when anisotropy and dissipation are involved, according to findings by Herrera et al. [113, 114]. In the presence of pressure anisotropy, the stability criterion modifies and takes the following form,

$$\begin{aligned} \Gamma < \frac{4}{3} + \left[ -\frac{4}{3}\frac{(P^{\text {tot}}_r - P^{\text {tot}}_t)}{|(P^{\text {tot}}_r)'|r}\right] , \end{aligned}$$
(70)

where the prime displays differentiation with regard to the radial coordinate r. For unstable regions, the Newtonian limit, \(\Gamma < 4/3\), is generated by the vanishing of the second term in (70), which occurs by relativistic contributions.

However, the adiabatic index can be modified by radial heat transfer dissipation or the occurrence of density inhomogeneities. It has been shown by Moustakidis [115] that the critical value for the adiabatic index is given by,

$$\begin{aligned} \Gamma _{crit} = \frac{4}{3} + \frac{19}{21}\frac{M}{R}, \end{aligned}$$
(71)

where the stellar model’s compactness is represented by the ratio M/R. Moustakidis [115] argued that stability versus radial perturbations ensures the stability of relativistic fluid configurations if \(\Gamma >\Gamma _{crit}\). The Chandrasekhar stability criterion is satisfied by our complexity-free anisotropic stellar models in f(Q)-gravity theory generated by gravitational decoupling, as shown in Fig. 4, since the adiabatic index \(\Gamma \) is rising and exceeds 4/3 everywhere in the anisotropic stellar models for each \(\alpha \). It is worth noting that the stronger stability criterion, \(\Gamma _{crit}\), which is not satisfied in pure f(Q)-gravity theory, i.e., \(\Gamma _{0}<\Gamma _{crit}\) for \(\alpha =0\), (where \(\Gamma _{0}\) denotes the central values of the adiabatic index \(\Gamma \)) but this has been ensured in f(Q)-gravity in the presence of gravitational decoupling, i.e., \(\Gamma _{0}>\Gamma _{crit}\), as illustrated in Table 1. This demonstrates how stable configurations can be generated from unstable models using the gravitational decoupling approach.

5.4 Energy conditions

In this section, we discuss the energy conditions (ECs) to understand the geodesics of the Universe. Such conditions can be established by using the well-known Raychaudhury’s equations [116] which satisfy the following equations under the attractive gravity,

$$\begin{aligned}{} & {} R_{\epsilon \nu } u^\epsilon u^\nu \ge 0,\end{aligned}$$
(72)
$$\begin{aligned}{} & {} R_{\epsilon \nu } n^\epsilon n^\nu \ge 0, \end{aligned}$$
(73)

where \(u^\nu \) and \(n^\nu \) denote the vector field and null vector. Therefore, under the anisotropic matter distribution, the energy conditions in f(Q) recovered from standard GR as [41],

$$\begin{aligned}{} & {} \mathrm{(i)}~~ \text {null~ energy~ condition~(NEC)}:~~\nonumber \\ {}{} & {} \quad \rho ^{\text {tot}}+P_r^{\text {tot}} \ge 0,~~~~~ \end{aligned}$$
(74)
$$\begin{aligned}{} & {} \mathrm{(ii)}~~ \text {weak~ energy~ condition~(WEC)}: ~~\nonumber \\ {}{} & {} \quad \rho ^{\text {tot}}\ge 0,~~~ \rho ^{\text {tot}}+P_r^{\text {tot}} \ge 0, ~ \end{aligned}$$
(75)
$$\begin{aligned}{} & {} \mathrm{(iii)}~~ \text {strong~ energy~ condition~(SEC)}:~~\nonumber \\ {}{} & {} \quad \rho ^{\text {tot}}+P_r^{\text {tot}}+2\,P_t^{\text {tot}} \ge 0,~~~~~ \end{aligned}$$
(76)
$$\begin{aligned}{} & {} \mathrm{(iv)} ~~\text {dominant~ energy~ condition~(DEC)}:~~ ~~\nonumber \\ {}{} & {} \quad ~\rho ^{\text {tot}}\ge 0,~ \rho ^{\text {tot}}-|P_r^{\text {tot}}|\ge 0,~~~\rho ^{\text {tot}}-|P_t^{\text {tot}}|\ge 0.~~~ \end{aligned}$$
(77)

Since total pressures (\(P_r^{\text {tot}}\) & \(P_t^{\text {tot}}\)) and total energy density are positive throughout the model which can be visualized from Fig. 2. Then NEC, WEC, and SEC energy conditions are automatically fulfilled. Only we need to check the dominant energy condition (DEC) for the model. For this purpose, we draw the Fig. 5 for the dominant energy condition. From this Fig. 5, it is observed that the dominant energy condition is also fulfilling for our model.

Fig. 5
figure 5

The behavior of (\(\rho ^{\text {tot}}-P_r^{\text {tot}}\)) and (\(\rho ^{\text {tot}}-P_t^{\text {tot}}\)) versus radial coordinate r with same constant values as used in Fig. 3

Full size image

5.5 Mass measurements of anisotropic star via equi-mass diagram on \(R-\alpha \), \(R-\beta _1\), and \(\alpha -\beta _1\) planes

In this section, we measure the mass of the anisotropic star through the equi-mass diagram on different \(R-\alpha \), \(R-\beta _1\), and \(\alpha -\beta _1\) planes. Figure 6 shows the mass distribution on \(R-\alpha \) plane with fixing \(\beta _1=0.66~\text {km}^2\). It can be observed that if we increase the radius R and fix \(\alpha \), then the mass of the star is also increasing. On the other hand, if we fix the radius between 0 to 10, then no deviation in mass is observed for all \(\alpha \in [0,0.18]\) but when \(r\ge 10\), then we start observing that the mass is increasing with increasing \(\alpha \). This increment is maximum when \(R=13.44~\text {km}\). The maximum mass is observed \(2.3~M_{\odot }\) for \(\alpha =0.18\) and \(R=13.44~\text {km}\).

Fig. 6
figure 6

The equi-mass diagram on \(R-\alpha \) plane with constant value \(C=0.0043~\text {km}^{-2}\), and \(\beta _1=0.66~\text {km}^{2}\)

Full size image
Fig. 7
figure 7

The equi-mass diagram on \(R-\beta _1\) plane with constant value \(C=0.0043~\text {km}^{-2}\), and \(\alpha =0.1\)

Full size image

Now we move to Fig. 7, which is showing the equi-mass diagram on \(R-\beta _1\) plane with fixing \(\alpha =0.1\). As we can observe clearly from this figure that the pattern of mass distribution on the \(R-\beta _1\) plan is similar to the \(R-\alpha \) plane as discussed above. It is important to mention that the star becomes too massive when we increase \(\beta _1\) with \(R=13.44~\text {km}\). This implies that the total mass of the anisotropic star in f(Q)-gravity can be controlled by coupling parameter \(\beta _1\).

Finally, the last Fig. 8 is showing for the mass distribution on \(\alpha -\beta _1\) plane with fixed radius \(R=13.44~\text {km}\). As we can observe that if we fix \(\beta _1 \in [0.6,1.2]\) and increase \(\alpha \), then mass also increases but this increment can be clearly noticed when \(\beta _1\) is high. Similarly, if \(\beta _1\) increases with fixing \(\alpha \in [0,0.18]\), the mass is also increasing. This implies that the mass of the objects depends on both parameters \(\alpha \) and \(\beta _1\).

6 Energy exchange between the sources \(T_{\epsilon \nu }\) and \(T^\theta _{\epsilon \nu }\)

Before going to discuss the direct analysis of the energy exchange between the sources, it is necessary to mention why the energy exchange is required in the context of extended gravitational decoupling. In this regard, Ovalle [60] proved that both sources \(T_{\epsilon \nu }\) and \(T^\theta _{\epsilon \nu }\) can be successfully decoupled as long as there is the exchange of energy between them. This concept can be understood by the following explanations: Since the Einstein tensor \(G^{\{H,W\}}_{\epsilon \nu }\) for the line element (45) fulfills its corresponding Bianchi identity, then the energy-momentum tensor \(T_{\epsilon \nu }\) is conserved in this spacetime geometry, which is shown by Eq. (44), explicitly we can write as,

$$\begin{aligned} \bigtriangledown ^{\{H,W\}}_\epsilon \, T^{\epsilon }_ {\nu }=0, \end{aligned}$$
(78)
Fig. 8
figure 8

The equi-mass diagram on \(\alpha -\beta _1\) plane with constant value \(C=0.0043~\text {km}^{-2}\), and \(R=13.44\)

Full size image
Fig. 9
figure 9

Left panel: The variation of energy exchange \(\Delta E\) on \(r-\alpha \) plane for \(C=0.0043~\text {km}^{-2}\), \(\beta _1=0.66~\text {km}^2\) and \(A/B=-0.5\). Right panel: The variation of energy exchange \(\Delta E\) on \(r-\alpha \) plane for \(C=0.0043~\text {km}^{-2}\), \(\beta _1=0.66~\text {km}^2\) and \(A/B=0.5\)

Full size image
Fig. 10
figure 10

Left panel: The variation of energy exchange \(\Delta E\) on \(r-\beta _1\) plane for \(C=0.0043~\text {km}^{-2}\), \(\alpha =0.1\) and \(A/B=-0.5\). Right panel: The variation of energy exchange \(\Delta E\) on \(r-\beta _1\) plane for \(C=0.0043~\text {km}^{-2}\), \(\alpha =0.1\) and \(A/B=0.5\)

Full size image
Fig. 11
figure 11

Left panel: The variation of energy exchange \(\Delta E\) on \(\beta _1-\alpha \) plane for \(C=0.0043~\text {km}^{-2}\), \(R=13.44~\text {km}\) and \(A/B=-0.5\). Right panel: The variation of energy exchange \(\Delta E\) on \(r-\beta _1\) plane for \(C=0.0043~\text {km}^{-2}\), \(R=13.44~\text {km}\) and \(A/B=0.5\)

Full size image

where \(\bigtriangledown ^{\{H,W\}}\) implies the above divergence is calculated in the connection to the metric (45). We note that

$$\begin{aligned} \bigtriangledown _\epsilon \, T^{\epsilon }_{ \nu } = \bigtriangledown ^{\{H,W\}}_\epsilon \, T^{\epsilon }_{\nu }-\frac{\alpha \,\eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu , \end{aligned}$$
(79)

here the divergence shown in the left-hand side is calculated in connection to the deformed spacetime given by Eq. (15). In view of Eqs. (17) and (18), the Eq. (4) leads,

$$\begin{aligned}{} & {} -\frac{H^{\prime }}{2}\,({T}^0_{0}-{T}^1_{1})+({T}^1_{1})^{\prime }-\frac{2}{r}\,({T}^2_{2}-{T}^1_{1})-\frac{\alpha \eta ^{\prime }}{2} ({T}^0_{0}-{T}^1_{1}) \nonumber \\ {}{} & {} -\frac{\Phi }{2} \Big ([T^\theta ]^0_0-[T^\theta ]^1_1\Big ) +\Big ([T^\theta ]^{1}_{1}\Big )^{\prime }-\frac{2}{r}\,\Big ([T^\theta ]^{2}_{2}-[T^\theta ]^{1}_{1}\Big )=0,\nonumber \\ \end{aligned}$$
(80)

As expected, the Eq. (78) will provides the explicit form,

$$\begin{aligned}{} & {} -\frac{H^{\prime }}{2}\,({T}^0_{0}-{T}^1_{1})+({T}^1_{1})^{\prime }-\frac{2}{r}\,({T}^2_{2}-{T}^1_{1})=0,~~~~ \end{aligned}$$
(81)

which is a linear combination of the Einstein field equations (41)–(43). Thus we can confirm that the source \(T_{\epsilon \nu }\) has been successfully decoupled from the system (26)–(28). Finally, by considering the condition (78), the Eq. (80) gives,

$$\begin{aligned}{} & {} \bigtriangledown _\epsilon \, T^{\epsilon }_{ \nu } =-\frac{\alpha \, \eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu , \end{aligned}$$
(82)

and

$$\begin{aligned}{} & {} \bigtriangledown _\epsilon \, [T^\theta ]^{\epsilon }_{ \nu }= \frac{\alpha \, \eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu . \end{aligned}$$
(83)

In the above equations, the divergence is calculated in connection to the deformed spacetime (15). Also, the Eq. (83) is a linear combination of “quasi-Einstein” field equations (46)–(48) in f(Q)-gravity. Based on the above explanation, it can be clearly observed that both sources \(T_{\epsilon \nu }\) and \(T^{\theta }_{\epsilon \nu }\) can be successfully decoupled as long as there is an exchange of energy between both the sources.

Later on a critical phenomenon of the energy exchange between both sources \(T_{\epsilon \nu }\) and \(T^{\theta }_{\epsilon \nu }\) was initially discussed by Ovalle et al. [117] and Contreras & Stuchlik [118]. According to them, the energy exchange between the sources was denoted by \( \Delta E\) and determined by the formula,

$$\begin{aligned} \Delta E=\frac{\eta ^\prime }{2} \big (p + \rho \big ). \end{aligned}$$
(84)

Since p and \(\rho \) are positive then from above equation (84, if \(\eta ^\prime >0\) means \(\Delta E>0\), then Eq. (83) yields \(\bigtriangledown _\epsilon \, [T^\theta ]^{\epsilon }_{ \nu }>0\). In this situation, the new source \( {T^\theta }_{\epsilon \nu }\) is giving energy to the environment while the opposite occurs when \(\eta ^\prime <0\).

Then, using Eqs. (53), (54) and (59) into Eq. (84), we find the expression for Energy exchange,

$$\begin{aligned} \Delta E= & {} -3 C \beta _1 r H_1(r) \Big [A \sqrt{2-C^2 r^4+C r^2} (3-C^2 r^4 \nonumber \\{} & {} +2 C r^2)+B \left( 2 C r^2+3\right) \left( C r^2-2\right) ^2\Big ]\Big /\Big [2 \left( C r^2+1\right) ^2 \nonumber \\ {}{} & {} \times \Big \{B \left( 2 C^2 r^4+C r^2-10\right) -A \left( C r^2+1\right) \nonumber \\ {}{} & {} \quad \times \sqrt{2-C^2 r^4+C r^2}\Big \}\Big ]. \end{aligned}$$
(85)

Figure 9 shows the distribution of energy exchange (\(\Delta E\)) between the relativistic fluids on the \(r-\alpha \) plane for the constant value \(A/B=-0.5\) (left panel) and \(A/B=0.5\) (right panel) with fixed \(C=0.0043~\text {km}^{-2}\) and \(\beta _1=0.66~\text {km}^{-2}\). It can be observed from both the left and right panels of this Fig. 9 that the \(\Delta E\) is positive. This shows that the new source \(T^\theta _{\epsilon \nu }\) always gives the energy to the perfect fluid matter distribution. Also, there is no energy exchange between the fluid distributions near the core for all \(\alpha \in [0.6, 1.2]\). But the value of \(\Delta E\) is maximum and positive at \(\alpha \approx 0.025\) when \(7\le r \le 11\) and \(9\le r \le 12\) for \(A/B=-0.5\) and \(A/B=0.5\), respectively. The magnitude of the maximum value decreases and moves near the boundary when A/B increases. Also, the value of \(\Delta E\) is ruled out for \(\alpha < 0.025\).

The energy exchange between the relativistic fluids on \(r-\beta _1\) plane is shown in Fig. 10 for \(A/B=-0.5\) (left panel) and \(A/B=0.5\) (right panel) with fixed \(C=0.0043~\text {km}^{-2}\) and \(\alpha =0.1~\text {km}^{-2}\). It can be observed from both figures that \(\Delta E\) is positive at each point of \(r-\beta _1\) plane which shows the new source \(T^\theta _{\epsilon \nu }\) is giving the energy to the perfect fluid matter distribution in this case also. Also, there is no energy exchange between the relativistic fluids near the core i.e. when \( r\le 1\) but when \(r>1\), then \(\Delta E\) increases with increasing \(\beta _1\). The maximum value of \(\Delta E\) is achieved between \(6\le r \le 10\) at \(\beta _1=1.2~\text {km}^{-2}\) which is \(\Delta E=0.0053\) and \(\Delta E=0.0054\) for \(A/B=-0.5\) (left panel) and \(A/B=0.5\) (right panel), respectively. This implies that when A/B increases then \(\Delta E\) will also increase. The next Fig. 11 shows the mass distribution on \(\beta _1-\alpha \) plane with fixed radius \(r=13.44~\text {km}\) for \(A/B=-0.5\) (left panel) and \(A/B=0.5\) (right panel). For fixing \(\beta _1\) and increasing \(\alpha \), the energy exchange \(\Delta E\) decreases while it is increasing for increasing \(\beta _1\) and fixed \(\alpha \). It is also noticed that \(\Delta E\) is positive throughout the \(\beta _1-\alpha \) plane which means the new source is giving the energy to the environment. Furthermore, the maximum value of \(\Delta E\) in both cases is achieved when \(\beta _1 \approx 1.2\) and \(\alpha \approx 0.3\). Also, we observe that \(max\{\Delta E\}_{A/B=-0.5} < max\{\Delta E\}_{A/B=0.5} \) which implies \(max\{\Delta E\}\) is increasing when A/B increases. Furthermore, the value of \(\Delta E\) is ruled out for \(\alpha <0.03\). Finally, we concluded that both constants \(\beta _1\) and \(\alpha \) play an important role to predict how much amount of energy is exchanged between the sources.

7 Concluding remarks

In this work, we have successfully investigated the complexity-free spacetime for anisotropic self-gravitating stellar configurations generated by gravitational decoupling in f(Q)-gravity theory. In this context, the gravitational decoupling via CGD approach basically enlarged spherical isotropic solutions by incorporating an anisotropic gravitational source. It should be noted that we have employed this CGD technique and transformed both the temporal and radial metric potentials, which divides the decoupled system of non-linear field equations in f(Q)-gravity into two subsystems. One set corresponding to the seed source and the other one involves extra source terms. The effects of a new gravitational source have been introduced to the well-known perfect fluid solution that corresponds to Buchdahl’s space-time geometry in order to test the consistency of the CGD approach with this f(Q)-gravity theory. While the conservation equation for the matter sources expressed in (46) has shown the energy exchange between the two sources. Moreover, all the solution’s constants were determined by joining the interior spacetime with exterior Schwarzschild (Anti-) de Sitter spacetime at the pressure-free boundary \(r=R\).

The eventual model has been carefully analyzed and obeys the necessary conditions for viability inside the stellar fluid’s interior. The effective energy density and effective pressure stresses are physically well-behaved and reflect the properties for realistic stellar objects. For anisotropic solutions, we have found that the magnitude of effective pressure stresses rises when the decoupling constant, denoted by \(\alpha \), increases, as well as the effective tangential pressure, dominates its radial counterpart which results in a repulsive force aids in balancing the inwardly directed gravitational force. Moreover, the behavior of the effective anisotropy factor rises as \(\alpha \) rises, highlighting the fact that the decoupling constant \(\alpha \) significantly affects the force’s ability to be strengthened due to anisotropy. Our model is stable for all chosen values of the decoupling constant, \(\alpha \), and the contributions from the non-metricity scalar, Q, denoted by \(\beta _1\), according to a stability analysis employing superluminal speeds based on Herrera’s cracking concept and the anisotropic generalization of the Chandrasekhar adiabatic index. However, the most crucial point is that when gravitational decoupling is taken into account, the stronger stability criterion,\(\Gamma _{crit}\), which is not satisfied in pure f(Q)-gravity theory, i.e., \(\Gamma _{0}<\Gamma _{crit}\) for \(\alpha =0\), becomes ensured in f(Q)-gravity, i.e., \(\Gamma _{0}>\Gamma _{crit}\). This shows how the gravitational decoupling approach can generate stable configurations from unstable models. An intriguing finding is the mass measurements of anisotropic star predicted by equi-mass diagram on different \(R-\alpha \), \(R-\beta _1\), and \(\alpha -\beta _1\) planes. Here we showed that our equi-mass diagram predicts a maximum mass of \(2.3~M_{\odot }\) for \(\alpha =0.18\) when \(R=13.44~\text {km}\), and the star becomes excessively massive when we increase \(\beta _1\) with \(R=13.44~\text {km}\). Moreover, the total mass of the anisotropic star in f(Q)-gravity can be controlled by both parameters \(\alpha \) and \(\beta _1\). This experiment has shown how useful the gravitational decoupling approach is for constructing astrophysical models that are coherent with empirical occurrences.