Evidence of $A_{CP}(D^0\rightarrow \pi ^+\pi ^-)$ implies observable CP asymmetry in the $D^0\rightarrow \pi ^0\pi ^0$ decay

Abstract

Inspired by the recent measurement of CP asymmetry in the individual mode on LHCb, we study CP asymmetry of the $D\rightarrow \pi \pi$ system in the isospin and topological analysis. The ratio between penguin and tree amplitudes $P/(T+C)$ in the $D\rightarrow \pi \pi$ system is found to be greater than two in most values of the relative strong phase. And $D^0\rightarrow \pi ^0\pi ^0$ is a potential mode to reveal the CP asymmetry of the order of $10^{-3}$, which would be observed by Belle II in the future. The large CP asymmetry in the $D\rightarrow \pi \pi$ system might be understood in the t-channel final-state interaction.

1 Introduction

CP asymmetry in D meson decay, which is defined as

$$\begin{aligned} A_{CP}(D\rightarrow f) \equiv \frac{\Gamma (D\rightarrow f)-\Gamma (\overline{D}\rightarrow \overline{f})}{\Gamma (D\rightarrow f)+\Gamma (\overline{D}\rightarrow \overline{f})}, \end{aligned}$$

(1)

provides a window to test the Standard Model (SM) and search for new physics (NP) in the up-type quark weak decay in hadrons. The LHCb collaboration observed CP asymmetry of charm decay in 2019 [1],

$$\begin{aligned} \Delta A_{CP}{} & {} \equiv A_{CP}(D^0\rightarrow K^+K^-)-A_{CP}(D^0\rightarrow \pi ^+\pi ^-)\nonumber \\{} & {} =(-1.54\pm 0.29)\times 10^{-3}. \end{aligned}$$

(2)

After that, many experimental efforts are devoted to the measurement of CP asymmetry and mixing parameters in charm system [2,3,4,5,6,7,8]. In theoretical aspect, there are two controversial viewpoints for the observed CP asymmetry difference in literature, regarding it as signal of new physics [9,10,11,12], or the non-perturbative QCD enhancements to penguin [13,14,15,16,17,18,19,20,21]. It attributes to the large ambiguities in evaluating penguin topologies and the absence of more information given by experiments.

Very recently, the LHCb collaboration reported the first evidence of non-vanishing CP asymmetry in the individual decay of $D^0\rightarrow \pi ^+\pi ^-$ by measuring $\Delta A_{CP}$ and CP asymmetry in the $D^0\rightarrow K^+K^-$ decay [22]. The CP asymmetries in the $D^0\rightarrow K^+K^-$ and $D^0\rightarrow \pi ^+\pi ^-$ decays are given by

$$\begin{aligned} A_{CP}(D^0\rightarrow K^+K^-)&= (0.77\pm 0.57)\times 10^{-3}, \end{aligned}$$

(3)

$$\begin{aligned} A_{CP}(D^0\rightarrow \pi ^+\pi ^-)&= (2.32\pm 0.61)\times 10^{-3}. \end{aligned}$$

(4)

CP asymmetry in the individual mode is more significant compared to the difference between two decay modes because it allows us to extract more knowledge of non-perturbative QCD. The newest data indicates a very large U-spin breaking in the $D^0\rightarrow K^+K^-$ and $D^0\rightarrow \pi ^+\pi ^-$ modes, which is beyond the naive expectations of $\varepsilon \sim m_s/\Lambda _\textrm{QCD}\sim 30\%$ [23].

In this work, we analyze the implications of the new measurement of CP asymmetry in the $D^0\rightarrow \pi ^+\pi ^-$ decay. By applying the isospin and topological analysis, we show the ratio between penguin and tree amplitudes in the $D\rightarrow \pi \pi$ system is greater than 2 in most values of strong phase. And CP asymmetry in the $D^0\rightarrow \pi ^0\pi ^0$ decay could reach to be $\mathcal {O}(10^{-3})$, which is available on Belle II in the future. The large CP asymmetry in the $D\rightarrow \pi \pi$ system might be understood in the t-channel final-state interaction (FSI) [24,25,26,27,28,29,30,31,32,33,34,35,36,37].

This paper is organized as follows. In Sect. 2, we analyze CP asymmetry in the $D\rightarrow \pi \pi$ system in the isospin and topological analysis. In Sect. 3, we try to explain the large CP asymmetry in charm in the final state interaction. And Sect. 4 is a short summary.

2 Isospin and topological analysis

In the $D\rightarrow \pi \pi$ system, $(D^0,D^+)$ form an isospin doublet, $(\pi ^+,\pi ^0,\pi ^-)$ form an isospin triplet. Isospin decompositions of the $D^0\rightarrow \pi ^+\pi ^-$, $D^0\rightarrow \pi ^0\pi ^0$ and $D^+\rightarrow \pi ^+\pi ^0$ modes are

$$\begin{aligned} \mathcal {A}(D^0\rightarrow \pi ^+\pi ^-){} & {} = \frac{1}{2\sqrt{3}}\mathcal {A}_{3/2}+\frac{1}{\sqrt{6}}\mathcal {A}_{1/2}, \end{aligned}$$

(5)

$$\begin{aligned} \mathcal {A}(D^0\rightarrow \pi ^0\pi ^0){} & {} = \frac{1}{\sqrt{6}}\mathcal {A}_{3/2}-\frac{1}{2\sqrt{3}}\mathcal {A}_{1/2}, \end{aligned}$$

(6)

$$\begin{aligned} \mathcal {A}(D^+\rightarrow \pi ^+\pi ^0){} & {} =\frac{\sqrt{6}}{4}\mathcal {A}_{3/2}, \end{aligned}$$

(7)

in which $\mathcal {A}_{3/2}$ and $\mathcal {A}_{1/2}$ are the amplitudes with $\Delta I = 3/2$ and $\Delta I = 1/2$, respectively. Topological decompositions of the $D\rightarrow \pi \pi$ modes can be expressed as

$$\begin{aligned} \mathcal {A}(D^0\rightarrow \pi ^+\pi ^-){} & {} = \lambda _d\,(T+E+\mathcal {P}_\textrm{b})-\lambda _b\,\mathcal {P}, \end{aligned}$$

(8)

$$\begin{aligned} \mathcal {A}(D^0\rightarrow \pi ^0\pi ^0){} & {} = \frac{1}{\sqrt{2}}\lambda _d\,(C-E-\mathcal {P}_\textrm{b})+\frac{1}{\sqrt{2}}\lambda _b\,\mathcal {P}, \end{aligned}$$

(9)

$$\begin{aligned} \mathcal {A}(D^+\rightarrow \pi ^+\pi ^0){} & {} =\frac{1}{\sqrt{2}}\lambda _d\,(T+C), \end{aligned}$$

(10)

where $\lambda _d=V^*_{cd}\,V_{ud}$ and $\lambda _b=V^*_{cb}\,V_{ub}$. The contributions from the penguin operators $O_{3-6}$ and the chromomagnetic penguin operator $O_{8g}$ are neglected in Eqs. (8)$\sim$(10). T, C and E denote the tree amplitudes and $\mathcal {P}$ and $\mathcal {P}_\textrm{b}$ denote the penguin amplitudes. $\mathcal {P}_\textrm{b}$ is the difference between $\mathcal {P}_d$ and $\mathcal {P}_s$, $\mathcal {P}_\textrm{b} = \mathcal {P}_d - \mathcal {P}_s$, and $\mathcal {P}=\mathcal {P}_s$. $\mathcal {P}_d$ and $\mathcal {P}_s$ are the topologies with d and s in the quark loop respectively. In literature such as [38], $\mathcal {P}$ is written as penguin plus penguin annihilation diagrams, $\mathcal {P}+2\,\mathcal{P}\mathcal{A}$. In order to math the isospin amplitudes, the quark compositions of D and $\pi$ mesons are defined as $D^0 = -c\overline{u}$, $D^+ = c\overline{d}$, $\pi ^+ = u\overline{d}$, $\pi ^0 = \frac{1}{\sqrt{2}}\,(d\overline{d} - u\overline{u})$ and $\pi ^- = -d\overline{u}$ in Eqs. (8)$\sim$(10). By comparing Eqs. (8)$\sim$(10) with Eqs. (5)$\sim$(7), the relations between isospin amplitudes and topological amplitudes are found to be

$$\begin{aligned} \mathcal {A}_{3/2}{} & {} = \frac{2\sqrt{3}}{3}\lambda _d(T+C), \end{aligned}$$

(11)

$$\begin{aligned} \mathcal {A}_{1/2}{} & {} = \sqrt{6}\lambda _d\left( E+\mathcal {P}_\textrm{b}+\frac{2}{3}T-\frac{1}{3}C\right) -\sqrt{6}\lambda _b \mathcal {P}. \end{aligned}$$

(12)

Equations (11) and (12) can also be derived from the effective Hamiltonian of charm decay by analyzing the isospin structure of tree and penguin operators, see literature such as Ref. [39] for details.

Fig. 1

Ratio of penguin and tree amplitudes $P/(T+C)$ dependent on the strong phase $\delta _p$ in the cases of negative (left) and positive (right) strong phase $\delta _I$. The gray bands represent the uncertainties, and the blue solid and dashed lines are $P/(T+C)=2$ and $-2$ respectively

Fig. 2

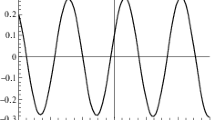
CP asymmetry in the $D^0\rightarrow \pi ^0\pi ^0$ decay dependent on $\delta _p$ in the cases of negative (left) and positive (right) $\delta _I$. The horizontal pink shadow is $1\sigma$ experimental limitation to date [40, 42]. The blue shadow is the expected statistical uncertainties on Belle II at $50\textrm{ab}^{-1}$ data set [43]

In the SM, $\lambda _b$ is much smaller than $\lambda _d$, $\lambda _b/\lambda _d \sim \mathcal {O}(10^{-4})$ [40]. The last term in Eq. (12) can be neglected safely in the branching fractions. We define an approximate $\Delta I =1/2$ amplitude without the $\lambda _b\, P$ term as

$$\begin{aligned} \mathcal {A}^\prime _{1/2} = \sqrt{6}\,\lambda _d\,\left( E+\mathcal {P}_\textrm{b}+\frac{2}{3}T-\frac{1}{3}C\right) . \end{aligned}$$

(13)

$\mathcal {A}^\prime _{1/2}$ can be written as

$$\begin{aligned} \mathcal {A}^\prime _{1/2} = \mathcal {A}^{\prime s}_{1/2}\,e^{i\,\delta _{I}}, \end{aligned}$$

(14)

with magnitude $\mathcal {A}^{\prime s}_{1/2}$ and relative strong phase $\delta _{I} =\delta _{1/2} - \delta _{3/2}$. The strong phase of $\mathcal {A}_{3/2}$ is usually set to be zero. The isospin amplitudes $\mathcal {A}_{3/2}$ and $\mathcal {A}^\prime _{1/2}$ can be extracted from the branching fractions of three $D\rightarrow \pi \pi$ modes which are given by [40]

$$\begin{aligned} \mathcal {B}r(D^0\rightarrow \pi ^+\pi ^-)= & {} (1.454\pm 0.024)\times 10^{-3},\nonumber \\ \qquad \mathcal {B}r(D^0\rightarrow \pi ^0\pi ^0)= & {} (0.826\pm 0.025)\times 10^{-3}, \nonumber \\ \mathcal {B}r(D^+\rightarrow \pi ^+\pi ^0)= & {} (1.247\pm 0.033)\times 10^{-3}. \end{aligned}$$

(15)

The partial decay width $\Gamma$ is parameterized to be

$$\begin{aligned} \Gamma (D\rightarrow \pi \pi ) = \frac{|P_c|}{8\pi m^2_{D}}|\mathcal {A}(D\rightarrow \pi \pi )|^2, \end{aligned}$$

(16)

in which $P_c$ is the c.m. momentum in the rest frame of D meson. The hadronic parameters $\mathcal {A}_{3/2}$, $\mathcal {A}^{\prime s}_{1/2}$ and $\delta _{I}$ are extracted to be

$$\begin{aligned} \mathcal {A}_{3/2}= & {} (0.447\pm 0.006)\times 10^{-6}\,\textrm{GeV},\nonumber \\ \mathcal {A}^{\prime s}_{1/2}= & {} (1.090\pm 0.009)\times 10^{-6}\,\textrm{GeV}, \nonumber \\ \delta ^n_{I}= & {} (-86.66\pm 1.31)^\circ ,\nonumber \\ \delta ^p_{I}= & {} (86.66\pm 1.31)^\circ . \end{aligned}$$

(17)

There are two solutions for the strong phase $\delta _I$. Superscripts n and p are used to distinguish the negative and positive solutions. Equation (17) is consistent with the result given by Ref. [41].

To analyze CP asymmetries in the $D\rightarrow \pi \pi$ modes, we parameterize the penguin amplitude $\mathcal {P}$ as

$$\begin{aligned} \lambda _b\,\mathcal {P} = |\lambda _b|\,P\,e^{i\,(\delta _p - \gamma )}, \end{aligned}$$

(18)

in which P and $\delta _p$ are the magnitude and strong phase (with respect to $A_{3/2}$) of penguin amplitude respectively. $\gamma$ is phase parameter of the CKM matrix, known as $\phi _3$ in the unitarity triangle. In the SM, $\gamma$ is fitted to be $1.144\pm 0.027$ [40]. The weak phase of $\lambda _d$ is negligible compared to $\gamma$. With the isospin and topological amplitudes, CP asymmetries of the $D^0\rightarrow \pi ^+\pi ^-$ and $D^0\rightarrow \pi ^0\pi ^0$ decays are derived to be

$$\begin{aligned}{} & {} A_{CP}(D^0\rightarrow \pi ^+\pi ^-)\nonumber \\{} & {} \quad = 4\sqrt{3}\,\frac{|\lambda _b|}{\lambda _d}\,\frac{ \,P\!\sin \gamma \!\!\,\left( \!\!\sqrt{2}\,\mathcal {A}_{1/2}^{\prime s}\sin (\delta _I{-}\delta _p){-}\mathcal {A}_{3/2}\sin \delta _p\right) \!\! }{2(\mathcal {A}_{1/2}^{\prime s})^2{+}\mathcal {A}_{3/2}^2{+}2\sqrt{2}\,\mathcal {A}_{1/2}^{\prime s}\mathcal {A}_{3/2}\cos \delta _I},\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}{} & {} A_{CP}(D^0\rightarrow \pi ^0\pi ^0)\nonumber \\{} & {} \quad = 2\sqrt{3}\,\frac{|\lambda _b|}{\lambda _d}\,\frac{ \,P\!\sin \gamma \!\!\,\left( \!\!\sqrt{2}\,\mathcal {A}_{1/2}^{\prime s}\sin (\delta _I{-}\delta _p){+}2\,\mathcal {A}_{3/2}\sin \delta _p\right) \!\! }{(\mathcal {A}_{1/2}^{\prime s})^2{+}2\,\mathcal {A}_{3/2}^2{-}2\sqrt{2}\,\mathcal {A}_{1/2}^{\prime s}\mathcal {A}_{3/2}\cos \delta _I}. \nonumber \\ \end{aligned}$$

(20)

In Eqs. (19) and (20), the first term in numerator is the CP asymmetry in $\mathcal {A}_{1/2}$ and the second term is the interference between $\mathcal {A}_{1/2}$ and $\mathcal {A}_{3/2}$.

There are two non-determined parameters in Eqs. (19) and (20), P and $\delta _p$. If the scenario of no new physics effect is assumed, we can solve P as a function of $\delta _p$ according to the experiment result of $A_{CP}(D^0\rightarrow \pi ^+\pi ^-)$. The ratio between penguin and tree amplitudes $P/(T+C)$ dependent on $\delta _p$ is plotted in Fig. 1. One can find $P/(T+C)$ is greater than 2 in most values of $\delta _P$ in both negative and positive $\delta _I$. It suggests the penguin topology is enhanced by non-perturbative QCD in the $D\rightarrow \pi \pi$ system. More generally, it is possible that the large penguin topologies exist in other singly Cabibbo-suppressed charmed hadron decay modes, leading to observable CP asymmetries. Topology $\mathcal {P}_\textrm{b}$ is comparable to the tree amplitudes, contributing to a large $SU(3)_F$ breaking effect in the singly Cabibbo-suppressed charm decays and affecting the branching fractions. Thus $\mathcal {P}_\textrm{b}$ cannot be neglected in the global fit of the D meson or baryon non-leptonic weak decays.

With the function of $P(\delta _p)$, we get the function of $A_{CP}(D^0\rightarrow \pi ^0\pi ^0)$ dependent on $\delta _p$, which is plotted in Fig. 2. $A_{CP}(D^0\rightarrow \pi ^0\pi ^0)$ is expected to be $\mathcal {O}(10^{-3})$ at most values of $\delta _p$, which is available on Belle II at $50\textrm{ab}^{-1}$ data set. At some particular values of $\delta _p$, $A_{CP}(D^0\rightarrow \pi ^0\pi ^0)$ could reach to be $\mathcal {O}(10^{-2})$. So CP asymmetry in the $D^0\rightarrow \pi ^0\pi ^0$ decay might be the next observed CP asymmetry in charm sector. On the other hand, if CP asymmetries of the $D^0\rightarrow \pi ^+\pi ^-$ and $D^0\rightarrow \pi ^0\pi ^0$ decays are well determined by experiments, the magnitude and strong phase of penguin $\mathcal {P}$ can be extracted without model calculations. It will deepen the understanding of non-perturbative QCD in charm scale.

Fig. 3

Ratio R dependent on $\delta _p$ in the cases of negative (left) and positive (right) $\delta _I$, in which the horizontal pink shadow is $1\sigma$ experimental limitation to date taken from HFLAV [44]

Fig. 4

Final-state interaction effects: s-channel (resonance) and t-channel (rescattering) contributions to one particle exchange

Fig. 5

Penguin diagram and re-scattering contribution to the penguin diagram

In experiments, the ratio R is used to test new physics in the $\Delta I = 3/2$ amplitude, which is defined by [45, 46]

$$\begin{aligned} R=\frac{|\mathcal {A}(\pi ^+\pi ^-)|^2-|\overline{\mathcal {A}}(\pi ^+\pi ^-)|^2 +|\mathcal {A}(\pi ^0\pi ^0)|^2-|\overline{\mathcal {A}}(\pi ^0\pi ^0)|^2 -\frac{2}{3}(|\mathcal {A}(\pi ^+\pi ^0)|^2-|\overline{\mathcal {A}}(\pi ^+\pi ^0)|^2)}{|\mathcal {A}(\pi ^+\pi ^-)|^2+|\overline{\mathcal {A}}(\pi ^+\pi ^-)|^2 +|\mathcal {A}(\pi ^0\pi ^0)|^2+|\overline{\mathcal {A}}(\pi ^0\pi ^0)|^2 +\frac{2}{3}(|\mathcal {A}(\pi ^+\pi ^0)|^2+|\overline{\mathcal {A}}(\pi ^+\pi ^0)|^2)}. \end{aligned}$$

(21)

With the isospin and topological amplitudes of $D\rightarrow \pi \pi$ modes, ratio R is derived to be

$$\begin{aligned} R= 6\sqrt{6}\,\frac{|\lambda _b|}{\lambda _d}\,\frac{ \,\mathcal {A}_{1/2}^{\prime s}\,P\,\sin \gamma \,\sin (\delta _I-\delta _p) }{3\,(\mathcal {A}_{1/2}^{\prime s})^2+11\,\mathcal {A}_{3/2}^2} \end{aligned}$$

(22)

in the SM. According to Eq. (22), ratio R is determined by CP asymmetry in the $\Delta I = 1/2$ amplitude. The dependence of ratio R on $\delta _p$ is plotted in Fig. 3. It is found that $R \sim \mathcal {O}(10^{-3})$ in the most values of $\delta _p$.

3 Estimation in the final-state interaction

In the $D\rightarrow \pi \pi$ system, the penguin contribution is $\lambda _d\mathcal {P}_d+\lambda _s\mathcal {P}_s$. Considering all the tree amplitudes are proportional to $\lambda _d$ in the $D\rightarrow \pi \pi$ modes, we write penguin amplitudes as $\lambda _d\mathcal {P}_d+\lambda _s\mathcal {P}_s = \lambda _d\mathcal {P}_d-(\lambda _d+\lambda _b)\mathcal {P}_s = \lambda _d\mathcal {P}_\textrm{b}-\lambda _b\mathcal {P}_s$ in Eqs. (8)$\sim$(10). The CP asymmetry is induced by the interference between $\lambda _b\mathcal {P}_s$ with other decay amplitudes. In this section, we discuss how large the penguin amplitude $\mathcal {P}_s$ could be in the final-state interaction.

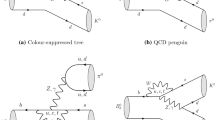
For the two-body heavy meson weak decay, the FSI effect can be modeled as exchange of one particle between two particles generated from the short-distance tree emitted process. There are s-channel and t-channel contributions in the final state interaction, which are depicted in Fig. 4. In the s-channel contribution, the resonance state in the $D\rightarrow \pi \pi$ decay has the quantum number $J^{PC}=0^{++}$ derived from the final states. Ref. [18] suggests that $f_0(1710)$ playing an important role in enhancing the penguin amplitude. However, the CP asymmetry ratio between $D^0\rightarrow \pi ^+\pi ^-$ and $D^0\rightarrow K^+K^-$ modes is expected to be $-1.06$, which is different from the experimental result. It is attributed to the suppression by the ratio of branching fraction, $\mathcal {B}r(f_0(1710)\rightarrow \pi \pi )/\mathcal {B}r(f_0(1710)\rightarrow KK)\approx 0.4$. If the t-channel contribution is included, the large CP asymmetry in the $D\rightarrow \pi \pi$ might be understood in the FSI.

An approach to relate topological diagram to the re-scattering triangle diagram was proposed in Ref. [20]. The re-scattering contribution in the penguin amplitude can be described by Fig. 5. In the topological diagram $\mathcal {P}$ in Fig. 5, indices i, j, k and l present the light quark u, d or s in the charm decay. $\mathcal {P}$ diagram can be obtained by twisting quark lines from a short-distance T diagram, as shown in the second diagram, $L(\mathcal {P})$, in Fig. 5. $L(\mathcal {P})$ forms a triangle diagram at hadron level, which is the third diagram in Fig. 5. In the triangle diagram, the vertex in the left is a weak vertex and the other two vertexes are strong vertexes. The quark loop in penguin can be understood as the light quark $q_l$ exited from the weak vertex goes through three propagators in the triangle diagram then returns to the weak vertex.

Fig. 6

Triangle diagrams contributing to CP asymmetries in the $D\rightarrow \pi \pi$ system

Fig. 7

Theoretical prediction for the ratio $|P/(T+C)|$ with $\eta$ varying from $-1.6\sim 1.6$ (blue) and $t=m_t^2$ (red)

There are two triangle diagrams contributing to the penguin diagram $\mathcal {P}_s$ shown in Fig. 6. The left diagram presents $KK\rightarrow \pi \pi$ scattering and the right diagram presents $K^*K^*\rightarrow \pi \pi$ scattering. Compared to Ref. [23], the $K^*K^*\rightarrow \pi \pi$ scattering is included in the final state interaction. Since the weak vertex of triangle diagram is a short-distance T diagram, the factorization approach is used to estimate the weak decay amplitude. It is parameterized as the decay constant of the emitted meson and the transition form factor of another meson. For the amplitude of total triangle diagram, there are several calculational methods, in which the treatment of hadronic loop integration is different [24,25,26,27,28,29,30]. In this work, the intermediate states are treated to be on their mass shell and then the optical theorem and Cutkosky cutting rule are used to calculate the absorptive part. The calculation details can be found in Ref. [27].

Considering the exchanged meson being generally off-shell, a form factor is introduced as $F(t) = (\Lambda ^2-m_t^2)/(\Lambda ^2-t)$ to compensate the off-shell effect [47], where t and $m_t$ are the momentum square and mass of the exchanged meson respectively. F(t) is normalized to unity at the on-shell situation $t=p^2_{t}=m_t^2$. The cutoff $\Lambda$ is parameterized as $\Lambda = m_{t} + \eta \Lambda _\textrm{QCD}$ with $\Lambda _\textrm{QCD} = 330\,\textrm{MeV}$ for the charm decay. The parameter $\eta$ cannot be calculated from the QCD method.

The dependence of the ratio $|P/(T+C)|$ on the parameter $\eta$ is displayed in Fig. 7. It is found that $|P/(T+C)|$ is very sensitive to $\eta$. With $\eta$ varying in the range between $-1.6$ and 1.6, $|P/(T+C)|$ varies from zero to four. The large $|P/(T+C)|$ in some area indicates that the large penguin is accessible in the non-perturbative QCD. If we set $t=m_t^2$, $|P/(T+C)|$ is expected to be 1.96. It is consistent with the penguin amplitude extracted from CP asymmetry in the $D^0\rightarrow \pi ^+\pi ^-$ mode.

4 Summary

We studied CP asymmetry in the $D\rightarrow \pi \pi$ system based on the isospin and topological analysis. According to the new measurement of CP asymmetry in the $D^0\rightarrow \pi ^+\pi ^-$ decay, we concluded that CP asymmetry in the $D^0\rightarrow \pi ^0\pi ^0$ decay could reach to be $\mathcal {O}(10^{-3})$, which is available on Belle II in the future. Besides, the large CP asymmetry in the $D\rightarrow \pi \pi$ system might be explained by the t-channel final-state interaction.