1 Introduction

In the field of mathematics, topological defects are solutions of non-linear differential equations [1]. On the other hand, in physics, topological defects are regions that separate different states [2]. A well-intuitive and well-known example are the domain walls in electromagnetic materials that separate different states in the same sample of magnetic material [3], which arise for several reasons, such as intrinsic properties of the material, external fields, temperature and pressure variations, etc. However, in addition to the domain walls, there are also other types of defects, for example, of a linear nature, such as disclinations and dislocations [4, 5], and of a punctual nature [4], such as impurities and vacancies, which can arise in elastic media, generally investigated in crystallography [6].

Based on theories of the primordial universe [2], there are predictions that in the Universe there are cosmological objects analogous to the topological defects mentioned above, that is, domain walls [1, 7], defects of a linear nature, such as the cosmic string [8,9,10,11] and dislocations [12] associated with curvature and torsion in space-time, respectively, and the global monopole [13]. It is noteworthy that the latter is one of the most quoted to be observed in the scope of observational cosmology [2].

In particular, the global monopole (GM) has been investigated in several areas of physics, for example, in observational cosmology [2], in scenarios f(R) theory [14, 15], in presence of Wu-Yang magnetic monopole [16] and in the gravitating magnetic monopole [17], the polarization of the fermionic vacuum [18] and Casimir effect [19]. There are also studies of this type of defect in quantum mechanical, non-relativistic and relativistic systems. In the case of non-relativistic quantum mechanics, there are studies on the harmonic oscillator [20, 21], on a particle interacting with a Kratzer potential [22], on a charged particle-magnetic monopole scattering [23], on a particle subjected to the self-interaction potential [24], on the Hulthén potential [25] and thermodynamics systems [26]. In a relativistic context, GM has been investigated on the hydrogen atom and the pionic atom [27], on the exact solutions of scalar bosons in the presence of the Aharonov-Bohm and Coulomb potentials [28] and on the Klein–Gordon and Dirac oscillators [29,30,31].

Recently, gravitational effects have been investigated on quantum particles. These studies are possible through non-trivial metrics arising from the solutions of Einstein’s equations. In order to understand the primordial Universe, these non-trivial solutions come up with information or parameters associated with the “fossils” of the first minutes of the Universe, including topological defects. Therefore, through mathematical tools capable of absorbing this information in the mathematical description of fundamental particles, it is possible to analytically describe fundamental particles such as spin-0 bosons and spin-1/2 fermions in these non-trivial geometries with the presence of topological charges. As examples to be cited, we have the following studies: scalar solutions in Kerr–Newman and Friedmann–Robertson–Walker spacetimes both containing a cosmic string [32], relativistic quantum dynamics of scalar and spin-0 particles in Safka-Witten spacetime [33], Klein–Gordon [32, 34,35,36,37,38], Dirac [39] and Weyl [40] particles in Gödel-type spacetime and on a scalar particle in Ellis-Bronnikov-type wormhole spacetime [41, 42].

It is noteworthy that the geometries mentioned above represent a drop in the ocean with regard to the topologically charged geometries proposed in the theoretical framework. Recently, a topologically charged spacetime has been proposed which has drawn a lot of attention in the scientific community. This is the gravitational field generated by a GM within the so-called Eddington-inspired Born-Infeld gravity (EiBI-gravity) [43]. Such a solution was originally obtained by Lambaga and Ramadhan [44]. The authors coupled the energy-momentum tensor referring to the external region of the core of Barriola and Vilenkin’s GM [13] to the EiBI-gravity field equations through the metric-affine formalism. It is worth noting that in [45], the authors also considered non-canonical GM models within EiBI-gravity and obtained regular black hole solutions. However, there is still no study in the literature on the quantum dynamics of a spin-0 boson in the EiBI GM spacetime. Therefore, the purpose of this work is to analytically describe solutions of the bound state of a spin-0 boson with and without interaction in this non-trivial geometry.

The structure of this paper is as follows: in Sect. 2, we investigate the KGO for a massive scalar particle in EiBI spacetime, and through analytical studies, we obtain the energy spectrum for bound states; in Sect. 3, we analyze the bosonic Klein–Gordon oscillator (KGO) in that same spacetime and by using analytical methods, we obtain the relativistic energy profile for this interaction; finally, in Sect. 4, we present the conclusions.

2 Klein–Gordon oscillator

In Refs. [44, 45] show that the spacetime generated by a source of matter, such as that related to the region outside the GM core [13], is described by the following line element in spherical coordinates:

$$\begin{aligned} ds^2= & {} -(1-\kappa ^2\eta ^2)dt^2+\frac{r^2dr^2}{(1-\kappa ^2\eta ^2)(r^2+\epsilon \kappa ^2\eta ^2)}\nonumber \\{} & {} +r^2(d\theta ^2+\sin ^{2}{\theta }d\phi ^2) \, \end{aligned}$$
(1)

where \(\kappa ^2=8\pi G\), being G the gravitational constant and \(\eta \) is the energy scale of the spontaneous symmetry breaking. The Eddington parameter \(\epsilon \) controls the non-linearity of the EiBI-gravity. In [46] it was shown that the cohesion of astrophysical objects by their own gravity imposes \(\kappa ^2\epsilon <10^{-2} \frac{m^5}{kg\ s^2}\) for the case of neutron stars. We can further rescale the (1): \(t\rightarrow \sqrt{1-\kappa ^2\eta ^2}\) and \(\epsilon \rightarrow \varepsilon \kappa ^2\eta ^2\) to get

$$\begin{aligned} ds^2= & {} -dt^2+\frac{dr^2}{\alpha ^2(1+\frac{\varepsilon }{r^2})}\nonumber \\{} & {} +r^2(d\theta ^2+\sin ^{2}{\theta } d\phi ^2) \, \end{aligned}$$
(2)

with \(\alpha ^2=1-\kappa ^2\eta ^2\). For negative values of the parameter \(\epsilon \) such a solution describes a topologically charged wormhole [45]. In fact, many implications have already been studied admitting this possibility [41, 42]. For \(\epsilon >0\), the above metric describes a GM spacetime within EiBI-gravity.

KGO equation is constructed from the Klein–Gordon equation by considering the redefinition of the four-dimensional linear momentum through a non-minimal coupling \({\hat{p}}_\mu \rightarrow {\hat{p}}_\mu +im\omega {X_ \mu }\) [37, 47, 49], where \(\omega \) is the frequency of the relativistic oscillator and m is the rest mass of the scalar field. This relativistic oscillator model was proposed based on the relativistic oscillator model for spin-1/2 particles, known in the literature as the Dirac oscillator [50]. KGO became a successful relativistic quantum model for the harmonic oscillator due to the possibility of solving it analytically and for recovering the Shoröndinger oscillator in the non-relativistic limit. This relativistic oscillator model has been investigated in Minkowski spacetime [51,52,53], in possible Lorentz symmetry breaking scenarios [54, 55], by interacting with a magnetic screw dislocation [56, 57] and in a Kaluza-Klein theory [58, 59].

The expression that defines the Klein–Gordon oscillator is given by

$$\begin{aligned} \frac{1}{\sqrt{-g}}(\partial _{\mu }+m\omega X_{\mu })(\sqrt{-g}g^{\mu \nu })(\partial _{\nu }-m\omega X_{\nu })\phi - m^2\phi =0,\nonumber \\ \end{aligned}$$
(3)

where \(g=\text {det}(g_{\mu \nu })\) and \(g^{\mu \nu }\) is the inverse of the metric tensor. We also have the radial direction where the KGO is located \(X_{\mu }=(0,r,0,0)\).

Replacing the components of the metric tensor Eq. (2) together with its inverse in the expression referring to KGO, we have

$$\begin{aligned}{} & {} -\frac{\partial ^2\phi }{\partial {t}^2} + \alpha ^2\left( 1+\frac{\epsilon }{r^2}\right) \frac{\partial ^2\phi }{\partial {r}^2}+\left( \frac{2\alpha ^2}{r}+ \frac{\alpha ^2\epsilon }{r^3}\right) \frac{\partial \phi }{\partial {r}}\nonumber \\{} & {} \quad - m^2\phi - 3m\omega \alpha ^2\phi -m^2\omega ^2\alpha ^2\left( r^2+\epsilon \right) \phi \nonumber \\{} & {} \quad - \frac{2m\omega \epsilon \alpha ^2}{r^2}\phi + \frac{1}{r^2}\left[ \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left( \sin \theta \frac{\partial }{\partial \theta }\right) \right. \nonumber \\{} & {} \quad \left. +\frac{1}{\sin ^2\theta }\frac{\partial ^2}{\partial \varphi ^2}\right] \phi =0. \end{aligned}$$
(4)

By using the method of separation of variables, we define that the scalar field is written in terms of new functions \(\phi \left( t,r,\theta ,\varphi ,\right) = {e}^{-iE{t}}f\left( r\right) Y_{l,m}(\theta ,\varphi )\), where \(Y_{l,m}(\theta ,\varphi )\) are the spherical harmonics, f(r) is the radial wave function and E represents the energy eigenvalues of the system. With the following definition

$$\begin{aligned}{} & {} \left[ \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left( \sin \theta \frac{\partial }{\partial \theta }\right) +\frac{1}{\sin ^2\theta }\frac{\partial ^2}{\partial \varphi ^2}\right] Y_{l,m}(\theta ,\varphi )\nonumber \\{} & {} \quad =-l(l+1)Y_{l,m}(\theta ,\varphi ), \end{aligned}$$
(5)

and by substituting Eq. (5) into Eq. (3) we obtain the following second order differential equation

$$\begin{aligned}{} & {} \left( 1+\frac{\epsilon }{r^2}\right) f''\left( r\right) +\left( \frac{2}{r}+ \frac{\epsilon }{r^3}\right) f'\left( r\right) \nonumber \\{} & {} \quad +\left[ K_{1}^2 -\frac{K_{2}^2}{r^2}-K_{3}^2r^2\right] f\left( r\right) =0, \end{aligned}$$
(6)

where we define the parameters

$$\begin{aligned} K_{1}^2= & {} \frac{E^2-m^2-3m\omega \alpha ^2-m^2\omega ^2\alpha ^2\epsilon }{\alpha ^2}, \nonumber \\ K_{2}^2= & {} \frac{l\left( l+1\right) + 2m\omega \epsilon \alpha ^2}{\alpha ^2}, \qquad K_{3}^2= m^2\omega ^2. \end{aligned}$$
(7)

In order to solve Eq. (6), let us consider the change \(f\left( r\right) = e^{-\frac{K_{3}{r^2}}{2}}g\left( r\right) \). This redefinition must be valid for all r. It should be well behaved in origin \(r\rightarrow {0}\) and spatial infinities \(r\rightarrow {\pm }\infty \). In this way, Eq. (6) is rewritten as follows,

$$\begin{aligned}{} & {} \left( 1+\frac{\epsilon }{r^2}\right) g''\left( r\right) + \left[ \frac{2}{r}- \frac{2\epsilon {K_{3}}}{r}+ \frac{\epsilon }{r^3}-2K_{3}r\right] g'\left( r\right) \nonumber \\{} & {} \quad +\left[ \left( K_{1}^2-3K_{3} +\epsilon {K_{3}^2}\right) -\frac{\left( K_{2}^2 + 2\epsilon {K_{3}}\right) }{r^2}\right] g\left( r\right) =0.\nonumber \\ \end{aligned}$$
(8)

From now on, let us define the change of variable \(u=1+\frac{r^2}{\epsilon }\) into Eq. (8), from which we obtain the following second-order differential equation

$$\begin{aligned}{} & {} \frac{d^2g}{du^2}+ \frac{dg}{du}\left[ -K_3\epsilon + \frac{1}{2u} + \frac{1}{u-1}\right] \nonumber \\{} & {} \quad + g\left( u\right) \left[ \left( \frac{P_{1}+P_{2}}{u}\right) - \left( \frac{P_{2}}{u-1}\right) \right] =0, \end{aligned}$$
(9)

where we define the new parameters

$$\begin{aligned} P_{1}=\frac{\epsilon }{4}\left( K_{1}^2-3K_{3}+\epsilon {K^{2}_{3}}\right) , \qquad \qquad P_{2}= \frac{\left( K_{2}^2+ 2\epsilon {K_{3}}\right) }{4}.\nonumber \\ \end{aligned}$$
(10)

Eq. (9) is the confluent Heun equation [60,61,62] and \(g\left( u\right) \) is the confluent Heun function given as follows

$$\begin{aligned} g\left( u\right)= & {} H_c\left( -K_{3}\epsilon ;-\frac{1}{2},0,\frac{\epsilon {K^{2}_1}}{4}+ \frac{\epsilon ^2{K^{2}_3}}{4},\frac{1}{4}-\frac{{K^{2}_2}}{4}\right. \nonumber \\{} & {} \quad \left. -\frac{{K^{2}_1}\epsilon }{4}-\frac{\epsilon ^2{K^{2}_3}}{4},u\right) . \end{aligned}$$
(11)

Equation (9) has singular points, of which the origin is a regular singular point. In this sense, Eq. (9) admits solutions around the origin given in power series form [63]

$$\begin{aligned} g\left( u\right) = \sum _{j=0}^{\infty }c_j{u}^{j}. \end{aligned}$$
(12)

Thus, by substituting Eq. (12) into Eq. (9) we obtain a relation between the coefficients \(c_{1}\) and \(c_{0}\) and the recurrence relation

$$\begin{aligned} c_1= & {} -2c_0\left( P_1 + P_2\right) , \end{aligned}$$
(13)
$$\begin{aligned} c_{j+2}= & {} \frac{c_j\left[ P_1-j\epsilon {K_3}\right] + c_{j+1}\left[ \left( j+1\right) \left( j+ \frac{3}{2}+ \epsilon {K_3}\right) -\left( P_1 +P_2\right) \right] }{\left( j+2\right) \left( j+\frac{3}{2}\right) }.\nonumber \\ \end{aligned}$$
(14)

In order to find bound state solutions we must truncate the confluent Heun series (12) to obtain finite degree polynomials of order n. This is possible by truncating the confluent Heun series (12) through the recurrence relation (14) imposing that \(c_{n+1}=0\), with \(j=n-1\). Thus, the recurrence relation Eq. (14) is rewritten

$$\begin{aligned} c_n= \frac{c_{n-1}\left[ \left( n-1\right) \epsilon {K_3}-P_1\right] }{\left[ n\left( n+\frac{1}{2}+\epsilon {K_3}\right) -\left( P_1 + P_2\right) \right] }, \end{aligned}$$
(15)

where \(n=1,2,3,\ldots \) represent the radial modes of the system. It is only possible to analyze Eq. (15) imposing values for the radial mode n, due to the dependence of the coefficients \(c_n\) and \(c_{n-1}\). Therefore, let us consider the radial mode \(n=1\), which represents the lowest energy state of the relativistic quantum system. Therefore, substituting \(n=1\) into Eq. (15), we obtain the following expression

$$\begin{aligned} c_1= \frac{c_0{P_1}}{\left[ \left( P_1 + P_2\right) -\left( \frac{3}{2}+\epsilon {K_3}\right) \right] }. \end{aligned}$$
(16)

Thus, by combining Eqs. (13) and (16), in which they relate coefficients \(c_0\) and \(c_1\), we find a second-degree algebraic equation in the variable \(P_1\) that contains the energy term

$$\begin{aligned}{} & {} P_1^2+ P_1\left( 2P_2-1-\epsilon {K_3}\right) \nonumber \\{} & {} \qquad + P_2\left[ P_2-\frac{1}{2}\left( 3+2\epsilon {K_3}\right) \right] =0. \end{aligned}$$
(17)

Therefore, the solution of Eq. (17) gives us, in terms of the parameter \(E=E_{l,1}\), the solution

$$\begin{aligned} E_{l,1}= & {} \pm \Bigg [m^2+ 4m\omega \alpha ^2 - \frac{l\left( l+1\right) }{\epsilon } \nonumber \\{} & {} +\frac{2\alpha ^2}{\epsilon } \pm \frac{\alpha ^2}{\epsilon }\sqrt{4+4m^2\omega ^2{\epsilon ^2}+16m\omega {\epsilon }+\frac{2l\left( l+1\right) }{\alpha ^2}}\Bigg ]^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(18)

Equation (18) represents the allowed energy values for the lowest energy state of KGO in EiBI spacetime. By Comparing to Eq. (18) with the results obtained in Refs. [29, 47] we can see that the KGO has its energy profile drastically modified, that is, in Refs. [29, 47], the energy spectrum of KGO is determined by a closed expression, while the KGO in EiBI spacetime can’t determine a closed expression for its energy spectrum; due to gravitational effects intrinsic aspects of this non-trivial topology characterized by the metric given in Eq. (1), it is only possible to determine allowed values of energy for the quantum system by imposing values of n to Eq. (15) separately. Furthermore, the lowest energy state of the system is not defined by the radial mode \(n=0\), as in Refs. [29, 47], but by the radial mode \(n=1\). In addition, we can note that the allowed energy values for the lowest energy state of KGO depend on the parameter associated with the GM, \(\alpha \).

By making \(\omega =0\) in Eq. (18), we have

$$\begin{aligned} E_{l,1}=\pm \Bigg [m^2 - \frac{l\left( l+1\right) }{\epsilon } +\frac{2\alpha ^2}{\epsilon } \pm \frac{\alpha ^2}{\epsilon }\sqrt{4+\frac{2l\left( l+1\right) }{\alpha ^2}}\Bigg ]^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(19)

that is, the allowed energy values for the lowest energy state of a scalar particle in EiBI spacetime. This means that, even without interaction, the particle continues to have discrete energy, characterizing the confinement, which comes from gravitational effects.

We can observe through Eqs. (18) and (19) that, by taking the limit of \(\epsilon \rightarrow {-a^2}\) we recover the energy profiles of a scalar particle [41] and of KGO [42] in a topologically charged Ellis-Bronnikov space-time, respectively. The focus of this work is totally focused on the analysis of the positive part of the \(\epsilon \) parameter, by making our analysis more generally.

In Fig. 1, we define some values for the constants \(\alpha \) and we perform the evolution of the parameters \(\omega /m\). In this way, we can have a visual representation for the energy levels for the ground state. Since on this occasion, we consider \(m^2\epsilon \) constant. Likewise, we define some values for the constant \(\alpha \) and provide the evolution of the parameters \(m^2\epsilon \). Now, we keep the relationship between the parameters \(\omega /m\) constant and obtain a visual representation of the ground state of the energy spectrum (see Fig. 2).

The eigenfunction corresponds to the ground state of the energy spectrum Eq. (18) is described by the first term of the polynomial of the confluent Heun equation Eq. (12), defined as \(g_{l,1}=c_0 + c_1{u}\). Therefore, the general solution contained in the general ansatz \(f_{l,1}\left( r\right) =e^{-\frac{K_{3}{r^2}}{2}}g_{l,1}\left( r\right) \) is explicitly rewritten in the form below

$$\begin{aligned} f_{l,1}\left( r\right) ={c_0}e^{-\frac{{m\omega }{r^2}}{2}}\left[ 1-2\left( P_1 +P_2\right) \left( 1+\frac{r^2}{\epsilon }\right) \right] . \end{aligned}$$
(20)

We can see that the eigenfunction (20) for the lowest energy state of the quantum system is influenced by the GM and the KGO, since it depends on the parameters \(P_1\) and \(P_2\), which in turn depend on the parameters associated with the topological defect, \(\alpha \), and the relativistic scalar oscillator, \(\omega \).

Fig. 1
figure 1

In both graphs contained in the figures on the right and left, we have \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(\omega /m\). In the figure on the left, we have the continuous blue curve that represents the positive sign inside the square root Eq. (18) and the red curve continues the negative sign also from inside the root of Eq. (18). We fixed \(m^2\epsilon =l=1\) and also did \(\alpha =0.2\). The dotted lines indicate the negative energy values. In the figure on the right, we carry out the same process now by varying the parameter \(\alpha =0.6\)

Full size image
Fig. 2
figure 2

In both figures we are visualizing \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(m^2\epsilon \). In the figure on the left, we have the continuous blue curve that represents the positive sign inside the square root Eq. (18) and the red curve continues the negative sign also from inside the root of Eq. (18). We fixed \(\omega /m=l=1\) and also did \(\alpha =0.2\). The dotted lines indicate the negative energy values. In the figure on the right, we carry out the same process now by varying the parameter \(\alpha =0.5\)

Full size image

3 KGO plus a gravitational Mie-type potential

In this second part of the work, we are interested in the study of a massive particle with spin zero, now being influenced by the Born-Infeld spacetime curvature scalar. In a way, we want to verify how the parameter that accompanies the geometric term \(\xi \) modifies the energy spectrum. Furthermore, investigate how the Born-Infeld term can be seen as a perturbation of the global monopole metric, by modifying both the spectrum and its eigenfunctions. In this case, Eq. (3) is redefined as

$$\begin{aligned}{} & {} \frac{1}{\sqrt{-g}}(\partial _{\mu }+m\omega X_{\mu })(\sqrt{-g}g^{\mu \nu })(\partial _{\nu }-m\omega X_{\nu })\phi \nonumber \\{} & {} \quad - \left( \xi {R}+m^2\right) \phi =0, \end{aligned}$$
(21)

where \(\xi \) is the coupling constant that binds to the geometric term. We are by considering that this oscillator is in the same direction as the case treated in the previous section \(X_{\mu }=(0,r,0,0)\). The curvature scalar is defined as follows

$$\begin{aligned} R=\frac{2\epsilon \alpha ^2}{r^4} + \frac{2\left( 1-\alpha ^2\right) }{r^2}. \end{aligned}$$
(22)

Equation (22) reminds us of a particular case of a well-known potential in the study of molecular atomic physics, known in the literature as Mie-type potential [64, 65]. This type of potential describes the interaction between two atoms which form a diatomic molecule and is given in the form

$$\begin{aligned} V(r)=V_0\left[ \left( \frac{\sigma }{\kappa -\sigma }\right) \left( \frac{r_0}{r}\right) ^\kappa -\left( \frac{\sigma }{\kappa -\sigma }\right) \left( \frac{r_0}{r}\right) ^\sigma \right] , \end{aligned}$$
(23)

where \(\sigma \) and \(\kappa \) are parameters and \(V_0\) is the interaction energy between two atoms separated by the distance \(r_0\) in a molecular system. For \(\sigma =2\) e \(\kappa =1\), for example, we recover the Kratzer–Fues potential [66,67,68]. By taking \(\sigma =4\) and \(\kappa =2\) into Eq. (23), we obtain \(V(r)\rightarrow 1/r^4+1/r^2\), a possible particular case of the Mie-type potential. Therefore, based on this discussion, due to the mathematical structural analogy, we can consider Eq. (22) or \(\xi R\) as a gravitational Mie-type potential. In this way, from Eqs. (2), (5) and (22) into Eq. (21) we have

$$\begin{aligned}{} & {} \left( 1+\frac{\epsilon }{r^2}\right) Z''\left( r\right) + \left( \frac{2}{r}+\frac{\epsilon }{r^3}\right) Z'\left( r\right) \nonumber \\{} & {} \quad + \left[ \Omega _1^2-\frac{\Omega _2^2}{r^2}-\Omega _3^2{r^2}-\frac{\Omega _4^2}{r^4}\right] Z\left( r\right) =0, \end{aligned}$$
(24)

with

$$\begin{aligned} \Omega _1^2= & {} \frac{E^2-m^2-3m\omega \alpha ^2-m^2\alpha ^2\omega ^2\epsilon }{\alpha ^2}, \qquad \Omega _3^2= m^2\omega ^2 \end{aligned}$$
$$\begin{aligned} \Omega _2^2= & {} \frac{l\left( l+1\right) + 2\epsilon {m\omega }\alpha ^2 + 2\xi \left( 1-\alpha ^2\right) }{\alpha ^2}, \qquad \Omega _4^2= 2\xi \epsilon .\nonumber \\ \end{aligned}$$
(25)

From now on, let us consider the redefinition of the radial wave function \(Z\left( r\right) =e^{-\frac{\Omega _3{r^2}}{2}}{r}^{|\Omega |} \beta \left( r\right) \) into Eq. (24) and by remembering that \(|\Omega |=\frac{\Omega _4}{\sqrt{\epsilon }}\) we obtain

$$\begin{aligned}{} & {} \left( 1+\frac{\epsilon }{r^2}\right) \beta ''\left( r\right) + \left[ \frac{2}{r}\left( 1+|\Omega |-\epsilon \Omega _3\right) + \frac{\epsilon }{r^3}\left( 1+2|\Omega |\right) \right. \nonumber \\{} & {} \quad \left. - 2\Omega _3{r}\right] \beta '\left( r\right) + \left[ \frac{\zeta _1}{r^2} + \zeta _2\right] \beta \left( r\right) =0. \end{aligned}$$
(26)

where we define the new parameters

$$\begin{aligned} \zeta _1= & {} |\Omega |^2 -2\epsilon |\Omega |\Omega _3 + |\Omega | -2\epsilon \Omega _3 -\Omega _2^2, \nonumber \\ \zeta _2= & {} \Omega _1^2 -3\Omega _3 + \epsilon \Omega _3^2 -2|\Omega |\Omega _3. \end{aligned}$$
(27)

Next, we perform the change of variables given by \(s=-\frac{r^2}{\epsilon }\), then, Eq. (26) becomes

$$\begin{aligned}{} & {} \beta ''\left( s\right) + \left[ \epsilon \Omega _3 + \frac{\left( 1+|\Omega |\right) }{s}+ \frac{\frac{1}{2}}{s-1}\right] \beta '\left( s\right) \nonumber \\{} & {} \quad +\left[ \frac{-\frac{\zeta _1}{4}}{s}+ \frac{\left( \frac{\zeta _1-\epsilon \zeta _2}{4}\right) }{s-1}\right] \beta \left( s\right) =0. \end{aligned}$$
(28)

Equation (28) is the confluent Heun equation [60,61,62], and \(\beta \left( s\right) \) is the confluent Heun function defined in the form:

$$\begin{aligned} \beta \left( s\right)= & {} H_c\left( \epsilon \Omega _3,|\Omega |,-\frac{1}{2}, -\frac{\epsilon \Omega _1^2}{4}-\frac{\epsilon ^2\Omega _3^2}{4},\frac{1}{4}\right. \nonumber \\{} & {} \left. +\frac{|\Omega |^2}{4}-\frac{\Omega _2^2}{4},s\right) . \end{aligned}$$
(29)

Analogously to what was done in the previous section, Eq. (28) can also be solved by using power series, that is, by using the so-called Fröbenius method [63]

$$\begin{aligned} \beta \left( s\right) =\sum _{j=0}^{\infty }d_j{s}^{j}. \end{aligned}$$
(30)

Therefore, substituting Eq. (30) in Eq. (28), we obtain a relation between the coefficients \(d_0\) and \(d_1\) and recurrence relation:

$$\begin{aligned} d_1= & {} \frac{\zeta _1{d_0}}{4\left( 1+|\Omega |\right) }, \end{aligned}$$
(31)
$$\begin{aligned} d_{j+2}= & {} \frac{\epsilon \left( \Omega _3{j}\!-\!\frac{\zeta _2}{4}\right) d_{j}\!+\!\left[ \left( \frac{\zeta _1}{4}\right) \!+\!\left( j+1\right) \left( j+\frac{3}{2}\!+\!|\Omega |\!-\!\epsilon \Omega _3\right) \right] d_{j+1}}{\left( j+2\right) \left( j+2+|\Omega |\right) }.\nonumber \\ \end{aligned}$$
(32)

As we have discussed in the previous section, the confluent Heun series becomes a polynomial of degree \(n=j+1\) when

$$\begin{aligned} d_n= \epsilon \frac{d_{n-1}\left[ \left( \frac{\zeta _2}{4}\right) +\Omega _3\left( 1-n\right) \right] }{\left[ \left( \frac{\zeta _1}{4}\right) +n\left( n+\frac{1}{2}+|\Omega |-\epsilon \Omega _3\right) \right] }, \end{aligned}$$
(33)

where \(n=1,2,3,\ldots \) represent the radial modes of the system.

Let us follow the steps from Eqs. (15) to (16), then, we write

$$\begin{aligned} d_1= \frac{\epsilon \left( \frac{\zeta _2}{4}\right) d_0}{\left[ \left( \frac{\zeta _1}{4}\right) + \frac{3}{2} +|\Omega |-\epsilon \Omega _3\right] }. \end{aligned}$$
(34)

We verified that tor there is compatibility between the results of the bosonic scalar field and the case referring to KGO under effects of the scalar curvature, it is necessary that the parameter \(|\Omega |=-\frac{\Omega _4}{\sqrt{\epsilon }}=-\sqrt{2\xi }\), by making the parameter \(\xi \) positive and defined. Thus, we have that the allowed values for the lowest energy state of the system defined by the radial mode \(n=1\) are given by

$$\begin{aligned} E_{l,1}= & {} \pm \left\{ m^2+ 6m\omega \alpha ^2 -2m\omega \alpha ^2\left( \frac{\Omega _4}{\sqrt{\epsilon }}\right) \right. \nonumber \\{} & {} \left. + \frac{\alpha ^2}{4\epsilon \left( 1-\frac{\Omega _4}{\sqrt{\epsilon }}\right) }\left[ \zeta _1^2 +4\zeta _1\left( \frac{3}{2}-m\omega \epsilon -\frac{\Omega _4}{\sqrt{\epsilon }}\right) \right] \right\} ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(35)

In Eq. (35), we can note that the parameter \(\xi \) that accompanies the curvature scalar, contributes to modifying the energies of the bosonic KGO. The characteristic term of the Born-Infeld metric \(\epsilon \) can be seen as a correction for the GM metric. And therefore, it should also corroborate modifications in the energy spectrum.

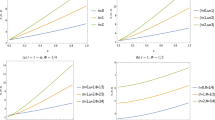
We can observe in the Figs. 3, 4, 5 and 6 that we have created a graphical representation to describe some energy configurations for the ground state, contained in Eq. (35). First, in the Figs. 3 and 4 we set \(m^2\epsilon =1\) and vary the parameters \(\alpha \) and \(\xi \) through the function \(\omega /m\). And later, in the Figs. 5 and 6 we kept the reason \(\omega /m\) fixed and varied the same parameters \(\alpha \) and \(\xi \) through the function \(m^2\epsilon \).

Another result that we can construct from Eq. (35) is the case of a bosonic scalar field. That it is enough to consider the frequency of KGO in the limit of \(\omega \rightarrow {0}\). Thus, the spectrum refers to the ground state of this model is described by

$$\begin{aligned} E_{l,1}= & {} \pm \Bigg [m^2+ \frac{\alpha ^2}{\epsilon \left( 1-\sqrt{2\xi }\right) }\left( \xi ^2+\frac{11\xi }{2}+ \frac{l^2(l+1)^2}{4\alpha ^4}\right. \nonumber \\{} & {} \left. + \frac{\xi ^2(1-\alpha ^2)^2}{\alpha ^4} + \frac{\xi {l}(l+1)(1-\alpha ^2)}{\alpha ^4}\right) \nonumber \\{} & {} +\frac{\alpha ^2}{\epsilon \left( 1-\sqrt{2\xi }\right) }\left( \frac{l(l+1)+2\xi (1-\alpha ^2)}{\alpha ^2}\right) \nonumber \\{} & {} \times \left( \frac{3}{2}\sqrt{2\xi }-\xi \!-\!\frac{3}{2}\right) \!-\!\frac{\alpha ^2}{\epsilon \left( 1-\sqrt{2\xi }\right) }\frac{3}{2}\sqrt{2\xi }\left( 1\!+\!2\xi \right) \Bigg ]^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(36)

which represents the allowed values for the lowest energy state of a scalar field subject to the gravitational Mie-type potential arising from the curvature scalar. We can notice that the energy profile of the system is drastically modified.

The eigenfunction corresponding to the ground state of the bosonic KGO is defined through the expression below

$$\begin{aligned} Z_{l,1}\left( r\right) ={c_0}e^{-\frac{m\omega }{2}r^2}{r}^{-\sqrt{2\xi }}\left[ 1-\frac{\zeta _1{r^2}}{4\epsilon \left( 1-\sqrt{2\xi }\right) }\right] . \end{aligned}$$
(37)

which carries information on the dependency of KGO interaction and on the spacetime topology adopted as background.

Fig. 3
figure 3

In both graphs contained in the figures on the right and left, we have \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(\omega /m\). In the figure on the left, we have the setting of the parameter \(\alpha =0.1\) and two values of the parameter \(\xi \). The continuous curves represent the positive sign of the spectrum Eq. (35) and the dotted curves the negative sign of the spectrum. In the figure on the right, the same process was carried out, now with the parameter \(\alpha =0.5\). Was fixed \(m^2\epsilon =l=1\)

Full size image
Fig. 4
figure 4

In both graphs contained in the figures on the right and left, we have \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(\omega /m\). In the figure on the left, we have the setting of the parameter \(\xi =0.1\) and two values of the parameter \(\alpha \). The continuous curves represent the positive sign of the spectrum Eq. (35) and the dotted curves the negative sign of the spectrum. In the figure on the right, the same process was carried out, now with the parameter \(\xi =0.4\). Was fixed \(m^2\epsilon =l=1\)

Full size image
Fig. 5
figure 5

In both figures we are visualizing \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(m^2\epsilon \). In the figure on the left, we fixed the parameter \(\alpha =0.1\) and varied some values for the parameter \(\xi \). The continuous curves represent the positive sign of the energy spectrum Eq. (35) and the dotted curves the negative sign. On the curve on the right, we fix the parameter \(\alpha =0.3\) and vary the parameter \(\xi \). In both cases, we set \(\omega /m=l=1\)

Full size image
Fig. 6
figure 6

In both figures we are visualizing \(\arrowvert \frac{E_{l,1}}{m}\arrowvert \) as a function of \(m^2\epsilon \). In the figure on the left, we fixed the parameter \(\xi =0.1\) and varied some values for the parameter \(\alpha \). The continuous curves represent the positive sign of the energy spectrum Eq. (35) and the dotted curves the negative sign. On the curve on the right, we fix the parameter \(\xi =0.3\) and vary the parameter \(\alpha \). In both cases, we set \(\omega /m=l=1\)

Full size image

4 Conclusion

In the present work, we study quantum dynamics in Born–Infeld space-time. First, we focus on investigating the effects of a massive particle subjected to KGO, through analytical methods, we construct the energy spectrum referring to the ground state and its corresponding eigenfunction. Looking at the energy spectrum Eq. (18), we can directly observe how the Born–Infeld parameter \(\epsilon \) modifies it.

Furthermore, we show that it is possible to adapt the energy spectrum Eq. (18) for negative values of the \(\epsilon \) parameter and retrieve the KGO case for the topologically charged Ellis-Bronnikov spacetime [42]. We also built a graphical representation for some configurations of the energy spectrum Eq. (18) referring to the ground state (see Figs. 1 and 2).

We investigated a second model, now the massive bosonic particle subjected to the effects of a KGO. In the same way, we build the energy spectrum through analytical methods and in Eq. (18) we stipulate the expression referring to the ground state of energy and later in the equation Eq. (37) the corresponding eigenfunction. We show that not considering the limit of \(\omega \rightarrow {0}\) in the energy spectrum Eq. (36), we can construct the ground state of a massive bosonic particle under the effects of the Born–Infeld parameter \(\epsilon \).

A graphical representation was also constructed to make visual some of the ground state configurations contained in the spectrum Eq. (35). We can observe in the Figs. 3, 4, 5 and 6 that both the parameter accompanying the curvature scalar \(\xi \) and the parameter \(\alpha \), are correlated for the construction of the spectrum. Depending on the values assigned to these parameters, the energy spectrum may diverge. For example, when we consider \(m^2\epsilon \rightarrow {0}\) (see Figs. 5 and 6).