1 Introduction

A fundamental mark of quantum mechanics is the superposition principle, which leads naturally to the phenomenon of coherence and interference, as appropriate for isolated or ideal quantum systems. In contrast, realistic quantum systems are never completely isolated from their environment. For such open quantum systems, there is always a source of decoherence due to the interaction or entanglement of the system with the environment or the surrounding [1,2,3]. Such entanglement may influence what we observe locally upon measurement of the system, even from a classical point of view. Quantum decoherence leads to quantum to classical transition and ensures consistency between quantum and classical predictions for the observed system [4].

Quantum decoherence is rapidly gaining interest in the research community, chiefly in the context of interacting quantum field theories [5, 6]. Decoherence should be closely related to the loss or ignorance of information of an open quantum system and as we have mentioned above, is usually formulated in the setup of system plus environment. It can be characterised via various correlations, like the mutual information, discord and the entanglement entropy. Decoherence can be studied in many different scenarios. A general model of decoherence for a non-relativistic quantum particle interacting with a weak stochastic gravitational perturbation was studied in [7, 8]. Decoherence generation from an accelerated time-delay source for an inertial observer is studied in [9]. The decoherence via the gravitational interaction of the dark matter with its environment, consisting of ordinary matter is analysed in [10]. Perhaps one of the most interesting outcome of the decoherence mechanism could be the classicalisation of the primordial inflationary quantum field theoretic perturbations, leading to the large scale structures in the sky we observe today. We refer our reader to [11,12,13,14,15,16,17,18,19,20,21] and references therein for some such discussions.

As of the issue of quantifying decoherence, different strategies exist in the non-equilibrium quantum field theory, e.g. [5, 22,23,24,25,26] and also the references therein. In the conventional approach to compute decoherence, one traces out the inaccessible environmental degrees of freedom to obtain a reduced density matrix of the system, which in general is a mixed one. Using this reduced density matrix one quantifies the decoherence generated in the system in terms of the von Neumann entropy, e.g. [25, 27,28,29,30,31,32,33,34,35,36,37,38]. Another way to tackle the decoherence problem is to consider the master equation approach [39,40,41,42]. In this work, we shall instead be interested in using the correlator approach proposed in [43,44,45], in order to compute the decoherence in terms of the von Neumann entropy due to observer’s lack of ability to know all correlation functions of the system and the environment, eventually characterising the effective loss of information for the system.

Precisely, there can be n-point correlators which can be generated using the n-particle irreducible effective action [5, 46, 47], capturing the information of interaction between the system and its surrounding. In a realistic scenario however, it is certainly impossible for an observer to quantify the correlators of all orders exactly. Thus one needs to consider a practical scenario allowing us to compute only some finite order correlators such as the 2-point or 4-point Gaussian ones. The ignorance of the higher-order Gaussian and non-Gaussian correlators of the system and surrounding leads to the lack of information, generation of quantum decoherence and hence a non-zero entropy defined in some suitable manner. However, we also note that due to progresses in cold atom experiments, simulating quantum field theory models and measuring higher-order correlations becomes an experimentally relevant problem. For example in [48], multipoint correlation functions in both in and out of equilibrium quantum field theories have been experimentally studied to show the deviation of Gaussianity due to the presence of interaction.

In this work we have considered an open quantum field theory at zero temperature, consisting of bosons and fermions, in order to study the decoherence and subsequent entropy generation via the approach proposed in [43,44,45]. Specifically, we have considered a scalar field coupled to fermions via the Yukawa interaction, treating the scalar as the system and the fermions as the surrounding. We shall work in the flat spacetime, and the present work is to be understood as a warm up exercise before we attempt this problem in the context of the early inflationary universe paradigm, where the late time non-perturbative secular effects may be present. Some earlier analysis on open quantum systems with scalars and fermions can be found in [49,50,51,52].

The rest of the paper is organised as follows. In Sect. 2, we have described the model we are considering and the assumptions we are making along with their justifications. Further, following [43,44,45] and references therein, we have defined the von Neumann entropy of the system in terms of the phase space area. In Sect. 2.1, we have outlined the in–in or the Schwinger–Keldysh or the closed time path formalism which will be required to compute the relationship between the statistical propagator with that of the Wightman functions, i.e. the two point functions relevant for our computations. In Sect. 3 we have computed the 2-loop 2-particle irreducible (2PI) effective action using the Schwinger–Keldysh formalism and have found out the Kadanoff–Baym equations for our model. These are basically the equations of motion for the loop corrected two point functions in an interacting quantum field theory, containing self energy corrections. In Sect. 3.1, we have renormalised the Kadanoff–Baym equations by renormalising the self-energy of the scalar field. Finally in Sect. 4, we have computed the phase space area, the statistical propagator and the entropy of the system, which can be thought of as a quantifier of the decoherence generated on the system due to the interaction with the surrounding and the subsequent ignorance of the higher order correlators. The variation of the entropy and phase space area with respect to the rest mass of the system as well as the Yukawa coupling strength is obtained. Finally, in Sect. 5 we conclude our work. The fermions will be taken to be massless, for the sake of simplicity of computation. We shall use the technical formalism of [44, 45], developed in the context when both system and environment are scalar fields.

Fig. 1
figure 1

Self energy diagrams for the scalar field at one and two loop order for the Yukawa coupling. The broken lines denote fermions whereas the solid lines denote the scalar. We shall restrict our computations to \({\mathcal {O}}(g^2)\) only. See main text for discussion

Full size image

We shall work with the mostly positive signature of the metric in \(d=(4-\epsilon )\)-dimensional \((\epsilon =0^+)\) Minkowski spacetime and will set \(c=\hbar =1\) throughout.

2 The basic setup

We consider a hermitian massive scalar field \(\phi (x)\) coupled to fermions by the Yukawa interaction,

$$\begin{aligned} S= & {} \int {\textrm{d}}^{\scriptscriptstyle {d}}\!x \left[ -\frac{1}{2} (\partial _\mu \phi ) (\partial ^{\mu } \phi ) - \frac{1}{2} m^{2}\phi ^{2}-\frac{i}{2}{\bar{\psi }}\gamma ^{\mu }\partial _{\mu }\psi \right. \nonumber \\{} & {} \left. -g {\bar{\psi }}\psi \phi \right] . \end{aligned}$$
(1)

Since we are working with the mostly positive signature of the metric, the \(\gamma ^{\mu }\)’s satisfy the anti-commutation,

$$\begin{aligned}{}[\gamma ^{\mu },\gamma ^{\nu }]_+= -2\eta ^{\mu \nu } \textbf{I}. \end{aligned}$$

As we have mentioned earlier, the scalar \(\phi (x)\) will play the role of the system, interacting with the environment \(\psi (x)\), \({\overline{\psi }}(x)\). We assume that the environment is at zero temperature and is in its vacuum state.

We assume that our observer (observing the system) can measure two point correlation functions only. Note that a tree level two point function is essentially Gaussian. A quantum corrected such function may or may not be Gaussian. Higher correlations containing the effect of interaction, such as the three point correlators, are non-Gaussian. We have to work on perturbative corrections to the self energy and will restrict ourselves to one loop, \({\mathcal {O}}(g^2)\). Note also that the two loop \({\mathcal {O}}(g^4)\) diagrams of Fig. 1 contains backreaction of the system on the environment, which will be ignored. Restricting ourselves only to one loop seems justified at least when the Yukawa coupling constant g is not too strong and second, in particular when there is no secular effect at late times. Note also that since the fermions are taken to be massless, there can be decay of the system (i.e., the scalar) into fermion-anti-fermion pairs starting at \({\mathcal {O}}(g^2)\). However, this decay involves three point correlators between the system and the surrounding, with on shell process also going on within the surrounding which is unobserved by the observer. Hence we shall ignore such decay in our computations. As we have stated in the preceding section, the lack of observer’s ability to measure higher order correlators due to the system-environment interaction essentially leads to lack of information for the system and it decoheres. This lack of information or decoherence will be quantified by the von Neumann entropy, as follows.

A quantum system can be represented by the density matrix that holds all information about the system. One can calculate various correlators from the density matrix. In particular, different two point correlators are given as [53]

$$\begin{aligned} \langle \phi (x)\phi (x^{\prime })\rangle= & {} {\textrm{Tr}}\left[ {\rho }(t) \phi (x)\phi (x^{\prime }) \right] \nonumber \\ \langle \pi (x)\pi (x^{\prime })\rangle= & {} {\textrm{Tr}}\left[ \rho (t) \pi (x)\pi (x^{\prime }) \right] \nonumber \\ \frac{1}{2}\langle [\phi (x),\pi (x^{\prime })]_+\rangle= & {} \frac{1}{2}{\textrm{Tr}}[{\rho }(t) [\phi (x),\pi (x^{\prime })]_+]\nonumber \\:= & {} \partial _{t'}F_{\phi }(x,x') \end{aligned}$$
(2)

where the first one is the Wightman function, \(\pi (x)={\dot{\phi }}(x)\) is the momentum conjugate to the scalar field and the quantity \(F_{\phi }(x,x')\) is called the statistical propagator defined as

$$\begin{aligned} F_{\phi }(x,x'):= & {} \frac{1}{2} {\textrm{Tr}} \left( \rho (t)[\phi (x), \phi (x')]_+ \right) \nonumber \\= & {} \frac{1}{2} {\textrm{Tr}} \left[ \rho (t) ( \phi (x)\phi (x') + \phi (x')\phi (x)) \right] . \end{aligned}$$
(3)

Thus the statistical propagator is basically the Wightman function symmetrised in x and \(x'\). For a given density operator \(\rho (t)\) (pure or mixed), the statistical propagator tells us about how the states are occupied. One can also relate this to the average particle density. We shall focus only on the above two point correlators and their quantum corrections, as a practical scenario.

In the spatial momentum space, the statistical propagator reads,

$$\begin{aligned} F(|{\vec {k}}|,t,t')=\int d^3\Delta {\vec {x}} \, F_{\phi }(t,{\vec {x}},t',\vec {x'}) e^{-\imath {\vec {k}}\cdot \Delta {\vec {x}}}. \end{aligned}$$
(4)

One also defines the phase space area for each spatial momentum mode as the Fourier transform of the quantity

$$\begin{aligned} 4\Big [\langle \phi (x)\phi (x^{\prime })\rangle \langle \pi (x)\pi (x^{\prime })\rangle - \left( \frac{1}{2}\langle [\phi (x),\pi (x^{\prime })]_+\rangle \right) ^2 \Big ]_{t=t'}, \end{aligned}$$

given by

$$\begin{aligned} \Delta _{|{\vec {k}}|}^{2}(t)=4 \left[ F(|{\vec {k}}|,t,t')\partial _{t}\partial _{t'}F(|{\vec {k}}|,t,t') - (\partial _{t}F(|{\vec {k}}|,t,t'))^{2} \right] _{t=t'}\nonumber \\ \end{aligned}$$
(5)

where we have used the equal time limits of Eqs. (2) and (4). In order to see the analogy of this construction with that of ordinary quantum mechanics, let us recall the generalised uncertainty relation (with \(\hbar =1\)),

$$\begin{aligned}{} & {} \left\langle q^{2}\right\rangle \left\langle p^{2}\right\rangle - \left[ \left\langle \frac{1}{2}[q, p]_+\right\rangle \right] ^{2}= \frac{1}{4}\quad (\text {pure state}) \nonumber \\{} & {} \left\langle {q}^{2}\right\rangle \left\langle p^{2}\right\rangle -\left[ \left\langle \frac{1}{2}[q, p]_+\right\rangle \right] ^{2}>\frac{1}{4} \quad (\text {mixed state}). \end{aligned}$$
(6)

Combining the two above, we write

$$\begin{aligned} \left\langle q^{2}\right\rangle \left\langle p^{2}\right\rangle -\left[ \left\langle \frac{1}{2}[q,p]_+\right\rangle \right] ^{2}=\frac{\Delta ^2}{4}. \end{aligned}$$
(7)

Thus the quantity \(\Delta \ge 1\), interpreted as the phase space area, can be thought of as a measure of the impurity of the quantum state. One plausible way to understand the increase in \(\Delta \) is the transfer of momentum between the system and the environment, thereby increasing the momentum uncertainty. Putting these all in together, the loss or ignorance of information due to the inaccessibility of all the correlations in the system, environment and between them, is characterised via the von Neumann entropy for our field theoretic continuum system [53],

$$\begin{aligned} S_{|{\vec {k}}|}(t)= & {} \frac{ \Delta _{|{\vec {k}}|}(t)+1}{2} \ln \left( \frac{\Delta _{|{\vec {k}}|}(t)+1}{2}\right) \nonumber \\{} & {} - \frac{ \Delta _{|{\vec {k}}|}(t)-1}{2} \ln \left( \frac{\Delta _{|{\vec {k}}|}(t)-1}{2}\right) . \end{aligned}$$
(8)

One can also relate the phase space area with the statistical particle number density per mode as

$$\begin{aligned} n_{|{\vec {k}}|}(t) = \frac{ \Delta _{|{\vec {k}}|}(t)-1}{2}. \end{aligned}$$
(9)

We shall see below that \(\Delta _{|{\vec {k}}|}(t)\) becomes identity in the absence of the Yukawa interaction.

For our purpose, we need to compute the various two-point functions in the in–in or the Schwinger–Keldysh formalism, which we outline below.

2.1 Propagators in the in–in formalism

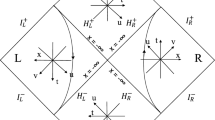
The Schwinger–Keldysh or the in–in formalism is useful for studying the quantum dynamics of a system in a non-equilibrium scenario [54, 55]. Using this, one can meaningfully compute the causal expectation value of an operator with respect to some suitable initial state. Precisely, one follows the time evolution of an operator from some initial state at \(t = t_0\), without having the knowledge of appropriate late time states. Evolution of an operator from \(t_0\) to t requires a time-ordered evolution and then it is brought back to the initial time following an anti-time ordered evolution t to \(t_0\), as depicted in Fig. 2.

Thus in the in–in formalism, the expectation value of an operator O(t) with respect to some initial density operator \(\rho (t_{0})\) (defined in the Heisenberg picture) is given by,

$$\begin{aligned} \langle O(t) \rangle= & {} {\textrm{Tr}}\left[ \rho (t_{0})O(t)\right] \nonumber \\= & {} {\textrm{Tr}}\left[ \rho (t_{0}) \left\{ {\overline{T}} \exp \left( \imath \int _{t_0}^t {\textrm{d}}t^{\prime } H(t^{\prime })\right) \right\} O(t_{0})\right. \nonumber \\{} & {} \times \left. \left\{ T \exp \left( -\imath \int _{t_0}^t {\textrm{d}} t'' H(t'') \right) \right\} \right] \end{aligned}$$
(10)

where \({\overline{T}}\) stands for the anti-time ordering, and H(t) is the Hamiltonian. The generating functional for the corresponding path integral for Eq. (1), subject to Fig. 2 is given by

Fig. 2
figure 2

Schwinger–Keldysh contours with finite and infinite initial and final times

Full size image
$$\begin{aligned}{} & {} {\mathcal {Z}}[J_{+}^{\phi }, J_{-}^{\phi }, J_{+}^{\psi }, J_{-}^{\psi }, \rho (t_0)] \nonumber \\{} & {} \quad =\int \! {\mathcal {D}}\phi ^{+}_{0}{\mathcal {D}}\phi ^{-}_{0} [{\mathcal {D}}\psi ^{+}_{0}] [{\mathcal {D}}\psi ^{-}_{0}] \langle \phi ^{+}_{0}, \psi ^{+}_{0}| { \rho }(t_{0})|\phi ^{-}_{0}, \psi ^{-}_{0} \rangle \nonumber \\{} & {} \qquad \times \int _{\phi _{0}^{+}}^{\phi _{0}^{-}}\! {\mathcal {D}}\phi ^{+}{\mathcal {D}}\phi ^{-} \delta [\phi ^{+}(t_{f}\!)-\phi ^{-}(t_{f}\!)]\!\nonumber \\{} & {} \qquad \times \int _{\psi _{0}^{+}}^{\psi _{0}^{-}} \![{\mathcal {D}}\psi ^{+}][{\mathcal {D}}\psi ^{-}] [\delta [\psi ^{+}(t_{f}\!)-\psi ^{-}(t_{f}\!)]] \nonumber \\{} & {} \qquad \times \textrm{exp}\left[ \imath \int {\textrm{d}}^{d-1} {\vec {x}}\int _{t_{0}}^{t_{f}} {\textrm{d}}t^{\prime } \left( {\mathcal {L}}[\phi ^{+},\psi ^{+},t']-{\mathcal {L}}[\phi ^{-},\psi ^{-},t']\right. \right. \nonumber \\{} & {} \qquad \left. \left. +J_{+}^{\phi }\phi ^{+} + J_{-}^{\phi }\phi ^{-} + [J_{+}^{\psi } \psi ^{+}] + [J_{-}^{\psi }\psi ^{-}] \right) \right] \end{aligned}$$
(11)

where for notational convenience we have written \([{\mathcal {D}}\psi ]={\mathcal {D}}\bar{\psi }{\mathcal {D}}\psi \), \([J_{+}^{\psi } \psi ^{+}]= J_{+}^{\psi } \psi ^{+}+\bar{\psi }^{+}\bar{J_+}^{{\bar{\psi }}^+} \) etc. The fields \(\phi ,\, \psi ,\,\bar{\psi } \) have their sources \(J^{\phi }\), \(J^{\psi }\) \({\bar{J}}^{{\bar{\psi }}}\) respectively. Note that there are two species of fields and sources for each category. The \(+\) sign denotes forward evolution in time whereas the − sign denotes backward evolution. The \(\delta \)-function ensures the field configurations are the same on the final hypersurface at \(t=t_f\). The expectation values of n-point functions can be found by taking functional differentiation of the generating functional Eq. (11) with respect to the sources J’s, for instance

$$\begin{aligned}{} & {} \left. {\textrm{Tr}}\left[ {\rho }(t_{0}) {\overline{T}}[\phi (x_1)\dots \phi (x_n)] T[\phi (y_1)\dots \phi (y_k)] \right] \right. \nonumber \\{} & {} \quad \left. = \frac{\delta ^{n+k}{\mathcal {Z}}[J, \rho (t_0)] }{\imath \delta \! J_{-}^{\phi }(x_{1})\cdots \imath \delta \! J_{-}^{\phi }(x_{n}) \imath \delta \! J_{+}^{\phi }(y_{1})\cdots \imath \delta \! J_{+}^{\phi }(y_{k})} \right| _{J = 0}.\nonumber \\ \end{aligned}$$
(12)

With the help of the above, we now define the following propagators for the scalar field,

$$\begin{aligned} \imath \Delta ^{++}_{\phi }(x,x^{\prime })= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) T[\phi (x^{\prime })\phi (x)] \right] \nonumber \\= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) \phi ^+(x)\phi ^+(x^{\prime })\right] \nonumber \\= & {} \left. \frac{\delta ^2{\mathcal {Z}}[J, \rho (t_0)]}{\imath \delta \! J_{+}^{\phi }(x) \imath \delta \! J_{+}^{\phi }(x^{\prime })} \right| _{J=0} \end{aligned}$$
(13a)
$$\begin{aligned} \imath \Delta ^{--}_{\phi }(x,x^{\prime })= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) {\overline{T}} [ \phi (x^{\prime })\phi (x)] \right] \nonumber \\= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) \phi ^-(x^{\prime })\phi ^-(x)\right] \nonumber \\= & {} \left. \frac{\delta ^2{\mathcal {Z}} [J, \rho (t_0)]}{\imath \delta \! J_{-}^{\phi }(x)\imath \delta \! J_{-}^{\phi }(x^{\prime })} \right| _{J=0} \end{aligned}$$
(13b)
$$\begin{aligned} \imath \Delta ^{-+}_{\phi }(x,x^{\prime })= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) \phi (x)\phi (x^{\prime })\right] \nonumber \\= & {} {\textrm{Tr}}\left[ {\rho }(t_{0}) \phi ^-(x)\phi ^+(x^{\prime })\right] \nonumber \\= & {} \left. \frac{\delta ^2{\mathcal {Z}} [J, \rho (t_0)] }{\imath \delta \! J_{-}^{\phi }(x)\imath \delta \! J_{+}^{\phi }(x^{\prime })} \right| _{J=0} \end{aligned}$$
(13c)
$$\begin{aligned} \imath \Delta ^{+-}_{\phi }(x,x^{\prime })= & {} {\textrm{Tr}}\left[ {\rho }(t_{0})\phi (x^{\prime })\phi (x)\right] \nonumber \\= & {} {\textrm{Tr}}\left[ {\rho }(t_{0})\phi ^-(x^{\prime })\phi ^+(x)\right] \nonumber \\= & {} \left. \frac{\delta ^2{\mathcal {Z}} [J, \rho (t_0)] }{\imath \delta \! J_{+}^{\phi }(x)\imath \delta \! J_{-}^{\phi }(x^{\prime })} \right| _{J=0} \end{aligned}$$
(13d)

where we have taken \(t>t'\) above. The time ordered and the anti-time ordered propagators are respectively the Feynman and anti-Feynman propagators and the rest are the two Wightman functions. One can also write

$$\begin{aligned} \imath \Delta ^{++}_{\phi }(x,x^{\prime })= & {} \theta (t-t^{\prime })\imath \Delta ^{-+}_{\phi }(x,x^{\prime }) + \theta (t^{\prime }-t)\imath \Delta ^{+-}_{\phi }(x,x^{\prime }) \nonumber \\ \imath \Delta ^{--}_{\phi }(x,x^{\prime })= & {} \theta (t^{\prime }-t)\imath \Delta ^{-+}_{\phi }(x,x^{\prime }) + \theta (t-t^{\prime })\imath \Delta ^{+-}_{\phi }(x,x^{\prime }).\nonumber \\ \end{aligned}$$
(14)

These propagators and Wightman functions also satisfy the following properties,

$$\begin{aligned} \imath \Delta ^{++}_{\phi }(x,x^{\prime }) + \imath \Delta ^{--}_{\phi }(x,x^{\prime })= & {} \imath \Delta ^{-+}_{\phi }(x,x^{\prime }) +\imath \Delta ^{+-}_{\phi }(x,x^{\prime }) \end{aligned}$$
(15)
$$\begin{aligned} \imath \Delta ^{-+}_{\phi }(x,x^{\prime })= & {} \imath \Delta ^{+-}_{\phi }(x^{\prime },x). \end{aligned}$$
(16)

The retarded and the advanced propagators, useful for our later purpose, are respectively defined as

$$\begin{aligned} \imath \Delta ^{\textrm{r}}_{\phi }(x,x^{\prime })= & {} \imath \Delta ^{++}_{\phi }(x,x^{\prime }) - \imath \Delta ^{+-}_{\phi }(x,x^{\prime }) \end{aligned}$$
(17a)
$$\begin{aligned} \imath \Delta ^{\textrm{a}}_{\phi }(x,x^{\prime })= & {} \imath \Delta ^{++}_{\phi }(x,x^{\prime }) - \imath \Delta ^{-+}_{\phi }(x,x^{\prime }). \end{aligned}$$
(17b)

One also defines the spectral two point function and the statistical propagator as (e.g. [44]),

$$\begin{aligned} \imath \Delta ^{c}_{\phi } (x,x^{\prime })= & {} {\textrm{Tr}}\left( {\rho }(t_{0}) [\phi (x),\phi (x^{\prime })]\right) \nonumber \\= & {} \imath \Delta ^{-+}_{\phi }(x,x^{\prime }) - \imath \Delta ^{+-}_{\phi }(x,x^{\prime })\nonumber \\ F_{\phi }(x,x')= & {} \frac{1}{2} {\textrm{Tr}}\left[ {\rho }(t_{0}) [ \phi (x),\phi (x')]_+ \right] \nonumber \\= & {} \frac{1}{2}\Big (\imath \Delta ^{-+}_{\phi }(x,x') + \imath \Delta ^{+-}_{\phi }(x,x')\Big ). \end{aligned}$$
(18)

The spectral function can tell us about the states of the system and the spectrum, but it does not hold any information on how these states are occupied. The statistical propagator on the other hand, gives information about how the states are populated. Hence the latter is much relevant to study decoherence and entropy [22] (also references therein).

The free Feynman, anti-Feynman and the Wightman functions satisfy

$$\begin{aligned}{} & {} (\partial _x^2 - m^2)\imath \Delta ^{ss'}_{\phi }(x,x^{\prime }) = \imath s \delta _{ss'}\delta ^{\scriptscriptstyle {D}}\!(x-x^{\prime })\nonumber \\{} & {} \quad (s,s'=\pm ,\text { no sum on }s). \end{aligned}$$
(19)
Fig. 3
figure 3

Contributions to the 2PI effective action up to two loop order. The solid lines denote \(\phi \)-propagators, whereas the dashed lines correspond to \(\psi \)-propagators. The tadpoles will not make any contribution. See main text for discussion

Full size image

The propagators for the fermionic field can be defined in a likewise manner, keeping in mind the anti-commutations satisfied by them and the replacement of the d’Alembertian \(\partial ^2\) by . We shall consider a zero temperature field theory, and hence various averages such as in Eq. (13) are to be understood simply as the vacuum expectation values below.

With these equipments, we are now ready to compute the loop correction to the two-point functions and to find out the Kadanoff–Baym equation, i.e. the equation of motion satisfied by them.

3 Derivation of the Kadanoff–Baym equations

The Kadanoff–Baym equations are integro-differential equations satisfied by the two-point functions in an interacting quantum field theory [56]. It is well known that the one particle irreducible effective action, when varied with respect to some background field, gives rise to the quantum corrected field equation. Likewise, the 2PI effective action, when varied with respect to the two point functions, yields equation of motion satisfied by them known as the Kadanoff–Baym equations. Since the 2PI effective action contains quantum corrections, we obtain extensions of free theory equations like Eq. (19), essentially containing the effect of loops. One can obtain the 2PI effective action as a double Legendre transform from the generating functional for connected Green functions with respect to the linear source J and also another quadratic source [22, 47, 57,58,59]. These equations contain the effects of the non-local self energy.

We expand the effective action corresponding to Eq. (1) up to two loop order as

$$\begin{aligned}{} & {} \Gamma [{\phi }^{s},{\psi }^{s},{{\bar{\psi }}}^s, \imath \Delta _{\phi }^{ss^{\prime }},\imath {}S^{ss^{\prime }}_{\psi }] \nonumber \\{} & {} \quad = S[{\phi }^{s},{\psi }^{s}] + \frac{\imath }{2} {\textrm{Tr}} \ln [ (\imath \Delta _{\phi }^{ss^{\prime }})^{-1}] {-\imath } {\textrm{Tr}} \ln [(\imath {}S^{ss^{\prime }}_{\psi })^{-1}] \nonumber \\{} & {} \qquad +\frac{1}{2} {\textrm{Tr}} \frac{\delta ^{2}\! S[{\phi }^{s},{\psi }^{s}]}{\delta \!{\phi }^{s} \delta \! {\phi }^{s^{\prime }}} \imath \Delta _{\phi }^{ss^{\prime }} - {\textrm{Tr}} \frac{\delta ^{2} S[{\phi }^{s},{\psi }^{s}]}{\delta \! {{\bar{\psi }}}^{s} \delta \! {\psi }^{s^{\prime }}} \imath {}S^{ss^{\prime }}_{\psi } \nonumber \\{} & {} \qquad + \Gamma ^{(2)}[{\phi }^{s},{\psi }^{s},\imath \Delta _{\phi }^{ss^{\prime }},\imath {}S^{ss^{\prime }}_{\psi }] \end{aligned}$$
(20)

where \(s,s'=\pm \), and \(\imath {}S^{ss^{\prime }}_{\psi }\) are the fermion propagators. \(\Gamma ^{(2)}\) denotes the 2PI contribution to the effective action at two loop, as shown in Fig. 3. Note however that since we are considering massless fermions, the tadpoles vanish. Even with a massive fermion, the tadpoles can be completely renormalised away in the flat spacetime. Thus we need to consider only the sunset like diagram of Fig. 3. We now explicitly write down the parts of Eq. (20) containing quantum corrections as

(21a)
(21b)
(21c)

where the last line corresponds to the first of Fig. 3.

We now vary the effective action with respect to the bosonic and the fermionic propagators, \(i\Delta _{\phi }\) and \(iS_{\psi }\), to obtain the equations of motion

$$\begin{aligned} \frac{ \delta \Gamma [\imath \Delta _{\phi }^{ss^{\prime }}, \imath {}S^{ss^{\prime }}_{\psi } ]}{\delta \imath \Delta _{\phi }^{ss^{\prime }}} = 0, \quad \text {and}\quad \frac{\delta \Gamma [\imath \Delta _{\phi }^{ss^{\prime }},\imath {}S^{ss^{\prime }}_{\psi } ]}{\delta \imath {}S^{ss^{\prime }}_{\psi }} = 0 \end{aligned}$$
(22)

explicitly giving respectively

(23a)
(23b)

We next multiply Eqs. (23a) and (23b) respectively by \(s \imath \Delta ^{s^{\prime }s^{\prime \prime }}_{\phi }(x^{\prime },x^{\prime \prime })\) and \(s \imath {}S^{s^{\prime }s^{\prime \prime }}_{\psi }(x^{\prime },x^{\prime \prime })\) (from the right), and then integrate over \(x^{\prime }\) and sum over \(s^{\prime }=\pm \). Recalling that the integration over the product of the propagator and its inverse gives a \(\delta \)-function, we obtain the one-loop Kadanoff–Baym equations

(24a)
(24b)

where we have abbreviated the one loop the self-energies as

$$\begin{aligned} \imath M^{ss^{\prime \prime }}_{\phi }(x,x')= & {} -\imath g^{2} \textrm{Tr}[iS^{ss'}_\psi (x,x')iS^{s's}_\psi (x',x)]\nonumber \\= & {} -2ss^{\prime \prime }\frac{\delta \Gamma ^{(2)}[\imath \Delta _{\phi }^{ss^{\prime }}, \imath {}S^{ss^{\prime }}_{\psi } ]}{\delta \imath \Delta ^{s^{\prime \prime }s}_{\phi }} \end{aligned}$$
(25a)
$$\begin{aligned} \imath M^{ss^{\prime \prime }}_{\psi }(x,x')= & {} \imath g^{2} \imath {}S^{s^{\prime \prime }s}_{\psi }(x',x) \imath \Delta ^{ss^{\prime \prime }}_{\phi }(x,x')\nonumber \\= & {} ss^{\prime \prime }\frac{\delta \Gamma ^{(2)}[\imath \Delta _{\phi }^{ss^{\prime }}, \imath {}S^{ss^{\prime }}_{\psi } ]}{\delta \imath {}S^{s^{\prime \prime }s}_{\psi }}. \end{aligned}$$
(25b)

Since we are considering the scalar to be our system which is observed, we shall consider only the scalar self energy, Eq. (25a). The corresponding Feynman diagram is given by the first of Fig. 1. Accordingly, by expanding the summations, we rewrite Eq. (24a) as

$$\begin{aligned}{} & {} (\partial _{x}^{2}-m^{2}) \imath \Delta ^{++}_{\phi }(x,x^{\prime }) \nonumber \\{} & {} \quad - \int {\textrm{d}}^{\scriptscriptstyle {d}}\! y \left[ \imath M^{++}_{\phi }(x,y)\imath \Delta ^{++}_{\phi }(y,x^{\prime }) \right. \nonumber \\{} & {} \quad \left. - \imath M^{+-}_{\phi }(x,y)\imath \Delta ^{-+}_{\phi }(y,x^{\prime })\right] = \imath \delta ^{\scriptscriptstyle {d}}(x-x^{\prime }) \end{aligned}$$
(26a)
$$\begin{aligned}{} & {} (\partial _{x}^{2} - m^{2})\imath \Delta ^{+-}_{\phi }(x,x^{\prime })\nonumber \\{} & {} \quad - \int {\textrm{d}}^{\scriptscriptstyle {d}}\!y \left[ \imath M^{++}_{\phi }(x,y)\imath \Delta ^{+-}_{\phi }(y,x^{\prime }) \right. \nonumber \\{} & {} \quad \left. - \imath M^{+-}_{\phi }(x,y)\imath \Delta ^{--}_{\phi }(y,x^{\prime })\right] =\, 0 \end{aligned}$$
(26b)
$$\begin{aligned}{} & {} (\partial _{x}^{2} - m^{2})\imath \Delta ^{-+}_{\phi }(x,x^{\prime }) \nonumber \\{} & {} \quad - \int {\textrm{d}}^{\scriptscriptstyle {d}}\!y \left[ \imath M^{-+}_{\phi }(x,y)\imath \Delta ^{++}_{\phi }(y,x^{\prime }) \right. \nonumber \\{} & {} \quad \left. - \imath M^{--}_{\phi }(x,y)\imath \Delta ^{-+}_{\phi }(y,x^{\prime })\right] =\, 0 \end{aligned}$$
(26c)
$$\begin{aligned}{} & {} (\partial _{x}^{2}-m^{2})\imath \Delta ^{--}_{\phi }(x,x^{\prime }) \nonumber \\{} & {} \quad - \int {\textrm{d}}^{\scriptscriptstyle {d}}\!y \left[ \imath M^{-+}_{\phi }(x,y)\imath \Delta ^{+-}_{\phi }(y,x^{\prime }) \right. \nonumber \\{} & {} \quad \left. - \imath M^{--}_{\phi }(x,y)\imath \Delta ^{--}_{\phi } (y,x^{\prime })\right] =-\imath \delta ^{\scriptscriptstyle {d}}(x-x^{\prime }). \end{aligned}$$
(26d)

Setting \(g=0\) above makes the self energies vanishing, thereby reproducing the free theory results of Eq. (19). Note also that even though the self energies appearing in the above equations are of one loop order, we may integrate these equations to find out the propagators, eventually non-perturbative in the coupling constant. In other words, the Kadanoff–Baym equations gives a framework to resum the self energies. This seems to be in particular useful in the context of the primordial cosmic inflation, where late time secular effects may be present, necessitating resummation, e.g. [60,61,62].

We shall solve Eq. (26) by going to the momentum space. We define the Fourier transform

$$\begin{aligned} \imath \Delta _{\phi }^{ss^{\prime }}(x,x')= & {} \int \frac{{\textrm{d}}^{\scriptscriptstyle {d}}k}{(2\pi )^{\scriptscriptstyle {d}}} \imath \Delta _{\phi }^{ss^{\prime }}(k)\textrm{e}^{\imath k \cdot (x-x')} \end{aligned}$$
(27)

in terms of which Eq. (26) become

$$\begin{aligned} (-k^2-m^{2}- \imath M^{++}_{\phi }(k)) \imath \Delta ^{++}_{\phi }(k) + \imath M^{+-}_{\phi }(k) \imath \Delta ^{-+}_{\phi }(k)= & {} \, \imath \end{aligned}$$
(28a)
$$\begin{aligned} (-k^2 - m^{2} -\imath M^{++}_{\phi }(k) )\imath \Delta ^{+-}_{\phi }(k) + \imath M^{+-}_{\phi }(k)\imath \Delta ^{--}_{\phi }(k)= & {} 0 \end{aligned}$$
(28b)
$$\begin{aligned} (-k^2 - m^{2} + \imath M^{--}_{\phi }(k) )\imath \Delta ^{-+}_{\phi }(k) - \imath M^{-+}_{\phi }(k)\imath \Delta ^{++}_{\phi }(k)= & {} 0 \end{aligned}$$
(28c)
$$\begin{aligned} (-k^2-m^{2} + \imath M^{--}_{\phi }(k))\imath \Delta ^{--}_{\phi }(k) - \imath M^{-+}_{\phi }(k)\imath \Delta ^{+-}_{\phi }(k)= & {} -\imath \nonumber \\ \end{aligned}$$
(28d)

where \(k^2=k_{\mu }k^{\mu }=-k_{0}^{2}+|{\vec {k}}|^{2}\). Solving these coupled algebraic equations, we can find out various two point functions. For example, on subtracting Eq. (28b) from Eq. (28c), we have the momentum space expression for the advanced propagator Eq. (17b),

$$\begin{aligned} \imath \Delta ^{\textrm{a}}_{\phi }(k) = \imath \Delta ^{++}_{\phi }(k)-\imath \Delta ^{-+}_{\phi }(k)= \frac{-\imath }{ k^2+m^{2}+\imath M^{\textrm{a}}_{\phi }(k)}\nonumber \\ \end{aligned}$$
(29)

where the advanced self-energy \(\imath M^{\textrm{a}}_{\phi }(k)\) is given by

$$\begin{aligned} \imath M^{\textrm{a}}_{\phi }(k) = \imath M^{++}_{\phi }(k) - \imath M^{-+}_{\phi }(k) = \imath M^{+-}_{\phi }(k) - \imath M^{--}_{\phi }(k). \end{aligned}$$

Likewise we find the Wightman functions

$$\begin{aligned} \imath \Delta ^{-+}_{\phi }(k)= & {} \frac{ - \imath M^{-+}_{\phi }(k) \imath \Delta ^{\textrm{a}}_{\phi }(k)}{k^2+m^{2}+\imath M^{\textrm{r}}_{\phi }(k)} \end{aligned}$$
(30a)
$$\begin{aligned} \imath \Delta ^{+-}_{\phi }(k)= & {} \frac{ - \imath M^{+-}_{\phi }(k) \imath \Delta ^{\textrm{a}}_{\phi }(k)}{k^2+m^{2}+\imath M^{\textrm{r}}_{\phi }(k)} \end{aligned}$$
(30b)

where the retarded self-energy \(\imath M^{\textrm{r}}_{\phi }(k)\) is given by

$$\begin{aligned} \imath M^{\textrm{r}}_{\phi }(k) = \imath M^{++}_{\phi }(k) - \imath M^{+-}_{\phi }(k) = \imath M^{-+}_{\phi }(k) - \imath M^{--}_{\phi }(k). \end{aligned}$$

Substituting Eq. (29) into Eqs. (30a) and (30b), we finally obtain the momentum space expression of the statistical propagator Eq. (18),

$$\begin{aligned} F_{\phi }(k){} & {} =-\frac{ \imath \Delta ^{\textrm{a}}_{\phi }(k) (\imath M^{-+}_{\phi }(k)+\imath M^{+-}_{\phi }(k))}{2(k^2+m^{2}+\imath M^{\textrm{r}}_{\phi }(k))} \nonumber \\ {}{} & {} =\frac{\imath (\imath M^{-+}_{\phi }(k)+\imath M^{+-}_{\phi }(k))}{2(\imath M^{\textrm{r}}_{\phi }(k)-\imath M^{\textrm{a}}_{\phi }(k))}\Bigg (\frac{1}{k^2+m^2+\imath M^{\textrm{a}}_{\phi }(k)}\nonumber \\{} & {} \quad -\frac{1}{k^2+m^2+\imath M^{\textrm{r}}_{\phi }(k)}\Bigg ). \end{aligned}$$
(31)

Recall that the statistical propagator will yield the expression of the phase space area and entropy, Eqs. (5) and (8). Thus in order to compute the statistical propagator, we need to determine various self-energies, as appearing in Eq. (31). However, note that the above expressions are not renormalised. Hence we shall use the renormalised self energies in Eq. (31), in order to compute the entropy. Also in particular, note that since the self energies are \({\mathcal {O}}(g^2)\), the only coupling constant dependence of the above expression comes in the denominator of the terms within the parenthesis. Thus the expression for the statistical propagator is actually non-perturbative and contains the resummed self-energy corresponding to the series of one-loop diagrams (i.e., the first of Fig. 1), owing to the Kadanoff–Baym equations.

3.1 The retarded self-energy and its renormalisation

In this section, we compute the self-energy \(\imath M_{\phi }^{ss^{\prime }}(x,x')\) and find out the renormalised retarded self-energy, \(\imath M_{\phi ,{\textrm{ren}}}^{\textrm{r}}(x,x')= \imath M_{\phi ,{\textrm{ren}}}^{++}(x,x') - \imath M_{\phi }^{+-}(x,x')\), to be useful for our future purpose. Due to the subtraction of the two propagators, it is easily done in coordinate space. Necessary techniques in order to deal with such coordinate space computations can be seen in, e.g. [63, 64].

The fermion propagator \(\imath {}S^{ss^{\prime }}_{\psi }(x,x')\) is obtained by acting on the massless scalar field propagator,

(32)

The Poincaré invariant biscalar distance functions with appropriate \(i\epsilon \) prescription, \(\Delta x_{ss^{\prime }}^{2}(x,x')\), necessary for the in–in formalism are defined as

$$\begin{aligned} \Delta x_{++}^{2}(x,x')= & {} - \left( \left| t - t' \right| - i \epsilon \right) ^{2} + | {\vec {x}} - {\vec {x}}'|^{2} \end{aligned}$$
(33a)
$$\begin{aligned} \Delta x_{+-}^{2}(x,x')= & {} - \left( t - t' + i \epsilon \right) ^{2} + | {\vec {x}} - {\vec {x}}'|^{2} \end{aligned}$$
(33b)
$$\begin{aligned} \Delta x_{-+}^{2}(x,x')= & {} - \left( t - t' - i \epsilon \right) ^{2} + | {\vec {x}} - {\vec {x}}'|^{2} \end{aligned}$$
(33c)
$$\begin{aligned} \Delta x_{--}^{2}(x,x')= & {} - \left( \left| t - t' \right| + i \epsilon \right) ^{2} + | {\vec {x}} - {\vec {x}}'|^{2}. \end{aligned}$$
(33d)

The one loop scalar self-energy \(\imath M_{\phi }^{++}(x,x')\) is readily found from Eqs. (25a) and (32)

$$\begin{aligned} \imath M_{\phi }^{++}(x,x')= - \frac{\imath g^{2}\Gamma ^{2}(\frac{d}{2})}{ \pi ^{\scriptscriptstyle {d}}} \frac{1}{ \Delta x_{++}^{2\scriptscriptstyle {d}-2}(x,x')}. \end{aligned}$$
(34)

Similarly, we can find out the other self-energies \(\imath M_{\phi }^{--}(x,x')\), \(\imath M_{\phi }^{+-}(x,x')\) and \(\imath M_{\phi }^{-+}(x,x')\) using the suitable \(i\epsilon \) prescriptions as given in Eq. (33). We will now identify the divergence of Eq. (34). Note first that for an arbitrary exponent \(\alpha \), we have

$$\begin{aligned} \frac{1}{\Delta x_{++}^{2 \alpha }(x,x')} = \frac{1}{4(\alpha -1)(\alpha - \frac{d}{2})} \partial ^{2} \frac{1}{\Delta x_{++}^{2(\alpha -1)}(x,x')}. \end{aligned}$$
(35)

Furthermore, we can write

$$\begin{aligned} \partial ^{2} \frac{1}{\Delta x_{++}^{\scriptscriptstyle {d}-2}(x,x')} = \frac{4 \pi ^{\frac{d}{2}}}{\Gamma (\frac{d-2}{2})} \imath \delta ^{\scriptscriptstyle {d}} (x-x'). \end{aligned}$$
(36a)

For the other distance functions of Eq. (33), we have

$$\begin{aligned} \partial ^{2} \frac{1}{\Delta x_{--}^{\scriptscriptstyle {d}-2}(x,x')}= & {} - \frac{4 \pi ^{\frac{d}{2}}}{\Gamma (\frac{d-2}{2})} \imath \delta ^{\scriptscriptstyle {d}} (x-x') \end{aligned}$$
(36b)
$$\begin{aligned} \partial ^{2} \frac{1}{\Delta x_{+-}^{\scriptscriptstyle {d}-2}(x,x')}= & {} \,0=\, \partial ^{2} \frac{1}{\Delta x_{-+}^{\scriptscriptstyle {d}-2}(x,x')}. \end{aligned}$$
(36c)

We now rewrite Eq. (34) using Eqs. (35) and (36a) as

$$\begin{aligned}{} & {} \imath M_{\phi }^{++}(x,x')= - \frac{\imath g^{2} \Gamma ^{2}(\frac{d}{2}-1) }{16 \pi ^{\scriptscriptstyle {d}}} \frac{1}{(d-3)(d-4)} \nonumber \\{} & {} \qquad \times \left[ \partial ^{4}\left\{ \frac{1}{ \Delta x_{++}^{2\scriptscriptstyle {d}-6}(x,x')} - \frac{\mu ^{\scriptscriptstyle {d}-4}}{ \Delta x_{++}^{\scriptscriptstyle {d}-2}(x,x')} \right\} \right. \nonumber \\{} & {} \qquad \left. + \frac{ 4 \pi ^{\frac{d}{2}} \mu ^{\scriptscriptstyle {d}-4} }{\Gamma (\frac{d-2}{2})} \imath \delta ^{\scriptscriptstyle {d}} (x-x') \right] \end{aligned}$$
(37)

where \(\mu \) is an arbitrary mass scale. We now Taylor expand the terms inside the curly brackets around \(d=4\) to obtain,

$$\begin{aligned} \imath M_{\phi }^{++}(x,x')= & {} - \frac{\imath g^{2} \Gamma (\frac{d}{2}-1) \mu ^{d-4} }{4 \pi ^{\frac{d}{2}} (d-3)(d-4)}\partial ^2 \imath \delta ^{\scriptscriptstyle {d}} (x-x') \nonumber \\{} & {} + \frac{\imath g^{2}}{32 \pi ^{4}} \partial ^{4}\left[ \frac{\ln (\mu ^{2}\Delta x_{++}^{2}(x,x'))}{ \Delta x_{++}^{2}(x,x')}\right] \nonumber \\{} & {} + {\mathcal {O}}(d-4). \end{aligned}$$
(38)

The first term of the above expression contains an ultraviolet divergence around \(d=4\) which we have separated and the second term contains a non-local contribution to the self-energy. Since the divergence contains a \(\partial ^2\), we have to add a scalar field strength renormalisation counterterm \((\phi \rightarrow (1+\delta Z)^{1/2}\phi ).\) This yields in the action an additional kinetic term

$$\begin{aligned} \int d^d x\left[ \frac{1}{2} \delta Z \phi \, \partial ^2 \phi \right] \end{aligned}$$

where we have ignored a total divergence. The amputated version of the Feynman diagram corresponding to the above term involves two functional differentiations with respect to the two scalar field operators, yielding two \(\delta \)-functions. Integrating either of them, and choosing

$$\begin{aligned} \delta Z= \frac{ g^{2} \Gamma (\frac{d}{2}-1) \mu ^{d-4} }{4 \pi ^{\frac{d}{2}} (d-3)(d-4)}, \end{aligned}$$
(39)

we remove the divergence of Eq. (38). Note that such renormalisation could also be performed at the level of the Kadanoff–Baym equations, Eq. (26). In that case, the counterterm contribution is achieved by replacing the self energies \(\imath M_{\phi }^{++}(x,x')\) and \(\imath M_{\phi }^{--}(x,x')\), which contain divergent contributions, by the amputated counterterm contribution corresponding to \(\delta Z\) given above.

\(\imath M_{\phi }^{--}(x,x')\) is given by just the complex conjugation of Eq. (38)

$$\begin{aligned} \imath M_{\phi }^{--}(x,x')= & {} \frac{\imath g^{2} \Gamma (\frac{d}{2}-1) \mu ^{d-4}}{4 \pi ^{\frac{d}{2}} (d-3)(d-4)}\partial ^2\imath \delta ^{\scriptscriptstyle {d}} (x-x') \nonumber \\{} & {} - \frac{\imath g^{2}}{32 \pi ^{4}} \partial ^{4}\left[ \frac{\ln (\mu ^{2}\Delta x_{--}^{2}(x,x'))}{ \Delta x_{--}^{2}(x,x')}\right] \nonumber \\{} & {} + {\mathcal {O}}(d-4). \end{aligned}$$
(40)

The divergence appearing in the above expression can be tackled as above, with the counterterm Eq. (39). Thus the renormalised expressions for the above two self-energies are given by

$$\begin{aligned} \imath M_{\phi ,{\textrm{ren}}}^{++}(x,x')= & {} \frac{\imath g^{2}}{32 \pi ^{4}} \partial ^{4}\left[ \frac{\ln (\mu ^{2}\Delta x_{++}^{2}(x,x'))}{ \Delta x_{++}^{2}(x,x')}\right] \nonumber \\= & {} (\imath M_{\phi ,{\textrm{ren}}}^{--}(x,x'))^{\star }. \end{aligned}$$
(41)

Also, choosing the suitable pole prescription from Eq. (33), \(\imath M_{\phi }^{+-}(x,x')\) and \(\imath M_{\phi }^{-+}(x,x')\) are determined by

$$\begin{aligned} \imath M_{\phi }^{+-}(x,x')= & {} \frac{\imath g^{2}}{32 \pi ^{4}} \partial ^{4}\left[ \frac{\ln (\mu ^{2}\Delta x_{+-}^{2}(x,x'))}{ \Delta x_{+-}^{2}(x,x')}\right] \nonumber \\= & {} (\imath M_{\phi }^{-+}(x,x'))^{\star }. \end{aligned}$$
(42)

Note that \(\imath M_{\phi }^{+-}(x,x')\) and \(\imath M_{\phi }^{-+}(x,x')\) do not need any renormalisation as they do not contain any divergence around \(d = 4\), as can be readily verified from Eq. (36c). From Eqs. (41) and (42), we now have the renormalised retarded self-energy

$$\begin{aligned}{} & {} \imath M_{\phi ,{\textrm{ren}}}^{\textrm{r}}(x,x')= \imath M_{\phi ,{\textrm{ren}}}^{++}(x,x') - \imath M_{\phi }^{+-}(x,x') \nonumber \\{} & {} \quad = \frac{\imath g^{2}}{32 \pi ^{4}} \partial ^{4}\left[ \frac{\ln (\mu ^{2}\Delta x_{++}^{2}(x,x'))}{ \Delta x_{++}^{2}(x,x')} - \frac{\ln (\mu ^{2}\Delta x_{+-}^{2}(x,x'))}{ \Delta x_{+-}^{2}(x,x')}\right] .\nonumber \\ \end{aligned}$$
(43)

Using now

$$\begin{aligned} \frac{\ln \Delta x^2}{\Delta x^2}=\frac{1}{8} \partial ^2 (\ln ^2 \Delta x^2-2\ln \Delta x^2) \end{aligned}$$
(44)

we can write the nonlocal terms of Eq. (43) as,

$$\begin{aligned}{} & {} \frac{\ln \left( \mu ^{2} \Delta x_{++}^{2}\right) }{\Delta x_{++}^{2}}-\frac{\ln \left( \mu ^{2} \Delta x_{+-}^{2}\right) }{\Delta x_{+-}^{2}}=\frac{\partial ^{2}}{8}\left[ \ln ^{2}\left( \mu ^{2} \Delta x_{++}^{2}\right) \right. \nonumber \\{} & {} \quad \left. -2 \ln \left( \mu ^{2} \Delta x_{++}^{2}\right) -\ln ^{2}\left( \mu ^{2} \Delta x_{+-}^{2}\right) +2 \ln \left( \mu ^{2} \Delta x_{+-}^{2}\right) \right] .\nonumber \\ \end{aligned}$$
(45)

Breaking now the logarithms into real and complex parts, we have

$$\begin{aligned}{} & {} \ln ^{2}\left( \mu ^{2} \Delta x_{++}^{2}\right) -2 \ln \left( \mu ^{2} \Delta x_{++}^{2}\right) -\ln ^{2}\left( \mu ^{2} \Delta x_{+-}^{2}\right) \nonumber \\{} & {} \qquad +2 \ln \left( \mu ^{2} \Delta x_{+-}^{2}\right) =4 \pi i (\ln \mu ^2 (\Delta t^2 - \Delta x^2)-1)\nonumber \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times \theta (\Delta t^2-\Delta x^2). \end{aligned}$$
(46)

Putting these all in together the renormalised retarded self-energy, Eq. (43), takes the form

$$\begin{aligned} \imath M_{\phi ,{\textrm{ren}}}^{\textrm{r}}(x,x')= & {} \frac{g^{2}}{64 \pi ^{3}} \partial ^{6}\left[ \theta (\Delta t^2-\Delta x^2)\theta (\Delta t) \right. \nonumber \\{} & {} \left. \left\{ 1- \ln \left( \mu ^{2}(\Delta t^{2}-\Delta x^{2})\right) \right\} \right] . \end{aligned}$$
(47)

The step functions appearing above ensure that the retarded self-energy is non-vanishing only if \(\Delta t>0\) and \(\Delta t^2-\Delta x^2>0\). This ensures the expected causal characteristics of the retarded self-energy.

As we have stated earlier, we wish to make a momentum space computation of the entropy and hence the statistical propagator, Eq. (31). The relevant renormalised expressions, including that of various self energies are found in Appendices A and B. In particular, the Fourier transform of Eq. (47) is done in Appendix B. Using these ingredients, we wish to compute the von Neumann entropy in the following section.

4 Phase space area and entropy

Renormalised expression for the statistical propagator is given by the renormalised version of Eq. (31)

$$\begin{aligned} F_{\phi }(k)= & {} \frac{\imath (\imath M^{-+}_{\phi }(k)+\imath M^{+-}_{\phi }(k))}{2(\imath M^{\textrm{r}}_{\phi , \textrm{ren}}(k)-\imath M^{\textrm{a}}_{\phi , \textrm{ren}}(k))}\Bigg (\frac{1}{k^2+m^2+\imath M^{\textrm{a}}_{\phi , \textrm{ren}}(k)}\nonumber \\{} & {} -\frac{1}{k^2+m^2+\imath M^{\textrm{r}}_{\phi , \textrm{ren}}(k)}\Bigg ). \end{aligned}$$
(48)

The renormalisation of the various self-energies has been performed in the preceding section and Appendices A and B. Substituting now Eqs. (66), (69) and (71) into the above equation, we find after some algebra

$$\begin{aligned}{} & {} F_{\phi }(k) = - \frac{\imath }{2} {\textrm{sgn}}(k^{0}) \theta (k_{0}^{2}-|{\vec {k}}|^{2})\nonumber \\{} & {} \quad \times \left[ \frac{1}{k^2+m^{2}+\frac{g^{2}k^2}{8 \pi ^{2}}\ln \left( \frac{k^2}{4\mu ^{2}} \right) - \frac{\imath g^{2}k^2}{8\pi }{\textrm{sgn}}(k^{0})\theta ((k^{0})^{2}-|{\vec {k}}|^{2})}\right. \nonumber \\{} & {} \quad \left. - \frac{1}{k^2+m^{2}+\frac{g^{2}k^2}{8 \pi ^{2}}\ln \left( \frac{k^2}{4\mu ^{2}} \right) + \frac{\imath g^{2}k^2}{8\pi }{\textrm{sgn}}(k^{0})\theta ((k^{0})^{2}-|{\vec {k}}|^{2})} \right] . \nonumber \\ \end{aligned}$$
(49)
Fig. 4
figure 4

Variation of the statistical propagator, Eq. (49), with respect to the dimensionless variable \(k^0/\mu \), where we have taken \(|{\vec {k}}|/\mu =1\), \(m/\mu =1\) and the Yukawa coupling strengths \(g=0.5\) (black curve), \(g=1.3\) (red curve)

Full size image
Fig. 5
figure 5

Variation of the statistical propagator, Eq. (49), with respect to the dimensionless variable \(k^{0}/\mu \), where we have taken \(|{\vec {k}}|/\mu =1\), \(m/\mu =1.3\) and the Yukawa coupling strengths \(g=0.5\) (green curve), \(g=1.3\) (blue curve). Comparison with Fig. 4 shows lesser numerical value of the statistical propagator with increasing \(m/\mu \). See main text for discussion

Full size image

We have plotted the above statistical propagator with respect to the dimensionless variable \(k^0/\mu \) in Figs. 4 and 5. Note that as the Yukawa coupling g gets smaller, \(F_{\phi }(k)\) approaches a \(\delta \)-function dispersion, as expected from Eq. (49). However as g increases, the \(\delta \)-function peak becomes broadened to a quasi-particle peak like that of the Breit–Wigner kind. Further broadening of the peak with increasing g implies that the resonance becomes broadened and we can no longer sensibly talk about a quasi-particle. Also, these plots show that with the increase in \(m/\mu \), the peak gets shifted towards the higher values of \(k^0/\mu \) with a decrease in the value of the statistical propagator, which means that the corresponding state becomes less populated.

Now in order to compute the entropy, we would use the definition of the same in terms of the phase space area and the three momentum, Eqs. (5) and (8). We shall assume the mass of the scalar field to be time independent. However, one can also consider time-dependent mass as a signature of a non-equilibrium system, as has been considered in [44]. A time dependent mass function will break the time translation invariance, inducing an explicit proper time dependence on the statistical propagator. We also note that in standard quantum field theories, one generally talks about the early or late times when the system is in equilibrium and it is found in some eigenstates of the free Hamiltonian. For a system which is out-of-equilibrium however, an exact distinction between energy states is unclear. A standard approach in such scenario is the adiabatic approximation, in which one specifies a reference set of approximate states under the assumption of a slowly varying dynamical background. Using the projection of system’s evolution onto these approximate states, one may hope to study its dynamics at intermediate times. There are schemes to truncate the adiabatic expansion of the system to form the aforementioned approximate basis set at intermediate times. For example in [44, 45], the Bogoliubov transformations are used to achieve the same.

For turning on the perturbation non-adiabatically which we have not considered here, we consider replacing the coupling constant g with \(g\rightarrow g\,\theta (t-t_0)\). The step function changes the limit of integration Eq. (26) from \(-\infty \) to \(t_0\) and \(t_0\) to some final time. The self energies vanish in the absence of interaction and would only contribute for the second time interval. Thus it is clear that the Schwinger–Keldysh contours presented in Fig. 2 are not equivalent to this abrupt switching case. Note that turning on the interaction abruptly may certainly lead to particle creation, which may significantly modify the statistical propagator. Some relevant discussion on this can be seen in e.g. [44].

Using now the Fourier transforms, we have from Eq. (49)

$$\begin{aligned} F_{\phi }(|{\vec {k}}|,0)= & {} \int _{-\infty }^{\infty } \frac{{\textrm{d}}k^{0}}{2\pi } F_{\phi }(k) \end{aligned}$$
(50a)
$$\begin{aligned} \left. \partial _{t} F_{\phi }(|{\vec {k}}|, \Delta t) \right| _{\Delta t =0}= & {} - \imath \int _{-\infty }^{\infty } \frac{{\textrm{d}}k^{0}}{2\pi } k^{0} F_{\phi }(k) \end{aligned}$$
(50b)
$$\begin{aligned} \left. \partial _{t'}\partial _{t} F_{\phi }(|{\vec {k}}|, \Delta t) \right| _{\Delta t =0}= & {} \int _{-\infty }^{\infty } \frac{{\textrm{d}}k^{0}}{2\pi } (k^{0})^{2} F_{\phi }(k). \end{aligned}$$
(50c)

Substituting now Eq. (49) into the above integrals, we have evaluated them numerically. For example, for \(|{\vec {k}}|/\mu =1\), \(m/\mu =2\) and \(g=0.5\), we find the numerical value of the phase space area Eq. (5), to be

$$\begin{aligned} \Delta \approx 2.69, \end{aligned}$$
(51)

which is indeed greater than unity and hence indicating a non-vanishing von Neumann entropy, as dictated by Eq. (8). We have further analysed the variation of the phase space area with respect to the dimensionless system mass \(m/\mu \), by fixing all the other parameters in Fig. 6. Thus \(\Delta \) decreases monotonically with increasing \(m/\mu \) and asymptotically reaches unity, indicating very small or almost vanishing entropy. This corresponds to the fact that with the increasing mass, the system becomes more stable, i.e., it becomes difficult for the surrounding to disturb a heavier system.

Fig. 6
figure 6

Variation of the dimensionless phase space area \(\Delta \), with respect to the dimensionless mass parameter \(m/\mu \) of the system, where we have taken \(|{\vec {k}}|/\mu =1\) and, for \(g=0.5\) (blue curve), \(g=1\) (red curve) and \(g=1.5\) (green curve). See main text for discussion

Full size image

From Eq. (8), we obtain the non-vanishing von Neumann entropy corresponding to the phase space area of Eq. (51) (\(|{\vec {k}}|/\mu =1\), \(m/\mu =2\) and \(g=0.5\))

$$\begin{aligned} S \approx 1.27. \end{aligned}$$
(52)

We have also analysed the variation of the entropy with respect to the system mass by fixing all the other parameters in Fig. 7. Due to the aforementioned reason as that of the phase space area, the entropy is decreasing with the increasing \(m/\mu \).

Fig. 7
figure 7

Variation of the von Neumann entropy with respect to the dimensionless mass parameter \(m/\mu \) of the system. We have taken \(|{\vec {k}}|/\mu =1\) and, \(g=0.5\) (blue curve), \(g=1\) (red curve) and \(g=1.5\) (green curve). As of the phase space area, Fig. 6, the entropy also decreases monotonically with increasing \(m/\mu \). See main text for discussion

Full size image

As we have emphasised earlier, such non-vanishing entropy is due to the coupling between the system and the environment along with the ignorance of all kinds of correlations between them for an observer located in the practical world. The non-trivial statistical propagator gives up phase space for the system field that previously was inaccessible to it. Such increase in the accessible phase space for the system in turn, implies that less information about the system field is accessible to the observer, and hence we observe a non-vanishing von Neumann entropy. Due to this reason, as our results show, the increase in the coupling strength increases the von Neumann entropy.

5 Conclusion

This work studies the decoherence and subsequent entropy generation using the non-equilibrium effective field theory for the Yukawa interaction in the Minkowski spacetime, using the correlator approach of [43,44,45]. The scalar is treated as the system, whereas the fermions as the surrounding and it is assumed that the surrounding or the environment is in its vacuum state. We have assumed as the simplest realistic scenario that the observer measures only the leading and next to the leading order, two point correlators for the system. The ignorance about all the other correlators yields the generation of entropy.

We have constructed the Kadanoff–Baym equations from the 2-loop 2PI effective action, i.e. the quantum corrected equations satisfied by the two point correlators in the in–in formalism in Sect. 3. In Sect. 3.1, we renormalise our results and finally compute the phase space area, the statistical propagator and the entropy in Sect. 4. Note that all the results found in the preceding section are explicitly independent of time, owing to the fact that we have not taken any time dependent background field or time dependent mass. Discussion on the latter scenario can be seen in [44].

For a fixed value of all the relevant parameters such as mass, coupling, momentum and energy, we observe a higher numerical value of phase space area and entropy in (cf., Sect. 4), compared to the scenario when both the system and the surrounding are scalars [44]. This is due to the fact that the Yukawa coupling is dimensionless whereas the cubic coupling considered in [44] is dimensionfull, leading to different momentum dependence in the statistical propagator Eq. (49). Although we note that the qualitative aspects of the variation of the entropy (e.g. Fig. 7) for both the cases are similar.

Finally, we note that the entire above analysis might seem to rest upon the implicit assumption that the observer cannot measure the correlations corresponding to the fermions. For the case when the fermions represent a thermal bath and the scalar is initially at zero temperature, such distinction between the system and the environment seems obvious. For the zero temperature case we have considered presently, however, such distinction might seem albeit arbitrary. For example, we do not have any explicit hierarchy of scales of physical quantities here which decides such partitioning. Moreover, we could also have computed the correlators corresponding to the fermions instead. Thus for the zero temperature field theory, the above analysis is based upon the fact that the observer only measures the correlations for the scalar field, and the effect of fermions comes only as virtual particles inside a loop. Such implicit assumption is justified only when the system is much ‘small’ compared to the surrounding, i.e., when it can be considered as a ‘bath’ at zero temperature. This seems to have some qualitative similarity with the standard formalism of tracing out the fermionic degrees of freedom and look into the effective scalar field dynamics. Now, since we are ignoring a part of the theory, it would lead to an entropy, as we have obtained above. An obvious extension of this would be to go to the two loop self energies of Fig. 1, which contains some effect of system’s backreaction onto the surrounding. Perhaps more importantly, one should also consider the three-point scalar-fermion-anti-fermion correlators containing the effect of the decay of the scalar. This would involve constructing an effective action generating those correlators. We reserve these works as future tasks.

As we have emphasised earlier, understanding such decoherence mechanism can be very important in the early inflationary universe scenario, which is in fact our chief motivation. Even though this also must be a zero-temperature case, the short and the super-Hubble wavelength parts of the scalar field might give us some clue to naturally identify the system and the surrounding. Some related works, using formalism different from this paper can be seen in [65,66,67]. Most importantly, for a massless minimal scalar in an inflationary background, we may expect the appearance of late time, non-perturbative secular effects. Resumming them non-perturbatively using the Kadanoff–Baym equations could be a challenging task. We hope to return to these issues in our future publications.