Abstract
We analyze the properties of the black hole surface gravity by using an alternative approach based upon the use of light surfaces that are represented by certain characteristic frequencies. To this end, we rewrite the Kerr line element in terms of the characteristic frequencies, which allows us to obtain copies of the Kerr geometries (black hole–clusters) as the parameters vary. In particular, we replace the spin parameter \(a=J/M\) with the corresponding characteristic frequencies so that the line element describes only black holes. This new representation is particularly adapted to analyze how the surface gravity behaves as the black hole passes from one state to another. It turns out that the spins \(a={\sqrt{3}}/{2} M\) and \(a=1/\sqrt{2} M\) for black holes and \(a/M=\sqrt{9/8}\) for naked singularities are of particular relevance for the analysis of the surface gravity properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this work, we study the black hole (BH) surface gravity by using certain light surfaces of the corresponding geometry. We focus in particular on the axially symmetric, vacuum and asymptotically flat Kerr geometry. In general terms, given an object and its surface, we can define surface gravity as the (gravitational) acceleration a test particle in the proximity of the object is subject to. More precisely, a BH surface gravity is the acceleration, as exerted at infinity, of a test particle located in close proximity to the BH outer horizon, which is necessary to keep it at the horizon. For static BHs, it can be expressed as the force exerted at infinity to hold a test particle at close proximity of the horizon. Notice that the locally exerted force at the horizon is infinite. A similar definition holds for stationary BHs and, in general, for BHs with “well defined” Killing horizons.
Surface gravity is a classical geometrical concept playing a major role in BH thermodynamics – [1]. Bekenstein first suggested the analogy leading to the concepts of BH entropy and temperature and the formulation of classical BH thermodynamics – [2, 3]. However, the introduction of a temperature leads naturally to inquire about a possible BH radiation emission, regulated by the temperature defined by its surface gravity. An interpretation of this suggestion has been realized in the quantum (semi-classical) frame. BH thermal radiation has been shown to be the result of quantum mechanical effects governed by the BH temperature and, therefore, its surface gravity (Hawking semiclassical radiation). The surface gravity regulates also the probability of a negative energy particle tunneling through the horizon – [4]. Because it radiates, one can expect the BH mass to decrease and eventually disappear, but the actual fate of the BH and the informations carried in the BH during and before the evaporation process, the possible existence of remnant at the end of process and the entropy evolution are matters of an ongoing debate – see for example [5].
At the core of quantum physics and the quantization of gravity as a geometric theory, the information paradox and the actual fate of a BH, following the characteristic thermal emission, are examples of controversial aspects of the surface gravity physics. A further aspect still under examination concerns the (classical) geometrical nature of the singularity, the very definition of surface gravity, and the nature of singularity in interaction with the surrounding matter and fields. Note, in fact, that the surface gravity of a black hole is defined only when it is in equilibrium”, i.e., stationary. It should be noted that while surface gravity for stationary black holes is well defined (as there is a well defined Killing horizon where the Killing vector is normalized to unit at spatial infinity), this is not the case for dynamical black holes [6, 7]. The surface gravity for a Killing horizon is defined by the fact that the Killing vector is a non-affinely parametrized geodesic on the Killing horizon (based on the fact that a global Killing vector field \(\mathcal {L}^a\) becomes null on the event horizon). The Zeroth Law states that the surface gravity \(\ell \) of a stationary black hole is constant over the event horizon.
In this work, we will use the properties of the Killing vector \(\mathcal {L}^{a}\), which is defined as \(\mathcal {L}^{a}\partial _{a}=\partial _t+\omega \partial _\phi \) in terms of the Killing fields of “time translations” and axial symmetry of the Kerr geometry. \(\mathcal {L}^{a}\) is a null vector at the horizons, where \(\omega =\omega _H^\pm \) are known as the angular velocities or frequencies of the horizons.
The Kerr horizons are Killing horizons (a Killing horizon is a hypersurface where a Killing vector of the metric becomes null) with respect to the Killing vector \(\mathcal {L}^{a}\). Then, \(\nabla _b (\mathcal {L}_a\mathcal {L}^a)\) is normal to the Killing horizon. \(\mathcal {L}_\mathcal {N}\equiv (\mathcal {L}_b\mathcal {L}^b)\) is constant and zero on the Killing horizon by definition. The vector \(\mathcal {L}^a\) is also normal to the horizon, where it satisfies the condition \(\mathcal {L}^a\nabla _a\mathcal {L}^b=\ell \mathcal {L}^b\). The surface gravity can be defined, therefore, in terms of the null generators of the horizon. \(\ell \) is constant on each null generator of the horizon, but can be different on each generator.
We consider the null vector \(\mathcal {L}^{a}\) in all points of the Kerr geometries (including naked singularities), the horizons being particular cases. The set of geometries and null orbits a(r) with the same null frequency \(\omega \) (which is, therefore, also a horizon frequency) can be represented as a curve on a plane \(a-r\), extended plane, where the curves of all the BH horizons is the envelope surface of all the curves. In a fixed spacetime, the solutions of the condition \(\mathcal {L}_\mathcal {N}=0\) determine replicas of the horizon, which are special light surfaces – [8,9,10,11,12,13,14].
A BH transition from a state to another, which is accompanied by a change of the characteristic parameters, is regulated by the laws of BH thermodynamics. An analysis of the BHs transitions developed in the light surfaces frame is presented in [15]. Actually, we associate a transition to the values of the stationary BH state parameters mass, temperature and entropy before and after the transition, which become regulated by the quantities, horizon frequency and surface gravity, before the transition. It is therefore important to relate different states of BHs. Here, in particular, we rephrase alternatively the BH surface gravity concept in terms of the angular momentum of the horizon, defined as a function of light-surfaces characteristic frequency. In particular, in Sect. 3, we study accelerations and surface gravity in the extended plane, using light-surfaces and their characteristics, and consider replicas of the acceleration.
The plan of the article is detailed as follows. In Sect. 2, the Kerr geometry is introduced. The relation between Killing horizons and characteristic frequencies is discussed in Sect. 2.1. Frequencies and angular momentum of the horizons in the extended plane are discussed in Sect. 2.2. Section 3 deals with the concept of surface gravity in the extended plane, using light-surfaces. We introduce the accelerations \(\ell \) and \(\kappa \) in terms of the characteristic frequencies and evaluate them in the extended plane. Then, the acceleration \(\ell \) is studied in Sect. 3.1. The concepts of replicas and inner horizon confinement are considered in Sect. 3.2. The variation of the acceleration \(\kappa \) and its extreme points in the extended plane, are considered in Sect. 3.3. Then, in Sect. 3.4, the accelerations \(\ell \) and \(\kappa \) are studied on the horizon curve and on special points of the extended plane. The discussion and final remarks are included in Sect. 4. The additional vector \(\bar{\ell }\), which is related to the acceleration \(\ell \), is considered in Sect. A. In Sect. B, we detail the construction of the extended plane. In Sect. C, we summarize some results that are used in several parts of this work. In Sect. D, we consider more closely the metric tensor on the extended plane. This section provides alternative representations of the BH geometries, using the BHs–NSs correspondence through light-surfaces in the extended plane. We evaluate the metric line element in terms of the light-surface parameters such as the origin spin \(a_0\), the tangent radius \(r_g\), and tangent spin \(a_g\). Therefore, the metric tensors of the extended planes are the subject of study in Sect. D.1.
2 The Kerr geometry
The metric tensor of the Kerr geometry can be written in Boyer–Lindquist (BL) coordinates \( \{t,r,\theta ,\phi \}\) as follows
where
and \(r\in [0,+\infty )\), \(t\in [0,+\infty )\), \(\theta \in [0,\pi ]\) and \(\phi \in [0,2\pi ]\). Here M is the (ADM and Komar) mass parameter and the specific angular momentum is given as \(a=J/M\), where J is the total angular momentum of the gravitational source. For simplicity and when otherwise is not specified, here and in the following, we consider dimensionless parameters defined as \(r\rightarrow r/M\) and \(a\rightarrow a/M\). We also introduce the quantity \(\sigma \equiv \sin ^2\theta \).
The radii
are the outer and inner Killing horizons, respectively and \(r_{\epsilon }^+\) and \(r_\epsilon ^-\) represent the outer and inner ergosurfaces, respectively.Footnote 1 The case \(a=0\) corresponds to the static spherically symmetric Schwarzschild solution, where \(r_+=2M\) and there is no ergosurface. For an extreme BH, \(a=\pm M\), the horizons coincide \(r_\pm =M\).
Naked singularities (NSs) are defined for \(a^2>M^2\). The surfaces \(r_{\epsilon }^\pm \) in NS spacetimes are well defined, when \(\sqrt{1-\sigma }\in [-M/a, M/a] \). Since the metric is independent of \(\phi \) and t, the covariant components \(p_{\phi }\) and \(p_{t}\) of a particle four-momentum are conserved along its geodesics. Consequently, \( {E} \equiv -g_{ab}\xi _{t}^{a} p^{b}\) and \(L \equiv g_{ab}\xi _{\phi }^{a}p^{b}\ \) are constants of motion for test particle orbits, where \(\xi _{t}=\partial _{t} \) is the Killing field representing the stationarity of the Kerr geometry and \(\xi _{\phi }=\partial _{\phi } \) is the rotational Killing field (the vector \(\xi _{t}\) becomes spacelike in the ergoregion). The constant L may be interpreted as the axial component of the angular momentum of a test particle following timelike geodesics and E as representing the total energy of the test particle coming from radial infinity, as measured by a static observer at infinity. The motion on the fixed plane \(\sigma =1\) is restricted to that plane (\(u^\theta =0\)) because the Kerr metric is symmetric under reflections with respect to the equatorial hyperplane \(\theta =\pi /2\). Due to the symmetries of the metric tensor (1), the test particle dynamics is invariant under the mutual transformation of the parameters \((a,L)\rightarrow (-a,-L)\) so that the analysis of circular motion can be restricted to the case of positive values of a for corotating \((L>0)\) and counterrotating \((L<0)\) orbits [16,17,18,19,20].
2.1 Killing horizons and characteristic frequencies
The results we discuss in this work follow from the investigation of the properties of the Killing vector \(\mathcal {L}=\partial _t +\omega \partial _{\phi }\), where \(\omega \) is a constant. The quantity \({\mathcal {L}_\mathcal {N}}\equiv \mathcal {L}\cdot {\mathcal {L}}=g_{tt} + 2g_{t\phi }\omega + g_{\phi \phi }\omega ^2\) becomes null for photon-like particles with orbital frequencies \(\omega _{\pm }\).
Metric bundles (\(\mathcal{M}\mathcal{B}\)s) correspond to the solutions of the condition \({\mathcal {L}_\mathcal {N}}=0\), providing a relation among \((r, \theta , M, a, \omega )\), where \(\omega \) is called the characteristic \(\mathcal{M}\mathcal{B}\) frequency. More precisely, \(\mathcal{M}\mathcal{B}\)s are defined as the solutions of \( a_{\omega }\equiv a:\mathcal {L}_{\mathcal {N}}=0\), for a given frequency \(\omega =\) constant. The explicit solution \(a_\omega \) on the equatorial plane \((\sigma =1)\) was presented in [8], and for \(\sigma \ne 1\) in [10]. For concreteness, we present here the solution of \(\mathcal {L}_{\mathcal {N}}=0\) for the spin a on the equatorial plane,
which is a relation among the three dimensionless variables \((a/M, r/M, \omega M)\), where \(M>0\) can be eliminated by using dimensionless variables r, a and \(\omega \).
A particular null vector \(\mathcal {L}\) is defined by \(\omega =\omega (r_{\pm })\equiv \omega _H^\pm \), defining the Killing horizons of the metric. The corresponding Killing vectors \(\mathcal {L}_{\pm } \) are generators of Killing event horizons [8,9,10, 13, 14, 21]. In the case \(a = 0\) (where \(\omega =0\)), \(\xi _t\) (now generator of \(r_+\)) is hypersurface-orthogonal. The solutions \(r_s(\omega ,a,\theta )\equiv r:{\mathcal {L}_\mathcal {N}}=0\) define light surfacesFootnote 2 characterized by the null frequencyFootnote 3\(\omega \).
The characteristic bundle frequency \(\omega \) is, therefore, per definition the orbital frequency of a circularly orbiting photon and also the BH horizon frequency \(\omega _H^{\pm }\). Here, we simplify the analysis by considering mainly \(a\ge 0\), \(\sin \theta \ge 0\) and \(\omega \ge 0\). The last assumption restricts, in fact, the analysis to corotating photon orbits. The case of counter-rotating photons is detailedFootnote 4 in [10].
Extended plane
\(\mathcal{M}\mathcal{B}\)s can be represented as curves in the plane (a/M, r/M), or \((\mathcal {A}/M,r/M)\), “extended plane”, where \(\mathcal {A}\equiv a\sqrt{\sigma }\), therefore each point of the extended plane can be represented by the couple of values (a/M, r/M), or \((\mathcal {A}/M,r/M)\). The extended plane \(a/M-r/M\) for \(\sigma =1\) (equatorial planes) is illustrated in Fig. 1, where also the \(\mathcal{M}\mathcal{B}\)s defined in Eq. (4) are represented. \(\mathcal{M}\mathcal{B}\)s analysis can therefore be done in terms of the \(\mathcal{M}\mathcal{B}\)s curves and regions on the extended plane. The light-surfaces with fixed a are given by the crossing of all the \(\mathcal{M}\mathcal{B}\)s with the line \(a=\) constant in the extended plane.
The axis \(r=0\) (central singularity) is the bundle origin, which corresponds to the spin \(a_0\) or \(\mathcal {A}_0\), bundle origin spin, where the subindex 0 denotes the spin parameter and the quantity \(\mathcal {A}\) is the origin of the bundle (axis \(a(\mathcal {A}_0)=\) constant). For \(r=0\), there is \(a_0=1/(\omega \sqrt{\sigma })\) or \(\mathcal {A}_0=1/\omega \).
In the plane \(a/M-r/M\), the horizon curve is \(a_{\pm }=\sqrt{r(2M-r)}\in [0,M]\) (boundary of the black region in Fig. 1). Each line \(a_{\pm }=\) constant in this plane is a BH geometry, where the inner horizons are for \(r\in [0,M]\) on the line \(a_{\pm }\), while \(r\in [M,2M]\) contains the outer horizons – see Fig. 1. The maximum of the curve \(a_{\pm }\) is the point \(a=M\) and \(r=M\), which is the horizon in the extreme Kerr BH (Fig. 1). The Schwarzschild BH is for \(a=0\); therefore, it corresponds to the zeros of the metric bundles curves, where \(r=2M\) is its horizon, and in the extended plane it coincides also with the outer ergosurface on the equatorial plane of all the Kerr BHs and NSs – Fig. 1.
Each bundle curve in the extended plane is tangent to the horizon curve \(a_{\pm }(r)\) at a point r of the inner horizon or the outer horizon; therefore, the characteristic frequency of the bundle \(\omega \) is also the horizon frequency at the tangent point (r, a). Thus, the frequency of the (inner or outer) horizon r of the BH geometry with spin a is distinguished as the tangent point on \(a_{\omega }\). The horizon curve is the envelope surface of the metric bundles.
A lookup table with the main symbols and relevant \(\mathcal{M}\mathcal{B}\)s notations is in Table 1. The main properties are summarized in Table 2 and in Sect. (C).
From the \(\mathcal{M}\mathcal{B}\)s definition it follows that, for a fixed value of \(\omega \), in each geometry of the bundle \(a_{\omega }\) defined by the characteristic frequency \(\omega \), there is at least one point \(p=(r,\theta )\) defined by the bundle curve, where the photon circular orbit frequency is \({\omega }\). The bundle is tangent to the horizon curve at one point only; therefore, this defines uniquely the BH with the characteristic frequency \({\omega }\) and, consequently, bundles can contain either only BHs or BHs and NSs.
As the solutions \(\omega : \mathcal {L}_\mathcal {N}=0\), for each point \((a,r,\theta )\), are generally the two frequencies \(\omega _\pm \), this implies that there are two bundles crossing at any point of the extended plane. Bundles are not defined in the region \(]r_-,r_+[\) of BH spacetimes, but they are defined in the region \(r\in [0,2\,M]\) of NSs. The bundle on the equatorial plane \(\sigma =1\), tangent to the extreme Kerr BH, has characteristic frequency \(\omega =\omega _H^{\pm }=1/2\) and contains only NSs, the tangent point is at \(a=M\), and its origin is \(a_0=2M=1/\omega \).
The light surfaces defining \(\mathcal{M}\mathcal{B}\)s provide also a connection between BHs and NSs, a reinterpretation of NS solutions, and an alternative definition of BH horizons in the extended plane. They are also used to introduce the concept of horizon replicas, which, in principle, can be observed in regions close to the rotation axis of the Kerr BH. The properties of the spacetime in the bundle can be reconstructed from the properties of the BH horizon.
Extended plane \(a/M-r/M\) on the equatorial plane. Metric bundles (\(\mathcal{M}\mathcal{B}\)s) with angular momentum \((L_f)=1/\omega =constant\) are shown for different \((L_f)\), where \(\omega \) is the \(\mathcal{M}\mathcal{B}\)s characteristic frequency. Horizons angular momentum \((L_f)_H^{\pm }(r)\) and angular velocity (frequency) \(\omega _H^{\pm }(r)\) are defined in Eq. (8) as functions of \(r\in [0,2M]\). The bundles at \((L_f)=\) constant are denoted at the curves on the equatorial plane. There is \((L_f)_H^{\pm }(r)=\mathcal {A}_0\equiv a \sqrt{\sigma }=1/\omega _{H}^{\pm }(r)\), where \(\mathcal {A}_0\) is the bundle origin spin and \(\sigma \equiv \sin ^2\theta \). On the equatorial plane (\(\sigma =1\)), there is \(\mathcal {A}=a\). Black region is the BHs region with the outer and inner horizons \(a_\pm \), respectively, as functions of r/M. A horizontal line on the extended plane at \(\sigma =1\) is a fixed spacetime \(a/M=\) constant. In particular, \(a=0\) corresponds to the Schwarzschild BH spacetime and \(a=M\) to the extreme Kerr BH. The frequencies of the inner and outer horizons curve are clearly distinguished. Note that \(\omega _H^-=(L_f)_H^+\) for \(a=4/5\). The frequency \(\omega ^{\pm }_H=1/2\) and angular momentum \((L_f)_H^\pm =2=\mathcal {A}_0\), correspond to the extreme Kerr BH. On the equatorial plane, the point \(r=2M\) is the outer ergosurface (the Schwarzschild BH horizon for \(a=0\))
Replicas
Within the metric bundles formalism, certain orbits are identified as replicas – Fig. 1. These are light-like (circular) orbits having the same frequency as the black hole \(\omega _H^+\), which is also the bundle characteristic frequency. In general, we say that a property \(\mathcal {Q}(\omega (r))\), which is a function of the frequency \(\omega \) and is defined on an orbit with radius r, is “replicated” on an orbit \(r_1\ne r\) if \(\omega (r)=\omega (r_1)\). Eventually, this relation can include a polar angle dependence with \(\omega (r, \sigma )=\omega (r_1,\sigma _1)\), where \(\sigma \equiv \sin ^2\theta \). Moreover, it can be demonstrated that the number of orbits satisfying this condition is two.
Clearly, the curve defined by the classes of points \((r,r_1)\) define the bundles, which can include eventually the dependence from \(\sigma \) such that \(\mathcal {Q}(\omega (r,\sigma ))= \mathcal {Q}(\omega (r_1,\sigma _1))\) and \(\omega (r,\sigma )=\omega (r_1,\sigma _1)\) (in units of the BH mass). In this sense, the regions \((r,\sigma )\) and \((r_1,\sigma _1)\) can be interpreted as presenting replicas of the proprieties \(\mathcal {Q}\).
In general, if r is a circle very close to the central singularity, then the second point \(r_1\) is located far from the central singularity. Therefore, we can extend the definition by saying that replicas in the extended plane \(a/M-r/M\), are special set of points \(\{p_i\}_{i=1}^\kappa \) corresponding to equal (positive) limiting frequency \(\omega >0\) [8, 10, 45, 46]. It has been proved that there is a maximum of \(\kappa =2\) on the section of the extended plane \(a>0\), for a fixed plane \(\sigma \).
We can generalize the definition of bundle to group geometries on the basis of an equal value of a property \(\mathcal {Q}\), but the convenience of the choice of orbital limiting frequencies for photon is manifold, since this definition is naturally related to the geometry symmetries and it has numerous relevant astrophysical applications.
Horizon confinement
In the context of replicas, we also introduce the concept of horizon confinement. Indeed, we say that there is a replica when in the spacetime it is possible to find at least a couple of points having the same value for the property \(\mathcal {Q}\). Then, we say that there is a confinement, when that value is not replicated. In the Kerr spacetime, part of the inner horizon frequencies are “confined”.
The confinement analysis, which is the study of the topology of the curves \({\omega }=\) constant in the extended plane, provides information about the local properties of the spacetime replicated in regions more accessible to observes; for example, in the case of properties defined in the proximity of the BH poles or of the inner horizons. Replicas also connect measurements in different spacetimes characterized by the same value of the property \(\mathcal {Q}\). Particularly, from their definition it follows that replicas connect two null vectors, \( \mathcal {L}(r_+,a,\sigma )\) and \( \mathcal {L}(r_p,a,\sigma _p)\), where \(r_+\) is the outer Killing horizon (we also consider the special case \(\sigma =\sigma _p\)).
An observer can register the presence of a replica at the point p of the BH spacetime with spin \(a_p\), belonging to a Killing bundle. The observer will find the replica of the BH horizon frequency \(\omega _H^+(a_p)\) at the point p; therefore, her/his orbital stationary frequency is \(\omega _p\in ]\omega _{\bullet },\omega _{\star }[\) for two frequencies (\(\omega _{\bullet },\omega _{\star }\)), where one of the frequencies is the outer horizon’s frequency \(\omega _H^{+}\), replicated on a pair of orbits \((r_+,r_p)\). The second light-like frequency is the frequency of a horizon in a BH spacetime. The relation between the two frequencies \((\omega _{\star },\omega _{\bullet })\) is determined by a characteristic ratio, which we also study (when a transition occurs from a BH state to a new state, one of the two characteristic frequencies \(\omega _\pm \) also changes).
The explicit \(\mathcal{M}\mathcal{B}\)s definition is based upon the use of stationary null orbits frequencies, constraining matter circular orbits. The \(\mathcal{M}\mathcal{B}\)s definition is tightly connected in the Kerr geometry to the (light-like and time-like) stationary observers, i. e., observers with a tangent vector which is a Killing vector, that is, whose four-velocity \(u^\alpha \) is a linear combination of the two Killing vectors \(\xi _{\phi }\) and \(\xi _{t}\); therefore, \( u^\alpha =\gamma \mathcal {L}^{\alpha }= \gamma (\xi _t^\alpha +\omega \xi _\phi ^\alpha \)), where \(\gamma \) is a normalization factor and \(d\phi /{dt}={u^{\phi }}/{u^t}\equiv \omega \). The dimensionless quantity \(\omega \) is the orbital frequency of the stationary observer. Because of the spacetime symmetries, the coordinates r and \(\theta \) of a stationary observer are constants along its worldline, i. e., a stationary observer does not see the spacetime changing along its trajectory. Specifically, the causal structure defined by timelike stationary observers is characterized by a frequency bounded in the range \(\omega \in ]\omega _-,\omega _+[\). Static observers are defined by the limiting condition \(\omega =0\) and cannot exist in the ergoregion. Therefore, the limiting frequencies \(\omega _{\pm }\), which are photon orbital frequencies, solutions of the condition \(\mathcal {L_{N}}=0\), determine the frequencies \(\omega _H^{\pm }\) of the Killing horizons, as well as the bundles characteristic frequencies.
In the next section, we shall relate the energy and angular momentum functions of circularly orbiting photons to the bundle characteristic frequency, and we use the extended plane representation to identify and discuss different features of the Kerr solutions as replicas, proposed to study BHs transitions, and confinements, which are considered in the study of NSs and some properties of the inner horizons. One main motivation for this alternative representation of the whole family of Kerr solutions is to illuminate the BH transitions implied by BH thermodynamics, focusing on the surface gravity and its variations in the extended plane, which we will introduce in Sect. 2.3 and discuss in details in Sect. 3.
2.2 Frequencies and angular momentum
It is convenient to write explicitly the angular velocity (frequency) \(\omega \) and the specific angular momentum \((L_f)\):
The case of an orbiting circular particle is defined by the constraint \(u^r=0\). Explicitly, for stationary observers (timelike particles) the frequencies have to be in the range bounded by the light-like orbital frequencies
which are also the bundle characteristic frequencies. The horizons angular velocities \(\omega _H^{\pm }\) are the frequencies \(\omega _{\pm }\) evaluated on the outer and inner horizons, respectively, with the “horizons angular momentum” \((L_f)_H^{\pm }\).
In the following, when not otherwise specified, we denote by \((L_f)\) the light-like-orbital momentum given in Eq. (6), which is also the BH horizon angular momentum. Curves with constant \(\omega \) and constant \((L_f)\) satisfy \(g_{\phi \phi }/g_{tt}=(L_f)/\omega =\) constant. The saddle point of the curve \((L_f)(\omega ^{\pm })\) as a function of r is \(r_-/M=1/2\), which is the inner horizon of the BH spacetime, where \((L_f)(\omega ^{\pm })={2}/{\sqrt{3}}=1/\omega \). Note that in this case \(a=\omega _-\). The saddle point of the function \(\omega (r)\) is located on the outer horizon \(r_+/M={3}/{2}\), where \(L=2 \sqrt{3}=1/\omega \). Evaluating these quantities on the extended plane, where the horizons are \(a_{\pm }=\sqrt{r(2-r)}\), we get
where \(r=r_g\) is a point of the horizon curve. Moreover, \(\omega ^{\pm }_H=(L_f)_H^\pm =1\) for \(r=2/5 M\). The inner horizon for a spacetime with \(a/M=4/5\) is related to the inner horizon confinement (and, therefore, to the NS bottleneck region discussed in [13, 14]). Note that in terms of Eq. (7) this implies \((L_f)_H^-=\omega _H^-\) – see Fig. 2.
Left panel: horizons angular velocity (frequency) \(\omega _H^{\pm }(r)\) and horizons angular momentum \((L_f)_H^{\pm }(r)\) defined in Eq. (8) as functions of \(r\in [0,2M]\). The horizon curve radius (tangent radius of the metric bundle with the horizon curve) is plotted in the extended plane. There, \((L_f)_H^{\pm }(r)=\mathcal {A}_0=1/\omega _{H}^{\pm }(r)\), where \(\mathcal {A}_0\) is the bundle origin spin. The point \(r/M=2/5\) corresponds to the inner horizon point of a BH geometry with \(a/M=4/5\), where \((L_f)_H^{\pm }(r))=\omega _H^{\pm }(r)=1\), is explicitly plotted. Center panel: horizons angular velocity (frequency) \(\omega _H^{\pm }(r)\) and horizons angular momentum \((L_f)_H^{\pm }(r)\), as defined in Eq. (7) for the outer and inner horizon \(r_{\pm }(a)\), respectively, as functions of the spin \(a\in [0,M]\). In this case, the frequencies of the inner and horizons curve are clearly distinguished. Note that \(\omega _H^-=(L_f)_H^+\) for \(a=4/5\). The frequency \(\omega ^{\pm }_H=1/2\) and angular momentum \((L_f)_H^\pm =2=\mathcal {A}_0\), corresponding to the extreme Kerr BH, are plotted. Right panel: equatorial plane, light surfaces condition \((L_f)=constant\) for different spins. The extreme Kerr spacetime corresponds to the green curve. Right panel: the bundles at \((L_f)=\) constant are denoted at the curves on the equatorial plane. Note the coincidence with the bundles at \(\omega =1/(L_f)=\) constant. The dashed and dotted lines also show the saddle points of the angular velocity and angular momentum
The spin \(a/M=4/5\), corresponding to \(r_-/M=2/5\) and \(r_+/M=8/5\), determines the boundary spin for the inner horizon confinement – see Eq. (C5). In this context, we show that an analogue definition of the metric Killing bundle can be provided in terms of the angular momentum \((L_f)\) defining the bundles \({(L_f)}=\) constant. We discuss the main characteristics in Fig. 2 and the relation with the bundles \({\omega }=\) constant, considering Eq. (8).
The relevant aspect at the angular momentum of the horizon for fixed frequency is the bundle origin \(\mathcal {A}_0\) and, therefore, we can express the horizon confinement in terms of the horizon angular momentum. Explicitly, on the equatorial plane,
The two bundles transform with \(\omega =1/(L_f)\), which means substitution of the characteristic frequency of the bundle with its origin. Note also the limit \(\lim \limits _{r\rightarrow 0}(L_f)=a\). It is also clear that the replicas at equal \(\omega \) and \((L_f)\) are those at equal \(g_{\phi \phi }/g_{tt}\).
Left: the acceleration \(\ell \) evaluated on the spin \(a_g(\omega )\) tangent to the BH horizons for different photon frequencies \(\omega \) and on the horizon curve \(a_{\pm }\) in extended plane. \(\omega =0.5\) corresponds to the frequency of the extreme BH. The maximum is for \(\omega =r/\sqrt{3}\) (minimum curve of the right panel in dimensionless units). Center: \(\ell \) as function of the tangent radius \(r_g(\omega )\). The gray curve is \(\ell \) on the horizons \(r_{\pm }\) as function of the spin a/M. Note the limiting value \(a=M\). Right panel: \(a_{\pm }\) is the horizon curve in the extended plane. The radius \(r_{\clubsuit }^{\pm }\), spin \( a_{\clubsuit }\), and spin \( a_{\square }\) are defined in Eqs. (36), (35), and (31)
2.3 Surface gravity and BH thermodynamics
In [15], BH thermodynamics has been explored in the extended plane in terms of the metric bundles, considering the bundle frequency \(\omega \) and the acceleration \(\ell \). For completeness, we review here the main results. Here, we use the notation \((\pm )\) to indicate quantities evaluated on the horizons \(r_{\pm }\). We can rephrase BH transitions as the problem of finding replicas in the extended plane relating the parameters \(\mathcal {P}_{\pm }=(\ell ^{\pm }, \omega ^{\pm }_H)\), evaluated on the points r and \(r_p\) along the horizon curve. Consequently, there exists a quantity \(\kappa \) such that \(\mathcal {P}_{\pm }(r)=\kappa \mathcal {P}^*_{\pm }(r_p)\). The notation \((*)\) represents a change in sign in one or more components. While the frequency \(\omega \) is always positive (according to the sign of J), the surface gravity \(\ell \) can be negative, when evaluated on a point of the inner horizon; therefore, it can be \(\ell _H^{\pm }(r_p)=\ell _H^-<0\). For the surface gravity there can be replicas on the curve of the horizons, which depend on a and r and connect inner and outer horizons; this is clearly illustrated in Fig. 3. We introduce the quantities \(\ell ^-_+(r)\equiv \ell _H^-(r)/\ell _H^+(r)\) and \(\omega ^-_+(r)\equiv \omega _H^-(r)/\omega _H^+(r)\) and define \(\ell _-^+(a)\equiv \ell _H^+(a)/\ell _H^-(a)\) and \( \omega _-^+(a)\equiv \omega _H^+(a)/\omega _H^-(a)\) so that \( \omega _-^+(a)=- \ell _-^+(a)\). Furthermore, using the relation \(\ell _+^-(r)=-\omega _+^-(r)\), we obtain
where all quantities are functions of the tangent radius \(r\in [0,2M]\) and
are functions of the tangent spin \(a\in [0,M]\), see also Eq. (10). These relations distinguish the case \(\ell _{H}^\pm =\pm \omega _H^\pm \) occurring for \(a=a_{\gamma }\equiv 1/\sqrt{2}\), where \(\omega _H^{\pm }(r)=\ell _H^{\pm }(r)=\mathcal {Q}_{\ell \omega }^{+}\equiv {1}/{\sqrt{2}}-{1}/{2}\) for \(r=r_+= \left( \sqrt{2}+2\right) /2\). Therefore, for this spacetime the variation has a special form when written in the extended plane \(\delta M^\pm =\mathcal {Q}_{\ell \omega }^{\pm }\delta \tilde{M}^{\pm }\) (where \(\delta \tilde{M}^{\pm }\equiv \pm \delta A^\pm _{area}+\delta J^\pm )\), where \(\mathcal {Q}_{\ell \omega }^{-}=\omega _H^-={1}/{2}+{1}/{\sqrt{2}}=-\ell _H^-\). A further notable case is the spin \(a/M=\sqrt{{8}/{9}}\) where \((\ell _H^-,\omega _H^-)-=2(-\ell _H^+,\omega _H^+)\).
Now we extend the problem of finding replicas by searching the solutions of the following problem that relates the outer horizon \(r_+\) to an inner horizon \(r_-=r\)
i.e. \(\left( \omega (r_p),\ell (r_p)\right) =s\left( \omega (r),-\ell (r)\right) \), without loss of generality we fix \(s\ge 0\). It can be proved that \(r/r_p=s\) with \( r_p\equiv {2}/({s+1})\). Within this solution, \((r,r_p)\) represent a horizon parametrization, radii r and \( r_p\) correspond to the horizons of the BH spacetime with \(a(r)=a(r_p)\) i.e.
For \(s<1\), we have that \(r=r_-\) and \(r_p=r_+\), while for \(s>1\), we obtain \(r=r_+\) and \(r_p=r_-\). The limiting case \(s=1\) corresponds to the extreme Kerr BH, while \(a(r_p)\) can be seen as analogue to the tangent curve \(a_g(\omega )\) of the horizon. Note that the factor s depends on the spin, i.e., \(s\equiv [({2-a^2})\mp 2 \sqrt{({1-a^2})}]/{a^2}\).
The acceleration \(\ell \) and BH surface gravity \(\ell _H^+=\ell (r_+)\) (\(r_+\) is the outer horizon) as functions of the tangent point \(r_g\) (left-upper panel), the bundle frequency \(\omega \) (central upper panel), the origin spin \(a_0\) (right upper panel), and the radius \(r\in [M,2M]\) (outer horizon range) evaluated at the horizon curve \(a_+\) (bottom left panel) and for different spins \(a/M\in [0,1]\) (inside panel) for different values of \(\sigma =\sin ^2\theta \). Bottom right panel: Horizons frequencies \(\omega _H^{\pm }\) and surface gravities \((\ell (a_{\pm })\), as functions of the radius r/M
3 Black holes surface gravity in the extended plane
In this section, we use metric bundles to study the properties of the BH surface gravity in the extended plane. We investigate the accelerations \(\ell \) and \(\kappa \) as functions of the bundles characteristics. These accelerations are affine coefficients (or accelerations of pre-geodesics) of the principal null geodesics, where \( \kappa =- \ell \) on \(\theta =0\). The quantities we use in this work are evaluated in the entire extended plane, i.e., we consider also the region \(r\in [0,r_-]\) for \(a\in [0,M]\), including the inner horizons. In this way, we will also be able to evaluate particular transitions and relate the acceleration in the \(\mathcal{M}\mathcal{B}\)s with the surface gravity.
We start considering the acceleration \(\ell \)
which has been introduced in Sect. 1 by using the Killing tensor \(\mathcal {L}\). In Sect. A, we introduce \(\ell \) as the acceleration of a null vector \(\bar{\ell }\): \(\nabla _{\bar{\ell }} \bar{\ell }^b=\ell \bar{\ell }^b\), with \(\bar{\ell }^a\bar{\ell }_a=0\). This vector is well defined for NS and BH geometries.
On the horizon curve, \(a_{\pm }\), in the extended plane, we have that
On the radii \(r_{\pm }\), we find the surface gravity \(\ell (r_+)\) and the quantities
Note that on the extended plane, at \(a=a_g=M\), which is the maximum of the horizon curve as an envelope surface, the surface gravity is null. The point \((r_g=M, a_g=M)\) represents in the extended plane the extreme Kerr BH geometry, while \(a_g=0\) and \(r_g=2M\) correspond to the limiting static case of the Schwarzschild geometry. We also note the asymptotic condition \(r\rightarrow +\infty \) on the function \(\ell (a_{\pm })\) in the extended plane; this is a function of r extended beyond the definition range of \(a_{\pm }\), where \(r\in [0,2\,M]\). We analyze the acceleration on the horizon curves \(a=a_g(\omega )\in [0,M]\), and \(r=r_g(\omega )\in [0,2M]\) as functions of the bundle characteristic frequencies \(\omega \in [0,+\infty ]\) and as functions of \((a_0\ge 0,\sigma \in [0,1])\), the origin spin of the bundle and \(\sigma =\sin ^2\theta \). Consequently, we obtain the acceleration on the horizons in the extended plane as a function of these quantities, identifying the metric bundles and constructing the horizons as envelope surface of tangent metric bundles curves.
We introduce also the null vectors \(\kappa ^{\star }\equiv \frac{(r^2+a^2)}{(2\rho ^2)}\partial _t- \frac{\Delta }{2\rho ^2}\partial _r+ \frac{a}{2\rho ^2}\partial _\phi \) and \(\ell ^{\star }\equiv \frac{(r^2+a^2)}{\Delta }\partial _t+ \partial _r+\frac{a}{\Delta }\partial _{\phi }\), with \(\textbf{g}(\kappa ^{\star },\ell ^{\star })=-1\). The vector \(\kappa ^{\star }\) has an “acceleration” term (pre-geodesic) \(\nabla _{\kappa ^{\star } }\kappa ^{\star } = \kappa \kappa ^{\star }\). It is simple to see that the acceleration of \(\ell ^{\star }\) is null or, in other words, \(\ell ^{\star }\) is geodesic.Footnote 5
Furthermore, the acceleration \(\kappa \) is defined as
On the horizons curves \(a_{\pm }\) and on the radii \(r_{\pm }\), we obtain, respectively,
In Sect. 3.1, we focus on the properties of the acceleration \(\ell \), exploring the inner horizon confinement and replicas in Sect. 3.2 and the variation of the acceleration \(\kappa \) in Sect. 3.3. Moreover, the accelerations \(\ell \) and \(\kappa \) on the horizon are studied in Sect. 3.4.
The accelerations \(\ell \) and \(\kappa \) in the extended plane, as functions of different bundle quantities for different values of \(\sigma =\sin ^2\theta \), including the Schwarzschild and extreme BH limiting cases. Bottom left and right panels: analysis of the constant accelerations, \(\kappa =\) constant and \(\ell =\) constant, in terms of the bundle origin \(\mathcal {A}_0\) and tangent spin \(a_g\). Center line right panel: The accelerations \(\ell _H^{\pm }\) on the horizons are shown as functions of \(r^{\mp }\). For the extreme Kerr BH, there is \(\ell _H^{\pm }=0\). The inner panel illustrates the acceleration \(\ell \) on the horizons as function of the tangent spin \(a_g\). The limiting Schwarzschild case is also shown, where \(\ell =1/4\). Center line left, central panels and upper line panels: the accelerations \((\ell ,\kappa )\) as functions of the tangent radius \(r_g\), the bundle origin \(\mathcal {A}_0\), the bundle frequency \(\omega \) for different planes \(\sigma \)
Upper left panel: the acceleration \(\ell (r;a,\sigma )\) as function of a/M and \(r/\sqrt{3}\) on the equatorial plane \(\sigma =1\). \(a_{\pm }\) are the horizons in the extended plane. Two notable curves are \(r=\sqrt{3} a\) and \(r=a/\sqrt{3}\), expressing the acceleration equivalently as a function of a and r, respectively – see Eq. (46). Gray region corresponds to BH region in the extended plane. \(\ell =0\) is the surface gravity of the extreme Kerr BH. The asymptotic value \(\ell =1/4\) is the surface gravity of the Schwarzschild BH. Upper center panel: \(\ell (r;a,\sigma )\) as functions of r/M. Here \(\ell _{\pm }=\ell (a_{\pm })\) are accelerations on the horizons curves in the extended plane (surface gravity). Upper right panel: curves \(\ell (a,r)=\) constant in the extended plane; the BH region and extreme BH cases are highlighted. Bottom left panel: Curves \(a_{\spadesuit }^{\pm }(r,\ell )=\) constant, according to Eq. (20), in the \(r-\ell \) plane, \(r_{\ell }\) is defined in Eq. (23). Bottom center panel: the acceleration \(\ell _{\odot }\) and origin spin \(a_0^{\odot }\) as functions of the characteristic bundle frequency \(\omega \) – see Eq. (57),(23). Inside panel: spin bundle tangent spin \(a_g^{\odot }\). Bottom right panel: the accelerations \(\ell _u^{\pm }\) and \(\ell _{J}^{\pm }\) of Eq. (24) as function of the origin spin \(\mathcal {A}_0=a_0\sqrt{\sigma }\), where \(\sigma =\sin ^2\theta \)
3.1 The acceleration \(\ell \)
In this section, we focus on the acceleration \(\ell \) in the extended plane, its behavior on the horizons \(\ell _{H}^{\pm }\), and the particular curves of constant \(\ell \). Moreover, we investigate the behavior of the surface gravity on the extended plane. We also discuss the extreme points of the acceleration, which highlights the particular BH geometry with \(a/M=\sqrt{3}/2\). Then, we introduce the concept of bottleneck and proceed to investigate the connection between the BH bottleneck region and some properties of the acceleration \(\ell \) in the extended plane. Finally, we investigate the scalar \(\ell \) evaluated on the light surfaces and metric bundles (Fig. 4).
The acceleration \(\ell \) and the linearized horizons
In the extended plane, we also consider the inner BHs horizons. We can express the acceleration \(\ell \) on the inner horizon in terms of the acceleration on the outer horizon (the surface gravity) and viceversa, considering the functions \(\ell _H^-(\ell _H^+)\) and \(\ell _H^+(\ell _H^-)\), respectively,
which are shown in Fig. 5. As noted in Eq. (12), the accelerations \(\ell _H^+\) and \(\ell _H^-\) can be related by the proportional factor s.
Constant acceleration \(\ell \)
The metric bundles are collections of Kerr geometries characterized by the same limiting photon frequency \(\omega \) at a point r (depending on the plane \(\sigma \)). We can explore the acceleration \(\ell \) on the points of a metric bundle and the curves of \(\ell =\) constant in the extended plane. The study of geometries and orbits with equal acceleration \(\ell \) is, in fact, the analysis of the replicas with respect to \(\ell \). Particularly, we investigate the zero acceleration \(\ell =0\) (the value for the extreme Kerr BH) and distinguish affine parameterized null geodesics, focusing on the horizons curves. Moreover, we look for a point (a, r) in the extended plane, with acceleration \(\ell _H^+\) (surface gravity) of a BH geometry for a fixed spin \(a\in [0,M]\) – Sect. 3.2. Firstly, we consider a fixed geometry with spin a. We obtain the following classes of geometries having equal acceleration, \(\ell (r,a)=\ell \)=constant, on a point r.
Considering \( \ell (r,a)=\ell >0\) (related to the outer horizons points), we obtain
Note that \(a_{\spadesuit }^{\pm }\) is defined also for \(\ell <0\). Importantly, the region of the extended plane where \(\ell =0\) is discriminated from the curve \(a=\pm r\), related to the extreme Kerr BH, where \(r=M\) with horizon frequency \(\omega _H^{\pm }=1/2\) – Fig. 6.
Considering also negative values, \(\ell (r,a)=\ell <0\) (inner horizons values), we obtain
In the BH case, \(\ell <0\) only for \(r\in [0,M]\) and \(a\in ]r,M]\) – Fig. 6. On the other hand, in the NS case, \(\ell >0\) only for \(r>M\) and \(a\in ]M,r[\), distinguishing, therefore, the BHs and NSs through the accelerations. Note that \(\kappa =-\ell \) for \(\sigma =0\), i.e., on the rotation axis. We now consider the acceleration \(\ell \) on the notable curves in the extended plane.
The acceleration \(\ell \) on the horizon curves in the extended plane: BH surface gravity
Here we reconsider the function \(\ell (a_{\pm })\), the BH surface gravity on the extended plane of Eq. (15), on the horizons \(a_{\pm }\). We also consider the function \(r_{\ell }:\ell (r)=\ell (a_{\pm }(r))=\ell =\) constant and obtain the orbits
– Fig. 6.
We can express the acceleration \(\ell (r,a)\) considering the origin \(a_0=\mathcal {A}_0\) of the bundle on the horizons curves \(r_{\pm }(\mathcal {A}_0)\), where \(a_0\in [0,M]\), as
Assuming the spin \(a=a_g(\mathcal {A}_0)\) on the horizons curve and evaluating on the horizon \(r=r_{\pm }\), we obtain
where \(r_+ (a_g (\mathcal {A}_ 0)) \ge r_ + (\mathcal {A}_0)\). These relations highlight the values \(\mathcal {A}_0=\pm 1\) and \(\mathcal {A}_0=\pm 2\) related to the tangency of the bundles to the extreme Kerr BH in the extended plane – Fig. 6.
Extremes of the accelerations and the spin \(a/M=\sqrt{3}/2\)
Notably, the acceleration \(\ell \) has extreme points as a function of r and a, implying that the surface gravity has some extremes for BH spacetimes, as evaluated in the extended plane. Here, we first consider the curves \(r=r_g\) and \(a=a_g\), representing the horizons curves as envelope surface of the metric bundles. The extreme points of \(\ell \), as function of r and a, are \(r=\sqrt{3}a\) and \(a=\sqrt{3}r\), respectively, where \(\ell =-{1}/{8 r^2},\ell ={1}/{8 a^2})\) (or equivalently \(\ell =-{3}/{8 a^2}, \ell =-{3}/{8 r^2})\).
We now consider the function \( \ell (r, a)\). There is an extreme as function of r (\(\partial _r\ell (r, a) = 0 \)) on the orbit \(r_o = \sqrt{3} a\), where the acceleration is \(\ell (r_o, a) = {1}/({8 a^2})\). For a BH, where \(a\in [0,M] \), there is \(r_o\in [0, \sqrt{3}M]\). The radius \(r_o\) on the horizon curve in the extended plane, where \(r_o = 3/2M \), is a point of the outer horizon for the spacetime with spin \(a/M = {\sqrt{3}}/{2}\). Assuming \(r_o = a_ 0 \sqrt{3}\), where \(a = a_ 0\), and setting \(r_o = r_g\), we obtain \(a_0=a_0^{\odot }\equiv {2}/{\sqrt{3}\left( 4\omega ^2 + 1 \right) }\) – see Fig. 6.
We consider now the acceleration as function of the spin a. Then, \(\partial _a\ell (r, a) = 0 \) for \( a_o = \sqrt{3} r \), where the acceleration is \(\ell (a_o, r) = - {1}/{8 r^2} \); therefore, it is related to an inner horizon in the extended plane. We look particularly for the solutions in the BH region of the extended plane, for \(a\in [0, M] \), which is for \(r\in [0,{M}/{\sqrt{3}}]\), a region of the inner horizons. Restricting to the horizon curve, remarkably, we find the solution for \(r_o= M/2 \), which is the inner horizon of the BH spacetime with \(a/M = \sqrt{3}/2\). Therefore, the extremes of the acceleration \(\ell \) for a and r constitute, respectively, the inner and outer horizon for the BH with spin \(a/M = \sqrt{3}/2\). (Note that the curve \(\ell (r) = \ell (a_ {\pm }, r)\) has no extremes as a function of r; similarly for \(\ell (\mathcal {A}_0) = \ell (a_g(\mathcal {A}_ 0), r_\pm (\mathcal {A}_ 0))\), a part of the case \(\mathcal {A}_0=0\).)
Acceleration and bottleneck
Here, we interpret the bottleneck in the extended plane, introduced and discussed in [13, 14]. The bottleneck is a restriction in the structure of the light surfaces of some naked singularities, which is defined by the null condition \(\mathcal {L}\cdot \mathcal {L}=0\). The solutions of this condition, written in the form \(r_s^{\pm }(\omega ;a)\), determine the bundles in terms of the photon orbital angular velocity \(\omega \) and the dimensionless spin a/M – Fig. 7. Analogously, the bottleneck region appears on the plane \(r/M-L_H^{\pm }\) as illustrated in Fig. 2. Here, we present some basic concepts of the definition of bottlenecks and their relation to bundles and repulsive gravity effects. From Fig. 7, it follows that the bottleneck is a region around the point \(r=M\) and \(\omega =1/2\), that is, the extreme Kerr BH in the region \(a\in [M,2M]\) or, equivalently, a region around the point \(r=M\) and \( \hat{L}=2\) characterized by repulsive gravity effects. This regions contains circular geodesics with \(L=0\) (ZAMOs) and \(E=0\) [8, 9, 16,17,18,19,20,21, 45, 46]. To analyze the bottleneck region, we can consider the distance \(\Delta \omega _{\pm }=\textbf{c}\) where \(\Delta \omega _{\pm }\equiv \left. (\omega _+-\omega _-)\right| _{\pi /2}\) with \(\textbf{c}=0\) on the horizon curves \(a_{\pm }\). We evaluate the minimum values of \(\textbf{c}\) for NSs, obtaining for \(\partial _r \Delta \omega _{\pm }=0\) the solutions
and for \(\partial _a \Delta \omega _{\pm }=0\)Footnote 6
It is clear from Fig. 8 that the bottleneck region can be defined in terms of functions \(a_{\delta }^a\).
Bottleneck in the extended plane (equatorial plane \(\sigma =1\), where \(\sigma \equiv \sin ^2\theta \)). Light surfaces \(r_s^{\pm }(\omega ;a)\), solutions of equation from the null condition \(\mathcal {L}\cdot \mathcal {L}=0\), as functions of the frequency \(\omega \) (quantity \((L_f)\equiv 1/M\) is the angular momentum), for different spacetimes, where at \(r=0\) there is \(\omega =M/a\). The extreme BH spacetime and the bottleneck region are pointed out
Analysis of the difference \(\Delta \omega _{\pm }=\textbf{c}\) for \(\textbf{c}=\) constant (left upper panel) and for selected values of \(\textbf{c}=\) constant (right upper panel). The black region represent black holes in the extended plane. Curves with \(\textbf{c}=\) constant are represented as functions \(a=a_z^{\pm }\) (right upper panel). The bottleneck region is highlighted. Black, black dashed, and black dotted-dashed curves are the extremes of \(a_\delta ^{\pm }\) of Eq. (26) as functions of a: \(\partial _a \Delta =0\) for \(a_{\delta }^a\), or as functions of r for \(a_{\delta }^\pm \). Right bottom panel: the function \(\textbf{c}_0\) for the Schwarzschild spacetime, where \(a_z^{\pm }=0\). Bottom left panel: the frequencies difference \(\Delta \omega _{\pm }\) on its extreme curves \(a_{\delta }^a\) and \(a_{\delta }^\pm \)
Upper line panels and bottom left panel: solutions of \(\Delta \omega _{\pm }=\) constant for a fixed spacetime, where \(\Delta \omega _{\pm }\equiv \omega _+-\omega _-\) and \(\omega _{\pm }\), in terms of two points \((r,r_p)\) on the equatorial plane for different spacetime spins with the limiting cases of Schwarzschild (\(a=0\)), extreme BH (\(a=M\)), and NSs. The event horizons for BH geometries and the bottleneck regions for NSs are shown. The difference \(\Delta \omega _{\pm }\) is null on the horizons and reaches an inferior limit in the bottleneck. Bottom center panel: solutions of \(\partial _{r_p}\Delta \omega _{\pm }=0\) for different spins. Bottom Right panel: solutions of \(\partial _a\Delta \omega _{\pm }=0\) for different spins (according to the right panel color-notation)
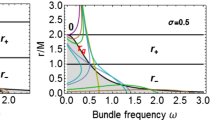
The acceleration \(\ell \) on the light surfaces \(r_{s}^{\pm }\), Eq. (28). It is also shown in Fig. 17 as function of the spin a/M in the extended plane for selected values of the bundle characteristic frequencies \(\omega \) and different values of the planes \({\sigma }\equiv \sin ^2\theta \) (denote on each curves). EBH denotes the extreme Kerr BH, where the tangent spin is \(a_g=M\) and the origin spin is \(\mathcal {A}_0=a_0\sqrt{\sigma }=2M\). The gray curve represents the equatorial plane \(\sigma =1\). The curves for the tangent spin \(a_g(\omega )\), tangent to the curve \(\ell (r_+)\), and \(a_0\) are also identified. The second line-left panel shows explicitly the origin spin \(a_0\) as crossing with the lines at \(\sigma =1\) (gray curve), the tangent spin \(a_g\) and the surface gravity \(\ell (r_\pm )\). A difference appears for the case \(\omega <1\) and \(\omega >1 \) and \(\omega =2\) related to the appearance of the bottleneck. See also Figs. 12 and Figs 13. Figure 11 represent \(\ell \) on the metric bundles \(a_{\omega }\)
We note the limiting spin \(a=1.16M\). Analogously, we consider the minimization of the frequencies differences for a couple of points \((r,r_p)\). This problem is addressed in Fig. 9, which illustrate the role of horizons, photon orbits, and bottlenecks. See also Fig. 9.
Acceleration \(\ell \) on the light surfaces \(r_s^\pm \)
We start considering the following solutions of the condition \(\mathcal {L}\cdot \mathcal {L}=0\) on the equatorial plane (\(\sigma =1\))
which define the equatorial light surfaces – see Fig. 10. Then, we consider \(\ell (r_s^\pm )\) (acceleration on the light surfaces) on the equatorial plane. The characteristic bundle frequency tangent to the horizon curve in \(a_g=M\), corresponding to the extreme BH, is \(\omega =1/2\) with origin \(a_0=2M\in {NS}\). In any plane \(\sigma \), there is \(a_0=2M/\sqrt{\sigma }\ge 2M\). From Figs. 10 and 11, it follows that the case \(\sigma =1\) contains an extreme case for the surfaces of gravity that collect the bundles \(\omega =\) constant, characterized by a tangent spin \(a_g(\omega )\) with origin \(a_0=1/\sqrt{\sigma }\omega >a_g(\omega )\).
The bundle origin \(a_0\) can be obtained from the curves of Fig. 10, as the folding of the curve \(\ell (r_s)\), evaluated on the light surfaces at \(\sigma =1\) (this occurs only for \(\sigma =1\)). The tangent spin \(a_g\) corresponds to the crossing with the surface gravity curves, i.e., the curves \(\ell =\ell (r_{\pm })\). The bundle origins \(a_0\), for bundles with equal frequencies, arise from the crossing of the curves with the reference curve at \(\sigma =1\) – see Fig. 10. Note that \(a_0(\sigma =1)\le a_0(\sigma <1)\). More precisely, the tangent spin \(a_g\) can be found from the crossing with the curve \(\ell _H^+\equiv \ell (r_+)>0\), the BH surface gravity, if \(\omega <1/2\), while the crossing is at \(a_g=M\) for \(\ell =0\), which is the extreme BH surface gravity with horizon frequency \(\omega =1/2\). Finally, \(\ell _H^-\equiv \ell (r_-)<0\) for \(\omega >1/2\), corresponding to the inner horizon tangency with origin partially in the NS bottleneck region.
The acceleration \(\ell \) (surface gravity, \(\ell ({a_{\pm }})\)) on the metric bundles \(a_{\omega }\) of Eq. (29) for different bundle frequencies \(\omega \) and on the equatorial plane. \(\ell (a_{\pm })\) is the horizon curve shown on the plane \(\ell -r\). The extreme BH case corresponds to \((a=M, \ell (a_{\pm })=0)\) and the Schwarzschild case to \((a=0, \ell (a_{\pm })=1/4)\). The upper-left panel is a zoom of the region of negative acceleration of the inside panel. Curves for some \(\omega \) are tangent and confined by \(\ell (a_{\pm })\), constraining BHs and NSs transitions and representing the acceleration variation on the metric bundles. The functions \(\ell ({a_{\pm }})\) for the surface gravity are shown for a fixed bundle frequency in NS \(\omega =\{1/7,0.5, 0.3,1\}\) on different planes \(\sigma \). See also Figs. 10 and 12
In Fig. 10, we consider the acceleration \(\ell \) on the light surface \(r_s^{\pm }\) and on the horizons \(\ell (r_{\pm })\), with characteristic frequencies of the bundles fixed for different planes. We note that the function \(\ell (r_-)\) represents a limiting case of the selected curves. At fixed frequency, the acceleration is evaluated on all the points r in different spacetimes a of the bundle curves. It is clear that the equatorial plane, \(\sigma =1\) (gray curve), is a limiting case, where the curves crossing represents the bundles origins \(a_0=1/(\omega \sqrt{\sigma })\). The tangent spin of the bundle is provided by the bending of the curves. We note the different behaviors for \(\omega <1/2\) (extreme Kerr BH) and for \(\omega >1/2\). It is clear that \(\ell _H^+=\omega _H^+\) for the spin \(a=1/\sqrt{2}\) (and \(\ell _H^-=-\omega _H^-\)), where \(r_{\gamma }^-=r_{\epsilon }^+\), that is, the outer ergosurface on the equatorial plane of the BH, which is a geodesic orbit of the (corotating) photon.
On the equatorial plane, \(\ell (r_s^\pm )=-\omega ^2\), for \(a=a_0={1}/{\omega }\), and \(\ell (r_s^\pm )=-1/a_0^{2}\) for \(\omega ={1}/{a_0}\).
On the metric bundles
On the bundles, \(a_{\omega }(r,\omega ,\sigma )\), on the equatorial plane, we obtainFootnote 7
Analysis of the tangency conditions of the metric bundles and the confinement of the horizon in the extended plane, on the equatorial plane \(\sigma =1\), in terms of the surface gravity and accelerations. Upper line – left panel: the BH region is in gray. \(r_g\) (red curve) is the radius of the metric bundles tangent to the horizons; therefore, \(r_g\) correspond to the the BHs horizons in the extended plane. Here it is shown as function of the frequency, see Eq. (29). The extreme case of the Kerr spacetime, \(\ell =0\), is shown (black thick curve). The acceleration \( \ell (a)\) as function of r/M for different values of the bundle frequency \(\omega \) are shown. The curves \(\ell \)=constant can be tangent and confined by \(\ell (a_{\pm })\). \(a_\omega \) is the metric bundle with frequency \(\omega \) and origin \(a_0\). The frequencies \(\omega \in \{0,1/2\}\) are the limiting values for the Schwarzschild and extreme Kerr BH, respectively. In the NS case, curves are not confined and cross the case \(\omega =1\). Bottom right panel: the curves \(\ell (a_{\omega _3})\)=constant – see also Figs. 11, 10 – on the plane r-\(\omega \), for \(\sigma =1\). The extreme BH case is \(\ell =0\). The BH region is in gray
which are represented in Fig. 11, where the acceleration \(\ell \) as function of r/M is shown on the equatorial plane and on different planes for different characteristic frequencies \(\omega \) of the bundle. For a fixed frequency, the curves are tangent to the curves of acceleration evaluated on the horizons. In this respect, we consider bundles with equal tangent spins \(a_g\), where \(r_g^p/r_g=\mathcal {A}_0^p/\mathcal {A}_0=\omega /\omega ^p\), with \(\mathcal {A}_0^p/(\mathcal {A}_0^p+4)=\mathcal {A}_0/(\mathcal {A}_0+4)\), and quantities \(\mathcal {Q}\) and \(\mathcal {Q}^p\) refer to two different bundles with equal tangent spin \(a_g\), relating therefore inner and outer horizons – see Sect. C.
3.2 On the inner horizon confinement and replicas
In this section, we consider again the replicas and confinement problem. We consider again the acceleration \(\ell _H^{\pm }=\ell (r_{\pm })\) on the horizons \(r_{\pm }(a)\), and the accelerations \(\ell (a_{\pm })\) on the curves \(a_{\pm }\).
- The curves \(r_{\pm }\)::
-
We consider the couple (a, r) for
$$\begin{aligned}{} & {} \ell _H^-=\ell (r,a) \quad \text{ on }\quad r=r_-,\\\nonumber{} & {} \ell _H^+=\ell (r,a) \quad \text{ on }\quad r=r_+\ . \end{aligned}$$(30)
We obtain the following solutions \(r=r_{\clubsuit }^{\pm }\) for the replicas of the horizons \( r_{\pm }\)
where \(x\equiv \sqrt{1-a^2}\) – Fig. 3. Notice the values \(r/M=3/2\) and the spin \(a/M=\sqrt{3}/2\). Alternatively,
Equivalently, we obtain the solution for the geometry \(a=a_{\clubsuit }(r)\):
See Fig. 3 for the outer horizon replicas. Notice that \(a_{\clubsuit }\rightarrow M\) for \(r\rightarrow +\infty \).
- The curves \(a_{\pm }\)::
-
For this case
$$\begin{aligned}{} & {} \ell (a_{\pm })=\ell , \quad \text{ on }\quad a_{\pm } \quad \text{ and }\quad a_{\square }\equiv \frac{\sqrt{r^2 (r+1)}}{\sqrt{1-r}}<1.\nonumber \\ \end{aligned}$$(36)
There are no radii r in the extended plane for the surface gravity \(\ell _H^-\) – Fig. 11 – in the same space-time (confinement of the inner horizon considered in [8, 10, 45, 46]). Note that the function \(a_{\square }\) is well defined only for \(r<M\) which includes the case of the inner horizons in the extended plane.
Upper Left-panel: \(\ell (r_s^-)=\) constant in the plane \(\omega -a\). The horizon frequencies \(\omega _{H}^{\pm }\) and the limiting the acceleration \(\ell \) are shown. \(r_s^-\) is a light surface on the equatorial plane. Upper Right panel: \(\ell (r_s^{\pm })\) as function of a/M for different values of \(\omega \) on the equatorial plane \(\sigma =1\). The frequency \(\omega \) denotes the bundle characteristic frequency, the horizon frequency and the photon circular orbital frequency. \(\omega =1/2\) is the horizon frequency of the extreme Kerr BH. The spin \(a_0\) is the bundle spin origin on the equatorial plane. \(a_g\) is the spin of the bundle tangent to the horizon curve in the extended plane. Bottom left-panel: \(\ell \) as function of \(\omega \) and a/M (inside panel) and \(\ell \) on the functions signed on the curves. \(\omega _H^{\pm }(a)\) are the horizon frequencies as functions of the BH spins. Bottom right panel: the accelerations on the horizons \(\ell _H^{\pm }\). The quantity \(\ell _H^+\) is the surface gravity evaluated on the light surfaces and the horizon frequencies. The horizon frequencies \(\omega _H^\pm \) are shown as functions of the BH spin a/M. The special spin \(a/M=1/\sqrt{2}\) is shown. See Figs. 10 and 11
Analysis of \(a_p^{\Bbbk }\) and \(r_p^{\Bbbk }\), of Eq. (37), relating two different geometries with equal accelerations \(\ell \). Bottom panels: (\(a_p^{\Bbbk }\), \(r_p^{\Bbbk }\)) as functions of the spin in the extended plane for different radii r. The origin line \(r=0\) is denoted by a black thick curve. The extreme Kerr spacetime is for \(r=M\) and \(r=2\,M\) is for the Schwarzschild geometry. Upper central and right panels: \(a_p^{\Bbbk }\) and \(r_p^{\Bbbk }\) are represented as functions of r for different spins (denoted on each curve). Left upper panel: the quantity \(a_p^{\Bbbk }=\) constant and \(r_p^{\Bbbk }=\) constant in the plane \(a-r\). The black region is the horizon in the extended plane; the black lines represent the extreme BH with \(r=M\) and \(a=M\)
The second problem we consider here is \(\ell (a_{\pm }(r_p),r_p)=\ell (a,r)\), that is, we look for the pairs of points (a, r) and \((a_p,r_p)\) in the extended plane, relating two different geometries \((a,a_p)\) with equal accelerations. We analyze the situation for two general points \((r,r_p)\) while the case of the points on the horizons curve constitute a special case. There are the following two solutions:
- (A):
-
For the horizon \(a_{\pm }\)
$$\begin{aligned}{} & {} \ell (a_{\pm }(r_p),r_p)=\ell (a,r)\quad \text{ where }\nonumber \\{} & {} r_p=r_p^{\Bbbk }=\frac{\left( a^2+r^2\right) ^2}{\chi _{\circledcirc }}, \end{aligned}$$(37)with \(\chi _{\circledcirc }\equiv a^4+2 a^2 \left( r^2+1\right) +r^2(r^2-2)\), where the maximum of the replica \(r_p^{\Bbbk }\) is \( r_p=1 + {3}/{(4 r^2-3)}\), for couples (a, r) satisfying the relation \( a={r}/{\sqrt{3}}\).
- (B):
-
We consider the replicas according to the geometry spin \(a_p\) defined as
$$\begin{aligned}{} & {} \ell (r_{\pm }(a_p))=\ell (a,r)\quad \text{ for }\nonumber \\{} & {} a_p=a_p^{\Bbbk }\equiv \frac{\left( a^2+r^2\right) \sqrt{\chi _\circledcirc +2(a^2-r^2)}}{\sqrt{\chi _\circledcirc ^2}}, \end{aligned}$$(38)– Fig. 14. The spin \(a_p^{\Bbbk }\) has a maximum \(a_p^{\Bbbk }=r\), for \(a=r\), and a minimum \(a_p^{\Bbbk }={2 r \sqrt{2(2 r^2-3 )}}/{\sqrt{ \left( 3-4 r^2\right) ^2}}\), for \(a={r}/{\sqrt{3}}\), which confirms \(a=r\) and \(a={r}/{\sqrt{3}}\) as special functions in this analysis.
3.3 Variation of the acceleration \(\kappa \)
The condition \(\kappa =-\ell \) (equal point and geometry) is valid only on the limiting point \(\sigma =0\), which corresponds to the BH axis. The analysis of this case allows us to study \(\mathcal{M}\mathcal{B}\)s close to the rotation axis. It is, therefore, important to consider the dependence of \(\kappa \) from the plane \(\sigma \). Therefore, we explore the acceleration \(\kappa \) in different bundles with equal \(\sigma \) – see also Appendix (C)). Below, we analyze the variation of the acceleration \(\kappa \) on special portions of the extended plane.
- The zeros of the:
-
accelerations \(\kappa \) (the geodesics curves).
We analyze the zeros of the acceleration \(\kappa \) of Eq. (17), i.e.,
$$\begin{aligned}{} & {} \kappa =0\quad \text{ for }\quad r_{\Theta }^{\pm }\equiv \frac{1}{2} a \left[ a \sigma \pm \sqrt{\sigma \left( a^2 \sigma -4\right) +4}\right] ,\nonumber \\{} & {} \quad (a\ne 0),\quad \text{ or } \text{ alternatively } \text{ for } \quad \nonumber \\{} & {} \quad a=a_{\Theta }\equiv \pm \frac{r}{\sqrt{(r-1) \sigma +1}} \end{aligned}$$(39)The points \(r=M\) and \(a=M\) or \(\mathcal {A}_0=a_0\sqrt{\sigma }=2M\) are special cases – Fig. 15. Importantly, on the horizons \(k(a_{\pm })=0\) for \(r=M\) and any \(\sigma \). Moreover, the solution of \(k(r_{\pm })=0\) is at \(a=M\) (the extreme Kerr spacetime) for any plane. Therefore the analysis show the geometries related by the acceleration \(\kappa \). More generally, in the extended plane, the condition \(\kappa =\) constant has solutions \(a_{\kappa }^1=a_{\complement }^-\) and \(a_{\kappa }^2=a_{\complement }^+\) where
$$\begin{aligned}{} & {} a_{\complement }^\mp \equiv \flat \frac{\sqrt{\frac{r [2 \kappa r (\sigma -1)+\sigma ]-\sigma +1\mp \sqrt{r^2 \left[ \sigma ^2-8 \kappa (\sigma -1)^2\right] +4 \kappa r^3 (\sigma -1) \sigma -2 r (\sigma -1) \sigma +(\sigma -1)^2}}{\kappa (\sigma -1)^2}}}{\sqrt{2}} \end{aligned}$$(40)(with \(\flat \equiv \pm \)). On the equatorial plane, \(\sigma =1\), there is an extremum for r at \(r={3 a^2}/{2}\) (where \(\kappa =-{4}/({27 a^4})\)).
- Dependence of:
-
\(\kappa \) from \(\sigma \). The variation of \(\kappa \) in terms of the plane \(\sigma \) leads to the extreme points
$$\begin{aligned}{} & {} \partial _\sigma \kappa =0\quad \text{ for }\quad \sigma =\sigma _{\sim } \end{aligned}$$(41)$$\begin{aligned}{} & {} \sigma _{\sim }\equiv \frac{a^2 (r+1)+(r-3) r^2}{a^2 (1-r)} \nonumber \\{} & {} \quad \text{ where }\quad \kappa _{\sim }=\frac{(r-1)^2}{4 r\Delta }. \end{aligned}$$(42)In particular, on the equatorial plane, we find
$$\begin{aligned}{} & {} r_{I}^{\mp }\equiv \frac{1}{2}\left( 3\mp \sqrt{9-8 a^2}\right) , \quad \text{ or }\nonumber \\{} & {} a_{r_I}^{\pm }\equiv \pm \frac{\sqrt{(3-r) r}}{\sqrt{2}}. \end{aligned}$$(43)There is the special value \(a/M= \sqrt{{9}/{8}}\) for NSs in the bottleneck region. The spin range is constrained to \(a/M\in ]0,\sqrt{9/8}]\), where, for \(a/M=\sqrt{9/8}\), there is \(r_{I}^{\mp }/M=3/2\) – Fig. 16 – and \(r=3M\) (and \(r=0\)) corresponds to the static limit of Schwarzschild where \(a_{r_I}=0\) as represented in Fig. 16.
- Dependence of:
-
\(\kappa \) on the horizons from \(\sigma \). The dependence on \(\sigma \) is intrinsic in the definition of \(\kappa \) and, on the horizons, if parameterized in terms of the bundle origin \(\mathcal {A}_0\) – see Appendix (C). (This clearly does not contradict the rigidity theorem, the dependence on the \(\theta \) angle comes from the particular parameterization adopted for the \(\mathcal{M}\mathcal{B}\)s) On the horizon \(a_{\pm }\), the acceleration \(\kappa \) has the extreme points, as function of the plane \(\sigma \) in the extended plane, or
$$\begin{aligned}{} & {} \partial _\sigma \kappa (a_{\pm })=0 \quad \text{ for }\quad r=M, \quad \text{ and }\quad r=2M, \end{aligned}$$(44)that is, for the Kerr spacetime and the Schwarzschild spacetime. More precisely, by considering the accelerations on the horizons \(r_{\pm }(a)\), we find that
$$\begin{aligned}{} & {} \partial _{\sigma }\kappa (r_+)=0,\quad \text{ for }\quad \left( a=\pm M,\quad a=0\right) ,\nonumber \\{} & {} \partial _{\sigma }\kappa (r_-)=0,\quad \text{ for }\quad a=\pm M, \end{aligned}$$(45)– Fig. 15.
- Dependence of:
-
\(\kappa \) from the spin a: The following extreme points exist:
$$\begin{aligned}{} & {} \partial _a\kappa =0 \quad \text{ for }\quad a=0,\quad \text{ and }\nonumber \\{} & {} a_{\ominus }^{\pm }\equiv \pm \sqrt{r^2 \left[ \frac{2}{(r-1) \sigma +1}+\frac{1}{1-\sigma }\right] }, \end{aligned}$$(46)$$\begin{aligned}{} & {} \text{ where }\quad \kappa _{\ominus }^{\pm }\equiv \kappa (a_{\ominus }^{\pm }) =-\frac{[(r-1) \sigma +1]^2}{4 r^2 (\sigma -1) [(r-2) \sigma +2]}. \nonumber \\ \end{aligned}$$(47)In particular, for NS and extremeFootnote 8 BH, we find the extremes
$$\begin{aligned}{} & {} a\ge M: \quad \sigma =0,\quad r = a/\sqrt{3}; \\{} & {} \nonumber \text{ and } \text{ on } \quad \sigma \in ] 0,1[ \quad \text{ there } \text{ is }\quad r = r_{\ominus } \quad \text{ where } \\{} & {} \nonumber r_{\ominus }\equiv \frac{2 \tilde{g} \cos \left[ \frac{1}{3} \arccos \left( \frac{3 \sqrt{3} (\sigma -1)^3}{\sigma ^3 \tilde{g}^{3}}\right) \right] }{\sqrt{3}}-\frac{1}{\sigma }+1,\\{} & {} \nonumber \tilde{g}\equiv \sqrt{\frac{(1-\sigma ) \left[ \sigma \left( a^2 \sigma -3\right) +3\right] }{\sigma ^2}}. \end{aligned}$$(48)In the case of BHs, where \(a/M\in [-1,1]\), we find
$$\begin{aligned}{} & {} \text{ for }\quad r\ge r_+\quad \text{ in }\quad \sigma \in [0,1] \nonumber \\{} & {} \text{ for }\quad r\ge 2 \quad \text{ at } \quad a=0 \end{aligned}$$(49)$$\begin{aligned}{} & {} \text{ for }\quad r\in [0,r_-]:\quad \text{-- } \text{ at }\quad a\in \Bigg ]\frac{\sqrt{3}}{2},1\Bigg ]:\nonumber \\{} & {} \quad \left( \sigma =0, \quad r=\sqrt{\frac{a^2}{3}}\right) ;\quad \left( \sigma \in ]0,1[,\quad r=r_{\ominus }\right) \end{aligned}$$(50)$$\begin{aligned}{} & {} \text{--at }\quad a\in \Bigg ]0,\frac{\sqrt{3}}{2}\Bigg ],\quad \left( \sigma =2-\sqrt{\frac{1}{1-a^2}},\quad r=r_-\right) ;\nonumber \\{} & {} \quad \left( \sigma \in \Bigg ]2-\sqrt{\frac{1}{1-a^2}},1\Bigg [,\quad r=r_{\ominus }\right) \end{aligned}$$(51)where we highlight the region outside the outer horizon and inside the inner horizon; moreover, the limiting spin \(a={\sqrt{3}}/{2}\) and the curves \( r=\sqrt{{a^2}/{3}}\) for the poles are evidenced – see Fig. 6.
- Dependence of:
-
\(\kappa \) from r: We focus on a fixed orbit r in a spacetime with a fixed spin a and we analyze the dependence of the acceleration \(\kappa \) from r. On the horizontal lines of the extended plane, where \(a=\) constant, the acceleration \(\kappa \) is not constant with respect to r and there are extremes at \( r=r_{\triangleleft \triangleright }^{\pm }\), that is,
$$\begin{aligned}{} & {} \partial _r\kappa =0,\quad \text{ for } \nonumber \\{} & {} \sigma \in [0,1[,\quad r=r_{\triangleleft \triangleright }^{\pm }\equiv \left\{ \frac{a^2 \sigma }{2}+\tilde{b}\cos \left[ \frac{1}{3} \arccos \left( \frac{a^2 \sigma }{\tilde{b}}\right) \right] ,\right. \nonumber \\{} & {} \left. \frac{a^2 \sigma }{2}-\tilde{b}\cos \left[ \frac{1}{3} \left( \arccos \left[ \frac{a^2 \sigma }{\tilde{b}}\right] +\pi \right) \right] \right\} \end{aligned}$$(52)respectively, with \(\tilde{b}\equiv \sqrt{a^2 [\sigma (a^2 \sigma -4)+4]}\), while on the equatorial plane (\(\sigma =1\)), we obtain \( r= {3 a^2}/{2} \) – see Fig. 16. Or alternatively in terms of spin, for \(a= a_{\triangleleft \triangleright }^{\pm }\) where
$$\begin{aligned}{} & {} a_{\triangleleft \triangleright }^{\pm }\equiv \flat \frac{\sqrt{\frac{r \left[ -3 (r-2) \sigma \pm \sqrt{r \sigma [(9 r-28) \sigma +28]+36 (\sigma -2) \sigma +36}-6\right] }{(\sigma -1) \sigma }}}{\sqrt{2}},\nonumber \\{} & {} \quad \text{ with }\quad \flat =\pm . \end{aligned}$$(53)
Upper line. Left panel: \(a_{\Theta }=\) constant in the \(r-\sigma \) plane with \(\sigma \equiv \sin ^{2}\theta \) – see Eq. (39). The Schwarzschild case corresponds to \(r=2M\), the extreme BH Kerr to \(r=M\). Bottom panels: the accelerations \(\kappa \) and \(\ell \) on the horizons \(r_{+}\) and \(a_{\pm }\) (in the extended plane). The curves correspond to different values of \(\sigma \). We plot the curves \(\kappa =\) constant at different planes \(\sigma \) in the extended plane. The BH region is in gray
Upper left panel: the curves \(\sigma _\sim =\) constant of Eq. (41) in the extended plane. The black region is the BH. Central panel: the curves \(\kappa ({\sigma _\sim })=\kappa _\sim =\) constant are shown in the extended plane. Right panel: \(r_{\pm }\) are the outer and inner horizons, \(r_{I}^{\pm }\) are defined in Eq. (43). The accelerations \(\kappa \) and \(\ell \) are shown as functions of the dimensionless BH spin a/M. Second line, left panel: the curves \(\kappa _{\ominus }=\) constant and \(a_{\ominus }=\) constant, Eq. (46), are plotted. Center and right panel: \(\kappa _{\ominus }\) and \(a_{\ominus }\) as functions of r for different planes \(\sigma \equiv \sin ^2\theta \). Bottom line. Left panel: the curves \(a^{\pm }_{\lhd \rhd }=\) constant, right panel curves, \(r_{\lhd \rhd }^{\pm }=\) constant defined in Eq. (52)
In the next section we conclude this analysis explicitly considering the accelerations in terms of \(\ell \) and \(\kappa \).
3.4 The accelerations \(\ell \) and \(\kappa \) on the horizon in the extended plane
We focus on the accelerations \(\ell \) and \(\kappa \) on special points of the metric bundles in the extended plane, considering the horizon \(r_{\pm }\) and \(a_{\pm }\). Specifically, we consider the curves \((a_g,r_g)\) tangent to the horizons as functions of characteristic frequency of the bundle \(\omega \) and the bundle origin spin \(\mathcal {A}_0\). We summarize some of the results found in the previous analysis and frame them in an overall view of the new framework.
Below, we discuss the following seven cases:
- (i):
-
On \(r_g\), where \(a=a_g(r_g)\): On the horizon curve, where \(a=a_g(r_g)\), in terms of \(r_g\) we obtain
$$\begin{aligned}{} & {} k(r_g)=\frac{1-r_g}{r_g [(r_g-2) \sigma +2]}\quad \text{ and }\quad \ell (r_g)=\frac{r_g-1}{2 r_g}.\nonumber \\ \end{aligned}$$(54)In the case of an extreme BH, \(r_g=M\), we find \(\ell (r_g)=\kappa (r_g)=0\). On \(r_g=2M\), which is the horizon in the Schwarzschild spacetime or the outer ergosurface on the equatorial plane of the Kerr BH, we obtain \(\kappa (r_g)=-1/4=-\ell (r_g)\). The acceleration \(\kappa \), however, depends on the plane \(\sigma \) and, therefore, on the bundle origin. Considering the variation on the plane \(\sigma \), we obtain the following extremes at a fixed tangent point
$$\begin{aligned}{} & {} \partial _\sigma k=0\quad \text{ for }\quad r_g=M,\quad r_g=2M. \end{aligned}$$(55)Condition \(\partial _{\sigma }\kappa =0\) provides the extreme plane for the acceleration \(\kappa (r_g)\) (\(\ell (r_g)\) is, indeed, independent of \(\sigma \)). The analysis of the extreme points with respect to the plane does not provide information on the acceleration on the horizons, which are independent of \(\sigma \), but on the origin of the bundle (dependent on \(\sigma \), with a fixed tangent point).
- (ii):
-
For \(a=a_g(\mathcal {A}_0)\) and \(r=r_g(\mathcal {A}_0)\): The accelerations \(\ell \) and \(\kappa \) on the horizons, \(r_{\pm }\) or \(a_{\pm }\), can be expressed more conveniently in terms of \(a_g(\mathcal {A}_0)\) (tangent spin) and tangent radius \(r=r_g(\mathcal {A}_0)\) as functions of \(\mathcal {A}_0=a_0\sqrt{\sigma }\)
$$\begin{aligned}{} & {} \kappa (\mathcal {A}_0,\sigma )=-\frac{\mathcal {A}_0^4-16}{4 \mathcal {A}_0^2 \left[ \mathcal {A}_0^2+4(1- \sigma )\right] }\quad \text{ and }\nonumber \\{} & {} \ell (\mathcal {A}_0)=\frac{1}{4}-\frac{1}{\mathcal {A}_0^2} \end{aligned}$$(56)represented in Figs. 4, 5 – see also Eq. (23). Note that \(\kappa (\mathcal {A}_0,\sigma )\) in Eq. (56) depends explicitly on \(\sigma \) and the bundle origin \(\mathcal {A}_0\). As expected, zero acceleration occurs for \(\mathcal {A}_0=a_0\sqrt{\sigma }=2M\), corresponding to the Kerr extreme BH as tangent point on the horizon curve.
- (iii):
-
For \(r=r_g(\omega )\) and \(a=a_g(\omega )\): We now consider the accelerations \((\kappa ,\ell )\) on the horizon curves in terms of the bundle characteristic frequency \(\omega \), assuming \(r=r_g(\omega )\) and \(a=a_g(\omega )\). Then,
$$\begin{aligned}{} & {} \kappa (\omega ,\sigma )=\frac{16 \omega ^4-1}{16 (1-\sigma ) \omega ^2+4}, \quad \text{ and }\nonumber \\{} & {} \ell =\ell _{\odot }(\omega )=\frac{1}{4}-\omega ^2, \end{aligned}$$(57)are the accelerations on the horizons in the extended plane as functions of the bundles (horizons) frequencies. Here \(\ell _{\odot }\) has been defined in Eq. (23) and represented in Fig. 6 – see also Figs. 4, 5.
- (iv):
-
For \(r=r_g\) and on the bundle origin \(a=a_0(r_g,\sigma )\): On the vertical lines of the extended plane, \(r=r_g=\) constant (bundle tangent radius to the horizon curve), in terms of the bundle origin \(a=a_0(r_g,\sigma )\), the accelerations are
$$\begin{aligned} \kappa (r_g,\sigma )= & {} -\frac{(r_g-2) \sigma [(r_g [r_g+2]-4) \sigma +4]}{r_g [([r_g-2] r_g+4) \sigma -4]^2}\quad \text{ and }\nonumber \\ \ell (r_g,\sigma )= & {} \frac{(r_g-2) \sigma [(r_g-2) r_g \sigma +4]}{r_g [(r_g-2) r_g \sigma -4]^2}. \end{aligned}$$(58)In this analysis, as there is \(a=a_0\ge 0\), we describe BHs and NSs on the orbits \(r_g\in [0,2]\).
- (v):
-
On the origin \(\mathcal {A}_0(r_g,\sigma )=a_0\sqrt{\sigma }\) and \(r_g=r_{g}(\mathcal {A}_0)\): Similarly to the previous situation, we consider the spin bundle origin and the tangent radius of the horizon curve. These quantities are considered as functions of the origin \(\mathcal {A}_0=a_0\sqrt{\sigma }\), where \(a_0=\mathcal {A}_0/\sqrt{\sigma }\):
$$\begin{aligned}{} & {} \kappa (\mathcal {A}_0,\sigma )=\frac{\left( \mathcal {A}_0^2+4\right) ^2 \sigma \left[ \left( \mathcal {A}_0^4-4 \mathcal {A}_0^2-16\right) \sigma +\left( \mathcal {A}_0^2+4\right) ^2\right] }{\mathcal {A}_0^2 \left[ \left( \mathcal {A}_0^2+4\right) ^2-\left( \mathcal {A}_0^4+4 \mathcal {A}_0^2+16\right) \sigma \right] ^2}\nonumber \\{} & {} \quad \text{ and }\ \ell (\mathcal {A}_0,\sigma )=\frac{\left( \mathcal {A}_0^2+4\right) ^2 \sigma \left[ 4 \sigma -\left( \mathcal {A}_0^2+4\right) ^2\right] }{\mathcal {A}_0^4 \left[ 4 \sigma +\left( \mathcal {A}_0^2+4\right) ^2 \right] ^2} \end{aligned}$$(59) - (vi):
-
On the horizon curve \(r_g(a_0,\omega )\) and the origin spin \(a_0=1/\omega \sqrt{\sigma }\): We now consider \(r=r_g\in [0,2M]\) (tangent radius of the bundle with the horizon curve) and \(a=a_0\) (bundle origin spin) in terms of \(\omega \), the bundle characteristic frequency. Then,
$$\begin{aligned} \kappa (\omega ,\sigma )= & {} -\frac{\sigma \left( 4 \omega ^3+\omega \right) ^2 \left[ 16 (\sigma -1) \omega ^4+4 (\sigma -2) \omega ^2-\sigma -1\right] }{\left[ 16 (\sigma -1) \omega ^4+4 (\sigma -2) \omega ^2+\sigma -1\right] ^2},\nonumber \\ \ell (\omega )= & {} \frac{\sigma \omega ^2 \left( 4 \omega ^2+1\right) ^2 \left[ 4 \omega ^2 \left( \sigma -4 \omega ^2-2\right) -1\right] }{\left[ 4 \omega ^2 \left( \sigma +4 \omega ^2+2\right) +1\right] ^2}.\nonumber \\ \end{aligned}$$(60)The accelerations are evaluated for NSs and BHs (as \(a=a_0\)) on the points \(r_g\in [0,2M]\).
- (vii):
-
For \(r_g={\mathcal {A}_0 a_g}/{2}\) and \(a=a_0= \mathcal {A}_0/\sqrt{\sigma }\): In this case, we consider the acceleration \(\kappa \) as function of \((\mathcal {A}_0,r_g,a_g)\). Then, in terms of the tangent radius \(r_g={\mathcal {A}_0 a_g}/{2}\) and spin \(a=a_0= \mathcal {A}_0/\sqrt{\sigma }\), we obtain
$$\begin{aligned} \kappa (\mathcal {A}_0, a_g,\sigma )= & {} \frac{4 \sigma \left[ \sigma \left( 2 \mathcal {A}_0 a_g-a_g^2-4\right) +4\right] }{\mathcal {A}_0^2 \left[ \left( a_g^2-4\right) \sigma +4\right] ^2},\nonumber \\ \ell (\mathcal {A}_0, a_g,\sigma )= & {} \frac{4 \sigma \left( a_g^2 \sigma -4\right) }{\mathcal {A}_0^2 \left( a_g^2 \sigma +4\right) ^2} \end{aligned}$$(61)– see Fig. 5.
The analysis carried out in this section will also be resumed in Sect. D, considering the metric tensor on the extended plane similarly to the analysis of the accelerations \(\kappa \) and \(\ell \).
4 Discussion and final remarks
The concept of extended plane can be used to describe BH transitions from the \(\mathcal{M}\mathcal{B}\)s view-point, for instance, a transition from the tangent spin \(a_{g}(0)\) for the BH(0) to \(a_{g}(1)\) for the BH(1), corresponding to a transition between the respective tangent \(\mathcal{M}\mathcal{B}\)s. Consequently, we can also describe transitions in terms of the origin frequency and the tangent radius of the bundle. In this new perspective, the transition from a state (0) to a new state (1) is essentially regulated by the characteristics of the initial state, such as the BH surface gravity \(\ell _H^+(0)\) evaluated on the outer horizon, entering the entropy/temperature terms, and by the work term, which is expressed through the bundle frequency \(\omega _H^+\). We have expressed the relation between surface gravities in terms of the tangency conditions of the bundles with the horizon curve and in terms of the bundle curves in the extended plane, leading to the alternative view-point in terms of replicas, i.e., orbits of the bundles located at \(r>r_+\) (and some being in the \(r<r_-\) region). In this sense, we describe the state transitions in terms of metric bundles transitions.
This work investigates also the properties of naked singularity geometries, which correspond to exact solutions of Einstein equations and whose existence in Nature is still a subject of debate. For instance, from a theoretical point of view, the metric tensors for over-spinning (or over-charged) singular geometries still remain to be consistently framed in GR, particularly, in the context of BH physics, including aspects of the progenitor collapse, the BH scattering, and the consequent BH horizons formation.
Representation of the extended plane of the Kerr geometry. Upper Left panel: the space \((\mathcal {A}_0/M,r/M\)), where \(\mathcal {A}_0\equiv a_0\sqrt{\sigma }\) is the bundle origin and \(\sigma =\sin ^2\theta \). The relation (B1), discussed in Sect. B, refers to this plane. The metrics on the different parts of the extended plane are detailed in Sect. D.1. Upper center-second panel: Horizons representation in the plane \(r/M-r/M\). The outer and inner BH horizons \(r_{\pm }\) as functions of \(r_{\mp }\). Third upper line panel: the lower triangle (BH) corresponds to the BH triangle in the left and central panels. Four triangles are constructed per symmetry to indicate the corresponding sections of the extended planes. Upper right panel: the left panel comes from the right panel upper line. The consequent transformation leads to the center bottom panel. Bottom panel: the function \(\mathcal {A}_{tangent}\) of Eq. (B1) as function of \(\mathcal {A}_0=a_0\sqrt{\sigma }\), where \(a_0\) is the bundle origin spin, \(\sigma \equiv \sin ^2\theta \), and \(a_g\) is the bundle tangent spin. The functions \(a_{ex}\) and \( a_{ex}^a\) of Eq. (B6) are also plotted
A sideline of this analysis, we exploit the particular black holes-naked singularities correlation proposed in [8,9,10]. In particular, we focused on the bottleneck region, which is a structure of the light surfaces observed in some naked singularities [8,9,10, 47, 48] and associated with some repulsive gravity effects characterizing NSs [16,17,18,19,20, 49,50,51,52,53,54,55]. Naked singularities, in classical GR, are characterized by repulsive gravity effects. In the Kerr spacetime, for example, the effects of repulsive gravity are very well identified in the motion of test particles. Moreover, this phenomenon occurs also in the field of spherically symmetric naked singularities, as the static and electrically charged solution of Reissner and Nordström. In the case of a Kerr spacetime, there is a specific set of NSs characterized by this phenomenon and a special region of circular orbits, where effects attributable to a repulsive gravity force could, in principle, be detected. This region corresponds to the NS bottleneck.
We connected the light surfaces properties to the bottleneck region of NSs. The origin \(\mathcal {A}_0\) of the bundle with frequency \(\omega \) coincides with the horizon angular momentum. We established a connection between the concepts of \(\mathcal{M}\mathcal{B}\)s and bottleneck region in NSs- Sect. 2.2, redefining metric bundles in terms of the angular momentum of the horizon defined in terms of the characteristic bundle frequency. In the first part of this analysis (Sect. 2), we introduced the concept of metric bundles and discussed the main properties in the extended plane, enlightening along this analysis the fundamental spins of the Kerr spacetimes, according to their properties in the extended plane. In Sect. 3, we studied the accelerations and surface gravity in the extended plane using metric bundles, considering the case of replicas of the acceleration.
The accelerations \((\ell , \kappa )\), related to the surface gravity definition, are defined on the horizon points in the extended plane.
In Sect. D, we rewrite the metric tensor on parts of the extended plane, providing alternative representations of the BH geometries in terms of the BHs–NSs correspondence and creating clusters of BH copies with respect to a new metric parameter, recovered from the bundles representations as curves in the extended plane.
Metric bundles, in the context of astrophysical observations, can have a direct impact on BH astrophysics. Firstly, light surfaces, which are the solutions \(r=r(a_{\omega },\omega )\) with respect to metric bundles \(a_{\omega }\), play a relevant role in constraining the energy extraction mechanism from BHs, which regulates, for example, the Blandford–Znajek process. They also constrain the properties of the accretion disks and the Grad-Shafranov equations for the force free magnetosphere around a BH. More precisely, the energy extraction process can take place regulated by the light surfaces which are, in general, two surfaces, one surface located outside the horizon \(r_+\) and one within the ergoregion \(]r_+,r_{\epsilon }^+[\). Re-parameterizing with functions defined on the extended plane, we obtain structures constituted by replicas of the metric tensor describing the same geometries or portions of the same geometry in the extended plane. The replicas can also be used to describe the physics on the BH axis, extracting information detectable in regions far from the horizons. We use the characteristic quantities of the bundles to generate the schemes of Fig. 17. We also used the BH surface gravity to obtain replicas, which generate multiple copies of the geometry (up to four) and tensors clusters, representing multiple copies of a geometry or portions, according to the value of the metric parameter.
The \(\mathcal{M}\mathcal{B}\)s analysis of metric bundles enlightens the fundamental spins of the Kerr spacetimes, according to the properties in the extended plane. Consequently, some notable spins are pointed out: BHs (\(a={\sqrt{3}}/{2} M\), \(a=1/\sqrt{2} M\)), and NS \(a/M=\sqrt{9/8}\), on the basis of the variation of the gravity surface \( \ell \) in the state transitions from black hole to black hole. In this new framework particular geometries and points of the geometries are studied as the curves \( rM= {3 a^2}/{2}\) (in relation to some properties on the singularity equatorial plane) and, in relation to the properties on the singularity axis the curves \(a=r\), \(a={r}/\sqrt{3}\) and \(a=r\sqrt{3}\). Finally we summarise the situation for the spins as follows
- BH:
-
spacetimes with spin \(a_{\gamma }\equiv \sqrt{1/2}\). In the BH geometry with spin \(a_{\gamma }\equiv \sqrt{1/2}\), it is \(\ell _{H}^\pm =\pm \omega _H^\pm \) and the analysis in Sect. 2.3. This result implies that in this spacetime the transitions are essentially regulated by the characteristic bundle frequency. In this case, \(r_{\gamma }^-=r_{\epsilon }^+\), that is, the outer ergosurface on the equatorial plane of the BH is a geodesic orbit of the (corotating) photon – see also Fig. 13. In this geometry, \(\omega (r) = s \ell (r)\) at the same point r. We obtain \(r=1\mp \sqrt{{1}/({s^2+1})}\) for \(s<0\) and \(s\ge 0\), respectively. For \(s=\pm 1\), we obtain \(r=r_\pm =1\pm {1}/{\sqrt{2}}\), outer and inner horizons, respectively, for BHs with spin \(a/M=1/\sqrt{2}\). In other words, if we consider \(\ell _H^{\pm } (\omega ) = s\omega \), then for \(s = \pm 1\), we obtain \(\omega = \pm \left( 1\pm \sqrt{2} \right) /2\), corresponding to \(a/M = 1/\sqrt{2}\). Furthermore, \(\partial _a^{(2)}\ln s=0\) for \( a= a_{\gamma }\equiv {M}/{\sqrt{2}}\), where \(s\equiv \omega ^+_-\equiv \omega _H^+/\omega _H^-\), see Eq. (C2) and [15].
- BH:
-
spacetime spin \(a/M=4/5\). It is \(\omega ^{\pm }_H=(L_f)_H^\pm =1\) from Eq. (8) for \(r=2/5 M\), the inner horizon for the BH spacetime \(a/M=4/5\), related to the inner horizon confinement and, therefore, to the NS bottleneck region – see. The spin \(a_g=4M/5\) determines the bundle confinement as expressed in Eq. (C5).
- BH:
-
spacetime spin \(a/M=\sqrt{3}/2\). The analysis of the extremes of the accelerations \(\ell \), solutions \(\partial _r \ell =0\), enlightens the role of the BH spin \(a/M=\sqrt{3}/2\). The radius \(r_o\), solution of \(\partial _r\ell =0\), is on the horizon curve in the extended plane, where \(r_o = 3/2M \), which is the outer horizon of the BH spacetime with spin \(a/M = {\sqrt{3}}/{2}\) – see Fig. 6. Restricting to the horizon curve, we find the solution for \(r_o= M/2 \), which is the inner horizon of the BH spacetime with \(a/M = \sqrt{3}/2\). Therefore, the extremes of the acceleration \(\ell \) for a and r constitute, respectively, the inner and outer horizon for the BH with spin \(a/M = \sqrt{3}/2\). (That is \(\partial _a \ell = 0\) for \( r_a = a/\sqrt{3}\), while \(\partial _r \ell = 0\) for \(r_r = \sqrt{3} a\); however, \(r_a = r_ - \) and \(r_r = r_ +\) for \( a/M = \sqrt{3}/2\)). In Fig. 3, we note the values \(r/M=3/2\) and the spin \(a/M=\sqrt{3}/2\). The saddle point of \((L_f)(\omega ^{\pm })\) as function of r is \(r_-/M=1/2\), which is the inner horizon of the BH spacetime, where the momentum and velocity are \((L_f)(\omega ^{\pm })={2}/{\sqrt{3}}=1/\omega \). (Note that in this case \(a=\omega _-\)). The saddle point of the function \(\omega (r)\) is for the same BH spacetime on the outer horizon \(r_+/M={3}/{2}\) where \((L_f)=2 \sqrt{3}=1/\omega \).
- NS:
-
spacetime spin \(a/M= \sqrt{9/8}\). In the variation of the acceleration \(\kappa \) in terms of the plane \(\sigma \), we found in Eq. (43) the special value \(a/M= \sqrt{{9}/{8}}\) for NSs in the bottleneck region. The spin range is constrained to \(a/M\in ]0,\sqrt{9/8}]\), where for \(a/M=\sqrt{9/8}\) it is \(r_{I}^{\mp }/M=3/2\) – see Eq. (49) and Fig. 16.
- NS:
-
spacetime spin \(a/M=2/\sqrt{3}\). The origin spin \(\mathcal {A}_0=2/\sqrt{3}\) is a saddle point for the area, and it is also the saddle point for the angular momentum corresponding to the frequency \(\omega =1/(L_H)\) of the inner horizon \(r_-/M=1/2\) for the spacetime \(a=\omega \), whose frequency of the outer horizon is a saddle point for the frequency – see Eq. (7).
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
It is \(r_+<r_{\epsilon }^+\) on the planes \(\theta \ne 0\) and it is \(r_{\epsilon }^+=2M\) on the equatorial plane \(\theta =\pi /2\), where \(r_-=0\). Moreover, \(0<r_{\epsilon }^-<r_-<r_+<r_{\epsilon }^+\) for \(\sigma \ne 0\) and \(a\in ]0,M[\). For \(\sigma =0\), the functions \(r_{\epsilon }^\pm \) satisfy the properties \(0<r_{\epsilon }^-=r_-<r_+=r_{\epsilon }^+\).
Light surfaces are defined essentially as solutions of the condition \({\mathcal {L}_\mathcal {N}}=0\). The concept of light surfaces is used in astrophysics with reference to the “velocity of light” surfaces, which are widely applied in the analysis of the magnetosphere of black holes and Pulsars – see for example [22, 23]. Light surfaces are defined as regions, where the speed of a particle moving purely toroidally equals the light velocity. In all generality, a light surface can be defined as the set of of points in which \(\mathcal {L}\equiv \xi _t+\omega \xi _\phi \) (co-rotating vector) is null, i.e., regions of spacetime in which observers would have to move at the speed of light in order to co-rotate. (In the bundles’ framework, we consider also the counter-rotating condition for fixed \(\omega <0\).) In the case of electromagnetic fields in the Kerr spacetime with \(\omega < \omega _H^+\), light surfaces are surfaces at which the magnetic field lines rotate (with \(\omega \)) at the speed of light. (Note that \(\omega < \omega _H^+\) is the condition for the outer horizon tangency in the bundle approach, and it constraints the energy extraction from the BH via the Blandford–Znajek mechanism.). In the Kerr BH spacetime, there are two light surfaces. The inner one is inside the ergoregion and is interpreted as due to the frame dragging effect [24,25,26,27,28,29], and the outer one is located outside the ergoregion. Outside the exterior light surface, co-rotating particles would have to move faster than light. The outer light surface corresponds to the Pulsar light cylinder only asymptotically (\(r=1/\omega \sqrt{\sigma }\)). Similarly to the stationary observers, the BH magnetosphere, rigidly rotating with angular velocity \(\omega \), is divided into regions of sub-luminal and super-luminal rotation, depending on the sign of \(\mathcal {L}_N\equiv \mathcal {L}\cdot \mathcal {L}\). The separating surfaces, defined via \(\mathcal {L}_N=0\), are light surfaces [30,31,32]. Therefore, outside of the outer light surface, magnetic field lines would rotate with velocities faster than the speed of light (respect to ZAMOs). Inside the inner light surface, which is located inside the outer ergoregion, magnetic field lines would (counter)rotate super-luminally with respect to the ZAMO. Light surfaces can, therefore, be defined as the surfaces separating sub-luminal and super-luminal (co-rotating) motion [28,29,30, 33,34,35,36,37,38,39,40]. The consequences of the existence of horizons replicas on the BH magnetosphere is the subject of a future analysis.
The quantities considered in this analysis are conformal invariants of the metric and inherit some of the properties of the Killing vector \(\mathcal {L}\).
The notion of co-rotation and counter-rotation motion in NSs must be attentively discussed. In test particles analysis and accretion tori models, for slowly spinning NSs (\(a\in ]M,1.3[\)), there are circular geodesic orbits with \((E\le 0,L\le 0)\) and \((E\ge 0,L\le 0)\) on the equatorial plane of the ergoregion. However, these solutions correspond to the relativistic angular velocity (the Keplerian velocity with respect to static observers at infinity \(d\phi /dt\)) \(\omega >0\); therefore, in this sense, they are all co-rotating with respect to the static observers at infinity – see, for example, [19, 41,42,43,44].
We also note that the couple \((\ell ^{\star },\kappa ^{\star })\) can be used to define the the Walker-Penrose Killing tensor as \(K\equiv \rho ^2(\ell ^{\star }_{\flat }\otimes \kappa ^{\star }_{\flat }+\kappa ^{\star }_{\flat } \otimes \ell ^{\star }_{\flat })+r^2 \textbf{g}\), where \(\flat \) is for the covariant form of the vectors (1-form of the vector through the metric g duality).
Equation \(\Delta \omega _{\pm }=\textbf{c}\) can be solved for the spins \(a_z^{\pm }\equiv \sqrt{\left( {r^2 \left[ 2-\textbf{c}^2 r (r+2)\right] \pm 2 \sqrt{r^3 \left[ r-4 \textbf{c}^2 (r+2)\right] }}\right) /{\textbf{c}^2 (r+2)^2}}\), where \(a_z^-=a_z^+=0\) so that \(\textbf{c}= \pm {2 \sqrt{r-2}}/{r^{3/2}}\). Furthermore, it is clear that the values of \(\textbf{c}\) such that \(a_z^{\pm }=0\), which corresponds to the Schwarzschild case, have as extreme case \(r=3M\). That is, \(a_z\) are curves with equal difference in frequency, which is null, as expected, on the horizon in the extended plane – Fig. 8.
We consider, for \(\sigma =1\), the third solution for the metric bundles \(a_{\omega ,3}=({1-2 \omega ^2})/{\omega }\) related to the horizon curve, which is a limiting condition. Considering the acceleration \(\ell \), we represent this case as the confinement of the curves \(\ell (a_{\omega })\) for \(\omega \) in the inner horizon curve in Fig. 12. On the equatorial plane, it is possible to see that, assuming \(\omega >0\), the bundles are defined for \(r\in ]0,r_{\upsilon }^{(+)}]\), where \(r_{\upsilon }^{(+)}\equiv \sqrt{\frac{\omega ^2+1}{\omega ^2}}-1\) and for the upper boundary of this range \(a=2r_{\upsilon }^{(+)}\omega \).
There is \(a= 1/\sqrt{2}\): \( r_{\gamma }^-=r_{\epsilon }^+\), and \(a/M= 2(\sqrt{2}-1): r_{mbo}^-=r_{\epsilon }^+\), \(a/M=\sqrt{8/9}\) \(r_{mso}^-=r_{\epsilon }^+\), and \( a/M=2\sqrt{2}\) for naked singularities, where \(r_{mso}^-=r_{\epsilon }^+\). Radii \((r_{\gamma }^-,r_{mbo}^-,r_{mso}^-)\) are the corotating last circular orbit (photon orbit), marginally bounded orbit, and marginally stable orbit, respectively.
For \( r_g={a_g}/{2 \omega }\) it is \( \textrm{d}r_g={\textrm{d}a_g}/{2 \omega }-{a_g \textrm{d}\omega }/{2 \omega ^2}\), considering \(a_g\) and \(\omega \) independent.
Note that for \(r=r_g(\omega )\), there is \( \textrm{d}r_g/\textrm{d}\omega =-(a_g(\omega )^2/\omega )\).
Note that considering \(\mathcal {A}_0\) as independent parameter, we could take for \( r=r_g(\mathcal {A}_0)\) the term \( \textrm{d}r_g={a_g^2 \textrm{d}\mathcal {A}_0}/{\mathcal {A}_0}\), or explicit \(\mathcal {A}_0=a_0\sqrt{\sigma }\). In this case, for \( r=r_g(a_0,\sigma )\), we obtain \(\textrm{d}r_g=a^2_g \left( {\textrm{d}a_0}/{a_0}+\textrm{d}\theta \sqrt{(1-\sigma )/{\sigma }}\right) \). Notably, this implies a modification of the \(g_{\theta \theta }\) component and for \(g_{rr}\).
In this case we should consider that for \(r=r_g(\omega )\), we obtain \( \textrm{d}r_g/\textrm{d}\omega =-(a_g(\omega )^2/\omega )\).
For \( r_g(a_0,\sigma )\) we have that \(\textrm{d}r_g=a_g^2 \left( {\textrm{d}a_0}/{a_0}+\textrm{d}\theta \sqrt{({1-\sigma })/{\sigma }}\right) \).
Note that for \(r=r_g(\omega )\), it is \( \textrm{d}r_g/\textrm{d}\omega =-(a_g(\omega )^2/\omega )\).
For \( r_g={a \mathcal {A}_0}/{2}\) it is \( \textrm{d}r_g=\mathcal {A}_0\textrm{d}a/2+a\textrm{d}\mathcal {A}_0/2\) with \(\mathcal {A}_0\) independent parameter.
For \( r_g=2[1-{ a}/{\mathcal {A}_0}]\), in this case \( \textrm{d}r_g={2 (a \textrm{d}\mathcal {A}_0-\mathcal {A}_0 \textrm{d}a)}/{\mathcal {A}_0^2}\)
References
J.M. Bardeen, B. Carter, S.W. Hawking, Commun. Math. Phys. 31, 2 (1973)
J.D. Bekenstein, Phys. Rev. D 7, 2333 (1973)
J.D. Bekenstein, Phys. Rev. D 12, 3077 (1975)
S.W. Hawking, Commun. Math. Phys. 43, 199–220 (1975)
J. Polchinski, Contribution to: TASI, 353–397 (2015)
A.Y. Nielsen, CQGra 25(8), 085010 (2008)
M. Pielahn, G. Kunstatter, A.B. Nielsen, Phys. Rev. D. 84(10), 104008 (2011)
D. Pugliese, H. Quevedo, Eur. Phys. J. C 79(3), 209 (2019)
D. Pugliese, H. Quevedo. Eur. Phys. J. C 78(1), 69 (2018)
D. Pugliese, H. Quevedo, Eur. Phys. J. C 81(3), 258 (2021)
D. Pugliese, G. Montani, Entropy 22, 402 (2020)
D. Pugliese, Z. Stuchlík, Class. Quantum Gravity 38(14), 14 (2021)
D. Pugliese, H. Quevedo, Nucl. Phys. B 972, 115544 (2021)
D. Pugliese, H. Quevedo, Gen. Relat. Gravit. 53(10), 89 (2021)
D. Pugliese, H. Quevedo, submitted (2022)
D. Pugliese, H. Quevedo, R. Ruffini, Phys. Rev. D 83, 024021 (2011)
D. Pugliese, H. Quevedo, R. Ruffini, Phys. Rev. D 83, 104052 (2011)
D. Pugliese, H. Quevedo, R. Ruffini, Eur. Phys. J. C 77(4), 206 (2017)
D. Pugliese, H. Quevedo, R. Ruffini, Phys. Rev. D 84, 044030 (2011)
D. Pugliese, H. Quevedo, R. Ruffini, Phys. Rev. D 88(2), 024042 (2013)
D. Pugliese, H. Quevedo, Eur. Phys. J. C 75(5), 234 (2015)
B. Punsly, Black Hole Gravitohydromagnetics (Springer, Berlin–Heidelberg, 2009)
M. Camenzind, Compact Objects in Astrophysics: White Dwarfs, Neutron Stars and Black Holes (Springer, Berlin, Heidelberg, 2007)
H.-Y. Pu, M. Nakamura, K. Hirotani, Y. Mizuno, K. Wu, K. Asada, Astrophys. J. 801, 56 (2015)
D.A. Uzdensky, Astrophys. J. 603, 652–662 (2004)
A. Tchekhovskoy, R. Narayan, J.C. McKinney, Astrophys. J. 711, 50–63 (2010)
Z. Pan, Phys. Rev. D 98, 043023 (2018)
R.D. Blandford, R.L. Znajek, MNRAS 179, 433–456 (1977)
R.L. Znajek, MNRAS 179, 457 (1977)
S.S. Komissarov, MNRAS 350, 427–448 (2004)
D.A. Uzdensky, Astrophys. J. 620, 889–904 (2005)
J.F. Mahlmann, P. Cerda-Duran, M.A. Aloy, MNRAS 477(3), 3927–3944 (2018)
S.S. Komissarov, J.C. McKinney, MNRAS 377, L49–L53 (2007)
D.A. Macdonald, MNRAS 211, 313–329 (1984)
J.C. McKinney, MNRAS 368, 1561–1582 (2006)
B. Crinquand, B. Cerutti, G. Dubus, K. Parfrey, A. Philippov, A &A 650, A163 (2021)
I. Contopoulos, D. Kazanas, C. Fendt, Astrophys. J. 511, 351–358 (1999)
I. Contopoulos, D. Kazanas, D.B. Papadopoulos, Astrophys. J. 765, 113 (2013)
J.C. McKinney, R. Narayan, MNRAS 375, 531–547 (2007)
A. Nathanail, I. Contopoulos, Astrophys. J. 788, 186 (2014)
Z. Stuchlik, BAICz 31, 129 (1980)
Z. Stuchlik, BAICz 32, 68 (1981)
K. Adamek, Z. Stuchlik, CQGra 30, 205007 (2013)
P. Slaný, Z. Stuchlík, CQGra 22, 3623 (2005)
D. Pugliese, H. Quevedo, arXiv:1910.02808 [gr-qc] (2019)
D. Pugliese, H. Quevedo, arXiv:1910.04996 [gr-qc] (2019)
C. Chakraborty, M. Patil, P. Kocherlakota et al., Phys. Rev. D 95(8), 084024 (2017)
S. Mukherjee, R.K. Nayak, Astrophys. Space Sci. 363(8), 163 (2018)
S.L. Shapiro, S.A. Teukolsky, Am. Sci. 79(4), 330–343 (1991)
M. Patil, P.S. Joshi, D. Malafarina, Phys. Rev. D 83, 064007 (2011)
V.S. Manko, E. Ruiz, Phys. Lett. B 791(10), 26–29 (2019)
O. Luongo, H. Quevedo, Phys. Rev. D 90(8), 084032 (2014)
T. Harada, Pramana 63, 741–754 (2004)
J.W. Maluf, Gen. Relat. Gravit. 46, 1734 (2014)
F. de Felice, A &A 45, 65 (1975)
Acknowledgements
This work was partially supported by UNAM-DGAPA-PAPIIT, Grant No. 114520 and Conacyt-Mexico, Grant no. A1-S-31269.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The vector \(\bar{\ell }\)
Here we discuss the properties of the acceleration \(\ell \) as determined by the vector \(\bar{\ell }=f_t u^t+f_r u^r+f_\phi u^\phi \), where \(u^\alpha \equiv \partial _{\alpha }\) and \(\nabla _{\varvec{\ell }} \bar{\ell }^b=\ell \bar{\ell }^b\) with \(\bar{\ell }^a\bar{\ell }_a=0\). We obtain the condition \(f_{\phi }(r,\theta )/ f_t(r,\theta )={a}/({a^2+r^2})\), with
See Fig. 18. (Note that \(\bar{\ell }^{\pm }\) are well defined for NSs and BHs with the exclusion of the horizons). In BH spacetimes it is \(\bar{\ell }^+=\frac{2r \rho ^2}{\sqrt{\Delta ^2} \left( a^2+r^2\right) }\kappa ^* \) and \(\bar{\ell }^-=-{r}/({a^2+r^2})\ell ^*\), as introduced in Sect. 3. Note that the vectors \(\bar{\ell }^{\pm }\) are well defined also in NS geometries.
Components \(\left\{ f_t,f_r,f_{\phi }\right\} \) of the vector \(\bar{\ell }^{\pm }\), defined in Eq. (A1), and the acceleration \(\ell \) as function of the parameter \(\tau \) for different spacetime spins a/M
Upper line: orbits of a photon with four-velocity vector \(\bar{\ell }^{\pm }\) on the equatorial plane; see Eq. (A1). The black region represents the central black hole. The gray region is the ergoregion. Different spins are considered. Below panels: coordinates and relativistic velocities (\(\omega \), \(\dot{r}\)) are plotted
For \(t'\equiv f_t\) and \(r'\equiv f_r\), there exists a turning point (i.e. \(\partial _r t'=\partial _r r'=0\)) at is \(r=\pm a \), where
This solution tends to 0 for large NS spins, while for extreme Kerr BH (on the horizon), \(t'\) and \(\phi '\equiv f_{\phi }\) are not well defined and \(r'=-1/2\). Then \(\partial _r \phi ' = 0\) for \( r_ {al}^{\mp } \), where \(r_ {al}^{-}\) is defined for \(r > M\) at \(a =M\) and \(r_ {al}^{+}\in ]r_-,r_+[\):
where
With \(r_0\equiv r(0)\), we obtain
where \(\textbf{W}(z)\) is the Lambert \(\textbf{W}\) function (known also as product logarithm or omega function), which is a solution for \(w: z=we^w\), and
The equation \(r=r_{\pm }\) is satisfied for \(\tau = \tau _{\pm }\)
respectively. See Fig. 19.
Appendix B: Black holes in the extended plane: clusters metrics
In this section, we discuss in detail the construction of the extended plane [8, 10]. Here, we present the set of transformations considered in Fig. 17 as follows:
which are part of the boundaries of the BHs regions in Fig. 17, where, in particular,
constituting the vertices of the BH regions in Fig. 17-central panel. These definitions determine a tangent line to the horizon curve in the extended plane, through the points \(\mathcal {A}_0 (a_0)\) (bundle origin) and the tangent point. The quantity \(\mathcal {A}_0\) is a parameter in the relations \(\mathcal {A}^{\star }_{\star }=a(r)\)), where \(\mathcal {A}^{\star }_{\star }=\{\mathcal {A}_0(r),\mathcal {A}_{tangent},\mathcal {A}_{tan}^0,\mathcal {A}_{r}^*\}\) is one of the quantities of Eq. (B1). Then, we define \(r_{ex}:\mathcal {A}_{tan}^0(\mathcal {A}_0,r_{ex})=a\) such that \(r_{ex}=r_{ex}(a,\mathcal {A}_0)\), where \(a_{ex}: \partial _{\mathcal {A}_0}r_{ex}(a_{ex})=0\), and \(r_{ex}^a:\mathcal {A}_{tangent}(\mathcal {A}_0,r_{ex}^a)=a\) with \(a_{ex}^a: \partial _{\mathcal {A}_0}r_{ex}^a(a_{ex}^a)=0\). It is explicitly
The four regions of Fig. 17 are outlined in this analysis also through the inertial mass, the surface gravity \(\ell \) and the BH area in the extended plane, as functions of the origin spin \(\mathcal {A}_0\), the characteristic frequency of \(\omega \) of the bundles, and the tangent radius (the first law of BH thermodynamics in the extended plane is defined along the boundary of these regions). The first graph is an adapted graphical representation of the extended plane. In the BH region, there are four regions whose boundaries are \( r_{\pm }\) and \(a_{\pm }\) in the two planes, with base points \(\{r=0,a=0\}\), \(r_{\epsilon }^+=\{r=2,a=0\}\) and \(a=M\), \( \mathcal {A}=1\). Analogously, in the plane \(r/M-r/M\) the boundaries are the functions \(r_+(r_-)\) and \(r_{-}(r_+)\), that is, \(r_{\pm }(r_{\mp })=-r_{\mp }+2M \). Considering the curves of Eq. (B1) and using \(r_g=r_g(\mathcal {A}_0)\) and \(a_g=a_g(\mathcal {A}_0)\), with the origin spin \(\mathcal {A}_0={2r_{\pm }}/{a_g}\) and \(\mathcal {A}_0={2\sqrt{r_g}}/{\sqrt{2-r_g}}\), we can express the curves in terms of the irreducible mass in [15].
Appendix C: Metric bundle properties
In this section, we summarize the main features of the metric bundles used in this work. We also list the main definitions in Table 2. The bundles frequencies relations We consider special bundle frequency relations by using the following quantities
(Note that here \(s=\omega ^+_-\) as introduced in Sect. 2.3). The value \(s=1/4\) (and then \(s=4\)) is, therefore, a remarkable frequency ratio (note that for a fixed tangent spin \(a_g\), we obtain \(s\le 1\)). We now go back to the frequency analysis, introducing the following “resonance” solutions:
Confinement Confined bundles, with origin in a BH, have tangent spin \(a_g/M\in [0,4/5]\). Specifically,
Appendix D: Black holes in the extended plane: cluster metrics
The previous analysis on quantities evaluated on the metric bundles and the results of [15] on classical BH thermodynamics in the extended plane, motivates us to look for a unique representation of the metric properties in the extended plane. We use NSs to study BHs, following a frame inherent in in \(\mathcal{M}\mathcal{B}\) formalism.
Some aspects of the Kerr solution have been rewritten in the extended plane, studying properties unfolding along all the solutions. Here, we re-consider the line element adapting it to this new frame. We explore the symmetries envisaged in the extended plane to re-define the BHs and NSs metric tensors. We consider clusters of copies of BHs in the extended plane, evaluating the line elements on sections of the extended plane and parametrizing metric bundles characteristics, introducing in the metric tensor \(\mathcal{M}\mathcal{B}\) parameters as cluster parameters. With these re-parametrizations with functions defined in the extended plane, we obtain structures constituted by replicas of the metric tensor describing the same geometries or portions of the same geometry in the extended plane. We describe BH geometries, taking into account the existence of NS solutions in the extended plane and making use of the BH–NS correspondence.
We consider the line element evaluated on the metric bundle in terms of the \(\mathcal{M}\mathcal{B}\) characteristics \(\mathcal {Q}\) such as the origin spin \(a_0\), the tangent radius \(r_g\), and the tangent spin \(a_g\). According to the different evaluations, we describe entire or partial collections of BHs and NSs. Each point (r, a) (or \((r,a,\sigma )\)) of the extended plane corresponds to a geometry or a section, as a specific hyper-plane. By evaluating the tensor \({g}(\cdot ,\cdot )\) along a specific element \(\mathcal {Q}\) of the plane, we obtain a collection of metrics \(\textbf{g}\{\mathcal {Q}\}\). There are different interpretations of the tensors on the extended plane, depending on how we consider the dependence on the new metric parameters. Notably, in some cases, the metric tensors depend on two spin parameters, the origin \(a_0\) and the tangent spin \(a_g\). Then, assuming \(a=a_g(\omega )\), there are two tensors parametrized by the two bundle characteristic frequencies, for \( \omega \in ]1/2,+\infty ]\) and for \( \omega \in [0,1/2[\), respectively, describing one BH geometry (defined by the tangent spin \(a_g\)). In general, we can obtain copies of the same BH geometry, corresponding to different values of the parameters (“BH clusters”). For any metric tensor we consider, in particular, the singular points \(\mathcal {S}_g\) and the limits \(\{\lim \limits _{\mathcal {Q}}\}\) listed in Table 3. In Table 4, the different cases we explore below are summarized. We mainly concentrate on the components \(g_{tt}\), and \( g_{rr}\) of the metric tensor \(g(\cdot ,\cdot )\). This analysis consider the sections of the extended plane of Fig. 17. Following the re-parametrization with \(r={{r}}(\mathcal {Q}_i)\) for a set \(\{\mathcal {Q}_i\}_i\) of parameters, we do not consider the variations \(\partial _{\mathcal {Q}_i} {{r}}(\mathcal {Q}_i)\). Finally, we exclude in this analysis the counterrotating case, i.e., \(\omega <0\) (or \(a_0<0\)), and we use the even term \(\sigma \equiv \sin ^2\theta \).
In some representations we shall distinguish the planes \(\sigma =4/5\) and \(\sigma =1/2\). The metric can describe BH or BHs and NSs. In some cases the BH spin is assumed to be the \(\mathcal{M}\mathcal{B}\)tangent. The metric describes, therefore, the geometry on the horizon curve in the extended plane, and the tensor in the new frame describes only BH solutions. The limiting cases of the Schwarzschild spacetime and the Kerr extreme BH are also recovered.
1.1 D.1 Tensors of the extended planes
Introducing the following quantities
we shall consider in the following points the tensors of Table 4.
(a) Tensor \(\textbf{g}\{a_0,r_g\}\). Setting \(a=a_0={1}/({\sqrt{\sigma } \omega })\) and \(r=r_g={a_g}/{2 \omega }\), the tensor has two spin parameters, the tangent spin \(a_g\in [0,M]\) and the origin spin \(a_0\ge 0\), which is the geometry spin. The tensor describes a collection of BHs and NSs, with spin \(a_0\), on the horizon curve \(r_g\) in the extended plane, when the relation \(r=r_g=a_g/(2 \omega )\) holds (spin \(a_g\), frequency \(\omega \), and \(a_0\sqrt{\sigma }\) are related by the bundles). The metric describes, therefore, the geometry on the horizon curve \(r_g\in [0,2M]\) in the extended plane, with spin equal to the origin bundle spin \(a_0\) parametrized by the plane \(\sigma =\sin ^2\theta \). It should be noted that for every \(a_g\) there are two frequencies and two radii \(r_g\), with the exception of the extreme BH Kerr spacetime. The spacetime with \(a=a_0\) is distinguished by the bundle frequency \(\omega \), which also distinguishes BHs and NSs, fixing also \(a_g\) and \(r_g\) and \(\sigma \). Therefore, \(a_g\) and \(\omega \) are not independent parameters as for any \(\omega \) there is a unique pair \((a_g,r_g)\) and for a fixed \(a_g\) there are two frequencies \(\omega \). Thus, considering \(\sigma \) as a parameter for the origin, we obtain the couple \((a_g, \omega )\). If we set \(\omega \), there is one spin \(a_g\) and two corresponding metric tensors for the two \(\omega \)s, respectively. The metric tensor is explicitlyFootnote 9
The singular points defined in Table 3 are for
(\(\checkmark \) indicates not well-defined quantities). The relation \(r_g(a_g)\) holds on the specific curves of the extended plane. The characteristic bundle frequency is defined by a horizon point in the extended plane. On the other hand, for fixed \(\omega \), the parameter \(a_0\) can be used also to obtain a variation of \(\sigma \). (Then, we can consider the spin \(a_g\) as a free parameter for a new parametrization of \(r_g\ge 0\).). The following limits hold:
see Table 3. In the case \(a_g=0\) (the static spacetime), there is \(r_g=0\), which is the singularity, and it is interesting to note that we can obtain the Schwarzschild metric, considering \(\omega \) independent from \(a_g\). The limits for the characteristic frequency of the bundle are
according to Table 3.
(b) Tensor \(\textbf{g}\{a_{\pm }\}\). With \(a=a_{\pm }= \sqrt{r (2-r)}\), we write the metric tensor \(\textbf{g}(\cdot ,\cdot )\) on the horizon curve in the extended plane \((a>0)\), assuming therefore \(a\in [0,M]\) and describing BHs on the horizons points. The radius r is bounded in the horizon range \(r\in [0,2M]\). However, importantly for any \(r\in [0,2\,M]\) there is one and only one BH geometry with spin \(a\in ]0,M[\). Viceversa, any spin a corresponds to two radii \((r,r_p)\) and for any geometry a(r) there is couple of radii \(r=r_{\pm }\), which are vertical lines of the extended plane. The metric tensor is
The singular points are
(see Table 3 ). The interpretation of the metric follows from the limiting cases:
where \(r_g=0\) is the Schwarzschild singularity, \(r_g=M\) there is the extreme Kerr BH, and \(r_g=2M\) is the horizon in the Schwarzschild spacetime.
\({\textbf {(c) Tensor}} \quad \textbf{g}\{a_g,r_g\}\). We set \(a=a_g=2 r_g \omega \) and \( r=r_g\). The metric tensor is evaluated on the horizon curve \(r_g\) in the extended plane (where \(\textrm{d}r=\textrm{d}r_g\)). It describes BHs spacetimes (\(a=a_g\in [0,M]\)) depending on the bundle characteristic frequency \(\omega \), where the spin parameter a is evaluated on the horizon curve \(a_g\). There are different interpretations for the tensor \(\textbf{g}\{a_g,r_g\}\), depending on the interpretation of the tensor parameters. The terms \(\omega \), \(a_g\), and \(r_g\) are not independent, as \(a_g=2 r_g \omega \) holds only for specific relations between \(r_g\) and \(\omega \). We consider two main interpretations: 1. In the first interpretation we vary \(\omega \) as a free parameter, generating a representation of the spin \(a_g\) dependent on the radius \(r_g\ge 0\) (which has as special cases \(r_g\in [0,2M]\)). This tensor describes Kerr NSs and BHs, where \(r_g=r\) is a free variable of the metric. 2. The second interpretation is a special case of the former one, where \(a=a_g\) and \(r=r_g\); therefore, the tensor describes BHs on the horizon curves. For any spin \(a_g\) there are two characteristic frequencies and radii \(r_g\); therefore, for any geometry there are two metric tensors. Explicitly,
The different interpretations of the metrics become clearer with the analysis of the metric singularities,
where the horizon curve emerges for the solutions of \(g_{rr}^{-1}=0\). The limits for the frequency parameter are (see Table 3)
where the first case, \(\omega =0\), represents, as expected, the Schwarzschild static metric with \( r_g\ge 0\). (Note that in this interpretation the asymptotic limit \(\omega =\infty \) does not correspond to the static limit). Finally, the limiting conditions for the horizon radius in the extended plane \(r_g\) are
according to Table 3.
(d) Tensor \(\textbf{g}\{a_g,r_g\}\). We consider \( a=a_g(r_g)={4 \omega }/({4 \omega ^2+1})\), where \(r=r_g={2}/({4 \omega ^2+1})\); therefore, the metric tensor is evaluated on the horizon curve in the extended plane for the BH geometry with spin \(a=a_g(\omega )\), where \(\omega \) is the horizon frequency. We note that for a fixed \(a_g\in ]0,M[\) there are two frequencies \(\omega =\omega _H^{\pm }\). The metric tensor isFootnote 10
(In this case we have to consider \(\textrm{d}r=-(a_g^2/\omega )\textrm{d}\omega \)). The quantity \(\chi _{\dag }\) is introduced in Eq. (D9), where \({g}_{tt}=0\) for \(\omega =0\). Therefore, for any characteristic frequency there is one couple \((r_g,a_g)\) and the second frequency corresponds to a different \(r=r_g\) with the same spin \(a=a_g\).
Considering the frequency limits, as in Table 3, we obtain
The limit for \(\omega =1/2\) corresponds to the extreme Kerr BH and the Schwarzschild case at the points \((a=0, r=2M)\) and \((a=0, r=0)\).
\({\textbf {(e) Tensor}}\quad \textbf{g}\{a_g\}\). We set \(a=a_g=4 {{\omega }/{\left( 4 \omega ^2+1\right) }}\). In this evaluation, the spin of the geometry is the tangent spin \(a_g\) of the metric bundles to the horizon curve. Therefore, the geometry describes BH solutions. The spin is identified through the characteristic frequency of the bundles \(\omega \). The set \(\textbf{g}\{a_g\}\) is split into two sets, corresponding to the bundles of Eq. (C1) tangent to the inner and outer horizon of a fixed spacetime. A fixed frequency \(\bar{\omega }\) identifies a BH geometry, with metric tensor \(\textbf{g}_{\bar{\omega }}(\cdot ,\cdot )\) with the spin \(\bar{a}=a_g(\bar{\omega })\), and there is the corresponding geometry \(\textbf{g}_{\hat{\omega }}(\cdot ,\cdot )\) defined by the spin \(\hat{a}=a_g(\hat{\omega })=a_g(\bar{\omega })=\bar{a}\). Therefore, the metric tensors \(\textbf{g}_{\bar{\omega }}(\cdot ,\cdot )\) and \(\textbf{g}_{\hat{\omega }}(\cdot ,\cdot )\) describe parts of the same geometry (horizontal line of the extended plane \(a_g\)), one referring to the inner horizon frequency, for \(\omega >1/2\), and all the bundles tangent to the inner horizon \(r_-(a_g)\), differentiating with respect to the plane \(\sigma \) only; and the second set for the outer horizon frequency \(\omega \in ]0,1/2[\). The frequency \(\omega =1/2\) corresponds to the extreme Kerr BH spacetime, where \(\bar{\omega }=\hat{\omega }=1/2\) and the two tensors \(\textbf{g}_{\bar{\omega }}(\cdot ,\cdot )\) and \(\textbf{g}_{\hat{\omega }}(\cdot ,\cdot )\) coincide. There are two limiting cases for the tensor \(\textbf{g}_{\bar{\omega }}(\cdot ,\cdot )\), the Schwarzschild spacetime for \(\omega \rightarrow 0\) and \(\omega \rightarrow +\infty \), the Kerr extreme BH described by condition \(\omega =1/2\).
The metric tensor \({\textbf{g}}_{\omega }(\cdot ,\cdot )\) components are:
According to Table 3, the singular point are
The horizon curve is clearly a metric singularity. The limiting conditions on the metric are (see Table 3 )
and, as expected, for \(\omega =\{0,\infty \}\) we obtain the Schwarzschild metric with \(a_g=0\).
(f) Tensor \(\textbf{g}\{a_g\}\). In this case, the BH spin is assumed to be the tangent spin of the bundle \(a_g= {4 a_0 \sqrt{\sigma }}/({a_0^2 \sigma +4})\) to the horizon in the extended plane. Therefore, the metric tensor describes BHs with \(a_g\in [0,M]\). A metric spin parameter is \(a_0\ge 0\) which is the bundle origin. However, the BH geometry with spin \(a_g\) is described, for different \(\sigma \), by different origins \(a_0\) associated to two frequencies \(\omega =1/(a_0\sqrt{\sigma })\) for the two horizons of the BH with \(a=a_g\), respectively. For each spin \(a_g\), there are two couples \((a_0,\sqrt{\sigma })\), corresponding to the two frequencies \((\omega =1/(a_0\sqrt{\sigma }))\) of the inner and outer horizon. In order to analyze, for a fixed geometry \(a_g\), all planes \(\sigma \in [0,1]\), the origin \(a_0\) must vary. Any value of \(\sigma \) describes a geometry at fixed \(a_0\). Otherwise, fixing \(a_0\) and varying \(\sigma \), we obtain a collection of BH spacetimes.
Explicitly, the metric tensor \(\textbf{g}\{a_g\}\) components are
and the singular points are (see Table 3)
The limits for the bundle origins \(a_0\) are (see Table 3)
Therefore, also in this case for \(a_0=0\) and \(a_0=\infty \) (where \(a_g=0\)), we obtain the Schwarzschild spacetime.
(g) Tensor \(\textbf{g}\{a_g,r_g\}\). The metric tensor \(\textbf{g}({\cdot ,\cdot })\) is evaluated on the horizon curve in the extended plane. In this case, \( a=a_g={4 \mathcal {A}_0}/({\mathcal {A}_0^2 +4})\) and \(r=r_g={2 \mathcal {A}_0^2 }/({\mathcal {A}_0^2 +4})\). The spin parameter \(a=a_g\in [0,M]\) is parameterized with the variable \(\mathcal {A}_0=a_0\sqrt{\sigma }\); therefore, while the metric tensor \(\textbf{g}(\cdot ,\cdot )\) describes BHs, the metric spin parameter varies in the NS range \(\mathcal {A}_0\in [0,\infty [\). Similarly, the radius r is evaluated on the horizon curve \(r_g\in [0,2M]\) as function of its origin \(a_0\) and plane \(\sigma \). Clearly, since \(\mathcal {A}_0=1/\omega \), the metric tensor can be also set in terms of \(\omega \) onlyFootnote 11. Eventually, we can also restrict the analysis to the equatorial plane, where \(\mathcal {A}_0=a_0\) and \(a_0\in [0,2\,M]\) for the inner horizon tangency and \(a_0>2M\) for the outer horizon tangency.
Explicitly, the metric tensor is
Then, \({g}_{tt}=0\) for \( \sigma =0\), and \({g}_{tt}=\infty \) for \( a_0=0\) and \( \sigma =1\). The limiting cases for the origin spin \(a_0\) are (Table 3)
Thus, there are infinite couples \(\{a_0,\sqrt{\sigma }\}\) of two different classes \(\{a_0,\sqrt{\sigma }\}_\pm : \; a_0\sqrt{\sigma }=1/\omega _H^{\pm }\), respectively, describing the same geometry \(a_g\) for different planes \(\sigma \).
(h) Tensor \(\textbf{g}\{r_g,a_g\}\). In this case, \(r=r_g={a_g}/{2 \omega }\), and \(a=a_g\). Therefore, the metric tensor describes BHs \((a\in [0,M])\), where \(r=r_g(a_g,\omega )\in [0,2\,M]\), while \(\omega \in [0,1/2]\) for the outer horizon and \(\omega \in ]1/2,+\infty ]\) for the inner horizon of the geometry. The tensor describes a collection of horizons for BH spacetimes, with restrictions on \(a_g\) and \(\omega \), where the relation \(r=r_g={a_g}/{2 \omega }\) holds. Considering \(\omega \) as free parameter, then \(r\ge 0\) is the radial variable re-parameterized by \(\omega \), not evaluated therefore on the horizon curve. Otherwise, for a spin \(a_g\) there are two frequencies (\(\omega _1,\omega _2)\) and, therefore, two metric tensors. The tensor is
where \(\chi _{\dag }\equiv [1-4(\sigma -1) \omega ^2]\). The singular points for the metric tensors, according to Table 3, are \( \mathcal {S}_g: \left( a_g= -\frac{4 \omega }{\chi _{\dag }}; a_g= 0; a_g= 0; a_g= a_g(\omega ) \right) \) as expected, the horizon curve is a singular point. The limiting conditions for the spin are
and for the frequency we obtain (Table 3)
However, in the limits (D23) and (D22) it has to be considered that the frequencies \(\omega \) and the tangent spin \(a_g\) are not independent. For \(a_g=M\) it is \(\omega =1/2\) and, in general, for fixed \(a_g\) there are two frequencies.
(i) Tensor \(\textbf{g}\{r_g,a_g\}\). In this case, \( a=a_g={2 r_g}/{a_0 \sqrt{\sigma }}\) and \(r=r_g\). Thus, as \(a=a_g\in [0,M]\), the tensor describes BH geometries using NSs with origin spin \(a_0\in [0,\infty ]\). However, this case depends on the plane \(\sigma \). Here we assume \(r_g\in [0,2M]\), being the horizon curve (therefore it should be considered \(\textrm{d}r=\textrm{d}r_g\)). Since \(\omega =1/(a_0 \sqrt{\sigma })\), \(r_g\) and \(\omega \) is not independent, in fact, for each \((a_0 \omega )\) there is one \(r_g\) such that \(a=a_g={2 r_g}/{a_0 \sqrt{\sigma }}\). The tensor is
The singular points are \( \mathcal {S}_g:\bigg ( \bigg \{r_g= \frac{2 a_0^2 \sigma }{ p_{\bullet }(a_0)}\bigg \}; \{r_g= 0\}; \{r_g= 0\}; \{r_g= r_g(\mathcal {A}_0)\} \bigg ) \), see Table 3 – with limits
We note that for \(a=a_0=\infty \), as expected, the tangent point to the horizon curve corresponds to the Schwarzschild geometry where \(r_g=r\). Finally, the limiting conditions on the radius \(r_g\) are
– Table 3.
(l) Tensor \(\textbf{g}\{a_0\}\). Here we assume that the geometry spin is \(a=a_0={1}/({\omega \sqrt{\sigma }})\), the bundle origin. For any plane \(\sigma \) we can consider the properties of a fixed geometry \(a_0\) by varying \(\omega \) and, therefore, the corresponding bundle. The modified metric tensor is
The singular points of the metric are for \(g_{tt}=0\), for \(r= 1\pm {\sqrt{\sigma \omega ^2 \left[ \sigma \left( \omega ^2+1\right) -1\right] }}/{\sigma \omega ^2}\), and \(g_{rr}^{-1}= 0\) for \( r=1\pm \sqrt{ {\left( \sigma \omega ^2-1\right) }/{\sigma \omega ^2}} \). The limiting conditions on the frequencies are
– Table 3. We note that the static case emerges for the asymptotic condition \(\omega \rightarrow \infty \).
(m) Tensor \(\textbf{g}\{a_0,r_g\}\). We set \(a=a_0={2 \sqrt{r_g}}/{\sqrt{\sigma (2 -r_g) }}\) and \(r=r_g\). In this case, the metric has diverse interpretations. We can consider a generic free radial variable \(r\ge 0\) or, viceversa, the tangent radius \(r_g\in [0,2\,M]\) and the origin spin changes for each plane \(\sigma \). The geometry describes BHs and NSs as the spin parameter \(a_0\) is the bundle origin. The metric tensor is
The singular points of the tensor are
The limiting conditions are
(n) Tensor \(\textbf{g}\{a_0\}\). In this case, \( a=a_0={2 \sqrt{r_g}}/ {\sqrt{(2-r_g) \sigma }}\). The metric is parameterized by the spin parameter a, which is the origin \(a_0\) of the bundle in the extended plane, or by \(a_0(r_g,\sigma )\) as function of the tangent radius \(r_g\in [0,2M]\), while the radial variable is \(r\ge 0\). The tensor describes Kerr BHs and NSs, extreme Kerr BH and Schwarzschild BHs.
Then,
The metric singularities are
(Table 3) The limiting conditions on the tangent radius \(r_g\) are
where the limiting condition \(r_g=2M\) corresponds to the static solution.
(o) Tensor \(\textbf{g}\{a_0,r_g\}\). In this evaluation, we consider the spin parameter to be the origin spin \(a=a_0={1}/{\omega \sqrt{\sigma }}\), while we assume \(r=r_g(\omega )\), the tangent radius on the horizon in the extended plane. The metric element depends on the characteristic frequency \(\omega \) and the planeFootnote 12\(\sigma \). The metric describes BHs and NSs, but for every point \(\omega \) a point \(r_g\) on the horizon curve is fixed, while \(a_0\) is fixed by setting \(\sigma \). We stress here that \(r_g\) is independent from \(\sigma \). Fixing \(\omega \), we set a vertical line on the extended plane. For any plane \(\sigma \) we study a different geometry (horizontal line \(a=a_0\)). In each geometry, we consider the radius \(r_g\), which is a horizon point only in one BH spacetime.
Explicitly, the metric tensor components are
The metric singularities are
Table 3. We note the special plane \(\sigma =1/2\). The limits on \(\omega \) give
The first limit constitutes the case of naked singularity \(a_0=\infty \) with horizon \(r_g=2M\). The case \(\omega =\infty \) corresponds to the static and spherically symmetric geometry where \(r_g=2M\). We note also the singular value \(\sigma =4/5\).
(p) Tensor \(\textbf{g}\{a_0,r_g\}\). We set \(a=a_0\) and \(r=r_g={2 a_0^2 \sigma }/({a_0^2 \sigma +4})\). Therefore, \(a_0\in [0,+\infty [\) describes both BHs and NSs, but the metric tensor is evaluated on the curve \(r_g(\mathcal {A}_0)\) of the extended plane as a function of the spin and the plane \(\sigma \). Then, \(r=r_g\in [0,2M]\) is the tangent curve for all \(a_0\) and for all \(\sigma \), describing a set of geometries on the curves \(r_g\), where the spin parameter is the bundle origin. For every geometry \(a_0\) the orbits \(r_g(a_0)\) are described for every \(\sigma \). Thus, the frequency and the tangent spin, which is the bundle frequency \(\omega =1/(a_0\sqrt{\sigma })\), can be evaluated for every \(\sigma \in [0,1]\). Then, the value \(\omega =1/a_0\sqrt{\sigma }\) corresponds to one radius \(r_g\) on the horizon curve. The metric tensor components areFootnote 13
where \(\tilde{s}\equiv \sigma \left[ a_0^4 (\sigma -1) \sigma +4 a_0^2 (\sigma -2)+16\right] -16\). Then, \({g}_{tt}=0\) for \(\sigma \in [{1}/{2},1[\) and \(a_0\equiv \pm 2 \sqrt{{(({\sigma }/{\sqrt{(1-\sigma ) \sigma }})-1)/{\sigma }}})\), and \({g}_{tt}=\infty \) for \((\sigma =1, a_0=0)\), and \({g}_{rr}=\infty \) on the equatorial plane for \((a_0=0,\sigma =1)\). The limits for origin spins \(a_0\), according to Table 3, are
(q) Tensor \(\textbf{g}\{a_g,r_g\}\). Here we consider \(a=a_g={4 a_0 \sqrt{\sigma }}/({a_0^2 \sigma +4})\in [0,1]\) and \(r=r_g={2}/({4 \omega ^2+1})\in [0,2]\). The tensor is associated to BH geometries with the spin parameter \(a_0\) for NSs. The radius is evaluated along the curve \(r_g(\omega )\); consequently, in any spacetime for any value of \(\omega \), it is \(r=r_g(\bar{\omega })\in [0,2M]\). However, \(a_g\) is not independent from \(r_g\) as \(\omega =1/(a_0\sqrt{\sigma })\) for any \(\sigma \) and for any \(a_g\) there are two values of \(r_g\) corresponding to two horizons. Alternatively, if we consider a and r as independent, we can take \(r\ge 0\) for the fixed \((a_0,\sqrt{\sigma })\). By making explicit the dependence from \(\sigma \), we consider \(\sigma \) as a metric parameter and, therefore, at fixed spacetime \(a=a_g\), we can consider all planes \(\sigma \in [0,1]\) varying \(a_0\).
Explicitly, the tensor isFootnote 14:
where \(\tilde{y}\equiv \left[ \frac{1}{\left( 4 \omega ^2+1\right) ^2}-\frac{4 a_0^2 (\sigma -1) \sigma }{\left( a_0^2 \sigma +4\right) ^2}\right] \). Then,
There is a singularity at the origin \(a_0\), corresponding to \(r=0\).
The limits for the origins are
where
(see Table 3). The first and the last limit, \(a_0=0\) and \(a_0=\infty \), lead to the static case of the Schwarzschild geometry where \(a_g=0\), as the tangent point to the horizon on the point is \(r=r_g=2M\).
The limiting conditions for the frequencies are
with
In the following cases, we shall consider the metric tensor \(\textbf{g}(\cdot ,\cdot )\), on the curves of Eq. (B1) and on the metric bundle curve on the equatorial plane.
(r) Tensor \(\textbf{g}\{{{\textbf {()}}}_2\}\). For \(r={a \mathcal {A}_0}/{2}\), we consider the metric tensor on the curve \({{\textbf {()}}}_2\) of Eq. (B1). In this case, the variable r is interpreted as a radius on the extended plane and the two spins, a and \(\mathcal {A}_0=a_0 \sqrt{\sigma }\), as parameters. The tensor describes BHs and NSs on particular pointsFootnote 15 determined by \(r={a \mathcal {A}_0}/{2}\). This holds for \(r=r_g\) and \(a=a_g\); thus, it is clear that at fixed a we can always consider r as re-parameterized with a variable \(\mathcal {A}_0\), eventually interpreted as independent from \(\theta \), and the plane \(\sigma \) as a free parameter. Therefore, we explore BH geometries (\(a_g\in [0,M]\)) using NSs \(\mathcal {A}_0\ge 0\). These relations, however, do not fix the spins \((a,\mathcal {A}_0)\), which are not independent since for fixed \(a=a_g\) there are two radii \(r_g\) and two values of \(\mathcal {A}_0\).
Explicitly, the tensor is
It is interesting to note the singular points
which include the origin \(r=0\) and the horizon curve, interpreted as the collection of tangent curves of the bundles – Table 3. The limits are
and
(s) Tensor \(\textbf{g}\{{{\textbf {()}}}_1\}\). For \(r=2\left( 1-{a}/{\mathcal {A}_0}\right) \), we consider the metric tensor on the curve \({{\textbf {()}}}_1\) fromFootnote 16 of Eq. (B1). Then, \(a\ge 0\) while \(\mathcal {A}_0\) is the origin parameter and \(r=r(a)\ge 0\) at fixed \(\mathcal {A}_0>a\). The geometry described by the metric is defined by the spin a; consequently, in order to vary r the bundles origin have to be varied.
The tensor is
The singular points are
There is a singularity at \(a=a_g\) – Table 3. The limits are
In this case, we assumed \(a=a_g\in [0,M]\), which describes BHs in the extended plane. Other limits are
(t) Tensor \(\textbf{g}\{{{\textbf {()}}}_2\}\). Considering curve \({{\textbf {()}}}_2\) we assume \( a={2 r}/{\mathcal {A}_0}\). In this case, we have a different metric spin a(r) for any radius r; we consider geometries along the horizon curve on the extended plane. Thus, we can change the origin \(\mathcal {A}_0\equiv a_0\sqrt{\sigma }\) in order to consider, for any a(r), all the values of the poloidal angle. Then,
The tensor singularities are \( \mathcal {S}_{g}: \Big (r= \frac{\mathcal {A}_0}{2 c_{\bullet }}; r= 0; r= 0; r=r_g \Big ) \). The the central singularity is at \(r=0\) and the horizon curves – Table 3. The limit conditions lead to
Note that the Schwarzschild metric is for the limit \(\mathcal {A}_0=a_0\sqrt{\sigma }=+\infty \), while the static geometry does not correspond to the limit \(\mathcal {A}_0=0\).
(u) Tensor \(\textbf{g}\{{{\textbf {()}}}_1\}\). Setting \(a=\mathcal {A}_0\left( 1-{r}/{2}\right) \), the metric spin \(a\ge 0\) is function of the origin spin \(\mathcal {A}_0=a_0\sqrt{\sigma }\). The tensor is related for each r to a different geometry and, therefore, to a collection of sections of different geometries for different origins \(\mathcal {A}_0\). For convenience, a parameter can be understood as a variable per-plane, so that it can be considered as independent from the polar angle and r, where \(a=\mathcal {A}_0\) for \( r=0\). For \(r=2M\) we obtain the Schwarzschild spacetime. This metric, however, describes points of BHs and NSs.
The metric tensor is
where
The singular points, according to Table 3, are
We note the role of the ergoregion \(r=r_{\epsilon }^+=2M\) and of the horizon \(r=r_g\) in the extended plane. The limiting conditions on the origin \(\mathcal {A}_0\) are
For \(\mathcal {A}_0=0\) we obtain the Schwarzschild geometry, while for \(\mathcal {A}_0=\infty \) the tensor describes a limiting case of NSs.
(v) Tensor \(\textbf{g}\{a_{\omega }^\pm \}\). We now consider the metric tensor on the metric bundles, curves \(a_{\omega }^\pm \) of the extended plane, on the equatorial plane \(\sigma =1\). The metric \(\textbf{g}(\cdot ,\cdot )\) provides a collections of points (a, r), for fixed frequency \(\omega \), where \(a=a_{\omega }^\pm (\omega ,r)\). Thus, at fixed characteristic frequency \(\omega \) of the bundle, we obtain the points \((a,r,\theta ,\phi )\), including the horizons points. Any point \(({r},\omega )\) describes a different geometry (excluding the case of replicas and considering negative frequencies). For fixed r, by varying the characteristic frequency, i.e., the metric bundle, we analyze the properties of the metric tensor on the vertical lines of the extended plane for different spins. For fixed frequencies, i.e., for fixed bundles, by varying r we analyze the properties of the point (a, r) in the extended plane.
Explicitly, the tensor is
The singular points of the metric are
see Table 3 – which shows the presence of metric singularities for \(r=r_{\epsilon }^+\) and on the horizon \(r_g\) in the extended plane. The limits are
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Pugliese, D., Quevedo, H. On black hole surface gravity. Eur. Phys. J. C 83, 370 (2023). https://doi.org/10.1140/epjc/s10052-023-11345-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-11345-w