Lower bound on the time-to-mass ratio of closed circular motions around spinning and charged naked singularities

Abstract

It has recently been conjectured that circular trajectories (geodesic as well as non-geodesic) around central compact objects are characterized by the time-to-mass universal lower bound $T_{\infty }/M>{{\mathcal {C}}}$, where $\{T_{\infty },M\}$ are respectively the orbital period as measured by flat-space asymptotic observers and the mass of the central compact object, and $\mathcal{C}=O(1)$ is a dimensionless constant of order unity. In the present paper we prove that this dimensionless bound is respected by circular orbits around central naked singularities. Intriguingly, it is explicitly proved that the orbital-time-to-mass ratio $T_{\infty }/M$ around a central super-spinning singularity remains finite even in the $r\rightarrow 0$ limit of circular orbits with infinitesimally small radial coordinates (which are characterized by a diverging time-to-radius ratio, $T_{\infty }/r\rightarrow \infty$). In particular, we reveal the fact that the shortest orbital period around a super-spinning naked singularity is given by the dimensionless relation $T_{\infty }/M=2\pi$. In addition, we explore the functional behavior of the time-to-mass ratio of circular trajectories around super-charged (non-vacuum) naked singularities and prove that the dimensionless ratio $T_{\infty }/M(r)$ is bounded from below, where M(r) is the gravitational mass contained within the orbital radius of the test particle.

1 Introduction

The orbital motions of test particles in curved spacetimes provide valuable information on the physical properties of highly compact objects. Hence, the motions of particles in curved spacetimes of black holes and horizonless naked singularities have been extensively studied by physicists and mathematicians within the framework of general relativity during the last five decades (see [1,2,3] and references therein).

A physical quantity of particular importance for the analysis of circular trajectories of test particles in curved spacetimes is the orbital period $T_{\infty }$ of the particle as measured by asymptotic observers. One may expect the orbital period $T_{\infty }$ of a test particle around a central compact object to be bounded from below by a fundamental lower bound which is of the order of the mass M of the central object (we use gravitational units with $G=c=1$, in which case time and mass have units of length) [4].

In particular, using a naive analysis that ignores red-shift effects (the gravitational time dilation effect) and frame-dragging effects in rotating curved spacetimes (below we shall analyze in detail these physically important effects), one deduces that the orbital period around a central compact object of radius R is expected to be bounded from below by the simple dimensionless relation $T_{\infty }/R\ge 2\pi$. In addition, in curved spacetimes with no naked singularities the characteristic radius of the central compact object is bounded from below by its mass, $R > rsim M$. Thus, the minimally allowed orbital period around a central compact object in spacetimes with no naked singularities (that is, in spacetimes in which the radii of compact objects are bounded from below by the simple relation $R > rsim M$) is expected to be bounded from below by a dimensionless relation of the form

$$\begin{aligned} \left( {{T_{\infty }}\over {M}}\right) _{\text {min}} > rsim 2\pi . \end{aligned}$$

(1)

Interestingly, it has recently been proved [4] that, among all possible trajectories (both geodesic and non-geodesic) that circle a central black hole, the co-rotating equatorial null circular geodesic determines the shortest possible orbital period $T_{\infty }$ as measured by flat-space asymptotic observers [4] (see also the physically interesting work [5]). In particular, it has been proved [4] that, among all spinning Kerr black holes of mass M, the maximally rotating (extremal) black hole is characterized by the smallest dimensionless orbital-time-to-mass ratio¹:

$$\begin{aligned} \left( {{T_{\infty }}\over {M}}\right) _{\text {min}}=4\pi \ \ \ \ \ \text {for extremal Kerr black holes}. \end{aligned}$$

(2)

It is important to emphasize that the suggested lower bound (1) on the dimensionless orbital-time-to-mass ratio is based on the above mentioned assumption that the curved spacetime contains no naked singularities, in which case the radius of the central compact object is bounded from below by the simple dimensionless relation $R/M > rsim 1$.

In the present compact paper we raise the following physically interesting question: Is there a fundamental lower bound on the time-to-mass ratio of orbital motions around naked singularities?

In order to address this important question, in the present paper we shall study the orbital motions of test particles around super-spinning and super-charged naked singularities. Interestingly, below we shall explicitly prove that the orbital motions of test particles around naked singularities are characterized by a dimensionless time-to-mass lower bound.

2 Circular trajectories around super-spinning Kerr naked singularities

In the present section we shall analyze the two-dimensional functional behavior of the orbital period $T_{\infty }(r,a)$ around rotating Kerr naked singularities.² Using the Boyer–Lindquist spacetime coordinates, the Kerr naked singularity is described by the curved line element [2, 3, 6]

$$\begin{aligned} ds^2= & {} -\left( 1-{{2Mr}\over {\rho ^2}}\right) dt^2-{{4Mar\sin ^2\theta }\over {\rho ^2}}dt d\phi \nonumber \\ {}{} & {} +{{\rho ^2}\over {\Delta }}dr^2 +\rho ^2d\theta ^2\nonumber \\ {}{} & {} +\left( r^2+a^2+{{2Ma^2r\sin ^2\theta }\over {\rho ^2}}\right) \sin ^2\theta d\phi ^2, \end{aligned}$$

(3)

where the physical parameters M and $J\equiv Ma$ are respectively the mass and angular momentum of the spacetime. The metric functions in (3) are given by the spatially-dependent expressions

$$\begin{aligned} \Delta \equiv r^2-2Mr+a^2; \quad \rho ^2\equiv r^2+a^2\cos ^2\theta . \end{aligned}$$

(4)

Note that an horizonless super-spinning naked singularity is characterized by the dimensionless spin-to-mass ratio³

$$\begin{aligned} {{a}\over {M}}>1. \end{aligned}$$

(5)

We consider test particles that move along circular trajectories in the equatorial plane ($\theta =\pi /2$) of the Kerr naked singularity (3). Our goal is to determine the shortest possible orbital period around the central singularity as measured by asymptotic observers. We shall therefore consider test particles that move as close as possible to the speed of light,⁴$^{,}$⁵ in which case the radius and spin dependent orbital period $T_{\infty }(r;M,a)$ as measured by asymptotic observers can be obtained from the curved line element (3) with the properties⁶

$$\begin{aligned} ds=dr=d\theta =0\quad \text {and}\quad \Delta \phi =\pm 2\pi . \end{aligned}$$

(6)

In particular, substituting (6) into (3), one finds the functional relation

$$\begin{aligned} T_{\infty }(r;M,a)=2\pi \cdot {{\sqrt{\Delta }\mp {{2Ma}\over {r}}}\over {1-{{2M}\over {r}}}}\ \end{aligned}$$

(7)

for the orbital period as measured by asymptotic observers, where the upper/lower signs in the functional expression (7) correspond respectively to co-rotating/counter-rotating trajectories around the central singularity.⁷

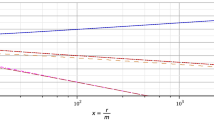
Intriguingly, taking cognizance of the functional relation (7) one deduces that, for co-rotating orbits, the time-to-mass ratio $T_{\infty }/M$, which characterizes the circular trajectories around the central super-spinning singularity (3), remains finite even in the $r\rightarrow 0$ limit of infinitesimally small radii (in which case the circular orbits are characterized by a diverging time-to-radius ratio, $T_{\infty }/r\rightarrow \infty$ ).

In particular, from Eq. (7) one finds the limiting functional behavior

$$\begin{aligned}{} & {} T_{\infty }(r\rightarrow 0;M,a) \nonumber \\ {}{} & {} \quad =2\pi \cdot \Big [a+{{r^2}\over {2a}}+O\Big ({{Mr^3}\over {a^3}}\Big )\Big ]\ \ \ \ \text {for}\ \ \ \ r\rightarrow 0 \end{aligned}$$

(8)

for co-rotating circular trajectories in the small radii $r\rightarrow 0$ regime. From Eqs. (5) and (8) one obtains the dimensionless lower bound

$$\begin{aligned} {{T_{\infty }}\over {M}}>2\pi \ \ \ \ \text {for}\ \ \ \ r\rightarrow 0 \end{aligned}$$

(9)

on the orbital-time-to-mass ratio in the $r\rightarrow 0$ limit.

Taking cognizance of Eqs. (5) and (7) one finds that, for a given value r of the radial coordinate that characterizes the closed trajectory around the central singularity, the orbital period $T_{\infty }(a;r)$ of a co-rotating trajectory as measured by asymptotic observers has a minimum for the dimensionless spin ratio⁸

$$\begin{aligned} \Big ({{a}\over {M}}\Big )_{\text {min}}=\text {max}\left\{ \sqrt{{{4r}\over {r+2M}}},1^{+}\right\} \ . \end{aligned}$$

(10)

Substituting Eq. (10) into Eq. (7), one obtains the dimensionless functional expressions

$$\begin{aligned} T_{\infty }=2\pi \cdot \sqrt{r(r+2M)}\ \ \ \ \text {for}\ \ \ \ \ r>{2\over 3}M\ \end{aligned}$$

(11)

and

$$\begin{aligned} T_{\infty }=2\pi \cdot {{r-M-{{2M^2}\over {r}}}\over {1-{{2M}\over {r}}}}\ \ \ \ \text {for}\ \ \ \ \ r\le {2\over 3}M\ \end{aligned}$$

(12)

for the radius-dependent shortest possible orbital period around the central spinning singularity. The radially-dependent expressions on the r.h.s of (11) and (12) are monotonically increasing functions of the radial coordinate r. This fact implies that the orbital period is minimized in the $r\rightarrow 0$ limit to yield the finite dimensionless time-to-mass ratio

$$\begin{aligned} \left( {{T_{\infty }}\over {M}}\right) _{\text {min}}\rightarrow (2\pi )^{+}\ \ \text {for} \ \ \{a/M\rightarrow 1^{+} \ \ \text {and}\ \ r\rightarrow 0\}\quad \end{aligned}$$

(13)

for the shortest possible orbital period around the central super-spinning Kerr naked singularity.

3 Circular trajectories around super-charged (non-vacuum) naked singularities

In the present section we shall analyze the two-dimensional functional behavior of the orbital period $T_{\infty }(r,Q)$ around super-charged (non-vacuum) naked singularities.⁹ The charged Reissner–Nordström naked singularity is characterized by the curved line element [2, 3]

$$\begin{aligned} ds^2= & {} -\Big (1-{{2M}\over {r}}+{{Q^2}\over {r^2}}\Big )dt^2+\Big (1-{{2M}\over {r}}+{{Q^2}\over {r^2}}\Big )^{-1}dr^2 \nonumber \\ {}{} & {} +r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2, \end{aligned}$$

(14)

where the physical parameters M and Q are respectively the total mass and electric charge of the spacetime. Note that an horizonless naked singularity is characterized by the dimensionless super-critical charge-to-mass ratio¹⁰

$$\begin{aligned} {{Q}\over {M}}>1. \end{aligned}$$

(15)

Since our goal is to determine the shortest possible orbital period around the central charged singularity, we shall consider test particles whose velocities are as close as possible to the speed of light $^4$, in which case the orbital period around the central singularity can be obtained from the curved line element (14) with the properties $ds=dr=d\theta =0$ and $\Delta \phi =\pm 2\pi$¹¹:

$$\begin{aligned} T(r;M,Q)={{2\pi r}\over {\sqrt{1-{{2M}\over {r}}+{{Q^2}\over {r^2}}}}}. \end{aligned}$$

(16)

The radius-dependent electromagnetic energy density associated with an electric charge Q is given by the expression $T^0_0=Q^2/8\pi r^4$ [7]. Thus, the electromagnetic energy $E_{\text {elec}}(r)=\int ^{\infty }_{r}T^0_0 4\pi r^2dr$ outside a charged sphere of radius r is given by the expression

$$\begin{aligned} E^{\text {outside}}_{\text {elec}}(r)={{Q^2}\over {2r}}, \end{aligned}$$

(17)

which implies that the gravitational mass M(r) contained within a sphere of radius r is given by the relation

$$\begin{aligned} M(r)=M-{{Q^2}\over {2r}}. \end{aligned}$$

(18)

We shall now address the following physically interesting question: Is the orbital period around a super-charged central singularity is bounded from below by a function of the mass parameter M(r),¹² [8,9,10,11,12,13,14]?

We first point out that Eq. (18) yields the simple inequalities

$$\begin{aligned} T_{\infty }>0>M(r)\ \ \ \ \text {for}\ \ \ \ r<{{Q^2}\over {2M}}. \end{aligned}$$

(19)

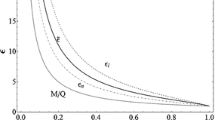
It is therefore physically interesting to analyze the functional behavior of the dimensionless orbital-time-to-mass ratio $T_{\infty }/M(r)$ of circular trajectories in the complementary regime

$$\begin{aligned} r\ge {{Q^2}\over {2M}}\ \end{aligned}$$

(20)

which, taking cognizance of the characteristic inequality (15) for super-charged naked singularities, yields the relation

$$\begin{aligned} r>{1\over 2}M. \end{aligned}$$

(21)

From Eqs. (15), (16) and (18) one deduces that, for a given value r of the radial coordinate that characterizes the closed orbital motion around the central super-charged naked singularity (14), the dimensionless time-to-mass ratio ${{T_{\infty }}/{M(r)}}$, which is given by the functional expression

$$\begin{aligned} {{T_{\infty }}\over {M(r)}}={{2\pi r}\over {\sqrt{1-{{2M}\over {r}}+{{Q^2}\over {r^2}}}\cdot \Big (M-{{Q^2}\over {2r}}\Big )}}, \end{aligned}$$

(22)

has a minimum for the dimensionless charge parameter¹³$^{,}$¹⁴

$$\begin{aligned} \Big ({{Q}\over {M}}\Big )_{\text {min}}= \text {max}\left\{ \sqrt{{{2r(1-r/3M)}\over {M}}},1^{+}\right\} \ \ \ \ \text {for}\ \ \ \ r\le 3M. \end{aligned}$$

(23)

Substituting (23) into Eq. (22), one obtains the dimensionless functional expressions

$$\begin{aligned}{} & {} {{T_{\infty }}\over {M(r)}}=2\pi \cdot 3\sqrt{3}\ \ \ \ \ \nonumber \\{} & {} \quad \text {for}\ \ \ \ \ {{r}\over {M}}\in \left( {{3-\sqrt{3}}\over {2}},{{3+\sqrt{3}}\over {2}}\right) \end{aligned}$$

(24)

and¹⁵

$$\begin{aligned}{} & {} {{T_{\infty }}\over {M(r)}}=2\pi \cdot {{r}\over {M\big |1-{{M}\over {r}}\big |\cdot \big (1-{{M}\over {2r}}\big )}}\ \ \ \ \ \nonumber \\{} & {} \quad \text {for}\ \ \ \left\{ {{r}\over {M}}\in \left( {1\over 2},{{3-\sqrt{3}}\over {2}}\right] \ \ \text {or}\ \ {{r}\over {M}}\in \left[ {{3+\sqrt{3}}\over {2}},3\right] \right\} .\nonumber \\ \end{aligned}$$

(25)

From Eqs. (24) and (25) one deduces that circular trajectories around the central super-charged naked singularity (14) in the entire radial interval ${{r}\over {M}}\in ({{3-\sqrt{3}}\over {2}},{{3+\sqrt{3}}\over {2}})$ [with the corresponding relation (23) for the electric charge of the central singularity] are characterized by the finite dimensionless ratio

$$\begin{aligned} \Big [{{T_{\infty }}\over {M(r)}}\Big ]_{\text {min}}=6\sqrt{3}\pi \ \end{aligned}$$

(26)

for

$$\begin{aligned} {{r}\over {M}}\in \Big ({{3-\sqrt{3}}\over {2}},{{3+\sqrt{3}}\over {2}}\Big )\ \ \ \text {with}\ \ \ {{Q}\over {M}}= \sqrt{{{2r(1-r/3M)}\over {M}}}. \end{aligned}$$

(27)

The analytically derived dimensionless relation (26) determines the smallest possible orbital-time-to-mass ratio for circular trajectories around the central super-charged naked singularity.

4 Summary

Motivated by the conjectured lower bound (1) on the dimensionless time-to-mass ratio that characterizes closed orbital motions of test particles around massive compact objects, in the present compact paper we have studied, using analytical techniques, the physical and mathematical properties of circular trajectories around central naked singularities.¹⁶

Interestingly, we have proved that the time-to-mass ratio $T_{\infty }/M$ of an orbital motion around a super-spinning naked singularity is finite (bounded from below) even in the $r\rightarrow 0$ limit of infinitesimally small radii (in which case the circular orbits are characterized by the diverging time-to-radius dimensionless relation $T_{\infty }/r\rightarrow \infty$). In particular, it has been proved that the orbital periods of circular motions around super-spinning naked singularities are characterized by the lower bound [see Eq. (13)]

$$\begin{aligned} T_{\infty }>2\pi \cdot M\ \ \ \ \ \text {for super-spinning naked singularities}. \end{aligned}$$

(28)

In addition, we have explored the functional behavior of the time-to-mass ratio for orbital motions of test particles around super-charged (non-vacuum) naked singularities and revealed the fact that the orbital period $T_{\infty }$ is bounded from below by the gravitational mass contained within the orbital radius of the test particle. In particular, we have proved that orbital periods around super-charged naked singularities are characterized by the inequality [see Eqs. (19) and (26)]

$$\begin{aligned} T_{\infty }\ge 6\sqrt{3}\pi \cdot M(r)\ \ \ \text {for super-charged naked singularities}. \end{aligned}$$

(29)

Finally, we would like to note that the time-to-mass lower bounds discussed in the present paper may be of observational importance in future detectors. In particular, far away observers who measure the orbital periods of test bodies around central compact objects may in principle use the analytically derived relations (28) and (29) in order to derive upper bounds on the masses of the observed compact objects [15].