1 Introduction

Mazur and Motola first proposed the notion of a gravitational vacuum star (gravastar) as an alternative to the black hole [1, 2]. In other words, gravastars are free of any kind of singularity. The gravastar consists of three regions as follows [3,4,5,6,7,8,9,10,11,12]. The interior region (\(0<r<r_{1}\)) has a vacuum explain by the dark energy, with equation of state (EOS) \(p=-\rho \). Shell region (\(r_{1}<r<r_{2} \)) consists of ultra-stiff perfect fluid with EoS \(p=\rho \) that first reported, by Zeldovich and Novikov in context of cosmology [13, 14]. The exterior region (\(r>r_{2}\)) is a vacuum region with EOS \(p=0\) which can be described by Schwarzschild, Kerr and Kerr–Neumann, Reissner–Nordström metrics as requested under the situation. Commonly described the Schwarzschild [15, 16] and Reissner–Nordström metric [17, 18] depending the gravastar is charged and rotating or not.

In 1992, Bãnados, Teitelboim, and Zanelli proposed a new black hole solution by considering three-dimensional gravity with negative cosmological constant [19]. The existence of such black holes, generally called BTZ black holes. Also, in subsequent works [20, 21], the three-dimensional black holes were seriously investigated, particularly in the context of the anti-de Sitter (AdS)/conformal field theory (CFT) correspondence (or AdS/CFT correspondence) [22]. Indeed the study of BTZ black holes is beneficial to comprehension gravitational interactions in low-dimensional spacetime [23]. In this regard, some interesting works on three-dimensional black holes have been perused in Refs. [24,25,26,27,28,29,30].

Notably, when faced with the computational and conceptual challenges of quantum gravity, one is compelled to find simple models to overcome these significant challenges; ideally, ones that preserve some of the original conceptual complexities while simplifying the computational effort. An example of such a model is general relativity (GR) in \(\mathbf {2+1-}\) dimensions. Spacetime geometry in \(\mathbf {2+1-}\) dimensions shares many fundamental issues with theories in \(\mathbf {3+1-}\) dimensions, which is an excellent laboratory for many theoretical approaches. In addition, fundamental physics, especially field theories in \(\mathbf {2+1-}\) dimensions such as quantum hall effect, cosmic topology, parity violation, cosmic strings, and induced masses enjoy curious properties which invite dedicated studies [31,32,33,34,35,36,37,38]. On the other hand, it has been shown that the classical black holes (such as BTZ black holes) cannot exist in de Sitter spacetime [39]. So, we consider the AdS case for gravastars in \(\mathbf {2+1-}\) dimensional spacetime.

Magueijo and Smolin [40] obtained the gravity’s rainbow which is the generalization of doubly special relativity for curved spacetimes. The gravity’s rainbow produces a rectification to the spacetime that becomes substantial as soon as the particle’s energy–momentum approaches the Planck energy. So that in this formalism, connectivity and curvature are related to the energy. In fact, in the gravity’s rainbow, the gravitational effects, in addition toas well as a possible explanation for the absence of black holes at the LHC creating curvature in spacetime, create different effects those are proportional to different wavelengths in the structure of spacetime. Thus gravity’s rainbow is a falsification of spacetime defined by two arbitrary functions \(L(\varepsilon )\) and \( H(\varepsilon )\) (they are called the rainbow functions). This theory could provide a solution for information paradox [41, 42], the existence of remains for black holes after vaporization [43], as well as a possible explanation for the absence of black holes at the LHC [44]. In astrophysical point of view, it has been shown that the maximum mass of neutron stars can be more than three times the mass of Sun [45, 46]. Indeed the mass of neutron stars is an increasing function of rainbow functions [45,46,47]. In the context of gravity, it has been pointed out that by considering appropriate scaling for the energy functions, the Horava-Lifshitz gravity can be related to the gravity’s rainbow [48]. In the context of black holes, various studies focusing on the effects of gravity’s rainbow on the thermodynamics of black holes have been made in Refs. [49,50,51,52,53,54]. Also, it has been shown that the second law of thermodynamics and cosmic censorship surmise are refracted owing to the rainbow effect [55]. The rainbow functions have a very considerable effect on the information flux of black holes [56]. Alencar et al. [57], studied the influence of gravity’s rainbow on the global Casimir effect around a static small black hole at zero and the finite temperature. In addition, combination of gravity’s rainbow with modified theories of gravity such as F(R) and F(T) theories [58,59,60,61], Rastall gravity [62], massive gravity [63], dilaton gravity [64], have been also made. In the context of cosmology, attention of gravity’s rainbow could dispel the big bang singularity [65,66,67]. In addition, the primary singularity problem [68] and stability of Einstein’s static universe in gravity’s rainbow have been investigated [69].

In order to detect a non-singular replaced to BTZ black holes, it is necessary to explore gravastars in three-dimensional spacetime. Usmani et al. [70] have presented a new model of a gravastar admitting conformal motion which includes a charged interior for four-dimensional spacetime. Their exterior has been discussed by a Reissner–Nordström line element instead of Schwarzschild one. The gravastar model in higher dimensional spacetime defined in Refs. [18, 71, 72]. Later Rahaman et al. [73] have designed an uncharged gravastar in three-dimensional AdS spacetime. The exterior region of this gravastar corresponds to the outer three-dimensional AdS spacetime of BTZ black holes. Then, they extended the gravastar in three-dimensional AdS spacetime by adding the electrical charge [74]. Other works on the (un)charged gravastar models with their physical features have been studied in Refs. [12, 75,76,77,78,79,80,81,82,83,84,85,86]. Also, many gravastars have been studied in the framework of modified theories of gravity. For example, the gravastar solution in the f(R, T) gravity model has been evaluated in Refs. [87,88,89]. The gravastar solution in f(G, T) gravity model has been analyzed in [90]. The structure of a gravastar admitting conformal motion for a specific model of energy–momentum squared gravity has been studied in Ref. [91]. Isotropic static spherically symmetric uncharged gravastars under the framework of braneworld gravity by using the metric potential of Kuchowicz type have been found in Ref. [92]. Ghosh et al. [93] extracted the gravastar solutions in Rastall gravity. Considering F(R, G) theory of gravity, the gravastar model has been evaluated in Ref. [94]. Debnath has discussed the geometry of the four-dimensional charged gravastar model in Rastall-gravity’s rainbow [95].

The basic motivation of the work is to study the gravastar in three-dimensional AdS spacetime, both charged and uncharged states, in the context of gravity’s rainbow theory with the isotropic fluid. Also, we research the nature of physical parameters and study the stability of thin-shell gravastars for three-dimensional (un)charged AdS in this theory of gravity. In this regard, the general formalism of gravity’s rainbow by using the deformation of the standard energy–momentum relation, could be obtained

$$\begin{aligned} E^{2}L^{2}(\varepsilon )-p^{2}H^{2}(\varepsilon )=\mu ^{2}, \end{aligned}$$
(1)

where \(\varepsilon =\frac{E}{E_{p}}\). Here p, E, \(\mu \) and \(E_{p}= \sqrt{\frac{\hbar c^{5}}{G}}\) are the momentum, energy, mass of a test particle and Planck energy, respectively. Also, \(L(\varepsilon )\) and \( H(\varepsilon )\) are called the rainbow functions. It is significant that there are three known cases for the rainbow function;

  • The first is related to the hard spectra caused gamma-ray bursts [96], with the form

    $$ \begin{aligned} L(\varepsilon )=\frac{e^{\beta \varepsilon }-1}{\beta \varepsilon } \quad \& \quad H(\varepsilon )=1. \end{aligned}$$
    (2)

  • The second set of rainbow functions comes from considering the constancy of the velocity of light [97],

    $$\begin{aligned} L(\varepsilon )=H(\varepsilon )=\frac{1}{1-\lambda \varepsilon }. \end{aligned}$$
    (3)

  • The third is motivated by studying the conducted in loop quantum gravity and noncommutative geometry as [98, 99]

    $$ \begin{aligned} L(\varepsilon )=1\quad \& \quad H(\varepsilon )=\sqrt{1-\eta \varepsilon ^{n}}, \end{aligned}$$
    (4)

    where \(\beta \), \(\lambda \), \(\eta \) and n are constants those can be adjusted by experiment. It is notable that at low energy levels, the rainbow functions satisfy the following relations,

    $$ \begin{aligned} \lim _{\varepsilon \longrightarrow 0}L(\varepsilon )=1 \quad \& \quad \lim _{\varepsilon \longrightarrow 0}H(\varepsilon )=1. \end{aligned}$$
    (5)

The following recipe can be used to build an energy dependent spacetime,

$$\begin{aligned} {\widehat{g}}(\varepsilon )=\eta ^{ab}e_{a}(\varepsilon )\otimes e_{b}(\varepsilon ), \end{aligned}$$
(6)

where \(e_{0}(\varepsilon )=\frac{1}{L(\varepsilon )}{\widetilde{e}}_{0}\) and \( e_{i}(\varepsilon )=\frac{1}{H(\varepsilon )}{\widetilde{e}}_{i}\). Also, \( {\widetilde{e}}_{0}\) and \({\widetilde{e}}_{i}\) being the energy independent frame fields. Considering Eq. (6), we obtain a three-dimensional spacetime describing the interior spacetime of a compact object model in gravity’s rainbow as

$$\begin{aligned} {ds}^{2}=\frac{f(r)}{L^{2}(\varepsilon )}{dt}^{2}-\frac{1}{H^{2}(\varepsilon )}\left( \frac{{dr}^{2}}{g(r)}+r^{2}{d\theta }^{2}\right) , \end{aligned}$$
(7)

where f(r) and g(r) are functions of r. Also, \(L(\varepsilon )\) and \( H(\varepsilon )\) depend on \(\varepsilon =E/E_{p}\). By considering that the metric coefficients are dependent on the energy of the test particle, the spacetime geometry becomes energy dependent.

The structure of present work is as follows; in Sect. 2, we deal with the geometry of uncharged gravastar, and also we calculate the solutions in the three regions of gravastar. Also in this section, we analyze the physical aspects of the gravastar model parametersl. Section 3 studies the geometry of the charged gravastar, where the solutions of the all regions of the charged gravastar are calculated. Then we examine the physical aspects of the parameters of charged gravastar model. Section 4 investigates the matching of thin shell gravastars’ interior and exterior regions for three-dimensional uncharged and charged AdS in gravity’s rainbow. In Sect. 4.2 we study the stability of thin shell gravastars. Finally, some conclusions are drawn in Sect. 5.

2 Three-dimensional uncharged gravastars in gravity’s rainbow

In this section, we obtain the solutions of field equations for gravastar in gravity’s rainbow without electromagnetic field, and analyze its geometrical as well as physical interpretations. As it was mentioned in previous section, there are three regions of the gravastar structured as follows; (i) interior region \(R_{1}\): \(0<r<r_{1}\) with the equation of state (EOS) follows \(p=-\rho \), (ii) shell region \(R_{2} \): \(r_{1}<r<r_{2}\) with EOS follows \(p=\rho \), (iii) exterior region \(R_{3}\): \(r_{2}<r\) with EOS follows \(p=\rho =0\).

The field equation with the energy-dependent cosmological constant \(\Lambda (\varepsilon )\) and perfect fluid distribution in gravity’s rainbow is as follows

$$\begin{aligned} R_{\alpha \beta }-\frac{1}{2}Rg_{\alpha \beta }+\Lambda \left( \varepsilon \right) g_{\alpha \beta }=-8\pi \left( T_{\alpha \beta }^{PF}\right) , \end{aligned}$$
(8)

where R refers to the Ricci scalar, \(\Lambda (\varepsilon )\) is the cosmological constant which depends on \(\varepsilon \), and \(R_{\alpha \beta } \) is the Ricci tensor. Here, we consider the matter distribution in the interior of a compact object as a perfect fluid model given by

$$\begin{aligned} T_{\alpha \beta }^{PF}=(\rho +p)u_{\alpha }u_{\beta }-pg_{\alpha \beta }, \end{aligned}$$
(9)

where p, \(\rho \), \(u_{\alpha }\) are the fluid pressure, matter-energy density and velocity three-vector of a fluid element, respectively. The Einstein’s field equations with a negative energy-dependent cosmological constant (\(\Lambda (\varepsilon )<0\)), for the spacetime explained by Eq. ( 7) with the energy–momentum tensor described in Eq. (9), yield (rendering \(G=c=1\))

$$\begin{aligned}{} & {} \frac{H^{2}(\varepsilon )g^{\prime }(r)}{2r}=8\pi \rho (r)+\Lambda (\varepsilon ), \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{H^{2}(\varepsilon )g(r)f^{\prime }(r)}{2rf(r)}=-8\pi p(r)+\Lambda (\varepsilon ), \end{aligned}$$
(11)
$$\begin{aligned}{} & {} -\frac{H^{2}(\varepsilon )g(r)f^{\prime 2}(r)}{4f^{2}(r)}+\frac{ H^{2}(\varepsilon )g^{\prime }(r)f^{\prime }(r)}{4f(r)}+\frac{ H^{2}(\varepsilon )g(r)f^{\prime \prime }(r)}{2f(r)}\nonumber \\{} & {} \quad =-8\pi p(r)+\Lambda (\varepsilon ). \end{aligned}$$
(12)

where the prime and double prime define the first and second derivatives with respect to r, respectively. Now, the generalized Tolman–Oppenheimer–Volkov (TOV) equation can be written as

$$\begin{aligned} p^{\prime }+(p+\rho )\frac{f^{\prime }}{2f}=0. \end{aligned}$$
(13)

2.1 Interior region of gravastar

The interior region \(R_{1}\) (\(0<r<r_{1}=D\)) of the gravastar follows EoS \( p=-\rho \). We advert that this type of EoS is available in the works and is known as a degenerate vacuum, false vacuum, or \(\rho \)-vacuum [100,101,102,103] and represents a repellent pressure. Therefore by using the result given in Eq. (13), we can obtain the following interior

$$\begin{aligned} \rho =constant=\rho _{v}. \end{aligned}$$
(14)

Here we define this constant as \(\rho _{v}=H_{0}^{2}/2\pi \) [73], where \(H_{0}\) refers to the Hubble parameter. In other word, it can be described as follows,

$$\begin{aligned} p=-\rho _{v}. \end{aligned}$$
(15)

Now, by using Eqs. (10) and (11), we get the solutions for g(r) and f(r) from the field equations as,

$$\begin{aligned} g(r)=f(r)=A+\frac{\left( \Lambda (\varepsilon )+4H_{0}^{2}\right) r^{2}}{ H^{2}(\varepsilon )}, \end{aligned}$$
(16)

where A is an integration constant. From the above equation, it can be seen that the obtained metric is free from any central singularity. So, the active gravitational mass M(r) can be expressed at in the following form

$$\begin{aligned} M(r)=\int _{0}^{D}2\pi r\rho dr=\frac{H_{0}^{2}D^{2}}{2}. \end{aligned}$$
(17)

Here, it is observed that for the interior region, the physical parameters such as pressure, density and gravitational mass, do not depend on the rainbow functions. We also note that the quantities g(r) and f(r) depend on the rainbow function \(H(\varepsilon )\).

2.2 Exterior region of gravastar

For the vacuum exterior region, EoS is given by \(p=\rho =0\). The solution corresponds to the static BTZ black hole in gravity’s rainbow is written as follows [104, 105],

$$\begin{aligned} f(r)=g(r)=-m_{0}-\frac{\Lambda (\varepsilon )r^{2}}{H^{2}(\varepsilon )}, \end{aligned}$$
(18)

where the parameter \(m_{0}\) is an integration constant related to the total mass of black hole.

2.3 Sell of gravastar

Here we study a thin shell including ultra-relativistic fluid of soft quanta obeying EoS as \(p=\rho \). This assumption has already been used by various authors, which is known as a stiff fluid that refers to a Zeldovich Universe to investigate some cosmological [106,107,108] and astrophysical phenomena and astrophysical events [109,110,111]. It is not simple to solve the field equations within the non-vacuum region \(R_{2}\), i.e., within the shell. However, we can obtain an analytic solution within the framework of very thin shell limit, \(0<g(r)\equiv h<<1\). The reason of using this very thin shell limit is that in this limit, it can be set h to be zero to the first order. Therefore, the field equations (10–12), with \( p=\rho \), can be written as,

$$\begin{aligned} h^{\prime }=\frac{4r\Lambda (\varepsilon )}{H^{2}(\varepsilon )}. \end{aligned}$$
(19)

Integrating Eq. (19) yields

$$\begin{aligned} h=g(r)=B+\frac{2\Lambda (\varepsilon )r^{2}}{H^{2}(\varepsilon )}. \end{aligned}$$
(20)

By equating Eqs. (11) and (12), one gets

$$\begin{aligned} -\frac{1}{2}\left( {\frac{f^{\prime }}{f}}\right) ^{2}+\frac{1}{2}\left( \frac{g^{\prime }}{g}\right) \left( \frac{f^{\prime }}{f}\right) +\frac{ f^{\prime \prime }}{f}=\frac{f^{\prime }}{rf}, \end{aligned}$$
(21)

therefore, the other function is

$$\begin{aligned} f(r)={\left( C_{1}+C_{2}\frac{H^{2}(\varepsilon )}{4\Lambda (\varepsilon )} \sqrt{B+\frac{2\Lambda (\varepsilon )r^{2}}{H^{2}(\varepsilon )}}\right) } ^{2}, \end{aligned}$$
(22)

where B, and \(C_{1}\) are integration constants. It is notable that \(C_{2}\) is a constant with a dimension as (length)\(^{-2}\) that is considered for the sake of having a dimensionless term. Also, from the conservation (Eq. (13)), and using EOS \(p=\rho \), one can obtain

$$\begin{aligned} p=\rho =p_{0}{\left( C_{1}+C_{2}\frac{H^{2}(\varepsilon )}{4\Lambda (\varepsilon )}\sqrt{B+\frac{2\Lambda (\varepsilon )r^{2}}{H^{2}(\varepsilon )}}\right) }^{-2}, \end{aligned}$$
(23)

where \(p_{0}\) being an integration constant.

2.4 Physical parameters

2.4.1 Proper length

We note that the radius of inter boundary of shell is \(r_{1}=D\) and the radius of the exterior boundary of shell is \(r_{2}=D+\delta \), where \(\delta \) is the proper thickness of shell which is considered to be very small (i.e., \(\delta<<1\)). The proper length of shell is described as \( l=\int _{D}^{D+\delta }\sqrt{\frac{1}{g(r)}}dr\) [1]. Applying the mentioned definition, we extract the proper length in gravity’s rainbow, which is given by

$$\begin{aligned} l=\int _{D}^{D+\delta }\sqrt{\frac{1}{H^{2}(\varepsilon )g(r)}}dr. \end{aligned}$$
(24)

Since g(r) is complicated in the shell region, it is not simple to obtain the analytical form of above integral. Here we assume \(\sqrt{\frac{1}{g(r)}}= \frac{dF(r)}{dr}\), so from the above integral can be written

$$\begin{aligned} l= & {} \frac{1}{H(\varepsilon )}\int _{D}^{D+\delta }\frac{dF(r)}{dr}dr=\frac{ F(D+\delta )-F(D)}{H(\varepsilon )} \nonumber \\\approx & {} \frac{\delta }{H(\varepsilon )}\frac{dF(r)}{dr}\mid _{_{r=D}}= \frac{\delta }{H(\varepsilon )}\sqrt{\frac{1}{g(r)}}\mid _{_{r=D}}. \end{aligned}$$
(25)

Since \(\delta<<1\) (\(O(\delta ^{2})\approx 0\)), according to the above manipulation, it can be considered only the first-order term of \(\delta \). So for this approximation, the proper length will be equal to

$$\begin{aligned} l\approx \frac{\delta }{H(\varepsilon )}\sqrt{\frac{1}{B+\frac{2\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}}. \end{aligned}$$
(26)

From the above result, we understand that the proper length of thin shell of the gravastar is proportional to the thickness (\(\delta \)) of shell. Also it is observed that the proper length of thin shell depends on the rainbow function \(H(\varepsilon )\).

2.4.2 Energy

It is assumed that the energy inside the gravastar has dark energy, which actually the repulsive force from the interior comes from this energy. The energy content within the shell region of the gravastar described as \( E=\int _{D}^{D+\delta }{2\pi }r\rho dr\) [1]. So, we obtain the energy content within the thin shell in gravity’s rainbow, which is given as

$$\begin{aligned} E=\frac{1}{H^{2}(\varepsilon )}\int _{D}^{D+\delta }2\pi r\rho dr. \end{aligned}$$
(27)

Similarly, as done above, by expanding \(F(D+\delta )\) binomially about D and taking the first order of \(\delta \), we obtain the following relation,

$$\begin{aligned} E\approx \frac{2\pi p_{0}\delta D}{H^{2}(\varepsilon ){\left( C_{1}+C_{2} \frac{H^{2}(\varepsilon )}{4\Lambda (\varepsilon )}\sqrt{B+\frac{2\Lambda (\varepsilon )D^{2}}{H^{2}(\varepsilon )}}\right) }^{2}}. \end{aligned}$$
(28)

2.4.3 Entropy

Mazur and Mottola [1, 2] showed that the entropy density is zero in the interior region \(R_{1}\) of the gravastar. But, the entropy within the thin shell in gravity’s rainbow can be expressed by

$$\begin{aligned} S=2\pi \int _{D}^{D+\delta }\sqrt{\frac{1}{H^{2}(\varepsilon )g(r)}}s(r)rdr, \end{aligned}$$
(29)

where s(r), the entropy density for the local temperature T(r), is given by

$$\begin{aligned} s(r)=\frac{\alpha ^{2}k_{B}^{2}T(r)}{4\pi \hbar ^{2}}=\frac{\alpha k_{B}}{ \hbar }\sqrt{\frac{p(r)}{2\pi }}. \end{aligned}$$
(30)

In above equation, \(k_{B}\) is Boltzmann constant, \(\hbar \) is Reduced Planck constant and \(\alpha ^{2}\) is a dimensionless constant. The entropy within the thin shell can be written as

$$\begin{aligned} S= & {} \frac{\alpha k_{B}\sqrt{2\pi p_{0}}}{\hbar H(\varepsilon )}\nonumber \\{} & {} \!\! \times \int _{D}^{D+\delta }\frac{rdr}{\sqrt{B\!+\!\frac{2\Lambda (\varepsilon )r^{2}}{ H^{2}(\varepsilon )}}\!\left( C_{1}+C_{2}\frac{H^{2}(\varepsilon )}{4\Lambda (\varepsilon )}\sqrt{B\!+\!\frac{2\Lambda (\varepsilon )r^{2}}{H^{2}(\varepsilon )}}\right) }.\nonumber \\ \end{aligned}$$
(31)

Similarly, by expanding \(F(D+\delta )\) binomially about D, it is obtained

$$\begin{aligned} S\!\approx \!\frac{D\delta \alpha k_{B}\sqrt{2\pi p_{0}}}{\hbar H(\varepsilon ) \sqrt{B\!+\!\frac{2\Lambda (\varepsilon )D^{2}}{H^{2}(\varepsilon )}}\!\left( C_{1}+C_{2}\frac{H^{2}(\varepsilon )}{4\Lambda (\varepsilon )}\sqrt{B\!+\!\frac{ 2\Lambda (\varepsilon )D^{2}}{H^{2}(\varepsilon )}}\right) }.\nonumber \\ \end{aligned}$$
(32)

Here we have plotted the physical parameters, the proper length l, the energy E, and the entropy S versus the rainbow function (\(H(\varepsilon ) \)) in Figs. 1, 2 and 3, respectively. From these figures, we see that all three parameters of the shell of gravastar decrease versus the rainbow function \(H(\varepsilon )\).

Fig. 1
figure 1

The proper length (l) vs the rainbow function (\(H(\varepsilon )\)). We have chosen \(\delta =0.01\), \(D=1\), \(\Lambda ( \varepsilon )=-\,1\), and \(B=1\)

Full size image
Fig. 2
figure 2

The energy E vs the rainbow function (\(H(\varepsilon )\)). We have chosen \(\delta =0.01\), \(D=1\), \(\Lambda (\varepsilon )=-\,1\), \(C_{1}=10\), \(C_{2}=1\), \(p_{0}=1\), and \(B=1\)

Full size image
Fig. 3
figure 3

The entropy S vs the rainbow function (\(H(\varepsilon )\) ). We have chosen \(\delta =0.01\), \(D=1\), \(\Lambda (\varepsilon )=-\,1\), \(C_{1}=10\), \(C_{2}=1\), \(p_{0}=1\), and \(B=1\)

Full size image

3 Three-dimensional charged AdS gravastars in gravity’s rainbow

The Einstein–Hilbert action coupled to the energy-dependent cosmological constant and electromagnetism is given by

$$\begin{aligned} I=\int {d}^{3}{x}\sqrt{-g}\left( \frac{R-2\Lambda \left( \varepsilon \right) }{16\pi }-\frac{1}{4}F_{\mu \nu }F^{\mu \nu }+L_{m}\right) , \end{aligned}$$
(33)

where \(L_{m}\) is Lagrangian for the matter. It is assumed that the fluid source consists of natural matter and an electromagnetic field. The Einstein–Maxwell equations with the energy-dependent cosmological constant \( \Lambda (\varepsilon )\) for a charged perfect fluid distribution is as follows [112],

$$\begin{aligned} R_{\alpha \beta }-\frac{1}{2}Rg_{\alpha \beta }+\Lambda \left( \varepsilon \right) g_{\alpha \beta }=-8\pi \left( T_{\alpha \beta }^{PF}+T_{\alpha \beta }^{EM}\right) , \end{aligned}$$
(34)

where the energy–momentum tensor \(T_{\alpha \beta }^{EM}\) for normal matter is given by

$$\begin{aligned} T_{\alpha \beta }^{PF}=(\rho +p)u_{\alpha }u_{\beta }-pg_{\alpha \beta }, \end{aligned}$$
(35)

here \(\rho \), p, \(u_{i}\) are respectively, matter-energy density, fluid pressure and velocity three-vector of a fluid element. The energy–momentum tensor for electromagnetic field is described by,

$$\begin{aligned} T_{\alpha \beta }^{EM}=-\frac{1}{4}\left( F_{\gamma }^{\alpha }F_{\beta \gamma }-\frac{1}{4}g_{\alpha \beta }F_{\gamma \kappa }F^{\gamma \kappa }\right) , \end{aligned}$$
(36)

where \(F_{\alpha \beta }\) is the electromagnetic field and depends on current three-vector,

$$\begin{aligned} J^{\gamma }=\sigma (r)u^{\gamma }, \end{aligned}$$
(37)

as

$$\begin{aligned} F_{;\beta }^{\alpha \beta }=-4\pi J^{\alpha }. \end{aligned}$$
(38)

where \(\sigma (r)\) is the proper charge density. The three-velocity is considered as \(u_{\alpha }=\delta _{\alpha }^{t}\), and eventually, the electromagnetic field tensor can be described as

$$\begin{aligned} F_{\alpha \beta }=E(r)\left( \delta _{\alpha }^{t}\delta _{\beta }^{r}-\delta _{\alpha }^{r}\delta _{\beta }^{t}\right) , \end{aligned}$$
(39)

where E(r) is the electric field.

For a the charged fluid source with density \(\rho (r)\), pressure p(r) and electric field E(r), the Einstein–Maxwell equations in the gravity’s rainbow can be described as follows,

$$\begin{aligned}{} & {} \frac{H^{2}(\varepsilon )g^{\prime }(r)}{2r} =8\pi \rho (r)+\Lambda (\varepsilon )+E^{2}(r), \end{aligned}$$
(40)
$$\begin{aligned}{} & {} \frac{H^{2}(\varepsilon )g(r)f^{\prime }(r)}{2rf(r)} =-8\pi p(r)+\Lambda (\varepsilon )+E^{2}(r), \end{aligned}$$
(41)
$$\begin{aligned}{} & {} -\frac{H^{2}(\varepsilon )g(r)f^{\prime 2}(r)}{4f^{2}(r)}+\frac{ H^{2}(\varepsilon )g^{\prime }(r)f^{\prime }(r)}{4f(r)}+\frac{ H^{2}(\varepsilon )g(r)f^{\prime \prime }(r)}{2f(r)} \nonumber \\{} & {} \quad =-8\pi p(r)+\Lambda (\varepsilon )-E^{2}(r). \end{aligned}$$
(42)

Now, for a charged fluid distribution, the generalized TOV equation can be expressed as

$$\begin{aligned} p^{\prime }+(p+\rho )\frac{f^{\prime }}{2f}=\frac{1}{8\pi r^{2}} (r^{2}E^{2})^{\prime }, \end{aligned}$$
(43)

where \(E\equiv E(r)\), and the electric field E is as follows

$$\begin{aligned} E(r)=\frac{4\pi }{r}\int _{0}^{r}\frac{x\sigma (x)dx}{H(\varepsilon )\sqrt{ g(r)}}=\frac{q(r)}{r}. \end{aligned}$$
(44)

The parameter \(\frac{\sigma (x)}{H(\varepsilon )\sqrt{g(r)}}\), which is inside the above integral, is considered as the volume charge density. It should be noted that the charge density volume is a polynomial function of r. Therefore, we use the condition

$$\begin{aligned} \frac{\sigma (x)}{H(\varepsilon )\sqrt{g(r)}}=\sigma _{0}r^{m}, \end{aligned}$$
(45)

were m is an arbitrary constant introduced as a polynomial index and the constant \(\sigma _{0}\) is related to as the central charge density. By using the result in Eq. (45), one obtains from Eq. (44),

$$\begin{aligned} E(r)= & {} \frac{4\pi \sigma _{0}}{m+2}r^{m+1}, \end{aligned}$$
(46)
$$\begin{aligned} q(r)= & {} \frac{4\pi \sigma _{0}}{m+2}r^{m+2}. \end{aligned}$$
(47)

Now, we analyze the solutions of field equations for charged gravastar (here, charge is created by electromagnetic field) and discuss its geometry as well as physical interpretations.

3.1 Interior region of charged gravastar

In search for interior solution which is free of any mass-singularity at the origin, our configuration is supported by an interior region \(R_{1}\) (\( 0<r<r_{1}=D\)) of the charged gravastar with equation of state \(p=-\rho \). Hence by using the result given in Eqs. (40) and (43), we obtain the following interior,

$$\begin{aligned} \rho (r)= & {} -p(r)=\frac{2\pi \sigma _{0}^{2}\left( D^{2m+2}-r^{2m+2}\right) }{(m+1)(m+2)}, \end{aligned}$$
(48)
$$\begin{aligned} g(r)= & {} C_{0}+\frac{\left[ 16\pi \int _{0}^{r}x\rho (x)dx+2\int _{0}^{r}xE^{2}(x)dx+\Lambda \left( \varepsilon \right) r^{2} \right] }{H^{2}(\varepsilon )}, \end{aligned}$$
(49)
$$\begin{aligned} f(r)= & {} g(r)=C_{0}+\frac{\left[ \frac{16\pi ^{2}\sigma _{0}^{2}r^{2}D^{2m+2} }{(m+1)(m+2)}-\frac{16\pi ^{2}\sigma _{0}^{2}r^{2m+4}}{(m+1)({m+2})^{3}} +\Lambda \left( \varepsilon \right) r^{2}\right] }{H^{2}(\varepsilon )}, \nonumber \\ \end{aligned}$$
(50)

where \(C_{0}\) is an integration constant. We note from Eq. (50) that \(C_{0}\) is a nonzero integration constant. We get the charge density for the electric field in the following form,

$$\begin{aligned} \sigma (r)= & {} \sigma _{0}r^{m}\left( C_{0}+\frac{1}{H^{2}(\varepsilon )}\left[ \frac{16\pi ^{2}\sigma _{0}^{2}r^{2}D^{2m+2}}{(m+1)(m+2)}\right. \right. \nonumber \\{} & {} \left. \left. -\frac{16\pi ^{2}\sigma _{0}^{2}r^{2m+4}}{(m+1)({m+2})^{3}}+\Lambda (\varepsilon ) r^{2} \right] \right) ^{1/2}. \end{aligned}$$
(51)

We can obtain the active gravitational mass of the interior region of the charged gravastar as follows

$$\begin{aligned} M(r)= & {} \frac{1}{H^{2}(\varepsilon )}\int _{0}^{D}2\pi r\left( \rho +\frac{E^{2} }{8\pi }\right) dr\nonumber \\= & {} \frac{(2m^{2}+8m+6)\pi ^{2}\sigma _{0}^{2}D^{2m+4}}{ H^{2}(\varepsilon )(m+2)^{3}(m+1)}. \end{aligned}$$
(52)

A characteristic feature of a stellar compact object is that the internal gravitational mass and radius of the star system are directly proportional to each other, which is shown by Eq. (52). Here, it can be also observed via Eq. (48) that the physical parameters such as pressure and density are dependent on the charge. However, in this connection, we note an interesting point; the mentioned physical parameters are not dependent on the energy-dependent cosmological constant \(\Lambda \left( \varepsilon \right) \) and rainbow functions for the interior region. We also observe that the quantities g(r), f(r), M(r), and \(\sigma (r)\) depend not only on the rainbow function \(H(\varepsilon )\), but also on the charge.

3.2 Exterior region of charged gravastar

In order to discuss the exterior region of charged gravastar whose EoS is given by \(p=\rho =0\), we take the solution corresponds to a static charged BTZ black hole in the gravity’s rainbow described as follows [113],

$$\begin{aligned} f(r)=g(r)=-m_{0}-\frac{\Lambda \left( \varepsilon \right) r^{2}}{ H^{2}(\varepsilon )}-\frac{2q^{2}L^{2}(\varepsilon )}{l^{2}}\ln \left( \frac{ r}{l}\right) , \end{aligned}$$
(53)

where the parameter q is an integration constant referred to the total charge of the black hole. Furthermore, l is a constant with the length dimension that is considered for the sake of having a dimensionless logarithmic argument. For \(q=0\), the above metric reaches to the uncharged BTZ black hole in gravity’s rainbow.

3.3 Sell of charged gravastar

In the shell region, it is assumed that the thin shell region contains stiff perfect fluid which follows EoS \(p=\rho \). For this EoS, it is complex to get to the answer the solution from the field equations. Similar to the uncharged case, we shall consider the limit \(0<g(r)\equiv h<<1\) in the thin shell to obtain the analytical solution within the thin shell. Assuming this approximation (h to be zero) with \(p=\rho \), the field equations (40)–(42), can be recast in the following forms,

$$\begin{aligned}{} & {} h^{\prime } =\frac{4r(\Lambda \left( \varepsilon \right) +E^{2})}{ H^{2}(\varepsilon )}, \end{aligned}$$
(54)
$$\begin{aligned}{} & {} \frac{H^{2}(\varepsilon )h^{\prime }f^{\prime }(r)}{4f(r)} =-2E^{2}. \end{aligned}$$
(55)

By integrating Eq. (54), we get

$$\begin{aligned} g(r)=A_{0}+\frac{2\Lambda \left( \varepsilon \right) r^{2}}{ H^{2}(\varepsilon )}+\frac{32\pi ^{2}\sigma _{0}^{2}r^{2m+4}}{ H^{2}(\varepsilon )\left( m+2\right) ^{3}}, \end{aligned}$$
(56)

where \(A_{0}\) is an integrating constant. Using this value in Eq. (55 ), it is obtained another metric coefficient as,

$$\begin{aligned} f(r)=F_{0}\left( {{\Lambda \left( \varepsilon \right) +\frac{16\pi ^{2}\sigma _{0}^{2}r^{2m+2}}{{(m+2)}^{2}}}}\right) ^{\frac{-1}{m+1}}, \end{aligned}$$
(57)

where \(F_{0}\) is an integration constant. Also, using the generalized TOV equation (43) one can get

$$\begin{aligned} 8\pi p(r)=8\pi \rho (r)=\left( \frac{m+2}{m}\right) \left( \Lambda (\varepsilon )+\frac{16\pi ^{2}\sigma _{0}^{2}r^{2m+2}}{(m+2)^{2}}\right) ,\nonumber \\ \end{aligned}$$
(58)

the Eq. (58) shows that the energy-dependent cosmological constant has a important contribution to the pressure and density parameters of the shell of charged gravastar in an additive manner.

3.4 Physical parameters of charged gravastar

3.4.1 Proper length

The radius of inner and outer surfaces of the shell of gravastar are \(r_{1}=D\) and \(r_{2}=D+\delta \), respectively. Similar to the previous case (uncharged case), and by assuming \(\sqrt{\frac{1}{g(r)}}=\frac{dF(r)}{dr }\), the proper thickness between two boundaries can be described as,

$$\begin{aligned} l= & {} \frac{1}{H(\varepsilon )}\int _{D}^{D+\delta }\frac{dF(r)}{dr}dr=\frac{ F(D+\delta )-F(D)}{H(\varepsilon )} \nonumber \\\approx & {} \frac{\delta }{H(\varepsilon )}\frac{dF(r)}{dr}\mid _{_{r=D}}= \frac{\delta }{H(\varepsilon )}\sqrt{\frac{1}{g(r)}}\mid _{_{r=D}}. \end{aligned}$$
(59)

As we know \(\delta<<1\), so \(O(\delta ^{2})\approx 0\). According to this approximation, the proper length is given by,

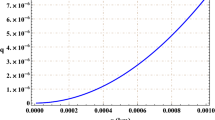
$$\begin{aligned} l\approx \frac{\delta }{H(\varepsilon )}\left( A_{0}+\frac{2\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}+\frac{32\pi ^{2}\sigma _{0}^{2}D^{2m+4}}{H^{2}(\varepsilon ){(m+2)}^{3}}\right) ^{-1/2}.\nonumber \\ \end{aligned}$$
(60)

From the above result, we understand that the proper length of the thin shell of the charged gravastar is proportional to the shell’s thickness \( \delta \). Also it is observed that the proper length of thin shell of the charged gravastar depends on the electric field \(\sigma _{0}\), the radius D, the rainbow function \(H(\varepsilon )\), the energy-dependent cosmological constant \(\Lambda (\varepsilon )\), and also m. The proper length l have been plotted versus thickness \(\delta \) and radius D in Figs. 4 and 5, respectively. In Fig. 4, it can be seen a linear relationship between proper length and thickness of the shell. Also from Fig. 5, we see that the proper length l decreases as radius D increases.

Fig. 4
figure 4

The proper length l vs thickness \(\delta \). We have chosen \(\sigma _{0}=4\), \(D=1\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\). \(m=2\) and \(H(\varepsilon )=1.1\)

Full size image
Fig. 5
figure 5

The proper length l vs radius D. We have chosen \(\sigma _{0}=4\), \(\delta =0.01\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=2\) and \(H(\varepsilon )=1.1\)

Full size image

3.4.2 Energy

The energy content within the shell region of the charged gravastar is defined in the following form [74],

$$\begin{aligned} E=\int _{D}^{D+\delta }2\pi \left( \rho +\frac{E^{2}}{8\pi }\right) rdr. \end{aligned}$$
(61)

We use Eq. (61), to calculate the energy content within the thin shell region of the charged gravastar in gravity’s rainbow as follows,

$$\begin{aligned} E= & {} \frac{2\pi \int _{D}^{D+\delta }\left( \rho +\frac{E^{2}}{8\pi }\right) rdr}{H^{2}\left( \varepsilon \right) } \nonumber \\= & {} \frac{(m+2)\Lambda \left( \varepsilon \right) \left[ {(D+\delta )} ^{2}-D^{2}\right] }{8mH^{2}\left( \varepsilon \right) }\nonumber \\{} & {} +\frac{16\pi ^{2}\sigma _{0}^{2}(m+1)\left[ {(D+\delta )}^{2m+4}-D^{2m+4}\right] }{4m{ (m+2)}^{3}}. \end{aligned}$$
(62)

According to this fact that the thickness \(\delta \) of shell is very small, \( \delta<<1\), it can be expanded binomially about D. Taking the first order of \(\delta \), we obtain,

$$\begin{aligned} E\approx \frac{\delta }{H^{2}(\varepsilon )}\left[ \frac{(m+2)\Lambda \left( \varepsilon \right) D}{4m}+\frac{16\pi ^{2}\sigma _{0}^{2}(m+1)D^{2m+3}}{2m{ (m+2)}^{2}}\right] .\nonumber \\ \end{aligned}$$
(63)

We observe that the energy content in the shell region is proportional to the thickness \(\delta \) of the shell. In addition, we see that the energy of charged gravastar depends on the electric field \(\sigma _{0}\) of gravastar, the radius D, the rainbow function \(H(\varepsilon )\), the energy-dependent cosmological constant \(\Lambda (\varepsilon )\), and also m. We have plotted the energy content E in the shell versus thickness \(\delta \) and radius D in Figs. 6 and 7, respectively. As one can see the energy content E in the shell increases with the thickness \( \delta \) of shell of the charged gravastar (Fig. 6) as well as the radius D (Fig. 7).

Fig. 6
figure 6

The energy E vs thickness \(\delta \). We have chosen \( \sigma _{0}=4\), \(D=1\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=2\) and \(H(\varepsilon )=1.1\)

Full size image
Fig. 7
figure 7

The energy E vs radius D. We have chosen \(\sigma _{0}=1\), \(\delta =0.01\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \( m=2\) and \(H(\varepsilon )=1.1\)

Full size image

3.4.3 Entropy

We obtain the entropy within the thin shell of charged gravastar in three-dimensional spacetime as

$$\begin{aligned} S=2\pi \int _{D}^{D+\delta }\sqrt{\frac{1}{H^{2}(\varepsilon )g(r)}}rs(r)dr, \end{aligned}$$
(64)

where s(r) is the entropy density, which is given by Eq. (30). So for the entropy within the thin shell, we can write

$$\begin{aligned} S= & {} \frac{1}{2H(\varepsilon )}\int _{D}^{D+\delta }\frac{\alpha k_{B}}{\hbar }\nonumber \\{} & {} \times \sqrt{\frac{m+2}{m}\left[ \Lambda \left( \varepsilon \right) r^{2}+\frac{ 16\pi ^{2}\sigma _{0}^{2}r^{2m+4}}{{(m+2)}^{2}}\right] }{\mathcal {A}} _{1}^{-1/2}dr.\nonumber \\ \end{aligned}$$
(65)

where \({\mathcal {A}}_{1}=A_{0}+\frac{2\Lambda \left( \varepsilon \right) r^{2} }{H^{2}(\varepsilon )}+\frac{32\pi ^{2}\sigma _{0}^{2}D^{2\,m+4}}{ H^{2}(\varepsilon ){(m+2)}^{3}}\). To extract the entropy in the following form, we use the approximation \(\delta \ll 1\), and expand the above integrand about D and retain terms up to the first order of \(\delta \),

$$\begin{aligned} S\!\approx \!\frac{\delta \alpha k_{B}}{2H(\varepsilon )\hbar }\sqrt{\frac{m+2}{m }\!\left[ \Lambda \left( \varepsilon \right) D^{2}\!+\!\frac{16\pi ^{2}\sigma \! _{0}^{2}D^{2m\!+\!4}}{{(m+2)}^{2}}\right] }{\mathcal {A}}_{2}^{-1/2}.\nonumber \\ \end{aligned}$$
(66)

where \({\mathcal {A}}_{2}=A_{0}+\frac{2\Lambda \left( \varepsilon \right) D^{2} }{H^{2}(\varepsilon )}+\frac{32\pi ^{2}\sigma _{0}^{2}D^{2\,m+4}}{ H^{2}(\varepsilon ){(m+2)}^{3}}\). Equation (66) reveals that the entropy in the shell region of the charged gravastar in three-dimensional energy-dependent spacetime is proportional to the thickness \(\delta \) of the shell, the electric field \(\sigma _{0}\), the radius D, the rainbow function \(H(\varepsilon )\), the energy-dependent cosmological constant \( \Lambda (\varepsilon )\), and m. We have drawn the entropy S within the shell versus the thickness \(\delta \) and radius D in Figs. 8 and 9, respectively. The entropy S increases when the thickness \(\delta \) and the radius D increase.

Fig. 8
figure 8

The entropy S vs thickness \(\delta \). We have chosen \( \sigma _{0}=4\), \(D=1\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=2\) and \(H(\varepsilon )=1.1\)

Full size image
Fig. 9
figure 9

The entropy S vs radius D. We have chosen \(\sigma _{0}=4 \), \(\delta =0.01\), \(A_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=1\) and \(H(\varepsilon )=1.1\)

Full size image

4 Junction condition between interior and exterior regions

According to this fact that gravastar consists of three regions, interior region, thin shell region, and exterior region, using the Darmois–Israel formalism [114,115,116], one can study the matching between the surfaces of the interior and exterior regions. For this purpose, we define \(\Sigma \) as the junction surface located at \(r=D\). In the gravity’s rainbow, the metric 7 considered on the junction surface. It appears that the metric coefficients at the junction surface \(\Sigma \) are continuous, but their derivatives might not be continuous at \(\Sigma \). Using the extrinsic curvature of \(\Sigma \) at \(r=D\), in the joining surface S, it is possible to determine the surface stress-energy and surface tension of the junction surface S.

According to the Lanczos equation [117], stress-energy surface \( S_{ij}\) is defined as follows,

$$\begin{aligned} S_{ij}=-\frac{1}{8\pi }\left( \eta _{ij}-\delta _{ij}\eta _{kk}\right) . \end{aligned}$$
(67)

Then, the discontinuity in the second fundamental form is expressed as follows,

$$\begin{aligned} \eta _{ij}=K_{ij}^{+}-K_{ij}^{-}, \end{aligned}$$
(68)

where \(K_{ij}\) describes the extrinsic curvature. The signs “−” and “\(+\)” are related to the gravastar’s interior and exterior regions, respectively. The components of the extrinsic curvature tensor on both surfaces of the shell region read

$$\begin{aligned} K_{ij}^{\pm }=\left[ -n_{\nu }^{\pm }\left( \frac{\partial ^{2}x_{\nu }}{ \partial \xi ^{i}\partial \xi ^{j}}+\Gamma _{\alpha \beta }^{\nu }\frac{ \partial x^{\alpha }}{\partial \xi ^{i}}\frac{\partial x^{\beta }}{\partial \xi ^{j}}\right) \right] , \end{aligned}$$
(69)

where \(\xi ^{i}\) represent the intrinsic coordinates on the shell, and \(-n_{\nu }^{\pm }\) are the normal unit \((n^{\nu }n_{\nu }=1)\) vectors

$$\begin{aligned} n_{\nu }^{\pm }=\pm \left( {g^{\alpha \beta }\frac{\partial f}{\partial x^{\alpha }}\frac{\partial f}{\partial x^{\beta }}}\right) ^{-\frac{1}{2}} \frac{\partial f}{\partial x^{\nu }}. \end{aligned}$$
(70)

Now, from Lanczos equation spacetime, the stress-energy surface tensor can be written as \(S_{ij}=diag(\varrho ,P)\), where \(\varrho \) is the surface energy density and P is the surface pressure, respectively. So according to the general formalism for three-dimensional spacetime [118] and using the above equations, and also by setting \(r=D\), for uncharged gravastars, we obtain

$$\begin{aligned} \varrho _{uncharged}(D)= & {} \frac{-1}{8\pi D}\left( \sqrt{-m_{0}-\frac{ \Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}\right. \nonumber \\{} & {} \left. -\sqrt{A+ \frac{(\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{H^{2}(\varepsilon )}}\right) , \end{aligned}$$
(71)
$$\begin{aligned} P_{uncharged}(D)= & {} \frac{1}{8\pi }\left( \frac{-\frac{\Lambda \left( \varepsilon \right) D}{H^{2}(\varepsilon )}}{\sqrt{-m_{0}-\frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}}\right. \nonumber \\{} & {} \left. -\frac{\frac{ (\Lambda (\varepsilon )+4H_{0}^{2})D}{H^{2}(\varepsilon )}}{\sqrt{A+\frac{ (\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{H^{2}(\varepsilon )}}}\right) . \end{aligned}$$
(72)

For charged gravastars, we have

$$\begin{aligned} \varrho _{charged}(D)= & {} \frac{-1}{8\pi D}\left( \sqrt{{\mathcal {N}}_{1}}- \sqrt{C_{0}+{\mathcal {N}}_{2}+\frac{\Lambda \left( \varepsilon \right) D^{2}}{ H^{2}(\varepsilon )}}\right) , \nonumber \\\end{aligned}$$
(73)
$$\begin{aligned} P_{charged}(D)= & {} \frac{1}{8\pi }\left( \frac{-\frac{\Lambda \left( \varepsilon \right) D}{H^{2}(\varepsilon )}-\frac{\frac{q^{2}L^{2}( \varepsilon )}{l^{2}}}{D}}{\sqrt{{\mathcal {N}}_{1}}}\right. \nonumber \\{} & {} \left. -\frac{\frac{\frac{16\pi ^{2}\sigma _{0}^{2}(m^{2}+2m+3)}{{(m+2)}^{2}(m+1)}D^{2m+3}+\Lambda \left( \varepsilon \right) D}{H^{2}(\varepsilon )}}{\sqrt{C_{0}+{\mathcal {N}}_{2}+ \frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}} \right) , \end{aligned}$$
(74)

where \({\mathcal {N}}_{1}\) and \({\mathcal {N}}_{2}\) are

$$\begin{aligned} {\mathcal {N}}_{1}= & {} -m_{0}+\frac{\Lambda \left( \varepsilon \right) D^{2}}{ H^{2}(\varepsilon )}-\frac{2q^{2}L^{2}(\varepsilon )}{l^{2}}\ln \left( \frac{ D}{l}\right) , \end{aligned}$$
(75)
$$\begin{aligned} {\mathcal {N}}_{2}= & {} \frac{16\pi ^{2}\sigma _{0}^{2}(m^{2}+2m+3)D^{2m+4}}{{ H^{2}(\varepsilon )(m+2)}^{3}(m+1)}. \end{aligned}$$
(76)

It is notable that \(\varrho _{uncharged}\) and \(P_{uncharged}\) are related to the line energy density and line pressure of uncharged gravastar in gravity’s rainbow, respectively. Also, \(\varrho _{charged}\) and \(P_{charged}\), are related to the line energy density and the line pressure of charged gravastar in this gravity, respectively. We have drawn our results for the line energy density and line pressure versus radius D for both state of charged and uncharged in Figs. 10, 11, 12 and 13. It is clear that the line energy density for both state of charged and uncharged gravastars increases (see Figs. 10 and 12). But the line pressure for both state of charged and uncharged gravastars decreases as radius D increases (see Figs. 11, 13).

Fig. 10
figure 10

The line energy density \(\varrho _{uncharged}\) vs radius D. We have chosen \(m_{0}=-80\), \(H_{0}=70\), \(A=1\), \(\Lambda (\varepsilon )=-\,1\), and \(H(\varepsilon )=1.1\)

Full size image
Fig. 11
figure 11

The line pressure \(P_{uncharged}\) vs radius D. We have chosen \( m_{0}=-80\), \(H_{0}=70\), \(A=1\), \(\Lambda (\varepsilon )=-\,1\), and \(H( \varepsilon )=1.1\)

Full size image
Fig. 12
figure 12

The line energy density \(\varrho _{charged}\) vs radius D. We have chosen \(m_{0}=-80\), \(L(\varepsilon )=1.1\), \(H(\varepsilon )=1.1\), \(\sigma _{0}=4\), \(C_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=1\), \(q=1\), and \(l=1\)

Full size image
Fig. 13
figure 13

The line pressure \(P_{charged}\) vs radius D. We have chosen \( m_{0}=-80\), \(L(\varepsilon )=1.1\), \(H(\varepsilon )=1.1\), \( \sigma _{0}=4\), \(C_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=1\), \(q=1\), and \(l=1\)

Full size image

4.1 Equation of state of thin-shell gravastars in gravity’s rainbow

The equation of state parameter \( \omega (r)\) (at \(r=D\)) is described as follows

$$\begin{aligned} \omega (D)=\frac{P(D)}{\varrho (D).} \end{aligned}$$
(77)

Therefore, using equations for line energy density and line pressure, we can obtain the equation of state parameter in the following form,

$$\begin{aligned} \omega _{uncharged}(D)=\frac{\frac{\frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}{\sqrt{-m_{0}-\frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}}+\frac{\frac{(\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{H^{2}(\varepsilon )}}{\sqrt{A+\frac{(\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{H^{2}(\varepsilon )}}}}{\sqrt{-m_{0}-\frac{ \Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}-\sqrt{A+ \frac{(\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{H^{2}(\varepsilon )}}},\nonumber \\ \end{aligned}$$
(78)

for charged

$$\begin{aligned}{} & {} \omega _{charged}(D)\nonumber \\{} & {} \quad =\frac{\frac{-\frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}-\frac{q^{2}L^{2}(\varepsilon )}{l^{2}D}}{\sqrt{ {\mathcal {N}}_{1}}}-\frac{\frac{\frac{16\pi ^{2}\sigma _{0}^{2}(m^{2}+2m+3)}{{ (m+2)}^{2}(m+1)}D^{2m+4}+\Lambda \left( \varepsilon \right) D^{2}}{ H^{2}(\varepsilon )}}{\sqrt{C_{0}+{\mathcal {N}}_{2}+\frac{\Lambda \left( \varepsilon \right) D^{2}}{H^{2}(\varepsilon )}}}}{\sqrt{{\mathcal {N}}_{1}}- \sqrt{C_{0}+{\mathcal {N}}_{2}+\frac{\Lambda \left( \varepsilon \right) D^{2}}{ H^{2}(\varepsilon )}}}, \end{aligned}$$
(79)

in which \(\omega _{uncharged}\), and \(\omega _{charged}\) are the equation of state parameters for uncharged and charged gravastars. We have plotted the equation of state parameters \(\omega _{uncharged}\), and \(\omega _{charged}\) vs radius \({\textbf{D}}\) in Figs. 14 and 15, respectively.

Fig. 14
figure 14

\(\omega _{uncharged}\) vs radius D. We have chosen \( m_{0}=-4\), \(H_{0}=70\), \(A=1\), \(\Lambda (\varepsilon )=-\,1\), and \(H( \varepsilon )=1.1\)

Full size image
Fig. 15
figure 15

\(\omega _{charged}\) vs radius D. We have chosen \(m_{0}=-4\), \(L(\varepsilon )=1.1\), \(H(\varepsilon )=1.1\), \(\sigma _{0}=4\), \(C_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=1\), \(q=1\), and \(l=1\)

Full size image

From these figures, we see that the equation of state parameter increase as the radius increases, but it keeps a negative sign for both charged and uncharged states.

4.2 Stability of thin-shell gravastars in gravity’s rainbow

In this section, we want to study the stability of thin-shell gravastars for three-dimensional uncharged and charged AdS in gravity’s rainbow. The stable and unstable formations of thin-shell gravastars can be analyzed through the behavior of \(\eta \) as an effective parameter in determining the stability regions of the respective solutions that defined as follows [119],

$$\begin{aligned} \eta (r)=\frac{P^{\prime }(r)}{\varrho ^{\prime }(r)}. \end{aligned}$$

The parameter \(\eta \) can be interpreted as the squared speed of sound satisfying \(0\le \eta \le 1\) commonly. It is obvious that the speed of sound should not exceed the speed of light. But, to check the stability of the gravastar, this limitation may not be satisfied on the surface layer [120, 121]. The parameter \(\eta \) for uncharged gravastar in \(r=D\) can be written in the following form,

$$\begin{aligned}{} & {} \eta _{uncharged}(D)\nonumber \\{} & {} \quad =\frac{-\frac{\Lambda \left( \varepsilon \right) ^{2}D^{2}}{{\mathcal {N}}_{3}^{\frac{3}{2}}H^{4}(\varepsilon )}-\frac{\Lambda \left( \varepsilon \right) }{\sqrt{{\mathcal {N}}_{3}}H^{2}(\varepsilon )}+ \frac{(\Lambda \left( \varepsilon \right) +4H_{0}^{2})^{2}D^{2}}{{\mathcal {N}} _{4}^{\frac{3}{2}}H^{4}(\varepsilon )}-\frac{\Lambda \left( \varepsilon \right) +4H_{0}^{2}}{\sqrt{{\mathcal {N}}_{4}}H^{2}(\varepsilon )}}{\frac{\sqrt{ {\mathcal {N}}_{3}}-\sqrt{{\mathcal {N}}_{2}}}{D^{2}}+\frac{\frac{\Lambda \left( \varepsilon \right) D}{\sqrt{{\mathcal {N}}_{3}}H^{2}(\varepsilon )}+\frac{ (\Lambda \left( \varepsilon \right) +4H_{0}^{2})D}{\sqrt{{\mathcal {N}}_{4}} H^{2}(\varepsilon )}}{D}},\nonumber \\ \end{aligned}$$
(80)

where \({\mathcal {N}}_{3}\) and \({\mathcal {N}}_{4}\) are

$$\begin{aligned} {\mathcal {N}}_{3}= & {} -m_{0}-\frac{\Lambda \left( \varepsilon \right) D^{2}}{ H^{2}(\varepsilon )}, \end{aligned}$$
(81)
$$\begin{aligned} {\mathcal {N}}_{4}= & {} A+\frac{(\Lambda (\varepsilon )+4H_{0}^{2})D^{2}}{ H^{2}(\varepsilon )}. \end{aligned}$$
(82)

Therefore, we analyze the stability of gravastar configurations by analyzing the sign of the parameter \(\eta \). Because the expression is complicated, we use the graphical behavior of \(\eta _{uncharged}(D)\) in Fig. 16. In this figure, we examine that thin-shell of three-dimensional uncharged gravastars in gravity’s rainbow expresses stable behavior for very values of D.

Fig. 16
figure 16

\(\eta _{uncharged}\) vs radius D. We have chosen \( m_{0}=-80 \), \(H_{0}=70\), \(A=1\), \(\Lambda (\varepsilon )=-\,1\), and \(H( \varepsilon )=1.1\)

Full size image

We obtain the parameter \(\eta \) for charged garavastars in the following form

$$\begin{aligned}{} & {} \eta _{charged}(D)\nonumber \\{} & {} \! \!=\frac{\left( \frac{\frac{-\Lambda \left( \varepsilon \right) }{H^{2}(\varepsilon )}\!+\!\frac{L^{2}(\varepsilon )q^{2}}{l^{2}D^{2}}}{ \sqrt{{\mathcal {N}}_{1}}}\!-\!\frac{\left( \frac{\Lambda \left( \varepsilon \right) D}{H^{2}(\varepsilon )}\!+\!\frac{q^{2}L^{2}(\varepsilon )}{l^{2}D} \right) \! \left( \frac{2\Lambda \!\left( \varepsilon \right) D }{ H^{2}(\varepsilon )}\!+\!\frac{2q^{2}L^{2}(\varepsilon )}{l^{2}D}\right) }{2 {\mathcal {N}}_{1}^{\frac{3}{2}}}\!-\!\frac{\frac{(2m+3)(m+2){\mathcal {N}}_{2}}{D^{2}} \!+\!\Lambda \left( \varepsilon \right) }{\sqrt{C_{0}+{\mathcal {N}}_{2}\!+\!\Lambda \left( \varepsilon \right) D^{2}}}+{\mathcal {N}}_{5}\right) }{\frac{\sqrt{ {\mathcal {N}}_{1}}-\sqrt{C_{0}\!+\!{\mathcal {N}}_{2}\!+\!\Lambda \left( \varepsilon \right) D^{2}}}{D^{2}}\!+\!\frac{\frac{\frac{\Lambda \left( \varepsilon \right) D }{H^{2}(\varepsilon )}\!+\!\frac{L^{2}(\varepsilon )q^{2}}{l^{2}D}}{\sqrt{ {\mathcal {N}}_{1}}}\!+\!\frac{\frac{2{\mathcal {N}}_{2}}{D}+\frac{m{\mathcal {N}}_{2}}{D} \!+\!\Lambda \left( \varepsilon \right) D}{\sqrt{C_{0}+{\mathcal {N}}_{2}\!+\!\Lambda \left( \varepsilon \right) D^{2}}}}{D}},\nonumber \\ \end{aligned}$$
(83)

where \({\mathcal {N}}_{5}\) is the following function,

$$\begin{aligned} {\mathcal {N}}_{5}=\frac{\left( \frac{(m+2){\mathcal {N}}_{2}}{D}+\Lambda \left( \varepsilon \right) D\right) \left( \frac{2(m+2){\mathcal {N}}_{2}}{D}+2\Lambda \left( \varepsilon \right) D\right) }{2\left( {{C_{0}+{\mathcal {N}} _{2}+\Lambda \left( \varepsilon \right) D}^{2}}\right) ^{3/2}}. \end{aligned}$$

We study the graphical behavior of \(\eta _{charged}(D)\) in Fig. 17. This figure examines how the thin shell of three-dimensional charged gravastars in gravity’s rainbow expresses stable behavior. As one can see, the charged three-dimensional gravastars in gravity’s rainbow are stable object (Fig. 17).

Fig. 17
figure 17

\(\eta _{charged}\) vs radius D. We have chosen \(m_{0}=-80\), \(L(\varepsilon )=1.1\), \(H(\varepsilon )=1.1\), \(\sigma _{0}=4\), \(C_{0}=1\), \(\Lambda (\varepsilon )=-\,1\), \(m=1\), \(q=1\), and \(l=1\)

Full size image

5 Conclusion

In fact, the gravastar is the short form of Gravitationally vacuum stars which has given a new idea in the gravitational system. Such a stellar model which is free from any singularity, can be considered an alternative to black holes. Gravastar can be described through the interior region, thin shell region, and exterior region. In this paper, we studied the gravastars in the contexts of both three-dimensional AdS spacetime and gravity’s rainbow theory. We discussed the geometry of the uncharged gravastar model in gravity’s rainbow. In the interior region, the gravastar follows the equation of state (EoS) \(p=-\rho \). Some physical quantities such as energy density, pressure and gravitational mass were obtained for the interior region. In the exterior region, we found the vacuum exterior region whose EoS is given by \(p=\rho =0\). The solution corresponds to a static BTZ black hole in the gravity’s rainbow. In the shell region, the fluid source follows the EoS \(p=\rho \). In this region, we considered the thickness the shell of the gravastar to be very small, because we assumed that the interior and exterior regions join together at a location. Employing the approximation \( 0<g(r)\equiv h \ll 1\), we found the analytical solutions within the thin shell of the uncharged gravastar. Next, we calculated the physical parameters such as the proper length of the thin shell, energy, and entropy inside the thin shell of the uncharged gravastar, and showed that these parameters are directly proportional to the proper thickness of the shell (\(\delta \)) due to the approximation \(\delta<<1\). Also, we investigated the physical parameters such as the proper length l, the energy E, and the entropy S versus the rainbow function \(H(\varepsilon )\). Here, we saw that all three parameters of the shell of the uncharged gravastar decreasing function of rainbow function \(H(\varepsilon )\). In the next section, While considering a new model of charged gravastar in connection to the electrovacuum exterior three-dimensional AdS spacetime in the context of gravity’s rainbow theory, we investigated the role of electromagnetic field on an isotropic stellar model. To do this, we first wrote the Einstein–Maxwell’s field equations in the framework of the gravity’s rainbow. Then, we obtained the geometry of charged gravastar model. Some physical quantities such as energy density, pressure and gravitational mass were obtained for the interior region. In the exterior region, we found the electrovacuum exterior region. Solution corresponds to a static, charged BTZ black hole in the gravity’s rainbow. In the shell region, under approximation \(0<g(r)\equiv h<<1\), we obtained the analytical solutions within the thin shell of the charged gravastar. We computed the physical parameters such as the proper length of the thin shell, energy, and entropy inside the thin shell of the charged gravastar, and showed that these parameters are directly proportional to the proper thickness of the shell (\(\delta \)) due to the approximation \(\delta \ll 1\). These physical parameters significantly depend on the rainbow function \( H(\varepsilon )\). From the results of calculations, we saw that the proper length of the shell, energy, and entropy inside the shell of the charged gravastar increase as thickness increases. Also, the proper length decreases as the radius increases. The energy and entropy inside the shell always increase as the radius increases. Besides, by using the Darmois–Israel formalism, the matching between the surfaces of interior and exterior regions of the gravastars were studied. According to the matching conditions, the line energy density and the line pressure were obtained for both charged and uncharged states. Our results show that the line density increase as the radius increases, but the line pressure always decreases as the radius increases, but keeps the negative sign for both charged and uncharged states. Also, the equation of state parameter on the surface was obtained which shows that the equation of state parameter increase by increasing the radius. Here we saw that there is a negative sign for both charged and uncharged states. Finally, we explored the stable regions of uncharged and charged gravastar in gravity’s rainbow.