Abstract
The conformal anomaly and anomaly-induced effective action represent useful and economic ways to describe semiclassical contributions to the action of gravity. We discuss the anomaly in the case when the background is formed by metric and scalar fields and formulate the induced action in two standard covariant forms. The analysis of induced action at low energies reveals existing connection to the renormalization group and effective potential. The classification of anomalous terms is extended to the scalar background and ambiguities in the total derivative terms in the anomaly are considered using Pauli–Villars regularization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The conformal anomaly [1,2,3,4,5] and anomaly-induced effective action [6, 7] (see also [8, 9] for review and further references) play an important role in the description of loop corrections in the semiclassical approach. Even in the context of the Standard Model (SM) one can use the conformal anomaly at high energies, which can be still much below the Planck scale where the full quantum gravity is supposed to become relevant. For example, energy range of inflation, of the order \(10^{11}{-}10^{14}\) GeV form a scenario when the conformal anomaly may apply perfectly well since the masses of the SM particles is negligible while the Planck energies are far beyond.
One of the fundamental features of the Standard Model of weak interactions is the Higgs mechanism of providing masses to W and Z bosons and fermions. The use of conformal symmetry was traditionally invoked to improve on the naturalness of the Standard Model (see, e.g., Refs. [10, 11]). On the other hand, there is a growing interest in the quantum effects on Higgs scalar, related to the vacuum instability at high energies (in the UV), including the effects of curved spacetime [12,13,14]. Although several mechanisms have been proposed to resolve this issue, the subject does not look completely clear. Thus, it may be interesting to consider in detail the quantum contributions to the scalar action in the UV, using the powerful formalism of integrating conformal anomaly.
The anomaly in a metric-scalar theory, including self-interaction in the scalar sector, has been well discussed in the literature using different methods [15,16,17,18] (see also references therein), however we hope to add several relevant aspects to the subject. In what follows, we derive and discuss the trace anomaly and the anomaly-induced effective action for the case when the background is formed by metric and also by scalar fields. Our considerations cover the limits of consistency of the approach based on anomaly, that includes the discussion of ambiguities in the anomaly and induced action.
Last, but not least, we show how to evaluate the anomaly-based contributions at low energies. Indeed, taking the IR limit in a massless theory is a non-trivial issue. In our opinion, a better understanding of the corresponding approximation and its relation to other approaches look interesting by themselves.
The paper is organized as follows. In Sect. 2 we describe the anomaly for arbitrary particle contents of the semiclassical theory. Section 3 discusses the anomaly-induced effective action of metric and scalar field. Section 4 is devoted to the analysis of ambiguity in the anomaly, extending the results of the previous works on the subject [19, 20]. In Sect. 5, we consider the low-energy limit of induced action and the connection with renormalization group and effective potential of scalar fields. Finally, in Sect. 6 we draw our conclusions and discuss a few open issues, especially those related to conformal quantum gravity. Throughout the paper, we use pseudo-Euclidean notations, regardless of the Wick rotation to Euclidean signature space is assumed when we refer to the heat kernel results.
2 Conformal anomaly with scalar fields
Consider first the toy model with N copies of Dirac spinor fields \({\Psi }_k\) and a single real scalar field \(\Phi \) in curved space,
with nonminimal parameter \( \xi =\frac{1}{6}\). Other couplings include scalar self-interaction \(\lambda \) and Yukawa constant h. The conformal model (1) is useful owing to its simplicity and generality. The last means the presence of fermions with Yukawa interaction provide renormalization of the kinetic term for the scalar field already at the one-loop level. The total derivative term \({{\,\mathrm{\square }\,}}\Phi ^2\) with arbitrary parameter \(\tau \) is required to have renormalizable theory. The renormalization of this term is very important, as we shall see in what follows.
The generalization to an arbitrary conformal multiscalar model with spinor, vector fields, and an arbitrary gauge group is not complicated. The general action has the form \(S(\Phi ,\Psi ,A,g)\), where \(\Phi \), \(\Psi \), A and g are scalars, fermions, vectors and metric.
On top of the general covariance, this model is also invariant under the transformation called local conformal symmetry,
The renormalizable theory on curved backgrounds (see, e.g. [21, 22] for the introduction) requires the conformal vacuum term
where
is the square of the Weyl tensor and \(E_4=R_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu } - 4 R_{\alpha \beta }R^{\alpha \beta } + R^2\) is the integrand of the Gauss–Bonnet topological term.
Regardless the surface terms \({{\,\mathrm{\square }\,}}\Phi ^2\), \(E_4\), and \({{\,\mathrm{\square }\,}}R\) are not conformal, the symmetry holds in the corresponding Noether identity corresponding to (2),
where \(d_\Phi =-1\) is the conformal weight of the background scalar field. If including fermions and vectors, the weights are \(d_\Psi =-\frac{3}{2}\) and \(d_A=0\).
According to the existing general proof [23] (see also [22] for a simplified version), the one-loop divergence \(\bar{\Gamma }^{(1)}_{div}\) in the theory (1) is conformal invariant. This means, in dimensional regularization,
where \(\varepsilon \equiv (4\pi )^{2}(n-4)\) and the local functional \(\int d^{4}x \sqrt{-g} \Delta {\mathcal {L}}_c \) is conformal i.e., satisfies (5).
On the other hand, the renormalized one-loop effective action
violates Noether identity. Here \(\bar{\Gamma }^{(1)}=\bar{\Gamma }^{(1)}_{div}+\bar{\Gamma }^{(1)}_{fin} \) is non-renormalized one-loop contribution and \(\Delta S^{(1)}\) includes local counterterms introduced to cancel the UV divergences. The breaking of the symmetry due to quantum corrections characterizes the conformal anomaly [1,2,3,4].
The expression for the divergences in our model (1) is
where \((\nabla \Phi )^2 = g^{\mu \nu }\partial _\mu \Phi \,\partial _\nu \Phi \). In the limit \(n \rightarrow 4\), the integral in the expression (8) satisfies (5).
In the general case, when the theory includes scalars, spinors and vectors, the one-loop conformal invariance implies that the one-loop divergences have the form
where \(\widetilde{\beta }_{\lambda } =\beta _\lambda + 4\lambda \gamma _\Phi \). The gamma function \(\gamma _\Phi \) and the beta functions w, b, c, \(\beta _\lambda \) and \(\beta _\tau \) depend on the particle contents of the theory.
The coefficients w, b and c are the one-loop \(\beta \)-functions in the vacuum sector. They depend only on the number of fields of different spins [22, 24],
In the particular case of (8), \(N_0=1\), \(N_{1/2}=N\) and \(N_1=0\). In the scalar sector, \(\beta _\lambda \), \(\gamma _\Phi \) and \(\beta _\tau \) depend on the gauge group, coupling constants and other details of the model. In the simple example (8) considered above,
The anomaly cannot be derived completely using the identity (5) because of the problems with surface terms [5, 24]. However, following the scheme of [9, 19], one can obtain the anomaly by taking variational derivative with respect to the conformal factor,
Here \( \big | \) means the replacement \(\bar{g}_{\mu \nu } \rightarrow g_{\mu \nu }\), \(\bar{\Phi } \rightarrow \Phi \), and \(\sigma \rightarrow 0\).
It is remarkable that the general form of the divergences in the scalar sector remains qualitatively the same (8) in any other conformal model with a scalar field or fields. Thus, the general structure of the anomaly (16) holds on. The main modification concerns corresponding renormalization group functions. In particular, there are no dramatic changes if the scalar is complex and multi-component. For the MSM Higgs we have to make the following replacements in both divergences and anomaly:
and the rest is the same.
As another example, consider the SU(2) model [25]
where scalars and spinors are in the adjoint representation of the gauge group, \( G^{a}_{\mu \nu }=\nabla _\mu A^{a}_{\nu }-\nabla _\nu A^{a}_{\mu }+g\varepsilon ^{abc}A^{b}_{\mu }A^{c}_{\nu }\), and \(({{\mathcal {D}}}_{\mu }\Phi )^{a}=\delta ^{ab}\nabla _\mu \Phi ^{b} +ig\varepsilon ^{acb}A^{c}_{\mu }\Phi ^{b} \) is the covariant derivative of scalars (or the same for spinors). In this theory, the coefficients in the scalar sector are [21]
One can also find the coefficients for other cases, such as GUT-like models (e.g. [26]) and the Minimal Standard Model [27]. As we have mentioned above, the general structure of anomaly (16) remains and only the coefficients get modified.
At this point we can make a classification of the scalar-dependent structures in the anomaly (16), similar to that of [4, 28] in the purely metric case. There are
-
(i)
Real conformal terms, such as \(C^2\), \(\Phi ^4\) and \(\,(\nabla \Phi )^2 + \frac{1}{6}R\Phi ^2\). It proves useful introducing special notation for the generalized conformal structures in the anomaly,
$$\begin{aligned}{} & {} X_c = (\nabla \Phi )^2 + \dfrac{1}{6}\,R\Phi ^2 {,} \nonumber \\{} & {} Y(g_{\mu \nu },\Phi ) = wC^2 - \gamma _\Phi X_c + \dfrac{1}{4!}\,\widetilde{\beta }_{\lambda }\Phi ^4. \end{aligned}$$(22) -
(ii)
Unique topological term \(E_4\), independent on the extra fields such as scalars.
-
(iii)
Total derivatives, in the present case \(\Box R\) and \(\Box \Phi ^2\). In the next section we shall see that these terms are generated by local terms in the induced action. Whether or not these terms can be regarded as irrelevant, depends on the model, as we shall discuss in what follows.
Let me mention that the topological term remains unique in higher (even, at least) dimensions [29]. However, there is no general proof that the total derivatives in the anomaly can be always generated by local actions regardless this is the case in dimension six and, in general, for all available examples.
3 Integration of anomaly with a scalar field
To anomaly-induced effective action of the background fields \(g_{\mu \nu }\) and \(\Phi \) is a solution to the equation
Such a solution for a purely gravitational case was found in [6, 7] and represents a four dimensional generalization of the Polyakov action [30] in two dimensions. There are generalizations including torsion [31, 32] and the parity-violating term [33]. Also, the general solution for an arbitrary even dimension was obtained in [29].
The first observation is that the total derivative terms in the anomaly \(\langle {\mathcal {T}} \rangle \) can be obtained using the relations
The conformal invariants can be kept together with \(C^2\) as in Eq. (22), simplifying a lot the derivation of anomaly-induced action. Furthermore, we will need the relation
where \( \Delta _4 \) is the Paneitz operator [34,35,36]
satisfying \(\sqrt{-g}\Delta _4=\sqrt{-\bar{g}}\bar{\Delta }_4\). In what follows we use the compact notation \(\int _x\equiv \int d^4 x\sqrt{-g(x)}\). The fundamental relation (26) is the main element that enables the integration of anomaly, as it provides the formula
that is valid for an arbitrary conformal functional \(A[g_{\mu \nu },\Phi ]=A[\bar{g}_{\mu \nu },\bar{\Phi }]\).
The simplest solution can be obtained directly from (23), (24), (25) and (26), in the form
where \(\sqrt{-g} = \sqrt{-{{\bar{g}}}} e^{4\sigma }\) and \(R = e^{-2\sigma }\big [{{\bar{R}}} - 6({{\bar{\nabla }}}\sigma )^2 - 6 \bar{{{\,\mathrm{\square }\,}}} \sigma \big ]\). In (29), \(S_c[{{\bar{g}}}_{\mu \nu },{{\bar{\Phi }}}]=S_c[g_{\mu \nu },\Phi ]\) is an “integration constant” for Eq. (29) i.e., the conformal functional that cannot be obtained from anomaly and, therefore, has no direct relation to the UV divergences.
An alternative, non-local covariant solution of (23) requires introducing Green function for the Paneitz operator,
Using (28) and the general scheme [29], we obtain (see e.g. [22] for the details)
Rewriting (31) in the symmetric form, we get
Finally, we rewrite the result (32) in the local representation by introducing two auxiliary fields \(\varphi \) and \(\psi \) [37] (see also [33, 38] for an alternative presentation). The result is
Let us note that the non-local covariant expression (31) is a particular case of the formula given in the recent work [39] (there were also particular examples for other fields, e.g., [33, 40]). As we already mentioned above, this structure is quite general and actually holds in any even-dimensional spacetime [29]. A remarkable feature of the solutions (31) and (33) is that the induced effective action, as given in these formulas, is invariant under global conformal transformations (2), i.e., with \(\sigma =const\). However, this invariance does not contradict the fact that the global conformal symmetry of the theory is anomalous.
The forms (29), (31) and (33) are equivalent, regardless for the non-cosmological applications (see, e.g., [9] and references therein) (33) is more useful owing to covariance and locality. The phenomenological generalization for light massive quantum fields has been constructed in [41, 42] for the simplest form (29).
Concerning zero-order cosmology i.e., for the dynamics of the conformal factor of the metric, we note that there is a significant difference between the purely metric background and the solution with scalar, such as (33). In the metric case, the functional \(S_c\) is irrelevant because the metric is defined by (2) with \(\,e^\sigma = a(\eta )\), where \(\eta \) is conformal time. As a result, \(S_c\) does not depend on \(a(\eta )\), and the anomaly-induced effective action looks like an exact form of quantum corrections at the one-loop level. Furthermore, assuming that the general structure of anomaly does not change at higher loops, the unique detail that may change beyond the one-loop order concerns the beta functions. In the scalar case, anomaly includes extra terms (16) and, on the other hand, the functional \(S_c\) depends on the scalar fields \(\Phi \). Thus, the solution (33) cannot be regarded as exact anymore. The status of this solution is like one of the purely metric background in the case of black hole solution or other similar situations [9].
Another important question is whether the form of anomaly may be the same at higher loops, if the initial quantum theory includes scalar fields. To address this issue we have to explore in detail the effective action of scalar field at one loop, including the corresponding ambiguities. This will be the subject of the next section.
The last important item to note is that the expressions (29), (31) and (33) are valid only for massless conformal fields. In case of massive Higgs or other massive fields contributing to \(\widetilde{\beta }_\lambda \), \(\gamma _\Phi \), w, b, c and \(\beta _\tau \), these results can be regarded as UV approximation. In the case of \(\widetilde{\beta }_\lambda \), \(\gamma _\Phi \), w and c this fact can be confirmed by direct analysis of the nonlocal form factors [43,44,45].
4 Ambiguities in the total derivative terms
Let us discuss the existence of ambiguities in the beta functions of the surface terms c and \(\beta _\tau \) of (16). We already know from (24) and (25) that these terms produce \(\int d^4x\sqrt{-g}R^2\) and \(\int d^4x\sqrt{-g}R\Phi ^2\) finite terms in the induced action.
The case of the \(c{{\,\mathrm{\square }\,}}R\)-term was extensively discussed in the literature as mainly unsolved problem coming from the choice of regularization. In this respect, it is worth mentioning the book [24] and important review paper [5]. In a more conclusive way, the problem was considered in [19] for the particular example of a real scalar field. The ambiguity in the coefficient \(\beta _\tau \) has been considered in [20] for the two examples, i.e., the self-interacting scalar and the Yukawa model. In the last case the theory had a purely background scalar field and took into account quantum effects of a fermion. The analysis in Ref. [19] included various types of regularization. One of the main points was that there is an ambiguity in the choice of the Weyl-squared counterterm, related to the possibility to choose the counterterm with \(C^2(d)\) with \(d=n+\gamma (n-4)\), instead of \(C^2(4)\) [3] or a more simple version with \(C^2(n)\). It was shown that this ambiguity is completely equivalent to the freedom of introducing a finite \(\int d^4x\sqrt{-g}R^2\)-term in the classical vacuum action (3). As this term produces \({{\,\mathrm{\square }\,}}R\) in the Noether identity (5), the \({{\,\mathrm{\square }\,}}R\)-term in the anomaly gets modified and looks ambiguous. Another example of a qualitatively similar ambiguity, not related to the choice of \(C^2(d)\), is the Pauli–Villars regularization, that shows an ambiguity for the beta function c [20].
The important difference between c and \(\beta _\tau \) is that introducing an \(R^2\)-term into the lagrangian of vacuum does not spoil the symmetry for the quantum fields and can be regarded as kind of “legitimate” procedure. The situation is opposite for the \(\Phi ^2\)-term. Changing the coefficient of this term in the classical lagrangian from \(\frac{1}{6}\) to any \(\xi \ne \frac{1}{6}\) breaks down the conformal symmetry in the sector of quantum fields. Then, the one-loop divergences become conformally non-invariant i.e., they do not have special structure of (9). In this case, one needs an independent renormalization of \(\xi \) in the action (1), hence the conformal value \(\xi = \frac{1}{6}\) cannot be a fixed point of the renormalization group flow. Strictly speaking, without conformal symmetry there is no sense to speak about anomaly. Thus, the \({{\,\mathrm{\square }\,}}\Phi ^2\)-type ambiguity is a critical issue for the quantization of any quantum theory with scalar fields.
Since for the \({{\,\mathrm{\square }\,}}\Phi ^2\) term there is no ambiguity in the dimensional regularization, in what follows we extend the Pauli–Villars – based analysis [19, 20] to arbitrary model with scalars, fermions and vectors. As we shall see below, this extension is not completely trivial. As before, we assume that there is only a single real scalar \(\Phi \), but without imposing restrictions on gamma and beta functions in the divergences (9).
Pauli–Villars regularization requires introducing the set of scalar or spinor fields (regulators) [46,47,48] with the specially chosen masses \(m_i\) and with indefinite Grassmann parity. We will need the one-loop contributions of an individual scalar regulator \(\varphi _i\) with the mass \(m_i\) in the external background of the scalar field \(\Phi \) and metric,
where \(\kappa \) is an artificial coupling which will prove useful later on, while \(m_i\) and \(\xi _i\) are masses and non-minimal parameters for the scalars regulators.
The contribution of the regulator may enter with either positive or negative sign, depending on the statistics of \(\varphi _i\). In both cases, we can use the expression for the effective action which was calculated using the heat kernel method [49, 50] in [43, 44, 51], including for the metric-scalar background [45] (an independent equivalent calculation was reported in [52]) and also using Feynman diagrams [22, 43, 44, 53]. The result, for the bosonic statistics, has the form
where \(\tau _i = {{\,\mathrm{\square }\,}}/m_i^2\) and we use the compact notations
where \(\gamma \approx 0.577\) is the Euler–Mascheroni constant. The expressions for the non-local form factors \(k_W\), \(k_R\), \(k_\kappa \) and \(k_\xi \) can be found in [45]. For us it is sufficient to remember that (i) the UV logarithmic factors are always proportional to \(\,\text{ ln }\,\mu ^2\), as shown below; (ii) in the IR limit \(m_i \rightarrow \infty \) all these form factors vanish as \(\,{{\mathcal {O}}}(\tau _i)\).
In the conformal limit, \(m_i \rightarrow 0\) and \(\widetilde{\xi }_i \rightarrow 0\), the finite part in (35) boils down to
All the terms here violate local conformal symmetry. The first two terms in the integrand are nonlocal and correspond to the one-loop divergences in the Weyl-squared and \(\Phi ^4\) terms, respectively. The last two terms are local and correspond to the total derivative, \({{\,\mathrm{\square }\,}}R\) and \({{\,\mathrm{\square }\,}}\Phi ^2\) terms in the anomaly via (24) and (25). One can say that (37) is an alternative to (32) form of the effective action responsible for anomaly [54, 55], but we shall use this expression as an instrument to explore the ambiguity.
The procedure of Pauli–Villars regularization starts from (35) and requires the set of auxiliary (regulator) fields (34) with \(i = 1,\ldots ,N\). For exploring the ambiguity, these fields should have general \(\widetilde{\xi }_i\). Each field has a degeneracy \(s_i\) multiplied by 1 in the case of bosonic, or \(-2\) for the fermionic statistics. Starting from the simplest case of a single scalar \(\Phi \), we label it as \(\varphi _0\), assuming \(\widetilde{\xi }_0=0\) and \(s_0=1\). Then the Pauli–Villars regularized effective action can be defined as
The \(i=0\) term is given by (37) plus the divergent part \({{\mathcal {O}}}(1/\epsilon )\). Consider \(m_i=\mu _i M\), where M is the dimensional parameter of regularization and \(\mu _i\) are dimensionless coefficients to be defined. We can choose \(\mu _i\) in such a way that the \({{\mathcal {O}}}(1/\epsilon )\) terms in (38) cancel out and the auxiliary dimensional regularization becomes irrelevant. In fact, we could replace it by the covariant cut-off in the heat-kernel integral, as it was done in [19, 20].
The Pauli–Villars conditions eliminating \({{\mathcal {O}}}(1/\epsilon )\) terms and (in case of covariant cut-off) also the quadratic and quartic divergences, have the form
Some explanation is in order. The condition (39) provides cancellation of quartic divergences and also Weyl-squared \({{\mathcal {O}}}(1/\epsilon )\) terms. The two conditions (40) eliminate quadratic divergences in the cut-off scheme. Finally, the conditions (41) eliminate logarithmic divergences (i.e., \({{\mathcal {O}}}(1/\epsilon )\)) of the cosmological constant and \(R^2\)-types.
A possible solution to these conditions corresponds to \(N=5\) and
This solution is also valid for combinations of the conditions in (40) and (41), i.e.,
required for the \(R\Phi ^2\) divergence. Using (38), we arrive at the following expression for conformal anomaly in the covariant Pauli–Villars regularization for a single scalar field,
where \(\gamma _\Phi = 0\) and we define
As in [20], we find a dependence on the parameters of Pauli–Villars for the coefficients of the total derivative terms \(\square \Phi ^2\) and \(\square R\).
One can note that there is an ambiguity in both terms \({{\,\mathrm{\square }\,}}\Phi ^2\) and \({{\,\mathrm{\square }\,}}R\), related to the choice of \(\xi _i\) in the scalar regulators. The point is that we can choose \(\widetilde{\xi }_i=\mu ^2_i\) like it is done in the relation (44) or alternatively, take \(\widetilde{\xi }_i\equiv 0\), that also solves the system of equations (39), (40) and (41). In the latter case, we recover the standard value for those anomaly terms which are common for all regularizations that do not explicitly break conformal invariance.
The remaining question is whether we can remove all the divergences (9) in the general theory by using the Pauli–Villars regulators. This cannot be done with the regulators of only scalar type, because those do not cancel the \(X_c\) term that does not appear in the formula (35). Thus, we need to add the regulators of another type, producing the kinetic scalar counterterm.
Thus, let us introduce spinor regulators with indefinite Grassmann parity, as suggested in [20]. The operator which we put in the bilinear form is
where \(\varphi _j = \tilde{m}_j + h\Phi \), also \(\tilde{m}_j = \nu _jM\) is the mass of the regulator and \(\Phi \) is the background scalar (with generalizations to a multiscalar case described in Sect. 2). It is easy to get
The analog of (35) in the described fermionic case has the form [20, 45]
The finite nonlocal form factors \(k^f_W\) and \(k^f_R\) can be found in the second reference in [43, 44] and we used notations
The cancelation of the vacuum \(N_{1/2}\)-dependent part of (9) can be done using regulators (50) and the action
where \(j=0\) correspond to each of the physical fermions. This means, we shall need \(N_{1/2}\) copies of each of these regulators, exactly as we need \(N_0\) copies in the scalar case. The conditions for the coefficients \(t_j\) and \(\nu _j\) are completely similar to (39), (40), and (41) if we assume \(N_f=5\) and replace \(s_i \rightarrow t_j\) and \(\mu _i \rightarrow \nu _j\), this time with \(\widetilde{\xi }_j \equiv 0\). Correspondingly, the solution is given by (42) and (43) with the same replacements.
At this point we can make two relevant observations. The first is that the cancelation of the \(\Phi \)-dependent terms in (9) can be provided by the tuning of the artificial couplings \(\kappa \) and h in the regulator actions (38) and (53). This can be provided for any scalar contents and, correspondingly, for any \(\beta _\lambda \) and \(\gamma _\Phi \), even regardless of the possible gauge fixing ambiguity in the last quantity. Thus, we do not need to worry about the dependence on the scalar \(\Phi \) in the rest of our consideration.
The second point is as follows. Looking at the expressions (10), (11), and (12) it is clear that the cancelation of divergences for a general set \(N_{0,\,1/2,\,1}\) cannot be done only with scalar and fermion regulators. Thus, we need to introduce vector regulators to take care about \(N_1\)-dependent part. This regulator do not need to depend on \(\Phi \) owing to the first observation. Here we meet an aparent problem because the regulator should be massive and the massless limit in the gravitational form factors are known to manifest discontinuity [56]. However, the solution of this problem is known for a long time [46,47,48]. The regulator fields are unphysical and do not need to satisfy the same conditions of consistency as physical fields, such as correspondence between spin and statistics, or the absence of the unphysical modes. Thus, we can define the regulators for the vector part in the form
where
and \(\check{m}^2_k = \rho _k M\) is the mass of the regulator. It is important that in (55) we have double contribution of the scalar mode, like in the massless Faddeev–Popov ghosts cases. This is different from the single contribution in case of a massive vector [56, 57]. This feature guarantees the cancelation of the divergences in the \(N_1\) vacuum part of (9) if we chose the conditions similar to (39), (40), and (41) for the coefficients \(r_k\) and \(\rho _k\), take \(N_v=5\) and replace \(s_i \rightarrow r_k\) and \(\mu _i \rightarrow \rho _k\), of course with \(\widetilde{\xi }_k \equiv 0\), as in the fermion case. The solution is (42) and (43) with the appropriate replacements. The explicit form of (55), with the full set of nonlocal form factors, can be found in the second reference in [43, 44] or easily extracted from [56].
Thus, we have proven that the cancelation of divergences is possible for any particle contents and beta functions of the underlying model. The ambiguity is present and is given by (46). Let us stress that, despite the local terms satisfy the power counting in the theory, the ambiguity described above cannot be fixed by the change of renormalization parameter \(\mu \) because the corresponding terms are not present in the initial classical action and are not subject of the UV renormalization. This aspect of the theory was previously discussed in the classical paper [58] and more recently in [20]. The ambiguity in the local terms can be fixed only by introducing these nonconformal terms from the very beginning with arbitrary coefficients, that can be fixed by experiment and not by a particular regularization scheme.
5 Anomaly-induced effective action in the IR
In this section, we explore the anomaly-induced action at low energies, i.e. in the IR. The scheme which we shall use is partially similar to the one presented in [40, 59] for the electromagnetic and metric background. In what follows, we shall see that the scalar case provides interesting novelties and unexpected connection to other approaches.
For our purposes, the most useful version of the effective action is not (33) but the nonlocal form (31). Then, our approximations are as follows.
-
(i)
All matter fields are (at least approximately) massless and all \(\xi _i\approx \frac{1}{6}\), such that the conformal symmetry holds at the classical level. In this case, the anomaly-induced action is a good-quality approximation.
-
(ii)
Scalar terms \( \Phi ^4\) and \(X_c\) are dominating over the curvature terms, i.e.,
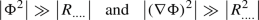 (56)
(56)for all the components of the curvature tensor
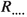 .
. -
(iii)
As always in general relativity, the IR limit means that the gravitational field is weak.Footnote 1 According to this assumption, the dominating metric-dependent quantities are those which do not vanish in the linear order in the metric perturbations \(h_{\mu \nu }\) over the flat background. In particular, this implies
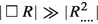 for all curvature contractions. Thus, the scalar-dependent terms and \({{\,\mathrm{\square }\,}}R\)-terms represent the most relevant part of the anomaly-induced effective action. In general, the anomaly in the vacuum sector is a sub-leading part in the given approximation and has to be treated as auxiliary element to arrive at the scalar-dependent contributions.
for all curvature contractions. Thus, the scalar-dependent terms and \({{\,\mathrm{\square }\,}}R\)-terms represent the most relevant part of the anomaly-induced effective action. In general, the anomaly in the vacuum sector is a sub-leading part in the given approximation and has to be treated as auxiliary element to arrive at the scalar-dependent contributions.
The non-local structures in the induced action reduce to a more simple form because
The leading terms in the expression (22) are those with \(\Phi \) and \({{\,\mathrm{\square }\,}}R\), hence
where we splitted Y into two parts according to (22).
After a small algebra, the nonlocal part of expression (31) boils downFootnote 2 to become
The last formula is interesting and deserves a few observations.
(i) The first integral in this expression shows that there is a modified coefficient of the local \(R^2\)-term in the IR. Let us note that this modification is a direct consequence of that the \(R^2\)-term was hidden the first line of Eq. (31) under the flat space limit. In this way we just recover the b term in the induced anomaly action in that limit. According to (11), the addition to the coefficient of \(R^2\) has the value b/18, hence it is negative and its magnitude is about 0.01–1. The effect is insufficient to explain the huge coefficient (about \(5\times 10^8 \)) of the \(R^2\)-term in the Starobinsky model [60, 61] and we still have the challenging problem of deriving this coefficient, as discussed recently in [62].
It is worth noting that the classical \(R^2\) term required to explain the observations in the inflationary model [60, 61] leads to the propagating scalar mode of the metric in the flat-space limit, exactly as it is the case for Einstein’s gravity corrected by anomaly [39]. Anyway, it is quite interesting, from the theoretical side, that the quantum effects may enlarge the spectrum of the gravitational waves in the initially conformal theory, where the scalar mode is absent.
(ii) In the symmetry-breaking regime, we have \(\Phi \approx v\) i.e., the scalar field is approximately a constant. Then the second integral in (59) takes the form
In the last summand we meet the first order term \(R\,\square ^{-1}R\) of the known nonlocal expression [63]. Physically, this may be the case for the Standard Model Higgs scalar, at the energies greater than the typical value \(v=246\) GeV. At this scale, the anomaly is an appropriate approximation and, compared to the Planck energy or the GUT scale, this may be an IR region.
Let us note that the terms \(R\,\square ^{-1}R\), \(R\,(\square ^{-1}R)^2\), etc, have the same global scaling as the usual R-term. For this reason, including these terms with the properly chosen coefficients may produce a small deviation from GR in the cosmological setting. In particular, these terms may serve as a replacement of a small cosmological constant in the phenomenological description of the acceleration of the Universe. Remarkably, we can arrive at these terms starting from the conformal anomaly and taking the low-energy approximation as described above.
It is remarkable that even in the next orders of the IR approximation, we do not meet the terms \({{\mathcal {O}}}(Y^2)\) because these structures don’t appear in the induced action (31). As a consequence, the anomaly-induced action does not generate \(R {{\,\mathrm{\square }\,}}^{-2}R\)-type terms. It is known that these terms cannot be obtained, also, from the spontaneous symmetry breaking by the curvature expansion [64]. The interest to derive such a structure is because it is used for the phenomenological description of the accelerated expansion of the Universe [65] (see also references therein), replacing the cosmological term. However, it is not easy to obtain it from the quantum considerations, at least at the one-loop order.
(iii) Let us come back to the formula (59) and consider \(g_{\mu \nu }=\bar{g}_{\mu \nu }e^{2\sigma }\) and \(\Phi =\bar{\Phi }e^{-\sigma }\). Assuming a weak gravitational field, in the linear in \(\sigma \) approximation we get
where \(\bar{{{\,\mathrm{\square }\,}}}=\bar{g}^{\mu \nu }\partial _\mu \partial _\nu \). Then, after integration with the delta function, we arrive at
with a local expression in the integrand. This output is rather natural, but still amusing. It confirms explicitly that the anomaly-induced action is, in fact, a local version of the renormalization group corrected classical action. The usual constant scaling parameter in curved space [21, 23] is replaced by the local function \(\sigma \), making curved spacetime renormalization group closer to applications [9].
Regarding (62) as a loop correction to the classical action of scalar field, the effective action of scalar field can be obtained by the changes
as it should be under the renormalization group - based improvement. In particular, one can use this approach to recover the one-loop effective potential. For this, one has to follow the procedure:
that is coherent with the scalar part of (2). At the end, one has to replace \(\bar{\Phi }\) by \(\Phi \) and \(\bar{g}_{\mu \nu }\) by \(g_{\mu \nu }\), as we did in the previous sections.
For the one-loop effective potential, in this way we arrive at
where \(\widetilde{\beta }_{\lambda } =\beta _\lambda + 4\lambda \gamma _\Phi \). Formula (65) requires only the renormalization conditions to become the standard expression for the massless conformal theory in curved spacetime [21], that is a direct extension of the Coleman and Weinberg potential [66]. One can include \(X_c\) term together with \(R\Phi ^2\) and get the first term in the derivative expansion of effective action. This would be completely equivalent to the renormalization-group based method [21, 67]. This equivalence may be observed in the scattering of gravitational perturbations on a flat background, as it was recently considered in [39]. The relation between the anomaly-induced action and the effective potential (65) shows that this equivalence can be extended to other applications.
The procedure of deriving the effective potential and other terms in the effective actions from anomaly is expected to work only for those terms which have UV logarithmic divergences and are not related to the masses of quantum fields. The anomaly picks up the UV sector of quantum corrections and it is not a surprise that, with certain skills, one can recover the corresponding terms, e.g. in the potential.
6 Conclusions and discussions
We have formulated the anomaly-induced effective action in curved spacetime with additional background scalars. The result is given in the covariant nonlocal form (29), it is also presented as local action (33) using two auxiliary scalars. The prescription for deriving the induced effective actions is pretty well-known, including a very general form [29] and enables one to add extra fields, as we did with scalars. Let us note that the non-covariant form of induced metric-scalar action has been previously obtained in [41, 42], including for light massive quantum fields. We hope that the covariant forms obtained above can be also extended to the light massive fields case, but at the moment this remains an unsolved problem.
The most complicated new results of the present work are the extension of the Pauli–Villars regularization ambiguities for the local terms in the effective action to an arbitrary quantum theory including scalar fields and, especially, the consideration of the low-energy limit in the induced effective action.
The problem of ambiguities has been previously addressed in [19, 20] for pure gravity and for the case of a single real scalar field. The extension of this analysis to an arbitrary gauge model required a new type of fine tuning for the scalar and spinor regulators, in the part of their coupling to background scalars, and also introducing massive vector field regulators in such a way that the massless limit does not show a usual discontinuity. We have described how this can be done in Sect. 4. The main output of this part of our work is that there is always an ambiguity in the one-loop finite quantum correction of the \(R\Phi ^2\)-type.
The main question related to the conformal symmetry and anomaly is whether the general structure of anomaly or, equivalently, the form of induced action (29) can be preserved beyond the one-loop level. Our results show that, starting from the two-loop approximation, preserving the structure of anomaly requires a fine tuning of the Pauli–Villars regulators, such that the combination \(\beta _\tau + 3\rho \) i.e., the coefficient of \({{\,\mathrm{\square }\,}}\Phi ^2\) term in the anomaly (46), vanish. Since the only instrument to provide this cancelation is the choice of \(\widetilde{\xi }_i = 0\) or \(\widetilde{\xi }_i = \mu _i^2\) in (47), this cancelation looks impossible.
What happens after that can be described as follows. The non-local anomalous terms do not produce UV divergences. In contrast, the local \(R\Phi ^2\) term does. The one-loop \(R\Phi ^2\) looks exactly as the classical non-conformal term with an extra \(\hbar \). Then, for the second (superficial) integration in the two-loop diagrams this term produces the \({{\mathcal {O}}}(\hbar ^2)\) term with the \(1/\epsilon \) divergence. Consequently, the two-loop beta-function for \(\xi \) has no fixed point at \(\xi =\frac{1}{6}\) and the whole conformal framework breaks down. Taking the described situation into account, at the two-loop order of the theory with scalars we have to deal with \(\xi \ne \frac{1}{6}\) and the theory becomes essentially non-conformal. Thus, the general expectation is that beyond the first loop, the structure of anomaly and the anomaly-induced action becomes qualitatively different and the conformal symmetry can be regarded only as an approximation. It is worth mentioning that this scenario is known in the literature both from the direct higher-loop calculations [16] in the \(\phi ^4\) theory and, most important, from the general analysis of the conformal Ward identities [23]. In this work, we clarified the role of regularization in this scenario. The last observation in this part is that, qualitatively the same situation takes place with the term \({{\,\mathrm{\square }\,}}R\) in all possible versions of conformal quantum gravity theory.
Our analysis of the low-energy limit in the anomaly-induced action has been performed in the way regarded standard in general relativity. This approach led us to the reduced form (59) of the action. This expression manifested a few qualitatively new properties. First of all, we have found a new contribution to the local \(R^2\) term in the IR. Second, in the IR we can reproduce, starting from the induced action, the non-local structure \(R{{\,\mathrm{\square }\,}}^{-1}R\) introduced earlier in the literature [43, 44], especially used in cosmology on the purely phenomenological ad hoc basis [63]. On the other hand, it is not possible to generate \(R{{\,\mathrm{\square }\,}}^{-2}R\) term, also existing in the literature on modified gravity [65]. Third, we confirmed that the anomaly-induced action represents a useful local version of the renormalization group in curved spacetime. In particular, it turns out possible to recover the effective potential of the conformal scalar field starting from the induced action.
Data Availability
This manuscript has associated data in a data repository. [Authors’ comment: This is a theoretical paper, and it has no associated experimental data.]
Notes
This means that in GR the low-energy approximation is actually a weak curvature limit.
On top of this, there is a usual local part, i.e., \(- \int _x\,\Big (\frac{2 b+3c}{36}R^2 + \frac{\beta _\tau }{6} R\Phi ^2\Big ).\)
References
D.M. Capper, M.J. Duff, L. Halpern, Photon corrections to the graviton propagator. Phys. Rev. D 10, 461 (1974)
D.M. Capper, M.J. Duff, Neutrino corrections to the graviton propagator. Nucl. Phys. B 82, 147 (1974)
M.J. Duff, Observations on conformal anomalies. Nucl. Phys. B 125, 334 (1977)
S. Deser, M.J. Duff, C. Isham, Nonlocal conformal anomalies. Nucl. Phys. B 111, 45 (1976)
M.J. Duff, Twenty years of the Weyl anomaly. Class. Quantum Gravity 11, 1387 (1994). arXiv:hep-th/9308075
R.J. Riegert, A non-local action for the trace anomaly. Phys. Lett. B 134, 56 (1984)
E.S. Fradkin, A.A. Tseytlin, Conformal anomaly in Weyl theory and anomaly free superconformal theories. Phys. Lett. B 134, 187 (1984)
I. Antoniadis, E. Mottola, \(4-D\) quantum gravity in the conformal sector. Phys. Rev. D 45, 2013 (1992)
I.L. Shapiro, Effective action of vacuum: semiclassical approach. Class. Quantum Gravity 25, 103001 (2008). arXiv:0801.0216
W.A. Bardeen, On naturalness in the standard model. FERMILAB-CONF-95-391-T
K.A. Meissner, H. Nicolai, Conformal symmetry and the Standard Model. Phys. Lett. B 648, 312 (2007). arXiv:hep-th/0612165
J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Riotto, A. Strumia, Higgs mass implications on the stability of the electroweak vacuum. Phys. Lett. B 709, 222 (2012). arXiv:1112.3022
M. Holthausen, K.S. Lim, M. Lindner, Planck scale boundary conditions and the Higgs mass. JHEP 02, 037 (2012). arXiv:1112.2415
J. Elias-Miro, J.R. Espinosa, G.F. Giudice, H.M. Lee, A. Strumia, Stabilization of the electroweak vacuum by a scalar threshold effect. JHEP 06, 031 (2012). arXiv:1203.0237
I.T. Drummond, G.M. Shore, Conformal anomalies for interacting scalar fields in curved spacetime. Phys. Rev. D 19, 1134 (1979)
S.J. Hathrell, Trace anomalies and \(\lambda \varphi ^{4} \) theory in curved space. Ann. Phys. 139, 136 (1982)
M.A. Valle, M.A. Goni, Conformal transformation of the one-loop effective action for \(\lambda \varphi ^{4} \) theory. Phys. Rev. D 36, 615 (1987)
M.S. Alves, J. Barcelos-Neto, Path integrals and the trace anomaly in a self-interacting scalar theory. Mod. Phys. Lett. A 4, 115 (1989)
M. Asorey, E.V. Gorbar, I.L. Shapiro, Universality and ambiguities of the conformal anomaly. Class. Quantum Gravity 21, 163 (2004). arXiv:hep-th/0307187
M. Asorey, G. de Berredo-Peixoto, I.L. Shapiro, Renormalization ambiguities and conformal anomaly in metric-scalar backgrounds. Phys. Rev. D 74, 124011 (2006). arXiv:hep-th/0609138
I.L. Buchbinder, S.D. Odintsov, I.L. Shapiro, Effective Action in Quantum Gravity (IOP Publishing, Bristol, 1992)
I.L. Buchbinder, I.L. Shapiro, Introduction to Quantum Field Theory with Applications to Quantum Gravity (Oxford University Press, Oxford, 2021)
I.L. Buchbinder, On Renormalization group equations in curved space-time. Theor. Math. Phys. 61, 393 (1984)
N.D. Birrell, P.C.W. Davies, Quantum Fields in Curved Space (Cambridge University Press, Cambridge, 1982)
B.L. Voronov, I.V. Tyutin, Models of asymptotically free massive fields. Yad. Fiz. 23, 664 (1976)
I.L. Buchbinder, I.L. Shapiro, E.G. Yagunov, The asymptotically free and asymptotically conformal invariant Grand Unification theories in curved space-time. Mod. Phys. Lett. A 5, 1599 (1990)
Y. Yoon, Y. Yoon, Asymptotic conformal invariance of SU(2) and standard models in curved space-time. Int. J. Mod. Phys. A 12, 2903 (1997). arXiv:hep-th/9612001
S. Deser, A. Schwimmer, Geometric classification of conformal anomalies in arbitrary dimensions. Phys. Lett. B 309, 279 (1993). arXiv:hep-th/9302047
F.M. Ferreira, I.L. Shapiro, Integration of trace anomaly in \(6D\). Phys. Lett. B 772, 174 (2017). arXiv:1702.06892
A.M. Polyakov, Quantum geometry of bosonic strings. Phys. Lett. B 207, 211 (1981)
I.L. Buchbinder, S.D. Odintsov, I.L. Shapiro, Nonsingular cosmological model with torsion induced by vacuum quantum effects. Phys. Lett. B 162, 92 (1985)
J.A. Helayel-Neto, A. Penna-Firme, I.L. Shapiro, Conformal symmetry, anomaly and effective action for metric-scalar gravity with torsion. Phys. Lett. B 479, 411 (2000). arXiv:gr-qc/9907081
S. Mauro, I.L. Shapiro, Anomaly-induced effective action and Chern–Simons modification of general relativity. Phys. Lett. B 746, 372 (2015). arXiv:1412.5002
E.S. Fradkin, A.A. Tseytlin, Asymptotic freedom on extended conformal supergravities. Phys. Lett. B 110, 117 (1982)
E.S. Fradkin, A.A. Tseytlin, One-loop beta function in conformal supergravities. Nucl. Phys. B 203, 157 (1982)
S. Paneitz, A Quartic conformally covariant differential operator for arbitrary pseudo-Riemannian manifolds, MIT preprint, 1983. SIGMA 4, 036 (2008). arXiv:0803.4331
I.L. Shapiro, A.G. Jacksenaev, Gauge dependence in higher derivative quantum gravity and the conformal anomaly problem. Phys. Lett. B 324, 286 (1994)
P.O. Mazur, E. Mottola, Weyl cohomology and the effective action for conformal anomalies. Phys. Rev. D 64, 104022 (2001). arXiv:hep-th/0106151
E. Mottola, Scalar gravitational waves in the effective theory of gravity. JHEP 07, 043 (2017). arXiv:1606.09220. [Erratum: JHEP 09, 107 (2017)]
M. Giannotti, E. Mottola, Trace anomaly and massless scalar degrees of freedom in gravity. Phys. Rev. D 79, 045014 (2009). arXiv:0812.0351
I.L. Shapiro, J. Solà, Massive fields temper anomaly-induced inflation: the clue to graceful exit? Phys. Lett. B 530, 10 (2002). arXiv:hep-ph/0104182
A.M. Pelinson, I.L. Shapiro, F.I. Takakura, On the stability of the anomaly-induced inflation. Nucl. Phys. B 648, 417 (2003). arXiv:hep-ph/0208184
E.V. Gorbar, I.L. Shapiro, Renormalization group and decoupling in curved space. JHEP 02, 021 (2003). arXiv:hep-ph/0210388
E.V. Gorbar, I.L. Shapiro, Renormalization group and decoupling in curved space, II. The standard model and beyond. JHEP 02, 021 (2003). arXiv:hep-ph/0303124
G. de Berredo-Peixoto, E.V. Gorbar, I.L. Shapiro, On the renormalization group for the interacting massive scalar field theory in curved space. Class. Quantum Gravity 21, 2281 (2004). arXiv:hep-th/0311229
A.A. Slavnov, The Pauli–Villars regularization for nonabelian gauge theories. Theor. Math. Phys. 33, 210 (1977)
T.D. Bakeyev, A.A. Slavnov, Higher covariant derivative regularization revisited. Mod. Phys. Lett. A 11, 1539 (1996). arXiv:hep-th/9601092
M. Asorey, F. Falceto, Geometric regularization of gauge theories. Nucl. Phys. B 327, 427 (1989)
A.O. Barvinsky, G.A. Vilkovisky, Covariant perturbation theory (II). Second order in the curvature. General algorithms. Nucl. Phys. B 333, 471 (1990)
I.G. Avramidi, Covariant methods of study on the nonlocal structure of effective action. Yad. Fiz. (Sov. J. Nucl. Phys.) 49, 1185 (1989)
S.A. Franchino-Viñas, T. de Paula Netto, I.L. Shapiro, O. Zanusso, Form factors and decoupling of matter fields in four-dimensional gravity. Phys. Lett. B 790, 229 (2019). arXiv:1812.00460
K.A. Meissner, H. Nicolai, Effective action, conformal anomaly and the issue of quadratic divergences. Phys. Lett. B 660, 260 (2008). arXiv:hep-th/0710.2840
A. Codello, O. Zanusso, On the non-local heat kernel expansion. J. Math. Phys. 54, 013513 (2013). arXiv:1203.2034
A.O. Barvinsky, Y.V. Gusev, G.A. Vilkovisky, V.V. Zhytnikov, The one loop effective action and trace anomaly in four-dimensions. Nucl. Phys. B 439, 561 (1995). arXiv:hep-th/9404187
A.O. Barvinsky, A.G. Mirzabekian, V.V. Zhytnikov, Conformal decomposition of the effective action and covariant curvature expansion. in 6th Moscow Quantum Gravity (1995). arXiv:gr-qc/9510037
I.L. Buchbinder, G. de Berredo-Peixoto, I.L. Shapiro, Quantum effects in softly broken gauge theories in curved spacetimes. Phys. Lett. B 649, 454 (2007). arXiv:hep-th/0703189
A.O. Barvinsky, G.A. Vilkovisky, The generalized Schwinger–DeWitt technique in gauge theories and quantum gravity. Phys. Rep. 119, 1 (1985)
L.S. Brown, J.C. Collins, Dimensional renormalization of scalar field theory in curved space-time. Ann. Phys. 130, 215 (1980)
E. Mottola, R. Vaulin, Macroscopic effects of the quantum trace anomaly. Phys. Rev. D 74, 064004 (2006). arXiv:gr-qc/0604051
A.A. Starobinsky, A new type of isotropic cosmological models without singularity. Phys. Lett. B 91, 99 (1980)
A.A. Starobinsky, The perturbation spectrum evolving from a nonsingular initially de-Sitter cosmology and the microwave background anisotropy. Sov. Astron. Lett. 9, 302 (1983)
T.D.P. Netto, A.M. Pelinson, I.L. Shapiro, A.A. Starobinsky, From stable to unstable anomaly-induced inflation. Eur. Phys. J. C 76, 544 (2016). arXiv:1509.08882
S. Deser, R.P. Woodard, Nonlocal cosmology. Phys. Rev. Lett. 99, 111301 (2007). arXiv:astro-ph/0706.2151
E.V. Gorbar, I.L. Shapiro, Renormalization group and decoupling in curved space 3. The case of spontaneous symmetry breaking. JHEP 02, 060 (2004). arXiv:hep-ph/0311190
M. Maggiore, L. Hollenstein, M. Jaccard, E. Mitsou, Early dark energy from zero-point quantum fluctuations. Phys. Lett. B 704, 102 (2011). arXiv:1104.3797
S.R. Coleman, E.J. Weinberg, Radiative corrections as the origin of spontaneous symmetry breaking. Phys. Rev. D 7, 1888 (1973)
I.L. Buchbinder, J.J. Wolfengaut, Renormalization group equations and effective action in curved space-time. Class. Quantum Gravity 5, 1127 (1988)
Acknowledgements
W.C.S. and P.R.B.V. are grateful to CAPES for supporting their Ph.D. projects. The work of M.A. is partially supported by Spanish MINECO/FEDER Grant PGC2018-095328-B-I00 and DGA-FSE Grant 2020-E21-17R. I.Sh. is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq (Brazil) under the Grant 303635/2018-5 and by Fundação de Amparo à Pesquisa de Minas Gerais - FAPEMIG, under the project PPM-00604-18.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Asorey, M., e Silva, W.C., Shapiro, I.L. et al. Trace anomaly and induced action for a metric-scalar background. Eur. Phys. J. C 83, 157 (2023). https://doi.org/10.1140/epjc/s10052-023-11293-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-11293-5



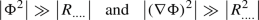
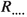 .
.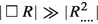 for all curvature contractions. Thus, the scalar-dependent terms and
for all curvature contractions. Thus, the scalar-dependent terms and