1 Introduction

After it was proposed in the 1920s, Kaluza–Klein (KK) theory [1, 2] was discussed repeatedly over the past 100 years. The essential idea of this theory is that the observable physical phenomena of our four-dimensional world can be reduced from a five-dimensional fundamental theory. According to string theory, the existence of extra dimensions is inevitable. Various models containing extra dimensions were proposed and discussed seriously as effective theories at certain energy level. In the braneworld scenario [3,4,5,6], our world is described as a four-dimensional brane embedded in a higher-dimensional spacetime called bulk and extra dimensions are suggested to be extended far more larger than they were thought before [4], or even infinite [3, 6].

The development of extra dimension theories gives new insight into fundamental physics. Nevertheless, the reasons that introduce the concept of extra dimensions are quite different. In KK theory, the fifth dimension was proposed in order to unify the four-dimensional gravity and electromagnetic force by regarding the electromagnetic field as the fifth component of the metric. In Arkani-Hamed–Dimopoulos–Dvali (ADD) model [4] and Randall–Sundrum (RS)-1 model [5], the existence of extra dimensions provides an alternative mechanism to resolve the gauge hierarchy problem in particle physics. On the other hand, some efforts have been made to explore the possibility of infinite extra dimensions, such as RS-2 model [6] and domain wall model [3]. Combining the above two models [3, 6], one can obtain the model of a brane with thickness (called thick brane) in a five-dimensional curve spacetime with an infinite extra dimensions. Such brane is called thick brane. In contrast, the branes in the RS-1 and RS-2 models are called thin branes since they are a pure four-dimensional hypersurface without thickness.

We may regard thin brane as an approximation to thick brane if the thickness of a brane can be neglected. However, there is a significant difference between thin brane and thick brane. In a thick brane model, there are no special dimensions as “extra dimensions” since the four-dimensional fields in the Standard Model, which are described by zero modes of some higher-dimensional fields, are lived in the bulk. However, those zero modes are localized around the thick brane and they can not propagate along extra dimensions. For a thin brane model, there are some very special extra dimensions and all the matter fields are confined on a hypersurface, i.e., the brane. Both thin and thick branes have their respective advantages. For example, thin brane resolves the hierarchy problem, while thick brane has its application in holographical QCD.

For all kinds of extra dimension theories, an important question is why we stay in a four-dimensional world and do not observe these extra dimensions. In the original KK theory it was explained by compacting the extra dimension into a tiny circle with size of Planck scale so that we can not find it in current experiments even if we actually occupy the whole volume of the five dimensions. In ADD model and RS-1/RS-2 model, it is a prior hypothesis that all matter fields are confined on a four-dimensional hypersurface embedded in five-dimensional spacetime. In the thick brane model which we mainly concern in this paper, all fields live in the bulk and the extra dimension extends infinitely, but the matter fields is trapped in a very narrow region along the extra dimension. This mechanism is called as localization. There are a lot of references for the thick brane models and localization of gravity and matter fields [7,8,9,10,11,12,13,14,15,16,17,18,19,20], see Refs. [21,22,23,24,25,26] for reviews.

Another principal problem need to be considered is how to recover ordinary four-dimensional theory such as electroweak gauge theory and general relativity from the underlying five-dimensional theory. It leads to the idea that ordinary four-dimensional physics corresponds to some five-dimensional physics. From the very popular AdS/CFT perspective, our ordinary four-dimensional physics, as a field theory living on the boundary of a five-dimensional spacetime, is totally equivalent to a gravitational theory in the bulk. On the other hand, in KK theory, domain wall model and brane model, it is accomplished by reducing the high-dimensional fundamental theory to the four-dimensional effective one, which is realized by integrating the high-dimensional action over extra dimensions.

Most of the works about localization of a scalar field on a thick brane focus on free field and few works discuss the self-interaction of a scalar field in the bulk as well as its effective theory on a thick brane. In this paper we will investigate the effective action of a self-interacting scalar field on a thick brane. We first assume a five-dimensional fundamental action of a self-interacting scalar field. Then we employ the KK reduction procedure to derive the four-dimensional effective actions of the scalar KK modes. The effective action should be coincident with the action in current four-dimensional theory. Furthermore, the five-dimensional interaction will bring new four-dimensional particles and new interaction terms between them. This will make some significant prophecies on particle collision at higher energy level.

The organization of this paper is as follows. In Sect. 2, we give a general formulation for the KK reduction of a five-dimensional action of a self-interacting scalar field. In Sect. 3, we consider two brane solutions and obtain two kinds of typical potentials which demonstrate some significant properties of the four-dimensional effective action. Finally, in Sect. 4 we devote to the conclusions and discussions.

2 KK reduction of action

Let us first consider a free massless scalar field in five-dimensional spacetime:

$$\begin{aligned} S=\int \sqrt{-g}\,d^{5}x\left( -\frac{1}{2} g^{MN} \partial _{M}\phi \partial _{N}\phi \right) . \end{aligned}$$
(1)

The five-dimensional metric is proposed as

$$\begin{aligned} ds^2 = g_{MN} dx^M dx^N = e^{2A(z)} \left( {\tilde{g}}_{\mu \nu }(x^\lambda ) dx^\mu dx^\nu +dz^2 \right) , \nonumber \\ \end{aligned}$$
(2)

where M, N and \(\mu ,\nu \) are the five-dimensional and four-dimensional coordinate indices, \(z=x^{5}\) is the extra dimensional coordinate, and \({\tilde{g}}_{\mu \nu }(x^\lambda )\) is the reduced four-dimensional metric at any fixed position of the extra dimensional coordinate \(z=z_0\) by a constant factor \(e^{2A(z_0)}\). Usually, we can set \(e^{2A(0)}=1\) by using the degree of freedom of the coordinate transformation \(x^\mu \rightarrow {\bar{x}}^{\mu } = e^{A(0)} x^\mu \).

In order to reduce the five-dimensional fundamental action (1) to a four-dimensional effective one, we separate the variables of extra dimension from ordinary four dimensions

$$\begin{aligned} \phi (x^{\mu },z) =\underset{n}{\sum }\varphi _{n}(x^{\mu })f_{n}(z), \end{aligned}$$
(3)

which is called the KK decomposition. Substituting the above decomposition into the action (1), we have

$$\begin{aligned} S= & {} -\frac{1}{2}\int \sqrt{-{\tilde{g}}} d^{4}x\int e^{5A(z)}\,dz \underset{n,m}{\sum }\ \big (f_{n}f_{m} {\partial }_{\mu }\varphi ^{n}\partial _{\nu }\varphi _{m}\nonumber \\{} & {} +\,\varphi _{n}\varphi _{m}\partial ^{5}f_{n}\partial _{5}f_{m}\big ). \end{aligned}$$
(4)

The field equation corresponding to the action (1) is the five-dimensional Klein–Gordon equation:

$$\begin{aligned} g^{MN}\nabla _{M}\nabla _{N}\phi =0. \end{aligned}$$
(5)

By virtue of the KK decomposition (3), the above Klein–Gordon equation (5) can be converted to two equations. One is the familiar four-dimensional Klein–Gordon equation of four-dimensional modes \(\varphi _{n}(x^{\mu })\) and another is an eigenvalue equation of the extra-dimensional part \(f_{n}(z)\):

$$\begin{aligned} ({\square }^{(4)}-\zeta _{n})\varphi _{n}(x^{\mu })= & {} 0, \end{aligned}$$
(6)
$$\begin{aligned} (\partial _{z}^{2}+3(\partial _{z}A)\partial _{z})f_{n}(z)= & {} \zeta _{n}f_{n}(z), \end{aligned}$$
(7)

where \({\square }^{(4)}={\tilde{g}}^{\mu \nu }\nabla _{\mu }\nabla _{\nu }\). With the redefinition of the field

$$\begin{aligned} \chi _{n}(z)=e^{\frac{3}{2}A}f_{n}(z), \end{aligned}$$
(8)

Equation (7) becomes a one-dimensional Schrödinger-like equation

$$\begin{aligned} \left[ -\partial _{z}^{2}+V(z)\right] \chi _{n}(z)=\zeta _{n}\chi _{n}(z), \end{aligned}$$
(9)

where the effective potential is

$$\begin{aligned} V(z)=\frac{3}{2}\partial _{z}^{2}A+\frac{9}{4}(\partial _{z}A)^{2}. \end{aligned}$$
(10)

If the eigenstate \(\chi _{n}(z)\) of the Schrödinger-like equation is a normalizable bound state, the corresponding KK mode is localized on a brane, in the sense that the energy density of the field actually distributes in a finite region of the extra dimension and one can obtain the four-dimensional action of the KK mode \(\varphi _{n}(x^{\mu })\). To this end, we require the normalization condition as well as in quantum mechanics:

$$\begin{aligned} \int \chi _{n}\chi _{m}\,dz=\delta _{nm}, \end{aligned}$$
(11)

or equivalently

$$\begin{aligned} \int e^{3A(z)}f_{n}f_{m}\,dz=\delta _{nm}, \end{aligned}$$
(12)

which could be inferred from Eq. (9) that

$$\begin{aligned} \int e^{3A(z)}\partial _{z}f_{n}\partial _{z}f_{m}\,dz=\delta _{nm}\sqrt{\zeta _{n}\zeta _{m}}, \end{aligned}$$
(13)

where m, n are not summarized here. The ground state with \(\zeta _0=0\) is called the zero mode and is interpreted as the ordinary four-dimensional scalar field that we have observed on the brane.

By virtue of the normalized conditions (12) and (13), the action (1) is reduced to

$$\begin{aligned} S_{\text {eff}}=\int \sqrt{-{\tilde{g}}} d^{4}x \left[ -\frac{1}{2}\underset{n}{\sum }\ \left( \partial ^{\mu }\varphi _{n}\partial _{\mu }\varphi _{n}+\zeta _{n}\varphi _{n}^{2} \right) \right] , \end{aligned}$$
(14)

where \({\partial }^{\mu } \equiv {\tilde{g}}^{\mu \nu } \partial _{\nu }\) and \(\zeta _{n}\) is the eigenvalue of Eq. (7) and it can be proven to be nonnegative. The result is interpreted as a family of four-dimensional scalar fields with different masses and \(\sqrt{\zeta _{n}}\) is called induced mass originating from extra dimension. It can be seen in another way that a massless particle in five-dimensional spacetime satisfies the following relation

$$\begin{aligned} {\tilde{g}}^{\mu \nu } p_{\mu }p_{\nu } = - (p_{5})^2. \end{aligned}$$
(15)

In case of a nonzero momentum along the extra dimension, the four-dimensional particle on the brane has an effective mass \(m=|p_{5}|\).

It should be underlined that in our formulation, by virtue of the KK decomposition of the scalar field, the equation for the extra dimensional part \(f_{n}(z)\) of the scalar field decouples from the equation of the four-dimensional part \(\varphi _{n}(x^{\mu })\). This guarantees we can study physics on the brane, otherwise we will be blind to a dynamical variable and we never have complete dynamical equations. The approach of the effective action on the brane accords with such an assertion that all observers have a right to describe physics using an effective theory based only on the variables they can access. In particle physics we have met this concept in the renormalization group theory. To describe particle interactions at 10 GeV in the lab, we do not need to know what happens at \(10^{14}\) GeV. We have also seen that this concept is demonstrated in the cosmic censorship that a horizon protects our predictive ability on the basis of general relativity from a singularity. In the braneworld scenario here, if observers are confined on brane, they should still be able to study physics using only the variables accessible to them without having to know what happens outside of the brane.

So far the scalar field is free. We would like to include interaction by adding a perturbative interaction potential \(U(\phi )\) in the action (1):

$$\begin{aligned} S_{\text {int}}=-\int \sqrt{-{\tilde{g}}}\, d^{4}x\int dz\,e^{5A(z)}\,U(\phi ). \end{aligned}$$
(16)

We expect that the following four-dimensional effective interaction term can be given by integrating the above interaction term over the extra dimension:

$$\begin{aligned} S_{\text {int}}^{(4)} =-\int \sqrt{-{\tilde{g}}}\, d^{4}x\,U^{(4)}(\varphi (x^{\mu })), \end{aligned}$$
(17)

where

$$\begin{aligned} U^{(4)}(\varphi (x^{\mu }))=\int dz\,e^{5A(z)}\,U\left( \phi \left( x^{\mu },z\right) \right) . \end{aligned}$$
(18)

It is just an integral projection from five-dimensional spacetime to our four-dimensional one. Comparing to the ordinary four-dimensional action which only involves the zero mode \(\varphi _{0}\)

$$\begin{aligned} S_{0}^{(4)}=\int \sqrt{-{\tilde{g}}}\, d^{4}x \left[ -\frac{1}{2} \left( \partial ^{\mu }\varphi _{0}\partial _{\mu }\varphi _{0} +\zeta _{0}\varphi _{0}^{2} \right) -U_{0}^{(4)}(\varphi _{0}) \right] ,\nonumber \\ \end{aligned}$$
(19)

it can be seen that

$$\begin{aligned} S^{(4)}= & {} S_{0}^{(4)} + \int \sqrt{-{\tilde{g}}}\, d^{4}x \Big [-\frac{1}{2}\underset{n\ge 1}{\sum } \big (\partial ^{\mu }\varphi _{n}\partial _{\mu }\varphi _{n}\nonumber \\{} & {} +\zeta _{n}\varphi _{n}^{2} \big ) -\left( U^{(4)}(\varphi )-U_{0}^{(4)}(\varphi _{0}) \right) \Big ]. \end{aligned}$$
(20)

The second term in the four-dimensional action (20) is new and totally originates from the extra dimension. It predicts not only new massive particles but also new interactions: \(S_{\text {int}}^{(4)}\) contains more terms other than the ordinary four-dimensional interaction \(S_{0\, \text {int}}^{(4)}=-\int d^{4}x\,U_{0}^{(4)}\). It contains all possible interactions of various KK modes \(\varphi _{n}\).

In this paper we will investigate the interaction of a quartic form

$$\begin{aligned} U=\lambda \phi ^{4}=\lambda \bigg [\underset{n}{\sum }\varphi _{n}(x^{\mu })f_{n}(z)\bigg ]^{4}. \end{aligned}$$
(21)

It can be expressed in a four-dimensional effective action as

$$\begin{aligned} S_{\text {int}}^{(4)} =-\int \sqrt{-{\tilde{g}}}\, d^{4}x\,\lambda \underset{klmn}{\sum }\gamma _{klmn}\varphi _{k}\varphi _{l}\varphi _{m}\varphi _{n}, \end{aligned}$$
(22)

where

$$\begin{aligned} \gamma _{klmn}=\int e^{5A(z)}\,dzf_{k}f_{l}f_{m}f_{n}. \end{aligned}$$
(23)

As we known in general, \(f_{k},f_{l},f_{m},f_{n}\) are four different or same KK modes. From the four-dimensional viewpoint, there are a family of scalar KK particles with different masses \(\sqrt{\zeta _{n}}\). They interact with each other with the form (22). The coupling constant \(\lambda \gamma _{klmn}\) is exactly the scattering amplitude on tree level with the Feynman diagram showed in Fig. 1. We will calculate them in the next section.

Fig. 1
figure 1

The Feynman diagram for (22)

Full size image

Furthermore, there is a very interesting difference between the cases of interactive and free scalar fields. It is convinced that we cannot measure the distribution of the field on extra dimension since we are restricted on the brane. What we could measure on brane is just the mass spectrum of the KK particles. So a problem arises: can we discover the metric of five-dimensional spacetime while the observers and all our observations are confined on a four-dimensional brane?

This question is equivalent to the quantum mechanics problem that, can we reconstruct the shape of a potential V(z) from its eigenvalue spectrum \(\{E_{n}\}\)? Unfortunately, the answer is negative. For example, the Morse potential

$$\begin{aligned} V(z)=C_{1}^{2}+e^{-2z}-(2C_{1}+1)e^{-z} \end{aligned}$$
(24)

and the Scarf (hyperbolic) potential

$$\begin{aligned} V(z)= & {} -[C_{1}(C_{1}+1)-C_{2}^{2}]\text {sech}^2 z\nonumber \\{} & {} +\,(2C_{1}+1)C_{2}\tanh z ~\text {sech}z +C_{1}^{2} \end{aligned}$$
(25)

have exactly the same eigenenergies:

$$\begin{aligned} E_{n}=C_{1}^{2}-(C_{1}-n)^{2}, \end{aligned}$$
(26)

even though the potentials and eigenfunctions are quite distinct. Here \(C_{1}\) and \(C_{2}\) are constants and \(-\infty<z<\infty \). In fact, we could learn form supersymmetric quantum mechanics that there are a large number of potentials that have the same eigenenergies and are related with each other by the so called isospectral deformations. We do not strive for the details here. There seems to be an inevitable conclusion: the five-dimensional metric can not be known if we just stay on the brane. Nevertheless, interactions of various KK modes will change this situation.

With a fundamental interaction, say, \(\phi ^{4}\), we could measure not only the mass spectrum \(\{m_{n}\}\) of the KK particles, but also the coupling constants \(\{\lambda \gamma _{klmn}\}\), which would distinguish the potentials corresponding to the same eigenvalues. The point is that the coupling constants in Eq. (23) involve eigenfunctions \(\{f_{n}\}\), which are distinct for different potentials. So we have seen the significance of interaction: the effective coupling constants reveal the structure of five-dimensional spacetime which cannot be inferred by the free fields on the brane. On the other hand, the interaction provides channels that KK particles transform into each other. The massive KK modes may decay to the zero mode, while they can also be produced from collision of the zero mode particles.

3 Properties of the effective action

We have seen that the effective potential of the KK modes is only determined by the warp factor A(z) in the bulk metric (2):

$$\begin{aligned} V(z)=\frac{3}{2}\partial _{z}^{2}A+\frac{9}{4}(\partial _{z}A)^{2}, \end{aligned}$$
(27)

which determines the KK modes \(f_{n}\) as well as the effective coupling constants \(\lambda \gamma _{klmn}\). In this paper, we only use some explicit forms of the warp factor A(z) instead of going into the details of solving the field equations for the background spacetime, which depend on the chosen gravitational theory and the background fields generating the thick brane. We will discuss two kinds of typical potentials which demonstrate some significant properties of the four-dimensional effective action.

In Refs. [27, 28], the authors presented the de Sitter braneworld model, in which an induced 3-brane with spatially flat cosmological background is considered. The action and the five-dimensional metric for this braneworld model are given by

$$\begin{aligned} S= & {} \int d^5x\sqrt{-g} \frac{1}{2\kappa ^2_5} ( R -2\Lambda _5), \end{aligned}$$
(28)
$$\begin{aligned} ds^2= & {} e^{2A(z)}\Big [-dt^2+a(t)^2(dx_1^2+dx_2^2+dx_3^2)+dz^2\Big ],\nonumber \\ \end{aligned}$$
(29)
Fig. 2
figure 2

The shape of the potential (33)

Full size image
Fig. 3
figure 3

The Feynman diagrams for (38)–(40)

Full size image

where \(\kappa ^2_5=1/M_*^3\) with \(M_*\) being the five-dimensional fundamental scale, \(\Lambda _5\) is the bulk cosmological constant, and a(t) is the scale factor of the brane. The brane solution is [27, 28]

$$\begin{aligned} A(z)= & {} \ln \left( \frac{H}{b}\textrm{sech}(Hz)\right) , \end{aligned}$$
(30)
$$\begin{aligned} a(t)= & {} e^{Ht}, \end{aligned}$$
(31)
$$\begin{aligned} \Lambda _5= & {} 6 b^2, \end{aligned}$$
(32)

where 1/b parameterizes the thickness of the brane, the parameter H is the Hubble parameter. The relation between the effective four-dimensional cosmological constant on the brane and the Hubble parameter H is \(\Lambda _4 = 3H^2\). In this paper, we consider the special case of \(b=H\) for simplicity. For the de Sitter braneworld model, the corresponding potential is the P\(\ddot{\textrm{o}}\)schl–Teller (PT) potential

$$\begin{aligned} V(z)=\frac{3}{4}H^{2}\left[ 3-5\text {sech}^{2}(Hz)\right] , \end{aligned}$$
(33)

which is shown in Fig. 2. For this potential, we have two bound states. The first one is the ground state, i.e., the zero mode

$$\begin{aligned} \chi _{0}(z)=e^{\frac{3}{2}A}f_{0}(z)=\sqrt{\frac{2H}{\pi }}\text {sech}^{\frac{3}{2}}(Hz) \end{aligned}$$
(34)

with mass

$$\begin{aligned} m_{0}=\sqrt{\zeta _{0}}=0. \end{aligned}$$
(35)

The second one is the first massive KK mode

$$\begin{aligned} \chi _{1}(z)=e^{\frac{3}{2}A}f_{1}(z)=\sqrt{\frac{2H}{\pi }}\text {sech}^{\frac{3}{2}}(Hz)\sinh (Hz) \end{aligned}$$
(36)

with mass

$$\begin{aligned} m_{1}=\sqrt{\zeta _{1}}=\sqrt{2}H. \end{aligned}$$
(37)

Here, we can see that the parameter H can be viewed as the new physics energy scale since it determines the mass of the new particle (the first massive KK particle) beyond the Standard Model. Obviously the masses are determined by the warp factor A(z) in the bulk metric. The two bound states are in fact two kinds of KK particles on the brane.

The two KK modes interact with each other via the four-dimensional effective interactions from the fundamental scalar potential \(\phi ^{4}\). The effective coupling constants are calculated as follows:

$$\begin{aligned} \lambda \gamma {}_{0000}&=\int e^{5A(z)}\,dzf_{0}^{4}=\frac{3H\lambda }{2\pi }, \end{aligned}$$
(38)
$$\begin{aligned} \lambda \gamma {}_{0011}&=\int e^{5A(z)}\,dzf_{0}^{2}f_{1}^{2}=\frac{H\lambda }{2\pi }, \end{aligned}$$
(39)
$$\begin{aligned} \lambda \gamma {}_{1111}&=\int e^{5A(z)}\,dzf_{1}^{4}=\frac{3 H\lambda }{2\pi }, \end{aligned}$$
(40)
$$\begin{aligned} \lambda \gamma {}_{0001}&=\gamma {}_{0111}=0, \end{aligned}$$
(41)

which show that there are three kinds of interactions between these two KK modes. The corresponding Feynman diagrams are shown in Fig. 3.

It can be seen that, like the mass spectrum of the KK modes, the effective coupling constants are determined by the warp factor A(z). Both of them origin from the extra dimension. However, they associate two independent parameters H and \(\lambda \). We should assume that the zero mode stands for the four-dimensional particle which has already been observed (so that \(H\lambda \) can be fixed) and has a self-interacting \(\lambda \gamma {}_{0000}\varphi _{0}^{4}\).

Provided that we make zero mode particles collide with enough energy, it should be observed in reaction new particles that correspond to the first excited mode \(f_{1}\) (so that H and \(\lambda \) can be fixed) as well as zero mode. On tree level the magnitudes of the reaction are just the effective coupling constants. The cross sections of the above two processes are

$$\begin{aligned} d\sigma _{00}= & {} (2\pi )^{2}\delta ^{4}(p_{3}+p_{4}-p_{1}-p_{2}) \frac{9 H^{2}\lambda ^{2}}{\left( -4p_{1}\cdot p_{2}\right) }\nonumber \\{} & {} *\frac{d^{3}{\vec {p}_{3}}}{(2\pi )^{3}2p_{3}^{0}} \frac{d^{3}{\vec {p}_{4}}}{(2\pi )^{3}2p_{4}^{0}}, \end{aligned}$$
(42)
$$\begin{aligned} d\sigma _{11}= & {} (2\pi )^{2}\delta ^{4}(p_{3}+p_{4}-p_{1}-p_{2}) \frac{\pi ^{2} H^{2}\lambda ^{2}}{\left( -16p_{1}\cdot p_{2}\right) }\nonumber \\{} & {} * \frac{d^{3}{\vec {p}_{3}}}{(2\pi )^{3}2p_{3}^{0}} \frac{d^{3}{\vec {p}_{4}}}{(2\pi )^{3}2p_{4}^{0}}, \end{aligned}$$
(43)

where \(p_{1}\) and \(p_{2}\) are 4-momenta of the initial state particles and \(p_{3}\) and \(p_{4}\) are 4-momenta of the final state ones. The total cross sections are the integral of the phase space of the final states

$$\begin{aligned} \sigma _{00}= & {} \frac{1}{4\pi {}^{3}} \frac{9 H^{2}\lambda ^{2}}{-8p_{1}\cdot p_{2}}, \end{aligned}$$
(44)
$$\begin{aligned} \sigma _{11}= & {} \frac{1}{4\pi {}^{3}} \frac{ H^{2}\lambda ^{2}}{-8p_{1}\cdot p_{2}} \frac{\sqrt{\left( {p_{1}^{0}+p_{2}^{0}}\right) ^{2} -8H^{2}} }{\left( p_{1}^{0}+p_{2}^{0}\right) }. \end{aligned}$$
(45)

We see that the branch ratio

$$\begin{aligned} R(00\rightarrow 11)= & {} \frac{\sigma _{11}}{\sigma _{00}+\sigma _{11}} \nonumber \\= & {} 1-\frac{9\left( {p_{1}^{0}+p_{2}^{0}}\right) }{\sqrt{\left( {p_{1}^{0}+p_{2}^{0}}\right) ^{2}-8H^{2}} +9\left( p_{1}^{0}+p_{2}^{0}\right) }\nonumber \\ \end{aligned}$$
(46)

is significant only if the initial energy \(p_{1}^{0}+p_{2}^{0}\) is high enough. The above results show that the cross sections and branch ratio are related to the fundamental coupling \(\lambda \) in five dimensions and the new physics energy scale H.

Note that, the decay of the first excited mode \(f_{1}\) into three zero modes \(f_{0}\) is prohibited. It implies that there exist some “selected rules” in the interactions between KK particles just like transitions between states in quantum mechanics. From our discussion in the end of Sect. 2, in the case of the PT potential, there must be plenty of \(f_{1}\) particles on the brane.

Although the above PT potential illustrates some main features of the effective action, it is a little simple because it only has two kinds of KK particles on the brane. There is more interesting content in the case of harmonic potential since all of its eigenstates are bound states and we have a series of infinite localized KK particles in four dimensions. Therefore, we can investigate how the four-dimensional effective interactions vary while the KK modes go higher.

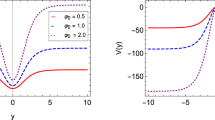
To this end, we consider the flat thick brane model generated by a mimetic scalar field with a Lagrange multiplier [29]. The action of this theory is given by

$$\begin{aligned} S=\int d^5x\sqrt{-g}\left( \frac{R}{2\kappa ^2_5} + \lambda \big (\partial _M \phi \partial ^M \phi -U\big )-V \right) , \end{aligned}$$
(47)

where \(U=U(\phi )\) and \(V=V(\phi )\) are functions of the scalar field phi, and \(\lambda \) is a Lagrange multiplier. For simplicity, one can choose the natural unit with \(\kappa ^2_5=1\). One of the solutions for the flat thick brane metric (2) with \({\tilde{g}}_{\mu \nu }=\eta _{\mu \nu }\) is given by [29]

$$\begin{aligned} A= & {} -k^{2}z^{2}, \end{aligned}$$
(48)
$$\begin{aligned} \phi= & {} v \left( \frac{kz}{\sqrt{1+k^2z^2}}\right) ^\gamma , \end{aligned}$$
(49)

where the parameter k is the scale parameter which controls the thickness of the brane. Here, we do not list the expressions of \(\lambda \), U, and V. For this brane solution, this warp factor A(z) can generate a harmonic potential in a form of

$$\begin{aligned} V(z)=9k^{4}z^{2}-3k^{2}. \end{aligned}$$
(50)

The eigenfunction is

$$\begin{aligned} \chi _{n}(z)= & {} e^{\frac{3}{2}A}f_{n}(z) \nonumber \\= & {} \left( \frac{3k^{2}}{\pi }\right) ^{\frac{1}{4}} \frac{1}{\sqrt{2^{n}n!}}e^{-\frac{3}{2}k^{2}z^{2}}H_{n}(\sqrt{3}kz), \end{aligned}$$
(51)

where \(H_{n}\) is the Hermitian polynomial

$$\begin{aligned} H_{n}(\xi )=(-1)^{n}e^{\xi ^{2}}\frac{{{\textrm{d}^{n}} e ^{-\xi ^{2}}}}{\textrm{d}\xi ^{n}}. \end{aligned}$$
(52)

The four-dimensional induced mass, i.e., the eigenvalue is

$$\begin{aligned} \zeta _{n}=m_{n}^{2}=6k^{2}n,\quad n=0,1,2,\ldots \end{aligned}$$
(53)

and the effective coupling constant is

$$\begin{aligned} \lambda \gamma _{klmn}=\lambda \int e^{5A(z)}f_{k}f_{l}f_{m}f_{n}\,dz. \end{aligned}$$
(54)

Here, we can also see that the parameter k is related to the new physics energy scale.

Notice that, if we add a constant c in the potential (50), the induced mass will be changed, meanwhile the effective coupling constant remains unchanged since we have the same configurations for the KK modes. This constant term c may come from the five-dimensional mass term of the scalar field. Thus, we get new induced masses but the same effective coupling constants, i.e., the effective interaction on the brane is independent of the five-dimensional mass of the scalar field.

It is assumed that only the zero mode \(\varphi _{0}\) and the interaction \(\lambda \gamma {}_{0000}\varphi _{0}^{4}\) have been observed on the brane. So they are the “ordinary” particles and the four-dimensional \(\varphi ^{4}\) interaction, respectively. As demonstrated before, the excited KK modes emerge and interact with each other when we increase energy of particle collision to sufficiently high level.

Note that Eq. (54) is an integration result. The integrand is too complicated to be figured out for the general modes (k, l, m, n). Hence, we consider the effective coupling constant between KK particles for some lower fixed modes of them. The effective coupling constant of the lowest mode (0, 0, 0, 0) is

$$\begin{aligned} \lambda \gamma {}_{0000} =\frac{3 k\lambda }{\sqrt{5 \pi }}. \end{aligned}$$
(55)

This value will be considered as a unit in the following calculations. The rest results will be presented numerically.

Table 1 The values of \(\gamma _{nnnn}\) in unit of \(\gamma _{0000}\)
Full size table
Table 2 The values of \(\gamma _{00mn}\) in unit of \(\gamma _{0000}\)
Full size table

Firstly let us check the “nnnn” interaction, i.e., the interaction in form of \(\varphi _n^{4}\) between the same KK modes. We see that all kinds of KK particles have a \(\varphi _{n}^{4}\) interaction. However, as the quantum number n increasing, the coupling varies form weak to extraordinary strong, see Table 1. Unlike the mass of the n-th excited KK particle which linearly depends on the quantum number n, the effective coupling constant seems to increase as an exponential-like function of n. It may be amazing that, even though the interaction in five-dimensional spacetime is assumed to be weak, the four-dimensional effective interaction on brane is not necessarily weak. In fact, it can be very strong.

Next, we consider the “00mn” interactions, i.e., the interaction terms containing two zero modes and two massive modes \(\varphi _{m},~\varphi _{n}\). Such interactions correspond to the process that two zero mode particles scatter into two KK particles in modes n and m. The tree level amplitude is exactly \(\lambda \gamma {}_{00mn}\). The result is listed in Table 2. Obviously, there is a selected rule: \(\gamma _{00mn}\) has a nonzero value only if \(m+n\) is even. This can be easily proven from the parities of the eigenfunctions. Another significant thing is that the sign of nonzero \(\gamma _{00mn}\) becomes positive and negative alternately, which means the effective interaction becomes repulsion and attraction alternately.

On the other hand, the relation between the nonvanishing \(\gamma _{00mn}\) and m, n is interesting. Figure 4 shows how the magnitude of the interaction varies. It can be seen from Table 2 and Fig. 4 that \(\left| \gamma _{00mn}\right| _{\text {nonzero}}\) reaches the maximum at \(m=n\) for a fixed m and decreases with “the distance between m and n” \(|m-n|\). It also can be see that \(\left| \gamma _{00mn}\right| _{\text {nonzero}}\) tend to zero when \(n\rightarrow \infty \). Thus we have a conclusion that a scatter process including one or two very high excited KK states can be neglected.

Fig. 4
figure 4

The relations between nonzero \(\left| \gamma _{00mn}\right| \) in unit of \(\gamma _{0000}\) versus n for \(m=0,2,8\)

Full size image
Fig. 5
figure 5

Illustration for the total cross section \(\sigma _{mn}\) in (57) in unit of \(\sigma _{00}\)

Full size image
Table 3 The values of \(\Gamma _{n000}\) in unit of \(10^{-9}k^{3}\) for even n
Full size table
Table 4 The values of \(\Gamma _{n100}\) in unit of \(10^{-9}k^{3}\) for odd n
Full size table

The cross section of the process \(00\rightarrow mn\) is

$$\begin{aligned} d\sigma _{mn}= & {} (2\pi )^{4}\delta ^{4}(p_{3}+p_{4}-p_{1}-p_{2}) \frac{\left| \gamma _{00mn}\right| ^{2}}{\left( -4p_{1}\cdot p_{2}\right) }\nonumber \\{} & {} *\frac{d^{3}\vec {p}_{3}}{(2\pi )^{3}2p_{3}^{0}} \frac{d^{3}\vec {p}_{4}}{(2\pi )^{3}2p_{4}^{0}}, \end{aligned}$$
(56)

where the subscripts 1 and 2 refer to the initial state particles and 3 and 4 refer to the final state particles. Integrating it we obtain the total cross section

$$\begin{aligned} \sigma _{mn}=\frac{1}{4\pi }\frac{\left| \gamma _{00mn}\right| ^{2}}{\left( -p_{1}\cdot p_{2}\right) }\frac{{p^{2}}}{2(p_{1}^{0}+p_{2}^{0})^{2}}, \end{aligned}$$
(57)

where

$$\begin{aligned} {p^{4}}= & {} \big (p_{1}^{0}+p_{2}^{0}\big )^{4} -2\big (p_{1}^{0}+p_{2}^{0}\big )^{2}m_{3}^{2}\nonumber \\{} & {} -2\big (p_{1}^{0}+p_{2}^{0}\big )^{2}m_{4}^{2} -2m_{3}^{2}m_{4}^{2}+m_{3}^{4}+m_{4}^{4}, \end{aligned}$$
(58)

it characterizes the size of the final state phase space. It can be shown that the total cross section will decline with m, n, see Fig. 5 for illustration. For a fixed center mass energy \(E=p_{1}^{0}+p_{2}^{0}\) of the two zero mode particles, the total cross section is zero when \(m_{3}+m_{4} > E\).

Let us assume that we have very high initial energy so that a large number of reaction branches are turned on. The branch ratio \(R(00\rightarrow 00)\) is always the largest one. When the initial energy \(p_{1}^{0}+p_{2}^{0}\gg m_{3}\) and \(p_{1}^{0}+p_{2}^{0}\gg m_{4}\), the variation of the size of the final state phase space is negligible and the branch ratio \(R(00\rightarrow mn)\) grows with n and reaches its maximum at \(n=m\), behaving just like \(\left| \gamma _{00mn}\right| \). On the other hand, larger value of n or m suppresses the scattering amplitude drastically, as well as suppresses the size of the final state phase space.

Therefore, the observable branch ratios \(R(00\rightarrow mn)\) mainly come from the ones with smaller m and n. Furthermore, in an inclusive process in which the final state involves a KK mode n, the branch ratios of the processes that the final state includes another KK mode close to n are the most significant.

The “000n” interaction is especially important because it represents the amplitude that a KK particle decays to three zero mode particles. We could deduce the decay rate \(\Gamma _{n000}\) of a KK particle of mode n from \(\gamma _{000n}\):

$$\begin{aligned} \Gamma _{n000}=\sum _{f}(2\pi )^{4}\delta (p_{f}^{0}-2k\sqrt{6n})\delta ^{3}({\vec {p}}_{f})\lambda ^{2}\left| \gamma {}_{000n}\right| ^{2},\nonumber \\ \end{aligned}$$
(59)

where the subscript f denotes the final state. The values of \(\Gamma _{n000}\) in unit of \(10^{-9}k^{3}\) are shown in Table 3. For the even modes n, the decay rate \(\Gamma _{n000}\) decreases with mode number n. For the odd modes, the decay channels \(n\rightarrow 000\) do not exist. Instead, they have nonzero \(\Gamma _{n100}\), see Table 4.

The above two Tables 3 and 4 show the same regular pattern: the decay rate vanishes when the mode number increases. The KK particle with higher modes seem “isolate” from the zero mode in the decay process.

For a KK particle with mode n, it could decay to three lower mode particles, so there are various decay channels \(n\rightarrow klm\). The lifetime \(\tau \) of the particle is the reciprocal of the sum of its decay rates into all possible final states. Checking the lifetime of the KK particles, we find that particles with higher mode have longer lifetime (see Fig. 6). The KK particles with higher modes may be practically stable.

Note that the mass spectrum of the KK modes, the cross sections, the branch ratio, the decay rate and the lifetime of a KK particle are also affected by the fundamental coupling \(\lambda \) in five dimensions and the new physics energy scale k in the second model.

Fig. 6
figure 6

The lifetimes of the KK particles

Full size image

4 Conclusions and discussions

In this paper we have investigated the effective action on the brane from two five-dimensional braneworld models with a perturbation interaction of a scalar field. We have discussed how a five-dimensional interaction affects on our four-dimensional world, in the cases of PT and harmonic potentials. We demonstrated some common features of these effects, not just of these certain potentials. These conclusions could be applied to more general interactions other than \(\phi ^{4}\).

The first conclusion is that one or more KK particles will appear if we improve the energy of particle collision, and new interactions between those KK particles, including the zero mode particle, will arise at the same time. The properties of these interactions can be seen by calculating the effective coupling constants. Nevertheless, the new particles corresponding to higher KK modes are more difficult to discover, not only due to the requirement of higher energy, but also for the diminishing of the involved effective interaction.

There is a obvious tendency of the effective coupling constants: \(\gamma _{klmn}\) tends to vanish when k, l, m, n “depart” from each other. Especially, the zero mode \(\varphi _{0}\) seems to decouple from other KK modes \(\varphi _{n}\) with large n.

With properties of KK particles, we might have an interesting observation. The KK particles with higher modes have larger masse and longer lifetime, and it almost does not interact with the ordinary matter in four-dimensional world if its mode number n is large enough. Exactly, this is one of the features of dark matter. Therefore, the KK particles with higher modes might be a candidate of dark matter if they are localized on the brane.

In the future work, we would like to study the interaction between KK fermions and KK vectors from \({\bar{\varPsi }}\gamma ^{M}A_{M}\varPsi \). The method is analogous to what we performed in this paper. However, there are significant differences between them. For a spinor field, the left and right components of the zero mode can not been localized on brane at the same time [15, 16, 25, 30,31,32,33,34,35]. If we regard the zero mode particle as an electron, a contradiction would arise since it has been observed that electrons have both chiralities. On the other hand, the four-dimensional effective electrodynamics may not be gauge invariant, as a result of the massive KK modes of a vector field.