1 Introduction

Any reasonable modern cosmological model must include Dark Energy (DE). Nevertheless, the nature and origin of Dark Energy remain a mystery despite its fundamental importance in modern theoretical cosmology [1,2,3]. As it is well known, a cosmological model made of only matter and radiation cannot lead to accelerated solutions to the universe as predicted by Einstein’s Theory of General Relativity (GR) [4]. This kind of solution is obtained by including a constant \(\varLambda \) in Einstein’s field equations [5], i.e., by adding the contribution of the dark energy. Despite its simplicity, such accelerated cosmological model is in exceptional agreement with a vast amount of observational data. Such a cosmological model is known as the concordance cosmological model or the \(\varLambda \)CDM model. Nevertheless, \(\varLambda \) suffers from the cosmological constant ongoing problem [6, 7]. Additionally, this \(\varLambda \)–problem is amplified by the current values estimation of the Hubble constant \(H_0\), using high red-shift CMB data and local measurements at low red-shift data, e.g., [8,9,10,11]. In fact, the value of the \(H_0\) computed by the PLANCK Collaboration [12, 13], \(H_0 = \) (67–68) km/(Mpc s), is lower than the value estimated from local measurements [14, 15], \(H_0 =\) (73–74) km/(Mpc s). This \(H_0\) tension points to a cosmological model with new physics [16,17,18,19].

Over the years, this incomplete picture of the cosmological concordance model has motivated the arrival of many new and alternative models. We can classify recent DE cosmological models into two generic categories: (i) alternative theories of gravity for which the solutions have additional corrective terms compared to the standard case; (ii) by employing a new dynamical degree of freedom by means of a convenient equation-of-state. In the first class of models, one finds, for instance, Scalar-Tensor theories of gravity [20,21,22,23], brane-world models [24,25,26,27,28] and f(R) theories of gravity [29,30,31,32]; and for the second class, one finds models such as k-essence [33], phantom [34], quintessence [35], quintom [36], or tachyonic [37]. For a good review article on the dynamics of dark energy see for instance [38].

In this work, we will focus our study on the generalized Chaplying gas equation-of-state [39], widely used in many cosmological model extensions. Here, we study the properties of relativistic astrophysical objects, where we opt to use the same equation of state.

In studies of compact relativistic astrophysical objects the authors usually focus on stars made of an isotropic fluid, where the radial pressure \(P_r\) equals the tangential pressure \(P_\bot \). However, celestial bodies are not always made of isotropic fluid only. In fact under certain conditions the fluid can become anisotropic. The review article of Ruderman [40] mentioned for the first time such a possibility: this author makes the observation that relativistic particle interactions in a very dense nuclear matter medium could lead to the formation of anisotropies. The study on anisotropies in relativistic stars has received a boost by the subsequent work of [41]. Interestingly, Ivanov [42] has shown that by considering a compact object to be an anisotropic star, the effects of shear, electromagnetic field, etc, can be automatically taken into account. Indeed, anisotropies can arise in many scenarios of a dense matter medium, like phase transitions [43], pion condensation [44], or in presence of type 3A super-fluid [45]. See also [46,47,48] for more recent works on the topic, and references therein. In these works relativistic models of anisotropic quark stars were studied, and the energy conditions were fulfilled. In particular, in [46] an exact analytical solution was obtained, in [47] an attempt was made to find a singularity free solution to Einstein’s field equations, and in [48] the Homotopy Perturbation Method was employed, which is a tool that facilitates to tackle Einstein’s field equations. What is more, alternative approaches have been considered to incorporate anisotropies into known isotropic solutions [49,50,51].

Beyond the collisionless dark matter paradigm, self-interacting dark matter has been proposed as an attractive solution to the dark matter crisis at galactic scales [52]. In this scenario one can imagine relativistic stars made entirely of self-interacting dark matter, see e.g. [53,54,55]. In a similar way, given that the current cosmic acceleration calls for dark energy, very recently a couple of works appeared in the literature, where the authors entertain the possibility that stars made of dark energy or more generically exotic matter just might exist [56, 57].

These exotic stars are unique objects like any other compact object that manifest themselves across many multi-messenger signals like gravitational waves, neutrinos, cosmic rays and electromagnetic radiation from radio up to gamma-rays. For instance, we will be able to test many of these stellar models using the data from the present and next generation of gravitational wave detectors such as LIGO, Virgo, KAGRA and LISA.

In the present work, we propose to study non-rotating dark energy stars with anisotropic matter assuming a generalized equation-of-state of the form \(p = -B^2/\rho + A^2\rho \) (with A and B being constants). A simplified version of this, known as a Chaplygin equation-of-state, was introduced in Cosmology long time ago to unify the description of non-relativistic matter and the cosmological constant [58,59,60]. Such a generic equation-of-state is originated by a viscose matter, that when considered in a cosmological context gives rise to the unification of dark matter and dark energy [39].

2 Relativistic spheres within GR

We will consider a static, spherically symmetric object (static fluid), and we will assume locally certain anisotropy, bounded by a spherical surface \(\varSigma \). The line element considering Schwarzschild–like coordinates is written as

$$\begin{aligned} ds^2=e^{\nu } dt^2 - e^{\lambda } dr^2 - r^2 d\varOmega ^2, \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) are, as always, the corresponding metric potential, depending on the radial coordinate only, and \(d\varOmega ^2\equiv \left( d\theta ^2 + \sin ^2\theta d\phi ^2 \right) \) correspond to the element of solid angle. We will take: \(x^0=t; \, x^1=r; \, x^2=\theta ; \, x^3=\phi \). The classical Einstein field equations for a vanishing cosmological constant are:

$$\begin{aligned} G^\nu _\mu =8\pi G T^\nu _\mu , \end{aligned}$$
(2)

with G being Newton’s constant, taken to be unity for simplicity. Now, in the comoving frame, the physical matter content is an anisotropic fluid of energy density \(\rho \), radial pressure \(P_r\), and tangential pressure \(P_\bot \). Thus, the covariant energy–momentum tensor in (local) Minkowski coordinates is \(T^{\mu }_{\nu } =\{ \rho , P_r, P_\bot , P_\bot \}\) and the field equations can be written as:

$$\begin{aligned} \rho= & {} -\frac{1}{8\pi }\left[ -\frac{1}{r^2}+e^{-\lambda } \left( \frac{1}{r^2}-\frac{\lambda '}{r} \right) \right] , \end{aligned}$$
(3)
$$\begin{aligned} P_r= & {} -\frac{1}{8\pi }\left[ \frac{1}{r^2} - e^{-\lambda } \left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \right] , \end{aligned}$$
(4)
$$\begin{aligned} P_\bot= & {} \frac{1}{32\pi }e^{-\lambda } \left( 2\nu ''+\nu '^2 - \lambda '\nu ' + 2\frac{\nu ' - \lambda '}{r}\right) , \end{aligned}$$
(5)

where the derivatives with respect to r are denoted by primes.

As it is well known, we can combine the last equations to produce the hydrostatic equilibrium equation (also known as the generalized Tolman–Opphenheimer–Volkoff equation), i.e.,

$$\begin{aligned} -\frac{1}{2}\nu '\left( \rho + P_r\right) -P'_r+\frac{2}{r}\left( P_\bot -P_r\right) =0. \end{aligned}$$
(6)

Conveniently, we can express this equilibrium equation as the balance between the following three forces: gravitational (\(F_g\)), hydrostatic (\(F_r\)) and anisotropic (\(F_p\)), which we define as

$$\begin{aligned} F_g=-\frac{\nu '\left( \rho + P_r\right) }{2},\; F_r= -P'_r\; \textrm{and}\; F_p=\frac{2\varPi }{r}. \end{aligned}$$
(7)

where \(\varDelta \equiv \varPi =P_\bot -P_r\). Accordingly, Eq. (6), now reads

$$\begin{aligned} F_g+F_r+F_p=0. \end{aligned}$$
(8)

The previous Eq. (8) establishes that this compact star results from the equilibrium between these three different forces [61]. It is worth noticing that if \(F_p=0\), we obtain the standard TOV equation. In particular, in cases where \(P_\bot >P_r\) (or \(\varPi >0\)), \(F_p>0\) causes a repulsive force in Eq. (8) that counteracts the attractive force given by \(F_g+F_r\). In the reverse case of \(P_\bot <P_r\) (or \(\varPi <0\)), \(F_p<0\) is also an attractive force that adds to the other ones.

Alternatively, we can remove the \(\nu '\)-dependence in Eq. (6) to obtain a more convenient equation, namely

$$\begin{aligned} P'_r=-\frac{(m + 4 \pi P_r r^3)}{r \left( r - 2m\right) }\left( \rho + P_r\right) +\frac{2}{r}\left( P_\bot -P_r\right) , \end{aligned}$$
(9)

To do that, we have used the relation

$$\begin{aligned} \frac{1}{2}\nu ' = \frac{m + 4 \pi P_r r^3}{r \left( r - 2m\right) }, \end{aligned}$$
(10)

In addition, m is the mass function, obtained by:

$$\begin{aligned} R^3_{232}=1-e^{-\lambda }=\frac{2m}{r}, \end{aligned}$$
(11)

or,

$$\begin{aligned} m = 4\pi \int ^{r}_{0} {\tilde{r}}^2\rho \ d{\tilde{r}}. \end{aligned}$$
(12)

Now, let us rewrite the energy-momentum tensor as follow

$$\begin{aligned} T^{\mu }_{\nu }=\rho u^{\mu }u_{\nu }- P h^{\mu }_{\nu }+\varPi ^{\mu }_{\nu }, \end{aligned}$$
(13)

Firstly, we set the four-velocity as \(u^{\mu } = (e^{-\frac{\nu }{2}},0,0,0)\), and the four acceleration, \(a^\alpha =u^\alpha _{;\beta }u^\beta \), whose any non–vanishing component is \(a_1 = -\nu ^{\prime }/2\). Subsequently, the set \(\{ \varPi ^{\mu }_{\nu }, \varPi , h^{\mu }_{\nu }, s^{\mu }, P \}\) is taken according to

$$\begin{aligned} \varPi ^{\mu }_{\nu }= & {} \varPi \bigg (s^{\mu }s_{\nu }+\frac{1}{3}h^{\mu }_{\nu }\bigg ) \end{aligned}$$
(14)
$$\begin{aligned} \varPi= & {} P_{\bot }-P_r \end{aligned}$$
(15)
$$\begin{aligned} h^\mu _\nu= & {} \delta ^\mu _\nu -u^\mu u_\nu \end{aligned}$$
(16)
$$\begin{aligned} s^{\mu }= & {} (0,e^{-\frac{\lambda }{2}},0,0) \end{aligned}$$
(17)
$$\begin{aligned} P\equiv & {} \frac{1}{3}\Bigl ( P_{r}+2P_{\bot } \Bigl ) \end{aligned}$$
(18)

with the properties \(s^{\mu }u_{\mu }=0\), \(s^{\mu }s_{\mu }=-1\). For the exterior solution, we match the problem with Schwarzschild spacetime, i.e.,

$$\begin{aligned} ds^2= \left( 1-\frac{2M}{r}\right) dt^2 - \left( 1-\frac{2M}{r}\right) ^{-1} dr^2 - r^2 d\varOmega ^2. \nonumber \\ \end{aligned}$$
(19)

The problem should be supplemented using certain boundary conditions on the surface \(r=r_\varSigma =\text {cte}\). Thus, we demand the continuity of the first and the second fundamental forms across that surface, which means

$$\begin{aligned} e^{\nu _\varSigma }= & {} 1-\frac{2M}{r_\varSigma }, \end{aligned}$$
(20)
$$\begin{aligned} e^{-\lambda _\varSigma }= & {} 1-\frac{2M}{r_\varSigma }, \end{aligned}$$
(21)
$$\begin{aligned} \left[ P_r\right] _\varSigma= & {} 0, \end{aligned}$$
(22)

where subscript \(\varSigma \) represent that the quantity is evaluated on the boundary surface \(\varSigma \). Finally, notice that last three equations are the necessary (and also sufficient) conditions for a smooth matching of the two metrics (1) and (19) on the surface \(\varSigma \).

3 Anisotropic matter: complexity factor

In what follows, we will briefly summarize the underlying physics behind the definition of the complexity factor, focusing on the astrophysical relevance of such quantity. Let us first start mentioning the seminal paper by Herrera [62], where a new and non-trivial way to reveal when static self-gravitating objects are anisotropic was properly introduced. Even more, this new definition tried to fix two problems present in preliminary definitions of complexity. The first problem appears when the probability distribution (which appear in the definition of “disequilibrium” and information) is replaced by the energy density of the fluid distribution [63]. The second problem is manifest when we recognize that previous definitions of complexity consider the energy density of the fluid only, ignoring another relevant components as pressure. Thus, the new definition introduced by L.H. try to make progress by fixing the above mentioned issues.

Originally, the new definition of the complexity factor was investigated only under a mathematical point of view (see [64,65,66,67] and references therein). However, the real value of such definition becomes evident when we use it as a supplementary condition to close the set of differential equations of a self-gravitational system. What is more, the complexity factor could be used as a self-consistent way to incorporate anisotropies [68, 69], see also [70,71,72,73,74,75,76,77] and references therein.

As was previously pointed out, the complexity factor appears in the orthogonal splitting of the Riemann tensor for static self-gravitating fluids with spherical symmetry, and for a detailed step-by-step computation, we should see the original paper [62] and also [78]. Thus, albeit we will avoid a profound discussion regarding the orthogonal decomposition of the Riemann tensor, we need to define the following quantities:

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(23)
$$\begin{aligned} Z_{\alpha \beta }= & {} R^{*}_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta } = \frac{1}{2}\eta _{\alpha \gamma \epsilon \mu } R^{\epsilon \mu }_{\quad \beta \delta } u^{\gamma } u^{\delta }, \end{aligned}$$
(24)
$$\begin{aligned} X_{\alpha \beta }= & {} R^{*}_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }= \frac{1}{2}\eta _{\alpha \gamma }^{\quad \epsilon \mu } R^{*}_{\epsilon \mu \beta \delta } u^{\gamma } u^{\delta }, \end{aligned}$$
(25)

Please, notice that the symbol \(*\) represent the dual tensor, namely

$$\begin{aligned} R^{*}_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }R_{\alpha \beta }^{\quad \epsilon \mu } \end{aligned}$$
(26)

and \(\eta _{\epsilon \mu \gamma \delta }\) is the well-known Levi–Civita tensor. Taking advantage of the decomposition of the Riemann tensor, we rewrite the set of scalars \(\{Y_{\alpha \beta }, Z_{\alpha \beta }, X_{\alpha \beta }\}\) in term of the physical variables, i.e.,

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{4\pi }{3}(\rho +3 P)h_{\alpha \beta }+4\pi \varPi _{\alpha \beta }+E_{\alpha \beta }, \end{aligned}$$
(27)
$$\begin{aligned} Z_{\alpha \beta }= & {} 0, \end{aligned}$$
(28)
$$\begin{aligned} X_{\alpha \beta }= & {} \frac{8\pi }{3} \rho h_{\alpha \beta }+4\pi \varPi _{\alpha \beta }-E_{\alpha \beta }. \end{aligned}$$
(29)

Notice that the corresponding tensor \(E_{\alpha \beta }\) (defined as \(E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }\)) is given by

$$\begin{aligned} E_{\alpha \beta }=E \bigg (s_\alpha s_\beta +\frac{1}{3}h_{\alpha \beta }\bigg ), \end{aligned}$$
(30)

with

$$\begin{aligned} E=-\frac{e^{-\lambda }}{4}\left[ \nu ^{\prime \prime } + \frac{{\nu ^{\prime }}^2-\lambda ^{\prime } \nu ^{\prime }}{2} - \frac{\nu ^{\prime }-\lambda ^{\prime }}{r}+\frac{2(1-e^{\lambda })}{r^2}\right] , \nonumber \\ \end{aligned}$$
(31)

satisfying the following properties:

$$\begin{aligned} E^\alpha _{\,\,\alpha }=0,\quad E_{\alpha \gamma }= E_{(\alpha \gamma )},\quad E_{\alpha \gamma }u^\gamma =0. \end{aligned}$$
(32)

Even more, as was also demonstrated by [79], the tensors \(\{ Y_{\alpha \beta }, Z_{\alpha \beta }, X_{\alpha \beta } \}\) can be represented in term of alternative scalar functions. Considering the tensors \(X_{\alpha \beta }\) and \(Y_{\alpha \beta }\) in the static case, the so-called structure scalars \(X_T, X_{TF}, Y_T, Y_{TF}\) can be written in term of the physical variables as follow:

$$\begin{aligned} X_T= & {} 8\pi \rho , \end{aligned}$$
(33)
$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3} \int ^r_0{{\tilde{r}}^3 \rho ' d{\tilde{r}}} , \end{aligned}$$
(34)
$$\begin{aligned} Y_T= & {} 4\pi ( \rho + 3 P_r-2\varPi ) , \end{aligned}$$
(35)
$$\begin{aligned} Y_{TF}= & {} 8\pi \varPi - \frac{4\pi }{r^3} \int ^r_0{{\tilde{r}}^3 \rho ' d{\tilde{r}}} . \end{aligned}$$
(36)

From Eqs. (34)–(36), the local anisotropy of pressure is determined by \(X_{TF}\) and \(Y_{TF}\) via the following relation:

$$\begin{aligned} 8\pi \varPi = X_{TF} + Y_{TF} . \end{aligned}$$
(37)

The vanishing complexity condition, \(Y_{TF}=0\), implies the following relation between the energy density and the anisotropic factor

$$\begin{aligned} \varPi (r) = \frac{1}{2r^3} \, \int ^r_0{{\tilde{r}}^3 \rho '({\tilde{r}}) d{\tilde{r}}} \end{aligned}$$
(38)

The last condition has also been significantly investigated along years introducing, via alternative ansatzs, several concrete forms of the anisotropy \(\varPi \equiv P_{\perp } - P_r \) and different equations of state (see for instance [49, 80,81,82,83,84,85,86,87,88,89,90,91] and references therein). Given that a profound comprehension of the idea of complexity is still under construction, the connection between \(\varPi \) (or more precisely, any equation of state \(P_{\bot } \equiv P_{\bot }(\rho )\)) and the definition of complexity factor \(Y_{TF}\) is still missing.

Fig. 1
figure 1

Anisotropic DE stars within complexity factor: mass function in solar masses (left panel), anisotropic factor (middle panel), and energy density and pressures (right panel) versus radial coordinate throughout the star

Full size image
Fig. 2
figure 2

Anisotropic DE stars within complexity factor: Speed of sounds (left panel) and relativistic adiabatic index (right panel) versus radial coordinate throughout the star

Full size image
Fig. 3
figure 3

Anisotropic DE stars within complexity factor: Energy conditions versus radial coordinate throughout the star

Full size image

4 Discussion

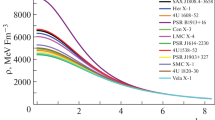
In the present paper we have investigated anisotropic stars made of exotic matter in light of the by now well-known complexity formalism. In particular, we compute for the first time numerical solutions of realistic compact distribution of matter, and compare our solution against the conventional formalism, both within GR. We take advantage of a generalized Chaplyin equation-of-state to close the system. After the numerical computation shown, in figures, how several relevant quantities of the star evolve. In particular, we notice that: (i) the mass function increase, the anisotropic factor decrease and the energy density and pressures decrease throughout the star, (ii) the speed of sound, radial and tangential, increase and decrease, respectively, and both are lower that \(c_0^2 \equiv 1\), the relativistic adiabatic index, \(\varGamma (r)\), increase and it is always higher than \(\varGamma _0 \equiv 4/3\), (iii) the corresponding energy conditions are also satisfied. Thus, in light the these numerical results, we can confirm that the complexity factor formalism is a solid approach to obtain well-defined solutions in the context of compact stars (Figs. 1, 2, 3).

Fig. 4
figure 4

Anisotropic DE stars considering a more standard approach and assuming small a: Mass function in solar masses (left panel), anisotropic factor (middle panel), and sound speeds (right panel) versus radial coordinate throughout the star

Full size image
Fig. 5
figure 5

Anisotropic DE stars considering a more standard approach and assuming large a: Mass function in solar masses (left panel), anisotropic factor (middle panel), and sounds speed (right panel) versus radial coordinate throughout the star

Full size image
Fig. 6
figure 6

Mass-to-radius profiles in two alternative approaches: Left: Profiles for the 3 models corresponding to the curves following the complexity formalism. Right: Profiles for the 3 models corresponding to curves obtained in the conventional scenario

Full size image

As a supplementary check, we have obtained, numerically again, interior solutions using a more standard approach, i.e., adding external constraints to close the system of differential equations. As a toy model, we have considered an anisotropic factor, \(\varPi (r)\), as follows

$$\begin{aligned} \varPi (r) = - \bigg (\frac{r}{a}\bigg )^2 \, \rho (r) \end{aligned}$$
(39)

characterized by a dimensionful parameter, a, with dimensions of length, which encodes the strength of the anisotropy. This form of anisotropic factor was previously employed in [82]. Its mathematical form may be justified as follows: It is a simple expression fulfilling the basic requirements, namely the anisotropic factor has the correct dimensions, it is manifestly negative, and it vanishes at the center of the star, \(\varPi (r=0)=0\). Moreover, we consider two concrete cases: (i) large values of a and (ii) small values of a, assuming the following numerical values

$$\begin{aligned} a \longrightarrow {\left\{ \begin{array}{ll} a_{\text {large}} = 30~{\text {km}} \\ a_{\text {small}} = 10~{\text {km}} \end{array}\right. } \end{aligned}$$
(40)

Although it is not necessary to do so, given the ansatz above for the anisotropic factor, one may derive the following differential equation

$$\begin{aligned} \varPi '(r) = \frac{2}{r} \, \varPi (r) - \frac{r^2}{a^2} \, \rho '(r), \end{aligned}$$
(41)

which looks very similar to the differential equation

$$\begin{aligned} \varPi '(r) = - \frac{3}{r} \, \varPi (r) + \frac{\rho '(r)}{2}. \end{aligned}$$
(42)

obtained using Eq. (36) and the vanishing complexity condition \(Y_{TF}=0\). Equation (41) may be derived in a straightforward manner as follows: First, taking the derivative with respect to r of both sides of Eq. (39)

$$\begin{aligned} - \varPi '(r) = \frac{1}{a^2} \, [ 2 r \rho + r^2 \, \rho '(r) ], \end{aligned}$$
(43)

and then making use once more of the definition of the anisotropic factor

$$\begin{aligned} \frac{\varPi (r)}{r} = - \frac{r}{a^2} \, \rho (r). \end{aligned}$$
(44)

Our main result may be summarized as follows: When the normalized anisotropy, \(\varPi (r)/B\), is comparable, i.e. same order of magnitude, to the one studied within the complexity factor formalism, the solution is not realistic, since causality is violated, as shown in Fig. 4 for the small a case. On the contrary, when the solution is realistic satisfying all the criteria, the star is characterized by a similar mass and at the same time by a much lower anisotropic factor. This is displayed in Fig. 5 for the large a case, where it is clear that the star is much less anisotropic in comparison to Fig. 1.

Finally, we show in Fig. 6 the mass-to-radius profiles (mass in solar masses versus radius in km) for three models, both within the complexity factor formalism (left panel) and in a more standard approach for the case of large a (right panel). The three models considered here are the following

$$\begin{aligned} A = \sqrt{0.4}, \; \; \; \; \; B = 0.23 \times 10^{-3} \,\, {\text {km}}^{-2} \end{aligned}$$
(45)

for Model 1,

$$\begin{aligned} A = \sqrt{0.425}, \; \; \; \; \; B = 0.215 \times 10^{-3} \,\, {\text {km}}^{-2} \end{aligned}$$
(46)

for Model 2, and

$$\begin{aligned} A = \sqrt{0.45}, \; \; \; \; \; B = 0.2 \times 10^{-3} \,\, {\text {km}}^{-2} \end{aligned}$$
(47)

for Model 3. The shape of the curves shows that the radius of the star acquires a maximum value first, and then the mass of the star, too, acquires its maximum mass. Although in both cases the anisotropic factor is negative, the complexity factor formalism predicts smaller and lighter objects as compared to the conventional approach (Fig. 7).

Fig. 7
figure 7

Mass-to-radius profiles for Model 1 for different cases: (i) considering isotropic matter (dashed), (ii) utilizing the vanishing complexity factor formalism (cyan), and (iii) using the conventional method (three curves in between for \(a=100\) km (less anisotropic), 50 km (middle), 25 km (more anisotropic)

Full size image

We notice that the complexity factor is an effective method to include modifications in the stellar structure of compact stars resulting from the presence of new physical processes responsible for the appearance of anisotropy contributions. Consequently, the TOV equations for such stars are altered by the existence of a new anisotropic force. Unlike in the case of an isotropic star, the TOV equations balance three forces: gravity, hydrostatic and anisotropic forces.

Finally, in the last figure we show the mass-to-radius relationships both for isotropic and for anisotropic stars within both approaches for the case of Model 1. First we obtain the M-R profile for stars made of isotropic matter (dashed line). Then we study anisotropies within the vanishing complexity formalism, and we obtain the curve in cyan. Next, when we consider the conventional method, since now the ansatz for the anisotropic factor is characterized by a continuous parameter, we can observe the impact of that parameter on the profiles, corresponding to the other 3 curves in the figure. Increasing the anisotropy, the profile is gradually shifted towards the one corresponding to complexity. But at some point causality is violated, and therefore the solution is not realistic/viable any more. That is precisely the point where we must stop. The last allowed profile remains quite far away from the one obtained within complexity.

5 Conclusions

To summarize our work, we have obtained interior solutions of exotic stars made of dark energy, taking into account the presence of anisotropies and adopting the extended Chaplygin gas equation-of-state. The anisotropic factor is treated employing the formalism based on the complexity factor, and the structure equations have been integrated numerically. The solutions are shown to be well-behaved and realistic. Moreover, we have made a comparison with another more conventional approach, where the form of the anisotropic factor is introduced by hand.