Exploration of trace anomaly contribution to proton mass based on light vector meson photoproduction

Abstract

In the quantum chromodynamics, the mass source of the proton is decomposed into four parts by the energy momentum tensor: quark energy term, gluon energy term, quark mass term and trace anomaly term. And the trace anomaly term is the most crucial contribution for studying the internal structure of the proton. In this work, under the definition of the vector meson dominant model, the trace anomaly contribution of the proton is extracted from the experimental data of light vector mesons $\rho$, $\omega$ and $\phi$ photoproduction at the near-threshold, which are ($0.53\pm 0.15$)$\%$, ($1.47\pm 0.48$)$\%$ and ($2.73\pm 0.54$)$\%$, respectively. Further, combined with the results extracted from the heavy vector meson $J/\psi$ photoproduction, the distribution of the trace anomaly contribution with the vector meson mass is given for the first time. These results may provide important theoretical information for determining the range of the trace anomaly contribution and for further understanding the origin of the proton mass.

1 Introduction

The emergence of the quantum chromodynamics Energy Momentum Tensor (EMT) provides a direct computational standard for understanding various properties of hadrons [1], such as mass, spin [2], angular momentum  [3,4,5], mechanical properties [1, 4, 6,7,8,9,10,11], etc. All these attributes are the essential properties of hadrons, which are valuable to further exploring the internal structure of hadrons. As the most basic and stable hadron, the study of the internal structure of the proton is one of the most meaningful topics to be discussed [7, 12].

The proton is composed of quarks and gluons, with a total mass of $M_{N}=0.938$ GeV. However, the distribution of quarks and gluons inside the proton and their respective percentages of the total mass has been an ambiguous question. The first mass decomposition of the proton originated in 1995, Ji [13, 14] decomposed the mass source of the proton into four terms based on the EMT $T^{\mu \nu }$ of hadronic states: the quark energy term $M_{q}$, the gluon energy term $M_{g}$, the quark mass term $M_{m}$ and the trace anomaly term $M_{a}$. Also related to EMT focusing on the decomposition of $T^{00}$ comes from the work of Lorcé [15] and Hatta [16]. Lorcé’s [15] decomposition consists of two schemes: a two-term decomposition and a four-term decomposition. Hatta [16] primarily concentrates on the regularization scheme to prove that the trace anomaly solely comes from the gluon momentum energy tensor, while the quark mass term just comes from the quark energy tensor. Beyond that, a revisiting of the mass decomposition is developed by Metz et al. [12], who reviewed the previous similarities and differences in the origin of the proton mass and concluded that any decomposition at most exists two independent terms. This is because the existence of the forward limit leads to the EMT matrix element having two independent form factors [15]. The most striking point is that using independent operators [17] in their four-term decomposition computations yields the trace anomaly term $M_{a} =0$, which is different from the results of other mass decomposition. The above research investigates the source of protons in terms of momentum energy tensor and whether other ways exist to enable us to comprehend the decomposition of the proton.

A novel approach in Ref. [18] is proposed to relate the differential cross sections of vector meson photoproduction to the trace anomaly with the vector meson dominate (VMD) model. The trace anomaly contribution of the proton [19] is studied employing $J/\psi$ photoproduction data GlueX experiment [20] at JLab, respectively. A new report [21] recently measured a new set of the differential data of $J/\psi$ photoproduction at $E\in [9.10,10.60]$ GeV and extracted the trace anomaly contribution of the proton with VMD. One finds that the trace anomaly contribution extracted from the heavy meson photoproduction data varies rapidly with energy, indicating that the trace anomaly is very sensitive to the energy and has a strong dependence. This causes considerable confusion in the conclusive determination of the trace anomaly contribution of the proton. Therefore, it is necessary to study the trace anomaly contribution in terms of the cross section of light vector mesons photoproduction at the near-threshold.

As the most familiar light vector mesons, $\rho$, $\omega$ and $\phi$ have accumulated considerable experimental data [22,23,24,25,26,27] during years of development. In this work, based on the photoproduction experimental data of the three mesons, the trace anomaly contribution of the proton is extracted by VMD model and analyzed as a function of R at the near-threshold range. Here, R is proportional to the center of mass energy W, representing the ratio of the final momentum $|\textbf{p}_3|$ to the initial momentum $|\textbf{p}_1|$. In addition, since the two gluon exchange model is reliable in predicting the mass radius of the proton [6], the trace anomaly contribution of the proton is expected based on the two gluon exchange model. Combined with the result extracted from the photoproduction data of the three vector mesons at the near-threshold, the trace anomaly contribution of the proton is systematically discussed.

The outline of the paper is organized as follows. The expression of the mass decomposition of the proton, the vector meson dominate and the two gluon exchange models are described in Sect. 2, along with a detailed discussion of trace anomaly. The results of trace anomaly coherence are presented in Sect. 3. A simple summary and discussion is presented in Sect. 4.

2 Formalism

2.1 Mass decomposition of the proton

Starting with the EMT, $T^{\mu \nu }$ is decomposed into the traceless term $\bar{T}_{\mu \nu }$ and trace term $\hat{T}^{\mu \nu }$ [13, 14],

$$\begin{aligned} T^{\mu \nu }=\bar{T}^{\mu \nu }+\hat{T}^{\mu \nu } \end{aligned}$$

(1)

where the traceless $\bar{T}_{\mu \nu }$ contains contributions from gluon and quark, and the trace $\hat{T}^{\mu \nu }$ includes contributions from quark mass and trace anomaly. A more detailed decomposition is,

$$\begin{aligned} \begin{aligned}&\bar{T}^{\mu \nu }=\bar{T}^{\mu \nu }_{q}(\mu ^2)+\bar{T}^{\mu \nu }_{g}(\mu ^2), \\&\hat{T}^{\mu \nu }=\hat{T}^{\mu \nu }_{m}(\mu ^2)+\hat{T}^{\mu \nu }_{a}(\mu ^2). \end{aligned} \end{aligned}$$

(2)

which can be seen that $\bar{T}^{\mu \nu }$ and $\hat{T}^{\mu \nu }$ are energy conserved, but the components depend on the energy scale $\mu ^2$. Then, the EMT is expressed as a sum of four terms,

$$\begin{aligned} T^{\mu \nu }=\bar{T}^{\mu \nu }_{q}(\mu ^2)+\bar{T}^{\mu \nu }_{g}(\mu ^2)+\hat{T}^{\mu \nu }_{m}(\mu ^2)+\hat{T}^{\mu \nu }_{a}(\mu ^2). \end{aligned}$$

(3)

Introduce the matrix element of the energy momentum tensor in the proton state $|P\rangle$, then the left side of Eq. (2) is normalized as

$$\begin{aligned} \begin{aligned}&\left\langle P\left| \bar{T}^{\mu \nu }\right| P\right\rangle =\left( P^{\mu } P^{\nu }-\frac{1}{4} g^{\mu \nu } M^{2}_{N}\right) / M_{N}, \\&\left\langle P\left| \hat{T}^{\mu \nu }\right| P\right\rangle =\frac{1}{4} g^{\mu \nu } M_{N} . \end{aligned} \end{aligned}$$

(4)

where $g^{\mu \nu }$ is metric tensor of space. The normalization requires Lorentzian invariant while renormalization scales independently. In the rest frame, the total energy of the mass of the whole EMT can be defined by the Hamiltonian form, which is

$$\begin{aligned} \begin{aligned}&\left\langle \bar{T}^{00}\right\rangle \mid _{P=0}\;=\frac{3}{4} M_{N}, \\&\left\langle \hat{T}^{00}\right\rangle \mid _{P=0}\;=\frac{1}{4} M_{N}. \end{aligned} \end{aligned}$$

(5)

That is, the trace part is $25\%$ of the proton total mass $M_{N}$, which means $\left\langle P\left| \hat{T}^{00}_{m}\right| P\right\rangle +\left\langle P\left| \hat{T}^{00}_{a}\right| P\right\rangle =M_{N}/4$. Under the Hamiltonian operator, Eq. (3) can be reformulated as [15],

$$\begin{aligned} \mathcal {H}=\mathcal {H}_{q}+\mathcal {H}_{g}+\mathcal {H}_{m}+\mathcal {H}_{a}. \end{aligned}$$

(6)

Hence, in the rest frame, the mass decomposition of the proton is derived from Eq. (6),

$$\begin{aligned} M_{N}=M_{q}+M_{g}+M_{m}+M_{a}. \end{aligned}$$

(7)

The four mass components with Hamiltonian form are parameterized as,

$$\begin{aligned} \begin{aligned} M_{q}&=\frac{3}{4}\left( a-\frac{b}{1+\gamma _{m}}\right) M_{N} \\ M_{g}&=\frac{3}{4}(1-a) M_{N} \\ M_{m}&=\frac{4+\gamma _{m}}{4\left( 1+\gamma _{m}\right) } b M_{N} \\ M_{a}&=\frac{1}{4}\left( 1-b\right) M_{N}. \end{aligned} \end{aligned}$$

(8)

where b is trace anomaly parameter, a is the momentum fraction of the quarks and $\gamma _{m}$ is the anomalous dimension of the quark mass [16, 28, 29]. In the chiral limit and low energy scattering, $b=0$, the proton’s mass is entirely due to the contribution of gluon quantum fluctuations. In this case, $M_{m}=0$ and $M_{a}=M_{N}/4$.

2.2 Vector meson dominate

In Eq. (8), the fourth term is needed to compute the trace anomaly contribution $M_{a}/M_{N}$. This item contains a trace anomaly parameter b, which is the key to determining the contribution of trace anomaly. Therefore, the vector mesons dominate (VMD) model is developed to calculate parameter b and $M_{a}/M_{N}$.

The differential cross section at $t=t_{min}$ for $\gamma N$ $\rightarrow$ $V N$ process can be expressed with the VMD model,

$$\begin{aligned} \begin{aligned} \left. \frac{d \sigma _{\gamma N \rightarrow V N}}{d t}\right| _{t=t_{min}}&=\left. \frac{3 \Gamma _{V \rightarrow e^{+} e^{-}}}{\alpha _{em} m_{V}}\left( \frac{\textbf{p}_3}{\textbf{p}_1}\right) ^{2} \frac{d \sigma _{V N \rightarrow V N}}{d t}\right| _{t=t_{min}}\\&=\left. \frac{3 \Gamma _{V \rightarrow e^{+} e^{-}}}{\alpha _{em} m_{V}} R^{2} \frac{d \sigma _{V p \rightarrow V p}}{d t}\right| _{t=t_{min}}, \end{aligned} \end{aligned}$$

(9)

with

$$\begin{aligned} \textbf{p}_1=\frac{W^{2}-m_{N}^{2}}{2 W}, \end{aligned}$$

(10)

$$\begin{aligned} \textbf{p}_3=\sqrt{\frac{\left[ W^{2}-\left( m_{V}+m_{N}\right) ^{2}\right] \left[ W^{2}-\left( m_{V}-m_{N}\right) ^{2}\right] }{4 W^{2}}}, \end{aligned}$$

(11)

where $\alpha _{em}=1/137$ is the fine coupling constant, $\Gamma _{V \rightarrow e^{+} e^{-}}$ is the lepton decay width, $M_{N}$ is the mass of the proton, $m_{V}$ is the mass of the light meson ($\rho$, $\omega$ and $\phi$), and $R=|\textbf{p}_3|/|\textbf{p}_1|$ represents the ratio of the final momentum to the initial momentum. The $\left. \frac{d \sigma _{V N \rightarrow V N}}{d t}\right| _{t=t_{min}}$ is the elastic scattering in Eq. (9),

$$\begin{aligned} \left. \frac{d \sigma _{V N \rightarrow V N}}{d t}\right| _{t=t_{min}}=\frac{1}{64 \pi } \frac{1}{m_{V}^{2}\left( \lambda ^{2}-m_{N}^{2}\right) }\left| F_{V N}\right| ^{2}, \end{aligned}$$

(12)

where $\lambda =(W^{2}-m^{2}_{V}-m^{2}_{N})/(2m_{V})$ is the nucleon energy [18]. In the low energy region, the elastic scattering amplitude $F_{V N}$ of the particle is denoted as [30],

$$\begin{aligned} F_{V N}=r_{0}^{3} d_{2} \frac{2 \pi ^{2}}{27} 2 M_{N}^{2}\left( 1-b\right) , \end{aligned}$$

(13)

with the Bohr radius of meson and Wilson coefficient [30, 35],

$$\begin{aligned}{} & {} r_{0}=\left( \frac{4}{3 \alpha _{s}}\right) \frac{1}{m_{q}}, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} d_{n}^{(1 S)}=\left( \frac{32}{N_{c}}\right) ^{2} \sqrt{\pi } \frac{\Gamma \left( n+\frac{5}{2}\right) }{\Gamma (n+5)}, \end{aligned}$$

(15)

where $m_{q}$ is the mass of the constituent quark, $\alpha _{s}$ is the strong coupling constant and b is trace anomaly parameter. From the above derivations, it can be found that the primary factor affecting parameter b is the cross section of vector meson photoproduction. In addition, $m_V$, $\alpha _s$, $m_q$ and $\Gamma _{e^+e^-}$ are related to the specific type of vector meson and the energy scale of the corresponding quark energy region, and also have an impact on the value of b. Their specific values are shown in Table 1.

Table 1 The lepton decay width $\Gamma _{V \rightarrow e^{+}e^{-}}$, the constituent quark mass $m_{q}$, meson mass $m_{V}$ and the strong coupling parameter $\alpha _{s}$ for $\rho$, $\omega$ and $\phi$ [24, 31,32,33,34]

Stay away from the chiral limit, the contribution of QCD trace anomaly to proton mass can be represented by the factor $1-b$. By the fourth term of Eq. (8), Eq. (13) becomes

$$\begin{aligned} F_{V N}=r_{0}^{3} d_{2} \frac{2 \pi ^{2}}{27} 2 M_{N}^{2} 4 \frac{M_{a}}{M_{N}}. \end{aligned}$$

(16)

When the center of mass energy W approaches the threshold, $t_{min}$ $\rightarrow$ $t_{max}$, the relation between the total and differential cross sections of vector meson photoproduction is [36],

$$\begin{aligned} \left. \sigma _{\gamma N \rightarrow V N}(W_{thr})=4 |\textbf{p}_1| |\textbf{p}_3|\frac{d \sigma _{\gamma N \rightarrow V N}}{d t} \right| _{W_{thr},t=t_{thr}}, \end{aligned}$$

(17)

where $\Delta =|t_{max}-t_{min}|=4 |\textbf{p}_1| |\textbf{p}_3|$ [37], $t_{thr}=-m_v^2 M_N/(m_V+M_N)$ at $W_{thr}$. Therefore, the Eq. (9) is represented as [36],

$$\begin{aligned} \begin{aligned} \left. \frac{d \sigma _{\gamma N \rightarrow J / \psi N}}{d t}\right| _{t=t_{t h r}, W_{t h r}}&=\left. \frac{d \sigma _{\gamma N \rightarrow J / \psi N}}{d t}\right| _{t=t_{\min }, W_{t h r}} \\&=\frac{\sigma _{\gamma N \rightarrow J / \psi N}\left( W_{t h r}\right) }{4\left| p_1\right| \cdot \left| p_{3}\right| }. \end{aligned} \end{aligned}$$

(18)

From the above statement, we can calculate the trace anomaly contribution $M_{a}/M_{N}$ from the total and differential cross sections ($d \sigma /d t|_{t=t_{min}}$ and $d \sigma /d t|_{t=t_{thr}}$) of vector mesons at the near-threshold.

2.3 Two gluon exchange model

Studying the photoproduction reaction of vector mesons can not only provide insight into the behaviour of the photoproduction cross section of vector mesons but also explore the related properties of the proton, such as the source of mass, mass radius and mechanical properties of the proton [1, 6,7,8,9,10,11]. And also, some models [38, 39] have been used to reproduce the cross section of vector meson photoproduction. In particular, in low energy regions, vector meson photoproduction is usually described by the exchange of two or three gluons. The process can be described as splitting photons into $q\bar{q}$ which exchanges the two gluons to scatter the initial proton. Eventually, the $q\bar{q}$ pair hadrons form the final vector meson, as shown in Fig. 1. This is the two gluon exchange model based on perturbation QCD, which can be directly related to the gluon distribution function $xg(x,m_{V}^{2})$. Due to the existing partial distribution functions such as CTEQ6M [40], GRV98 [41], NNPDF [42] , CJ15 [43, 44], and IMParton16 [45]. It isn’t easy to interpret the relevant photoproduction experimental data of vector mesons at the near-threshold. Therefore, the parameterized gluon distribution function $xg(x,m_{V}^{2})$ $=$ $A_{0}x^{A_{1}}(1-x)^{A_{2}}$ [46, 47] is introduced in this work. Here, $A_{0}$, $A_{1}$ and $A_{2}$ are free parameters, in which $A_0$ has the most significant influence on the cross section size of vector meson photoproduction.

Fig. 1

The Feynman diagrams of the two gluon exchange model for vector mesons photoproduction

Therefore, combined with $xg(x,m_{V}^{2})$, the differential cross section of the two gluon exchange model is [48]

$$\begin{aligned} \frac{d \sigma }{d t}=\frac{\pi ^{3} \Gamma _{e^{+} e^{-}} \alpha _{s}}{6 \alpha m_{q}^{5}}\left[ x g\left( x, m_{V}^{2}\right) \right] ^{2} \exp \left( b_{0} t\right) , \end{aligned}$$

(19)

where $b_{0}$ is the slope which can be determined by experimental data. The total cross section of vector meson photoproduction is expressed by integrating Eq. (19) from $t_{min}$ to $t_{max}$,

$$\begin{aligned} \sigma (W)=\int _{t_{min}}^{t_{max}}\frac{d \sigma }{d t}d t. \end{aligned}$$

(20)

Here, $t_{min}$ ($t_{max}$) is expressed as [46, 49]

$$\begin{aligned} t_{min}(t_{max})=\left( \frac{m_{1}^2-m_{3}^2-m_{2}^2+m_{4}^2}{2W}\right) ^{2}-(p_{1cm}\mp p_{3cm})^{2}, \end{aligned}$$

(21)

where $p_{icm}$ $=$ $\sqrt{E_{icm}^{2}-m_{i}^{2}}$ ($i=1,3$), $E_{1cm}$ $=$ $(W^{2}+m_{1}^{2}-m_{2}^{2})/(2W)$ and $E_{3cm}$ $=$ $(W^{2}+m_{3}^{2}-m_{4}^{2})/(2W)$.

3 Results

In our previous work [6, 50], the mass radius of the proton and the scattering length of $\phi$-N were predicted with the two gluon exchange model, which is in good agreement with those extracted directly from the experimental data. This phenomenon indicates that the two gluon exchange model is reliable for studying the physical properties of the proton. Therefore, in this work, we concentrate on the cross section of $\phi$ photoproduction at the near-threshold predicted by the two gluon exchange model to extract the trace anomaly contribution $M_{a}/M_{N}$ of the proton. The relevant parameters for $\gamma p$ $\rightarrow$ $\phi p$ based on the two gluon exchange model are list in Table 2. In addition, $\rho$ and $\omega$ are not composed of pure $q\bar{q}$, but a mixture of ud quarks. So the trace anomaly contributions are extracted directly from the experiment data of $\rho$ and $\omega$ meson [25,26,27].

Table 2 The slope $b_{0}$ and parameters $A_{0}, A_{1}, A_{2}$ for the two gluon exchange model

With Eq. (9), the $M_{a}/M_{N}$ is extracted by the differential cross sections $d \sigma / d t|_{t=t_{min}}$ of $\phi$ photoproduction at the near-threshold. The $M_{a}/M_{N}$ extracted from the CLAS [23] and LEPS data [22] of $\phi$ photoproduction at different energies is shown in Fig. 2, where the center of mass energy W is converted into the corresponding R. There appears to be an overall upward trend here. The average trace anomaly contribution $\sqrt{\left\langle (M_{a}/M_{N})^{2}\right\rangle }$ is calculated as ($5.02\pm 0.32$)$\%$. The blue line represents the result of extraction of the differential cross section of $\phi$ predicted by the two gluon exchange model, which increases with R. The $\sqrt{\left\langle M_{a}/M_{N})^{2}\right\rangle }=(5.59\pm 0.78)$ $\%$. Here, the interval of R is [0, 0.66].

Fig. 2

The function of the trace anomaly contribution with R based on the differential cross section $d \sigma / d t|_{t=t_{min}}$ of $\phi$ predicted by the two gluon exchange model (the blue line). The olive-green squares are extracted from the CLAS [23] and LEPS [22]. Compared with the result obtained by heavy vector meson photoproduction, the extraction of $M_{a}/M_{N}$ from the $\phi$ photoproduction is relatively flat with the change of energy. Here, the blue band is the error bar of $A_0$

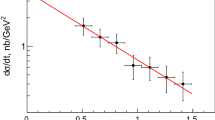
Unlike the trace anomaly contribution obtained from the differential cross section, $M_{a}/M_{N}$ extracted from the total cross section of $\phi$ photoproduction grows relatively gently with R, as shown in Fig. 3. The $\sqrt{\left\langle (M_{a}/M_{N})^{2}\right\rangle }=(2.51\pm 0.45$)$\%$ is from the two gluon exchange model and $\sqrt{\left\langle (M_{a}/M_{N})^{2}\right\rangle }=(2.60\pm 0.15$)$\%$ is extracted from the CLAS data [24]. Relating Figs. 2 and 3, at the point closest to the threshold, the $M_{a}/M_{N}$ extracted from the total and differential cross sections of $\phi$ photoproduction predicted by the two gluon exchange model are adjacent, which takes into account the error bars. Moreover, the average value calculated from the total cross section at $R\in [0,0.66]$ is almost close to the $M_{a}/M_{N}$ calculated from the differential cross section at the threshold $R=0$ (the $M_{a}/M_{N}$ is ($2.17\pm 0.30$)$\%$). This indicates that the trace anomaly extracted from the total cross section is the minimum of the trace anomaly extracted from the differential cross section.

Fig. 3

The trend of the trace anomaly contribution with R based on total cross section of $\phi$ predicted by the two gluon exchange model (the blue line). The magenta diamond is extracted from the CLAS data [24]. Here, the blue band is the error bar of $A_0$

A recent literature [21] has measured a new set of the differential cross sections of $J/\psi$ photoproduction and extracted the trace anomaly contribution. The results indicate that the $M_{a}/M_{N}$ increases with the energy W, which is consistent with the results obtained by the differential cross section of $\phi$ photoproduction. This phenomenon shows that the trace anomaly is very sensitive and dependent on energy. However, it does not suggest that the consequence extracted from the total cross section of $\phi$ is incorrect. It’s just because the trace anomaly contribution from the differential cross section is more reasonable to demonstrate the growing relationship.

The reason for the sensitive problem is that the minimum momentum transfer $t_{min}$ of vector mesons changes very rapid with the increase of W. Although the $t_{min}$ of light vector meson does not vary with W as quickly as that of heavy vector meson, the sensitivity still exists. Fortunately, the differential cross section at $t=t_{thr}$ provides an opportunity to limit the energy sensitivity problem. As is shown in the Fig. 4, the $t=t_{min}$ has a decreasing trend with W, while $t=t_{thr}$ has no such tendency.

Fig. 4

The momentum transfers for the $t_{min}$ and $t_{thr}$ as a function of W for the reaction of $\gamma p$ $\rightarrow$ $\phi p$. The blue line is for the $t=t_{min}$, and the red dashed line is for the $t=t_{thr}$

Under the definition of Eq. (18), $M_{a}/M_{N}$ is extracted from the differential cross sections $d \sigma / d t|_{t=t_{thr}}$ of the $\phi$ photoproduction at the near-threshold. As shown in Fig. 5, the energy sensitivity of $M_{a}/M_{N}$ based on the $\phi$ photoproduction is decreased. Not at all as fast as Fig. 2. The average value calculated based on the two gluon exchange model is $(2.88\pm 0.40)\%$. Table 3 lists the results calculated through experimental data of $\phi$, and the average value is $(2.90\pm 0.23)\%$. Combined with the results extracted from the total cross section before, the trace anomaly contributions of the two are almost consistent, taking the error bar into account. Therefore, considering all the results from the total and differential cross sections of $\phi$, the root mean square (RMS) can be calculated as $(2.73\pm 0.54)\%$.

Table 3 The trace anomaly contribution $M_{a}/M_{N}$ based on the $d \sigma / d t|_{t=t_{thr}}$ of meson $\phi$ from the CLAS [23] and LEPS data [22]. The average is ($2.90\pm 0.23$)$\%$

Fig. 5

The function of the trace anomaly contribution with R based on the differential cross section $d \sigma / d t|_{t=t_{thr}}$ of $\phi$ predicted by the two gluon exchange model. The notation and the blue band is the same as in Fig. 2

Based on the experimental differential cross section of $\rho$ [26, 27] at $W\in [1.79,1.94]$ and $\omega$ [25] at $W\in [1.73,2.38]$ measured in the SAPHIR Collaboration [25,26,27], the trace anomaly contributions extracted directly with the VMD model are listed in Tables 4 and 5. Near the threshold, $M_{a}/M_{N}$ obtained from $\rho$ and $\omega$ photoproduction data is tiny, with average values of ($0.53\pm 0.15$)$\%$ and ($1.47\pm 0.48$)$\%$, respectively. In order to apparently observe the trace anomaly distribution extracted from the $\rho$, $\omega$ and $\phi$ photoproduction cross section, W is transformed into the corresponding R here, which is shown in Fig. 6. $M_{a}/M_{N}$ extracted based on the differential cross section of light vector meson account for a very small fraction of the proton mass.

Table 4 The result extracted from the experimental data of $\rho$ photoproduction [26, 27], where $W=1.79$, 1.82, 1.87, 1.94 GeV are from Ref. [26] and $W=1.92$ GeV is from Ref. [27]. The average is $(0.53\pm 0.15)\%$

Table 5 The trace anomaly contribution extracted from the experimental data of $\omega$ photoproduction [25]. The average is $(1.47\pm 0.48)$ $\%$

Fig. 6

The trace anomaly contributions $M_{a}/M_{N}$ as a function of R extracted from the $d \sigma / d t|_{t=t_{thr}}$ of three light vector mesons photoproduction [22, 23, 25,26,27]. The olive green square is the result from $\gamma p$ $\rightarrow$ $\phi p$ from the CLAS [23] and LEPS data [22]. The blue diamond is extracted from the data of $\omega$ derived by SAPHIR Collaboration [25]. The purple circle represents the $M_{a}/M_{N}$ extracted from the $\rho$ experimental data developed by SAPHIR Collaboration [26, 27]

Table 6 The $M_{a}/M_{N}$ extracted from the differential cross section of $\rho$, $\omega$, $\phi$, and $J/\psi$

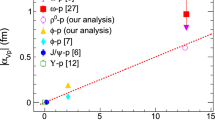
In the previous work [51], the $M_a/M_N$ extracted from the differential cross section of $J/\psi$ photoproduction is $(3.50\pm 0.70)\%$. Combined with the results of this work, the trace anomaly contribution obtained from the light vector meson and heavy vector meson is listed in Table 6. These results indicate that the trace anomaly contribution accounts for a small fraction of the proton mass. Figure 7 shows the trace anomaly distribution extracted from different vector mesons, which can be observed that the trace anomaly contribution is proportional to the mass of the meson. The red line is a function fitted through the results from $\omega$, $\phi$ and $J/\psi$ photoproduction,

$$\begin{aligned} \frac{M_a}{M_N} = \exp {\left[ 1.50 - (0.66\pm 0.39)\frac{1}{m_V}\right] }. \end{aligned}$$

(22)

One find that the trace anomaly contribution extracted from the $\rho$ meson photoproduction cross section is obviously small. The main reason is that the width of the $\rho$ meson is too large, so that the decay width $\Gamma _{\rho \rightarrow e^{+}e^{-}}$ is more than one order of magnitude larger than $\Gamma _{\omega \rightarrow e^{+}e^{-}}$ (as shown in Table 1), and finally the extracted trace anomaly contribution is suppressed. If the partial width $\Gamma _{\rho \rightarrow e^{+}e^{-}}$ of the $\rho$ meson is replaced by $\Gamma _{\omega \rightarrow e^{+}e^{-}}$, the trace anomaly contribution extracted from the $\rho$ photoproduction cross section is very close to that extracted from the $\omega$ photoproduction cross section.

Fig. 7

The distribution of the trace anomaly contributions obtained from different vector mesons photoproduction. The blue diamond, the orange pentagram, the olive green square, and the purple circle represent the results from $J/\psi$ [51], $\phi$, $\omega$, and $\rho$, respectively

4 Conclusion

At present, the trace anomaly contribution in the proton has been extracted from the total cross section and differential cross section at $t=t_{min}$ of $\phi$ photoproduction at the near-threshold. The results show that the extraction by $d \sigma /d t|_{t=t_{min}}$ is very sensitive to energy. To eliminate this energy dependence, the differential cross section at $t=t_{thr}$ is employed and successfully solved the problem. Combined with the results extracted from the total cross section of $\phi$, the RMS is calculated as $(2.73\pm 0.54)\%$. Furthermore, the trace anomaly contributions extracted from the cross sections of $\rho$ and $\omega$ photoproduction are $(0.53\pm 0.15)\%$ and $(1.47\pm 0.48)\%$, respectively. In our previous work [51], the trace anomaly contribution was extracted as $(3.50\pm 0.70)\%$ from $J/\psi$ photoproduction. By comparing and analyzing the results, it is found that the trace anomaly contribution increases linearly with the increase of the mass of the vector meson. This result is not only helpful to determine the size range of the trace anomaly contribution, but also provides an important reference for us to understand the differences in the physical mechanism of different vector meson photoproduction. In the future, we will carry out research in this area.

A new mass decomposition [12] in 2020, also starting from the energy momentum tensor $T^{00}$, divides the proton mass into four terms. In their calculations, the trace anomaly term $M_{a}/M_{N}=0$ is considered, and the proton’s mass is primarily composed of the other three parts. Although a lot of work has been done on the source of the proton mass, all of them focus on the difference between the normal and abnormal contributions, especially the trace anomaly contribution, how much it contributes to the proton mass is still the target of our further investigation. In addition, an interesting result [52] is that someone calculated the trace anomaly contribution of the hydrogen atom is also very small. All these results demonstrate that the trace anomaly contribution is still ambiguous. Therefore, acquiring more vector meson photoproduction data is necessary to investigate the source of proton mass further. In the future, the EIC facility [53, 54] and JLab may have the opportunity to design more experiments to probe the proton’s internal structure and explain the source of proton mass more reasonably.