1 Introduction

In 1975, Hawking pointed out that black holes will end theirs lives with evaporation [1], which significantly supported the picture of the Bekenstein entropy, that a black hole can be reckon as a thermodynamic system [2]. However, a question soon arose, due to its breaking the law of information conservation in conflict with the quantum theory, which is the so-called black hole information paradox. About a half century passed, in 2016, Hawking, Perry, and Strominger (HPS) revisited this problem, and proposed soft hairy black hole that might provide a resolution to the information paradox [3, 4].

The studies on the soft hairy black hole would involve the global spacetime structure from the event horizon to the asymptotically flat zone. Therefore, it is interesting to examine whether the influence from the soft hair can be observed. Recently, it becomes possible, because Event Horizon Telescope (EHT) presented the images of the black holes in M87 [5,6,7,8,9,10], and just recently in our galaxy [11], and opened a new way to investigate the physics in strong field regime of gravity for the black holes.

A black hole can not only bend lights but also swallow them. As a result, a shaded zone exists in the field of vision of an observer, and is thus called the black hole shadow. It is the interpretation for the images of the black holes. Originally, it was developed based on the theoretical works of Synge [12] and Bardeen [13]. By extracting information of a black hole from its shadow, one can tell the difference of the spacetime geometry for different black holes, and provide a way to explore properties of the black hole, such as reflection coefficients on the horizon [14], quantum structure [15, 16] and naked singularity [17], or test general relativity [18,19,20,21] and the No-hair theorem [22,23,24,25].

Due to the interests of information paradox, the shadow of the soft hairy black hole has been explored in Refs. [25, 26]. The supertranslation hair, as a type of soft hair, is of great interesting, because it was suggested that the supertranslated black hole carries conservation charges at classical level [4], and thus might have observable effect in classical physics. Ref. [26] investigated the photon sphere of the supertranslated Vaidya black hole in the equatorial plane, which suggested that the changes of the photon sphere might lead to a distinguishable shadow. Since the supertranslated black hole has less space-time symmetries compared to the parameterized Kerr black hole, in Ref. [25], the authors simulated the light rays for calculating the shadow of the supertranslated black holes. Both of them argued that the supertranslation hair could be observable. However, in our point of view, the supertranslation hair was implanted by introducing a diffeomorphism to a black hole [4], which might suggest no observed effects. In this paper, we will clarify this point according to some explicit calculations.

The rest of the paper is organized as follows. In Sect. 2, we calculate the shadow of the supertranslated Schwarzschild black hole. Differed from previous studies, we obtain 4-velocities and trajectories of the bending light rays around the supertranslated Schwarzschild black hole by making use of diffeomorphism. In Sect. 3, we give a general derivation for the shadow of a supertranslated black hole in asymptotically flat space-time. In Sect. 4, the conclusions and discussions are summarized.

2 The shadow of Schwarzschild black hole with supertranslation hair

In this section, we would briefly list results of supertranslated Schwarzschild black hole proposed by HPS, and then show the procedure for obtaining the shadow of the supertranslated Schwarzschild black holes.

2.1 Schwarzschild black hole with supertranslation hair

As proposed by HPS [4], the supertranslation hair on Schwarzschild black hole is given by introducing the supertranslations,

$$\begin{aligned} g_{\mu \nu }^{{ (\mathrm hairy)}} = g_{\mu \nu }^{{(\mathrm bald)}} +{\mathcal {L}}_{\zeta } g_{\mu \nu }^{{(\mathrm bald)}}, \end{aligned}$$
(1)

which is also the procedure of implanting supertranslation hair on Schwarzschild black hole. The quantities in Eq. (1) will be illustrated in the following part of this paper. The metric of bald Schwarzschild black hole \(g_{\mu \nu }^{(\mathrm bald)}\) in advanced Bondi coordinate (v,r,\(\theta \),\(\phi \)) is given by

$$\begin{aligned} \textrm{d} s^2 = - \left( 1 - \frac{2 M}{r} \right) \textrm{d} v^2 + 2 \textrm{d} v \textrm{d} r + r^2 \gamma _{A B} \textrm{d} \Theta ^A \textrm{d} \Theta ^B, \end{aligned}$$
(2)

where M is the mass of the black hole, \(\Theta ^A\) denotes the angular coordinates \(\theta \) or \(\phi \). The \({\mathcal {L}}_\zeta \) is the Lie derivative along the supertranslation vector \(\zeta \) that is formulated as [4, 27, 28],

$$\begin{aligned} \zeta = f (\theta , \phi ) \partial _{v} - \frac{1}{2} D^2 f (\theta , \phi ) \partial _r + \frac{1}{r} D^A f (\theta , \phi ) \partial _A. \end{aligned}$$
(3)

where D is the covariant derivative with respect to the metric on the unit two sphere, and the \(f(\theta ,\phi )\) is an arbitrary function that is proportional to the first order weak-field expansion. Here, the \(\zeta \) is also the asymptotical Killing vector in Schwarzschild space-time. Expanding the \(f(\theta ,\phi )\) into spherical harmonics,

$$\begin{aligned} f(\theta ,\phi )=\sum _{lm}a_{lm}Y_{lm}(\theta ,\phi ), \end{aligned}$$
(4)

one can find infinite number of choices of l and m that can give different asymptotical Killing vectors. In particular, in the case of \(l=0\), \(\zeta \) is generator of the temporal translation. And in the case of \(l=1\) and \(m=-1,0,1\), \(\zeta \) are generators of the three spatial translations, respectively. Finally, on the left hand side of Eq. (1), the supertranslated Schwarzschild metric \(g_{\mu \nu }^{ (\mathrm hairy)}\) in advanced Bondi coordinate takes the form of

$$\begin{aligned} \textrm{d} s^2= & {} - \left( 1 - \frac{2 M}{r} - \frac{M}{r^2} D^2 f \right) \textrm{d} v^2 + 2 \textrm{d} v \textrm{d} r\nonumber \\{} & {} - D_A \left( 2 f - \frac{4 M}{r} f + D^2 f \right) \textrm{d} v \textrm{d} \Theta ^A\nonumber \\{} & {} + (r^2 \gamma _{A B} + 2 r D_A D_B f - r \gamma _{A B} D^2 f) \textrm{d} \Theta ^A \textrm{d} \Theta ^B,\nonumber \\ \end{aligned}$$
(5)

in which the metric depends on the angular coordinates \(\theta \) and \(\phi \) due to the function \(f(\theta ,\phi )\). It seems to bring complexity in the calculation of the propagation of light.

2.2 Propagation of light and photon sphere

In order to calculate shadow of a black hole, one should obtain solutions of null geodesic equations at first. From complexity of the metric shown in Eq. (5), it seems to be a tough task to deal with the geodesic equations. In this section, we will show that the 4-velocities and the trajectories of light rays can be obtained by using diffeomorphism, namely, the procedure of implanting the supertranslation hair. Directly solving the geodesic equations for the supertranslated Schwarzschild black hole is not necessary.

First of all, one should work out the 4-velocities of light rays for the bald Schwarzschild black hole in the Bondi coordinate. Based on the Hamilton–Jacobi method for geodesic equations [29], we obtain 4-velocities of light rays in static coordinates \((t,r,\theta ,\phi )\) for the bald Schwarzschild black hole (see Eqs. (10)–(13) in ref. [30]). And then the 4-velocities in static coordinates are transformed into Bondi coordinate by using \(v=t+r+2M\log (r/2M -1)\), namely

$$\begin{aligned} p^{v, (\mathrm bald)}= & {} E\left( \frac{r}{r-2M}\right) \left( 1+\sqrt{\frac{r^{3}+2M\kappa -r\kappa }{r^3}}\right) , \end{aligned}$$
(6a)
$$\begin{aligned} p^{r, (\mathrm bald)}= & {} E\sqrt{\frac{r^{3}+2M\kappa -r\kappa }{r^3}}, \end{aligned}$$
(6b)
$$\begin{aligned} p^{\theta , (\mathrm bald)}= & {} \frac{E}{r^2}\sqrt{\kappa -\frac{\lambda ^2}{\sin ^2\theta }}, \end{aligned}$$
(6c)
$$\begin{aligned} p^{\phi , {(\mathrm bald)}}= & {} \frac{E\lambda }{r^2\sin ^2\theta }, \end{aligned}$$
(6d)

where E, \(\kappa \equiv K/E^2\) and \(\lambda \equiv L/E\) are three integral constants corresponding to the energy, the total angular momentum, and the angular momentum with respect coordinate \(\phi \) for a light ray at infinity.

According to the above arguments, the 4-velocities of light rays around the supertranslated Schwarzschild black hole can be obtained by using the supertranslations,

$$\begin{aligned} p^{\mu , (\mathrm hairy)} = p^{\mu , (\mathrm bald)} + {\mathcal {L}}_\zeta p^{\mu , (\mathrm bald)}, \end{aligned}$$
(7)

where the \(\zeta \) is the supertranslation vector given in Eq. (3), and the components of the 4-velocities \(p^{\mu , (\mathrm hairy)}\) are presented as follows,

(8a)
$$\begin{aligned} p^{r, (\mathrm hairy)}= & {} \frac{1}{r^2}\left( 2 \sqrt{\kappa - \lambda ^2 \csc ^2 \theta }\right. \nonumber \\{} & {} \times \left. \left( - \partial ^{3}_{\theta }f - \cot \theta \partial ^{2}_{\theta }f +\csc ^2 \theta \partial _{\theta }f \right. \right. \nonumber \\{} & {} \left. \left. - \csc ^2 \theta \partial _{\theta }\partial ^{2}_{\phi }f \!+\!2 \cot \theta \csc ^2 \theta \partial ^{2}_{\phi }f\right) \right) \nonumber \\{} & {} + \frac{2 \lambda \csc ^2 \theta }{r^2}\left( \partial ^{2}_{\theta }\partial _{\phi }f\!+\! \cot \theta \partial _{\theta }\partial _{\phi }f \!+\!\csc ^2 \theta \partial ^{3}_{\phi }f\right) \nonumber \\{} & {} +4\sqrt{\frac{2 \kappa M +r^3 -\kappa r}{r^3}}, \end{aligned}$$
(8b)
$$\begin{aligned} p^{{\theta }, (\mathrm hairy)}= & {} \frac{E}{r^3}\Bigg ( - r \partial ^{2}_{\theta }f \sqrt{\kappa - \lambda ^2 \csc ^2 \theta }\nonumber \\{} & {} + \frac{\lambda ^2 r \cot \theta \csc ^2 \theta \partial _{\theta }f}{\sqrt{\kappa - \lambda ^2\csc ^2 \theta }} - \lambda r \csc ^2 \theta \partial _{\theta }\partial _{\phi }f\nonumber \\{} & {} +\sqrt{\kappa \!-\! \lambda ^2 \csc ^2 \theta } \left( \partial ^{2}_{\theta }f \!+\! \cot \theta \partial _{\theta }f \!+\! \csc ^2 \theta \partial ^{2}_{\phi }f\right) \nonumber \\{} & {} + r \sqrt{\kappa - \lambda ^2 \csc ^2\theta }\Bigg ), \end{aligned}$$
(8c)
$$\begin{aligned} p^{{\phi }, (\mathrm hairy)}= & {} \frac{E \csc ^2 \theta }{r^3} \Bigg (-r \sqrt{\kappa - \lambda ^2 \csc ^2 \theta } \partial _{\theta }\partial _{\phi }f\nonumber \\{} & {} + 2 r \cot \theta \sqrt{\kappa \!-\! \lambda ^2 \csc ^2 \theta } \partial _{\phi }f \nonumber \\{} & {} - 2\lambda r \cot \theta \partial _{\theta } f \!+\! \lambda \left( 1 -r\right) \csc ^2 \theta \partial ^{2}_{\phi } f \!+\! \lambda \partial ^{2}_{\theta }f \nonumber \\{} & {} + \lambda \cot \theta \partial _{\theta } f + \lambda r \Bigg ). \end{aligned}$$
(8d)

Based on the diffeomorphism, it is not difficult to find that the 4-velocities of the light rays in Eq. (8) are exactly the solutions of geodesic equations with respect to the metric in Eq. (5).

From the 4-velocities given in Eq. (8), the worldlines of the light rays \(\gamma ^\mu (\lambda )\) in supertranslated Schwarzschild spacetime can also be obtained by using diffeomorphism. The geodesic equations for the worldlines of light rays \({\bar{\gamma }}^\mu \) in bald Schwarzschild space-time are given by

$$\begin{aligned} \frac{\textrm{d}{\bar{\gamma }}^{\mu }}{\textrm{d}\lambda }= & {} p^{\mu ,(\mathrm bald)}. \end{aligned}$$
(9)

After implanting the supertranslation hair, the geodesic equations take the form of

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\lambda }({\bar{\gamma }}^{\mu } + \delta {\gamma }^{\mu })= & {} p^{\mu , (\mathrm bald)}+{\mathcal {L}}_{\zeta }p^{\mu , (\mathrm bald)}, \end{aligned}$$
(10)

where \(\delta \gamma ^\mu \) indicates a small change for the \({\bar{\gamma }}\) ascribed from the supertranslation hair. Using Eqs. (9) and (10), we obtain the solution \(\delta \gamma ^{\mu }=\zeta ^{\mu }\). Therefore the worldline of a light ray around the supertranslated Schwarzschild black hole is formulated as

$$\begin{aligned} \gamma ^{\mu }={\bar{\gamma }}^{\mu }+\zeta ^{\mu }. \end{aligned}$$
(11)

It shows that each event on the null geodesic is shifted by the supertranslation vector. Since a finite \(\zeta ^\mu \) can not shift the “endpoint” of a null geodesic from the singularity inside the black hole to spatial infinity, the fact that the light rays finally escape away from or fall into the black hole will not be changed after implanting supertranslation hair.

Fig. 1
figure 1

Ray-tracing simulations for the light rays (blue and orange curves) around a supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{20}(\theta ,\phi )\) (left panel), and \(f(\theta ,\phi )=\frac{M}{5}Y_{30}(\theta ,\phi )\) (right panel), respectively. The black circle represents the photon sphere for the bald black hole, and the red circle represents the photon sphere for the supertranslated Schwarzschild black hole. The orange curves represent the light rays that are almost tangent to the photon sphere, which determine the edge of the shadow on observers’ projection plane

Full size image
Fig. 2
figure 2

Distorted photon spheres of the supertranslated Schwarzschild black holes described by Eq. (3) and (4) with \(a_{lm}=\frac{M}{5}\). For comparison, the photon sphere of the bald Schwarzschild black hole is plotted in the translucent sphere

Full size image

The photon sphere for Schwarzschild black hole is the assemble of the unstable circle orbits of the light rays, which determines whether a bending light ray approaching the black hole can escape to infinity again. In this sense, it describes critical escape orbits for a light ray. Since implanting supertranslation hair does not change whether a light ray can escape to infinity or not, the 4-velocities of the light rays in critical escape orbits for the supertranslated Schwarzschild black hole can be formulated as

$$\begin{aligned} p^{\mu , (\mathrm hairy)}_c = p^{\mu , (\mathrm bald)}|_{\kappa =27M^2} + {\mathcal {L}}_\zeta (p^{\mu , (\mathrm bald)}|_{\kappa =27M^2}), \end{aligned}$$
(12)

where the subscript ‘c’ denotes the light rays in the critical escape orbits.

We will further illustrate Eq. (12) with ray-trace simulations. In Fig. 1, we show the trajectories of the light rays \(\gamma ^\mu \) in Eq. (11) for the supertranslated Schwarzschild black hole by numerically solving the Eq. (6), and then associating it with Eq. (11). It shows that the photon sphere, which locates at \(r=3M\) (the black circle) for the bald black hole, is distorted (the red circle) for the supertranslated Schwarzschild black hole. The orange curves represent the light rays that are almost tangent to the photon sphere. One can observe that these light rays are determined by integrating constant \(\kappa =27M^2\), which are the same as those in bald Schwarzschild space-time.

Based on Eq. (11), one can also obtain the distorted photon sphere for other types of supertranslation hairs. In Fig. 2, we plot the distorted photon spheres for selected l and m in Eq. (4). It shows that the photon sphere get more distorted for the larger l. Because the positive and negative m in Eq. 4 share the same shape of the photon sphere, we only show the cases of \(m \ge 0\) for illustration.

2.3 The shadow of a supertranslated Schwarzschild black hole

For the supertranslated Schwarzschild black hole, it was suggested that the distorted photon sphere might lead to a distinguishable shadow [26]. In this section, we will calculate the shadow in details. For distant observers, the shadow described by the coordinates \((\alpha ,\beta )\) on the observers’ projection plane is given by [12, 13]

$$\begin{aligned} \alpha\equiv & {} - \frac{r\sin \theta \textrm{d}\phi }{\textrm{d}r}\bigg |_{x^i_\textrm{obs}} = -r_{o}\sin \theta _{o}\frac{p^{{\phi }, (\mathrm hairy)}_{c}}{p^{{r}, (\mathrm hairy)}_{c}}\bigg |_{x^i_\textrm{obs}}\nonumber \\ {}= & {} -\frac{\lambda + \partial _{\phi }f(\theta _{o},\phi _{o})}{r_{o}\sin \theta _{o}}, \end{aligned}$$
(13)
$$\begin{aligned} \beta\equiv & {} \frac{r \textrm{d}\theta }{\textrm{d}r}\bigg |_{x^i_\textrm{obs}} = r_{o} \frac{p^{{\theta }, (\mathrm hairy)}_{c}}{p^{{r}, (\mathrm hairy)}_{c}}\bigg |_{x^i_\textrm{obs}}\nonumber \\ {}= & {} \frac{\sqrt{\kappa -\lambda ^2 \csc ^2 \theta _{o}}+ \partial _{\theta }f(\theta _{o},\phi _{o})}{r_{o}}, \end{aligned}$$
(14)

where \(x^i_\textrm{obs}=(r_o,\theta _o,\phi _o)\) is the location of an observer, and we have used Eq. (12) for evaluating the 4-velocities \(p^{\mu , (\mathrm hairy)}_c\). Here, the \(\kappa \) and \(\lambda \) are determined by the critical escape orbits, and the values of them are exactly the same as those for bald Schwarzschild space-time as discussed in Eq. (12).

Based on Eqs. (13) and (14), the shape and size of the shadow remain the same as those for bald Schwarzschild black hole, but the position of the shadow is shifted by \(\delta \alpha =-\partial _\phi f/(r_0\sin \theta _0)\) and \(\delta \beta =\partial _\theta f/r_0\) on the projection plane. It can be clearly shown by eliminating the \(\lambda \) in Eqs. (13) and (14), and then one can obtain the curve equation in coordinates \((\alpha ,\beta )\),

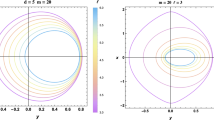
$$\begin{aligned} \left( \alpha +\frac{ \partial _{\phi }f}{r_{o}\sin \theta _{o}}\right) ^2+\left( \beta -\frac{ \partial _{\theta }f}{r_{o}}\right) ^2=\frac{\kappa }{r^2_{o}}. \end{aligned}$$
(15)

The curve equation represents a circle with radius \(\sqrt{\kappa }/r_0\) and centre \((-\partial _\phi f/(r_0\sin \theta _0),\partial _\theta f/r_0)\) on projection plane. For illustrations, we plot the shadows of the supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{33}(\theta ,\phi )\) and \(f(\theta ,\phi )=\frac{M}{5}Y_{31}(\theta ,\phi )\) for observers at equatorial plane \(\theta _0 = \frac{\pi }{2}\) in Figs. 3 and 4, respectively. For observers located at different \(\phi \) ranged from 0 to \(2\pi \), the center positions of the shadows would move from the red point to the other one shown in the plots. Comparing the two examples, one might find that the positions of the shadows with supertranslation hair \(f(\theta ,\phi )=\frac{M}{5}Y_{33}(\theta ,\phi )\) is shifted by a larger distance than that with \(f(\theta ,\phi )=\frac{M}{5}Y_{13}(\theta ,\phi )\). In Fig. 5, we plot the shadows of the supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{32}(\theta ,\phi )\) for observers at equatorial plane. In addition, the positions of the shadows for \(f(\theta ,\phi )=\frac{M}{5}Y_{30}(\theta ,\phi )\) are fixed at the origin of the coordinate \((\alpha ,\beta )\) on projection plane. Thus, we did not show the these here. Generally, for arbitrary types of supertranslation hairs described in Eqs. (3) and (4), the shadows on projection plane are completed described by Eq. (15). Here, we only showed the supertranslated Schwarzschild black hole with \(l=3\) for examples.

Although, the photon sphere get highly distorted, the supertranslation only leads to the shifted positions of the shadows on the projection plane.

Fig. 3
figure 3

The shadow of supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{33}(\theta ,\phi )\) for distant observers at equatorial plane \(\theta _0=\frac{\pi }{2}\), and at different \(\phi _o\) ranged from 0 to \(2\pi \), respectively. The photon rings on the projection plane are presented in the black circles, and red point–dashed line–red point represents the the centre of the shadows

Full size image
Fig. 4
figure 4

The shadow of supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{31}(\theta ,\phi )\) for distant observers at equatorial plane \(\theta _0=\frac{\pi }{2}\), and at different \(\phi _o\) ranged from 0 to \(2\pi \), respectively. The photon rings on the projection plane are presented in the black circles, and red point–dashed line–red point represents the the centre of the shadows

Full size image
Fig. 5
figure 5

The shadow of supertranslated Schwarzschild black hole with \(f(\theta ,\phi )=\frac{M}{5}Y_{32}(\theta ,\phi )\) for distant observers at equatorial plane \(\theta _0=\frac{\pi }{2}\), and at different \(\phi _o\) ranged from 0 to \(2\pi \), respectively. The photon rings on the projection plane are presented in the black circles, and red point–dashed line–red point represents the the centre of the shadows

Full size image

3 A general derivation for the shadow of supertranslated black hole

Because the supertranslated black hole was implanted based on the diffeomorphism, we could extend the above calculation to an arbitrary asymptotically flat spacetime. For the shadow of a stationary black hole in the view of distant observers, the 4-velocities of light rays from the photon sphere can be generally expanded as

$$\begin{aligned} p^\mu = A^\mu (\theta ,\phi )+\frac{1}{r}B^\mu (\theta ,\phi )+\frac{1}{r^2}C^\mu (\theta ,\phi )+{\mathcal {O}}\left( \frac{1}{r^3}\right) , \nonumber \\ \end{aligned}$$
(16)

where \(A_\mu \), \(B_\mu \) and \(C_\mu \) are the expansion coefficients. Due to the asymptotically flat space-time, the leading order of the 4-velocities are proportional to the \({\mathcal {O}}(1)\), and the space-time are exactly the Minkowski space-time in the null infinity. Therefore, the motion of a photon formulated by Eq. (16) should obey the conservation laws, namely,

$$\begin{aligned} E= & {} p^0 = \sqrt{(p^r)^2+ r^2(p^\theta )^2 + r^2\sin ^2{\theta } (p^\phi )^2}, \end{aligned}$$
(17)
$$\begin{aligned} J= & {} r^2 \sqrt{(p^\theta )^2 + \sin ^2{\theta } (p^\phi )^2 }, \end{aligned}$$
(18)

where E and J are constants describing total energy and angular momentum of a photon, respectively. By making use of Eq. (18), the spatial components of the 4-velocities of the light rays in Eq. (16) reduce to

$$\begin{aligned} p^r= & {} A^r(\theta ,\phi )+\frac{1}{r}B^r(\theta ,\phi )+\frac{1}{r^2}C^r(\theta ,\phi )+{\mathcal {O}}\left( \frac{1}{r^3}\right) , \end{aligned}$$
(19a)
$$\begin{aligned} p^\theta= & {} \frac{1}{r^2}C^\theta (\theta ,\phi )+{\mathcal {O}}\left( \frac{1}{r^3}\right) , \end{aligned}$$
(19b)
$$\begin{aligned} p^\phi= & {} \frac{1}{r^2}C^\phi (\theta ,\phi )+{\mathcal {O}}\left( \frac{1}{r^3}\right) . \end{aligned}$$
(19c)

In the leading order, it seems reasonable that \(p^A\) is proportional to \({\mathcal {O}}(r^2)\), and \(p^r\) is proportional to \({\mathcal {O}}(1)\).

Based on Eq. (7), the supertranslated 4-velocities can be obtained by substituting the bald velocities with Eq. (19). It describes the motions of light in the space-time of a supertranslated black hole. For given coordinate conditions from the asymptotic symmetries [27], the supertranslated vectors with respect to an arbitrary supertranslated black hole could different from the form in Eq. (3), while it could be generally expressed in an asymptotic expansion [4], namely

$$\begin{aligned} \zeta= & {} f(\theta ,\phi )\partial _v+ \left( \zeta ^{r,(0)}(\theta ,\phi )+\frac{1}{r}\zeta ^{r,(1)}(\theta ,\phi )+{\mathcal {O}}\left( {\frac{1}{r^2}}\right) \right) \partial _r \nonumber \\{} & {} + \left( \frac{1}{r}\zeta ^{A,(1)}\left( \theta ,\phi \right) +\frac{1}{r^2}\zeta ^{A,(2)}(\theta ,\phi ) +{\mathcal {O}}\left( \frac{1}{r^3}\right) \right) \partial _A \end{aligned}$$
(20)

For different black holes, the coefficients \(\zeta ^{r,(0)}\), \(\zeta ^{r,(1)}\), \(\zeta ^{A,(2)}\) and \(\zeta ^{A,(2)}\) should be different.

In order to obtain the influence of the supertranslation on the shadow of a black hole, we evaluate the (\(\alpha \),\(\beta \)) with the supertranslated 4-velocities by making use of Eqs. (6), (19) and (20), namely,

$$\begin{aligned} \alpha ^\textrm{hairy}= & {} -r_{o}\sin \theta _{o}\frac{p^{{\phi }, (\mathrm hairy)}_{c}}{p^{{r}, (\mathrm hairy)}_{c}}\bigg |_{r\rightarrow \infty } \nonumber \\= & {} -r_{o}\sin \theta _{o}\left( \frac{\frac{1}{r^2}C^\phi +\frac{1}{r^2}A^r\zeta ^{\phi ,(1)}+{\mathcal {O}}\left( \frac{1}{r^3} \right) }{A^r+{\mathcal {O}}\left( \frac{1}{r} \right) } \right) \nonumber \\= & {} -\frac{\sin \theta _{o}}{r_o}\left( \frac{C^\phi }{A^r}+\zeta ^{\phi ,(1)}\right) +{\mathcal {O}}\left( \frac{1}{r^2_o} \right) \end{aligned}$$
(21a)
$$\begin{aligned} \beta ^\textrm{hairy}= & {} r_{o} \frac{p^{{\theta }, (\mathrm hairy)}_{c}}{p^{{r}, (\mathrm hairy)}_{c}}\bigg |_{r\rightarrow \infty }\nonumber \\= & {} \frac{1}{r_o}\left( \frac{C^\theta }{A^r}+\zeta ^{\theta ,(1)}\right) +{\mathcal {O}}\left( \frac{1}{r^2_o} \right) , \end{aligned}$$
(21b)

Since we have known \(\zeta ^{A,(1)} \rightarrow D^A f(\theta ,\phi )\) with \(r\rightarrow \infty \), one might find that the results in Eq. (21) are consistent with that for supertranslated Schwarzschild black holes in Eqs. (13) and (14). At least for distant observers, the supertranslation can only affect the positions of the shadows on the projection plane. It is noted that the results can be reproduced by choosing different coordinate systems in Minkowski space-time (at null infinity). Therefore, no observed effect on the shadow of a supertranslated black hole can be given.

4 Conclusions and discussions

We investigate the shadow for supertranslated Schwarzschild black hole proposed by Hawking, Perry and Strominger [3]. The calculation on the shadow of supertranslated Schwarzschild black hole turns to be much easier, if the supertranslated 4-velocities and the trajectories of the light rays are used. Based on this approach, we showed that the photon sphere gets distorted due to the supertranslation hairs, the position of the shadow on the projection plane is shifted by the supertranslation vector and depends on the location of the observer, and the size and shape of the shadow are the same as those of bald black hole. For the shifted position of the shadows, it can be originated from different choice of coordinate systems in Minkowski space-time. Therefore, there is no observed effect on the shadow of a supertranslated black hole.

This paper is partly inspired by pioneers’ studies [25, 26] that suggests observable effects from the supertranslated black holes by observing its shadow. We clarified that the shadow can not be used as an observable for indicating the soft hairs. Perhaps, the supertranslated black holes could have possible observed effects at quantum level.