1 Introduction

The gravitational particle creation in Friedman Universe expansion is an important theoretical issue [1,2,3,4,5] that has been intensively studied for decades [6,7,8,9,10,11,12,13]. Based on adiabaticity and non-back-reaction approximation for a slowly time-varying Hubble function H(t), one adopted the semi-classical WKB approaches to calculating the particle production rate, which is exponentially suppressed \(e^{-M/H}\) for massive particles \(M\gg H\). However, the non-adiabatic back-reactions of particle creations on the Hubble function can be large and have to be taken into account. The non-adiabatic back-reactions of massive particle productions have a quantum time scale \({\mathcal O}(1/M)\) that is much smaller than classical Universe evolution time scale \({\mathcal O}(1/H)\). To properly include the back-reaction of particle production on Universe evolution, one should separate fast components \({\mathcal O}(1/M)\) from slow components \({\mathcal O}(1/H)\) in the Friedman equation. Many efforts [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] have been made to study non-adiabatic back-reaction and understand massive particle productions without exponential suppression. It is important for reheating, possibly accounting for massive dark matter and total entropy of the present Universe [15, 16, 32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].

In this article, we consider the \(\tilde{\Lambda }\)CDM scenario [54] of dark energy and matter interactions, in which the cosmological term \(\tilde{\Lambda }\) is time-varying and the Friedman equations for a flat Universe become

$$\begin{aligned} H^2= & {} \frac{8\pi G}{3}\rho ;\nonumber \\ \dot{H}= & {} -\frac{8\pi G}{2}(\rho + p)\quad {=-\frac{8\pi G}{2}(\rho _{_M}+ p_{_M})}, \end{aligned}$$
(1.1)

where energy density \(\rho \equiv \rho _{_M}+\rho _{_\Lambda }\) and pressure \(p\equiv p_{_M}+p_{_\Lambda }\). Equation of state \(p_{_\Lambda }=-\rho _{_\Lambda }\) is for the cosmological constant term (dark energy). Equation of state \(p_{_M}=\omega _{_M}\rho _{_M}\) is for the matter that represents relativistic (radiation) and non-relativistic components. The second equation of (1.1) is the generalised conservation law (Bianchi identity) for including time-varying cosmological term \(\rho _{_\Lambda }(t)\equiv \tilde{\Lambda }/(8\pi G)\). It reduces to the usual equation \(\dot{\rho }_{_M} + (1+\omega _{_M})H\rho _{_M}=0\) for time-constant \(\rho _{_\Lambda }\). The second equation of (1.1) shows that due to the matter’s gravitational attractive nature, \(\dot{H} <0\) and H decreases in time. Equation (1.1) are not the same as the Friedman equations with the constant cosmological term \(\Lambda \) or the scalar field \(\phi \) of inflation potential \(V(\phi )\).

2 Slow and fast components’ separation

In the \(\tilde{\Lambda }\)CDM scenario, we adopt the approach [27] to describe the decomposition of slow and fast components: scale factor \(a=a_\textrm{slow}+a_\textrm{fast}\), Hubble function \(H=H_\textrm{slow}+H_\textrm{fast}\), cosmological term and matter density \(\rho _{_{\Lambda ,M}}=\rho ^\textrm{slow}_{_{\Lambda ,M}}+\rho ^\textrm{fast}_{_{\Lambda ,M}}\) and pressure \(p_{_{\Lambda ,M}}=p^\textrm{slow}_{_{\Lambda ,M}}+p^\textrm{fast}_{_{\Lambda ,M}}\). The fast components vary much faster in time, but their amplitudes are much smaller than the slow components. According to the order of small ratio \(\lambda \) of fast and slow components, the Friedman equations (1.1) are decomposed into two sets. The slow components \({\mathcal O}(\lambda ^0)\) obey the same equations as usual Friedman equations (“macroscopic” \({\mathcal O}(H_\textrm{slow}^{-1})\) equations)

$$\begin{aligned} H_\textrm{slow}^2= & {} \frac{8\pi G}{3}(\rho _{_M}^\textrm{slow}+\rho _{_\Lambda }^\textrm{slow});\nonumber \\ \quad \dot{H}_\textrm{slow}= & {} -\frac{8\pi G}{2}(\rho _{_M}^\textrm{slow} +p_{_M}^\textrm{slow}), \end{aligned}$$
(2.1)

where \(H_\textrm{slow}=\dot{a}_\textrm{slow}/a\approx \dot{a}_\textrm{slow}/a_\textrm{slow}\), time derivatives \(\dot{H}_\textrm{slow}\) and \(\dot{a}_\textrm{slow}\) relate to the macroscopic “slow” time variation scale \({\mathcal O}(1/H)\). The faster components \({\mathcal O}(\lambda ^1)\) obey new (“microscopic” \({\mathcal O}(M^{-1})\) equations),

$$\begin{aligned} H_\textrm{fast}= & {} \frac{8\pi G}{2\times 3H_\textrm{slow}}(\rho _{_M}^\textrm{fast}+\rho _{_\Lambda }^\textrm{fast});\nonumber \\ \dot{H}_\textrm{fast}= & {} -\frac{8\pi G}{2}(\rho _{_M}^\textrm{fast} +p_{_M}^\textrm{fast}), \end{aligned}$$
(2.2)

where \(H_\textrm{fast}=\dot{a}_\textrm{fast}/a\approx \dot{a}_\textrm{fast}/a_\textrm{slow}\), time derivatives \(\dot{H}_\textrm{fast}\) and \(\dot{a}_\textrm{fast}\) relate to the microscopic “fast” time variation scale \({\mathcal O}(1/M)\), and slow components are approximated as constants in “fast” time variation. For the cosmological term, equation of state \(p_{_\Lambda }=-\rho _{_\Lambda }\) becomes \(p_{_\Lambda }^\textrm{slow,fast}=-\rho _{_\Lambda }^\textrm{slow,fast}\) respectively at order \({\mathcal O}(\lambda ^0)\) and \({\mathcal O}(\lambda ^1)\). In due course, we shall clarify the equation of state \(p_{_M}=\omega _{_M}\rho _{_M}\) for the matter term, associating to the fast and slow components respectively. Equation (2.2) for the fast components are different from their counterparts [27] for the case of Friedman equations with a single inflation field \(\phi \) and its potential \(V(\phi )\). They are novel equations to investigate the nature of dark energy and matter interactions in the \(\tilde{\Lambda }\)CDM scenario.

In the fast component Eq. (2.2), we adopt the approach [14] to describe the fast components of matter density \(\rho _{_M}^\textrm{fast}\) and pressure \(p_{_M}^\textrm{fast}\). They are due to the non-adiabatic production of particle and antiparticle pairs in fast time variation \(H_\textrm{fast}=\dot{a}_\textrm{fast}/ a_\textrm{slow}\) and its time derivative \(\dot{H}_\textrm{fast}\). As new results, we find quantum coherent oscillation of fast and microscopic components \(H_\textrm{fast}\), \(\rho _{_\Lambda }^\textrm{fast}\), \(\rho _{_M}^\textrm{fast}\) and \(p_{_M}^\textrm{fast}\), due to microscopic back reactions at the time scale \({\mathcal O}(M^{-1})\). The quantum pair production and oscillation of \(\rho _{_M}^\textrm{fast}\) and \(p_{_M}^\textrm{fast}\) can form a macroscopic state of massive pair plasma, contributing to slow and macroscopic components \(\rho _{_M}^\textrm{slow}\) and \(p_{_M}^\textrm{slow}\) at the time scale \({\mathcal O}(H^{-1})\). In the \(\tilde{\Lambda }\)CDM scenario, we consider the time-varying cosmological term \(\rho _{_\Lambda }^\textrm{slow}\) drives the inflation (quasi-de Sitter phase) [8, 15, 55,56,57]. We study how such a macroscopic state of massive pair plasma affects (back-reacts on) the Friedman equation (2.1) by slowly decreasing \(\rho _{_\Lambda }^\textrm{slow}\) and \(H_\textrm{slow}\), leading to slowing-down effects on the inflation.

3 Quantum pair production and oscillation

A quantised massive scalar matter field inside the Hubble sphere volume \(V\sim H^{-3}_\textrm{slow}\) of Friedman Universe reads

$$\begin{aligned} \Phi (\textbf{x},t)= & {} \sum _n A_n Y_n(\textbf{x})\psi _n(t). \end{aligned}$$
(3.1)

Here we assume that the field exponentially vanishes outside the horizon \(H^{-1}_\textrm{slow}\), i.e., the particle horizon \((a_\textrm{slow}H_\textrm{slow})^{-1}\) of comoving Hubble radius, and \(\int _V Y_n(\textbf{x}) Y^\dagger _{n'}(\textbf{x})h^{1/2}d^3x=\delta _{nn'}\). The principal quantum number “n” stands for for quantum states of physical wave vectors \(k_n\) and \(k_0=0\) for the ground state.Footnote 1 The \(A_n\) and \(A_n^\dagger \) are time-independent annihilation and creation operators satisfying the commutation relation \([A_n^\dagger ,A_n]=\delta _{n,n'}\). The time-separate equation for \(\psi _n(t)\) is

$$\begin{aligned} \partial _t^2\psi _n(t) + \omega _n(t)^2\psi _n(t)=0,\quad \omega _n(t)^2=k^2_n+M^2, \end{aligned}$$
(3.2)

and Wronskian-type condition \(\psi _n(t)\partial _t\psi ^*_n(t) - \psi ^*_n(t)\partial _t\psi _n(t)=i\). Expressing

$$\begin{aligned} \psi _n(t)\!= & {} \!\frac{1}{(2V\omega _n)^{1/2}}\left( \alpha ^*_n(t) e^{-i\int ^t\omega _n dt}+\beta ^*_n(t) e^{i\int ^t\omega _n dt}\right) \nonumber \\ \end{aligned}$$
(3.3)

in terms of \(\alpha _n(t)\) and \(\beta _n(t)\), Eq. (3.2) becomes

$$\begin{aligned} \partial _t\alpha _n(t)= & {} C_n e^{-2i\int ^t\omega _n dt}\beta _n(t);\nonumber \\ \partial _t\beta _n(t)= & {} C_n e^{2i\int ^t\omega _n dt}\alpha _n(t), \end{aligned}$$
(3.4)

and \(|\alpha _n|^2-|\beta _n|^2=1\), where \(C_n\equiv 3\,H\omega _n^{-2}[k_n^2/3 +M^2/2]\). In an adiabatic process for slowly time-varying \(H=H_\textrm{slow}\), namely quasi static case \(H\approx \mathrm{const.}\), the particle state \(\alpha _n(0)=1\) and \(\beta _n(0)=0\) evolve to \(|\alpha _n(t)|\gtrsim 1\) and \(|\beta _n(t)|\not =0\). Positive and negative frequency modes get mixed, leading to particle productions of probability \(|\beta _n(t)|^2\propto e^{-M/H_\textrm{slow}}\).

We will focus on studying particle production in non-adiabatic processes for rapidly time-varying \(H_\textrm{fast}\), \(\alpha _n\) and \(\beta _n\) in the ground state \(n=0\) of the lowest lying massive mode \(M\gg H\). First, we recall that Parker and Fulling introduced the transformation [14],

$$\begin{aligned} A_0=\gamma ^*B + \delta B^\dagger ,\quad B=\delta A^\dagger _0-\gamma A_0, \end{aligned}$$
(3.5)

\([B,B^\dagger ]=1\), and two mixing constants obeying \(|\gamma |^2-|\delta |^2=1\). For a given \(A_n\) and its Fock space, the state \(|{\mathcal N}_\textrm{pair}\rangle \) is defined by the conditions \(A_{n\not =0}|{\mathcal N}_\textrm{pair}\rangle =0\) and

$$\begin{aligned} B^\dagger B |{\mathcal N}_\textrm{pair}\rangle ={\mathcal N}_\textrm{pair}|{\mathcal N}_\textrm{pair}\rangle . \end{aligned}$$
(3.6)

The \(B^\dagger \) and B are time-independent creation and annihilation operators of the pair of mixed positive frequency \(A_0\) particle and negative frequency \(A_0^\dagger \) antiparticle. The state \(|{\mathcal N}_\textrm{pair} \rangle \) contains \({\mathcal N}_\textrm{pair}=1,2,3,\ldots \) pairs, and \(|{\mathcal N}_\textrm{pair}=0 \rangle \) is the ground state of non-adiabatic interacting system of fast varying \(H_\textrm{fast}\) and massive pair production and annihilation.Footnote 2 It is a coherent superposition of states of particle and anti-particle pairs. In this coherent condensate state \(|{\mathcal N}_\textrm{pair} \rangle \) and \({\mathcal N}_\textrm{pair}\gg 1\), neglecting higher mode \(n\not =0\) contributions, they obtained the negative quantum pressure and positive quantum density of coherent pair field, see Eqs. (59) and (60) of Ref. [14],

$$\begin{aligned} p^\textrm{fast}_{_M}= & {} -\frac{M(2{\mathcal N}_\textrm{pair }+1)}{2\pi ^2 V}\Big \{\textrm{Re}[\gamma ^*\delta (|\alpha |^2+|\beta |^2)]\nonumber \\{} & {} +(2|\delta |^2+1)\textrm{Re}(\alpha ^*\beta e^{2iMt})\Big \}, \end{aligned}$$
(3.7)
$$\begin{aligned} \rho ^\textrm{fast}_{_M}= & {} \frac{M(2{\mathcal N}_\textrm{pair }+1)}{\pi ^2 V}\Big \{\textrm{Re}[\gamma \delta ^*\alpha \beta )]\nonumber \\{} & {} +(|\delta |^2+1/2)(|\beta |^2+1/2)\Big \}, \end{aligned}$$
(3.8)

where \(\omega _{n=0}=M\), \(\alpha _{n=0}=\alpha \) and \(\beta _{n=0}=\beta \). Pressure (3.7) and density (3.8) were adopted for studying the avoidance of cosmic singularity in curved Universe. In their sequent article [58], the authors confirm Eqs. (3.7) and (3.8) by studying the regularization of higher mode contributions to the energy-momentum tensor of a massive quantized field in closed, flat and hyperbolic spatial spaces. The natures of the massive coherent pair state \(|{\mathcal N}_\textrm{pair}\rangle \) (3.6) of the pressure (3.7) and density (3.8) are rather generic for non-adiabatic production of massive particles in curved spacetime.

Following their approach for the ground state \(k_n=0\), we arrive at the same quantum pressure (3.7) and density (3.8). In our case, we consider the state (3.6) as a coherent condensate state of very massive \(M\gg H_\textrm{slow}\) and large number \({\mathcal N}_\textrm{pair}\gg 1\) pairs, and \(M(2{\mathcal N}_\textrm{pair}+1)\) in (3.7) and (3.8) can be larger than the Planck mass \(m_\textrm{pl}\). Therefore higher mode \((k_n\not =0)\) contributions could be neglected. Their regularization and corrections will be studied in future. In this article, we adopt (3.7) and (3.8) as the fast components \(\rho ^\textrm{fast}_{_M}\) and \(p^\textrm{fast}_{_M}\) in Eq. (2.2) to find their non-adiabatic back-reactions on fast components \(H_\textrm{fast}\) and \(\rho ^\textrm{fast}_{_\Lambda }\).

Using negative \(p^\textrm{fast}_{_M}\) (3.7) and positive definite \(\rho ^\textrm{fast}_{_M}\) (3.8), we search for a solution of fast component Eq. (2.2) and quantum fluctuating mode Eq. (3.4) in the period \([-t,t]\) of the microscopic time \(t\sim H^{-1}_\textrm{fast}\). It is around the macro-scopic time \(t_\textrm{slow}\sim H^{-1}_\textrm{slow}\), when the slow components \(a_\textrm{slow}\), \(H_\textrm{slow}\), \(\rho ^\textrm{slow}_{_{M,\Lambda }}\) and \(p^\textrm{slow}_{_{M,\Lambda }}\) are valued, following the Friedman equations (2.1). The integrals \(\int ^t\omega _n dt\) are over the microscopic time t characterised by the Compton time scale 1/M. Its lower limit is \(t=0\) by setting \(t_\textrm{slow}=0\) as a reference time, when \(a_\textrm{fast}(0)=0\),

$$\begin{aligned} H_\textrm{fast}(0)=\dot{a}_\textrm{fast}/a_\textrm{slow}=0;\quad \alpha (0)=1,\quad \beta (0)=0. \end{aligned}$$
(3.9)

The real value \(\gamma ^*\delta \) condition in Eqs. (3.7) and (3.8) leads to the time symmetry: \(a^\textrm{fast}(t)=a^\textrm{fast}(-t)\), \(\alpha (t)=\alpha ^*(-t)\) and \(\beta (t)=\beta ^*(-t)\) [14]. When \(t\leftrightarrow -t\), positive and negative frequency modes interchange. Here we use \(a_\textrm{slow}\not =0\), \(H_\textrm{slow}\not =0\) and co-moving radius \((Ha)^{-1}\approx (H_\textrm{slow}a_\textrm{slow})^{-1}\) of Hubble volume \(V\sim H_\textrm{slow}^{-3}\).

In microscopic time t of unit \(m_\textrm{pl}^{-1}\), we numerically solve “microscopic” Eqs. (2.2), (3.4), (3.7) and (3.8) that are non-linearly coupled equations at time scale \({\mathcal O}(M^{-1})\). In addition to massive pairs production and coherent state (3.6) formation, we find (Fig. 1) that the system undergoes quantum pair oscillation, namely the quantum pressure \(p^\textrm{fast}_{_M}\) (3.7) and density \(\rho ^\textrm{fast}_{_M}\) (3.8) coherently oscillating with \(H_\textrm{fast}\) and \(\rho ^\textrm{fast}_{_\Lambda }\). Figure 1 shows results for \(C_0 = (3/2)H_\textrm{fast}\) and verified condition \(|\alpha |^2-|\beta |^2=1\). In the quantum period of microscopic time t, the negative quantum pressure \(p^\textrm{fast}_{_M}< 0\) and “microscopic” \({\mathcal O}(M^{-1})\) back-reaction effects lead to the quantum pair oscillation characterised by the frequency \(\omega =M\) of massive quantised pair fields. The positive quantum pair density \(\rho ^\textrm{fast}_{_M}> 0\) indicates particle creations without \(e^{-M/H}\) suppression. It is consistent with increasing Bogoliubov coefficient \(|\beta (t)|^2\) that mixes positive and negative energy modes. The sum \(\rho ^\textrm{fast}_{_M}+ p^\textrm{fast}_{_M} >0\) is positive definite, leading to the decreasing \(H_\textrm{fast}(t)\) (2.2). As a consequence, for time \(t>0\), the fast components \(H_\textrm{fast}\) and \(\rho ^\textrm{fast}_{_\Lambda }\) decrease in time, in order for pair production. Whereas for time \(t<0\), \(H_\textrm{fast}\) and \(\rho ^\textrm{fast}_{_\Lambda }\) increases, due to pair annihilation. The small \(a_\textrm{fast}(t)\) varies around \(a_\textrm{slow}\) at \(t_\textrm{slow}\equiv 0\). Note that \(p^\textrm{fast}_{_M}\) (3.7) and \(\rho ^\textrm{fast}_{_M}\) (3.8) represent the quantum pressure and density of massive coherent pair state (3.6) in short quantum time sales \({\mathcal O}(1/M)\). They do not follow an usual equation of state of classical matter.

We numerically solve non-linearly back-reacting Eqs. (2.2), (3.4), (3.7) and (3.8) for fast components at the microscopic scale. As a result, one of our findings in this article is the high-frequency \({\mathcal O}(M^{-1})\) oscillation of quantum pair state’s pressure \(p^\textrm{fast}_{_M}\) and density \(\rho ^\textrm{fast}_{_M}\), coherently with the oscillations of the fast components \(H_\textrm{fast}\), \(\dot{H}_\textrm{fast}\) and \(\rho _{_\Lambda }^\textrm{fast}\), see Fig. 1, Figs. 3 and 4 in supplemental material. By showing the highly non-adiabatic nature of pair-production processes, we present the novel dynamics and quasi-classical state of collective oscillations, in addition to the coherent state \(|{\mathcal N}_\textrm{pair}\rangle \) (3.6) of massive pair production [14]. Such quantum pair oscillation phenomenon is dynamically analogous to the quasi-classical plasma oscillation of electron-positron pair production in an external electric filed E [59] and pair production rate is not exponentially suppressed by \(e^{-\pi M^2/E}\) [60]. This analogy motivates us to model the quantum coherent pair state \(|{\mathcal N}_\textrm{pair}\rangle \) (3.6) and oscillating dynamics (Fig. 1) as a quasi-classical plasma state of effective energy density and pressure to study their impacts on the Friedman equation (2.1) in the \(\tilde{\Lambda }\)CDM scenario.

Fig. 1
figure 1

The quantum pair density and pressure oscillations in time are shown using \(M=10^{-2} m_\textrm{pl}\), \(H_\textrm{slow}= 10^{-5} m_\textrm{pl}\), \({\mathcal N}_\textrm{pair}=10^{8}\) and \(\delta = 1\). The Planck unit \(m_\textrm{pl}=(1/8\pi G)^{1/2}=1\) is adopted for presenting numerical results, namely the time “t” is in the unit of the Planck time, the quantum pair density \(\rho ^\textrm{fast}_{_M}\) and pressure \(p^\textrm{fast}_{_M}\) are in the unit of the Planck density. It shows that \(\rho ^\textrm{fast}_{_M}\) and \(p^\textrm{fast}_{_M}\) are not small, but their oscillating amplitudes \(\delta \rho ^\textrm{fast}_{_M}/\rho ^\textrm{fast}_{_M}\) and \(\delta p^\textrm{fast}_{_M}/p^\textrm{fast}_{_M}\) are about \({\mathcal O}(10^{-3})\). For a long time \(t> 10^4\), the coherent oscillations approach stable configurations in time, and amplitude damping effects appear. For more details and figures, see Fig. 3 in Appendix of Supplemental Material

Full size image

4 Massive pair plasma state

As shown in Fig. 1, massive pair quantum pressure \(p^\textrm{fast}_{_M}\) (3.7) and density \(\rho ^\textrm{fast}_{_M}\) (3.7) can be significantly large and rapidly oscillate with the fast components \(H_\textrm{fast}\) and \(\rho ^\textrm{fast}_{_\Lambda }\) (2.2) in microscopic time and space. Their oscillating amplitudes are not dampen in time, and it is therefore expected to form a massive pair plasma state in a long macroscopic time. However, to study their effective impacts on the classical Friedman equations (2.1) evolving in macroscopic time and space, we have to discuss two problems coming from scale difference \(M\gg H\). First, it is impossible to even numerically integrate slow and fast component coupled Eqs. (2.1,2.2) due to their vastly different time scales. On this aspect, we consider their non-vanishing averages \(\langle \cdot \cdot \cdot \rangle \) over the microscopic period in time. Figure 1 shows \(\langle \rho ^\textrm{fast}_{_M}+ p^\textrm{fast}_{_M}\rangle \) and other averages of fast oscillating components do not vanish. Second the spatial dependence of pair quantum pressure \(p_\textrm{fast}\) (3.7) and density \(\rho _\textrm{fast}\) (3.7) are unknown, since they are obtained by using the vacuum expectation value of field \(\Phi (\textbf{x},t)\) energy-momentum tensor over entire space. For the case \(M\gg H_\textrm{slow}\), the Compton length \(M^{-1}\) of ground state \(n=0\) is much smaller than the Hubble horizon \(H^{-1}_\textrm{slow}\). Therefore, the massive coherent pair state (3.6–3.8) and quantum plasma oscillation of Fig. 1 well localise inside the Hubble sphere. We speculate that their location should be near to the Horizon rather than at the centre, because of isotropic homogeneity extending up to the horizon.

Based on these considerations and non-vanishing averages of fast oscillating components (Fig. 1) over microscopic time period, we assume the formation of massive pair plasma state at macroscopic time scale \({\mathcal O}(H^{-1}_\textrm{slow})\). We describe such macroscopic state as a perfect fluid state of effective number \(n^H_{_M}\) and energy \(\rho ^H_{_M}\) densities as,

$$\begin{aligned}{} & {} \rho ^H_{_M} \equiv 2\chi m^2 H^2_\textrm{slow},\quad n^H_{_M} \equiv \chi m H^2_\textrm{slow};\nonumber \\{} & {} \qquad m^2 \equiv \sum _fg_d^fM^2_f, \end{aligned}$$
(4.1)

and pressure \(p^H_{_M}=\omega ^H_{_M} \rho ^H_{_M}\). The \(\omega ^H_{_M}\approx 0\) for \(m\gg H_\textrm{slow}\) and its upper limit is 1/3. The introduced mass parameter m represents possible particle masses \(M_f\), degeneracies \(g_d^f\) and the mixing coefficient \(\delta \) (3.5). The degeneracies \(g_d^f\) plays the same role of pair number \({\mathcal N}_\textrm{pair}\) in Eq. (3.8), namely \(\sum _f g_d^f\approx (2{\mathcal N}_\textrm{pair}+1)\). We explain the reasons why the densities (4.1) are proportional to \(\chi m H^2_\textrm{slow}\), rather than \(H^3_\textrm{slow}\) from the entire Hubble volume V. The “surface area” factor \(H^2_\textrm{slow}\) is attributed to the spherical symmetry of Hubble volume. The “radial size” factor \(\chi m\) comes from the layer width \(\lambda _m \) introduced as an effective parameter to describe the properties (i) for \(m\gg H_\textrm{slow}\) the massive pair plasma is localised as a spherical layer and (ii) its radial width \(\lambda _m < H^{-1}_\textrm{slow}\) depends on the massive pair plasma oscillation dynamics,Footnote 3 rather than the \(H_\textrm{slow}\) dynamics govern by the Friedman equations (2.1). The width parameter \(\chi \) expresses the layer width \(\lambda _m = (\chi m)^{-1} \gg 1/m\) in terms of the effective Compton length 1/m,

$$\begin{aligned} \lambda _m=(\chi m)^{-1} < H^{-1}_\textrm{slow},\quad 1\gg \chi > (H_\textrm{slow}/m). \end{aligned}$$
(4.2)

Because parameters m and \(\chi m\) represent time-averaged values over fast time oscillations of massive pair plasma state, we consider m and \(\chi m\) as approximate constants in slowly varying macroscopic time. However, the typical m and \(\chi m\) values should be different for Universe evolution epochs, since the fast-component equations for massive pair productions and oscillations depend on the \(H_\textrm{slow}\) value, see Sect. 3. Their values have to be fixed by observations. On the other hand, in the approximation without separating fast and slow components, we have consistently obtained the mean density \(n^H_{_M} \approx \chi m H^2\) (4.1) and \(\chi \approx 1.85\times 10^{-3}\) by studying massive fermion pair productions in an exact De Sitter spacetime of \(H=\mathrm{const.}\) and scaling factor \(a(t)=e^{iHt}\) [30, 31].

We have to point out the following. (i) The pressure \(p^H_{_M}\) and density \(\rho ^H_{_M}\) (4.1) are effective descriptions of the massive pair plasma state in macroscopic scales. It results from the coherence condensation state (3.6,3.7,3.8) and oscillating dynamics (Fig. 1) in microscopic scales. (ii) They play the role of “slow” components contributing to the “macroscopic” \({\mathcal O}(H^{-1}_\textrm{slow})\) Friedman equations (1.1) or (2.1). It means that in the Friedman equations (2.1), the matter density \(\rho ^\textrm{slow}_{_M}\) and pressure \(p^\textrm{slow}_{_M}\) contains contributions from (a) the normal matter state of pressure and density and (b) the massive pair plasma state of pressure and density \(p^H_{_M}=\omega ^H_{_M}\rho ^H_{_M}\). These two sets may interact with each other. We shall study the massive pair plasma state effects on each epoch of the Universe’s evolution. Here we start to study its effects on inflation. Henceforth sub- and super-scripts “slow” are dropped.

5 Massive pair plasma state effect on inflation

To start this section, we recall the Ref. [61], showing that the massive pair state \(|{\mathcal N}_\textrm{pair}\rangle \) (3.6) of the large occupation number \({\mathcal N}_\textrm{pair}\gg 1\) is a quasi-classical state equivalently to the FLRW model filled by a massive classical scalar field. The author obtained the analytical solution of the slowly evolving quasi-de Sitter stage for inflation. Here, we study the state \(|{\mathcal N}_\textrm{pair}\rangle \) in the \(\tilde{\Lambda }\)CDM scenario by showing the fast oscillating components \(H_\textrm{fast}\) and \(\rho _{_\Lambda }^\textrm{fast}\) produce the massive particle pairs. Moreover, the massive pair state’s energy density and pressure in coherent oscillation with \(H_\textrm{fast}\) and \(\rho _{_\Lambda }^\textrm{fast}\) can thus form a quasi-classical and massive plasma state (4.1). We will study at the macroscopic time scale \({\mathcal O}(H^{-1})\) how the time-varying cosmological term \(\rho _{_\Lambda }^\textrm{slow}\) derives the inflation and how the quasi-classical and massive plasma state (4.1) slows down the inflation. It is different from the inflation model of a massive scalar field of the potential \(V(\phi )\propto M^2\phi ^2\) in the FLRW metric.

In this section, we show that the inflation is driven by the cosmological term \(\rho _{_\Lambda }(t)\) (gravitationally repulsive) and it is slowed down by the massive pair plasma state (4.1) (gravitationally attractive). The latter is formed at the expense of the former energy. Suppose that during inflation the normal matter state of pressure and density is absent, and only massive pair plasma state of pressure and density \(p^H_{_M}=\omega ^H_{_M}\rho ^H_{_M}\) (4.1) is present. The “macroscopic” \({\mathcal O}(H^{-1})\) Friedman equations (1.1) become

$$\begin{aligned} H^2= & {} \frac{8\pi G}{3}(\rho _{_\Lambda }+\rho ^H_{_M}),\nonumber \\ \dot{H}= & {} -\frac{8\pi G}{2}(\rho ^H_{_M}+p^H_{_M}). \end{aligned}$$
(5.1)

These Eq. (5.1), time-varying “dark energy” \(\rho _{_\Lambda }=\tilde{\Lambda }/(8\pi G)\), massive plasma state \(\rho ^H_{_M}\) and \(p^H_{_M}\) (4.1) give a “macroscopic” back-reacting system at the scale \({\mathcal O}(H^{-1})\), yielding a slowly time-decreasing H for the quasi-de Sitter phase (6.2) discussed below. This should be differentiated from the “microscopic” \({\mathcal O}(M^{-1})\) back-reacting system of Eqs. (2.2), (3.4), (3.7) and (3.8), yielding the quantum pair coherent oscillation discussed before. It is a difficult task to analyse \({\mathcal O}(M^{-1})\) and \({\mathcal O}(H^{-1})\) dynamics numerically since two scales \(M\gg H\) are very different. It is the reason why we split the fast \({\mathcal O}(M^{-1})\) components from the slow \({\mathcal O}(H^{-1})\) components, and introduce at the scale \({\mathcal O}(H^{-1})\) the massive pair plasma state of effective density \(\rho ^H_{_M}\) and pressure \(p^H_{_M}\) (4.1). They are microscopic time averages over fast components (3.7,3.8) and contribute to slow components in Friedman equation (5.1).

In the inflation epoch, the time-varying cosmological term \(\rho _{_\Lambda }\) is dominant over the massive pair plasma state \(\rho ^H_{_M}\), e.g., \(\rho _{_\Lambda }\gg \rho ^H_{_M}\). The former derives the inflation, while the latter slowly slows it down. Assuming initial values of “cosmological constant” \(\tilde{\Lambda }(0)=\Lambda \) and \(H(0)= (\Lambda /3)^{1/2}\)Footnote 4, Eqs. (5.1) show that the scalar factor \(a\sim \exp (\Lambda /3)^{1/2}t\) is exponentially inflated in time if the massive pair plasma state is absent \(\rho ^H_{_M}=p^H_{_M}\equiv 0\). As the consequence of the nontrivial massive pair plasma state (\(\rho ^H_{_M}\not =0, p^H_{_M}\approx 0\)) and its back reaction on H via \(\dot{H} <0\) of Eq. (5.1), H and \(\tilde{\Lambda }\) decrease in time, become dynamically time dependent. Thus inflation is slowed down to its end.

6 Inflation and tensor-to-scalar ratio

As the macroscopic time t varies at the scale \(H^{-1}\), what is the rate of pair production in connection with the massive pair plasma state density (4.1) changing and contributing to the matter density. To quantitatively describe these dynamics, we estimate the total number of particles produced inside the Hubble sphere \(N\approx n^H_{_M}H^{-3}/2\) and mean pair production rate w.r.t. macroscopic time variation dt,

$$\begin{aligned} \Gamma _M \approx \frac{dN}{2\pi dt}\approx \frac{\chi m}{4\pi } \epsilon ,\quad \epsilon \equiv -\frac{\dot{H}}{H^2}. \end{aligned}$$
(6.1)

Here we neglect the back-reactions of slow time-varying components H, \(\rho _{_{\Lambda ,M}}\) and \(p_{_{\Lambda ,M}}\) on fast components \(H_\textrm{fast}\), \(\rho ^\textrm{fast}_{_M}\) and \(p^\textrm{fast}_{_M}\). The modified Friedman equations (5.1) and rate (6.1) are basic equations to quantitatively describe inflation, effective mass m and width \(\chi \) parameters are fixed by observations.

In inflation, the H is larger than the mean pair production rate \(H>\Gamma _M\), Eq. (5.1) are governed by cosmological term \(\rho _{_\Lambda }\) and induced massive pair plasma state of density \(\rho ^H_{_M}\) (4.1) and pressure \(p^H_{_M}\approx 0\). From Eqs. (4.1) and (5.1), we analytically obtain the inflationary solution of slowly decreasing H (slow-rolling dynamics)

$$\begin{aligned} H \approx H_*(a/a_*)^{-\epsilon },\quad \epsilon \approx \chi (m/m_\textrm{pl})^2\ll 1, \end{aligned}$$
(6.2)

where \(a_*\) and \(H_*\) are the characteristic inflation scale corresponding to the interested quantum modes of pivot scale \(k_*\) crossed the horizon \((c_sk_*=H_*a_*)\) for CMB observations. Here, the interested quantum modes refer to the primordial curvature perturbations of the standard scenario. We will discuss separately the possibly interesting quantum modes of quantum pair coherent oscillations presented in the previous Sect. 3. Therefore, the scalar, tensor power spectra and their ratio read [65]

$$\begin{aligned} \Delta ^2_{_{\mathcal R}} \!= & {} \! \frac{1}{8\pi ^2}\frac{H^2_*}{m^2_\textrm{pl}\,\epsilon \,c_s}, ~\Delta ^2_h \!=\! \frac{2}{\pi ^2}\frac{H^2_*}{m^2_\textrm{pl}};~ r\!\equiv \! \frac{\Delta ^2_h}{\Delta ^2_{_{\mathcal R}}}=16\,\epsilon \, c_s, \nonumber \\ \end{aligned}$$
(6.3)

where the time-dependent background sound velocity \(c_s< 1\), and the spectra index \(n_s\approx 1-2\epsilon \) at the leading order of scale-invariance deviations. Based on two CMB observational values at the pivot scale \(k_*=0.\,05\, (\textrm{Mpc})^{-1}\) [66]: (i) the spectral index \(n_s\approx 0.965\), from Eq. (6.2) we obtain

$$\begin{aligned} \epsilon \approx \chi (m_*/m_\textrm{pl})^2\lesssim (1-n_s)/2\approx 0.0175, \end{aligned}$$
(6.4)

and the \(m_*\) is the mass scale (4.1) corresponding to the pivot scale; (ii) the scalar amplitude \(A_s=\Delta ^2_{_{\mathcal R}}(k_*) \approx 2.1\times 10^{-9}\), Eq. (6.3) gives

$$\begin{aligned} H_*=3.15\times 10^{-5}\,(r/0.1)^{1/2}m_\textrm{pl}. \end{aligned}$$
(6.5)

As a result, the energy-density ratio of pair plasma and cosmological term densities is

$$\begin{aligned} \frac{\rho ^H_{_M}}{\rho _{_\Lambda }}\Big |_{H_*} \approx \frac{2\chi (m_*H_*)^2}{3(m_\textrm{pl}H_*)^2} =\frac{2}{3}\chi \left( \frac{m_*}{m_\textrm{pl}}\right) ^2\approx 1.17\times 10^{-2},\nonumber \\ \end{aligned}$$
(6.6)

and \(H^2_*\approx \rho ^*_{_\Lambda }/(3m^2_\textrm{pl})\).

The inflation slows down and eventually ends at \(a=a_\textrm{end}\) and \(H=H_\textrm{end}\),

$$\begin{aligned} H_\textrm{end}=H_*\exp -(\epsilon \, N_\textrm{end}), \end{aligned}$$
(6.7)

where \(N_\textrm{end}=\ln \left( a_\textrm{end}/a_*\right) \) is the e-folding numbers from the inflation scale \(H_*\) to the inflation ending scale \(H_\textrm{end}\). It can be preliminarily determined by the inflationary rate being smaller than the mean pair-production rate namely

$$\begin{aligned} H_\textrm{end}< \Gamma _M =(\chi m_*/4\pi )\,\epsilon . \end{aligned}$$
(6.8)

However, this inequality provides the upper bound on \(H_\textrm{end}\), whose value should be calculated by studying the dynamical transition from inflation to reheating. Using Eqs. (6.7) and (6.8), we give the upper limit on the tensor-to-scalar ratio r in terms of the e-folding numbers \(N_\textrm{end}\),

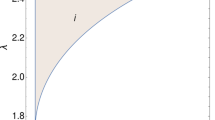
$$\begin{aligned}{} & {} r< 1.01 \times 10^8 \left( \frac{\Gamma _M}{m_\textrm{pl}}\right) ^2 e^{2\epsilon N_\textrm{end}}\nonumber \\{} & {} \quad = 7.97\times 10^4 \chi (1-n_s)^3e^{(1-n_s) N_\textrm{end}} \end{aligned}$$
(6.9)

where \(\epsilon =\chi (m_*/m_\textrm{pl})^2=(1-n_s)/2\) (6.4) is used. Non-vanishing \(\chi \) implies \(r\not =0\). In Fig. 2, we plot the upper limit (6.9) compared with data and other inflation models. The range of width parameter \(\chi \) values is discussed in Eq. (4.2). The inequalities \(\lambda _m\gg 1/m\) and \(m\gg H\) implies \(\chi \ll 1\). For Fig. 2 and calculations below, we chose the reference value \(\chi \sim 10^{-3}\) at the same order of \(\chi \approx 1.85\times 10^{-3}\) that we approximately obtained for massive fermion pair productions in an exact De Sitter spacetime [30, 31].

From Eq. (6.7), the inflation ending scale \(H_\textrm{end}\) is given by

$$\begin{aligned} H_\textrm{end}\approx & {} H_*e^{-(1-n_s)N_\textrm{end}/2} \approx (0.42,0.35)H_*, \end{aligned}$$
(6.10)

for \(N_\textrm{end}= (50,60)\) and \(r=(0.02,0.028)\). It shows small H-variation

$$\begin{aligned} H^2_\textrm{end} = \frac{ \rho ^\textrm{end}_{_\Lambda } + \rho ^{H\mathrm end}_{_M}}{3m^2_\textrm{pl}}\gtrsim \frac{ \rho ^\textrm{end}_{_\Lambda }}{3m^2_\textrm{pl}}; \quad \frac{\rho ^{H\mathrm end}_{_M}}{\rho ^\textrm{end}_{_\Lambda }}\ll 1, \end{aligned}$$
(6.11)

and \(\rho ^\textrm{end}_{_\Lambda }\approx 3 m^2_\textrm{pl}H^2_\textrm{end}\). Equations (6.6) and (6.11) imply the time-varying \(\Lambda (t)\propto H^2\) “area law” in inflation.

We would like to point out that the quasi-de Sitter phase (slow-rolling dynamics) for inflation undergoes when \(\rho _{_\Lambda }\) and H slowly decrease in time. In this epoch, \(H>\Gamma _M\), the massive plasma state energy density \(\rho ^{H}_{_M}\) is much smaller than \(\rho _{_\Lambda }\) (6.6), and slowly increases in time. Therefore \(\rho ^{H}_{_M}\) back-reaction on \(\rho _{_\Lambda }\) is small, leading to slowly time-decreasing \(\rho _{_\Lambda }\) that predominately governs the H evolution, slowly decreasing in time from \(H_*\) and \(H_\textrm{end}\) (6.10). At the inflation end \(H \lesssim \Gamma _M\) and the transition to \(H < \Gamma _M\), the quantum pair production and oscillation play an important role. The “dark-energy” density \(\rho _{_\Lambda }\) decreases rapidly and converts to the energy density \(\rho ^{H}_{_M}\) of massive pairs. As a result, \(\rho ^{H}_{_M}\) becomes comparable with, then predominates over \(\rho _{_\Lambda }\), e.g., a matter-dominate episode \(\rho ^{H}_{_M}\gg \rho _{_\Lambda }\) and \(\rho _{_\Lambda }\rightarrow 0\) (\(\tilde{\Lambda }\rightarrow 0\)). Moreover, massive pairs decay to light particles and decay rate \(\Gamma ^{^\textrm{de}}_M > H\). The massive pairs’ energy density converts to the radiation energy density \(\rho _{_R}\), leading to the radiation-dominant reheating. The situations are similar to discussions in Refs. [32, 33]. On this issue, we present in Ref. [53] preliminary analysis and will publish lengthy calculations and final results in a separate article.

Fig. 2
figure 2

On the Figure 5 of Ref. [67], the upper limit (6.9) is plotted for \(\chi =10^{-3}\). The red zone bound by the e-folding number \(N_\textrm{end}=N=50,60\) curves agrees with the blue constraint zone. The constraint on the tensor-to-scalar ratio r also agrees with the upper limit \(r<0.044\) from the recent observation [68]. The Figure 5 of Ref. [67] comes from Figure 28 of Ref. [69] and Figure 8 of Ref. [66]. Their figure captions indicate inflation models studied. For example, the yellow region shows the loci of approximately constant e-folding number N, assuming simple \(V(\phi )\propto (\phi /m_\textrm{pl})^p\) single-field inflation. It shows that the red zone of the \(\tilde{\Lambda }\)CDM is distinct from the constrained zones of other inflation models

Full size image

7 Comparison with other inflation models

We compare and contrast the \(\tilde{\Lambda }\)CDM scenario to inflation models with scalar field potentials. We emphasise that the quantum scalar field \(\Phi \) and Eqs. (3.1–3.8) describe the state and dynamics of massive pair productions in the Friedman Universe with dark energy density \(\rho _{_\Lambda }\). They are not inflation field \(\phi \), potential \(V(\phi )\), \(3m_\textrm{pl}^2H^2=\dot{\phi }^2/2 +V(\phi )\), \(\rho _\phi =\dot{\phi }^2/2 + V(\phi )\) and \(p_\phi =\dot{\phi }^2/2 - V(\phi )\) in inflation models. However, we can find some correspondences between inflation models and the present scenario (4.1,5.1)

$$\begin{aligned}{} & {} \dot{\phi }^2 \Leftrightarrow \rho ^{H}_{_M} + p^{H}_{_M}\approx \rho ^{H}_{_M}, \nonumber \\{} & {} V(\phi ) \Leftrightarrow \rho _{_\Lambda } + (\rho ^{H}_{_M} - p^{H}_{_M})/2 \approx \rho _{_\Lambda }. \end{aligned}$$
(7.1)

The slow-roll condition \(V(\phi )\gg \dot{\phi }^2/2\) corresponds to \(\rho _{_\Lambda } \gg \rho ^{H}_{_M}\) for \(\rho ^H_{_M}\approx (2\chi m^2/3\,m^2_\textrm{pl}) \rho _{_\Lambda }\). It leads to \(\dot{\rho }_{_\Lambda } \Leftrightarrow \dot{V}=\dot{\phi }V^\prime \) and \(\dot{\rho }^H_{_M} \Leftrightarrow (1/2)d(\dot{\phi }^2)/dt =\dot{\phi }\ddot{\phi }\). As a result, the second equation in (5.1) corresponds to the classical equation of motion for \(\phi \): \(\ddot{\phi }+3H\dot{\phi }+V^\prime (\phi )=0\). These correspondences imply that the \(\Lambda \)CDM scenario (4.1, 5.1) could be effectively expressed in terms of inflation field \(\phi \) and peculiar potentials \(V(\phi )\).

We have to mention the pioneer \(R+R^2\) inflation model [15], which agrees with the observational constraints on the spectral index \(n_s\) and tensor-to-scalar ratio r. It is worthwhile to see the connection between the \(\tilde{\Lambda }\)CDM scenario and the \(R+R^2\) model from the viewpoints of the asymptotic safety [70] and cosmological observations [71, 72]. The non-local UV-complete gravitational and particle field theory of higher derivatives [73] or holonomy fields along a loop [Eq. (133)] of Ref. [62] can have fixed points [54, 63, 70]. Their scaling domains can realise the effective and quasi-classical field theory of gravity and particles. One has to investigate, in agreement with observations, the following issues. If there is one scaling domain for the inflation dynamics. What are effectively relevant operators, \(\langle T^{\mu \nu }_M\rangle \), \(\tilde{\Lambda }\), R and \(R^2\). What are scaling laws for these operators as the cosmological scale changing. How we use an effective potential approach to describe the dynamics of these relevant operators. These are subjects for future studies.

8 Singularity-free pre-inflation and large-scale anomaly

It is worthwhile to mention the results for pre-inflation in the \(\tilde{\Lambda }\)CDM scenario. In the pre-inflation, when the Hubble scale \(H\sim H_\textrm{fast}=\dot{a}_\textrm{fast}/a_\textrm{fast}\) and all slow components are zero, namely \(a_\textrm{slow}=0, H_\textrm{slow}=0\), \(p_{_{M,\Lambda }}^\textrm{slow}=0\) and \(\rho _{_{M,\Lambda }}^\textrm{slow}=0\), see Sect. 1. The \(H_\textrm{fast}\) and \(a_\textrm{fast}\) dynamical evolutions are govern by the fast components \(\rho _{_\Lambda }^\textrm{fast}\), \(\rho _{_M}^\textrm{fast}\) and \(p_{_M}^\textrm{fast}\). The Friedman equations (1.1) become

$$\begin{aligned} H^2_\textrm{fast}=\frac{8\pi G}{3}(\rho ^\textrm{fast}_{_\Lambda }+\rho _{_M}^\textrm{fast}),~\dot{H}_\textrm{fast} =-\frac{8\pi G}{2}(\rho _{_M}^\textrm{fast} + p_{_M}^\textrm{fast}),\nonumber \\ \end{aligned}$$
(8.1)

with \(\rho _{_M}^\textrm{fast}\) (3.7) and \(p_{_M}^\textrm{fast}\) (3.8) in a spherical Hubble volume \(V\sim H^{-3}_\textrm{fast}\). The initial values are (3.9), but \(H^2_\textrm{fast}(0)\approx (m^{-2}_\textrm{pl}/3)\rho ^\textrm{fast}_{_\Lambda }(0)\not =0\) and \(a_\textrm{fast}(0)\not =0\), due to nontrivial cosmological term \(\rho ^\textrm{fast}_{_\Lambda }(0)=\Lambda /(8 \pi G)\) and \(\Lambda \sim m_\textrm{pl}^2/a_\textrm{fast}^2(0)\). The \(\Lambda \) value is about the Planck scale, attributed to the nature of quantum gravity. Numerically integrating Eqs. (3.4), (3.7), (3.8) and (8.1), we show that quantum pair production and oscillation do not decrease the scale factor \(a_\textrm{fast}(t)\), which instead exponentially increases, leading to inflation. It concludes that the Universe does not contract to a spacetime singularity of infinite density and gravity. The results show that the weak energy condition of \(\rho ^\textrm{fast} = \rho ^\textrm{fast}_{_M} + \rho ^\textrm{fast}_{_\Lambda }>0\) and \(\rho ^\textrm{fast} + p^\textrm{fast} =\rho ^\textrm{fast}_{_M} + p^\textrm{fast}_{_M}>0\) is satisfied, but the strong energy condition \(\rho ^\textrm{fast} + 3p^\textrm{fast} = \rho ^\textrm{fast}_{_M} + 3p^\textrm{fast}_{_M} -2 \rho ^\textrm{fast}_{_\Lambda }>0\) is violated for details see Fig. 4 in Supplemental Material.

Using Friedman equations (5.1) and \(\epsilon \)-rate \(\epsilon =-\dot{H}/H^2\) (6.1), we recast the scalar spectrum (6.3) of primordial curvature perturbations as

$$\begin{aligned} \Delta ^2_{_{\mathcal R}} (k)\approx & {} \frac{1}{12\pi ^2}\frac{\rho _{_\Lambda }}{c_s\chi m^2 m^2_\textrm{pl} (1+\omega ^H_{_M})}. \end{aligned}$$
(8.2)

From pre-inflation \(H> H_*\) to inflation \(H\approx H_*\), \(\rho _{_\Lambda }\) and \(c_s\) are almost constants, and the variation \(\omega ^H_{_M}\) is 1/3 at most. Therefore the scalar spectrum \(\Delta ^2_{_{\mathcal R}} (k)\) (8.2) decreases 3/4, as the scalar spectrum goes to the large distance scale of CMB observations, exploring the high-energy scale of horizon crossing. It probably explains the large-scale anomaly of the low amplitude of the CMB power spectrum at low-\(\ell \) multipole, e.g., the CMB power spectrum drops 3/4 at \(\ell =2\). These are new features of the \(\tilde{\Lambda }\)CDM scenario in the pre-inflation epoch. However, present discussions are preliminary, and further studies are required.

9 Discussions on dark-matter density perturbations

Since dark matter dominates over the normal matter today, we suppose that major massive pairs produced in pre-inflation, inflation and reheating should be dark-matter particles. In addition to quantum pair oscillating modes (Fig. 1), the pair plasma oscillation appears when the massive pair plasma density \(\rho ^H_{_M}\) is large enough. The acoustic wave of the density perturbation \(\delta \rho ^H_{_M}/\rho ^H_{_M}\) is formed and described by the sound velocity \(c^{M}_s=(\partial p^H_{_M}/ \partial \rho ^H_{_M})^{1/2}=(\omega ^H_{_M})^{1/2}\). We might call these primordial modes as dark-matter density perturbations to distinguish them from curvature perturbations. The quantum pair oscillating modes and massive pair plasma acoustic density perturbations exited and reentered the horizon, which should imprint on both CMB and matter density power spectra. The phenomenon is similar to the usual discussions on the curvature perturbation modes imprinting on the CMB power spectra. In addition, dark-matter density perturbations in reheating exited and reentered the horizon could account for baryogenesis. Reference [74] presents the preliminary results. However, detailed discussions and quantitative calculations are required to see if these primordial dark-matter density perturbations are interesting modes to confront with observations. To end this article, it is worthwhile to mention that in Refs. [54, 75, 76],Footnote 5 we study in the \(\tilde{\Lambda }\)CDM scenario the very slowly varying “dark-energy” \(\tilde{\Lambda }\) interacting with radiation and matter from the reheating \(\rho _{_\Lambda }\ll \rho _{_{M,R}}\) to the present time \(\rho _{_\Lambda }>\rho _{_{M,R}}\). Reference [77, 78] shows their relevance for relieving the \(H_0\) tension.