Electroweak baryogenesis in the CP-violating two-Higgs doublet model

Abstract

Recently we presented the upgrade of our code BSMPT for the calculation of the electroweak phase transition (EWPT) to BSMPT v2 which now includes the computation of the baryon asymmetry of the universe (BAU) in the CP-violating 2-Higgs-Doublet Model (C2HDM). In this paper we use BSMPT v2 to investigate the size of the BAU that is obtained in the C2HDM with the two implemented approaches FH and VIA to derive the transport equations, by taking into account all relevant theoretical and experimental constraints. We identify similarities and differences in the results computed with the two methods. In particular, we analyse the dependence of the obtained BAU on the parameters relevant for successful baryogenesis. Our investigations allow us to pinpoint future directions for improvements both in the computation of the BAU and in possible avenues taken for model building. Recently, it was argued that the source term in the VIA method vanishes at leading order which would have consequences for the derived BAU in this method.

1 Introduction

The Standard Model (SM) of particle physics has seen a great success with the commissioning of the Large Hadron Collider (LHC) where the last missing piece of the SM, the Higgs boson, was discovered in 2012 by the LHC experiments ATLAS [1] and CMS [2]. The success story is clouded by the fact that there are remaining puzzles that cannot be explained within the SM. While the discovered Higgs boson behaves very SM-like [3,4,5,6] open questions like the observed baryon-antibaryon asymmetry $\eta$ of the universe [7] call for new physics extensions. The asymmetry can be generated dynamically through electroweak baryogenesis [8,9,10,11,12,13,14,15,16] provided the three Sakharov conditions [17] are fulfilled. These are baryon number violation, C and CP violation and departure from the thermal equilibrium. The mechanism requires the electroweak phase transition (EWPT), which proceeds through bubble formation, to be of strong first order [14, 16] so that the baryon number violating sphaleron transitions in the false vacuum [18, 19] can be suppressed. Although all three Sakharov conditions are in principle met by the SM a strong first order EWPT (SFOEWPT) can only be realized for an SM Higgs boson mass around 70-80 GeV [20] which is in contradiction with the experimentally measured 125 GeV [20]. Additionally, the amount of CP violation in the SM that stems from the Cabibbo–Kobayashi–Maskawa (CKM) matrix is not large enough to quantitatively reproduce the measured value of $\eta$ [16, 21]. These problems can be remedied by extended Higgs sectors that provide additional sources of CP violation and further scalar bosons that may trigger an SFOEWPT. An example is the 2-Higgs-Doublet Model (2HDM) where an SFOEWPT can be realized in accordance with all relevant theoretical and experimental constraints both for a CP-conserving [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] and a CP-violating Higgs potential [42,43,44,45,46,47,48,49,50,51].

Denoting by $v_c$ the vacuum expectation value (VEV) at the critical temperature $T_c$ which is defined as the temperature where two degenerate global minima exist, a value of $v_c/T_c$ larger than one is indicative for an SFOEWPT [11, 52]. There are several programs on the marked that allow for the computation of the minima of extended Higgs sectors¹ and the strength of the phase transition. Thus, Vevacious [55, 56] allows to find the global minima of the one-loop effective potential with many scalars. CosmoTransitions [57] is a tool that analyses the different vacua of theories with single or multiple scalar fields in order to determine the critical temperatures, the super-cooling temperatures and the bubble wall profiles separating the different phases and that also describes their tunnelling dynamics. The C++ package PhaseTracer [58] finds the cosmological phases and the critical temperatures for phase transitions for any scalar potential by tracing the minima of the effective potential as function of the temperature change. We have published the C++ code BSMPT [59, 66] for the calculation of the strength of the EWPT of extended Higgs sectors by determining the critical VEV $v_c$ at the temperature $T_c$. For this we compute the loop-corrected effective potential at finite temperature [60,61,62] including the daisy resummation of the bosonic masses [63]. For efficient parameter scans in the models under investigation we use a renormalisation scheme that keeps the loop-corrected Higgs masses and mixing angles at their tree-level values and applied it to investigations in the 2HDM [35], the C2HDM [50, 64] and the Next-to-2HDM (N2HDM) [64].

While the SFOEWPT is a necessary condition for successful baryogenesis the question still remains to be answered if the model is able to generate the observed baryon asymmetry of the universe after taking into account all relevant constraints. The baryon asymmetry that can be estimated by assuming that all cosmic microwave background photons are the result of thermal annihilation of the baryon pairs is given by [65]

$$\begin{aligned} \frac{n_B - n_{{\bar{B}}}}{n_B + n_{{\bar{B}}}} \approx \eta \equiv \frac{n_B}{n_\gamma } = (6.2 \pm 0.4) \cdot 10^{-10} \;, \end{aligned}$$

(1.1)

where $n_B$ ($n_{{\bar{B}}}$) is the (anti-)baryon density and $n_\gamma$ the photon density of today’s universe. Recently, we published the upgrade BSMPT v2 [66]. It not only extends the existing code to include the computation of the strength of the EWPT for the already implemented models (the 2HDM, C2HDM and the N2HDM) by the complex singlet extension of the SM (CxSM). But its major upgrade is the implementation of the computation of the baryon asymmetry of the universe for the C2HDM in two different approximations, the so-called FH [67,68,69,70] and the VIA approach [71,72,73,74]. In that paper, we explained our treatment of the wall profile and described in detail the two approaches for the computation of the BAU, as well as the code, the system requirements, the installation and the usage of the program. We complemented the manual by a more general discussion on the approaches and approximations that we used.

The purpose of this work now is to apply our code BSMPT v2 to the computation of the BAU in the C2HDM. For recent computations of the BAU in the C2HDM, see also [75] and references therein. We want to investigate how the two different approaches used in the literature compare to each other.² While the approaches lead to quite different results we will analyse where they show similar behaviour and what are the crucial parameters that influence the possible size of $\eta$. Our goal is to find out if in principle it is possible to obtain a BAU in the C2HDM that is compatible with the observed value while at the same time applying the relevant theoretical and experimental constraints. We furthermore investigate the inclusion of different fermion species, top, bottom and $\tau$, in the VIA approach and their impact on the BAU. The paper will give us more insights in the effects of the various approaches used to compute the BAU and will pinpoint different directions to be taken both for future model building and for improvement of the computation.

Recently, the source term of the VIA method was re-derived in [82]. Relying solely on 1-particle-irreducible self-energy diagrams it was found that the source term vanishes at leading order (LO) both for bosons and for fermions, both in the perturbative and in the resummed approach. This would effect the results of the VIA approach derived in this paper and their discussion, as will be outlined below.

The paper is organized as follows. In Sect. 2 we introduce the C2HDM and set our notation. We briefly comment on the computation of the EWPT and take the occasion to present the improvement of our renormalisation scheme of the C2HDM implemented in BSMPT v2.2. Section 3 is devoted to the calculation of the BAU. We discuss in detail our calculation of the bubble wall profile and summarize the computation of the BAU in the FH and in the VIA approach, an extensive description is given in [66]. Section 4 contains our numerical analysis. After the description of the applied constraints and our parameter scan, we discuss the newly implemented counterterms in the C2HDM before moving on to the presentation of the results on the outcome of the BAU in the two applied approaches, and the dependence on the bubble wall velocity. We investigate the interplay between wall thickness and overall mass scale of the Higgs spectrum and analyse the behaviour of both approaches with respect to the parameters that are crucial for successful BAU. Finally, we present the effect of additional fermions included in the VIA computation. We conclude in Sect. 5.

Table 1 Left: definition of the 2HDM types through the allowed couplings between fermions and Higgs doublets. Right: corresponding ${\mathbb {Z}}_2$ parity assignments to the left-handed quark and lepton doublets, Q, L, and the right-handed singlets of the up-type and down-type quarks, $u_R$ and $d_R$, and right-handed leptons $l_R$

2 The complex two-Higgs doublet model

We give a brief introduction in the scalar sector of the C2HDM [83,84,85] and refer for a more detailed discussion of the model to [50, 86]. The scalar potential of the C2HDM is a simple extension of the SM Higgs sector with an additional $\textrm{SU}(2)$ Higgs doublet

$$\begin{aligned} V_{\text {C2HDM}}&= m_{11}^2 \Phi _1^{\dagger }\Phi _1 + m_{22}^2 \Phi _2^{\dagger }\Phi _2 + \frac{\lambda _1}{2} \left( \Phi _1^{\dagger }\Phi _1\right) ^2 \nonumber \\&\quad + \frac{\lambda _2}{2} \left( \Phi _1^{\dagger }\Phi _1\right) ^2+ \lambda _3 \left( \Phi _1^{\dagger }\Phi _1\right) \left( \Phi _2^{\dagger }\Phi _2\right) \nonumber \\&\quad + \lambda _4 \left( \Phi _1^\dagger \Phi _2\right) ^2 + \Bigg [ \frac{\lambda _5}{2} \left( \Phi _1^\dagger \Phi _2\right) ^2 \nonumber \\&\quad - m_{12}^2 \left( \Phi _1^\dagger \Phi _2\right) + h.c. \Bigg ] , \end{aligned}$$

(2.1)

with a softly broken discrete $\mathbb Z_2$ symmetry under which $\Phi _1\rightarrow \Phi _1$ and $\Phi _2\rightarrow -\Phi _2$. This $\mathbb Z_2$ symmetry ensures the absence of flavour-changing neutral currents (FCNC) at tree level and allows for different types of the C2HDM depending on how the Higgs doublets couple to the fermions. The different possibilities are listed in Table 1. For simplicity only Type I and II are discussed in this analysis. All Lagrangian parameters are real due to the hermiticity of the potential except for $m_{12}^2$ and $\lambda _5$ which can be complex as we allow for CP violation. Upon electroweak symmetry breaking (EWSB) the two Higgs doublets acquire vacuum expectation values (VEVs) around which they can be expanded in terms of the charged CP-even and CP-odd field components $\rho _i$ and $\eta _i$ and the neutral CP-even and CP-odd fields $\zeta _i$ and $\psi _i$ ($i=1,2$). The general tree-level vacuum structure of the 2HDM allows for three different possible vacua, the normal EW-breaking vacuum, a CP-breaking and a charge-breaking (CB) vacuum. As was shown in Refs. [87,88,89] these vacua cannot coexist simultaneously at tree level. Higher-order corrections or finite temperature effects might break this statement, hence we allow for a more general vacuum structure in the analysis. Denoting the corresponding VEVs by $\omega _{1,2}$ for the normal vacuum, and by $\omega _{\text {CP}}$ and $\omega _{\text {CB}}$ for the CP-breaking and the charge-breaking minimum, respectively, the expansion of the two Higgs doublets $\Phi _i$ around the VEVs is given by

$$\begin{aligned} \Phi _1&= \frac{1}{\sqrt{2}} \begin{pmatrix} \rho _1 + \textrm{i}~\eta _1 \\ \zeta _1 + \omega _1 + \textrm{i}~\psi _1 \end{pmatrix} \nonumber \\ \Phi _2&= \frac{1}{\sqrt{2}} \begin{pmatrix} \rho _2 + \omega _{\text {CB}}+\textrm{i}~\eta _2 \\ \zeta _2 + \omega _2 + \textrm{i}~\left( \psi _2 + \omega _{\text {CP}}\right) \end{pmatrix} , \end{aligned}$$

(2.2)

with

$$\begin{aligned} {\langle {\Phi _1}\rangle }&= \frac{1}{\sqrt{2}}\begin{pmatrix} 0 \\ \omega _1 \end{pmatrix} \quad \text{ and } \quad {\langle {\Phi _2}\rangle } = \frac{1}{\sqrt{2}} \begin{pmatrix} \omega _{\text {CB}}\\ \omega _2 + \textrm{i}~\omega _{\text {CP}}\end{pmatrix} , \end{aligned}$$

(2.3)

where the bracket ${\langle {\dots }\rangle }$ indicates the vacuum state. The vacuum structure at zero temperature is denoted as

$$\begin{aligned} v_i \equiv \omega _i\big \vert _{T=0} \quad i = 1,2,\textrm{CP},\textrm{CB} , \end{aligned}$$

(2.4)

with

$$\begin{aligned} v_{\text {CP}}=v_{\text {CB}} \equiv 0 . \end{aligned}$$

(2.5)

This ensures that we end up in the physical minimum given by the normal EW tree-level minimum at zero temperature. A non-zero value for the CB VEV would break electric charge conservation and introduce massive photons. Therefore, all parameter points showing such unphysical vacuum structures are neglected in the analysis as well as those breaking CP invariance. The VEVs of the normal EW minimum are related to the SM VEV by

$$\begin{aligned} v_1^2+v_2^2 \equiv v^2 \approx \left( 246~\text {GeV}\right) ^2 . \end{aligned}$$

(2.6)

The minimum conditions of the potential read

$$\begin{aligned} \frac{\partial V_{\text {tree}}}{\partial \Phi _i^{\dagger }}\big \vert _{\Phi _j={\langle {\Phi _j}\rangle }} \overset{!}{=}\ 0 ,\quad i,j\in \lbrace 1,2\rbrace , \end{aligned}$$

(2.7)

where ${\langle {\Phi _j}\rangle }=(0,v_j/\sqrt{2})^T$ at $T=0$ lead to the tadpole conditions

$$\begin{aligned} m_{11}^2&= \text{ Re }(m_{12}^2) \frac{v_2}{v_1} - \frac{\lambda _1}{2} v_1^2 - \frac{\lambda _3+\lambda _4+\text{ Re }\lambda _5}{2} v_2^2 \end{aligned}$$

(2.8a)

$$\begin{aligned} m_{22}^2&= \text{ Re }(m_{12}^2) \frac{v_1}{v_2} - \frac{\lambda _2}{2} v_2^2 - \frac{\lambda _3+\lambda _4+\text{ Re }\lambda _5}{2} v_1^2 \end{aligned}$$

(2.8b)

$$\begin{aligned} \text{ Im } m_{12}^2&= \text{ Im } \lambda _5 \frac{v_1v_2}{2} , \end{aligned}$$

(2.8c)

which allow us to trade the Lagrangian parameters $m_{11}^2$, $m_{22}^2$ for the zero-temperature EW VEVs $v_1$ and $v_2$. Equation (2.8c) relates the two phases of the complex parameters $m_{12}^2$ and $\lambda _5$, and we follow the conventions defined in [86].

The mass eigenstates of the charged sector, the charged Higgs bosons $H^\pm$ and the charged Goldstone bosons $G^\pm$, are obtained through the rotation

$$\begin{aligned} \begin{pmatrix} G^\pm \\ H^\pm \end{pmatrix} =&R_\beta \begin{pmatrix} \frac{1}{\sqrt{2}} \left( \rho _1 \pm \textrm{i}~\eta _1 \right) \\ \frac{1}{\sqrt{2}} \left( \rho _2 \pm \textrm{i}~\eta _2 \right) \end{pmatrix} \end{aligned}$$

(2.9)

with the rotation matrix

$$\begin{aligned} R_\beta =&\begin{pmatrix} \cos (\beta ) &{} \sin (\beta ) \\ -\sin (\beta ) &{} \cos (\beta ) \end{pmatrix} \end{aligned}$$

(2.10)

and the mixing angle $\beta$ defined through

$$\begin{aligned} \tan \beta =&\frac{v_2}{v_1} . \end{aligned}$$

(2.11)

Applying the same rotation matrix to the CP-odd fields yields the neutral Goldstone boson $G^0$ and the CP-odd field $\zeta _3$ as

$$\begin{aligned} \begin{pmatrix} G^0 \\ \zeta _3 \end{pmatrix} =&R_\beta \begin{pmatrix} \psi _1 \\ \psi _2 \end{pmatrix} . \end{aligned}$$

(2.12)

The mass eigenstates of the neutral Higgs sector, $H_k~(k=1,2,3)$, are then given by

$$\begin{aligned} \begin{pmatrix} H_1 \\ H_2\\ H_3 \end{pmatrix} =R \begin{pmatrix} \zeta _1\\ \zeta _2\\ \zeta _3 \end{pmatrix} , \end{aligned}$$

(2.13)

with the rotation matrix ($c_i \equiv \cos \alpha _i,$ $s_i \equiv \sin \alpha _i$, $i=1,2,3$)

$$\begin{aligned} R = \begin{pmatrix} c_1c_2 &{} s_1 c_2 &{} s_s \\ -\left( c_1 s_2s_3+ s_1 c_3\right) &{} c_1 c_3 - s_1 s_2 s_3 &{} c_2 s_3 \\ -c_1s_2c_3+s_1 s_3 &{} -\left( c_1 s_3+s_1s_2c_3\right) &{} c_2 c_3 \end{pmatrix} . \end{aligned}$$

(2.14)

Without loss of generality the mixing angles $\alpha _i$ can be chosen in the interval

$$\begin{aligned} -\frac{\pi }{2}\le \alpha _i < \frac{\pi }{2} . \end{aligned}$$

(2.15)

The rotation Eq. (2.13) yields a diagonal mass matrix

$$\begin{aligned} R M^2_{\text {Scalar}} R^T = {\text {diag}}(m_{H_1}^2,m_{H_2}^2,m_{H_3}^2) , \end{aligned}$$

(2.16)

with mass ordered neutral Higgs boson masses

$$\begin{aligned} m_{H_1}\le m_{H_2}\le m_{H_3} . \end{aligned}$$

(2.17)

The C2HDM potential can then be expressed in terms of the following nine independent input parameters

$$\begin{aligned} v ,\quad \tan \beta ,\quad \alpha _{1,2,3} ,\quad m_{H_i} ,\quad m_{H_j} ,\quad m_{H^{\pm }}\,\quad \text {and}\,\quad \text{ Re }(m_{12}^2) .\nonumber \\ \end{aligned}$$

(2.18)

Here, $m_{H_i}$ and $m_{H_j}$ denote any two of the three neutral Higgs bosons, with one of them being the 125 GeV scalar. The remaining mass is expressed in terms of the other two Higgs boson masses and elements of the rotation matrix defined in Eq. (2.14) through the relation [90]

$$\begin{aligned} \sum \limits _{k=1}^{3} m_{H_k}^2 R_{k3} \left( R_{k2} \tan \beta - R_{k1} \right) = 0 , \end{aligned}$$

(2.19)

so that it is no direct input parameter in our parameter scan.

2.1 Computation of the phase transition

In [35, 50, 59] we presented in detail the computation of the loop-corrected effective potential at finite temperature from which we deduce the critical VEV $v_c$ at the critical temperature $T_c$, which denotes the temperature where the symmetric and non-symmetric vacuum become degenerate. For values of $\xi _c = v_c/T_c \ge 1$ we have a strong first order EWPT [11, 52]. We have chosen the renormalisation conditions of the loop-corrected effective potential such that not only the VEV and all physical Higgs boson masses, but also all mixing matrix elements remain at their tree-level values. This choice allows us to effectively determine in a parameter scan of the model parameter points that are compatible with the theoretical and experimental constraints without the need to resort to an iterative procedure as we can directly use the tree-level mass values and mixing angles as input parameters. In the CP-violating 2HDM, however, the determination of the counterterm potential from the parametrisation of the tree-level potential is not sufficient to render all masses and mixing values equal to their tree-level values. At one-loop level new flavour-violating structures are induced due to CP violation. This has to be taken into account in the construction of the counterterm potential which is hence given by

$$\begin{aligned} V_{\text {CT}}= & {} \frac{\delta m_{11}^2}{2} \omega _1^2 + \frac{\delta m_{22}^2}{2} (\omega _2^2+\omega _{\text {CP}}^2 + \omega _{\text {CB}}^2) \nonumber \\{} & {} - \delta \text{ Re }(m_{12}^2) \,\omega _1\omega _2 + \delta \text{ Im }(m_{12}^2) \,\omega _1\omega _{\text {CP}} + \frac{\delta \lambda _1}{8} \omega _1^4 \nonumber \\{} & {} + \frac{\delta \lambda _2}{8} (\omega _2^2+\omega _{\text {CP}}^2+\omega _{\text {CB}}^2)^2 +\frac{\delta \lambda _3}{4} \omega _1^2\nonumber \\{} & {} \left( \omega _{2}^2 +\omega _{\text {CP}}^2 + \omega _{\text {CB}}^2\right) + \frac{\delta \lambda _4}{4} \omega _1^2\left( \omega _2^2+\omega _{\text {CP}}^2\right) \nonumber \\{} & {} + \frac{\delta \text{ Re }(\lambda _5)}{4} \omega _1^2 \left( \omega _2^2-\omega _{\text {CP}}^2\right) - \frac{\delta \text{ Im }(\lambda _5)}{2} \omega _1^2\omega _2\omega _{\text {CP}} \nonumber \\{} & {} + \delta T_1 \, \omega _1 + \delta T_2 \, \omega _2 + \delta T_{\text {CP}} \, \omega _{\text {CP}} \nonumber \\{} & {} - \frac{\delta \text{ Im }(\lambda _6)}{2} \omega _1^{3} \omega _{\text {CP}} - \frac{\delta \text{ Im }(\lambda _7)}{2} \omega _1 \omega _{\text {CP}}\nonumber \\{} & {} \times (\omega _2^2+\omega _{\text {CP}}^2+\omega _{\text {CB}}^2) . \end{aligned}$$

(2.20)

This form of the counterterm potential differs by the last two terms from the one given in Ref. [50]. A check of the results given in [50] shows, however, that the difference induced by the two new terms is negligible so that the results given in [50] do not change significantly.

We apply the following renormalisation conditions [50]

$$\begin{aligned} \partial _{\phi _i} \left. V_{\text {CT}} (\phi )\right| _{\phi = \langle \phi ^c \rangle _{T=0}}= & {} - \partial _{\phi _i} \left. V_{\text {CW}} (\phi ) \right| _{\phi = \langle \phi ^c \rangle _{T=0}} \end{aligned}$$

(2.21)

$$\begin{aligned} \partial _{\phi _i} \partial _{\phi _j}\left. V_{\text {CT}} (\phi )\right| _{\phi = \langle \phi ^c\rangle _{T=0}}= & {} - \partial _{\phi _i} \partial _{\phi _j}\left. V_{\text {CW}} (\phi )\right| _{\phi = \langle \phi ^c\rangle _{T=0}}, \nonumber \\ \; \end{aligned}$$

(2.22)

with the Coleman–Weinberg potential $V_{\text {CW}}$ given in [50],

$$\begin{aligned} \phi _i \equiv \{ \rho _1, \eta _1, \rho _2, \eta _2, \zeta _1, \psi _1, \zeta _2, \psi _2 \} \;, \end{aligned}$$

(2.23)

and the field configuration $\langle \phi ^c \rangle _{T=0}$ in the minimum at $T=0$,

$$\begin{aligned} \langle \phi ^c \rangle _{T=0} = (0,0,0,0,v_1,0,v_2,0) \;. \end{aligned}$$

(2.24)

These conditions ensure the EW minimum to be a local minimum at $T=0$, which we check numerically to be the global one, and that the masses and mixing angles remain at their tree-level values at $T=0$. Since the conditions are not enough to fix all renormalisation constants, we have to choose two of them and set them equal to $t_1$ and $t_2 \in {\mathbb {R}}$, respectively. This results in the following counterterms in terms of the derivatives of the potential,

$$\begin{aligned}&\delta m_{11}^2 = t_1 v_2^2 - \frac{3}{2} H^\text {CW}_{\psi _1, \psi _1} - \frac{v_2 }{2 v_1} H^\text {CW}_{\psi _1, \psi _2}+ \frac{1}{2} H^\text {CW}_{\zeta _1, \zeta _1} + \frac{v_2 }{2 v_1}H^\text {CW}_{\zeta _1, \zeta _2} \end{aligned}$$

(2.25a)

$$\begin{aligned}&\delta m_{22}^2 = t_1 v_1^2 - \frac{v_1 }{2 v_2}H^\text {CW}_{\psi _1, \psi _2} - \frac{3}{2} H^\text {CW}_{\psi _2, \psi _2} + \frac{v_1 }{2 v_2}H^\text {CW}_{\zeta _1, \zeta _2} + \frac{1}{2} H^\text {CW}_{\zeta _2, \zeta _2} \end{aligned}$$

(2.25b)

$$\begin{aligned}&\delta \textrm{Im}\left( m_{12}^2\right) = \frac{1}{2} H^\text {CW}_{\zeta _1, \psi _2} + \frac{v_2 }{2 v_1}H^\text {CW}_{\zeta _2, \psi _2} + \frac{3 }{2 v_2}N^\text {CW}_{\psi _1} \end{aligned}$$

(2.25c)

$$\begin{aligned}&\delta \textrm{Re}\left( m_{12}^2\right) = t_1 v_1 v_2 + H^\text {CW}_{\psi _1, \psi _2} \end{aligned}$$

(2.25d)

$$\begin{aligned}&\delta \lambda _1 = -\frac{v_2^2}{v_1^2} t_1 + \frac{1}{v_1^2} H^\text {CW}_{\psi _1, \psi _1} - \frac{1}{v_1^2} H^\text {CW}_{\zeta _1, \zeta _1} \end{aligned}$$

(2.25e)

$$\begin{aligned}&\delta \lambda _2 = -\frac{ v_1^2}{v_2^2} t_1 + \frac{1}{v_2^2}H^\text {CW}_{\psi _2, \psi _2} - \frac{1}{v_2^2}H^\text {CW}_{\zeta _2, \zeta _2} \end{aligned}$$

(2.25f)

$$\begin{aligned}&\delta \lambda _3 = -t_1 + \frac{H^\text {CW}_{\eta _1, \eta _2}}{v_1 v_2} - \frac{1}{v_1^2}H^\text {CW}_{\eta _2, \eta _2} + \frac{H^\text {CW}_{\psi _2, \psi _2}}{v_1^2} - \frac{H^\text {CW}_{\zeta _1, \zeta _2}}{v_1 v_2} \end{aligned}$$

(2.25g)

$$\begin{aligned}&\delta \lambda _4 = t_1 + \frac{2 }{v_1^2}H^\text {CW}_{\eta _2, \eta _2} - \frac{2 }{v_1^2}H^\text {CW}_{\psi _2, \psi _2} \end{aligned}$$

(2.25h)

$$\begin{aligned}&\delta \textrm{Re}\lambda _5 = t_1 \end{aligned}$$

(2.25i)

$$\begin{aligned}&\delta \textrm{Im}\lambda _5 = -\frac{2 v_1}{v_2}~t_2 - \frac{2 }{v_2^2}H^\text {CW}_{\zeta _1, \psi _1} \end{aligned}$$

(2.25j)

$$\begin{aligned}&\delta T_\text {CB} = -N^\text {CW}_{\rho _2} \end{aligned}$$

(2.25k)

$$\begin{aligned}&\delta T_1 = v_1 H^\text {CW}_{\psi _1, \psi _1} + v_2 H^\text {CW}_{\psi _1, \psi _2} - N^\text {CW}_{\zeta _1} \end{aligned}$$

(2.25l)

$$\begin{aligned}&\delta T_2 = v_1 H^\text {CW}_{\eta _1, \eta _2} + v_2 H^\text {CW}_{\eta _2, \eta _2} - N^\text {CW}_{\zeta _2} \end{aligned}$$

(2.25m)

$$\begin{aligned}&\delta T_\text {CP} = -\frac{v_1 }{v_2} N^\text {CW}_{\psi _1}- N^\text {CW}_{\psi _2} \end{aligned}$$

(2.25n)

$$\begin{aligned}&\delta \textrm{Im}\lambda _6 = t_2 \end{aligned}$$

(2.25o)

$$\begin{aligned}&\delta \textrm{Im}\lambda _7 = \frac{ v_1^2}{v_2^2} t_2+ \frac{v_1 }{v_2^3}H^\text {CW}_{\zeta _1, \psi _1} + \frac{1}{v_1 v_2}H^\text {CW}_{\zeta _2, \psi _2} \;, \end{aligned}$$

(2.25p)

with

$$\begin{aligned} H^{\text {CW}}_{\phi _i,\phi _j}&\equiv \partial _{\phi _i} \partial _{\phi _j}\left. V_{\text {CW}} (\phi )\right| _{\phi = \langle \phi ^c\rangle _{T=0}} \end{aligned}$$

(2.26)

$$\begin{aligned} N^{\text {CW}}_{\phi _i}&\equiv \partial _{\phi _i} \left. V_{\text {CW}} (\phi ) \right| _{\phi =\langle \phi ^c\rangle _{T=0}} . \end{aligned}$$

(2.27)

For the procedure on the treatment of the infrared divergences for the Goldstone bosons in the Landau gauge that arrive in the second derivative of the Coleman Weinberg potential [91,92,93,94,95,96,97] we refer to Ref. [35].

3 Calculation of the electroweak baryogenesis

Before we go into the details of the computation of the BAU, $\eta$, we first sketch the general idea of EWBG. The EWPT triggers the expansion of bubbles that contain the broken phase with a non-vanishing VEV $\langle \phi \rangle \ne 0$ within the surrounding symmetric phase with $\langle \phi \rangle = 0$. CP-violating interactions generate a net-asymmetry of the left-handed fermions in front of the bubble wall. Baryon-number violating sphaleron processes convert the left-handed fermions into baryons and vice versa. While the bubbles are expanding the baryons diffuse through the bubble wall. Inside the bubble, in the broken phase, the sphaleron decay rate is strongly suppressed so that the conversion between baryons and left-handed particles does not continue. The suppression requires an EWPT that is of strong first order. The criterion for a strong first-order EWPT is given by $\xi _c = v_c/T_c \gtrsim 1$ [11, 52], where $v_c$ denotes the critical VEV at the critical temperature $T_c$. The critical temperature $T_c$ is defined as the temperature where two degenerate global minima exist.

In order to determine $\xi _c$ we compute the loop-corrected effective potential at finite temperature. Since the effective potential at finite temperature was already discussed in full detail in [50, 59, 64] for the C2HDM including the presentation of the adapted renormalisation scheme and the thermal corrections, we skip the discussion here and refer to the previous works. Still, we want to make two remarks here. In contrast to the value of the effective potential at the minimum, the VEV determined from the effective potential is gauge dependent. The issue of gauge dependence has been analysed in the literature [36, 62, 98,99,100,101,102,103]. Gauge-invariant approaches have been proposed within simpler models applying certain approximations. While a gauge-invariant treatment for the analysis of the EWPT would certainly be preferred, this is beyond the scope of this paper. The effective potential also depends on the renormalisation scale $\mu$. For discussions of the effective three-dimensional theory instead of the conventional perturbative approach, we refer to [41, 104,105,106,107,108,109,110,111,112,113,114,115,116].

In the following we present the calculation of the actual BAU, $\eta$, to set the applied conventions and notation. In this analysis two non-local approaches for the determination of $\eta$ are compared. The first approach is based on the semi-classical force [67,68,69,70] yielding a set of fluid equations. We will refer to this approach as FH. The FH ansatz works for thick bubble walls, so that the wall thickness $L_W$ is assumed to be larger than the typical de-Broglie wavelength of the particles in front of the bubble wall. The typical wavelength of a particle in the plasma is given by the inverse temperature $T^{-1}$ implying that the Wenzel–Kramers–Brillouin (WKB) approach used in FH is valid for bubble walls with

$$\begin{aligned} 1\ll L_W T_c , \end{aligned}$$

(3.1)

where $T_c$ denotes the critical temperature at which the electroweak phase transition takes place. Additionally, only small wall velocities are assumed in[69, 70]. This allows us to simplify the resulting transport equations further. As mentioned recently in Ref. [81] this can be generalized to arbitrary wall velocities even above the speed of sound of the plasma. The ansatz for arbitrary wall speeds is left for further future investigations.

The second approach is based on the competing VEV-insertion approximation (VIA) [71,72,73,74]. VIA formulates the quantum transport equations in the Closed Time Path (CTP) or Schwinger–Keldysh formalism [117,118,119]. To extract the respective source terms the fermionic two-point functions of the corresponding particles are expanded at LO in the spatially varying Higgs field VEV v(z), where z denotes the perpendicular distance to the wall. The next-to-leading order (NLO) contributions to the CP-violating source terms and the relaxation rates have been calculated recently [120], but they are not used in this analysis. We will comment below on the recent results of [82] which find that the LO source term vanishes in the VIA approach. VIA also allows us to include additional leptons in the transport equations such as the $\tau$-lepton [121]. Including leptons in the transport equations has the advantage that the generated densities are not suppressed by strong sphaleron interactions and that the chiral flux of the leptons can diffuse more efficiently in the plasma. In this way the $\tau$ contributions might enhance the produced BAU. We will compare different VIA systems including only top quarks (t), top and bottom quarks ($t+b$) and finally top and bottom quarks as well as $\tau$ leptons ($t+b+\tau$). VIA can be understood as an expansion in v(z)/T, whereas FH corresponds to an expansion in $\left( L_W T\right) ^{-1}$. Both approaches rely on the bubble wall dynamics and its profile. In the analysis we treat the bubble wall velocity as open parameter and use the standard assumption that the nucleating bubble is treated in the bubble rest frame and approximated by a planar wall so that the only parameter needed in both approaches is the wall profile depending on the space-time coordinate z referring to the wall distance. Furthermore, we use a two-step approach in both cases to calculate $\eta$. In the first step we solve the (quantum) transport equations for the left-handed fermion excess $n_L$ in front of the bubble wall, and in the second step this fermion asymmetry triggers the generation of the baryon asymmetry via the electroweak sphaleron transition.

3.1 Calculation of the bubble wall profile

To describe the bubble wall profile the kink solution is used by which the VEV profile as a function of the bubble wall distance z is described as [69, 70]

$$\begin{aligned} f(z) = \frac{f_0}{2}\left( 1-\tanh \frac{z}{L_W}\right) , \end{aligned}$$

(3.2)

where f(z) is the value of the VEV at given z and $f_0$ the value of the VEV inside the broken phase. Furthermore, the wall thickness $L_W$ is given by [69]

$$\begin{aligned} L_W = \frac{v_c}{\sqrt{8 V_b}} , \end{aligned}$$

(3.3)

with $v_c$ being the critical VEV at the electroweak phase transition and $V_b$ the barrier height between both degenerate global minima (at the critical temperature $T_c$). The numerical values of the critical VEV $v_c$ and the critical temperature $T_c$ for a given parameter point are obtained from BSMPT v2, which also calculates $L_W$. For this, BSMPT v2 determines the tunnel path between both global minima numerically. Starting with the direct connection between both minima, the straight path as a first guess for the tunnel path can be parametrised as

$$\begin{aligned} \quad \vec {\omega }(t)&= \vec {\omega }_s + t \vec {n} \end{aligned}$$

(3.4)

$$\begin{aligned} \vec {n}&= \vec {\omega }_b-\vec {\omega }_s , \end{aligned}$$

(3.5)

where $\vec {\omega }_{s/b}$ is the VEV configuration of the symmetric and broken minimum, respectively, and $t\in \left[ 0,1\right]$. Successively, the global minima in the orthogonal planes along the straight path are determined. They form a grid that approximates the tunnel path between the two degenerate minima. The barrier height $V_b$ is then obtained as the difference between the maximum value of the effective potential along this path and the value of the effective potential at $v_c$.

Fig. 1

Normalised deviation from the straight line path at each step i along the path where $\vec {\omega }_l$ are the points along the direct line from $\vec {\omega }_s$ to $\vec {\omega }_b$. $\vec {\omega }_p$ refers to the found global minimum in the orthogonal planes. The colour code denotes the various possible minima, $\omega _1$ (red), $\omega _2$ (blue) and $\omega _{\text {CP}}$ (green). Red and blue points are on top of each other and are almost zero

For a more detailed discussion of the numerical method we refer to the manual of BSMPT v2. In Fig. 1 the result for one example parameter point of the C2HDM³ is given. The figure displays the squared difference between the found VEV vector $\vec {\omega }_p (t)$ of the tunnel path and the straight connection $\vec {\omega }_l (t)$ between both minima normalised to the squared difference between the broken and symmetric VEVs at each step i (corresponding to discrete values of $t\in [0,1]$),

$$\begin{aligned} \Delta \omega _i^2 = \frac{|\vec {\omega }_{p,i}-\vec {\omega }_{l,i}|^{2 }}{n_i^2} \;, \end{aligned}$$

(3.6)

for $\omega _i=\omega _1$ (red), $\omega _2$ (blue) and $\omega _{\text {CP}}$ (green), versus the parameter t. Both electroweak VEVs $\omega _1$ and $\omega _2$ do not show any deviation from the direct connection, only for the CP-violating VEV of the C2HDM, $\omega _{\text {CP}}$, there is a significant deviation. Similar observations were made in [70] showing that the straight line is a good first approximation of the tunnel path, but the CP-violating VEV was not taken into account in [70]. By determining $L_W$ and the general VEV configuration at the critical temperature⁴ the bubble wall profile can be parametrised in both approaches, VIA and FH, by using Eq. (3.2).

Both approaches require the complex phases of the leptons and quarks as a function of the bubble wall distance z. In the following, we give the explicit formulas for the C2HDM case by making use of Eq. (3.2). Through the possibility of a CP-violating VEV at non-zero temperature the quark and lepton masses can become complex.⁵ For the type I version of the C2HDM where all leptons and quarks are coupled to the second Higgs doublet $\Phi _2$, the Yukawa Lagrangian yields the following mass terms

$$\begin{aligned} m_i(z)= \frac{y_{i}}{\sqrt{2}} \left( \omega _2(z)-\textrm{i}~\omega _{\text {CP}}(z)\right) , \end{aligned}$$

(3.7)

where $y_i$ is the zero-temperature Yukawa coupling of the respective particle i and $\omega _2$, $\omega _{\text {CP}}$ the VEVs defined in Eq. (2.3). For the type II C2HDM Eq. (3.7) only holds for the up-type quarks. For the leptons and down-type quarks the VEV $\omega _1$ of the Higgs doublet $\Phi _1$ gives rise to the mass term and no complex part is introduced there, so that the masses are real. Defining the complex mass of the particle i as

$$\begin{aligned} m_i (z)= & {} \frac{y_{i}}{\sqrt{2}} \left( \omega _2(z)-\textrm{i}~\omega _{\text {CP}}(z)\right) = \frac{y_i}{\sqrt{2}} \sqrt{\omega _2^2+\omega _{\text {CP}}^2} \nonumber \\{} & {} \times \exp \left( \textrm{i}~\arg \left( \omega _2\!-\! \textrm{i}~\omega _{\text {CP}}\right) \right) \equiv \vert m_i(z)\vert \exp (\textrm{i}~\theta ^{(i)}(z)) , \nonumber \\ \end{aligned}$$

(3.8)

allows us to parametrise the phase evolution as a function of the wall distance as

$$\begin{aligned} \theta ^{(i)}(z) = \left( \theta _{\text {brk}}^{(i)} - \frac{\theta _{\text {brk}}^{(i)}-\theta _{\text {sym}}^{(i)}}{2} \left( 1+\tanh \frac{z}{L_W}\right) \right) , \end{aligned}$$

(3.9)

where $\theta _{\text {brk}}$ is the phase in the broken minimum and $\theta _{\text {sym}}$ the one in the symmetric minimum, respectively. Note that the phase in the totally symmetric minimum with all VEVs vanishing is arbitrary, so that we chose $\theta _{\text {sym}}$ as the phase of the symmetric minimum plus an infinitesimal shift along the tunnel path so that we have a smooth phase along the tunnel path. For further details, we refer to [66]. The broken and symmetric phases for the particle i are given by

$$\begin{aligned} \theta _{\text {brk}}^{(i)} \!=\! \arg \left( \omega _{2,c}^{(i)}-\textrm{i}~\omega _{\text {CP},c}^{(i)}\right) ,\quad \theta _{\text {sym}}^{(i)} = \arg \left( \omega _{2,\text {s}}^{(i)}-\textrm{i}~\omega _{\text {CP,s}}^{(i)}\right) ,\nonumber \\ \end{aligned}$$

(3.10)

where the index c denotes the critical VEVs and s the VEVs in the symmetric phase. For a more detailed description of the numerical approach we refer again to the manual of BSMPT v2 [66].

3.2 Semi-classical force approach

The semi-classical force method uses the existence of a complex fermion mass. This complex mass induces in the presence of a varying Higgs background a semi-classical force term which can be deduced by applying the WKB approximation [69, 70, 81], or from the closed-time-path (CTP) formalism of thermal field theory [122,123,124,125], yielding

$$\begin{aligned} F = - \frac{\left( m^2\right) ^{\prime }}{2E_0} \pm s \frac{\left( m^2\theta ^{\prime }\right) ^{\prime }}{2 E_0 E_{0,z}}\mp \frac{\theta ^{\prime }m^2\left( m^2\right) ^{\prime }}{4 E_0^3 E_{0,z}} , \end{aligned}$$

(3.11)

where $E_0$ is the conserved energy of the quasi-particles in front of the bubble wall in the rest frame of the wall, $E_{0,z}^2=E_0^2-\vec {p}_{\parallel }$ with the momentum $\vec p_{\parallel }$ parallel to the bubble wall and $\left( \dots \right) ^{\prime }$ denotes the derivative with respect to the wall distance z. For better readability we skipped the z dependences of $m,\theta , E_0$, and $E_{0,z}$ in Eq. (3.11). The mass m and the phase $\theta$ are defined as in Eq. (3.8) and s denotes the spin of the particle. The first term in Eq. (3.11) corresponds to the classical solution since the particle changes its mass in the varying Higgs background while moving and conserves CP, whereas the second and third part besides the spin are dependent on the particle’s nature ($+$ particle/− antiparticle) and therefore induce CP violation. This part is only present if the particle has a complex mass phase. Allowing for small kinetic perturbations $\delta f_i$ in the distribution functions $f_i$ of the particle species i we have (the $+(-)$ refers to fermions (bosons), $\beta =1/T$),

$$\begin{aligned} f_i = \frac{1}{\text {e}^{\beta \left[ \gamma _W \left( E_0+v_W p_z\right) -\mu _i\right] }\pm 1} + \delta f_i , \end{aligned}$$

(3.12)

with the Lorentz boost factor $\gamma _W=1/\sqrt{1-v_W^2}$ of the wall. The chemical potential $\mu _i$ describing the departure from chemical equilibrium, allows us to express the Boltzmann equations for the near-equilibrium system as

$$\begin{aligned} {{\textbf {L}}}[f_i]\equiv \left( v_g\partial _z + F \partial _{p_z}\right) f_i = \mathcal C[f_i] , \end{aligned}$$

(3.13)

where ${{\textbf {L}}}[f_i]$ is the Liouville operator, $v_\textrm{g}$ the group velocity of the WKB wave package given by [70]

$$\begin{aligned} v_\textrm{g} = \frac{p_z}{E_0} \left( 1 \pm \frac{s}{2} \theta ^{\prime } \frac{m^2}{E_0^2 E_{0,z}} \right) , \end{aligned}$$

(3.14)

and F denotes the semi-classical force given in Eq. (3.11). The collision integral $\mathcal C[f_i]$ is model dependent and can be linked to the interaction rates of the thermal bath [78]. The force term splits into a CP-even and two CP-odd terms. Additionally, since the CP-even and CP-odd components are equal at first order, the perturbations $\mu _i$ around the chemical equilibrium have to be expanded to the second order in the CP-odd terms in order to account for CP-violating effects. We therefore solve the Boltzmann equation separately for $\mu _{e/o}$and $\delta f_{i,e/o}$,

$$\begin{aligned} \mu _i =&\mu _{i,1e} + \mu _{i,2o} + \mu _{i,2e} , \quad \delta f_i = \delta f_{i,1e} + \delta f_{i,2o} + \delta f_{i,2e} , \end{aligned}$$

(3.15)

where e(o) corresponds to the CP-even (odd) part. The indices 1 and 2 indicate the order in the gradient expansion used in [69]. To simplify the actual solution of the transport equation in Eq. (3.13), only the two lowest moments of the equation are taken into account, the zeroth and first moment of Eq. (3.13). The weighted average are defined as follows for the zeroth and the first moment, respectively,

$$\begin{aligned} {\langle {X}\rangle } = \frac{\int d^3p X(p)}{\int d^3 f_{0+}^{\prime }(m=0)} ,\quad {\langle {\frac{p_z}{E_0}X}\rangle } = \frac{\int d^3p \frac{p_z}{E_0}X(p)}{\int d^3 f_{0+}^{\prime }(m=0)} , \nonumber \\ \end{aligned}$$

(3.16)

where the derivative of the massless fermion distribution function

$$\begin{aligned} f_{0+}^{\prime }(m=0) \equiv f_i|_{i=\textrm{fermion},\mu _i=0,\delta f_i=0,v_W=0} \end{aligned}$$

(3.17)

is chosen as normalisation.⁶ By defining the plasma velocity

$$\begin{aligned} u_i \equiv \left\langle {\frac{p_z}{E_0}\delta f_i}\right\rangle \end{aligned}$$

(3.18)

the Liouville operator in Eq. (3.13) on the one side produces source terms and on the other side relates the chemical potentials and plasma velocities with thermal transport coefficients, denoted $K_i$. The only missing pieces are the zeroth and the first moments of the collision integrals

$$\begin{aligned} {\langle {\mathcal C[f_i]}\rangle }\quad \text {and}\quad \left\langle {\frac{p_z}{E_0}\mathcal C[f_i]}\right\rangle , \end{aligned}$$

(3.19)

which can be expressed in terms of the inelastic and total interaction rates, $\Gamma _{\text {inel}}$ and $\Gamma _{\text {tot}}$, respectively[78],

$$\begin{aligned} {\langle {\mathcal C[f_i]}\rangle } = \Gamma _{\text {inel}} \sum \mu _i\quad \text {and}\quad \left\langle {\frac{p_z}{E_0}\mathcal C[f_i]}\right\rangle = - \Gamma _{\text {tot}} u . \end{aligned}$$

(3.20)

The second-order CP-odd chemical potential is given by the difference of the chemical potential of the particle and the one of the anti-particle,

$$\begin{aligned} \mu _{i,2} ={}&\mu _{i,2o} - {\bar{\mu }}_{i,2o} . \end{aligned}$$

(3.21)

The index i denotes the involved particle species, given by the top quark and its charged conjugated, t and $t^c$, the bottom quark b and the Higgs boson h. The chemical potential of the corresponding antiparticle is denoted by ${\bar{\mu }}_i$. The transport equations include Yukawa interactions, strong sphaleron transitions and W-boson scattering. The top transport equations can then be written as [69, 70]

$$\begin{aligned} 0&= 3 v_WK_{1,t} \left( \partial _z \mu _{t,2} \right) + 3v_WK_{2,t} \left( \partial _z m_t^2 \right) \mu _{t,2} + 3 \left( \partial _z u_{t,2} \right) \nonumber \\&\quad - 3\Gamma _y \left( \mu _{t,2} + \mu _{t^c,2} + \mu _{h,2} \right) - 6\Gamma _M \left( \mu _{t,2} + \mu _{t^c,2} \right) \nonumber \\&\quad - 3\Gamma _W \left( \mu _{t,2} - \mu _{b,2} \right) \nonumber \\&\quad - 3\Gamma _{ss} \left[ \left( 1+9 K_{1,t} \right) \mu _{t,2} + \left( 1+9 K_{1,b} \right) \mu _{b,2} \right. \nonumber \\&\quad \left. + \left( 1-9 K_{1,t} \right) \mu _{t^c,2} \right] , \end{aligned}$$

(3.22a)

$$\begin{aligned} 0&= 3v_WK_{1,b} \left( \partial _z \mu _{b,2}\right) + 3 \left( \partial _z u_{b,2} \right) \nonumber \\&\quad - 3\Gamma _y \left( \mu _{b,2} + \mu _{t^c,2} + \mu _{h,2} \right) \nonumber \\&\quad - 3\Gamma _W \left( \mu _{b,2} - \mu _{t,2} \right) \nonumber \\&\quad - 3\Gamma _{ss} \left[ \left( 1 + 9K_{1,t}\right) \mu _{t,2} + (1+9K_{1,b}) \mu _{b,2} \right. \nonumber \\&\quad \left. + (1-9K_{1,t}) \mu _{t^c,2} \right] , \end{aligned}$$

(3.22b)

$$\begin{aligned} 0&= 3 v_WK_{1,t} \left( \partial _z \mu _{t^c,2} \right) + 3v_WK_{2,t} \left( \partial _z m_t^2 \right) \mu _{t^c,2} \nonumber \\&\quad + 3 \left( \partial _z u_{t^c,2} \right) \nonumber \\&\quad - 3\Gamma _y \left( \mu _{t,2} + \mu _{b,2} + 2\mu _{t^c,2} + 2\mu _{h,2} \right) \nonumber \\&\quad - 6\Gamma _M \left( \mu _{t,2} + \mu _{t^c,2} \right) \nonumber \\&\quad - 3\Gamma _{ss} \left[ \left( 1+9 K_{1,t}\right) \mu _{t,2} + \left( 1+9K_{1,b}\right) \mu _{b,2} \right. \nonumber \\&\quad \left. + \left( 1-9K_{1,t}\right) \mu _{t^c,2} \right] , \end{aligned}$$

(3.22c)

$$\begin{aligned} 0&= 4v_WK_{1,h} \left( \partial _z \mu _{h,2}\right) + 4\left( \partial _z u_{h,2}\right) \nonumber \\&\quad - 3\Gamma _y \left( \mu _{t,2} + \mu _{b,2} + 2\mu _{t^c,2} + 2\mu _{h,2} \right) - 4\Gamma _h \mu _{h,2} , \end{aligned}$$

(3.22d)

$$\begin{aligned} S_t&= -3K_{4,t} \left( \partial _z \mu _{t,2}\right) + 3v_W{\tilde{K}}_{5,t} \left( \partial _z u_{t,2}\right) \nonumber \\&\quad + 3v_W{\tilde{K}}_{6,t} \left( \partial _z m_t^2 \right) u_{t,2} + 3\Gamma _t^\textrm{tot} u_{t,2} , \end{aligned}$$

(3.22e)

$$\begin{aligned} 0&= -3K_{4,b} \left( \partial _z \mu _{b,2} \right) + 3v_W{\tilde{K}}_{5,b} \left( \partial _z u_{b,2}\right) \nonumber \\&\quad + 3\Gamma _b^\textrm{tot} u_{b,2} , \end{aligned}$$

(3.22f)

$$\begin{aligned} S_t&= -3K_{4,t} \left( \partial _z \mu _{t^c,2}\right) + 3v_W{\tilde{K}}_{5,t} \left( \partial u_{t^c,2}\right) \nonumber \\&\quad + 3v_W{\tilde{K}}_{6,t} \left( \partial _z m_t^2\right) u_{t^c,2} + 3\Gamma _t^\textrm{tot} u_{t^c,2} , \end{aligned}$$

(3.22g)

$$\begin{aligned} 0&= -4K_{4,h} \left( \partial _z \mu _{h,2} \right) + 4v_W{\tilde{K}}_{5,h} \left( \partial _z u_{h,2} \right) \nonumber \\&\quad + 4\Gamma _h^\textrm{tot} u_{h,2} , \end{aligned}$$

(3.22h)

with the source term of the top quark⁷

$$\begin{aligned} S_t =&-v_W K_{8,t} \partial _z \left( m_t^2 \partial _z \theta \right) + v_W K_{9,t} \left( \partial _z \theta \right) m_t^2 \left( \partial _z m_t^2\right) . \end{aligned}$$

(3.23)

Analogous to the chemical potential Eq. (3.21) the transport equations only depend on the differences between the CP-odd components of the plasma velocities of the particles, $u_{i,2o}$, and of their antiparticles, ${\bar{u}}_{i,2o}$,

$$\begin{aligned} u_{i,2} = u_{i,2o} - {\bar{u}}_{i,2o} . \end{aligned}$$

(3.24)

For the strong sphaleron rate $\Gamma _{ss}$ and the top Yukawa rate $\Gamma _y$ we use⁸ [70, 126, 127]

$$\begin{aligned} \Gamma _{ss} = 4.9 \times 10^{-4} T_c , \quad \Gamma _y = 4.2 \times 10^{-4} T_c \end{aligned}$$

(3.25)

The W-exchange rate is approximated by the total Higgs interaction rate $\Gamma _h^{\text {tot}}$ [70]. The Higgs number violating rate is given by [126]

$$\begin{aligned} \Gamma _h = \frac{m_W^2(z,T_c)}{50 T_c} , \end{aligned}$$

(3.26)

where the W-mass is determined numerically at given temperature $T_c$ and wall distance z by BSMPT v2. The spin-helicity flipping rate $\Gamma _M$ for the top quark is implemented as [126]

$$\begin{aligned} \Gamma _M = \frac{m_t^2(z,T_c)}{63 T_c} , \end{aligned}$$

(3.27)

where again the mass of the top quark is determined numerically at given distance and temperature $T_c$. The total interaction rates in Eq. (3.22) can be related to the diffusion constants $D_i$ of the quarks and Higgs bosons as [69, 70]

$$\begin{aligned} D_t = \frac{K_{4,t}}{K_{1,t} \Gamma _t^\textrm{tot}} ,\quad D_b = \frac{K_{4,b}}{K_{1,b} \Gamma _b^\textrm{tot}} ,\quad D_h = \frac{K_{4,h}}{K_{1,t} \Gamma _h^\textrm{tot}} . \end{aligned}$$

(3.28)

The thermal transport coefficients are defined as

$$\begin{aligned} K_{1,i}&= - {\left\langle {\frac{p_z^2}{E_0} \partial _E^2 f_{i,0} }\right\rangle } , \end{aligned}$$

(3.29a)

$$\begin{aligned} K_{2,i}&= {\left\langle {\frac{\partial _E^2 f_{i,0}}{2E_0} }\right\rangle } , \end{aligned}$$

(3.29b)

$$\begin{aligned} K_{4,i}&= {\left\langle {\frac{p_z^2}{E_0^2} \partial _E f_{i,0} }\right\rangle } , \end{aligned}$$

(3.29c)

$$\begin{aligned} {\tilde{K}}_{5,i}&= \left[ \frac{p_z^2}{E_0} \partial _E f_{i,0} \right] , \end{aligned}$$

(3.29d)

$$\begin{aligned} {\tilde{K}}_{6,i}&= \left[ \frac{E_0^2-p_z^2}{2E_0^3} \partial _E f_{i,0} \right] , \end{aligned}$$

(3.29e)

$$\begin{aligned} K_{8,i}&= {\left\langle {\frac{\vert p_z\vert \partial _E f_{i,0}}{2E_0^2 E_{0z}} }\right\rangle } , \end{aligned}$$

(3.29f)

$$\begin{aligned} K_{9,i}&= {\left\langle {\frac{\vert p_z\vert }{4E_0^3 E_{0z}} \left( \frac{\partial _E f_{i,0}}{E_0} - \partial _E^2 f_{i,0} \right) }\right\rangle } , \end{aligned}$$

(3.29g)

with the expectation values given by

$$\begin{aligned} {\left\langle {X}\right\rangle }&= \frac{\int \textrm{d}^3p X(p)}{\int \textrm{d}^3p \partial _E f_{0+}(m=0)} ,\nonumber \\ \left[ X\right]&= \frac{\int \textrm{d}^3p X(p)}{\int \textrm{d}^3p f_{i,0,v_W}} = \frac{\int \textrm{d}^3p X(p)}{\int \textrm{d}^3p f_{i,0}|_{v_W=0}} \end{aligned}$$

(3.30)

and the distribution functions

$$\begin{aligned} f_{i,0}&= \left. f_{i}\right| _{\mu _i = 0, \delta f_i = 0, v_W= 0} ,\nonumber \\ f_{0+}&= \left. f_{i}\right| _{i=\textrm{fermion},\mu _i=0,\delta f_i = 0, v_W= 0} , \nonumber \\ f_{i,0,v_W}&= f_{i,0} + v_Wp_z \partial _{E_0} f_{i,0} . \end{aligned}$$

(3.31)

The first two equations describe the distribution function in chemical equilibrium. The third one is the Taylor series of the distribution in chemical equilibrium for small wall velocities. Note that the assumption of small wall velocities is explicitly used to simplify the thermal transport coefficients in Eq. (3.29). To keep the full wall velocity dependence in the transport equations it is required to adapt the thermal transport coefficients in Eq. (3.29). The implementation of the full dependence as discussed in Ref. [81] is left for future work.

In the numerical implementation, the chemical potentials and the plasma velocities are assumed to vanish at $z\approx 4 L_W$ as a boundary condition. The factor 4 of the wall thickness has no physical interpretation and it was checked that this choice in the numerical set-up has no impact on the end result. Furthermore, with the choice of the kink profile the corresponding VEV profile already has negligibly small values at $z\approx 4 L_W$ implying that the choice of this boundary condition is justified.

The differential system of equations in Eq. (3.22) is solved numerically in BSMPT v2. For that the thermal coefficients in Eq. (3.29) are evaluated numerically for a given two-dimensional grid in squared mass and temperature and interpolated as a bi-cubic spline to optimize the run time of the calculation. The numerical solution of the transport equation system in Eq. (3.22) is performed by using the numerical c++ library boost [128] implemented in BSMPT v2. Solving the transport equations of Eq. (3.22) yields the chemical potentials $\mu _i$ of each particle species. Assuming local baryon number conservation the chemical potential of the left-handed quarks is then given by [70]

$$\begin{aligned} \mu _{B_L} =&\frac{1}{2} \left( 1+4K_{1,t}\right) \mu _{t,2} + \frac{1}{2} \left( 1+4K_{1,b}\right) \mu _{b,2} - 2K_{1,t} \mu _{t^c,2} , \end{aligned}$$

(3.32)

which triggers the generation of the baryon asymmetry in the electroweak sphaleron transition.

The actual value of the BAU can then be calculated from the solution of the transport equations since we assume that the weak sphaleron transition rate ${\tilde{\Gamma }}_{ws}$ is much smaller than all contributing interaction rates of the thermal plasma. In this way we can first calculate the produced left-handed fermion asymmetry in front of the bubble wall and in the second step we calculate the produced baryon asymmetry due to the electroweak sphaleron transition. The produced BAU can be calculated with [69, 70]

$$\begin{aligned} \eta _B= & {} \frac{n_B}{s}=\frac{405 \Gamma _{ws}}{4\pi ^2 v_w g_* T_c}\int _0^\infty dz \mu _{B_L}(z) \gamma (z)\nonumber \\{} & {} \times \exp \left( -\frac{45\Gamma _{ws}}{4v_W} \int _{-\infty }^z dz^\prime \gamma (z^\prime ) \right) , \end{aligned}$$

(3.33)

with the bubble wall velocity $v_W$, the effective degrees of freedom of the universe at electroweak temperatures $g_*\simeq 106.75$. For simplicity, we calculate the produced BAU at the critical temperature $T_c$. For the sphaleron transition rate ${\tilde{\Gamma }}_{ws}$ we choose a z-dependent ansatz

$$\begin{aligned} {\tilde{\Gamma }}_{ws} = \Gamma _{ws} \gamma (z) , \end{aligned}$$

(3.34)

with $\Gamma _{ws}\simeq 1.0\cdot 10^{-6} T_c$ and [129]

$$\begin{aligned} \gamma (z) = \exp \left( - a f(z)/T \right) \;, \quad a=37 , \end{aligned}$$

(3.35)

and the VEV profile f(z) given in Eq. (3.2). The implementation of the nucleation temperature in BSMPT, that should actually be used, is left for future work. For a detailed theoretical derivation of the top transport equations in Eq. (3.22) we refer to Refs. [69, 70] and for a detailed description of the implementation of the top transport equations in BSMPT v2 we refer to the manual of BSMPT v2 [66].

3.3 The VEV-insertion approximation

The VEV-insertion approximation (VIA) can be understood as an expansion in v(z)/T in which the fermionic two-point function is expanded in terms of the VEV. The mass fluctuations induced by the varying Higgs background (v(z)) are treated as perturbations that interact with the thermal bath. By including these thermal interactions CP-conserving and CP-violating source terms for the right-/left-handed fermion densities can be found. These sources generate a net-asymmetry between left- and right-handed fermions in front of the bubble wall, which again is then translated in the two-step approach into the baryon asymmetry via the electroweak sphaleron transition. Starting with the quantum transport equations derived in the finite temperature CTP formalism [117,118,119, 130, 131] the Schwinger-Dyson equation for a Weyl fermion current can be derived as [73, 132]

$$\begin{aligned} \partial _{\mu }j_i^{\mu }&= - \int d^3z \int \limits _{-\infty }^{\infty } dz_0 \textrm{Tr}\left[ \Sigma _i^{>}(x,z)S_i^{<}(z,x)\right. \nonumber \\&\quad - S_i^>(x,z)\Sigma _i^<(z,x)\nonumber \\&\quad \left. + S_i^<(x,z)\Sigma _i^>(z,x) - \Sigma _i^<(x,z)S_i^>(z,x) \right] , \end{aligned}$$

(3.36)

with $i=L,R$ for the left- and right-handed fermion, respectively. The Wightman functions $S^{\lambda }$ ($\lambda =>,<$) and the corresponding self-energies $\Sigma ^{\lambda }$ are defined in [73]. Again the bubble is assumed to be planar and the reference frame is the bubble rest frame which allows us to reformulate the left-hand side of Eq. (3.36). By using the diffusion approximation and Fick’s law the left-/right-handed current of the particle species i can be expressed in terms of the distribution function $n_{L/R,i}$ of the left-/right-handed particle species i,

$$\begin{aligned}{} & {} \partial _{\mu }j^{\mu }_{R/L,i}(x)\approx v_w n_{R/L,i}^{\prime }- D_{R/L,i} \nabla ^2 n_{R/L,i} \nonumber \\{} & {} \quad \approx v_wn_{R/L,i}^{\prime }-D_{R/L,i} n_{R/L,i}^{\prime \prime } , \end{aligned}$$

(3.37)

with the diffusion constant $D_{R/L,i}$ for the respective particle i and $\left( \dots \right) ^{\prime }$ corresponding to the derivative with respect to the wall distance z. The thermal corrections and the complex phases of the masses allow us to write the mass terms of the quarks/leptons $\Psi$ as follows

$$\begin{aligned} \mathcal L \supset - \frac{f_i\left( T,\phi _b\right) }{\sqrt{2}} {\bar{\Psi }}_L \Psi _R +\text { h.c.}, \end{aligned}$$

(3.38)

where $f_i \left( T,\phi _b\right) \in \mathbb C$ parametrises the interaction strength as a function of the Higgs background field $\phi _b$ and the temperature T. Using Eq. (3.38) allows us to cast the right-hand side of Eq. (3.36) in a CP-conserving part and a CP-violating part [73]

(3.39)

with the right-handed CP-violating source term for the particle species i given by

(3.40)

with the colour factor $N_c=3(1)$ for quarks (leptons) and the 4-momentum k of the fermions. $f_i^{\prime }$ corresponds to the derivative of the interaction strength in Eq. (3.38) with respect to the wall distance z. The left-/right-handed dispersion relation reads⁹

$$\begin{aligned} \epsilon _{L/R}^{i} =\omega _{L/R}^i + \textrm{i}~\Gamma _{T,L/R}^i \equiv \sqrt{k^2 +\left( m^i_{T,L/R}\right) ^2}-\textrm{i}~\Gamma ^i_{T,L/R}\,,\nonumber \\ \end{aligned}$$

(3.41)

with the thermal mass $m^i_{T}~\left( i=t,b,\tau \right)$, the thermal decay width $\Gamma _{T}^i$ and the Fermi–Dirac distribution $n(x)=\left( \text {e}^x+1\right) ^{-1}$. For simplicity, we assume the thermal widths to be approximately degenerate for left- and right-handed particles,

$$\begin{aligned} \Gamma ^{i}_{L,T}\approx \Gamma ^{i}_{T,R}\approx \Gamma ^{i}_{T}\approx 0.16 T , \end{aligned}$$

(3.42)

and for the thermal masses we use [120]

$$\begin{aligned}&\left( m_{T,R}^q\right) ^2 = \left( \frac{g_1^2}{18} + \frac{g_3^2}{6} + \frac{y_q^2}{8}\right) T^2 , \end{aligned}$$

(3.43)

$$\begin{aligned}&\left( \delta m^q\right) ^2 \equiv \left( m_{T,R}^q\right) ^2-\left( m_{T,L}^q\right) ^2 =\left( \frac{5 g_1^2}{96} - \frac{3g_2^2}{32} + \frac{y_q^2}{16}\right) T^2 , \end{aligned}$$

(3.44)

$$\begin{aligned}&\left( m_{T,R}^l\right) ^2 = \left( \frac{g_1^2}{8} + \frac{y_q^2}{8}\right) T^2 , \end{aligned}$$

(3.45)

$$\begin{aligned}&\left( \delta m^l\right) ^2 \equiv \left( m_{T,R}^l\right) ^2-\left( m_{T,L}^l\right) ^2 =\left( \frac{3 g_1^2}{32} - \frac{3g_2^2}{32} - \frac{y_q^2}{16}\right) T^2 , \end{aligned}$$

(3.46)

where q corresponds to the quark and l to the lepton type, respectively. The gauge couplings $g_i$ ($i=1,2,3$) are those of the SM gauge groups $\textrm{SU}(3)\times \mathrm {SU_L}(2)\times U(1)_Y$ and $y_q$ denotes the Yukawa coupling of the respective quark. For quarks, the difference of the left- and right-handed thermal masses is not significant and taking the limit of exactly degenerate masses in Eq. (3.40) would be a valid approximation. For leptons, however, this is not the case. Therefore, we expand Eq. (3.40) for small $\left( \delta m^i\right) ^2$ of quarks and leptons. As a second step we exploit $\Gamma _T \ll T$ allowing us to simplify Eq. (3.40) significantly, leading to

(3.47)

with the shorthand notation

$$\begin{aligned} \delta \omega = \frac{\left( \delta m\right) ^2}{2\sqrt{k^2+\left( m_R\right) ^2}} . \end{aligned}$$

(3.48)

Note that, for better readability, we again neglect the index i. The CP-conserving interactions $S_{CP}$ in Eq. (3.36) contain the Yukawa interaction rates, where we use the approximation of[133],

$$\begin{aligned} \Gamma _y^{\text {quark}} \approx 0.19 \alpha _s y_q^2 T \text {,}\,\quad \Gamma _y^{\text {lepton}}\approx 0.28\alpha _w y_{\tau }^2T , \end{aligned}$$

(3.49)

with the zero-temperature Yukawa couplings $y_q$ and $y_{\tau }$ of the quarks and $\tau$ leptons, respectively. $\alpha _s$ corresponds to the strong coupling and $a_w$ to the SU(2) coupling of the SM. The CP-conserving source term reads

$$\begin{aligned} S_{CP} = \Gamma ^+_M+ \mu _+ + \Gamma ^-_M \mu _- , \end{aligned}$$

(3.50)

with $\mu _\pm = \mu _L\pm \mu _R$ and the relaxation rates are given by[73]

$$\begin{aligned} \Gamma _M^{\pm ,(i)}&= \frac{6}{T^2}\cdot \frac{N_c}{2\pi ^2T}\vert f_i\vert ^2 \int \frac{k^2dk}{\omega _L\omega _R}\text{ Im }\nonumber \\&\quad \times \left[ -\frac{\left( h(\epsilon _L)\mp h(\epsilon _R^*)\right) }{\epsilon _R^*-\epsilon _L}\left( \epsilon _L\epsilon _R^*-k^2\right) \right. \nonumber \\&\quad \left. +\frac{\left( h(\epsilon _L)\mp h(\epsilon _R)\right) }{\epsilon _L+\epsilon _R}\left( \epsilon _L\epsilon _R+k^2\right) \right] , \end{aligned}$$

(3.51)

where h denotes the derivative of the Fermi–Dirac distribution given by

$$\begin{aligned} h(x) = \frac{\text {e}^{x}}{\left( \text {e}^x +1\right) ^2} . \end{aligned}$$

(3.52)

Note that the relaxation rate in Eq. (3.51) is actually rescaled due to the high temperature expansion of the chemical, potential

$$\begin{aligned} n = \frac{T^2}{6}\mu \kappa + \mathcal O(\mu _i^3) , \end{aligned}$$

(3.53)

that enters the transport equations, with n denoting the number density and $\kappa$ the statistical factor for fermions (F,$+$) and bosons (B,−), respectively¹⁰ [74], given by

$$\begin{aligned} \kappa (x) = \kappa _i(0) \frac{c_{F,B}}{\pi ^2} \int \limits _{m/T}^{\infty } dx \frac{x \text {e}^x}{\left( \text {e}^x\pm 1\right) ^2} \sqrt{x^2-m^/T^2} . \end{aligned}$$

(3.54)

As before, we apply the expansion in small mass differences $\left( \delta m\right) ^2$ and for $\Gamma _T\ll T$ in Eq. (3.51), simplifying the integration significantly,

$$\begin{aligned} \Gamma ^{-,(i)}_M&= \frac{6}{T^2}\cdot \frac{N_c}{2\pi ^2T}\vert f_i\vert ^2 \int \frac{ dk k^2 }{\omega ^2}\nonumber \\&\quad \times \left( -\frac{k^2}{\Gamma _T}+\frac{\omega ^2}{\Gamma _T} + \frac{k^2\Gamma _T}{\omega ^2} + \left( \frac{k^2}{\omega \Gamma _T}-\frac{2 k^2 \Gamma _T}{\omega ^3}\right) \delta \omega \right) h_f(\omega ) \nonumber \\&\quad +{{\mathcal {O}}}\left( \delta \omega ^2;\left( \frac{\Gamma _T}{T}\right) ^2;h_f^{\prime }\right) . \end{aligned}$$

(3.55)

Note that

$$\begin{aligned} \Gamma ^{+,(i)}\sim \left( \dots \right) \delta \omega \cdot h_f^{\prime }(\omega )+\mathcal O\left( \delta \omega ^2;\left( \frac{\Gamma _T}{T}\right) ^2;h_f^{\prime }\right) \;.\nonumber \\ \end{aligned}$$

(3.56)

We drop $\Gamma ^{+,(i)}$ for simplicity and also to be consistent with Ref. [121] which we follow for the formulation of the full set of transport equations [121]. The net number density, i.e. the number density of particles minus antiparticles, is denoted as follows

$$\begin{aligned}&n_q = n_{t_L} + n_{b_L} , \quad n_t = n_{t_R} , \quad n_b = n_{b_R} , \end{aligned}$$

(3.57a)

$$\begin{aligned}&n_l = n_{\nu _L} + n_{\tau _L} , \quad n_{\tau } = n_{\tau _R} , \quad n_{\nu } = n_{\nu _L} , \end{aligned}$$

(3.57b)

$$\begin{aligned}&n_{h_k} = n_{h^0_k}+n_{h^{\pm }_k} , \end{aligned}$$

(3.57c)

where $n_{X_{L/R}}$ is the distribution function of the left- or right-handed particle species X. The index k denotes the doublets $\phi _k = (h_k^{\pm },h_k^0)$. The strong sphaleron rate allows us to relate the densities of the light quarks via

$$\begin{aligned} n_{q_1} = n_{q_2} = -2 n_u = - 2 n_d = -2 n_s = -2n_c , \end{aligned}$$

(3.58)

so that only one of them needs to be considered, which we choose to be $n_u$. Note that the distribution functions are used and not the chemical potentials. The question of which interactions should be included in the transport equations depends on the timescale of the diffusion process. By assuming the two-step approach, first the generated left-handed asymmetry in front of the bubble wall is calculated and in the second step this asymmetry is translated to the actual baryon asymmetry via an electroweak sphaleron transition. The diffusion system is then given by [121]

(3.59a)

(3.59b)

(3.59c)

(3.59d)

$$\begin{aligned}&\partial _{\mu }j_{\nu }^{\mu } = 0 , \end{aligned}$$

(3.59e)

(3.59f)

$$\begin{aligned}&\partial _{\mu }j_{h_k}^{\mu } = + \Gamma _y^{(t)} \mu _Y^{(t)} -\Gamma _y^{(b)}\mu _Y^{(b)} + \Gamma _y^{(u)}\mu _Y^{(u)}-\Gamma _y^{(\tau )}\mu _Y^{(\tau )} , \end{aligned}$$

(3.59g)

$$\begin{aligned}&\partial _{\mu }j_u^{\mu } = + \Gamma _{ss} \mu _{ss} , \end{aligned}$$

(3.59h)

with the Yukawa rates $\Gamma _y^{(i)}~\left( i=t,b,\tau \right)$, the relaxation rates $\Gamma _M^{(i)}$ (defined as $\Gamma ^{-,(i)}_M$ in Eq. (3.51)), the strong sphaleron rate

$$\begin{aligned} \Gamma _{ss} = 14 \alpha _s^4 T_c , \end{aligned}$$

(3.60)

and the respective source terms . Note that the light leptons decouple completely from the system, since there is no corresponding strong sphaleron interaction. It is also possible to neglect the $\tau$ lepton in the system of transport equations by setting the associated Yukawa rates to zero. Analogously, the bottom quark can be decoupled. Assuming $m_b\approx 0$ one can then also drop u in the system of transport equations due to the relation $u=b$ for massless bottom quarks. The rescaled chemical potentials in Eq. (3.59) are given by

$$\begin{aligned} \mu _M^{(t)}&=\left( \frac{n_t}{\kappa _t} - \frac{n_q}{\kappa _{q}}\right) , \nonumber \\ \mu _Y^{(t)}&= \left( \frac{n_t}{\kappa _t}-\frac{n_q}{\kappa _q}-\sum _k\frac{h_k}{\kappa _{h_k}}\right) , \end{aligned}$$

(3.61a)

$$\begin{aligned} \mu _M^{(b)}&= \left( \frac{n_b}{\kappa _b} - \frac{n_q}{\kappa _{q}}\right) , \nonumber \\ \mu _Y^{(b)}&= \left( \frac{n_b}{\kappa _b}-\frac{n_q}{\kappa _q}+\sum _k\frac{h_k}{\kappa _{h_k}}\right) , \end{aligned}$$

(3.61b)

$$\begin{aligned} \mu _M^{(\tau )}&= \left( \frac{n_{\tau }}{\kappa _\tau } - \frac{n_l}{\kappa _{l}}\right) , \nonumber \\ \mu _Y^{(\tau )}&= \left( \frac{n_{\tau }}{\kappa _\tau }-\frac{n_l}{\kappa _l}+\sum _k\frac{n_{h_k}}{\kappa _{h_k}}\right) , \end{aligned}$$

(3.61c)

$$\begin{aligned} \mu _{ss}&= \left( \frac{2 n_q}{\kappa _q} -\frac{n_t}{\kappa _t} - \frac{n_b}{\kappa _b}-\frac{8 n_u}{\kappa _{L}}-\frac{4 n_u}{\kappa _R}\right) , \end{aligned}$$

(3.61d)

where the statistical factor $\kappa _i$ is defined in but: Eq. (3.54). Note that $\kappa _{L/R}$ refers to left-/right-handed massless quarks, respectively. Using Eq. (3.37) allows us to express the system of transport equations in Eq. (3.59) as a system of second order coupled differential equations (ODE). The ODE is solved by using the C++ library Boost::Odeint[134] which we embedded in the BSMPT framework. For technical details of the numerical solution of the ODE we refer to [66].

The solution of the quantum transport equations given in Eq. (3.59) allows us to calculate the produced BAU in a second step. In this second step, the thermalization of the left-handed excess in front of the bubble to baryons through sphaleron transitions has to be solved. The thermal system is described by the differential equation [121]

$$\begin{aligned} -v_W n_B^{\prime } - D n_B^{\prime \prime } =- N_f \Gamma _{ws}\left( \mu _{ws}+\mu ^0_{ws}\right) , \end{aligned}$$

(3.62)

with the bubble wall velocity $v_W$, the baryon asymmetry distribution function $n_B$, the diffusion constant D, the family number $N_f$ and the electroweak sphaleron transition rate $\Gamma _{ws}$. The chemical potentials in the last bracket split into two parts. The first part describes the chemical potentials of the left-handed fermions which are dynamically produced during the thermalization. The second part $\mu _{ws}^0$ denotes the initial condition, which biases the electroweak sphaleron transitions in the first place. Hence, the initial condition $\mu _{ws}^0$ is given by the sum of all left-handed fermionic chemical potentials of the solution of Eq. (3.59)

$$\begin{aligned} \mu _{ws}^0= & {} \sum _{\text {fam.}}\left( 3\mu _{q_L}+\mu _{l_L}\right) =\sum _{\text {fam.}}\left( \frac{6}{T^2}\right) \left( 3~\frac{n_{q_L}}{\kappa _q}+\frac{n_{l_L}}{\kappa _l}\right) \nonumber \\\simeq & {} \frac{1}{2}\left( \frac{6}{T^2}\right) \sum _\text {fam.}\left( n_{q_L}+n_{l_L}\right) \equiv \frac{1}{2}\left( \frac{6}{T^2}\right) n_L^0 . \end{aligned}$$

(3.63)

Note that we applied the high-temperature expansion for the chemical potentials to use the particle distribution functions $n_x$. The factor is absorbed in the transition rate. In the second step, we used the zero-temperature statistical factors for quarks and leptons, respectively. Since the strong sphaleron rate is large compared to the electroweak sphaleron transition rate, the involved chemical potentials of the left- and right-handed quark can be related to each other,

$$\begin{aligned} 0=\mu _{ss} \sim \sum _{\text {fam.}}\left( n_{q_L}-n_{u_R}-n_{d_R}\right) . \end{aligned}$$

(3.64)

This allows us to relate the baryon asymmetry $n_B$ with the left-handed quark density as

$$\begin{aligned} n_B = \frac{2}{3}\sum _\text {fam.}n_{q_L} . \end{aligned}$$

(3.65)

Since electroweak sphaleron transitions conserve $B-L$, the baryon asymmetry can be related with the left-handed lepton density

$$\begin{aligned} n_B = \sum _\text {fam.} n_{l_L} , \end{aligned}$$

(3.66)

which finally allows us to formulate the differential equation for the BAU

$$\begin{aligned} -v_W n_B^\prime - D n_B^{\prime \prime } = -{\tilde{\Gamma }}_{ws} \left( \frac{3}{2}n_L^0 + {\mathcal {R}} n_B\right) , \end{aligned}$$

(3.67)

with the SM relaxation term . The Eq. (3.67) can be solved numerically with the help of BSMPT v2, where we use for the rescaled electroweak sphaleron transition rate

$$\begin{aligned} {\tilde{\Gamma }}_{ws} = 6\cdot \kappa \alpha _w^5 T_c , \end{aligned}$$

(3.68)

with the electroweak gauge coupling $\alpha _w$ and some numerical prefactor $\kappa$ of the order one. This value has a rather large theoretical error and is determined to be [135, 136]

$$\begin{aligned} \kappa = 29\pm 6 . \end{aligned}$$

(3.69)

Assuming a z-dependent sphaleron rate as in Eq. (3.34) we obtain in the limit $4D\Gamma _{ws}\mathcal{R} \ll v_W^2$ for the BAU [121]

$$\begin{aligned} \eta = - \frac{3\Gamma _{ws}}{2v_W s} \int _0^\infty dz n_L (z) \gamma (z) \exp \left( - \frac{\mathcal{R} \Gamma _{ws}}{v_W} \int _{-\infty }^z dz^\prime \gamma (z^\prime ) \right) \;. \nonumber \\ \end{aligned}$$

(3.70)

4 Numerical analysis

The main goal of our analysis is to investigate how the two different approaches applied in the literature to compute the BAU compare to each other and what are the crucial parameters that influence the possible size of $\eta$. We furthermore want to understand how the requirement of a strong first order EWPT combined with the strict experimental constraints on the still allowed CP violation interacts with the goal to generate a BAU compatible with the observations. Before we present our results, however, we first give the details of our parameter scan.

4.1 Minimisation of the effective potential

For the numerical determination of the strength of the phase transition $\xi _c$, we use BSMPT v2.2 [66] which extends BSMPT [59] by the computation of the electroweak baryogenesis in the C2HDM¹¹, and we extend the C2HDM parameter scan discussed in [64]. The search for parameter points that provide a strong first order EWPT, that are compatible with the Higgs data and that simultaneously produce the correct amount of baryon asymmetry is a non-trivial task so that we had to increase significantly the amount of scanned points compared to the scan performed in [64]. Since the numerical determination of $\xi _c$ is not the main emphasis of this paper we refer to [35, 50, 64] for the detailed discussion of the impact of the requirement of a strong first order EWPT on the collider phenomenology.

Table 2 Parameter ranges for the C2HDM TI input parameters used in ScannerS

Table 3 Parameter ranges for the C2HDM TII input parameters used in ScannerS

4.2 Constraints and parameter scan

In the following we list the numerical values of the input parameters used in the analysis where we focus on the C2HDM Type I (TI) and II (TII). In the parameter scan, one of the neutral Higgs bosons, called h in the following, is required to have a mass of $m_h=125.09~\text {GeV}$ [20] and behave SM-like. The remaining two neutral Higgs bosons will be denoted as $h_{\downarrow }$ and $h_{\uparrow }$, where $m_{h_{\downarrow }}<m_{h_{\uparrow }}$. We explicitly allow for all three possible mass hierarchies

$$\begin{aligned} \text {M}_{\text {I}}:\quad&m_h<m_{h_{\downarrow }}<m_{h_{\uparrow }}, \end{aligned}$$

(4.1a)

$$\begin{aligned} \text {M}_{\text {II}}:\quad&m_{h_{\downarrow }}<m_h<m_{h_{\uparrow }}, \end{aligned}$$

(4.1b)

$$\begin{aligned} \text {M}_{\text {III}}:\quad&m_{h_{\downarrow }}<m_{h_{\uparrow }}<m_h , \end{aligned}$$

(4.1c)

The scan ranges for the input parameters of the C2HDM TI are given in Table 2 and for the C2HDM TII in Table 3.

As for the remaining SM parameters, we use the fine structure constant taken at the Z boson mass scale [137, 138],

$$\begin{aligned} \alpha _{\text {EM}}^{-1}(M_Z^2) = 128.962 \;, \end{aligned}$$

(4.2)

and the masses for the massive gauge bosons are chosen as [137, 138]

$$\begin{aligned} m_W = 80.385~\text {GeV}\quad \text {and }\quad m_Z=91.1876~\text {GeV}. \end{aligned}$$

(4.3)

The lepton masses are set to [137, 138]

$$\begin{aligned} m_e=0.511~\textrm{MeV},\quad m_{\mu }=105.658~\textrm{MeV},\quad m_{\tau } = 1.777~\text {GeV}, \end{aligned}$$

(4.4)

and the light quark masses to [138]

$$\begin{aligned} m_u = m_d = m_s = 100~\textrm{MeV} . \end{aligned}$$

(4.5)

To be consistent with the CMS and ATLAS analyses, we take the on-shell top quark mass as [138, 139]

$$\begin{aligned} m_t = 172.5~\text {GeV}\, \end{aligned}$$

(4.6)

and the recommended charm and bottom quark on-shell masses [138]

$$\begin{aligned} m_c=1.51~\text {GeV}\quad \text {and} \quad m_b = 4.92~\text {GeV}. \end{aligned}$$

(4.7)

We choose the complex parametrisation of the CKM matrix [137, 140]

$$\begin{aligned}{} & {} V_{\text {CKM}}\nonumber \\{} & {} \quad = \begin{pmatrix} c_{12}c_{13} &{} s_{12}c_{13} &{} s_{13}\text {e}^{-\textrm{i}~\delta }\\ -s_{12}c_{23}-c_{12}s_{23}s_{13}\text {e}^{\textrm{i}~\delta } &{} c_{12}c_{23}-s_{12}s_{23}s_{13} \text {e}^{\textrm{i}~\delta } &{} s_{23}c_{13}\\ s_{12}s_{23}-c_{12}c_{23}s_{13}\text {e}^{\textrm{i}~\delta } &{} - c_{12}s_{23}-s_{12}c_{23}c_{13}\text {e}^{\textrm{i}~\delta } &{} c_{23}c_{13} \end{pmatrix} ,\nonumber \\ \end{aligned}$$

(4.8)

where $s_{ij}=\sin \theta _{ij}$ and $c_{ij}=\cos \theta _{ij}$. The angles are given in terms of the Wolfenstein parameters

$$\begin{aligned} s_{12} = \lambda ,\quad s_{13}\text {e}^{\textrm{i}~\delta } = A \lambda ^3\left( \rho +\textrm{i}~\eta \right) ,\quad s_{23} = A \lambda ^2 , \end{aligned}$$

(4.9)

with [64]

$$\begin{aligned} \lambda =0.22537 ,\quad A =0.814 \quad \rho = 0.117\quad \eta = 0.353 . \end{aligned}$$

(4.10)

Note that we take into account a complex phase $\delta$ in the CKM matrix as an additional source for CP violation. The impact of the complex CKM phase compared to that of the complex phase induced by the VEV configuration is negligible, however. Finally, the electroweak VEV is set to

$$\begin{aligned} v=1/\sqrt{\sqrt{2}G_F}=246.22~\text {GeV}. \end{aligned}$$

(4.11)

The parameter points under investigation have to fulfil experimental and theoretical constraints. For the generation of such parameter points we use the C++ program ScannerS v2.0.0 [141,142,143,144]. ScannerS allows us to check for boundedness from below of the tree-level potential and uses the tree-level discriminant of [145] to ensure the electroweak vacuum to be the global minimum at tree level. By using BSMPT it is also possible to check for the NLO electroweak vacuum to be the global minimum of the potential. Only parameter points providing a stable NLO electroweak vacuum at zero temperature are taken into account for the analysis. We furthermore demand an approximated NLO unitarity as described in Ref. [64]. To be consistent with recent flavour constraints, we test for the compatibility with ${\mathcal {R}}_b$ [146, 147] and $B\rightarrow X_s \gamma$ [147,148,149,150,151] in the $m_{H^{\pm }}-\tan \beta$ plane. For the C2HDM TII, this implies that the charged Higgs mass has to be above 580 GeV [151] whereas in the C2HDM TI this bound is much weaker and is strongly correlated with $\tan \beta$. CP violation is severely constrained by the electric dipole moment (EDM) measurements. ScannerS checks for compatibility with the EDMs [152] where the most stringent limit is provided by the ACME Collaboration [153]. The compatibility with the Higgs measurements is taken into account by ScannerS through HiggsBounds [154,155,156] and HiggsSignals [157]. For the parameter scan the versions HiggsBounds5.7.1 and HiggsSignals2.4.0 are used. For the determination of the strength of the EWPT and the actual calculation of the BAU we use our new code BSMPT v2.2 [66]. For this analysis, we chose in the counterterm potential, cf. Eq. (2.20), $t_1=0$ and $t_2$ such that for the counterterms $\delta \text{ Im } \lambda _{6,7}$ we have $\delta \text{ Im } \lambda _{6}=\delta \text{ Im } \lambda _{7}$.¹² The wall velocity which is an input parameter in BSMPT v2.2 is set as

$$\begin{aligned} v_W = 0.1 \;. \end{aligned}$$

(4.12)

Altogether we found 186 parameter points that fulfil all experimental and theoretical constraints and simultaneously provide a strong first order EWPT. We start the analysis with the discussion of the additional counterterms, followed by the discussion of the found BAUs in the FH and VIA approaches. Afterwards, we investigate the impact of the chosen bubble wall velocity and finally, we take the full sample of parameter points in our analysis and compare both approaches applied in the computation of the BAU.

4.3 Discussion of the counterterms

We start by discussing the influence of the radiatively generated counterterms $\delta \text{ Im } \lambda _{6,7}$. In Fig. 2 we plot the size of $\delta C \equiv \delta \text{ Im } \lambda _6 = \delta \text{ Im } \lambda _7$ for all points of our parameter scan that fulfil the described constraints and have $\xi _c \ge 1$, as a function of $|\text{ Im } \lambda _5|$. The colour code indicates the size of $|\text{ Im }(m_{12}^2)|$ in GeV$^2$. The plot clearly shows that the new counterterm scales with the imaginary parts of $\lambda _5$ and $m_{12}^2$ and thus with the complex phase allowing for explicit CP-violation. In the CP-conserving limit these imaginary parts would vanish so that no flavour violation is generated radiatively and hence no such counterterms would be required.¹³ We also checked different choices of the free parameter $t_2$ relevant for the determination of $\delta \text{ Im } \lambda _{6,7}$, cf. Eqs. (2.25a)–(2.25p), by setting e.g. $\delta \text{ Im } \lambda _6=0$, and found that the overall behaviour of the results remained basically the same. The default setting of BSMPT v2.2 is hence $t_1=0$ and $t_2$ such that $\delta \text{ Im } \lambda _6 = \delta \text{ Im } \lambda _7$, which can be changed, however, by the user if desired. We finally remark that since our renormalisation scheme is set up such that the Higgs masses and mixing remain at their tree-level values no dangerous FCNCs are induced at tree level through the loop-corrected potential.¹⁴

Fig. 2

The absolute value of the counterterm $\delta C \equiv \delta \text{ Im } \lambda _6 = \delta \text{ Im } \lambda _7$ for all points passing our constraints with $\xi _c\ge 1$ as function of $|\text{ Im } \lambda _5|$. The colour code denotes the size of $|\text{ Im }(m_{12}^2)|$ in GeV$^2$

4.4 The amount of generated baryon asymmetry

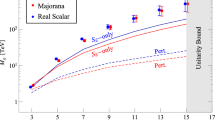
In Fig. 3 we show the computed generated baryon asymmetry $\eta$ for our allowed scan points in type 1, denoted TI, (violet points) and type 2, denoted TII, (green triangles) in the FH and in the VIA approach, both normalised to the observed baryon asymmetry $\eta _{\text {obs}}$. In the VIA approach the massive t, b and $\tau$ contributions are taken into account. The impact of the different inclusions will be discussed later. We first remark that both approaches for the derivation of the quantum transport equations are correlated in the sense that they predict the largest BAU for the same parameter points. However, the VIA method predicts BAU values that are two to three orders of magnitude larger than those obtained in the FH method. This issue has been discussed in the literature [81] leading to some criticism with respect to the validity of the approximations made in the VIA method. It was argued that the expansion applied in the derivation of the source term for the top quark might break down because of the large top quark mass [81, 120]. This might be the reason why it is possible to generate such large values in comparison to the FH method for the BAU. Still, also in the VIA method for the parameter points passing the constraints of our scan the obtained BAU is not compatible with the observed value. We did not find any benchmark point that provides the sufficient amount of BAU together with a small bubble wall velocity within the FH or the VIA approach.

Fig. 3

BAUs in the FH approach versus the VIA approach, including t, b and $\tau$ contributions in the latter, both normalised to the observed value. Results for the C2HDM TI are shown as violet points, those for the C2HDM TII as green triangles

In a recent work [82] published after the finalization of our manuscript, it was argued that the source term of the VIA method vanishes at LO. Since the LO appearance of the VIA source generates larger asymmetries, its vanishing could hence move the results of the VIA and the FH approach closer to each other. We show below that the BAU of the VIA approach lies up to several orders of magnitude above the one of the FH approach. In order to show and investigate the impact of the new findings, however, one would have to implement the resulting transport equations for the case of the vanishing LO source term. This would also nessecitate the calculation of the source term at NLO and the adaption of the transport equations to account for NLO effects. Only then, we could investigate the impact and compare the two methods and make meaningful statements. This is far beyond the present paper, however. Without being able to comment on this further, we point out to the reader that the results presented for the VIA method should be taken with caution, if the recent findings of [82] can be seen in an upgraded future study with BSMPT. The actual size of the baryon asymmetry found in the VIA approach would be changed. We believe, however, that the dependence of the BAU on the parameters would show a similar behaviour as discussed later in the paper. We find below that it is in the VIA method along the same lines as in the FH method. Furthermore, toy models with additional source terms can mimic the effects of additional source terms at NLO which are discussed here for the SM fermion content at LO. For discussions of the impact of additional fermion sources see e.g. [121, 159]. The exact dependence requires, however, the NLO analysis. While the numerical impact of the new insights of [82] cannot be judged by us, our analysis of the LO dependence of the VIA results can still pinpoint directions in model building such that the proper treatment at NLO leads to a sufficient amount of BAU.

When we compare both types of C2HDM we see that in type 2 we have a constant ratio between both approaches while type 1 shows a stronger difference in the FH and VIA results. Overall, however, the results in both C2HDM types are rather similar so that in the following we will discuss both types of C2HDM together.

Table 4 Input parameters of the benchmark point BMPI discussed in Sect. 4.5: the parameter point is defined for the C2HDM TI

Fig. 4

BMPI: BAU normalised to the observed value obtained in the FH approach (left) and in the VIA approach (right) as function of the wall velocity $v_W$. Results are shown in the VIA approach for the inclusion of the t, b and $\tau$ contributions (violet points), of the t and b contributions (blue triangles), and of the t contributions only (green triangles)

4.5 Dependence on the bubble wall velocity

As stated above, we set $v_W=0.1$ in our scans. Here now, we want to discuss the dependence of the BAU on $v_W$ in both approaches. For this we choose a specific benchmark point out of our sample of allowed scan points. The input parameters for this point, called BMPI in the following, are listed in Table 4. For this point we have a critical VEV and temperature of 234.401 GeV and of 211.237 GeV, respectively, and hence $\xi _c=1.1096$. The complex phase of the top quark mass is $\theta _t =15.641$, the wall thickness $L_W=0.0177~\text {GeV}^{-1}$ and $L_W T_c=3.744\gg 1$. Starting from this benchmark point we vary $v_W$ while keeping all parameters fixed and compute the corresponding BAU.

The result is shown in Fig. 4 which depicts the BAU in the FH approach (left) and in the VIA approach right, both normalised to the observed BAU as a function of $v_W$. In the VIA approach we show results for the case where the massive t, b and $\tau$ contributions are taken into account in the transport equations (violet points), where only t and b are included (blue triangles), and with t contributions solely (green triangles).

As can be inferred from the left plot, the FH approach exhibits a mild dependence on $v_W$ for small $v_W$. The FH approach uses an explicit expansion for small wall velocities and is only valid in this regime. The mild dependence on $v_W$ ensures that the choice of the input value for $v_W$ does not impact the resulting BAU significantly. If the bubble wall velocity approaches the plasma sound speed $v_W \approx 1/\sqrt{3}$, however, the BAU predicted in the FH approach, first rises steeply and then plummets. Recently it was found by the authors of [81] by re-deriving the fluid equations without making the approximation of small $v_W$ that the sound speed barrier can safely be crossed. In this context, also some mistakes in the previous derivation of the FH approach were pointed out. Their numerical comparison of both old and new results showed that they agree for small wall velocities and deviate by less than 30% for $v_W=0.1$ in the predicted BAU, which is also the wall velocity that we use in our analysis. The new approach will be implemented in the next upgrades of BSMPT v2.2. The VIA method shows a similarly mild dependence on $v_W$ as the FH approach. The VIA method does not apply an expansion in small $v_W$, but assumes small velocities, so that the choice of $v_W=0.1$ is reasonable.

4.6 Wall thickness and mass scale

As discussed in Sect. 3, the FH ansatz works for thick bubble walls. With the typical particle wavelength in the plasma given by the inverse temperature $T^{-1}$ this implies the requirement

$$\begin{aligned} 1 \ll L_W T_c \;. \end{aligned}$$

(4.13)

In Fig. 5, we see for the allowed C2HDM TI and TII points the values of $L_W T_c$ as a function of the average mass scale

$$\begin{aligned} {\overline{m}} = \frac{1}{4} \left( \sum _{i_=1}^3 m_{H_i} + m_{H^\pm } \right) \;. \end{aligned}$$

(4.14)

The colour code denotes the values of the critical temperature $T_c$. Apart from a few outliers, there are two regions in the plot, given by small average mass values with $2.7 \lesssim L_W T_c \lesssim 11.5$ on the one hand and larger average mass values where $3.7 \lesssim L_W T_c \lesssim 17.9$. While both lighter and heavier spectra can lead to $L_W T_c$ large enough such that the FH approach can be applied we find more parameter points in regions with light mass spectra and low $L_W T_c$.

Fig. 5

$L_W T_c$ versus the average mass scale ${\overline{m}}$ (definition, see text) for the allowed C2HDM TI and TII parameter points. The colour code denotes the critical temperature $T_c$

4.7 Scaling behaviour of both approaches

Important parameters for successful baryogenesis and for the approaches used in the computation are the complex phase $\theta _t$ of the top quark mass, the strength of the phase transition $\xi _c$, and $L_W T_c$. The phase $\theta _t$ indicates the amount of CP violation which is required for electroweak baryogenesis. The source terms in the transport equations are proportional to the phase factor. The strength $\xi _c$ of the phase transition can be viewed as a parameter describing the dynamics of the phase transition. Its importance has been discussed in the literature (see e.g. [70]). A stronger EWPT, i.e. larger $\xi _c$, is expected to produce more BAU. The bubble wall thickness times the critical temperature, $L_W T_c$, is required to be large for the FH method to be applicable. The wall thickness $L_W$ itself is used for the parametrisation of the bubble wall profile and can be understood as a parameter describing the state of the bubble. The bubble wall dynamics is given by the wall velocity $v_W$, which we have set, however, to a fixed value, $v_W=0.1$, for all of our parameter points.

Fig. 6

Normalised BAU in the FH approach (left) and the VIA$-\tau$ approach (right) as a function of the tuning parameter combination $(\theta _t \xi _c L_W T_c)$ for the allowed parameter points. The colour code indicates the average mass scale ${\overline{m}}$

In Fig. 6 the normalised BAU is shown for our allowed C2HDM TI and TII points as function of the tuning parameter combination $(\theta _t \xi _c L_W T_c)$ for the FH approach (left) and the VIA$-\tau$ approach, i.e. including massive t, b and $\tau$ contributions, (right). The colour code indicates the size of the average mass scale ${\overline{m}}$. In both approaches the BAU clearly increases with rising $\theta _t \xi _c L_W T_c$. We also see that larger values of BAU are obtained for a larger average mass scale ${\overline{m}}$.

The insights that we have gained so far allow us to discuss in more detail what are the limiting factors in obtaining a large enough BAU. A prerequisite for successful BAU is a $\xi _c$ above one. The influence of $\xi _c$ on $\eta$ should not be too strong here, as all $\xi _c$ values that we could obtain in accordance with the applied constraints range only between 1 and at most 1.62. The baryon-antibaryon asymmetry is found to increase with the CP-violating phase as expected so that we need a large CP-violating phase for sufficient generation of a baryon-antibaryon asymmetry. The CP-violating phase, however, is severely constrained by the EDM measurements. Furthermore, an overall heavier spectrum is advantageous for the amount of BAU as we have just seen. On the other hand a strong first order EWPT favours a Higgs mass spectrum where the Higgs bosons are close to each other in the intermediate mass range [50, 64] and hence mix strongly. Constraints from the oblique S, T, U parameters force the charged Higgs mass to be degenerate with one of the neutral Higgs bosons and constrain large mass differences between Higgs states that are considerably mixed so that scenarios with large mass gaps cannot be realized. Moreover, we have seen that while large values of $L_W T_c$ as required in the FH ansatz can be realized, a lot of parameter points gather around low $L_W T_c$ for an overall light mass spectrum. These contradictory requirements on the overall Higgs mass spectrum may explain why it is difficult to reach large enough BAU.

Fig. 7

BAU in the FH approach (left) and the VIA$-\tau$ approach (right) as a function of $L_W T_c$ for the allowed parameter points and $h_1$ being the SM-like Higgs boson $h_{\text {SM}}$ (violet dots), $h_2$ being SM-like (dark-green triangles), and $h_3=h_{\text {SM}}$ (green crosses)

The only parameter to be discussed with respect to the amount of BAU is $L_W T_c$ which we will do next. Figure 7 shows the dependence of the BAU in the FH approach (left) and the VIA$-\tau$ approach (right) normalised to the observed value as a function of $L_W T_c$ for the allowed parameter points. The colour and shape code indicates which of the three neutral Higgs bosons is the SM-like one. Both for FH and VIA$-\tau$ we have a larger BAU in the case of $h_1$ being SM-like and for $L_W T_c$ being larger, i.e. $L_W T_c \gtrsim 5$. Actually, both approaches show a similar dependence on $L_W T_c$ indicating an agreement in the diffusion description of both approaches with the FH approach predicting less BAU, however. This can also be inferred from Fig. 8 which shows the ratio of the BAU in the FH approach and in the VIA$-\tau$ approach as a function of $L_W T_c$ for the allowed parameter points. Their ratio varies by somewhat more than one order of magnitude at most. For all three possible mass orderings we find parameter points, where $L_W T_c$ is large for this mass ordering and where both methods can be applied.

4.8 The effect of additional fermions

In Fig. 9 we display, for the allowed points, the ratio of the baryon asymmetry computed in the VIA$-t$ approach where only the top quark has been included and the one computed in the VIA$-\tau$ approach with the top, bottom and $\tau$ contributions included in the transport equations. The left plot shows the ratio as function of $L_W T_c$ and the right one shows the ratio as function of $L_W$. The colour code indicates the critical temperature. The inclusion of additional fermions can have an increasing effect on $\eta$ for $L_W \gtrsim 0.02~\text {GeV}^{-1}$. As we have fixed the bubble wall velocity and thereby the diffusion timescale, respectively, the diffusion length scale, the only length scale in the system that can be different in the parameter points is the wall thickness. The wall thickness gives the length along which the bubble profile is changing. The varying Higgs profile triggers non-zero source terms so that in this region the diffusion process takes place. The additional massive particles ($\tau$ and bottom) with their respective source terms can hence produce more efficiently a left-handed asymmetry for thick bubble walls resulting in an enhanced BAU compared to the case where only the top quark contribution is taken into account. Unfortunately, the effect is tiny, however, for our parameter sample that is compatible with all allowed constraints. Note finally that the impact of different temperatures $T_c$ is marginal as can be seen by comparing the left and the right figure.

Fig. 8

Ratio of the BAU in the FH approach and in the VIA$-\tau$ approach as a function of $L_W T_c$ for the allowed parameter points and $h_1$ being the SM-like Higgs boson $h_{\text {SM}}$ (violet dots), $h_2$ being SM-like (dark-green triangles), and $h_3=h_{\text {SM}}$ (green crosses)

Fig. 9

Ratio between the BAU computed in the VIA$-t$ approach and the VIA$-\tau$ approach as a function of $L_W T_c$ (left) and $L_W$ (right) for all allowed parameter points. The colour code indicates the critical temperature $T_c$

5 Conclusions

In this paper we investigated the question if in principle it is possible to generate in the C2HDM a baryon asymmetry that is compatible with the observed value after taking into account all relevant theoretical and experimental constraints. For this we used the recent upgrade BSMPT v2.2 to calculate the BAU in two different approaches, the FH and the VIA approach. Our goal was to investigate differences and similarities of the two methods and in particular the dependence of the obtained value of $\eta$ on the various parameters that are relevant for the BAU in order to single out future directions for upgrades of the implementation and for model building.

We found that both approaches show the same overall behaviour in the sense that large BAU in the FH approach also yields large values in the VIA approach, with the $\eta$ values computed with FH being two to three orders of magnitude smaller that those obtained from VIA. The dependence on the wall velocity is mild in the FH approach for small $v_W$ but diverges for velocities near the sound speed. Recently, however, a re-derivation of the fluid equations showed that the sound speed barrier can be safely crossed [81]. While the results for $\eta$ in the old and new approach differ by less than 30% for $v_W=0.1$ the new results of [81] will be implemented in future upgrades of our code. The application of FH requires values of $L_W T_c > 1$. In our analysis we found that for parameter points compatible with the constraints large values of $L_W T_c$ can be realized both for lighter and heavier overall mass spectra with more points being found for lighter mass spectra and at low $L_W T_c$. It turns out, however, that an overall heavier mass spectrum is advantageous for the BAU. The combination of an SFOEWPT and the applied constraints on the other hand forbids large mass gaps. These findings explain why it is difficult to generate a large enough BAU in the C2HDM compatible with the observed values. Additionally, we need large CP-violating phases which is in contradiction with the strict constraints from the EDM measurements. As for the impact of $L_W T_c$, $\eta$ shows a similar behaviour in the FH and the VIA approach in the region of large values of $L_W T_c$. Towards smaller values the computed $\eta$ with the FH method slightly increases. Finally, we found that the inclusion of additional fermions besides the top quark in the transport equations in the VIA approach has a slightly increasing effect on $\eta$. This indicates that models with additional fermions might be advantageous for the BAU, a direction that we investigate in a forthcoming publication.

We point out that the investigations performed here were at LO in the VIA approach. The recent results of [82] published after the finalization of our manuscript, argued, however, that the source term of the VIA method vanishes at LO. The impact of this result on our findings cannot be judged without implementing the new findings. This nessecitates the calculation of the source term at NLO and the adaption of the transport equations to account for NLO effects, which is cleary beyond the scope of this paper. This would be a new publication on its own that we plan for the future. We hence point out to the reader, that the results of the VIA method should be taken with caution considering the recent findings.

Clearly, the requirement of an SFOEWPT, of a sufficiently large amount of CP violation and of compatibility with the stringent theoretical and experimental constraints challenges the generation of a BAU that is compatible with the observed value. However, the differences in the results of the calculations from the different methods applied as well as new insights in the derivation of the bubble wall velocity leave room for improvement of the computation of $\eta$. Together with possible avenues for model building to facilitate an SFOEWPT, to possibly generate CP violation spontaneously at non-zero temperature thus alleviating the EDM constraints, or to include new fermions e.g. to increase the obtained value for $\eta$, this gives ample room for further promising investigations in the context of the dynamical generation of the BAU through electroweak baryogenesis.