Production of double heavy quarkonia at super Z factory

Abstract

Within the color singlet model, we calculate the exclusive production of double charmonia, double bottomonia, and double $B_c$ mesons at future super Z factory. The two heavy quarkonia or $B_c$’s are either two S-wave Fock states ($^1S_0, ~^3S_1$), or one S-wave and one P-wave states ($^1P_1,~^3P_J~(J=0,1,2)$). The top three $Z^0$ propagated channels in cross sections for double charmonia are $\sigma {(J/\psi +h_c)}_{Z^0}=(454.0^{+39.1}_{-59.2})\times 10^{-5} fb, \sigma {(\eta _c+\chi _{c2})}_{Z^0}=(284.2^{+22.2}_{-35.3})\times 10^{-5} fb$, and $\sigma {(\eta _c+\chi _{c0})}_{Z^0}=(137.0^{+9.9}_{-16.4})\times 10^{-5} fb$. For double bottomonia, they are $\sigma {(\eta _b+\Upsilon )}_{Z^0}=(428.6^{+67.9}_{-60.9})\times 10^{-4} fb, \sigma {(\Upsilon +\chi _{b2})}_{Z^0}=(230.6^{+23.6}_{-22.2})\times 10^{-4} fb$, and $\sigma {(\Upsilon +\Upsilon )}_{Z^0}=(119.9^{+18.4}_{-16.6})\times 10^{-4} fb$. For double $B_c$ mesons, they are $\sigma {(B_c^{*+}+B_c^{*-})}_{Z^0}=(1150^{+87}_{-84})\times 10^{-3} fb$, $\sigma {(B_c^{*+}+\chi _{bc2}^-)}_{Z^0}=(1133^{-16}_{+22})\times 10^{-3} fb$, and $\sigma {(\eta _{bc}^++B_c^{*-})}_{Z^0}=(634.6^{+47.8}_{-45.8})\times 10^{-3} fb$. Here the uncertainties come from the varying masses of constituent heavy quarks, which bring up to 20% corrections. The cross sections of double $B_c$ mesons are roughly one order of magnitude larger than those of the double bottomonia, and two orders of magnitude larger than those of the double charmonia. To make it helpful for experimental study, we present the total cross sections $\sigma$ as functions of CM energy $\sqrt{s}$, $\sigma$ as functions of the renormalization scale $\mu$, the angle distributions $d\sigma /dcos\theta$, and the $p_T$ distributions $d\sigma /dp_{t}$. We also find that the initial state radiation can bring about 30–40% suppresions when 1%$m_Z$ energy is losing, and cross sections can increase by about 2–3 times or decrease by an order of magnitude when adopting different potential models which becomes the major source of uncertainty. The numerical results show that it might be not optimistic for the experimental observation, but it is still far from excluded at the FCC-ee and also the CEPC running in the Z factory mode.

1 Introduction

The Large Hadron Collider (LHC) provides a direct probe of the high energy frontier of particle physics. We also have the BESIII experiment at the BEPC running at the $\tau$-charm energy region and the Belle II experiment at the super KEKB running as a B factory. As a supplementary, we further need another electron-positron collider to make precise study on the $W^{\pm },~Z^0$, and Higgs physics running at proper energy regions. The Circular Electron Positron Collider (CEPC) provides three operation modes, corresponding to the Higgs factory running at center-of-momentum (CM) energy $\sqrt{s}=240$ GeV, the Z factory at $\sqrt{s}=91.2$ GeV, and the WW threshold scan around $\sqrt{s}\sim 160$ GeV. For the Z-factory mode, the CEPC would have the $Z^0$ event yields of $7\times 10^{11}$ [1]. The first stage of Future Circular Collider (FCC) is an electron-positron collider (FCC-ee), which would operate at the Z resonance for 4 years. It has even larger $Z^0$ event yields of $7\times 10^{12}$, since its total integrated luminosity is about nine times as that of CEPC [2]. The future electron-positron colliders would provide nice platforms for the precise study on $Z^0$ physics. Note that, the Electron Positron Linear Collider also has the similar GigaZ running mode [3], and a super Z factory has also been proposed by another Chinese group [4].

The production of heavy quarkonium is a multiscale problem for probing the quantum chromodynamics (QCD) theory. The heavy quarkonium is a bound state consisting of a heavy quark and a heavy antiquark, i.e. the $Q\bar{Q}^\prime$ ($Q,~Q^\prime = c$ or b quarks) bounding systems. The production of the heavy quarkonium has three different momentum scales: the heavy quark mass $\sim m_Q$, the momentum of the heavy quark or antiquark in the quarkonium rest frame $\sim m_Q v$, and the kinetic energy of the heavy quark or antiquark $\sim m_Q v^2$. Here, v is the relative velocity between the constituent heavy quark and antiquark in the quarkonium rest frame. The typical values are $v^2=0.1$ for $b\bar{b}$ quarkonium, and $v^2=0.3$ for $c\bar{c}$ quarkonium. Because of $m_Q \gg m_Q v \gg m_Q v^2$, the creation of the constituent $Q\bar{Q}^\prime$ pair can be calculated perturbatively, while the hadronization of $Q\bar{Q}^\prime$ pair to a physical color-singlet quarkonium is nonperturbative. So the production of heavy quarkonium has been a hot topic on exploring the QCD at both the perturbative and nonperturbative energy regions, which provides rich physics on strong interation. For more information on the current status of heavy quarkonium, please refer to some reviews [5,6,7,8,9].

Considering the fact that the constituent heavy quark and antiquark inside the quarkonium have the nonrelativistic nature, we can use the nonrelativistic QCD (NRQCD) factorization framework [10, 11] to factor the production of heavy quarkonium into the perturbative creation of the constituent $Q\bar{Q}^\prime$ pair and the nonperturbative hadronization of the heavy quark pair. The NRQCD factorization formulation consists of the short-distance coefficients and long-distance matrix elements. The short-distance coefficients stand for the hard creation of the heavy constituent $Q\bar{Q}$ pair and can be calculated perturbatively with the method of the Feynman diagrams. The long-distance matrix elements stand for the nonperturbative hadronization of the binding $Q\bar{Q}$ pair with definite $J^{PC}$ quantum numbers into the physical heavy quarkonium. Our calculation are in the color singlet model (CSM) [12,13,14], which require the intermediate $Q\bar{Q}$ pair and the final quarkonium have the same quantum numbers. Under this assumption, the long-distance matrix elements then can be related to the radial wave functions (or their derivatives) of the heavy quarkonium at the origin, which can be extracted from the decays of the quarkonim and can be calculated within the potential models [15,16,17,18,19,20,21,22,23,24] or potential NRQCD [25] or lattice QCD [26]. Thus there are no free nonperturbative parameters in CSM.

In the calculation of the short-distance coefficients in the NRQCD framework, the squared amplitudes become complicated and lengthy especially for the production of the P-wave quarkonium. To simplify the calculation, we adopt the “improved trace technology” [27,28,29,30,31,32], which is based on the helicity amplitude method. In which, the amplitudes have been expressed directly as the linear combinations of independent Lorentz structures before the polarization sum. This method helps a lot to overcome the problem of time-consuming calculation for the production of the P-wave quarkonium.

The production of double heavy quarkonia has been studied extensively both at the LHC and B factories. The hadronic production of double $J/\psi$ has always been a hot topic because $J/\psi$ can be very easy to be detected by its leptonic decays and this channel can be used to explore the distribution of gluons in a proton at the LHC [33,34,35,36,37,38,39,40]. In addition, the photoproduction of double $J/\psi$ [41], the production of double heavy quarkonia through diffractive interactions [42], the production of double heavy quarkonia through photon-photon interaction [43, 44], and the hadronic production of double $B_c$ mesons [45] have also been studied. The production of double heavy quarkonia through electron-positron annihilation has been widely explored at B factories. In particular, the production of $J/\psi + \eta _c$ at B factories once challenged the NRQCD framework. At the leading order (LO) within NRQCD formulation, its total cross section is about 2–6 fb [46,47,48]. However, the measurements at B factories by the Belle and BaBar collaborations show that the cross section is much bigger, around 20 fb [49, 50]. This large discrepancy between theory and experiment can be reduced by the QCD next-to-leading order (NLO) corrections [51, 52] and the relativistic corrections in the NRQCD [46, 53, 54]. Recently, this issue has been solved by the QCD next-to-next-to-leading corrections [55], which gives consistent estimate with the BaBar measurement.

The future Z factory is another platform to study the production of double heavy quarkonia through the $Z^0$ boson decays. Although these exclusive processes are rare, we have the advantages of the vast $Z^0$ events and the clear background provided by the fully reconstructed quarkonia at the electron positron collider running as a Z factory. This provide us another opportunity of studying the interplay between the perturbative and nonperturbative regimes in the hadronization of heavy quark pair into quarkonia. The production of the double charmonia at LO at such Z factory is discussed in Refs. [56, 57]. The QCD NLO corrections to the production of double charmonia are also studied [58, 59], which shows that NLO corrections are also important near the $Z^0$ mass pole. The QCD NLO corrections to the paired S-wave $B_c^{(*)}$ production are obtained, where the NLO corrections are small at $Z^0$ pole [60]. The associated S-wave charmonium-bottomonium production at LO at $Z^0$ pole are explored in Ref. [61]. In the present paper, we shall study the production of double charmonia, double bottomonia, and double $B_c$ mesons at the future Z factory, where the case of two S-wave ($^1S_0, ~^3S_1$) states and the case of one S-wave and one P-wave ($^1P_1, ~^3P_J$ ($J=0,1,2$)) states are considered. To make our work more helpful in future experimental researches, we shall discuss the dependences of cross sections on the center-of-momentum energy and the running renormalization scale, the differential angle distribution, the transverse momentum distribution, and the uncertainties caused by the masses of constituent heavy quarks and the radial wave functions (or their derivatives) of the heavy quarkonium at the origin.

The rest of this paper is organized as follows. In Sect. 2, we introduce the prescription of the production of double heavy quarkonium within the CSM framework. In Sect. 3, we first present the total cross sections, then discuss their differential distributions and the uncertainties. Section 4 is reserved for a summary.

Fig. 1

Feynman diagrams for electron positron annihilation into double heavy quarkonia or $B_c$’s through the virtual photon and $Z^0$ boson

2 Formulations

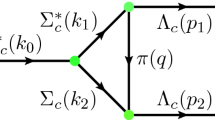
The Feynman diagrams for the exclusive production of double heavy quarkonia or $B_c$ mesons in $e^-(p_1) e^+(p_2) \rightarrow \gamma ^*/Z^0 \rightarrow H_1[n](q_1) + H_2[n^\prime ](q_2)$ are displayed in Fig. 1, where $H_{1(2)}$ represent the heavy quarkonia or $B_c$’s and $[n^{(\prime )}]$ represent the spin and orbit angular momentum states $[^1S_0], ~[^3S_1], ~[^1P_1]$, and $[^3P_J]$ ($J=0,1,2$). Here all the intermediated Fock states are in color singlet model (CSM). The differential cross sections can be factored into the short-distance coefficients and the long-distance matrix elements [10, 11],

$$\begin{aligned} d\sigma (H_1,H_2)= & {} d\hat{\sigma }((Q^\prime \bar{Q})[n]\nonumber \\ {}{} & {} +(Q\bar{Q^\prime })[n^\prime ]) {\langle \mathcal{O}[n] \rangle } {\langle \mathcal{O}[n^\prime ] \rangle }. \end{aligned}$$

(1)

The short-distance coefficients $\hat{\sigma }$ describe the short-distance production of two Fock states $(Q^\prime \bar{Q})[n]$ and $(Q\bar{Q^\prime })[n^\prime ]$ ($Q,~Q^\prime =c$ or b quarks) with the spin and orbit angular momentum states [n] and $[n^\prime ]$, respectively. In CSM, the non-perturbative long-distance matrix elements ${\langle \mathcal{O}[n^{(\prime )}] \rangle }$ describe the hadronization of the Fock state $(Q\bar{Q^\prime })[n^{(\prime )}]$ into the physical heavy quarkonia $H_{1(2)}$ in the same quantum states $[n^{(\prime )}]$.

The short-distance differential cross section $d\hat{\sigma }$ are perturbatively calculable,

$$\begin{aligned} d\hat{\sigma }=\frac{1}{4\sqrt{(p_1\cdot p_2)^2-m^4_{e}}} \overline{\sum } \big |\mathcal{M}([n],[n^\prime ])\big |^{2} d\Phi _2, \end{aligned}$$

(2)

where $\overline{\sum }$ stands for the average over the spin of the initial electron and positron, and sum over the color and spin of the two Fock states. In the $e^-e^+$ center-of-momentum (CM) frame, the two-body phase space can be simplified as

$$\begin{aligned} d{\Phi _2}= & {} (2\pi )^4 \delta ^{4}\left( p_1+p_2 - \sum _{f=1}^2 q_{f}\right) \prod _{f=1}^2 \frac{d^3{\vec {q}_f}}{(2\pi )^3 2q_f^0} \nonumber \\= & {} \frac{{\mid \vec {q}_1}\mid }{8\pi \sqrt{s}}d(cos\theta ). \end{aligned}$$

(3)

Here, $s=(p_1+p_2)^2$ stands for the squared CM energy. The magnitude of the 3-momentum ${|\vec {q}_1|}=\sqrt{\lambda [s, M^2_{1}, M^2_{2}] }/2\sqrt{s}$, where $M_{1(2)}$ are the masses of two heavy quarkonia $H_{1(2)}$ and $\lambda [a, b, c]= (a - b - c)^2 - 4 b c$. The $\theta$ is the angle between the momentum $\vec {p_1}$ of the electron and the momentum $\vec {q_1}$ of the quarkonium $H_1[n]$.

The hard scattering amplitude $\mathcal{M}([n],[n^\prime ])$ in Eq. (2) can be read directly from the Feynman diagrams in Fig. 1,

$$\begin{aligned} i\mathcal{M}([n],[n^\prime ])= \sum _{j=1}^4 \bar{v}_{l^\prime } (p_2) \mathcal{V}^\mu u_l (p_1) \mathcal{D}_{\mu \nu } \mathcal{A}^\nu _j, \end{aligned}$$

(4)

where j represents the number of Feynman diagrams, and $l^{(\prime )}$ are the spins of the initial leptons. The vertex $\mathcal {V}^\mu$ and the propagator $\mathcal {D_{\mu \nu }}$ for the virtual photon and $Z^0$ propagated processes have different forms,

$$\begin{aligned} \mathcal {V}^\mu= & {} \alpha ( -i e e_Q\gamma ^\mu ) + \beta \frac{-i g}{4 cos\theta _W} \gamma ^\mu (1-4 e_Q sin^2 \theta _W-\gamma ^5), \nonumber \\ \mathcal {D_{\mu \nu }}= & {} \alpha \frac{-i g_{\mu \nu }}{p^2} + \beta \frac{-i g_{\mu \nu }}{p^2-m^2_Z+i m_Z \Gamma _Z}. \end{aligned}$$

(5)

In which, $\alpha =1, \beta =0$ is for virtual photon propagated processes, and $\alpha =0, \beta =1$ is for $Z^0$ propagated processes. e is the unit of the electric charge, $e_Q=1,2/3,-1/3$ for the leptons, c quark, and b quark, respectively. g is the weak interaction coupling constant, and $\theta _W$ represents the Weinberg angle. $p=p_1+p_2$ is the 4-momentum of the propagator. $m_Z$ and $\Gamma _Z$ are the mass and the total decay width of $Z^0$ boson.

The explicit expressions of the Dirac $\gamma$ matrix chains $\mathcal{A}^\nu _j~(j=1,2,3,4)$ in Eq. (4) for the case that both two quarkonia or $B_c$’s are the S-wave states ($[^1S_0]$ , $[^3S_1]$) can be formulated as

(6)

Here, S and L are the spin and the orbit angular momentum of the Fock states $[n^{(\prime )}]$. $q_{11}=\frac{m_{Q_1}}{M_{1}}{q_1}+q$ and $q_{12}=\frac{m_{Q_1^\prime }}{M_{1}}{q_1}-q$ are the momenta of the two constituent heavy quarks of the quarkonium $H_1[n](q_1)$ with q being the relative momentum between them and $M_{1}=m_{Q_1}+m_{{Q}_1^\prime }$. $q_{21}=\frac{m_{Q_2^\prime }}{M_{2}}{q_2}+q^\prime$ and $q_{22}=\frac{m_{{Q}_2}}{M_{2}}{q_2}-q^\prime$ are the momenta of the two quarks of the quarkonium $H_2[n^\prime ](q_2)$ with $q^\prime$ being the relative momentum between them and $M_{2}=m_{Q_2^\prime }+m_{{Q}_2}$. The two projectors $\Pi ^{(S,L=0)}_{q_k}$ ($k=1, 2$) in Eq. (6) have the following forms

(7)

For spin-singlet state $[^1S_0]$, $\epsilon _a(q_k)=1$ and $\gamma ^a=\gamma ^5$; for spin-triplet state $[^3S_1]$, $\epsilon _a(q_k)=\varepsilon _{\alpha }(q_k)$ is its polarization vector and $\gamma ^a=\gamma ^\alpha$ is the Dirac matrix with Lorentz index $\alpha$. For the S-wave states, the relative momentum q and $q^{\prime }$ are set to zero directly. In CSM, $\delta _{ij}/\sqrt{N_c}$ is the color operator for color-singlet projector of the heavy quarkonium with $N_c=3$.

We shall consider the case that one of two quarkonia or $B_c$ mesons $H_2[n^\prime ](q_2)$ is a P-wave state ($[^1P_1]$, $[^3P_J~(J=0,1,2)]$). The expressions of $\mathcal{A}^\nu _j~(j=1,2,3,4)$ for this case can be expressed in those for both S-wave case,

$$\begin{aligned} \mathcal{A}^{\nu (S=0, L=1)}_j= & {} \varepsilon _\beta (q_2) \left. \frac{d}{d q^\prime _\beta } \mathcal{A}^{\nu (S=0, L=0)}_j \right| _{q=0,q^\prime =0}, \nonumber \\ \mathcal{A}^{\nu (S=1, L=1)}_j= & {} \varepsilon ^J_{\alpha \beta } (q_2)\left. \frac{d}{d q^\prime _\beta } \mathcal{A}^{\nu (S=1, L=0)}_j \right| _{q=0,q^\prime =0}. \end{aligned}$$

(8)

In which, $\varepsilon _\beta (q_2)$ is the polarization vector of the $[^1P_1]$ state, and $\varepsilon ^{J}_{\alpha \beta }(q_2)$ is the polarization tensor for $[^3P_J]$ states with $J=0,1,2$. The derivatives over the relative momentum $q^\prime _\beta$ of the quarkonium or $B_c$ meson $H_2[n^\prime ]$ will give complicated and lengthy amplitudes. The relative momentum $q^\prime$ is set to zero after taking the derivatives.

To get compact analytical expression of the complicated P-wave channels and also to improve the efficiency of numerical evaluation, we adopt the “improved trace technology” to simplify the amplitudes $\mathcal{M}([n],[n^\prime ])$ at the amplitude level before evaluating the polarization sum. To shorten this manuscript, we don’t present the prescription. For detailed techniques and examples, one can refer to the literatures [27,28,29,30,31,32].

When manipulating the squared amplitudes $|\mathcal{M}([n], [n^\prime ])|^{2}$ in Eq. (2), we need to sum over the polarization vectors of the heavy quarkonia. For the spin-triplet state $[^3S_1]$ or the spin-singlet state $[^1P_1]$ with 4-momentum p, the polarization sum is given by [11]

$$\begin{aligned} \sum _{J_z}\varepsilon _{\alpha } \varepsilon _{\alpha ^\prime } = \Pi _{\alpha \alpha ^\prime } \equiv -g_{\alpha \alpha ^\prime }+\frac{p_{\alpha } p_{\alpha ^\prime }}{p^2}, \end{aligned}$$

(9)

where $J_z=S_z$ or $L_z$ for $[^3S_1]$ and $[^1P_1]$ states, respectively. In the case of $[^3P_J]$ states, the polarization sum should be performed by the selection of appropriate total angular momentum quantum number J. The sum over polarization tensors is given by [11]

$$\begin{aligned} \varepsilon ^{0}_{\alpha \beta } \varepsilon ^{0*}_{\alpha ^\prime \beta ^\prime }= & {} \frac{1}{3} \Pi _{\alpha \beta }\Pi _{\alpha ^\prime \beta ^\prime }, \\ \sum _{J_z}\varepsilon ^{1}_{\alpha \beta } \varepsilon ^{1*}_{\alpha ^\prime \beta ^\prime }= & {} \frac{1}{2} (\Pi _{\alpha \alpha ^\prime }\Pi _{\beta \beta ^\prime }- \Pi _{\alpha \beta ^\prime }\Pi _{\alpha ^\prime \beta }), \\ \sum _{J_z}\varepsilon ^{2}_{\alpha \beta } \varepsilon ^{2*}_{\alpha ^\prime \beta ^\prime }= & {} \frac{1}{2} (\Pi _{\alpha \alpha ^\prime }\Pi _{\beta \beta ^\prime }+ \Pi _{\alpha \beta ^\prime }\Pi _{\alpha ^\prime \beta })-\frac{1}{3} \Pi _{\alpha \beta }\Pi _{\alpha ^\prime \beta ^\prime }, \end{aligned}$$

for total angular momentum $J=0,1,2$, respectively.

At last we discuss the hadronization of the Fock states into the physical heavy quarkonia, which is described by the nonperturbative color-singlet matrix element $\langle \mathcal{O}([n^{(\prime )}])\rangle$ in Eq. (1). The heavy-quark spin symmetry provides relations between matrix elements for the various spin states [10],

$$\begin{aligned} \langle \mathcal{O}([^3S_1]) \rangle= & {} \langle \mathcal{O}([^1S_0]) \rangle [1+O(v^2)],\nonumber \\ \langle \mathcal{O}([^3P_J]) \rangle= & {} \langle \mathcal{O}([^1P_0]) \rangle [1+O(v^2)]. \end{aligned}$$

(10)

Here, v is the relative velocity between the constituent heavy quark and antiquark in the quarkonium or $B_c$ rest frame. Further, vacuum-saturation approximation together with the heavy-quark spin symmetry can be used to express all the color-singlet matrix elements in terms of the radial wave functions at the origin $R_{S}(0)$ for S-wave states and their first derivatives at the origin $R^\prime _{P}(0)$ for P-wave states [10],

$$\begin{aligned} \langle \mathcal{O}([^1S_0])\rangle= & {} \frac{1}{4\pi } \big |R_{S}(0)\big |^2 [1+O(v^4)],\nonumber \\ \langle \mathcal{O}([^3S_1])\rangle= & {} \frac{1}{4\pi } \big |R_{S}(0)\big |^2 [1+O(v^4)],\nonumber \\ \langle \mathcal{O}([^1P_1])\rangle= & {} \frac{3}{4\pi } \big |R^\prime _{P}(0)\big |^2 [1+O(v^2)],\nonumber \\ \langle \mathcal{O}([^3P_J])\rangle= & {} \frac{3}{4\pi } \big |R^\prime _{P}(0)\big |^2 [1+O(v^2)]. \end{aligned}$$

(11)

Since the relativistic corrections are at order $v^2$ or evern higher in NRQCD, we can adopt the same values of matrix elements for both the spin-singlet and spin-triplet states. Moreover, the radial wave functions (or their derivatives) of the heavy quarkonia or $B_c$ mesons at the origin can be extracted from the decays of the quarkonia or $B_c$’s in experiments, and be calculated within the potential models [15,16,17,18,19,20,21,22,23,24] or potential NRQCD [25] or lattice QCD [26].

Table 1 The masses (units: GeV) of the constituent quarks, and the squared radial wave functions at the origin $|R_{S}(0)|^2$ (units: GeV$^3$) and their first derivatives at the origin $|R^\prime _{P}(0)|^2$ (units: GeV$^5$) for the charmonia, bottomonia and $B_c$ mesons within the BT-potential model [62]. The uncertainties of radial wave functions (or their first derivatives) at the origin are caused by the corresponding varying quark masses

3 Phenomenology

3.1 Input parameters

For the numerical analysis, masses of the constituent c and b quarks for heavy quarkonia and $B_c$ mesons are displayed in Table 1. The mass of a heavy quarkonium is always set to be the sum of the masses of its constituent quarks $M_{i}=m_{Q_i}+m_{Q^\prime _i}~(i=1,2)$, which ensures the gauge invariance of the hard scattering amplitude under the NRQCD framework. Thus we adopt different constituent quark masses for the S- and P-wave heavy quarkonia and $B_c$ mesons. In our previous work [62], the radial wave functions at the origin $|R_{S}(0)|^2$ and the first derivatives of radial wave functions at the origin $|R^\prime _{P}(0)|^2$ for various heavy quarkonia and $B_c$ mesons have been calculated under five different potential models. In this work, we adopt the results of the Buchmüller and Tye potential model (BT-potential) [15, 16, 62], which are also presented in Table 1. The uncertainties of radial wave functions (or their derivatives) at the origin are caused by the corresponding varying quark masses, which would be taken into consideration when we discuss the uncertainties caused by varying quark masses in Sect. 3.3. The LO running strong coupling constant $\alpha _s$ is adopted, which leads to $\alpha _s(2m_c)=0.26$ for charmonia and $B_c$ mesons, and $\alpha _s(2m_b)=0.18$ for bottomonia. Other parameters have the following values [63]: the Fermi constant $G_F=\frac{\sqrt{2}g^2}{8m_W^2}=1.16639 \times 10^{-5}$ GeV$^{-2}$ with $m_W= 80.399$ GeV, the fine structure constant $\alpha =e^2/4\pi =1/130.9$, the Weinberg angle $\theta _W=\arcsin \sqrt{0.23119}$, and the $Z^0$ boson mass $m_Z =91.1876$ GeV and its total decay width $\Gamma _{Z^0}=2.4952$ GeV.

3.2 Total and differential cross sections

Table 2 Cross sections (units: fb) for the production of the double heavy quarkonia and $B_c$ mesons in $e^+e^-$ annihilation at $\sqrt{s}=m_Z$ within the BT-potential model [62]. The subscripts $\gamma ^*$ and $Z^0$ are for virtual photon and $Z^0$ boson propagated processes, respectively. The top three channels in each column are in bold face

The total cross sections for the production of double heavy quarkonia and $B_c$ mesons via $e^- e^+ \rightarrow \gamma ^*/Z^0 \rightarrow H_1[n] + H_2[n^\prime ]$ at CM energy $\sqrt{s}=91.1876$ GeV are listed in Table 2. From this table, one could draw a conclusion that the contributions from virtual photon propagated processes are negligible in comparison with $Z^0$ propagated processes at future super $Z^0$ factory. The top three $Z^0$ propagated channels for the production of double charmonia, double bottomonia, and double $B_c$ mesons are

$$\begin{aligned} \sigma {(J/\psi +h_c)}_{Z^0}> & {} \sigma {(\eta _c+\chi _{c2})}_{Z^0}> \sigma {(\eta _c+\chi _{c0})}_{Z^0}> \dots , \nonumber \\ \sigma {(\eta _b+\Upsilon )}_{Z^0}> & {} \sigma {(\Upsilon +\chi _{b2})}_{Z^0}> \sigma {(\Upsilon +\Upsilon )}_{Z^0}> \dots , \nonumber \\ \sigma {(B_c^{*+}+B_c^{*-})}_{Z^0}> & {} \sigma {(B_c^{*+}+\chi _{bc2}^-)}_{Z^0}> \sigma {(\eta _{bc}^++B_c^{*-})}_{Z^0} > \dots \nonumber \\ \end{aligned}$$

(12)

In Ref. [56], Chen et al. calculate the cross sections for the production of the double charmonia for S- and P-wave states in CSM. If the same input parameters are adopted, our estimations in Table 2 are consistent with theirs.

Fig. 2

Total cross sections versus the CM energy $\sqrt{s}$ and the renormalization scale $\mu$, the differential angle distributions d$\sigma$/dcos$\theta$, and the $p_t$ distributions d$\sigma$/d$p_t$ at $\sqrt{s}=m_Z$ for the double charmonium production. The diamond black line, cross magenta line, dashed cyan line, solid red line, dotted blue line, and the dash-dotted green line are for the top six $Z^0$ propagated channels in Table 2: $J/\psi +h_c$, $\eta _c+\chi _{c2}$, $\eta _c+\chi _{c0}$, $J/\psi +J/\psi$, $\eta _c+h_c$, and $J/\psi +\chi _{c2}$, respectively

For the Z factory operation mode at CEPC, the designed integrated luminosity with two interaction point and in 2 years is $16~ab^{-1}$ [1]. Then we can estimate the events of the production of double heavy quarkonia and $B_c$ mesons. The top three channels for double charmonia are 73 $J/\psi +h_c$ events, 45 $\eta _c+\chi _{c2}$ events, and 22 $\eta _c+\chi _{c0}$ events. The top three channels for double bottomonia are 686 $\eta _b+\Upsilon$ events, 369 $\Upsilon +\chi _{b2}$ events, and 192 $\Upsilon +\Upsilon$ events. The top three channels for double $B_c$ mesons are $1.84\times 10^4$ $B_c^{*+}+B_c^{*-}$ events, $1.81\times 10^4$ $B_c^{*+}+\chi _{bc2}^-$ events, and $1.02\times 10^4$ $\eta _{bc}^++B_c^{*-}$ events. We take the $J/\psi +h_c$ channel as an example to discuss its observation at CEPC. The $J/\psi$ event can be fully reconstructed through the leptonic decay $J/\psi \rightarrow l^+ l^-$ ($l=e,\mu$) whose branching fraction is about 12% [63]. The $h_c$ can be reconstructed through the decay chain $h_c \rightarrow \eta _c+ \gamma \rightarrow (\text {hadronic decays})+\gamma$ with the $(50\pm 9)$% branching fraction of $h_c \rightarrow \eta _c + \gamma$ [63] and about total 43% branching fraction of the sixteen hadronic decays of $\eta _c$.¹ Thus with 2 years’ data, we can obtain only 2 events of $J/\psi +h_c$ in the Z factory mode at the CEPC. Although the events of double bottomonia and double $B_c$ meosns are larger than the events of double charmonia by about one and two orders of magnitude respectively, the observations for the production of them are also not optimistic because of the bigger suppression factors from their decays.² In one word, 2 years’ operation time for Z factory mode at the CEPC is not sufficient to make the study on the production of double heavy quarkonia and $B_c$ mesons. And the observation of such decays at the CEPC with sizable sample might indicates the presence of new production mechanism, for example the contributions of color-octet Fock states might dominate.

The FCC-ee would run as a super Z factory in its first 4 years with the designed integrated luminosity of $150~ab^{-1}$ [2], which is about nine times of that at CEPC. Then the events of the top three channels for double charmonia, double bottomonia and double $B_c$ mesons are about 9 times of those at the CEPC. Taking the double charmonium channels as an example, we can obtain 681 $J/\psi +h_c$ events, 426 $\eta _c+\chi _{c2}$ events, and 206 $\eta _c+\chi _{c0}$ events. For the $J/\psi +h_c$ channel, we might reconstruct about 18 signals at the detector after considering the suppressions from the branching fractions. But if we further consider the reconstruction efficiency in experiments, the prospects are not optimistic. Anyway, the Z factory operation mode at future FCC-ee would be a better choice to study the production of double heavy quarkonia and $B_c$ mesons than at CEPC. It is worth noting that the CMS collaboration at the LHC carry out the search for Z boson decays into $J/\psi$ and $\Upsilon$ pairs very recently [64]. No evidence is found in the channels of $Z\rightarrow J/\psi J/\psi$, $Z \rightarrow \Upsilon (1S) \Upsilon (1S)$ and $Z \rightarrow \Upsilon (nS) \Upsilon (mS)$, but the upper limits for the branching fractions at 95% confidence level are presented.

Fig. 3

Total cross sections versus the CM energy $\sqrt{s}$ and the renormalization scale $\mu$, the differential angle distributions d$\sigma$/dcos$\theta$, and the $p_t$ distributions d$\sigma$/d$p_t$ at $\sqrt{s}=m_Z$ for the double bottomonium production. The diamond black line, cross magenta line, dashed cyan line, solid red line, dotted blue line, and the dash-dotted green line are for the top six $Z^0$ propagated channels in Table 2: $\eta _b+\Upsilon$, $\Upsilon +\chi _{b2}$, $\Upsilon +\Upsilon$, $\Upsilon +\chi _{b1}$, $\Upsilon +\chi _{b0}$, and $\Upsilon +h_{b}$, respectively

Fig. 4

Total cross sections versus the CM energy $\sqrt{s}$ and the renormalization scale $\mu$, the differential angle distributions d$\sigma$/dcos$\theta$, and the $p_t$ distributions d$\sigma$/d$p_t$ at $\sqrt{s}=m_Z$ for the double $B_c$ production. The diamond black line, cross magenta line, dashed cyan line, solid red line, dotted blue line, and the dash-dotted green line are for the top six $Z^0$ propagated channels in Table 2: $B_c^{*+}+B_c^{*-}$, $B_c^{*+}+\chi _{bc2}^-$, $\eta _{bc}^++B_c^{*-}$, $B_c^{*+}+\chi _{bc0}^-$, $B_c^{*+}+\chi _{bc1}^-$, and $\eta _{bc}^++\chi _{bc0}^-$, respectively

In Figs. 2, 3 and 4, we display the total cross sections $\sigma (\sqrt{s})$ as functions of the CM energy $\sqrt{s}$, the total cross sections $\sigma (\mu )$ as functions of the renormalization scale $\mu$ in running strong coupling constant $\alpha _s(\mu )$, the differential angle distributions d$\sigma$/dcos$\theta$ and the $p_t$ distributions d$\sigma$/d$p_t$ at $\sqrt{s}=m_Z$ for the double charmonia, the double bottomonia and the double $B_c$ mesons, respectively. In those figures, we only exhibit the curves of top six $Z^0$ propagated processes in Table 2. Note that the figure legends in those three figures are different.

In the plots for total cross sections with running CM energy $\sqrt{s}$ in Figs. 2, 3 and 4, one can observe the dramatic peaks of cross section caused by the $Z^0$ resonance clearly. In the future super Z factory, the beam energy can be controlled with a very high accuracy. The natural beam energy spread scales as $\sigma _E/E$ with the energy resolution $\sigma _E$ at the energy E. At FCC-ee, the spread is 27 MeV [65]. At CEPC, the expected accuracy is the order of 100 keV for the Z factory operation [1]. However, the initial state radiation (ISR) at an electron-positron collider may make the CM energy $\sqrt{s}$ deviates from the $Z^0$ mass pole heavily. The influence of ISR on the production rates can be identified as the deviations of $\sqrt{s}$ from $m_Z$. In Table 3, we display the top six cross sections for the double heavy quarkonia and $B_c$ mesons with the deviations of both 1%$m_Z$ and 3%$m_Z$. It is found that the total cross sections decrease by about 30–40% when CM energy $\sqrt{s}$ deviates from the $Z^0$ pole even by only 1%$m_Z$, which reflects the effects of ISR.

Table 3 The deviations of cross sections (units: $\times 10^{-3}$ fb) for the top six channels for the production of double charmonia, double bottomonia, and double $B_c$ mesons when the CM energy $\sqrt{s}$ deviates from the $Z^0$ mass pole by 1%$m_Z$ and 3%$m_Z$. The top three channels are in bold face

The dependence of total cross sections on the renormalization scale $\mu$ in the running strong coupling $\alpha _s(\mu )$ is usually large in the leading order calculation. With its interpretation as an estimate of the contribution from missing higher order, it might be indicative. In the plots for total cross sections with running scale $\mu$ in Figs. 2, 3 and 4, we find that the cross sections always decrease monotonically as the scale increases with a more smooth trend at higher energy.

The differential angle distributions $d\sigma /dcos\theta$ for the double charmonia, double bottomonia and the double $B_c$ mesons are also displayed Figs. 2, 3 and 4, respectively. The distribution $d\sigma /dcos\theta$ can be obtained easily with the help of the differential phase space in Eq. (3). Here, $\theta$ is the angle between the momentum $\vec {p_1}$ of the electron and the momentum $\vec {q_1}$ of the heavy quarkonium. It is found that the distribution of the production of $\Upsilon +\chi _{b0}$ is quite flat, while other distributions have either a slight bulge or a slight hollow. We can derive the $p_t$ distribution $d\sigma /dp_t$ with the help of angle distributions as follows

$$\begin{aligned} \frac{d\sigma }{dp_t}=\left| \frac{dcos\theta }{dp_t}\right| \left( \frac{d\sigma }{dcos\theta }\right) =\frac{p_t}{|\vec {q}_1| \sqrt{|\vec {q}_1|^2-p^2_t}} \left( \frac{d\sigma }{dcos\theta }\right) , \nonumber \\ \end{aligned}$$

(13)

where ${|\vec {q}_1|}=\sqrt{\lambda [s, M^2_{1}, M^2_{2}]} /2\sqrt{s}$ is the magnitude of the 3-momentum of the heavy quarkonium. As are shown in Figs. 2, 3 and 4, the differential cross sections versus $p_t$ of all channels are monotonically increasing. This is understood because the $p_t$ distribution is proportional to $p_t/\sqrt{|\vec {q}_1|^2-p^2_t}$ and the distribution $d\sigma /dcos\theta$ changes relatively smoothly.

3.3 Uncertainties

Table 4 Uncertainties of the total cross sections (units: $\times 10^{-5}~fb$) caused by constituent quark masses under B.T. model, and by four other potential models for $Z^0$ propagated channels of double charmonia at $\sqrt{s}=m_Z$. The percentages in brackets are the ratios of the maximum or minimum in other potential models to the estimates under the B.T. model

Table 5 Uncertainties of the total cross sections (units: $\times 10^{-4}~fb$) caused by constituent quark masses under B.T. model, and by four other potential models for $Z^0$ propagated channels of double bottomonia at $\sqrt{s}=m_Z$. The percentages in brackets are the ratios of the maximum or minimum in other potential models to the estimates under the B.T. model

Table 6 Uncertainties of the total cross sections (units: $\times 10^{-3}~fb$) caused by constituent quark masses under B.T. model, and by four other potential models for $Z^0$ propagated channels of the double $B_c$ mesons at $\sqrt{s}=m_Z$. The percentages in brackets are the ratios of the maximum or minimum in other potential models to the estimates under the B.T. model

To obtain reliable estimates at leading order calculation, we discuss the main uncertainty sources of the cross sections of the double quarkonium or $B_c$ production in this subsection. For the input parameters, the Fermi constant $G_F$, the fine structure constant $\alpha$, the Weinberg angle $\theta _W$, and the mass and width of the $Z^0$ boson are either relatively precise or an overall factor. So we shall explore the uncertainties caused by masses of constituent heavy quarks, the radial wave functions or their first derivatives at the origin³. We only discuss the uncertainties of the $Z^0$ propagated channels since the contributions of virtual photon channels are smaller by three orders of magnitude at least at super Z factory.

The uncertainties of cross sections caused by both varying quark masses and the radial wave functions or their first derivatives at the origin at $\sqrt{s}=m_Z$ are presented in Tables 4, 5 and 6 for the double charmonia, double bottomonia, and double $B_c$ mesons, respectively. The uncertainties caused by varying masses are displayed in the second columns which are calculated in the BT-potential model [62], and the mass deviations are 0.1 GeV for $m_c$ and 0.2 GeV for $m_b$ (see explicit values in Table 1). Here, the affects of the varying masses on the radial wave functions or their first derivatives at the origin are also taken into consideration, which makes them not being the overall factors any more. The values from the third to the sixth columns in Tables 4, 5 and 6 are the estimates with the radial wave functions or their first derivatives at the origin calculated in other four potential models. The four models are the QCD-motivated potential with one-loop correction given by John L. Richardson (J. potential) [17], the QCD-motivated potential with two-loop correction given by K. Igi and S. Ono (I.O. potential) [18, 19], the QCD-motivated potential with two-loop correction given by Yu-Qi Chen and Yu-Ping Kuang (C.K. potential) [19, 20], and the QCD-motivated Coulomb-plus-linear potential (Cor. potential) [19, 21,22,23,24]. The formula and latest values of those wave functions or their first derivatives at the origin have been discussed in our earlier work [62]. It is shown that the cross sections change dramatically when we choose different potential models, which bring the largest uncertainties. For the production of the double charmonia, we always obtain the maximum under the B.T. potential model and obtain the minimum under the I.O. potential model. For the production of the double bottomonia, we always obtain the maximum under the B.T. potential model and obtain the minimum under the C.K. potential model. For the production of the double $B_c$ mesons, we always obtain the maximum under the I.O. potential model and obtain the minimum under the C.K. potential model. In the Tables 4, 5 and 6, percentages in brackets are the ratios of the maximum or minimum relative to the estimates under the B.T. model.

4 Summary

In the present work, we study the production of the double heavy quarkonia or $B_c$ mesons in $e^-(p_1) e^+(p_2) \rightarrow \gamma ^*/Z^0 \rightarrow H_1[n](q_1) + H_2[n^\prime ](q_2)$ within the CSM framework, where $H_{1(2)}$ represent the heavy quarkonia or $B_c$ mesons and $[n^{(\prime )}]$ represent the color-singlet Fock states $[^1S_0], ~[^3S_1], ~[^1P_1]$, and $[^3P_J]$ ($J=0,1,2$). For a sound estimation at the future super Z factory, total cross sections $\sigma$ as functions of CM energy $\sqrt{s}$, $\sigma$ as functions of the renormalization scale $\mu$, the angle distributions $d\sigma /dcos\theta$, and the $p_T$ distributions $d\sigma /dp_{t}$ are studied, which are shown in Figs. 2, 3 and 4 for the double charmonia, double bottomonia, and double $B_c$ mesons, respectively. We further discuss the uncertainties of the cross sections caused by the varying masses of constituent quarks, and the non-perturbative matrix elements under different potential models.

In Table 2, it is found that the production rates of double $B_c$ meson channels are roughly one order of magnitude greater than those of double bottomonium channels with the same Fock states, and are roughly two orders of magnitude greater than those of the double charmonium channels with the same Fock states. For CEPC running in Z factory mode, we obtain $\mathcal {O}(1)$ events of $J/\psi +h_c$ signal because of the big suppression factors of the fully reconstructed of both heavy charmonia. For the Z factory mode at FCC-ee, we might catch over a dozen of such rare events, but it is pessimistic for the observation in experiments after taking the reconstruction efficiency into account. However, since the color-singlet model predictions often turn out to undershoot data by one or even more orders of magnitude in many quarkonium production processes, therefore a detection of the considered processes at the FCC-ee and also the CEPC is still far from excluded. As shown in Table 3, the ISR may bring about 30–40% suppresions when the CM energy $\sqrt{s}$ deviates from the $Z^0$ pole even by only 1%$m_Z$. For the uncertainty analyses in Tables 4, 5 and 6, we find that the masses of constituent quarks can bring up to about 20% corrections to the cross sections. And the total cross sections can increase by about 2–3 times or decrease by an order of magnitude when adopting different potential models, which would be the major source of uncertainty.