1 Introduction

It is known that the law of gravitational entropy is inspired by the thermodynamics of a black hole, due to its proper geometric configuration and the spatial location in spacetime. In this sense, it is revealed the relationship between thermodynamics and gravity in the studies [1, 2], where the entropy of a black hole is proportional to its surface area, \(S=\frac{A}{4G}\), and its surface gravity is related to a temperature [3]. Accordingly, from a thermodynamic point of view, Jacobson first showed that the equation of state of space-time is exactly the standard Einstein equations. This is a significant step because determining the relationship between thermodynamics and gravity has made it easier to consider the concept of dark energy from a thermodynamic perspective [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. In this direction, cosmic spacetime, as a whole, can be considered a thermodynamics system to study the second law of thermodynamics (cosmological entropy law). The surface area of the apparent horizon of this system is associated with entropy, which is similar to the black hole entropy. Since the universe is expanding, the volumetrical of the horizon is expanding, and thus entropy increases with cosmic time. The moving matter inside the horizon also has entropy due to its energies. The sum of the entropy of the apparent horizon and the matter (the generalized form of entropy) should show an increasing trend with cosmic time or must be greater than zero when taking the Clausius relation into account. From a thermodynamic point of view, for example, zero entropy denotes a perfect structure [24] without the disorder. Particularly in the early inflation of the universe [25, 26] entropy can be less than zero, and this may be related to the creation of dark energy or extra dimensions [24]. On the other hand, in general, the early inflation of the universe is identified by a scalar field. Hence, we can consider the potential of scalar inflation, \(V=\phi ^{n}\), which expresses a chaotic case [27] in the most general sense. In this study, we show that there may be wide-range of chaotic potential models, including the \(\sim \phi ^{\frac{2}{3}}\), \(\sim \phi ^{\frac{4}{5}}\) potentials that emerge in the context of string theory [28,29,30,31,32]. For this, we use the Friedmann equations, which are modified by the non-additive Tsallis entopic proposal [33],

$$\begin{aligned} S_{A}=\delta A^{\beta }. \end{aligned}$$
(1)

We study the inflation of the early universe under the constant-roll condition [8, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58] and determine some potential values appearing in the string landscape [59,60,61] with small values of the scalar-to-tensor ratio. In consequence of the negative entropy case, we concluded that under the constant-roll field of the theory, a quintessence dark energy [62] in the early universe should exist. This case is obtained in a wide range of the power-term of the potential, \(0.5<n<1.2\), which also includes a type of string-chaotic potential.

2 Modified Friedmann equations

From a thermodynamics perspective, it was obtained the Friedmann equations in the studies [7, 63]. In the background of the line element which describes a homogeneous and isotropic spacetime geometry, i.e., Friedmann–Robertson–Walker metric,

$$\begin{aligned} ds^{2}=h_{ab}dx^{a}dx^{b}+R^{2}_{A}d\Omega ^{2}_{2}, \end{aligned}$$
(2)

with the two dimensional metric, \(h_{\alpha \beta }=diag(-1,a^{2}/(1-kr^{2})\) (\(x^{0}=t\), \(x^{1}=r)\) and the radius of the area, \(R_{A}=ar\), the first Friedmann equation in view of non-extensive Tsallis entropy relation are given by [7, 20]

$$\begin{aligned} \left( H^{2}+\frac{k}{a^{2}}\right) ^{2-\beta }=\frac{8\pi L_{p}^{2}}{3}\rho _{\phi }, \end{aligned}$$
(3)

Herein, we define \(\delta \equiv \frac{(2-\beta )(4\pi )^{1-\beta }}{4\beta L_{p}^{2}}\), and \(\delta \) is an unknown constant given by (1). We deal with the positive energy density, i.e., non-ghost fields, so it can be observed that the upper bound of the non-additive parameter is \(\beta <2\). However, we consider the matter contents inside the early universe as a scalar field description \(T_{\alpha }^{\beta }=diag(-\rho _{\phi },p_{\phi })\). Hence, under a canonical scalar field consideration \(L_{\phi }=X-V(\phi )\), we have the pressure and the energy density, \(\rho _{\phi }=\frac{\dot{\phi }^{2}}{2}+V(\phi ),\,\,\,\,\,\,p_{\phi }=\frac{\dot{\phi }^{2}}{2}-V(\phi )\), which shows the continuity equation,

$$\begin{aligned} \dot{\rho }_{\phi }+3H(\rho _{\phi }+p_{\phi })=0. \end{aligned}$$
(4)

In a clear form, it can be written the Klein-Gordon equation,

$$\begin{aligned} \ddot{\phi }+3H\dot{\phi }+V_{\phi }=0. \end{aligned}$$
(5)

On the other hand, one can easily derive the second Friedmann equation by using Eq. (4) and time derivative of the Eq. (3),

$$\begin{aligned}{} & {} (2-\beta )(1-\epsilon )\left( H^{2}+\frac{k}{a^{2}}\right) ^{1-\beta }H^{2} \nonumber \\{} & {} \quad +\frac{(2\beta -1)}{2}\left( H^{2}+\frac{k}{a^{2}}\right) ^{2-\beta }=-\,4\pi p_{\phi }. \end{aligned}$$
(6)

2.1 The constant-roll inflation field of Tsallis cosmology

In this title, we investigate the phenomenological implications of the constant-roll condition on the Friedmann equations given by Eqs. (3), (6). After obtaining the non-additive parameter as a fixed field for inflation, we expand our discussion to other parameters. It is known that the inflation of the universe is measured by the inflation parameters, i.e., the scalar spectral index parameter and the tensor-to-scalar ratio, and for a minimally coupled scalar theory is given by [66,67,68]

$$\begin{aligned} n_{s}\simeq 1-4\epsilon _{1}-2\epsilon _{2} ,\quad r=16\epsilon _{1}, \end{aligned}$$
(7)

with the slow-roll indices [67]

$$\begin{aligned}{} & {} \epsilon _{1}=-\frac{\dot{H}}{H^{2}},\,\,\,\,\,\,\nonumber \\{} & {} \epsilon _{2}=\frac{\ddot{\phi }}{H\dot{\phi }}. \end{aligned}$$
(8)

In general, the small values of the parameters \(\epsilon _{1}\ll 1,\,\,\epsilon _{2}\ll 1\) are required to exist the inflation. But, the imposing the slow-roll condition, \(\frac{\dot{\phi }^{2}}{2}\ll 1\), only on \(\epsilon _{1}\ll 1\) is sufficient to occur the inflation. In addition, a more general form of the constant-roll condition is given by

$$\begin{aligned} \ddot{\phi }=\gamma H\dot{\phi }, \end{aligned}$$
(9)

where \(\gamma \) is some dimensionless real parameter. It is clear that \(\gamma \simeq 0\) leads to the slow-roll condition and \(\gamma =-3\) corresponds to the ultra slow-roll condition [64] which has the flatness of the potential \(V_{\phi }=0\). It is seen that the constant-roll condition has an effect only on \(\epsilon _{2}\) parameter which is required to be \(\epsilon _{2}=\gamma \). For a flat spacetime dimensions \(k=0\), when taking into account, the assumption \(\frac{\dot{\phi }^{2}}{2}\ll 1\) the Eqs. (3), (6) and (5) become

$$\begin{aligned}{} & {} H^{2}\simeq \left( \frac{8\pi }{3}\right) ^{\frac{1}{2-\beta }}V(\phi )^{\frac{1}{2-\beta }}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \dot{H}\simeq -\frac{3\dot{\phi }^{2}}{2(2-\beta )}\left( \frac{8\pi }{3}\right) ^{\frac{1}{2-\beta }}V(\phi )^{\frac{\beta -1}{2-\beta }}, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \dot{\phi }=-\frac{V_{\phi }}{(\gamma +3)H}. \end{aligned}$$
(12)

The slow-roll indices are eqaul to,

$$\begin{aligned}{} & {} \epsilon _{1}=\frac{3\dot{\phi }^{2}}{2(2-\beta )V(\phi )},\quad \epsilon _{2}=\gamma \end{aligned}$$
(13)

It is worth emphasizing that the slow-roll indices, and consequently, the inflation parameters (7) should be calculated at the horizon crossing point(\(k=aH\)) as the fluctuations in the inflation field [71, 72] (scalar field \(\phi \)) become crucial at this point. Here, k shows the comoving wave vectors [63, 73]. We assume that the inflation begins where the fluctuations of the field occur during the horizon crossing. Hence, the e-foldings number N, which determines the amount of inflation, can be written as

$$\begin{aligned} N=\int _{t_{*}}^{t_{end}}H(t)dt, \end{aligned}$$
(14)

where \(t_{*}\) and \(t_{end}\) show the horizon crossing time and end of the inflation time, respectively. In terms of the scalar field, we can write

$$\begin{aligned} N=\int _{\phi _{*}}^{\phi _{end}}\frac{H}{\dot{\phi }}d\phi , \end{aligned}$$
(15)

with the value of the scalar field at the horizon crossing, \(\phi _{*}\). In the present study, we deal with the chaotic potentials which are given by

$$\begin{aligned} V(\phi )=V_{0}\phi ^{n}, \end{aligned}$$
(16)

where \(V_{0}\) is some positive parameter with mass dimensions \(m^{4-n}\) with the definition \(n>0\).

To find \(\phi _{*}\) it is necessary to know the value of the scalar field at the end of inflation. Accordingly, the first slow return parameter at the end of inflation is known to have the value \(\epsilon _{1}(\phi _{end})\simeq 1\), so we get

$$\begin{aligned} \phi _{end}= & {} \Bigg [\Bigg (\frac{8\pi G}{3}\Bigg )^{\frac{1}{2-\beta }}\nonumber \\{} & {} \times \frac{2(2-\beta )(\gamma +3)^{2}}{3n^{2}}V_{0}^{\frac{\beta -1}{2-\beta }}\Bigg ]^{\frac{2-\beta }{(n-2)(2-\beta )-n}}. \end{aligned}$$
(17)

Hence, the e-foldings number can be written as

$$\begin{aligned} N= & {} -\frac{(\gamma +3)}{n}\Bigg (\frac{8\pi G}{3}\Bigg )^{\frac{1}{2-\beta }}\nonumber \\{} & {} \times \frac{V_{0}^{\frac{\beta -1}{2-\beta }(2-\beta )}}{[4-n+\beta (n-2)]}\nonumber \\{} & {} \times \left[ \phi _{end}^{\frac{4-n+\beta (n-2)}{2-\beta }}-\phi _{*}^{\frac{4-n+\beta (n-2)}{2-\beta }}\right] . \end{aligned}$$
(18)

As a result, the value of the scalar field at the horizon crossing is obtained as follows,

$$\begin{aligned} \phi _{*}= & {} \Bigg \{\Bigg (\frac{8\pi G}{3}\Bigg )^{\frac{-1}{2-\beta }}V_{0}^{\frac{1-\beta }{2-\beta }}\nonumber \\{} & {} \times \Bigg (\frac{3n^{2}}{2(2-\beta )(\gamma +3)^{2}}+\frac{Nn}{(\gamma +3)}\nonumber \\{} & {} \times \Bigg (\frac{8\pi G}{3}\Bigg )^{-\frac{1}{2-\beta }}\nonumber \\{} & {} \times \frac{[4-n+\beta (n-2)]}{(2-\beta )V_{0}^{\frac{\beta -1}{2-\beta }}}\Bigg \}^{\frac{(\beta -2)}{n-4+\beta (2-n)}}. \end{aligned}$$
(19)

The resulting slow-roll parameters are determined as follows,

$$\begin{aligned} n_{s}= & {} 1-\frac{12n}{3n+2(\gamma +3)(4-n+\beta (n-2))N}-2\gamma , \nonumber \\ r= & {} \frac{48n}{3n+2(\gamma +3)(4-n+\beta (n-2))N} \end{aligned}$$
(20)

It should be emphasized that the inflation parameters depend on the power-term n of the potential, the constant-roll parameter gamma, and the non-additive Tsallis parameter beta. By fixing one of these three parameters, it is possible to discuss the inflation field of the universe across the remaining two parameters. Making this choice brings a multitude of possibilities. Hence, we will determine the reasonable value of the constant-roll parameter for this theory, using the relationship between the inflation parameters appearing in (20). Since we investigate the inflation in the background of the constant-roll field, in this fixed field, non-additive Tsallis entopic parameter can be investigated together with the scalar potential. In a range of n, which also includes the chaotic potential models developed in the context of string theory, we specify the structure of spacetime according to the positive and negative values of the \(\beta \) parameter.

2.2 Graphical analysis of the constant-roll field under observational constraints

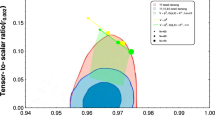
In this title, some graphical presentations of the fixed field are shown in the framework of the observational data. The latest Planck data [65] indicate the ranges of the scalar spectral index parameter and the tensor-to-scalar ratio, respectively, as follows,

$$\begin{aligned} n_{s}=0.9649\pm 0.0042,\quad r<0.064. \end{aligned}$$
(21)

From (20) the inflation parameters can be written as follows,

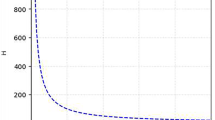
$$\begin{aligned} n_{s}=\frac{4-r-8\gamma }{4}. \end{aligned}$$
(22)

The observational intervals given by (21) produce a good value for \(\gamma \) which is 0.018, with small value of \(r=0.013\). The Fig. 1. is plotted independently from the values of n and \(\beta \). In other words, the observational boundaries of the inflation parameters determine the constant-roll parameter, so we immobilize the value of the constant-roll parameter at 0.018. Also, we determine that the tensor-to-scalar ratio is in the range \(r<0.0132\).

Fig. 1
figure 1

It is shown the relationship between the \(n_{s}\) and r in this figure. We choose the range values \(\gamma =[0,0.018]\), \(r=[0,0.064]\). The vertical axis indicates the value of the spectral index parameter

Full size image

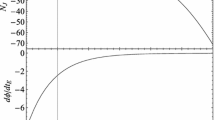
In Figs. 2 and 3, we find some values for \(n_{s}\) and r, with negative values \(\beta \) in agreement with the observation data. As n values increase, the absolute values of \(\beta \) increase but remain negative, i.e., when \(0.6<n<2\), \(\beta \) has large negative values. For \(n=2\) the observational bounds do not hold. For \(n>2\), the negative energy density cases appear due to \(\beta >2\).

Fig. 2
figure 2

The spectral index parameter (vertical axis) is plotted in the ranges \(\beta =[-10,2]\), \(n=[0,1.1]\) with the values \(\gamma =0.018\), \(N=60\)

Full size image

In Figs. 4 and 5, we investigate the possible positive values of the \(\beta \). In this case, for \(n>0\) but small values of it, the condition \(\beta >0\) is valid. In other words, small values of n result in \(\beta >0\), with \(r<0.0132\).

Fig. 3
figure 3

The figure shows the behavior of the tensor-to-scalar ratio (vertical axis). We use the ranges \(\beta =[-10,2]\), \(n=[0,1.1]\) with the values \(\gamma =0.018\), \(N=60\)

Full size image
Fig. 4
figure 4

The behavior of the spectral index parameter is shown. We use the ranges \(n=[0, 4]\) and \(\beta =[0,2]\) with the values \(\gamma =0.018\), \(N=60\)

Full size image
Fig. 5
figure 5

The behavior of the tensor-to-scalar ratio is shown. We use the ranges \(n=[0, 4]\) and \(\beta =[0,2]\) with the values \(\gamma =0.018\), \(N=60\)

Full size image

We conclude, in short, that for string-chaotic inflation models \(n=\frac{2}{3}\), \(n=\frac{4}{5}\), negative values of the \(\beta \) appear, and we determine that the quadratic potential form, \(n=2\) is not observed in the theory. On the other hand, if values of n are very small but not in the range of \(0.5<n <1.2\), positive values of \(\beta \) can be appeared with \(r<0.0132\).

3 Closing remarks

In the framework of thermodynamics, entropy tends to increase in usual systems. The cosmological entopic setup has been developed by considering the geometric structure of a black hole. In the entropy expression written for the apparent horizon of the universe, one can infer that the horizon area increases when the universe expands, so the entropy increases. On the other hand, the total entopic change generally must always be positive, even if the entropy of matter moving inside the horizon is negative. Non-additive Tsallis entropy refers to a kind of total entropy. In this study, we investigate the constant-roll condition in the context of the Tsallis entropic cosmology and discuss its application to the high-energy era of the universe. Within the reasonable value of the constant-roll parameter in which the parameter is as a fixed field, we obtain some results that are quite consistent with the observation data. We find that the Tsallis parameter takes negative values for range \(0.5<n<1.2\) with \(r<0.0132\), where negative values of the \(\beta \) have different physical meanings. The tendency of total entropy to decrease may mean the creation of dark energy or extra dimensions [24] in the tissue of spacetime. This points to a quintessence type of dark energy in the constant-roll inflation field. One can show this case by using the equation of state (EoS) parameter, \(w_{\phi }=\frac{p_{\phi }}{\rho _{\phi }}\). The EoS parameter can be written as \(w_{\phi }=\frac{\epsilon _{1}(2-\beta )-3}{\epsilon _{1}(2-\beta )+3}\), where we used the Eqs. (12), (13), and (19). Also, note that \(\epsilon _{1}\) is explicitly in the form,

$$\begin{aligned} \epsilon _{1}=\frac{3n}{3n+2(\gamma +3)(4-n+\beta (n-2))N}. \end{aligned}$$
(23)
Fig. 6
figure 6

The figure shows the behavior of the EoS parameter (vertical axis). We use the ranges \(n=[0, 1.1]\) and \(\beta =[-10,2]\) with the values \(\gamma =0.018\), \(N=60\)

Full size image

In Fig. 6, it can be easily seen that any value of the \(\beta \) leads to de Sitter vacua \(w_{\phi }=-1\) for \(n=0\), but we deal with the case \(n\ne 0\), so a quasi-de Sitter phase \(w_{\phi }\sim -1\) emerges for the range \(0.001<n<0.3\). However, one can see that the trend toward negative values of \(\beta \) indicates the presence of the quintessence type of dark energy. Especially in the \(0.5<n<1.2\) interval, this dynamic form of dark energy emerges. In addition to the string-chaotic inflation models \(n=\frac{2}{3}\) and \(n=\frac{4}{5}\), all potential values in the range of \(0.5<n<1.2\) under the small values of tensor-to-scalar ratio can be included in string-chaotic potential models and so in string landscape. It is known that quintessence dark energy [69] naturally emerges from string theory landscape solutions [62] and this may be a realistic approach to defining the structure of spacetime tissue [24]. Furthermore, dark energy solutions in the theory produce negative solutions of \(\Lambda \) instead of positive ones, which correspond to anti-de Sitter vacua [69, 70]. So, in the present study, we show that the inflation evolves from a quasi-de Sitter state to a quintessence dark energy when the phenomenological constant-roll condition is present. Also, when the increasing \(\beta \) leads to the n value approach 2, the inflation parameters do not give the desired result at the quadratic potential value.

According to the constant-roll field in our discussion, the value \(\beta =1\) leads to small positive values of n. This value or \(\beta >0\) corresponds to the quasi-de Sitter vacua, as discussed above, which is the known conventional solution of Friedmann cosmology. Whereas, the values of n, which can be included in the string landscape, should be in the \(0.5<n<1.2\) interval corresponding to the quintessence dark energy, where Tsallis entropy decreases in the field when \(\beta \) is negative. This case may indicate a matter-like formation in the universe from a thermodynamic point of view. If so, the universe should be in the proper phase state (i.e., quintessence phase) after the de Sitter vacuum. In particular, it may lead to both opening up extra dimensions [24] in the tissue of spacetime and the creation of normal matter. Therefore, when compared with the Bekenstein entropy relationship \(S=\frac{A}{4G}\) with \(A=4\pi R_{A}^{2}\), the Tsallis entropic proposal, which proposes a modification, reveals two phases. The first is a quasi-de Sitter-like vacuum state with the value \(\beta =1\) or \(\beta >0\), and the second is a quintessence type of dark energy with \(\beta <0\). This dual-phase state, which takes place in the constant-roll inflation field, shows an increasing entropy at the beginning and a decreasing entropy after it. To further our discussion and show our conclusions clearly, the left side of Eq. (3) can be handled as a dual system, and for the flat case \(k=0\), we can write \((H^{2})^{2-\beta _{+}}+(H^{2})^{2-\beta _{-}}=\frac{8\pi L_{p}^{2}}{3}\rho _{\phi }\). Herein, \(\beta _{-}\) and \(\beta _{+}\) show the expressions that identify negative and positive values of \(\beta \). If the universe starts to expand from a quasi-de Sitter vacuum, where \(\beta >0\), one can see that the inflation is driven by the system’s first term when compared with the second one. However, the system switches to the chaotic potential regime at once, accelerating expansion continues under the dominance of the quintessence dark energy. Here the second term immediately becomes dominant with negative \(\beta \) values. Therefore, it reveals the existence of the quintessence type of dark energy for the early universe, with a modification advantage compared to the Bekenstein entropy proposal of the nonadditive Tsallis parameter. As a result, we have determined a wide range of string-chaotic potentials in range \(\beta <0\). This process occurs in the constant-roll field with changes in the nonadditive Tsallis parameter, where the quintessence type of dark energy emerges in this field.