1 Introduction

The series of observational evidence [1,2,3,4,5] since 1998 put the standard cosmology in a dilemma. It is a conflict in the choice of gravity theory and in the choice of the matter contained. The standard cosmology with Einstein gravity and normal matter (matter satisfying strong energy condition) cannot support the above observational results. So the cosmologists have been trying the following two options to accommodate the observational prediction of the present accelerated era of expansion: (i) Einstein gravity with some exotic matter (having large negative pressure known as dark energy) (ii) modified gravity theory with usual matter. In the present work the second alternative has been considered to examine the observational results. Modified gravity theory comes in a natural way to accommodate the tensions in the present expansion rate of the universe. Also, this modification of gravity theory is an alternative way of modifying the standard model of particle physics through dark matter. The most natural and obvious extension of Einstein-Hilbert action is to replace the Ricci scalar R by an arbitrary function f(R), the well-known f(R) gravity theory. This modified gravity theory has been tested to explain the late-time cosmic acceleration [6], and it supports the local gravitational tests [7,8,9,10,11,12,13].

In the recent past, a further modification has been proposed by Harko et al. [14], considering the Einstein-Hilbert action as f(R, T) with T, the trace of the energy-momentum tensor. The quantum effect in the form of conformal anomaly is a possible justification behind the introduction of the matter part in the gravity Lagrangian. However, this gravity model depends on the source term due to the coupling in the matter and gravity and as a consequence, there is a hypothetical force term perpendicular to the four-velocity and test particles do not have a geodesic path. Further, the field equations become very complicated. Subsequently, a simple choice in the form of f(R, T) has been proposed [15] in an unorthodox manner as \(f(R,T)=R+h(T)\), with justification that the test particles will move along the geodesics. Though the electromagnetic field cannot be accommodated with this choice of f(R, T). However, for perfect fluid this choice shows that h(T) should be power-law in T with power depending on the constant equation of state parameter. In the present work, the choice of h(T) are the followings (i) power-law in T (ii) logarithm of T (iii) a linear combination of power-law and log(T) and (iv) a product of them. The motivation of the present work is to examine which of the four choices of h(T) supports the observational data. The plan of the paper is as follows: In Sect. 2, a brief description of f(R, T) gravity theory has been presented. Four specific models of f(R, T) gravity have been proposed in Sect. 3. While Sect. 4 deals with the numerical investigation of these models with respect to the observational data. The paper ends with a conclusion in Sect. 5.

2 f(R, T) gravity theory: a brief description

In this gravity theory, the complete action of f(R, T) gravity can be written as [14]

$$\begin{aligned} {\mathcal {A}}=\int \left[ \frac{1}{16\pi G}f(R,T)+{\mathcal {L}}_m\right] \sqrt{-g}d^4x \end{aligned}$$
(1)

where \(T=T_{\mu \nu }g^{\mu \nu }\) is the trace of the energy-momentum tensor \(T_{\mu \nu }\) , obtained from the matter Lagrangian density as [16]

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}{\mathcal {L}}_m)}{\delta g^{\mu \nu }} \end{aligned}$$
(2)

Further, if \({\mathcal {L}}_m\) depends only on \(g_{\mu \nu }\) but not its derivatives, then the above form for \(T_{\mu \nu }\) simplifies to

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu }{\mathcal {L}}_m-2\frac{\partial {\mathcal {L}}_m}{\partial g^{\mu \nu }}. \end{aligned}$$
(3)

Now the variation of the action (1) with respect to the metric gives the field equations for f(R, T) gravity as [14]

$$\begin{aligned}{} & {} f_RR_{\mu \nu }+\left( g_{\mu \nu }\square -\nabla _\mu \nabla _\nu \right) f_R-\frac{1}{2}g_{\mu \nu }f(R,T)\nonumber \\{} & {} \quad =8\pi G T_{\mu \nu }-\left( T_{\mu \nu }+\Theta _{\mu \nu }\right) f_T \end{aligned}$$
(4)

with

$$\begin{aligned} \Theta _{\mu \nu }= & {} g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}=-2T_{\mu \nu }+g_{\mu \nu }{\mathcal {L}}_m-2g^{\alpha \beta }\frac{\partial ^2{\mathcal {L}}_m}{\partial g^{\mu \nu }\partial g^{\alpha \beta }},\nonumber \\ f_R= & {} \dfrac{\partial f(R,T)}{\partial R},\quad f_T=\dfrac{\partial f(R,T)}{\partial T}. \end{aligned}$$

One should note that the field equations for f(R) gravity can be recovered from Eq. (4) if f(R, T) is replaced by f(R). Further, one may recover GR if \(f(R,T)=R\) while \(\Lambda \)CDM model will be recovered if \(R+2\Lambda \) (\(\Lambda \), a cosmological constant) with matter in the form of dust i.e. \(L_m=\rho \).

In the present work, a particular choice namely \(f(R,T)=R+h(T)\) is considered so that the field Eq. (4) simplifies to [15]Footnote 1

$$\begin{aligned} G_{\mu \nu }=\kappa \left[ T_{\mu \nu }-h'(T)(T_{\mu \nu }+\Theta _{\mu \nu })+\frac{1}{2}h(T)g_{\mu \nu }\right] . \end{aligned}$$
(5)

In the context of perfect fluid (which we shall consider in the following sections), the energy-momentum tensor has the following form

$$\begin{aligned} T_{\mu \nu }=(\rho +p)u_\mu u_\nu -pg_{\mu \nu } \end{aligned}$$
(6)

with matter Lagrangian as \({\mathcal {L}}_m=-p\). Here \(\rho \) and p are the energy density and thermodynamic pressure of the perfect fluid with restrictions on the four velocity \(u^\mu \) as

$$\begin{aligned} u_\mu u^\mu =1~;~~u^\mu \nabla _\nu u_\mu =0. \end{aligned}$$

The symmetric (0,2) tensor \(\Theta _{\mu \nu }\) simplifies to

$$\begin{aligned} \Theta _{\mu \nu }=-2T_{\mu \nu }-pg_{\mu \nu }. \end{aligned}$$
(7)

Now, considering the spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) space-time having metric

$$\begin{aligned} \textrm{d}s^2=-\textrm{d}t^2+a^2(t)\left( \textrm{d}x^2+\textrm{d}y^2+\textrm{d}z^2\right) , \end{aligned}$$
(8)

the modified Friedmann equations can be explicitly written as

$$\begin{aligned} 3H^2= & {} \kappa \rho _\textrm{m}+\kappa (\rho _\textrm{m}+p_\textrm{m})h'(T)+\frac{1}{2}\kappa h(T) \end{aligned}$$
(9)
$$\begin{aligned} 2{\dot{H}}+3H^2= & {} -\kappa p_\textrm{m}+\frac{1}{2}\kappa h(T) \end{aligned}$$
(10)

where a(t) is the cosmological scale factor, \(H\equiv \dfrac{{\dot{a}}}{a}\) is the Hubble parameter and \(\rho _\textrm{m}\), \(p_\textrm{m}\) are the energy density and thermodynamic pressure of the matter respectively. Now the above field Eqs. (9) and (10) may be written in the form of the standard FLRW equations as,

$$\begin{aligned} 3H^2= & {} ~\kappa \rho _{eff}~=\kappa \left( \rho _\textrm{m}+\rho _{fld}\right) \end{aligned}$$
(11)
$$\begin{aligned} 2{\dot{H}}+3H^2= & {} -\kappa p_{eff}=-\kappa \left( p_\textrm{m}+p_{fld}\right) \end{aligned}$$
(12)

where

$$\begin{aligned} \rho _{fld}= & {} (\rho _\textrm{m}+p_\textrm{m})h'(T)+\frac{1}{2}h(T) \end{aligned}$$
(13)
$$\begin{aligned} p_{fld}= & {} -\frac{1}{2}h(T) \end{aligned}$$
(14)

Here \(\rho _{fld}\) and \(p_{fld}\) are the energy density and pressure contributions respectively due to the modified gravity. These terms can be considered as equivalent contributions from a dark fluid component. Further, \(\rho _{eff}\) and \(p_{eff}\) are respectively the effective energy density and pressure of this f(R, T) gravity model.

Moreover, the conservation equations of individual component can be written as

$$\begin{aligned} {\dot{\rho }}_\textrm{m}+3H(\rho _\textrm{m}+p_\textrm{m})=0 \end{aligned}$$
(15)
$$\begin{aligned} {\dot{\rho }}_{fld}+3H(\rho _{fld}+p_{fld})=0 \end{aligned}$$
(16)

Solving Eq. (15), the energy density of the matter component can be obtained as

$$\begin{aligned} \rho _\textrm{m}=\rho _{m0}(1+z)^{3(1+\omega )} \end{aligned}$$
(17)

where we have considered the barotropic equation of state \(p_\textrm{m}=\omega \rho _\textrm{m}\) and \(z=\dfrac{1}{a(t)}-1\) is the cosmological redshift. Here \(\rho _{m0} > 0\), a constant that represents the current energy densities of matter. Further, the energy-momentum scalar can be obtained as \(T= (1-3\omega )\rho _\textrm{m}\).

3 f(R, T) gravity models

In this section, different models of f(R, T) gravity have been studied. In particular, we have considered four different choices of h(T), namely, power law form, logarithmic form, and their two combination forms as addition and multiplication.

3.1 Model I: \(f(R,T)=R+h_0 T^m\)

Here we have considered power law form of h(T) where \(h_0\), m are arbitrary constants. Substituting the above choice, one can simplify Eqs. (13) and (14) as

$$\begin{aligned} \rho _{fld}= & {} \frac{h_0}{2}(1-3w)^{m-1}(2m(1+\omega )+(1-3\omega ))\rho _\textrm{m}^m \end{aligned}$$
(18)
$$\begin{aligned} p_{fld}= & {} -\frac{h_0}{2}(1-3w)^{m}\rho _\textrm{m}^m, \end{aligned}$$
(19)

Hence, the equation of state for fluid \(\omega _{fld}=\dfrac{p_{fld}}{\rho _{fld}}=-\dfrac{(1-3\omega )}{2m(1+\omega )+(1-3\omega )} \) will be a constant. The first Friedmann equation for this model can be written as

$$\begin{aligned} H^2(z){} & {} =\dfrac{\kappa }{3}\left( \rho _{m0}(1+z)^{3(1+\omega )}\nonumber \right. \\{} & {} \quad \left. +\frac{h_0}{2}(1-3w)^{m-1}(2m(1+\omega )+(1-3\omega ))\right. \nonumber \\{} & {} \quad \times \left. \left\{ \rho _{m0}(1+z)^{3(1+\omega )}\right\} ^m\right) \end{aligned}$$
(20)

Now, defining another dimensionless parameter for Hubble parameter by \(E(z)=\dfrac{H(z)}{H_0}\), one may write

$$\begin{aligned} E^2(z){} & {} =\left( \Omega _{m0}(1+z)^{3(1+\omega )}\nonumber \right. \\{} & {} \quad \left. +\frac{h_0}{2}(1-3w)^{m-1}(2m(1+\omega )+(1-3\omega ))\right. \nonumber \\{} & {} \quad \times \left. \left\{ \Omega _{m0}(1+z)^{3(1+\omega )}\right\} ^m\right) \end{aligned}$$
(21)

where \(\Omega _{m0}=\dfrac{\rho _{m0}}{H_0^2}\) is the dimensionless density parameter.

3.2 Model II: \(f(R,T)=R+ 2h_0 \ln T\)

In this model, we choose logarithmic form of h(T) where \(h_0\) is an arbitrary constant.

In the background of homogeneous and isotropic FLRW space-time geometry, the first modified Friedmann equation can be explicitly expressed as

$$\begin{aligned} H^2(z){} & {} = \frac{\kappa }{3} \left[ \rho _{m0} (1+z)^{3(1+\omega )} +h_0\left( \frac{2(1+\omega )}{(1-3\omega )} \right. \right. \nonumber \\{} & {} \quad \left. \left. +\ln \left[ (1-3w)\rho _{m0} (1+z)^{3(1+\omega )}\right] \right) \right] \end{aligned}$$
(22)

Further, the energy density and pressure of the fluid are given by

$$\begin{aligned} \rho _{fld}= & {} h_0\left[ \dfrac{2(1+\omega )}{(1-3\omega )} +\ln \left[ (1-3w)\rho _\textrm{m}\right] \right] \nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} p_{fld}= & {} -h_0\ln \left[ (1-3w)\rho _\textrm{m}\right] \end{aligned}$$
(24)

and the equation of state for fluid will be \(\omega _{fld}=-\dfrac{\ln \left[ (1-3w)\rho _\textrm{m}\right] }{2\frac{(1+\omega )}{(1-3\omega )}+\ln \left[ (1-3w)\rho _\textrm{m}\right] } \).

3.3 Model III: \(f(R,T)=R+ h_0\left( \alpha _1 T^m +2\alpha _2 \ln T\right) \)

In this choice of f(R, T), \(h_0\), \(\alpha _1\), \(\alpha _2\) and m are arbitrary constants. For this choice, the first Friedmann equation is given by

$$\begin{aligned}{} & {} H^2(z) = \frac{\kappa }{3} \left[ \rho _{m0} (1+z)^{3(1+\omega )} \right. \nonumber \\{} & {} \quad + h_0\left( \alpha _1(1-3w)^{m-1}(2m(1+\omega )\right. \nonumber \\ {}{} & {} \quad +(1-3\omega ))\left\{ \rho _{m0} (1+z)^{3(1+\omega )}\right\} ^m\nonumber \\{} & {} \quad \left. \left. +\alpha _2\left\{ \frac{2(1+\omega )}{(1-3\omega )} +\ln \left[ (1-3w)\rho _{m0} (1+z)^{3(1+\omega )}\right] \right\} \right) \right] \nonumber \\ \end{aligned}$$
(25)

The energy density and the pressure of the fluid are given by

$$\begin{aligned} \rho _{fld}= & {} h_0\left[ \alpha _1(1-3w)^{m-1}(2m(1+\omega )+(1-3\omega ))\rho _\textrm{m}^m\nonumber \right. \\{} & {} \left. +\alpha _2\left( 2\frac{(1+\omega )}{(1-3\omega )} +\ln \left[ (1-3w)\rho _\textrm{m}\right] \right) \right] \end{aligned}$$
(26)
$$\begin{aligned} p_{fld}= & {} -h_0\left[ \frac{\alpha _1}{2}(1-3w)^{m}\rho _\textrm{m}^m + \alpha _2 \ln \left[ (1-3w)\rho _\textrm{m}\right] \right] \nonumber \\ \end{aligned}$$
(27)
Fig. 1
figure 1

Posterior distribution for the cosmological parameters of the four models using data sets I (Pantheon + BAO) and PLANCK18 prior has been considered

Full size image

3.4 Model IV: \(f(R,T)=R+ h_0 T^m \ln T \)

Here we choose h(T) as the product of the power law and Logarithmic form. From the first Friedmann equation, one has

$$\begin{aligned} H^2(z)= & {} \frac{\kappa }{3} \left[ \rho _{m0} (1+z)^{3(1+\omega )}\nonumber \right. \\{} & {} \left. + \frac{h_0}{2}(1-3w)^{m-1}\left\{ \rho _{m0} (1+z)^{3(1+\omega )}\right\} ^m\right. \nonumber \\{} & {} \times \left\{ 2(1+w)+(1-3w+2m(1+w))\right. \nonumber \\ {}{} & {} \left. \left. \ln \left[ (1-3w)\rho _{m0} (1+z)^{3(1+\omega )}\right] \right\} \right] \end{aligned}$$
(28)

The energy density and pressure of the fluid are given by

$$\begin{aligned} \rho _{fld}= & {} \frac{h_0}{2}(1-3w)^{m-1}\rho _\textrm{m}^m \nonumber \\{} & {} \times \big [ 2(1+w)+(1-3w+2m(1+w))\nonumber \\{} & {} \ln \left[ (1-3w)\rho _\textrm{m}\right] \big ] \nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} p_{fld}= & {} -\frac{h_0}{2}(1-3w)^{m}\rho _\textrm{m}^m \nonumber \\{} & {} \times \ln \left[ (1-3w)\rho _\textrm{m}\right] . \end{aligned}$$
(30)

and the equation of state for fluid is given by \(\omega _{fld}=-\dfrac{(1-3\omega )\ln \left[ (1-3w)\rho _\textrm{m}\right] }{2(1+w)+(1-3w+2m(1+w))\ln \left[ (1-3w)\rho _\textrm{m}\right] }\).

One may note that among these four models, model I coincides with \(\Lambda CDM\) cosmology for \(m=0\) while model III reduces to \(\Lambda CDM\) cosmology for the choice \(m=0\) and \(\alpha _2=0\). Further, it should be mentioned that model II and IV cannot recover the \(\Lambda CDM\) model for any choice of the parameter values.

Table 1 Best fit values of model parameters for the different models using data set I (Pantheon + BAO)
Full size table

4 Numerical analysis and observational constraint

In this section, our aim here is to constrain the cosmological parameters analyzing the observational data sets. In order to do so, we have modified the public version of the CLASS Boltzmann code to include the dark energy sector as a fluid. The MCMC code Montepython3.5 [17] has been used to estimate the relevant cosmological parameters.

In order to analyze, we use the cosmological datasets (Pantheon [18], BAO (BOSS DR12 [19], \(SMALLZ-2014\) [20]) and HST [21]) and a PLANCK18 prior has been imposed.

We have made the choice of flat priors on the base cosmological parameters as follows: the baryon density \(100\omega _b = [1.9, 2.5]\); cold dark matter density \(\omega _{cdm} = [0.0, 0.145]\); Hubble parameter \(H0 = [60, 80] {\text {km s}}^{-1}{\text {Mpc}}^{-1} \) and a wide range of flat prior has been chosen for \(w_{0b}=[-0.33, 0.33]\) and \(m=[-2,2]\).Footnote 2

Fig. 2
figure 2

Posterior distribution for the cosmological parameters of the four models using data set II (Pantheon +BAO + HST) and PLANCK18 prior has been considered

Full size image

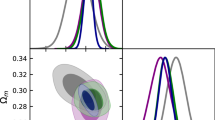
In order to make a comparison among the models, we have taken (Pantheon + BAO) as data set I and (Pantheon + BAO + HST) as dataset II. For the data set I, the posterior distributions of the cosmological parameters have been shown in Fig. 1 and the corresponding constraints are enlisted in the Table 1. Here from Table 1, one may say that, the best-fit values of all the cosmological parameters for model III are within the error bar of the observed data. While for the other three models, the best-fit values of these cosmological parameters are not in the error bar of the observed data. This is also reflected in the posterior distribution of the cosmological parameters Fig. 1. Further, it may be noted that the estimated values of all the parameters for model I and model IV are very close to each other. Also, the value for present time Hubble parameter i.e. H0 is estimated as very low values both for model I and model IV, while model II estimates it as a very high value, which do not match with recent observations. On the other hand, for model III, H0 is close to the observational value. However, from Fig. 1 it can be seen that the distribution of the parameters for all the models are distorted from the Gaussian nature.

Similar analysis has also been done for data set II by incorporating HST data together with the data set I. The posterior distribution of the cosmological parameters have been shown in Fig. 2 and the corresponding constraints have been enlisted in the Table 2. From Table 2 it is found that the value \(m=0\) lies inside the \(1\sigma \) region for model I and model III which implies that model I and model III recover \(\Lambda CDM\) cosmology as mentioned in the previous section. Figure 2 shows that data set II constrains all the parameters nicely and the nature of the distribution of the parameters are Gaussian. But in this case, all four models that have been considered show almost identical behaviour in respect of parameters i.e.,  it is difficult to identify any particular model based on this data set. In order to compare the models we will analyze Akaike Information Criterion (AIC) [22]and the Bayesian Information Criterion (BIC) [23] in the next section.

Table 2 Best fit values of model parameters for different models using data set II (Pantheon + BAO + HST)
Full size table

Using the best fit value of the cosmological parameters of the different models inferred from the dataset II, we have plotted the Hubble parameter H(z) with respect the redshift z and the deceleration parameter q(z) which is defined as

$$\begin{aligned} q(z)=-\frac{\ddot{a}a}{{\dot{a}}^2}=-\left( 1+\frac{{\dot{H}}}{H^2}\right) \end{aligned}$$
(31)

From the Figs. 3 and 4, it may seem that all these four models are almost identical if one considers \(z>0\) i.e., earlier time to present days. But the beauty is hidden in \(z<0\) i.e., in the future prediction. The present value of the deceleration parameter \(q_0\) is obtained as \(-0.485\) (model I), \(-0.35\) (model II), \(-0.484\) (model III), \(-0.487\) (model IV). That means the value of \(q_0\) for model I, III and IV matches with the recent observations. From Fig. 4 it is seen that Model I asymptotically approaches the quintessence era in the future (\(q\rightarrow -0.85\) as \(z\rightarrow -1\)). Model II & IV will enter a decelerating phase again in future. In the case of Model III, the universe will not only continue its accelerated expanding phase but also will go beyond the phantom region. Actually, model III predicts Big Rip in the future \((z\rightarrow -1)\).

Now using the best fit values of the parameters from Tables 1 and 2, \(\rho _0\) and \(h_0\) can be estimated as follows

 

Dataset I

Dataset II

 

\(\rho 0_{fld}\)

\(h_0\)

\(\rho 0_{fld}\)

\(h_0\)

Model I

2327

12694

3905

4806

Model II

4987.19

528.42

4170.96

445

Model III

3779.29

1291.46

3884.68

1630

Model IV

2361.03

4095.65

3868.73

1821

5 Information criteria and model comparison

In order to make a comparison among the models, here we apply the well known Akaike Information Criterion (AIC) [22]and the Bayesian Information Criterion (BIC) [23]. This allows us to examine which model best fits the observational data. Based on the information theory, AIC is an estimator of the Kullback–Leibler information with the property of asymptotically unbiasedness. Under the standard Gaussian error assumptions, the expression of AIC reads as [24,25,26]

$$\begin{aligned} AIC=-2\ln ({\mathcal {L}}_{max})+2k+\frac{2k(k-1)}{N_{tot}-k-1}~, \end{aligned}$$
(32)

where \({\mathcal {L}}_{max}\) is the maximum likelihood of the datasets, \(N_{tot}\) is the total data points and k is the number of parameters of the model. If the number of data points \(N_{tot}\) is large enough, then it reduces to \(AIC \approx - 2 \ln ({\mathcal {L}}_{max}) + 2k\). The AIC gives goodness of fit through the maximum likelihood, however, the additional term of the AIC acts as a penalty for models which have a large number of parameters. Whereas, the BIC is defined as [27, 28]

$$\begin{aligned} BIC=-2\ln ({\mathcal {L}}_{max})+kln(N_{tot})~. \end{aligned}$$
(33)

It is clearly seen that the penalty for BIC is higher than that of AIC. In general, the model having lower values of AIC and BIC corresponds to the model that best fits the data.

Table 3 The values for the AIC and BIC for the different models
Full size table

The values of AIC and BIC for all the models have been reported in Table 3. From the table, it is seen that Model I and IV have good observational support for Data set I, and for data set II there is good support for Model I, III, IV according to AIC analysis. Whereas, from BIC analysis, it can be found that Model II has observational support for data set I, and all these four models support observational results for data set II. Now if one makes \(\Delta AIC\) and \(\Delta BIC\) analysis i.e., one compares these four models with the \(\Lambda \)CDM model, the result is the same. One may note an interesting feature that the \(\Delta AIC\) for model I, III and IV are negative, that means the maximum likelihood of these three models is marginally higher than that of the \(\Lambda \)CDM. Consequently, one can say that these three models with data set II are slightly preferred over the \(\Lambda CDM\). Further, among these three models, Model III has the least \(\Delta AIC\) and \(\Delta BIC\) values. Moreover looking both at the AIC and BIC values it can be concluded that Model-I and Model III are best favoured models for dataset I and dataset II respectively. Since the distribution of the parameters for Data set I is not Gaussian, hence excluding the result for data set I, one can conclude that model III has best observational support with respect to these datasets.

6 Conclusion

A detailed study of the f(R, T) gravity theory has been done with a widely used form of f(R, T), namely \(f(R,T)=R+h(T)\) and four possible form of h(T) namely power-law form, logarithm form, an additive and product form of them. Perfect fluid with constant equation of state is chosen as the matter component for the model. However, the modified field equations are equivalent to field equations in Einstein gravity with non-interacting two-fluid system. The other fluid component (known as effective fluid) is also a perfect fluid with constant equation of state (depending on the state parameter of the usual fluid). The parameters involved in these four models are estimated from the observation data due to the data set I (Pantheon [18], BAO [19, 20]) and data set II (Pantheon [18], BAO [19, 20] and HST [21]) with prior from PLANCK18 data set [29].

From the observational analysis, it is found that only model III for data set I matches with the observational result. However, the distribution of the parameters for all the models has a distortion from the Gaussian nature which motivates us to further study with the data set II. For data set II, we have found that all the four models show almost identical behaviour.

Fig. 3
figure 3

It represents the dimensionless \(H(z)/H_0 \) vs z plot

Full size image
Fig. 4
figure 4

It shows the deceleration parameter q(z) vs z plot

Full size image

Next, the cosmological parameters, namely, the Hubble parameter H and the deceleration parameter q have been plotted against the redshift parameter z to show their behaviour with the evolution of the universe. Figure 3 shows that the Hubble parameter gradually decreases with the evolution of the universe for all the four models. However, some interesting features are found in Fig. 4 for the deceleration parameter. For all the four models q evolves almost identically till the present era, making a transition from deceleration to accelerating phase. But model I and model III will continue to be in accelerating era of evolution while model II and model IV will make a transition from accelerating phase to again decelerated era of evolution. Further, the present time value of the deceleration parameter for model I, III, IV matches with the recent observations. Moreover, the model III predicts Big Rip in the future infinity. On the other hand, from AIC and BIC analysis, model I, III, IV with data set II are slightly preferred over the \(\Lambda \)CDM. Finally, it can be concluded that Model-I with data set I and Model III with data set II are the best favoured models. Since the distribution of the parameters for Data set I is not Gaussian, one can conclude that model III is the best model with respect to these datasets.